Dual-Channel Heterogeneous Graph Neural Network for Automatic Algorithm Recommendation

Abstract

Automatic algorithm selection is a critical challenge in data-driven decision-making due to the proliferation of available algorithms and the diversity of application scenarios, with no universally optimal solution. Traditional methods, including rule-based systems, grid search, and single-modal meta-learning, often struggle with high computational cost, limited generalization, and insufficient modeling of complex dataset-algorithm interactions, particularly under data sparsity or cold-start conditions. To address these issues, we propose a Dual-Channel Heterogeneous Graph Neural Network (DCHGNN) for automatic algorithm recommendation. Datasets and algorithms are represented as nodes in a heterogeneous bipartite graph, with edge weights defined by observed performance. The framework employs two channels, one for encoding the textual descriptions and the other for capturing the meta-features of the dataset. Cross-channel contrastive learning aligns embeddings to improve consistency, and a random forest regressor predicts algorithm performance on unseen datasets. Experiments on 121 datasets and 179 algorithms show that DCHGNN achieves an average relative maximum value of 94.8%, outperforming baselines, with 85% of predictions in the high-confidence range $[0.9, 1]$. Ablation studies and visualization analyses confirm the contributions of both channels and the contrastive mechanism. Overall, DCHGNN effectively integrates multimodal information, mitigates sparsity and cold-start issues, and provides robust and accurate algorithm recommendations.

1. Introduction

With the proliferation of machine learning applications in managerial tasks such as demand forecasting and risk assessment, automated algorithm selection has become critical to overcome algorithm overload and scenario heterogeneity [1]. While traditional methods like rule-based systems and grid search suffer from poor generalization and high computational cost [2,3], meta-learning and graph-based approaches have emerged as promising alternatives by leveraging historical performance meta-data [4] or modeling dataset-algorithm interactions as graphs [5]. Nevertheless, four core challenges remain: (1) limited representational capacity of meta-features for complex multimodal data; (2) inability of single-model frameworks to balance automation and precision at scale; (3) neglect of high-order structured interactions between datasets and algorithms; and (4) performance degradation under data sparsity or cold-start scenarios due to insufficient meta-knowledge or incomplete graph structures.

To address these limitations, several recent works have explored graph-based and meta-learning based approaches for algorithm selection. Graph-based fine-grained model selection for multi-source domain (GFMS) constructs a library of source models, exploits graph neural networks (GNNs) to learn feature-model associations and dataset similarities, and blends over multiple source models rather than selecting just one, showing strong performance in cross-domain image classification tasks [6]. Cohen et al. [7] proposed MARCO-GE, which also MARCO-GE similarly represents datasets as graphs and applies a Graph Convolutional Networks to learn embeddings; it then trains a ranking meta-model to recommend clustering algorithms across a large suite of datasets, algorithms, and clustering evaluation measures, outperforming previous meta-learning baselines. To enhance the sparsity performance and improve the accuracy of recommendations, Cohen-Shapira et al. [8] used graph convolutional networks to aggregate structural information from dataset-algorithm performance graphs, and proposed a meta-learning method for algorithm recommendation. Together, these efforts suggest that integrating graph structure, embedding representations, and meta-models can significantly improve algorithm and model recommendation under challenges such as dataset variability, sparsity, and domain migration. These methods effectively model the interaction between the dataset and the algorithm, but mainly operate on isomorphic graphs or rely on single-modal features, thus lacking a framework to integrate multimodal data and handle complex scene tasks.

Inspired by this, this paper proposes a novel dual-channel heterogeneous graph neural network framework for algorithm recommendation. The framework embeds datasets and algorithms as nodes in a heterogeneous bipartite graph, with edge weights determined by algorithm performance. A dual-channel heterogeneous graph attention mechanism learns fine-grained representations of dataset-algorithm relationships, reinforced through cross-channel contrastive learning to ensure consistency. Finally, a random forest regressor is used to predict the performance on unseen datasets, enabling accurate algorithm recommendation.

The main contributions of this work are summarized as follows:

• Dual-channel heterogeneous graph framework: We model datasets and algorithms as nodes in a heterogeneous bipartite graph and design Semantic and Meta HGNN Channels to fuse textual descriptions and numerical meta-features, capturing rich dataset-algorithm interaction patterns beyond single-modal approaches.
• Cross-channel contrastive learning: We introduce a contrastive learning mechanism to align embeddings from the two channels, improving consistency and robustness of node representations and alleviating the negative impact of data sparsity.
• Extensive experimental validation: Through experiments on 121 datasets and 179 algorithms—including baseline comparisons, ablation studies, visualization analyses, and case studies—we demonstrate that DCHGNN outperforms state-of-the-art methods in both accuracy and stability, and effectively addresses challenges such as data sparsity and cold-start scenarios.

2. Related Work

2.1. Automated Algorithm Recommendation

Meta-learning has long served as a key technical framework for automatic algorithm recommendation, and its core idea lies in learning the mapping rules between dataset characteristics and algorithm performance from historical task data, thereby predicting the optimal algorithm for new tasks. This type of method mainly relies on numerical meta-features to construct meta-models and has achieved mature applications in early algorithm recommendation scenarios. The meta-models in existing studies mainly include rule-based, distance-based, regression-based, and ensemble learning-based meta-models.

The rule-based meta-model generates selection rules for each candidate algorithm. When the meta-features meet the selection rules, it indicates that the corresponding candidate algorithm is the appropriate one for the task. Ali et al. [9] used the rule-based learning algorithm C5.0 to describe which types of algorithms are suited to solving which types of classification problems. Azadeh et al. [10] extracted 18 types of dataset meta-features and used Classification and Regression Trees (CART) to select the optimal algorithm from six candidate algorithms. Distance-based meta-models measure the distance between tasks using meta-features. Their basic idea is that algorithms exhibit similar performance on similar tasks, and the similarity between tasks can be quantified and calculated through meta-feature distance. For a new task, the appropriate algorithm for it is predicted by using the applicable algorithms of other tasks that are closest to it in distance. Common distance metrics include Euclidean distance, Manhattan distance, cosine distance, and Jaccard index [11,12,13,14]. In addition, some studies map the algorithm selection problem to a regression problem. They train meta-models using task meta-features and the performance metric values of candidate algorithms, input the meta-features of a new task into each meta-model to obtain predicted performance metric values, and output the appropriate algorithm by comparing the predicted performance of each algorithm. Lorena et al. [15] used the Support Vector Regression (SVR) algorithm as the meta-model and constructed 28 meta-models respectively for 14 candidate regression algorithms and two types of regression problem meta-features. Diego et al. [16] trained meta-models on each meta-dataset using the Linear Regression (LR) algorithm. They predicted the performance metric values of candidate algorithms on new datasets through these meta-models, thereby forming a ranking of the predicted algorithms. Garcia et al. [17] employed three regression meta-algorithms including SVR to predict the performance metric values of five candidate classification algorithms. They compared the application effects of different types of meta-features based on the prediction biases. Some scholars have constructed meta-models with strong generalization performance and algorithm selection performance by introducing the idea of ensemble learning. Random forest (RF) is one of the widely used meta-models in meta-learning-based algorithm selection research. Owing to its ability to evaluate feature importance, random forest can clearly identify the impact of dataset meta-features on model selection. It also balances accuracy and interpretability in small-to-medium-sized tasks, thus becoming a benchmark method in numerous studies [18]. Auto-sklearn, as a representative automated machine learning framework, further optimizes the meta-learning process by integrating Bayesian optimization technology. It constructs a search space covering multiple algorithms and their hyperparameters, and dynamically adjusts the search direction based on historical performance feedback to efficiently screen out the optimal algorithm configuration for a specific dataset. Feurer et al. [19] verified through a large number of experiments that Auto-sklearn outperforms manual parameter tuning in standard classification and regression tasks, and its highly encapsulated framework reduces the application threshold for automatic algorithm recommendation.

However, traditional meta-learning-based methods have obvious limitations. Firstly, they have a single dependence on feature modalities. These methods can only process structured numerical meta-features and completely ignore unstructured information such as dataset text descriptions (e.g., domain semantics, task objective explanations) and algorithm principle texts. This leads to a significant decline in recommendation accuracy in cross-domain scenarios. For example, when recommending algorithms for a medical text classification dataset, traditional methods cannot capture the semantic association between medical domain and text processing algorithms, resulting in the possible recommendation of algorithms more suitable for image data. Secondly, they ignore the interaction structure between datasets and algorithms. These methods treat datasets and algorithms as independent entities and do not model the implicit association relationships between them, such as the high-frequency adaptation between a certain type of dataset and a certain type of algorithm. Finally, in data-sparse or cold-start scenarios (e.g., a new dataset with no historical interaction records), the meta-model lacks sufficient information support for prediction, and its generalization ability is severely limited.

2.2. Graph Representation Learning for Recommendation

Graph representation learning (GRL) has become a fundamental paradigm for modeling relational and structured data in recommender systems. By capturing high-order dependencies and complex interaction patterns, GRL provides a powerful mechanism to go beyond shallow feature engineering and leverage the relational nature of user-item data. Early works primarily focused on general principles of GNNs and representation learning [20,21,22,23], while more recent surveys have systematically summarized their applications in recommendation [24,25], social recommendation [26], and dynamic graphs [27]. Collectively, these studies highlight the capability of graph-based methods to address long-standing challenges such as data sparsity, scalability, and the cold-start problem, thereby motivating a growing body of research on graph-based recommendation frameworks.

A large number of concrete models have been proposed to demonstrate the effectiveness of GRL in diverse recommendation scenarios. For instance, Liu et al. [28] introduced a multi-perspective social recommendation model built upon GCNs, emphasizing the role of social ties. Ge et al. [29] exploited cross-modal graph representations to enhance news recommendation, showing how heterogeneous modalities can be aligned within a graph structure. Wang et al. [30] applied network representation learning to point-of-interest (POI) recommendation, effectively capturing geographical and social relations, while Amara et al. [31] recently proposed a multi-view GNN framework to integrate heterogeneous signals for more robust predictions. These works collectively underline the flexibility of GRL in adapting to different domains, data modalities, and recommendation settings.

Building on these foundations, heterogeneous graph neural networks (HGNNs) have emerged as a particularly powerful extension for recommendation tasks, as they explicitly model multiple types of nodes, relations, and semantic contexts. Fan et al. [32] pioneered a metapath-guided HGNN for intent recommendation, demonstrating the benefit of semantic path-based message passing. Shi et al. [33] further proposed a general HGNN framework, showing that heterogeneous semantics can yield significant performance gains compared to homogeneous graphs. Notably, Yang et al. [34] developed Heterogeneous Graph Attention Networks (HGAT) with a dual-level attention mechanism, significantly enhancing node representation learning in sparse short-text scenarios. Similarly, Fan et al. [35] proposed the framework GraphRec, which extended social recommendation by jointly modeling user-item interactions and social relations through attentive graph aggregation. More specialized designs have also been developed: Cai et al. [36] introduced an inductive HGNN to mitigate the user cold-start problem; Pang et al. [37] applied a heterogeneous global graph neural network to session-based recommendation; Sang et al. [38] explored adversarial training to improve robustness; Wei et al. [39] studied privacy-preserving HGNNs; and Yan et al. [40] developed a federated HGNN framework for secure and distributed recommendation. These lines of research collectively demonstrate the versatility and adaptability of HGNNs to address both algorithmic and practical challenges.

Taken together, the above advances clearly indicate that GRL, in particular HGNNs, provides a principled way to capture multi-type interactions and complex semantic structures in recommendation tasks. Motivated by these developments, our work introduces a dual-channel heterogeneous GNN framework tailored for algorithm recommendation. Specifically, the framework integrates dataset descriptions, meta-features, and algorithm properties into a unified graph-based representation, enabling the model to learn richer structural semantics and ultimately deliver more accurate and generalizable algorithm recommendation outcomes.

3. Materials and Methods

3.1. Overview

Motivated by recent advances in graph neural networks and meta-recommendation, this paper proposes a dual-channel heterogeneous graph meta-learning framework (DCHGNN) for algorithm recommendation, as shown in Figure 1. The framework comprises four core components as the following: (1) heterogeneous graph construction, (2) dual-channel representation learning, (3) cross-channel contrastive learning, and (4) performance prediction. We provide the details of each component and their interrelationships below.

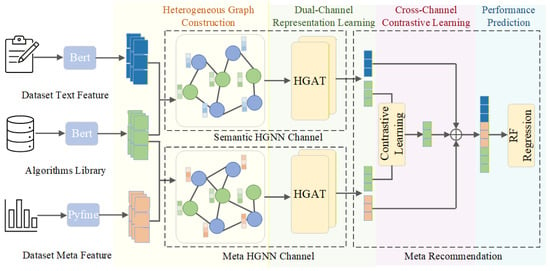
Figure 1. Overview of the proposed DCHGNN framework for algorithm recommendation. The framework employs a dual-channel heterogeneous graph attention mechanism, maintaining semantic (textual) and meta-feature channels in parallel to model dataset-algorithm relationships, leverages contrastive learning to refine representations, and relies on RF regression for meta-recommendation.

The framework adopts a sequential yet deeply integrated pipeline design where modules are interconnected through well-defined input-output relationships. The process initiates with the heterogeneous graph construction module, which formulates the recommendation problem as a bipartite graph structure, providing the fundamental computational topology and initial features for the entire system. This graph structure is then fed into the dual-channel representation learning module, where two parallel graph neural networks extract complementary feature representations from semantic and numerical perspectives respectively. The outputs from both channels are then processed by the cross-channel contrastive learning module, which serves as the critical bridge between representation learning and final prediction. This module employs a contrastive learning mechanism that aligns the dual-channel representations in a shared latent space, explicitly enhancing representational consistency and robustness against channel-specific noise. The resulting fused dataset-algorithm pair representations are subsequently delivered to the performance prediction module. Finally, the fused high-quality embeddings serve as the input for the performance prediction module. In this module, a random forest regressor accomplishes accurate prediction of algorithm performance on unseen datasets, enabling automated recommendation.

Throughout this pipeline, graph construction serves as the foundation, dual-channel learning acts as the feature engine, fusion and contrastive mechanisms are key to enhancing generalization capability, and the prediction module represents the ultimate value realization of all preceding processing. Particularly noteworthy is that contrastive learning functions as a supervisory signal that directly influences and optimizes the representation learning process through backpropagation, forming a cross-module closed-loop optimization that ensures all components work synergistically rather than in isolation.

3.2. Problem Definition

Algorithm recommendation aims to identify suitable algorithms for a new dataset by considering dataset characteristics, task type, and evaluation criteria. Let the dataset set be denoted as $D=\{d_1,d_2,\dots ,d_n\}$, the algorithm set as $A=\{a_1,a_2,\dots ,a_m\}$, and the performance matrix as $P\in {\mathbb{R}}^{n\times m}$, where each entry $p_{ij}$ represents the performance (e.g., classification accuracy) of algorithm $a_j$ when applied to dataset $d_i$.

The goal of algorithm recommendation is to learn a mapping function as the following:

$$f:D\times A\to \mathbb{R},$$

such that for a new dataset $d^{*}\in D$, the predicted performance of algorithm $a_j$ can be obtained as the following:

$${\widehat{p}}_{*j}=f(d^{*},a_j),$$

where ${\widehat{p}}_{*j}$ denotes the estimated accuracy of algorithm $a_j$ on dataset $d^{*}$. Based on these predictions, the system recommends the algorithm(s) expected to achieve the best performance for the unseen dataset.

3.3. Data Preparation

To effectively learn the mapping function f, it is crucial to represent datasets and algorithms in a way that captures their characteristics and interactions. This requires collecting comprehensive descriptive and performance data for both datasets and algorithms, as well as any domain-specific semantic information that can enrich these representations. Accordingly, this study collected experimental results of 179 algorithms across 121 datasets from the UCI repository (http://archive.ics.uci.edu, accessed on 1 September 2024), Kaggle (https://www.kaggle.com/, accessed on 1 September 2024) and openML [41]. These datasets are widely used in the classification field and are representative of practical classification problems. We further integrated domain-specific semantic information from Wikipedia to construct a heterogeneous knowledge network. Based on these sources, we organized the data into four complementary components to support heterogeneous graph representation learning as the following:

Dataset Text Description: Dataset text description contains the basic characteristics of datasets (e.g., name, number of instances, number of attributes, maximum number of classes), domain-specific semantic descriptions, and annotator notes. Its core value lies in establishing explicit associations between datasets and domain knowledge. We extracted the text descriptions of dataset from the UCI repository, detailed in Table 1.

Table 1. Dataset text description.

Field	Description
title	Dataset name
num_instances	Number of instances (integer)
num_attributes	Number of attributes (integer, excluding label)
has_missing	Whether missing values exist (boolean)
attribute_names	List of all attribute names (including label, optional if unspecified)
attribute_types	Data type of each attribute (nominal/continuous/integer)
class_distribution_skewed	Whether the label distribution is skewed (boolean)
source_owner	Providing institution or original owner of the dataset
donor	Dataset donor
date_received	Date when the dataset was received
task_type	classification/regression/both (task type)
target_name	Label name
notes	Brief summary of the dataset task objective and challenges

Dataset Meta-Feature: Dataset meta-features were extracted using the open-source library PyFME [42], as it provides a standardized, reproducible, and comprehensive toolkit widely used in meta-learning research to characterize dataset complexity and statistical properties. In total, 111 meta-features were extracted across five categories, encompassing general, statistical, information-theoretic, model-based, and landmarking features, as shown in Table 2.

Table 2. Extracted 111 meta-features grouped into five categories.

Category	Meta-Features
General (18)	attr_to_inst, cat_to_num, eq_num_attr, freq_class.mean, freq_class.sd, inst_to_attr, nr_attr, nr_bin, nr_cat, nr_class, nr_cor_attr, nr_disc, nr_inst, nr_norm, nr_num, nr_outliers, ns_ratio, num_to_cat
Statistical (44)	can_cor.mean, can_cor.sd, cor.mean, cor.sd, cov.mean, cov.sd, eigenvalues.mean, eigenvalues.sd, g_mean.mean, g_mean.sd, gravity, h_mean.mean, h_mean.sd, iq_range.mean, iq_range.sd, kurtosis.mean, kurtosis.sd, lh_trace, mad.mean, mad.sd, max.mean, max.sd, mean.mean, mean.sd, median.mean, median.sd, min.mean, min.sd, p_trace, range.mean, range.sd, roy_root, sd.mean, sd.sd, sd_ratio, skewness.mean, skewness.sd, sparsity.mean, sparsity.sd, t_mean.mean, t_mean.sd, var.mean, var.sd, w_lambda
Info theory (11)	attr_conc.mean, attr_conc.sd, attr_ent.mean, attr_ent.sd, class_conc.mean, class_conc.sd, class_ent, joint_ent.mean, joint_ent.sd, mut_inf.mean, mut_inf.sd
Model based (24)	leaves, leaves_branch.mean, leaves_branch.sd, leaves_corrob.mean, leaves_corrob.sd, leaves_homo.mean, leaves_homo.sd, leaves_per_class.mean, leaves_per_class.sd, nodes, nodes_per_attr, nodes_per_inst, nodes_per_level.mean, nodes_per_level.sd, nodes_repeated.mean, nodes_repeated.sd, tree_depth.mean, tree_depth.sd, tree_imbalance.mean, tree_imbalance.sd, tree_shape.mean, tree_shape.sd, var_importance.mean, var_importance.sd
Landmarking (14)	best_node.mean, best_node.sd, elite_nn.mean, elite_nn.sd, linear_discr.mean, linear_discr.sd, naive_bayes.mean, naive_bayes.sd, one_nn.mean, one_nn.sd, random_node.mean, random_node.sd, worst_node.mean, worst_node.sd

Algorithm Descriptive Data: This module includes algorithm names, hyperparameter configurations (e.g., kernel function for SVM, tree depth range for random forest), performance statistics (e.g., average accuracy across datasets), and textual descriptions of algorithm principles. Standardized algorithm descriptions enable a multidimensional representation of algorithm characteristics.

To construct the algorithm description data, this study employed an automated pipeline based on the DeepSeek Chat API. Specifically, algorithm names were first parsed from a prepared text file and sequentially processed by a script that generated standardized prompts. The key details are provided in the Appendix A. Each prompt was strictly formatted to query the official documentation of R, Matlab, Caret, and Weka libraries, requiring the model to return results exclusively in JSON format with six predefined fields: algorithm name, category, input data type and format, number of variables, output data type and format, and theoretical foundation. The model responses were subsequently post-processed by removing code block delimiters and extraneous characters, followed by JSON parsing. Finally, the extracted information was aggregated to form the structured algorithm description dataset.

Dataset-Algorithm Interaction Data: This module records the performance of each dataset across multiple algorithms [43]. The accuracy metric was chosen as the edge weight between datasets and algorithms, serving as a measure of their compatibility. Although accuracy has certain limitations, such as sensitivity to class imbalance, its interpretability and broad applicability make it a widely accepted benchmark for cross-domain comparisons.

3.4. Dual-Channel Heterogeneous Graph Construction

In the graph construction stage, datasets and algorithms are regarded as two types of nodes, and the performance evaluation results between them are used as edge weights to form a bipartite graph. To fully leverage the heterogeneous information available, we introduce a dual-channel design combined with a contrastive learning mechanism, enabling the model to jointly exploit both textual descriptions and numerical meta-features of datasets. This approach allows the framework to capture complementary aspects of dataset characteristics, leading to more comprehensive and informative feature representations.

The heterogeneous interaction graph is denoted as $G=(V,E)$, where $V=D\cup A$ is the set of nodes, consisting of dataset nodes D and algorithm nodes A; $E=\{(d_i,a_j)\mid p_{ij}\ne 0\}$ is the set of edges, representing the interactions between datasets and algorithms, with edge weight $w_{ij}=p_{ij}$. The dual-channel design consists of the following:

Semantic HGNN Channel: The semantic HGNN channel encodes the semantic information of datasets and algorithms into a heterogeneous graph. Specifically, textual descriptions of datasets and algorithms are first transformed into high-dimensional embeddings using BERT, due to its strong capability in capturing contextual semantics from dataset descriptions. These embeddings serve as the initial node features for datasets and algorithms in the graph. Edges between dataset and algorithm nodes are weighted by algorithm performance metrics (e.g., accuracy), enabling the model to learn fine-grained semantic relationships between datasets and algorithms. By leveraging this channel, the framework can reason about which algorithms are likely to perform well on a given dataset based on textual semantic similarity and historical performance.

Meta HGNN Channel: In the meta HGNN channel, dataset meta-features are explicitly extracted and used as the node features for dataset nodes. These meta-features capture intrinsic statistical, information-theoretic, model-based, and landmarking characteristics of the datasets, providing complementary structural information beyond textual descriptions. Algorithm nodes, on the other hand, inherit their features from the BERT embeddings computed in the semantic HGNN channel, ensuring consistency across channels. The edges between dataset and algorithm nodes continue to represent performance metrics (e.g., accuracy), allowing the graph to encode both the intrinsic properties of datasets and their historical algorithm performance. By combining meta-features with semantic embeddings, the meta HGNN channel enhances the model’s ability to reason about dataset-algorithm suitability, particularly when textual descriptions alone are insufficient.

3.5. Heterogeneous Graph Attention Network Representation Learning

To model the above heterogeneous graphs, we proposed a novel heterogeneous graph attention mechanism, maintaining two parallel channels on the graph: the semantic (textual description) channel and the meta (numerical meta-feature) channel. Node features from different sources were first projected into a shared message space using dedicated linear transformations. The attention mechanism then performs importance-weighted aggregation over each central node’s neighbors.

Specifically, at each layer, the neighbor representations are weighted by attention coefficients ${\alpha }_{ij}$, summed, and passed through a nonlinear transformation to produce the node’s layer-wise representation. By stacking multiple layers, the receptive field of each node is gradually expanded, and complementary semantic information across the two channels is captured. This hierarchical, dual-channel aggregation ultimately yields heterogeneous graph representations suitable for downstream tasks such as algorithm recommendation. The update functions of semantic HGNN channel and meta HGNN channel at the l-th layer are defined as the following:

$$h^{\left(sema\right),l}=\sigma \left(\sum _j{\alpha }_{ij}{W}_{sema}{h}_j^{\left(sema\right),\left(l-1\right)}\right),$$

$$h^{\left(meta\right),l}=\sigma \left(\sum _j{\alpha }_{ij}{W}_{meta}{h}_j^{\left(meta\right),\left(l-1\right)}\right),$$

where $h^{\left(sema\right),l}$ and $h^{\left(meta\right),l}$ are the outputs of the semantic and meta channels respectively; $\sigma (·)$ is a nonlinear activation function; $W_{sema}$ and $W_{meta}$ are channel-specific transformation matrices; $h_j^{(l-1)}$ is the representation of neighbor node j at layer $l-1$; and ${\alpha }_{ij}$ is the attention coefficient computed as the following:

$${\alpha }_{ij}=\mathrm{softmax}\left(\mathrm{LeakyReLU}\left({\alpha }^T[W{h}_i\Vert W{h}_j]\right)\right),$$

where $\alpha$ is a learnable attention vector, and applying the LeakyReLU nonlinearity.

3.6. Cross-Channel Contrastive Learning

Since the two channels capture information from different modalities, their embeddings may diverge if left unconstrained, potentially degrading recommendation performance. To address this, we introduced a contrastive learning mechanism to enforce consistency between the two channels, thereby enhancing robustness, reducing sparsity, and promoting information sharing.

For a dataset $d_i$, let $N\left(d_i\right)$ denote its neighboring algorithm nodes. For each algorithm $a_j\in N\left(d_i\right)$, its normalized representations in the two channels are as the following:

$$Z_{a_j}^{\left(\mathrm{sema}\right)}={\displaystyle \frac{h_{a_j}^{\left(\mathrm{sema}\right)}}{\parallel h_{a_j}^{\left(\mathrm{sema}\right)}{\parallel }_2}},$$

$$Z_{a_j}^{\left(\mathrm{meta}\right)}={\displaystyle \frac{h_{a_j}^{\left(\mathrm{meta}\right)}}{\parallel h_{a_j}^{\left(\mathrm{meta}\right)}{\parallel }_2}}.$$

For a dataset $d_i$, the contrastive loss for algorithm $a_j\in N\left(d_i\right)$ is defined as the following:

$$L_{\mathrm{contrast}}(a_j\mid d_i)=-log{\displaystyle \frac{exp\left(\mathrm{sim}(Z_{a_j}^{\left(\mathrm{sema}\right)},Z_{a_j}^{\left(\mathrm{meta}\right)})/\tau \right)}{{\sum }_{a_k\in N\left(d_i\right)}exp\left(\mathrm{sim}(Z_{a_j}^{\left(\mathrm{sema}\right)},Z_{a_k}^{\left(\mathrm{meta}\right)})/\tau \right)}},$$

where the positive pair is formed by the same algorithm node across two channels, i.e., $(Z_{a_j}^{\left(\mathrm{sema}\right)},Z_{a_j}^{\left(\mathrm{meta}\right)})$, and the negative pairs are cross-channel embeddings of different algorithms in the same neighborhood. $\tau$ is a temperature parameter.

Finally, the overall contrastive loss is averaged across all datasets and their neighboring algorithms as follows:

$$L_{\mathrm{contrast}}={\displaystyle \frac{1}{\left|D\right|}}\sum _{d_i\in D}{\displaystyle \frac{1}{\left|N\right(d_i\left)\right|}}\sum _{a_j\in N\left(d_i\right)}{L}_{\mathrm{contrast}}(a_j\mid d_i).$$

3.7. Random Forest Regression for Performance Prediction

The task of algorithm recommendation can be formulated as a regression problem where the goal is to predict the dataset-algorithm edge weight (i.e., accuracy). After the heterogeneous graph attention network learning phase, we obtain node embeddings from both channels. The embeddings of algorithm nodes from the two channels are averaged to form a unified representation. The embeddings of dataset nodes from the two channels are concatenated to preserve complementary information. The resulting dataset-algorithm pair representation is then used as input to a random forest regressor with the observed accuracy serving as the target label. Model training is performed using a leave-one-out strategy where one dataset is held out as the test set while the model is trained on the remaining datasets, as shown in Figure 2.

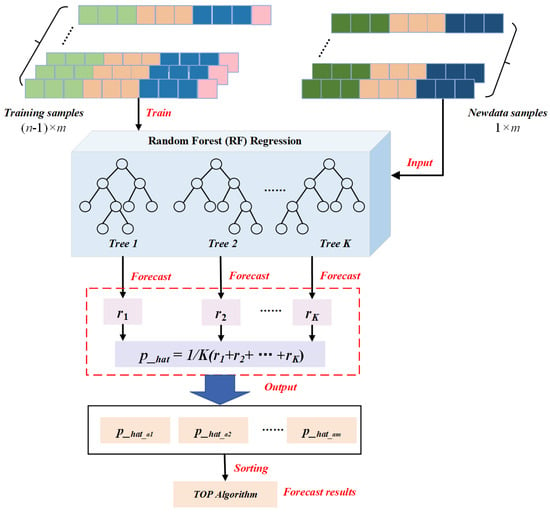
Figure 2. Random forest regressor for algorithm recommendation. The message aggregation features of algorithms and datasets obtained by the heterogeneous graph attention network, are combined with the accuracy rate to form $(n-1)\times m$ training samples, and trains a random forest regressor consisting of K decision trees. For the new dataset, its aggregated information features of the attention mechanism are combined with the dual-channel features of m algorithms respectively to form m testing samples, and then input into the regressor to obtain the recommendation algorithm with largest prediction value.

Through this process, the regressor predicts the performance of all algorithms on the unknown dataset, selecting the algorithm with the highest predicted value as the recommended algorithm for this dataset.

4. Experimental Results and Analysis

4.1. Baseline Methods

To validate the effectiveness of the proposed framework, we compared it against four representative baselines:

• Random Forest (RF) [44]: An ensemble learning method based on decision trees. RF builds multiple decision trees and aggregates their predictions to improve accuracy and reduce overfitting. It is widely used and has demonstrated competitive performance across various datasets.
• Auto-Sklearn [45]: An automated machine learning (AutoML) framework built on scikit-learn. It leverages Bayesian optimization for algorithm selection and hyperparameter tuning, enabling efficient model search and strong performance on diverse tasks.
• LightGCN [46]: A lightweight graph neural network designed for recommendation tasks. It simplifies traditional GCN by removing feature transformation and nonlinear activation, retaining only neighborhood aggregation. This design makes it highly efficient for large-scale user-item graphs while maintaining strong recommendation performance.
• HGAT [34]: Heterogeneous Graph Attention Network designed for semi-supervised classification. HGAT extends the standard graph attention mechanism to heterogeneous graphs, effectively capturing node- and edge-type-specific interactions to learn expressive node representations, and has demonstrated strong performance on classification tasks.

4.2. Evaluation Metric

We adopted the Relative Maximum Value (RMV) [47] to evaluate the performance of algorithm recommendation. RMV measures the ratio between the performance of the algorithm selected by the predictive model and that of the true best-performing algorithm on the dataset, and it is defined as the following:

$$RMV={\displaystyle \frac{Accurac{y}_{\mathrm{prediction}}}{Accurac{y}_{\mathrm{top}}}}$$

(1)

where $Accurac{y}_{\mathrm{prediction}}$ denotes the accuracy of the algorithm recommended by the model, obtained by selecting the algorithm with the highest predicted performance score and then retrieving its actual accuracy on the corresponding dataset. $Accurac{y}_{\mathrm{top}}$ represents the accuracy of the true top-performing algorithm, which serves as the performance upper bound. We records the accuracy performance of each dataset across multiple algorithms [43].

Accuracy is defined as the following:

$$Accuracy={\displaystyle \frac{TP+TN}{TP+FP+TN+FN}}$$

(2)

where TP, FP, TN, and FN denote the numbers of true positives, false positives, true negatives, and false negatives, respectively.

To evaluate the consistency between the predicted accuracy ${\mathrm{Accuracy}}_{\mathrm{prediction}}$ and the true accuracy ${\mathrm{Accuracy}}_{\mathrm{top}}$, this study introduces the Expected Calibration Error (ECE), which measures the degree to which the predicted confidence aligns with the actual performance. A lower ECE indicates better calibration and higher reliability of the prediction model.

First, the predicted accuracies ${\mathrm{Acc}}_{{\mathrm{pred}}_i}\in [0,1]$ are divided into M equally spaced intervals:

$$B_m=\{i\mid {\mathrm{Acc}}_{{\mathrm{pred}}_i}\in (b_{m-1},b_m]\},m=1,2,\dots ,M.$$

(3)

For each interval $B_m$, the average predicted accuracy and the average true accuracy are computed as the following:

$$\mathrm{conf}\left(B_m\right)={\displaystyle \frac{1}{|B_m|}}\sum _{i\in B_m}{\mathrm{Acc}}_{{\mathrm{pred}}_i},$$

(4)

$$\mathrm{acc}\left(B_m\right)={\displaystyle \frac{1}{|B_m|}}\sum _{i\in B_m}{\mathrm{Acc}}_{{\mathrm{top}}_i}.$$

(5)

Finally, the Expected Calibration Error (ECE) is calculated as the following:

$$\mathrm{ECE}=\sum _{m=1}^M{\displaystyle \frac{|B_m|}{N}}|\mathrm{acc}\left(B_m\right)-\mathrm{conf}\left(B_m\right)|,$$

(6)

where N denotes the total number of samples.

In this study, ECE serves as an evaluation metric to verify whether the predicted performance scores of algorithms are well-calibrated with their actual observed results. A smaller ECE value reflects that the model’s predicted confidence is more consistent with true accuracy, thus indicating stronger reliability and trustworthiness of the meta-recommendation framework.

4.3. Overall Results

Table 3 and Table 4 summarize the Average RMV and RMV distribution across all methods. The results indicate that our proposed DCHGNN framework achieves the highest overall performance, with an Average RMV of 94.8%, outperforming traditional ensemble methods (RF), AutoML approaches (Auto-Sklearn), and state-of-the-art graph-based models (LightGCN, HGAT). Notably, 85% of the predictions fall within the $[0.9,1]$ confidence interval, while predictions in the low-performance range $[0,0.6]$ are completely eliminated ( 0%), highlighting the model’s ability to generate highly reliable recommendations. Beyond accuracy, we further evaluated the calibration quality of predicted performance using the Expected Calibration Error (ECE). As shown in Table 3, DCHGNN achieves an ECE of 0.042, which is lower than all graph-based and AutoML baselines, and only slightly higher than the random forest method. This suggests that while RF exhibits naturally strong calibration due to its ensemble averaging mechanism, DCHGNN achieves a comparable level of reliability while maintaining a significantly higher predictive accuracy. Therefore, DCHGNN provides not only precise but also well-calibrated recommendations, effectively balancing performance and confidence consistency.

Table 3. Average RMV and calibration comparison.

Method	RF	Auto-Sklearn	LightGCN	HGAT	DCHGNN
Average RMV	93.8%	92.8%	93.1%	93.9%	94.8%
ECE	0.039	0.050	0.057	0.055	0.042

Table 4. RMV distribution comparison.

RMV Interval	RF	Auto-Sklearn	LightGCN	HGAT	DCHGNN
$[0,0.6]$	1%	2%	3%	1%	0%
$(0.6,0.7]$	0%	2%	1%	2%	0%
$(0.7,0.8]$	2%	3%	5%	3%	2%
$(0.8,0.9]$	17%	13%	10%	12%	13%
$[0.9,1]$	80%	80%	81%	82%	85%

Compared to other graph-based methods, DCHGNN substantially reduces the proportion of low-confidence predictions, indicating that the dual-channel architecture and contrastive learning strategy stabilize node embeddings and enhance model robustness. By jointly leveraging semantic textual features and numerical meta-features, DCHGNN captures complementary information that single-channel approaches (e.g., HGAT or LightGCN) fail to exploit, leading to more accurate and reliable recommendations. The superior performance across multiple RMV intervals demonstrates that DCHGNN generalizes well to diverse datasets, maintaining strong confidence even in challenging cases.

Overall, the experimental analysis confirms that DCHGNN not only improves average predictive performance but also enhances calibration and reliability, validating the effectiveness of the dual-channel heterogeneous graph approach in achieving both accuracy and trustworthiness.

4.4. Robustness Evaluation

To address the concern that our reported improvements might be contingent on the specific choice of RF as the final performance predictor, we conducted additional experiments employing a diverse set of regression models. These include linear regression, gradient boosted trees (GBT), and multi-layer perceptron (MLP). As shown in Table 5 and Table 6, clearly demonstrate that the superiority of our DCHGNN framework is consistent across different predictive models.

Table 5. Average RMV under different prediction methods.

Method	Linear	GBT	MLP	RF
Average RMV	88.71%	93.72%	91.39%	94.8%

Table 6. RMV distribution comparison under different prediction methods.

RMV Interval	Linear	GBT	MLP	RF
$[0,0.6]$	6%	2%	2%	0%
$(0.6,0.7]$	3%	2%	3%	0%
$(0.7,0.8]$	6%	4%	5%	2%
$(0.8,0.9]$	17%	9%	16%	13%
$[0.9,1]$	69%	83%	74%	85%

The results show that RF achieves the highest average RMV (94.80%), indicating strong predictive performance. In contrast, while GBT yield comparable average RMV values (93.72%), it exhibits a larger proportion of lower RMV scores, particularly in the [0, 0.8] range. This suggests that random forest is not only more accurate but also more robust across diverse datasets. The superior performance of random forest can be attributed to its ability to capture complex interactions among features with minimal risk of overfitting, confirming its effectiveness as the meta-classifier for algorithm selection.

To further validate the proposed method’s predictive stability and resilience in real-world scenarios where data imperfections are common, we conducted a comprehensive robustness evaluation. As shown in Table 7 and Table 8, This experiment simulates increasingly noisy and incomplete graph structures by simultaneously removing true edges and introducing non-existent edges at varying interference ratios: 0.1, 0.15, 0.2, 0.25, and 0.3. This dual-perturbation strategy effectively corrupts the original data topology, testing the proposed method’s dependency on reliable connectivity and its ability to maintain performance under structural degradation.

Table 7. Average RMV under different interference ratios.

Ratio	0.1	0.15	0.2	0.25	0.3	No Interference
Average RMV	93.38%	91.05%	88.53%	88.73%	91.20%	94.8%

Table 8. RMV distribution comparison under different interference ratios.

RMV Interval	0.1	0.15	0.2	0.25	0.3	No Interference
$[0,0.6]$	0%	4%	7%	7%	3%	0%
$(0.6,0.7]$	2%	3%	2%	3%	2%	0%
$(0.7,0.8]$	7%	6%	7%	4%	5%	2%
$(0.8,0.9]$	11%	12%	10%	10%	13%	13%
$[0.9,1]$	80%	75%	74%	76%	76%	85%

The results confirm that our method maintains strong predictive performance even under significant data corruption. The key finding is that performance degrades gracefully rather than collapsing. The distribution across RMV intervals reveals crucial insights into the method’s stability. Most notably, the proportion of high-confidence predictions (RMV $\ge 0.9$) remains consistently strong across all perturbation levels. Even at 0.3 perturbation ratio, 76% of samples maintain this high-confidence status compared to 85% in the no interference scenario. This suggests that the method’s core predictive capability remains largely intact for the majority of instances, with confidence scores accurately reflecting the reduced but still substantial reliability.

The observed robustness can be attributed to the inherent design of the DCHGNN framework. The dual-channel architecture provides complementary views of the data, potentially mitigating the impact of corrupted connections in one channel. Furthermore, the rich heterogeneous information integrated into the node representations may allow the model to rely on feature-based evidence when topological information becomes unreliable. This resilience to structural noise strongly supports the practical deployment of DCHGNN in real-world environments where data quality and completeness are frequently compromised.

4.5. Statistical Significance Test

Although the proposed model achieves numerically superior performance compared to baseline methods, it is important to verify whether the observed improvements are statistically significant rather than arising from random fluctuations. Since the RMV score distributions do not satisfy the normality assumption, we adopt the non-parametric Wilcoxon signed-rank test for paired comparisons across datasets.

The hypotheses are formulated as follows:

$$\left\{\begin{array}{cc}{H}_0:\mathrm{median}\left(d_i\right)=0,\hfill & (\mathrm{no}\mathrm{significant}\mathrm{difference})\hfill \\ H_1:\mathrm{median}\left(d_i\right)>0,\hfill & (\mathrm{the}\mathrm{proposed}\mathrm{method}\mathrm{outperforms}\mathrm{the}\mathrm{baseline})\hfill \end{array}\right.$$

For each dataset $i=1,2,\dots ,n$, let $x_i={\mathrm{RMV}}_i^{\mathrm{DCHGNN}}$ and $y_i={\mathrm{RMV}}_i^{\mathrm{Baseline}}$. The paired difference is computed as the following:

$$d_i=x_i-y_i,$$

and samples with $d_i=0$ are removed. The absolute differences $|d_i|$ are ranked in ascending order, assigning ranks $R_i\in \{1,2,\dots ,n\}$. The test statistic is then obtained as the sum of ranks corresponding to positive differences:

$$W^{+}=\sum _{d_i>0}{R}_i.$$

For a one-sided test evaluating whether the proposed method is significantly better, the statistic $W=W^{+}$ follows an approximately normal distribution under $H_0$ with the following:

$$E\left[W^{+}\right]={\displaystyle \frac{n(n+1)}{4}},\mathrm{Var}\left(W^{+}\right)={\displaystyle \frac{n(n+1)(2n+1)}{24}}.$$

The standardized test statistic is computed as the following:

$$Z={\displaystyle \frac{W^{+}-E\left[W^{+}\right]-0.5}{\sqrt{\mathrm{Var}\left(W^{+}\right)}}},$$

where $0.5$ is the continuity correction term. The corresponding p-value is calculated by the following:

$$p=1-\mathsf{\Phi }\left(Z\right),$$

where $\mathsf{\Phi }(·)$ denotes the cumulative distribution function of the standard normal distribution.

The Wilcoxon signed-rank test was conducted between DCHGNN and each baseline method across multiple datasets. The results indicate that the performance difference between DCHGNN and Auto-Sklearn is statistically significant ($p=0.0036<0.05$), confirming that the observed improvement is unlikely due to random variation. Compared with RF ($p=0.0716>0.05$), the result is close to the significance threshold, showing a potential upward trend in performance. In contrast, the differences with LightGCN ($p=0.6733$) and HGAT ($p=0.6952$) are not statistically significant, suggesting comparable performance levels.

Overall, the statistical results demonstrate that DCHGNN achieves a significant performance advantage over traditional AutoML-based models while maintaining competitive results with advanced graph-based architectures, highlighting both the effectiveness and stability of the proposed dual-channel heterogeneous graph framework.

4.6. Ablation Study

To investigate the contribution of key components, we conducted ablation experiments under four settings as the following:

• w/o Con: Employing the dual-channel framework without the contrastive learning mechanism
• w/o Meta: Employing a single channel without incorporating meta-features
• w/o Sema: Employing a single channel without incorporating dataset textual description features
• w/o Dual: Employing a single channel without removing any features. The meta-features were first normalized to zero mean and unit variance. The dataset node features were then obtained by directly column-wise concatenating the textual embeddings and the normalized meta-features without any further post-processing.

The ablation results in Table 9 and Table 10 reveal several important insights. First, removing contrastive learning leads to the most significant performance degradation, with the Average RMV dropping to 90.6%. This highlights the crucial role of contrastive learning in aligning the two channels and improving the consistency of learned representations. Second, excluding meta-features reduces performance to 91.6%, suggesting that dataset meta-information provides complementary structural cues that are not captured by textual descriptions alone. Third, removing description features yields the lowest score (88.2%), indicating that semantic information extracted from textual descriptions is indispensable for accurate algorithm recommendation. Finally, using a single concatenated channel achieves 92.0%, which outperforms some individual feature settings but still falls short of the dual-channel architecture, confirming the advantage of explicitly modeling and fusing heterogeneous information through separate channels.

Table 9. Average RMV scores for ablation studies.

Method	w/o Con	w/o Meta	w/o Sema	w/o Dual	DCHGNN
Average RMV	90.6%	91.6%	88.2%	92.0%	94.8%

Table 10. Distribution of RMV scores across ablation settings.

RMV Interval	w/o Con	w/o Meta	w/o Sema	w/o Dual	DCHGNN
$[0,0.6]$	6%	3%	6%	3%	0%
$(0.6,0.7]$	3%	2%	1%	2%	0%
$(0.7,0.8]$	3%	6%	8%	5%	2%
$(0.8,0.9]$	10%	9%	18%	12%	13%
$[0.9,1]$	78%	80%	67%	78%	85%
Total	100%	100%	100%	100%	100%

Overall, the proposed framework consistently surpasses all ablation variants, achieving the highest average RMV (94.8%) and the most stable RMV distribution. These findings validate the necessity of jointly incorporating contrastive learning, meta-features, and the dual-channel design, each of which plays a pivotal role in enhancing robustness and ensuring reliable recommendation quality.

4.7. Parameter Sensitivity Analysis

To further investigate the robustness and reproducibility of our method, we analyzed the sensitivity of three key hyperparameters: the contrastive loss temperature ($\tau$), the embedding dimension, and the learning rate, the results are shown in Table 11, Table 12 and Table 13 and Figure 3.

Table 11. Sensitivity analysis for embedding dimension hyperparameter.

RMV Interval	64	128	256	512
$[0,0.6]$	6%	6%	0%	1%
$(0.6,0.7]$	4%	2%	0%	2%
$(0.7,0.8]$	6%	5%	2%	5%
$(0.8,0.9]$	12%	13%	13%	12%
$[0.9,1]$	72%	74%	85%	80%
Total	100%	100%	100%	100%

Table 12. Sensitivity analysis for contrastive loss temperature hyperparameter.

RMV Interval	0.1	0.15	0.2	0.3
$[0,0.6]$	0%	0%	4%	6%
$(0.6,0.7]$	0%	0%	1%	2%
$(0.7,0.8]$	5%	2%	4%	6%
$(0.8,0.9]$	17%	13%	12%	13%
$[0.9,1]$	78%	85%	79%	73%
Total	100%	100%	100%	100%

Table 13. Sensitivity analysis for learning rate hyperparameter.

RMV Interval	$1\times {10}^{-4}$	$5\times {10}^{-4}$	$1\times {10}^{-3}$	$5\times {10}^{-3}$
$[0,0.6]$	1%	3%	0%	0%
$(0.6,0.7]$	2%	1%	0%	1%
$(0.7,0.8]$	4%	4%	2%	7%
$(0.8,0.9]$	21%	15%	13%	12%
$[0.9,1]$	72%	77%	85%	80%
Total	100%	100%	100%	100%

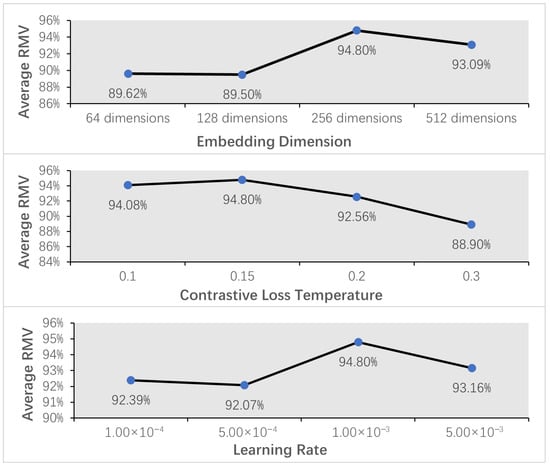
Figure 3. Sensitivity analysis regarding the embedding dimensions, temperature parameters and learning rates.

The embedding dimension is a key determinant of the model’s representational capacity. Our experiments tested dimensions of 64, 128, 256, and 512. As shown in Figure 3 and Table 11, the results indicate that performance does not increase monotonically with dimensionality. The optimal average RMV was achieved with a dimension of 256. While a higher dimension of 512 yielded a competitive result, the performance slightly decreased, suggesting potential redundancy. Conversely, lower dimensions of 64 and 128 resulted in notably inferior performance, indicative of insufficient representational power. Therefore, an embedding dimension of 256 is identified as the ideal trade-off between model expressiveness and generalization.

The temperature parameter $\tau$ governs the penalty on hard negative samples in the contrastive loss, critically influencing the structure of the embedding space. We evaluated the model performance with $\tau$ ranging from 0.1 to 0.3. As shown in Figure 3 and Table 12, the model achieves its peak performance at $\tau =0.15$, attaining an average RMV of 94.80% and the highest proportion of samples with an RMV score ≥ 0.9. A deviation from this optimal value leads to a performance degradation. Specifically, a lower $\tau$ may cause the model to over-penalize hard negatives, while a higher $\tau$ excessively softens the loss, resulting in a significant drop in the average RMV to 88.90%. This analysis validates that $\tau =0.15$ optimally facilitates inter-channel embedding consistency, thereby maximizing the matching performance.

The learning rate is pivotal for the optimization dynamics. We compared rates from $1\times {10}^{-4}$ to $5\times {10}^{-3}$. As shown in Figure 3 and Table 13, the analysis reveals that a learning rate of $1\times {10}^{-3}$ provides the best convergence efficiency and final performance, yielding the highest average RMV. Lower learning rates of $1\times {10}^{-4}$ and $5\times {10}^{-4}$ likely lead to insufficient or slower convergence, resulting in lower average RMVs of 92.39% and 92.07%, respectively. This confirms that a learning rate of $1\times {10}^{-3}$ enables the model to converge stably and efficiently to a superior optimum.

This extensive sensitivity analysis strongly reinforces the robustness and reproducibility of our proposed method, as it demonstrates consistent high performance under the chosen hyperparameter settings while clearly quantifying the impact of their variation.

4.8. Visualization of Algorithm Representations

To further assess the effectiveness of the proposed DCHGNN model, we conducted a t-SNE visualization of algorithm representations after training and compared them with the BERT-initialized algorithm node features. The study includes 179 algorithms grouped into nine major categories. As shown in Figure 4, a clear difference can be observed between the two visualizations. In the right figure (BERT-initialized features, before training), nodes of different colors—representing different algorithm categories—are largely mixed, with blurred class boundaries and dispersed intra-class distributions. In contrast, the left figure (features after DCHGNN training) exhibits compact clusters within each category and clear separations between categories. This result demonstrates that the proposed model effectively captures intra-class similarities and inter-class differences among algorithms, thereby enhancing the discriminative ability of the learned representations.

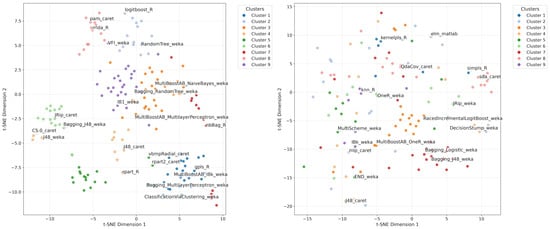
Figure 4. Visualization of algorithm representations after DCHGNN training (left, silhouette score: 0.27) and before training (right, silhouette score: 0.41).

To provide a clearer understanding of the algorithm representations learned by the DCHGNN model, we summarized the results of clustering into nine major categories in Table 14. Most algorithms within each cluster belong to the same family, while a few exceptions from different types are also present. For example, Cluster 1, labeled as partial least squares and principal component regression, also includes the algorithm bagging_DecisionStump_weka. This phenomenon arises because our model learns algorithm representations based on the scale of algorithm-data interactions, rather than strictly following the conventional taxonomy of algorithms. As a result, the DCHGNN framework captures both the dominant family structures and cross-family relationships in the embedding space.

Table 14. Clustering results of 179 algorithms into nine major categories.

Cluster	Representative Algorithms
Cluster 1: Partial Least Squares and Principal Component Regression	pls_caret, gpls_R, spls_R, simpls_R, kernelpls_R, widekernelpls_R, mars_R, dpp_C, PenalizedLDA_R, mlp_matlab, avNNet_caret, pcaNNet_caret, bagging_DecisionStump_weka.
Cluster 2: Neural Networks	mlp_matlab, mlp_caret, avNNet_caret, pcaNNet_caret, elm_matlab, elm_kernel_matlab, rbf_caret, RBFNetwork_weka, cascor_C, bdk_R, pnn_matlab, lvq_R, svm_C, gaussprRadial_R.
Cluster 3: Boosting Methods	AdaBoostM1_weka, adaboost_R, LogitBoost_weka, logitboost_R, MultiBoostAB_NaiveBayes_weka, MultiBoostAB_J48_weka, RacedIncrementalLogitBoost_weka, Decorate_weka, RandomForest_weka, REPTree_weka, fda_caret, stepLDA_caret.
Cluster 4: Decision Trees	DecisionStump_weka, RandomTree_weka, REPTree_weka, rpart_R, rpart_caret, J48_weka, J48_caret, C5.0Tree_caret, ctree_caret, rforest_R, rf_caret, AttributeSelectedClassifier_weka.
Cluster 5: Other Ensembles	RandomCommittee_weka, Bagging_HyperPipes_weka, MultiScheme_weka, END_weka, Dagging_weka, Vote_weka, MetaCost_weka, Stacking_weka, CostSensitiveClassifier_weka, LWL_weka, HyperPipes_weka.
Cluster 6: Rule-based Methods	PART_weka, JRip_caret, JRip_weka, OneR_weka, Ridor_weka, DTNB_weka, ZeroR_weka, DecisionTable_weka, ConjunctiveRule_weka, naiveBayes_R, NaiveBayesUpdateable_weka, gcvEarth_caret.
Cluster 7: Bagging	Bagging_DecisionStump_weka, Bagging_J48_weka, Bagging_NaiveBayes_weka, Bagging_PART_weka, Bagging_RandomForest_weka, bagging_R, treebag_caret, plsBag_R, nbBag_R, svmBag_R, nnetBag_R, cforest_caret.
Cluster 8: Discriminant Analysis	lda_R, lda2_caret, rrlda_R, sda_caret, slda_caret, PenalizedLDA_R, sparseLDA_R, qda_caret, rda_R, fda_R, mda_caret, pda_caret, pam_caret.
Cluster 9: Nearest Neighbor Methods	knn_R, knn_caret, IBk_weka, IB1_weka, KStar_weka, NNge_weka, lvq_caret, lvq_R, pnn_matlab, VFI_weka, Logistic_weka, ClassificationViaRegression_weka, LWL_weka, RBFNetwork_weka.

4.9. Case Study

To validate the effectiveness of the proposed framework, we conducted empirical analyses on two benchmark datasets: Yeast and Zoo. The Yeast dataset, created by Kenta Nakai’s team at the Institute of Molecular and Cellular Biosciences, Osaka University (1996) and included in the UCI machine learning repository, is suitable for heterogeneous feature recommendation tasks. It consists of 1484 protein instances, encompassing 10 biochemical feature attributes and non-numeric localization labels. The Zoo dataset, also available in the UCI repository, exhibits biological classification features that align well with algorithm recommendation scenarios. It contains 101 animal instances with seven class labels and 16 mixed-type features, including both categorical and integer attributes. These datasets allow for a comprehensive evaluation of the framework’s ability to handle multi-dimensional, heterogeneous data.

Based on these datasets, the framework generates algorithm recommendation sequences using graph-based representation learning. For the Yeast dataset, the top five recommended algorithms are: RRFglobal_caret, elm_kernel_matlab, rbfDDA_caret, rforest_R, and IBK_weka. For the Zoo dataset, the top five algorithms are: parRF_caret, dkp_C, knn_R, rforest_R, and rf_caret. Table 15 summarizes the performance comparison between local validation and interaction-based evaluation.

Table 15. Top five algorithm recommendation performance (sorted by recommendation rank).

Dataset	Algorithm	Local Validation Accuracy	Interaction Data Accuracy
Yeast	RRFglobal_caret	0.58	0.60
	elm_kernel_matlab	0.62	0.62
	rbfDDA_caret	0.58	0.59
	rforest_R	0.60	0.64
	IBK_weka	0.62	0.51
Zoo	parRF_caret	0.96	0.98
	dkp_C	0.98	0.98
	knn_R	0.94	0.96
	rforest_R	0.94	0.95
	rf_caret	0.95	0.96

The Yeast dataset poses a challenging scenario due to larger instance numbers, blurred inter-class boundaries, and potential noise or redundant features. Consequently, overall accuracies are lower and performance varies more across algorithms. The best algorithm accuracy on the interaction data for Yeast is 0.64, closely matching the top five recommended algorithms. This demonstrates that the framework is robust to noise and distributional shifts. In contrast, the Zoo dataset presents a relatively regular classification task with predominantly discrete or integer features and well-defined class boundaries. All top five recommended algorithms perform consistently well, with local and interaction-based accuracy exceeding 0.94. This indicates that the proposed model successfully captures the discrete and structured characteristics of the Zoo data, prioritizing tree- and nearest-neighbor-based algorithms. Across both datasets, the model consistently recommends algorithm sets that align well with the intrinsic data structure, further validating its effectiveness and generalization capability in algorithm recommendation tasks.

4.10. Time Complexity Analysis

To evaluate computational efficiency, this paper compared the proposed framework with a representative baseline, Auto-sklearn, which performs algorithm selection by executing candidate models on the given dataset. During its search process, Auto-sklearn trains and validates multiple algorithms using cross-validation to estimate performance, resulting in substantial computational overhead. In contrast, our framework generates algorithm recommendations directly through graph-based inference, without training or re-evaluating candidate algorithms on the target dataset.

Theoretical Complexity. Let N denote the number of dataset instances, F the number of extracted meta-features, M the number of candidate algorithms, and E the number of edges in the constructed algorithm–feature graph.

For Auto-sklearn, the time complexity can be approximated as the following:

$$\mathcal{O}(M\times T_{\mathrm{train}}\times K)$$

where $T_{\mathrm{train}}$ is the average training time per model and K is the number of cross-validation folds. This cost scales linearly with both the number of candidate algorithms and their respective training/validation iterations, leading to high computational demand.

In contrast, the proposed DCHGNN framework performs a single-pass inference on the heterogeneous graph, where node embeddings are computed and propagated via message passing. Its computational cost can be approximated as the following:

$$\mathcal{O}(E+N\times F)$$

which depends mainly on the graph size (nodes and edges) and feature dimensionality. Since no model retraining or iterative search is required, the total cost remains nearly constant across datasets, ensuring scalability to large-scale tasks.

Empirical Comparison. We further conducted inference-time comparisons using the same Yeast and Zoo datasets. Two evaluation schemes were considered: (1) comparing accuracy within equal inference time, and (2) comparing inference time when achieving the same target accuracy threshold. Since Auto-sklearn requires at least 30 s of search time while our model completes inference in approximately 15 s, we report results following the second scheme. The maximum search time for Auto-sklearn was set to 20 min. Table 16 summarizes the detailed inference time comparison.

Table 16. Inference time comparison between the proposed DCHGNN and Auto-sklearn.

Dataset	Target Accuracy (≥)	Proposed Model Time	Auto-Sklearn Time
Yeast	0.58	15.6 s	117.4 s
Zoo	0.96	15.8 s	116.1 s

As shown in Table 16, the proposed model exhibits a significant advantage in computational efficiency. For the Yeast dataset, our model completed inference in 15.6 s while evaluating 179 candidate algorithms and providing the optimal recommendation. In contrast, Auto-sklearn required 117.4 s to reach a comparable accuracy (0.5897), during which it explored 35 algorithm configurations. For the Zoo dataset, our model achieved 0.96 accuracy in 15.7 s, whereas Auto-sklearn required 116.1 s and 54 trials to reach 0.9677 accuracy.

Overall, the proposed framework achieves approximately a 7.5 times speed advantage while maintaining comparable recommendation accuracy. Theoretically, its single-pass inference complexity of $\mathcal{O}(E+N\times F)$ further supports its superior scalability compared to the iterative $\mathcal{O}(M\times T_{\mathrm{train}}\times K)$ search in Auto-sklearn. These results collectively verify that the proposed model serves as an efficient and deployable solution for real-world algorithm recommendation systems.

5. Conclusions

In this work, we proposed DCHGNN, a dual-channel heterogeneous graph neural network framework for automatic algorithm recommendation. By modeling datasets and algorithms as nodes in a bipartite graph and integrating semantic textual features with numerical meta-features through two complementary channels, the framework captures complex dataset-algorithm interaction patterns that single-modal approaches cannot fully exploit. A cross-channel contrastive learning mechanism aligns the embeddings of both channels, enhancing representation consistency and robustness, while a random forest regressor predicts algorithm performance on unseen datasets. Unlike existing graph-based recommendation models such as LightGCN and HGAT, which rely primarily on single-modal features and homogeneous message passing, DCHGNN integrates semantic textual information and numerical meta-features within a dual-channel design. This enables the model to capture richer dataset-algorithm interaction patterns and maintain representation consistency, even under sparse or cold-start conditions.

Extensive experiments on 121 datasets and 179 algorithms demonstrate that DCHGNN consistently outperforms state-of-the-art baselines in recommendation accuracy and stability. Ablation studies and visualization analyses confirm the importance of dual-channel design, meta-features, and contrastive learning. The proposed framework effectively addresses challenges such as data sparsity and cold-start scenarios, providing a scalable, reliable, and adaptive solution for real-world data-driven tasks. While the current evaluation primarily focuses on tabular classification tasks, a common and challenging benchmark in automated machine learning, the general architecture of DCHGNN is designed to be modality-agnostic. Future work will systematically extend and validate the framework’s effectiveness across diverse data modalities, including image, text, and time-series domains, to further demonstrate its broader applicability and generalization capabilities. Additionally, we will explore dynamic graph modeling, support for a broader range of task types, and enhanced interpretability, further extending the applicability and impact of this approach in data-driven decision-making.