Game-Based Consensus of Switching Multi-Agent Systems

Abstract

This paper investigates the leader–follower consensus problem for a class of second-order multi-agent systems. These systems are composed of both discrete-time and continuous-time subsystems and are governed by switching dynamics. Within the framework of a fixed directed topology involving multiple leaders, two control strategies are formulated. One applies separate control protocols to the continuous and discrete subsystems, while the other adopts an unified sampled-data control protocol. First, a multi-player game model is established based on the analysis and simulation of conflict behaviors among agents, and the existence of a unique Nash equilibrium(NE) for the system is proven. Then, based on the Nash equilibrium, a continuous–discrete-time game-based switching control system is formulated. Furthermore, the results confirm that the proposed system achieves consensus under both control strategies, even under arbitrary switching patterns. Finally, the performance of the approach is verified through numerical simulations.

1. Introduction

During the past few years, increasing attention has been devoted to multi-agent systems (MASs), which consist of autonomous agents cooperating through interaction to complete tasks [1]. Among studies on MASs (e.g., controllability [2,3,4], stabilizability [5,6], containment control [7,8], leader-following consensus [9,10,11]), consensus remains one of the primary research directions.

The concept of consensus was first introduced by DeGroot [12], who proposed a model demonstrating how agents can reach an agreement in parameter estimation. This work laid the foundation for subsequent research on consensus in MASs. Olfati-Saber [13] studied the problem of average consensus in connected undirected graphs and extended it to cases involving time delays and switched topologies. The work of Ren and Beard [14] demonstrated that for multi-agent systems under directed topologies, the existence of a spanning tree in the communication graph is the fundamental criterion for achieving consensus. Liu and Ji [15] introduced a flexible dynamic event-triggering approach related to the triggering threshold and addressed consensus in MASs with general linear dynamics, resulting in significantly reduced communication requirements. It is worth noting that the above results are only applicable to linear systems. A significant advancement was made by Liu et al. [16], who derived consensus criteria for nonlinear systems subject to both fixed and switching topologies. For MASs with communication topologies involving negative weights, Tian et al. [17] established a unified framework. Their work provides necessary and sufficient conditions for consensus under such conditions.

The aforementioned studies concentrated exclusively on MASs with a single type of dynamics and did not consider the more prevalent hybrid MASs encountered in practical engineering applications, which comprise two interacting components: subsystems with discrete-time (DT) dynamics [18] and subsystems with continuous-time (CT) dynamics. Numerous instances of such systems exist [19,20]; consequently, investigating the coordinated control of hybrid MASs is of substantial practical significance and application value. For example, in human–robot systems, commands from humans are discrete, while the movements of the robot are continuous [21]. Zheng et al. [22,23] investigated the consensus problem in first-order and second-order hybrid MASs under fixed directed communication topologies. By analyzing various communication strategies between DT and CT agents, they established a foundational framework for hybrid systems interactions.

In practical scenarios, various hybrid systems could be formulated as switching systems, wherein the dynamical behavior of agents may switch arbitrarily between DT and CT dynamics. Such switching behavior commonly arises in applications including power systems and automatic speed regulation systems. For instance, a system might be controlled by either physical or digital regulators, governed by switching rules between these regulators. When addressing the issue of long sampling periods, a discretized model of CT dynamics is considered; whereas for high-precision and short-sampling-period systems, it is necessary to handle time-varying values. Consequently, the system functions as a switching system that coordinates continuous-time and discrete-time dynamics. Zhai et al. [24] conducted a stability analysis of continuous–discrete systems using a Lie algebraic technique. On the basis of this, Zheng et al. [25] used classic protocol control methods to achieve consistency under switching dynamics. In addition, Lin et al. [26] also conducted research on finite time control and quantified control to achieve consensus. Liu et al. [27,28] proposed two control protocols for the consensus control of second-order MASs concerning switching dynamics, and provided several sufficient and necessary conditions to guaranteeing consensus regarding network topology and sampling period.

As the demand for reducing energy consumption in MASs continues to grow in practical applications, game theory has been applied for distributed control of MASs. Each agent in MASs functions as an independent player, making individual decisions based on local information exchange with its neighbors. By defining utility functions for the agents and assuming they adjust their behavior to optimize their utility, the collaborative task can be modeled as a distributed game.Ma et al. [29] analyzed games between CT and DT MASs, establishing sufficient/necessary conditions for consensus in the resulting hybrid system and proposing a method to accelerate convergence. Wang et al. [30] broadened the result to the more general scenario of an arbitrary number of interacting subsystems. A data-driven approach was employed by Xie et al. [31] to address the multi-player nonzero-sum game in unknown linear systems, enabling the derivation of dynamic output feedback Nash strategies using only input–output data. Motivated by the aforementioned works, this paper examines the consensus problem for second-order MASs with switching dynamics under a leader–follower framework, using a game-theoretic approach. In contrast to existing game-theoretic approaches [29,30,31], our work is distinguished by its integration of switching CT-DT dynamics with a non-cooperative game among multiple leaders. While prior studies primarily focus on systems with a single type of dynamics or cooperative interactions, this study explicitly models the strategic competition between leaders under arbitrary switching patterns, establishing a unique framework that bridges game theory and hybrid system control.

Relative to the existing literature, the principal contributions of our work are delineated as follows.

• The competitive behaviors among multiple leaders in MASs are modeled as a non-cooperative game, within which the individual cost function for each player is designed. Solving this game reveals that it admits a unique Nash equilibrium solution.
• Based on the formulated game, two control strategies are developed for consensus attainment. One employs distinct CT and DT inputs for the respective subsystems, while the other utilizes a unified sampled-data control protocol for both, thus avoiding controller frequent switching.
• Two sufficient and necessary conditions are established for the proposed control protocols.

The proposed framework finds potential applications in several real-world domains where hybrid continuous–discrete dynamics and competitive interactions coexist. For instance, in smart grid systems, multiple distributed energy resources (leaders) may compete to optimize their own profits while coordinating with local controllers (followers) to maintain frequency and voltage stability—a scenario naturally captured by our non-cooperative game model. Similarly, in multi-robot collaborative systems, such as warehouse logistics or search-and-rescue missions, robots may switch between continuous motion and discrete decision-making modes, while competing for tasks or resources. Our unified sampled-data control protocol can effectively avoid frequent controller switching and ensure consensus under dynamic topologies. These examples illustrate the practical relevance and generality of our theoretical results.

The paper is organized as follows. Section 2 introduces the necessary preliminaries. The main theoretical results are developed in Section 3 and Section 4. Section 5 presents numerical simulations to illustrate the findings. The work is concluded in Section 6.

Some notations and symbols are listed in Table 1.

Table 1. Notation Summary.

Symbol	Definition
$\mathbb{R}$	Set of real numbers
$\mathbb{N}$	Set of nonnegative integers
${\mathbb{N}}^{+}$	Set of positive integers
$I_n$	Identity matrix of dimension n
${\mathbf{1}}_n$	Column vector of ones of length n
${\mathbf{0}}_n$	Column vector of zeros of length n
$\mathcal{G}$	Directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$
$\mathcal{V}$	Set of nodes (agents)
$\mathcal{E}$	Set of directed edges
$\mathcal{A}$	Adjacency matrix $\left[a_{ij}\right]$
L	Laplacian matrix $\left[l_{ij}\right]$
$x_i,v_i$	Position and velocity of agent i
$u_i$	Control input of agent i
$\alpha ,\beta$	Coupling gains in control protocols
${\zeta }_i$	State vector of agent i, ${\zeta }_i={(x_i,v_i)}^T$
$t_k$	Sampling instant
h	Sampling period
${\kappa }_i,{\vartheta }_i$	Cost weights in the game-theoretic framework
$\mathrm{\Xi },K,Q,H$	Matrices defined in the Nash equilibrium analysis
$\lambda ,\epsilon$	Eigenvalues of Laplacian and game control matrices
$V_f,V_l$	Sets of followers and leaders
$P_f,P_l$	Sets of follower and leader players in game framework
$c,d$	Superscripts denoting continuous-time and discrete-time systems

2. Preliminaries

2.1. Graph Theory

Consider a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, defined by a node set $\mathcal{V}=\{v_1,\dots ,v_N\}$, a set of directed edges $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ and an adjacency matrix $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$. A directed edge $e_{ij}$ in $\mathcal{G}$ is represented as the ordered pair $(v_i,v_j)$, indicating the direction of information flow from $v_j$ to $v_i$. The adjacency matrix satisfies: $a_{ij}>0$ if $e_{ij}\in \mathcal{E}$, else $a_{ij}=0$; $a_{ii}=0$; and $a_{ij}=a_{ji}$ if the graph is undirected. The Laplacian matrix $L=\left[l_{ij}\right]\in {\mathbb{R}}^{N\times N}$ of G has entries defined by

$$l_{ij}=\left\{\begin{array}{cc}\sum _{j\in N_i}{a}_{ij},\hfill & \mathrm{if}i=j,\hfill \\ -a_{ij},\hfill & \mathrm{if}i\ne j.\hfill \end{array}\right.$$

A graph is connected when a path exists between every pair of distinct nodes. A tree is a connected subgraph that contains no cycles. A directed spanning tree of G is a directed tree that contains every node in G. A directed spanning forest comprises multiple directed spanning trees that share no common vertices.

2.2. System Model

Consider a MAS with second-order switching dynamics, consisting of n followers and m leaders, labeled as $V=\{1,2,\dots ,n+m\}$, where $n+m\in {\mathbb{N}}^{+}$. The set of followers is denoted as $V_f=\{v_1,v_2,...,v_n\}$, and the set of leaders is denoted as $V_l=\{v_{n+1},v_{n+2},...,v_{n+m}\}$. In a MAS considering second-order switching dynamics, all agents are subject to both CT and DT switching dynamics. The follower state of the CT dynamical system is described as

$$\left\{\begin{array}{c}{\dot{x}}_i^c\left(t\right)=v_i^c\left(t\right),\hfill \\ {\dot{v}}_i^c\left(t\right)=u_i^c\left(t\right),i=1,2,\dots ,n,\hfill \end{array}\right.$$

(1)

the leader state of the CT dynamical system is expressed as

$$\left\{\begin{array}{c}{\dot{x}}_i^c\left(t\right)=v_i^c\left(t\right),i=1,2,\dots ,n,\hfill \\ {\dot{v}}_i^c\left(t\right)=0,i=n+1,n+2,\dots ,n+m,\hfill \end{array}\right.$$

(2)

the follower state of DT dynamical systems is represented as

$$\left\{\begin{array}{c}{x}_i^d\left(t_{k+1}\right)=x_i^d\left(t_k\right)+v_i^d\left(t_k\right),\hfill \\ v_i^d\left(t_{k+1}\right)=v_i^d\left(t_k\right)+u_i^d\left(t_k\right),\hfill \end{array}\right.$$

(3)

the leader state of DT dynamical systems is set to

$$\left\{\begin{array}{c}{x}_i^d\left(t_{k+1}\right)=x_i^d\left(t_k\right)+v_i^d\left(t_k\right),\hfill \\ v_i^d\left(t_{k+1}\right)=v_i^d\left(t_0\right),\hfill \end{array}\right.$$

(4)

For agent i, its position $x_i(·)$, velocity $v_i(·)$, and control input $u_i(·)$ are all real-valued states, i.e., $x_i(·),v_i(·),u_i(·)\in \mathbb{R}$. The superscripts c and d indicate that agent i is part of the CT and DT dynamical systems, respectively. $v_i\left(t_0\right),i\in V_l$ represents the initial velocity state of the leaders. Since the leader states are unaffected by the other agents, we assume in this paper that the velocity state of the leaders at any time is the same as the initial value. We use a control protocol for CT systems, where each agent constantly observes its own state and the states of its neighbors. The control input is given by

$$u_i^c\left(t\right)=\beta \sum _{j\in N_i}{a}_{ij}\left[v_j\left(t\right)-v_i\left(t\right)\right]+\alpha \sum _{j\in N_i}{a}_{ij}\left[x_j\left(t\right)-x_i\left(t\right)\right],$$

(5)

the control protocol that each agent can observe their own state and neighboring states at the sampling time is used for DT systems, the corresponding control input is defined as

$$u_i^d\left(t_k\right)=\beta \sum _{j\in N_i}{a}_{ij}\left[v_j\left(t_k\right)-v_i\left(t_k\right)\right]+\alpha \sum _{j\in N_i}{a}_{ij}\left[x_j\left(t_k\right)-x_i\left(t_k\right)\right],$$

(6)

where $\alpha ,\beta >0$ are the coupling gains.

Thus, systems (1) and (3) can be written as

$$\left\{\begin{array}{c}{\dot{x}}_i^c\left(t\right)=v_i^c\left(t\right),\hfill \\ {\dot{v}}_i^c\left(t\right)=\beta \sum _{j\in N_i}{a}_{ij}\left[v_j\left(t\right)-v_i\left(t\right)\right]+\alpha \sum _{j\in N_i}{a}_{ij}\left[x_j\left(t\right)-x_i\left(t\right)\right],i=1,2,\dots ,n,\hfill \end{array}\right.$$

(7)

and

$$\left\{\begin{array}{c}{x}_i^d\left(t_{k+1}\right)=v_i^d\left(t_k\right)+x_i^d\left(t_k\right),\hfill \\ v_i^d\left(t_{k+1}\right)=v_i^d\left(t_k\right)+\beta \sum _{j\in N_i}{a}_{ij}\left[v_j\left(t_k\right)-v_i\left(t_k\right)\right]+\alpha \sum _{j\in N_i}{a}_{ij}\left[x_j\left(t_k\right)-x_i\left(t_k\right)\right].\hfill \end{array}\right.$$

(8)

For the systems (1) and (2), let ${\zeta }_i\left(t\right)={\left(\begin{array}{c}{x}_i\left(t\right),v_i\left(t\right)\end{array}\right)}^T$. Then, the states of followers and leaders are respectively given as follows

$${\dot{\zeta }}_i\left(t\right)=A{\zeta }_i\left(t\right)-\sum _{j=1}^n{l}_{ij}B{\zeta }_i\left(t\right),i=1,2,\dots ,n,$$

(9)

$${\dot{\zeta }}_i\left(t\right)=A{\zeta }_i\left(t\right),i=n+1,n+2,\dots ,n+m.$$

(10)

where $A=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$ and $B=\left[\begin{array}{cc}0& 0\\ \alpha & \beta \end{array}\right]$. Within the leader–follower framework, L is structured as $L=\left[\begin{array}{cc}{L}_f& L_{fl}\\ L_{fl}^T& L_l\end{array}\right]$, where $L_f\in {\mathbb{R}}^{n\times n}$ and $L_l\in {\mathbb{R}}^{m\times m}$ are the submatrices associated with the followers and leaders, respectively. $L_{fl}\in {\mathbb{R}}^{n\times m}$, and $L_{fl}^T\in {\mathbb{R}}^{m\times n}$ are the connection matrix between leaders and followers.

Let $\zeta \left(t\right)={\left({\zeta }_1^T\left(t\right),{\zeta }_2^T\left(t\right),\dots ,{\zeta }_{n+m}^T\left(t\right)\right)}^T$, then (1) and (2) can be characterized as

$$\dot{\zeta }\left(t\right)=\left(\left[\begin{array}{cc}{I}_n\otimes A& {\mathbf{0}}_{n\times m}\\ {\mathbf{0}}_{m\times n}& I_m\otimes A\end{array}\right]-\left[\begin{array}{cc}{L}_f\otimes B& L_{fl}\otimes B\\ {\mathbf{0}}_{m\times n}& {\mathbf{0}}_{m\times m}\end{array}\right]\right)\zeta \left(t\right),$$

simplifying it yields

$$\dot{\zeta }\left(t\right)=\left[\begin{array}{c}\left(I_{n+m}\otimes A\right)-\left(L\otimes B\right)\end{array}\right]\zeta \left(t\right).$$

(11)

For the DT systems (3) and (4), by applying a similar transformation, one obtains

$$\zeta \left(t_{k+1}\right)=\left[\left(I_{n+m}\otimes C\right)-\left(L\otimes D\right)\right]\zeta \left(t_k\right),$$

(12)

where $\zeta \left(t_k\right)={\left({\zeta }_1^T\left(t_k\right),{\zeta }_2^T\left(t_k\right),...,{\zeta }_{n+m}^T\left(t_k\right)\right)}^T$, ${\zeta }_i\left(t_k\right)={\left(x_i\left(t_k\right),v_i\left(t_k\right)\right)}^T$, $C=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right],D=\left[\begin{array}{cc}0& 0\\ \alpha & \beta \end{array}\right]$.

Lemma 1

([32]). $\mathcal{M}=\left(m_{ij}\right)\in {\mathbb{R}}^{n\times n}$ is regarded as strictly diagonally dominant (SDD) if $\left|m_{ii}\right|>{\sum }_{j=1,j\ne i}^n\left|m_{ij}\right|$, $i\in V$. The SDD matrix is invertible.

Lemma 2

([33]). A quadratic complex coefficient polynomial is given as

$$g\left(s\right)=s^2+{\omega }_{1}s+{\omega }_2,$$

where ${\omega }_1$ and ${\omega }_2$ are complex numbers. If $g\left(s\right)$ satisfies $Re\left({\omega }_1\right)>0$ and $Re\left({\omega }_1\right)Im\left({\omega }_1\right)Im\left({\omega }_2\right)+R{e}^2\left({\omega }_1\right)Re\left({\omega }_2\right)-I{m}^2\left({\omega }_2\right)>0$, then it is called Hurwitz stable.

Lemma 3

(Gersghorin Circle Theorem [14]). Let $\mathcal{B}=\left(b_{ij}\right)\in {\mathbb{R}}^{n\times n}$ and let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ denote its eigenvalues. Then ${\lambda }_i\in {\bigcup }_{i=1}^n{G}_i,i\in 1,2,\dots ,n,$ where $G_i=\left\{z\mid |z-b_{ii}|\le {\sum }_{j=1,j\ne i}^n\left|b_{ij}\right|\right\}.$

Lemma 4

([23]). For a stochastic matrix $\mathcal{S}=\left(s_{ij}\right)\in {\mathbb{R}}^{n\times n},$ the eigenvalue ${\mathbf{1}}_n$ always exists with corresponding eigenvector ${\mathbf{1}}_n$. The absolute values of all other eigenvalues lie within the unit circle.

2.3. Conceptualization and Representation in Game Theory

We consider a CT-DT switching dynamic system with n follower players and m leader players. The set of follower players is defined as $P_f=\{p_1,p_2,\dots ,p_n\}$, and the set of leader players is defined as $P_l=\{p_{n+1},p_{n+2},\dots ,p_{n+m}\}$. The state of player $p_i$, $i=1,2,\dots ,n+m$ at the game moment $t=t_k$ is defined as ${\zeta }_i\left(t\right)\in \mathbb{R}$. The competitive behavior among agents in the switching system is cast as a multi-player game, denoted by $\mathbb{G}(P,S_i,C_i)$, which is expressed as follows.

Players: The set of all players is defined as $P=P_f\cap P_l$.

Strategy: All players are assumed to make their strategy choices independently and simultaneously. Each player $p_i,i\in P$, selects a strategy from its own strategy set $S_i\in \mathbb{R}$, and competes against its opponents with the objective of minimizing its own cost function $f_i(·)$. Define $t^{-}$ as the moment right before the game (i.e., the instantaneous time prior to the strategy update at t). If a player changes its state ${\zeta }_i\left(t\right)$ through selecting a strategy, the player will have reached the state ${\zeta }_i\left(t^{-}\right)$ just before time $t^{-}$.

Cost: The leader players $p_i,i\in P_l$ are assumed to be upper-level decision-makers, who compete exclusively with other leaders, not with followers. Its cost function is governed by the cost of changing one’s state ${\left[\begin{array}{c}{\zeta }_i\left(t_{k+1}\right)-{\zeta }_i\left(t_{k+1}^{-}\right)\end{array}\right]}^T\left[\begin{array}{c}{\zeta }_i\left(t_{k+1}\right)-{\zeta }_i\left(t_{k+1}^{-}\right)\end{array}\right]$ and the cost of divergence with other leader players ${\displaystyle \frac{1}{q_i}}{\sum }_{j\in N_i}{h}_{ij}{[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_j\left(t_{k+1}\right)]}^T[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_j\left(t_{k+1}\right)]$. Therefore, the cost function of the leader player $p_i,i\in P_l$ is defined as

$$\begin{array}{cc}\hfill f_i\left(t_{k+1}\right)& ={\kappa }_i{\left[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_i\left(t_{k+1}^{-}\right)\right]}^T\left[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_i\left(t_{k+1}^{-}\right)\right]\hfill \\ \hfill & +{\vartheta }_i{\displaystyle \frac{1}{q_i}}\sum _{j\in N_i}{h}_{ij}{\left[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_j\left(t_{k+1}\right)\right]}^T\left[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_j\left(t_{k+1}\right)\right],\hfill \end{array}$$

(13)

where ${\kappa }_i$ and ${\vartheta }_i$ represent the cost weight of the change in its own state and the cost weight of divergence with other players, respectively, $q_i={\sum }_{j\in N_i}{h}_{ij}>0,0<{\kappa }_i,{\vartheta }_i<1\mathrm{and}{\kappa }_i+{\vartheta }_i=1$. In addition, the follower players $p_i,i\in P_f$ do not engage in competitive behavior among leader players but instead follow the directives of the leaders and adjust their own states subject to the instructions. Consequently, the cost function of the follower players $p_i,i\in P_f$ is defined as

$$f_i\left(t_{k+1}\right)={\left[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_i\left(t_{k+1}^{-}\right)\right]}^T\left[{\zeta }_i\left(t_{k+1}\right)-{\zeta }_i\left(t_{k+1}^{-}\right)\right].$$

(14)

Definition 1.

In a multi-player game $\mathbb{G}$, there exists a Nash equilibrium solution if it satisfies

$$f_i\left(s_i^{\ast },{\mathbf{s}}_{-i}^{\ast }\right)\le f_i\left(s_i,{\mathbf{s}}_{-i}^{\ast }\right),\forall s_i\in S_i,i\in P,$$

(15)

where the cost $f_i(s_i,{\mathbf{s}}_{-i})$ for player $p_i$ depends on their strategy $s_i\in S_i$ and the strategy profile ${\mathbf{s}}_{-i}$ of other players. Thus, no player gains from unilaterally deviating from the equilibrium ${\mathbf{s}}^{\ast }$.

Remark 1.

All players are rational and selfish. They seek to minimize their state changes and reduce discrepancies with their opponents, which is applicable in many practical situations. For example, in tariff negotiations, each country aims to uphold its tariffs while reaching a consensus with other countries, requiring a balance between its own interests and discrepancies with others. In social networks, individuals typically maintain their own viewpoints while seeking consensus, necessitating compromises to balance personal preferences with group alignment.

3. Main Results

Consider a CT-DT switching dynamic MAS on a directed graph $\mathcal{G}$. Assume that each agent in the system satisfies $q_i={\sum }_{j\in N_i}{h}_{ij}>0$, and that the interactions among these agents are modeled as a game $\mathbb{G}(P,S_i,C_i)$. The cost functions of the leader players and the follower players correspond to Equations (13) and (14), respectively. Let the state set of followers be ${\zeta }_f\left(t_k\right)={\left[{\zeta }_1\left(t_k\right),{\zeta }_2\left(t_k\right),...,{\zeta }_n\left(t_k\right)\right]}^T$ and the state set of leaders be ${\zeta }_l\left(t_k\right)={\left[{\zeta }_{n+1}\left(t_k\right),{\zeta }_{n+2}\left(t_k\right),...,{\zeta }_{n+m}\left(t_k\right)\right]}^T$. And $\zeta \left(t_k\right)={\left[\begin{array}{c}{\zeta }_f\left(t_k\right),{\zeta }_l\left(t_k\right)\end{array}\right]}^T$.

Theorem 1.

The game $\mathbb{G}(P,S_i,C_i)$ has a unique NE $\left({\zeta }_1^{\ast }\left(t_{k+1}\right),...,{\zeta }_i^{\ast }\left(t_{k+1}\right),{\zeta }_{n+m}^{\ast }\left(t_{k+1}\right)\right)$ with ${\zeta }^{\ast }\left(t_{k+1}\right)={\tilde{\mathrm{\Xi }}}^{-1}\tilde{K}\zeta \left(t_{k+1}^{-}\right)$ holding, where

$\tilde{\mathrm{\Xi }}=\left[\begin{array}{cc}{I}_n& \\ & \mathrm{\Xi }\end{array}\right]$, $\mathrm{\Xi }=I_m-QH$, $Q=diag\left\{{\displaystyle \frac{{\vartheta }_1}{q_1}},{\displaystyle \frac{{\vartheta }_2}{q_2}},...,{\displaystyle \frac{{\vartheta }_m}{q_m}}\right\}$, $H=\left[\begin{array}{cccc}{h}_{11}& h_{12}& \dots & h_{1m}\\ h_{21}& h_{22}& \dots & h_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ h_{m1}& h_{m2}& \dots & h_{mm}\end{array}\right]$ and $\tilde{K}=\left[\begin{array}{c}{I}_n\\ & K\end{array}\right]$, $K=diag\left\{{\kappa }_1,{\kappa }_2,...,{\kappa }_m\right\}$.

Proof of Theorem 1.

For $p_i,i\in P_f$, $f_i\left({\zeta }_i\left(t_{k+1}\right)\right)$ has a global minimum solution ${\zeta }_i^{\ast }\left(t_{k+1}\right)$, which satisfies

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial f_i\left({\zeta }_i\left(t_{k+1}\right)\right)}{\partial {\zeta }_i\left(t_{k+1}\right)}}{|}_{\left({\zeta }_1^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_n^{\ast }\left(t_{k+1}\right)\right)}=0,\hfill \\ {\displaystyle \frac{{\partial }^2{f}_i\left({\zeta }_i\left(t_{k+1}\right)\right)}{{\partial }^2{\zeta }_i\left(t_{k+1}\right)}}{|}_{\left({\zeta }_1^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_n^{\ast }\left(t_{k+1}\right)\right)}>0,\hfill \end{array}\right.$$

(16)

for $p_i,i\in P_l$, if ${\mathbf{\zeta }}_j^{\ast }\left(t_{k+1}\right)$, $j\in P_l,j\ne i$ is fixed, obviously $f_i\left({\zeta }_i\left(t_{k+1}\right),{\mathbf{\zeta }}_j^{\ast }\left(t_{k+1}\right)\right)$ is a quadratic function with respect to ${\zeta }_i\left(t_{k+1}\right)$, thus $f_i\left({\zeta }_i\left(t_{k+1}\right),{\mathbf{\zeta }}_j^{\ast }\left(t_{k+1}\right)\right)$ has a global minimum solution ${\zeta }_i^{\ast }\left(t_{k+1}\right)$ satisfying

$$\left\{\begin{array}{c}{\left.{\displaystyle \frac{\partial f_i\left({\zeta }_i\left(t_{k+1}\right),{\zeta }_j\left(t_{k+1}\right)\right)}{\partial {\zeta }_i\left(t_{k+1}\right)}}\right|}_{\left({\zeta }_{n+1}^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_{n+m}^{\ast }\left(t_{k+1}\right)\right)}=0,\hfill \\ {\left.{\displaystyle \frac{{\partial }^2{f}_i\left({\zeta }_i\left(t_{k+1}\right),{\zeta }_j\left(t_{k+1}\right)\right)}{{\partial }^2{\zeta }_i\left(t_{k+1}\right)}}\right|}_{\left({\zeta }_{n+1}^{\ast }\left(t_{k+1}\right)\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_{n+m}^{\ast }\left(t_{k+1}\right)\right)}>0.\hfill \end{array}\right.$$

(17)

According to (15)–(17), the game $\mathbb{G}(P,S_i,C_i)$ has a unique NE solution. Furthermore, $\left({\zeta }_1^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),{\zeta }_{n+m}^{\ast }\left(t_{k+1}\right)\right)$ is the NE solution if and only if

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial f_i\left({\zeta }_i\left(t_{k+1}\right)\right)}{\partial {\zeta }_i\left(t_{k+1}\right)}}{|}_{\left({\zeta }_1^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_n^{\ast }\left(t_{k+1}\right)\right)}=0,i\in P_f,\hfill \\ {\displaystyle \frac{\partial f_i\left({\zeta }_i\left(t_{k+1}\right),{\zeta }_j\left(t_{k+1}\right)\right)}{\partial {\zeta }_i\left(t_{k+1}\right)}}{|}_{\left({\zeta }_{n+1}^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_i^{\ast }\left(t_{k+1}\right),\dots ,{\zeta }_{n+m}^{\ast }\left(t_{k+1}\right)\right)}=0,i\in P_l.\hfill \end{array}\right.$$

(18)

By solving (18), one obtains

$$\left\{\begin{array}{cc}{\zeta }_i^{\ast }\left(t_{k+1}\right)={\zeta }_i\left(t_{k+1}^{-}\right),\hfill & i\in P_f,\hfill \\ {\zeta }_i^{\ast }\left(t_{k+1}\right)-{\displaystyle \frac{{\vartheta }_i}{q_i}}\sum _{j\in N_i}{h}_{ij}{\zeta }_j^{\ast }\left(t_{k+1}\right)={\kappa }_i{\zeta }_i\left(t_{k+1}^{-}\right),\hfill & i\in P_l.\hfill \end{array}\right.$$

(19)

Let $H=\left[\begin{array}{cccc}{h}_{11}& h_{12}& \dots & h_{1m}\\ h_{21}& h_{22}& \dots & h_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ h_{m1}& h_{m2}& \dots & h_{mm}\end{array}\right]$ with $h_{11}=h_{22}=\dots =h_{mm}=0$. The Equation (19) can be written in matrix form as

$$\left[\begin{array}{cc}{I}_n& \\ & \mathrm{\Xi }\end{array}\right]\left[\begin{array}{c}{\zeta }_f^{\ast }\left(t_{k+1}\right)\\ {\zeta }_l^{\ast }\left(t_{k+1}\right)\end{array}\right]=\left[\begin{array}{cc}{I}_n& \\ & K\end{array}\right]\left[\begin{array}{c}{\zeta }_f\left(t_{k+1}^{-}\right)\\ {\zeta }_l\left(t_{k+1}^{-}\right)\end{array}\right],$$

(20)

where $\mathrm{\Xi }=I_m-QH\in {\mathbb{R}}^{(n+m)\times (n+m)}$, $Q=diag\left\{{\displaystyle \frac{{\vartheta }_1}{q_1}},{\displaystyle \frac{{\vartheta }_2}{q_2}},...,{\displaystyle \frac{{\vartheta }_m}{q_m}}\right\}$ and $K=diag\left\{{\kappa }_1,{\kappa }_2,...,{\kappa }_m\right\}\in {\mathbb{R}}^{(n+m)\times (n+m)}$. For convenience, let $\tilde{\mathrm{\Xi }}=\left[\begin{array}{cc}{I}_n& \\ & \mathrm{\Xi }\end{array}\right]\in {\mathbb{R}}^{m\times m}$, $\tilde{K}=\left[\begin{array}{c}{I}_n\\ & K\end{array}\right]\in {\mathbb{R}}^{m\times m}$, then (20) could be rewritten as $\tilde{\mathrm{\Xi }}{\zeta }^{\ast }\left(t_{k+1}\right)=\tilde{K}\zeta \left(t_{k+1}^{-}\right)$. Observing $\tilde{\mathrm{\Xi }}=\left(e_{ij}\right)\in {\mathbb{R}}^{(n+m)\times (n+m)}$, it can be found that

$$\sum _{j=1,j\ne i}^{n+m}\left|e_{ij}\right|<1=\left|e_{ii}\right|,i\in P,$$

which implies that $\tilde{\mathrm{\Xi }}$ is strictly diagonally dominant. By Lemma 1 the $\tilde{\mathrm{\Xi }}$ is invertible. Therefore, we have

$${\zeta }^{\ast }\left(t_{k+1}\right)={\tilde{\mathrm{\Xi }}}^{-1}\tilde{K}\zeta \left(t_{k+1}^{-}\right).$$

(21)

As a consequence, game $\mathbb{G}(P,S_i,C_i)$ has the unique Nash equilibrium $\left({\zeta }_1^{\ast }\left(t_{k+1}\right),...,{\zeta }_i^{\ast }\left(t_{k+1}\right),{\zeta }_{n+m}^{\ast }\left(t_{k+1}\right)\right)$ with ${\zeta }^{\ast }\left(t_{k+1}\right)={\tilde{\mathrm{\Xi }}}^{-1}\tilde{K}\zeta \left(t_{k+1}^{-}\right)$ holding. □

This theorem establishes the existence of a unique Nash Equilibrium (NE) in the game involving multiple leaders and followers. It signifies that each leader can find an optimal balance between minimizing its own state deviation and reducing disagreements with other leaders. The followers, in contrast, do not engage in competition and simply adjust their states according to the leaders’ directives. The existence of this unique NE not only provides a stable optimization objective for the system but also forms a solid foundation for designing the subsequent consensus control protocols.

All agents participate in the game $\mathbb{G}(P_i,S_i,C_i)$, and adjust their states at the next time step based on the NE. Under the framework of the game, embedding the CT system (11) into (21) yields

$$\begin{array}{cc}\hfill \dot{\zeta }\left(t\right)& ={\tilde{\mathrm{\Xi }}}^{-1}\tilde{K}\left[\left(I_{n+m}\otimes A\right)-\left(L\otimes B\right)\right]\zeta \left(t\right)\hfill \\ \hfill & =\left[\begin{array}{cc}{I}_n^{-1}& \mathbf{0}\\ \mathbf{0}& {\mathrm{\Xi }}^{-1}\end{array}\right]\left[\begin{array}{cc}{I}_n& \mathbf{0}\\ \mathbf{0}& K\end{array}\right]\left[\begin{array}{cc}{I}_n\otimes A-L_f\otimes B& -L_{fl}\otimes B\\ \mathbf{0}& I_m\otimes A\end{array}\right]\zeta \left(t\right)\hfill \\ \hfill & =\left[\begin{array}{cc}{I}_n\otimes A-L_f\otimes B& -L_{fl}\otimes B\\ \mathbf{0}& {\mathrm{\Xi }}^{-1}K\otimes A\end{array}\right]\zeta \left(t\right)\hfill \\ \hfill & =\left(\begin{array}{c}\left[\begin{array}{c}{I}_n\otimes A\\ \mathbf{0}& {\mathrm{\Xi }}^{-1}K\otimes A\end{array}\right]-\left[\begin{array}{cc}{L}_f\otimes B& L_{fl}\otimes B\\ \mathbf{0}& \mathbf{0}\end{array}\right]\end{array}\right)\zeta \left(t\right)\hfill \\ \hfill & =\left[\left(\mathrm{\Psi }\otimes A\right)-\left(L\otimes B\right)\right]\zeta \left(t\right),\hfill \end{array}$$

(22)

where $\mathrm{\Psi }=\left[\begin{array}{c}{I}_n\\ & {\mathrm{\Xi }}^{-1}K\end{array}\right]$. Similarly, embedding the DT system (12) into (21) yields

$$\zeta \left(t_{k+1}\right)=\left[\begin{array}{c}\left(\mathrm{\Psi }\otimes C\right)-\left(L\otimes B\right)\end{array}\right]\zeta \left(t_k\right).$$

(23)

By analyzing the matrix ${\mathrm{\Xi }}^{-1}K=\left(c_{ij}\right)\in {\mathbb{R}}^{m\times m}$, we can conclude that

$$\begin{array}{cc}\hfill \mathrm{\Xi }{\mathbf{1}}_m& =\left[\begin{array}{cccc}1& -{\displaystyle \frac{{\vartheta }_1}{q_1}}{h}_{12}& \dots & -{\displaystyle \frac{{\vartheta }_1}{q_1}}{h}_{1m}\\ -{\displaystyle \frac{{\vartheta }_2}{q_2}}{h}_{21}& 1& \dots & -{\displaystyle \frac{{\vartheta }_2}{q_2}}{h}_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ -{\displaystyle \frac{{\vartheta }_m}{q_m}}{h}_{m1}& -{\displaystyle \frac{{\vartheta }_m}{q_m}}{h}_{m2}& \dots & 1\end{array}\right]\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}1-{\displaystyle \frac{{\vartheta }_1}{q_1}}\sum _{j\in N_{n+1}}{h}_{(n+1)j}\\ 1-{\displaystyle \frac{{\vartheta }_2}{q_2}}\sum _{j\in N_{n+2}}{h}_{(n+2)j}\\ ⋮\\ 1-{\displaystyle \frac{{\vartheta }_m}{q_m}}\sum _{j\in N_{n+m}}{h}_{(n+m)j}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}1-{\vartheta }_1\\ 1-{\vartheta }_2\\ ⋮\\ 1-{\vartheta }_m\end{array}\right],\hfill \end{array}$$

(24)

and $K{\mathbf{1}}_m=diag\left\{{\kappa }_1,{\kappa }_2,\dots ,{\kappa }_m\right\}{\mathbf{1}}_m={\left[{\kappa }_1,{\kappa }_2,\dots ,{\kappa }_m\right]}^T$. Since the weight factors satisfy ${\vartheta }_i+{\kappa }_i=1$, we have $K{\mathbf{1}}_m={\left[1-{\vartheta }_1,1-{\vartheta }_2,...,1-{\vartheta }_m\right]}^T$. Thus, we obtain

$${\mathrm{\Xi }}^{-1}K{\mathbf{1}}_m={\mathbf{1}}_m.$$

(25)

According to the foregoing, it can be known that $\mathrm{\Xi }=I_m-QH$, assume that the eigenvalues of $QH=\left(b_{ij}\right)\in {\mathbb{R}}^{m\times m}$ are ${\lambda }_i$, $i=n+1,n+2,\dots ,n+m$. Based on Lemma 3, we obtain ${\lambda }_i\in {\bigcup }_{j=n+1}^{n+m}{\mathcal{G}}_i$, where

$$\begin{array}{cc}\hfill {\mathcal{G}}_i& =\left\{c||c-b_{ii}|\le \sum _{j=n+1,j\ne i}^{n+m}|b_{ij}|\right\}\hfill \\ & =\left\{c||c|\le \sum _{j=n+1,j\ne i}^{n+m}|{\displaystyle \frac{{\vartheta }_i}{q_i}}{h}_{ij}|\right\}\hfill \\ & =\left\{c||c|\le \left|{\vartheta }_i\right|<1\right\}.\hfill \end{array}$$

It means $\left|{\lambda }_i\right|<1$.Thus

$${\mathrm{\Xi }}^{-1}={\left(I_m-QH\right)}^{-1}=\sum _{n=0}^{\infty }{\left(QH\right)}^n=I_n+QH+{\left(QH\right)}^2+\dots .$$

(26)

Clearly, each element of the matrix $QH$ is nonnegative. Accordingly, the inverse matrix ${\mathrm{\Xi }}^{-1}$ is nonnegative and possesses positive diagonal entries. According to (25) and (26), ${\mathrm{\Xi }}^{-1}K$ is a stochastic matrix with positive diagonal elements. By Lemma 4, the eigenvalue ${\mathbf{1}}_n$ corresponds to the eigenvector ${\mathbf{1}}_m$, while the other eigenvalues satisfy $\left|{\lambda }_i\right|<1$.

The Jordan canonical form of L associated with the directed graph $\mathcal{G}$ is defined as $J=\mathrm{diag}(J_1,J_2,\dots ,J_r),$ where Jordan block $J_d$ is given by

$$J_d={\left(\begin{array}{cccc}{\lambda }_d& 1& \dots & 0\\ 0& {\lambda }_d& \ddots & ⋮\\ ⋮& \ddots & \ddots & 1\\ 0& 0& 0& {\lambda }_d\end{array}\right)}_{N_d\times N_d},$$

where ${\lambda }_d$ is an eigenvalue of L with algebraic multiplicity $N_d$, $d=1,2,\dots ,r$. Moreover, these multiplicities satisfy $N_1+N_2+\dots +N_r=n+m.$

Let J denote the Jordan canonical form of L, such that $L=PJ{P}^{-1}$. The columns of the nonsingular matrix P comprise the right eigenvectors of L, and the rows of $P^{-1}$ comprise the left eigenvectors. Letting $\xi \left(t\right)=\left(P^{-1}\otimes I_2\right)\zeta \left(t\right)$, the CT game control system (22) is cast to

$$\begin{array}{cc}\hfill \dot{\xi }\left(t\right)& =\left(I_2\otimes P^{-1}\right)\left[\left(\mathrm{\Psi }\otimes A\right)-\left(L\otimes B\right)\right]\zeta \left(t\right)\hfill \\ \hfill & =\left[\left(A\mathrm{\Psi }\otimes P^{-1}\right)-\left(B\otimes J{P}^{-1}\right)\right]\zeta \left(t\right)\hfill \\ \hfill & =\left[\left(A\otimes \mathrm{\Psi }\right)-\left(B\otimes J\right)\right]\xi \left(t\right).\hfill \end{array}$$

(27)

By the system (23), through a similarity transformation, we obtain the DT game control system as

$$\xi \left(t_{k+1}\right)=\left[\left(\mathrm{\Psi }\otimes C\right)-\left(J\otimes D\right)\right]\xi \left(t_k\right).$$

(28)

Lemma 5

([28]). Assume that the directed graph $\mathcal{G}$ contains a directed spanning tree, the CT-DT switching dynamic MAS can achieve consensus if ${lim}_{t\to \infty }∥{\xi }_i\left(t\right)∥=0,$ ${lim}_{k\to \infty }∥{\xi }_i\left(t_k\right)∥=0,$ where $i=2,3,\dots ,n+m$.

We have made the following assumptions.

A1

The graph $\mathcal{G}$ admits a directed spanning forest.

A2

The control gain simultaneously satisfies conditions (29) and (30).

$$\left\{\begin{array}{c}{\displaystyle \frac{{\beta }^2}{\alpha }}>\underset{u_i\in \wedge \left(L\right)}{max}{\displaystyle \frac{{\mathrm{Im}}^2\left(u_i\right)}{\mathrm{Re}\left(u_i\right){\left|u_i\right|}^2}},\hfill \\ {\displaystyle \frac{{\kappa }_i^2}{{\vartheta }_i}}>\underset{{\epsilon }_i\in \wedge \left({\mathrm{\Xi }}^{-1}K\right)}{max}{\displaystyle \frac{\mathrm{Re}\left({\epsilon }_i\right)}{{\mathrm{Im}}^2\left({\epsilon }_i\right)}},\hfill \end{array}\right.$$

(29)

$$\left\{\begin{array}{c}4Re\left(u_i\right)>{\left|u_i\right|}^2\left(2\beta -\alpha \right),\hfill \\ \left(\alpha +\beta \right){\left|u_i\right|}^2\left[\left({\alpha }^2-\alpha \beta -2{\beta }^2\right){\left|u_i\right|}^2+4Re\left(u_i\right)\right]>4{Im}^2\left(u_i\right)\alpha ,\hfill \end{array}\right.$$

(30)

where $u_i$ is the eigenvalue of L, ${ϵ}_i$ is the eigenvalue of the game control matrix ${\mathrm{\Xi }}^{-1}K$.

Theorem 2.

Consensus is achieved in the CT-DT switching MAS (27)–(28) if and only if A1 and A2 are satisfied.

Proof of Theorem 2.

(Sufficiency) Let $\mathrm{\Gamma }=\mathrm{\Psi }\otimes A-J\otimes B$, $\mathrm{\Pi }=\mathrm{\Psi }\otimes C-J\otimes B$, then (27) and (28) could be expressed as $\dot{\xi }\left(t\right)=\mathrm{\Gamma }\xi \left(t\right),$ $\xi \left(t_{k+1}\right)=\mathrm{\Pi }\xi \left(t_k\right).$ Note that $\mathrm{\Gamma }\mathrm{\Pi }=\mathrm{\Pi }\mathrm{\Gamma }$, for any initial state $\xi \left(t_0\right)$, we have

$$\xi \left(t\right)=e^{\mathrm{\Gamma }t}{\mathrm{\Pi }}^k\xi \left(t_0\right).$$

(31)

Since $J=P^{-1}LP$, where P is a nonsingular matrix. Hence, the characteristic polynomial of $\mathrm{\Gamma }$ is

$$\begin{array}{cc}\hfill & det\left(\lambda I_{2(n+m)}-\mathrm{\Gamma }\right)\hfill \\ \hfill =& det\left(\begin{array}{cc}\lambda I_{2n}-I_n\otimes A+J_f\otimes B& {\mathbf{0}}_{2n\times 2m}\\ {\mathbf{0}}_{2m\times 2n}& \lambda I_{2m}-{\mathrm{\Xi }}^{-1}K\otimes A\end{array}\right)\hfill \\ \hfill =& \prod _{i=1}^{n}det\left(\begin{array}{cc}{\lambda }_i& -1\\ u_i\alpha & {\lambda }_i+u_i\beta \end{array}\right)\prod _{j=n+1}^{n+m}det\left(\begin{array}{cc}{\lambda }_j& -{\epsilon }_j\\ 0& {\lambda }_j\end{array}\right)\hfill \\ \hfill =& \prod _{i=1}^{n}det\left({\lambda }_i^2+{\lambda }_i{u}_i\beta +u_i\alpha \right)\prod _{j=n+1}^{n+m}det\left({\lambda }_j^2+{\epsilon }_j\right)\hfill \\ \hfill =& \prod _{i=1}^n{f}_i^c\left(\lambda \right)\prod _{j=n+1}^{n+m}{g}_i^c\left(\lambda \right),\hfill \end{array}$$

(32)

where $f_i^c\left({\lambda }_i\right)={\lambda }_i^2+{\lambda }_i{u}_i\beta +u_i\alpha$, $g_i^c\left({\lambda }_i\right)={\lambda }_j^2+{\epsilon }_j$. Substituting $\lambda =i\varpi$ into $f_i^c\left(\lambda \right)$ and $g_i^c\left(\lambda \right)$, we obtain

$$f_i^c\left(\mathbf{i}\varpi \right)=-{\varpi }^2+\beta \left(Re\left(u_i\right)+\mathbf{i}Im\left(u_i\right)\right)\mathbf{i}\varpi +\alpha \left(Re\left(u_i\right)+\mathbf{i}Im\left(u_i\right)\right)$$

and

$$g_i^c\left(\mathbf{i}\varpi \right)=-{\varpi }^2+\mathrm{Re}\left({\epsilon }_i\right)+\mathbf{i}Im\left({\epsilon }_i\right).$$

The determinant of the block matrix is computed as follows. Since the matrix is block upper triangular, we have

$$det(\lambda I-\mathrm{\Gamma })=det(\lambda I_{2n}-(I_n\otimes A-J_f\otimes B))·det(\lambda I_{2m}-({\mathrm{\Xi }}^{-1}K\otimes A)).$$

For the first term, corresponding to the follower subsystem, we note that $J_f$ is block diagonal (Jordan form of $L_f$), so

$$det(\lambda I_{2n}-(I_n\otimes A-J_f\otimes B))=\prod _{i=1}^{n}det\left(\lambda I_2-\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]+u_i\left[\begin{array}{cc}0& 0\\ \alpha & \beta \end{array}\right]\right),$$

which simplifies to

$$\prod _{i=1}^{n}det\left(\begin{array}{cc}\lambda & -1\\ u_i\alpha & \lambda +u_i\beta \end{array}\right)=\prod _{i=1}^n({\lambda }^2+u_i\beta \lambda +u_i\alpha ).$$

For the second term, corresponding to the leader subsystem under game-based control, we have

$$det(\lambda I_{2m}-({\mathrm{\Xi }}^{-1}K\otimes A))=\prod _{j=n+1}^{n+m}det\left(\lambda I_2-{\epsilon }_j\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\right)=\prod _{j=n+1}^{n+m}det\left(\begin{array}{cc}\lambda & -{\epsilon }_j\\ 0& \lambda \end{array}\right),$$

which gives

$$\prod _{j=n+1}^{n+m}\left({\lambda }^2\right),$$

therefore, the full characteristic polynomial is

$$det(\lambda I-\mathrm{\Gamma })=\prod _{i=1}^n({\lambda }^2+u_i\beta \lambda +u_i\alpha )·\prod _{j=n+1}^{n+m}{\lambda }^2.$$

This confirms that the eigenvalues of $\mathrm{\Gamma }$ are the roots of $f_i^c\left(\lambda \right)={\lambda }^2+u_i\beta \lambda +u_i\alpha$ for $i=1,\dots ,n$, and $\lambda =0$ (with multiplicity $2m$) for the leaders. The stability of the system depends on the Hurwitz stability of $f_i^c\left(\lambda \right)$, which is analyzed in the subsequent steps.

The relevant pairs of the real part and the imaginary part are $m\left(\varpi \right)=-{\varpi }^2+\alpha Re\left(\varpi \right)-\beta Im\left(u_i\right)\varpi$ and $n\left(\varpi \right)=\alpha Im\left(u_i\right)+\beta Re\left(u_i\right)\varpi$, respectively. $f_i^c\left({\lambda }_i\right)$ is Hurwitz stable if and only if the following requirements are met:

• The polynomial $m\left(\varpi \right)$ possesses two distinct real roots, denoted by $m_2>m_1$;
• The crossing condition $m_2>n_1>m_1$ is satisfied, where $n_1$ is the unique root of $n\left(\varpi \right)$;
• $n^{\prime }\left(0\right)m\left(0\right)-n\left(0\right)m^{\prime }\left(0\right)>0$.

The two roots of $m\left(\varpi \right)=0$ are $m_1={\displaystyle \frac{\beta Im\left(u_i\right)-\sqrt{{\beta }^2{Im}^2\left(u_i\right)+4\alpha Re\left(u_i\right)}}{-2}}$ and $m_2={\displaystyle \frac{\beta Im\left(u_i\right)+\sqrt{{\beta }^2{Im}^2\left(u_i\right)+4\alpha Re\left(u_i\right)}}{-2}},$ which satisfy (1). The root of $n\left(\varpi \right)=0$ is $n_1=-{\displaystyle \frac{\alpha Im\left(u_i\right)}{\beta Re\left(u_i\right)}}$, according to condition (2), ${\displaystyle \frac{{\beta }^2}{\alpha }}>{\displaystyle \frac{{\mathrm{Im}}^2\left(u_i\right)}{\mathrm{Re}\left(u_i\right){\left|u_i\right|}^2}}$ is obtained. It can be seen from the expression of $m\left(\varpi \right)$ and $n\left(\varpi \right)$ that $m\left(\begin{array}{c}0\end{array}\right)=\alpha Re\left(\begin{array}{c}{u}_i\end{array}\right)$,$m^{\prime }\left(\begin{array}{c}0\end{array}\right)=-\beta Im\left(\begin{array}{c}{u}_i\end{array}\right)$,$n\left(\begin{array}{c}0\end{array}\right)=\alpha Im\left(\begin{array}{c}{u}_i\end{array}\right)$ and $n^{\prime }\left(0\right)=\beta Re\left(u_i\right)$. According to condition (3), we get $\alpha \beta {\left|u_i\right|}^2>0$. For $g_i^c\left(\mathbf{i}\varpi \right)$, follow the steps above, ${\displaystyle \frac{{\kappa }_i^2}{{\vartheta }_i}}>{\displaystyle \frac{\mathrm{Re}\left({\epsilon }_i\right)}{{\mathrm{Im}}^2\left({\epsilon }_i\right)}}$ is obtained. After organizing, if the condition (29) in Theorem 1 holds, the CT game control system is Hurwitz stable, indicateing all the eigenvalues of $\mathrm{\Gamma }$ have negative real parts.

Similarly, in the DT game control setting, the characteristic polynomial of $\mathrm{\Pi }$ is

$$\begin{array}{cc}\hfill & det\left(\lambda I_{2(n+m)}-\mathrm{\Pi }\right)\hfill \\ \hfill =& det\left(\begin{array}{cc}\lambda I_{2n}-I_n\otimes C+J_f\otimes B& {\mathbf{0}}_{2n\times 2m}\\ {\mathbf{0}}_{2m\times 2n}& \lambda I_{2m}-{\mathrm{\Xi }}^{-1}K\otimes C\end{array}\right)\hfill \\ \hfill =& \prod _{i=1}^{n}det\left(\begin{array}{cc}{\lambda }_i-1& -1\\ u_i\alpha & {\lambda }_i-1+u_i\beta \end{array}\right)\prod _{j=n+1}^{n+m}det\left(\begin{array}{cc}{\lambda }_j-{\epsilon }_j& -{\epsilon }_j\\ 0& {\lambda }_j-{\epsilon }_j\end{array}\right)\hfill \\ \hfill =& \prod _{i=1}^{n}det\left({\lambda }_i^2+\left(u_i\beta -2\right){\lambda }_i+1+u_i\alpha -u_i\beta \right)\prod _{j=n+1}^{n+m}det\left({\lambda }_j^2-2{\lambda }_j{\epsilon }_j+{\epsilon }_j^2\right)\hfill \\ \hfill =& \prod _{i=1}^n{f}_i^d\left({\lambda }_i\right)\prod _{j=n+1}^{n+m}{g}_j^d\left({\lambda }_i\right),\hfill \end{array}$$

(33)

where $f_i^d\left({\lambda }_i\right)={\lambda }_i^2+\left(u_i\beta -2\right){\lambda }_i+1+u_i\alpha -u_i\beta$ and $g_i^d\left({\lambda }_i\right)={\lambda }_j^2-2{\lambda }_j{\epsilon }_j+{\epsilon }_j^2$. However, under DT dynamics, the appropriate stability criterion is Schur stability rather than Hurwitz stability. To this end, bilinear transformations $\lambda ={\displaystyle \frac{s+1}{s-1}}$ is applied. Then we get

$${\overline{f}}_i^d\left(s\right)={\left(s-1\right)}^2{f}_i^d\left({\displaystyle \frac{s+1}{s-1}}\right)=u_i\alpha s^2+2\left(u_i\beta -u_i\alpha \right)s+u_i\alpha -2u_i\beta +4,$$

and

$${\tilde{g}}_j^d\left(s\right)=s^2+{\displaystyle \frac{2s}{1-2{\epsilon }_j}}+{\displaystyle \frac{1+2{\epsilon }_j+{\epsilon }_j^2}{1-2{\epsilon }_j}}.$$

Considering $u_i\alpha \ne 0,1-2{\epsilon }_j\ne 0$, we have

$${\tilde{f}}_i^d\left(s\right)=s^2+2\left({\displaystyle \frac{\beta }{\alpha }}-1\right)s+1-2{\displaystyle \frac{\beta }{\alpha }}+{\displaystyle \frac{4}{u_i\alpha }},$$

and

$${\tilde{g}}_j^d\left(s\right)=s^2+{\displaystyle \frac{2s}{1-2{\epsilon }_j}}+{\displaystyle \frac{1+2{\epsilon }_j+{\epsilon }_j^2}{1-2{\epsilon }_j}}.$$

Hence, Hurwitz stability of ${\tilde{f}}_i^d\left(s\right)$ and ${\tilde{g}}_j^d\left(s\right)$ leads to Schur stability of $f_i^d\left(s\right)$ and $g_j^d\left(s\right)$. The proof of Hurwitz stability is similar to the previous text. According to conditions (a)–(c), we obtain $\left(\begin{array}{c}2\beta -\alpha \end{array}\right)<{\displaystyle \frac{4Re\left(\begin{array}{c}{u}_i\end{array}\right)}{{\left|\begin{array}{c}{u}_i\end{array}\right|}^2}}$, $(\alpha +\beta )|u_i{|}^2\left[\left({\alpha }^2-\alpha \beta -2{\beta }^2\right){\left|u_i\right|}^2+4Re\left(u_i\right)\right]>4{Im}^2\left(u_i\right)\alpha$ and $4Re\left(u_i\right)>{\left|u_i\right|}^2\left(2\beta -\alpha \right)$. Correspondingly, ${\tilde{g}}_j^d\left(s\right)$ is Hurwitz stable if

$$\left\{\begin{array}{c}4{Im}^2\left({\epsilon }_j\right)>\left(4{\left|{\epsilon }_j\right|}^2-1\right)\gamma ,\hfill \\ \gamma \left(1+2Re\left({\epsilon }_j\right)\right)+{\left|{\epsilon }_j\right|}^2{Im}^2\left({\epsilon }_j\right)+2{Im}^2\left({\epsilon }_j\right)>0,\hfill \\ \left(1+2Re\left({\epsilon }_j\right)\right)\left(4Im\left({\epsilon }_j\right)+\gamma \left(1-4{\left|{\epsilon }_j\right|}^2\right)\right)>\left(1-4{\left|{\epsilon }_j\right|}^2\right)\left(4Re\left({\epsilon }_j\right)+7{\left|{\epsilon }_j\right|}^{2}Im\left({\epsilon }_j\right)\right),\hfill \end{array}\right.$$

where $\gamma =2{\left|{\epsilon }_j\right|}^{2}Re\left({\epsilon }_j\right)+4Re\left({\epsilon }_j\right)+5{\left|{\epsilon }_j\right|}^2+1$. After calculating, if the condition (30) in Theorem 1 is satisfied, the DT game control system is Schur stable, which means all eigenvalues of $\mathrm{\Pi }$ are within the unit circle.

Therefore, when A1 and A2 in Theorem 2 are satisfied, system (31) meets Definition 2, which means the CT-DT switching dynamic MAS can achieve consensus.

(Necessity) Suppose the directed communication graph $\mathcal{G}$ does not contain a directed spanning forest, meaning a minimum of one follower cannot receive information from the leader. This implies that the state of that follower is not influenced by the leader, and thus, the system cannot achieve consensus. If the CT-DT switching dynamic MAS can achieve consensus under arbitrary switching, Definition 2 must be satisfied, so that $f_i^c$, $g_i^c$ is necessarily Hurwitz stable and $f_i^d$, $g_i^d$ is Schur stable. This can suggest the necessity. □

Remark 2.

The system operates in two distinct modes—CT game control and DT game control—between which it switches arbitrarily. Only one mode is active at any time.

This theorem provides the necessary and sufficient conditions for achieving consensus in the Continuous–Discrete switching multi-agent system. Condition A1 requires the communication graph to contain a directed spanning forest, which ensures that information can flow from the leaders to all followers. Condition A2 imposes constraints on the control gains $\alpha$ and $\beta$, guaranteeing system stability under arbitrary switching dynamics. Collectively, these conditions ensure that all agents’ states converge to a common value, even as the system switches arbitrarily between continuous-time and discrete-time dynamics.

4. Control Input with Sampled Data

To provide a clearer and more intuitive overview of the proposed control system architecture, a block diagram illustrating the interaction among the game-based decision-making module, the unified sampled-data controller, and the switching multi-agent system is presented in Figure 1.

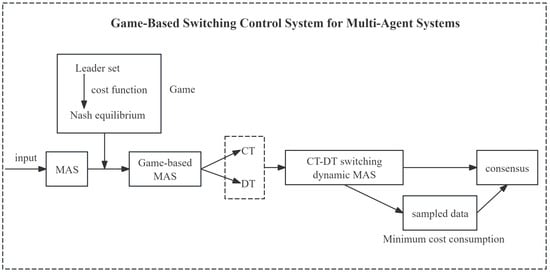
Figure 1. Game-Based Switching Control System for Multi-Agent Systems.

We use the same control protocol for systems (1) and (3), the sampled data protocol is designed as

$$u_i\left(·\right)=\alpha \sum _{i\in N_i}{a}_{ij}\left[x_j\left(t_k\right)-x_i\left(t_k\right)\right]+\beta \sum _{j\in N_i}{a}_{ij}\left[v_j\left(t_k\right)-v_i\left(t_k\right)\right].$$

(34)

Under this protocol, the system (1) is updated to

$$\dot{\phi }\left(t\right)=\left(I_{n+m}\otimes A\right)\phi \left(t\right)-\left(L\otimes B\right)\phi \left(t_k\right),$$

(35)

where $\phi \left(\begin{array}{c}t\end{array}\right)={\left(\begin{array}{c}{\phi }_1^T\left(\begin{array}{c}t\end{array}\right),{\phi }_2^T\left(\begin{array}{c}t\end{array}\right),...,{\phi }_{n+m}^T\left(\begin{array}{c}t\end{array}\right)\end{array}\right)}^T$, ${\phi }_i\left(\begin{array}{c}t\end{array}\right)={\left(\begin{array}{c}{x}_i\left(\begin{array}{c}t\end{array}\right),v_i\left(\begin{array}{c}t\end{array}\right)\end{array}\right)}^T$. Under the influence of the game framework, the CT system is updated to the CT game control system

$$\dot{\phi }\left(t\right)=\left(A\otimes \mathrm{\Psi }\right)\phi \left(t\right)-\left(B\otimes L\right)\phi \left(t_k\right).$$

(36)

Let $\varphi \left(t\right)=\left(P^{-1}\otimes I_2\right)\phi \left(t\right)$, then (36) could be written as

$$\dot{\varphi }\left(t\right)=\left(P^{-1}\otimes I_2\right)\dot{\phi }\left(t\right)=\left(\mathrm{\Psi }\otimes A\right)\varphi \left(t\right)-\left(J\otimes B\right)\varphi \left(t_k\right).$$

(37)

For DT game control systems, by similar transformations, we have

$$\varphi \left(t_{k+1}\right)=\left(\begin{array}{c}\mathrm{\Psi }\otimes C\end{array}\right)\varphi \left(\begin{array}{c}t\end{array}\right)-\left(\begin{array}{c}J\otimes B\end{array}\right)\varphi \left(\begin{array}{c}{t}_k\end{array}\right),$$

(38)

where $C=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$.

We have made the following assumptions.

B1

$\mathcal{G}$ contains a directed spanning forest.

B2

The control gain of the system simultaneously satisfies (39) and (40).

$$\left\{\begin{array}{c}{\displaystyle \frac{2\left(1-c_{ij}\right)\beta +\alpha }{\alpha c_{ij}}}>h,\hfill \\ {\left(1-c_{ij}^2-c_{ij}{\displaystyle \frac{\mathrm{Re}\left(u_i\right)}{{\left|u_i\right|}^2}}h\left(\beta +{\displaystyle \frac{\alpha }{2}}h\right)\right)}^2-{\left(c_{ij}+1\right)}^3\left(\beta +{\displaystyle \frac{\alpha }{2}}h\right){\displaystyle \frac{\mathrm{Im}\left(u_i\right)}{{\left|u_i\right|}^2}}h>0,\hfill \end{array}\right.$$

(39)

$$\left\{\begin{array}{c}4Re\left(u_i\right)>{\left|u_i\right|}^2\left(2\beta -\alpha \right),\hfill \\ \left(\alpha +\beta \right){\left|u_i\right|}^2\left[\left({\alpha }^2-\alpha \beta -2{\beta }^2\right){\left|u_i\right|}^2+4Re\left(u_i\right)\right]>4{Im}^2\left(u_i\right)\alpha .\hfill \end{array}\right.$$

(40)

Theorem 3.

The CT-DT switching MAS (37)–(38) achieves consensus if and only if conditions B1 and B2 are satisfied.

• The proof of Theorem 3 is given in Appendix A.

Remark 3.

This protocol implements a unified sampled-data control framework applicable to both CT and DT systems. During system switching, the controller avoids frequent switching between two control strategies, it only needs to adjust the dynamic behavior of the system.

This theorem introduces a unified sampled-data control protocol applicable to both CT and DT subsystems. Its primary advantage lies in avoiding frequent controller switching during system mode changes, thereby simplifying implementation. Conditions B1 and B2 pertain to the graph structure and the constraints on control gains and the sampling period h, respectively. These conditions ensure the system converges to consensus even with sampled information. This control strategy is particularly suitable for practical hybrid systems that require a unified control framework.

5. Simulations

Consider a directed graph consisting of 7 agents, where R1, R2, R3 are leaders and F1, F2, F3, F4 are followers, as shown in Figure 2. Clearly, it contains a spanning forest.

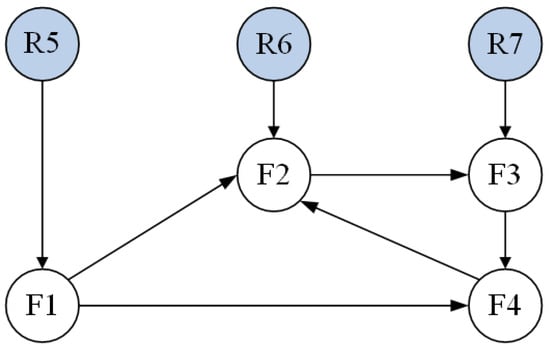
Figure 2. Directed graph of CT-DT switching MAS.

The Laplacian matrix L is constructed from the directed graph topology shown in Figure 1. For a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, the Laplacian matrix $L=\left[l_{ij}\right]$ is defined by

$$l_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{k\in N_i}}{a}_{ik},\hfill & \mathrm{if}i=j,\hfill \\ -a_{ij},\hfill & \mathrm{if}i\ne j,\hfill \end{array}\right.$$

where $a_{ij}>0$ if there exists a directed edge from agent j to agent i, otherwise $a_{ij}=0$. Based on the communication topology in Figure 1, the adjacency matrix $\mathcal{A}$ is first determined. Subsequently, the Laplacian matrix L is computed as follows

$$L=\left[\begin{array}{ccccccc}1& 0& 0& 0& -1& 0& 0\\ -1& 3& 0& -1& 0& -1& 0\\ 0& -1& 2& 0& 0& 0& -1\\ -1& 0& -1& 2& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right],$$

whose eigenvalue are $u_1=u_2=u_3=0$, $u_4=1$, $u_5=1.2451$, $u_{6,7}=2.8774\pm 0.7449i$. The matrix is partitioned according to the leader–follower structure, where the first four rows and columns correspond to followers F1–F4, and the last three rows and columns correspond to leaders R1–R3. Then the eigenvalues of ${\mathrm{\Xi }}^{-1}K$ could be calculated as ${ϵ}_1=1$, ${ϵ}_2=0.6308$, ${ϵ}_3=0.1692$. The initial state of each agent is specified as $x\left(t_0\right)={\left[\begin{array}{c}-24,-18,30,0,24,-6,12\end{array}\right]}^T$ and $v\left(t_0\right)={\left[\begin{array}{c}-10,0,12,22,-8,20,-16\end{array}\right]}^T$, The initial position vector and velocity vector are intentionally set to be dispersed in both magnitude and direction. This setup ensures that the system starts from a challenging configuration, thereby effectively demonstrating the convergence capability of the control protocols. The following example is completed to verify the correctness of Theorems 2 and 3.

Example 1.

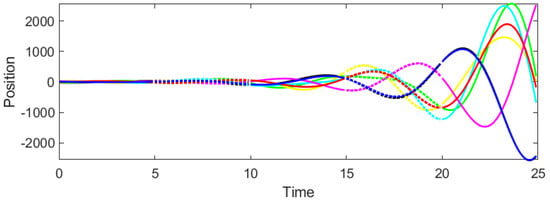
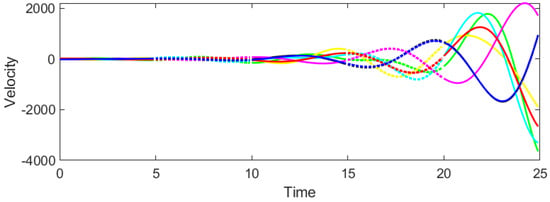
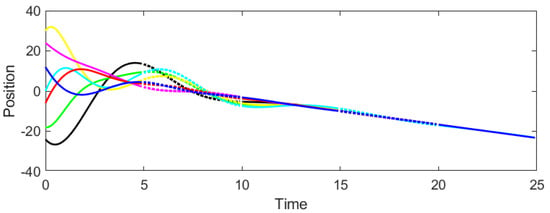
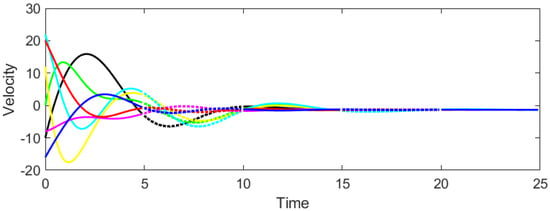
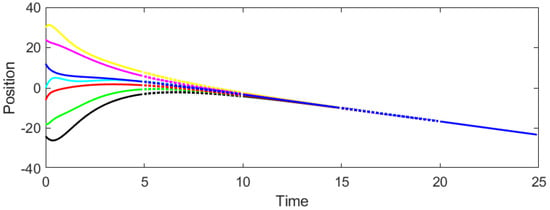
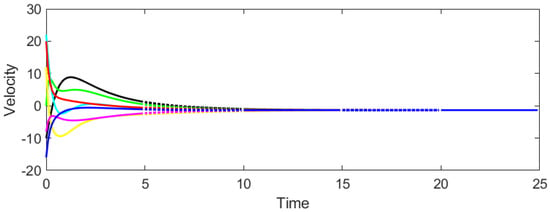
Consider the CT-DT switching system (1)–(4) under protocol (31) and stochastic switching, with $\alpha =0.5$. According to Theorem 2, the admissible interval of β is derived as $0.1039<\beta <2.15$. Then we select $\beta =0.05$ and $\beta =0.6$ to test whether consensus could be achieved. It can be seen from Figure 3 and Figure 4 that when $\beta =0.05$, the system cannot reach consensus. Instead, when $\beta =0.6$, Figure 5 and Figure 6 signify that the system achieves consensus, which verifies the precision of Theorem 2.

Figure 3. Response of agent positions for $\alpha =0.5$, $\beta =0.05$.

Figure 4. Evolution of agent velocities for $\alpha =0.5$, $\beta =0.05$.

Figure 5. Response of agent positions for $\alpha =0.5$, $\beta =0.6$.

Figure 6. Evolution of agent velocities for $\alpha =0.5$, $\beta =0.6$.

As shown in Figure 3 and Figure 4, the system fails to achieve consensus. The positions and velocities of the agents diverge over time, indicating instability. This aligns with Theorem 2, as $\beta =0.05$ violates the gain condition (29), leading to the loss of Hurwitz/Schur stability in the error dynamics.

Figure 5 and Figure 6 demonstrate that all agents successfully achieve consensus. The position and velocity trajectories converge to common values, confirming the theoretical prediction. The convergence is smooth and occurs within approximately 15 s, illustrating the effectiveness of the proposed game-based control strategy under switching dynamics.

Example 2.

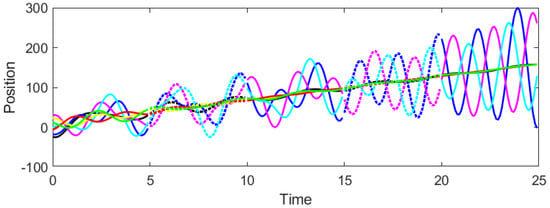
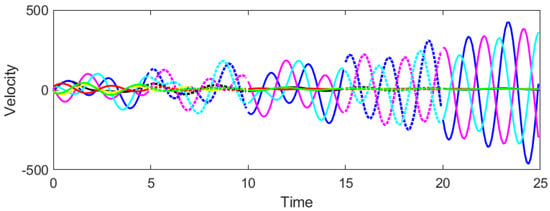
Under protocol (34) with stochastic switching, the CT-DT system (1)–(4) is analyzed with the parameter value set to $\alpha =0.33$. From Theorem 3, we get the admissible interval β is $0.1313<\beta <1.756$. Afterwards we set $\beta =0.5$ to determine the appropriate range for h with 0 < h < 1.143. We select $h=0.8$ and $h=1.5$. Figure 7 and Figure 8 demonstrate that the system achieves consensus when $h=0.8$. In contrast, Figure 9 and Figure 10 show that consensus is not attained when $h=1.5$, thereby confirming the validity of Theorem 3.

Figure 7. Response of agent positions for $\alpha =0.33$, $\beta =0.5$ and $h=0.8$.

Figure 8. Evolution of agent velocities for $\alpha =0.33$, $\beta =0.5$ and $h=0.8$.

Figure 9. Response of agent positions for $\alpha =0.33$, $\beta =0.5$ and $h=1.5$.

Figure 10. Evolution of agent velocities for $\alpha =0.33$, $\beta =0.5$ and $h=1.5$.

Figure 7 and Figure 8 show that the system achieves consensus. The trajectories converge steadily, validating the sampled-data control approach. The smaller sampling period ensures sufficient data updates to maintain stability under switching.

Figure 9 and Figure 10 reveal that consensus is not attained. The system exhibits oscillatory and divergent behavior, consistent with the violation of the maximum allowable sampling period This underscores the critical role of the sampling period in $h_{max}=1.143$ maintaining system stability under sampled-data control.

Remark 4.

The initial states selected in the simulations are representative of a general case with significant initial disagreement. In practice, the proposed control strategies are robust to variations in initial conditions, as the consensus achievement is structurally ensured by the directed spanning forest in the communication graph and the designed game-based control laws.

To address the practical contribution and performance of the proposed method, we provide a comparative analysis based on the convergence behavior observed in our simulations. While the primary goal of this paper is to establish the theoretical foundation and prove consensus achievement under the game-theoretic framework, the simulation results inherently demonstrate favorable performance characteristics.

This convergence performance can be favorably compared with existing non-game-theoretic approaches for switching systems. Compared to the classic consensus protocols for switched systems in [25], which often exhibit slower convergence due to passive reaction to neighborhood errors, our game-based approach enables agents (especially leaders) to proactively adjust their strategies by anticipating others’ actions. This strategic behavior, guided by the cost functions, leads to a more coordinated and efficient path to consensus, as reflected in the swift settling time in our results.Compared to the sampled-data control method in [27], our unified protocol (Example 2) not only avoids frequent controller switching but also, as seen in Figure 7 and Figure 8, maintains a fast convergence rate. This suggests that the integration of the game-theoretic decision-making process enhances the system’s coordination efficiency even under a unified control structure.

6. Conclusions and Future Work

In this paper, the leader–follower consensus problem in second-order MASs with switching dynamics, composed of both DT and CT subsystems, is investigated. The competitive interactions among multiple leaders are modeled as a multi-player game, with the competition mechanism characterized by the designed game rules. A cost function is assigned to each player, who aims to minimize their own cost for global optimization, and the unique NE of the game is derived. Based on this, two types of linear control protocols are proposed to achieve consensus. The first protocol employs CT control for CT subsystems and DT control for DT subsystems, leading to sufficient and necessary conditions on the network topology and coupling gain for consensus. The second protocol adopts a unified sampled-data control algorithm for both subsystems, with corresponding sufficient and necessary conditions established. Numerical simulations under various scenarios validate the effectiveness of both control strategies in dynamic switching topologies. Future research will focus on consensus control in switching dynamical systems with constraints on sampled position data or communication delays.