A Vectorization Approach to Solving and Controlling Fractional Delay Differential Sylvester Systems

Abstract

This paper addresses the solvability and controllability of fractional delay differential Sylvester matrix equations with non-permutable coefficient matrices. By applying a vectorization approach and Kronecker product algebra, we transform the matrix-valued problem into an equivalent vector system, enabling the derivation of explicit solution representations using a delayed perturbation of two-parameter Mittag-Leffler-type matrix functions. We establish necessary and sufficient conditions for controllability via a fractional delay Gramian matrix, providing a computationally verifiable criterion that requires no commutativity assumptions. The theoretical results are validated through numerical examples, demonstrating effectiveness in noncommutative scenarios where classical methods fail.

1. Introduction

Fractional delay differential equations (FDDEs) provide a framework for modeling a broad spectrum of mechanical and technological phenomena. Their applicability extends to numerous scientific and technical disciplines, such as diffusion processes, control theory, and epidemiological and financial modeling; see [1,2,3,4,5,6,7,8] and references therein. These equations naturally arise in systems where hereditary properties and fractional-order dynamics coexist with matrix-valued interactions.

In the realm of fractional delay differential equations, substantial progress has been made in developing solution representations using various techniques, including the method of steps and delayed matrix functions [9,10,11,12,13,14,15]. These developments have facilitated stability analysis, iterative learning control, and relative controllability investigations; see, for example, [9,16,17,18,19].

Parallel to these theoretical advances, control theory for fractional-order systems has found diverse applications spanning vibration control in mechanical systems [20], stability analysis of power networks [21,22], fractional-order epidemic models [23], and robust control design for time-delay systems [24,25,26]. Moreover, while the controllability of Sylvester-type systems has been explored in the absence of delays [27,28,29,30], and for fractional or impulsive variants [31,32,33], recent work by Appa Rao and Prasad [28] studied the controllability and observability of Sylvester matrix dynamical systems on time scales. Sadek et al. [32] discussed the controllability and observability of the fractional differential Sylvester matrix equations in the absence of delays of the form

$$\begin{array}{c}\left({}^{C}D_{0^{+}}^{\alpha }X\right)\left(\vartheta \right)=\mathbb{A} X\left(\vartheta \right)+X\left(\vartheta \right) \mathbb{B}+\mathbb{E}U\left(\vartheta \right)\mathbb{F}, \mathrm{for} \vartheta \in \mathit{\Delta }:=\left[0,\infty \right),\\ X\left(0\right)=X_0, \end{array}$$

(1)

with $\mathbb{B}=\mathit{\Theta }$ and $\mathbb{F}=\mathbb{I}$, using the conformable fractional derivative, where $\mathbb{I}$ is the identity matrix, the operator ${}^{C}D_{0^{+}}^{\alpha }$ signifies the Caputo fractional derivative of order $\alpha$ and $0<\alpha \le 1$ and the lower limit is taken to be zero; $X={\left(X_1,X_2,\dots ,X_n\right)}^{\mathrm{T}}:\left[0,{\vartheta }_f\right)\to {\mathbb{R}}^{n\times p}$ is a solution satisfying (1). For every $\vartheta \in \mathit{\Delta }$, $U\left(\vartheta \right)\in {\mathbb{R}}^{m_1\times m_2}$ represents the control input, $\mathbb{A}$, $\mathbb{B}$, $\mathbb{E}$, and $\mathbb{F}$ are $n\times n$, $p\times p$, $n\times m_1$, and $m_2\times p$ constant real nonzero matrices, respectively. Cuchta et al. [34] investigated linear quadratic tracking problems. Additional theoretical and application aspects are explored in studies by Zhang et al. [20], Biswal et al. [21], Das and Samanta [23], Bouazza et al. [24], Boudjerida and Seba [25], Fiuzy and Shamaghdari [26], and Singh and Pandey [31]. In 2025, Sadek [33] studied the exact solutions and controllability of (1).

However, despite these advances, the closed-form solutions and controllability analysis of fractional delay differential Sylvester matrix equations with distributed delays and control inputs under non-permutable matrix coefficients remain largely unexplored.

Therefore, this paper bridges this theoretical gap by establishing a comprehensive framework for analyzing the representation of solutions and controllability of the non-homogeneous linear fractional delay differential Sylvester matrix equation (FDDSE) of the form

$$\begin{array}{ccc}\hfill \left({}^{C}D_{0^{+}}^{\alpha }X\right)\left(\vartheta \right)=& \mathbb{A} X\left(\vartheta \right)+X\left(\vartheta \right)\hfill & \hfill \mathbb{B}+\mathbb{S} X\left(\vartheta -\sigma \right)+X\left(\vartheta -\sigma \right) \mathbb{J}\hfill \\ & +\mathbb{E}U\left(\vartheta \right)\mathbb{F},\hfill & \hfill \mathrm{for} \vartheta \in \mathit{\Delta }:=\left[0,{\vartheta }_f\right],\hfill \\ \hfill X\left(\vartheta \right)=& \mathit{\Phi }\left(\vartheta \right),\hfill & \hfill \mathrm{for} \vartheta \in [-\sigma ,0],\hfill \end{array}$$

(2)

where the operator ${}^{C}D_{0^{+}}^{\alpha }$ signifies the Caputo fractional derivative of order $\alpha$, where $0<\alpha \le 1$, and the lower limit is taken to be zero, $\vartheta$ is the independent variable, $\sigma$ is a positive constant delay, $X={\left(X_1,X_2,\dots ,X_n\right)}^{\mathrm{T}}:\left[-\sigma ,{\vartheta }_f\right)\to {\mathbb{R}}^{n\times p}$ is a solution satisfying (2) for every $\vartheta \in \mathit{\Delta }$, $U\left(\vartheta \right)\in {\mathbb{R}}^{m_1\times m_2}$ represents the control input, $\mathbb{A}$, $\mathbb{B}$, $\mathbb{S}$, $\mathbb{J}$, $\mathbb{E}$, and $\mathbb{F}$ are $n\times n$, $p\times p$, $n\times n$, $p\times p$, $n\times m_1$, and $m_2\times p$ constant real nonzero matrices, respectively, and the initial condition is provided by the continuous matrix function $\mathit{\Phi }:\left[-\sigma ,0\right)\to {\mathbb{R}}^{n\times p}$, which is standard and ensures the well-posedness of the delay system by supplying the complete history required for the solution to evolve forward in time $\vartheta$.

The presence of delay terms $\mathbb{S}$ $X\left(\vartheta -\sigma \right)$ and $X\left(\vartheta -\sigma \right)$$\mathbb{J}$ introduces infinite-dimensional dynamics, rendering classical Kalman-type rank conditions insufficient and necessitating novel functional-analytic or operator-theoretic approaches [35,36,37]. Sylvester-type systems of the form (2) arise naturally in the modeling of coupled and multi-agent systems. For instance, they can describe the dynamics of networks where the state of each agent is a matrix (e.g., a covariance matrix in estimation problems or a stress tensor in continuum mechanics), and the coupling between agents involves both instantaneous ($\mathbb{A}X\left(\vartheta \right)+X\left(\vartheta \right)\mathbb{B}$) and delayed ($\mathbb{S}X(\vartheta -\sigma )+X(\vartheta -\sigma )\mathbb{J}$) interactions. The fractional derivative operator ${}^{C}D_{0^{+}}^{\alpha }$ captures sub-diffusive processes or memory effects in the material or network dynamics. The control term $\mathbb{E}U\left(\vartheta \right)\mathbb{F}$ allows for actuation that can be applied through specific input channels, making the framework highly relevant for control design in complex, interconnected systems with memory, such as large-scale power grids, multi-robot formations, or chemical reaction networks. Furthermore, the core analytical challenge in solving System (2) stems from its matrix-valued nature and the non-commutativity of its coefficients, which prevents the direct application of standard scalar or vector solution techniques. To overcome this, we employ a vectorization approach coupled with Kronecker product algebra. This methodology is uniquely powerful for several reasons: (i) It systematically transforms the complex matrix-valued differential equation into an equivalent, higher-dimensional vector system, which is structurally simpler to analyze. (ii) The Kronecker product formalism elegantly handles the mixed-multiplication terms (for example, $\mathbb{A} X\left(\vartheta \right), X\left(\vartheta \right) \mathbb{B},$ $\mathbb{S} X\left(\vartheta -\sigma \right),$ and $X\left(\vartheta -\sigma \right) \mathbb{J}$) that are intrinsic to the Sylvester structure, converting them into standard linear algebraic operations. (iii) This approach allows us to leverage the well-established theory of fractional delay differential vector equations, enabling the derivation of explicit solution representations without imposing restrictive commutativity conditions on the system matrices, a limitation prevalent in alternative methods.

This paper aims to bridge this theoretical gap by establishing the following:

(i)

Explicit representation formulas for the solution of (2) under both permutable and non-permutable assumptions on the coefficient matrices, utilizing a delayed perturbation of a two-parameter Mittag-Leffler-type matrix function adapted to the Sylvester structure, and generalizing and improving the corresponding results in [38].

(ii)

Necessary and sufficient conditions for the controllability of (2), formulated in terms of the system matrices $\mathbb{A}$, $\mathbb{B}$, $\mathbb{S}$, $\mathbb{J}$, $\mathbb{E}$, and $\mathbb{F}$, and the delay $\sigma$, without requiring commutativity, generalizing the corresponding results in [33].

(iii)

A constructive methodology based on Kronecker product transformations, delayed matrix function expansions, and vectorization techniques, enabling both theoretical analysis and numerical implementation.

(iv)

The derived results not only improve and generalize the existing literature on scalar and vector delay systems but also provide foundational tools for the control and stabilization of large-scale matrix dynamical systems arising in multi-agent networks, tensor-based models, and coupled PDE-ODE systems with memory.

To provide a clear and structured overview of the methodological framework developed in this paper, we present a systematic block diagram in Figure 1.

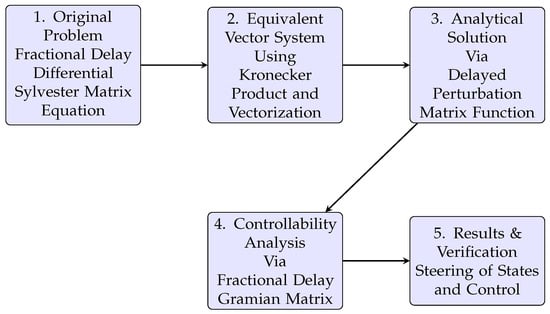
Figure 1. A schematic overview of the proposed methodology for solving and analyzing the controllability of fractional delay differential Sylvester matrix equations.

The remainder of this paper is organized as follows: In Section 2, we introduce the necessary notation and preliminary results. In Section 3, we derive the explicit solution representation for (2). In Section 4, we establish controllability criteria. Finally, we provide an illustrative example.

2. Preliminaries

In this section, we present some properties and rules for Kronecker products, the definition of the $\mathrm{Vec}$ operator, and the basic result related to the delayed perturbation of two-parameter Mittag-Leffler-type matrix function.

Definition 1

([4]). We recall the definition of the two-parameter Mittag-Leffler-type function:

$${\mathcal{E}}_{\alpha ,\gamma }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathit{\Gamma }(\alpha k+\gamma )}}, \mathit{for} \alpha >0, \gamma >0, z\in \mathbb{C}.$$

Of particular importance is the case $\gamma =1$, which reduces to the standard Mittag- Leffler function:

$${\mathcal{E}}_{\alpha }\left(z\right):={\mathcal{E}}_{\alpha ,1}\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathit{\Gamma }(\alpha k+1)}}.$$

Definition 2

([4]). Let $\tau :[-\sigma ,\infty )\to {\mathbb{R}}^n$ be a function. Its Caputo fractional derivative of order $\alpha \in (0 ,1)$ is given as

$$\left({}^{C}D_{0^{+}}^{\alpha }\tau \right)\left(\vartheta \right)={\displaystyle \frac{1}{\mathit{\Gamma }(1-\alpha )}}{\int }_0^{\vartheta }{(\vartheta -\xi )}^{-\alpha }{\tau }^{\prime }\left(\xi \right) \mathrm{d}\xi , \mathit{for} \vartheta >0.$$

Definition 3

([39]). Let $\mathbb{O}=\left[o_{ij}\right]\in {\mathbb{R}}^{m\times n}$ and $\mathbb{H}\in {\mathbb{R}}^{p\times q}$; then the Kronecker product of $\mathbb{O}$ and $\mathbb{H}$ written $\mathbb{O}\otimes \mathbb{H}$ is defined to be the matrix

$$\mathbb{O}\otimes \mathbb{H}=\left[\begin{array}{cccc}{o}_{11}\mathbb{H}& o_{12}\mathbb{H}& \cdots & o_{1n}\mathbb{H}\\ o_{21}\mathbb{H}& o_{22}\mathbb{H}& \cdots & o_{2n}\mathbb{H}\\ ⋮& ⋮& \ddots & ⋮\\ o_{m1}\mathbb{H}& o_{m2}\mathbb{H}& \cdots & o_{mn}\mathbb{H}\end{array}\right],$$

and is an $mp\times nq$ matrix.

Definition 4

([39]). Let $\mathbb{Z}=\left[Z_{ij}\right]\in {\mathbb{R}}^{n\times s}$. The vector operator $\mathrm{Vec}\left(\mathbb{Z}\right)$ is defined as

$$\mathrm{Vec}\left(\mathbb{Z}\right)={[Z_{11},Z_{21},\dots ,Z_{n1},\dots ,Z_{1s},Z_{2s},\dots ,Z_{ns}]}^T\in {\mathbb{R}}^{ns}.$$

Furthermore, we have the following properties of the Kronecker product and vector operator:

1.

${(\mathbb{A}\otimes \mathbb{B})}^{\mathrm{T}}={\mathbb{A}}^{\mathrm{T}}\otimes {\mathbb{B}}^{\mathrm{T}}$;

2.

$(\mathbb{A}\otimes \mathbb{B})(\mathbb{C}\otimes \mathbb{D})=(\mathbb{AC}\otimes \mathbb{BD})$;

3.

$\mathrm{Vec}\left(\mathbb{AB}\right)=({\mathbb{B}}^T\otimes \mathbb{A})\mathrm{Vec}\left(\mathbb{Y}\right)$.

Definition 5

([15]). Let $\mathbb{C}$ and $\mathbb{W}$ be $n\times n$ constant real nonzero matrices. We introduce the determining delay matrix equation for ${\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(k;s)\in {\mathbb{R}}^{n\times n}$ of the form

$${\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(k+1;s)=\mathbb{C} {\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(k;s)+\mathbb{W} {\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(k;s-\sigma ),$$

such that

$${\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(0;s)={\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(k;-\sigma )=\mathit{\Theta }, {\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(1;0)={\mathbb{I}}_n,$$

where $k=1$, 2, …, and $s=0$, σ, $2\omega$, ….

Definition 6

([15]). The delayed perturbation of a two-parameter Mittag-Leffler-type matrix function ${\mathcal{F}}_{\sigma ,\alpha ,\beta }^{\mathbb{C},\mathbb{W}}$ is defined as follows

$${\mathcal{F}}_{\sigma ,\alpha ,\beta }^{\mathbb{C},\mathbb{W}}\left(\vartheta \right):=\left\{\begin{array}{cc}\mathit{\Theta },& -\sigma \le \vartheta <0,\hfill \\ {\mathbb{I}}_n,& \vartheta =0,\hfill \\ {\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^{p-1}}{\displaystyle \frac{{\left(\vartheta -j\sigma \right)}^{i\alpha +\beta -1}}{\mathit{\Gamma }\left(i\alpha +\beta \right)}}{\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}\left(i+1;j\sigma \right),& (p-1)\sigma <\vartheta \le p\sigma .\hfill \end{array}\right.$$

3. Exact Solutions of a Fractional Delay Differential Matrix Equation

In this section, we derive the representation of a solution of problem (2). The following theorem shows an equivalence between the fractional delay differential Sylvester matrix Equation (2) for size $n\times p$ and the fractional delay differential system Equation (3) for size $np\times 1$.

Theorem 1.

Assume that $\mathbb{A}$, $\mathbb{B}$, $\mathbb{S}$, $\mathbb{J}$ are non-permutable $n\times n$, $p\times p$, $n\times n$, $p\times p$ constant real nonzero matrices, respectively. Let $\mathbb{X}\left(\vartheta \right)=\mathrm{Vec}\left(X\left(\vartheta \right)\right)$, $\mathbb{U}\left(\vartheta \right)=\mathrm{Vec}\left(U\left(\vartheta \right)\right)$, and $\mathit{\Psi }\left(\vartheta \right)=\mathrm{Vec}\left(\mathit{\Phi }\left(\vartheta \right)\right)$. Then the fractional delay differential Sylvester matrix Equation (2) is equivalent to the system

$$\begin{array}{cc}\hfill \left({}^{C}D_{0^{+}}^{\alpha }\mathbb{X}\right)\left(\vartheta \right)=& \mathbb{C} \mathbb{X}\left(\vartheta \right)+\mathbb{W} \mathbb{X}\left(\vartheta -\sigma \right)+\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(\vartheta \right), \mathit{for} \vartheta \in \left[0,\infty \right),\hfill \\ & \mathbb{X}\left(\vartheta \right)=\mathit{\Psi }\left(\vartheta \right), \mathit{for} \vartheta \in \left[-\sigma ,0\right],\hfill \end{array}$$

(3)

where $\mathbb{C}=\left({\mathbb{B}}^{\mathrm{T}}\otimes {\mathbb{I}}_n\right)+\left({\mathbb{I}}_p\otimes \mathbb{A}\right)$, $\mathbb{W}=\left({\mathbb{J}}^{\mathrm{T}}\otimes {\mathbb{I}}_n\right)+\left({\mathbb{I}}_p\otimes \mathbb{S}\right)$, and ${\mathbb{I}}_n$ is the identity matrix.

Proof. 

We apply the $\mathrm{Vec}$ operator to the Equation (2), and using the above properties of the Kronecker product, we have

$$\begin{array}{ccc}\hfill \left({}^{C}D_{0^{+}}^{\alpha }\mathbb{X}\right)\left(\vartheta \right)& =\hfill & \left[\left({\mathbb{B}}^{\mathrm{T}}\otimes {\mathbb{I}}_n\right)+\left({\mathbb{I}}_p\otimes \mathbb{A}\right)\right]\mathrm{Vec}\left(X\left(\vartheta \right)\right)\hfill \\ & & +\left[\left({\mathbb{J}}^{\mathrm{T}}\otimes {\mathbb{I}}_n\right)+\left({\mathbb{I}}_p\otimes \mathbb{S}\right)\right]\mathrm{Vec}\left(X\left(\vartheta -\sigma \right)\right)+\mathrm{Vec}\left(\mathbb{E}U\left(\vartheta \right)\mathbb{F}\right)\hfill \\ & =\hfill & \mathbb{C} \mathbb{X}\left(\vartheta \right)+\mathbb{W} \mathbb{X}\left(\vartheta -\sigma \right)+\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(\vartheta \right),\hfill \end{array}$$

and

$$\mathrm{Vec}\left(X\left(\vartheta \right)\right)=\mathrm{Vec}\left(\mathit{\Phi }\left(\vartheta \right)\right)=\mathit{\Psi }\left(\vartheta \right).$$

This completes the proof. □

Theorem 2.

The unique solution of (3) with the initial condition $\mathbb{X}\left(\vartheta \right)=\mathit{\Psi }\left(\vartheta \right)$ is

$$\begin{array}{cc}\hfill \mathbb{X}\left(\vartheta \right)& ={\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathbb{W}}(\vartheta +\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}(\vartheta -s)\left[\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s\hfill \\ \hfill & +{\int }_0^{\vartheta }{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}(\vartheta -s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(s\right)\mathrm{d}s.\hfill \end{array}$$

(4)

Proof. 

The proof of Formula (4) is similar to the proof of Corollary 1 in [15]. □

Corollary 1.

Let $\mathbb{A}$, $\mathbb{B}$, $\mathbb{S}$, $\mathbb{J}$ be permutable $n\times n$, $p\times p$, $n\times n$, $p\times p$ constant real non-zero matrices, respectively. Then the unique solution of (3) with the initial condition $\mathbb{X}\left(\vartheta \right)=\mathit{\Psi }\left(\vartheta \right)$ is

$$\begin{array}{cc}\hfill \mathbb{X}\left(\vartheta \right)& ={\mathcal{R}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathbb{W}}(\vartheta +\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{R}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}(\vartheta -s)\left[\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s\hfill \\ \hfill & +{\int }_0^{\vartheta }{\mathcal{R}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}(\vartheta -s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(s\right)\mathrm{d}s,\hfill \end{array}$$

where

$${\mathcal{R}}_{\sigma ,\alpha ,\beta }^{\mathbb{C},\mathbb{W}}\left(\vartheta \right):=\left\{\begin{array}{cc}\mathit{\Theta },& -\sigma \le \vartheta <0,\hfill \\ {\mathbb{I}}_n,& \vartheta =0,\hfill \\ {\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{j=0}^{p-1}}{\displaystyle \frac{{\left(\vartheta -j\sigma \right)}^{i\alpha +\beta -1}}{\mathit{\Gamma }\left(i\alpha +\beta \right)}}\left({\displaystyle \genfrac{}{}{0pt}{}{i}{j}}\right){\mathbb{C}}^{i-j}{\mathbb{W}}^j,& (p-1)\sigma <\vartheta \le p\omega .\hfill \end{array}\right.$$

Corollary 2.

Let $\mathbb{A}=\mathbb{B}=\mathit{\Theta }$, which leads to $\mathbb{C}=\mathit{\Theta }$ in (3). Suppose that $\mathbb{S}$ and $\mathbb{J}$ are non-permutable $n\times n$ and $p\times p$ constant real non-zero matrices, respectively. Then the solution $\mathbb{X}\left(\vartheta \right)$ of (3) can be expressed as

$$\begin{array}{cc}\hfill \mathbb{X}\left(\vartheta \right)& ={\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathit{\Theta },\mathbb{W}}(\vartheta +\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathit{\Theta },\mathbb{W}}(\vartheta -s)\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^{\vartheta }{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathit{\Theta },\mathbb{W}}(\vartheta -s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(s\right)\mathrm{d}s,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\sigma ,\alpha ,\beta }^{\mathit{\Theta },\mathbb{W}}\left(\vartheta \right)& =\sum _{i=0}^{\infty }\sum _{j=0}^{p-1}{\displaystyle \frac{{\left(\vartheta -j\sigma \right)}^{i\alpha +\beta -1}}{\mathit{\Gamma }\left(i\alpha +\beta \right)}}{\mathit{{\rm Y}}}^{\mathit{\Theta },\mathbb{W}}\left(i+1;j\sigma \right)\hfill \\ \hfill & =\sum _{i=0}^{⌊{\displaystyle \frac{\vartheta }{\sigma +1}}⌋}{\displaystyle \frac{{\left(\vartheta -i\sigma \right)}^{i\alpha +\beta -1}}{\mathit{\Gamma }\left(i\alpha +\beta \right)}}{\mathbb{W}}^i\hfill \\ \hfill & ={\left(\vartheta -i\sigma \right)}^{\beta -1}{\mathcal{E}}_{\alpha ,\beta }\left(\mathbb{W}{\left(\vartheta -i\sigma \right)}^{\alpha }\right).\hfill \end{array}$$

Corollary 3.

Let $\mathbb{S}=\mathbb{J}=\mathit{\Theta }$, which leads to $\mathbb{W}=\mathit{\Theta }$ in (3). Suppose that $\mathbb{A}$ and $\mathbb{B}$ are non-permutable $n\times n$ and $p\times p$ constant real non-zero matrices, respectively. Then the solution $\mathbb{X}\left(\vartheta \right)$ of (3) can be expressed as

$$\begin{array}{cc}\hfill \mathbb{X}\left(\vartheta \right)& ={\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathit{\Theta }}(\vartheta +\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathit{\Theta }}(\vartheta -s)\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^{\vartheta }{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathit{\Theta }}(\vartheta -s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(s\right)\mathrm{d}s,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\sigma ,\alpha ,\beta }^{\mathbb{C},\mathit{\Theta }}\left(\vartheta \right)& =\sum _{i=0}^{\infty }\sum _{j=0}^{p-1}{\displaystyle \frac{{\left(\vartheta -j\sigma \right)}^{i\alpha +\beta -1}}{\mathit{\Gamma }\left(i\alpha +\beta \right)}}{\mathit{{\rm Y}}}^{\mathbb{C},\mathit{\Theta }}\left(i+1;j\sigma \right)\hfill \\ \hfill & =\sum _{i=0}^{\infty }{\displaystyle \frac{{\vartheta }^{i\alpha +\beta -1}}{\mathit{\Gamma }\left(i\alpha +\beta \right)}}{\mathbb{C}}^i={\vartheta }^{\beta -1}{\mathcal{E}}_{\alpha ,\beta }\left(\mathbb{C}{\vartheta }^{\alpha }\right).\hfill \end{array}$$

Remark 1.

Corollary 2 improves and extends the corresponding results in [38] by removing the commutativity assumptions, and adding delay terms.

4. Controllability

In this section, we derive the necessary and sufficient conditions for controllability of the system (3).

Definition 7

([40]). The systems (3) are controllable over the interval $\left[0,{\vartheta }_f\right]$ if it possesses the capability to transit any initial state $\mathbb{X}\left(\vartheta \right)={\mathbb{X}}_0$, $-\sigma \le \vartheta \le 0$ to a designated final state ${\mathbb{X}}_f$ through the application of a control law $\mathbb{U}\left(\vartheta \right)\in {\mathbb{R}}^{m_1\times m_2}$ valid within the interval $[0,{\vartheta }_f]$, such that (3) has a solution $\mathbb{X}:\left[-\sigma ,{\vartheta }_f\right]\to {\mathbb{R}}^n$ that satisfies $\mathbb{X}\left(\vartheta \right)={\mathbb{X}}_0$, $-\sigma \le \vartheta \le 0$, and $\mathbb{X}\left({\vartheta }_f\right)={\mathbb{X}}_f$ for all ${\mathbb{X}}_0$, ${\mathbb{X}}_f\in {\mathbb{R}}^{n\times p}$.

Definition 8.

The fractional delay Gramian matrix of system (3) is defined as follows:

$${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]={\int }_0^{{\vartheta }_f}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)(\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{{\mathbb{C}}^{\mathrm{T}},{\mathbb{W}}^{\mathrm{T}}}({\vartheta }_f-s)\mathrm{d}s,$$

(5)

where ${·}^{\mathrm{T}}$ denotes the transpose of the matrix.

Theorem 3.

The system (3) is controllable in $[0,{\vartheta }_f]$ if and only if the $np\times np$ symmetric controllability matrix ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ is positive definite. In this case, the control

$$\mathbb{U}\left(\vartheta \right)=(\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{{\mathbb{C}}^{\mathrm{T}},{\mathbb{W}}^{\mathrm{T}}}({\vartheta }_f-\vartheta ){\mathit{\Pi }}_{\sigma ,\alpha }^{-1}[0,{\vartheta }_f]\mu ,$$

(6)

where

$$\mu ={\mathbb{X}}_f-{\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathbb{W}}({\vartheta }_f+\sigma )\mathit{\Psi }\left(-\sigma \right)-{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left[\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s,$$

defined on $0\le \vartheta \le {\vartheta }_f$ transfers $\mathbb{X}\left(\vartheta \right)={\mathbb{X}}_0$, $-\sigma \le \vartheta \le 0$ to $\mathbb{X}\left({\vartheta }_f\right)={\mathbb{X}}_f$.

Proof. 

(⇒) Assume that ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ is positive definite. Then it is a nonsingular matrix, which guarantees that ${\mathit{\Pi }}_{\sigma ,\alpha }^{-1}[0,{\vartheta }_f]$ exists. Then the control defined by (6) exists. Now, substituting (6) into (4) with $\vartheta ={\vartheta }_f$ we have

$$\begin{array}{ccc}\hfill \mathbb{X}\left({\vartheta }_f\right)& =\hfill & {\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathbb{W}}({\vartheta }_f+\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left[\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s\hfill \\ & & +{\int }_0^{{\vartheta }_f}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)(\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{{\mathbb{C}}^{\mathrm{T}},{\mathbb{W}}^{\mathrm{T}}}({\vartheta }_f-s)\mathrm{d}s{\mathit{\Pi }}_{\sigma ,\alpha }^{-1}[0,{\vartheta }_f]\mu \hfill \\ & =\hfill & {\mathbb{X}}_f.\hfill \end{array}$$

Hence, (3) is controllable on $[0,{\vartheta }_f]$.

(⇐) Conversely, suppose that (3) is controllable on $[0,{\vartheta }_f]$, then we have to show that ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ is nonsingular. Since ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ is symmetric and positive semidefinite, there exists at least one non-zero arbitrary constant state $z\in {\mathbb{R}}^{np}$ such that

$$\begin{array}{cc}\hfill 0& =z^{\mathrm{T}}{\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]z={\int }_0^{{\vartheta }_f}{z}^{\mathrm{T}}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)(\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{{\mathbb{C}}^{\mathrm{T}},{\mathbb{W}}^{\mathrm{T}}}({\vartheta }_f-s)z\mathrm{d}s\hfill \\ \hfill & ={\int }_0^{{\vartheta }_f}\theta (s,{\vartheta }_f){\theta }^{\mathrm{T}}(s,{\vartheta }_f)\mathrm{d}s={\int }_0^{{\vartheta }_f}{\parallel \theta \parallel }^2\mathrm{d}s,\hfill \end{array}$$

(7)

where $\parallel \theta \parallel$ denotes the Euclidean norm in ${\mathbb{R}}^{np}$, and

$$\theta (s,{\vartheta }_f)=z^{\mathrm{T}}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right),$$

which implies that

$${\int }_0^{{\vartheta }_f}{\parallel \theta \parallel }^2\mathrm{d}s=0,$$

then

$$\theta (s,{\vartheta }_f):={\mathbf{0}}^{\mathrm{T}}, 0\le \vartheta \le {\vartheta }_f,$$

(8)

where $\mathbf{0}$ denotes the $np$-dimensional zero vector. Since (3) is controllable on $[0,{\vartheta }_f]$, there exists a control ${\mathbb{U}}_1\left(\vartheta \right)$ that drives the initial state to the zero state at ${\vartheta }_f$. That is,

$$\begin{array}{ccc}\hfill \mathbb{X}\left({\vartheta }_f\right)& =\hfill & {\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathbb{W}}({\vartheta }_f+\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left[\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s\hfill \\ & & +{\int }_0^{{\vartheta }_f}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right){\mathbb{U}}_1\left(s\right)\mathrm{d}s\hfill \\ & =\hfill & \mathbf{0},\hfill \end{array}$$

(9)

similarly, there exists a control ${\mathbb{U}}_2\left(\vartheta \right)$ that drives the initial state to $z\ne 0$ state at ${\vartheta }_f$. That is,

$$\begin{array}{ccc}\hfill \mathbb{X}\left({\vartheta }_f\right)& =\hfill & {\mathcal{F}}_{\sigma ,\alpha ,1}^{\mathbb{C},\mathbb{W}}({\vartheta }_f+\sigma )\mathit{\Psi }\left(-\sigma \right)+{\int }_{-\sigma }^0{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left[\left({}^{C}D_{0^{+}}^{\alpha }\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s\hfill \\ & & +{\int }_0^{{\vartheta }_f}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right){\mathbb{U}}_2\left(s\right)\mathrm{d}s\hfill \\ & =\hfill & z.\hfill \end{array}$$

(10)

From (9) and (10), we have

$$z={\int }_0^{{\vartheta }_f}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\left[{\mathbb{U}}_2\left(s\right)-{\mathbb{U}}_1\left(s\right)\right]\mathrm{d}s.$$

(11)

Multiplying (11) by $z^{\mathrm{T}}$, and using (8), we have

$$z^{\mathrm{T}}z={\int }_0^{{\vartheta }_f}{z}^{\mathrm{T}}{\mathcal{F}}_{\sigma ,\alpha ,\alpha }^{\mathbb{C},\mathbb{W}}({\vartheta }_f-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\left[{\mathbb{U}}_2\left(s\right)-{\mathbb{U}}_1\left(s\right)\right]\mathrm{d}s=0.$$

This leads to $z^{\mathrm{T}}z=0$, contradicting the fact that z is a nonzero vector. We conclude that ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ is positive definite and, as a result, nonsingular. The proof is complete. □

Remark 2.

Corollary 3 and Theorem 3 extend the corresponding results in [33] by adding the delay terms $\mathbb{S}$$X\left(\vartheta -\sigma \right)$ and $X\left(\vartheta -\sigma \right)$$\mathbb{J}$.

Remark 3

(Practical Interpretation of the Gramian Condition). The non-singularity of the fractional delay Gramian matrix ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ has a direct physical and control-theoretic interpretation. It guarantees that the control energy required to steer the system between two states is finite. In engineering terms, a non-singular Gramian implies that the control inputs $\mathbb{U}\left(\vartheta \right)$, acting through the input matrix $({\mathbb{F}}^{\mathsf{T}}\otimes \mathbb{E})$, can excite all possible state directions of the vectorized system over the time interval $[0,{\vartheta }_f]$, despite the presence of fractional damping and delayed coupling. Checking the positivity of ${\mathit{\Pi }}_{\sigma ,\alpha }[0,{\vartheta }_f]$ provides a verifiable certificate for whether the system is fully controllable, which is a prerequisite for effective stabilization and trajectory tracking in applications.

5. An Example

The following example illustrates the theoretical results.

Example 1.

Consider a control problem involving a fractional delay differential Sylvester matrix equation, given by

$$\begin{array}{c}\left({}^{C}D_{0^{+}}^{0.8}X\right)\left(\vartheta \right)=\mathbb{A} X\left(\vartheta \right)+X\left(\vartheta \right) \mathbb{B}+\mathbb{S} X\left(\vartheta -1\right)+X\left(\vartheta -1\right) \mathbb{J}\\ +\mathbb{E}U\left(\vartheta \right)\mathbb{F}, \mathit{for} \vartheta \in \mathit{\Delta }=\left[0,2\right],\\ X\left(\vartheta \right)=\mathit{\Phi }\left(\vartheta \right)=\left(\begin{array}{cc}\vartheta +1& 0\\ 0& \vartheta +1\end{array}\right), \mathit{for} \vartheta \in \left[-1,0\right],\end{array}$$

(12)

where

$$\begin{array}{cc}\hfill \mathbb{A}& =\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right), \mathbb{B}=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right), \mathbb{E}=\left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right),\hfill \\ \hfill \mathbb{S}& =\left(\begin{array}{cc}1& 0\\ -1& 2\end{array}\right), \mathbb{J}=\left(\begin{array}{cc}0& 3\\ 2& 0\end{array}\right), \mathbb{F}=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right).\hfill \end{array}$$

Then

$$\mathit{\Psi }\left(\vartheta \right)=\left(\begin{array}{c}\vartheta +1\\ 0\\ 0\\ \vartheta +1\end{array}\right), \left({}^{C}D_{0^{+}}^{0.8}\mathit{\Psi }\right)\left(\vartheta \right)={\displaystyle \frac{{\vartheta }^{0.2}}{\mathit{\Gamma }\left(1.2\right)}}\left(\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right),$$

$$\mathbb{C}=\left(\begin{array}{cccc}1& -1& 1& 0\\ 1& 1& 0& 1\\ 0& 0& 1& -1\\ 0& 0& 1& 1\end{array}\right), \mathbb{W}=\left(\begin{array}{cccc}1& 0& 2& 0\\ -1& 2& 0& 2\\ 3& 0& 1& 0\\ 0& 3& -1& 2\end{array}\right),$$

and

$$\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)=\left(\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 1& 0\\ 1& 0& 0& 0\\ 1& 0& 0& 0\end{array}\right), (\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}})=\left(\begin{array}{cccc}0& 0& 1& 1\\ 0& 0& 0& 0\\ 1& 1& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

Using Definitions 5 and 6, we compute

$${\mathcal{F}}_{1,0.8,0.8}^{\mathbb{C},\mathbb{W}}\left(\vartheta \right):=\left\{\begin{array}{c}\mathit{\Theta }, -1\le \vartheta <0,\\ {\mathbb{I}}_2, \vartheta =0,\\ {\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \frac{{\left(\vartheta \right)}^{\left(i+1\right)0.8-1}}{\mathit{\Gamma }\left(\left(i+1\right)0.8\right)}}{\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}\left(i+1;0\right), 0<\vartheta \le 1.\\ {\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \frac{{\left(\vartheta \right)}^{\left(i+1\right)0.8-1}}{\mathit{\Gamma }\left(\left(i+1\right)0.8\right)}}{\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}\left(i+1;0\right) \\ +{\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \frac{{\left(\vartheta -1\right)}^{i0.8+0.8-1}}{\mathit{\Gamma }\left(\left(i+1\right)0.8\right)}}{\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}\left(i+1;1\right), 1<\vartheta \le 2,\end{array}\right.$$

and, for $i\ge 0$, we deduce that

$${\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}\left(i+1;0\right)={\mathbb{C}}^i, {\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}\left(i+1;1\right)=i{\mathbb{WC}}^{i-1},$$

such that

$${\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(0;s)={\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(k;-1)=\mathit{\Theta }, {\mathit{{\rm Y}}}^{\mathbb{C},\mathbb{W}}(1;0)={\mathbb{I}}_2.$$

Thus

$${\mathcal{F}}_{1,0.8,0.8}^{\mathbb{C},\mathbb{W}}\left(\vartheta \right):=\left\{\begin{array}{c}\mathit{\Theta }, -1\le \vartheta \le 0,\\ {\mathbb{I}}_2, \vartheta =0,\\ {\vartheta }^{-0.2}{\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{\vartheta }^{0.8}\right), 0<\vartheta \le 1.\\ {\vartheta }^{-0.2}{\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{\vartheta }^{0.8}\right)+{\left(\vartheta -1\right)}^{0.6}\mathbb{W}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\vartheta }}\left[{\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{(\vartheta -1)}^{0.8}\right)\right], 1<\vartheta \le 2,\end{array}\right.$$

where

$${\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{\vartheta }^{0.8}\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(\mathbb{C}{\vartheta }^{0.8}\right)}^k}{\mathit{\Gamma }\left(0.8k+0.8\right)}}.$$

Using Theorem 2, we calculate the explicit solutions $\mathbb{X}\left(\vartheta \right)$ of (12), for $\vartheta \in \mathit{\Delta }$, as follows:

$$\begin{array}{cc}\hfill \mathbb{X}\left(\vartheta \right)& ={\int }_{-1}^0{\mathcal{F}}_{1,0.8,0.8}^{\mathbb{C},\mathbb{W}}(\vartheta -s)\left[\left({}^{C}D_{0^{+}}^{0.8}\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s\hfill \\ \hfill & +{\int }_0^{\vartheta }{\mathcal{F}}_{1,0.8,0.8}^{\mathbb{C},\mathbb{W}}(\vartheta -s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)\mathbb{U}\left(s\right)\mathrm{d}s.\hfill \end{array}$$

Following the definition in (5), we now construct the fractional delay Gramian matrix for system (12):

$${\mathit{\Pi }}_{1,\alpha }[0,2]={\int }_0^2{\mathcal{F}}_{1,0.8,0.8}^{\mathbb{C},\mathbb{W}}(2-s)\left({\mathbb{F}}^{\mathrm{T}}\otimes \mathbb{E}\right)(\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathcal{F}}_{1,0.8,0.8}^{{\mathbb{C}}^{\mathrm{T}},{\mathbb{W}}^{\mathrm{T}}}(2-s)\mathrm{d}s,$$

which implies that

$${\mathit{\Pi }}_{1,0,8}[0,2]=\left(\begin{array}{cccc}14.27& -53.23& 14.92& -50.56\\ -53.23& 306.22& -59.91& 302.96\\ 14.92& -59.91& 17.08& -54.61\\ -50.56& 302.96& -54.61& 334.28\end{array}\right)>0,$$

and

$${\mathit{\Pi }}_{1,0.8}^{-1}[0,2]=\left(\begin{array}{cccc}0.89& -0.052& -0.79& 0.05\\ -0.052& 0.06& 0.12& -0.04\\ -0.79& 0.12& 0.92& -0.08\\ 0.05& -0.04& -0.08& 0.04\end{array}\right).$$

Therefore, we see that ${\mathit{\Pi }}_{1,0,8}[0,2]$ is positive definite. Consequently, given any finite terminal condition ${\mathbb{X}}_f\in {\mathbb{R}}^{2\times 2}$ for which $\mathbb{X}\left(1\right)={\mathbb{X}}_f={(X_1,X_2,X_3,X_4)}^{\mathrm{T}}$, the associated control function $\mathbb{U}\left(\vartheta \right)$ is given by:

$$\begin{array}{cc}\hfill \mathbb{U}\left(\vartheta \right)& =(\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathcal{F}}_{1,0.8,0.8}^{{\mathbb{C}}^{\mathrm{T}},{\mathbb{W}}^{\mathrm{T}}}(2-\vartheta ){\mathit{\Pi }}_{1,0.8}^{-1}[0,2]\mu ,\hfill \\ & :=\left\{\begin{array}{c}\mathit{\Theta }, -1\le \vartheta \le 0,\\ (\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\mathit{\Pi }}_{1,0.8}^{-1}[0,2]\mu , \vartheta =0,\\ (\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\vartheta }^{-0.2}{\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{\vartheta }^{0.8}\right){\mathit{\Pi }}_{1,0.8}^{-1}[0,2]\mu , 0<\vartheta \le 1,\\ (\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}}){\vartheta }^{-0.2}{\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{\vartheta }^{0.8}\right){\mathit{\Pi }}_{1,0.8}^{-1}[0,2]\mu \\ +{\left((\mathbb{F}\otimes {\mathbb{E}}^{\mathrm{T}})(\vartheta -1\right)}^{0.6}\mathbb{W} \\ \times {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\vartheta }}\left[{\mathcal{E}}_{0.8,0.8}\left(\mathbb{C}{(\vartheta -1)}^{0.8}\right)\right]{\mathit{\Pi }}_{1,0.8}^{-1}[0,2]\mu , 1<\vartheta \le 2,\end{array}\right.\hfill \end{array}$$

where

$$\mu ={\mathbb{X}}_f-{\int }_{-1}^0{\mathcal{F}}_{1,0.8,0.8}^{\mathbb{C},\mathbb{W}}(2-s)\left[\left({}^{C}D_{0^{+}}^{0.8}\mathit{\Psi }\right)\left(s\right)-\mathbb{C}\mathit{\Psi }\left(s\right)\right]\mathrm{d}s.$$

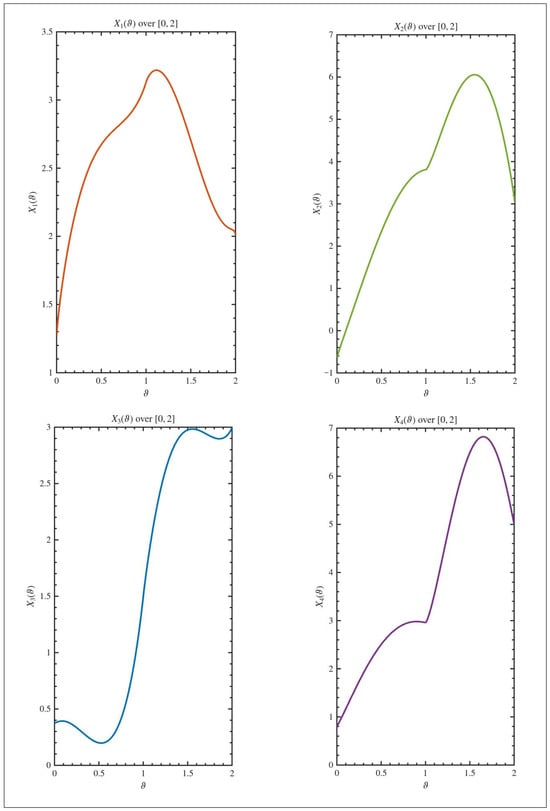
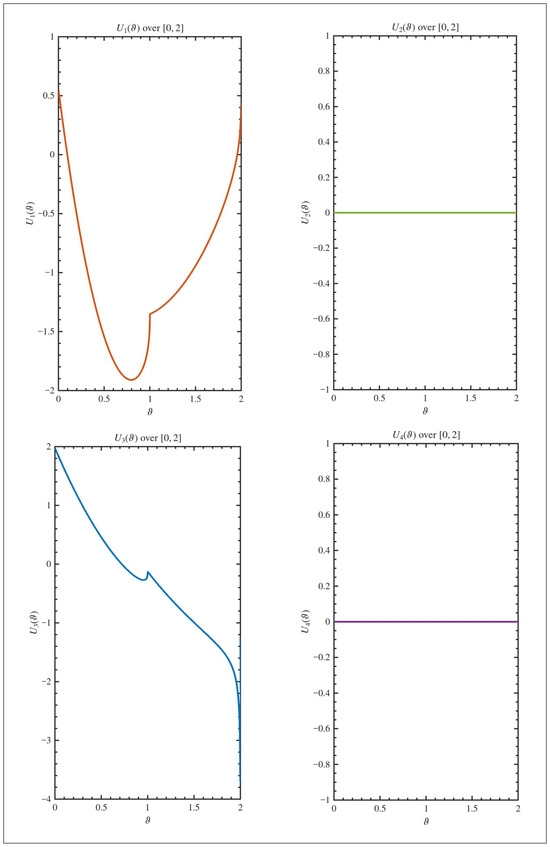
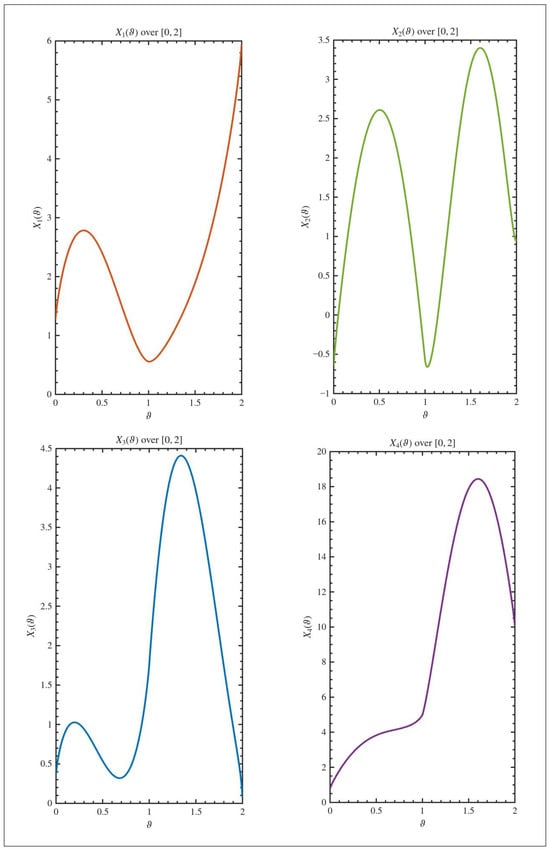
Hence the system (12) is controllable on $\left[0,2\right]$ by Theorem 3. To visualize the system behavior, we plot the state trajectories and control inputs for two different initial conditions. Figure 2 shows the state evolution $X\left(\vartheta \right)$ for the initial vector $X={(2,3,3,5)}^{\top }$, while Figure 3 displays the corresponding control functions $U_1\left(\theta \right),U_2\left(\theta \right),U_3\left(\theta \right),U_4\left(\theta \right)$ over the interval $[0,2]$. Similarly, Figure 4 illustrates the state $X\left(\vartheta \right)$ for $X={(6,1,0,10)}^{\top }$, and Figure 5 shows the associated control inputs. The graphical results in Figure 2, Figure 3, Figure 4 and Figure 5 provide compelling visual validation of our theoretical controllability criteria. Several key practical implications can be observed: (i) Despite significantly different initial conditions (${(2,3,3,5)}^{\top }$ vs. ${(6,1,0,10)}^{\top }$), the designed control laws successfully steer both systems to the desired terminal state, demonstrating the robustness of our controllability framework. (ii) The control inputs in Figure 3 and Figure 5 exhibit complex temporal patterns that account for both the fractional-order dynamics and the delay effects, highlighting the non-trivial nature of the control design. (iii) The state trajectories in Figure 2 and Figure 4 show smooth convergence to the target, confirming that the fractional delay Gramian-based control strategy effectively compensates for the system’s memory effects and delayed interactions. This comparative analysis underscores the practical utility of our approach for engineering applications where systems must be controlled from arbitrary initial states to desired configurations despite inherent delays and fractional-order dynamics.

Figure 2. The trajectory of the state $X\left(\vartheta \right)$ of system (12) in the interval $\vartheta \in [0, 2]$ when $X={\left(\begin{array}{c}{X}_1,X_2,X_3,X_4\end{array}\right)}^{\top }={\left(\begin{array}{c}2,3,3,5\end{array}\right)}^{\top }$.

Figure 3. The trajectory of the control functions $U_1\left(\vartheta \right)$, $U_2\left(\vartheta \right)$, $U_3\left(\vartheta \right)$, $U_4\left(\vartheta \right)$ for $\vartheta \in [0, 2]$ when $X={\left(\begin{array}{c}{X}_1,X_2,X_3,X_4\end{array}\right)}^{\top }={\left(\begin{array}{c}2,3,3,5\end{array}\right)}^{\top }$.

Figure 4. The trajectory of the state $X\left(\vartheta \right)$ of system (12) in the interval $\vartheta \in [0, 2]$ when $X={\left(\begin{array}{c}{X}_1,X_2,X_3,X_4\end{array}\right)}^{\top }={\left(\begin{array}{c}6,1,0,10\end{array}\right)}^{\top }$.

Figure 5. The trajectory of the control functions $U_1\left(\vartheta \right)$, $U_2\left(\vartheta \right)$, $U_3\left(\vartheta \right)$, $U_4\left(\vartheta \right)$ for $\vartheta \in [0, 2]$ when $X={\left(\begin{array}{c}{X}_1,X_2,X_3,X_4\end{array}\right)}^{\top }={\left(\begin{array}{c}6,1,0,10\end{array}\right)}^{\top }$.

Remark 4.

It is seen that, when $\alpha =1$, the conclusion of Theorem 5 in [38] is not applicable to the system (12) because our results impose minimal restrictions on the coefficient matrices: they are not required to commute. Therefore, our results improve some existing ones.

6. Conclusions

This study has successfully developed a comprehensive theoretical framework for analyzing fractional delay differential Sylvester matrix equations with non-permutable coefficient matrices. The principal contribution lies in establishing explicit solution representations through the innovative application of vectorization techniques and Kronecker product algebra, which effectively transform the original matrix-valued problem into a tractable vector system. The derived solutions, expressed in terms of delayed perturbations of two-parameter Mittag-Leffler-type matrix functions, generalize and improve existing results by eliminating restrictive commutativity assumptions.

A significant advancement presented in this work is the introduction of a fractional delay Gramian matrix, which provides the necessary and sufficient conditions for complete controllability. This criterion remains computationally verifiable even when system matrices do not commute, addressing a critical gap in the literature. The numerical example demonstrates the practical efficacy of our approach, confirming that both solution representation and controllability analysis remain robust in non-commutative and delay-rich environments where conventional methods are inapplicable.

Future research directions will focus on extending this framework to incorporate nonlinear perturbations, stochastic disturbances, and state-dependent delays under non-permutable matrix structures. Furthermore, development of efficient numerical schemes, such as Krylov subspace methods [41,42], for computing the delayed Mittag-Leffler functions and the Gramian matrix, is essential for applying this framework to large-scale engineering problems.