Runtime Verification Tool for the Calculus of Context-Aware Ambients

Abstract

A context-aware system is a system that adapts its behaviours in response to changes in the system’s environment (i.e., context). Ensuring the correctness of such a system is difficult because the state of the environment changes frequently in an unpredictable manner according to the laws of physics. Hence, formal verification techniques like model-checking and theorem proving do not work in many cases. Runtime Verification (RV) is a lightweight formal verification technique that consists of checking at runtime whether the execution of the system violates the requirements of the system. The Calculus of Context-aware Ambients (CCA) is a process calculus for modelling context-aware systems and reasoning about their behaviours. This paper proposes an RV tool for CCA, called ccaRV. Given a model of a system in CCA and a property of the system written in LTL (Linear Temporal Logic), ccaRV verifies automatically at runtime if the execution of the system violates the property. We propose a semantic approach to RV, where the RV mechanism is defined at the semantics level and not as an add-on. A consequence of this is that there is no need for generating a monitor from the property specification nor for the instrumentation of a system during verification. We define a labelled reduction relation for CCA, where the labels are used to capture the execution traces at the semantics level. Then we extend LTL with spatial operators and context expressions in order to formulate properties about the system context. We use a case study of the MQTT (Message Queue Telemetry Transport) protocol to evaluate the proposed RV approach. The results show that the ccaRV tool is scalable and its decisions are accurate.

1. Introduction

An important goal in software engineering is to produce software systems that are free from faults and runtime errors. However, achieving this goal has proven to be difficult in many cases, and in particular for context-aware systems where the behaviours of a system change dynamically to adapt to new situations. Many software verification techniques have been proposed that can help to assure the correctness of a piece of software. Software testing techniques [1] review the software code to detect faults (static analysis), or run the software in a variety of conditions in the search of software errors (dynamic analysis). Since exhaustive testing is impossible in general, software testing techniques cannot guarantee that a software works correctly in all conditions. Model checking techniques [2,3], in contrast, explore automatically all possible reachable states of (a model of) the software. However, they do not scale well and suffer from the state explosion problem when the number of reachable states is too large. Deductive verification techniques [4] can be used in some cases where model checking fails. Deductive verification techniques allow the generation of a collection of verification conditions (from the software and its specification) that must be proven to establish the correctness of the software. These verification conditions can be discharged using theorem-proving tools (e.g., HOL [5], Vampire [6], and CVC4 [7]). However, a deductive verification approach requires some specialist knowledge in formal methods and a detailed understanding of the correct behaviour of the software, which makes it not easily accessible to software engineers.

Runtime verification (RV) [8,9] is a lightweight software verification technique that checks the behaviour of the software automatically at runtime against a desired property. This technique is scalable and much easier to understand compared to model checking and theorem proving approaches [10]. Moreover, RV can allow the system to recover from errors by performing specific actions when errors are detected; these actions may be to reconfigure the system, to log the traces that lead to the errors, or to notify the user [11]. However, RV does not guarantee that all possible executions of the software satisfy the property. Traditional software verification techniques assume that the system requirements are fixed and do not change in response to changes in the system context. This is not the case for IoT systems. The requirements of an IoT system are predominantly context-dependent and the system adapts its behaviours as the context changes. Such systems are also known as context-aware systems or simply smart systems. Context is key to the behaviour of IoT systems and is constructed from data acquired through sensors. For example, a self-driving car uses context information such as location, direction, speed, and the objects in the surrounding environment to guide itself autonomously on the road. Commonly, IoT devices are resource-constrained devices, are often powered by batteries with low computational and memory capacity, communicate wirelessly, and are mobile. Thus, context such as the network bandwidth, device location, battery level, available memory, and the physical environment changes frequently and affects the behaviour of the software running on these devices. The formal verification of context-aware systems is more challenging because the context of a system can change in an unpredictable manner.

The interest of applying RV techniques to IoT systems is growing in the software verification community [12,13,14,15,16]. However, most works focus on the analysis of the execution traces generated by the software under test and do not consider the context under which these execution traces were generated. Context is extremely dynamic and changes in an unpredictable way in that it is practically impossible to reproduce in a testing laboratory. Making context an integral part of an RV technique is important for effective verification of IoT systems because it will be possible to discover faults caused by changes in the context. Current approaches think of RV as an add-on after the system has been implemented and involve in general the following tasks: (i) the system’s source code is instrumented to produce the execution traces; (ii) a monitor is generated from the formal specification of the property; (iii) the system and the monitor are run to perform the RV (online or offline). The Calculus of Context-aware Ambients (CCA) [17] is a process calculus for modelling context-aware systems and to reason about their behaviours. Specifications written in CCA are executable by the CCA interpreter ccaPL [18]. This paper proposes an RV tool for CCA, called ccaRV. As shown in Figure 1, the tool takes as input an CCA process and an LTL formula and produces in output a verification report that says whether the LTL formula has been violated during the execution of the CCA process. We propose a semantic approach to RV, where the RV mechanism is defined at the semantics level and not as an add-on. We define a labelled reduction relation for CCA, where the labels are used to capture the execution traces at the semantics level. Then we extend LTL with spatial operators and context expressions in order to formulate properties about the system context. We use a case study of the MQTT (Message Queue Telemetry Transport) protocol to evaluate the proposed RV approach. The results show that the ccaRV tool is scalable and its decisions are accurate. The contributions of this paper are fourfold:

• A novel labelled reduction semantics is proposed for CCA, where the traditional reduction relation is annotated with a label representing the execution trace of the reduction step (Section 2.2).
• A new property specification language is proposed that extends LTL with context expressions and other operators to cater for the specification of properties about both the system and its context (Section 2.3). A context expression defined in Table 1 is a logical formula upon the state of the environment (context). A formal semantics of the property specification language is given over an infinite sequence of states, where a state contains both the current context information and the trace of the last reduction step. In this way, the semantic model provides a holistic view of the system execution (Section 2.3).
  Table 1. Syntax of CCA.

  Production Rules			Description	Production Rules			Description
  $P,Q$	$::=$		(Processes)	$\kappa$	$::=$		(Context expressions)
  		$\mathtt{0}$	inactivity			$\mathtt{0}$	empty context
  		$P|Q$	parallel composition			$\mathtt{true}$	true
  		$\left\{P\right\}$	block			$\mathtt{false}$	false
  		$\left(\mathtt{new}n\right)P$	name restriction			$n=m$	name match
  		$!P$	replication			$\mathtt{this}$	hole
  		$n\left[P\right]$	ambient			$n\left[\kappa \right]$	location context
  		$<\kappa >M.P$	context-guarded prefix			${\kappa }_1|{\kappa }_2$	parallel composition
  		$\mathtt{if}<{\kappa }_1>M_1.P_1$	if-then			${\kappa }_1\mathtt{and}{\kappa }_2$	conjunction
  		…				${\kappa }_1\mathtt{or}{\kappa }_2$	disjunction
  		$<{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{fi}$				$\mathtt{not}\kappa$	negation
  		$\mathtt{if}<{\kappa }_1>M_1.P_1$	if-then-else			$\mathtt{next}\kappa$	spatial next modality
  		$\dots$				$\mathtt{somewhere}\kappa$	somewhere modality
  		$<{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{else}P\mathtt{fi}$
  		$\mathtt{let}{x}_1=e_1,\dots ,x_{\ell }=e_{\ell }\mathtt{in}P$	arithmetic
  		$\mathtt{find}{x}_1,\dots ,x_{\ell }:\kappa \mathtt{for}P$	search
  		$\mathtt{proc}x(y_1,\dots ,y_{\ell })P$	process abstraction
  M	$::=$		(Capabilities)	$\alpha$	$::=$		(Locations)
  		$\mathtt{skip}$	one transition			@	any parent
  		$\mathtt{in}n$	move into ambient n			$n@$	specific parent n
  		$\mathtt{out}$	move out of parent			#	any child
  		$\mathtt{del}n$	delete ambient n			$n\#$	specific child n
  		$\alpha \mathtt{recv}(y_1,\dots ,y_{\ell })$	receive data from $\alpha$			$::$	any sibling
  		$\alpha \mathtt{send}(z_1,\dots ,z_{\ell })$	send data to $\alpha$			$n::$	specific sibling n
  		$\alpha x(z_1,\dots ,z_{\ell })$	process abstraction call			$ϵ$	locally

• A novel RV mechanism is defined based on the labelled reduction semantics of CCA and the semantics of the property specification language (Definition 5). A consequence of this is that there is no need for generating a monitor from the property specification nor for the instrumentation of a system during verification. This RV mechanism is implemented into a software tool called ccaRV depicted in Figure 1 (Section 3.1).
• A formal specification of the MQTT protocol is given in CCA and used to evaluate the RV tool ccaRV. The MQTT protocol is de facto standard messaging protocol for IoT device communication as it is designed for resource-constrained devices and low-bandwidth, high-latency or unreliable networks. It is chosen as a case study for its scalability (Section 2.4). The experimental results show that ccaRV decisions are accurate and the RV overhead is low relative to the execution time, but increases with the size of system and the size of the property (Section 3.2).

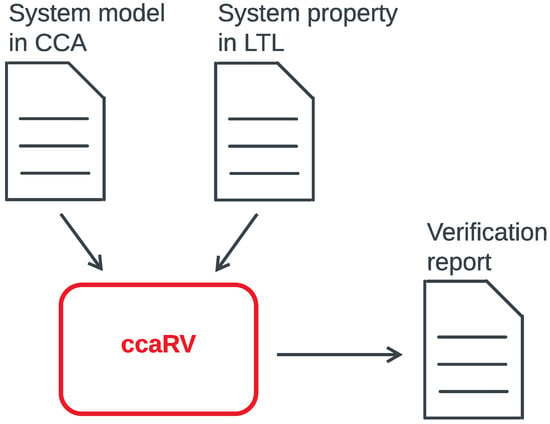
Figure 1. The CCA runtime verification tool ccaRV.

The remaining of the paper is structured as follows. Section 2 presents the syntax and the labelled reduction semantics of CCA, the syntax and the semantics of the property specification language, and a formal specification of the MQTT protocol. The ccaRV tool is presented in Section 3 as well as the experiment results. Section 4 discusses the related work and Section 5 concludes the paper and points to future research directions.

2. Materials and Methods

2.1. Overview of CCA

The Calculus of Context-aware Ambients (CCA) [17] is a process calculus for modelling the behaviour of context-aware, mobile, and concurrent systems. The concept of ambient is used in CCA to represent any entity in which a computation can take place. This is representedas $n\left[P\right]$, where n is the ambient’s name and P a process specifying the computation taking place in the ambient. We also say that the process P is executed by the ambient n. Ambients can communicate by sending messages to each other through a hand-shake message passing mechanism. A concurrent system can be specified as a parallel composition of ambients (see Section 2.1.2). An ambient can contain other ambients, forming a hierarchy of ambients. Such a hierarchical structure can be used to specified complex systems. An ambient can also be mobile, either by performing the movementcapabilities “$\mathtt{in}$” and “$\mathtt{out}$” (see Section 2.1.1) to move from one location to another or by being inside a moving ambient. Context-awareness is an important feature in CCA. Indeed, an ambient can be aware of its context so as to adapt its behaviour accordingly when the context changes. This is achieved using the notion of a context-guarded process, where the execution of a process is guarded by a context expression, which is a predicate over the state of the ambient hierarchy. The grammar in Table 1 describes formally the syntax of CCA, where P (or Q) denotes a process, M a capability, and $\kappa$ a context expression. We use the symbols n, x, y, and z to represent names. The formal semantics of CCA are presented in Section 2.2.

2.1.1. Capabilities

In CCA, a process is formed from atomic actions called capabilities. The syntax of a capability M is given in Table 1. The capability $\mathtt{skip}$ corresponds to one transition, i.e., one execution step. An ambient can perform the capability $\mathtt{in}n$ to move into a sibling ambient n. The capability $\mathtt{out}$ allows an ambient to move out of its parent ambient. Communications between ambients are performed using the output capability $\alpha \mathtt{send}(z_1,\dots ,z_{\ell })$ and the input capability $\alpha \mathtt{recv}(y_1,\dots ,y_{\ell })$, where the parameters are names and $\ell \ge 0$. The location $\alpha$ can be @ for any parent, $n@$ for a specific parent n, # for any child, $n\#$ for a specific child n, $::$ for any sibling, $n::$ for a specific sibling n, or $ϵ$ (empty string) for the executing ambient itself. An ambient of the form $n\left[\mathtt{0}\right]$ can be deleted using the capability $\mathtt{del}n$. A process abstraction x defined at a location $\alpha$ is called using a capability of the form $\alpha x(z_1,\dots ,z_{\ell })$, where the number of actual parameters, $\ell \ge 0$, must match the number of formal parameters of x.

2.1.2. Processes

The syntax of a process P is given in Table 1. The inactivity process $\mathtt{0}$ does nothing and terminates immediately. Two processes can be composed in parallel using the operator ‘|’. A process of the form $\left\{P\right\}$ behaves just like P. A name restriction $\left(\mathtt{new}n\right)P$ limits the scope of a new name n to the process P. The process $!P$ denotes a replication of the process P. A process of the form $<\kappa >M.P$ is guarded by a context expression (i.e., a predicate over contexts, see Section 2.1.3) $\kappa$. This process can execute only if the environment satisfies the condition $\kappa$. An if-then statement in CCA can have many branches, each guarded by a context expression. An if-then statement is blocking, i.e., it waits until one of the branches is executed. On the contrary, an if-then-else statement does not wait and executes the else-part if none of the branches of the then-part can be executed. The let-statement $\mathtt{let}{x}_1=e_1,\dots ,y_{\ell }=e_{\ell }\mathtt{in}P$ substitutes in P the values of the expressions to the variables. A search process $\mathtt{find}{x}_1,\dots ,x_{\ell }:\kappa \mathtt{for}P$ looks for a list of values for which the context expression $\kappa$ holds and substitutes those values in P. A definition of a process abstraction x has the form $\mathtt{proc}x(y_1,\dots ,y_{\ell })P$, where P is the body of the process abstraction and the list of formal parameters are between the parentheses. At the call of a process abstraction, the number of the actual parameters must match that of the formal parameters. Process abstractions are similar to procedures or functions in programming languages.

2.1.3. Context Expressions

A context is modelled in CCA as a process with possibly a single hole in it. A hole (represented by the symbol ⊙) in a context C is a placeholder for the process of which C is a context. For example, let us consider a system modelled by the process $n\left[P\right|m\left[Q\right|R\left]\right]|S$, where P, Q, R, S are processes. The context of the ambient m in that system is $n\left[P\right|\odot \left]\right|S$ and that of the process R is $n\left[P\right|m\left[Q\right|\odot \left]\right]|S$. The grammar in Table 2 depicts the syntax of a context, where P denotes a process. It is assumed that the following congruence rules hold over contexts: $\mathtt{0}|C\equiv C$, $\left\{C\right\}\equiv C$, and $C|P\equiv P|C$.

Table 2. Syntax of contexts.

Production Rules			Description
C	$::=$
		P	process
		⊙	hole
		$n\left[C\right]$	ambient
		$C|P$	parallel composition
		$\left(\mathtt{new}n\right)C$	restriction
		$\left\{C\right\}$	block

A context expression (CE in short) is a predicate over contexts. Table 1 presents the syntax of a context expression $\kappa$. A formal semantics of context expressions is given in Table 3, with respect to the context model of Table 2. The notation $C\vDash \kappa$ means that a context C satisfies a context expression $\kappa$. If a context express $\kappa$ is valid, i.e., is satisfied by all the contexts, we write $\vDash \kappa$.

Table 3. Satisfaction relation for context expressions.

	⊧	$\mathtt{true}$
C	⊧	$n=m$	if	$n=m$
C	⊧	$\mathtt{0}$	if	$C=\mathtt{0}$
C	⊧	$\mathtt{this}$	if	$C=\odot$
C	⊧	$\mathtt{not}\kappa$	if	$C\cancel{\vDash }\kappa$
C	⊧	${\kappa }_1|{\kappa }_2$	if	$\mathrm{exist}{C}_1,C_2\mathrm{such} \mathrm{that}C=C_1|C_2$$\mathrm{and}{C}_1\vDash {\kappa }_1\mathrm{and}{C}_2\vDash {\kappa }_2$
C	⊧	${\kappa }_1\mathtt{and}{\kappa }_2$	if	$C\vDash {\kappa }_1\mathrm{and}C\vDash {\kappa }_2$
C	⊧	$n\left[\kappa \right]$	if	$\mathrm{exists}{C}^{\prime }\mathrm{such} \mathrm{that}C=n\left[C^{\prime }\right]\mathrm{and}{C}^{\prime }\vDash \kappa$
C	⊧	$\mathtt{next}\kappa$	if	$\mathrm{exist}{C}^{\prime },n\mathrm{such} \mathrm{that}C=n\left[C^{\prime }\right]\mathrm{and}{C}^{\prime }\vDash \kappa$
C	⊧	$\mathtt{somewhere}\kappa$	if	$C\vDash \kappa$ or $\mathrm{exist}{C}^{\prime },n\mathrm{such} \mathrm{that}C=n\left[C^{\prime }\right]\mathrm{and}$$C^{\prime }\vDash \mathtt{somewhere}\kappa$

The CE $\mathtt{true}$ always holds, while the CE $\mathtt{false}$ (i.e., $\mathtt{not}\mathtt{true}$) never holds. A CE $n=m$ holds if the names n and m are identical. The CE $\mathtt{0}$ stands for the empty context $\mathtt{0}$. The CE $\mathtt{this}$ stands for the hole context. The propositional operators ($\mathtt{not}$, $\mathtt{and}$ and $\mathtt{or}$) keep their usual semantics. A CE ${\kappa }_1|{\kappa }_2$ holds for a parallel composition of two contexts such that ${\kappa }_1$ holds for one and ${\kappa }_2$ holds for the other. A CE $n\left[\kappa \right]$ holds for an ambient named n such that $\kappa$ holds inside that ambient. A CE $\mathtt{next}\kappa$ holds for a context if $\kappa$ holds for a child context of that context. A CE $\mathtt{somewhere}\kappa$ holds for a context if $\kappa$ holds for some sub-context of that context. Table 4 shows some examples of context expressions. The following section presents the formal semantics of CCA.

Table 4. Examples of context expressions.

Context Expression			Description
$has\left(n\right)$	=	$\mathtt{somewhere}\left(\mathtt{this}\right|n\left[\mathtt{true}\right]\left|\mathtt{true}\right)$	self contains n.
$at\left(n\right)$	=	$\mathtt{somewhere}\left(n\right[\mathtt{next}\left(\mathtt{this}\right|\mathtt{true}\left)\right]\left|\mathtt{true}\right)$	n contains self.
$at(n,m)$	=	$\mathtt{somewhere}\left(n\right[m\left[\mathtt{true}\right]\left|\mathtt{true}\right]\left|\mathtt{true}\right)$	n contains m.
$with\left(n\right)$	=	$\mathtt{somewhere}\left(n\right[\mathtt{true}\left]\right|\mathtt{next}\left(\mathtt{this}\right|\mathtt{true}\left)\right|\mathtt{true})$	self is with n.
$with(n,m)$	=	$\mathtt{somewhere}\left(n\right[\mathtt{true}\left]\right|m\left[\mathtt{true}\right]\left|\mathtt{true}\right)$	n is with m.
$contains\left(n\right)$	=	$\mathtt{somewhere}\left(\mathtt{this}\right|n\left[0\right]\left|\mathtt{true}\right)$	self contains $n\left[0\right]$.
$contains(d,n)$	=	$\mathtt{somewhere}\left(d\right[n\left[0\right]\left|\mathtt{true}\right]\left|\mathtt{true}\right)$	d contains $n\left[0\right]$.

2.2. A Labelled Reduction Semantics of CCA

This section presents the formal semantics of CCA based on a structural congruence and a labelled reduction relation. The structural congruence is denoted by ≡. It is the smallest congruence relation on processes that satisfies the axioms in Table 5. These axioms are used to manipulate the structure of processes. The axioms S1–S6 assert that the structural congruence is a commutative monoid for $(\mathtt{0},|)$. The axiom S7 says that the parallel composition of processes preserves the structural congruence. The axiom S8 says that an ambient $n\left[P\right]$ behaves the same as an ambient $n\left[Q\right]$ if P and Q are equivalent processes. The name restriction can be safely manipulated using the axioms S9–S13. The replication operator satisfies the axioms S14–S16. The axiom S17 states that the process abstraction definition is monotonic with respect to the structural congruence. A process guarded with $\mathtt{true}$ behaves the same as that process without guards (axiom S18). The axiom S19 states that if two processes are equivalent, then their context-guarded prefixes, with equivalent guards, are also equivalent. The let-statement unifies a name with the value of an expression; see the axiom S20, where $val\left(e_i\right)$ denotes the value of the expression $e_i$, for $i\ge 1$. We denoteby $\mathtt{fn}\left(Q\right)$, the set of the free names in a process Q. This set is calculated as in Table 6.

Table 5. Structural congruence relation for processes, where $\mathtt{fn}\left(Q\right)$ is the set of the free names in a process Q.

(S1)	$\mathit{P}\equiv \mathit{P}$
(S2)	$P\equiv Q\Rightarrow Q\equiv P$
(S3)	$P\equiv Q,Q\equiv R\Rightarrow P\equiv R$
(S4)	$P|\mathtt{0}\equiv P$
(S5)	$P|Q\equiv Q|P$
(S6)	$P\left|\right(Q\left|R\right)\equiv \left(P\right|Q\left)\right|R$
(S7)	$P\equiv Q\Rightarrow P|R\equiv Q|R$
(S8)	$P\equiv Q\Rightarrow n\left[P\right]\equiv n\left[Q\right]$
(S9)	$\left(\nu n\right)\left(\nu m\right)P\equiv \left(\nu m\right)\left(\nu n\right)P$
(S10)	$\left(\nu n\right)P|Q\equiv (\nu n\left)\right(P\left|Q\right)$  if $n\notin \mathtt{fn}\left(Q\right)$
(S11)	$\left(\nu n\right)m\left[P\right]\equiv m\left[\right(\nu n\left)P\right]$  if $n\ne m$
(S12)	$P\equiv Q\Rightarrow \left(\nu n\right)P\equiv \left(\nu n\right)Q$
(S13)	$\left(\nu n\right)\mathtt{0}\equiv \mathtt{0}$
(S14)	$!P\equiv P|!P$
(S15)	$!\mathtt{0}\equiv \mathtt{0}$
(S16)	$P\equiv Q\Rightarrow !P\equiv !Q$
(S17)	$P\equiv Q\Rightarrow \mathtt{proc}x(y_1,\dots ,y_{\ell })P\equiv \mathtt{proc}x(y_1,\dots ,y_{\ell })Q$
(S18)	$<\mathtt{true}>M.P\equiv M.P$
(S19)	$P\equiv Q,(\vDash \kappa \iff {\kappa }^{\prime })\Rightarrow <\kappa >M.P\equiv <{\kappa }^{\prime }>M.Q$
(S20)	$C(\mathtt{let}{x}_1=e_1,\dots ,x_{\ell }=e_{\ell }\mathtt{in}P)\equiv C\left(P\{val\left(e_1\right)/x_1,\dots ,val\left(e_{\ell }\right)/x_{\ell }\}\right)$

Table 6. Definition of the free names function $\mathtt{fn}$.

$\mathtt{fn}\left(\mathtt{0}\right)=\mathtt{fn}\left(\mathtt{out}\right)$	=	∅
$\mathtt{fn}\left(P\right|Q)$	=	$\mathtt{fn}\left(P\right)\cup \mathtt{fn}\left(Q\right)$
$\mathtt{fn}\left(\mathtt{new}nP\right)$	=	$\mathtt{fn}\left(P\right)\setminus \left\{n\right\}$
$\mathtt{fn}\left(n\right[P\left]\right)$	=	$\mathtt{fn}\left(P\right)\cup \left\{n\right\}$
$\mathtt{fn}(!P)$	=	$\mathtt{fn}\left(P\right)$
$\mathtt{fn}(<\kappa >P)$	=	$\mathtt{fn}\left(\kappa \right)\cup \mathtt{fn}\left(P\right)$
$\mathtt{fn}\left(\mathtt{proc}x(y_1,\dots ,y_{\ell })P\right)$	=	$\left\{x\right\}\cup (\mathtt{fn}\left(P\right)\setminus \{y_1,\dots ,y_{\ell }\})$
$\mathtt{fn}(\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{fi})$	=	$\underset{i=1}{\stackrel{\ell }{\cup }}\mathtt{fn}(<{\kappa }_i>M_i.P_i)$
$\mathtt{fn}(\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{else}P\mathtt{fi})$	=	$\underset{i=1}{\stackrel{\ell }{\cup }}\mathtt{fn}(<{\kappa }_i>M_i.P_i)\cup \mathtt{fn}\left(P\right)$
$\mathtt{fn}\left(\mathtt{in}n\right)$	=	$\left\{n\right\}$
$\mathtt{fn}(\alpha x(z_1,\dots ,z_{\ell }).P)$	=	$\mathtt{fn}\left(\alpha \right)\cup \{x,z_1,\dots ,z_{\ell }\}\cup \mathtt{fn}\left(P\right)$
$\mathtt{fn}(\alpha \mathtt{recv}(y_1,\dots ,y_{\ell }).P)$	=	$\mathtt{fn}\left(\alpha \right)\cup (\mathtt{fn}\left(P\right)\setminus \{y_1,\dots ,y_{\ell }\})$
$\mathtt{fn}(\alpha \mathtt{send}(z_1,\dots ,z_{\ell }).P)$	=	$\mathtt{fn}\left(\alpha \right)\cup \{z_1,\dots ,z_{\ell }\}\cup \mathtt{fn}\left(P\right)$
$\mathtt{fn}(@)=\mathtt{fn}(\#)=\mathtt{fn}(::)=\mathtt{fn}\left(ϵ\right)$	=	∅
$\mathtt{fn}(n@)=\mathtt{fn}(n\#)=\mathtt{fn}(n::)$	=	$\left\{n\right\}$
$\mathtt{fn}\left(\mathtt{true}\right)=\mathtt{fn}\left(\mathtt{false}\right)=\mathtt{fn}\left(\mathtt{this}\right)$	=	∅
$\mathtt{fn}(n=m)$	=	$\{n,m\}$
$\mathtt{fn}\left(\mathtt{not}\kappa \right)=\mathtt{fn}\left(\mathtt{next}\kappa \right)=\mathtt{fn}\left(\mathtt{somewhere}\kappa \right)$	=	$\mathtt{fn}\left(\kappa \right)$
$\mathtt{fn}\left({\kappa }_1\right|{\kappa }_2)$	=	$\mathtt{fn}\left({\kappa }_1\right)\cup \mathtt{fn}\left({\kappa }_2\right)$
$\mathtt{fn}\left(n\right[\kappa \left]\right)$	=	$\mathtt{fn}\left(\kappa \right)\cup \left\{n\right\}$
$\mathtt{fn}\left({\kappa }_1\mathtt{and}{\kappa }_2\right)$	=	$\mathtt{fn}\left({\kappa }_1\right)\cup \mathtt{fn}\left({\kappa }_2\right)$
$\mathtt{fn}\left({\kappa }_1\mathtt{or}{\kappa }_2\right)$	=	$\mathtt{fn}\left({\kappa }_1\right)\cup \mathtt{fn}\left({\kappa }_2\right)$

The rules in Table 7, Table 8 and Table 9 define the labelled reduction relation of processes, $\stackrel{s}{\to }$, where $P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}$ represents the process obtained by replacing each free occurrence of the name $y_i$ in P by $z_i$, $i=1,\dots ,\ell$. A substitution $\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}$ is sometimes denoted by $\delta$. The label s of a reduction relation is a string of one of the forms described in Table 10, which represents the trace of the reduction step. The first set of rules R1–R7 (in Table 7) defines the semantics of a process abstraction call. Thus, a process abstraction call is executed only if a definition of the process abstraction exists at the specified location. The next set of rules R8–R20 (in Table 8) deals with message passing communication between processes. The semantics of mobile and context-aware processes is given in Table 9. The mobility rules R21–R22 are inheritedfrom [19]. The rule R3 states that the capability $\mathtt{skip}$ denotes a single reduction step. An empty ambient (of the form $n\left[\mathtt{0}\right]$) can be deleted from the system (rule R24). The labelled reduction relation propagates across scopes (rule R25). The labelled reduction relation is closed under structural congruence (rule R26). The rule R27 says that a context-guarded prefix is executed only if the environment satisfies the guard. In this rule, $\delta$ stands for a substitution of names. The rule R28 states that one of the enabled branches of an if-then statement is chosen non-deterministically for execution. If no branch is enabled, then no reduction takes place. On the contrary, for the if-then-else statement, the else branch is executed if no other branch is enabled (see rules R29 to R30). Finally, the rule R31 defines the formal semantics of the search statement $\mathtt{find}$.

Table 7. Labelled reduction relation for process abstractions.

(R1)	$n[\mathtt{proc}x(y_1,\dots ,y_{\ell })P|x\{z_1,\dots ,z_{\ell }\}|R]\stackrel{t_8(n,x)}{\to }$
	$n\left[\mathtt{proc}x(y_1,\dots ,y_{\ell })P\right|P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\left|R\right]$
(R2)	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]|m[::x(z_1,\dots ,z_{\ell })|R]\stackrel{t_9(n,x,m)}{\to }$
	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]|m\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]$
(R3)	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]|m[n::x(z_1,\dots ,z_{\ell })|R]\stackrel{t_9(n,x,m)}{\to }$
	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]|m\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]$
(R4)	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P\left|m[@x(z_1,\dots ,z_{\ell })|R]\right]\stackrel{t_{10}(n,x,m)}{\to }$
	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P\left|m\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]\right]$
(R5)	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P\left|m[n@x(z_1,\dots ,z_{\ell })|R]\right]\stackrel{t_{10}(n,x,m)}{\to }$
	$n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P\left|m\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]\right]$
(R6)	$m[n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]|\#x(z_1,\dots ,z_{\ell })\left|R\right]\stackrel{t_{11}(n,x,m)}{\to }$
	$m\left[n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]\right|P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\left|R\right]$
(R7)	$m[n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]|n\#x(z_1,\dots ,z_{\ell })\left|R\right]\stackrel{t_{11}(n,x,m)}{\to }$
	$m\left[n\left[Q\right|\mathtt{proc}x(y_1,\dots ,y_{\ell })P]\right|P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\left|R\right]$

Table 8. Labelled reduction relation for message passing, where $\ell \ge 0$ is the number of parameters.

(R8)	$n[\mathtt{recv}(y_1,\dots ,y_{\ell }).P|\mathtt{send}(z_1,\dots ,z_{\ell }).Q\left|R\right]\stackrel{t_2(n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|Q\left|R\right]$
(R9)	$n[::\mathtt{recv}(y_1,\dots ,y_{\ell }).P|Q]|m[::\mathtt{send}(z_1,\dots ,z_{\ell }).R|S]\stackrel{t_5(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|Q]|m\left[R\right|S]$
(R10)	$n[::\mathtt{recv}(y_1,\dots ,y_{\ell }).P|Q]|m[n::\mathtt{send}(z_1,\dots ,z_{\ell }).R|S]\stackrel{t_5(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|Q]|m\left[R\right|S]$
(R11)	$n[m::\mathtt{recv}(y_1,\dots ,y_{\ell }).P|Q]|m[::\mathtt{send}(z_1,\dots ,z_{\ell }).R|S]\stackrel{t_5(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|Q]|m\left[R\right|S]$
(R12)	$n[m::\mathtt{recv}(y_1,\dots ,y_{\ell }).P|Q]|m[n::\mathtt{send}(z_1,\dots ,z_{\ell }).R|S]\stackrel{t_5(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|Q]|m\left[R\right|S]$
(R13)	$n[\#\mathtt{recv}(y_1,\dots ,y_{\ell }).P|m[@\mathtt{send}(z_1,\dots ,z_{\ell }).Q|R]\left|S\right]\stackrel{t_3(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|m\left[Q\right|R]\left|S\right]$
(R14)	$n[m\#\mathtt{recv}(y_1,\dots ,y_{\ell }).P|m[@\mathtt{send}(z_1,\dots ,z_{\ell }).Q|R]\left|S\right]\stackrel{t_3(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|m\left[Q\right|R]\left|S\right]$
(R15)	$n[\#\mathtt{recv}(y_1,\dots ,y_{\ell }).P|m[n@\mathtt{send}(z_1,\dots ,z_{\ell }).Q|R]\left|S\right]\stackrel{t_3(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|m\left[Q\right|R]\left|S\right]$
(R16)	$n[m\#\mathtt{recv}(y_1,\dots ,y_{\ell }).P|m[n@\mathtt{send}(z_1,\dots ,z_{\ell }).Q|R]\left|S\right]\stackrel{t_3(m,n,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|m\left[Q\right|R]\left|S\right]$
(R17)	$n[\#\mathtt{send}(z_1,\dots ,z_{\ell }).P|m[@\mathtt{recv}(y_1,\dots ,y_{\ell }).Q|R]\left|S\right]\stackrel{t_4(n,m,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\right|m\left[Q\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]\left|S\right]$
(R18)	$n[m\#\mathtt{send}(z_1,\dots ,z_{\ell }).P|m[@\mathtt{recv}(y_1,\dots ,y_{\ell }).Q|R]\left|S\right]\stackrel{t_4(n,m,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\right|m\left[Q\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]\left|S\right]$
(R19)	$n[\#\mathtt{send}(z_1,\dots ,z_{\ell }).P|m[n@\mathtt{recv}(y_1,\dots ,y_{\ell }).Q|R]\left|S\right]\stackrel{t_4(n,m,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\right|m\left[Q\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]\left|S\right]$
(R20)	$n[m\#\mathtt{send}(z_1,\dots ,z_{\ell }).P|m[n@\mathtt{recv}(y_1,\dots ,y_{\ell }).Q|R]\left|S\right]\stackrel{t_4(n,m,z_1,\dots ,z_{\ell })}{\to }$
	$n\left[P\right|m\left[Q\{z_1/y_1,\dots ,z_{\ell }/y_{\ell }\}\right|R]\left|S\right]$

Table 9. Labelled reduction relation for mobile and context-aware processes, where $\delta$ denotes a substitution of names and $ϵ$ stands for an empty string.

(R21)	$n[\mathtt{in}m.P|Q\left]\right|m\left[R\right]\stackrel{t_6(n,m)}{\to }m\left[n\right[P\left|Q\right]\left|R\right]$
(R22)	$m\left[n[\mathtt{out}.P|Q]\right|R]\stackrel{t_7(n,m)}{\to }n\left[P\right|Q]|m\left[R\right]$
(R23)	$\mathtt{skip}.P\stackrel{t_0}{\to }P$
(R24)	$\mathtt{del}n.P|n\left[\mathtt{0}\right]\stackrel{t_1\left(n\right)}{\to }P$
(R25)	$P\stackrel{s}{\to }Q\Rightarrow \left(\nu n\right)P\stackrel{s}{\to }\left(\nu n\right)Q$
(R26)	$P\equiv Q,Q\stackrel{s}{\to }{Q}^{\prime },Q^{\prime }\equiv P^{\prime }\Rightarrow P\stackrel{s}{\to }{P}^{\prime }$
(R27)	$C(M.P)\stackrel{s}{\to }{C}^{\prime }\left(P\delta \right)\Rightarrow C(<\kappa >M.P)\stackrel{s}{\to }{C}^{\prime }\left(P\delta \right)$ if $C\vDash \kappa$
(R28)	$C(<{\kappa }_i>M_i.P_i)\stackrel{s}{\to }{C}^{\prime }\left(P_i\delta \right)\Rightarrow$
	$C(\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{fi})\stackrel{s}{\to }{C}^{\prime }\left(P_i\delta \right)$, for some i, $1\le i\le \ell$.
(R29)	$C(\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{fi})\stackrel{s}{\to }{C}^{\prime }\left(P_i\delta \right)\Rightarrow$
	$C(\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{else}P\mathtt{fi})\stackrel{s}{\to }{C}^{\prime }\left(P_i\delta \right)$
(R30)	$C(\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{else}P\mathtt{fi})\stackrel{ϵ}{\to }C\left(P\right)$
	$\mathrm{if}\forall i\in [1,\ell ]\neg \exists (C^{\prime },s,\delta )\mathrm{such} \mathrm{that}C(<{\kappa }_i>M_i.P_i)\stackrel{s}{\to }{C}^{\prime }\left(P_i\delta \right)$.
(R31)	$C(\mathtt{find}{x}_1,\dots ,x_{\ell }:\kappa \mathtt{for}P)\stackrel{t_{12}(x_1,\dots ,x_{\ell },n_1,\dots ,n_{\ell })}{\to }C\left(P\{n_1/x_1,\dots ,n_{\ell }/x_{\ell }\}\right)$
	$\mathrm{if}C\vDash \kappa \{n_1/x_1,\dots ,n_{\ell }/x_{\ell }\}$

Table 10. General forms of the execution traces.

Notation	Execution Trace	Description
$t_0$	“skip”	capability “skip” is executed.
$t_1\left(n\right)$	“delete ambient ambient A”	ambient A is deleted.
$t_2(A,X)$	“local: A ===(X)===> A”	A sends message X to itself.
$t_3(A,B,X)$	“child to parent: A ===(X)===> B”	A sends a message X to its parent B.
$t_4(A,B,X)$	“parent to child: A ===(X)===> B”	A sends a message X to its child B.
$t_5(A,B,X)$	“sibling to sibling: A ===(X)===> B”	A sends a message X to its sibling B.
$t_6(A,B)$	“ambient A moves into ambient B”	A executes the capability “inB”.
$t_7(A,B)$	“ambient A moves out of ambient B”	A executes the capability “out”.
$t_8(A,T)$	“local call to the abstraction T in the ambient A”	A calls its own abstraction T.
$t_9(A,T,B)$	“call to the abstraction A::T in the ambient B”	B calls abstraction T of its sibling A.
$t_{10}(A,T,B)$	“call to the abstraction A@T in the ambient B”	B calls abstraction T of its parent A.
$t_{11}(A,T,B)$	“call to the abstraction A#T in the ambient B”	B calls abstraction T of its child A.
$t_{12}(x_1,\dots ,x_{\ell },$$n_1,\dots ,n_{\ell })$	“binding: $x_1$ -> $n_1$, …, $x_{\ell }$ -> $n_{\ell }$”	the variables $x_1,\dots ,x_{\ell }$ are bound to the names $n_1,\dots ,n_{\ell }$, by the $\mathtt{find}$ statement.

Definition 1 

(An enabled process). We say that a process P is enabled, denoted by $enabled\left(P\right)$, if there exists a process Q such that $P\stackrel{s}{\to }Q$, for some string of characters s. For example, the process $\mathtt{skip}.P$ is enabled (see the semantic rule R23), while the process $\mathtt{0}$ is not enabled.

Definition 2 

(An execution or run of a process). An execution or run of a process $P_0$ is a sequence of reductions $P_0\stackrel{s_1}{\to }{P}_1\stackrel{s_2}{\to }{P}_2\dots P_{n-1}\stackrel{s_n}{\to }{P}_n$, $n\ge 0$, such that $enabled\left(P_i\right)$ for all $i<n$ and if $n<\infty$, $\neg enabled\left(P_n\right)$.

Definition 3 

(A terminating execution). A terminating execution or run of a process $P_0$ is a finite sequence of reductions $P_0\stackrel{s_1}{\to }{P}_1\stackrel{s_2}{\to }{P}_2\dots P_{n-1}\stackrel{s_n}{\to }{P}_n$, $n\ge 0$, such that $P_n=\mathtt{0}$ and $enabled\left(P_i\right)$ for all $i<n$.

Definition 4 

(A continuation process). We say that a process Q is a continuation process of another process P, denoted by $P{\to }^{*}Q$, if there exists a finite sequence of reductions of the form $P\stackrel{s_1}{\to }{P}_1\stackrel{s_2}{\to }{P}_2\dots P_{n-1}\stackrel{s_n}{\to }Q$, $n\ge 0$ and $enabled\left(P_i\right)$ for all $i<n$.

Example 1 

(A specification of a persistent memory cell in CCA). A persistent memory cell is a data structure that stores a value persistently until the value is replaced by writing a new value to the memory cell. The value stored in a persistent memory cell can be read at any time by taking a copy of that value. Unlike a write action, a read action does not modify the content of a memory cell. A persistent memory cell that stores a pair of values can be specified in CCA as an ambient of the following form, where (z1,z2) is the initial content of the memory cell.

1. 

mem[

2. 

  !@recv().recv(v1,v2).{ @send(v1,v2).0 | send(v1,v2).0 }

3. 

 | !@recv(x1,x2).recv(y1,y2).{ send(x1,x2).0 | @send().0 }

4. 

 | send(z1,z2).0

5. 

]

To read the value of a memory cell mem, the following process segment must be used in parallel to the memory ambient: mem#send().mem#recv(x,y). This process segment communicates with the process in line 2 to get into the variables x and y a copy of the values stored in the memory cell. To write a pair of values (v1,v2) into a memory cell, the following process segment must be used in parallel to the memory ambient: mem#send(v1,v2).mem#recv(). This process segment synchronises with the process in line 3 to set (v1,v2) as the new content of the memory cell.

2.3. The Property Specification Language

RV consists of checking at runtime whether the execution of a process violates a given property. The grammar in Table 11 describes the syntax of the property specification language for ccaRV. It is an extension of the Linear Temporal Logic (LTL) [20] with new constructs like a context expression $\kappa$ (explained above), the predicate $\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("\mathtt{r}")$ (which holds if the string of characters r is a substring of the execution trace), and the operator post. A formula $\mathtt{p}\mathtt{o}\mathtt{s}\mathtt{t}f$ holds if the formula f is true in the final execution state.

Table 11. The syntax of LTL.

Production Rules			Description
$f,g$	$::=$
		$\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("\mathtt{r}")$	Trace predicate
		$\kappa$	Context expression
		$\mathtt{p}\mathtt{o}\mathtt{s}\mathtt{t}f$	Post-condition
		$f\&\&g$	Conjunction
		$f| |g$	Disjunction
		$f->g$	Implication
		$f<->g$	Equivalence
		$\mathtt{X}f$	Next (temporal)
		$f\mathtt{U}g$	Until
		$f\mathtt{V}g$	Release
		$f\mathtt{W}g$	Weak until
		$\left[\right]f$	Always
		$<>f$	Sometime
		$!f$	Negation

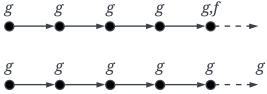
The propositional operators && (and), || (or), ! (negation), -> (implication), and <-> (equivalence) keep their usual semantics. Note that the spatial operators next and somewhere are defined in context expressions. Their semantics are explained in Section 2.1.3. The semantics of the temporal operators, over an infinite sequence of states, can be explained as follows. A formula $\mathtt{X}f$ is true in the current state if f is true in the next state. A formula $f\mathtt{U}g$ is true if f remains true at least until g becomes true in the current or a future state. A formula $f\mathtt{V}g$ is true if g remains true until and including the point where f first becomes true; if f never becomes true, g must remain true forever. A formula $f\mathtt{W}g$ is true if f is true permanently or until g becomes true. A formula $\left[\right]f$ is true if f is true at every state. Finally, a formula $<>f$ is true if f is true in the current state or sometime in the future. Table 12 illustrates graphically the semantics of the temporal formulas.

Table 12. Graphical illustration of the semantics of the temporal operators, where • represents a state, ⟶ denotes a single execution step, and $--->$ an infinite sequence of execution steps.

Formula	Graphical Semantics
f
$\mathtt{p}\mathtt{o}\mathtt{s}\mathtt{t}f$
$\mathtt{X}f$
$f\mathtt{U}g$
$f\mathtt{V}g$
$f\mathtt{W}g$
$\left[\right]f$
$<>f$

The formal semantics of a formula are defined over an infinite sequence of states $\sigma ={\sigma }_0{\sigma }_1{\sigma }_2\dots$, where a state is a pair ${\sigma }_i=(P_i,s_i)$ of a process $P_i$ (defined in Table 1) and a string $s_i$. We write $\sigma {\vDash }_{a}f$ to say that $\sigma$ satisfies a formula f. Let ${\sigma }^i={\sigma }_i{\sigma }_{i+1}\dots$ denote the suffix of $\sigma$ from the ith state, $i\ge 0$. Note that the first state of ${\sigma }^i$, ${\left({\sigma }^i\right)}_0$, is ${\sigma }_i$, for $i\ge 0$. The satisfaction relation ${\vDash }_a$ is defined as follows.

• $\sigma {\vDash }_a\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("\mathtt{r}")$ iff ${\sigma }_0=(P_0,s_0)$ and r is a substring of the string $s_0$.
• $\sigma {\vDash }_a\kappa$ iff ${\sigma }_0=(P_0,s_0)$ and $P_0\vDash \kappa$ (⊧ is defined in Table 3).
• $\sigma {\vDash }_a\mathtt{p}\mathtt{o}\mathtt{s}\mathtt{t}f$ iff there exists $i\ge 0$ such that ${\sigma }^i{\vDash }_{a}f$ and not $enabled\left(P_i\right)$ and for all $0\le k<i$, $enabled\left(P_k\right)$.
• $\sigma {\vDash }_a!f$ iff $\sigma {\cancel{\vDash }}_{a}f$.
• $\sigma {\vDash }_{a}f\left|\right|g$ iff $\sigma {\vDash }_{a}f$ or $\sigma {\vDash }_{a}g$.
• $\sigma {\vDash }_a\mathtt{X}f$ iff ${\sigma }^1{\vDash }_{a}f$.
• $\sigma {\vDash }_{a}f\mathtt{U}g$ iff there exists $i\ge 0$ such that ${\sigma }^i{\vDash }_{a}g$ and for all $0\le k<i$, ${\sigma }^k{\vDash }_{a}f$.

The semantics of the remaining formulas can be deduced from the following equalities.

• $f\&\&g=!(!f| |!g)$
• $f->g=!f| |g$
• $f<->g=\left(f->g\right)\&\&\left(g->f\right)$
• $f\mathtt{V}g=!(!f\mathtt{U}!g)$
• $<>f=\mathtt{t}\mathtt{r}\mathtt{u}\mathtt{e}\mathtt{U}f$
• $\left[\right]f=!<>!f$
• $f\mathtt{W}g=\left(f\mathtt{U}g\right)| |\left[\right]g$

We give some examples of LTL formulas in Example 2. The RV mechanism can now be formalised as in Definition 5.

Example 2. 

Examples of LTL formulas.

• $<>\left[\right]f$, i.e., eventually f holds forever. This is a safety property, i.e., nothing bad can happen.
• $\left[\right]<>f$, i.e., f always eventually holds. This is a liveness property, i.e., something good will always eventually happen.
• $<>\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("(\mathtt{X})")$, i.e., a message X is sent.
• $<>\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("(\mathtt{X})===>\mathtt{B}")$, i.e., a message X is received by ambient B.
• $<>\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("\mathtt{A}===(\mathtt{X})")$, i.e., a message X is sent by ambient A.
• $<>\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("\mathtt{A}===(\mathtt{X})===>\mathtt{B}")$, i.e., ambient A sent a message  X to ambient B.

Definition 5 

(Runtime Verification). An execution or run of a process $P_0\stackrel{s_1}{\to }{P}_1\stackrel{s_2}{\to }{P}_2\dots$$P_{n-1}\stackrel{s_n}{\to }{P}_n$, $n\ge 0$, does not violate an LTL formula f if $\sigma {\vDash }_{a}f$, where $\sigma =(P_0,ϵ)(P_1,s_1)(P_2,s_2)\dots$$(P_{n-1},s_{n-1})(P_n,s_n)(P_n,s_n)\dots$ and ϵ denotes an empty string. Note that the suffix ${\sigma }^n$ is an infinite sequence of the state $(P_n,s_n)$.

Definition 6 

(Partial satisfaction relation). We say that a process P partially satisfies a formula f, denoted by $P⊢f$, if there exists a run of the process P that does not violate the formula f.

Definition 7 

(Satisfaction relation). We say that a process P satisfies a formula f, denoted by $P{\vDash }_{s}f$, if every run of the process P does not violate the formula f.

Note that the partial satisfaction relation ⊢ guarantees the correctness of a single execution of a process, while the satisfaction relation ${\vDash }_s$ guarantees the correctness of all possible executions of a process. The relationship between the two is established by Theorem 1. In relation to RV, if the RV of a process P against an LTL formula f detects a violation then this proves that $P{\cancel{\vDash }}_{s}f$. If it does not, then it establishes that $P⊢f$.

Theorem 1. 

$P{\vDash }_{s}f$ implies $P⊢f$, for a process P and an LTL formula f.

The proof of Theorem 1 is straightforward from Definitions 6 and 7.

Theorem 2. 

If there exists a terminating execution for a process P, then $P⊢\mathtt{p}\mathtt{o}\mathtt{s}\mathtt{t}\mathtt{0}$.

Theorem 3. 

If t is a substring of s and P and Q are two processes such that $P\stackrel{s}{\to }Q$ and $Q⊢f$, then

$$P⊢\mathtt{X}\left(\mathtt{t}\mathtt{r}\mathtt{a}\mathtt{c}\mathtt{e}("t")\&\&f\right).$$

Theorem 4. 

If P and Q are two processes such that $P{\to }^{*}Q$ and $Q⊢f$, then

$$P⊢<>f.$$

The proofs of the Theorems 2–4 are given in Appendix A.

2.4. Case Study: The MQTT Protocol

2.4.1. Overview of the MQTT Protocol

The Message Queue Telemetry Transport (MQTT) protocol is a lightweight publish-subscribe messaging transport protocol developed for reliable machine-to-machine (M2M) communication over unreliable channels. It is an open, simple and easy-to-implement protocol developed for resource-constrained devices and high-latency, low-bandwidth, or unreliable networks. These make MQTT a suitable messaging protocol for IoT devices. The protocol runs over TCP/IP and other network protocols that provide ordered, lossless, bi-directional connections. A variant, MQTT-SN (MQTT for Sensor Networks), is used over other transport protocols such as UDP, Zigbee, or Bluetooth. MQTT is an OASIS (Organization for the Advancement of Structured Information Standards) standard [21,22] and an ISO (International Organization for Standardization) standard [23], for IoT connectivity. The MQTT protocol assumes two types of network entities: a message broker and a number of clients. Information is organised in a hierarchy of topics. A general architecture of the MQTT protocol is depicted in Figure 2. A client can act as a publisher by publishing a message on a topic, or as a subscriber to a topic to receive all the messages published on that topic, or both. A broker is a server that receives messages from publishers and pushes these messages to the subscribers of the corresponding topics. In this way the publishers do not need to know who the subscribers are and vice versa. If the broker receives a message on a topic for which there is no current subscribers, the message is discarded unless the publisher of the message instructs the broker to retain a copy of the message by setting the message’s retain flag to 1. The broker keeps only the latest retain message per topic. This retain message is automatically sent to a client when they subscribe to the topic, which is the latest known message on the topic.

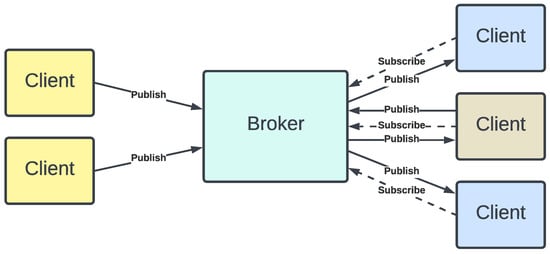
Figure 2. Architecture of the MQTT protocol.

There are 14 types of message packets in the MQTT protocol as summarised in Table 13. A client establishes a connection to a broker by sending a CONNECT packet to the broker. After connecting to a broker, a client can subscribe to a topic by sending a SUBSCRIBE packet to the broker or can publish a message on a topic using a PUBLISH packet. A client can cancel its subscription to a topic by sending an UNSUBSCRIBE packet to the broker. To end a connection with a broker, a client sends a DISCONNECT packet to the broker. The MQTT protocol provides three Quality of Service (QoS) levels that indicate the level of assurance for delivery of a PUBLISH packet between the sender and receiver:

• QoS 0 means at most one delivery. A packet is sent once; no acknowledgement is required. This is illustrated in Figure 3a. This also means the delivery is not guaranteed, the packet can get lost. Therefore, QoS level 0 is recommended when message loss is acceptable or the network bandwidth is at premium.
  

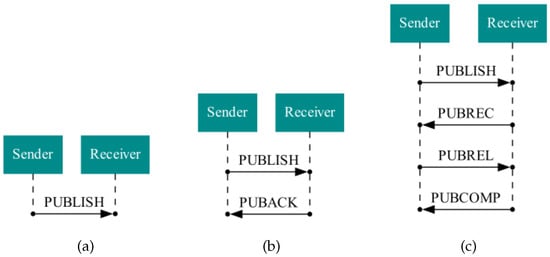  Figure 3. MQTT protocol control flow for each QoS.(a) QoS 0; (b) QoS 1; (c) QoS 2.
• QoS 1 means at least once delivery. A packet is sent repeatedly until acknowledgement is received. The packet delivery is guaranteed upon acknowledgement. This is illustrated in Figure 3b. This is the default QoS level and it offers the best trade-off between bandwidth and delivery guarantee.
• QoS 2 means exactly once delivery. A packet is sent once and is guaranteed to be delivered. There is an increased overhead associated with this quality of service. This is the highest quality of service, for use when neither loss nor duplication of messages are acceptable. The network traffic engendered by this QoS is illustrated in Figure 3c.

Table 13. MQTT packet types.

Name	Direction of Flow	Description
CONNECT	Client to Broker	Client request to connect to Broker
CONNACK	Broker to Client	Connect acknowledgment
PUBLISH	Client to Broker or	Publish message
	Broker to Client
PUBACK	Client to Broker or	Publish acknowledgment
	Broker to Client
PUBREC	Client to Broker or	Publish received
	Broker to Client
PUBREL	Client to Broker or	Publish release
	Broker to Client
PUBCOMP	Client to Broker or	Publish complete
	Broker to Client
SUBSCRIBE	Client to Broker	Client subscribe request
SUBACK	Broker to Client	Subscribe acknowledgment
UNSUBSCRIBE	Client to Broker	Unsubscribe request
UNSUBACK	Broker to Client	Unsubscribe acknowledgment
PINGREQ	Client to Broker	PING request
PINGRESP	Broker to Client	PING response
DISCONNECT	Client to Broker	Client is disconnecting

Table 13. MQTT packet types.

Name	Direction of Flow	Description
CONNECT	Client to Broker	Client request to connect to Broker
CONNACK	Broker to Client	Connect acknowledgment
PUBLISH	Client to Broker or	Publish message
	Broker to Client
PUBACK	Client to Broker or	Publish acknowledgment
	Broker to Client
PUBREC	Client to Broker or	Publish received
	Broker to Client
PUBREL	Client to Broker or	Publish release
	Broker to Client
PUBCOMP	Client to Broker or	Publish complete
	Broker to Client
SUBSCRIBE	Client to Broker	Client subscribe request
SUBACK	Broker to Client	Subscribe acknowledgment
UNSUBSCRIBE	Client to Broker	Unsubscribe request
UNSUBACK	Broker to Client	Unsubscribe acknowledgment
PINGREQ	Client to Broker	PING request
PINGRESP	Broker to Client	PING response
DISCONNECT	Client to Broker	Client is disconnecting

2.4.2. A Formal Specification of the MQTT Protocol in CCA

In this section, the behaviour of the MQTT protocol is formally described in CCA. A client and a broker can be represented as ambients in CCA. The behaviour of a client can be described by an ambient (aka client ambient) of the form in Listing 1, where the continuation process P represents a sequence of message exchanges between the client and the broker (e.g., SUBSCRIBE, PUBLISH, UNSUBSCRIBE, and DISCONNECT); and Q is a continuation process for processing the PUBLISH packets received from the broker. The line 2 allows a client to connect to the broker and then subscribe to topics or publish messages; while lines 3–8 are used for receiving messages from the broker and process them. Therefore, a client that only publishes messages need not contain the lines 3–8.

Listing 1. General form of a client ambient.

1.  clientId[ 2.   broker::send(CONNECT, clientId).broker::recv(ack).P 3.   | !broker::recv(packetType, _, topic, qos, retainFlag, payload).if 4.    < packetType=PUBLISH and qos=0 > Q 5.    < packetType=PUBLISH and qos=1 > broker::send(PUBACK).Q 6.    < packetType=PUBLISH and qos=2 > broker::send(PUBACK). 7.        broker::recv(pubrel).broker::send(PUBCOMP).Q 8.    fi 9.  ]

The first message packet a client can send to a broker is a CONNECT packet to establish a network connection with the broker. The broker acknowledges the connection by sending a CONNACK packet to the client. Then the client can subscribe to a topic by sending a SUBSCRIBE packet to the broker, which must respond with a SUBACK packet. The client will now receive from the broker all the messages published on that topic. In the course of a session, a client can also send a UNSUBSCRIBE packet to the broker to stop receiving messages on a specific topic. In this case, the broker will respond with a UNSUBACK packet. A PUBLISH packet can be sent by a client to a broker or by a broker to a client; in any case, the delivery process is guided by the QoS level of the packet (see Figure 3). Eventually, the client will send a DISCONNECT packet to close the network connection with the broker.

A topic is represented in CCA as a process abstraction (named after the topic), which sends each message published on the topic to all the clients that have subscribed to the topic. For each client C that connects to the broker successfully, a child ambient of the form $C\left[0\right]$ is created. This child ambient is deleted when the client disconnects from the broker. Similarly, when a client C subscribes to a topic T, a child ambient of the form $C\_T\left[0\right]$ is created. This child ambient is deleted when the client unsubscribes from the topic. The existence of these child ambients tells the broker whether a client is currently connected and what topics they have subscribed to. The context expression $contains\left(n\right)$, defined in Table 4, holds if the broker contains a child ambient of the form $n\left[0\right]$. The general form of a process abstraction for a topic is given in Listing 2. Basically, the process abstraction takes four arguments (a topic’s name, a QoS level, a retain flag, and a payload) and sends a PUBLISH packet to all the clients that have subscribed to the topic.

The general form of an ambient representing a broker (aka broker ambient) is given in Listing 3. The lines 3–5 correspond to the definitions of the process abstractions representing the topics managed by the broker. According to the MQTT protocol documentation [21] if a client sends a PUBLISH packet with a retain flag of 1, the broker must store the message and its QoS. Therefore, for each topic the broker ambient contains a persistent memory cell (defined in Example 1), named after the topic, which will store the retain message and the retain QoS of the topic (see lines 7–9 in Listing 3). Recall that the broker must send the retain message of a topic and the retain QoS to a client immediately after the client subscribes to the topic [21]. The lines 10–16 describe how the broker processes a CONNECT packet or a DISCONNECT packet received from a client. A child ambient of the form clientId[0] is created upon receiving a CONNECT from a client clientId, to mark that the client is connected (see line 13). This child ambient is deleted when the broker receives a DISCONNECT packet from the client (see line 15). In lines 18–29, a child ambient of the form clientId_topic is created when a client clientId subscribes to a topic (see lines 25–28); and this child ambient is deleted when the client unsubscribes from the topic (see line 32). The MQTT documentation says that when sending a PUBLISH Packet to a client, the server must set the retain flag to 1 if a message is sent as a result of a new subscription being made by a client. The broker must set the retain flag to 0 when a PUBLISH Packet is sent to a client because it matches an established subscription regardless of how the flag was set in the message it received. This requirement is specified in lines 20, 38, 40, 42, 44, 47, and 50 in Listing 3.

Listing 2. General form of a process abstraction representing a topic with N subscribers.

proc topic(topic, qos, retainFlag, payload){   if    < contains(clientId1) and contains(clientId1_topic) >      clientId1::send(PUBLISH,broker,topic,qos,retainFlag,payload).if        <qos=0> skip.0        <qos=1> clientId1::recv(ack).0        <qos=2> clientId1::recv(pubrec).clientId1::send(PUBREL).         clientId1::recv(pubcomp).0      fi    < not(contains(clientId1) and contains(clientId1_topic)) > skip.0   fi   | if    < contains(clientId2) and contains(clientId2_topic) >      clientId2::send(PUBLISH,broker,topic,qos,retainFlag,payload).if        <qos=0> skip.0        <qos=1> clientId2::recv(ack).0        <qos=2> clientId2::recv(pubrec).clientId2::send(PUBREL).         clientId2::recv(pubcomp).0      fi    < not(contains(clientId2) and contains(clientId2_topic)) > skip.0 fi | ... | if    < contains(clientIdN) and contains(clientIdN_topic) >      clientIdN::send(PUBLISH,broker,topic,qos,retainFlag,payload).if        <qos=0> skip.0        <qos=1> clientIdN::recv(ack).0        <qos=2> clientIdN::recv(pubrec).clientIdN::send(PUBREL).          clientIdN::recv(pubcomp).0      fi    < not(contains(clientIdN) and contains(clientIdN_topic)) > skip.0   fi }

Listing 3. General form of an ambient representing a broker.

1.  broker[ 2.      // One process abstraction per topic 3.      proc topic1(topic, qos, retainFlag, payload){ ... } 4.   | ... 5.   | proc topicK(topic, qos, retainFlag, payload){ ... } 6.    // One persistent memory cell per topic 7.   | topic1[ ... ] 8.   | ... 9.   | topicK[ ... ] 10.   | !::recv(packetType, clientId).if 11.        <packetType=CONNECT> clientId::send(CONNACK).if 12.          <contains(clientId)> skip.0 13.          <not contains(clientId)> skip.clientId[0] 14.         fi 15.        <packetType=DISCONNECT and contains(clientId)> del clientId.0 16.      fi 17.   | !::recv(packetType, clientId, topic).if 18.        <packetType=SUBSCRIBE> let x=clientId+_+topic in topic#send(). 19.         topic#recv(qos,msg).clientId::send(SUBACK). 20.          clientId::send(PUBLISH,broker,topic,qos,1,msg).if 21.           <qos=0 and contains(x)> skip.0 22.            <qos=1 and contains(x)> clientId::recv(ack).0 23.            <qos=2 and contains(x)> clientId::recv(pubrec). 24.              clientId::send(PUBREL).clientId::recv(pubcomp).0 25.            <qos=0 and not contains(x)> skip.x[0] 26.            <qos=1 and not contains(x)> clientId::recv(ack).x[0] 27.            <qos=2 and not contains(x)> clientId::recv(pubrec). 28.              clientId::send(PUBREL).clientId::recv(pubcomp).x[0] 29.         fi 30.        <packetType=UNSUBSCRIBE> let x=clientId+_+topic in topic#send(). 31.         topic#recv(qos,msg).clientId::send(UNSUBACK).if 32.           <contains(x)> del x.0 33.           <not contains(x)> skip.0 34.         fi 35.      fi 36.   | !::recv(packetType,clientId,topic,qos,retainFlag, payload).if 37.      <packetType=PUBLISH and qos=0 and retainFlag=1> topic#send(qos,payload). 38.         topic#recv().topic(topic,qos,0,payload).0 39.      <packetType=PUBLISH and qos=0 and retainFlag=0> 40.         topic(topic,qos,0,payload).0 41.      <packetType=PUBLISH and qos=1 and retainFlag=1> topic#send(qos,payload). 42.         topic#recv().clientId::send(PUBACK).topic(topic,qos,0,payload).0 43.      <packetType=PUBLISH and qos=1 and retainFlag=0> clientId::send(PUBACK). 44.         topic(topic,qos,0,payload).0 45.      <packetType=PUBLISH and qos=2 and retainFlag=1> topic#send(qos,payload) 46.         topic#recv().clientId::send(PUBREC).clientId::recv(pubrel). 47.         clientId::send(PUBCOMP).topic(topic,qos,0,payload).0 48.      <packetType=PUBLISH and qos=2 and retainFlag=0> clientId::send(PUBREC). 49.         clientId::recv(pubrel).clientId::send(PUBCOMP). 50.         topic(topic,qos,0,payload).0 51.      fi 52.  ]

2.4.3. An Example

Let us consider a simple IoT system composed of a motion sensor, a light sensor, a lamp and a CCTV camera. An arduino microcontroller is used to control the lamp and the camera based on the sensors’ outputs. The motion sensor outputs 1 if movement is detected nearby and 0 otherwise. The light sensor outputs the light level as a value between 0 and 1000. When it gets sufficiently dark (light level < 330) the microcontroller must turn the lamp on. The lamp is turned off otherwise. When movement is detected, the microcontroller must turn the CCTV camera on to record the scene; otherwise the camera is off. These devices communicate using the MQTT protocol, as depicted in Figure 4. It is assumed that the broker runs on some server in the network. The sensors are publishers and the actuators (i.e., the lamp and the camera) are subscribers. The microcontroller is both a publisher and a subscriber. The light sensor publishes the light level on the topic “light” and the motion sensor publishes its measurement on the topic “motion”. The microcontroller subscribes to both the “light” and the “motion” topics. It also publishes on two topics: the “lamp” topic to send control commands to the lamp, and the “camera” topic to control the camera. Consequently, the lamp subscribes to the “lamp” topic and the camera subscribes to the “camera” topic. The motion sensor and the light sensor are specified in Listing 4 using the general template provided in Listing 1. Note that these are pure publishers. The specifications of the lamp and the CCTV camera are given in Listing 5. The microcontroller is specified in Listing 6, and the full system specifications are given in Appendix B.

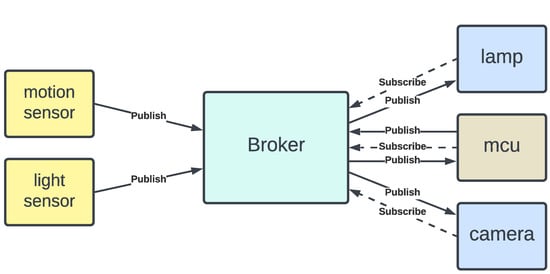
Figure 4. Architecture of a simple MQTT-based IoT system.

Listing 4. Specification of the motion sensor and the light sensor.

motion_sensor[   broker::send(CONNECT, motion_sensor).broker::recv(ack).   broker::send(PUBLISH, motion_sensor, motion, 1, 1, 1).   broker::recv(pubrec).broker::send(PUBREL).broker::recv(pubcomp).0 ] | light_sensor[   broker::send(CONNECT, light_sensor).broker::recv(ack).   broker::send(PUBLISH, light_sensor, light, 1, 1, 300).   broker::recv(pubrec).broker::send(PUBREL).broker::recv(pubcomp).0 ]

Listing 5. Specification of the lamp and the camera.

lamp[    !broker::recv(packetType, _, topic, qos, retainFlag, payload).if        <packetType=PUBLISH and qos=0 > skip.0        <packetType=PUBLISH and qos=1 > broker::send(PUBACK).0        <packetType=PUBLISH and qos=2 > broker::send(PUBREC).           broker::recv(pubrel).broker::send(PUBCOMP).0        fi    | broker::send(CONNECT, lamp).broker::recv(ack).        broker::send(SUBSCRIBE, lamp, lamp).broker::recv(suback).0 ] | camera[    !broker::recv(packetType, _, topic, qos, retainFlag, payload).if        <packetType=PUBLISH and qos=0> skip.0        <packetType=PUBLISH and qos=1> broker::send(PUBACK).0        <packetType=PUBLISH and qos=2> broker::send(PUBREC).           broker::recv(pubrel).broker::send(PUBCOMP).0     fi    | broker::send(CONNECT, camera).broker::recv(ack).        broker::send(SUBSCRIBE, camera, camera).broker::recv(suback).0 ]

Listing 6. Specification of the microcontroller.

mcu[     !broker::recv(packetType, _, topic, qos, retainFlag, payload).if         <packetType=PUBLISH and qos=0> Q(topic,payload,broker,mcu,lamp,camera).0         <packetType=PUBLISH and qos=1> broker::send(PUBACK).            Q(topic,payload,broker,mcu,lamp,camera).0         <packetType=PUBLISH and qos=2> broker::send(PUBREC).broker::recv(pubrel).            broker::send(PUBCOMP).Q(topic,payload,broker,mcu,lamp,camera).0         fi     | broker::send(CONNECT, mcu).broker::recv(ack).         broker::send(SUBSCRIBE, mcu, light).broker::recv(suback).         broker::send(SUBSCRIBE, mcu, motion).broker::recv(suback).0     | proc Q(topic,payload,broker,mcu,lamp,camera) {         if            <topic=light and payload<330> broker::send(PUBLISH,mcu,lamp,1,0,on).              broker::recv(puback).0            <topic=light and payload>=330> broker::send(PUBLISH,mcu,lamp,1,0,off).              broker::recv(puback).0            <topic=motion and payload=1> broker::send(PUBLISH,mcu,camera,1,0,on).              broker::recv(puback).0            <topic=motion and payload=0> broker::send(PUBLISH,mcu,camera,1,0,off).              broker::recv(puback).0         fi     } ]

3. Results

The formal semantics of CCA presented in Section 2.2 and the RV mechanism formalised in Definition 5 are implemented into a software tool in Java called ccaRV (for CCA Runtime Verification) [24]. The tool takes in input an CCA process and a property and checks at runtime if the execution of the process violates the property. This section presents an overview of the ccaRV tool and the experimental evaluation of the tool.

3.1. Overview of the ccaRV Tool

In order to verify an CCA process P against a property f with the ccaRV tool, one must write a program that consists of the process P and a declaration block that contains the property f. The grammar in Listing 7 describes the syntax of an ccaRV program. The keywords BEGIN_DECLS and END_DECLS delimit the declaration block. Note that ccaRV programs are case-sensitive. An example of an ccaRV program is given in Appendix B. Inside the declaration block, one can define context expressions using the keyword def. For example, defcontains(d,n) = { somewhere (d[n[0] | true] | true) }. One can also add the declaration of global names (using the keyword name) and the execution directives to control the execution of parallel processes.

Listing 7. Syntax of an ccaRV program, where P is a process and k is a context expression defined in Table 1; f is an LTL formula defined in Table 11; <Id> stands for an identifier (i.e., a name); e for the empty string; and <Val> is a non-negative integer number.

<Program> ::= <DeclarationBlock> P <DeclarationBlock> ::= e | "BEGIN_DECLS" <DeclarationList> "END_DECLS" <DeclarationList> ::= e | <Declaration> <DeclarationList> <Declaration> ::= "def" <Id> "(" <ParamList> ") = {" k "}" | "mode random"                 | "display code" | "length = " <Val> | "display congruence"                 | "name" <Id> <Params>                 | "ltl" (<Id> | e) "{" f "}" <ParamList> ::= e | <Id> <Params><Params> ::= e | "," <Id> <Params>

By default, the interleaving execution of parallel processes follows the FIFO (First In, First Out) policy in order to minimise the time a process waits to be executed. In the case of conflict (i.e., two or more processes are willing to execute), the sequential order as the processes appear in the program code applies. The execution directive mode random applies the FIFO policy, but in the case of conflict one of the conflicting processes is selected randomly for execution. In both cases, the process selected for execution performs only a single reduction and passes the control to another enabled process (if any). In practice, we strive for fair execution of concurrent processes so no process waits indefinitely for execution. The directive display code prints out the program code after each execution step. By default, only reduction steps are shown in the execution traces; the directive display congruence adds the congruence steps to the execution traces. The directive length = n causes the execution of the program to stop after n reductions, for some non-negative integer n. Global names are declared using the keyword name. The property for RV is specified using the keyword ltl followed by an LTL formula f between curly brackets. Optionally, a name can be given to the formula. Comments can be added anywhere in a program text in the same way as in the Java programming language.

The command line for executing an ccaRV program file myprog.cca is as follows.

$$\mathtt{java} -\mathtt{jar ccaRV}.\mathtt{jar} \left[-\mathtt{rn}\right]\mathtt{myprog}.\mathtt{cca}$$

The option -rn specifies the number n of runs, for some positive integer n. For example, with the option -r200 the process is executed 200 times and each run is checked against the property to verify. The default number of runs is one. This command line produces a verification report that tells for each run whether the property has been violated and how many execution steps have been performed. A verification report also shows the number of failed runs, the number of passed runs, and the total and average elapsed times. An excerpt of a verification report is shown in Figure 5. The execution trace of a failed run is logged till the point of failure in order to assist with debugging.

Figure 5. Example of a verification report.

3.2. Experimental Results

This section presents two sets of experiments designed to evaluate: (i) the accuracy of the RV decisions, and (ii) the RV overhead. The experiment environment comprised a 64-bit Toshiba laptop with an Intel Core i7 processor and 16 GB of RAM running a Windows 10 Pro operating system. The Java jar file for the ccaRV tool (version 1.0) used in the experiments can be obtained from [24]. It runs on Java RE version 11 and above. The source code of the ccaRV program for the first experiment is given in Appendix B and the source codes of the ccaRV programs for the second experiment can be generated using the Python program provided in Appendix C. All other applications were closed during the experiments.

3.2.1. Runtime Verification Accuracy

Consider the simple IoT system described in Section 2.4.3. The ccaRV program for this system can be found in Appendix B. Recall that the IoT devices communicate using an MQTT protocol. Sensor readings are published with the QoS 1 (see Listing 4). Since the purpose of RV is to detect the violation of a given property during the system execution, we have identified 10 properties that we know are violated or not based on the MQTT protocol requirements and the IoT system requirements. These properties are summarised in Table 14, where Z denotes any of the IoT devices and Y stands for a topic. For example, the property P7(Z,Y) is not violated if the client Z publishes on the topic Y without having subscribed to the topic Y. However, the property P7(Z,Y) is violated if the client Z subscribes to the topic Y before publishing (for the first time) on that topic. The property P7(Z,Y) is also violated if the client Z does not publish on the topic Y. The simple IoT system is verified for each of these properties using the command line:

$$\mathtt{java} -\mathtt{jar\; ccaRV}.\mathtt{jar} -\mathtt{r}\mathtt{2000}\mathtt{iot}.\mathtt{cca}$$

where iot.cca is the program file for the simple IoT system given in Appendix B. This means that for each property, the program is checked over 2000 runs in order to cover a large number of execution paths. The results are shown in Table 15, where “pass” means that no execution path violates the property, and “fail” means that one or more execution paths violate the property. It follows that the verification decisions of the ccaRV tool are accurate. Note that an RV decision “pass” does not guarantee the correctness of the system with respect to the corresponding property, since not all possible execution paths over all possible input values have been tested. But it gives more confidence that the system is correct with respect to that property.

Table 14. Property specifications.

Name	Property in LTL	Description
P1(Z)	[](trace("Z===(CONNECT")->	A client Z that sends a CONNECT
	<>trace("CONNACK)===>Z"))	request eventually receives
		a CONNACK acknowledgement.
P2	[](trace("SUBSCRIBE,camera")->	The camera requests a subscription
	<>trace("SUBSCRIBE,lamp"))	before the lamp.
P3(Z)	[](trace("Z===(PUBLISH")->	A device Z cannot publish
	contains(broker,Z))	if it is not connected to the broker.
P4	<>(trace("SUBSCRIBE,lamp,	The client lamp requests to subscribe
	motion"))	to the motion topic.
P5	[](trace("PUBLISH,	If the light level is <330 (e.g., 300),
	light_sensor,light,1,	eventually the lamp must turn on.
	1,300")-><>trace("1,0,on
	)===>lamp"))
P6	[](trace("PUBLISH,	If the light level is≥ 330 (e.g., 600),
	light_sensor,light,1,	eventually the lamp must turn off.
	1,600")-><>trace("1,0,off
	)===>lamp"))
P7(Z,Y)	<>((!contains(broker,Z_Y))	A client Z publishes on a topic Y
	&&trace("PUBLISH,Z,Y"))	it is not subscribed to.
P8	<>[](contains(broker,	The microcontroller mcu
	mcu_light))	subscribes to the light topic.
P9	<>(contains(broker,mcu)	The microcontroller mcu connects
	&&!contains(broker,lamp))	to the broker before the lamp.
P10	<>(trace("SUBSCRIBE,	The motion sensor subscribes to
	motion_sensor"))	a topic.

Table 15. RV accuracy.

Property	Expected Decision	Actual Decision over 2000 Runs
P1 (lamp)	pass	pass
P2	fail	fail
P3 (mcu)	pass	pass
P4	fail	fail
P5	pass	pass
P6	pass	pass
P7 (mcu, lamp)	pass	pass
P7 (motion_sensor, lamp)	fail	fail
P7 (camera, lamp)	fail	fail
P8	pass	pass
P9	fail	fail
P10	fail	fail

3.2.2. Runtime Verification Overhead

An RV overhead measures the additional load put on the system by an RV mechanism. This load must not affect the performance of the system too much for the RV mechanism to be practical and scalable. First, the system is run without RV, and the execution time is recorded. Then the system is run with the RV of some property. The difference in execution times is an estimate of the RV overhead. Three experiments are carried out to evaluate the RV overhead of the ccaRV tool. The first experiment considers the RV of a single MQTT system against a series of properties of increasing size. The size of a property is equal to 1 plus the number of (temporal, spatial, and Boolean) operators that occur in the property. We let 0 be the size of the property when RV is not applied during execution. The second experiment analyses the RV time overhead of context-related properties (context expressions) based on their sizes and the (execution) states at which they are verified. In the third experiment, a single property is checked against a series of MQTT systems of increasing size (i.e., the number of MQTT clients in a system). For the first experiment, we consider the MQTT-based IoT system presented in Section 2.4.3 and formally specified by the ccaRV program in Appendix B. This system is verified in ccaRV against a combination of the properties in Table 14. For each combination of properties, the system is run 200 times and the average execution time is measured, i.e.,

$$\mathtt{java} -\mathtt{jar\; ccaRV}.\mathtt{jar} -\mathtt{r}\mathtt{200}\mathtt{iot}.\mathtt{cca}$$

The 200 runs offer a good balance between the duration of the experiment and the coverage of the system execution paths. The results are given in Table 16 and depicted in Figure 6. It follows that the RV overhead increases with the size of the property.

Table 16. Average RV time over 200 runs with respect to the size of the property. The properties P1 to P7 are defined in Table 14. The property size 0 corresponds to an execution without RV, i.e., the baseline.

Property Size	Property in LTL	Average Execution Time (ms)	Standard Deviation (ms)
0	No property (baseline)	36.7	8.0
4	P1 (lamp)	38.4	8.4
13	P1 (lamp) && P3 (mcu)	45.2	8.9
16	P1 (lamp) && P3 (mcu) && P5	45.2	9.2
19	P1 (lamp) && P3 (mcu) && P5 && P1 (camera)	44.2	9.3
27	P1 (lamp) && P3 (mcu) && P5 && P1 (camera)
	&& P7 (mcu, lamp)	57.8	9.5
35	P1 (lamp) && P3 (mcu) && P5 && P1 (camera)
	&& P7 (mcu, lamp) && P7 (mcu, camera)	75.3	10.1

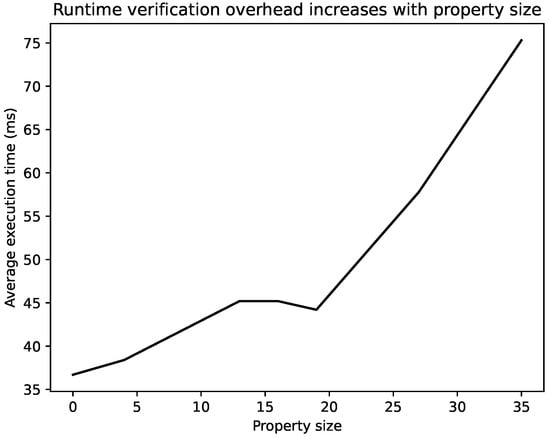
Figure 6. Graphical representation of the results in Table 16. It can be seen that the RV overhead increases with the size of the property. The property size 0 corresponds to an execution without RV.

The second experiment considers a number of context expressions of various sizes, describing specific locations in the ambient tree and compares the RV time of these context expressions at different execution states. These context expressions and their sizes are specified in Table 17. The temporal operator X (i.e., the temporal next) is used to determine the state at which a context expression is verified. For example, the context expression $\kappa$ is verified in the first state for the LTL formula $\kappa$, in the second state for the LTL formula $\mathtt{X}(\kappa )$, in the third state for the LTL formula $\mathtt{X}\left(\mathtt{X}\right(\kappa \left)\right)$, and so on. The MQTT-based IoT system presented in Section 2.4.3 is used for this experiment. Three execution states are chosen for this experiment: the initial state (state 0), the state 20 and the state 50. For each context expression in Table 17 and each of these states the system is run 200 times and the average RV time is measured. These measurements are summarised in Table 18. The results depicted in Figure 7 show that in each state the RV time increases with the size of the context expression; and for each context expression the RV time is practically the same across the states. These observations are due to the fact the ambient tree does not change much during the execution of this system.

Table 17. Examples of context expressions of various sizes. The size is equal to 1 plus the number of operators in the context expression.

Context Expression
Size	Specification
10	somewhere(broker[true]|true)&&
	somewhere(next(lamp[true]|true)|true)
22	somewhere(broker[true]|true)&&
	somewhere(next(lamp[true]|true)|true)&&
	somewhere(lamp[true]|camera[true]|true)&&
	somewhere(next(motion[true]|true)|true)
42	somewhere(broker[true]|true)&&
	somewhere(next(lamp[true]|true)|true)&&
	somewhere(lamp[true]|camera[true]|true)&&
	somewhere(next(motion[true]|true)|true)&&
	somewhere(broker[light[true]|true]|camera[true]|true)&&
	somewhere(mcu[true]|next(true)|true)
56	somewhere(broker[true]|true)&&
	somewhere(next(lamp[true]|true)|true)&&
	somewhere(lamp[true]|camera[true]|true)&&
	somewhere(next(motion[true]|true)|true)&&
	somewhere(broker[light[true]|true]|camera[true]|true)&&
	somewhere(mcu[true]|next(true)|true)&&
	somewhere(next(true)|camera[true]|true)&&
	somewhere(next(light[true]|next(true)|true)|true)

Table 18. Average RV time over 200 runs of context expressions of various sizes verified at specific states. The context expressions are defined in Table 17. The size 0 corresponds to an execution without RV, i.e., the baseline.

Context Expression Size	Average Execution Time (ms)			Standard Deviation (ms)
	State 0	State 20	State 50	State 0	State 20	State 50
0	35.7	35.7	35.7	8.1	8.1	8.1
10	36.2	36.5	36.3	8.2	8.2	8.3
22	37.1	37.2	36.9	8.1	7.8	9.6
42	37.5	37.7	36.9	8.2	9.8	8.9
56	38.6	38.5	38.3	11.9	10.8	8.3

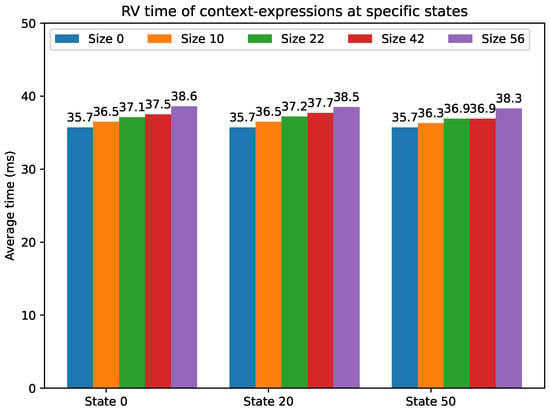
Figure 7. Comparison of RV time of context expressions of different sizes verified at different execution states.

For the third experiment, we consider a series of MQTT-based systems with 1 broker, 10 topics and a varying number of clients. The MQTT protocol is chosen in this experiment for its high scalability. The number of clients grows from 5 to 45, and each system comprises 40% of clients that are publishers, 40% of clients that are subscribers and 20% of clients that are both publishers and subscribers. The system is checked against the property <>(somewhere (broker[true] | true)), which says that the MQTT broker is eventually available. The results are recorded in Table 19. The column “Average execution time” shows the average execution time (without RV) of the system over 200 runs for each QoS level. The next column “Average verification time” shows the average execution time (with RV) of the system over 200 runs for each QoS level. The last column “Average verification overhead” shows the difference of the two execution times for each QoS level. The standard deviations of the measurements are given in Table 20. The graphs in Figure 8 show that the RV overhead increases with the size of the system. However, the QoS 0 incurs the least overhead and the QoS 1 the most. This is due to the difference in complexity of the MQTT protocol QoS levels as explained in Section 2.4.1. Moreover, Figure 9 shows that the RV overhead is small compared to the system execution time. Finally, Figure 10 confirms that QoS 0 is the fastest of the three MQTT protocol QoS levels. The MQTT-based systems used in this experiment can be reproduced automatically using the Python program in Appendix C.

Table 19. RV overhead for an MQTT protocol system. The first column represents the number of MQTT clients. The average time per run, in milliseconds (ms), is calculated over 200 runs.

Size	Average Execution Time (ms)			Average Verification Time (ms)			Average Verification Overhead (ms)
	QoS 0	QoS 1	QoS 2	QoS 0	QoS 1	QoS 2	QoS 0	QoS 1	QoS 2
5	23.1	25.7	26.2	28.2	27.2	30.4	5.1	1.5	4.2
10	64.0	71.9	72.6	72.4	75.4	87.8	8.4	3.5	15.2
15	143.0	159.5	160.8	150.5	165.2	179.7	7.5	5.7	18.9
20	238.7	276.4	271.5	253.7	315.5	283.3	15	39.1	11.8
25	397.4	458.1	448.6	430.8	558.1	505.7	33.4	100	57.1
30	615.2	721.3	694.9	672.1	825.1	741.5	56.9	103.8	46.6
35	925.1	1078.7	1048.7	997.2	1203.4	1158.5	72.1	124.7	109.8
40	1344.5	1563.2	1516.9	1438.2	1822.8	1650	93.7	259.6	133.1
45	1854.4	2154.2	2090.4	2013.4	2587	2309.7	159	432.8	219.3

Table 20. The standard deviation (over 200 runs) in milliseconds (ms) of the execution time and the verification time (in Table 19).

Size	Standard Deviation of Execution Time (ms)			Standard Deviation of Verification Time (ms)
	QoS 0	QoS 1	QoS 2	QoS 0	QoS 1	QoS 2
5	6.8	7.8	7.8	6.5	7.9	7.7
10	10.7	11.6	11.4	10.0	11.2	11.8
15	16.0	15.8	17.1	14.8	17.2	16.4
20	19.2	22.3	21.5	21.9	22.6	23.8
25	23.5	29.3	25.9	27.3	32.4	33.1
30	34.7	39.1	39.9	35.3	38.5	35.6
35	47.5	54.0	49.0	62.2	62.3	65.1
40	58.6	59.6	63.3	62.6	63.8	72.5
45	67.5	77.9	86.4	69.6	79.5	83.3

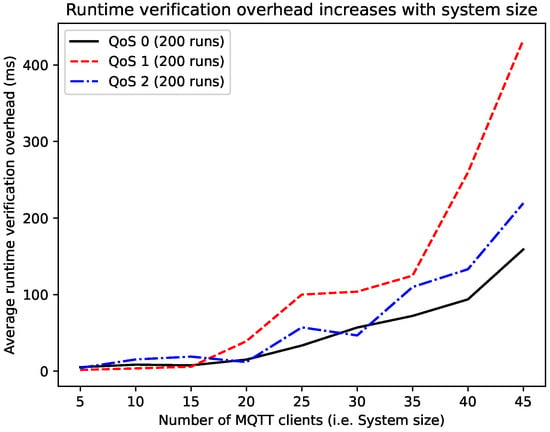
Figure 8. Comparison of RV overheads between MQTT QoS levels.

Figure 9. Comparison of the execution time and the RV time for each QoS level.

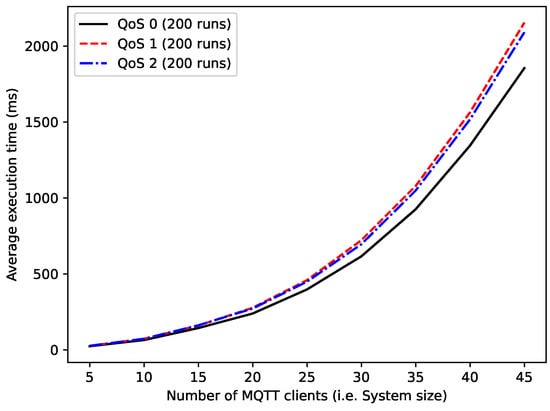
Figure 10. Comparison of the execution time of the three QoS levels of an MQTT protocol.

4. Discussion

RV is widely investigated in the literature. A survey presented in [25] addresses the problem of uncertainty in runtime monitoring and provided a detailed analysis of the different methods for handling incomplete traces. Similarly, [26] gives a survey on formal verification methods for smart contracts. LARVA [27] is an RV tool for Java programs that uses symbolic automata as the basis of the property specification language. ContractLAVA [28] is a LARVA-based RV tool for smart contracts. A study on the application of RV in robotics is carried out in [29]. They provide guidelines to help with the testing and verification of ROS (Robot Operating System)-based applications. Many researches have investigated the RV of distributed systems. Since a distributed system consists of subsystems that execute independently and interact through some message passing interfaces, the challenge is how to verify the correctness of a distributed system based on the different traces produced by the subsystems. The paper [30] proposes an approach to offline RV of distributed systems against interactions, which are formal models describing communications within a distributed system. They proposed a mechanism for spontaneously removing from subsystems the traces from an interaction that are no longer observed. A different approach is proposed in [31] that improves the asynchronous algorithm for RV of linearisability of concurrent algorithms [32]. They propose a generic methodology for building a lightweight runtime-verified linearisable algorithm from any presumably linearizable algorithm. All these approaches require the instrumentation of the program code for the purpose of RV. In our approach there is no need for the instrumentation of a program code because the RV mechanism is defined at the semantics level (see Definition 5).

Many approaches to decentralised monitoring in distributed systems have been investigated. Falcone [33] gives a review of some approaches to decentralized monitoring for systems with units of computation that are physically or logically distributed. An important challenge is how to synthesise decentralised monitors for a given property. The paper [34] proposes an approach for decentralised monitoring based on the Linear Temporal Logic (LTL). Similarly, ref. [35] argues that the LTL property to verify against needs to be decomposed into sub-formulae, which are then distributed amongst the local monitors attached to the subsystems of a distributed system. They propose an algorithm for distributing and monitoring LTL formulae, such that violations can be detected by local monitors alone. Ganguly et al. [36] propose an automata-based synchronous monitoring algorithm for the RV of synchronous distributed systems. In addition, ref. [37] proposes a framework to recommend efficient configurations of the monitoring system depending on the target specification using Machine Learning (ML). Past time CTL (Computation Tree Logic) is used in [38] to specify properties of IoT systems. They propose a procedure to derive, from a past-CTL formula, monitors that can be distributed on the edge devices. A domain-specific language for RV RML (Runtime Monitoring Language) is proposed in [39]. The formalization and implementation of RML is based on a trace calculus with fully deterministic rewriting semantics. Leotta et al. [16] propose an approach for RV of IoT systems based on the Prolog logic programming language. Compared to our approach, there is no need for generating a separate monitor for each property; rather a single monitor embedded in the semantics is used to evaluate any LTL formulae in accordance with Definition 5.

Some researchers have focused on developing tools for RV [40,41,42,43]. Aceto et al. [44] propose a synthetic benchmarking framework that targets the systematic evaluation of RV tools for message-based concurrent systems. An RV tool, detectEr, for software applications written in Erlang/OTP is presented in [45]. The tool runtime checks properties expressed in a safety fragment of the linear-time modal $\mu$-calculus. DAME [46] is an RV tool for multithreaded applications that detects violations of safety properties expressed in an epistemic logic, which is an extension of a past-time LTL. They propose an algorithm that automatically synthesizes decentralized monitors to evaluate the information at each thread and to detect and predict safety violations. In [47], an RV tool, R2U2, is presented that runs on an Arduino microcontroller and is designed to detect Aerobraking Control System (ACS) faults in rockets and trigger the appropriate mitigations. Compared to the ccaRV tool, none of these tools provides a mechanism for the RV of context-related properties.

It is challenging to design, develop, and validate a context-aware system that satisfies requirements, particularly when requirements can change at run time [48]. Fredericks et al. [49] propose run-time monitoring and adaptation of tests as suitable techniques for evaluating whether a Dynamic Adaptive System (DAS) satisfies, or is even capable of satisfying, its requirements given its current execution context. As stated in [50], systems that need to operate autonomously necessitate on-board RV technologies, to cater for the changing environment context. They identified important research questions to foster the discussion of ways to improve how to evaluate and compare tools for RV, particularly for cyber-physical systems. Some of these questions are addressed in [51] for unmanned aircraft systems to monitor safe operation with respect to operational limits such as geofencing. They propose an algorithm and describe parameters for the buffer distance used for the geo-fence boundary values. Ensuring the safety of complex Industrial Control Systems (ICSs) cannot be fully achieved during the design and development phases [52]. They propose a stream-based RV approach to ensure the safety of ICS at runtime. These works are closer to ours in the sense that the context of the system is catered for in the RV approaches. However, they still generate monitors from properties and introduce the system code, which are not necessary in our approach. Moreover, most of these works used artificially generated execution traces to evaluate the quality of their RV algorithms. In our case, real execution traces obtained from the actual execution of the system are used to evaluate the performance of our proposed approach.

5. Conclusions and Outlook

In this paper we have presented an RV tool for CCA called ccaRV. This tool can be used to verify that a system modelled in CCA satisfies desired properties. The property specification language is an extension of LTL with context expressions and other predicates so as to be able to specify context-dependent properties. This is particularly important for the verification of context-aware systems such as the IoT systems. A semantic approach to RV is proposed, where the RV mechanism is defined at the semantics level and not as an add-on. A consequence of this is that there is no need for the instrumentation of a system during verification. To achieve this, labelled reduction semantics is proposed for CCA, where a label represents the execution trace of a reduction step. The formal semantics of the property specification language is defined over an infinite sequence of states; each state in the sequence contains the current context and the execution trace of the last reduction step. Based on these semantics, the RV mechanism is formally defined and implemented into a software tool, ccaRV. This tool takes in input an CCA process and a property specified in LTL and produces a verification report that tells whether the execution of the process has violated the property. The ccaRV tool is evaluated using a case study of the MQTT protocol, which is de facto standard for IoT device communication. The results of the experiments show that the tool scales well and makes an accurate decision about whether a property is violated or not. In practice, the proposed ccaRV tool can be used during the development of a context-aware system (e.g., an IoT system) to verify that the system design specified in CCA satisfies the requirements of the system before the system is actually implemented in a high-level programming language like Java, C++, or Python.

In future work, we are interested in implementing the proposed semantic approach to RV for a high level programming language such as Python or Java. A key advantage of this approach is that users do not need to instrument their program code or to generate monitors for the property to verify. They just need to provide the property to check against their program. This is in contrast to current RV approaches that require that the program code be instrumented and the monitor be generated from the property to verify against.