Abstract
A decentralized control problem for vehicular platoon systems with heterogeneous dynamic behaviors is investigated in this paper. To simplify the controller design, a longitudinal model is established as an interconnected form. On this basis, a series of decentralized state feedback controllers are designed to ensure the individual stability, string stability and connective stability of the vehicular platoon system. Then, a new scenario in which additional vehicles are added to the platoon is also considered by developing an expanding construction system (ECS) based on the proposed longitudinal model. As a result, a corresponding controller can be designed as a new one of the decentralized controllers without changing the original control laws of the interconnected system. The stability conditions are presented with rigorous analysis by virtue of linear matrix inequality (LMI) for the interconnected system and the ECS. Simulation results are carried out to demonstrate the effectiveness of the proposed decentralized tracking controllers.
MSC:
93A15; 93C35
1. Introduction
Vehicle platoon control, also named string control [1,2], has been widely studied during the past five decades from various aspects since it is capable of improving traffic capacity and enhancing fuel efficiency; therefore there are many results to draw from within the research [3,4,5,6]. It is noteworthy that most of the early methods are based on centralized control [7], i.e., only a single controller obtains the system information and performs the control action, which may lead to poor reliability and expandability. In light of these constraints, a distributed control strategy is proposed with the development of computing techniques, and a main feature of this approach is that local communication among vehicles can be utilized.
A feedforward technique with communication is investigated and the string stability is achieved for a heterogeneous vehicle platoon with an arbitrary length [8]. The string stability is derived by employing wireless communication link [9]. Authors in [10] developed the concept of a semi-autonomous cruise system, and a small time gap can be achieved by the presented algorithm. Recently, some meaningful work [11,12,13] regarding the distributed tracking problem of truck platoon and vehicle platoon are introduced. However, most of the above achievements were realized by a wireless communication network.
In practical applications, uncertainties caused by various sources such as vehicle operation, sensor errors, and environmental conditions pose significant challenges to controller performance [14]. Currently, several studies [15,16,17] have been conducted to address the uncertainty. To reduce the influence of disturbances on the control performance of the vehicle exhaust system, robustness against external disturbances and sensor measurement errors is ensured based on the criterion [16]. In [17], a radial basis function neural network is considered to estimate uncertainties of vehicle parameters.
On the other hand, it is not easy to achieve accurate communication, and if the communication network between vehicles becomes invalid under attacks, the designed control law will take a risk of failure [18]. Meanwhile, when a vehicle adds to the platoon, the control protocols are required to redesigned due to the topology relationship changes, which may increase the algorithm complexity. To this end, some decentralized control methods [19,20,21,22] are introduced, i.e., the control law of each vehicle only employs its own acceleration and velocity, both of which are obtained via onboard sensors.
A decentralized control framework is established in [19] considering different road cases. In [20], the decentralized optimal control problem is addressed by minimizing travel time and energy consumption. In [21,22], the vehicle platoon systems are regarded as a large-scale network with overlapping structures, and then the inclusion conditions are utilized to deal with this kind of system by virtue of decomposition, contraction, and replacement, which constitute a considerably complicated calculation process. Although the results [19,20,21,22] can be used to address the issue caused by wireless communication networks, results are unavailable for a situation in which additional vehicles drive to the platoon.
Motivated by the above discussion, this work proposes a simple decentralized control method for multiple vehicle platoon systems without requiring complex computation. First, the vehicular platoon is constructed as an interconnected system with respect to the desired distance and velocity errors, instead of an overlapping form. Based on the interconnection relationship, the decentralized state feedback controllers are designed by virtue of Schur Complement Lemma and S-procedure. Further, the corresponding control laws are obtained via solving linear matrix inequalities (LMIs). Compared with the Riccati method [23,24,25], the LMI technique can directly verify the stability of the system by solving the matrix variables, which reduces the computational complexity. Note that a novel definition named plug and play control is proposed in [26,27] to deal with the case that a new part such as an actuator or a sensor is added to or removed from a single system. In [28], the author studies a situation of addition and removal of a system by employing the expanding construction method. Inspired by [26,27,28], in a situation involving adding a new vehicle one after another and the longitudinal construction of a vehicular platoon, it is easy to find the relationship between the new vehicular platoon and the original one. In this case, we establish a vehicle string with the expanding construction. Consequently, a control method is proposed for the newly added vehicle without changing the control laws of the original vehicle platoon. The stability analyses for the originally vehicle string and the newly added vehicle are given according to Lyapunov stability theorem, and the simulation results are utilized to show the effectiveness of the presented approach. The main contributions are summarized as follows:
- Different from [21,22], a new expanding construction system (ECS) is proposed for a vehicular platoon which can reduce the computing burden since the tanglesome matrix transformations are eliminated. By virtue of the ECS, when a new vehicle drives to the moving platoon, only the control law of the newly added vehicle is required to be designed while the original controllers of the platoon remain unchanged. Although [29] is also able to achieve this goal, the system matrix is required to be the Metzler matrix. Comparatively, the proposed method guarantees connective stability, and the Metzler system matrix no longer comes with the required conditions, thus facilitating its broad-ranging applications. In addition, the control scheme of the new vehicle is more flexible, and it can use the state feedback or output feedback, LQR, etc., which cannot be achieved in [29].
- A decentralized connection control strategy is presented in this work. Different from that in [30], the proposed method only uses the relative information on the position and velocity obtained by the onboard sensor, instead of the communication information between vehicles used in the controller proposed by [30]. As a result, the proposed control method can avoid the risk of controller failure caused by communication outage. Moreover, the ideal model for the leader vehicle varies depending on the surroundings, rather than being fixed with given values or a simple trajectory [31], which has certain practical significance.
- In addition to individual vehicle stability and string stability, connective stability is considered in this work. That is to say, even if the interconnected item between the vehicle and its front one is cut off, the proposed algorithm can still make sure that the whole platoon works well, i.e., connective stability is guaranteed despite the change in connective relationships. To the best of authors’ knowledge, there is no report that has investigated the vehicular platoon control problem from this perspective.
This paper is organized as follows: In Section 2, we establish the model of vehicular platoon systems. In Section 3 and Section 4, the decentralized connective controller design and a stability analysis of the original platoon system and expanded platoon system are given, respectively. Simulation examples are provided in Section 5, and the conclusions and future work are summarised in Section 6.
Notations: is the set of real numbers; denotes the absolute value of ; represents the transpose of ; stands for the diagonal matrix; is a positive definite matrix.
2. Vehicular Platoon Model
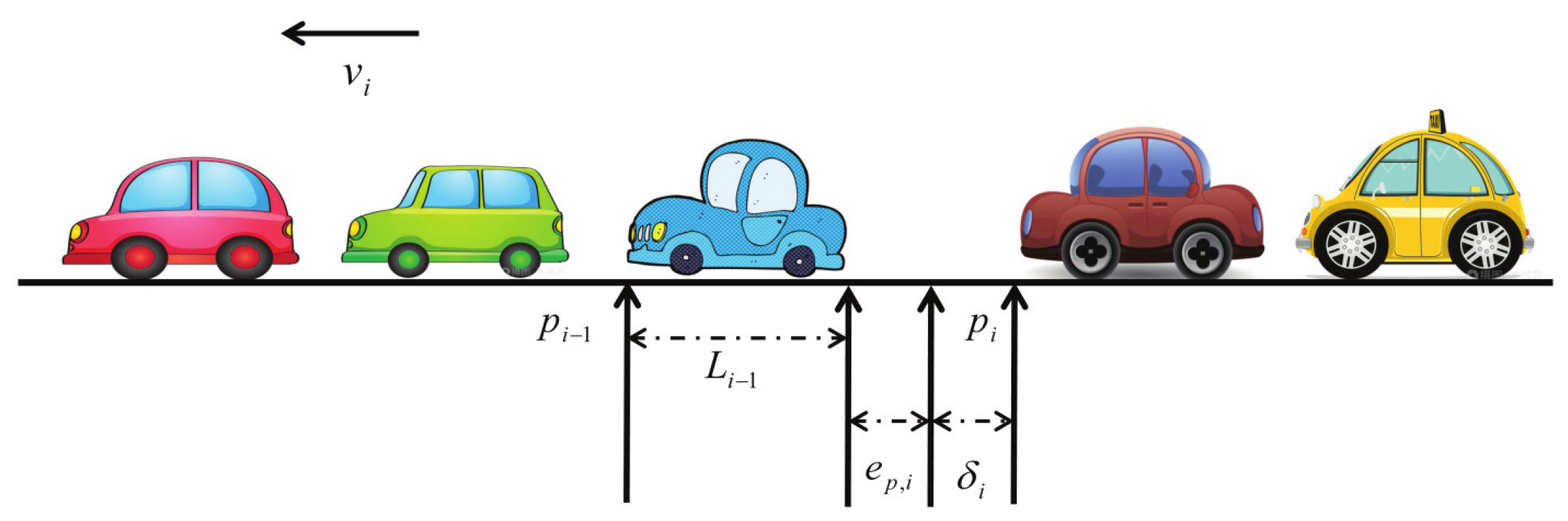
According to Newton’s second law, the vehicle (see Figure 1) can be established by
where , and are the position, velocity and acceleration of the vehicle, respectively. is the engine control input. is an engine time lag. Note that (1) can be regarded as a leading vehicle when .
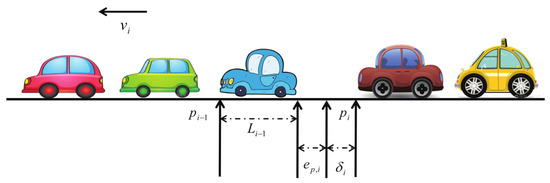
Figure 1.
Vehicular platoon running in a straight line.
Remark 1.
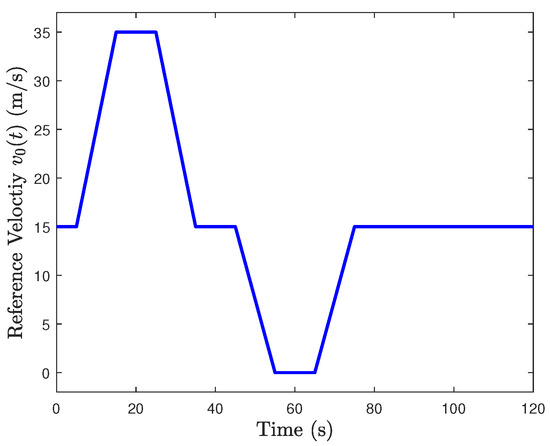
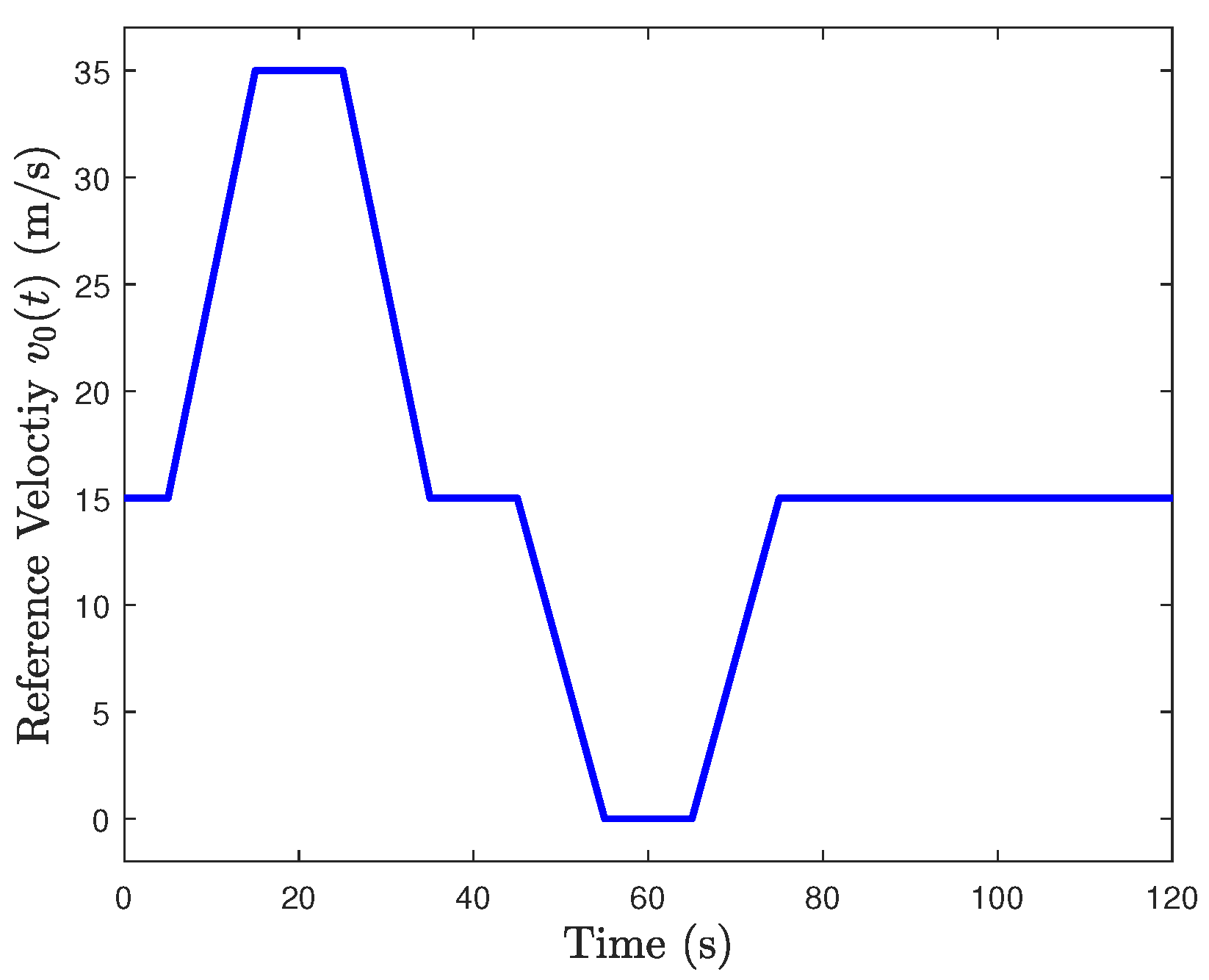
Compared with the second-order system, the third-order form is more accurate owing to the consideration of the engine dynamics. It follows from Figure 2 that the velocity of the leader vehicle is limited by the road environment, and its speed trajectory is modeled as shown in (2). Furthermore, for different practical cases, the trajectory is designed in different forms by analysing the road and weather conditions. In general, once the velocity of the leader is designed, it will no longer be possible to change. Although the time-varying velocity has also been considered in [32,33], it is a relatively simple curve, such as a profile formulated by a sine function, which makes it hard to describe complex road environments. Furthermore, we still believe that it is helpful to investigate the linear vehicular platoons from the new viewpoint, many ambitious studies have also been conducted in recent years [18,19,20,34].

Figure 2.
Trajectory of .
The position and velocity errors are defined as = , = −, where the known constants, and , are the vehicle length and the desired distance.
Computing the derivative of , and yields
Let and ; then, we have
where
with being the interconnection matrix.
Remark 2.
The vehicle model (4) is an interconnected model, which can be further built as a large-scale system with expanding construction to achieve connective stability. However, it is regarded as an overlapping structure model in [21,22], which may cause more complex calculations due to the decomposition, contraction and replacement of the matrix. Moreover, it is difficult to tackle the problem of adding a new vehicle in the platoon control model using the overlapping model in [21,22].
Remark 3.
It follows from in (4) that we consider a heterogeneous platoon in this paper rather than a homogeneous one [35,36,37]; hence, the constructed control laws are also heterogeneous, which can improve system performance [5].
The objective of this work is to design the decentralized control law to obtain individual vehicle stability (see Definition 1), string stability (see Definition 2), and connective stability (see Definition 3).
Definition 1.
In the platoon, if each vehicle can maintain the desired vehicle distance and velocity, i.e., and . Then, it is said to be stable for individual vehicles.
Definition 2
([33]). If given ϱ > 0, there is ϵ > 0, such that where represents or . Then, the tracking error of dynamics (1) is said to be string-stable.
Definition 3.
If the interconnected matrix is a matrix from one to zero, i.e., →, the system’s individual stability and string stability still can be guaranteed. Then, it is said to be connectively stable.
Remark 4.
According to [33], Definition 2 shows weak string stability, which means that the states of all vehicles in the platoon are bounded.
3. Main Results of Vehicles with Interconnected Form
A decentralized controller is designed as
Further, the above equation can be expressed as a compact form, that is
where , and
Before presenting the main result of this work, we first introduce the following assumption.
Assumption 1
([38]). The interconnection relationship satisfies
with being a constant and
Remark 5.
It should be pointed out that the interconnection relationship represents an influence of vehicle on vehicle ; therefore, it can be regarded as a disturbance. Assumption 1 is a boundedness condition and is reasonable since is a constant matrix and there always exist and such that the inequality (7) is satisfied.
Theorem 1.
The decentralized connective stability problem is solvable by virtue of , if the matrixes , , and parameters , so that (8) holds. Moreover, the gains can be computed by .
where is the identity matrix with appropriate dimensions and
Proof.
Select a Lyapunov function as
with
In order to stabilize the system, one has
which is equivalent to
Based on Assumption 1, this gives
□
Remark 6.
It follows from (12) that this is not an LMI due to the existence of items and . Among the existing methods, one of which is to let and . Another one is to let and . However, either way, the gain is computed by . Then, an important precondition is that the rank of matrix must be full, which is actually a strong assumption. In order to avoid this problem, in this paper, another handling approach is adopted which is less restrictive. The specific process is introduced below.
Pre- and post-multiplying and letting and produces
where = . This implies that Theorem 1 holds.
Stability Analysis: It follows from Theorem 1 that goes to zero when . Furthermore, it can be deduced from that the position and velocity errors will approach zero. Furthermore, as indicated by [37], the change in the matrix is considered in the restraint of the interconnected item; hence, the objective of this paper has been obtained.
4. Main Results of Vehicles with Expanding Construction Form
Based on the result of Section 3, we will consider a new situation in this section, that is, while the system (6) is normally running, a new vehicle is added to (6) one after another, which forms the expanding construction of large-scale systems. However, for the expanding construction system including () vehicles, the traditional method requires the design process in Section 3 to be repeated; hence, () control laws are calculated, which increases the computation complexity. In this section, we consider the relationship between the newly added ()th vehicle and the original N vehicles, and this relationship satisfies Assumption 2. Therefore, the proposed scheme only needs to compute the control law of the ()th vehicle, which greatly reduces the cost of controller design.
First of all, the newly added vehicle is modeled by
and based on a similar process, one can obtain
with , and
Hence, the vehicle system with expanding construction is established, i.e.,
with and
Similarly, for , we have the following assumption condition.
Assumption 2
([38]). The interconnection relationship satisfies
with being a constant and
Similarly to Remark 6, is regarded as a disturbance. Hence, Assumption 2 is also a boundedness condition.
Theorem 2.
The decentralized connective control problem including vehicles is solvable with and without changing the original control laws , if there exist matrices , , and parameters , such that inequalities (16) hold. Moreover, the control gain is determined by .
with , and
Proof.
Select a Lyapunov function as
with
Similarly, under Assumption 2, calculating the time derivative of and employing the S-procedure and Schur Complement Lemma lead to
where is a parameter and
Via pre- and post-multiplying and letting and , we have
where diag. This completes the proof of Theorem 2. □
Remark 7.
In this paper, the same controllers (i.e., state feedback) are designed for both the original vehicles and newly added vehicle. However, it is worth noting that the observer-based control technique still can be used for the newly added vehicle if its state is unmeasurable. Furthermore, if better performance is achieved, a corresponding control scheme can be adopted, such as pole placement, annular domain finite-time stability, LQR, etc., which will be the aim of our future work. As a consequence, the proposed method is more useful and practical.
Remark 8.
It is noted that the matrixes , , and parameters , with of the original system are known in the LMI of Theorem 2 since they have been computed by LMI (7). However, the global design not only needs to compute the matrixes , , and parameters , , but also the matrixes , , and parameters , , with also needing to be computed again. Hence, the computational complexity is lower when using the proposed method instead of the global design.
Stability Analysis: It follows from Theorem 2 that converges to zero when , which means that and are asymptotically stable. Moreover, and will also go to zero, that is, individual vehicle stability and string stability are achieved. In addition, because the change in the matrix is considered in the restraint of the interconnected item, the connective stability can be obtained.
5. Simulation Results
This section aims at verifying the correctness of the theoretical results, and it is divided into two subsections for interconnected systems (five vehicles) and for expanding construction systems (six vehicles), respectively. Firstly, the parameters of the leading vehicle are given as follows: m, m/s, and the reference velocity can be seen in Figure 2.
5.1. Simulation for Interconnected Form
First, the choices for the initial values and design parameters are given as follows: 0.5, 0, 0, 3, 0, 0, 0.1, , , and , .
It is worth noting that for , when is chosen as a large value, the position error and velocity error will converge slowly; when it is selected as the smaller value, then the errors converge faster. Therefore, a trade-off needs to be made based on the real situation. Furthermore, , , and are selected as positive numbers, but they have little influence on the convergence rate.
According to the initial values of , the interconnected relationship , and parameters , , and , matrices and with can be computed by solving the LMI (5). Then, the control gain can be calculated by and we have , = , = , = , = .
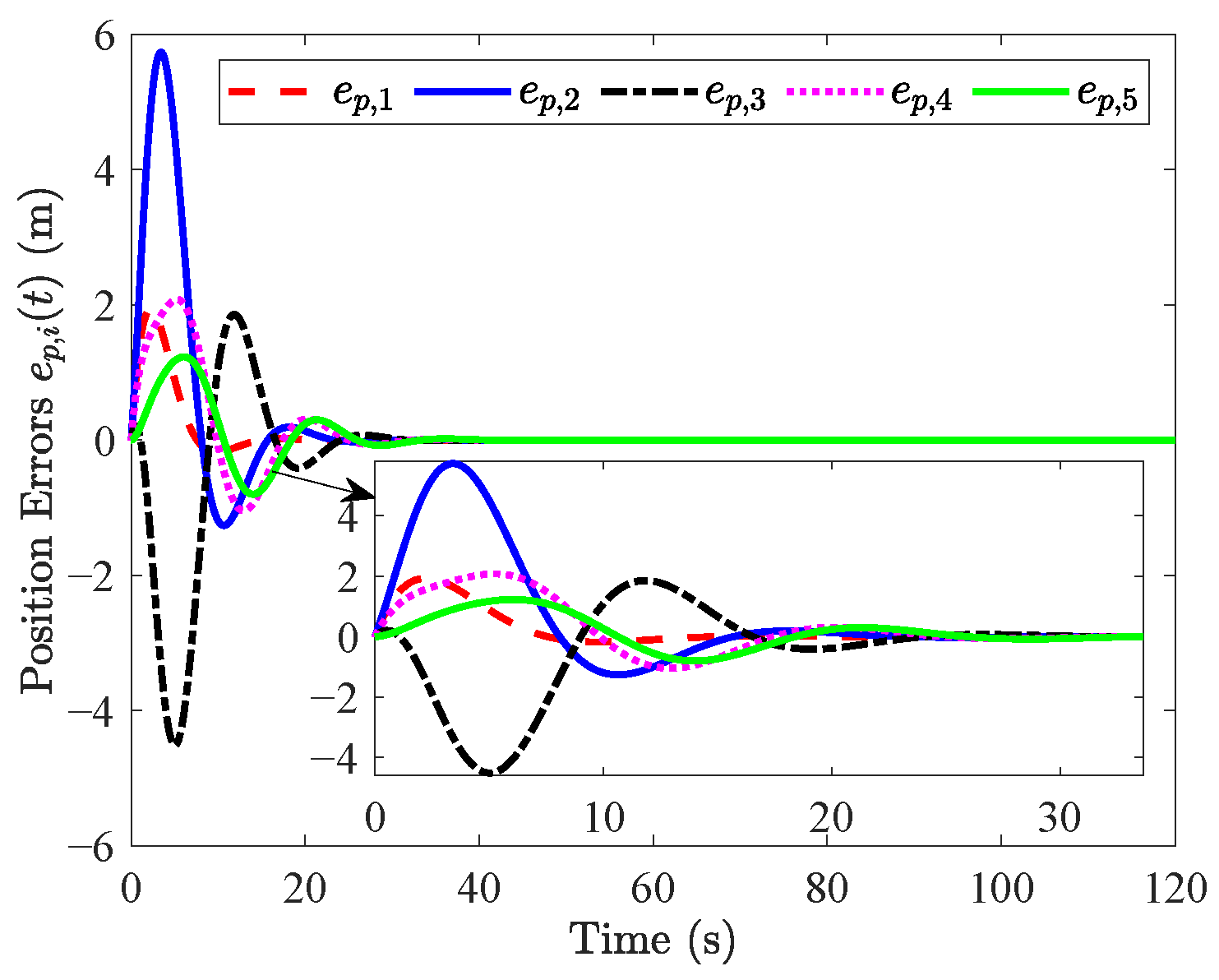
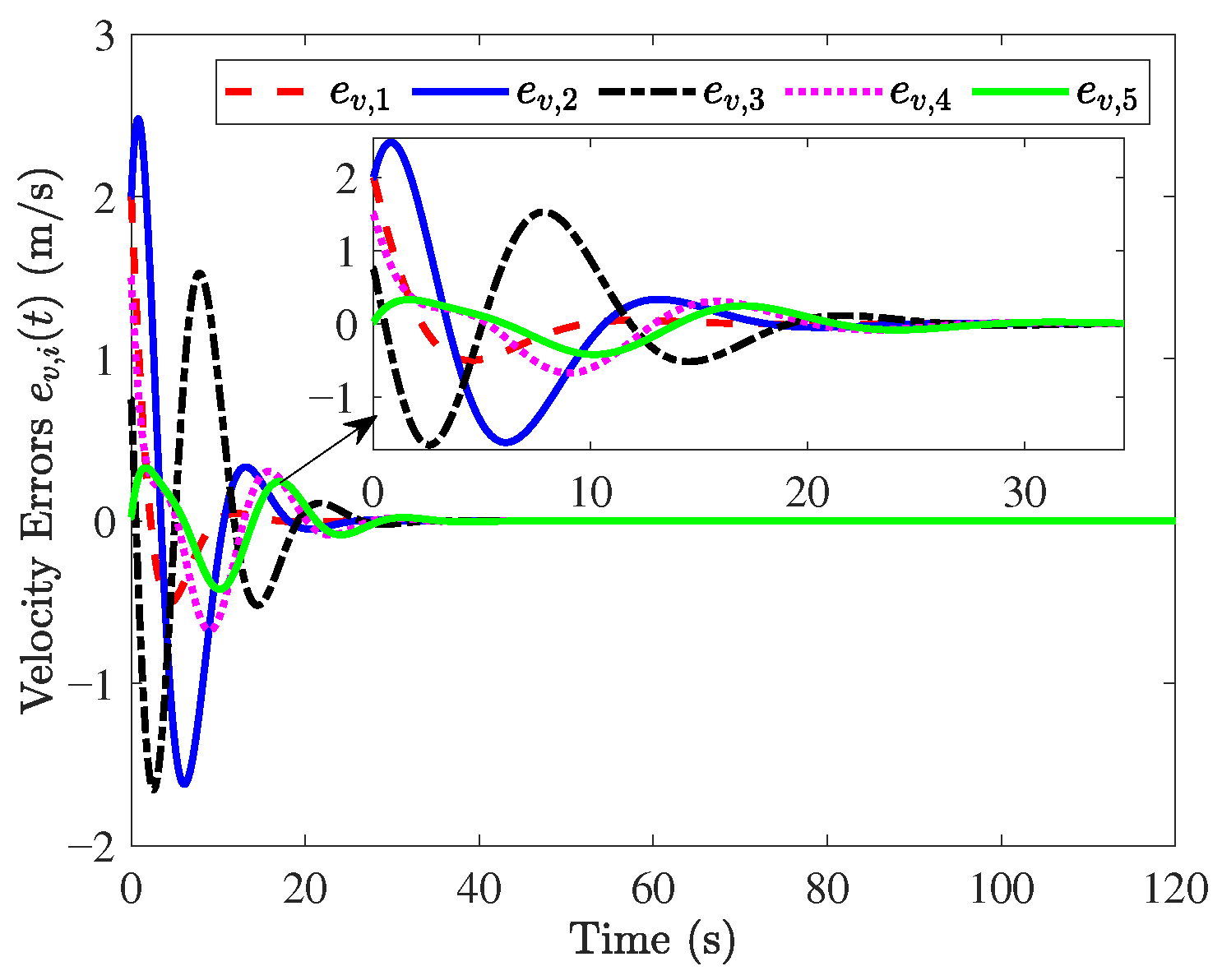
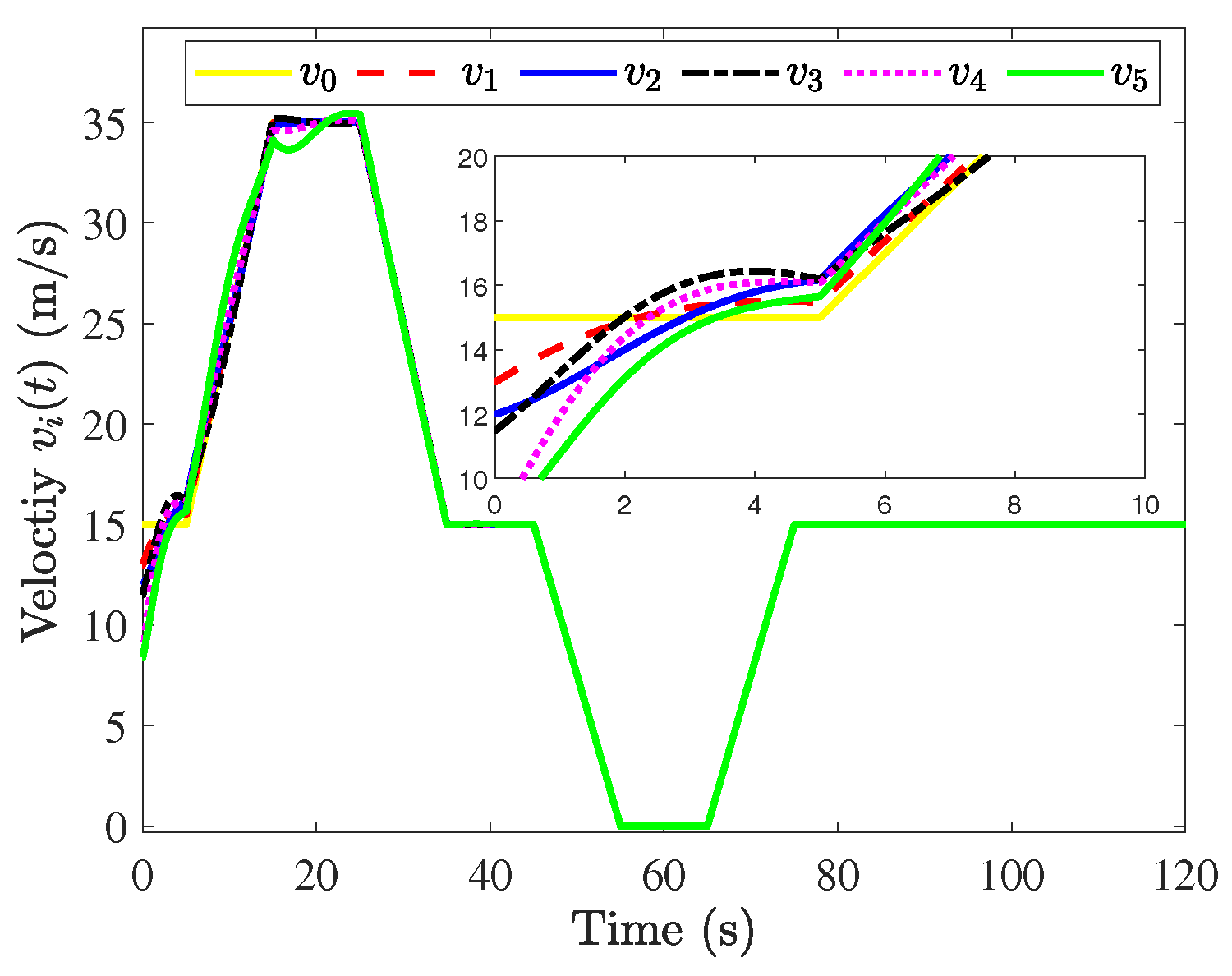
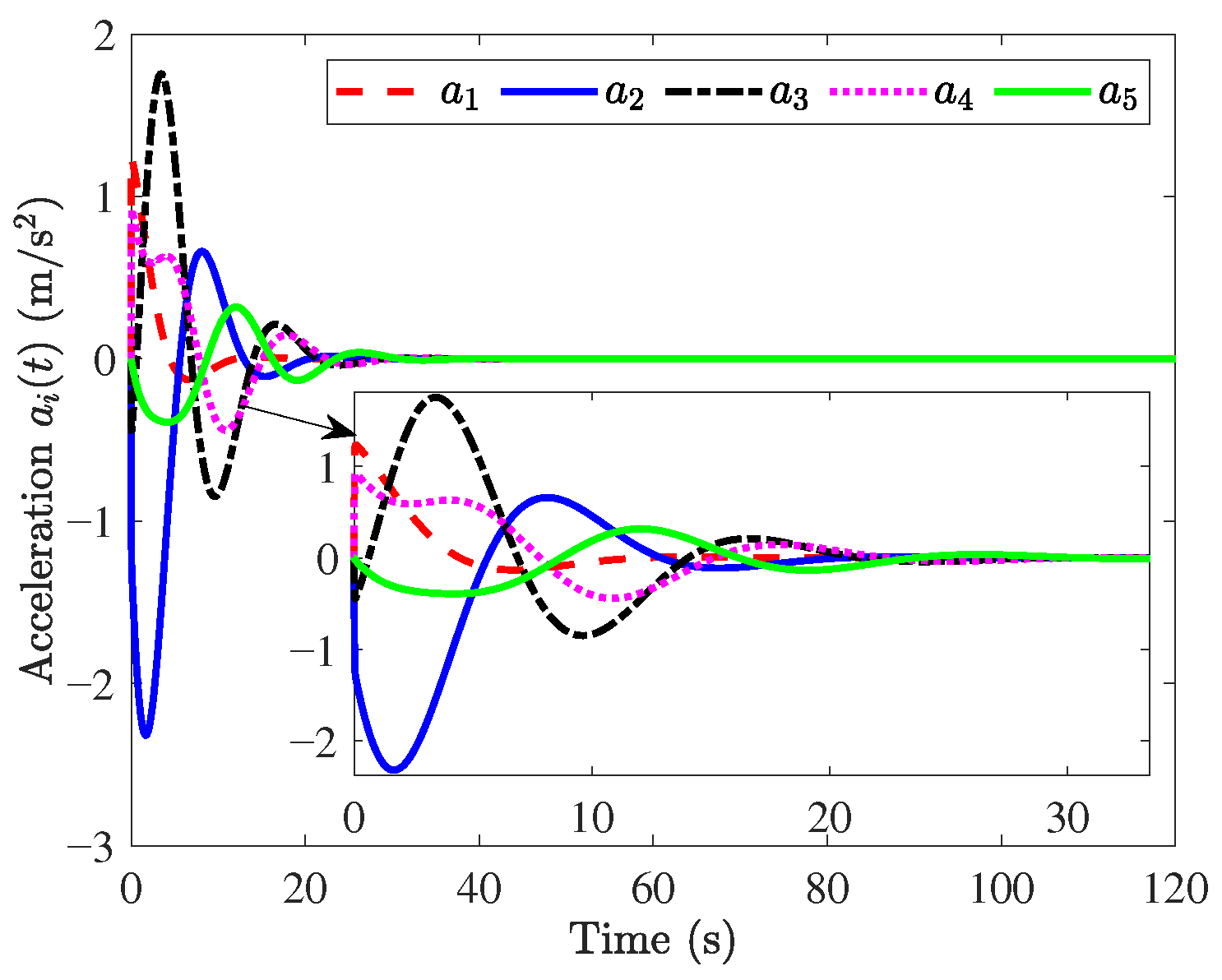
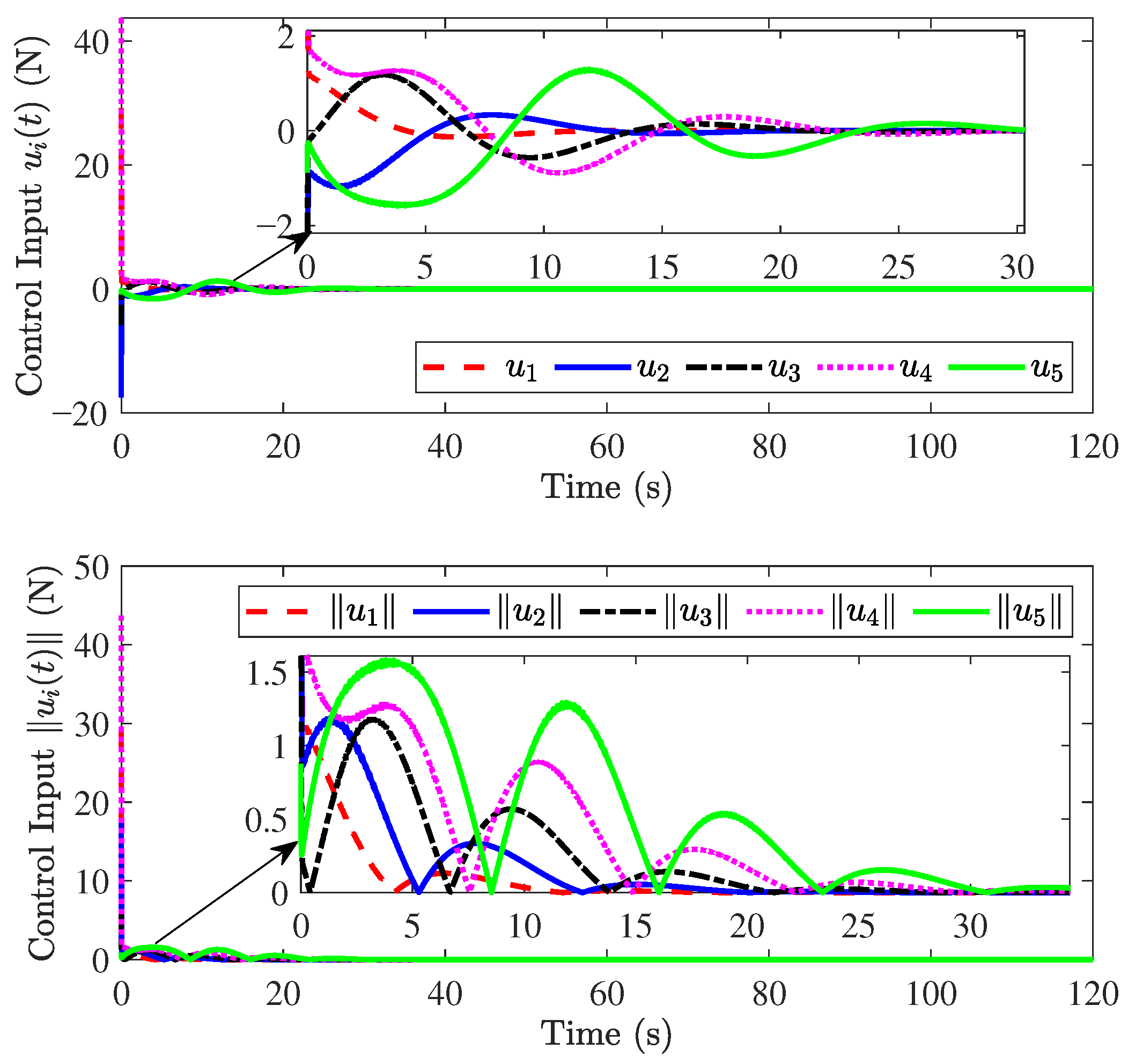
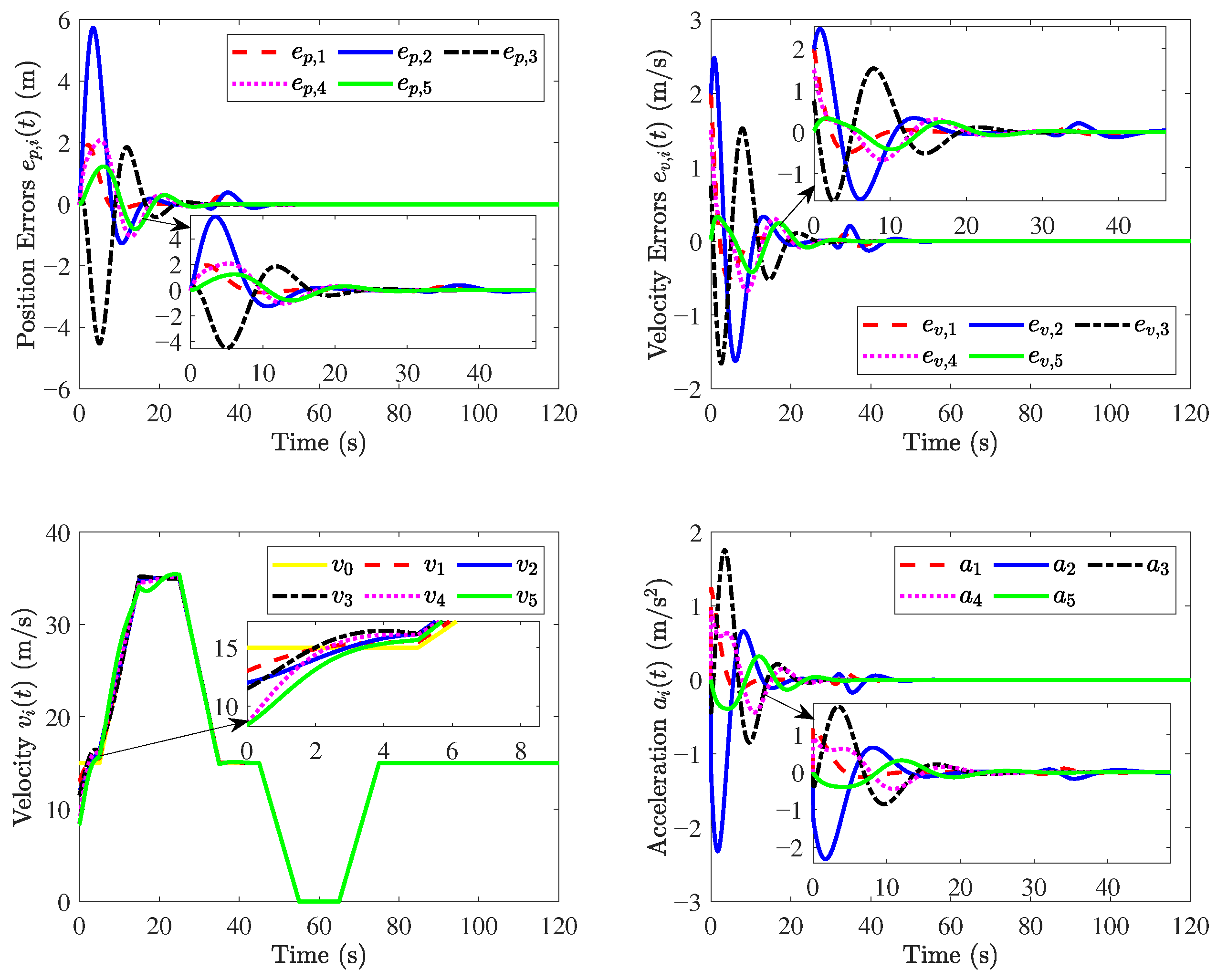
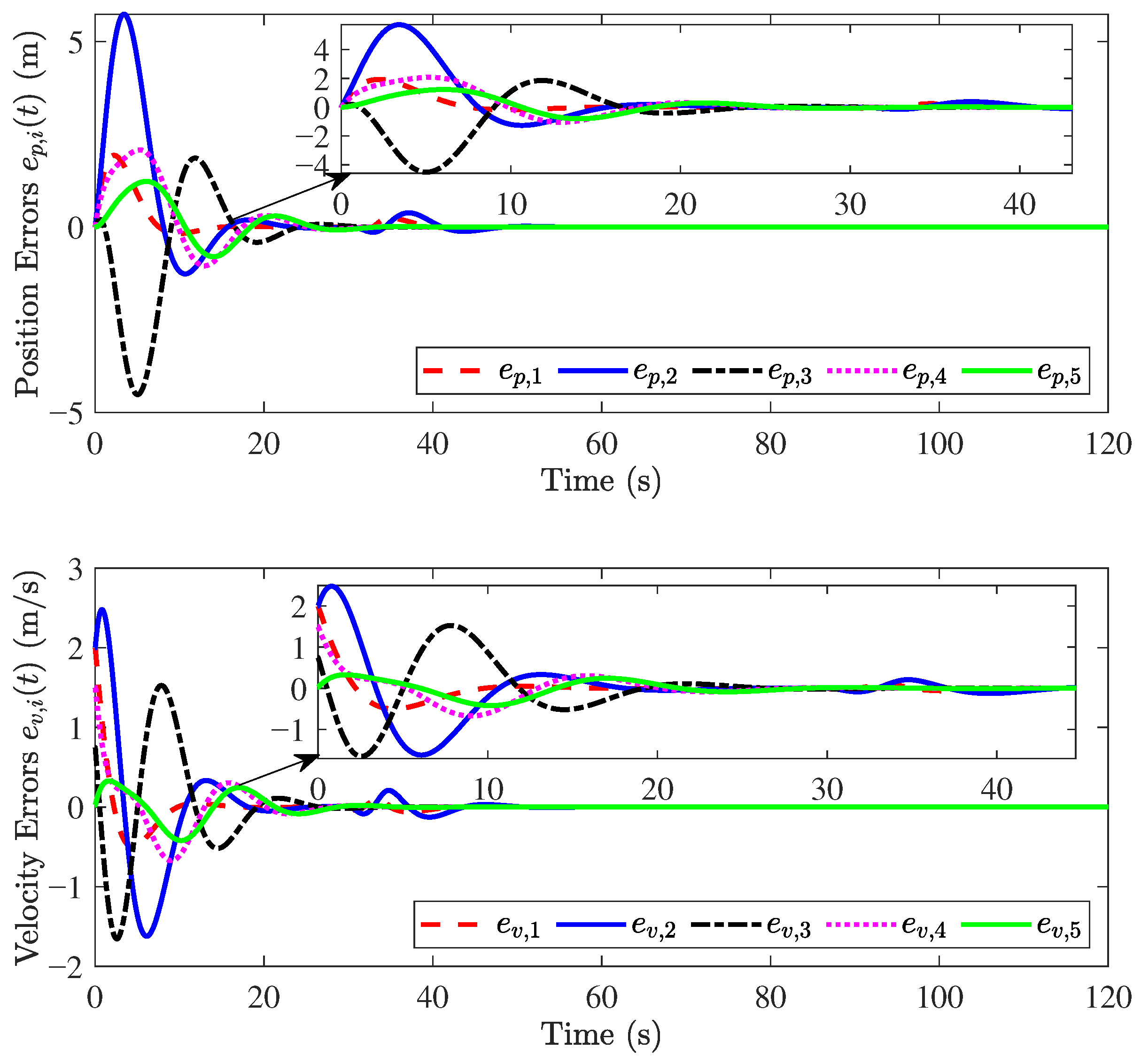
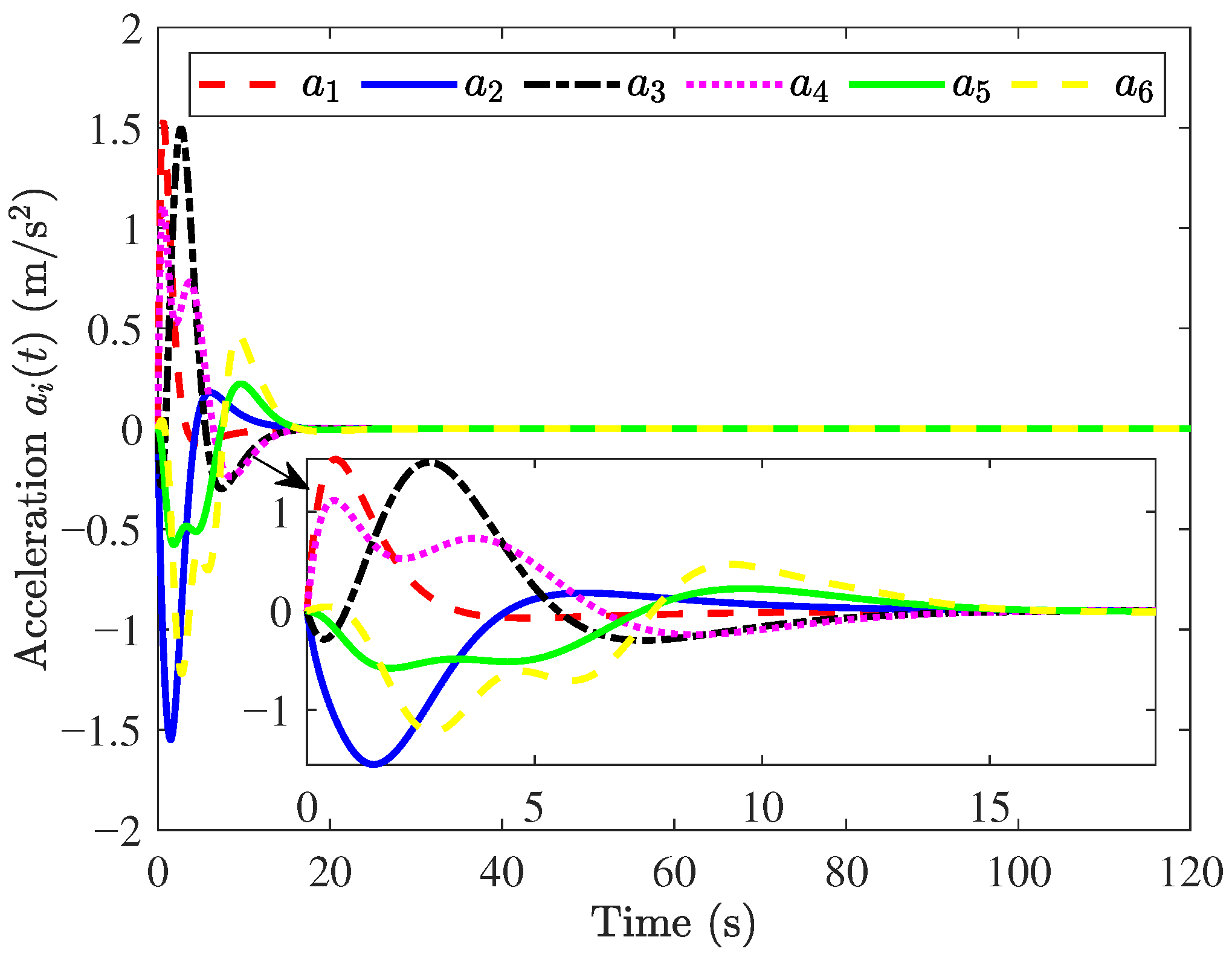
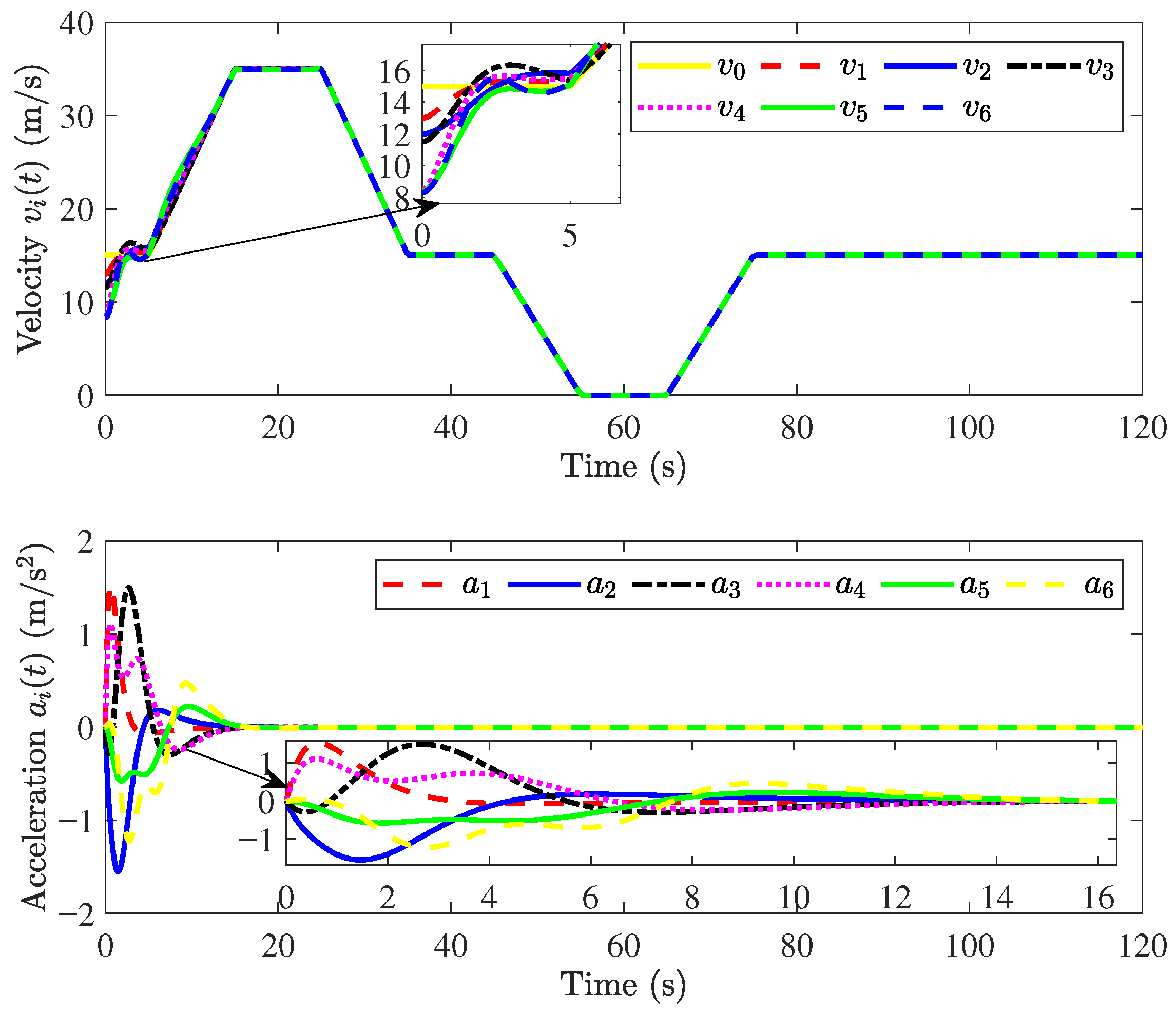
The simulation results are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Figure 3 and Figure 4 show that position errors and velocity errors converge to zero, which means that objectives (1) and (3) are obtained where the constant distance policy is adopted. It can be seen from Figure 5 that each vehicle tracks the reference velocity . In Figure 6, the responses of acceleration are given. It can be observed from Figure 7 that curves of the control input and its norm are shown.
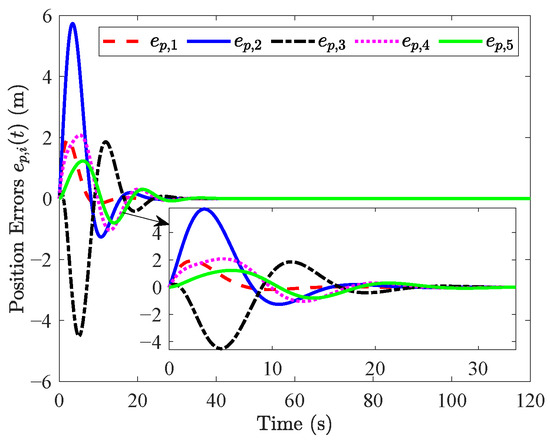
Figure 3.
Responses of .
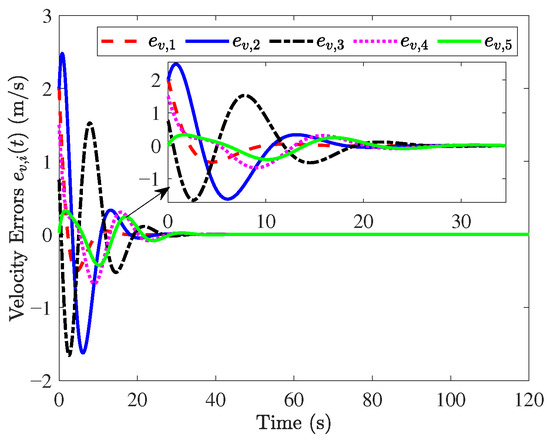
Figure 4.
Responses of .
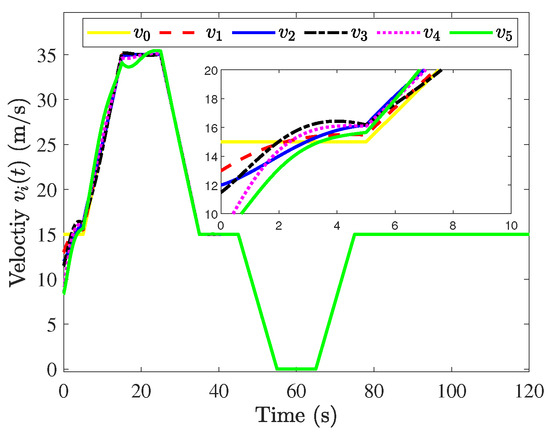
Figure 5.
Responses of .
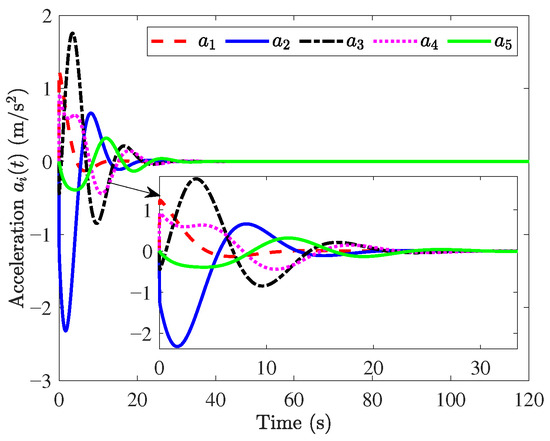
Figure 6.
Responses of .
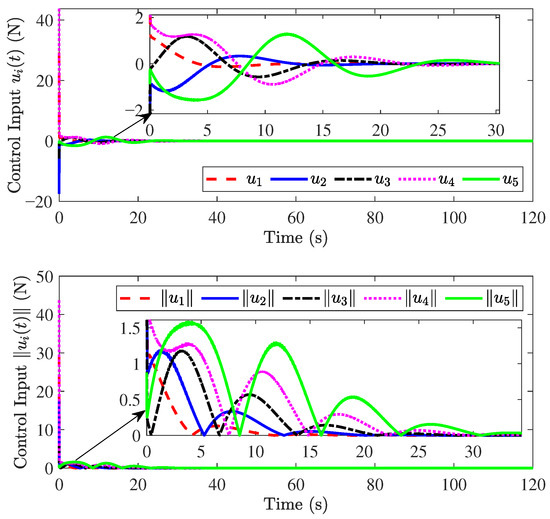
Figure 7.
Responses of and .
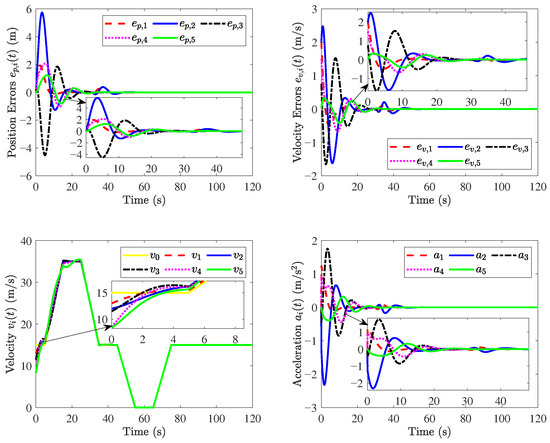
Figure 8.
Responses after cutting .
In order to explain objective (2), is changed to zero, and the corresponding results are shown in Figure 8, from which we can see that the trajectories are not affected. The reason lies in the fact that the change in the interconnected item from one to zero was considered during the process of controller design based on Assumption 1. As a result, when varies from one to zero, it does not affect the control performance of other vehicles and the platoon is not divided into two strings but runs well as a whole string.
Furthermore, an external disturbance is added to the first vehicle after the system runs for 30 s, and the result is shown in Figure 9, from which we can see that the string stability still can be guaranteed.
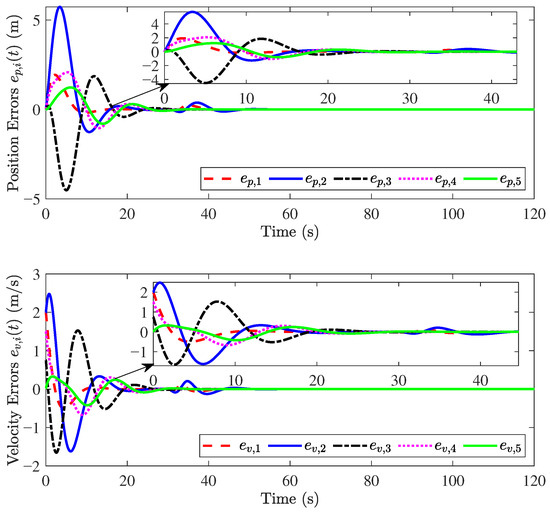
Figure 9.
Responses for the first vehicle with disturbance.
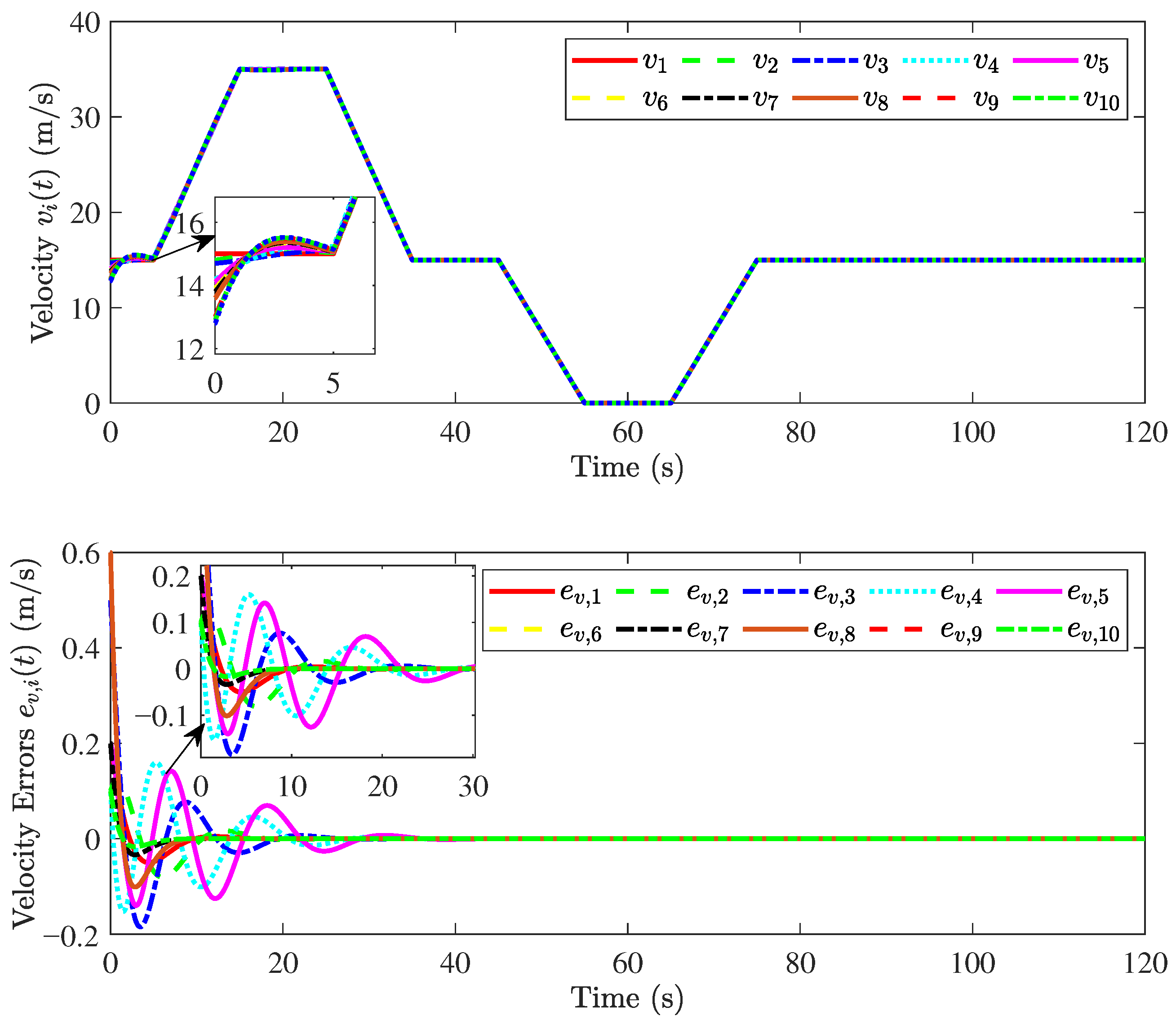
On the other hand, we increase the number of vehicles in the simulation result, and verify that the proposed method is still effective. The velocity and acceleration response curves of the ten vehicles are shown in Figure 10.
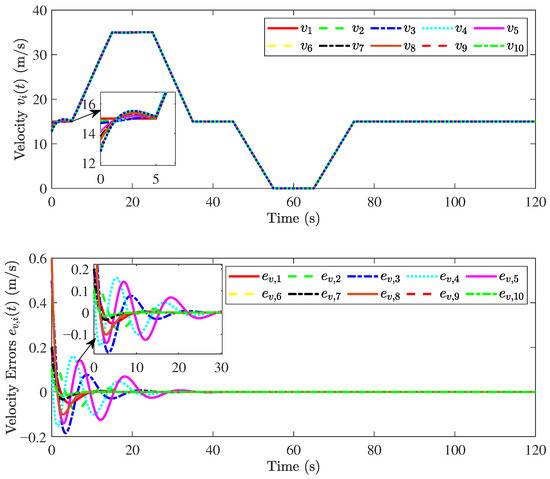
Figure 10.
Responses of ten vehicles and .
5.2. Simulation for Expanding Construction Form
In this subsection, we first provide the parameters for the newly added vehicle, that is,
According to Theorem 2, the control gain can be calculated without changing the original , .
The simulation results can be observed in Figure 11, Figure 12 and Figure 13. The velocity and acceleration of the 6th vehicle are shown in Figure 11 and Figure 12. Similarly, when is cut off, the result is shown in Figure 13. The above results illustrate that the proposed objectives are satisfied.
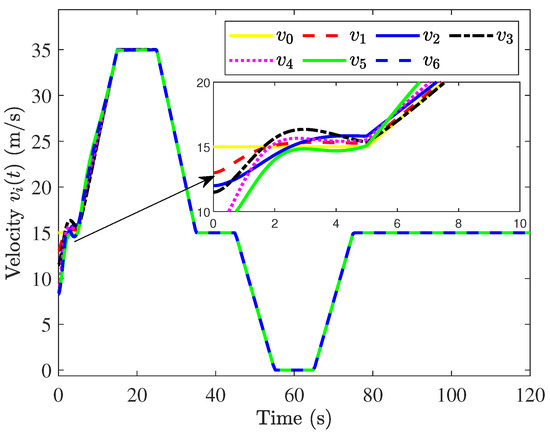
Figure 11.
Responses of .
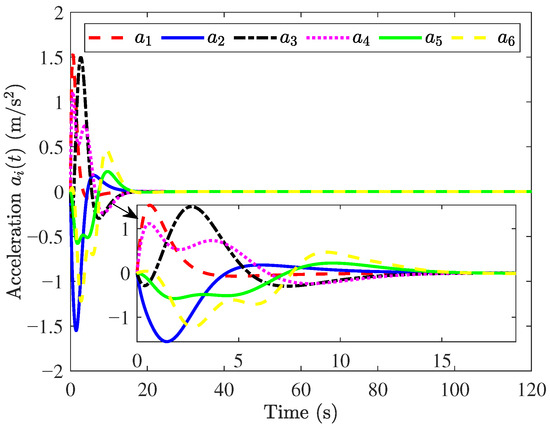
Figure 12.
Responses of .
Figure 13.
Responses after cutting .
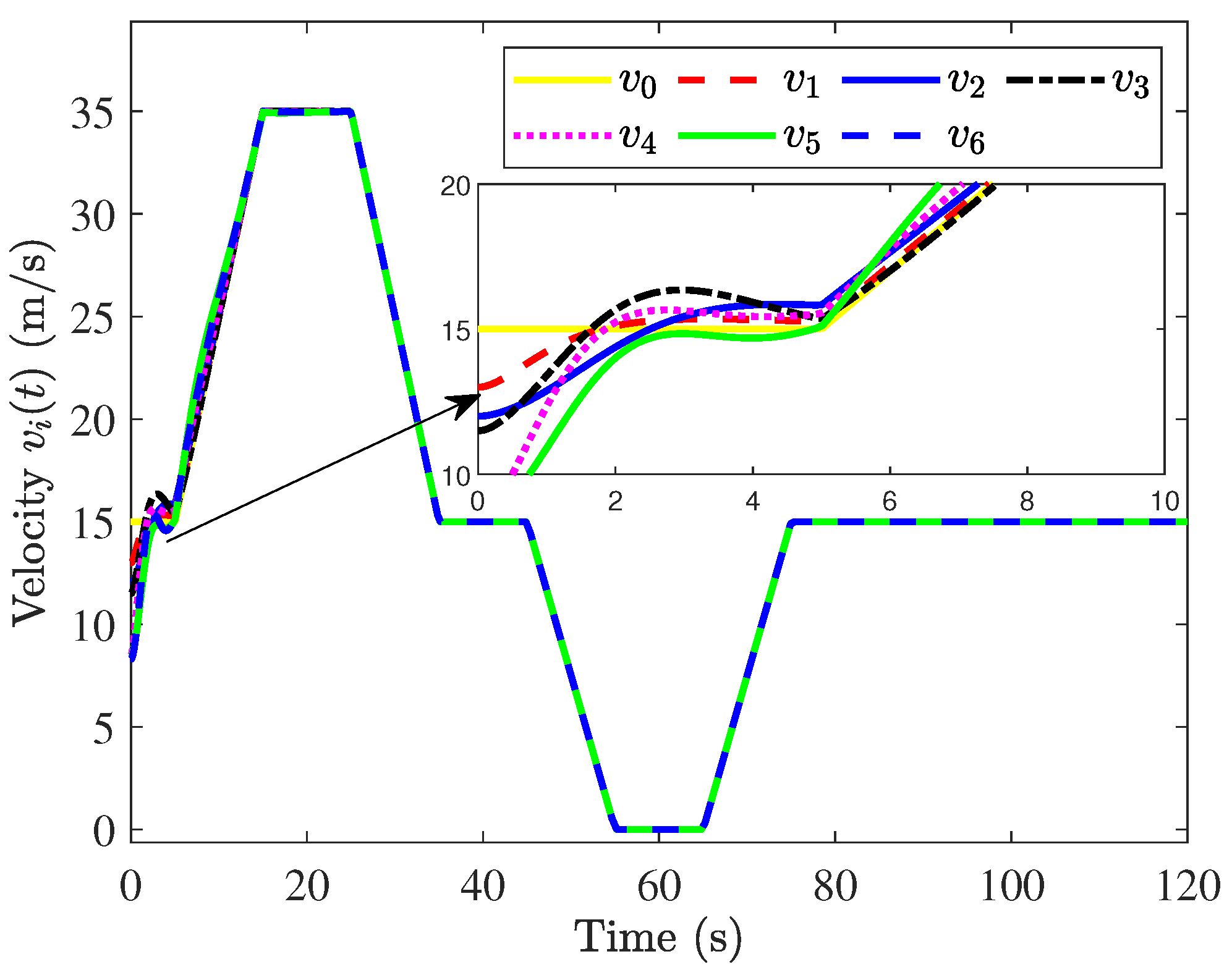
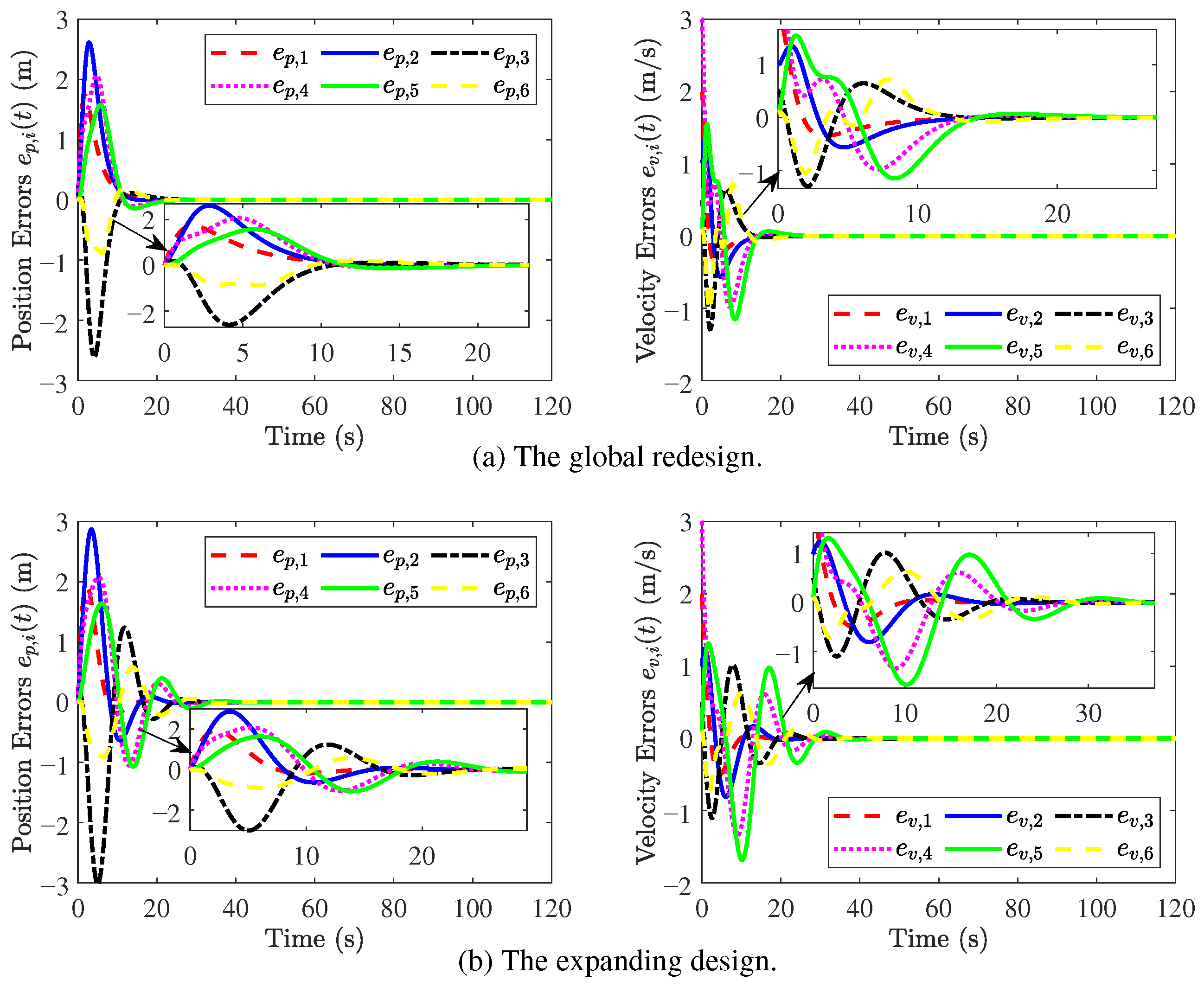
In addition, a comparison result between the expanding design and global redesign [39] is shown in Figure 14, from which the convergence rate of the position error and velocity error is faster by using the global redesign when a new vehicle is added to the original platoon. However, the global redesign algorithm is very complex since it needs to redesign all the controllers, and compute the corresponding gain matrices with the LMIs.
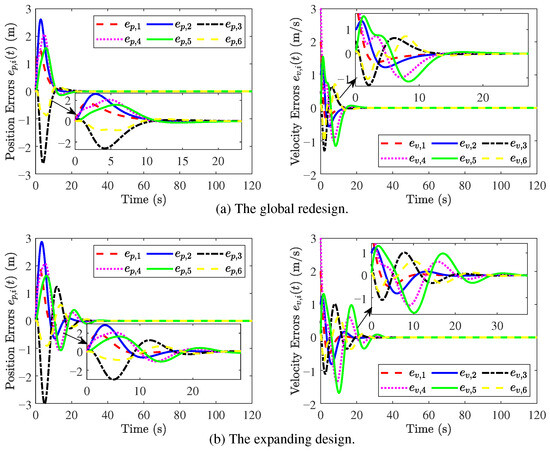
Figure 14.
Results of global redesign and expanding design.
6. Conclusions
The decentralized platoon control issue of multi-vehicle systems is investigated in this paper. In order to reduce the design complexity of the overlapping form, a longitudinal plant with an interconnected form is established at first. Then, for improving the algorithm flexibility, a vehicular platoon model is built as an expanding construction form, such that one can only design a controller for the newly added vehicle without changing the original control laws. Moreover, two sufficient conditions are introduced by the use of the LMI method. Finally, simulation results show the effectiveness of the presented approaches. Meanwhile, there still exist some interesting problems to be further investigated in the future, including how to extend the proposed method to nonlinear systems with different dimensions. It is noted that the designed method can be applied to multiarea interconnected power systems, as well multiple unmanned aerial vehicle systems and sensor networks, which will also be interesting explore in future work.
Author Contributions
Conceptualization, J.C.; methodology, Y.L. and L.W.; investigation, J.-K.W.; writing—original draft, J.-K.W.; writing—review & editing, J.C., Y.L. and L.W.; supervision, Y.L.; funding acquisition, Y.L. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (62373208, 62573249), the Taishan Scholar program of Shandong Province of China (tsqn202306218, tsqnz20221133), and the National Natural Science Foundation of Shandong Province (ZR2024YQ032, ZR2024QF026).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the correspondence contact information. This change does not affect the scientific content of the article.
References
- Bender, J.G. An overview of systems studies of automated highway systems. IEEE Trans. Veh. Technol. 1991, 40, 82–99. [Google Scholar] [CrossRef]
- Shladover, S.E. Review of the state of development of advanced vehicle control systems. Veh. Syst. Dyn. 1995, 24, 551–595. [Google Scholar] [CrossRef]
- Chu, K. Decentralized control of high speed vehicle strings. Transp. Sci. 1974, 8, 361–384. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Zhao, H.; Chang, T.; Yang, Y. Dynamic credible spectrum sharing based on smart contract in vehicular networks. Mathematics 2024, 12, 1929. [Google Scholar] [CrossRef]
- Studli, S.; Seron, M.M.; Middleton, R.H. From vehicular platoons to general networked systems: String stability and related concepts. Annu. Rev. Control 2017, 44, 157–172. [Google Scholar] [CrossRef]
- Liu, W.; Wei, Z.; Liu, Y.; Gao, Z. Adaptive Fixed-Time Safety Concurrent Control of Vehicular Platoons with Time-Varying Actuator Faults under Distance Constraints. Mathematics 2024, 12, 2560. [Google Scholar] [CrossRef]
- Levine, W.; Athans, M. On the optimal error regulation of a string of moving vehicles. IEEE Trans. Autom. Control 1966, 11, 355–361. [Google Scholar] [CrossRef]
- I-Jhayyish, A.M.H.A.; Schmidt, K.W. Feedforward strategies for cooperative adaptive cruise control in heterogeneous vehicle strings. IEEE Trans. Intell. Transp. Syst. 2018, 19, 113–122. [Google Scholar] [CrossRef]
- Naus, G.J.L.; Vugts, R.P.A.; Ploeg, J.; Molengraft, M.J.G.; Steinbuch, M. String-stable CACC design and experimental validation: A frequency-domain approach. IEEE Trans. Veh. Technol. 2010, 59, 4268–4279. [Google Scholar] [CrossRef]
- Rajamani, R.; Zhu, C. Semi-autonomous adaptive cruise control systems. IEEE Trans. Veh. Technol. 2002, 51, 1186–1192. [Google Scholar] [CrossRef]
- Guo, G.; Wang, Q. Fuel-efficient en route speed planning and tracking control of truck platoons. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3091–3103. [Google Scholar] [CrossRef]
- Chen, R.; Fan, Y.; Yuan, S.; Hao, Y. Vehicle collaborative partial offloading strategy in vehicular edge computing. Mathematics 2024, 12, 1466. [Google Scholar] [CrossRef]
- Wen, S.; Guo, G. Distributed trajectory optimization and sliding mode control of heterogenous vehicular platoons. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7096–7111. [Google Scholar] [CrossRef]
- Lan, J.; Zhao, D. Min-max model predictive vehicle platooning with communication delay. IEEE Trans. Veh. Technol. 2020, 69, 12570–12584. [Google Scholar] [CrossRef]
- Zhang, P.; Tian, D.; Zhou, J. Efficient robust model predictive control for behaviorally stable vehicle platoons. IEEE Trans. Intell. Transp. Syst. 2025, 26, 1671–1688. [Google Scholar] [CrossRef]
- Xu, L.; Zhuang, W.; Yin, G.; Bian, C.; Wu, H. Modeling and robust control of heterogeneous vehicle platoons on curved roads subject to disturbances and delays. IEEE Trans. Veh. Technol. 2019, 68, 11551–11564. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, J.; Hong, S. RBFNN-based adaptive event-triggered control for heterogeneous vehicle platoon consensus. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18761–18773. [Google Scholar] [CrossRef]
- Liu, A.; Li, T.; Gu, Y.; Dai, H. Cooperative extended state observer based control of vehicle platoons with arbitrarily small time headway. Automatica 2021, 129, 109678. [Google Scholar] [CrossRef]
- Malikopoulos, A.A.; Beaver, L.; Chremos, I.V. Optimal time trajectory and coordination for connected and automated vehicles. Automatica 2021, 125, 109469. [Google Scholar] [CrossRef]
- Xiao, W.; Cassandras, C.G. Decentralized optimal merging control for connected and automated vehicles with safety constraint guarantees. Automatica 2021, 123, 109333. [Google Scholar] [CrossRef]
- Yue, W.; Guo, G.; Wang, L.Y. Decentralized control of autonomous platoon under networked communication effect. J. Cent. South. Univ. 2011, 41, 144–151. [Google Scholar]
- Stankovic, S.S.; Stanojevic, M.J.; Siljak, D.D. Decentralized overlapping control of a platoon of vehicles. IEEE Trans. Control Syst. Technol. 2000, 8, 816–832. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S.; Huang, Y.F.; Gupta, V. Distributed algebraic Riccati equations in multi-agent systems. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 12–15 July 2022; pp. 1810–1817. [Google Scholar]
- Zeng, X.; Chen, J.; Hong, Y. Distributed optimization design of iterative refinement technique for algebraic Riccati equations. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 2833–2847. [Google Scholar] [CrossRef]
- Semsar-Kazerooni, E.; Khorasani, K. Optimal Consensus Seeking in a Network of Multiagent Systems: An LMI Approach. IEEE Trans. Syst. Man Cybern. B Cybern. 2010, 40, 540–547. [Google Scholar] [CrossRef]
- Stoustrup, J. Plug and play control: Control technology towards new challenges. Eur. J. Control 2009, 3, 311–330. [Google Scholar] [CrossRef]
- Bendtsen, J.; Trangbaek, K.; Stoustrup, J. Plug-and-play control modifying control systems online. IEEE Trans. Control Syst. Technol. 2013, 21, 79–93. [Google Scholar] [CrossRef]
- Tan, X.; Ikeda, M. Decentralized stabilization for expanding construction of large-scale systems. IEEE Trans. Automat. Control 1990, 35, 644–651. [Google Scholar] [CrossRef]
- Knorn, S.; Besselink, B. Scalable robustness of interconnected systems subject to structural changes. IFAC-PapersOnLine 2020, 53, 3373–3378. [Google Scholar] [CrossRef]
- Xie, S.; Russo, G. On the design of integral multiplex control protocols for nonlinear network systems with delays. arXiv 2022, arXiv:2206.03535. [Google Scholar]
- Liu, Y.; Yao, D.; Li, H.; Lu, R. Distributed cooperative compound tracking control for a platoon of vehicles with adaptive NN. IEEE Trans Cybern. 2022, 52, 7039–7048. [Google Scholar] [CrossRef]
- Guo, G.; Zhao, Z. Finite-time terminal sliding mode control of connected vehicle platoons. Control Theory Appl. 2023, 40, 149–159. [Google Scholar]
- Swaroop, D.; Hedrick, J.K. Direct adaptive longitudinal control of vehicle platoons. IEEE Trans. Veh. Technol. 2001, 50, 150–161. [Google Scholar] [CrossRef]
- Wen, S.; Guo, G. Cooperative adaptive cruise control of vehicles using a resource-efficient communication mechanism. IEEE Trans. Intell. Transp. Syst. 2019, 4, 127–140. [Google Scholar] [CrossRef]
- Cook, P.A. Stable control of vehicle convoys for safety and comfort. IEEE Trans. Autom. Control 2007, 52, 526–531. [Google Scholar] [CrossRef]
- Herman, L.; Martinec, D.; Hurak, Z.; Sebek, M. Nonzero bound on fiedler eigenvalue causes exponential growth of H-infinity norm of vehicular platoon. IEEE Trans. Autom. Control 2015, 60, 2248–2253. [Google Scholar] [CrossRef]
- Herman, L.; Martinec, D.; Veerman, J. Transients of platoons with asymmetric and different laplacians. Syst. Control Lett. 2016, 91, 28–35. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Liu, Y.; Gao, J. Organically structured control of large-scale systems with expanding construction based on state observation. Abstr. Appl. Anal. 2015, 19, 1–21. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Gao, J. Overlapping decentralized control based on dynamic output feedback for large-scale interconnected systems. J. Sys. Sci. Math. Sci. 2014, 34, 862–875. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).