Modeling SSE 50 ETF Returns and Option Pricing: Evidence from a Score-Driven GARCH-Jump Approach

Abstract

Modeling stock returns and option pricing in the presence of jumps remains a central challenge in financial economics. This paper employs a novel score-driven GARCH-jump model to analyze SSE (Shanghai Stock Exchange) 50 ETF returns and option pricing. The main findings are as follows. First, we use 50 ETF spot returns to estimate conditional volatility and jump intensity, and find that the SDSDJ (score-driven separate dynamic jumps) model significantly outperforms conventional GARCH-jump models in model fitting. Second, we evaluate both in-sample and out-of-sample pricing performance using data from 50 ETF options, and find that the SDSDJ model achieves the lowest in-sample pricing error among all benchmarks, while its simplified variant—the SDJ (score-driven jumps) model—delivers the most accurate out-of-sample results. Third, the superior pricing performance of both models is robust across different levels of moneyness and DTM (days-to-maturity).

1. Introduction

Modeling sudden jumps in asset prices is a critical topic in finance. Jumps—typically referring to large, abrupt price changes due to significant news—help explain why asset returns often have fat-tailed distributions and why option-implied volatilities exhibit pronounced “smiles”. Empirical evidence in the developed markets such as the U.S. market shows that jumps, while infrequent, can account for a non-trivial share of return variability (on the order of 5∼7% of total variance [1]). In emerging markets such as China, stock price fluctuations tend to be even more extreme, and existing studies document episodes of abnormal jumps and higher overall volatility than in mature markets [2]. These characteristics make accurate jump modeling particularly important for the Chinese stock market, as it deepens our understanding of return dynamics and improves option valuation in this market.

The Chinese stock market did not introduce exchange-traded equity options until 2015, when the Shanghai Stock Exchange launched the SSE 50 ETF option. Since then, the Chinese options market has expanded rapidly: By 2021, the average daily trading volume reached approximately 2.6 million contracts, making the SSE 50 ETF option one of the most actively traded ETF options. The annual trading volume increased from about 23 million contracts in 2015 to more than 300 million in 2024, reflecting the growing demand for hedging, arbitrage, and speculative activities. In particular, the introduction of SSE 50 ETF options has also impacted the underlying market. For example, Arkorful et al. [3] found that the introduction of these options significantly decreases the volatility of the SSE 50 ETF itself, as option trading attracts informed traders and improves the flow of information on the spot market. The rapid development of the Chinese options market provides a rich data source and a timely opportunity to investigate return-jump and volatility modeling, as well as option pricing, under a new market regime.

Despite the rapid growth of the SSE 50 ETF options markets, most empirical research on return modeling and option pricing focuses on U.S. indices (such as the S&P 500). The Chinese market differs in several important ways that warrant dedicated investigation [4,5]. First, the Chinese equity market is dominated by retail investors and is periodically shaped by regulatory interventions, resulting in regime shifts and clusters of large price movements. Second, capital controls and other restrictions can cause liquidity shocks around policy events, for example, daily price limits may also induce discontinuities. Third, the SSE 50 ETF options are physically delivered contracts that are adjusted for dividends—a feature uncommon in standard index options. Furthermore, the number of available strike prices is limited, and the cost of short-selling the underlying assets is much higher than in U.S. markets. Finally, implied volatility in the SSE 50 ETF options market is generally higher than in the U.S. These distinctive market characteristics highlight the limitations of traditional models and motivate the usage of context-specific approaches to volatility and jump modeling in the Chinese equity market.

A wide range of models have been developed to capture asset volatility dynamics in both continuous and discrete-time frameworks. Under the classic continuous-time framework, the stochastic volatility model proposed by Black and Scholes [6] and Heston [7], laid the theoretical foundation for option pricing under diffusion processes. On the discrete-time side, GARCH models have been proven to be very successful in capturing time-varying volatility. Building on this success, Duan [8] pioneered the GARCH option pricing model, showing that a GARCH-based approach can parsimoniously track time-varying volatility and even explain certain systematic pricing biases of the Black–Scholes model. Subsequently, Heston and Nandi [9] derived a closed-form option valuation formula for a GARCH process, providing the first convenient analytical pricing formula for a stochastic volatility model that can be estimated and implemented solely based on observables. Recently, Mozumder et al. [10] proposed a practitioner version of Heston and Nandi’s model.

However, empirical findings document that asset returns are occasionally disturbed by large jumps triggered by news or unexpected events. A growing body of literature links jumps to the arrival of big news (e.g., [2,11,12,13,14]). For instance, using an extensive news dataset, Jeon et al. [14] show that stock price jumps (in both frequency and size) are strongly related to news flows and their content, especially for firms with higher media visibility, analyst coverage, and institutional ownership. These evidences reinforce the view that jumps are not merely statistical outliers but are often tied to fundamental information events. To accommodate these discontinuities in returns, researchers have extended volatility models to include jump components in returns. In discrete time, numerous GARCH-jump models have been proposed for equities and exchange rates (e.g., [11,15]), where the return innovation has a mixture of a GARCH-driven continuous part and a jump-driven discontinuous part. These models have also been adapted to option pricing. For example, Duan et al. [16] developed approximation methods for GARCH-jump models, while Christoffersen et al. [17] estimated a model with time-varying jump intensity to price S&P 500 options. A consistent finding in the literature is that incorporating jumps improves pricing accuracy, and models with dynamic jump intensity outperform their static counterparts. For example, Christoffersen et al. [18] and Christoffersen et al. [17] verify that models allowing for jumps (especially with time-varying intensity) outperform those assuming purely continuous diffusion.

While GARCH and GARCH-jump-based models have been highly useful and progressed significantly in modeling returns [19,20] or option pricing [10,20], they update volatility using heuristic rules (e.g., lagged squared returns), which raise robustness concerns. This has motivated the development of score-driven volatility models—also known as dynamic conditional score (DCS) models—by Creal et al. [21] and Harvey [22]. Score-driven models take a different route: time-varying parameters (such as volatility or jump intensity) are updated each period using the score (i.e., the gradient) of the conditional log-likelihood, rather than ad hoc functions of past residuals. This generalized filtering mechanism guarantees that updates incorporate new information exactly as prescribed by the likelihood. Score-driven models have been developed rapidly [23] due to their flexibility in modeling time-varying parameters—such as volatility, skewness, kurtosis, tail risk, and correlations—through efficient likelihood-based updating. Incorporating the score-driven approach into option pricing models may improve the accuracy of option pricing, since it typically improves the volatility modeling—an input that directly determines option prices. In view of this, Ballestra et al. [24] recently proposed a score-driven GARCH-jump model, i.e., the SDSDJ (score-driven separate dynamic jumps) model, where both the conditional variance and the conditional jump intensity evolve according to auto-regressive updates driven by scaled score innovations. Their empirical application to S&P 500 returns and options demonstrates an excellent in-sample fitting and significant out-of-sample improvements, surpassing traditional GARCH-jump benchmarks. In particular, the score-driven model can accurately capture returns’ jump clustering and volatility dynamics, resulting in more reliable pricing of the S&P 500 options. These results suggest that score-driven jump models can offer a powerful tool for option valuation.

Unlike the extensive studies on the U.S. market, relatively few studies have examined option pricing in the Chinese market. For example, Huang et al. [5] compared discrete-time models on SSE 50 ETF options and found that specifications incorporating realized-volatility measures outperform standard GARCH models based solely on daily returns. Yang [25] introduced a GARCH option pricing model that includes a double-exponential jump component, and empirical results show that the model improves the fit on SSE 50ETF returns and options and provides relatively better in- and out-of-sample pricing performance. Recently, Chi et al. [26] evaluated GARCH-type option pricing models in the Chinese SSE 50 ETF market and find that these models (and their extensions) deliver superior in-sample fit, GARCH-based forecasts even outperform option-implied volatility in predicting realized volatility out of sample. However, to the best of our knowledge, the performance of score-driven GARCH-jump models for the Chinese stock market has not yet been investigated. In light of the unique market characteristics discussed above, as well as the good performance of score-driven models in other contexts, it is natural to investigate whether these models can enhance return filtering and option pricing in the SSE 50 ETF market.

This paper employs a novel score-driven GARCH-jump model to fit SSE (Shanghai Stock Exchange) 50 ETF returns and option pricing. The main findings are as follows. First, we use 50 ETF spot returns to estimate conditional volatility and jump intensity, and find that the SDSDJ model significantly outperforms conventional GARCH-jump models in model fitting. Second, we evaluate both in-sample and out-of-sample pricing performance using data from 50 ETF options, and find that the SDSDJ model achieves the lowest in-sample pricing error among all benchmarks, while its simplified variant—the SDJ (Score-driven jumps) model—delivers the most accurate out-of-sample results. Third, the superior pricing performance of both models is robust across different levels of moneyness and DTM (days-to-maturity).

The marginal contributions of this paper are threefold. First, we investigate the performance of score-driven GARCH-jump models in modeling SSE 50 ETF returns and option pricing in the Chinese stock market. Our study not only enriches existing studies on option pricing in the emerging markets, such as the Chinese stock market [5,25,26], but also provides evidence on jump behavior in the Chinese stock market [2,25]. Second, we obtain a novel out-of-sample finding. Although the empirical studies in Ballestra et al. [24] have shown that the dynamic score-driven GARCH-jump model outperforms its static counterpart for the U.S. stock market, rigorous out-of-sample option pricing evidence remains scarce. Using data from the Chinese market, we find that the SDJ model performs better than the SDSDJ model for out-of-sample option pricing. This empirical result suggests that, in some cases, the reduced generalization ability of dynamic GARCH-jump modeling may outweigh its flexibility, thereby allowing more parsimonious models to achieve superior performance. Last but not least, we also enrich the empirical applications of score-driven models in return modeling and option pricing.

The remainder of this article is organized as follows. Section 2 provides the data and an overview of the SSE 50 ETF options market. Section 3 introduces the methodology, including the SDSDJ and SDJ models, used in this paper. Section 4 presents and discusses the empirical results. Section 5 concludes the paper.

2. The Data and Features of the SSE 50 ETF Option Market

The underlying asset of the SSE (Shanghai Stock Exchange) 50 ETF options is the 50 ETF issued by Hua Xia Fund Asset Management Company. Covering the 50 largest high-liquidity blue-chip stocks listed on the SSE, the SSE 50 ETF accounted for approximately $4.1\%$ of the total market value (i.e., over $3.7$ trillion RMB) of all 1037 equity ETFs in China by the end of 2024. In this study, we use the daily returns of the SSE 50 ETF from 23 February 2005 to 28 October 2024, and the daily settlement prices of the 50 ETF option contracts from 9 February 2015, to 28 October 2024, as the sample. The data is sourced from the Wind Database, which is a reliable and widely used financial database in China.

Figure 1a plots the log-return time series of the 50 ETF, and Panel A of Table 1 gives its descriptive statistics. Apparently, we can find that the 50 ETF returns are highly volatile; there exists evidence of time-varying jumps, that jumps tend to cluster over time, and that the returns are characterized by a sharp peak and fat tails.

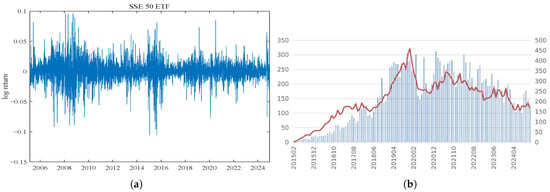
Figure 1. Log-return of SSE 50 ETF and trading volumn and open interest of 50 ETF options. (a) The log-return of 50 ETF; (b) trading volume and open interest of 50 ETF options, where the blue bars represent trading volume (in tens of thousands) and the red line represents open interest (in tens of thousands).

Table 1. Descriptive statistics.

Panel A: the daily log-return of SSE 50 ETF
	Mean	Std. error	Skewness	Kurtosis
SSE 50 ETF	3.04 × 10$-4$	1.64 × 10$-2$	−1.27 × 10$-1$	8.43
Panel B: Number of options
	DTM
Moneyness ($K/S_t$)	10–30	30–90	90–250	Total
<0.9	1471	2053	1030	4554
0.9–1.0	3209	3441	2864	9514
1.0–1.1	2800	3033	2543	8376
>1.1	1604	2066	1213	4883
Total	9084	10,593	7650	27,327

Notes: The sample period for the SSE 50 ETF is from 23 February 2005 to 28 October 2024, and that for the SSE 50 ETF options is from 9 February 2015 to 28 October 2024. DTM denotes days to maturity, and $K/S_t$ denotes moneyness, defined as the ratio of the strike price to the spot price.

The 50 ETF option was introduced on 9 February 2015 as a European-style, physically settled option written on the 50 ETF. Panel B of Table 1 gives the number of options sorted by moneyness and DTM, and the basic contract terms are provided in Table 2. As illustrated in Figure 1b, both daily trading volume and open interest increased dramatically from 2015 to 2024. Panel A of Table 3 lists the proportion of trading volume by option category. The following can be observed: First, ATM (at-the-money) and OTM (out-of-the-money) options account for more than $85\%$ of the total trading volume, while ITM (in-the-money) options account for less than $15\%$. Second, short- and medium-term options with DTM (days-to-maturity) of less than 60 days comprise over $90\%$ of the trading volume, whereas long-term options account for less than $10\%$. Therefore, in line with the literature (e.g., [24]), we restrict our selection to ATM and OTM options with maturities of up to one year (250 days) for pricing, as shown in Panel B of Table 1.

Table 2. Basic terms of the SSE 50 ETF option contracts.

Items	Descriptions
Underlying Asset	SSE 50 ETF
Option Types	Call options and Put options
Exercise Style	European-style
Contract Unit	10,000 units of the SSE 50 ETF
Expiration Months	Current month, next month, and the following two quarterly months
Expiration Date	The fourth Wednesday of the expiration month (postponed if it falls on a holiday)
Strike Prices	Typically 9 strike prices (1 at-the-money, 4 in-the-money, 4 out-of-the-money); strike intervals vary by price level
Trading Hours	9:30–11:30 AM and 1:00–3:00 PM (China Standard Time)
Trading Mechanism	T+0 (same-day trading allowed)
Quote Unit	Price quoted per ETF unit, in Chinese Yuan (RMB)
Settlement Method	Physical delivery (delivery of ETF units)
Types of Orders	Buy to Open/Sell to Open/Buy to Close/Sell to Close/Covered Call Opening/Covered Call Closing

Data Source: SSE website.

Table 3. Trading volume and implied volatility by moneyness and maturity.

Categories	Call	Put
Panel A: Percentage of Total Trading Volume (%)
DITM	$1.2$	$1.3$
ITM	$11.5$	$9.7$
ATM	$57.4$	$55.5$
OTM	$22.9$	$28.4$
DOTM	$7.0$	$5.1$
$\mathrm{DTM}<10$	$26.6$	$23.7$
10∼30	$47.2$	$47.9$
30∼60	$18.2$	$19.3$
60∼90	$1.5$	$2.1$
90∼180	$5.3$	$5.4$
$\mathrm{DTM}>180$	$1.2$	$1.6$
Panel B: Annualized Implied Volatility (%)
DITM	$23.4$	$36.4$
ITM	$31.3$	$27.0$
ATM	$22.2$	$23.1$
OTM	$20.1$	$23.9$
DOTM	$22.6$	$28.0$
$\mathrm{DTM}<10$	$32.6$	$37.9$
10∼30	$25.8$	$28.3$
30∼60	$22.9$	$25.8$
60∼90	$23.7$	$24.9$
90∼180	$21.8$	$25.4$
$\mathrm{DTM}>180$	$20.5$	$24.6$

Notes: The sample period is from 9 February 2015 to 28 October 2024. DITM stands for deep-in-the-money, ITM for in-the-money, ATM for at-the-money, OTM for out-of-the-money, and DOTM for deep-out-of-the-money. The critical thresholds of moneyness are 0.90, 0.98, 1.02, and 1.10.

Compared to their U.S. counterparts, SSE 50 ETF options exhibit several notable differences in contract specifications, regulatory practices, and market behavior. First, the number of strikes available is limited. At inception, the 50 ETF options offered only five strikes (one ATM, two OTM, and two ITM), which expanded to nine strikes (one ATM, four OTM, and four ITM) by early 2018. New strikes are added upon dividend adjustments, and seventeen such adjustments have been made since the launch of this product.

Second, option contracts are adjusted when dividends are paid on the underlying ETF. Specifically, if the ex-dividend price of the ETF is S and the cash dividend is d, the adjustment provides each holder with $S/(S-d)$ new contracts at a strike price of $(S-d)K/S$ for each original contract at strike K. Take call options as an example: when dividends are paid, the stock price decreases and the value of the call option is eroded; by adjusting the exercise price, the call option buyer can be protected. This leads to the following pricing identity:

$${\displaystyle \frac{S}{S-d}}{C}_t(S-d,{\displaystyle \frac{S-d}{S}}K,T)=C_t(S,K,T).$$

(1)

This mechanism effectively shields option holders from dividend-induced price drops—a feature not standard for index options such as SPX.

Finally, the Chinese market experiences higher price volatility [5]. For example, the average realized 10-day volatility of the 50 ETF from February 2015 to December 2024 was approximately $22.59\%$, compared to about $10\%$ for the S&P 500 (SPX). Moreover, by February 2018, the volatility premium (defined as VIX minus realized volatility) for the 50 ETF was approximately $16\%$ higher than that of SPX options.

These observations highlight fundamental differences between the Chinese and U.S. options markets, suggesting that pricing models useful for the U.S. may not be directly applicable to the Chinese context.

3. The Methodology

3.1. The SDSDJ and SDJ Models

We first introduce the SDSDJ model. Let $S_t$ denote the daily closing price series of SSE 50 ETF, then the log-return is $R_t=log(S_t+D_t)-log\left(S_{t-1}\right)$, including the dividend $D_t$. Following Christoffersen et al. [17] and Ballestra et al. [24], we use affine building blocks to model the log-return as follows:

$$R_t=r+\left({\lambda }_z-\frac{1}{2}\right)h_t+\left({\lambda }_y-\xi \right){\chi }_t+\sqrt{h_t}{Z}_t+y_t,$$

(2)

where r is the risk-free rate, $h_t$ is the conditional variance, and ${\chi }_t$ is the (expected) number of jumps per day. The terms ${\lambda }_z$ and ${\lambda }_y$ are risk premia for diffusion and jump risks under the physical measure, while the compensators $\frac{1}{2}{h}_t$ and $\xi {\chi }_t$ ensure that the conditional gross return has the expected value $exp\{r+{\lambda }_z{h}_t+{\lambda }_y{\chi }_t\}$. Specifically, the diffusion shock $Z_t$ is standard normal, and $y_t$ is defined as a compound Poisson process:

$$\begin{array}{cc}\hfill & y_t=\sum _{j=0}^{N_t}{X}_t^{\left(j\right)},\hfill \\ \hfill & \mathbb{P}\left(N_t=j\right)={\displaystyle \frac{e^{-{\chi }_t}{\chi }_t^j}{j!}},j=0,1,2,\dots \hfill \end{array}$$

(3)

where $N_t$ is the number of jumps arriving between times $t-1$ and t, and the jump size $X_t^{\left(j\right)}$ is a sequence of independent and identically distributed normal random variables, $X_t^{\left(j\right)}\sim \mathcal{N}(\mu ,{\tau }^2)$, as shown in Equation (3).

From an economic perspective, Equation (2) decomposes returns into a predictable risk-compensation part and two orthogonal surprise components: a continuous shock of variance $h_t$ and a rare-event jump $y_t$. This specification is consistent with the work of Maheu and Curdy [11], which proposes that an unobserved news process directs movements in prices, while the latent news process is assumed to consist of two distinct components—normal and unusual news events—which are identified by their effects on return volatility.

The key features of the SDSDJ model is that both the conditional volatility $h_t$ and conditional intensity ${\chi }_t$ are updated by a score-drivenfilter [21,22], which uses the score (the gradient of the predictive log-density) as the optimal direction in which to adjust latent states after each new observation. We use exponential links, $h_t=exp\left({\psi }_t\right)$ and ${\chi }_t=exp\left({\delta }_t\right)$, to enforce $h_t>0$ and ${\chi }_t>0$, and update

$$\begin{array}{cc}\hfill {\psi }_{t+1}& ={\omega }_{\psi }+{\alpha }_{\psi }{s}^h(R_t,{\psi }_t)+{\gamma }_{\psi }{s}^{\chi }(R_t,{\delta }_t)+{\beta }_{\psi }({\psi }_t-{\omega }_{\psi }),\hfill \\ \hfill {\delta }_{t+1}& ={\omega }_{\delta }+{\alpha }_{\delta }{s}^{\chi }(R_t,{\delta }_t)+{\gamma }_{\delta }{s}^h(R_t,{\psi }_t)+{\beta }_{\delta }({\delta }_t-{\omega }_{\delta }),\hfill \end{array}$$

(4)

where $s^h(·)$ and $s^{\chi }(·)$ are (scaled) scores of the one-step predictive density, as shown in Equation (A3). ${\alpha }_{\psi }$ and ${\alpha }_{\delta }$ represent own-score weight for volatility and jump intensity, while score weight ${\gamma }_{\psi }$ and ${\gamma }_{\delta }$ allow cross-effects (e.g., a burst of jump-like price moves can temporarily raise diffusive volatility, and vice versa), ${\beta }_{\psi }$ and ${\beta }_{\delta }$ control persistence, and $({\omega }_{\psi },{\omega }_{\delta })$ anchor long-run levels. The unknown parameter vector $\mathsf{\theta }=({\lambda }_z,{\lambda }_y,\mu ,\tau ,{\omega }_{\psi },{\alpha }_{\psi },{\gamma }_{\psi },{\beta }_{\psi },{\omega }_{\delta },{\alpha }_{\delta },{\gamma }_{\delta },{\beta }_{\delta })$ can be estimated by maximizing $l_{returns}\left(\mathsf{\theta }\right)$ (Equation (A1)).

It is remarked that the SDJ model is a special case of the SDSDJ model, where the jump intensity is a constant ($\chi$) rather than time-varying (${\chi }_t$). This is useful when the jump intensity is believed to be stable over the sample.

3.2. Option Valuation

In order to price the SSE 50 ETF options, risk neutralization is needed to convert the physical measure (real-world measure, $\mathbb{P}$) to the risk-neutral measure (equivalent martingale measure, $\mathbb{Q}$), which removes risk premia from returns and tilts the jump component to ensure discounted prices are martingales [17,24], then the log-return process and the iterative process under $\mathbb{Q}$-measure are given by

$$\begin{array}{cc}\hfill & R_t=ln\left({\displaystyle \frac{S_t}{S_{t-1}}}\right)=r-{\displaystyle \frac{1}{2}}{h}_t+\left({\lambda }_y-\xi \right){\chi }_t+V_t^{*}+y_t^{*},\hfill \\ \hfill & h_t=exp\left\{{\psi }_t\right\},{\chi }_t=exp\left\{{\delta }_t\right\}\hfill \\ \hfill & {\psi }_{t+1}={\omega }_{\psi }+{\alpha }_{\psi }{s}^{h,\ast }\left(V_t^{*},y_t^{*},{\psi }_t\right)+{\gamma }_{\psi }{s}^{{\chi }_{,\ast }}\left(V_t^{*},y_t^{*},{\delta }_t\right)+{\beta }_{\psi }\left({\psi }_t-{\omega }_{\psi }\right),\hfill \\ \hfill & {\delta }_{t+1}={\omega }_{\delta }+{\alpha }_{\delta }{s}^{\chi ,\ast }\left(V_t^{*},y_t^{*},{\delta }_t\right)+{\gamma }_{\delta }{s}^{h,\ast }\left(V_t^{*},y_t^{*},{\psi }_t\right)+{\beta }_{\delta }\left({\delta }_t-{\omega }_{\delta }\right),\hfill \end{array}$$

(5)

where $V_t^{*}\sim \mathcal{N}(0,h_t)$, $y_t^{*}$ is a compound Poisson process, whose jump intensity is ${\chi }_{t}exp({\Lambda }_y\mu +{\Lambda }_y^2{\tau }^2/2)$ and jump size follows $\mathcal{N}(\mu +{\Lambda }_y{\tau }^2,{\tau }^2)$, in which ${\Lambda }_y$ is the equivalent martingale measure (EMM) coefficient that capture the wedge between the physical and the risk-neutral measure. Under the $\mathbb{Q}$-measure, $s^{{\chi }_{,\ast }}(V_t^{*},y_t^{*},{\delta }_t)$ and $s^{h,\ast }(V_t^{*},y_t^{*},{\psi }_t)$ are the score functions given by Equation (A5).

Given current states $(h_t,{\chi }_t)$ and parameters, we obtain model-implied option values by simulating the risk-neutral return process and discounting expected payoffs as

$$O_t=exp\{-r\times \mathrm{DTM}\}{\mathbb{E}}^{\mathbb{Q}}\left[\Pi \left(S_T\right)\mid {\mathcal{F}}_t\right],$$

(6)

where $O_t$ is the option price, $\Pi \left(S_T\right)$ is the payoff of the option at maturity, and ${\mathcal{F}}_t$ is the information set available up to time t.

Fitting a dynamic model to a panel of option prices could be challenging, especially when the goal is to jointly estimate parameters using both returns and option prices [24]. Since it is important to consider both sources of information, we define a suitably weighted log-likelihood function that incorporates both the daily time series of log-returns and the panel of option contracts. While the log-likelihood for the daily returns, $l_{returns}\left(\mathsf{\theta }\right)$, is already provided in Equation (A1), modeling the option pricing errors requires additional assumptions. Formally, if we have N option prices, the option pricing error for the i-th contract, $u_i$, for $i=1,\dots ,N$, is defined as the relative implied volatility loss function:

$$u_i={\displaystyle \frac{I{V}_i^{MKT}-I{V}_i^{MOD}}{I{V}_i^{MKT}}},$$

(7)

where $I{V}_i^{MKT}$ and $I{V}_i^{MOD}$ denote the market- and model-implied volatilities of the i-th option, respectively, where the latter is computed according to the popular Black–Scholes model. Following Christoffersen et al. [17] and Ornthanalai [27], the likelihood associated with the error on implied volatility is computed through using a Gaussian specification:

$$l_{options}\left(\mathsf{\theta }\right)=-{\displaystyle \frac{N}{2}}ln\left(2\pi {\sigma }_u^2\right)-{\displaystyle \frac{1}{2}}\sum _{i=1}^N{\displaystyle \frac{u_i^2}{{\sigma }_u^2}}.$$

(8)

It is important to note that the number N of data points available for the option panel is different from the number T of daily returns. We follow Christoffersen et al. [17] and Ornthanalai [27], assign an equal weight to returns and option prices, and consider the following weighted joint (total) log-likelihood:

$$l_{joint}\left(\mathsf{\theta }\right)={\displaystyle \frac{T+N}{2}}{\displaystyle \frac{l_{returns}\left(\mathsf{\theta }\right)}{T}}+{\displaystyle \frac{T+N}{2}}{\displaystyle \frac{l_{options}\left(\mathsf{\theta }\right)}{N}}.$$

(9)

To assess the performance of the option pricing models, we follow Ballestra et al. [24], and employ the (percentage) IVRMSE (Implied Volatility Root Mean Square Error):

$$IVRMSE(\%)=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(I{V}_i^{MKT}-I{V}_I^{MOD})}^2}\times 100,$$

(10)

where N is the total number of option prices considered, and $I{V}_i^{MKT}$ and $I{V}_I^{MOD}$ denote the market and the model-implied volatilities of the i-th option, respectively.

3.3. Benchmark Models

To demonstrate the advantage of the score-driven GARCH-jump models, we choose the Black–Scholes [6], Heston and Nandi GARCH [9], GARCHJ (GARCH model with jumps [18]), and DVSDJ (dynamic volatility separate dynamic jumps [17]) as benchmark models.

Since the Black–Scholes model is so well known and widely used, we will not introduce it here. The Heston and Nandi GARCH model uses a closed-form solution as follows, rather than numerical methods (see Equation (A7)), where the underlying asset $S\left(t\right)$ follows the following process:

$$\begin{array}{cc}\hfill log\left(S\right(t\left)\right)& =log\left(S(t-\Delta )\right)+r+\lambda h\left(t\right)+\sqrt{h\left(t\right)}Z\left(t\right),\hfill \\ \hfill h\left(t\right)& =\omega +\sum _{i=1}^p{\beta }_{i}h(t-i\Delta )+\sum _{i=1}^q{\alpha }_i{(z(t-i\Delta )-{\gamma }_i\sqrt{h(t-i\Delta )})}^2,\hfill \end{array}$$

(11)

where r is the continuously compounded interest rate for the time interval $\Delta$, $Z\left(t\right)$ is a standard normal disturbance, and $h\left(t\right)$ is the conditional variance of the log return between $t-\Delta$ and t.

The GARCHJ model incorporates static jumps (i.e., Poisson process) into the GARCH option pricing model, whose return process is the same as Equation (2) and the iterative process is given by

$$h_{t+1}={\omega }_z+{\alpha }_z{\left(Z_t+{\displaystyle \frac{y_t}{\sqrt{h_t}}}-c_z\sqrt{h_t}\right)}^2+{\beta }_z{h}_t.$$

(12)

where $h_t$ is the conditional variance, $Z_t$ and $y_t$ are the normal and jump components of shocks for returns, respectively, and $({\omega }_z,{\alpha }_z,c_z,{\beta }_z)$ are parameters to be estimated.

The DVSDJ model is the generalized version of the GARCHJ model, where the jump intensity ${\chi }_t$ varies over time. The return process of the DVSDJ model is the same as Equation (2), and the iterative process is given by

$$\begin{array}{cc}\hfill & h_{t+1}={\omega }_z+{\beta }_z{h}_t+{\displaystyle \frac{{\alpha }_z}{h_t}}{\left(\sqrt{h_t}{Z}_t-c_z{h}_t\right)}^2+{\gamma }_z{\left(y_t-e_z\right)}^2,\hfill \\ \hfill & {\chi }_{t+1}={\omega }_y+{\beta }_y{\chi }_t+{\displaystyle \frac{{\alpha }_y}{h_t}}{\left(\sqrt{h_t}{Z}_t-c_y{h}_t\right)}^2+{\gamma }_y{\left(y_t-e_y\right)}^2.\hfill \end{array}$$

(13)

where $h_t$ is the conditional variance, ${\chi }_t$ is the dynamic jump intensity, $Z_t$ and $y_t$ are the normal and jump components of shock, respectively, and $({\omega }_z,{\alpha }_z,c_z,{\beta }_z,{\gamma }_z,e_z,{\omega }_y,{\alpha }_y,c_y,{\beta }_y,{\gamma }_y,e_y)$ are parameters to be estimated.

4. Empirical Results

4.1. In-Sample Fitting of Spot Returns

We use different GARCH-type models (H-N GARCH, GARCHJ, SDJ, DVSDJ, and SDSDJ model) to filter the conditional volatility and jump intensity of the 50 ETF spot returns. Since different models imply different conditional volatility and jump intensity for the same market, our objective is to identify which model achieves superior in-sample fitting.

Table 4 presents the maximum likelihood estimation results for these models. First, three different criteria—log-likelihood value, AIC, and BIC—are used to evaluate in-sample model fitting. From the table, we can find that, among all GARCH-type models, the novel SDSDJ model achieves the highest log-likelihood and the lowest AIC and BIC. Interestingly, the SDJ and DVSDJ models perform even worse than the plain vanilla Heston–Nandi GARCH model. Therefore, we demonstrate that score-driven GARCH-jump models provide better in-sample fitting. Second, as shown in the table, we find that none of the GARCH-type models produce significant coefficient estimates for ${\lambda }_y$, whereas the S&P 500 market exhibits a significant jump risk premium (e.g., ${\lambda }_y=0.6\%$; see [24]). However, ${\lambda }_z$ is significantly positive across models, indicating that investors are compensated for bearing the normal component of risk. Third, the jump size (denoted by $\mu$) of log-returns in the 50 ETF market is relatively small. As shown in the table, although all estimated $\mu$ values are negative—reflecting negatively skewed returns—their absolute magnitudes are small, in contrast to jump sizes of around $-1\%$ observed in the S&P 500 market. Lastly, similar to the S&P 500 market, there exists significant interaction between the normal and jump components for the SSE 50 ETF market. The relative magnitudes of $\gamma$ and $\alpha$ reflect the interaction between jump intensity and conditional variance. If $\gamma >\alpha$, the interaction is considered significant [24], which is also confirmed by the estimates in the table.

Table 4. Maximum likelihood estimation results for the spot return of 50 ETF.

	H-N GARCH	GARCHJ		SDJ		DVSDJ		SDSDJ
Parameters	Normal	Normal	Jump	Normal	Jump	Normal	Jump	Normal	Jump
$\lambda$	$1.74$ **	$4.06$ ***	$-1.98\times {10}^{-3}$	$4.65$ *	$8.14\times {10}^{-5}$	$4.08\times {10}^{-1}$ ***	$2.14\times {10}^{-3}$	$1.60$ ***	$5.07\times {10}^{-4}$
	$\left(0.87\right)$	$(8.03\times {10}^{-2})$	$(2.73\times {10}^{-3})$	$\left(2.64\right)$	$(1.96\times {10}^{-4})$	$(2.08\times {10}^{-2})$	$(6.08\times {10}^4)$	$(3.93\times {10}^{-1})$	$(2.63\times {10}^{-3})$
$\omega$	$-5.98\times {10}^{-6}$ ***	$-3.31\times {10}^{-6}$ ***		$-9.81$ ***		$1.87\times {10}^{-5}$	$-2.31\times {10}^{-1}$ ***	$-9.21$ ***	$7.70\times {10}^{-1}$ ***
	$(4.05\times {10}^{-7})$	$(9.15\times {10}^{-14})$		$(9.67\times {10}^{-2})$		$(2.61\times {10}^{-5})$	$(1.19\times {10}^{-2})$	$(2.71\times {10}^{-1})$	$(1.55\times {10}^{-1})$
$\beta$	$0.98$ ***	$9.87\times {10}^{-1}$ ***		$8.16\times {10}^{-1}$ ***		$7.82\times {10}^{-1}$ ***	$9.24\times {10}^{-1}$ ***	$8.92\times {10}^{-1}$ ***	$9.72\times {10}^{-1}$ ***
	$(2.90\times {10}^{-3})$	$(2.10\times {10}^{-3})$		$(3.08\times {10}^{-2})$		$(2.65\times {10}^{-3})$	$(1.25\times {10}^{-3})$	$(4.49\times {10}^{-2})$	$(7.39\times {10}^{-3})$
$\alpha$	$9.64\times {10}^{-6}$ ***	$3.60\times {10}^{-6}$ ***		$1.34\times {10}^2$ ***		$-2.58\times {10}^{-6}$	$1.50\times {10}^{-2}$ ***	$1.71\times {10}^3$ ***	$6.98\times {10}^{-2}$ ***
	$(8.51\times {10}^{-7})$	$(3.11\times {10}^{-7})$		$(4.96\times {10}^1)$		$(8.39\times {10}^{-6})$	$(2.25\times {10}^{-3})$	$(2.34\times {10}^1)$	$(1.81\times {10}^{-2})$
c		$4.21$ ***				$1.30\times {10}^2$ ***	$-4.51\times {10}^{-2}$ *
		$(1.83\times {10}^{-2})$				$\left(1.00\right)$	$(2.53\times {10}^{-2})$
$\gamma$	$10.59$ **					$3.45\times {10}^{-3}$ ***	$3.95$ ***	$1.48\times {10}^{-1}$	$4.96\times {10}^3$ ***
	$\left(4.34\right)$					$(8.07\times {10}^{-4})$	$(5.03\times {10}^{-2})$	$(1.30\times {10}^{-1})$	$(7.18\times {10}^1)$
e						$-5.75\times {10}^{-2}$ ***	$2.44\times {10}^{-1}$ ***
						$(1.10\times {10}^{-2})$	$(8.44\times {10}^{-3})$
$\mu$			$-1.13\times {10}^{-4}$ ***		$-9.90\times {10}^{-5}$ **		$-8.51\times {10}^{-3}$ ***		$4.22\times {10}^{-4}$ ***
			$(1.22\times {10}^{-5})$		$(2.00\times {10}^{-6})$		$(1.02\times {10}^{-3})$		$(2.67\times {10}^{-5})$
$\tau$			$2.79\times {10}^{-2}$ ***		$-1.90\times {10}^{-2}$ ***		$-2.63\times {10}^{-2}$ ***		$-1.30\times {10}^{-2}$ ***
			$(1.39\times {10}^{-3})$		$(6.31\times {10}^{-4})$		$(1.14\times {10}^{-3})$		$(2.86\times {10}^{-3})$
$\chi$			$1.03\times {10}^{-1}$ ***		$5.48\times {10}^{-1}$ ***
			$(1.85\times {10}^{-2})$		$(2.61\times {10}^{-2})$
log-likelihood	13,585	13,733		13,479		13,466		13,842
AIC	−27,160	−27,448		−26,942		−26,900		−27,660
BIC	−27,128	−27,390		−26,890		−26,796		−27,582

Notes: This table reports the maximum likelihood estimation results. The sample period is from 23 February 2005 to 28 October 2024. Columns labeled “Normal” contain estimates of parameters governing the normal component, and columns labeled “Jump” contain parameters governing the jump component. The standard errors in parentheses are based on the outer product of the gradient. *, **, and *** denote statistical significance at the 10%, 5%, and 1% levels, respectively.

Figure 2 plots the filtered conditional volatility for different models. As illustrated in Panel (a)–Panel (e), the 50 ETF has experienced two episodes of extreme volatility: the 2008 financial crisis and the 2015 Chinese stock market crash. Although the traditional GARCH model captures all market turbulence, its volatility peaks are not pronounced, exhibiting a relatively smooth pattern, and the same applies to the static GARCHJ model (Panel (b)). In contrast, the SDJ model (Panel (e)) and the SDSDJ model (Panel (e)) provide more significant peaks in modeling the conditional volatility of the 50 ETF.

Figure 2. This figure illustrates the time series plots of filtered conditional volatility. The sample period is from 23 February 2005 to 28 October 2024. (a) Heston and Nandi GARCH model; (b) GARCHJ model; (c) DVSDJ model; (d) SDJ model; (e) SDSDJ model.

Figure 3 presents the filtered jump intensity for different GARCH-jump models. Clearly, models with dynamic jump intensity (i.e., DVSDJ and SDSDJ) provide more significant peaks than the static models (i.e., GARCHJ and SDJ). One possible reason is that static models use constant jump intensities, making it difficult to distinguish between high- and low-jump intensity trading days. However, GARCH-jump models with dynamic jump models provide better estimates of the number of posterior jumps associated with market crises.

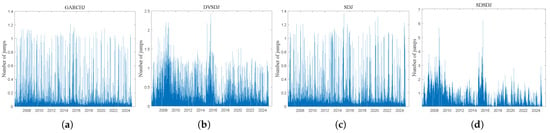
Figure 3. This figure illustrates the time series plots of filtered conditional jump intensity. The sample period is from 23 February 2005 to 28 October 2024. (a) GARCHJ model; (b) DVSDJ model; (c) SDJ model; (d) SDSDJ model.

Finally, we propose a general criterion for evaluating the quality of these volatility models: to what extent can the model strip out the predictable part of the log-return and assign a truly random and unpredictable part into the normal component ($Z_t$). Time series models with stronger explanatory power should yield $Z_t$ values that are closer to a standard normal distribution. Figure 4 illustrates the Q-Q plots of the normal innovation $Z_t$ for each GARCH model. As shown in the figure, $Z_t$ of traditional GARCH-type models deviates significantly from the standard normal distribution beyond $2\sigma$, while $Z_t$ of the SDSDJ model closely approximates a standard normal distribution within $3\sigma$.

Figure 4. This figure illustrates the Q-Q plots of the normal innovation $Z_t$. The sample period is from 23 February 2005 to 28 October 2024. (a) Heston and Nandi GARCH model; (b) GARCHJ model; (c) DVSDJ model; (d) SDJ model; (e) SDSDJ model.

4.2. Out-of-Sample Analysis for Spot Returns

To evaluate the predictive performance of the novel SDSDJ model and its rival models in 50 ETF spot returns, we follow Ballestra et al. [24] and forecast the 5% and 1% Value-at-Risk (VaR) from one to five days. We evaluate the predictive performance of these models across several crisis and relative stable periods by partitioning the dataset into five subperiods and conducting separate out-of-sample analyses: January 2005–August 2009 (including the 2008 global financial crisis), August 2009–December 2012 (a relatively stable period), January 2013–December 2017 (including the 2015 Chinese stock market crash), January 2018–December 2022 (including the COVID-19 pandemic), and December 2022–November 2024.

For each period, we estimate the model parameters using a rolling window with a width equal to $20\%$ of the total number of days in that period. That is, initially, we calibrate these models using the first $20\%$ of daily total returns from the SSE 50 ETF, reserving the remaining data for out-of-sample evaluations. Subsequently, for each day within the out-of-sample dataset, we re-estimate the parameters employing the latest $20\%$ daily return observations and generate forecasts for horizons ranging from one to five days.

Specifically, for the SDSDJ model, at each forecast date $t^{*}$, we generate 100,000 simulated return paths for $R_{t^{*}+l}$, with $l=1,2,3,4,5$, based on the return specification in Equation (2). This involves randomly generating the innovations $\sqrt{h_{t^{*}+l}}{Z}_{t^{*}+l}$ and $y_{t^{*}+l}$, with $h_t$ and ${\chi }_t$ evolving according to Equation (4). We follow similar simulation procedures for the GARCHJ, DVSDJ, and SDJ models. We then calculate the VaR at significance levels of $\alpha =5\%$ and $\alpha =1\%$ by determining empirical quantiles from the 100,000 simulated outcomes of $R_{t^{*}+l}$. Following Creal et al. [21], we evaluate the accuracy of the VaR forecast using the proportion-of-failures test proposed by Kupiec [28]. The null hypothesis for this out-of-sample test is defined as

H₀. 

The probability of model prediction failure equals $\alpha$.

Consequently, if the null hypothesis $H_0$ is rejected, it suggests that the model does not exhibit significant predictive power for VaR.

Table 5 reports the result of the likelihood ratio test. The empirical results indicate that the same model performs differently across high and low quantiles, and that market conditions also play a critical role in determining the model’s performance. For example, during the 2008 global financial crisis period (Panel A), at the $\alpha =1\%$ level, the SDJ and SDSDJ models exhibit superior performance, each with only one rejection. In contrast, the GARCHJ and DVSDJ models are rejected five times each. At the $\alpha =5\%$ level, however, each model demonstrates comparable and satisfactory performance. Interestingly, during the relatively stable period (Panel B), the SDSDJ model performs relatively better at $\alpha =1\%$ but worse at $\alpha =5\%$, while the GARCHJ model exhibits the opposite pattern. During the 2015 Chinese stock market crash period (Panel C), all models perform relatively well at the $\alpha =1\%$ level, but perform poorly at the $\alpha =5\%$ level. The performances of these models during the COVID-19 pandemic (Panel D) period show a pattern similar to that observed in the 2008 crisis: the SDSDJ model performs best at $\alpha =1\%$, whereas the GARCHJ model performs best at $\alpha =5\%$. In the most recent period (Panel E), the SDSDJ model performs well at both the $\alpha =1\%$ and $5\%$ levels.

Table 5. Out-of-sample VaR prediction for spot returns.

	Panel A: January 2005 to August 2009
	$\alpha =1\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$7.81$***$\left(0.01\right)$	$3.88$**$\left(0.05\right)$	$7.81$***$\left(0.01\right)$	$3.88$**$\left(0.05\right)$	$7.81$***$\left(0.01\right)$
SDJ	$4.53$**$\left(0.03\right)$	$2.31\left(0.13\right)$	$1.44\left(0.23\right)$	$0.76\left(0.38\right)$	$0.33\left(0.57\right)$
DVSDJ	$15.08$***$\left(0.00\right)$	$6.47$***$\left(0.01\right)$	$5.10$**$\left(0.02\right)$	$23.78$***$\left(0.00\right)$	$6.47$***$\left(0.01\right)$
SDSDJ	$4.56$**$\left(0.03\right)$	$0.67\left(0.41\right)$	$0.01\left(0.93\right)$	$0.01\left(0.93\right)$	$2.25\left(0.13\right)$
	$\alpha =5\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$1.07\left(0.30\right)$	$1.07\left(0.30\right)$	$0.54\left(0.46\right)$	$1.40\left(0.24\right)$	$1.07\left(0.30\right)$
SDJ	$0.59\left(0.44\right)$	$0.89\left(0.35\right)$	$0.89\left(0.35\right)$	$2.19\left(0.14\right)$	$0.59\left(0.44\right)$
DVSDJ	$0.56\left(0.45\right)$	$3.22$*$\left(0.07\right)$	$0.84\left(0.36\right)$	$2.07\left(0.15\right)$	$3.22$*$\left(0.07\right)$
SDSDJ	$0.00\left(0.98\right)$	$0.77\left(0.38\right)$	$2.08\left(0.15\right)$	$5.90$**$\left(0.02\right)$	$1.56\left(0.21\right)$
	Panel B: August 2009 to December 2012
	$\alpha =1\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$20.22$***$\left(0.00\right)$	$15.69$***$\left(0.00\right)$	$11.60$***$\left(0.00\right)$	$2.50\left(0.11\right)$	$1.55\left(0.21\right)$
SDJ	$0.86\left(0.35\right)$	$0.02\left(0.89\right)$	$0.02\left(0.89\right)$	$0.08\left(0.77\right)$	$1.53\left(0.22\right)$
DVSDJ	$0.19\left(0.66\right)$	$1.77\left(0.18\right)$	$1.77\left(0.18\right)$	$0.00\left(0.97\right)$	$6.31$***$\left(0.01\right)$
SDSDJ	$0.25\left(0.62\right)$	$0.61\left(0.44\right)$	$0.78\left(0.38\right)$	$3.31$*$\left(0.07\right)$	$0.61\left(0.44\right)$
	$\alpha =5\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$1.95\left(0.16\right)$	$2.99$*$\left(0.08\right)$	$1.13\left(0.29\right)$	$0.52\left(0.47\right)$	$0.28\left(0.60\right)$
SDJ	$3.65\left(0.06\right)$	$1.13\left(0.29\right)$	$12.56$***$\left(0.00\right)$	$10.86$***$\left(0.00\right)$	$7.93$***$\left(0.00\right)$
DVSDJ	$14.01$***$\left(0.00\right)$	$20.44$***$\left(0.00\right)$	$23.01$***$\left(0.00\right)$	$9.13$***$\left(0.00\right)$	$23.01$***$\left(0.00\right)$
SDSDJ	$5.93$***$\left(0.01\right)$	$5.93$***$\left(0.01\right)$	$4.89$**$\left(0.03\right)$	$15.00$***$\left(0.00\right)$	$15.00$***$\left(0.00\right)$
	Panel C: January 2013 to December 2017
	$\alpha =1\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$0.52\left(0.47\right)$	$0.52\left(0.47\right)$	$2.53\left(0.11\right)$	$2.53\left(0.11\right)$	$1.04\left(0.31\right)$
SDJ	$5.69$**$\left(0.02\right)$	$1.24\left(0.27\right)$	$3.12$*$\left(0.08\right)$	$0.00\left(0.97\right)$	$2.08\left(0.15\right)$
DVSDJ	$0.05\left(0.83\right)$	$0.76\left(0.38\right)$	$0.05\left(0.83\right)$	$2.21\left(0.14\right)$	$0.24\left(0.62\right)$
SDSDJ	$0.63\left(0.43\right)$	$2.89$*$\left(0.09\right)$	$0.63\left(0.43\right)$	$0.32\left(0.57\right)$	$0.04\left(0.84\right)$
	$\alpha =5\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$10.60$***$\left(0.00\right)$	$7.51$***$\left(0.01\right)$	$5.78$**$\left(0.02\right)$	$5.78$**$\left(0.02\right)$	$5.78$**$\left(0.02\right)$
SDJ	$3.75$**$\left(0.05\right)$	$8.70$***$\left(0.00\right)$	$5.44$**$\left(0.02\right)$	$3.75$**$\left(0.05\right)$	$9.99$***$\left(0.00\right)$
DVSDJ	$10.61$***$\left(0.00\right)$	$10.61$***$\left(0.00\right)$	$11.90$***$\left(0.00\right)$	$11.90$***$\left(0.00\right)$	$19.84$***$\left(0.00\right)$
SDSDJ	$10.40$***$\left(0.00\right)$	$7.14$***$\left(0.01\right)$	$11.65$***$\left(0.00\right)$	$11.65$***$\left(0.00\right)$	$17.60$***$\left(0.00\right)$
	Panel D: January 2018 to December 2022
	$\alpha =1\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$8.76$***$\left(0.00\right)$	$15.52$***$\left(0.00\right)$	$10.31$***$\left(0.00\right)$	$11.96$***$\left(0.00\right)$	$7.31$***$\left(0.01\right)$
SDJ	$0.80\left(0.37\right)$	$3.42$*$\left(0.06\right)$	$0.04\left(0.84\right)$	$5.97$***$\left(0.01\right)$	$2.37\left(0.12\right)$
DVSDJ	$0.76\left(0.38\right)$	$0.76\left(0.38\right)$	$7.09$***$\left(0.01\right)$	$0.02\left(0.89\right)$	$4.64$**$\left(0.03\right)$
SDSDJ	$3.68$*$\left(0.06\right)$	$7.86$***$\left(0.01\right)$	$2.59\left(0.34\right)$	$0.92\left(0.34\right)$	$0.07\left(0.79\right)$
	$\alpha =5\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$0.52\left(0.47\right)$	$0.77\left(0.38\right)$	$0.52\left(0.47\right)$	$2.27\left(0.13\right)$	$0.77\left(0.38\right)$
SDJ	$1.59\left(0.21\right)$	$2.08\left(0.15\right)$	$3.27$*$\left(0.07\right)$	$1.59\left(0.21\right)$	$0.53\left(0.47\right)$
DVSDJ	$23.95$***$\left(0.00\right)$	$13.38$***$\left(0.00\right)$	$30.97$***$\left(0.00\right)$	$10.70$***$\left(0.00\right)$	$36.49$***$\left(0.00\right)$
SDSDJ	$1.70\left(0.19\right)$	$0.34\left(0.56\right)$	$2.21\left(0.14\right)$	$4.20$**$\left(0.04\right)$	$5.03$**$\left(0.02\right)$
	Panel E: December 2022 to November 2024
	$\alpha =1\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$2.54\left(0.11\right)$	$5.78$**$\left(0.02\right)$	$2.54\left(0.11\right)$	$2.54\left(0.11\right)$	$4.03$**$\left(0.04\right)$
SDJ	$0.01\left(0.94\right)$	$0.34\left(0.56\right)$	$0.73\left(0.39\right)$	$1.35\left(0.24\right)$	$0.01\left(0.94\right)$
DVSDJ	$0.39\left(0.53\right)$	$0.30\left(0.58\right)$	$1.66\left(0.20\right)$	$0.30\left(0.58\right)$	$1.66\left(0.20\right)$
SDSDJ	$0.01\left(0.92\right)$	$0.01\left(0.92\right)$	$0.01\left(0.92\right)$	$0.43\left(0.51\right)$	$0.27\left(0.60\right)$
	$\alpha =5\%$
	$l=1$	$l=2$	$l=3$	$l=4$	$l=5$
GARCHJ	$1.91\left(0.17\right)$	$0.06\left(0.81\right)$	$0.06\left(0.81\right)$	$0.00\left(1.00\right)$	$0.56\left(0.46\right)$
SDJ	$7.84$***$\left(0.01\right)$	$2.43\left(0.12\right)$	$7.84$***$\left(0.01\right)$	$3.79$**$\left(0.05\right)$	$2.43\left(0.12\right)$
DVSDJ	$10.94$***$\left(0.00\right)$	$6.55$***$\left(0.01\right)$	$10.94$***$\left(0.00\right)$	$13.86$***$\left(0.00\right)$	$13.86$***$\left(0.00\right)$
SDSDJ	$0.80\left(0.37\right)$	$1.42\left(0.23\right)$	$0.80\left(0.37\right)$	$2.25\left(0.13\right)$	$2.25\left(0.13\right)$

Notes: We forecast the 5% and 1% Value-at-Risk (VaR) from one to five days ahead for each model. For each period, we estimate the model parameters using a rolling window comprising 20% of the days in the period, with the remaining data reserved for out-of-sample evaluation. The values reported are the likelihood ratio test statistic of Kupiec [28], with p-values in parentheses. *, ** and *** denote statistical significance at the 10%, 5%, and 1% levels, respectively.

Overall, the above empirical results suggest that the SDSDJ and SDJ models can effectively capture the extreme tail (e.g., $\alpha =1\%$) of the conditional return distribution. By contrast, traditional GARCH-type models are better suited for modeling non-extreme returns (e.g., $\alpha =5\%$) but yield notably relatively poorer out-of-sample fits when modeling extreme losses.

4.3. In-Sample Option Valuation

The GARCH-type models under $\mathbb{P}$-measure can be used to model the conditional volatility and jump intensity of spot returns, while those under $\mathbb{Q}$-measure can be used to price options. Here, we apply several risk-neutralized GARCH-type models, including the SDSDJ and SDJ models to price the 50 ETF options from 23 February 2015 to 20 December 2024.

Table 6 presents the joint MLE estimation results using both spot returns and corresponding options data. Similar to the MLE estimation results for using only spot returns, the SDSDJ model achieves the highest log-likelihood value and the lowest AIC and BIC among all GARCH-type models. However, we find that the DVSDJ model performs very poorly over the time horizon, with a log-likelihood of only 21,823—$50.12\%$ lower than that of the SDSDJ model. This empirical result supports the idea that incorporating score dynamics improves the performance of GARCH-jump models in option pricing. Furthermore, we find that the jump sizes $\mu$ are all negative, the values of $\beta$ lie between 0 and 1, and the estimates of ${\lambda }_y$ are all positive, indicating that the risk premium associated with the jump component is significantly positive. These findings are consistent with those of [17,18,24,27].

Table 6. Joint MLE estimation results using both SSE 50 ETF spot returns and options data.

	H-N GARCH	GARCHJ		SDJ		DVSDJ		SDSDJ
Parameters	Normal	Normal	Jump	Normal	Jump	Normal	Jump	Normal	Jump
$\lambda$	$1.98$ ***	$3.77$ ***	$1.78\times {10}^{-3}$ ***	$1.46\mathrm{E}1$ ***	$2.08\times {10}^{-3}$ ***	$8.39\times {10}^{-1}$	$1.99\times {10}^{-3}$	$8.23$ ***	$2.33\times {10}^{-3}$ ***
	$(8.89\times {10}^{-5})$	$(6.24\times {10}^{-2})$	$(2.35\times {10}^{-5})$	$(2.17\times {10}^{-1})$	$(7.58\times {10}^{-05})$	$\left(1.00\right)$	$\left(1.65\right)$	$(1.44\times {10}^{-2})$	$(1.08\times {10}^{-4})$
$\omega$	$1.07\times {10}^{-7}$	$7.27\times {10}^{-7}$ ***		$-8.92$ ***		$1.41\times {10}^{-5}$	$3.82\times {10}^{-4}$	$-6.39$ ***	$-1.72$ ***
	$(1.53\times {10}^{-5})$	$(2.00\times {10}^{-7})$		$(1.51\times {10}^{-2})$		$(1.59\times {10}^{-3})$	$\left(1.55\right)$	$(4.24\times {10}^{-2})$	$(4.33\times {10}^{-2})$
$\beta$	$9.04\times {10}^{-1}$ ***	$9.49\times {10}^{-1}$ ***		$9.96\times {10}^{-1}$ ***		$7.46\times {10}^{-1}$	$6.03\times {10}^{-1}$	$9.55\times {10}^{-1}$ ***	$9.04\times {10}^{-1}$ ***
	$\left(0.25\right)$	$(2.50\times {10}^{-3})$		$(1.65\times {10}^{-4})$		$\left(1.00\right)$	$\left(1.22\right)$	$(3.57\times {10}^{-4})$	$(8.54\times {10}^{-4})$
$\alpha$	$9.84\times {10}^{-6}$ ***	$4.94\times {10}^{-6}$ ***		$6.14\times {10}^{-1}$ ***		$-1.51\times {10}^{-6}$ ***	$4.13\times {10}^{-3}$	$-2.94\times {10}^{-1}$ ***	$3.70\times {10}^{-2}$ ***
	$(3.93\times {10}^{-7})$	$(7.01\times {10}^{-9})$		$(4.56\times {10}^{-3})$		$(4.20\times {10}^{-14})$	$\left(2.78\right)$	$(3.36\times {10}^{-3})$	$(6.90\times {10}^{-7})$
c		$-8.49$ ***				$1.14\mathrm{E}2$ ***	$7.48\mathrm{E}1$
		$(3.48\times {10}^{-1})$				$\left(1.00\right)$	$\left(1.00\right)$
$\gamma$	$79.71$ ***					$1.24\times {10}^{-2}$	$5.28\times {10}^{-1}$	$2.25\times {10}^{-1}$ ***	$3.24\times {10}^{-1}$ ***
	$\left(8.89\right)$					$\left(2.03\right)$	$\left(1.19\right)$	$(1.82\mathrm{E}-3)$	$(2.04\times {10}^{-2})$
e						$1.24\times {10}^{-3}$	$7.22\times {10}^{-1}$
						$\left(1.18\right)$	$\left(1.36\right)$
$\mu$			$-7.78\times {10}^{-4}$ ***		$-1.54\times {10}^{-3}$ ***		$-1.91\times {10}^{-2}$		$-9.31\times {10}^{-3}$ ***
			$(1.16\times {10}^{-5})$		$(1.31\times {10}^{-4})$		$\left(1.47\right)$		$(4.33\times {10}^{-8})$
$\tau$			$6.99\times {10}^{-3}$ ***		$1.73\times {10}^{-2}$ ***		$6.65\times {10}^{-3}$		$-1.75\times {10}^{-2}$ ***
			$(1.51\times {10}^{-4})$		$(2.76\times {10}^{-5})$		$\left(2.12\right)$		$(9.56\times {10}^{-6})$
$\chi$			$2.54\times {10}^{-1}$ ***		$1.18\times {10}^{-1}$ ***
			$(2.58\times {10}^{-5})$		$(3.06\times {10}^{-11})$
$\Lambda$		$-3.77$ ***	$1.44$ ***	$1.46\mathrm{E}1$ ***	$-3.70$ ***	$-8.39\times {10}^{-1}$	$-2.71$ ***	$8.23$ ***	$8.62$ ***
		$(6.24\times {10}^{-2})$	$(2.53\times {10}^{-1})$	$(2.17\times {10}^{-1})$	$(2.17\times {10}^{-1})$	$\left(1.00\right)$	$\left(1.00\right)$	$(1.44\times {10}^{-2})$	$(6.44\times {10}^{-1})$
log-likelihood	41,405	42,052		41,528		21,823		43,753
AIC	−82,800	−84,082		−83,036		−43,610		−87,478
BIC	−82,759	−83,992		−82,954		−43,463		−87,363

Notes: This table reports the joint estimation results based on Equation (9), covering the period from 9 February 2015 to 28 October 2024. Columns labeled “Normal” contain estimates of parameters governing the normal component, and columns labeled “Jump” contain parameters governing the jump component. The standard errors in parentheses are based on the outer product of the gradient. *** denote statistical significance at the 1% level.

We also employ the IVRMSE (%) criterion (implied Volatility Root Mean Square Error) to evaluate the performance of these models. Table 7 reports the in-sample IVRMSE for different option pricing models, both overall and across various moneyness and maturities. Panel A indicates that, overall, the SDSDJ model delivers the best performance, with an IVRMSE of only $8.11\%$, followed by the SDJ model ($8.81\%$) and the GARCHJ model ($9.08\%$), while the DVSDJ model performs the worst ($12.91\%$). Panel B shows that the pricing errors for OTM Put options are generally higher than those for OTM call options. Panel C reveals that short-term options tend to have higher pricing errors than long-term ones. As DTM increases, IVRMSE decreases—for example, the GARCHJ model performs better in the long term ($7.94\%$) than in the short term ($9.94\%$), and similar patterns are observed for the other models. Our primary concern is whether the SDSDJ model outperforms traditional GARCH-type models across different maturities and moneyness levels. The empirical results confirm that the SDSDJ model exhibits robust and consistently superior performance, with IVRMSE ranging from $7.52\%$ to $8.60\%$ across maturities, and from $7.55\%$ to $8.40\%$ across moneyness categories. Therefore, the empirical results confirm the robustness of its performance with respect to the option moneyness and maturities.

Table 7. In-sample IVRMSE (%) for different option pricing models.

	BSM	H-N GARCH	GARCHJ	SDJ	DVSDJ	SDSDJ
Panel A: Overall IVRMSE (%)
	8.88	10.11	9.08	8.81	12.91	8.11
Panel B: IVRMSE (%) sorted by moneyness
$K/S_t\in$
$[0.8,0.9]$	8.71	10.02	8.63	10.61	10.38	8.33
$(0.9,1.02]$	8.50	9.96	8.19	8.32	12.72	8.40
$(1.02,1.2]$	7.87	9.23	7.13	7.32	10.88	7.55
Panel C: IVRMSE (%) sorted by maturity
$\mathrm{DTM}\in$
$(-,30]$	9.51	11.98	9.94	10.22	14.62	8.60
$(30,90]$	8.52	9.86	8.49	7.55	11.38	7.78
$(90,-]$	8.08	9.44	7.94	7.62	11.69	7.52

Notes: This table reports the in-sample IVRMS (%) (implied Volatility Root Mean Squared Error) for different option pricing models, both overall and across various moneyness and maturities based on Equation (10). The sample period is from 9 February 2015 to 28 October 2024. DTM refers to the number of days-to-maturity, and $K/S_t$ refers to moneyness defined as the ratio of the strike price divided by the current price of the stock index.

4.4. Out-of-Sample Option Valuation

We also conduct out-of-sample analyses for option valuation. For each year, option contracts from the first half of that year are used to estimate the optimal parameters, which are then applied to price contracts in the second half of that year. The model-implied volatility is derived using the classic Black–Scholes formula. By comparing the model-implied and market-implied volatilities, we compute the out-of-sample IVRMSE (%) for each model.

Table 8 reports the out-of-sample IVRMSE (%) for different option pricing models, both overall, and across various moneyness and maturities. Panel A indicates that the SDJ model yields the lowest overall IVRMSE, while the SDSDJ model performs poorly out of sample. This may be attributed to the larger number of parameters, which can result in overfitting and consequently weaker out-of-sample performance, while more parsimonious models (such as Black–Scholes and SDJ) exhibit greater stability for out-of-sample option valuation performance. Panels B through D present results when the options sample is sorted by year, maturity, and DTM, respectively. We have the following discoveries. First, higher market volatility is usually associated with poorer out-of-sample model performance. For example, in 2020 and 2024, the IVRMSE for all models exceeds $7\%$, while in 2022 and 2023, it can be as low as $2.11\%$ (for the SDJ model). This substantial variation highlights the sensitivity of GARCH-type models to market conditions. During crisis periods, the performance of option pricing models generally deteriorates; however, the SDJ model remains the most robust among them. Second, pricing accuracy is higher for at-the-money options compared to deep out-of-the-money options, and the SDJ model still performs best across all moneyness categories. Finally, all models exhibit better performance in pricing long-term options, which is consistent with the in-sample findings.

Table 8. Out-of-sample IVRMSE (%) for different option pricing models.

	BSM	H-N GARCH	GARCHJ	SDJ	DVSDJ	SDSDJ
Panel A: Overall IVRMSE (%)
	6.15	8.88	7.12	5.59	6.38	8.30
Panel B: IVRMSE (%) sorted by year
2020	7.56	11.68	9.52	8.25	8.14	10.42
2021	5.38	9.27	7.01	3.50	4.22	9.11
2022	3.63	6.73	6.53	2.11	4.53	6.88
2023	3.50	5.29	3.96	2.11	3.46	3.15
2024	8.74	9.79	7.20	7.96	9.13	9.66
Panel C: IVRMSE (%) sorted by moneyness
$K/S_t\in$
$(-,0.9]$	9.10	14.20	11.90	9.95	10.63	12.90
$(0.9,1.02]$	4.31	4.43	3.82	3.62	4.44	5.20
$(1.02,1.2]$	7.77	12.93	9.69	4.81	6.86	10.58
Panel D: IVRMSE (%) sorted by maturity
$\mathrm{DTM}\in$
$(-,30]$	8.24	13.15	10.73	7.57	8.44	12.12
$(30,90]$	5.26	6.66	4.67	4.78	5.71	5.76
$(90,250]$	4.07	3.99	3.78	3.50	4.03	5.07

Notes: This table reports the out-of-sample IVRMSE (%) for different option pricing models, both overall and across various moneyness and maturities based on Equation (10). For each year from 9 February 2015 to 28 October 2024, all option contracts from the first half of the year are used to estimate the optimal parameters, then these parameters are applied to price option contracts in the second half of the year. The model-implied volatility is obtained using the classic Black–Scholes formula. DTM refers to the number of days-to-maturity, and $K/S_t$ refers to moneyness defined as the ratio of the strike price divided by the current price of the stock index.

To summarize, the empirical results on the out-of-sample option valuation in this section demonstrate that the score-driven GARCH-jump models outperform traditional approaches—including both GARCH-type models and the classic Black–Scholes model—in out-of-sample analyses for SSE 50 ETF options.

5. Conclusions

This paper employs a novel score-driven GARCH-jump model to analyze SSE 50 ETF returns and option pricing. Our analysis yields several key findings:

The SDSDJ (score-driven model with separate dynamic jumps) model achieves the highest log-likelihood and the lowest AIC and BIC values, indicating its superiority in-sample fitting to the 50 ETF return series. This model effectively captures both time-varying volatility and jump dynamics by utilizing score-driven filters.

According to the Kupiec likelihood ratio test, the GARCHJ (GARCH with jumps) model performs reasonably well in stable periods, but the SDSDJ and SDJ (score-driven model with jumps) models more accurately capture extreme losses in turbulent periods. This highlights the robustness of the SDSDJ framework for modeling fat-tailed returns and its value in risk management under stress.

The option pricing analysis shows that the SDSDJ model achieves the best in-sample performance across all GARCH-type models and has robust pricing accuracy across moneyness and maturities. However, its out-of-sample performance is less stable—likely due to overfitting, but its simplified variant—the SDJ model—delivers the most accurate out-of-sample results. These results imply a trade-off between model flexibility and generalizability, suggesting that while more flexible models like SDSDJ may offer better in-sample fits, more parsimonious models such as SDJ are better suited for practical out-of-sample option pricing under varying market conditions.

In summary, this study contributes to the literature on return modeling and option pricing in the Chinese equity markets using such score-driven GARCH-jump models. We document that the SDSDJ and SDJ models provide a unified framework for return modeling and option pricing, demonstrating robustness across different market conditions. These findings have important implications for regulators and practitioners, who may consider adopting the score-driven GARCH-type models for return modeling and option pricing, such as the recently introduced other stock index options in China; however, we leave this for future research.

Appendix A.1. Log-Likelihood and Score Functions

Following Ballestra et al. [24], the log-likelihood for Equation (2) (conditioning on $h_t,{\chi }_t$) is

$$\begin{array}{cc}\hfill l_{returns}\left(\mathsf{\theta }\right)=\ell (\mathsf{\theta }\mid R_t)& =lnf\left(\mathsf{\theta }\mid R_t\right)=ln\left[\sum _{j=0}^{\infty }exp\left\{-{\displaystyle \frac{1}{2}}ln\left(2\pi \right)-{\displaystyle \frac{1}{2}}ln\left(h_t+j{\tau }^2\right)\right.\right.\hfill \\ \hfill & \left.\left.-{\displaystyle \frac{{\left(R_t-r-\left({\lambda }_z-1/2\right)h_t-\left({\lambda }_y-\xi \right){\chi }_t-\mu j\right)}^2}{2\left(h_t+j{\tau }^2\right)}}-{\chi }_t-ln(j!)+jln\left({\chi }_t\right)\right\}\right],\hfill \end{array}$$

(A1)

where $\mathsf{\theta }=({\lambda }_z,{\lambda }_y,\mu ,\tau ,{\omega }_{\psi },{\alpha }_{\psi },{\gamma }_{\psi },{\beta }_{\psi },{\omega }_{\delta },{\alpha }_{\delta },{\gamma }_{\delta },{\beta }_{\delta })$. We model $(h_t,{\chi }_t)$ via Equation (4) with scores

$$\begin{array}{cc}\hfill {\nabla }_t^h& ={\displaystyle \frac{\partial lnf\left(R_t\right)}{\partial h_t}}{\displaystyle \frac{\partial h_t}{\partial {\psi }_t}},{\nabla }_t^{\chi }={\displaystyle \frac{\partial lnf\left(R_t\right)}{\partial {\chi }_t}}{\displaystyle \frac{\partial {\chi }_t}{\partial {\delta }_t}}.\hfill \end{array}$$

(A2)

Stabilized scores (scaled per Ballestra et al. [24]) are given by

$$\begin{array}{cc}\hfill s^h\left(R_t,{\psi }_t\right)=& {\displaystyle \frac{h_t^2}{\left(1+h_t+{\chi }_t{\tau }^2\right)\left(h_t+{\chi }_t{\tau }^2\right)}}\sum _{j=0}^{\infty }{\displaystyle \frac{f_j\left(R_t\right)}{f\left(R_t\right)}}{\displaystyle \frac{1}{\left[1+2{\left({\lambda }_z-1/2\right)}^2\left(h_t+j{\tau }^2\right)\right]}}{\displaystyle \frac{1}{1+{\mu }^2{j}^2}}\times \hfill \\ \hfill & \left({\displaystyle \frac{{\left(R_t-r-\left({\lambda }_z-1/2\right)h_t-\left({\lambda }_y-\xi \right){\chi }_t-\mu j\right)}^2}{h_t+j{\tau }^2}}+\right.\hfill \\ \hfill & \left.2\left({\lambda }_z-1/2\right)\left(R_t-r-\left({\lambda }_z-1/2\right)h_t-\left({\lambda }_y-\xi \right){\chi }_t-\mu j\right)-1\right),\hfill \\ \hfill s^{\chi }\left(R_t,{\delta }_t\right)=& \sum _{j=0}^{\infty }{\displaystyle \frac{f_j\left(R_t\right)}{f\left(R_t\right)}}{\displaystyle \frac{h_t}{\left[h_t+j{\tau }^2+{\chi }_t{\left({\lambda }_y-\xi \right)}^2\right]}}{\displaystyle \frac{1}{1+{\mu }^2{j}^2}}\times \hfill \\ \hfill & \left({\displaystyle \frac{\left({\lambda }_y-\xi \right)\left(R_t-r-\left({\lambda }_z-1/2\right)h_t-\left({\lambda }_y-\xi \right){\chi }_t-\mu j\right)}{h_t+j{\tau }^2}}+{\displaystyle \frac{j}{{\chi }_t}}-1\right),\hfill \end{array}$$

(A3)

where

$$f_j\left(R_t\right)={\displaystyle \frac{1}{\sqrt{2\pi (h_t+j{\tau }^2)}}}{e}^{-{\displaystyle \frac{{(R_t-r-({\lambda }_z-1/2)h_t-({\lambda }_y-\xi ){\chi }_t-\mu j)}^2}{2(h_t+j{\tau }^2)}}}{\displaystyle \frac{e^{-{\chi }_t}{\chi }_t^j}{j!}}.$$

(A4)

Appendix A.2. Likelihood-Ratio Backtest for VaR Exceedances [28]

Let $\alpha \in (0,1)$ and $I_t\left(\alpha \right)=\mathbf{1}\{{\mathrm{loss}}_t>{VaR}_{t|t-1}^{\alpha }\}$ for $t=1,\dots ,n$. With $x=\sum I_t\left(\alpha \right)$ and $\widehat{p}=x/n$, test

$$H_0:p=\alpha \mathrm{vs}.H_1:p\ne \alpha .$$

Binomial likelihoods:

$$L_0={(1-\alpha )}^{n-x}{\alpha }^x,L_1={(1-\widehat{p})}^{n-x}{\widehat{p}}^x.$$

LR statistic:

$${\mathrm{LR}}_{\mathrm{UC}}=-2ln\left(\frac{L_0}{L_1}\right)=-2\left[(n-x)ln\left(\frac{1-\alpha }{1-\widehat{p}}\right)+xln\left(\frac{\alpha }{\widehat{p}}\right)\right]\stackrel{d}{\to }{\chi }_1^2\left(\mathrm{under}{H}_0\right).$$

We report ${\mathrm{LR}}_{\mathrm{UC}}$ and p-values. (Edge cases $x\in \{0,n\}$ are flagged.)

Appendix A.3. Risk-Neutral Dynamics

Under the $\mathbb{Q}$ measure, the return and state updates are defined in Equation (5), in which the score terms are given by

$$\begin{array}{cc}\hfill s^{h,\ast }\left(V_t^{*},y_t^{*},{\psi }_t\right)=& {\displaystyle \frac{h_t^2}{\left(1+h_t+{\chi }_{t+1}{\tau }^2\right){\left(h_t+{\chi }_{t+1}{\tau }^2\right)}^2}}\sum _{j=0}^{\infty }{\displaystyle \frac{f_j^{*}\left(V_t^{*},y_t^{*},h_t\right)}{f^{*}\left(V_t^{*},y_t^{*},h_t\right)}}\hfill \\ \hfill & \times \left[{\displaystyle \frac{1}{1+{\mu }^2{j}^2}}{\displaystyle \frac{1}{1+2{\left({\lambda }_z-1/2\right)}^2\left(h_t+j{\tau }^2\right)}}\right.\hfill \\ \hfill & \left.\times \left({\displaystyle \frac{{\left(V_t^{*}+y_t^{*}-{\lambda }_z{h}_t-\mu j\right)}^2}{h_t+j{\tau }^2}}+2{\lambda }_z\left(V_t^{*}+y_t^{*}-{\lambda }_z{h}_t-\mu j\right)-1\right)\right],\hfill \\ \hfill s^{\chi ,\ast }\left(V_t^{*},y_t^{*},{\delta }_t\right)=& \sum _{j=0}^{\infty }{\displaystyle \frac{f_j^{*}\left(V_t^{*},y_t^{*},h_t\right)}{f^{*}\left(V_t^{*},y_t^{*},h_t\right)}}{\displaystyle \frac{1}{1+{\mu }^2{j}^2}}{\displaystyle \frac{h_t}{h_t+j{\tau }^2+{\chi }_t{\left({\lambda }_y-\xi \right)}^2}}\hfill \\ \hfill & \times \left({\displaystyle \frac{\left({\lambda }_y-\xi \right){\left(V_t^{*}+y_t^{*}-{\lambda }_z{h}_t-\mu j\right)}^2}{h_t+j{\tau }^2}}+{\displaystyle \frac{j}{{\chi }_t}}-1\right),\hfill \end{array}$$

(A5)

where

$$\begin{array}{cc}\hfill f_j^{*}(V_t^{*},y_t^{*},h_t)& ={\displaystyle \frac{1}{\sqrt{2\pi (h_t+j{\tau }^2)}}}{e}^{-{\displaystyle \frac{{(V_t^{*}+y_t^{*}-{\lambda }_z{h}_t-\mu j)}^2}{2(h_t+j{\tau }^2)}}}{\displaystyle \frac{e^{-{\chi }_t}{\chi }_t^j}{j!}},\hfill \\ \hfill \sum _{j=0}^{\infty }{\displaystyle \frac{f_j^{*}}{f^{*}}}& =1.\hfill \end{array}$$

(A6)

Appendix A.4. Benchmark Specifications

The closed-form option pricing formula for the Heston–Nandi GARCH model [9] is

$$\begin{array}{cc}\hfill C=& {\displaystyle \frac{1}{2}}S+{\displaystyle \frac{e^{-r\left(\tau \right)}}{\pi }}{\int }_0^{\infty }Re\left[{\displaystyle \frac{K^{-i\varphi }{f}^{*}(i\varphi +1)}{i\varphi }}\right]\mathrm{d}\varphi -\hfill \\ \hfill & {Ke}^{-r\tau }\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{\pi }}{\int }_0^{\infty }Re\left[{\displaystyle \frac{K^{-i\varphi }{f}^{*}\left(i\varphi \right)}{i\varphi }}\right]\mathrm{d}\varphi \right),\hfill \end{array}$$

(A7)

where C denotes the European call option price, S is the underlying asset price, K is the strike price, r is the risk-free interest rate, $\tau$ is the time to maturity, $e^{-r\tau }$ is the discount factor, $\varphi$ is the Fourier integration variable, $f^{*}(·)$ is the characteristic function under the Heston–Nandi GARCH model, i is the imaginary unit, and $Re[·]$ denotes the real part of a complex number.