Abstract
This paper presents a multiscale histogram excess-distribution strategy addressing the structural limitations (i.e., insufficient dark-region restoration, block artifacts, ringing effects, color distortion, and saturation loss) of contrast-limited adaptive histogram equalization (CLAHE) and retinex-based image-contrast enhancement techniques. This method adjusts the ratio between the uniform and weighted distribution of the histogram excess based on the average tile brightness. At the coarsest scale, excess pixels are redistributed to histogram bins initially occupied by pixels, maximizing detail restoration in dark areas. For medium and fine scales, the contrast enhancement strength is adjusted according to tile brightness to preserve local luminance transitions. Scale-specific lookup tables are bilinearly interpolated and merged at the pixel level. Background restoration corrects unnatural tone compression by referencing the original image, ensuring visual consistency. A ratio-based chroma adjustment and color-restoration function compensate for saturation degradation in retinex-based approaches. An asymmetric Gaussian offset correction preserves structural information and expands the global dynamic range. The experimental results demonstrate that this method enhances local and global contrast while preserving fine details in low light and high brightness. Compared with various existing methods, this method reproduces more natural color with superior image enhancement.
Keywords:
CLAHE; local contrast enhancement; tone continuity; detail preservation; noise suppression MSC:
68T45
1. Introduction
The image-contrast enhancement preprocessing technique is critical for securing visibility in dark regions and restoring fine details under poor illumination. Global histogram equalization (GHE) improves the overall contrast by redistributing the global pixel distribution according to the cumulative distribution function [1,2]. However, when different brightness distributions coexist in a scene, the histogram of specific tonal ranges becomes too flattened, causing the loss of texture and edge information and degrading the natural gradation [3,4].
Adaptive histogram equalization (AHE) was introduced to address these shortcomings by dividing the input image into small tiles and performing independent histogram equalization on each to enhance the local contrast that global methods often fail to capture [5]. However, AHE without clipping amplifies fine noise in dark regions, causing a small amount of noise to appear as exaggerated brightness variations, degrading the overall visual quality. Furthermore, abrupt differences in histogram distributions across adjacent tiles often cause blocking effects and boundary ringing artifacts. Local histogram equalization (LHE) was proposed as an alternative to GHE to mitigate these problems, and it has since been widely applied in image processing tasks [6]. By applying histogram equalization independently to multiple subregions, LHE adapts to local characteristics and enables more precise contrast enhancement.
Among LHE-based methods, contrast-limited AHE (CLAHE) is one of the most widely adopted approaches. The CLAHE method limits the number of pixels exceeding a predefined clip limit in each tile histogram and redistributes the excess uniformly across all bins, suppressing excessive noise amplification [7,8]. Nevertheless, CLAHE also has intrinsic limitations. The uniform redistribution of excess restricts the expansion capacity of the cumulative distribution function (CDF), preventing the sufficient restoration of fine structures in dark regions. Thus, the uniform redistribution mechanism of CLAHE tends to average out subtle local contrasts in low-light areas, failing to reveal adequate structural details.
Moreover, retinex-based methods are derived from the theory proposed by Land and McCann [9,10,11] and have evolved into single-scale retinex (SSR) and multiscale retinex (MSR) methods [12,13]. These techniques brighten dark regions by removing the illumination component [14,15,16,17,18]. However, they suffer from halo artifacts near sharp contrast transitions and color distortion and saturation loss [19,20]. Particularly, MSR often produces grayish tones in mid-brightness regions and reduces the overall saturation. Moreover, in the logarithmic reflectance estimation process of MSR, high-frequency emphasis filtering treats bright-region details as low-frequency illumination and removes them, resulting in the loss of fine structures in bright areas.
Hybrid approaches that combine CLAHE and retinex have been proposed, yet they also fail to overcome these drawbacks [21]. Multiscale CLAHE (M-S CLAHE) applies CLAHE at various tile sizes and merges the results to enhance local contrast and suppress blocking artifacts, where small tiles emphasize fine details and large tiles smooth tile boundaries. However, despite this multiscale framework, the uniform redistribution mechanism of CLAHE still limits restoration in extremely low-light regions. In addition, when combined with retinex, compounded distortions occur. Although retinex increases the overall brightness, structural details in dark regions remain unrecovered, and its low-frequency illumination removal process further eliminates fine details in bright regions [22]. Hence, the limitations of CLAHE in enhancing low-light contrast and the information loss of retinex in the bright regions overlap, exposing the structural vulnerabilities of these methods.
Despite numerous efforts, no existing method based on CLAHE, retinex, or hybrids has addressed the requirements of preserving structural details in dark and bright regions, maintaining tonal continuity, and suppressing color distortions. Therefore, a unified framework capable of overcoming these structural limitations systematically is necessary.
This paper proposes a multiscale histogram excess redistribution strategy based on the average brightness of each tile to overcome these structural limitations. At the coarsest grid scale, all clipped excess pixels are redistributed directly to the histogram bins initially occupied by pixels, maximizing detail restoration in dark regions. In contrast, at medium and fine grid scales, the ratio between uniform and weighted redistribution is adjusted according to the average tile brightness. This approach enables a controlled adjustment of the CDF, ensuring smooth and precise tonal transitions without excessive contrast or detail loss. The resulting scale-specific lookup tables (LUTs) are bilinearly interpolated at the pixel level and processed using a background restoration step to detect and correct unnatural background alterations by referencing the original image to maintain visual consistency. Afterward, average fusion across scales is performed to integrate the LUTs, followed by a logarithm-based color restoration function (CRF) to suppress color distortion.
Furthermore, an asymmetric Gaussian offset correction is incorporated to suppress noise amplification in dark regions, highlight details in mid-brightness areas, and prevent oversaturation in bright regions. This approach enables gradation expansion and structural preservation across the dynamic range. Without requiring prior denoising, the proposed method enhances image quality under low-light and high-contrast conditions. This method addresses the common limitations of CLAHE, retinex, and retinex-CLAHE, including the insufficient restoration of dark-region details, ringing artifacts, color distortion, saturation loss, and tonal inconsistency, delivering superior overall image enhancement performance. The novelty of the proposed approach lies in its multistage integration of adaptive histogram redistribution, scale-consistent interpolation, background restoration, and nonlinear post-processing, collectively enabling perceptual naturalness and structural fidelity beyond the capabilities of prior methods.
2. Related Work
2.1. Contrast-Limited Adaptive Histogram Equalization
Zuiderveld proposed CLAHE as an extension of AHE [6]. The CLAHE method incorporates a clip limit mechanism that enhances local contrast while suppressing excessive noise amplification to overcome the limitations of GHE [23,24]. The core principle of CLAHE is to divide the input image into a regular grid of tiles and perform histogram equalization independently in each tile while constraining the maximum frequency allowed in each histogram bin. When the pixel count at a given intensity level exceeds the predefined clip limit, the surplus pixels are regarded as excess and redistributed uniformly across all histogram bins. This redistribution process reduces sharp peaks in the histogram and suppresses excessive noise amplification, improving local contrast [25].
The primary advantage of CLAHE lies in its ability to suppress the noise amplification problem in AHE [8]. By applying the clip limit, CLAHE prevents the overemphasis of fine noise in dark regions, whereas bilinear interpolation across adjacent tiles alleviates artificial block boundary artifacts. Moreover, the local histogram analysis enables CLAHE to restore texture information that global approaches typically fail to preserve.
Despite these advantages, CLAHE has several limitations. First, determining an appropriate clip limit is challenging. If the clip limit is set too low, the effect of histogram equalization becomes negligible, and fine details in dark regions cannot be adequately restored [26]. Conversely, if the clip limit is set too high, noise amplification similar to AHE reoccurs, degrading the visual quality. This parameter dependency makes it difficult to guarantee consistent performance across diverse imaging conditions.
Second, CLAHE fails to restore adequate fine details in extremely low-light conditions. As reported by Reza, CLAHE is effective for images with moderate brightness levels [8]. However, for images with very low average brightness, no clip limit setting can sufficiently enhance details in dark regions. This limitation arises because the histogram clipping mechanism fails to provide adequate gradation expansion when the global brightness distribution is highly compressed.
Third, the uniform redistribution of excess pixels represents a fundamental limitation. In CLAHE, the clipped pixels are equally distributed across all histogram bins. This uniform redistribution constrains the increase in the CDF, significantly reducing the expansion capacity of the resulting LUT. Thus, the original structural characteristics of the histogram are distorted, and the formation of clear contrast is hindered in dark regions, leading to the loss of fine details. This problem is a drawback of CLAHE and cannot be addressed merely by adjusting parameters. Consequently, CLAHE-based image enhancement cannot fundamentally resolve various problems, such as noise amplification, detail distortion, color imbalance, and insufficient restoration of information in dark regions.
2.2. Retinex-Based Techniques
The retinex theory proposed by Land and McCann is an image-processing approach designed to model the color constancy mechanism of the human visual system [9]. The fundamental assumption of this theory is that an observed image can be expressed as the product of the illumination and reflectance components:
where denotes the input image, represents the illumination component, and indicates the reflectance component. The illumination component represents the overall brightness distribution of a scene and exhibits low-frequency characteristics. The reflectance component represents the intrinsic reflectance properties of objects and comprises high-frequency details. The objective of retinex-based methods is to remove illumination nonuniformity and accurately estimate the reflectance component, ensuring consistent visual quality regardless of lighting conditions.
2.2.1. Single-Scale Retinex
Jobson et al. proposed SSR, which restores the reflectance component by estimating the illumination using a Gaussian filter [12]. The mathematical formulation of SSR is given by the following:
where denotes the estimated reflectance component, indicates a two-dimensional (2D) Gaussian function with standard deviation , and the operator denotes the convolution. The convolution applies the filter across all positions of the image , computing a weighted sum at each location. The logarithmic operation converts the multiplicative relationship between illumination and reflectance into an additive form, facilitating the separation of illumination.
The advantage of SSR is its ability to enhance fine details in dark regions. According to Ismail et al., SSR restores hidden structural information in backlit conditions or heavily shadowed regions [27]. However, SSR exhibits several notable limitations. The first limitation is the halo effect. At edges with abrupt intensity transitions, Gaussian-based illumination estimation becomes inaccurate, causing ringing artifacts near boundaries. The second limitation is color distortion. The logarithmic transformation alters the original color balance, producing unnatural hue shifts, particularly in highly saturated regions. The third limitation is the overall desaturation, where SSR-processed images generally display reduced color saturation compared with the original. This reduction occurs because the logarithmic operation alters the relative ratios between color channels, and part of the color information may be misclassified as illumination and removed during decomposition. Such desaturation degrades visual fidelity and reduces perceptual preference.
2.2.2. Multiscale Retinex
The MSR method was introduced to overcome the limitations of SSR by employing Gaussian filters with multiple scales [13], formulated as follows:
where N denotes the number of scales, represents the weight assigned to each scale, such that , and indicates the 2D Gaussian filter with standard deviation . The convolutional operation applies each Gaussian filter to the input image . The outputs from multiple scales are linearly combined via the summation operator , yielding the final MSR response.
Typically, three scales are employed: small (enhancing fine details), medium (providing balanced contrast improvement), and large (suppressing global illumination nonuniformity). The MSR method alleviates several drawbacks of SSR, as the multiscale strategy mitigates excessive contrast amplification and reduces halo artifacts commonly observed in single-scale processing, improving the overall visual quality. Furthermore, MSR with color restoration incorporates a CRF to address color distortion problems [28].
- Despite these improvements, these methods still have critical limitations:
- Overall desaturation and residual halo artifacts:
- Although MSR improves on SSR, global desaturation persists. This limitation stems from its reliance on the gray world assumption. When an image violates this assumption, such as when one color dominates the scene or specific chromatic components are absent, the weighted averaging across scales drives colors toward gray, reducing saturation. Moreover, halo artifacts originating from the small-scale filters are not entirely eliminated despite compensation by larger scales.
- Loss of detail in bright regions:
- During logarithmic reflectance estimation, the Gaussian-based illumination approximation becomes inaccurate, suppressing fine structures in bright regions. The blurring effect of the Gaussian kernel excessively smooths edges, causing high-frequency texture information to be misclassified as part of the low-frequency illumination component and removed. This problem is pronounced in textured bright areas, resulting in significant information loss. Although Land’s original retinex theory assumes that the reflectance component faithfully represents the intrinsic properties of objects, practical implementations of MSR fail to achieve a complete separation between illumination and reflectance, diverging from this theoretical ideal.
2.3. CLAHE–Retinex Hybrid Approach
Several studies have attempted to exploit the complementary characteristics of CLAHE and retinex. Kim et al. proposed a model that combines retinex with multiscale CLAHE for high-dynamic range (HDR) tone compression, integrating the illumination estimation capability of retinex with the adaptive contrast enhancement of CLAHE [21]. The proposed hybrid strategies include sequential application, where retinex performs global illumination correction, followed by CLAHE for local contrast enhancement. Moreover, weighted averaging of the two outputs and selective integration in the frequency domain have been proposed to maximize the advantages of both methods.
These hybrid approaches are meaningful because they partially employ the strengths of each technique. Retinex contributes to global brightness improvement, whereas CLAHE enhances local contrast, and their combination alleviates some of the severe artifacts that occur when either method is applied independently. With an appropriately designed integration scheme, these methods can achieve superior visual quality in low-light conditions compared with using CLAHE or retinex alone.
However, despite these advantages, such combined methods still have structural limitations. First, the contrast enhancement constraints of CLAHE overlap with the loss of detail in bright regions using retinex. In addition, CLAHE redistributes excess pixels uniformly, restricting the growth of the CDF and causing insufficient contrast enhancement in dark regions. Moreover, retinex discards high-frequency content during illumination removal, suppressing fine details in bright areas. Thus, a dual distortion arises in which structural information vanishes at both extremes of the intensity range.
Second, the intrinsic artifacts of the two methods can reinforce each other. The CLAHE method frequently introduces block boundary artifacts, whereas retinex produces halo effects. When combined, these artifacts may yield more complex and visually distracting degradation. In addition, differences in their color-processing mechanisms can generate new distortions, such as hue inconsistency and saturation imbalance. These shortcomings are structural and cannot be eliminated by merely parameter tuning or post-processing.
2.4. Deep Learning Approaches
In recent years, deep-learning–based approaches have been actively investigated to overcome the structural limitations of traditional image contrast enhancement methods. Deep neural networks, including convolutional neural networks (CNNs), can learn the complex statistical characteristics of low-light images from large-scale datasets, thereby effectively alleviating issues such as parameter dependency, noise amplification, and tonal distortion commonly observed in rule-based algorithms.
Representative examples include LLENet, a network specifically designed for low-light image enhancement, which adaptively adjusts brightness and structure by directly learning from the input image [29]. Unlike pixel-level simple correction, LLENet performs higher-level representation learning, revealing details in dark regions while suppressing saturation in bright regions. This approach effectively reduces local contrast loss and color distortion problems observed in CLAHE or retinex methods.
Meanwhile, the application of deep learning techniques has expanded to practical domains such as terrain imagery and disaster detection [30]. For instance, a recent study on landslide extraction proposed a network that integrates a two-branch multiscale context feature extraction module (TMCFM), feature fusion exploiting static and dynamic context (FSDC), and a deeply supervised classifier (DSC). This architecture enabled precise detection by considering complex backgrounds and scale variations, successfully addressing challenges such as distinguishing bare land from vegetation, mitigating shadow interference, and handling landslides of various scales. The method achieved up to a 16.94% improvement in the intersection-over-union (IoU) metric compared to existing deep learning models. These results demonstrate that deep learning–based enhancement and analysis methods not only improve visual quality but also facilitate higher-level structural preservation and accurate semantic interpretation through contextual understanding and scale adaptivity.
The greatest advantage of learning-based approaches lies in their data-driven adaptability. While traditional methods often exhibit performance fluctuations depending on parameter selection, deep learning models can secure generalization capabilities by being trained on datasets encompassing diverse illumination and environmental conditions. Furthermore, networks can simultaneously address noise suppression, color restoration, and structural preservation, going beyond simple brightness adjustment.
Nevertheless, deep-learning–based approaches also face several limitations. First, constructing large-scale training datasets is essential, and performance degradation may occur if the dataset fails to sufficiently reflect real-world application conditions. Second, high computational costs and memory demands pose significant constraints for embedded devices or real-time applications. Third, the black-box nature of deep models makes it difficult to interpret results, and unexpected distortions or performance degradation may arise under specific conditions.
Therefore, although deep learning methods offer superior adaptability and representational power compared to traditional approaches, they also suffer from drawbacks such as data dependency and computational complexity. Recent studies have sought to address these challenges through lightweight network design, model compression via knowledge distillation, and hybrid architectures that integrate traditional methods such as CLAHE or retinex. This trend highlights that deep learning techniques are becoming a core direction not only for low-light image enhancement, but also for complex natural image processing tasks in general.
3. Proposed Method
Figure 1 illustrates the overall workflow of the proposed method, comprising five stages: multiscale histogram redistribution, interpolation and restoration, scale fusion, chroma compensation, and final nonlinear post-processing. The input image is first converted into gray scale, after which three tile partitions, coarse (4 × 4), medium (8 × 8), and fine (16 × 16), are applied.

Figure 1.
Flow chart of the proposed method.
At each scale, a blending-map-based strategy determines the uniform-to-weighted redistribution ratio according to the mean luminance of each tile. Then, the clipped excess is adaptively redistributed. A neighbor-tile-based adjustment compensates for abrupt luminance variations across tile boundaries to improve local consistency. In Figure 1, the red box indicates the region where this neighbor-tile-based adjustment was applied to correct local luminance discontinuities across tile boundaries. Pixel-level bilinear interpolation is applied to construct continuous LUTs, suppressing blocking artifacts and ensuring tonal continuity across tile boundaries. A background restoration stage corrects regions distorted by excessive local contrast enhancement, referencing the original image to maintain a natural appearance. The results from the three scales are integrated using average fusion (Σ), where fine-scale partitions emphasize local structures and coarse-scale partitions suppress block artifacts, balancing detail preservation and structural smoothness.
After scale fusion, an asymmetric Gaussian offset correction is applied. This process suppresses oversaturation in bright regions, enhances the sharpness of mid-tones, and preserves black levels in dark areas. In this way, it provides a nonlinear adjustment that complements the preceding linear fusion process. At this point, the original input image is converted from RGB to Lab for the first time, and the channels are separated. The fused luminance channel (, corrected with Gaussian offset) replaces the Lab L channel, while the chrominance channels a and b are taken from the original Lab image.
For chroma restoration, a two-step compensation strategy is employed. First, ratio-based chroma scaling adjusts the a and b channels proportionally to the ratio , with conditional clipping to prevent excessive saturation. This method produces an intermediate result by combining with the ratio-adjusted chroma channels. Building on this, a CRF is applied to mitigate interchannel imbalance and maintain structural consistency with the original chroma, resulting in a fully corrected chromatic representation.
Finally, the corrected Lab image is recomposed as (L = , a = = ), and this Lab image is transformed back into the RGB color space to yield the final enhanced image. This approach enhances the contrast, preserves structural details, and reproduces natural colors to ensure robust perceptual quality and global visual coherence.
3.1. Local Mean Luminance-Based Blending Map Generation
The input RGB image is converted to a grayscale image. An image of size is divided into tiles. This study adopts a multiscale approach by partitioning the image into grids of , , and , and generating independent blending maps for each scale. Each tile size is pixels, and tile is defined as the set of pixel coordinates in that region. For each tile, this approach performs histogram clipping and redistribution of excess counts, where the relative relationship between the local mean tile luminance and the global mean image luminance determines the redistribution scheme. The luminance of an input pixel is denoted by , and the mean luminance of tile is calculated as follows:
The blending map is a weighting matrix with values between 0 and 1, determined by the difference between the mean tile luminance and global mean luminance using the sigmoid function:
where ) represents the blending coefficient of tile ), and denotes the slope parameter controlling the sensitivity of the function to luminane variations. For some values of :
- : The curve becomes very flat, reflecting the intention of distributing nearly uniform weights across tiles.
- (adopted in this study): Provides a moderate slope, designed to ensure smooth transitions in mid-tone regions while maintaining a natural separation between dark and bright areas.
- : The curve becomes extremely steep, essentially acting like a threshold function, illustrating the risk of losing smooth transitions.
In this experiment, achieved an optimal trade-off that (i) preserves the local contrast in mid-luminance regions, (ii) enhances dark-region details without excessive amplification, and (iii) ensures smooth transitions between neighboring tiles. For the coarsest grid, identical weights were applied to all tiles regardless of luminance; therefore, no blending map is required.
3.2. Excess Redistribution Based on the Blending Map
This process constitutes the core of the overall algorithm, in which the clipped histogram excess of each tile is redistributed based on the blending map generated in Section 3.1. After clipping, the excess can either be uniformly spread across all bins or concentrated in the bins where pixels originally existed, following a weighted scheme.
The uniform redistribution strategy is effective in suppressing excessive noise amplification in flat regions with little information; however, it is limited in enhancing brightness and restoring fine structures in dark regions. In contrast, the weighted redistribution strategy concentrates the excess into bins that already contain pixels, increasing brightness in darker areas and better preserving structural details.
The proposed method adaptively combines uniform and weighted redistribution according to local luminance characteristics, applying the strengths of both approaches. This achieves a balance between visual quality and structural preservation across the entire image.
Figure 2 illustrates the proposed adaptive redistribution process. For an input image, the results using uniform redistribution and weighted redistribution are presented independently, highlighting the distinct characteristics of each strategy. Uniform redistribution maintains smoothness in background regions but fails to recover sufficient details in dark areas due to its limited contrast enhancement. Conversely, weighted redistribution emphasizes details in darker regions but often introduces excessive contrast or noise in flat background areas. In practice, the final LUT is generated by adaptively determining the ratio between the two strategies using the sigmoid-based blending map, maximizing their complementary strengths while mitigating drawbacks. This blended LUT is applied to produce the enhanced output image.
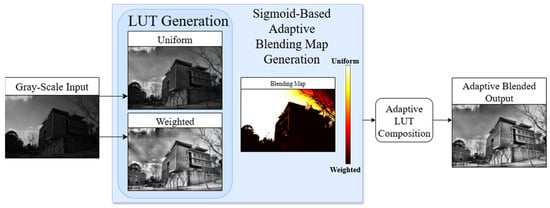
Figure 2.
Adaptive excess redistribution based on a sigmoid map.
For each tile , the excess is defined as the sum of the clipped pixel counts, expressed as follows:
where denotes the total excess in tile ), represents the number of pixels in the original histogram at bin , and indicates the clip limit defining the maximum allowed pixel count per bin. Only values exceeding the clip limit are accumulated, preventing overconcentration of pixels in specific bins and quantifying the total redistribution amount for processing. Negative excess is avoided by clipping at zero.
The excess is redistributed using two complementary schemes. First, the uniform redistribution scheme distributes the excess equally across all histogram bins. The redistributed excess for bin is defined as follows:
where denotes the total number of histogram bins. Equation (7) indicates that each histogram bin receives the same portion of the excess, independent of b. Any remainder resulting from integer division is randomly assigned to selected bins.
Second, the weighted redistribution scheme introduces the concept of local weights, reflecting the original bin counts and the distribution of the surrounding bins. This method ensures smoother and more continuous gradation expansion by adaptively emphasizing bins according to their local density. The local weight for bin is defined as follows:
The above equation computes the local weight by summing the histogram values within a ± 10 bin range centered at bin , with clipping applied to ensure that the range remains within [0, 255].
The local weight serves as the weighting criterion when allocating the excess to bin . The final redistributed excess for bin at iteration is determined as follows:
where denotes the set of valid bins eligible for redistribution. The value computed using Equation (9) is redistributed to the histogram via the weighted allocation process. This formulation proportionally distributes the remaining excess pixels at iteration according to the product of the original histogram value and the local weight .
If any undistributed excess remains while valid bins are still available, the same allocation procedure is iterated until the residual amount is exhausted. This iterative structure alleviates inefficiencies in integer-based allocation, ensuring a stable and continuous redistribution of the overall excess.
This study exclusively applies the weighted redistribution scheme to the coarsest tile grid (4 × 4) because large tiles typically cover broader spatial regions, where histogram distributions tend to be smoother and relative frequency differences between bins are mitigated. Consequently, the excess pixel count becomes larger, and redistributing such a substantial excess in a weighted manner across histogram bins where values already exist yields a more pronounced contrast enhancement effect.
In contrast, smaller tile grids, although advantageous for emphasizing fine structures, often exhibit locally uneven luminance distributions and unstable histogram bin populations. Applying the same weighted scheme under these conditions would likely lead to a disproportionate concentration of excess in specific bins, amplifying noise. Therefore, the proposed system confines the full weighted redistribution to the 4 × 4 grid, restoring structural details in dark regions while preventing noise amplification in smaller tiles, achieving a balanced enhancement outcome.
3.3. Neighbor-Tile-Based Adjustment
The initial blending map is computed by applying a sigmoid function to the mean luminance of each tile. Although this formulation automatically reflects the intrinsic luminance characteristics of each tile, it is limited because it does not sufficiently account for local contrast differences or luminance discontinuities across neighboring tiles.
A post-processing stage is introduced to address this limitation, where the blending weight of each tile is locally adjusted according to the luminance distribution of its neighboring tiles. Even if a tile has a relatively low blending weight, its value can be elevated if surrounded by multiple neighbors with higher weights, restoring local luminance balance more naturally. The correction ratio for the central tile ) is defined as follows:
where denotes the blending weight of the neighboring tile , and indicates the distance from the central tile ). The neighboring set includes the eight adjacent tiles (vertical, horizontal, and diagonal). A larger indicates that the central tile is surrounded by neighbors with stronger blending weights. To ensure local balance, the adjusted weight of the central tile is defined as , while enforcing a minimum bound .
Based on , the adjusted blending weight of the central tile is given by
where represents the lower bound for blending weights, set to 0.3 to prevent excessive noise amplification in flat regions.
By incorporating the blending weights and spatial arrangement of neighboring tiles, this adjustment enhances local consistency and alleviates abrupt luminance transitions across tile boundaries. Hence, the refined blending map offers smoother contrast transitions and improved visual naturalness.
3.4. Lookup Table Generation and Interpolation Based on Blending Weights
After the blending map adjustment is completed, an LUT is generated for each tile according to its blending weight, and the final pixel values are determined based on this LUT. This step integrates the histogram equalization results from the uniform and weighted redistributions according to the blending weights derived from the blending map. Furthermore, an interpolation procedure is incorporated to alleviate gradation discontinuities that may arise along the tile boundaries.
For each tile ), the LUT generated using the uniform redistribution () and the one generated using the weighted redistribution () are linearly combined according to the blending weight , as follows:
The resulting LUT reflects the local luminance characteristics and structural properties of the histogram, achieving simultaneous local contrast enhancement and noise suppression.
Bilinear interpolation is applied to eliminate tonal discontinuities along tile boundaries. For each pixel , its relative tile coordinates are denoted by and . The corrected pixel value is calculated by blending the four neighboring tile values as follows:
Applying bilinear interpolation during the LUT application can suppress brightness discontinuities and block artifacts around tile boundaries. This approach minimizes tonal breaks typically induced by tile-based processing and restores the overall luminance and gradation more smoothly and naturally.
3.5. Background Recovery
In the proposed contrast enhancement method, excessive amplification in certain regions may cause background distortion or form artificial boundaries. Drastic changes in background regions must be suppressed, and tonal discontinuities occurring at processing boundaries must be corrected to alleviate these problems. Thus, this study introduces a background recovery scheme that takes the original image and CLAHE-enhanced image as input, producing a visually natural and quality-improved final image . This process is implemented as a post-processing stage comprising three sequential steps: (i) identification and restoration of background regions, (ii) mitigation of discontinuities across adjacent pixels and tile boundaries, and (iii) refinement of residual distortions remaining along the recovered mask. Figure 3 illustrates the proposed pipeline overview.
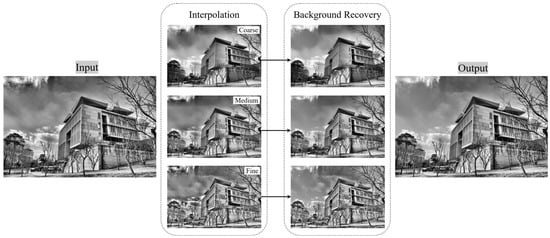
Figure 3.
Overenhancement artifact compensation.
For the given input, three interpolation results, coarse, medium, and fine, are initially generated, each corresponding to a different tile size. These scales capture distinct levels of structural details and background tone representations. During the background recovery stage, contrast overamplification observed in coarse-scale interpolation is attenuated, tonal imbalances across medium-scale regions are adjusted, and fine-scale textures are refined to suppress localized artifacts. This multiscale integration enables structural preservation and background stabilization.
Prior to recovery, large flat regions, such as the sky, exhibited uneven contrast, and dark artificial boundaries often emerged around cloud edges, resulting in visually distracting halos. After recovery, these discontinuities were substantially reduced, and the overall background tone was restored to a level closer to that of the original image. Structural components (e.g., buildings, tree branches, and fine textures) retained their sharpness without excessive contrast amplification. This balance between background smoothness and foreground clarity constitutes a critical advantage of the proposed method.
In summary, the background recovery scheme suppresses distortions and block artifacts typically encountered in conventional enhancement methods, while preserving structural sharpness and fine details. Thus, the final output image displays enhanced stability, improved perceptual quality, and a more visually natural appearance.
3.5.1. Background Mask Generation and Restoration
This stage identifies regions where excessive brightness reduction occurs due to contrast enhancement and restores these regions using the original image. First, the pixelwise luminance difference between the original and enhanced image is computed. The luminance difference at each coordinate is defined as follows:
where indicates that the pixel has become darker after enhancement. A darkened-region mask is generated as follows:
Next, the local flatness of the original image is analyzed. For each pixel, the mean luminance of its surrounding window, excluding the center pixel, is computed:
The flatness measure is defined as the absolute luminance difference between the center pixel and this local mean:
where W denotes the neighborhood excluding the center pixel. In practice, this operation can be implemented using a filtering kernel with the center weight set to zero.
The 75th percentile of the entire distribution of is selected as the threshold to determine the background region. The final background mask is defined as follows:
This 75th percentile criterion provides a statistically robust boundary encompassing sufficiently uniform regions likely to correspond to the background. Using a threshold that is too low excessively limits the restoration area, leading to insufficient background recovery. Conversely, a threshold that is too high includes structurally significant regions, resulting in detail loss. The empirical results in this study confirmed that the 75th percentile setting yields the most reliable separation between the background and foreground. For different percentile thresholds:
- Less than 50th percentile: The background region is defined too narrowly, resulting in insufficient restoration of actual background areas, leaving darkened regions and block artifacts.
- 75th percentile (adopted in this study): Provides a stable separation between background and detailed structures, enabling effective background restoration.
- 100th percentile: Almost all regions are classified as background, causing detailed structures to be included in the restoration and leading to blurred results.
Finally, for pixels where the background mask is activated, the restored image is updated by replacing the enhanced pixel value with that of the original image. The restored image, initially denoted by , is updated as follows:
3.5.2. Mitigation of Discontinuities Between Adjacent Pixels
For the restored image obtained in Section 3.5.1, a selective smoothing procedure based on local edge strength is applied to mitigate luminance discontinuities between adjacent pixels. First, horizontal and vertical Sobel operators are applied to compute the gradients and defined as follows:
and are convolved with the image to obtain the directional gradients:
where denotes the 2D discrete convolution. The edge magnitude is computed as
The threshold is set to the 85th percentile of the entire distribution of , and pixels over this threshold are regarded as strong edges to generate the mask:
This 85th percentile threshold identifies regions with significant structural transitions while excluding weak luminance fluctuations and background noise. By designating only the top 15% of pixels as edges, the method ensures that smoothing is applied selectively, preventing unnecessary blurring and preserving structural details. For pixels where , Gaussian-based smoothing is performed. A Gaussian kernel with standard deviation is defined as follows:
and is applied to to generate the smoothed image .
Next, within a local window centered at , the mean absolute luminance difference between the restored and original images is
If this value exceeds a predefined threshold, a blending weight is computed based on the local luminance variation, and the pixel value is updated using linear mixing of the restored and smoothed images:
The blending weight in Equation (28) increases linearly with the local luminance variation and is capped at a maximum value of 0.7, preventing excessive smoothing and avoiding the loss of fine details:
3.5.3. Mitigation of Discontinuities at Restored Mask Boundaries
In Section 3.5.1, the background mask was generated to restore flat background regions using the original image, improving the overall visual quality. However, this restoration may cause local gradation discontinuities between restored background regions and adjacent areas where no restoration is applied. An additional boundary smoothing operation is applied along the restored mask boundaries to address this problem.
- Boundary Mask ExtractionA morphological gradient operation is performed on to extract the transition boundary between background and nonbackground regions. Using a elliptical structuring element , the boundary mask is defined as follows:where denotes morphological dilation, which expands the boundary of the background mask using the structuring element . Equation (29) extracts only the pixels lying on the transition boundary by subtracting the original mask from its dilated version.
- Weighted Averaging on Boundary RegionsFor pixels where , a weighted average of the local intensity values is computed to ensure smooth luminance interpolation. In a local window , the Gaussian kernel is employed as the weighting function to compute the locally weighted mean intensity as follows:where represents a 2D Gaussian kernel that assigns higher weights to pixels closer to the center. This approach alleviates abrupt gradation transitions along the boundary while preserving the structural integrity of adjacent regions.
- Boundary Correction via Weighted BlendingThe final pixel intensity is updated by linearly blending the original and Gaussian-averaged values as follows:where represents the blending ratio, selected empirically to achieve natural boundary transitions while minimizing structural detail loss.
- Post-processing and NormalizationAfter all corrections, the pixel values of the resulting image are clipped to the range and converted into 8-bit unsigned integers. This stage prevents excessive contrast amplification and alleviates visual artifacts caused by boundary discontinuities. Thus, the background regions are restored as flat and noise-suppressed areas, whereas the structural details of foreground objects remain intact, enhancing the overall perceptual image quality.
3.6. Multiscale Image Fusion
This study generates multiple CLAHE results by applying various tile-grid-size configurations with the corresponding clip limits, averaging them to integrate the enhancement effects across various scales. Specifically, the tile configuration applies weighted redistribution across the entire histogram range, forming contrast in dark regions and clearly revealing fine details in low-light areas. The tile acts as a hybrid of small and large tile behaviors, achieving a balanced effect between global contrast enhancement and local contrast restoration. The tile, with its relatively small size, enhances contrast in regions rich in fine structures while maintaining flatness in featureless regions. This dual behavior preserves structural details and suppresses unnecessary contrast amplification. The scale-specific results are averaged to produce the final merged image , expressed as
where N denotes the number of scales used, which is three in this study.
3.7. Color Restoration and Gaussian Offset Post-Processing
The image obtained after CLAHE and multiscale merging is adjusted only in the channel of the Lab color space, whereas the chromatic channels and are retained from the original image. Thus, luminance is enhanced, but the color information remains unadjusted. Therefore, a color restoration procedure is necessary to maintain the original chromaticity while adapting it naturally to the adjusted channel.
3.7.1. Luminance-Based Ratio Adjustment and Color Restoration Function for Color Compensation
Ratio-based adjustment is employed for color restoration. The ratio is defined using the enhanced luminance and original luminance , reflecting the relative scaling of color according to luminance variation. A small constant is added to the denominator to ensure numerical stability:
The ratio is conditionally clipped according to the original luminance value to prevent color distortion caused by excessive saturation in certain regions. The clipping ranges are defined as follows:
In Equation (34), the threshold value of 20 is used to separate perceptually dark regions from normal luminance areas. Experimental evaluations confirmed that this cutoff minimizes color distortion while maintaining stable enhancement in dark regions. The clipped ratio is then applied to the chroma channels as
producing ratio-scaled chroma components.
Next, the CRF is applied to adjust the relative proportions of the chromatic channels. This process mitigates imbalances among channels arising from luminance enhancement. The CRF is defined as follows:
where denotes the pixel value at position in the original RGB image, and represents the sum of the three channels The parameters and α control the correction strength and luminance scaling ratio. This study empirically set and . Finally, the compensated chroma is obtained as
The CRF suppresses chromatic imbalance and saturation loss that may occur after luminance adjustment while maintaining structural consistency with the original color information. Thus, the two-step color compensation reduces discrepancies between the adjusted channel and original chromatic channels, ensuring natural color reproduction and overall visual coherence.
3.7.2. Asymmetric Gaussian Offset Adjustment
After color restoration using CRF, an additional asymmetric Gaussian-based offset is applied to the luminance () channel to enhance the sharpness of mid-tone regions and achieve visual balance between dark and bright areas. The proposed offset function is defined as an asymmetric Gaussian, applying variances to the left and right sides of a central luminance value :
where denotes the coefficient determining the maximum offset intensity, indicates the central luminance, and represent parameters controlling the distribution width for dark and bright regions, respectively. In this study, the parameters were empirically set to .
A conventional Gaussian function has a symmetric shape centered at , and thus applies the same adjustment strength to both dark and bright regions. However, the human visual system responds much more sensitively to subtle luminance variations in dark regions, while it is relatively less sensitive in bright regions, where saturation can easily occur. As a result, using a symmetric Gaussian leads to two problems.
First, there is insufficient restoration in dark regions. Since a symmetric Gaussian treats dark and bright regions in the same way, the shadows that require stronger compensation are not adequately enhanced. Consequently, the details in dark regions remain suppressed or insufficiently revealed.
Second, there is excessive enhancement and saturation in bright regions. Because the symmetric Gaussian applies the same level of adjustment to the highlights, unnecessary luminance amplification occurs in already bright areas, resulting in saturation and color distortion.
For these reasons, this study adopts an asymmetric Gaussian. By setting and differently, a narrower variance is applied to the dark side to actively enhance shadow details, while a wider variance is applied to the bright side to suppress excessive enhancement. This design aligns with the characteristics of the human visual system, improving detail visibility in dark regions while maintaining stable and natural tones in bright regions. Ultimately, the asymmetric Gaussian overcomes the limitations of the simple Gaussian, achieving balanced image enhancement across dark, mid-tone, and bright regions.
Mid-tone regions are further emphasized, dark regions are smoothly brightened, and bright regions are stably maintained without an excessive luminance increase by applying this offset to the luminance channel. Notably, when the input luminance L approaches the extremes (0 or 255), the function output sharply decreases, resulting in no additional offset. This preserves completely dark (black) and excessively bright (white) regions in their original state. Hence, this step serves as a post-processing stage that prevents luminance saturation and chromatic artifacts, while emphasizing the perceptual presence of mid-tone regions and enhancing the overall visual image quality.
3.8. Final Image Composition
This section describes the procedure for integrating all previously proposed processing steps to form the final output image. The overall system comprises four stages: (1) local contrast enhancement, (2) interpolation and background restoration, (3) color restoration and compensation, and (4) luminance offset adjustment and final synthesis.
First, CLAHE processes the input grayscale image based on the average luminance of each tile to enhance local details. The resulting tile-based LUT outputs are bilinearly interpolated to minimize unnatural transitions at the tile boundaries. Next, a background restoration procedure that considers the global luminance structure of the image is applied to correct regions that may become excessively dark or distorted in brightness due to CLAHE processing. As a result, the luminance-corrected intermediate image EnhancedL is produced.
In the color restoration stage, the and channels are extracted from the original RGB image, and the brightness-based ratio adjustment and CRF are applied to suppress color distortions caused by luminance changes. The CRF balances the corrected luminance image with the chrominance channels, producing the compensated chrominance channels and .
In the following step, an asymmetric Gaussian offset is applied to enhancedL to adjust the luminance distribution nonlinearly. This operation strengthens contrast in the mid-luminance regions while suppressing distortions in very dark or very bright regions, maintaining a stable luminance structure. Thus, the final luminance channel is obtained. Finally, the luminance channel is combined with the compensated chrominance channels and in the Lab color space, and then transformed back into the RGB color space to produce the final output image.
4. Simulation Results
4.1. Comparative Experiments
Figure 4 shows the input images used for the comparative experiments.

Figure 4.
Input images.
4.1.1. Global Tone Compression and Local Detail/Color Rendering Performance
Figure 5 presents the results of global tone mapping and local detail restoration using a color chart placed in an outdoor environment. The experiment was conducted under mixed illumination, where high- and low-luminance regions coexist, to evaluate the structural preservation and color fidelity across contrast ranges.
First, the LLE-NET method exhibited a generally low brightness level, leading to a narrow luminance range and insufficient tonal diversity. Consequently, brightness and chromatic variations appeared monotonous under complex illumination, limiting the reproduction of structural details and color contrast.
The M-S CLAHE method preserved details and color well in bright regions; however, excessive contrast amplification caused some tiles to appear overly dark, whereas the detail and color recovery in shadow regions remained limited, producing a darker tone overall. The retinex-CLAHE method brightened dark regions but blurred structures in bright areas and displayed noticeable color distortion due to saturation loss. The Reinhard method exhibited severe detail loss in highlight areas, whereas shadow regions were insufficiently elevated, inadequately revealing fine structures [31]. The iCAM06 method refined the tone adjustment but did not preserve fine structures and struggled with reproducing complex textures [32]. The L1L0 method suffered from saturation and chroma loss, inaccurately reproducing primary colors [33]. The method by Kwon et al. produced a hazy overall tone, reducing visual sharpness [34].

Figure 5.
Magnified color chart images: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.
In contrast, the proposed method stably preserved structural and chromatic information across the full tonal range by employing multiscale histogram redistribution and nonlinear offset correction. Unlike existing methods, the proposed method avoided excessive contrast amplification and highlight saturation. Magnified comparisons of the color chart further confirm that the proposed method faithfully reproduced primary colors in shadow and highlighted regions while recovering complex textures without structural loss. In Figure 5, the red boxes indicate the magnified regions used for detailed comparison, and the red lines represent the line-scan positions shown in Figure 6.

Figure 6.
Line-scan profiles for each method.
Figure 6 illustrates the line-scan results of the grayscale region at the bottom of the color chart in Figure 5. In addition, LLE-NET, M-S CLAHE, Reinhard, and L1L0 failed to represent gradations in bright regions, compressing the contrast range and producing dark-biased tones. The retinex-CLAHE method generated saturated highlights that obscured gradation distinctions while losing shadow levels, yielding an unnaturally bright appearance. The iCAM06 method and the method by Kwon et al. did not sufficiently enhance bright regions, resulting in a narrow dynamic range where shadows lacked depth and highlights lacked brightness.
In contrast, the proposed method clearly separated gradations across the entire tonal range and secured the widest global tone spectrum. Shadow and highlighted regions retained rich structural and chromatic detail, demonstrating the superiority of the proposed method in global tone compression and local detail and color rendering.
Figure 7, Figure 8, Figure 9 and Figure 10 qualitatively compare the color rendering performance with a color chart using each method in outdoor natural scenes and extremely low-light environments. The evaluation assessed the ability of the methods to suppress color distortion, preserve saturation, and faithfully reproduce primary colors under complex illumination.

Figure 7.
Comparison results in high-contrast shadow regions: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.


Figure 8.
Comparison of color and detail preservation in the color chart and wall regions: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.
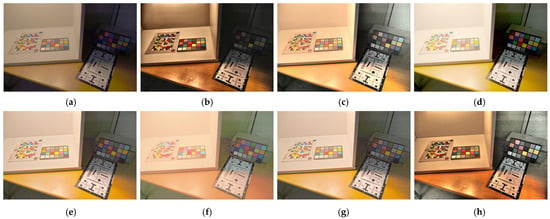
Figure 9.
Comparison of color reproduction in the color chart under bright and dark regions: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.

Figure 10.
Comparison of luminance and color reproduction in shadow regions: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.
The LLE-NET method produced an overall hazy appearance, where insufficient structural detail led to indistinct object boundaries and poor structural separation. Consequently, the differentiation of colors and shapes within the scene was degraded, resulting in reduced visual sharpness.
The M-S CLAHE method exhibited excessive saturation amplification in the color chart regions due to over-enhanced contrast, leading to gamut clipping and noticeable color distortion, with some colors appearing unnaturally vivid. Thus, the saturation distribution was inconsistent with the surrounding objects, producing visual disharmony and reduced naturalness.
In the retinex-CLAHE method, the unnatural expansion of color edges caused prominent halo artifacts along shadow boundaries in Figure 7. In Figure 8 and Figure 9, ringing artifacts were also observed, degrading visual quality. The hues of wooden surfaces and surrounding luminance information were distorted, reducing the stability of color reproduction. Although dark ceiling regions became visible due to the elevated luminance, a substantial loss of saturation was observed.
The Reinhard method followed a low-saturation tone-mapping strategy, flattening primary color information in the color chart and outdoor background. Saturation decreased sharply in mid-tone and highlighted regions, insufficiently separating indoor and outdoor contrasts.
The iCAM06, L1L0, and Kwon et al. methods commonly displayed reduced saturation and weakened color fidelity, leading to ambiguous correspondence between the color chart and actual scene. Specifically, L1L0 produced a strong achromatic tendency due to severe desaturation, which diminished the intercolor contrast and weakened the depth and texture representation.
In contrast, the proposed method demonstrated consistently superior color rendering. Across the illumination conditions, color distortions induced by luminance correction were suppressed, and primary colors were faithfully reproduced across the full tonal range (Figure 7, Figure 8 and Figure 9). Notably, in Figure 10, despite luminance enhancement in the shadow regions, saturation neither excessively increased nor decreased. Instead, the proposed method naturally reproduced the reddish tone of the wooden surface, the ceiling texture, the green of the trees, and the blue of the sky, closely resembling the real scene.
4.1.2. Regional Luminance Processing and Detail Preservation Performance
Figure 11, Figure 12 and Figure 13 present an extensive comparative analysis of each method with respect to dark-region restoration, noise suppression, bright-region detail preservation, and saturation control under challenging conditions, including underexposure and complex structural environments. Figure 11 illustrates an underexposed outdoor scene, where the evaluation focuses on the restoration of details in bright background regions (highlighted by red rectangles) and structural objects in dark regions, such as bicycles and scooters, and floor tiles. Figure 11 illustrates an underexposed outdoor scene, where the evaluation focuses on the restoration of details in bright background regions (highlighted by red rectangles) and structural objects in dark regions, such as bicycles and scooters, and floor tiles. In the original image, most structural details in the shadowed areas are indistinguishable due to overall underexposure, and the boundaries between the sky and buildings in bright regions are also unclear.


Figure 11.
Comparison of detail restoration and luminance balance in an underexposed outdoor scene: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.


Figure 12.
Comparison of chromaticity and structural detail preservation in scenes containing high-luminance regions: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.

Figure 13.
Comparison of gradation continuity and color tone reproduction around high-luminance transitions: (a) LLE-NET, (b) M-S CLAHE, (c) Retinex-CLAHE, (d) Reinhard [30], (e) iCAM06, (f) L1L0, (g) Kwon et al. [34], and (h) the proposed method.
Figure 12 compares the preservation of chromaticity and structural details in scenes with high-luminance regions, such as direct sunlight and open sky. The red rectangles indicate the magnified regions used for evaluating the preservation of fine details and tonal continuity in both bright and dark areas. This analysis emphasizes the effectiveness of retaining tonal continuity and fine details while avoiding luminance degradation in bright regions under mixed illumination. Magnifying the sky and dark regions marked by red rectangles allows for a clearer assessment of the characteristic behaviors of each method. The original image, captured under a strong backlight, reveals silhouetted foreground structures, with most of the details nearly unrecognizable.
Figure 11 and Figure 12 collectively reveal several recurring limitations of the existing methods. The first limitation concerns the imbalance in dark-region restoration. Although M-S CLAHE and Reinhard achieved noticeable brightness improvement compared to the original, they failed to recover sufficient fine structures in dark areas, leaving objects (e.g., bicycles and scooters in Figure 11) difficult to identify.
A second limitation is the trade-off between bright-region preservation and dark-region recovery. The LLE-NET method exhibited overall low contrast and insufficient structural detail, producing dark-biased tones and limiting the visibility of fine structures. Through multiscale contrast enhancement, M-S CLAHE partially suppressed luminance saturation in bright regions and retained high-intensity luminance, producing more distinct boundaries between the building and sky at the cost of introducing noise artifacts into the sky area.
In Figure 12, gradations of clouds and surrounding luminance structures were overly suppressed, yielding unnaturally darkened, shadow-like regions. Hence, gradation continuity around high-luminance transitions deteriorated. Retinex-CLAHE, Reinhard, iCAM06, L1L0, and the method by Kwon et al. displayed severe chromatic flattening in bright areas. In sky regions, saturation dropped markedly, leading to desaturated appearances, and the 3D structure and texture of the clouds disappeared, degenerating into flat grayish tones. Moreover, these methods inadequately reproduced natural luminance distributions and color temperature variations surrounding light sources, resulting in distorted tonal characteristics. Similarly, in dark regions, chromatic contrast was unnaturally exaggerated or suppressed, producing blurry structures and lifted black levels that undermined visual realism.
In contrast, the proposed method consistently mitigates these problems across both scenarios. By applying histogram excess redistribution guided by tile-averaged luminance, the method enhances luminance and restores fine structures in dark regions while adjusting the balance between the uniform and weighted redistribution to control amplification. Thus, details are restored without introducing excessive noise. In high-luminance regions, luminance and chromatic information are preserved, and smooth gradation transitions and chromatic consistency are maintained without luminance degradation or structural distortion. In Figure 11, the proposed method restores the structural details of buildings in bright backgrounds while suppressing sky noise and ensuring natural color reproduction. In shadow regions, various distinct details, such as floor tiles and the yellow tones and structure of scooters, are recovered. In Figure 12, the 3D shape of clouds, the natural blue tones of the sky, and luminance variations in light sources are preserved in bright areas, and distinct branches and structural details in dark regions are reconstructed. Notably, the bright edges of clouds seamlessly transition to their relatively darker shadowed portions, producing visually coherent tonal continuity across the scene.
Figure 13 extends this comparison by analyzing an HDR region that contains bright backgrounds and dark walls, with each subregion magnified for detailed examination. The red rectangles indicate the magnified regions used to evaluate text clarity and structural detail in dark wall areas, as well as color preservation and noise control in bright sky regions. In the original image, textual and structural information on wall surfaces is barely recognizable due to shadowing. The existing methods struggled to handle such extreme luminance contrasts. The M-S CLAHE method improved text visibility on signage but exaggerated luminance contrasts between the sky and walls, resulting in turbid highlights and unnatural tonalities. Noise was strongly emphasized in uniform sky regions, rendering the images visually rough. The retinex-CLAHE method alleviated some distortion, but the signage text remained blurred, reducing legibility and degrading the overall saturation. The Reinhard, iCAM06, L1L0, and Kwon et al. methods suppressed noise but displayed low overall contrast, leading to flattened local variations. Boundaries between clouds and building textures are obscured, and excessive luminance correction further diminishes saturation, erasing natural gradation transitions and weakening depth perception.
In contrast, the proposed method restores signage text and building-wall textures, clouds, and background details in a balanced manner. These are preserved while avoiding oversaturation or exaggerated contrast. In bright regions, the natural color of the sky and the 3D representation of clouds are maintained, while in dark regions, wall textures and text legibility are clearly preserved.
These superior results are achieved by the combined application of the background restoration algorithm, CRF, luminance ratio-based chroma compensation, and asymmetric Gaussian offset correction. Together, these components suppress oversaturation in bright regions while maintaining structural boundaries and chromatic consistency, delivering balanced image enhancement performance even in HDR scenarios.
In conclusion, in Figure 11, Figure 12 and Figure 13, the proposed method demonstrates substantial advantages in regional luminance processing and detail preservation. The proposed method bridges the trade-offs between dark-region visibility, bright-region fidelity, noise suppression, and color rendering, generating perceptually natural and structurally faithful results under diverse lighting conditions.
4.2. Quantitative Evaluation
The performance of the proposed method was validated via a series of quantitative evaluations using multiple no-reference and perceptual image quality metrics. This study employs the spatial-spectral sharpness (S3), maximum contrast with minimum artifacts (MCMA), natural image quality evaluator (NIQE), blind/referenceless image spatial quality evaluator (BRISQUE), and perception-based image quality evaluator (PIQE) to provide a comprehensive assessment of sharpness, contrast, naturalness, and distortion.
The S3 method quantifies image sharpness by considering spatial and spectral characteristics jointly, generating a sharpness index derived from local spectral gradients and the total variation [35]. A lower S3 score corresponds to superior sharpness preservation with fewer edge-related artifacts. The MCMA method evaluates the trade-off between contrast enhancement and artifact suppression by analyzing pixel-level and histogram-based features [36]. In this metric, smaller values indicate that contrast has been maximized without introducing undesirable artifacts.
The NIQE method is a completely blind quality assessment method that measures perceptual naturalness by quantifying deviations from the statistical regularities of the natural images [37]. Unlike full-reference metrics, this method does not require a pristine reference image, and lower NIQE values indicate that an enhanced image remains closer to the natural scene distribution. The BRISQUE method also operates in a no-reference setting, evaluating the degradation of naturalness via locally normalized luminance coefficients [38]. Again, lower values signify that distortions, such as noise or unnatural contrast, are less pronounced. Finally, PIQE estimates blockwise distortions, including compression artifacts and Gaussian noise, producing a spatial quality mask that derives an overall perceptual quality score [39]. A smaller PIQE score implies better visual quality with reduced blockiness and noise.
Together, these five metrics offer a complementary and multifaceted framework for evaluating image enhancement performance. Although S3 and MCMA emphasize structural fidelity and contrast handling, NIQE, BRISQUE, and PIQE capture perceptual naturalness and artifact suppression. This comprehensive evaluation ensures that the proposed method is assessed in terms of local contrast and sharpness and its ability to preserve the natural visual appearance without introducing undesirable distortion. The bar charts in Figure 14 present the quantitative scores of each method for all five metrics, along with their average values.
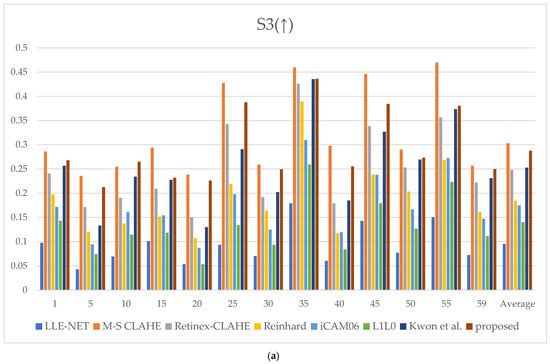
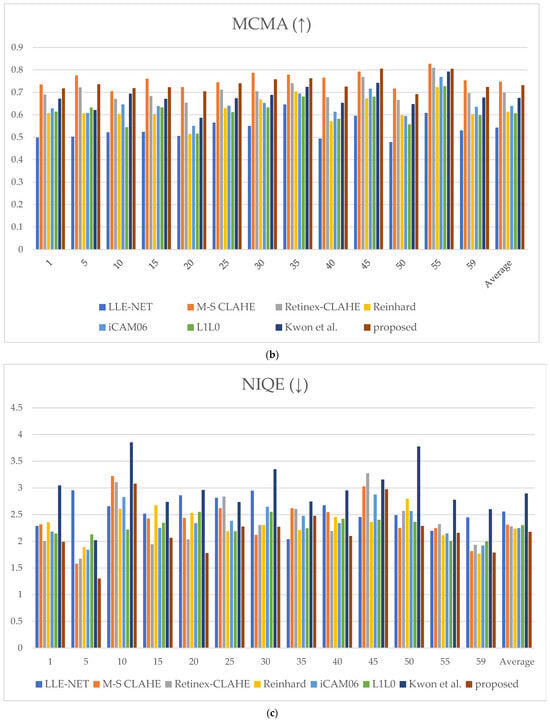
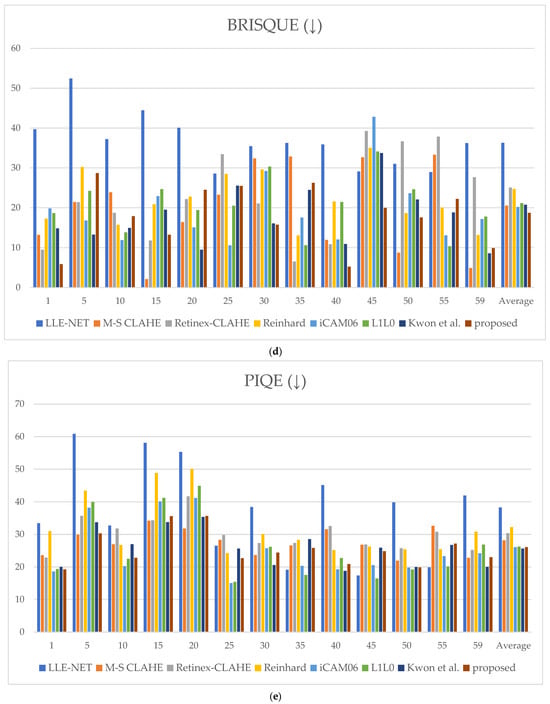
Figure 14.
Metric scores: (a) spatial–spectral sharpness measure (S3) score, (b) maximizing contrast with minimum artifact (MCMA) score, (c) naturalness image quality evaluator (NIQE) score, (d) blind/referenceless image spatial quality evaluator (BRISQUE) score, and (e) perception-based image quality evaluator (PIQE) score.
Table 1 summarizes the quantitative results in terms of average ± standard deviation for each metric. The proposed method not only achieved consistently favorable average scores but also exhibited relatively small deviations, indicating stable performance across diverse images. In contrast, although MS-CLAHE recorded competitive average scores, it showed large deviations, implying unstable behavior depending on image content. Consequently, when ranking individual images across metrics, the proposed method was superior in most cases, demonstrating both robustness and reliability in performance.

Table 1.
Quantitative evaluation of image quality metrics (average ± standard deviation).
Table 2 compares the average ranks of the methods obtained after applying the five metrics (i.e., S3, MCMA, NIQE, BRISQUE, and PIQE) to each image and ordering the scores accordingly. The values are not derived from a simple averaging of raw scores; instead, the relative ranks for each image were determined and aggregated to produce the mean rank. This approach better reflects the overall consistency and stability of performance across diverse scenes, rather than being influenced by deviations in specific cases.

Table 2.
Metric score comparison.
Thus, the proposed method ranked among the top in all metrics and achieved the best average rank in S3, NIQE, and BRISQUE. This result demonstrates that the method restores fine structures with clarity, minimizes detail loss, and produces outputs that are statistically closest to natural images, providing the most visually natural results. Furthermore, the minimal presence of distortions or artificial traces confirms that structural consistency is stably preserved.
For MCMA, the proposed method achieved an average rank of second place; however, the mean rank across images still belongs to the highest tier, indicating stable and competitive performance in contrast enhancement and artifact suppression. For PIQE, the difference from the top-ranked method was marginal, whereas the gap compared to lower-ranked methods was substantial. This outcome suggests that the proposed method also provides sufficiently stable quality concerning blocking artifacts and noise suppression.
In conclusion, the proposed method achieved consistently high performance, recording superior mean ranks across all metrics. Unlike conventional methods that vary in performance depending on the metric, the proposed approach offers a well-balanced image quality by preserving details, maintaining natural brightness and color, suppressing noise, and enhancing contrast. Therefore, the method demonstrates its superiority in terms of comprehensive image quality compared to the existing fusion-based techniques.
5. Discussions
The computational performance of the proposed multiscale CLAHE algorithm was analyzed based on a practical dataset (primarily at a resolution of 2144 × 1424), revealing the following characteristics.
The time complexity is theoretically O(), and performance measurements across various resolutions exhibited a strong linear correlation with . At a resolution of , the expected processing time was approximately 900–1200 s (15–20 min), demonstrating a predictable scalability with image size.
In terms of runtime efficiency, significant constraints were observed. Empirical results showed a processing speed of approximately MPixels/s, requiring around 17 min to process a single image. Notably, the bilinear interpolation stage accounted for about of the total runtime, representing the primary bottleneck.
The space complexity is with a memory consumption of approximately 10–12 MB at resolution, which is relatively efficient. The measured memory efficiency of 3.38 MB/MPixel indicates that the algorithm remains feasible on typical desktop environments.
From a real-time performance perspective, the current implementation is suitable only for quality-oriented batch processing. Processing 164 images is estimated to require 46–50 h, highlighting substantial time costs for large-scale applications.
These performance characteristics suggest that while the algorithm is suitable for research purposes or offline applications requiring high-quality results, optimization is essential for commercial or large-scale deployments. In particular, the integration of GPU acceleration, parallelization, and distributed processing could significantly improve its practicality. Furthermore, coupling with deep learning-based acceleration techniques may extend the applicability of the proposed method to real-time scenarios.
In addition, we examined the dependency of the proposed algorithm on its parameters. Most parameters did not cause substantial changes in the visual quality of the results, as they were not intended to drastically alter the image but rather to ensure smooth functional behavior and to suppress artificial boundaries or local noise. In this study, a systematic comparative analysis was conducted using a dataset of 164 images to carefully evaluate parameter variability. Based on this investigation, the selected values were chosen to provide stable and consistent performance. Therefore, the overall performance of the proposed method is not the outcome of overfitting to a specific dataset, but rather the result of a design aimed at maintaining reliable and robust quality across diverse conditions.
6. Conclusions
The proposed method introduces a novel multiscale adaptive histogram redistribution algorithm based on local brightness to address the structural limitations of CLAHE- and retinex-based image enhancement techniques, including the loss of detail in dark regions, gradation discontinuities along tile boundaries, highlight clipping, and color distortions. The proposed algorithm continuously adjusts the ratio between the uniform and weighted redistribution of histogram excess according to the average tile brightness, optimizing contrast enhancement across brightness ranges. Local distribution is corrected based on blending weights between adjacent tiles and distance-based information to alleviate gradation discontinuities at boundary regions and ensure overall spatial consistency.
The generated tilewise LUTs are smoothly connected at the pixel level via bilinear interpolation. After interpolation, the background is restored by referencing the original pixel values to recover shadow regions degraded by excessive tone compression, enhancing visual stability and structural preservation. The multiscale LUTs are averaged across scales, reflecting the detail enhancement effect of small tiles and the block-artifact suppression effect of large tiles. In the background restoration stage, regions distorted by excessive contrast adjustment are normalized based on the original image and corrected in consideration of the harmony with the surrounding gradation distributions, improving the overall naturalness of the image. In addition, a CRF based on the original chromatic components and ratio-based chroma compensation is applied to mitigate color distortion caused by luminance correction.
Furthermore, an asymmetric Gaussian offset correction technique is introduced to enhance the visual sharpness in mid-luminance regions and suppress highlight oversaturation. These post-processing modules contribute to gradation continuity and chromatic consistency. According to quantitative evaluation, the proposed algorithm satisfies performance requirements by preserving dark-region details, retaining highlight structural information, and minimizing color distortions, even without a separate noise reduction process. Compared with existing image enhancement methods (e.g., M-S CLAHE, retinex-CLAHE, Reinhard, iCAM06, L1L0, and the method by Kwon et al.), the proposed method consistently achieved superior results across the quantitative indices (i.e., S3, NIQE, BRISQUE, MCMA, and PIQE). The proposed method ranked first in three out of five metrics and second in the remaining two, demonstrating stable and well-balanced performance overall.
Moreover, the line-scan profile analysis confirmed the ability of the proposed method to preserve pixel-level contrast, and the subjective evaluation also verified its outstanding improvements in noise and halo suppression, structure restoration in dark regions, detail preservation in bright regions, color naturalness, and overall fidelity. In conclusion, this method systematically overcomes the structural limitations of conventional contrast enhancement techniques via a multistage processing framework comprising brightness-based excess redistribution, neighbor-tile blending correction, multiscale interpolation, background restoration, color restoration, and nonlinear offset post-processing. The proposed method satisfies the dual objectives of visual quality enhancement and structural information preservation in low-light and HDR imaging conditions. This method is expected to serve as a practical and scalable high-performance contrast enhancement technique for a wide range of image processing applications. In future research, it will be necessary to improve the settings of user parameters that reflect somewhat visual evaluations, and to conduct research on selecting more optimized parameters using HDR target image information.
Author Contributions
Conceptualization, S.-H.L. (Sung-Hak Lee); methodology, S.-H.J. and S.-H.L. (Sung-Hak Lee); software, S.-H.J.; validation, S.-H.J., D.-M.S., Y.-H.G., S.-H.L. (Seung-Hwan Lee) and S.-H.L. (Sung-Hak Lee); formal analysis, S.-H.J. and S.-H.L. (Sung-Hak Lee); investigation, S.-H.J. and S.-H.L. (Sung-Hak Lee); resources, S.-H.J. and S.-H.L. (Sung-Hak Lee); data curation, S.-H.J., D.-M.S., Y.-H.G., S.-H.L. (Seung-Hwan Lee) and S.-H.L. (Sung-Hak Lee); writing—original draft preparation, S.-H.J.; writing—review and editing, S.-H.L. (Sung-Hak Lee); visualization, S.-H.J.; supervision, S.-H.L. (Sung-Hak Lee); project administration, S.-H.L. (Sung-Hak Lee); funding acquisition, S.-H.L. (Sung Hak Lee). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Korea Creative Content Agency (KOCCA) grant funded by the Ministry of Culture, Sports and Tourism (MCST) in 2024 (Project Name: Development of optical technology and sharing platform technology to acquire digital cultural heritage for high quality restoration of composite materials cultural heritage, Project Number: RS-2024-00442410, Contribution Rate: 50%) and the Institute of Information & Communications Technology Planning & Evaluation (IITP)–Innovative Human Resource Development for Local Intellectualization program grant funded by the Korea government (MSIT) (IITP-2025-RS-2022-00156389, 50%).
Data Availability Statement
The data presented in this study are openly available at https://drive.google.com/drive/folders/1pOs7HyuOGYNznVOqfn9MwvBZsIYNf1W5 (accessed on 28 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Agaian, S.S.; Silver, B.; Panetta, K.A. Transform Coefficient Histogram-Based Image Enhancement Algorithms Using Contrast Entropy. IEEE Trans. Image Process. 2007, 16, 741–758. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Tang, G.; Gan, Z.; Cui, Z.; Liu, F. Enhancement Algorithm for Low Illumination Images Based on LIP Model. J. Nanjing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2017, 37, 98–106. [Google Scholar] [CrossRef]
- Lee, S.; Kim, N.; Paik, J. Adaptively Partitioned Block-Based Contrast Enhancement and Its Application to Low Light-Level Video Surveillance. SpringerPlus 2015, 4, 431. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive Histogram Equalization and Its Variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Nithyananda, C.R.; Ramachandra, A.C.; Preethi. Survey on Histogram Equalization Method Based Image Enhancement Techniques. In Proceedings of the 2016 International Conference on Data Mining and Advanced Computing (SAPIENCE), Ernakulam, India, 9–11 March 2016; pp. 150–158. [Google Scholar] [CrossRef]
- Zuiderveld, K.J. Contrast Limited Adaptive Histogram Equalization. In Graphics Gems IV; Heckbert, P.S., Ed.; Academic Press Professional, Inc.: San Diego, CA, USA, 1994; pp. 474–485. [Google Scholar] [CrossRef]
- Reza, A.M. Realization of the Contrast Limited Adaptive Histogram Equalization (CLAHE) for Real-Time Image Enhancement. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2004, 38, 35–44. [Google Scholar] [CrossRef]
- Land, E.H.; McCann, J.J. Lightness and Retinex Theory. J. Opt. Soc. Am. 1971, 61, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Land, E.H. The Retinex Theory of Color Vision. Sci. Am. 1977, 237, 108–129. Available online: https://www.jstor.org/stable/24953876 (accessed on 12 August 2025). [CrossRef] [PubMed]
- Land, E.H. Recent Advances in Retinex Theory and Some Implications for Cortical Computations: Color Vision and the Natural Image. Proc. Natl. Acad. Sci. USA 1983, 80, 5163–5169. [Google Scholar] [CrossRef]
- Jobson, D.J.; Rahman, Z.; Woodell, G.A. Properties and Performance of a Center/Surround Retinex. IEEE Trans. Image Process. 1997, 6, 451–462. [Google Scholar] [CrossRef]
- Jobson, D.J.; Rahman, Z.; Woodell, G.A. A Multiscale Retinex for Bridging the Gap between Color Images and the Human Observation of Scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef]
- Park, S.; Yu, S.; Moon, B.; Ko, S.; Paik, J. Low-Light Image Enhancement Using Variational Optimization-Based Retinex Model. IEEE Trans. Consum. Electron. 2017, 63, 178–184. [Google Scholar] [CrossRef]
- Tanaka, H.; Waizumi, Y.; Kasezawa, T. Retinex-Based Signal Enhancement for Image Dark Regions. In Proceedings of the 2017 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuching, Malaysia, 12–14 September 2017; pp. 205–209. [Google Scholar] [CrossRef]
- Liao, S.; Piao, Y.; Li, B. Low Illumination Color Image Enhancement Based on Improved Retinex. In Proceedings of the LIDAR Imaging Detection and Target Recognition 2017, Changchun, China, 15 November 2017; Volume 10605, p. 1060532. [Google Scholar] [CrossRef]
- Li, M.; Liu, J.; Yang, W.; Sun, X.; Guo, Z. Structure-Revealing Low-Light Image Enhancement via Robust Retinex Model. IEEE Trans. Image Process. 2018, 27, 2828–2841. [Google Scholar] [CrossRef]
- Hu, H.; Ni, G. Color Image Enhancement Based on the Improved Retinex. In Proceedings of the 2010 International Conference on Multimedia Technology (ICMT), Ningbo, China, 29–31 October 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Moore, A.; Allman, J.; Goodman, R.M. A real-time neural system for color constancy. IEEE Trans. Neural Netw. 1991, 2, 237–247. [Google Scholar] [CrossRef]
- Moore, A.; Allman, J.; Fox, G.; Goodman, R. A VLSI neural network for color constancy. In Advances in Neural Information Processing Systems, Proceedings of the 3rd Neural Information Processing Systems (NeurIPS 1990), Denver, CO, USA, 27–29 November 1990; Lippmann, R.P., Moody, J., Touretzky, D., Eds.; Morgan Kaufmann: San Mateo, CA, USA, 1990; pp. 370–376. Available online: https://proceedings.neurips.cc/paper_files/paper/1990/file/f8c1f23d6a8d8d7904fc0ea8e066b3bb-Paper.pdf (accessed on 12 August 2025).
- Kim, Y.-J.; Son, D.-M.; Lee, S.-H. Retinex Jointed Multiscale CLAHE Model for HDR Image Tone Compression. Mathematics 2024, 12, 1541. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Dhal, K.G.; Das, A.; Ray, S.; Gálvez, J.; Das, S. Histogram equalization variants as optimization problems: A review. Arch. Comput. Methods Eng. 2021, 28, 1471–1496. [Google Scholar] [CrossRef]
- Qi, Y.; Yang, Z.; Sun, W.; Lou, M.; Lian, J.; Zhao, W.; Deng, X.; Ma, Y. A comprehensive overview of image enhancement techniques. Arch. Comput. Methods Eng. 2022, 29, 583–607. [Google Scholar] [CrossRef]
- Thepade, S.D.; Pardhi, P.M. Contrast enhancement with brightness preservation of low light images using a blending of CLAHE and BPDHE histogram equalization methods. Int. J. Inf. Technol. 2022, 14, 3047–3056. [Google Scholar] [CrossRef]
- Campos, G.F.C.; Mastelini, S.M.; Aguiar, G.J.; Mantovani, R.G.; de Melo, L.F.; Barbon, S., Jr. Machine learning hyperparameter selection for contrast limited adaptive histogram equalization. J. Image Video Process. 2019, 2019, 59. [Google Scholar] [CrossRef]
- Ismail, M.K.; Al-Ameen, Z. Adapted single scale Retinex algorithm for nighttime image enhancement. Al-Rafidain J. Comput. Sci. Math. 2022, 16, 59–69. [Google Scholar] [CrossRef]
- Rahman, Z.-u.; Jobson, D.J.; Woodell, G.A. Retinex processing for automatic image enhancement. J. Electron. Imaging 2004, 13, 100–110. [Google Scholar] [CrossRef]
- Cao, X.; Yu, J. LLE-NET: A Low-Light Image Enhancement Algorithm Based on Curve Estimation. Mathematics 2024, 12, 1228. [Google Scholar] [CrossRef]
- Xie, Y.; Zhan, N.; Zhu, J.; Xu, B.; Chen, H.; Mao, W.; Luo, X.; Hu, Y. Landslide extraction from aerial imagery considering context association characteristics. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103950. [Google Scholar] [CrossRef]
- Reinhard, E.; Stark, M.; Shirley, P.; Ferwerda, J. Photographic tone reproduction for digital images. In Seminal Graphics Papers: Pushing the Boundaries; Akeley, K., Ed.; ACM: New York, NY, USA, 2023; Volume 2, pp. 661–670. [Google Scholar] [CrossRef]
- Kuang, J.; Johnson, G.M.; Fairchild, M.D. iCAM06: A refined image appearance model for HDR image rendering. J. Vis. Commun. Image Represent. 2007, 18, 406–414. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, J.; Zhang, D.; Cao, Z.; Zhang, L. A hybrid ℓ1–ℓ0 layer decomposition model for tone mapping. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4758–4766. [Google Scholar] [CrossRef]
- Kwon, H.-J.; Lee, S.-H. Contrast sensitivity based multiscale base–detail separation for enhanced HDR imaging. Appl. Sci. 2020, 10, 2513. [Google Scholar] [CrossRef]
- Vu, C.T.; Chandler, D.M. S3: A spectral and spatial sharpness measure. In Proceedings of the 2009 First International Conference on Advances in Multimedia (MMEDIA 2009), Colmar, France, 20–25 July 2009; pp. 37–43. [Google Scholar] [CrossRef]
- Abdoli, M.; Nasiri, F.; Brault, P.; Ghanbari, M. Quality assessment tool for performance measurement of image contrast enhancement methods. IET Image Process. 2019, 13, 833–842. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Venkatanath, N.; Praneeth, D.; Chandrasekhar, M.; Channappayya, S.S.; Medasani, S.S. Blind image quality evaluation using perception based features. In Proceedings of the 2015 Twenty First National Conference on Communications (NCC), Mumbai, India, 27 February–1 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).