Two-Side Merger and Acquisition Matching: A Perspective Based on Mutual Performance Evaluation Considering the Herd Behavior
Abstract
1. Introduction
2. Literature Review
2.1. DEA Cross Efficiency and Its Extensions
2.2. Efficiency Evaluation of M&A
2.3. Bounded Rationality in Partner Selection and Matching in M&A
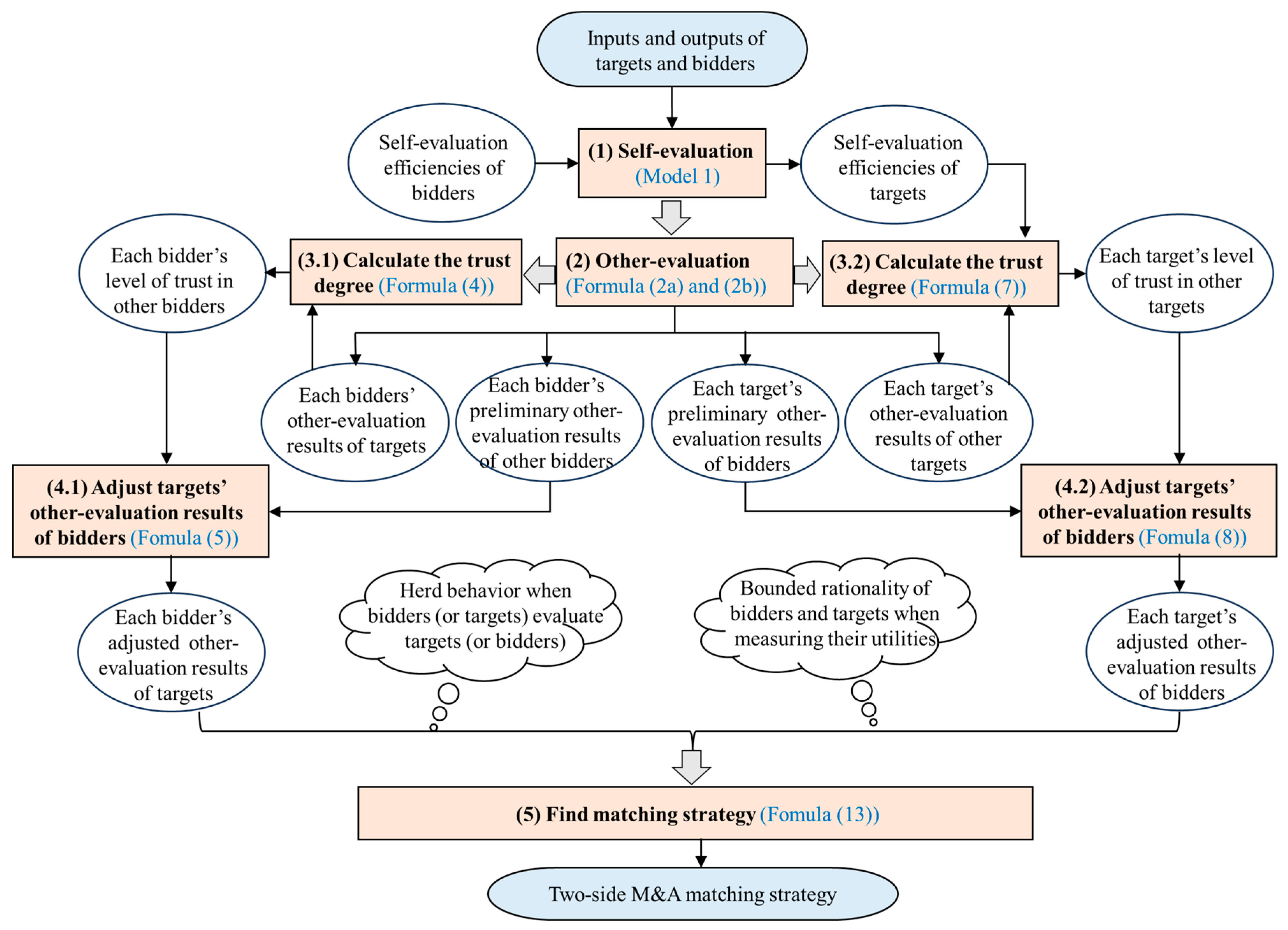
3. Our Proposed Two-Side M&A Matching Method
3.1. Mutual Evaluation Considering Herd Behavior
3.2. Matching Model Considering the Bounded Rationality of Bidders and Targets
3.3. Solution of the Matching Model
4. Application of Our Proposed Method
4.1. Data and Experiment
4.2. Sensitivity Analysis
4.3. Discussion
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Adjusted Other-Evaluation Results Under Different Herd Coefficients
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.70 | 1.03 | 0.57 | 1.28 | 0.98 | 0.91 | 1.06 | 1.82 | 1.41 | 1.22 | 1.93 | 1.65 | 1.05 | 0.58 | 1.28 | 0.86 | 1.14 | 1.74 | 0.75 | 0.82 | 0.63 | 1.00 | 1.27 | 1.17 | 0.72 | 0.91 |
| T 2 | 0.15 | 0.19 | 0.12 | 0.25 | 0.19 | 0.18 | 0.21 | 0.36 | 0.28 | 0.23 | 0.36 | 0.32 | 0.20 | 0.11 | 0.26 | 0.17 | 0.33 | 0.34 | 0.14 | 0.15 | 0.13 | 0.19 | 0.25 | 0.23 | 0.13 | 0.17 |
| T 3 | 0.56 | 0.81 | 0.45 | 1.01 | 0.78 | 0.72 | 0.84 | 1.45 | 1.12 | 0.97 | 1.53 | 1.31 | 0.83 | 0.46 | 1.01 | 0.68 | 0.94 | 1.38 | 0.60 | 0.65 | 0.50 | 0.79 | 1.00 | 0.94 | 0.57 | 0.72 |
| T 4 | 1.08 | 1.75 | 0.85 | 2.02 | 1.58 | 1.47 | 1.79 | 3.24 | 2.30 | 2.08 | 4.45 | 2.70 | 1.75 | 0.95 | 1.87 | 1.32 | 2.65 | 2.73 | 1.50 | 1.39 | 0.92 | 1.71 | 1.88 | 2.93 | 1.36 | 1.35 |
| T 5 | 0.79 | 1.20 | 0.66 | 1.50 | 1.15 | 1.05 | 1.22 | 2.06 | 1.62 | 1.43 | 2.11 | 1.90 | 1.23 | 0.68 | 1.49 | 1.00 | 0.97 | 2.03 | 0.85 | 0.95 | 0.71 | 1.16 | 1.49 | 1.23 | 0.83 | 1.08 |
| T 6 | 1.09 | 1.65 | 0.90 | 2.07 | 1.59 | 1.45 | 1.68 | 2.85 | 2.23 | 1.97 | 2.93 | 2.62 | 1.70 | 0.93 | 2.05 | 1.37 | 1.35 | 2.80 | 1.18 | 1.31 | 0.98 | 1.61 | 2.05 | 1.72 | 1.15 | 1.48 |
| T 7 | 1.17 | 1.89 | 0.92 | 2.19 | 1.71 | 1.59 | 1.93 | 3.49 | 2.49 | 2.25 | 4.75 | 2.92 | 1.89 | 1.03 | 2.03 | 1.43 | 2.83 | 2.96 | 1.61 | 1.50 | 1.00 | 1.85 | 2.04 | 3.12 | 1.47 | 1.47 |
| T 8 | 0.13 | 0.31 | 0.10 | 0.33 | 0.26 | 0.24 | 0.29 | 0.55 | 0.35 | 0.36 | 0.83 | 0.40 | 0.33 | 0.16 | 0.25 | 0.19 | 0.13 | 0.39 | 0.29 | 0.25 | 0.10 | 0.31 | 0.28 | 0.56 | 0.28 | 0.22 |
| T 9 | 0.06 | 0.14 | 0.04 | 0.13 | 0.11 | 0.11 | 0.14 | 0.28 | 0.18 | 0.17 | 0.59 | 0.21 | 0.13 | 0.07 | 0.09 | 0.08 | 0.38 | 0.20 | 0.16 | 0.11 | 0.05 | 0.14 | 0.10 | 0.42 | 0.13 | 0.07 |
| T 10 | 0.04 | 0.04 | 0.03 | 0.04 | 0.03 | 0.03 | 0.05 | 0.08 | 0.08 | 0.05 | 0.30 | 0.10 | 0.02 | 0.02 | 0.05 | 0.03 | 0.30 | 0.11 | 0.04 | 0.03 | 0.03 | 0.03 | 0.04 | 0.18 | 0.02 | 0.02 |
| T 11 | 0.46 | 0.68 | 0.38 | 0.86 | 0.66 | 0.60 | 0.69 | 1.17 | 0.92 | 0.81 | 1.17 | 1.08 | 0.70 | 0.39 | 0.86 | 0.57 | 0.54 | 1.16 | 0.48 | 0.54 | 0.41 | 0.66 | 0.86 | 0.68 | 0.47 | 0.62 |
| T 12 | 0.14 | 0.22 | 0.12 | 0.28 | 0.21 | 0.19 | 0.22 | 0.37 | 0.30 | 0.26 | 0.37 | 0.35 | 0.23 | 0.12 | 0.27 | 0.18 | 0.14 | 0.37 | 0.15 | 0.17 | 0.13 | 0.21 | 0.28 | 0.21 | 0.15 | 0.20 |
| T 13 | 0.30 | 0.08 | 0.10 | 0.08 | 0.06 | 0.06 | 0.08 | 0.22 | 0.09 | 0.10 | 0.32 | 0.11 | 0.08 | 0.05 | 0.05 | 0.04 | 0.22 | 0.10 | 0.10 | 0.07 | 0.04 | 0.08 | 0.06 | 0.22 | 0.08 | 0.04 |
| T 14 | 1.66 | 2.61 | 1.31 | 3.07 | 2.39 | 2.22 | 2.68 | 4.81 | 3.47 | 3.11 | 6.30 | 4.06 | 2.63 | 1.44 | 2.89 | 2.01 | 3.77 | 4.14 | 2.18 | 2.08 | 1.42 | 2.56 | 2.89 | 4.10 | 2.00 | 2.08 |
| T 15 | 0.26 | 0.13 | 0.18 | 0.15 | 0.11 | 0.10 | 0.10 | 0.43 | 0.14 | 0.14 | 0.39 | 0.15 | 0.21 | 0.13 | 0.12 | 0.08 | 0.06 | 0.13 | 0.13 | 0.12 | 0.09 | 0.12 | 0.09 | 0.24 | 0.14 | 0.09 |
| T 16 | 0.00 | 0.08 | 0.01 | 0.07 | 0.06 | 0.05 | 0.07 | 0.13 | 0.08 | 0.10 | 0.30 | 0.10 | 0.08 | 0.04 | 0.03 | 0.04 | 0.00 | 0.10 | 0.09 | 0.06 | 0.00 | 0.08 | 0.05 | 0.21 | 0.08 | 0.04 |
| T 17 | 0.42 | 0.63 | 0.35 | 0.80 | 0.61 | 0.56 | 0.64 | 1.09 | 0.86 | 0.75 | 1.09 | 1.00 | 0.65 | 0.36 | 0.79 | 0.53 | 0.50 | 1.08 | 0.44 | 0.50 | 0.38 | 0.61 | 0.79 | 0.63 | 0.44 | 0.57 |
| T 18 | 0.41 | 0.62 | 0.34 | 0.78 | 0.60 | 0.55 | 0.63 | 1.07 | 0.84 | 0.74 | 1.07 | 0.99 | 0.64 | 0.35 | 0.78 | 0.52 | 0.49 | 1.06 | 0.43 | 0.49 | 0.37 | 0.60 | 0.78 | 0.62 | 0.43 | 0.56 |
| T 19 | 0.06 | 0.14 | 0.04 | 0.13 | 0.11 | 0.10 | 0.14 | 0.27 | 0.17 | 0.17 | 0.58 | 0.21 | 0.12 | 0.07 | 0.09 | 0.08 | 0.37 | 0.19 | 0.16 | 0.11 | 0.05 | 0.14 | 0.10 | 0.41 | 0.13 | 0.07 |
| T 20 | 0.86 | 1.29 | 0.71 | 1.62 | 1.24 | 1.14 | 1.32 | 2.23 | 1.75 | 1.54 | 2.28 | 2.05 | 1.33 | 0.73 | 1.61 | 1.08 | 1.04 | 2.19 | 0.92 | 1.03 | 0.77 | 1.26 | 1.61 | 1.33 | 0.90 | 1.16 |
| T 21 | 0.39 | 0.58 | 0.32 | 0.73 | 0.56 | 0.51 | 0.59 | 1.00 | 0.79 | 0.69 | 1.00 | 0.93 | 0.60 | 0.33 | 0.73 | 0.49 | 0.46 | 0.99 | 0.41 | 0.46 | 0.35 | 0.57 | 0.73 | 0.58 | 0.40 | 0.53 |
| T 22 | 0.15 | 0.23 | 0.13 | 0.29 | 0.22 | 0.20 | 0.23 | 0.39 | 0.31 | 0.28 | 0.39 | 0.37 | 0.24 | 0.13 | 0.29 | 0.19 | 0.15 | 0.39 | 0.16 | 0.18 | 0.14 | 0.23 | 0.29 | 0.22 | 0.16 | 0.21 |
| T 23 | 0.37 | 0.52 | 0.30 | 0.65 | 0.50 | 0.47 | 0.54 | 0.94 | 0.72 | 0.62 | 0.97 | 0.84 | 0.53 | 0.30 | 0.66 | 0.44 | 0.65 | 0.89 | 0.38 | 0.42 | 0.33 | 0.51 | 0.65 | 0.60 | 0.36 | 0.46 |
| T 24 | 0.31 | 0.18 | 0.07 | 0.18 | 0.14 | 0.13 | 0.16 | 0.46 | 0.18 | 0.20 | 0.56 | 0.21 | 0.22 | 0.10 | 0.11 | 0.10 | 0.04 | 0.20 | 0.19 | 0.15 | 0.05 | 0.19 | 0.14 | 0.39 | 0.20 | 0.12 |
| T 25 | 0.12 | 0.18 | 0.10 | 0.22 | 0.17 | 0.15 | 0.18 | 0.30 | 0.24 | 0.21 | 0.30 | 0.28 | 0.18 | 0.10 | 0.22 | 0.15 | 0.13 | 0.30 | 0.12 | 0.14 | 0.10 | 0.17 | 0.22 | 0.17 | 0.12 | 0.16 |
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.62 | 0.88 | 0.50 | 1.11 | 0.85 | 0.79 | 0.92 | 1.59 | 1.22 | 1.05 | 1.66 | 1.43 | 0.90 | 0.50 | 1.12 | 0.74 | 1.10 | 1.51 | 0.65 | 0.70 | 0.55 | 0.86 | 1.10 | 1.02 | 0.62 | 0.78 |
| T 2 | 0.23 | 0.29 | 0.18 | 0.37 | 0.28 | 0.27 | 0.31 | 0.54 | 0.42 | 0.34 | 0.54 | 0.48 | 0.29 | 0.17 | 0.39 | 0.25 | 0.52 | 0.50 | 0.21 | 0.23 | 0.20 | 0.28 | 0.37 | 0.34 | 0.20 | 0.26 |
| T 3 | 0.52 | 0.73 | 0.42 | 0.92 | 0.71 | 0.65 | 0.76 | 1.32 | 1.02 | 0.87 | 1.38 | 1.19 | 0.74 | 0.41 | 0.93 | 0.62 | 0.95 | 1.25 | 0.53 | 0.58 | 0.46 | 0.71 | 0.91 | 0.85 | 0.51 | 0.65 |
| T 4 | 0.88 | 1.38 | 0.69 | 1.60 | 1.25 | 1.17 | 1.42 | 2.60 | 1.81 | 1.63 | 3.47 | 2.11 | 1.39 | 0.76 | 1.49 | 1.04 | 2.18 | 2.12 | 1.18 | 1.10 | 0.74 | 1.35 | 1.49 | 2.30 | 1.08 | 1.07 |
| T 5 | 0.68 | 1.02 | 0.56 | 1.29 | 0.98 | 0.90 | 1.04 | 1.76 | 1.38 | 1.22 | 1.79 | 1.62 | 1.06 | 0.58 | 1.27 | 0.85 | 0.79 | 1.74 | 0.72 | 0.81 | 0.61 | 1.00 | 1.28 | 1.04 | 0.71 | 0.92 |
| T 6 | 0.89 | 1.35 | 0.74 | 1.69 | 1.29 | 1.18 | 1.37 | 2.32 | 1.82 | 1.61 | 2.38 | 2.14 | 1.39 | 0.76 | 1.67 | 1.12 | 1.07 | 2.28 | 0.96 | 1.07 | 0.80 | 1.31 | 1.68 | 1.39 | 0.94 | 1.21 |
| T 7 | 0.95 | 1.48 | 0.74 | 1.72 | 1.34 | 1.25 | 1.52 | 2.78 | 1.95 | 1.75 | 3.68 | 2.27 | 1.49 | 0.81 | 1.61 | 1.12 | 2.31 | 2.29 | 1.26 | 1.18 | 0.80 | 1.45 | 1.60 | 2.44 | 1.16 | 1.16 |
| T 8 | 0.18 | 0.36 | 0.14 | 0.40 | 0.32 | 0.29 | 0.35 | 0.68 | 0.42 | 0.42 | 0.88 | 0.47 | 0.40 | 0.20 | 0.33 | 0.24 | 0.16 | 0.46 | 0.33 | 0.30 | 0.14 | 0.37 | 0.35 | 0.59 | 0.33 | 0.28 |
| T 9 | 0.09 | 0.17 | 0.06 | 0.16 | 0.13 | 0.13 | 0.18 | 0.35 | 0.22 | 0.21 | 0.71 | 0.26 | 0.15 | 0.08 | 0.12 | 0.10 | 0.56 | 0.23 | 0.20 | 0.14 | 0.07 | 0.17 | 0.13 | 0.52 | 0.15 | 0.08 |
| T 10 | 0.06 | 0.06 | 0.04 | 0.06 | 0.05 | 0.06 | 0.08 | 0.14 | 0.13 | 0.09 | 0.50 | 0.17 | 0.04 | 0.03 | 0.08 | 0.05 | 0.50 | 0.18 | 0.07 | 0.05 | 0.06 | 0.05 | 0.06 | 0.30 | 0.04 | 0.03 |
| T 11 | 0.44 | 0.65 | 0.36 | 0.83 | 0.63 | 0.58 | 0.67 | 1.12 | 0.89 | 0.78 | 1.12 | 1.04 | 0.68 | 0.37 | 0.82 | 0.55 | 0.49 | 1.12 | 0.46 | 0.52 | 0.39 | 0.64 | 0.82 | 0.64 | 0.45 | 0.59 |
| T 12 | 0.21 | 0.32 | 0.18 | 0.41 | 0.31 | 0.29 | 0.33 | 0.55 | 0.44 | 0.39 | 0.55 | 0.51 | 0.34 | 0.18 | 0.40 | 0.27 | 0.20 | 0.55 | 0.23 | 0.26 | 0.19 | 0.32 | 0.41 | 0.31 | 0.23 | 0.30 |
| T 13 | 0.50 | 0.06 | 0.17 | 0.06 | 0.05 | 0.05 | 0.06 | 0.25 | 0.07 | 0.07 | 0.25 | 0.08 | 0.06 | 0.04 | 0.05 | 0.04 | 0.37 | 0.07 | 0.07 | 0.05 | 0.07 | 0.06 | 0.04 | 0.17 | 0.06 | 0.03 |
| T 14 | 1.29 | 2.00 | 1.02 | 2.35 | 1.83 | 1.71 | 2.05 | 3.72 | 2.65 | 2.37 | 4.79 | 3.08 | 2.02 | 1.11 | 2.22 | 1.54 | 2.98 | 3.13 | 1.67 | 1.59 | 1.10 | 1.96 | 2.21 | 3.14 | 1.54 | 1.60 |
| T 15 | 0.43 | 0.13 | 0.29 | 0.18 | 0.13 | 0.12 | 0.10 | 0.59 | 0.15 | 0.14 | 0.37 | 0.15 | 0.27 | 0.18 | 0.17 | 0.10 | 0.11 | 0.13 | 0.13 | 0.14 | 0.15 | 0.13 | 0.10 | 0.19 | 0.15 | 0.10 |
| T 16 | 0.01 | 0.13 | 0.01 | 0.12 | 0.10 | 0.09 | 0.12 | 0.21 | 0.14 | 0.16 | 0.50 | 0.17 | 0.13 | 0.06 | 0.05 | 0.06 | 0.00 | 0.16 | 0.15 | 0.11 | 0.00 | 0.14 | 0.09 | 0.34 | 0.13 | 0.07 |
| T 17 | 0.41 | 0.62 | 0.34 | 0.78 | 0.60 | 0.55 | 0.63 | 1.06 | 0.84 | 0.74 | 1.06 | 0.98 | 0.64 | 0.35 | 0.78 | 0.52 | 0.46 | 1.05 | 0.43 | 0.49 | 0.37 | 0.60 | 0.78 | 0.61 | 0.43 | 0.56 |
| T 18 | 0.41 | 0.61 | 0.34 | 0.77 | 0.59 | 0.54 | 0.62 | 1.05 | 0.83 | 0.73 | 1.05 | 0.97 | 0.63 | 0.35 | 0.76 | 0.51 | 0.45 | 1.04 | 0.43 | 0.49 | 0.36 | 0.59 | 0.77 | 0.60 | 0.42 | 0.55 |
| T 19 | 0.09 | 0.17 | 0.06 | 0.16 | 0.13 | 0.13 | 0.18 | 0.35 | 0.22 | 0.21 | 0.70 | 0.26 | 0.15 | 0.08 | 0.12 | 0.10 | 0.55 | 0.23 | 0.20 | 0.13 | 0.07 | 0.17 | 0.13 | 0.51 | 0.15 | 0.08 |
| T 20 | 0.72 | 1.09 | 0.60 | 1.37 | 1.05 | 0.96 | 1.11 | 1.88 | 1.47 | 1.30 | 1.91 | 1.73 | 1.13 | 0.62 | 1.36 | 0.91 | 0.85 | 1.85 | 0.77 | 0.87 | 0.65 | 1.06 | 1.36 | 1.11 | 0.76 | 0.98 |
| T 21 | 0.39 | 0.58 | 0.32 | 0.74 | 0.56 | 0.51 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.60 | 0.33 | 0.73 | 0.49 | 0.43 | 0.99 | 0.41 | 0.46 | 0.35 | 0.57 | 0.73 | 0.57 | 0.40 | 0.53 |
| T 22 | 0.22 | 0.33 | 0.18 | 0.42 | 0.32 | 0.29 | 0.34 | 0.57 | 0.45 | 0.40 | 0.57 | 0.53 | 0.35 | 0.19 | 0.41 | 0.28 | 0.21 | 0.57 | 0.23 | 0.27 | 0.19 | 0.33 | 0.42 | 0.32 | 0.23 | 0.30 |
| T 23 | 0.38 | 0.52 | 0.31 | 0.66 | 0.51 | 0.47 | 0.55 | 0.95 | 0.73 | 0.62 | 0.98 | 0.86 | 0.53 | 0.30 | 0.68 | 0.45 | 0.75 | 0.90 | 0.38 | 0.42 | 0.34 | 0.51 | 0.66 | 0.61 | 0.36 | 0.47 |
| T 24 | 0.51 | 0.16 | 0.10 | 0.17 | 0.15 | 0.13 | 0.15 | 0.56 | 0.17 | 0.18 | 0.43 | 0.18 | 0.23 | 0.11 | 0.14 | 0.10 | 0.06 | 0.17 | 0.16 | 0.14 | 0.08 | 0.18 | 0.14 | 0.30 | 0.21 | 0.14 |
| T 25 | 0.19 | 0.29 | 0.16 | 0.37 | 0.28 | 0.26 | 0.30 | 0.50 | 0.40 | 0.35 | 0.50 | 0.46 | 0.30 | 0.17 | 0.37 | 0.24 | 0.21 | 0.50 | 0.20 | 0.23 | 0.17 | 0.28 | 0.37 | 0.29 | 0.20 | 0.27 |
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.30 | 0.71 | 0.46 | 1.00 | 0.92 | 0.38 | 0.42 | 0.38 | 0.51 | 0.67 | 0.64 | 0.36 | 0.47 |
| T 2 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.30 | 0.71 | 0.46 | 1.00 | 0.92 | 0.38 | 0.42 | 0.38 | 0.51 | 0.67 | 0.64 | 0.36 | 0.47 |
| T 3 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.30 | 0.71 | 0.46 | 1.00 | 0.92 | 0.38 | 0.42 | 0.38 | 0.51 | 0.67 | 0.64 | 0.36 | 0.47 |
| T 4 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 | 0.27 | 0.54 | 0.36 | 1.00 | 0.61 | 0.39 | 0.37 | 0.30 | 0.46 | 0.50 | 0.72 | 0.38 | 0.38 |
| T 5 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.56 | 0.41 | 0.54 |
| T 6 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.57 | 0.41 | 0.54 |
| T 7 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 | 0.27 | 0.54 | 0.36 | 1.00 | 0.61 | 0.39 | 0.37 | 0.30 | 0.46 | 0.50 | 0.72 | 0.38 | 0.38 |
| T 8 | 0.32 | 0.51 | 0.25 | 0.59 | 0.47 | 0.43 | 0.50 | 1.00 | 0.59 | 0.57 | 1.00 | 0.65 | 0.58 | 0.30 | 0.53 | 0.37 | 0.25 | 0.64 | 0.42 | 0.41 | 0.25 | 0.52 | 0.54 | 0.67 | 0.45 | 0.44 |
| T 9 | 0.16 | 0.25 | 0.11 | 0.24 | 0.19 | 0.20 | 0.27 | 0.55 | 0.33 | 0.30 | 1.00 | 0.37 | 0.21 | 0.12 | 0.20 | 0.15 | 1.00 | 0.33 | 0.29 | 0.20 | 0.12 | 0.24 | 0.19 | 0.75 | 0.22 | 0.12 |
| T 10 | 0.12 | 0.12 | 0.09 | 0.13 | 0.10 | 0.11 | 0.16 | 0.28 | 0.26 | 0.17 | 1.00 | 0.35 | 0.07 | 0.06 | 0.16 | 0.11 | 1.00 | 0.36 | 0.15 | 0.09 | 0.11 | 0.10 | 0.12 | 0.60 | 0.07 | 0.05 |
| T 11 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.56 | 0.41 | 0.54 |
| T 12 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.56 | 0.41 | 0.54 |
| T 13 | 1.00 | 0.01 | 0.32 | 0.02 | 0.02 | 0.02 | 0.01 | 0.31 | 0.03 | 0.01 | 0.06 | 0.02 | 0.01 | 0.04 | 0.06 | 0.02 | 0.75 | 0.01 | 0.02 | 0.01 | 0.15 | 0.01 | 0.01 | 0.04 | 0.01 | 0.00 |
| T 14 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 | 0.27 | 0.54 | 0.36 | 1.00 | 0.61 | 0.39 | 0.37 | 0.30 | 0.46 | 0.50 | 0.72 | 0.38 | 0.38 |
| T 15 | 0.86 | 0.15 | 0.58 | 0.24 | 0.19 | 0.17 | 0.10 | 1.00 | 0.18 | 0.14 | 0.30 | 0.15 | 0.43 | 0.31 | 0.29 | 0.15 | 0.22 | 0.11 | 0.13 | 0.18 | 0.31 | 0.13 | 0.13 | 0.08 | 0.19 | 0.15 |
| T 16 | 0.02 | 0.27 | 0.02 | 0.25 | 0.19 | 0.17 | 0.23 | 0.42 | 0.27 | 0.33 | 1.00 | 0.34 | 0.26 | 0.12 | 0.10 | 0.12 | 0.00 | 0.32 | 0.31 | 0.22 | 0.00 | 0.27 | 0.17 | 0.69 | 0.27 | 0.14 |
| T 17 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.57 | 0.41 | 0.54 |
| T 18 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.57 | 0.41 | 0.54 |
| T 19 | 0.16 | 0.25 | 0.11 | 0.24 | 0.19 | 0.20 | 0.27 | 0.55 | 0.33 | 0.30 | 1.00 | 0.37 | 0.21 | 0.12 | 0.20 | 0.15 | 1.00 | 0.33 | 0.29 | 0.20 | 0.12 | 0.24 | 0.19 | 0.75 | 0.22 | 0.12 |
| T 20 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.56 | 0.41 | 0.54 |
| T 21 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 0.99 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.56 | 0.41 | 0.54 |
| T 22 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.36 | 1.00 | 0.41 | 0.47 | 0.34 | 0.57 | 0.74 | 0.57 | 0.41 | 0.54 |
| T 23 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.30 | 0.71 | 0.46 | 1.00 | 0.92 | 0.38 | 0.42 | 0.38 | 0.51 | 0.67 | 0.64 | 0.36 | 0.47 |
| T 24 | 1.00 | 0.12 | 0.18 | 0.16 | 0.15 | 0.13 | 0.13 | 0.80 | 0.12 | 0.11 | 0.10 | 0.11 | 0.27 | 0.13 | 0.20 | 0.10 | 0.13 | 0.10 | 0.09 | 0.11 | 0.16 | 0.15 | 0.15 | 0.08 | 0.21 | 0.17 |
| T 25 | 0.39 | 0.58 | 0.32 | 0.74 | 0.56 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.60 | 0.33 | 0.73 | 0.49 | 0.42 | 1.00 | 0.41 | 0.46 | 0.35 | 0.57 | 0.74 | 0.57 | 0.40 | 0.53 |
Appendix B. Matching Results Under Different Herd Coefficients
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| T 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 12 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| T 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| T 22 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 25 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| T 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 12 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 15 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| T 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| T 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 22 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 24 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 25 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 12 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| T 15 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| T 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| T 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| T 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| T 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 24 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Appendix C. Matching Results Under Different Risk Attitudes
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| T 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| T 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| T 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 11 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| T 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 17 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 18 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 24 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 25 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
References
- Chang, T.S.; Lin, J.G.; Ouenniche, J. DEA-based Nash bargaining approach to merger target selection. Eur. J. Oper. Res. 2023, 305, 930–945. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Li, F.; Amirteimoori, A. Data-driven approach to find the best partner for merger and acquisitions in banking industry. Ind. Manag. Data Syst. 2021, 121, 879–893. [Google Scholar] [CrossRef]
- Li, F.; Liang, L.; Li, Y.; Emrouznejad, A. An alternative approach to decompose the potential gains from mergers. J. Oper. Res. Soc. 2018, 69, 1793–1802. [Google Scholar] [CrossRef]
- Wanke, P.; Maredza, A.; Gupta, R. Merger and acquisitions in South African banking: A network DEA model. Res. Int. Bus. Financ. 2017, 41, 362–376. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, J.; Chu, J.; Amirteimoori, A.; Sun, J. DEA-based models for best partner selection for merger. Rairo-Oper. Res. 2017, 51, 1345–1357. [Google Scholar] [CrossRef]
- Huang, Q.; Jiang, F.; Xie, F. The dark side of industry tournament incentives. Eur. Corp. Gov. Inst.–Financ. Work. Pap. 2020, 684. [Google Scholar] [CrossRef]
- Koi-Akrofi, G.Y. Mergers and acquisitions failure rates and perspectives on why they fail. Int. J. Innov. Appl. Stud. 2016, 17, 150–158. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lovell, C.K. Stochastic Frontier Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data envelopment analysis: Critique and extensions. New Dir. Program Eval. 1986, 32, 73–105. [Google Scholar] [CrossRef]
- Zhang, R.; Wei, Q.; Li, A.; Ren, L. Measuring efficiency and technology inequality of China’s electricity generation and transmission system: A new approach of network Data Envelopment Analysis prospect cross-efficiency models. Energy 2022, 246, 123274. [Google Scholar] [CrossRef]
- Jin, F.; Cai, Y.; Zhou, L.; Ding, T. Regret-rejoice two-stage multiplicative DEA models-driven cross-efficiency evaluation with probabilistic linguistic information. Omega-Int. J. Manag. Sci. 2023, 117, 102839. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Z.; Liang, L. A novel centralized cross-efficiency evaluation via explainable artificial intelligence in the context of big data. Eur. J. Oper. Res. 2025, 327, 247–262. [Google Scholar] [CrossRef]
- Wu, N.; Zhang, M.; Huang, Y.; Wang, J. Staged Resource Allocation Optimization under Heterogeneous Grouping Based on Interval Data: The Case of China’s Forest Carbon Sequestration. Mathematics 2024, 12, 2650. [Google Scholar] [CrossRef]
- Banerjee, A.V. A simple model of herd behavior. Q. J. Econ. 1992, 107, 797–817. [Google Scholar] [CrossRef]
- Rook, L. An economic psychological approach to herd behavior. J. Econ. Issues 2006, 40, 75–95. [Google Scholar] [CrossRef]
- Ajraldi, V.; Pittavino, M.; Venturino, E. Modeling herd behavior in population systems. Nonlinear. Anal.-Real. 2011, 12, 2319–2338. [Google Scholar] [CrossRef]
- Ma, J.; Wang, D.; McBean, E.A.; Su, J. A group decision-making method for public opinion response plans: Herd behavior and two-stage consensus-reaching. Expert Syst. Appl. 2025, 268, 126367. [Google Scholar] [CrossRef]
- Wu, D.D.; Zhou, Z.; Birge, J.R. Estimation of potential gains from mergers in multiple periods: A comparison of stochastic frontier analysis and Data Envelopment Analysis. Ann. Oper. Res. 2011, 186, 357–381. [Google Scholar] [CrossRef]
- Wu, D.D.; Luo, C.; Wang, H.; Birge, J.R. Bi-level programing merger evaluation and application to banking operations. Prod. Oper. Manag. 2016, 25, 498–515. [Google Scholar] [CrossRef]
- Al Tamimi, H.A.H.; Duqi, A.; Kanas, A.; Zervopoulos, P.D. Directional distance function DEA estimators for evaluating efficiency gains from possible mergers and acquisitions. J. Oper. Res. Soc. 2022, 73, 1240–1257. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, Y.M.; Shi, H.L. Mergers and acquisitions matching for performance improvement: A DEA-based approach. Econ. Res.-Ekon. Istraz. 2020, 33, 3545–3561. [Google Scholar] [CrossRef]
- Shi, H.L.; Wang, Y.M. A merger and acquisition matching method that considers irrational behavior from a performance perspective. IEEE Access 2020, 8, 45726–45737. [Google Scholar] [CrossRef]
- Saen, R.F.; Karimi, B.; Fathi, A. Unleashing efficiency potential: The power of non-convex double frontiers in sustainable transportation supply chains. Socio-Econ. Plan. Sci. 2025, 98, 102143. [Google Scholar] [CrossRef]
- Kaffash, S.; Azizi, R.; Huang, Y.; Zhu, J. A survey of data envelopment analysis applications in the insurance industry 1993–2018. Eur. J. Oper. Res. 2020, 284, 801–813. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Shadkam, E.; Khalili, S.M.; Kabirifar, K.; Yazdani, R.; Asgari Gashteroodkhani, T. A novel artificial intelligent approach: Comparison of machine learning tools and algorithms based on optimization DEA Malmquist productivity index for eco-efficiency evaluation. Int. J. Energy Sect. Manag. 2021, 15, 523–550. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.T. A compromise solution approach for efficiency measurement with shared input: The case of tourist hotels in Taiwan. Eur. J. Oper. Res. 2025, 321, 895–906. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Toloo, M.; Tone, K.; Izadikhah, M. Selecting slacks-based data envelopment analysis models. Eur. J. Oper. Res. 2023, 308, 1302–1318. [Google Scholar] [CrossRef]
- Guevel, H.P.; Ramón, N.; Aparicio, J. Benchmarking and Target Setting in Weight Restriction Context. Mathematics 2025, 13, 1175. [Google Scholar] [CrossRef]
- Ghiyasi, M.; Nasrabadi, N.; Emrouznejad, A. Inverse DEA based on cost and revenue efficiency in the absence of price information. Expert Syst. Appl. 2025, 284, 128028. [Google Scholar] [CrossRef]
- Lozano, S.; Villa, G. DEA-based pre-merger planning tool. J. Oper. Res. Soc. 2010, 61, 1485–1497. [Google Scholar] [CrossRef]
- Shi, X.; Li, Y.; Emrouznejad, A.; Xie, J.; Liang, L. Estimation of potential gains from bank mergers: A novel two-stage cost efficiency DEA model. J. Oper. Res. Soc. 2017, 68, 1045–1055. [Google Scholar] [CrossRef]
- Hsu, S.Y.; Lu, C.C.; Xiao, Y.H.; Chiu, Y.H. Two-stage evaluation of the pre-merger potential gains of Taiwan financial holding companies: Dynamic network slack-based measure analysis approach. Comput. Econ. 2024, 64, 2131–2178. [Google Scholar] [CrossRef]
- Santín, D.; Tejada, J. Is it worth it? Using DEA to analyze the efficiency gains and costs of merging university departments: A case study of the Complutense University of Madrid. Int. Trans. Oper. Res. 2025, 32, 2593–2619. [Google Scholar] [CrossRef]
- Soltanifar, M.; Ghiyasi, M.; Emrouznejad, A.; Sharafi, H. A novel model for merger analysis and target setting: A CSW-Inverse DEA approach. Expert Syst. Appl. 2024, 249, 123326. [Google Scholar] [CrossRef]
- Gerami, J. Strategic alliances and partnerships based on the semi-additive production technology in DEA. Expert Syst. Appl. 2024, 251, 123986. [Google Scholar] [CrossRef]
- Lozano, S. Using DEA to find the best partner for a horizontal cooperation. Comput. Ind. Eng. 2013, 66, 286–292. [Google Scholar] [CrossRef]
- Boamah, M.I.; Amin, G.R. Partner selection in business mergers: A data envelopment analysis approach. Rairo-Oper. Res. 2024, 58, 3107–3117. [Google Scholar] [CrossRef]
- Alam, N.; Lee Ng, S. Banking mergers–an application of matching strategy. Rev. Account. Financ. 2014, 13, 2–23. [Google Scholar] [CrossRef]
- Ullah, N.; Rashid, M.M. Merger and acquisition strategy for banks-an extensive contemporary literature review. Educ. Res. (IJMCER) 2024, 6, 41–55. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decisions under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Goursat, L. Essays on Matching with Limited Information and Bounded Rationality. Ph.D. Thesis, PSE—École d’Économie de Paris, Paris, France, 2024. [Google Scholar]
- Liu, H.H.; Song, Y.Y.; Yang, G.L. Cross-efficiency evaluation in data envelopment analysis based on prospect theory. Eur. J. Oper. Res. 2019, 273, 364–375. [Google Scholar] [CrossRef]
- Bikhchandani, S.; Hirshleifer, D.; Welch, I. Learning from the behavior of others: Conformity, fads, and informational cascades. J. Econ. Perspect. 1998, 12, 151–170. [Google Scholar] [CrossRef]

| Targets | ||||||
| DMU 1 | 12,030,000 | 26,053,000 | 6,574,000 | 321,590,000 | 260,071,000 | 874,492,000 |
| DMU 2 | 6,797,000 | 17,438,000 | 4,667,000 | 159,983,000 | 418,582,000 | 930,337,000 |
| DMU 3 | 9,433,000 | 24,857,000 | 4,847,000 | 171,910,000 | 399,795,000 | 922,214,000 |
| DMU 4 | 13,486,000 | 14,843,000 | 1,821,000 | 179,696,000 | 323,535,000 | 642,173,000 |
| DMU 5 | 2,906,278 | 7,143,995 | 1,049,107 | 21,369,509 | 111,246,751 | 284,800,984 |
| DMU 6 | 2,694,444 | 5,251,503 | 1,299,328 | 16,477,644 | 83,180,647 | 224,541,765 |
| DMU 7 | 2,674,738 | 5,599,066 | 1,238,290 | 63,273,007 | 66,710,323 | 145,275,378 |
| DMU 8 | 2,254,869 | 2,391,864 | 724,736 | 12,493,366 | 118,413,161 | 147,169,695 |
| DMU 9 | 1,822,000 | 3,902,000 | 734,000 | 84,268,000 | 116,053,000 | 26,039,000 |
| DMU 10 | 716,282 | 4,392,756 | 1,609,084 | 75,992,027 | 86,823,543 | 25,850,933 |
| DMU 11 | 1,130,000 | 3,824,000 | 732,000 | 3,611,000 | 45,833,000 | 143,259,000 |
| DMU 12 | 1,021,835 | 2,834,754 | 531,510 | 5,759,223 | 31,414,275 | 151,773,966 |
| DMU 13 | 3,065,000 | 408,000 | 49,000 | 30,522,000 | 2,936,000 | 75,981,000 |
| DMU 14 | 2,134,927 | 827474 | 195,004 | 16,895,877 | 46,229,666 | 66,651,806 |
| DMU 15 | 2,355,000 | 969,000 | 57,000 | 4,091,000 | 22,558,000 | 120,065,000 |
| DMU 16 | 874,000 | 75,000 | 17,000 | 14,999,000 | 56,740,000 | 57,972,000 |
| DMU 17 | 833,984 | 2,132,425 | 415,034 | 4,510,217 | 32,304,735 | 94,709,936 |
| DMU 18 | 806,063 | 2,007,746 | 396,230 | 3,295,262 | 30,936,413 | 90,940,461 |
| DMU 19 | 693,721 | 2,044,429 | 304,313 | 38,913,888 | 51,197,684 | 32,377,459 |
| DMU 20 | 826,942 | 2,392,684 | 342,382 | 8,213,749 | 26,942,302 | 85,234,124 |
| DMU 21 | 1,004,168 | 1,617,353 | 493,556 | 4,318,567 | 12,979,263 | 98,699,167 |
| DMU 22 | 478,939 | 1,880,615 | 463,911 | 3,467,026 | 24,619,079 | 82,616,342 |
| DMU 23 | 860,888 | 1,406,981 | 332,788 | 13,690,820 | 17,973,105 | 80,161,870 |
| DMU 24 | 2,767,499 | 196,097 | 177,247 | 2,958,018 | 15,679,177 | 95,246,115 |
| DMU 25 | 489,153 | 1,633,131 | 286,837 | 9,641,162 | 12,068,166 | 87,281,714 |
| Bidders | ||||||
| DMU 26 | 1,948,393 | 74,089 | 22,392 | 20,452,309 | 1,955,074 | 91,694,824 |
| DMU 27 | 654,536 | 1,437,922 | 323,041 | 2,592,121 | 22,348,994 | 74,874,375 |
| DMU 28 | 1,962,672 | 1,058,471 | 52,803 | 14,811,896 | 3,475,449 | 87,459,200 |
| DMU 29 | 530,498 | 1,122,359 | 200,962 | 2,811,159 | 16,234,808 | 75,525,219 |
| DMU 30 | 648,660 | 1,040,482 | 223,393 | 3,097,780 | 13,634,835 | 64,370,078 |
| DMU 31 | 688,114 | 1,088,034 | 240,598 | 4,488,941 | 12,960,589 | 61,953,747 |
| DMU 32 | 455,204 | 917,125 | 360,462 | 4,381,225 | 13,006,251 | 51,152,423 |
| DMU 33 | 413,000 | 138,000 | 27,000 | 7,223,000 | 12,503,000 | 54,765,000 |
| DMU 34 | 250,928 | 967,129 | 184,088 | 4,514,874 | 12,087,410 | 49,495,150 |
| DMU 35 | 250,398 | 1,070,095 | 221,349 | 1,231,922 | 15,511,046 | 46,312,248 |
| DMU 36 | 43,884 | 689,880 | 63,640 | 3,408,468 | 23,077,746 | 28,057,377 |
| DMU 37 | 99,028 | 787,196 | 157,252 | 2,658,890 | 9,934,276 | 35,463,205 |
| DMU 38 | 410,010 | 307,404 | 48,832 | 432,784 | 9,032,345 | 36,678,427 |
| DMU 39 | 557,418 | 475,005 | 47,617 | 1,412,929 | 5,967,721 | 27,828,008 |
| DMU 40 | 258,707 | 375,189 | 69,824 | 3,282,377 | 2,773,056 | 32,144,142 |
| DMU 41 | 294,276 | 641,672 | 123,855 | 2,055,884 | 4,649,921 | 28,034,702 |
| DMU 42 | 183,000 | 182,000 | 28,000 | 17,588,000 | 5000 | 10,210,000 |
| DMU 43 | 31,972 | 645,894 | 154,809 | 1,131,893 | 6,735,308 | 25,346,591 |
| DMU 44 | 233,451 | 514,566 | 91,005 | 1,256,897 | 9,114,602 | 18,637,162 |
| DMU 45 | 268,688 | 482,676 | 82,363 | 729,617 | 6,689,021 | 22,781,670 |
| DMU 46 | 519,103 | 359,248 | 44,772 | 5,514,050 | 100,813 | 25,840,618 |
| DMU 47 | 219,180 | 349,895 | 110,539 | 493,838 | 6,595,405 | 21,974,970 |
| DMU 48 | 171,946 | 418,399 | 128,227 | 1,118,529 | 3,994,800 | 25,734,653 |
| DMU 49 | 85,186 | 433,798 | 111,751 | 3,317,919 | 12,450,688 | 13,967,601 |
| DMU 50 | 378,901 | 225,266 | 70,767 | 382,072 | 8,106,359 | 21,904,069 |
| DMU 51 | 291,019 | 333,816 | 108,763 | 428,629 | 3,817,790 | 24,918,765 |
| Self-Evaluation Results of Targets | Self-Evaluation Results of Bidders | ||||||
|---|---|---|---|---|---|---|---|
| T 1 | 0.48 | T 14 | 0.36 | B 1 | 1.00 | B 14 | 0.56 |
| T 2 | 0.70 | T 15 | 0.70 | B 2 | 0.59 | B 15 | 0.86 |
| T 3 | 0.50 | T 16 | 1.00 | B 3 | 0.58 | B 16 | 0.59 |
| T 4 | 0.39 | T 17 | 0.55 | B 4 | 0.74 | B 17 | 1.00 |
| T 5 | 0.48 | T 18 | 0.55 | B 5 | 0.57 | B 18 | 1.00 |
| T 6 | 0.45 | T 19 | 0.77 | B 6 | 0.52 | B 19 | 0.66 |
| T 7 | 0.39 | T 20 | 0.47 | B 7 | 0.60 | B 20 | 0.66 |
| T 8 | 0.60 | T 21 | 0.56 | B 8 | 1.00 | B 21 | 0.60 |
| T 9 | 0.77 | T 22 | 0.69 | B 9 | 0.79 | B 22 | 0.84 |
| T 10 | 1.00 | T 23 | 0.56 | B 10 | 0.70 | B 23 | 0.92 |
| T 11 | 0.54 | T 24 | 0.57 | B 11 | 1.00 | B 24 | 1.00 |
| T 12 | 0.70 | T 25 | 0.77 | B 12 | 0.93 | B 25 | 0.76 |
| T 13 | 0.70 | B 13 | 0.71 | B 26 | 0.75 | ||
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 |
| T 2 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 |
| T 3 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 |
| T 4 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 |
| T 5 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 6 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 7 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 |
| T 8 | 0.32 | 0.51 | 0.25 | 0.59 | 0.47 | 0.43 | 0.50 | 1.00 | 0.59 | 0.57 | 1.00 | 0.65 | 0.58 | 0.32 | 0.51 | 0.25 | 0.59 | 0.47 | 0.43 | 0.50 | 1.00 | 0.59 | 0.57 | 1.00 | 0.65 | 0.58 |
| T 9 | 0.16 | 0.25 | 0.11 | 0.24 | 0.19 | 0.20 | 0.27 | 0.55 | 0.33 | 0.30 | 1.00 | 0.37 | 0.21 | 0.16 | 0.25 | 0.11 | 0.24 | 0.19 | 0.20 | 0.27 | 0.55 | 0.33 | 0.30 | 1.00 | 0.37 | 0.21 |
| T 10 | 0.12 | 0.12 | 0.09 | 0.13 | 0.10 | 0.11 | 0.16 | 0.28 | 0.26 | 0.17 | 1.00 | 0.35 | 0.07 | 0.12 | 0.12 | 0.09 | 0.13 | 0.10 | 0.11 | 0.16 | 0.28 | 0.26 | 0.17 | 1.00 | 0.35 | 0.07 |
| T 11 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 12 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 13 | 1.00 | 0.01 | 0.32 | 0.02 | 0.02 | 0.02 | 0.01 | 0.31 | 0.03 | 0.01 | 0.06 | 0.02 | 0.01 | 1.00 | 0.01 | 0.32 | 0.02 | 0.02 | 0.02 | 0.01 | 0.31 | 0.03 | 0.01 | 0.06 | 0.02 | 0.01 |
| T 14 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 | 0.38 | 0.46 | 0.28 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | 0.59 | 0.51 | 1.00 | 0.64 | 0.49 |
| T 15 | 0.86 | 0.15 | 0.58 | 0.24 | 0.19 | 0.17 | 0.10 | 1.00 | 0.18 | 0.14 | 0.30 | 0.15 | 0.43 | 0.86 | 0.15 | 0.58 | 0.24 | 0.19 | 0.17 | 0.10 | 1.00 | 0.18 | 0.14 | 0.30 | 0.15 | 0.43 |
| T 16 | 0.02 | 0.27 | 0.02 | 0.25 | 0.19 | 0.17 | 0.23 | 0.42 | 0.27 | 0.33 | 1.00 | 0.34 | 0.26 | 0.02 | 0.27 | 0.02 | 0.25 | 0.19 | 0.17 | 0.23 | 0.42 | 0.27 | 0.33 | 1.00 | 0.34 | 0.26 |
| T 17 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 18 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 19 | 0.16 | 0.25 | 0.11 | 0.24 | 0.19 | 0.20 | 0.27 | 0.55 | 0.33 | 0.30 | 1.00 | 0.37 | 0.21 | 0.16 | 0.25 | 0.11 | 0.24 | 0.19 | 0.20 | 0.27 | 0.55 | 0.33 | 0.30 | 1.00 | 0.37 | 0.21 |
| T 20 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.59 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 21 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 0.99 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 0.99 | 0.93 | 0.61 |
| T 22 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.38 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 |
| T 23 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 | 0.42 | 0.53 | 0.33 | 0.67 | 0.52 | 0.49 | 0.57 | 1.00 | 0.76 | 0.63 | 1.00 | 0.88 | 0.53 |
| T 24 | 1.00 | 0.12 | 0.18 | 0.16 | 0.15 | 0.13 | 0.13 | 0.80 | 0.12 | 0.11 | 0.10 | 0.11 | 0.27 | 1.00 | 0.12 | 0.18 | 0.16 | 0.15 | 0.13 | 0.13 | 0.80 | 0.12 | 0.11 | 0.10 | 0.11 | 0.27 |
| T 25 | 0.39 | 0.58 | 0.32 | 0.74 | 0.56 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.60 | 0.39 | 0.58 | 0.32 | 0.74 | 0.56 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.60 |
| T 1 | T 2 | T 3 | T 4 | T 5 | T 6 | T 7 | T 8 | T 9 | T 10 | T 11 | T 12 | T 13 | T 14 | T 15 | T 16 | T 17 | T 18 | T 19 | T 20 | T 21 | T 22 | T 23 | T 24 | T 25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.48 | 0.70 | 0.50 | 0.35 | 0.46 | 0.42 | 0.38 | 0.40 | 0.33 | 0.46 | 0.48 | 0.63 | 0.26 | 0.26 | 0.34 | 0.61 | 0.50 | 0.50 | 0.47 | 0.46 | 0.51 | 0.62 | 0.56 | 0.25 | 0.76 |
| T 2 | 0.48 | 0.70 | 0.50 | 0.35 | 0.46 | 0.42 | 0.38 | 0.40 | 0.33 | 0.46 | 0.48 | 0.63 | 0.26 | 0.26 | 0.34 | 0.61 | 0.50 | 0.50 | 0.47 | 0.46 | 0.51 | 0.62 | 0.56 | 0.25 | 0.76 |
| T 3 | 0.48 | 0.70 | 0.50 | 0.35 | 0.46 | 0.42 | 0.38 | 0.40 | 0.33 | 0.46 | 0.48 | 0.63 | 0.26 | 0.26 | 0.34 | 0.61 | 0.50 | 0.50 | 0.47 | 0.46 | 0.51 | 0.62 | 0.56 | 0.25 | 0.76 |
| T 4 | 0.44 | 0.68 | 0.48 | 0.39 | 0.42 | 0.40 | 0.39 | 0.54 | 0.55 | 0.61 | 0.40 | 0.48 | 0.25 | 0.36 | 0.31 | 1.00 | 0.44 | 0.44 | 0.62 | 0.39 | 0.39 | 0.50 | 0.49 | 0.23 | 0.55 |
| T 5 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.28 | 0.42 | 0.07 | 0.11 | 0.54 | 0.70 | 0.20 | 0.23 | 0.38 | 0.53 | 0.55 | 0.55 | 0.21 | 0.47 | 0.56 | 0.68 | 0.53 | 0.28 | 0.77 |
| T 6 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.29 | 0.42 | 0.08 | 0.12 | 0.54 | 0.69 | 0.20 | 0.23 | 0.38 | 0.54 | 0.55 | 0.55 | 0.22 | 0.47 | 0.56 | 0.69 | 0.53 | 0.28 | 0.77 |
| T 7 | 0.44 | 0.68 | 0.48 | 0.39 | 0.42 | 0.40 | 0.39 | 0.54 | 0.55 | 0.61 | 0.40 | 0.48 | 0.25 | 0.36 | 0.31 | 1.00 | 0.44 | 0.44 | 0.62 | 0.39 | 0.39 | 0.50 | 0.49 | 0.23 | 0.55 |
| T 8 | 0.32 | 0.64 | 0.44 | 0.35 | 0.45 | 0.42 | 0.29 | 0.60 | 0.32 | 0.32 | 0.45 | 0.53 | 0.16 | 0.34 | 0.36 | 1.00 | 0.48 | 0.49 | 0.39 | 0.40 | 0.43 | 0.54 | 0.44 | 0.27 | 0.52 |
| T 9 | 0.34 | 0.53 | 0.37 | 0.33 | 0.28 | 0.26 | 0.35 | 0.50 | 0.77 | 0.86 | 0.22 | 0.21 | 0.15 | 0.33 | 0.12 | 1.00 | 0.27 | 0.26 | 0.77 | 0.25 | 0.13 | 0.28 | 0.29 | 0.08 | 0.25 |
| T 10 | 0.31 | 0.37 | 0.27 | 0.20 | 0.16 | 0.14 | 0.29 | 0.20 | 0.60 | 1.00 | 0.12 | 0.12 | 0.11 | 0.15 | 0.05 | 0.39 | 0.14 | 0.13 | 0.67 | 0.17 | 0.08 | 0.17 | 0.21 | 0.03 | 0.23 |
| T 11 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.28 | 0.42 | 0.07 | 0.11 | 0.54 | 0.70 | 0.20 | 0.23 | 0.38 | 0.53 | 0.55 | 0.55 | 0.21 | 0.47 | 0.56 | 0.68 | 0.53 | 0.28 | 0.77 |
| T 12 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.28 | 0.42 | 0.07 | 0.11 | 0.54 | 0.70 | 0.20 | 0.23 | 0.38 | 0.53 | 0.55 | 0.55 | 0.21 | 0.47 | 0.56 | 0.68 | 0.53 | 0.28 | 0.77 |
| T 13 | 0.06 | 0.04 | 0.04 | 0.12 | 0.02 | 0.02 | 0.06 | 0.02 | 0.14 | 0.06 | 0.01 | 0.01 | 0.70 | 0.10 | 0.08 | 1.00 | 0.01 | 0.01 | 0.15 | 0.03 | 0.01 | 0.01 | 0.05 | 0.02 | 0.04 |
| T 14 | 0.44 | 0.68 | 0.48 | 0.39 | 0.42 | 0.40 | 0.39 | 0.54 | 0.55 | 0.61 | 0.40 | 0.48 | 0.25 | 0.36 | 0.31 | 1.00 | 0.44 | 0.44 | 0.62 | 0.39 | 0.39 | 0.50 | 0.49 | 0.23 | 0.55 |
| T 15 | 0.09 | 0.13 | 0.13 | 0.20 | 0.18 | 0.11 | 0.08 | 0.13 | 0.02 | 0.01 | 0.13 | 0.19 | 0.40 | 0.18 | 0.70 | 1.00 | 0.15 | 0.15 | 0.07 | 0.16 | 0.13 | 0.12 | 0.16 | 0.26 | 0.20 |
| T 16 | 0.17 | 0.45 | 0.30 | 0.25 | 0.28 | 0.26 | 0.20 | 0.56 | 0.51 | 0.50 | 0.25 | 0.21 | 0.01 | 0.29 | 0.13 | 1.00 | 0.28 | 0.28 | 0.49 | 0.22 | 0.12 | 0.29 | 0.19 | 0.09 | 0.15 |
| T 17 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.29 | 0.42 | 0.08 | 0.12 | 0.54 | 0.69 | 0.20 | 0.23 | 0.38 | 0.54 | 0.55 | 0.55 | 0.22 | 0.47 | 0.56 | 0.69 | 0.53 | 0.28 | 0.77 |
| T 18 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.29 | 0.42 | 0.08 | 0.12 | 0.54 | 0.69 | 0.20 | 0.23 | 0.38 | 0.54 | 0.55 | 0.55 | 0.22 | 0.47 | 0.56 | 0.69 | 0.53 | 0.28 | 0.77 |
| T 19 | 0.34 | 0.53 | 0.37 | 0.33 | 0.28 | 0.26 | 0.35 | 0.50 | 0.77 | 0.86 | 0.22 | 0.21 | 0.15 | 0.33 | 0.12 | 1.00 | 0.27 | 0.26 | 0.77 | 0.25 | 0.13 | 0.28 | 0.29 | 0.08 | 0.25 |
| T 20 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.28 | 0.42 | 0.07 | 0.11 | 0.54 | 0.70 | 0.20 | 0.23 | 0.38 | 0.53 | 0.55 | 0.55 | 0.21 | 0.47 | 0.56 | 0.68 | 0.53 | 0.28 | 0.77 |
| T 21 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.28 | 0.42 | 0.07 | 0.11 | 0.54 | 0.70 | 0.20 | 0.23 | 0.38 | 0.53 | 0.55 | 0.55 | 0.21 | 0.47 | 0.56 | 0.68 | 0.53 | 0.28 | 0.77 |
| T 22 | 0.38 | 0.66 | 0.47 | 0.30 | 0.48 | 0.45 | 0.29 | 0.42 | 0.08 | 0.12 | 0.54 | 0.69 | 0.20 | 0.23 | 0.38 | 0.54 | 0.55 | 0.55 | 0.22 | 0.47 | 0.56 | 0.69 | 0.53 | 0.28 | 0.77 |
| T 23 | 0.48 | 0.70 | 0.50 | 0.35 | 0.46 | 0.42 | 0.38 | 0.40 | 0.33 | 0.46 | 0.48 | 0.63 | 0.26 | 0.26 | 0.34 | 0.61 | 0.50 | 0.50 | 0.47 | 0.46 | 0.51 | 0.62 | 0.56 | 0.25 | 0.76 |
| T 24 | 0.08 | 0.13 | 0.09 | 0.10 | 0.10 | 0.10 | 0.06 | 0.14 | 0.02 | 0.01 | 0.09 | 0.13 | 0.29 | 0.17 | 0.26 | 1.00 | 0.11 | 0.11 | 0.04 | 0.09 | 0.14 | 0.11 | 0.13 | 0.57 | 0.13 |
| T 25 | 0.39 | 0.67 | 0.47 | 0.31 | 0.48 | 0.45 | 0.29 | 0.42 | 0.10 | 0.14 | 0.54 | 0.69 | 0.20 | 0.24 | 0.37 | 0.54 | 0.55 | 0.55 | 0.24 | 0.47 | 0.56 | 0.68 | 0.53 | 0.27 | 0.77 |
| T 1 | T 2 | T 3 | T 4 | T 5 | T 6 | T 7 | T 8 | T 9 | T 10 | T 11 | T 12 | T 13 | T 14 | T 15 | T 16 | T 17 | T 18 | T 19 | T 20 | T 21 | T 22 | T 23 | T 24 | T 25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.00 | 0.46 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.32 | 0.00 | 0.00 | 0.00 | 0.27 | 0.05 | 0.04 | 0.00 | 0.00 | 0.07 | 0.31 | 0.16 | 0.00 | 0.59 |
| T 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 |
| T 3 | 0.00 | 0.39 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.26 | 0.00 | 0.00 | 0.00 | 0.21 | 0.01 | 0.00 | 0.00 | 0.00 | 0.02 | 0.25 | 0.11 | 0.00 | 0.51 |
| T 4 | 0.11 | 0.72 | 0.21 | 0.00 | 0.07 | 0.01 | 0.00 | 0.37 | 0.40 | 0.56 | 0.02 | 0.23 | 0.00 | 0.00 | 0.00 | 1.54 | 0.13 | 0.11 | 0.57 | 0.00 | 0.00 | 0.27 | 0.23 | 0.00 | 0.39 |
| T 5 | 0.00 | 0.37 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.12 | 0.44 | 0.00 | 0.00 | 0.00 | 0.10 | 0.14 | 0.14 | 0.00 | 0.00 | 0.16 | 0.42 | 0.10 | 0.00 | 0.59 |
| T 6 | 0.00 | 0.48 | 0.05 | 0.00 | 0.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.55 | 0.00 | 0.00 | 0.00 | 0.20 | 0.23 | 0.23 | 0.00 | 0.06 | 0.25 | 0.53 | 0.18 | 0.00 | 0.71 |
| T 7 | 0.13 | 0.75 | 0.24 | 0.02 | 0.09 | 0.02 | 0.00 | 0.39 | 0.42 | 0.58 | 0.03 | 0.25 | 0.00 | 0.00 | 0.00 | 1.58 | 0.14 | 0.13 | 0.60 | 0.02 | 0.01 | 0.29 | 0.25 | 0.00 | 0.41 |
| T 8 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.68 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.30 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 11 | 0.00 | 0.22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.28 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | 0.00 | 0.00 | 0.03 | 0.26 | 0.00 | 0.00 | 0.42 |
| T 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.10 |
| T 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.43 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 14 | 0.22 | 0.89 | 0.34 | 0.10 | 0.18 | 0.11 | 0.08 | 0.51 | 0.54 | 0.71 | 0.12 | 0.35 | 0.00 | 0.00 | 0.00 | 1.79 | 0.24 | 0.23 | 0.73 | 0.10 | 0.09 | 0.39 | 0.35 | 0.00 | 0.53 |
| T 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.44 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 17 | 0.00 | 0.21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.24 | 0.00 | 0.00 | 0.39 |
| T 18 | 0.00 | 0.20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.24 | 0.00 | 0.00 | 0.39 |
| T 19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.29 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 20 | 0.00 | 0.39 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.14 | 0.47 | 0.00 | 0.00 | 0.00 | 0.12 | 0.16 | 0.16 | 0.00 | 0.00 | 0.18 | 0.44 | 0.12 | 0.00 | 0.62 |
| T 21 | 0.00 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.22 | 0.00 | 0.00 | 0.37 |
| T 22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.12 |
| T 23 | 0.00 | 0.25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.00 | 0.00 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.12 | 0.00 | 0.00 | 0.36 |
| T 24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| T 25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0.54 | 0.74 | 0.44 | 0.93 | 0.72 | 0.67 | 0.78 | 1.35 | 1.04 | 0.88 | 1.40 | 1.21 | 0.75 | 0.42 | 0.95 | 0.63 | 1.06 | 1.27 | 0.54 | 0.59 | 0.48 | 0.72 | 0.93 | 0.87 | 0.51 | 0.66 |
| T 2 | 0.30 | 0.39 | 0.24 | 0.49 | 0.38 | 0.35 | 0.41 | 0.73 | 0.55 | 0.46 | 0.73 | 0.64 | 0.39 | 0.22 | 0.52 | 0.34 | 0.71 | 0.67 | 0.28 | 0.31 | 0.27 | 0.37 | 0.49 | 0.46 | 0.26 | 0.34 |
| T 3 | 0.48 | 0.65 | 0.39 | 0.82 | 0.63 | 0.59 | 0.69 | 1.19 | 0.91 | 0.77 | 1.23 | 1.06 | 0.66 | 0.37 | 0.84 | 0.56 | 0.97 | 1.12 | 0.47 | 0.52 | 0.43 | 0.63 | 0.81 | 0.77 | 0.45 | 0.58 |
| T 4 | 0.68 | 1.01 | 0.52 | 1.17 | 0.92 | 0.86 | 1.04 | 1.96 | 1.33 | 1.18 | 2.48 | 1.52 | 1.03 | 0.56 | 1.11 | 0.77 | 1.71 | 1.52 | 0.87 | 0.81 | 0.57 | 0.99 | 1.09 | 1.67 | 0.80 | 0.80 |
| T 5 | 0.56 | 0.85 | 0.46 | 1.07 | 0.82 | 0.75 | 0.86 | 1.46 | 1.15 | 1.01 | 1.47 | 1.35 | 0.88 | 0.48 | 1.06 | 0.71 | 0.62 | 1.44 | 0.60 | 0.68 | 0.50 | 0.83 | 1.06 | 0.85 | 0.59 | 0.77 |
| T 6 | 0.69 | 1.04 | 0.57 | 1.31 | 1.00 | 0.92 | 1.06 | 1.79 | 1.41 | 1.24 | 1.83 | 1.65 | 1.08 | 0.59 | 1.29 | 0.87 | 0.78 | 1.77 | 0.74 | 0.83 | 0.62 | 1.02 | 1.30 | 1.06 | 0.73 | 0.94 |
| T 7 | 0.72 | 1.07 | 0.55 | 1.25 | 0.98 | 0.92 | 1.11 | 2.07 | 1.41 | 1.26 | 2.61 | 1.62 | 1.09 | 0.60 | 1.18 | 0.82 | 1.78 | 1.62 | 0.91 | 0.86 | 0.60 | 1.05 | 1.16 | 1.75 | 0.84 | 0.85 |
| T 8 | 0.24 | 0.42 | 0.19 | 0.48 | 0.38 | 0.35 | 0.41 | 0.81 | 0.49 | 0.48 | 0.93 | 0.54 | 0.47 | 0.24 | 0.41 | 0.29 | 0.20 | 0.53 | 0.36 | 0.34 | 0.18 | 0.43 | 0.43 | 0.63 | 0.38 | 0.34 |
| T 9 | 0.12 | 0.20 | 0.08 | 0.19 | 0.16 | 0.16 | 0.21 | 0.43 | 0.26 | 0.24 | 0.83 | 0.31 | 0.18 | 0.10 | 0.15 | 0.12 | 0.74 | 0.27 | 0.24 | 0.16 | 0.09 | 0.20 | 0.15 | 0.61 | 0.18 | 0.10 |
| T 10 | 0.09 | 0.09 | 0.06 | 0.09 | 0.07 | 0.08 | 0.11 | 0.20 | 0.18 | 0.12 | 0.70 | 0.24 | 0.05 | 0.04 | 0.11 | 0.07 | 0.70 | 0.25 | 0.10 | 0.06 | 0.08 | 0.07 | 0.08 | 0.42 | 0.05 | 0.04 |
| T 11 | 0.41 | 0.63 | 0.34 | 0.79 | 0.61 | 0.55 | 0.64 | 1.07 | 0.85 | 0.75 | 1.07 | 1.00 | 0.65 | 0.36 | 0.79 | 0.53 | 0.44 | 1.07 | 0.44 | 0.50 | 0.37 | 0.61 | 0.79 | 0.61 | 0.44 | 0.57 |
| T 12 | 0.28 | 0.43 | 0.23 | 0.54 | 0.42 | 0.38 | 0.43 | 0.73 | 0.58 | 0.51 | 0.73 | 0.68 | 0.45 | 0.24 | 0.54 | 0.36 | 0.27 | 0.73 | 0.30 | 0.34 | 0.25 | 0.42 | 0.54 | 0.41 | 0.30 | 0.39 |
| T 13 | 0.70 | 0.04 | 0.23 | 0.04 | 0.04 | 0.04 | 0.04 | 0.27 | 0.06 | 0.05 | 0.17 | 0.06 | 0.04 | 0.04 | 0.05 | 0.03 | 0.52 | 0.05 | 0.05 | 0.04 | 0.10 | 0.04 | 0.03 | 0.11 | 0.04 | 0.02 |
| T 14 | 0.93 | 1.38 | 0.72 | 1.62 | 1.27 | 1.19 | 1.43 | 2.63 | 1.82 | 1.63 | 3.27 | 2.11 | 1.41 | 0.77 | 1.55 | 1.07 | 2.19 | 2.12 | 1.16 | 1.10 | 0.78 | 1.36 | 1.53 | 2.17 | 1.07 | 1.11 |
| T 15 | 0.60 | 0.14 | 0.41 | 0.20 | 0.15 | 0.14 | 0.10 | 0.75 | 0.16 | 0.14 | 0.34 | 0.15 | 0.33 | 0.23 | 0.22 | 0.12 | 0.15 | 0.12 | 0.13 | 0.15 | 0.21 | 0.13 | 0.12 | 0.15 | 0.17 | 0.12 |
| T 16 | 0.01 | 0.19 | 0.02 | 0.17 | 0.13 | 0.12 | 0.16 | 0.29 | 0.19 | 0.23 | 0.70 | 0.24 | 0.18 | 0.09 | 0.07 | 0.09 | 0.00 | 0.22 | 0.21 | 0.15 | 0.00 | 0.19 | 0.12 | 0.48 | 0.19 | 0.10 |
| T 17 | 0.40 | 0.61 | 0.33 | 0.76 | 0.59 | 0.53 | 0.62 | 1.04 | 0.82 | 0.72 | 1.04 | 0.96 | 0.63 | 0.34 | 0.76 | 0.51 | 0.42 | 1.03 | 0.42 | 0.48 | 0.36 | 0.59 | 0.76 | 0.59 | 0.42 | 0.55 |
| T 18 | 0.40 | 0.60 | 0.33 | 0.76 | 0.58 | 0.53 | 0.61 | 1.03 | 0.81 | 0.72 | 1.03 | 0.95 | 0.62 | 0.34 | 0.75 | 0.50 | 0.42 | 1.02 | 0.42 | 0.48 | 0.36 | 0.59 | 0.76 | 0.59 | 0.42 | 0.55 |
| T 19 | 0.12 | 0.20 | 0.08 | 0.19 | 0.16 | 0.16 | 0.21 | 0.43 | 0.26 | 0.24 | 0.82 | 0.30 | 0.18 | 0.10 | 0.15 | 0.12 | 0.73 | 0.27 | 0.23 | 0.16 | 0.09 | 0.19 | 0.15 | 0.61 | 0.18 | 0.10 |
| T 20 | 0.59 | 0.89 | 0.49 | 1.12 | 0.86 | 0.78 | 0.90 | 1.53 | 1.20 | 1.06 | 1.55 | 1.41 | 0.92 | 0.50 | 1.11 | 0.74 | 0.65 | 1.51 | 0.63 | 0.71 | 0.53 | 0.87 | 1.11 | 0.89 | 0.62 | 0.80 |
| T 21 | 0.39 | 0.59 | 0.32 | 0.74 | 0.57 | 0.52 | 0.60 | 1.00 | 0.79 | 0.70 | 1.00 | 0.93 | 0.61 | 0.33 | 0.73 | 0.49 | 0.40 | 1.00 | 0.41 | 0.47 | 0.35 | 0.57 | 0.74 | 0.57 | 0.41 | 0.53 |
| T 22 | 0.28 | 0.44 | 0.24 | 0.55 | 0.42 | 0.38 | 0.44 | 0.74 | 0.58 | 0.52 | 0.74 | 0.69 | 0.45 | 0.25 | 0.54 | 0.36 | 0.27 | 0.74 | 0.30 | 0.35 | 0.25 | 0.43 | 0.55 | 0.42 | 0.30 | 0.40 |
| T 23 | 0.40 | 0.53 | 0.32 | 0.66 | 0.51 | 0.48 | 0.56 | 0.97 | 0.75 | 0.63 | 0.99 | 0.87 | 0.53 | 0.30 | 0.69 | 0.45 | 0.85 | 0.91 | 0.38 | 0.42 | 0.36 | 0.51 | 0.66 | 0.62 | 0.36 | 0.47 |
| T 24 | 0.70 | 0.15 | 0.13 | 0.17 | 0.15 | 0.13 | 0.15 | 0.65 | 0.15 | 0.15 | 0.30 | 0.15 | 0.25 | 0.12 | 0.16 | 0.10 | 0.09 | 0.14 | 0.13 | 0.13 | 0.11 | 0.17 | 0.14 | 0.21 | 0.21 | 0.15 |
| T 25 | 0.27 | 0.41 | 0.22 | 0.52 | 0.40 | 0.36 | 0.42 | 0.70 | 0.55 | 0.49 | 0.70 | 0.65 | 0.42 | 0.23 | 0.51 | 0.34 | 0.29 | 0.70 | 0.29 | 0.33 | 0.24 | 0.40 | 0.52 | 0.40 | 0.28 | 0.37 |
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | B 7 | B 8 | B 9 | B 10 | B 11 | B 12 | B 13 | B 14 | B 15 | B 16 | B 17 | B 18 | B 19 | B 20 | B 21 | B 22 | B 23 | B 24 | B 25 | B 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| T 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 12 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 15 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| T 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 22 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 24 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T 25 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Shi, H. Two-Side Merger and Acquisition Matching: A Perspective Based on Mutual Performance Evaluation Considering the Herd Behavior. Mathematics 2025, 13, 3268. https://doi.org/10.3390/math13203268
Wen Y, Shi H. Two-Side Merger and Acquisition Matching: A Perspective Based on Mutual Performance Evaluation Considering the Herd Behavior. Mathematics. 2025; 13(20):3268. https://doi.org/10.3390/math13203268
Chicago/Turabian StyleWen, Yao, and Hailiu Shi. 2025. "Two-Side Merger and Acquisition Matching: A Perspective Based on Mutual Performance Evaluation Considering the Herd Behavior" Mathematics 13, no. 20: 3268. https://doi.org/10.3390/math13203268
APA StyleWen, Y., & Shi, H. (2025). Two-Side Merger and Acquisition Matching: A Perspective Based on Mutual Performance Evaluation Considering the Herd Behavior. Mathematics, 13(20), 3268. https://doi.org/10.3390/math13203268






