You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Mathematics
Download PDF
  • Article
  • Open Access

10 September 2025

A Bibliometric and Topic Modeling Analysis of the p-Adic Theory Literature Using Latent Dirichlet Allocation

,
,
,
and
1
Departamento de Matemáticas y Estadística, Universidad del Norte, Barranquilla 080001, Colombia
2
Departamento de Matemáticas, Facultad de Educación y Ciencias, Universidad de Sucre, Sincelejo 700001, Colombia
3
Facultad de Ingeniería, Universidad del Magdalena, Santa Marta 470003, Colombia
4
Computer Science Department, Old Dominion University, Norfolk, VA 23508, USA
Mathematics2025, 13(18), 2932;https://doi.org/10.3390/math13182932
Version Notes
Order Reprints

Abstract

P-adic analysis, introduced by Kurt Hensel in the early 20th century, has developed into a fundamental area of mathematical research with broad applications in number theory, algebraic geometry, and mathematical physics. This study aims to examine the thematic evolution and scholarly impact of p-adic research through a comprehensive topic modeling and bibliometric analysis. Using classical bibliometric techniques (e.g., performance analysis, co-authorship, and co-citation networks) combined with Latent Dirichlet Allocation (LDA), we analyzed 7388 peer-reviewed documents published between 1965 and 2024. The computational workflow was conducted using R (version 4.4.1) and VOSviewer (version 1.6.20), which enabled the identification of 20 distinct research topics. These topics reveal both well-established and emerging areas, such as p-adic differential equations, harmonic analysis, and their connections to theoretical physics and cryptography. This study highlights key contributors, including Robert Coleman, Alain M. Robert, and Jean-Pierre Serre, whose work has shaped the development of the field. Temporal patterns observed in the topic distribution indicate dynamic shifts in research focus, while the interdisciplinary nature of recent contributions highlights the growing relevance of p-adic theory beyond pure mathematics. This analysis provides a data-driven overview of the intellectual structure of p-adic research, identifies underexplored areas, and suggests future directions for inquiry. The findings aim to support researchers in understanding historical trends, recognizing influential work, and identifying opportunities for further advancement and collaboration in the field.

1. Introduction

Introduced by Kurt Hensel in the early 20th century, p-adic analysis has become a central area of number theory, with important applications in mathematics and theoretical physics. The field focuses on the properties and structures of p-adic numbers and has recently experienced significant growth through the development of novel theoretical frameworks, advanced computational methods, and interdisciplinary applications [1,2,3,4,5,6,7,8,9,10,11,12].
This paper explores recent advances in p-adic analysis by identifying research topics through topic modeling, specifically using Latent Dirichlet Allocation (LDA) [13]. We aim to provide an in-depth examination of foundational theories and practical applications by focusing on four core areas: (1) fundamental concepts in p-adic theory; (2) methodological approaches, including computational tools and interdisciplinary frameworks; and (3) thematic developments in mathematical physics.
The workflow begins with a review of core concepts—such as p-adic numbers, their key properties, and fundamental theorems—followed by an examination of recent progress in areas such as p-adic differential equations, harmonic analysis, and their implications for number theory, algebraic geometry, and physics. We also discuss methodological considerations, including the computational tools and software employed, and highlight interdisciplinary connections that underscore the contemporary relevance of p-adic methods. This review concludes by synthesizing the main findings, identifying knowledge gaps, proposing future research directions, and reaffirming p-adic analysis as a dynamic and evolving field with profound implications for both mathematics and physics.
Through this analysis, we aim to provide a comprehensive resource for researchers and practitioners, encouraging collaboration and driving further advancements in the field. V. S. Vladimirov, I. V. Volovich, and B. Dragovich have made significant contributions to mathematical physics. Their pioneering works, such as Vladimirov’s Generalized functions over the field of p-adic numbers and Volovich’s p-adic quantum mechanics, have laid the foundation for exploring non-Archimedean structures in physics [12,14,15,16,17].
The works of A. Yu. Khrennikov and S. V. Kozyrev further illustrate the interdisciplinary scope of p-adic analysis, having developed applications such as p-adic neural networks and models of turbulence [18,19,20,21]. V. A. Avetisov and G. Parisi have also contributed to this intersection, applying p-adic methods to probability theory and statistical physics, as seen in their works on spontaneous replica symmetry breaking and p-adic models of complex systems [3,4,22].
Within the realm of mathematical physics, p-adic numbers serve as a bridge between number theory, functional analysis, and physical models. Researchers such as I. V. Volovich, A. N. Kochubei, and S. V. Kozyrev have made significant advances in the field [8,19,20,23,24,25,26,27,28,29,30,31,32].
Volovich and Vladimirov laid the theoretical groundwork in quantum mechanics and generalized functions over p-adic fields. At the same time, Kochubei contributed to the development of p-adic parabolic and stochastic differential equations. Kozyrev and Zelenov further enriched the field with their work on wavelet theory and mathematical physics [12,14,15,16,17,30,33,34,35,36].
Further contributions by Dragovich and Zúñiga-Galindo, in areas such as p-adic mathematical physics, parabolic equations, and Markov processes, have deepened our understanding. At the same time, Khrennikov’s work has offered valuable insights into p-adic probability theory and quantum mechanics [6,31,32,37,38].
Finally, important developments in ultrametric analysis, wavelet theory, and the application of p-adic methods have emerged from the work of Albeverio, Avetisov, Osipov, and collaborators [29,39,40]. This review provides a comprehensive and structured overview of these developments, highlighting the key principles, frameworks, and applications that underpin this fascinating interdisciplinary field.

2. Materials and Methods

2.1. Data Collection

We followed the PRISMA guidelines for systematic reviews to ensure a rigorous and transparent selection process [41]. During the identification phase, we searched the Scopus database for documents containing the term p-adic in titles, abstracts, or keywords. We selected this keyword for its specificity and consistency in representing the domain of p-adic theory. While bibliometric studies are common in broader scientific disciplines, we found no prior bibliometric analyses focused specifically on q-series, modular forms, or p-adic research. This gap reinforces the originality of our approach and supports the use of a precise, domain-defining keyword for retrieval. The initial screening yielded 8255 articles. In the eligibility stage, we excluded 867 records because of insufficient information, lack of access (e.g., missing abstracts or affiliation data), or duplication. The final dataset included 7388 articles for analysis (see Figure 1).
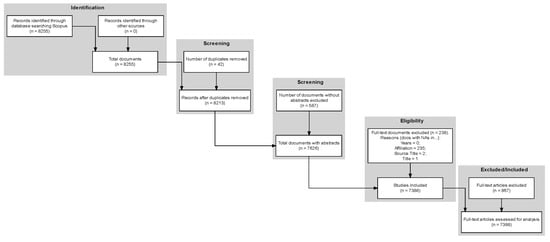
Figure 1. PRISMA flowchart: procedures and results by stage.

2.2. Bibliometric and Topic Modeling Analysis

This study integrated classical bibliometric methods and topic modeling to explore the intellectual and thematic structure of p-adic research. We employed bibliometric analysis to evaluate productivity, citation performance, and collaboration patterns, while topic modeling provided a semantic perspective on the evolution of themes. Following established frameworks [42,43], we analyzed productivity and citation patterns across countries, sources, and authors. Additionally, we examined the conceptual, intellectual, and social structures of the field through co-citation and co-authorship analyses, utilizing the bibliometrix R package (version 4.5.0) and VOSviewer (version 1.6.20) to visualize networks of collaboration and thematic evolution.
To identify latent research topics, we applied LDA, a generative probabilistic model commonly used in text mining to identify patterns of word co-occurrence across documents [13]. LDA assumes that each document is a mixture of various topics and that a distribution over words characterizes each topic. The process consisted of three main stages: (1) text preprocessing, (2) model construction, and (3) topic labeling. We cleaned and tokenized the texts using the LDAShiny package [44], intentionally avoiding stemming to preserve semantic clarity. We tested models with different numbers of topics (K = 4 to 30) and evaluated them using topic coherence metrics [45]. Two domain experts manually labeled the resulting topics based on the most relevant keywords, titles, and abstracts, following established best practices [46]. Finally, we analyzed topic trends over time and across journals using document–topic distributions. To quantify thematic shifts, we computed trend indices based on regression slopes and classified them as increasing, decreasing, or fluctuating, following the approach outlined in [47].

3. Results

3.1. General Information

Over the 59 years considered (1965–2024), we collected extensive data from 801 journals (Table 1). Table 1 summarizes the bibliometric profile of p-adic theory publications from 1965 to 2024. A total of 7388 documents from 801 sources were analyzed, with an annual growth rate of 2.38%. The average document age is 12.7 years, and the mean number of citations per document is 8.77. The majority of publications are articles (6774) and conference papers (345), with additional contributions from books, book chapters, and other formats. The dataset includes 4914 authors, of whom 1956 produced single-authored documents, resulting in 3855 such publications. Collaboration is reflected in an average of 1.72 co-authors per document and 19.02% international co-authorship.
Table 1. Primary data for bibliometric analysis of p-adic theory papers.
Thematic diversity is evident from 2727 Keywords Plus and 9717 author keywords. These indicators reflect the characteristics of a mature and theoretically grounded research field. The relatively modest annual growth rate (2.38%) and the high number of single-authored documents are consistent with disciplinary norms in pure mathematics, where individual scholarship remains prevalent. The average of 1.72 co-authors per document and the 19% rate of international collaboration suggest moderate global engagement—sufficient to sustain visibility, but not indicative of highly networked or interdisciplinary co-production. Meanwhile, the large number of author keywords (9717) highlights a growing diversification of research themes, likely driven by emerging applications in fields such as quantum physics, biological modeling, and number-theoretic cryptography. Overall, the data in Table 1 provide a solid foundation for understanding the evolution, authorship dynamics, and thematic expansion of p-adic research over the past six decades.
Figure 2 illustrates the evolution of p-adic research over time. The number of articles has grown steadily, particularly from 2015 to 2023. While the average number of citations per article showed variability before 1980, it has remained relatively stable since then.
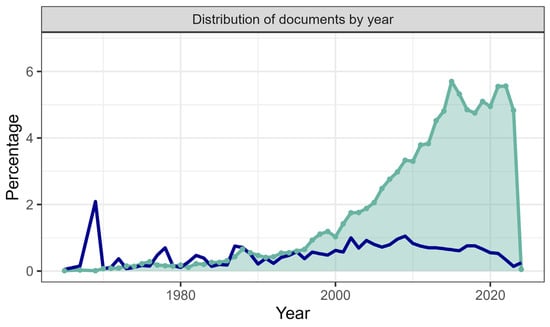
Figure 2. Distribution of citations and the number of articles in p-adic research over time. The green area shows the percentage of published articles per year, while the dark blue line represents the percentage of citations received each year.
This stability, alongside rising publication volume, suggests a continuous yet shifting research focus within the field. This pattern reflects a field that, while rooted in classical mathematical theory, has adapted to the dynamics of modern research. The post-2015 growth may be attributed to renewed interest in p-adic applications in physics, cryptography, and complex systems, as well as to the increased visibility of the field through dedicated publication venues and international collaborations. Moreover, the stable citation trend suggests consistent relevance of published work, even as thematic emphases evolve. These findings align with the broader bibliometric indicators presented in Table 1 and confirm that p-adic theory continues to generate sustained scholarly attention across multiple decades.
While part of the increase in publication output observed from 2015 onward may reflect growing interest and interdisciplinary applications within p-adic research itself, we acknowledge that this trend is also consistent with the broader global rise in scientific production across disciplines. Advances in digital publishing, open-access platforms, and increased research funding in several regions may have contributed to this overall growth. Nevertheless, the thematic consistency, sustained citation patterns, and emergence of dedicated journals suggest that the expansion of p-adic research also reflects genuine internal development within the field.

3.2. Sources

Table 2 presents the top 30 scientific journals that published research on p-adic theory between 1965 and 2024. The data highlight journal impact and productivity through indicators, such as total citations and the h-index.
Table 2. Top 30 scientific journals for p-adic research based on 7388 articles in the timespan 1965–2024.
Leading the list is the Journal of Number Theory, with 432 publications and a high citation count, reflecting sustained influence. P-Adic Numbers, Ultrametric Analysis, and Applications, which has been active since 2009, demonstrates a growing presence in the field. Other prominent journals include Compositio Mathematica, Transactions of the American Mathematical Society, and the Journal of Algebra, all of which contribute significantly to the development and dissemination of p-adic research.
This distribution of journals offers valuable insight into the intellectual positioning and interdisciplinary reach of the field. While journals such as Journal of Number Theory and Compositio Mathematica serve as core venues for number-theoretic work, the inclusion of Annals of Mathematics, Inventiones Mathematicae, and Asterisque points to the presence of foundational contributions that resonate across broader areas of pure mathematics. Notably, journals such as the Journal of High Energy Physics and Physics Letters B highlight the extension of p-adic theory into physics, particularly in the contexts of quantum theory and string theory, reflecting the interdisciplinary contributions of authors like Volovich and Khrennikov. The emergence of more recent and specialized journals, such as P-Adic Numbers, Ultrametric Analysis, and Applications, further signals the formalization of the field as a distinct and growing area of research. Collectively, these trends suggest that p-adic theory occupies a central but also expanding role in both theoretical mathematics and mathematical physics.

3.3. Authors

Table 3 lists the ten most prolific authors in p-adic research based on 7388 articles published between 1965 and 2024.
Table 3. Top ten most prolific authors in p-adic: analysis of 7388 articles in the timespan 1965–2024.
Kim T. stands out with 253 publications and 4930 citations, followed by Khrennikov A., Simsek Y., and Kim Ds., all of whom have made substantial contributions to the field. Their h-index values and citation counts reflect a strong and sustained academic influence. To complement this view, Table 4 presents five additional prominent authors whose contributions predate or extend beyond the 1965–2024 timespan.
Table 4. The other top five most prolific authors in p-adic research (1923–2024).
Among them, Volovich leads with 13,053 citations and an h-index of 55, followed by Kochubei and Kozyrev. Notably, Zuñiga-Galindo represents Latin America, while Vladimir Vasili’s early work, dating back to 1923, marks one of the earliest documented engagements in p-adic theory. Together, these tables offer a longitudinal perspective on the key contributors, highlighting both the historical foundations and ongoing development of p-adic research.
The presence of these authors at the top of the rankings is not coincidental. Scholars such as Kim T., Khrennikov A., and Volovich I. are widely recognized for their foundational and interdisciplinary contributions. For instance, Khrennikov has played a pivotal role in bridging p-adic theory with cognitive science and quantum mechanics, while Volovich is considered a pioneer in p-adic string theory. Kim T. and Simsek Y. have published extensively in number theory and special functions, often involving q-extensions and p-adic L-functions. Their prolific output and interdisciplinary reach likely explain their high publication and citation counts.
Although there are no prior bibliometric studies that focus exclusively on p-adic theory, the prominence of these names is consistent with their central roles in shaping the field, as evidenced by their frequent appearances in key journals and conferences on non-Archimedean mathematics. This alignment reinforces the validity of the bibliometric results and underscores the intellectual structure captured by the analysis.

3.4. Countries

Figure 3 illustrates the global distribution of p-adic research across 90 countries, based on 7388 publications from 1965 to 2024 (logarithmic scale).
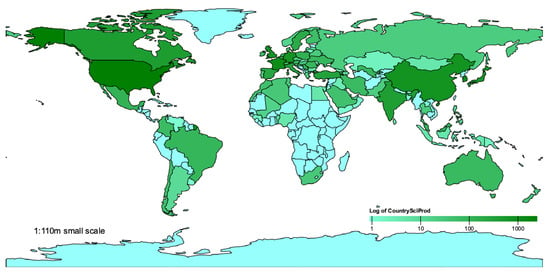
Figure 3. Global distribution (log scale) of 7388 papers on p-adic theory (1965–2024).
Table 5 presents the top 30 contributing countries, ranked by the number of publications and citations.
Table 5. Top 30 countries in p-adic research (1965–2024): Publications and citation metrics.
The United States leads with 2653 publications and 10,305 citations, reflecting its longstanding role in foundational research and international collaboration in p-adic theory. South Korea and France follow in terms of output-. Interestingly, Turkey (17.5) and Iran (15.4) exhibit the highest average citation rates, which may be attributed to a smaller but more impactful body of work, possibly centered around a few prolific authors, such as Simsek Y. and Rim S. Similarly, countries like Malaysia and Sweden also show strong citation averages despite lower output. This suggests the existence of concentrated centers of expertise or high-impact publications.
The presence of countries such as India, China, and Brazil indicates growing interest in the field across emerging scientific communities, though their average citation rates vary. The inclusion of Colombia in the top 30 reflects Latin America’s expanding participation in p-adic research, with authors like Zuñiga-Galindo W. contributing notably from the region. Overall, the data highlight a global engagement with p-adic theory, with both historically dominant countries and emerging contributors shaping the current research landscape.

3.5. Co-Authorship and Citation Analysis

Figure 4 presents co-authorship (a) and co-citation (b) networks in p-adic theory, generated using VOSviewer. In Figure 4a, the size of the nodes represents the number of publications per country, and the connecting lines indicate collaborative intensity. The United States, the United Kingdom, Germany, and France emerge as central actors with strong inter-country collaborations. Distinct clusters—such as a green cluster (U.S., India, Israel), a pink cluster (U.K., Germany), a red cluster (Brazil, Mexico), and a blue cluster (France, Italy)—reflect research partnerships and scientific alliances.
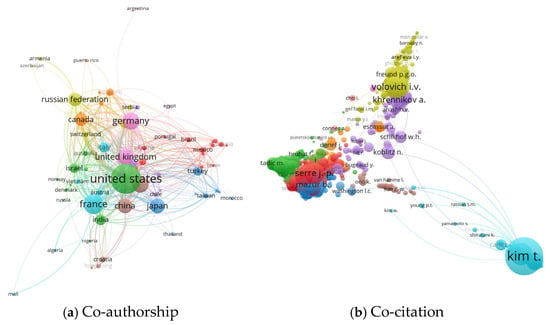
Figure 4. Co-authorship and co-citation networks in p-adic theory.
In Figure 4b, the nodes represent cited authors, with the node size proportional to the citation count. Notable authors, such as Kim T. and Serre J.-P., stand out for their high co-citation frequency. The clusters, indicated by color, group authors who are often cited together, suggesting thematic or regional specializations. For instance, the light blue cluster, led by Kim T., points to a well-defined thematic domain—likely linked to p-adic special functions and number-theoretic constructions—while the red cluster (e.g., Serre J.-P., Mazur B.) aligns with classical algebraic geometry and modular forms. The yellow cluster (Volovich I.V., Khrennikov A.) suggests a research front focused on p-adic models in physics and cognitive science.
These patterns reveal a fragmented yet intellectually rich field, where collaborations are influenced by both geographic proximity and shared thematic agendas. The prominence of well-established scholars in the co-citation network reflects the consolidation of theoretical cores, while the diversity of clusters indicates parallel developments in applied domains.
Due to the high complexity and number of nodes and edges involved, representing these networks in tabular format would result in an extensive and unintuitive dataset. Instead, the graphical visualization provides a more effective and interpretable overview of structural patterns, such as clustering, centrality, and international collaboration. This approach is widely used in bibliometric and scientometric research to reveal the intellectual and collaborative structures within a scientific domain.

3.6. Topic Identification

Table 6 summarizes the 20 topics, ranked by prevalence, identified by the LDA model that achieved the highest coherence score (0.11958), based on an analysis of 7388 articles published between 1965 and 2024. The terms listed in Table 6 (e.g., measur, structur, irreduc) are not typographical errors but rather the result of a preprocessing technique called stemming, which reduces words to their base or root forms. This is a common practice in natural language processing to group different morphological variants of a word under a common representation (e.g., “measuring”, “measured”, and “measurement” are all reduced to “measur”). In our case, we applied the Porter stemming algorithm through a text mining routine in R. This approach enhances the quality of topic modeling by mitigating sparsity caused by inflected forms of the same concept. Each topic is labeled and characterized by its prevalence and top terms.
Table 6. Summary of 20 topics identified by LDA in the p-adic theory literature (1965–2024).
The most prominent themes include group representations (t1, 6.31%, 841 articles) and locally compact topological groups (t18, 6.25%, 560 articles), indicating strong foundational interest. Topics such as the application of p-adic analysis (t5), K-theory (t19), local fields (t20), and Euler and Bernoulli polynomials (t17) also exhibit a substantial presence, with prevalence ranging from 5% to 6%. Several areas, including p-adic forms (t7), elliptic curves (t12), p-adic algebras (t6), and p-adic Galois theory (t14), reflect mid-level but focused research efforts. Lower-prevalence topics, including p-adic spectral theory (t10), p-adic functions and distributions (t2), and zeta functions (t4), represent niche or emerging lines of inquiry. Overall, the distribution highlights both well-established and specialized domains within p-adic research.
To validate the thematic coherence of the extracted topics, we examined representative papers from the dataset that exhibit high posterior probabilities for specific topics. For instance, t7 (p-adic forms) is exemplified by works such as “The P-adic Gross-Zagier formula on Shimura curves” [48], while t17 (Euler and Bernoulli polynomials) is closely reflected in “Higher order degenerate Hermite-Bernoulli polynomials arising from p-adic integrals on Zp” [49]. These connections demonstrate the alignment between the topics and influential publications in the field, supporting the interpretability of the LDA results. (The representative works cited in this paragraph are included in the reference list, although they are used solely for illustrative purposes to highlight internal consistency within the dataset analyzed).

3.7. Topic Trends

To identify topic trends, we analyzed the annual distribution of topic probabilities across all articles, as illustrated in Figure 5. The plots reflect regression models based on LDA, tracking thematic developments in p-adic theory from 1965 to 2024. The X-axis represents publication years, and the Y-axis shows the average topic proportion per year. The trends are color-coded: increasing (red), decreasing (blue), and stable (black).
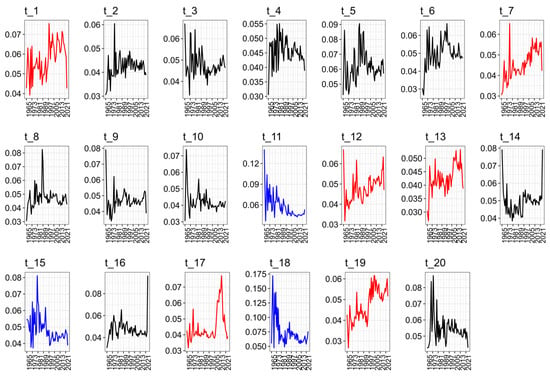
Figure 5. Trends of topic diagrams. Each line represents the estimated publication probability of a topic over time. The colors indicate the trend direction: red for increasing topics, blue for decreasing topics, and black for relatively stable topics.
Increasing Trends. Topics such as t1 (group representations), t7 (p-adic forms), t12 (elliptic curves), t13 (polynomials), t17 (Euler and Bernoulli polynomials), and t19 (K-theory) show upward trends, indicating growing academic interest. Notably, t12 maintains a stable but slightly rising trajectory, highlighting its continued relevance.
Decreasing Trends. Topics such as t11 (p-adic codes over rings), t15 (power series), and t18 (locally compact topological groups) exhibit a decline in publication probability over time. For example, t11 experienced intermittent peaks before tapering off, possibly reflecting a shift toward newer research directions.
Stable Trends. Topics with no significant trend include t2 (p-adic functions and p-adic distributions), t3 (p-adic sequences), t4 (zeta functions), t5 (application of p-adic analysis), t6 (p-adic algebras), t8 (p-adic integral equations), t9 (p-adic operators), t10 (p-adic spectral theory), t14 (p-adic Galois theory), t16 (p-adic dynamic systems), and t20 (local fields). These show consistent interest across decades, with some (e.g., t3: p-adic sequences, and t4: zeta functions) exhibiting minor fluctuations. Their stability suggests sustained scholarly engagement and foundational importance in p-adic research.

3.8. Topic Distributions Within Publication Sources

Figure 6 displays heatmaps of topic proportions across the top 30 journals (Figure 6a) and publication years (Figure 6b) in p-adic research. Both visualizations are organized using hierarchical clustering to reveal patterns in the distribution of topics.
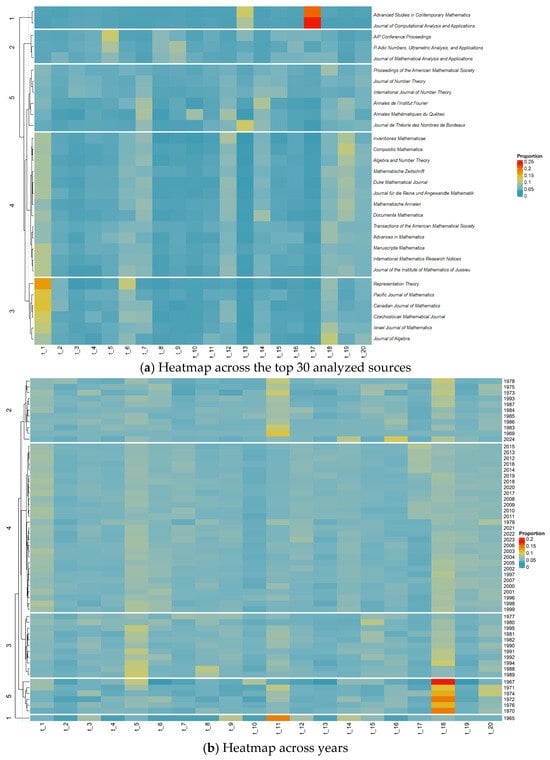
Figure 6. Heatmap depicting topic proportions across sources and years.
In Figure 6a, warmer colors (orange and red) indicate higher topic concentration within specific journals. For example, Advanced Studies in Contemporary Mathematics and the Journal of Computational Analysis and Applications demonstrate a strong focus on t17 (Euler and Bernoulli polynomials). In contrast, journals like the Journal of Number Theory and Proceedings of the American Mathematical Society exhibit more balanced topic distributions. t1 (group representations) is particularly prominent in journals such as the Journal of Algebra and the Israel Journal of Mathematics. Clusters 1 and 4 reflect journals with strong thematic specialization, while Clusters 3 and 5 show broader topic coverage.
In Figure 6b, the topic distributions are shown across years. The year 1965 (Cluster 1) stands out because of its high concentration in t11 (p-adic codes over rings). Clusters 2 and 5 include years with a strong focus on t18 (locally compact topological groups). Years from 1980 to 1982 exhibit a more even distribution across topics. Intense color patterns reflect historical moments of concentrated interest in specific areas, suggesting shifts in thematic focus and evolving research priorities over time.

4. Discussion

This study employed LDA and bibliometric analysis to examine the thematic structure, geographic distribution, and scholarly evolution of p-adic theory. The results offer a comprehensive overview of key research clusters, highlight emerging trends, and reveal collaboration patterns that shape the field’s development.
The application of LDA has revealed dynamic shifts in research interests over time. Increasing attention to topics such as p-adic forms (t7), elliptic curves (t12), and polynomials (t13) points to emerging research frontiers, potentially linked to recent advances and interdisciplinary applications in areas such as quantum computing and cryptography. In contrast, the declining prominence of topics like p-adic codes over rings (t11), power series (t15), and locally compact topological groups (t18) may reflect the resolution of foundational questions or a redirection of focus toward newer challenges. Broader academic and funding priorities could also influence these shifts.
To support continued growth in p-adic theory, it is essential to encourage collaboration across disciplines. Partnerships between mathematicians, physicists, and computer scientists can foster novel applications and innovation, a pattern seen in other scientific domains [50,51]. Equally important is the development of open-access repositories and advanced analytical tools to facilitate broader access to data and reproducibility of findings. While the LDA offers a robust quantitative framework, its insights are best interpreted in conjunction with expert judgment to ensure conceptual clarity and contextual depth.
Geographical analysis highlights the global nature of p-adic research and the importance of international collaboration. Differences in national research output suggest opportunities to strengthen exchange through international funding schemes, joint projects, and academic mobility. As emphasized by [52], transnational research networks enhance scientific capacity and innovation, especially in mathematically intensive fields.
The temporal heatmap analysis uncovered notable patterns of topic prevalence across clusters of years. For example, Cluster 1 (1965) shows a distinct concentration in p-adic codes over rings (t11), while Cluster 5 (1967–1970) reflects specialization in locally compact topological groups (t18). Cluster 2 (spanning 1973–1978, 1983–1987, 1993, and 2024) presents mixed but recurring attention to both topics. Cluster 3 further reinforces the significance of t18 and application-oriented topics, such as t5 (application of p-adic analysis). These patterns reflect how thematic focus evolves in response to scientific progress and community interest.
Another key point is the influence of authors from the Russian mathematical school. While their contributions are significant, the limited availability of citation data, particularly in widely used platforms such as Google Scholar, complicates bibliometric evaluation. This suggests a need for more inclusive and comprehensive indexing practices. Furthermore, the Journal of Pseudo-Differential Operators and Applications, established in 2010 by Birkhäuser (now part of Springer Nature), has emerged as a relevant outlet for p-adic research. Its broad thematic scope, including operator theory, algebra, and combinatorics, makes it particularly suitable for hosting research in this domain and supports the diffusion of specialized knowledge.
These findings align with trends observed in other mathematical domains, where emerging research areas often coincide with interdisciplinary applications and technological advances. For instance, the growing emphasis on topics like p-adic forms and elliptic curves resonates with similar thematic expansions in number theory, cryptography, and quantum information. Moreover, the increasing visibility of dedicated publication outlets, such as the Journal of Pseudo-Differential Operators and Applications, reflects a broader institutional support for specialized mathematical research. Such parallels help contextualize the development of p-adic theory within wider scientific movements and underscore the importance of continued cross-disciplinary engagement.
Despite its contributions, this study has limitations. It relies primarily on Scopus-indexed documents, which may exclude relevant non-English publications or regionally indexed journals. Additionally, the interpretation of LDA-generated topics involves subjective decisions in labeling and grouping. Furthermore, the increase in the number of publications observed, particularly after 2015, may not solely reflect internal developments in p-adic theory but may also align with a broader global trend in scientific output, supported by expanded research funding, open-access publishing platforms, and international collaborations. Keyword-related limitations must also be acknowledged: inconsistencies in author-defined keywords and the lack of standardization in mathematical terminology can affect topic granularity and coherence. Regarding methodological considerations, while the Bibliometrix package in R provides transparent and reproducible tools, alternative pipelines may yield variations depending on the preprocessing steps and parameter selection. Future research may address these constraints by incorporating cross-database triangulation and exploring advanced topic modeling techniques such as BERTopic, Top2Vec, or dynamic topic modeling, which leverage semantic embeddings and temporal evolution to improve topic interpretability and responsiveness to conceptual shifts in the literature.
In summary, this discussion highlights the importance of embracing interdisciplinary collaboration, expanding access to scholarly data, and fostering global research partnerships to sustain and advance p-adic theory. Future studies may consider applying dynamic topic modeling or cross-database analyses to further explore the evolution and interconnection of themes over time.

5. Conclusions

This study provides a comprehensive overview of the intellectual and thematic development of p-adic theory research over nearly six decades (1965–2024), drawing on 7388 publications indexed in Scopus. By applying LDA and bibliometric analysis, we identified 20 distinct topics and examined their temporal evolution, geographic distribution, and presence across top journals. This approach offers valuable insights into the structure, dynamics, and collaborative nature of the field.
The results reveal a diverse and evolving landscape. Foundational topics, such as Group representations (t1) and locally compact topological groups (t18), have historically played a central role. At the same time, areas like p-adic forms (t7), elliptic curves (t12), polynomials (t13), and K-theory (t19) have shown increasing prominence in recent years. Conversely, decreasing trends in topics such as p-adic codes over rings (t11) and power series (t15) may suggest a redirection of focus or the conclusion of earlier research trajectories. Stable trends in topics like zeta functions (t4), p-adic Galois theory (t14), and p-adic algebras (t6) indicate their enduring significance.
The analysis also highlights a broad international engagement in p-adic research, with leading contributions from the United States, Europe, and Asia. Thematic mapping across journals reveals varying degrees of specialization, with some journals, such as Advanced Studies in Contemporary Mathematics, showing concentrated thematic focus, and others, like the Journal of Number Theory, presenting a broader topical range.
The integration of LDA-based modeling with bibliometric techniques has proven effective for identifying thematic patterns, tracking historical trends, and highlighting underexplored areas. These findings have implications for scholars, research institutions, and funding bodies by offering a data-driven foundation for strategic decisions, interdisciplinary collaboration, and support for emerging areas. Future research may build on these results by incorporating additional databases, dynamic topic modeling, or author-level network analyses further to enrich our understanding of the field’s evolution.
These findings provide actionable insights for researchers, journal editors, and funding agencies. By identifying thematic trends and collaborative dynamics, this study offers a roadmap for future investigations and strategic publishing. The approach can also be applied to other mathematical domains, promoting evidence-based decision-making and supporting emerging areas through targeted collaboration and resource allocation.

Author Contributions

Conceptualization, H.L. and I.G.; investigation, I.G. and A.T.; methodology, H.L. and J.D.L.H.; project administration, H.L., I.G. and B.L.; supervision, H.L.; visualization, H.L. and B.L.; writing—original draft, B.L.; writing—review and editing, H.L. and J.D.L.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding. However, article processing charges were covered with institutional support from Universidad del Norte.

Data Availability Statement

The dataset used in this study was retrieved from the Scopus database and is publicly available at https://drive.google.com/file/d/1of0XsZY96xEU9ZUaO_cp5kbA4uRxi4Xs/view?usp=sharing. Researchers interested in replicating the analysis or exploring the data further may access it through the provided repository (accessed on 21 June 2025).

Acknowledgments

We acknowledge the institutional support of Universidad del Norte, Universidad de Sucre, Universidad del Magdalena, and Old Dominion University.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Albeverio, S.; Belopolskaya, Y. Stochastic processes in Q_p associated with systems of nonlinear PIDEs. p-Adic Numbers Ultrametric Anal. Appl. 2009, 1, 105–117. [Google Scholar] [CrossRef]
  2. Albeverio, S.; Khrennikov, A.; Kloeden, P. Memory retrieval as a p-adic dynamical system. Biosystems 1999, 49, 105–115. [Google Scholar] [CrossRef]
  3. Avetisov, V.A.; Bikulov, A.K.; Zubarev, A.P. First passage time distribution and the number of returns for ultrametric random walks. J. Phys. A Math. Theor. 2009, 42, 85003. [Google Scholar] [CrossRef][Green Version]
  4. Avetisov, V.A.; Bikulov, A.K.; Osipov, V.A. p-adic description of characteristic relaxation in complex systems. J. Phys. A Math. Gen. 2003, 36, 4239–4246. [Google Scholar] [CrossRef]
  5. Caruso, X. Computations with p-adic numbers. Les Cours Du CIRM 2017, 5, 1–75. [Google Scholar] [CrossRef]
  6. Dragovich, B.; Misic, N. p-adic hierarchical properties of the genetic code. Biosystems 2019, 185, 104017. [Google Scholar] [CrossRef]
  7. Fenimore, P.W.; Frauenfelder, H.; McMahon, B.H. Myoglobin, the hydrogen atom of biology and paradigm of complexity. Proc. Natl. Acad. Sci. USA 2003, 100, 8615–8617. [Google Scholar]
  8. Kozyrev, S.V. Ultrametric dynamics as a model of interbasin kinetics. J. Comput. Math. Anal. 2006, 41, 38–48. [Google Scholar]
  9. Oleschko, K.; Khrennikov, A.Y. Applications of p-adics to geophysics: Linear and quasilinear diffusion of water-in-oil and oil-in-water emulsions. Theor. Math. Phys. 2017, 190, 154–163. [Google Scholar] [CrossRef]
  10. Rodino, L.; Wong, M.W.; Zhu, H. Pseudo-Differential Operators: Analysis, Applications and Computations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
  11. Su, W.; Qiu, H. p-Adic calculus and its applications to fractal analysis and medical science. Facta Univ. Ser. Electron. Energetics 2008, 21, 339–347. [Google Scholar] [CrossRef]
  12. Vladimirov, V.S.; Volovich, I.V.; Zelenov, E.I. Spectral theory in p-adic quantum mechanics and representation theory. Sov. Math. Dokl. 1990, 41, 40–44. [Google Scholar] [CrossRef]
  13. Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
  14. Volovich, I.V. p-Adic string. Class. Quantum Gravity 1987, 4, L83–L87. [Google Scholar] [CrossRef]
  15. Volovich, I.V. Number theory as the ultimate physical theory. P-Adic Numbers Ultrametric Anal. Appl. 2010, 2, 77–87. [Google Scholar] [CrossRef]
  16. Vladimirov, V.S. Generalized functions over the field of p-adic numbers. Russ. Math. Surv. 1988, 43, 19–64. [Google Scholar] [CrossRef]
  17. Vladimirov, V.S.; Volovich, I.V. p-Adic quantum mechanics. Commun. Math. Phys. 1989, 123, 659–676. [Google Scholar] [CrossRef]
  18. Khrennikov, A.Y. Human subconscious as a p-adic dynamical system. J. Theor. Biol. 1998, 193, 179–196. [Google Scholar] [CrossRef]
  19. Khrennikov, A.Y.; Kochubei, A.N. p-Adic Analogue of the Porous Medium Equation. J. Fourier Anal. Appl. 2018, 24, 1401–1424. [Google Scholar] [CrossRef]
  20. Khrennikov, A.; Oleschko, K. An Ultrametric Random Walk Model for Disease Spread Taking into Account Social Clustering of the Population. Entropy 2020, 22, 931. [Google Scholar] [CrossRef]
  21. Khrennikov, A.; Oleschko, K.; López, M.C. Modeling Fluids Dynamics with Master Equations in Ultrametric Spaces Representing the Treelike Structure of Capillary Networks. Entropy 2016, 18, 249. [Google Scholar] [CrossRef]
  22. Aniello, P.; Mancini, S.; Parisi, V. A p-Adic Model of Quantum States and the p-Adic Qubit. Entropy 2023, 25, 86. [Google Scholar] [CrossRef] [PubMed]
  23. Avetisov, V.A.; Bikulov, A.K. Ultrametricity of the fluctuation dynamic mobility of protein molecules. Proc. Steklov Inst. Math. 2009, 265, 75–81. [Google Scholar] [CrossRef]
  24. Avetisov, V.A.; Bikulov, A.K.; Osipov, V.A. p-adic models of ultrametric diffusion in the conformational dynamics of macromolecules. Proc. Steklov Inst. Math. 2004, 245, 48–57. [Google Scholar]
  25. Chacón-Cortes, L.F.; García, I.G.; Torresblanca-Badillo, A.; Vargas, A. Finite time blow-up for a p-adic nonlocal semilinear ultradiffusion equation. J. Math. Anal. Appl. 2021, 494, 124599. [Google Scholar] [CrossRef]
  26. Gutiérrez-García, I.; Torresblanca-Badillo, A. Probability density functions and the dynamics of complex systems associated with some classes of non-archimedean pseudo-differential operators. J. Pseudo-Differ. Oper. Appl. 2021, 12, 12. [Google Scholar] [CrossRef]
  27. García, I.G.; Torresblanca-Badillo, A. Strong Markov processes and negative definite functions associated with non-Archimedean elliptic pseudo-differential operators. J. Pseudo-Differ. Oper. Appl. 2020, 11, 345–362. [Google Scholar] [CrossRef]
  28. García, I.G.; Torresblanca-Badillo, A. Some classes of non-archimedean pseudo-differential operators related to Bessel potentials. J. Pseudo-Differ. Oper. Appl. 2020, 11, 1111–1137. [Google Scholar] [CrossRef]
  29. Khrennikov, A.Y.; Kozyrev, S.V. Wavelets on ultrametric spaces. Appl. Comput. Harmon. Anal. 2005, 19, 61–76. [Google Scholar] [CrossRef]
  30. Zelenov, E.I. Quantum approximation theorem. P-Adic Numbers Ultrametric Anal. Appl. 2009, 1, 88–90. [Google Scholar] [CrossRef]
  31. Zúñiga-Galindo, W.A. Parabolic equations and Markov processes over p-adic fields. Potential Anal. 2008, 28, 185–200. [Google Scholar] [CrossRef]
  32. Zúñiga-Galindo, W.A. Pseudodifferential Equations Over Non-Archimedean Spaces; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
  33. Kochubei, A.N. Parabolic equations over the field of p-adic numbers. Izv. Math. 1991, 39, 1263–1280. [Google Scholar] [CrossRef]
  34. Kochubei, A.N. A Schrödinger-type equation over the field of p-adic numbers. J. Math. Phys. 1993, 34, 3420–3428. [Google Scholar] [CrossRef]
  35. Kochubei, A.N. Fundamental solutions of pseudodifferential equations associated with p-adic quadratic forms. Izv. Math. 1998, 62, 1169–1188. [Google Scholar] [CrossRef]
  36. Kochubei, A.N. Pseudo-Differential Equations and Stochastic over Non-Archimedean Fields; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
  37. Dragovich, B.; Khrennikov, A.Y.; Kozyrev, S.V.; Volovich, I.V. On p-adic mathematical physics. p-Adic Numbers Ultrametric Anal. Appl. 2009, 1, 1–17. [Google Scholar] [CrossRef]
  38. Dragovich, B.; Khrennikov, A.Y.; Kozyrev, S.V.; Volovich, I.V.; Zelenov, E.I. p-Adic mathematical physics: The first 30 years. p-Adic Numbers Ultrametric Anal. Appl. 2017, 9, 87–121. [Google Scholar] [CrossRef]
  39. Kozyrev, S.V. p-Adic Pseudodifferential Operators and p-Adic Wavelets. Theor. Math. Phys. 2004, 138, 322–332. [Google Scholar] [CrossRef]
  40. Kozyrev, S.V.; Osipov, V.A.; Avetisov, V.A. Nondegenerate ultrametric diffusion. J. Math. Phys. 2005, 46, 63302. [Google Scholar] [CrossRef]
  41. Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
  42. Aria, M.; Cuccurullo, C. bibliometrix: An R-tool for comprehensive science mapping analysis. J. Informetr. 2017, 11, 959–975. [Google Scholar] [CrossRef]
  43. Donthu, N.; Kumar, S.; Mukherjee, D.; Pandey, N.; Lim, W.M. How to conduct a bibliometric analysis: An overview and guidelines. J. Bus. Res. 2021, 133, 285–296. [Google Scholar] [CrossRef]
  44. De la Hoz-M, J.; Fernández-Gómez, M.J.; Mendes, S. LDAShiny: An R Package for Exploratory Review of Scientific Literature Based on a Bayesian Probabilistic Model and Machine Learning Tools. Mathematics 2021, 9, 1671. [Google Scholar] [CrossRef]
  45. Röder, M.; Both, A.; Hinneburg, A. Exploring the Space of Topic Coherence Measures. In Proceedings of the Eighth ACM International Conference on Web Search and Data Mining, Shanghai, China, 2–6 February 2015; pp. 399–408. [Google Scholar]
  46. Lewis, S.C.; Zamith, R.; Hermida, A. Content Analysis in an Era of Big Data: A Hybrid Approach to Computational and Manual Methods. J. Broadcast. Electron. Media 2013, 57, 34–52. [Google Scholar] [CrossRef]
  47. Xiong, H.; Cheng, Y.; Zhao, W.; Liu, J. Analyzing scientific research topics in manufacturing field using a topic model. Comput. Ind. Eng. 2019, 135, 333–347. [Google Scholar] [CrossRef]
  48. Disegni, D. The p-adic Gross–Zagier formula on Shimura curves, II: Nonsplit primes. J. Inst. Math. Jussieu 2023, 22, 2199–2240. [Google Scholar] [CrossRef]
  49. Khan, W.A.; Haroon, H. Higher order degenerate Hermite-Bernoulli polynomials arising from p-adic integrals on Zp. Iran. J. Math. Sci. Inform. 2022, 17, 171–189. [Google Scholar]
  50. Coccia, M. The evolution of scientific disciplines in applied sciences: Dynamics and empirical properties of experimental physics. Scientometrics 2020, 124, 451–487. [Google Scholar] [CrossRef]
  51. Smye, S.W.; Frangi, A.F. Interdisciplinary research: Shaping the healthcare of the future. Future Healthc. J. 2021, 8, e218–e223. [Google Scholar] [CrossRef]
  52. Dusdal, J.; Powell, J.J. Benefits, motivations, and challenges of international collaborative research: A sociology of science case study. Sci. Public Policy 2021, 48, 235–245. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams
Previous
Preface to the Special Issue on “Probability, Statistics and Random Processes”
Next