A Bibliometric and Topic Modeling Analysis of the p-Adic Theory Literature Using Latent Dirichlet Allocation
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Bibliometric and Topic Modeling Analysis
3. Results
3.1. General Information
3.2. Sources
3.3. Authors
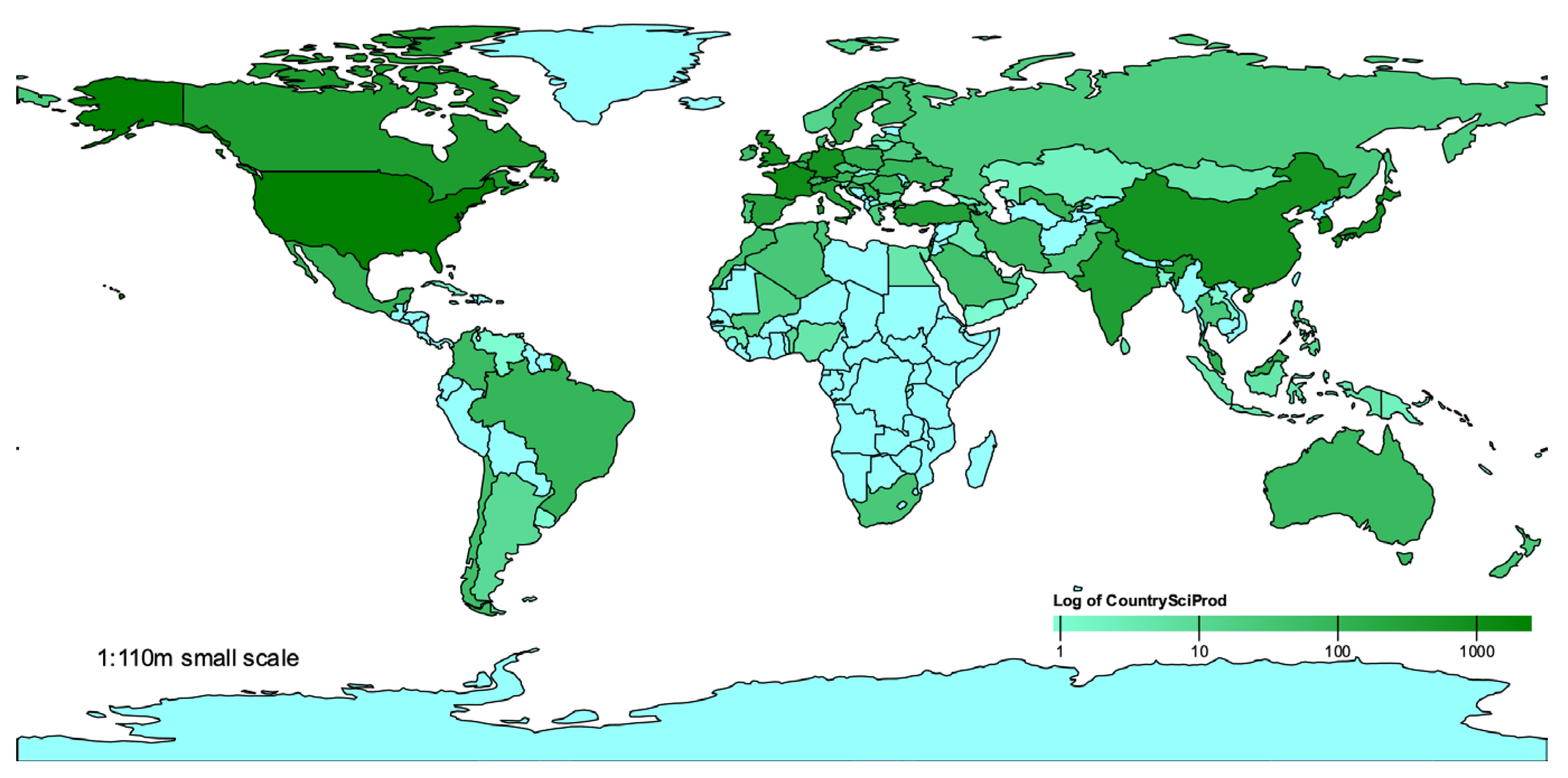
3.4. Countries
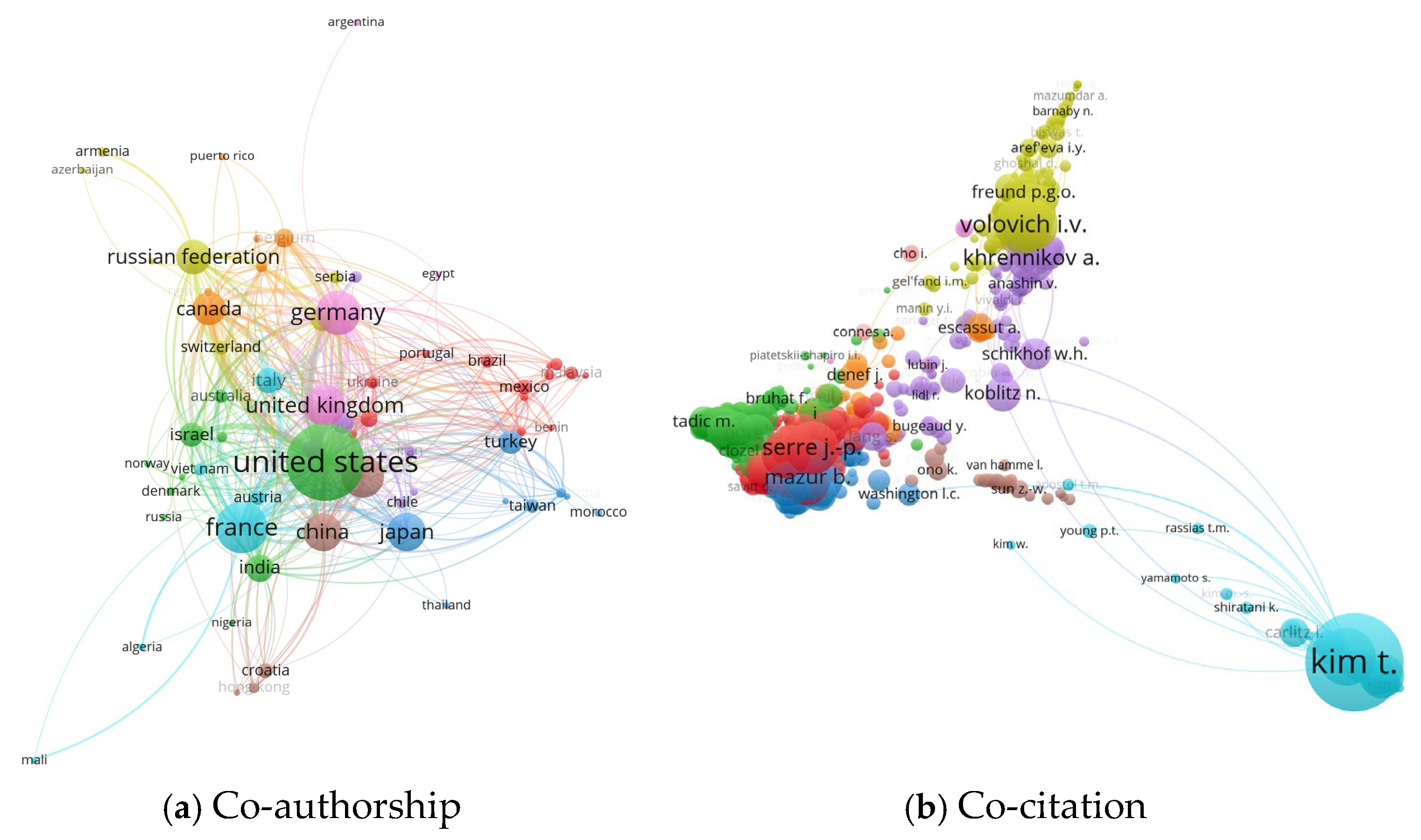
3.5. Co-Authorship and Citation Analysis
3.6. Topic Identification
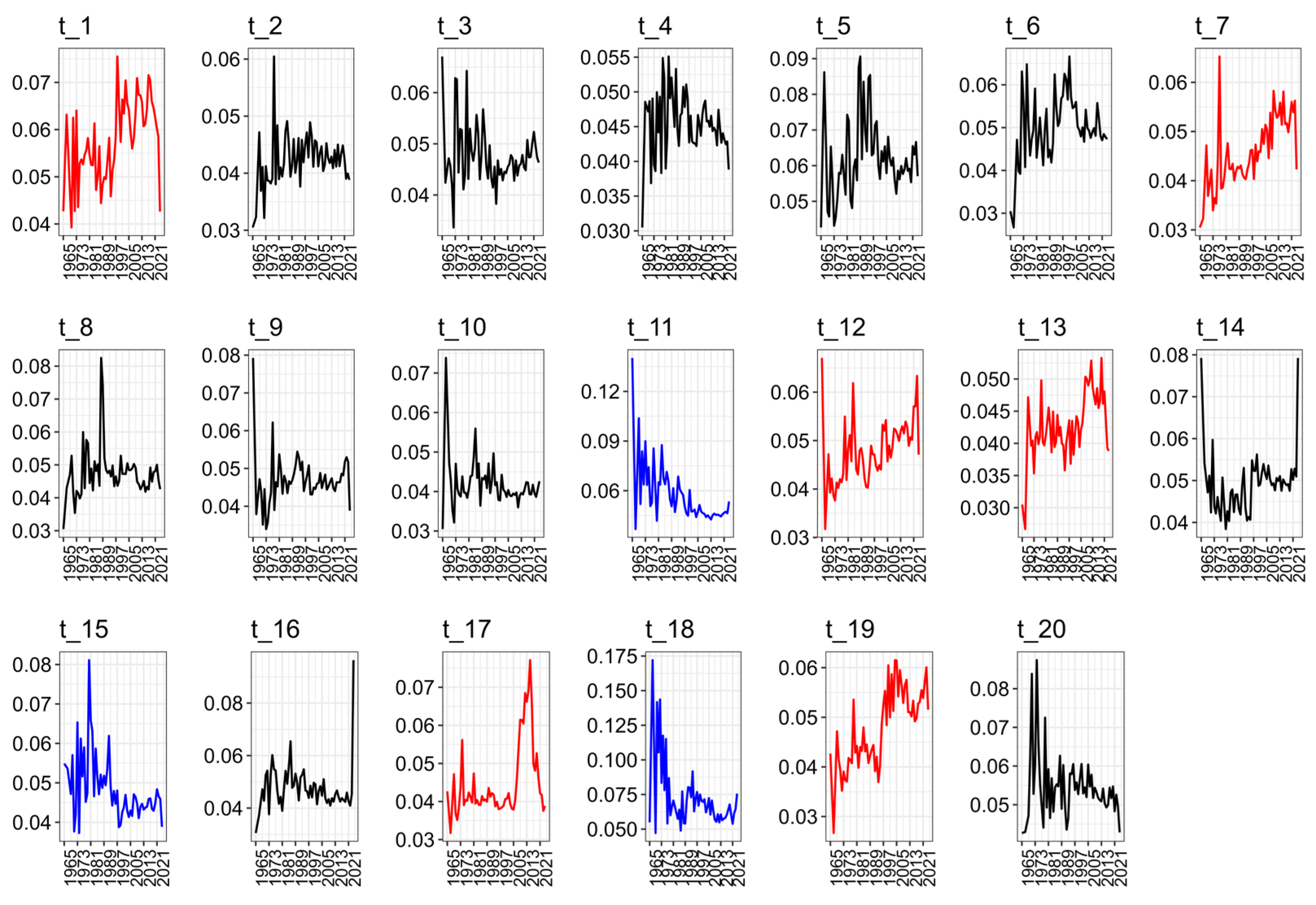
3.7. Topic Trends
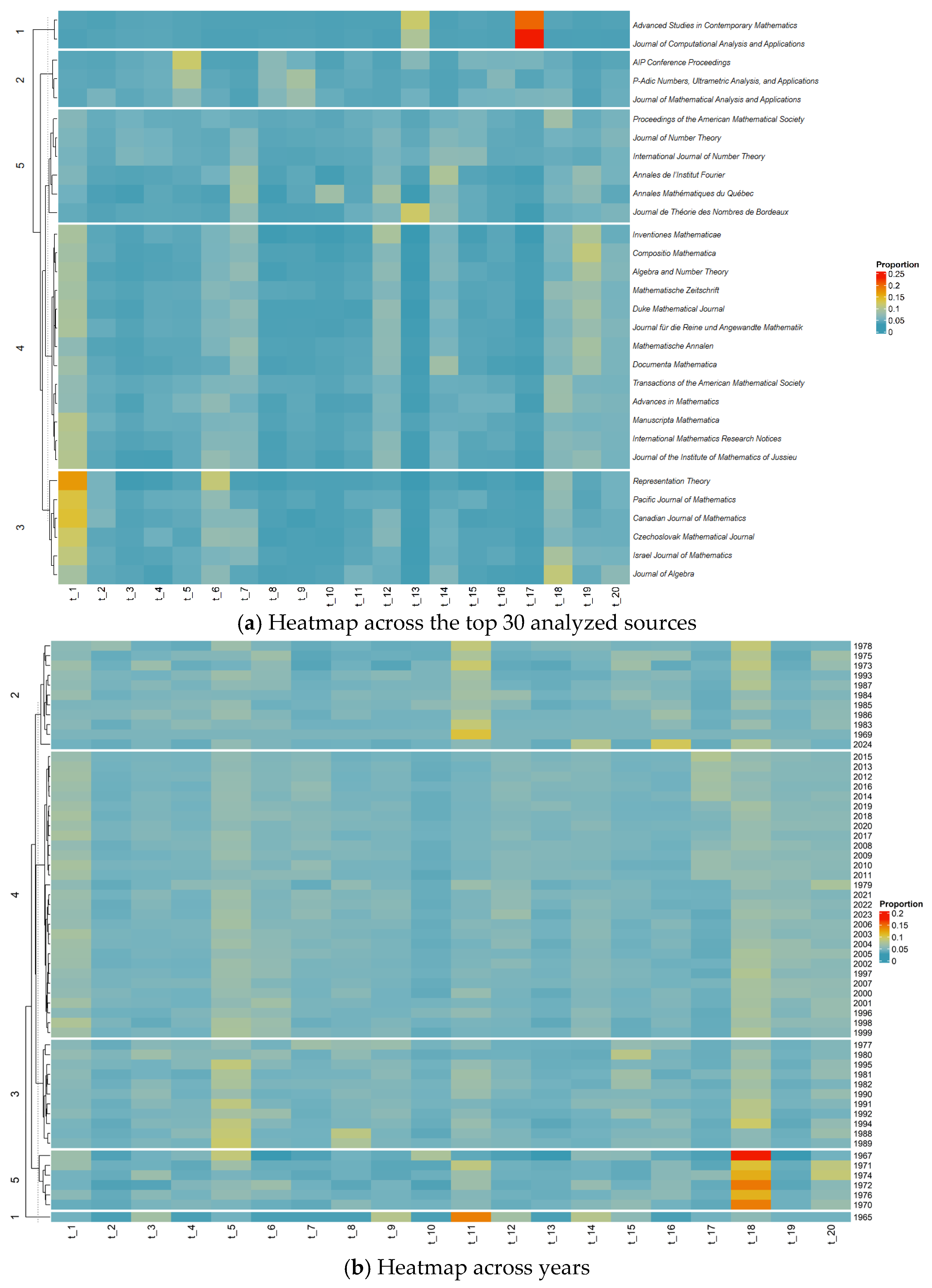
3.8. Topic Distributions Within Publication Sources
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Albeverio, S.; Belopolskaya, Y. Stochastic processes in Q_p associated with systems of nonlinear PIDEs. p-Adic Numbers Ultrametric Anal. Appl. 2009, 1, 105–117. [Google Scholar] [CrossRef]
- Albeverio, S.; Khrennikov, A.; Kloeden, P. Memory retrieval as a p-adic dynamical system. Biosystems 1999, 49, 105–115. [Google Scholar] [CrossRef]
- Avetisov, V.A.; Bikulov, A.K.; Zubarev, A.P. First passage time distribution and the number of returns for ultrametric random walks. J. Phys. A Math. Theor. 2009, 42, 85003. [Google Scholar] [CrossRef][Green Version]
- Avetisov, V.A.; Bikulov, A.K.; Osipov, V.A. p-adic description of characteristic relaxation in complex systems. J. Phys. A Math. Gen. 2003, 36, 4239–4246. [Google Scholar] [CrossRef]
- Caruso, X. Computations with p-adic numbers. Les Cours Du CIRM 2017, 5, 1–75. [Google Scholar] [CrossRef]
- Dragovich, B.; Misic, N. p-adic hierarchical properties of the genetic code. Biosystems 2019, 185, 104017. [Google Scholar] [CrossRef]
- Fenimore, P.W.; Frauenfelder, H.; McMahon, B.H. Myoglobin, the hydrogen atom of biology and paradigm of complexity. Proc. Natl. Acad. Sci. USA 2003, 100, 8615–8617. [Google Scholar]
- Kozyrev, S.V. Ultrametric dynamics as a model of interbasin kinetics. J. Comput. Math. Anal. 2006, 41, 38–48. [Google Scholar]
- Oleschko, K.; Khrennikov, A.Y. Applications of p-adics to geophysics: Linear and quasilinear diffusion of water-in-oil and oil-in-water emulsions. Theor. Math. Phys. 2017, 190, 154–163. [Google Scholar] [CrossRef]
- Rodino, L.; Wong, M.W.; Zhu, H. Pseudo-Differential Operators: Analysis, Applications and Computations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Su, W.; Qiu, H. p-Adic calculus and its applications to fractal analysis and medical science. Facta Univ. Ser. Electron. Energetics 2008, 21, 339–347. [Google Scholar] [CrossRef]
- Vladimirov, V.S.; Volovich, I.V.; Zelenov, E.I. Spectral theory in p-adic quantum mechanics and representation theory. Sov. Math. Dokl. 1990, 41, 40–44. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Volovich, I.V. p-Adic string. Class. Quantum Gravity 1987, 4, L83–L87. [Google Scholar] [CrossRef]
- Volovich, I.V. Number theory as the ultimate physical theory. P-Adic Numbers Ultrametric Anal. Appl. 2010, 2, 77–87. [Google Scholar] [CrossRef]
- Vladimirov, V.S. Generalized functions over the field of p-adic numbers. Russ. Math. Surv. 1988, 43, 19–64. [Google Scholar] [CrossRef]
- Vladimirov, V.S.; Volovich, I.V. p-Adic quantum mechanics. Commun. Math. Phys. 1989, 123, 659–676. [Google Scholar] [CrossRef]
- Khrennikov, A.Y. Human subconscious as a p-adic dynamical system. J. Theor. Biol. 1998, 193, 179–196. [Google Scholar] [CrossRef]
- Khrennikov, A.Y.; Kochubei, A.N. p-Adic Analogue of the Porous Medium Equation. J. Fourier Anal. Appl. 2018, 24, 1401–1424. [Google Scholar] [CrossRef]
- Khrennikov, A.; Oleschko, K. An Ultrametric Random Walk Model for Disease Spread Taking into Account Social Clustering of the Population. Entropy 2020, 22, 931. [Google Scholar] [CrossRef]
- Khrennikov, A.; Oleschko, K.; López, M.C. Modeling Fluids Dynamics with Master Equations in Ultrametric Spaces Representing the Treelike Structure of Capillary Networks. Entropy 2016, 18, 249. [Google Scholar] [CrossRef]
- Aniello, P.; Mancini, S.; Parisi, V. A p-Adic Model of Quantum States and the p-Adic Qubit. Entropy 2023, 25, 86. [Google Scholar] [CrossRef] [PubMed]
- Avetisov, V.A.; Bikulov, A.K. Ultrametricity of the fluctuation dynamic mobility of protein molecules. Proc. Steklov Inst. Math. 2009, 265, 75–81. [Google Scholar] [CrossRef]
- Avetisov, V.A.; Bikulov, A.K.; Osipov, V.A. p-adic models of ultrametric diffusion in the conformational dynamics of macromolecules. Proc. Steklov Inst. Math. 2004, 245, 48–57. [Google Scholar]
- Chacón-Cortes, L.F.; García, I.G.; Torresblanca-Badillo, A.; Vargas, A. Finite time blow-up for a p-adic nonlocal semilinear ultradiffusion equation. J. Math. Anal. Appl. 2021, 494, 124599. [Google Scholar] [CrossRef]
- Gutiérrez-García, I.; Torresblanca-Badillo, A. Probability density functions and the dynamics of complex systems associated with some classes of non-archimedean pseudo-differential operators. J. Pseudo-Differ. Oper. Appl. 2021, 12, 12. [Google Scholar] [CrossRef]
- García, I.G.; Torresblanca-Badillo, A. Strong Markov processes and negative definite functions associated with non-Archimedean elliptic pseudo-differential operators. J. Pseudo-Differ. Oper. Appl. 2020, 11, 345–362. [Google Scholar] [CrossRef]
- García, I.G.; Torresblanca-Badillo, A. Some classes of non-archimedean pseudo-differential operators related to Bessel potentials. J. Pseudo-Differ. Oper. Appl. 2020, 11, 1111–1137. [Google Scholar] [CrossRef]
- Khrennikov, A.Y.; Kozyrev, S.V. Wavelets on ultrametric spaces. Appl. Comput. Harmon. Anal. 2005, 19, 61–76. [Google Scholar] [CrossRef]
- Zelenov, E.I. Quantum approximation theorem. P-Adic Numbers Ultrametric Anal. Appl. 2009, 1, 88–90. [Google Scholar] [CrossRef]
- Zúñiga-Galindo, W.A. Parabolic equations and Markov processes over p-adic fields. Potential Anal. 2008, 28, 185–200. [Google Scholar] [CrossRef]
- Zúñiga-Galindo, W.A. Pseudodifferential Equations Over Non-Archimedean Spaces; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Kochubei, A.N. Parabolic equations over the field of p-adic numbers. Izv. Math. 1991, 39, 1263–1280. [Google Scholar] [CrossRef]
- Kochubei, A.N. A Schrödinger-type equation over the field of p-adic numbers. J. Math. Phys. 1993, 34, 3420–3428. [Google Scholar] [CrossRef]
- Kochubei, A.N. Fundamental solutions of pseudodifferential equations associated with p-adic quadratic forms. Izv. Math. 1998, 62, 1169–1188. [Google Scholar] [CrossRef]
- Kochubei, A.N. Pseudo-Differential Equations and Stochastic over Non-Archimedean Fields; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Dragovich, B.; Khrennikov, A.Y.; Kozyrev, S.V.; Volovich, I.V. On p-adic mathematical physics. p-Adic Numbers Ultrametric Anal. Appl. 2009, 1, 1–17. [Google Scholar] [CrossRef]
- Dragovich, B.; Khrennikov, A.Y.; Kozyrev, S.V.; Volovich, I.V.; Zelenov, E.I. p-Adic mathematical physics: The first 30 years. p-Adic Numbers Ultrametric Anal. Appl. 2017, 9, 87–121. [Google Scholar] [CrossRef]
- Kozyrev, S.V. p-Adic Pseudodifferential Operators and p-Adic Wavelets. Theor. Math. Phys. 2004, 138, 322–332. [Google Scholar] [CrossRef]
- Kozyrev, S.V.; Osipov, V.A.; Avetisov, V.A. Nondegenerate ultrametric diffusion. J. Math. Phys. 2005, 46, 63302. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
- Aria, M.; Cuccurullo, C. bibliometrix: An R-tool for comprehensive science mapping analysis. J. Informetr. 2017, 11, 959–975. [Google Scholar] [CrossRef]
- Donthu, N.; Kumar, S.; Mukherjee, D.; Pandey, N.; Lim, W.M. How to conduct a bibliometric analysis: An overview and guidelines. J. Bus. Res. 2021, 133, 285–296. [Google Scholar] [CrossRef]
- De la Hoz-M, J.; Fernández-Gómez, M.J.; Mendes, S. LDAShiny: An R Package for Exploratory Review of Scientific Literature Based on a Bayesian Probabilistic Model and Machine Learning Tools. Mathematics 2021, 9, 1671. [Google Scholar] [CrossRef]
- Röder, M.; Both, A.; Hinneburg, A. Exploring the Space of Topic Coherence Measures. In Proceedings of the Eighth ACM International Conference on Web Search and Data Mining, Shanghai, China, 2–6 February 2015; pp. 399–408. [Google Scholar]
- Lewis, S.C.; Zamith, R.; Hermida, A. Content Analysis in an Era of Big Data: A Hybrid Approach to Computational and Manual Methods. J. Broadcast. Electron. Media 2013, 57, 34–52. [Google Scholar] [CrossRef]
- Xiong, H.; Cheng, Y.; Zhao, W.; Liu, J. Analyzing scientific research topics in manufacturing field using a topic model. Comput. Ind. Eng. 2019, 135, 333–347. [Google Scholar] [CrossRef]
- Disegni, D. The p-adic Gross–Zagier formula on Shimura curves, II: Nonsplit primes. J. Inst. Math. Jussieu 2023, 22, 2199–2240. [Google Scholar] [CrossRef]
- Khan, W.A.; Haroon, H. Higher order degenerate Hermite-Bernoulli polynomials arising from p-adic integrals on Zp. Iran. J. Math. Sci. Inform. 2022, 17, 171–189. [Google Scholar]
- Coccia, M. The evolution of scientific disciplines in applied sciences: Dynamics and empirical properties of experimental physics. Scientometrics 2020, 124, 451–487. [Google Scholar] [CrossRef]
- Smye, S.W.; Frangi, A.F. Interdisciplinary research: Shaping the healthcare of the future. Future Healthc. J. 2021, 8, e218–e223. [Google Scholar] [CrossRef]
- Dusdal, J.; Powell, J.J. Benefits, motivations, and challenges of international collaborative research: A sociology of science case study. Sci. Public Policy 2021, 48, 235–245. [Google Scholar] [CrossRef]
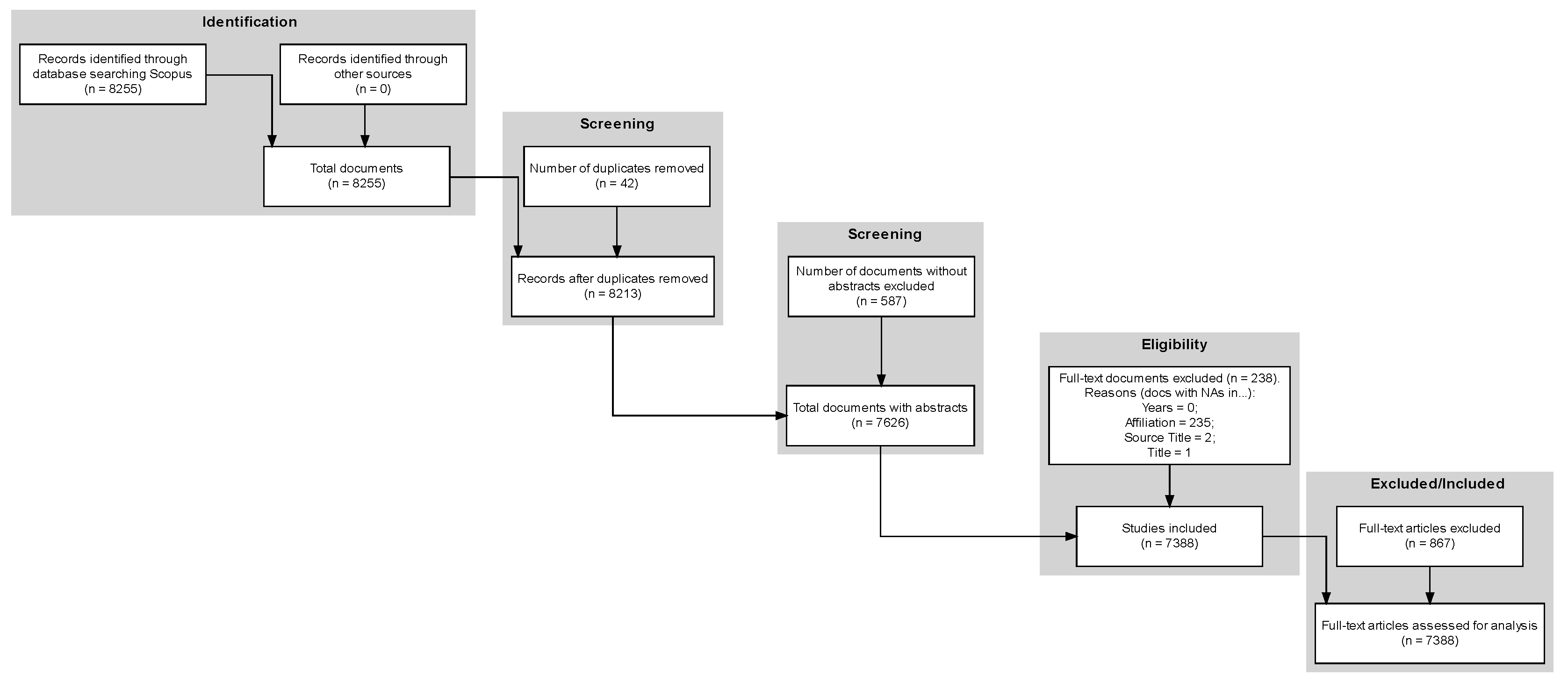
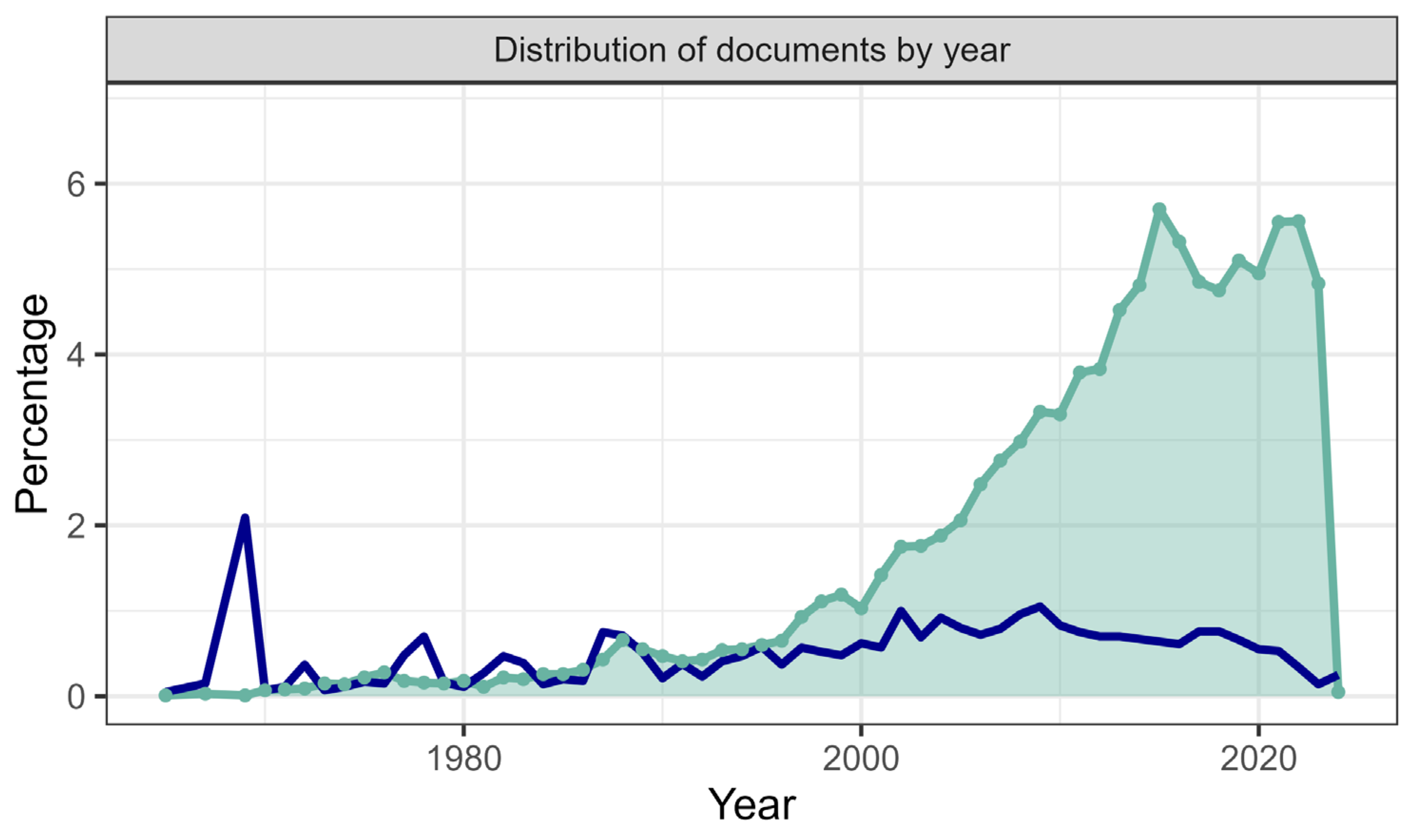
| Description | Result |
|---|---|
| Main information about data | |
| Timespan | 1965:2024 |
| Sources (journals, books, etc.) | 801 |
| Documents | 7388 |
| Annual growth rate % | 2.38 |
| Document average age | 12.7 |
| Average citations per doc | 8.765 |
| Document contents: | |
| Keywords Plus | 2727 |
| Author’s keywords | 9717 |
| Authors: | |
| Authors | 4914 |
| Authors of single-authored docs | 1956 |
| Authors collaboration | |
| Single-authored docs | 3855 |
| Co-authors per doc | 1.72 |
| International co-authorships % | 19.02 |
| Document types: | |
| Article | 6774 |
| Book | 26 |
| Book chapter | 182 |
| Conference paper | 345 |
| Other (editorial, erratum, note, review) | 61 |
| Rank | Source | Pub. | Cit. | h_Index | Year |
|---|---|---|---|---|---|
| 1 | Journal Of Number Theory | 432 | 3319 | 26 | 1969 |
| 2 | P-Adic Numbers, Ultrametric Analysis, And Applications | 178 | 1071 | 14 | 2009 |
| 3 | Compositio Mathematica | 170 | 2322 | 26 | 1996 |
| 4 | Transactions Of The American Mathematical Society | 157 | 1721 | 20 | 1972 |
| 5 | Journal Of Algebra | 151 | 850 | 15 | 1972 |
| 6 | Proceedings Of The American Mathematical Society | 139 | 881 | 16 | 1970 |
| 7 | Pacific Journal Of Mathematics | 120 | 882 | 16 | 1965 |
| 8 | Algebra And Number Theory | 106 | 720 | 14 | 2007 |
| 9 | Journal Fur Die Reine Und Angewandte Mathematik | 100 | 956 | 16 | 1981 |
| 10 | International Mathematics Research Notices | 97 | 675 | 13 | 2006 |
| 11 | Manuscripta Mathematica | 92 | 549 | 13 | 1972 |
| 12 | Israel Journal Of Mathematics | 80 | 793 | 13 | 1974 |
| 13 | Advances In Mathematics | 74 | 731 | 16 | 1986 |
| 14 | Canadian Journal Of Mathematics | 68 | 500 | 12 | 1996 |
| 15 | Duke Mathematical Journal | 67 | 1567 | 23 | 2002 |
| 16 | American Journal Of Mathematics | 67 | 827 | 17 | 1996 |
| 17 | Representation Theory | 66 | 544 | 12 | 1999 |
| 18 | Inventiones Mathematicae | 64 | 1509 | 23 | 1973 |
| 19 | Journal Of The Institute Of Mathematics Of Jussieu | 58 | 621 | 14 | 2003 |
| 20 | Advanced Studies In Contemporary Mathematics | 54 | 1522 | 20 | 2008 |
| 21 | Journal Of Mathematical Analysis And Applications | 54 | 681 | 16 | 2001 |
| 22 | Annales Scientifiques De L’Ecole Normale Superieure | 48 | 1041 | 21 | 1997 |
| 23 | Proceedings Of The Jangjeon Mathematical Society | 46 | 432 | 14 | 2009 |
| 24 | Asterisque | 45 | 1754 | 22 | 2002 |
| 25 | Annals Of Mathematics | 35 | 1395 | 23 | 2001 |
| 26 | Proceedings Of The London Mathematical Society | 33 | 342 | 12 | 1993 |
| 27 | Advances In Difference Equations | 32 | 328 | 12 | 2008 |
| 28 | Journal Of High Energy Physics | 29 | 1101 | 17 | 2000 |
| 29 | Physics Letters B | 28 | 893 | 15 | 1987 |
| 30 | Russian Journal Of Mathematical Physics | 26 | 2135 | 17 | 1999 |
| Rank | Author | Pub. | Cit. | h-Index | Year |
|---|---|---|---|---|---|
| 1 | Kim T. | 253 | 4930 | 32 | 2000 |
| 2 | Khrennikov A. | 123 | 1973 | 36 | 1993 |
| 3 | Simsek Y. | 61 | 1784 | 22 | 2005 |
| 4 | Kim Ds. | 96 | 907 | 18 | 2003 |
| 5 | Albeverio S. | 39 | 829 | 17 | 1994 |
| 6 | Mukhamedov F. | 37 | 576 | 16 | 2004 |
| 7 | Darmon H. | 28 | 532 | 14 | 2001 |
| 8 | Kedlaya Ks. | 33 | 574 | 14 | 2001 |
| 9 | Araci S. | 33 | 634 | 13 | 2011 |
| 10 | Rim S. | 52 | 514 | 13 | 2000 |
| Rank | Author | Cit. | h-Index | Year |
|---|---|---|---|---|
| 1 | Zuñiga-Galindo W. | 1561 | 23 | 1997 |
| 2 | Volovich I. | 13,053 | 55 | 1971 |
| 3 | Kozyrev S. | 3044 | 27 | 1994 |
| 4 | Kochubei A. | 5485 | 32 | 1973 |
| 5 | Vladimir V. | 2842 | x | 1923 |
| Rank | Country | Pub. | Cit. | Average Article Citations |
|---|---|---|---|---|
| 1 | USA | 2653 | 10,305 | 10 |
| 2 | South Korea | 1226 | 5154 | 15.4 |
| 3 | France | 1040 | 5055 | 10 |
| 4 | China | 786 | 1835 | 5.8 |
| 5 | Germany | 729 | 2831 | 8.9 |
| 6 | U.K. | 654 | 2089 | 7.8 |
| 7 | Japan | 590 | 2223 | 7.1 |
| 8 | Canada | 417 | 1699 | 10.9 |
| 9 | India | 378 | 842 | 6.4 |
| 10 | Italy | 298 | 766 | 7 |
| 11 | Turkey | 294 | 1992 | 17.5 |
| 12 | Israel | 249 | 757 | 7.3 |
| 13 | Spain | 213 | 409 | 6.2 |
| 14 | Sweden | 171 | 695 | 12.6 |
| 15 | Belgium | 133 | 282 | 6.3 |
| 16 | Netherlands | 125 | 224 | 5.9 |
| 17 | Poland | 121 | 322 | 6.7 |
| 18 | Mexico | 109 | 286 | 7.9 |
| 19 | Serbia | 101 | 289 | 8.3 |
| 20 | Malaysia | 99 | 357 | 11.2 |
| 21 | Brazil | 85 | 62 | 2.3 |
| 22 | Croatia | 83 | 445 | 7.5 |
| 23 | Uzbekistan | 83 | 227 | 9.1 |
| 24 | Romania | 81 | 54 | 2.5 |
| 25 | Ukraine | 80 | 132 | 4.6 |
| 26 | Austria | 79 | 132 | 4.7 |
| 27 | Switzerland | 72 | 131 | 5.5 |
| 28 | Australia | 70 | 137 | 6.5 |
| 29 | Iran | 66 | 401 | 15.4 |
| 30 | Colombia | 62 | 115 | 5 |
| Label | Prev. | Pub. | Top Terms | |
|---|---|---|---|---|
| t1 | Group representations | 6.31 | 841 | represent, local, correspond, irreduc, charact, gl, group, langland, unitari, admiss, supercuspid, princip, restrict, reduc, gln |
| t18 | Locally compact topological groups | 6.25 | 560 | group, finit, subgroup, compact, class, local, gener, free, isomorph, minim, pro, topolog, lie, abelian, dimens |
| t5 | Application of p-adic analysis | 6.12 | 714 | measur, model, structur, tree, state, quantum, base, probabl, physic, natur, real, consid, data, develop, exist |
| t19 | K-theory | 5.32 | 497 | varieti, cohomologi, smooth, project, hodg, étale, geometr, analyt, reduct, rigid, stabl, motiv, tate, semi, frobeniu |
| t20 | Local fields | 5.27 | 327 | field, characterist, finit, complet, algebra, residu, extens, field_characterist, local_field, degre, local, close, finit_field, absolut, ℚp |
| t17 | Euler and Bernoulli polynomials | 5.19 | 433 | polynomi, integr, Euler, ident, twist, symmetr, higher, interest, order, zp, bernoulli, ℤp, kim, degener, symmetri |
| t7 | p-adic forms | 5.15 | 481 | form, modular, curv, ellipt, modular_form, ordinari, classic, famili, automorph, hilbert, attach, deform, ellipt_curv, galoi_represent, slope |
| t12 | Elliptic curves | 5.15 | 357 | conjectur, quadrat, real, class, point, total, unit, case, rank, special, field, section, hold, refin, kato |
| t6 | p-adic algebras | 5.07 | 347 | algebra, connect, reduct, heck, categori, equival, group, reduct_group, heck_algebra, affin, orbit, split, doubl, functor, spheric |
| t14 | p-adic Galois theory | 4.99 | 347 | extens, modul, galoi, group, iwasawa, γ, φ, abelian, selmer, galoi_group, selmer_group, zp, prime, cyclotom, tate |
| t9 | p-adic operators | 4.73 | 350 | oper, space, differenti, continu, archimedean, condit, weight, fraction, banach, norm, suffici, role, pseudo, plai, basi |
| t11 | p-adic codes over rings | 4.73 | 262 | ring, algorithm, base, order, ideal, code, domain, factor, method, numer, matric, solv, root, techniqu, complex |
| t3 | p-adic sequences | 4.70 | 390 | integ, prime, sequenc, posit, odd, posit_integ, ℤ, odd_prime, ring_integ, pn, media, busi, mod, busi_media, infinit |
| t8 | p-adic integral equations | 4.67 | 274 | equat, solut, string, open, limit, exist, uniqu, random, class, asymptot, zero, amplitud, close, obtain, meromorph |
| t13 | Polynomials | 4.61 | 268 | number, polynomi, number_polynomi, gener, integr, bernoulli, bernoulli_number, combinatori, euler_number, special, gener_function, appli, neg, final, function |
| t15 | Power series | 4.51 | 293 | seri, coeffici, power, congruenc, sum, modulo, ℓ, exponenti, mod, hypergeometr, term, power_seri, degre, estim, gamma |
| t4 | Zeta functions | 4.48 | 225 | function, valu, multipl, zeta, root, zeta_function, complex, special, analyt, integr, term, trace, product, express, riemann |
| t16 | p-adic dynamic systems | 4.46 | 188 | system, ration, map, point, period, dynam, fix, approxim, dynam_system, complex, expans, ration_point, ration_number, find, ergod |
| t2 | p-adic functions and p-adic distributions | 4.27 | 118 | π, α, distribut, invari, σ, χ, ρ, τ, μ, squar, ω, β, ψ, δ, θ |
| t10 | p-adic spectral theory | 4.02 | 116 | qp, bound, λ, set, lower, subset, upper, larg, suffici, lower_bound, logic, degre, valu, upper_bound, defin |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Llinás, H.; Gutiérrez, I.; Torresblanca, A.; De La Hoz, J.; Llinás, B. A Bibliometric and Topic Modeling Analysis of the p-Adic Theory Literature Using Latent Dirichlet Allocation. Mathematics 2025, 13, 2932. https://doi.org/10.3390/math13182932
Llinás H, Gutiérrez I, Torresblanca A, De La Hoz J, Llinás B. A Bibliometric and Topic Modeling Analysis of the p-Adic Theory Literature Using Latent Dirichlet Allocation. Mathematics. 2025; 13(18):2932. https://doi.org/10.3390/math13182932
Chicago/Turabian StyleLlinás, Humberto, Ismael Gutiérrez, Anselmo Torresblanca, Javier De La Hoz, and Brian Llinás. 2025. "A Bibliometric and Topic Modeling Analysis of the p-Adic Theory Literature Using Latent Dirichlet Allocation" Mathematics 13, no. 18: 2932. https://doi.org/10.3390/math13182932
APA StyleLlinás, H., Gutiérrez, I., Torresblanca, A., De La Hoz, J., & Llinás, B. (2025). A Bibliometric and Topic Modeling Analysis of the p-Adic Theory Literature Using Latent Dirichlet Allocation. Mathematics, 13(18), 2932. https://doi.org/10.3390/math13182932








