Abstract
This study analytically investigates shear horizontal (SH) wave propagation in a layered structure consisting of a piezoflexoelectric (PFE) layer bonded to an elastic substrate, considering an imperfect interface. A frequency equation is derived by applying appropriate boundary and interfacial conditions, capturing the effects of flexoelectric coupling, interface imperfections, the layer thickness, and the material properties. The resulting dispersion relation reveals that both interface imperfections and the flexoelectric strength significantly alter the phase velocity of SH waves. Numerical simulations show that increasing flexoelectric coefficients or interface imperfections lead to notable changes in dispersion behavior. Comparative analyses under electrically open (EO)- and electrically short (ES)-circuited boundary conditions demonstrate their impacts on wave propagation. These findings offer new insights into the design and analysis of piezoflexoelectric devices with realistic interface conditions.
MSC:
74K35
1. Introduction
Piezoelectric materials exhibit a linear electromechanical coupling effect, characterized by the generation of electric charges under applied mechanical stress and, conversely, mechanical deformation in response to an electric field. This property is foundational to the operation of surface acoustic wave (SAW) devices, which serve as critical components in sensors, resonators, filters, oscillators, and other technologies within modern communication systems. Such devices typically consist of a thin piezoelectric film deposited on a rigid substrate.
Among the various acoustic wave modes, the propagation of shear horizontal (SH) waves along piezoelectric surfaces, particularly those composed of piezoelectric materials, has garnered significant research interest due to the inherent smart properties of piezoelectric materials, which facilitate the study of wave dynamics. Extensive investigations have been conducted on SH wave behavior in layered piezoelectric structures. For instance, Jin and Wang [1] analyzed Love wave propagation in a piezoelectric elastic piezoelectric layered system, while Wang [2] investigated SH waves in a piezoelectric layer bounded by a vacuum. Further studies have explored material gradation effects and Rayleigh wave propagation in piezoelectric media [3,4,5,6,7,8].
On the other hand, flexoelectricity, a form of higher-order electromechanical coupling, becomes significant at the nanoscale due to strong strain gradients and is present in all dielectric and semiconducting materials. The direct effect relates strain gradients to electric polarization, while the converse links electric field gradients to mechanical stress [9]. Other studies have incorporated the flexoelectric and surface effects in nanodielectrics and elastic media to address the behavior of SH waves [10,11,12]. Recent works [13,14,15,16] include vibration analysis and wave propagation in piezoelectric structures, as well as neural network-based hysteresis modeling. These studies show the wide range of applications for piezoelectric systems. They also highlight the rising significance of these systems in aerospace engineering. Additionally, studies of wave propagation have been conducted, taking into account Love waves [17], the effects of piezoelectric materials [18], and nonlinear energy harvesting [19]. The utilization of Rayleigh waves in centrosymmetric layers has been addressed and analyzed [20], while Singh and Singh [21] examined Bg waves in piezoflexomagnetic systems with interface imperfections. Another study has addressed the wave velocity in n-type piezoelectric semiconductors [22], while Singhal [23] investigated the surface wave velocity in flexoelectric rheological models.
Traditional analyses of layered piezoelectric systems have predominantly assumed idealized interfaces with perfect bonding, enforcing strict continuity conditions for both stress and displacement fields. However, practical fabrication processes inevitably introduce interfacial imperfections, which collectively compromise mechanical continuity and significantly influence the wave propagation characteristics. These interfacial defects have emerged as a critical research focus due to their substantial impacts on the performance and reliability of piezoelectric devices. Recent investigations have begun addressing these complexities. Notably, Biswas and Sahu [24] examined surface wave dispersion phenomena in functionally graded piezoelectric material (FGPM) bicomposites with flexoelectric effects, explicitly accounting for imperfect bonding conditions in fluid-loaded environments. Their work demonstrates how interfacial imperfections alter wave propagation behavior in smart material systems.
Recent advances in interfacial wave mechanics have extended to more complex material systems and boundary conditions. Kumar et al. [25] investigated Love wave propagation in flexoelectric–piezoelectric viscoelastic bilayers, incorporating dielectrically conducting imperfect interfaces. Simultaneously, Gupta et al. [26] examined shear horizontal (SH) wave behavior in functionally graded porous rock formations with fracture-induced interface irregularities, providing critical insights for geophysical sensing applications. Further extending the scope to multiferroic systems, Seema and Singhal [27] developed an analytical framework for SH wave transmission through magnetoelectroelastic media with mechanically imperfect interfaces, revealing substantial mode conversion effects at imperfection-affected boundaries.
Other investigations have significantly advanced our understanding of interface-dominated wave phenomena in smart material systems. Hemalatha and Kumar [28] studied shear horizontal (SH) wave propagation in rotating, functionally graded magnetoelectroelastic (FGMEE) structures, quantifying how imperfect bonding alters the dispersion characteristics under rotational effects. Subsequently, the work in [29] systematically extended these findings through comprehensive studies of SH wave dynamics in both functionally graded and magnetoelectroelastic media, incorporating complex interface conditions including geometric corrugations and mechanical imperfections.
Other studies, such as Masoumi et al. [30], have investigated the influence of flexoelectric effects on wave propagation in piezoelectric nanobeams by employing a nonlocal strain gradient-based higher-order beam model. Zhou et al. [31] developed a model to describe the propagation of mechanical waves in flexoelectric solids. Recent works [31,32,33] show that flexoelectricity and size effects strongly impact surface wave propagation in piezoelectric semiconductor layers, especially at the nanoscale.
The above literature review indicates that extensive studies have examined SH wave propagation in piezoelectric and flexoelectric materials and in layered systems with various interface types. However, most existing works either examine perfect interfaces or neglect the combined influence of piezoelectric and flexoelectric effects, limiting their applicability to realistic configurations. These methods, while effective for idealized conditions, fail to capture the wave behavior in practical systems, where interface imperfections and flexoelectric coupling coexist. To overcome this, the present study investigates SH wave propagation in a layered piezoflexoelectric (PFE) structure with an imperfect interface.
This analytical approach incorporates both piezoelectric and flexoelectric coupling along with interface imperfection to derive a frequency equation connecting the phase velocity and wave number. The resulting dispersion relation reveals the impacts of the material properties, interface quality, and flexoelectric strength. Numerical simulations under electrically open (EO) and electrically short (ES) boundary conditions provide insights into electromechanical wave behavior, demonstrating the need for the more realistic modeling of PFE structures in advanced applications.
2. Theoretical Formulation
In this study, we examine a PFE system comprising a finite-thickness PFE layer (thickness h) imperfectly bonded to an elastic substrate, as illustrated in Figure 1. A coordinate system is adopted, where the x-axis is oriented normal to the substrate surface, the y-axis aligns with the direction of SH wave propagation, and the z-axis corresponds to the direction of mechanical displacement. The analysis is conducted in a two-dimensional framework, assuming that all physical quantities vary with respect to the x and y coordinates. Distinct from previous studies, this work incorporates the flexoelectric effect in the modeling of the piezoelectric layer as well as the elastic substrate.
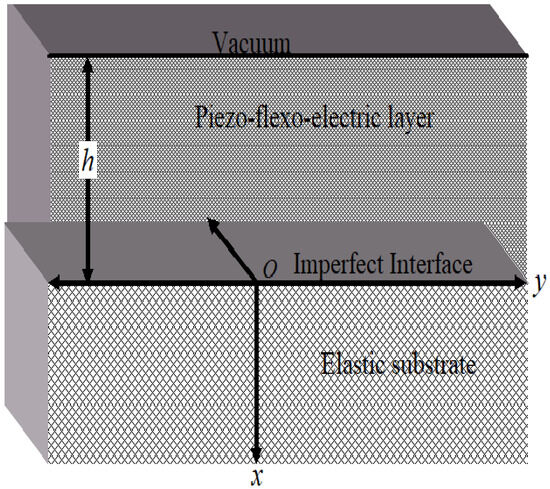
Figure 1.
Schematic illustration of the proposed model, consisting of a piezoflexoelectric layer with an elastic substrate.
The constitutive equations for a piezoelectric material that account for the flexoelectric effect can be formulated as follows [17]:
The values for strain gradients, electric field gradients, and the relevant material property tensors required to determine both direct and converse flexoelectric coefficients are adopted from the data presented in [17]. Following the variational approach outlined in [17], the governing equations for piezoflexoelectric (PFE) materials, in the absence of body forces, can be expressed as
Let denote the displacement components of a particle along the axes, respectively. Since SH waves propagate in the y-direction and induce motion solely along the z-axis, the displacement and potential fields remain unaffected. Therefore, the mechanical displacement associated with the electric and magnetic potentials can be simplified accordingly:
By applying Equations (1)–(4), the governing equation simplifies to the following final form for a piezoflexoeletric material layer:
To simplify the analysis, the substrate is modeled as a purely elastic medium, excluding the effects of both piezoelectricity and flexoelectricity. As a result, there is no coupling between the mechanical and electrical fields within the substrate. Additionally, higher-order stresses and electric quadrupole effects are neglected. Under these assumptions, the governing equations for the elastic substrate reduce to
and the electric potential for vacuum is governed by the Laplace equation, considering the air above the layer/region , as follows:
The superscripts (subscripts) “(1)” and “(2)” are used to denote the PFE layer and elastic substrate, respectively.
3. Solution to the Problem
3.1. Solution for the Piezoflexoelectric Layer
Assuming a time-periodic form for SH wave propagation, the solutions for a PFE layer with finite thickness h can be derived from Equation (5) under the assumption of harmonic wave behavior as
By applying Equation (8) in Equation (5), it can be systematically reduced to the following form:
Accordingly, the expressions for the displacement and electric potential, incorporating the effects of flexoelectricity, are formulated as
where are arbitrary constants and are listed in Appendix A.
3.2. Solution for the Elastic Substrate
Since SH waves are confined near the surface and attenuate with depth into the substrate, the solution must satisfy the boundary conditions and as . The substrate solution is obtained by assuming specific forms for the displacement and electric components as follows:
As a result, the explicit expressions for the elastic substrate solutions are derived as follows:
where are arbitrary constants and other coefficients are listed in Appendix A.
3.3. Solution for the Vacuum
Equation (7) is solved under the assumption that vanishes in the limit as ,
where is an unknown constant.
4. Boundary Conditions
The PFE layer is assumed to be imperfectly bonded to the elastic substrate, while its upper surface is considered traction-free. At the interface, the scalar potential, electric displacement, and mechanical displacement are treated as continuous fields. The corresponding mathematical formulations are provided below.
- 1.
- The surface located at is subjected to no external mechanical stress:
- 2.
- Imposed electrical condition at .
- (a)
- Electrically open (EO) case:
- (b)
- Electrically short (ES) case:
- 3.
- At , the interface is subject to the following constraints:
5. Spectral Dynamics of Wave Propagation
5.1. Electrically Open Case
By applying the boundary conditions (14), (15), and (17), which incorporate the mechanical and electrical continuity across the PFE layer, elastic substrate, and vacuum, and substituting the solution expressions (9), (12), and (13), we derive a homogeneous system for the EO case in terms of the unknown coefficients . The dispersion relation for SH wave propagation in a PFE layer overlying an elastic substrate, accounting for the flexoelectric effect, is obtained by expressing this system as a seventh-order determinant and setting it to zero, effectively eliminating the unknowns:
where is expressed as in Appendix A.
5.2. Electrically Short Case
By applying the boundary conditions (14), (16), and (17), which incorporate the mechanical and electrical continuity across the PFE layer and elastic substrate, and substituting the solution expressions (9) and (12), we derive a homogeneous system in terms of the unknown coefficients for the ES case. The dispersion relation for SH wave propagation in a PFE layer overlying an elastic substrate, accounting for the flexoelectric effect, is obtained by expressing this system as a sixth-order determinant and setting it to zero, effectively eliminating the unknowns:
where is defined as in Appendix A.
6. Results and Discussion
This section presents numerical results regarding the phase velocity dispersion characteristics of SH waves, explicitly accounting for flexoelectric effects. As a representative case, we consider a waveguide structure comprising a lead zirconate titanate 5H () ceramic layer over an glass-oriented substrate. Materials such as , piezoelectric ceramics, and quartz are frequently employed to support SH-polarized wave propagation due to their favorable electromechanical properties. Table 1 provides a detailed overview of all material parameters utilized throughout this investigation.

Table 1.
The composite material properties used in the model.
To enhance the clarity and streamline the analysis, the flexoelectric coefficients are considered equal, with their values selected from the range specified in the literature, i.e., C/m for the layer. The thickness of the PFE layer, denoted by h, is in the order of nanometers, highlighting its nanoscale dimensions. Air has a dielectric constant denoted by F/m, which reflects its ability to permit electric field propagation.
6.1. Effects of the Imperfect Interface Parameter
Figure 2 shows that increasing the imperfect interface parameter , ) (GPa) leads to a consistent rise in the phase velocity across the wave number range in the EO case. This indicates that greater interface compliance reduces the boundary constraints, allowing faster wave propagation. The effect is more pronounced at higher wave numbers, where wave–interface interactions are stronger. The distinct separation between the curves emphasizes the sensitivity of wave behavior to interface imperfections, which must be considered in the accurate modeling of EO layered systems.
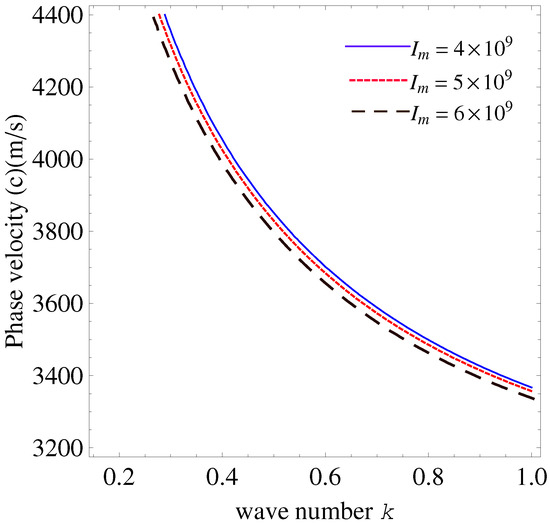
Figure 2.
Effects of imperfect interface parameter on wave number and phase velocity in electrically open case.
On the other hand, Figure 3 presents the influence of the imperfect interface parameter on the phase velocity variation in the ES case. The results show that, as increases, the phase velocity rises consistently across the wave number range. This trend reflects reduced interfacial constraints due to greater imperfection, facilitating faster wave propagation. The growing separation between the curves with increasing highlights the sensitivity of the wave behavior to the interface conditions, making it essential to consider imperfect interfaces in electrically short system designs. Comparing the EO and ES cases, both show an increase in phase velocity with the rising imperfect interface parameter , but the ES case exhibits a steeper rise. This indicates stronger sensitivity to the interface conditions in ES configurations compared to EO cases.
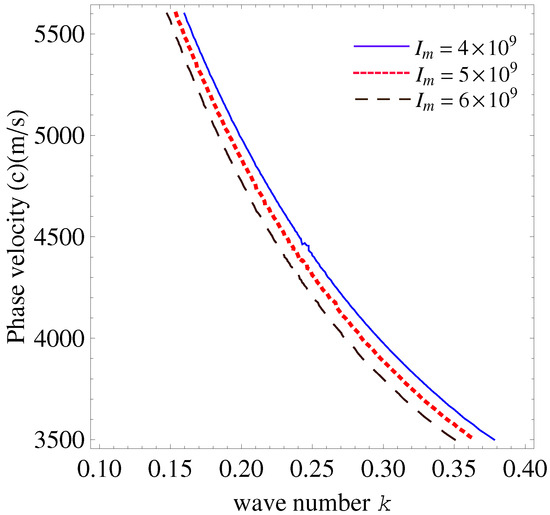
Figure 3.
Effects of imperfect interface parameter on wave number and phase velocity in electrically short case.
6.2. Effects of Layer Thickness Variation
Figure 4 illustrates the influence of varying the layer thickness h on the phase velocity of SH waves under EO boundary conditions. As the layer thickness increases from to , a noticeable rise in phase velocity is observed across the entire range of wave numbers. This trend reflects the enhanced wave confinement and increased stiffness effect with thicker layers. The dispersion curves also become steeper with higher h, indicating stronger dispersion behavior. These observations emphasize the sensitivity of the SH wave propagation characteristics to the structural geometry, particularly in piezoelectric or flexoelectric configurations.
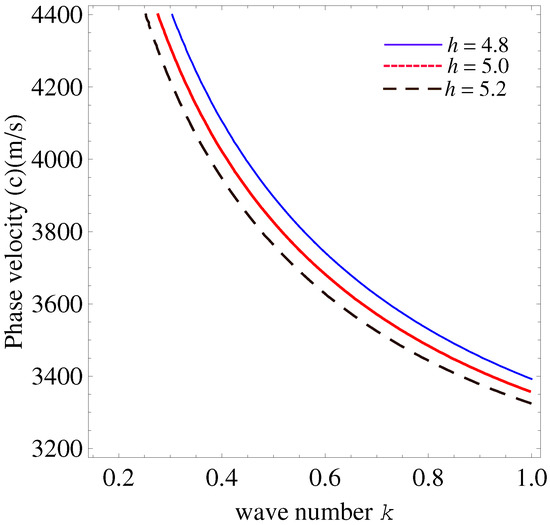
Figure 4.
Effects of layer thickness h on wave number and phase velocity in electrically open case.
The change in the SH wave phase velocity with respect to the layer thickness h under ES boundary conditions is shown in Figure 5. The phase velocity continuously increases over the wave number spectrum as h rises from to . This increase is a result of thicker layers producing a stronger effective response, which speeds up wave propagation. Furthermore, as the thickness increases, the dispersion behavior becomes more noticeable, highlighting the geometric dependence of the wave dynamics in these ES arrangements. For the same layer thickness, the ES scenario shows larger phase velocities than the EO example, suggesting a stronger electromechanical interaction. Furthermore, the dispersion curves for the ES design are steeper, indicating higher sensitivity to changes in thickness.
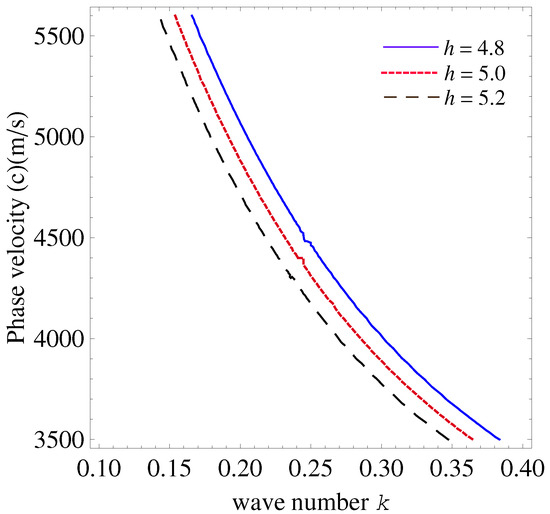
Figure 5.
Effects of layer thickness h on wave number and phase velocity in electrically short case.
6.3. Effects of Flexoelectric Parameter on Wave Propagation
The phase velocity variation with respect to the wave number k for various values of the flexoelectric coefficient (C/m) in an EO configuration is depicted in Figure 6. It is clear that the phase velocity increases noticeably over the whole wave number range when the flexoelectric parameter rises from to . This suggests that the wave propagation speed is improved by stronger flexoelectric coupling, especially at larger k values. The pattern demonstrates that, in the presence of open-circuit electrical boundary conditions, the flexoelectric effect has a substantial impact on the dispersive behavior of waves in dielectric materials.
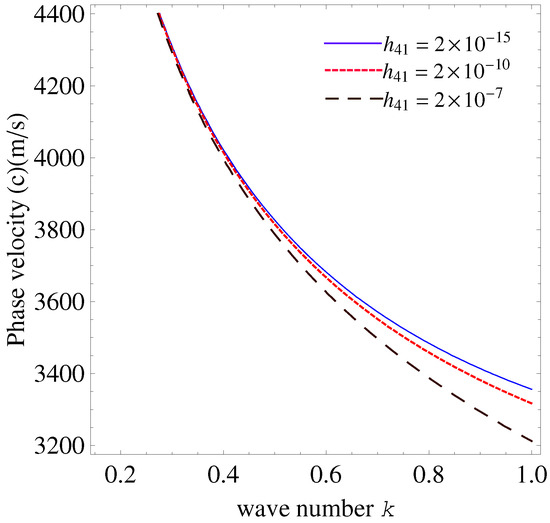
Figure 6.
Effects of flexoelectric parameter for layer on wave number and phase velocity in electrically open case.
Furthermore, the impact of the flexoelectric parameter , , on the phase velocity under ES boundary conditions is shown in Figure 7. The phase velocity increases steadily over the studied wave number range as rises from to . This behavior demonstrates how the wave speed in the medium is increased by stronger flexoelectric coupling. Higher wave numbers cause the impact to become more noticeable, suggesting that the flexoelectric contribution grows in importance in high-frequency regimes. In both the EO and ES cases, the phase velocity rises with the flexoelectric parameter; however, the ES case shows a greater rise, particularly for lower wave numbers. This suggests that the sensitivity of wave propagation to flexoelectric effects is strongly influenced by the electrical boundary conditions.
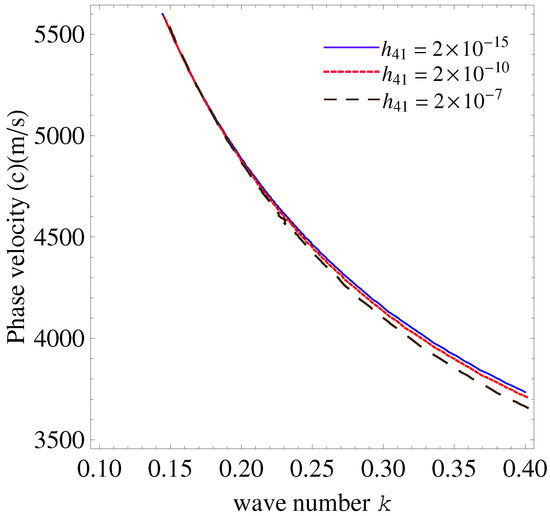
Figure 7.
Effects of flexoelectric parameter for layer on wave number and phase velocity in electrically short case.
The results show that the flexoelectric effect becomes more prominent at higher frequencies, where strain gradients are larger. At low frequencies, its influence is minimal, but, as the frequency increases, especially in the high-frequency regime, significant changes in phase velocity and attenuation are observed. These indicate the presence of critical frequencies where flexoelectricity starts to dominate the wave behavior. This frequency-dependent response suggests potential for the tuning of wave propagation via flexoelectric coupling in advanced device applications. Although the current results are based on precise symbolic computation using nominal values, a detailed uncertainty or sensitivity analysis will be explored in future work to evaluate the robustness of the model, particularly under nanoscale effects and possible fabrication tolerances.
7. Conclusions
This study examines the propagation characteristics of shear horizontal (SH) waves in a layered structure consisting of a piezoflexoelectric (PFE) layer imperfectly bonded to an elastic substrate. A comprehensive analysis of the dispersion relations is performed for both electrically open (EO) and electrically shorted (ES) boundary conditions. Our numerical results reveal that flexoelectric effects substantially influence the wave propagation dynamics, significantly affecting both the phase velocity and dispersion behavior, while potentially contributing to wave attenuation.
Our observations further demonstrate that SH waves’ phase velocities and dispersion properties are significantly influenced by the layer thickness and boundary conditions. Specifically, electrically short (ES) configurations exhibit stronger electromechanical coupling, higher phase velocities, and more distinct dispersion effects compared to electrically open (EO) configurations. The analysis indicates that an increase in the flexoelectric coefficient substantially elevates the phase velocity in both EO and ES cases, although this effect is more pronounced under ES conditions. This heightened sensitivity stems from the inherent differences in the electrical boundary conditions: ES configurations permit unrestricted charge movement, thereby enhancing electromechanical coupling within the piezoflexoelectric layer. Conversely, EO boundaries constrain charge redistribution, partially diminishing the flexoelectric response. These findings underscore the critical role of the electrical boundary conditions in regulating wave dispersion via flexoelectric coupling mechanisms.
To conclude, this study demonstrates that flexoelectric effects significantly influence the dispersion characteristics of surface acoustic waves (SAW) in nanoscale piezoelectric structures and must be accounted for in theoretical and practical analyses. The findings offer crucial insights for the development of miniaturized SAW devices with enhanced performance. Specifically, the results have important implications for the design of acoustic sensors and SAW-based components, where precise control over wave propagation is essential. Furthermore, these insights could contribute to the optimization of piezoflexoelectric structures for applications in energy harvesting and signal processing. Future research will involve validating the analytical predictions through finite element simulations to corroborate the observed dispersion and attenuation behaviors.
Author Contributions
Conceptualization: K.H., A.A. and M.T.; methodology: A.A. and K.H.; visualization, validation: K.H., M.T. and A.A.; draft writing: all authors. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge funding from the Deanship of Graduate Studies and Scientific Research, Jazan University, Saudi Arabia, through project number JU-20250271-DGSSR-RP-2025.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
The authors gratefully acknowledge funding from the Deanship of Graduate Studies and Scientific Research, Jazan University, Saudi Arabia, through project number JU-20250271-DGSSR-RP-2025.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| List of Abbreviations | |
| SH | Shear horizontal wave |
| PFE | Piezoflexoelectric |
| EO | Electrically open |
| ES | Electrically short |
| PZT | Piezoelectric material |
| SAW | Surface acoustic wave |
| FGPM | Functionally graded piezoelectric material |
| FGMEE | Functionally graded magetoelectroelastic |
| PZT-5H | Lead zirconate titanate 5H |
| Nomenclature | |
| imperfect interface parameter | |
| h | layer thickness |
| mass density | |
| stress tensor | |
| higher-order stress tensor | |
| displacement vector components | |
| electric flux | |
| electric quadrupole tensor | |
| elastic constant tensor | |
| piezoelectric constant | |
| electric permeability | |
| strain measure | |
| elastic deformation magnitude | |
| static electric potential | |
| d | converse flexoelectric tensor |
| f | direct flexoelectric tensor |
| strain gradient | |
| electric field gradient | |
| material property tensor | |
| wave number | |
| wave cycle length | |
| c | phase propagation velocity |
| vacuum electric permittivity | |
| silicon dioxide |
Appendix A
References
- Jin, F.; Wang, Z.K.; Wang, T.J. The propagation behavior of Love waves in a pre-stressed piezoelectric layered structure. Key Eng. Mater. 2000, 183, 755–760. [Google Scholar] [CrossRef]
- Wang, Q. Wave propagation in a piezoelectric coupled solid medium. J. Appl. Mech. 2002, 69, 819–824. [Google Scholar] [CrossRef]
- Manna, S.; Kundu, S.; Gupta, S. Love wave propagation in a piezoelectric layer overlying in an inhomogeneous elastic half-space. J. Vib. Control 2015, 21, 2553–2568. [Google Scholar] [CrossRef]
- Chaudhary, S.; Sahu, S.A.; Singhal, A. Analytic model for Rayleigh wave propagation in piezoelectric layer overlaid orthotropic substratum. Acta Mech. 2017, 228, 495–529. [Google Scholar] [CrossRef]
- Fang, X.; Wang, L.; Lou, J.; Fan, H.; Zhang, A.; Du, J. A unified model for investigating the propagation of SH surface waves in a piezoelectric layered medium. Int. J. Struct. Stab. Dyn. 2024, 24, 2450248. [Google Scholar] [CrossRef]
- Saroj, P.K. On propagation behavior of shear wave in piezoelectric-sandwiched structure. J. Adv. Dielectr. 2024, 14, 2440007. [Google Scholar] [CrossRef]
- Hemalatha, K.; Kumar, S.; Akshaya, A. Influence of corrugation on SH wave propagation in rotating and initially stressed functionally graded magneto-electro-elastic substrate. Geomech. Eng. 2025, 40, 79–88. [Google Scholar]
- Seema; Singhal, A. Mechanics of SH and anti-plane SH waves in orthotropic piezoelectric quasicrystal with multiple surface effect. Acta Mech. 2025, 236, 439–456. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef]
- Hu, S.; Shen, S. Electric field gradient theory with surface effect for nano-dielectrics. Comput. Mater. Contin. (CMC) 2009, 13, 63. [Google Scholar]
- Hemalatha, K.; Akshaya, A.; Qabur, A.; Kumar, S.; Tharwan, M.; Alnujaie, A.; Alneamy, A. Transverse Wave Propagation in Functionally Graded Structures Using Finite Elements with Perfectly Matched Layers and Infinite Element Coupling. Mathematics 2025, 13, 2131. [Google Scholar] [CrossRef]
- Shen, S.; Hu, S. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Wang, Y.Q. Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut. 2018, 143, 263–271. [Google Scholar] [CrossRef]
- Yamada, S.; Nambu, Y.; Chiba, M. Implementation and application of digitally controlled piezoelectric vibration absorbers to truss structures. Acta Astronaut. 2019, 156, 70–77. [Google Scholar] [CrossRef]
- Li, L.; Ren, Y.; Jin, Q. Wave propagation in piezoelectric doubly-curved panels considering thermal effects: Piezoelectricity-based synergistic effect analysi. Acta Astronaut. 2023, 204, 331–347. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, J.; Zhang, X.; Lu, B. Gird-search-based neural network modeling of piezoelectric hysteresis for gravitational wave inertial sensor. Acta Astronaut. 2025, 232, 132–142. [Google Scholar] [CrossRef]
- Yang, W.; Liang, X.; Shen, S. Love waves in layered flexoelectric structures. Philos. Mag. 2017, 97, 3186–3209. [Google Scholar] [CrossRef]
- Jiao, F.; Wei, P.; Li, Y. Wave propagation in piezoelectric medium with the flexoelectric effect considered. J. Mech. 2019, 35, 51–63. [Google Scholar] [CrossRef]
- Chu, L.; Li, Y.; Dui, G. Nonlinear analysis of functionally graded flexoelectric nanoscale energy harvesters. Int. J. Mech. Sci. 2020, 167, 105282. [Google Scholar] [CrossRef]
- Lv, S.; Shen, S. Rayleigh waves in a centrosymmetric flexoelectric layer attached to elastic substrate. Acta Mech. 2023, 234, 4649–4664. [Google Scholar] [CrossRef]
- Singh, S.; Singh, A. Bg waves in a piezo–flexo-magnetic layered model with impedance boundary and imperfect interface. Acta Mech. 2024, 235, 4339–4355. [Google Scholar] [CrossRef]
- Biswas, M.; Sahu, S.A. On the Rayleigh wave velocity in n-type piezoelectric semiconductors with enhanced flexoelectricity. Math. Mech. Solids 2025, 10812865251315937. [Google Scholar] [CrossRef]
- Seema; Singhal, A. Study of surface wave velocity in distinct rheological models with flexoelectric effect in piezoelectric aluminium nitride structure. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 29. [Google Scholar] [CrossRef]
- Biswas, M.; Sahu, S.A. Surface wave dispersion in imperfectly bonded flexoelectric-piezoelectric/FGPM bi-composite in contact of Newtonian liquid. Mech. Adv. Mater. Struct. 2023, 30, 2995–3012. [Google Scholar] [CrossRef]
- Kumar, S.; Kumari, R.; Singh, A.K. Love wave on a flexoelectric piezoelectric-viscoelastic stratified structure with dielectrically conducting imperfect interface. J. Acoust. Soc. Am. 2023, 154, 3615–3626. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Dutta, R.; Das, S. Flexoelectric effect on SH-wave propagation in functionally graded fractured porous sedimentary rocks with interfacial irregularity. J. Vib. Eng. Technol. 2024, 12, 1067–1087. [Google Scholar] [CrossRef]
- Seema; Singhal, A. Theoretical investigation of SH wave transmission in magneto-electro-elastic structure having imperfect interface using approximating method. Appl. Phys. A 2024, 130, 597. [Google Scholar] [CrossRef]
- Hemalatha, K.; Kumar, S. Propagation of SH wave in a rotating functionally graded magneto-electro-elastic structure with imperfect interface. J. Vib. Eng. Technol. 2024, 12, 8383–8397. [Google Scholar] [CrossRef]
- Hemalatha, K.; Kumar, S. Reflection of SH Wave at A Corrugated Interface of Functionally Graded Piezoelectric Half-Space. Int. J. Appl. Comput. Math. 2025, 11, 148. [Google Scholar] [CrossRef]
- Masoumi, A.; Amiri, A.; Talebitooti, R. Flexoelectric effects on wave propagation responses of piezoelectric nanobeams via nonlocal strain gradient higher order beam model. Mater. Res. Express 2019, 6, 1050d5. [Google Scholar] [CrossRef]
- Zhou, H.; Tian, X.; Deng, Q.; Sladek, J.; Sladek, V. Modeling mechanical waves propagation in flexoelectric solids. Smart Mater. Struct. 2024, 33, 035005. [Google Scholar] [CrossRef]
- Fang, X.; Wang, L.; Lou, J.; Fan, H.; Du, J. Flexoelectricity and size effects on SH surface waves in a nanoscale piezoelectric semiconductor layered medium. Appl. Math. Model. 2025, 141, 115928. [Google Scholar] [CrossRef]
- Wang, L.; Fang, X.; Lou, J.; Fan, H.; Zhang, A.; Du, J. Piezoelectric layer guided in-plane surface waves with flexoelectricity and gradient effects. Eng. Struct. 2024, 315, 118483. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).