1. Introduction
Within the paradigm of sustainable supply chain management, the reuse and overhaul of returned products—through recovery, rework, or remanufacturing—has been prioritized like never before, reflecting their growing importance in achieving both environmental and economic goals.
Dwicahyani et al. [
1] proposed a closed-loop supply chain model involving a retailer, manufacturer, and supplier, where the return rate functionally depends on the acceptance quality level of returned items. The manufacturer operates an imperfect regular production process that yields some defective units, which are inspected and either reworked, remanufactured using recoverable returns, or, if not fully recoverable, refurbished and sold in a secondary market at a discount.
Mahato and Mahata [
2] developed a profit-maximizing green EOQ model under capacity constraints by integrating order-size-dependent trade credit, all-unit discounts, partial backorder, and carbon emissions minimization. They demonstrated that retailers with limited in-house warehouse space can enhance both profitability and environmental performance by placing larger orders and renting additional storage capacity.
Inventory models that address recovery issues and environmental, social, and governance (ESG) considerations have received significant attention, as defining stock dynamics that align with ESG requirements is highly effective [
3]. However, the difference between considering and not considering recovery has not yet been thoroughly investigated and quantified. Since contemporary markets are highly competitive, cost-sensitive, and environmentally conscious, such issues remain challenging when market demand is sensitive to selling prices, stock inventory levels, and carbon emissions [
4]. Yu et al. [
5] considered an inventory model that integrated manufacturer–retailer operations in a closed-loop setup, where both customer demand and return behavior shift in response to price changes. Hasan et al. [
6] developed an eco-friendly inventory model that demonstrates how emissions are influenced by three types of carbon policies: taxes, offset schemes, and cap-and-trade systems.
Mabini et al. [
7] considered a multi-product model in the case of shortage. Wee [
8] optimized a joint pricing and replenishment model with price-dependent demand. Giri and Chaudhuri [
9] and Teng and Chang [
10] derived economic production quantity (EPQ) models with stock-dependent demand. Shaikh et al. [
11] addressed an inventory model with price- and stock-dependent demand. Other studies focused on recovery, rework, or remanufacturing. For instance, Schrady [
12] was the earliest to propose an EOQ model with recovery under deterministic demand. Subsequent researchers extended Schrady’s analysis: Nahmias and Revera [
13] investigated finite remanufacturing rates, and Koh et al. [
14] examined finite manufacturing and remanufacturing rates.
Until recently, the sustainability concept of ESG had attracted more attention for reasons beyond classical cost considerations. Maity et al. [
15] developed an eco-friendly EOQ model that accounts for carbon emissions using a pentagonal intuitionistic dense fuzzy framework. Khan et al. [
16] presented a model that integrates prepayment installments, pricing, and restocking decisions for product growth, considering demand that follows a power curve, nonlinear storage costs, and carbon regulation rules.
Hua et al. [
17] developed an EOQ model using the cap-and-trade mechanism to reduce carbon emissions. Inderfurth et al. [
18] derived lot-sizing decisions in a hybrid production/rework system considering defective products. Chung et al. [
19] developed a closed-loop inventory system for a vendor and a buyer considering a single manufacturing/remanufacturing cycle with constant demand. Yang et al. [
20] extended Chung et al.’s model to evaluate multiple manufacturing/remanufacturing cycles. Hovelaque and Bironneau [
21] investigated a sustainable EOQ model with carbon-emission-dependent demand. Helmrich et al. [
22] formulated an economic lot-sizing problem with emission capacity constraints. Ghosh et al. [
23] optimized a lot-sizing problem with a strict carbon cap policy and stochastic demand. Aljuneidi and Bulgak [
24] addressed a facility-location problem considering the carbon footprint of reverse logistics with constant demand. Chan et al. [
25] established a vendor–retailer–recycler inventory system by using a genetic algorithm. Konstantaras et al. [
26] optimized a closed-loop inventory system with time-varying demand and carbon tax regulations. Sarkar and Guchhait [
27] examined the impact of information asymmetry on green supply chains, incorporating cap-and-trade policies, service levels, and vendor-managed inventory strategies. They utilized RFID technology to mitigate asymmetry and improve coordination.
Carbon taxes determine prices, stabilizing the cost of emissions for firms and enabling predictable long-term planning. For instance, carbon taxes in Sweden and British Columbia have led to material reductions in emissions—transport emissions in Sweden fell by 11%, while British Columbia achieved a 5–15% decline. However, carbon taxes do not guarantee emission outcomes. If the rate is set too low, emissions reductions may fall short of targets, exposing weaknesses in the policy.
Conversely, cap-and-trade systems set a fixed emissions quantity and thus ensure compliance with environmental goals; however, they are prone to volatile price signals. This volatility discourages firms from making low-carbon investments due to the uncertainty of allowance costs. Hybrid designs address these trade-offs effectively. For example, incorporating a price floor and ceiling (“safety valve”) in cap-and-trade provides emission certainty while cushioning price volatility, thereby striking a balance between the virtues of both instruments. Empirical modeling suggests that hybrid systems yield superior outcomes compared to either approach alone. In China, pairing a carbon tax with its Emissions Trading System (ETS) is projected to reduce CO2 emissions by an additional 32 million tons by 2030 relative to relying solely on a cap-and-trade approach.
There are various instances where recovery technologies, such as eccentric disk pumps, have been introduced into hygienic manufacturing operations, resulting in significant improvements in the product recovery ratio and operational expenditures [
28]. Recovery strategies also support the development of new industry sectors. For instance, increased material costs motivate the automotive, personal computer, and cellular phone industries to reuse materials and items [
29]. Sarkar and Bhuniya [
30] developed a model focusing on flexible manufacturing and remanufacturing with green investments under variable demand. Their work emphasizes the integration of service facilities to enhance customer satisfaction and sustainability. Lin et al. [
31] analyzed when firms should remanufacture in-house vs. outsource under distinct sales/return lifecycles, explicitly addressing remanufacturing capacity/constraints that limit effective recovery. Sebatjane [
32] reviewed 140 papers on sustainable inventory models under carbon emission regulations, including carbon taxes, cap-and-trade schemes, and cap-and-offset schemes. A taxonomy was developed to classify existing models, and the reviewed studies were categorized accordingly. Research gaps were identified to outline a future research agenda.
Table 1 presents the differences between this and existing studies, offering a more detailed comparison with sustainable inventory models in the literature.
This study differs in that it integrates new and used products into a production line. Based on ISO-developed CE (Circular Economy) standards and the resource flow assessment of a full product lifecycle, the successful integration of new and used products into a single production line is second only to zero-resource utilization, extending product lifespan and promoting resource reuse. This model addresses the urgent need for raw materials and high energy efficiency in the manufacturing industry. Combining new and used products creates dual value within the company: not only are raw material consumption and waste emissions reduced, but new revenue-generating business models are created. Academia and industry have widely recognized that supply chain innovations centered on recycling, reuse, and remanufacturing can significantly reduce pressure on raw material extraction, mitigate the risk of resource depletion, and create new cost and environmental benefits (for example, in the application of recycled electric vehicle batteries, remanufacturing significantly reduces manufacturing costs and carbon footprint). This strategy leverages the potential of integrating the circular economy with international Industry 4.0 technologies, such as using smart manufacturing methods to promote closed resource loops and implementing reverse supply chain management, thereby improving manufacturing efficiency and supporting sustainable development.
Market demand is sensitive to selling price, stock inventory levels, and carbon emissions. A manufacturer with recovery is considered a system. There are two product sources: products can be purchased from an external vendor or produced within the recovery factory. Used products can be recycled and recovered as new products.
This study proposes a sustainable EOQ model, where the cycle time is assumed to be stably synchronized with that of the recovery process. This assumption is adopted because allowing production and recovery cycles to vary independently introduces realism at the expense of analytical simplicity. It can increase in-process inventory and cycle variability, reduce the cost efficiencies predicted by classic EOQ models, and require more complex, adaptive scheduling strategies. When cycles are not synchronized, the hidden inventory cost increases, potentially raising the total operational costs unless the model is reoptimized with revised data. Without synchronized cycles, discrepancies between production and recovery timings result in buffer accumulation, particularly at upstream bottlenecks. As the Theory of Constraints notes, this creates waste in flow and increases work-in-progress (WIP) inventory and lead time variability. A variable synchronization approach, by contrast, can reduce these inefficiencies [
4]. The effects of unsynchronized cycles can be summarized as follows: increased WIP inventory and higher holding costs disrupt the cost-optimal cycle, the EOQ assumptions no longer hold, and more complex scheduling (such as multiple deliveries and buffers) is required.
A total profit system (including sales revenue, minus the purchase cost of new and used products, minus the scrap disposal cost, minus the carbon emission cost, minus the classical and recovery setup costs, and minus the holding costs) is optimized to derive two independent decision variables: selling price and cycle time. The corresponding solution procedure is proposed in this study. Numerical examples are used to illustrate the difference in total profit when considering and not considering recovery. Sensitivity analysis is also conducted to identify significant parameters and their impact on decision variables. This research aims to help companies explore feasible solutions that both meet ESG standards while also increasing profits. The objective is to maximize the total profit of the sustainable inventory model, which considers limited recovery rates and demand sensitivity to price, carbon emissions, and stock conditions.
2. Mathematical Modelling
The mathematical model in this study is developed based on the following assumptions:
The replenishment rate is instantaneous, and the lead time is constant.
Market demand is sensitive to selling price, carbon emissions, and stock level.
The used product is recovered as a new product.
Cycle times for EOQ models and for recovery are assumed to be synchronized in a steady state.
Cap-and-trade regulations are adopted.
Notations are defined as in the following
Table 2:
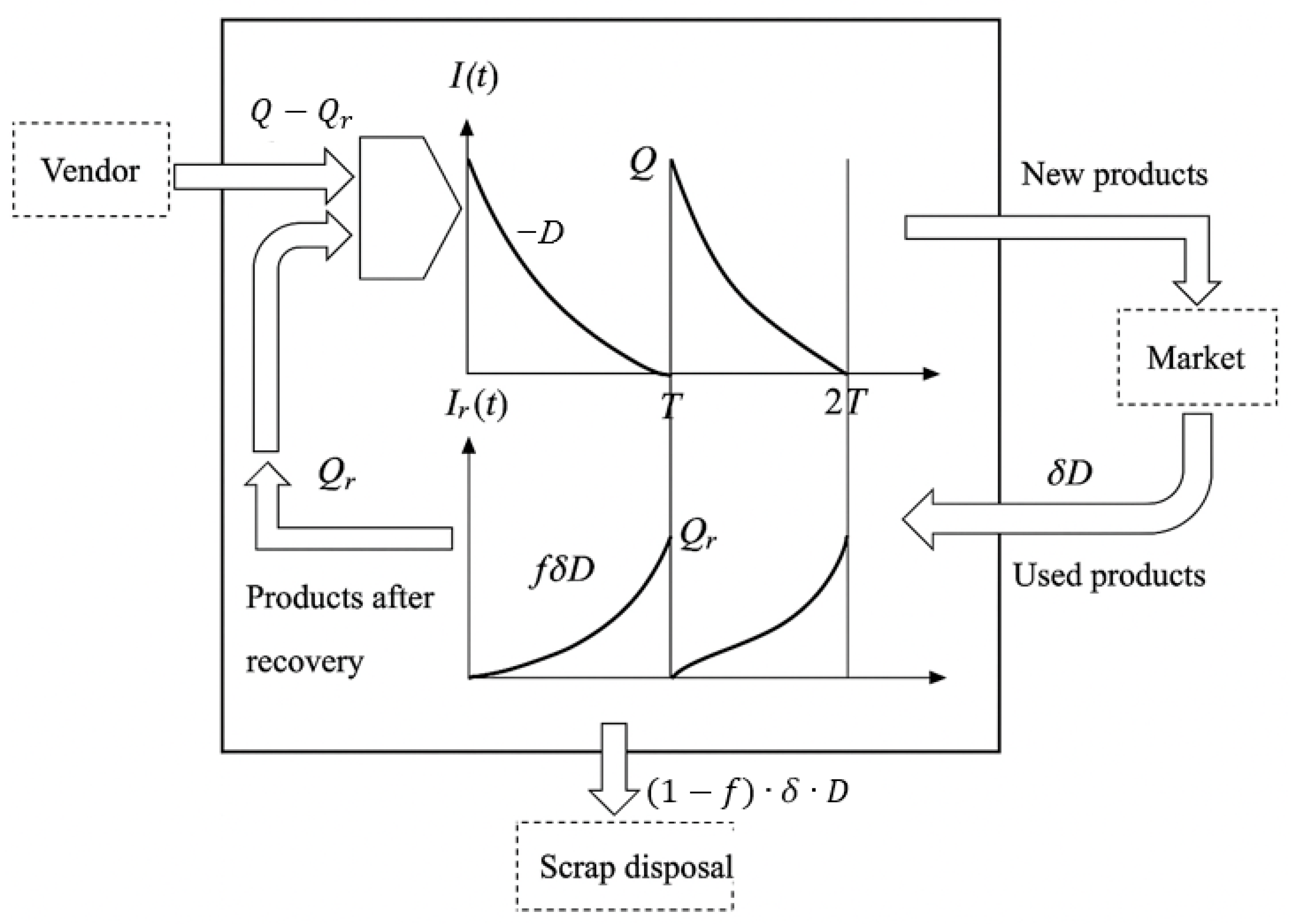
The flow of an EOQ model considering recovery in a mixed production system is illustrated in
Figure 1. There are two sources of incoming products: outside vendors and the recovery factory. The old products can be recycled and recovered, and their recycling rate and recovery rate are
δ and
f, respectively.
Since the inventory level is depleted due to a demand that is sensitive to selling price, carbon emissions, and stock on hand, the inventory levels of the EOQ model and recovery factory are represented by the following differential equations, respectively:
and
The boundary conditions are and .
The above equations were solved by Spiegel [
35]:
and
The lot size (denoted as
Q) and the recovery lot size (denoted as
Qr) can be expressed as
and
, respectively, as shown below:
and
The average demand can be obtained from the following:
The annual sales revenue (denoted as
SR) is formulated as
The annual purchase cost (denoted as
PC) is
The annual scrap disposal cost (denoted as
SDC) is
The annual carbon emission of the classical EOQ model (denoted as
Ec) is
The annual carbon emission of the recovery (denoted as
Er) is
The total carbon emission (denoted as
E) is defined in Equation (13), as the sum of
and
.
Solving the simultaneous equations of Equations (11)–(13), one can obtain
Ec and
Er, as shown in Equations (14) and (15), respectively:
and
Referring to Hua et al. [
17], the annual carbon emission cost (denoted as
CEC) can be expressed as
The annual classical cost (denoted as CC) excluding carbon-emission-related costs is
The annual recovery cost (denoted as
RC) is
The annual total profit (denoted as
TP) is
The optimization problem of maximizing
TP is a constrained nonlinear process, stated as
and is subject to Equations (12)–(14).
After substituting Equations (13)–(15) into Equations (8)–(10) and (16)–(18), there are two independent variables left, P and T, as shown in Equation (19).
Special Scenarios:
If the price-sensitive parameter β, carbon-emission-sensitive parameter κ, and stock-dependent parameter γ in Equation (19) are equal to zero, the demand is a constant, D = α, with independent variable (T) left. Then, one can solve the economic order cycle time by equating the first derivatives with respect to variable T to zero for the following five special scenarios:
For the EOQ model that neglects carbon emissions and recovery, where β, γ, κ, δ, Sc, Hc, Sr, Hr, Src, and Hrc are equal to zero, the economic order quantity and its cycle time are
which is the same as the classical EOQ formula.
- 2.
For the EOQ model that considers carbon emissions but neglects recovery, where β, γ, κ, δ, Sr, Hr, Src, and Hrc are zero, the economic order cycle time is
- 3.
For the EOQ model that considers recovery but neglects carbon emissions, where β, γ, κ, Sc, Hc, Src, and Hrc are zero, the economic order cycle time is
- 4.
For the EOQ model that considers recovery and carbon emissions, where β, γ, and κ are zero, the economic order cycle time is
- 5.
For the EOQ model that considers recovery, carbon emissions, and stock-dependent demand, where β and κ are zero, the economic order cycle time is
In the five abovementioned scenarios, since , the total profit increases monotonically with the selling price (P).
4. Numerical Example
The preceding theory can be illustrated by a practical numerical example, where the source data were provided by a local company, Yiming Co., Ltd., New Taipei City, Taiwan, which belongs to A&1 Group. The factory produces consumer goods and utensils through plastic injection molding and metal extrusion molding and sells to large-scale hypermarkets.
Setup cost per cycle, S = USD 280;
Holding cost per unit per year, H = USD 135;
Carbon emissions per setup, Sc = 56 units;
Carbon emissions for each holding unit per year, Hc = 45 units;
Recovery setup cost per cycle, Sr = USD 65;
Recovery holding cost per unit per year, Hr = USD 40;
Recovery carbon emissions per setup, Src = 14 units;
Recovery carbon emissions for each holding unit per year, Hrc = 13 units;
Unit purchase cost, c = USD 330;
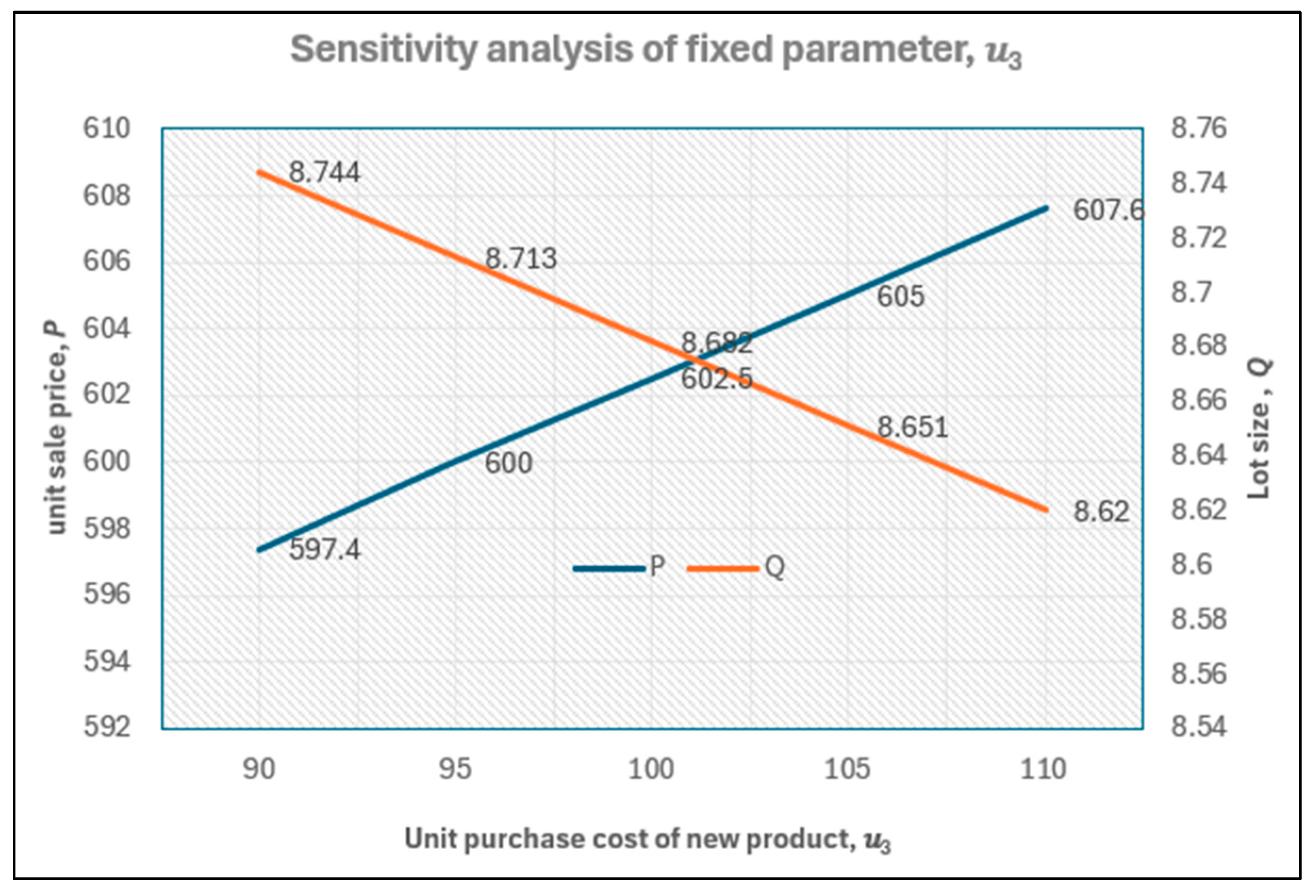
Unit purchase cost for used product from market, = USD 100;
Unit disposal cost for each recovery scrap, = USD 50;
Recycle rate of used product from market, δ = 0.8;
Yield rate from recovery, f = 0.85;
Unit carbon tax, = USD 2.5;
Carbon credit, Z = 300 units;
Unit carbon trading price, = USD 3;
Fixed demand parameter, α = 200;
Price-sensitive parameter, β = 0.18;
Carbon-emission-sensitive parameter, κ = 0.16;
Stock-sensitive parameter, γ = 0.25.
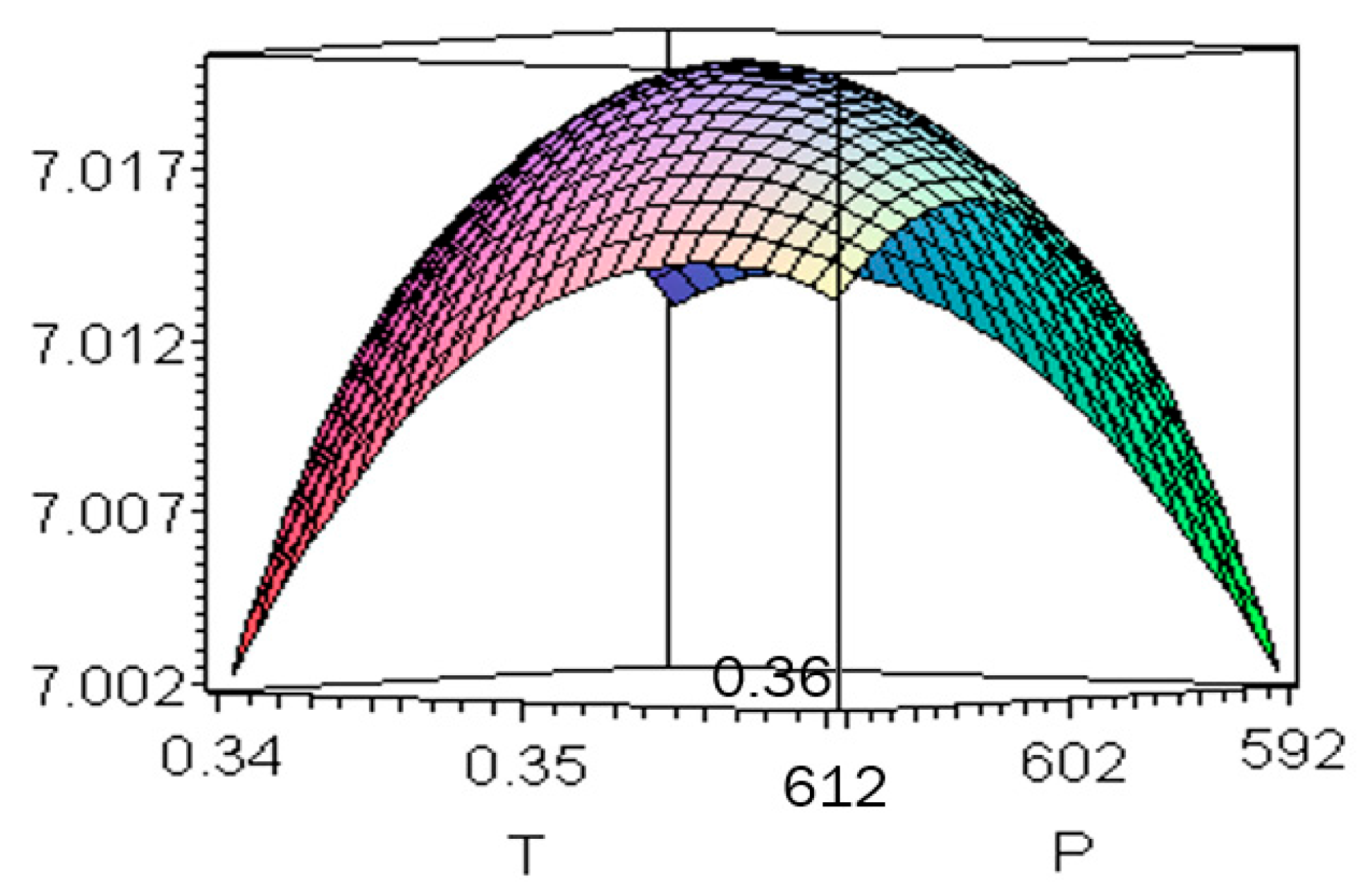
The graph of total profit with respect to
P and
T is shown in
Figure 2.
When recovery is considered, not only is the total profit higher than 15%, but the total cost is also 22% lower than the case without considering recovery, mainly because the purchase cost is 40% lower. Other reasons are that the selling price is 12% lower and the demand is 4% higher. This is a win–win policy for both sellers and consumers. The consumer can buy products at lower prices (−12%), and the seller can sell more products (+4%) and earn more profit (+15%). Please see
Table 3.
6. Concluding Remarks
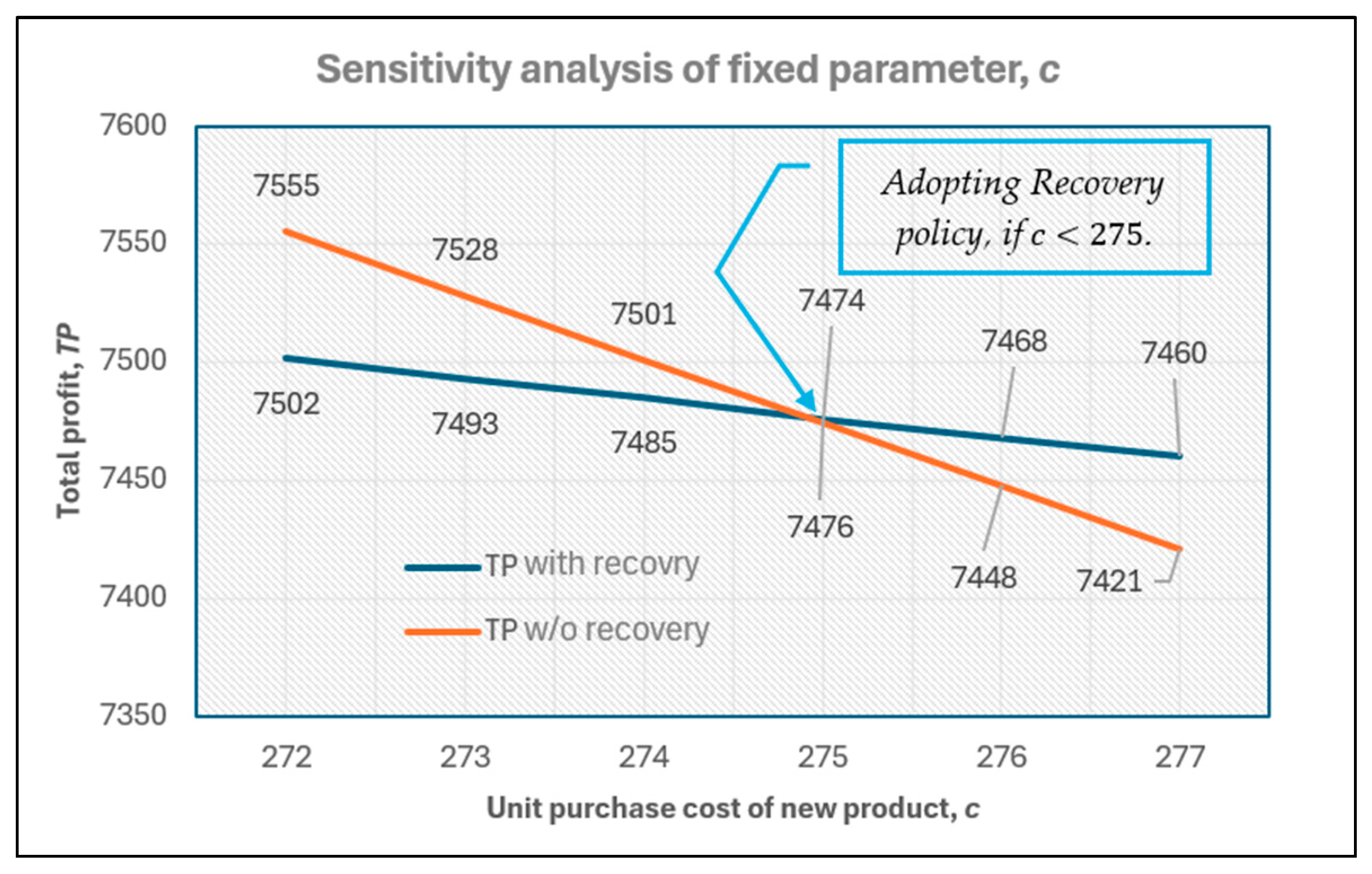
Unlike existing models, this study proposes an EOQ model with recovery, incorporating demand sensitivity to price, stock, and carbon emissions. The impact on recovery is comprehensively examined through sensitivity analysis. The following observations are made: (i) The recovery mechanism increases the total profit by approximately 15%. (ii) The primary reason for this increase is the reduction in purchase cost (−40%), rather than an increase in the selling price (see
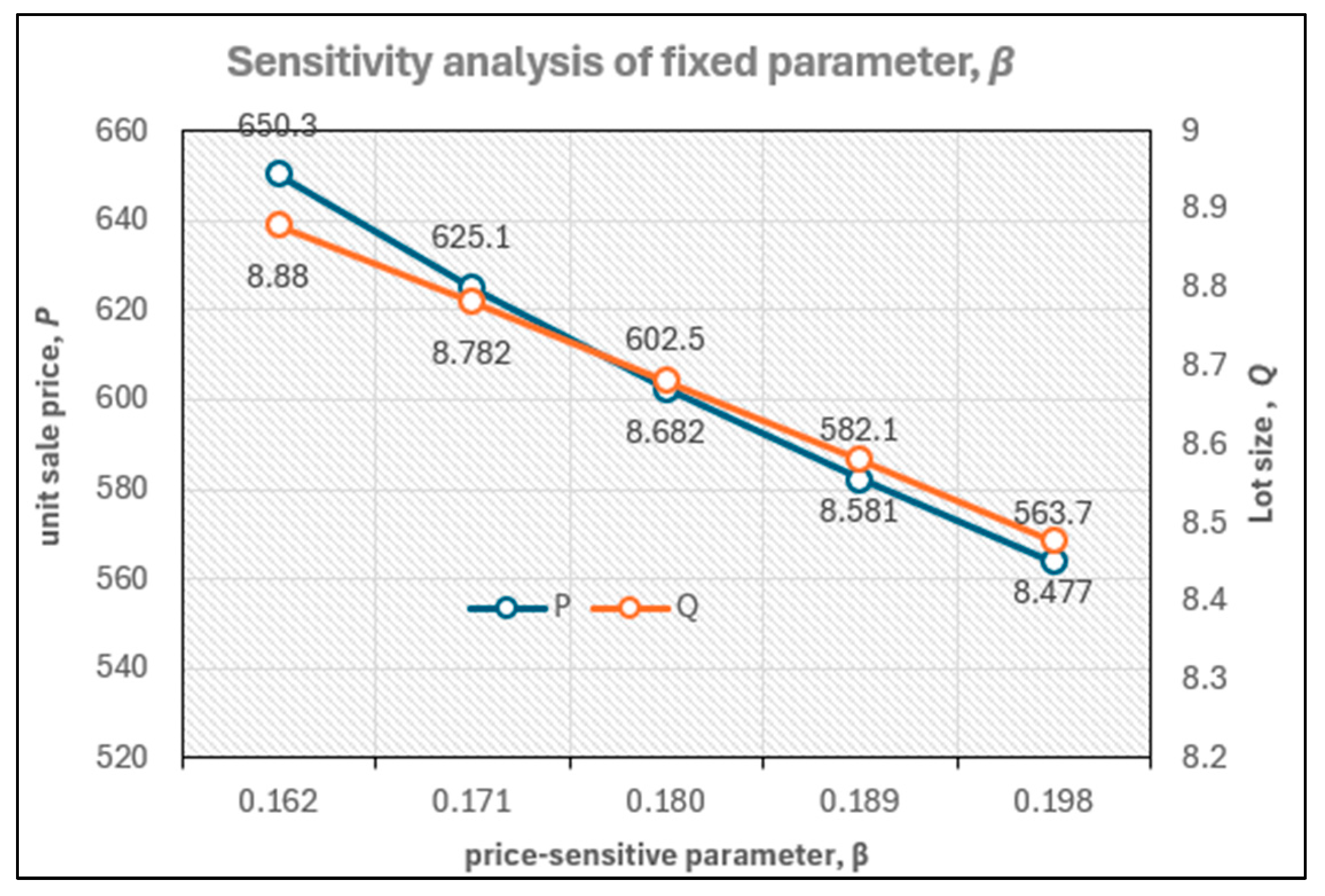
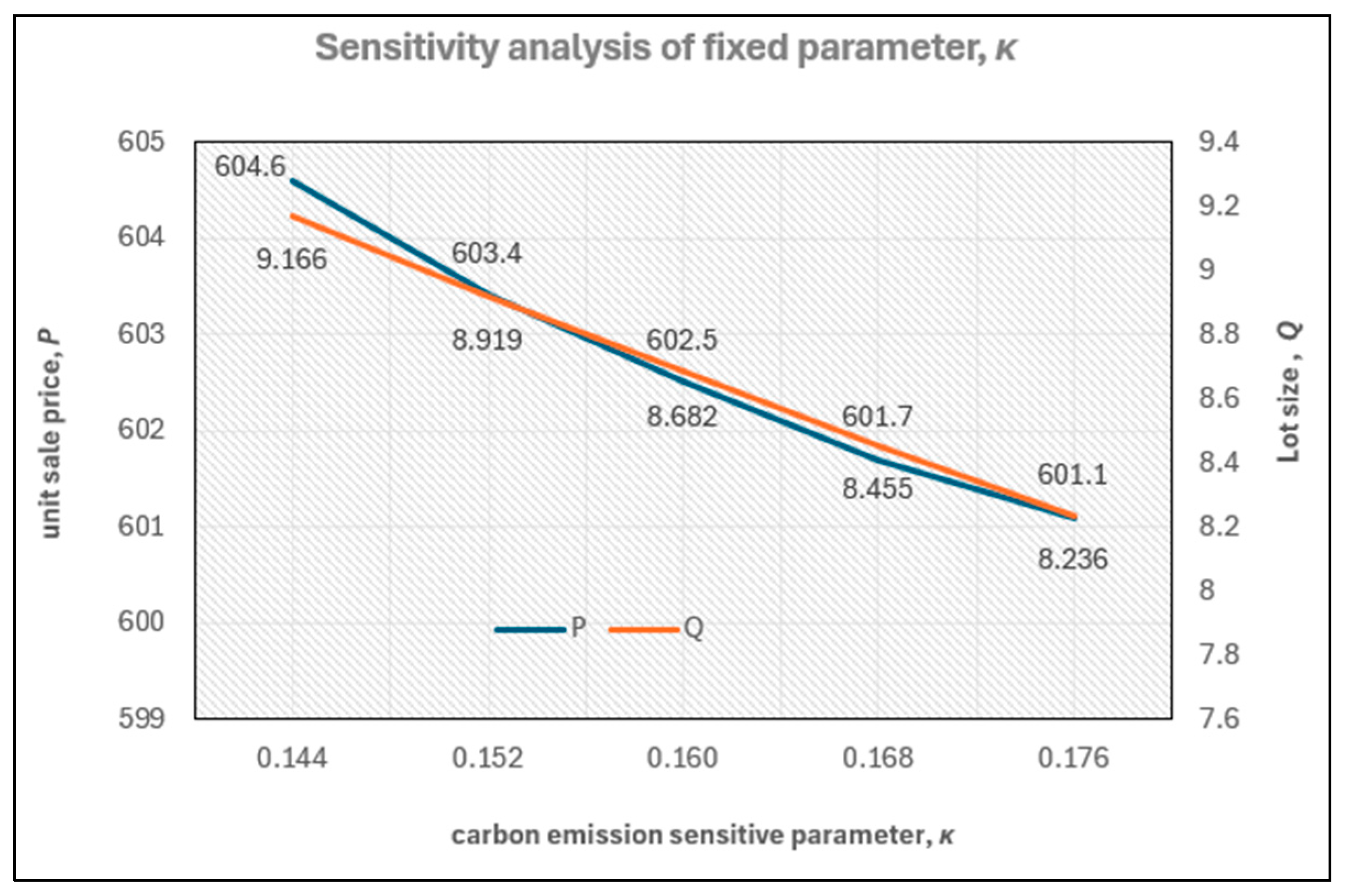
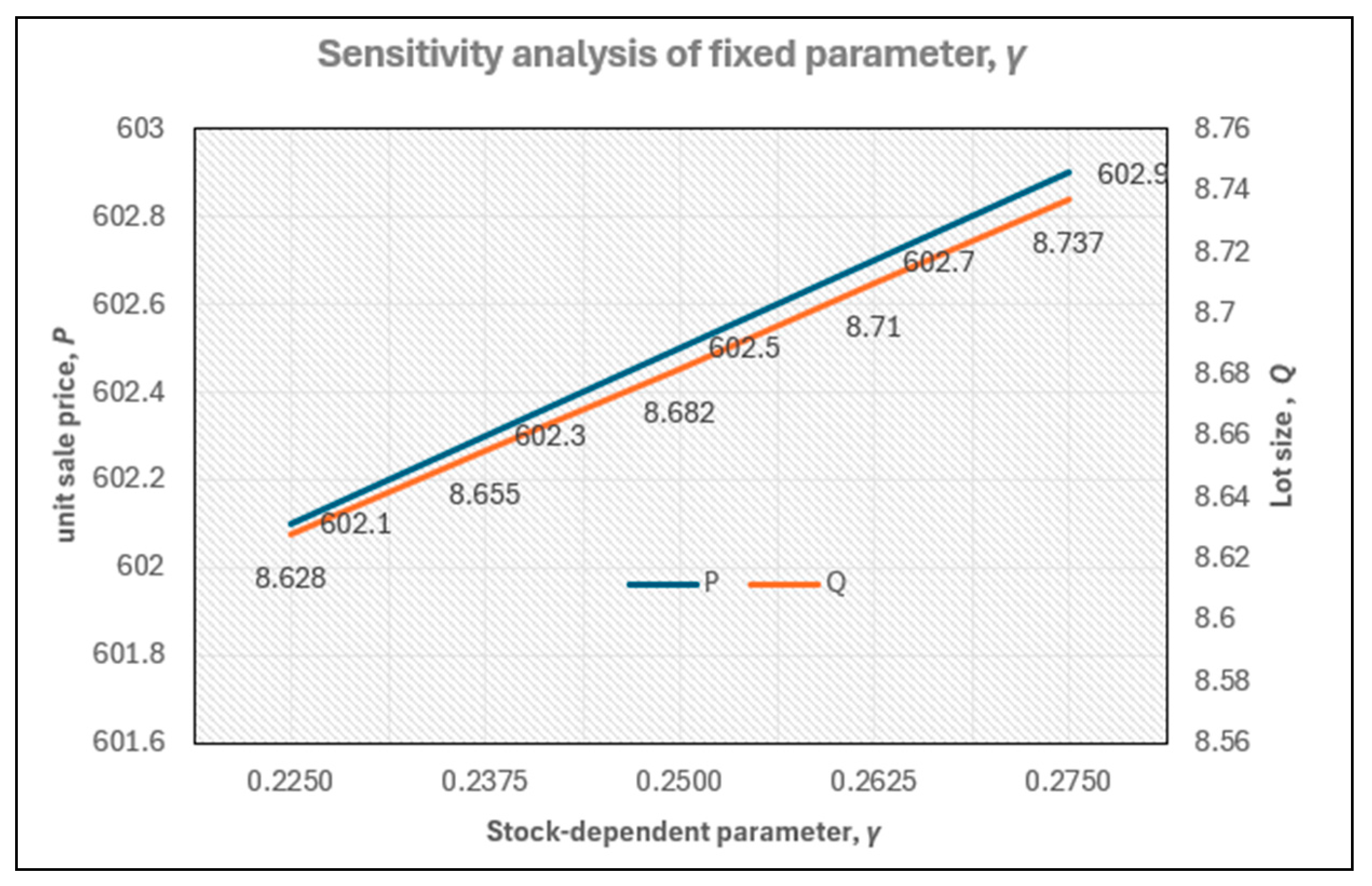
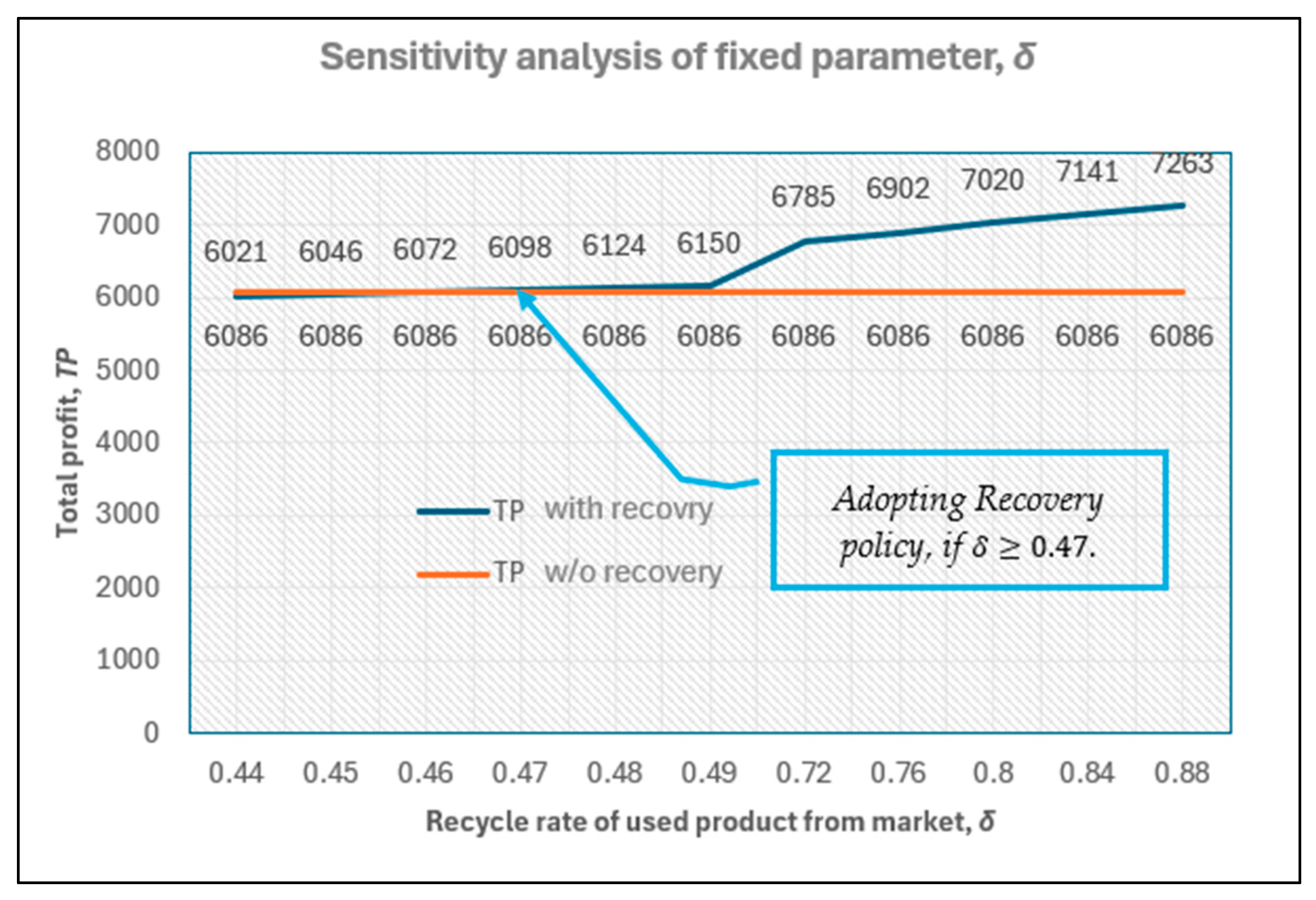
Table 3). (iii) The recovery mechanism benefits both the seller and consumer, resulting in a higher seller profit (+15%) and lower selling price (−12%), rather than benefiting only the seller. (iv) A critical unit purchase cost exists; if the unit purchase cost is lower than this value, it is not worth considering recovery. However, if the unit purchase cost exceeds this critical value, recovery is worth considering. Similar thresholds exist for other parameters, such as the recycling rate, yield rate, and unit purchase cost of used products. In other words, recovery is advantageous only if
c ≥ 275,
< 149,
f ≥ 0.70, or
δ ≥ 0.47 (please see
Figure 8,
Figure 10,
Figure 11 and
Figure 12). (v) In most cases, higher profit requires higher input costs. However, for budget-constrained enterprises, a unique solution is to adopt a recovery mechanism to achieve higher profits with lower costs (refer to
Figure 13).
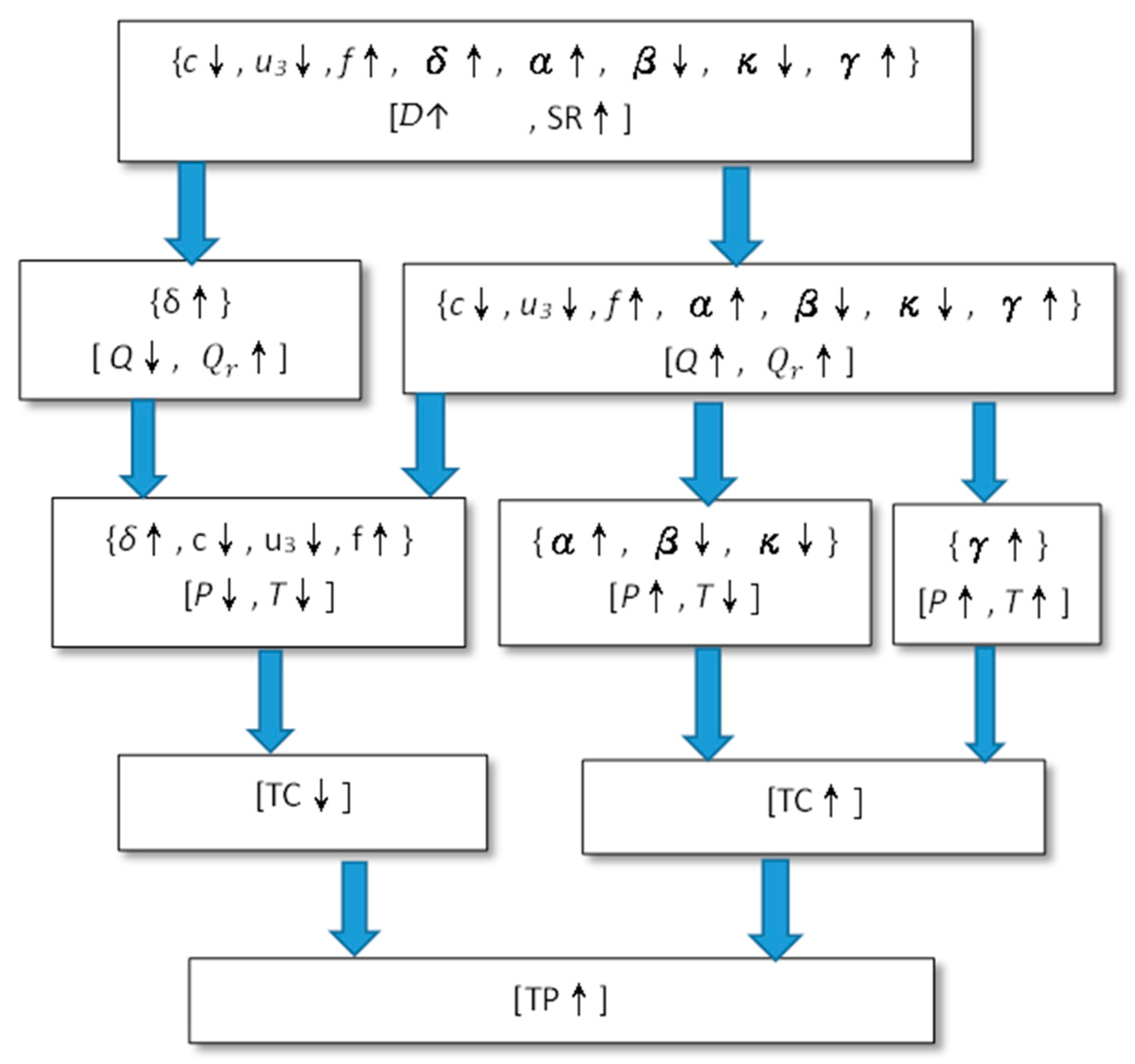
6.1. The Parameter Relationship Map
Based on
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10 and
Table 11, the relationship between parameters (
,
,
,
,
,
,
, and
) and decision variables (
P,
T,
,
,
SR,
TC,
TP,
PTPC) can be represented as a map, as shown in
Figure 13.
By adjusting purchase cost and recovery-related parameters (c↓, ↓, f↑, ↑), the seller can simultaneously reduce cost and increase profit, while the consumer pays a lower price. Conversely, changes in non-recovery-related parameters (↑, ↓, ↓, ↑) may increase seller profit, but at the expense of higher costs and higher consumer prices.
6.2. Managerial Implications, Limitations, Application and Future Research
The managerial implications of this study highlight the need for a shift in inventory management practices toward a more holistic approach that integrates sustainability into decision-making. By optimizing an inventory model that considers limited recovery rates and demand sensitivity to price, carbon emissions, and stock conditions, managers can better align their operations with both economic and environmental goals. When recovery is considered, the total profit increases by 15%, while the total cost decreases by 22% compared with the case without recovery, mainly because the purchase cost is 40% lower. Other contributing factors include a 12% reduction in the selling price and a 4% increase in demand. This represents a win–win policy for both sellers and consumers: consumers can buy products at lower prices (−12%), while sellers can sell more products (+4%) and earn higher profit (+15%). Adopting such an approach can lead to improved long-term profitability, compliance with regulatory standards, and a competitive edge in markets that are increasingly driven by sustainability considerations.
The model limitations, data, and application constraints, and directions for research and industrial application are summarized as follows:
The assumption of synchronized cycle times for EOQ and recovery may limit real-world applicability. Relaxing this assumption improves practical applicability but increases the complexity of the analytical framework.
Section 1 discusses this effect.
To address the data/application constraints of optimizing the proposed sustainable inventory model, further explanation is needed to enhance the model’s applicability and validity in practice.
A critical area for future research is the integration of stochastic elements to account for uncertainties in recovery rates, demand fluctuations, and supply chain disruptions, thereby strengthening the model’s performance under real-world conditions. Additionally, incorporating multi-objective optimization techniques could balance conflicting goals, such as minimizing carbon emissions while maximizing profit, thereby providing more comprehensive decision-making tools for managers. Expanding the model to consider circular economic principles, such as the reuse and recycling of materials, could further enhance its sustainability impact.
Future studies could also investigate the effects of different regulatory environments, such as varying carbon pricing mechanisms or environmental standards, on inventory decisions. This would provide valuable insights into how companies can effectively strategize across various regions. Another promising direction involves expanding the model to include multi-echelon supply chains, where sustainability considerations are coordinated across multiple layers of suppliers and distributors [
33]. Finally, the exploration of policy implications, such as the effects of carbon taxes or subsidies on inventory decisions, could provide valuable insights for both managers and policymakers seeking to balance economic and environmental objectives [
34].