The Instability in the Dimensions of Polynomial Splines of Mixed Smoothness over T-Meshes

Abstract

Mixed-smoothness splines facilitate localized control over smoothness; however, the issue of dimensional instability in mixed-smoothness spline spaces remains unstudied in the existing literature. This paper studies such instabilities over T-meshes, where different orders of smoothness are required across interior mesh segments. Using the smoothing cofactor-conformality method, we introduce a constraint on T-meshes to derive a stable dimension formula for mixed-smoothness spline spaces. Furthermore, we show dimensional instability in cases involving T-cycles and nested T-cycles. By defining a singularity factor for each T-cycle, we demonstrate that both dimensional instabilities and structural degenerations are associated with these singularity factors. The work contributes to a deeper understanding of spline spaces defined over non-tensor-product structures.

1. Introduction

Non-Uniform Rational B-splines (NURBSs) are widely employed in computer-aided design (CAD), geometric design (CAGD), manufacturing (CAM), engineering (CAE) and approximation theory [1,2]. However, NURBSs are fundamentally based on a tensor-product structure, requiring control points to lie on a topologically rectangular grid. Local refinement inevitably results in a large number of superfluous control points, imposing significant computational burdens on NURBS models [3,4].

To overcome the limitations of NURBS, Sederberg et al. [3] introduced T-splines, a point-defined spline defined on a T-mesh. T-splines offer greater flexibility for representing free-form surfaces and can control the surface shape with fewer control points. Furthermore, a specific class of T-splines, known as analysis-suitable T-splines, has been developed. Their basis functions are linearly independent and form a partition of unity [5,6]. Scott et al. [6] also presented a greedy algorithm for implementing local refinement in analysis-suitable T-splines. In addition, Pan et al. [7,8,9] showed how to generate hierarchical T-meshes with associated locally refined B-splines, which possess the property of local linear independence, form a non-negative partition of unity, and span the resulting spaces of $C^s$-smooth polynomial splines of degree $p=2s+1$. They are called RMB-splines, which are a type of locally refined spline.

There is another way to achieve local modification for tensor-product B-splines on rectangular meshes. Deng et al. first introduced the spline space over a T-mesh in [10], denoted as $S(m,n,\alpha ,\beta ,\mathcal{T})$. This space comprises bi-degree $(m,n)$ piecewise polynomials defined on T-mesh $\mathcal{T}$ with smoothness order $\alpha$ in the x direction and $\beta$ in the y direction. Using the B-net method, Deng et al. [10] derived the dimension of $S(m,n,\alpha ,\beta ,\mathcal{T})$ under the constraints $m\ge 2\alpha +1$ and $n\ge 2\beta +1$ for T-meshes without T-cycles. Huang et al. [11] obtained an equivalent dimension formula in a different form using the smoothing cofactor-conformality method [12,13]. Li et al. [14] refined the dimension formula in the same spline space by using the smoothing cofactor-conformality method under constraints involving the smoothness order, spline degree and the T-mesh structure as well. In addition, Li et al. [15] discussed the stability of the dimensions for general spline spaces, focusing their analysis on the conformality condition at a single interior vertex. Mourrain [16] introduced weighted T-meshes, over which the dimension could be computed in an explicit formula by using homological techniques. Li et al. [17] defined diagonalizable T-meshes, over which the dimensions of spline spaces are stable.

However, the study of bivariate splines on T-meshes poses an interesting challenge as the spline space dimension can depend on the geometry structure of the partition. As is known, for Morgan–Scott triangulation, the dimension of the spline space depends not only on the topological information of the partition, but also on its geometry structure [18,19,20]. Li et al. [21] and Berdinsky et al. [22] discovered the instability in the dimensions of spline spaces over certain T-meshes. In 2015, Guo et al. [23] revealed the instability of the dimension for a T-mesh with an independent simple T-cycle. Subsequently, in 2019, Li and Wang [24] demonstrated dimension instability for a T-mesh with nested T-cycles. However, the cases of instable dimensions in mixed-smoothness spline spaces over T-meshes remain unstudied.

Certain tasks require working with splines of mixed smoothness, at least locally, e.g., geometric objects containing $C^0$ feature lines and solutions to physical problems that show localized discontinuities. Local control over the smoothness can be very beneficial in such cases and can lead to great improvements in the quality of the output. In 2014, Mourrian [16] firstly analysed the dimension of spline spaces of different smoothness along the interior segments of a planar T-mesh by exploiting homological technique. Recently, Toshniwal and Villamizar [25] studied the stable dimensions of spline spaces of mixed smoothness along the interior edges on T-meshes via a homology-based approach. Currently, there is limited research on the dimension of mixed-smoothness spline spaces.

In this paper, we discuss the instability in the dimensions of mixed-smoothness spline spaces using the smoothing cofactor-conformality technique, which is the central novelty of this work relative to prior studies on mixed-smoothness splines. When different orders of smoothness are required across different mesh segments, we find some very interesting results. For the cases of one T-cycle and two- and three-nested T-cycles, the instability of dimension for mixed-smoothness spline spaces is associated with a geometric property depicted by a notation of a singularity factor. In addition, we give a stable dimension formula for mixed-smoothness splines over planar T-meshes via a constraint on the T-mesh using the smoothing cofactor-conformality technique.

The remainder of this paper is organized as follows. We review some definitions and notations regarding T-meshes in Section 2. In Section 3, we introduce a constraint on the T-mesh in order to obtain a stable dimension formula for mixed-smoothness spline spaces via the smoothing cofactor-conformality technique. In Section 4, we discuss the instability of the dimensions of mixed-smoothness spline spaces over certain T-meshes with a single T-cycle and two- and three-nested T-cycles respectively. Moreover, we show that dimensional instability and structural degeneration are related to a geometric property which is defined as singularity factor. Finally, conclusions are drawn in Section 5.

2. Preliminaries

In the following, we briefly review some definitions and notations of T-meshes and mixed-smoothness spline spaces over T-meshes and recall some preliminary knowledge about the smoothing cofactor method, which is a useful tool to analyse the dimensions of spline spaces. Some basic concepts in a mesh, such as segments, vertices, cells, etc., are defined as usual.

2.1. T-Meshes

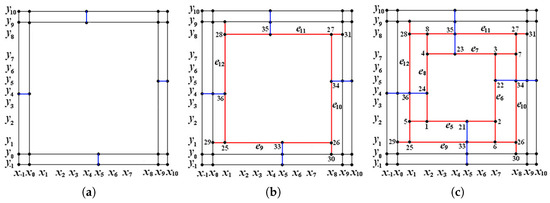
A T-mesh—a generalized rectangular grid that allows T-junctions arising from T-splines—classifies its interior mesh segments (referring to maximal interior mesh segments in the following paper) into three kinds: cross-cuts (e.g., $\overline{v_1{v}_2}$), where both endpoints lie on mesh boundaries; rays (e.g., $\overline{v_3{v}_{11}}$) with exactly one endpoint lying on the mesh boundary; and T-segments (e.g., $\overline{v_4{v}_{18}}$) whose endpoints are both interior vertices. Correspondingly, interior vertices are also classified into three kinds: free vertices (e.g., $v_{21},v_{22},v_{23}$) occurring at intersections of cross-cuts or rays; mono-vertices (e.g., $v_5,v_9,v_{16}$) formed at intersections of T-segments and cross-cuts or rays; and multi-vertices (e.g., $v_6,v_{15},v_{18}$) arising exclusively at intersections of T-segments. All examples are referenced from Figure 1a.

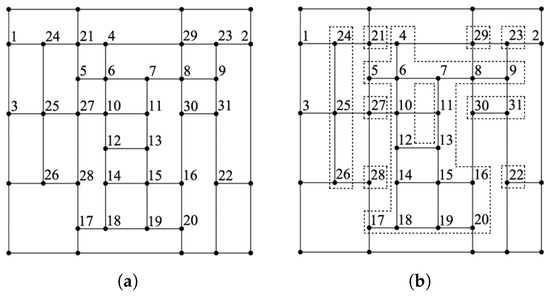
Figure 1. (a) A T-mesh. (b) Its T-connected components.

In this case, we refer to the two T-segments as T-connected; e.g, $\overline{v_7{v}_{19}}$ and $\overline{v_{14}{v}_{16}}$ are T-connected at vertex $v_{15}$. A T-connected component is defined as the union of all T-connected T-segments and their vertices—for example, the union of $\overline{v_4{v}_{18}},\overline{v_7{v}_{19}},\overline{v_5{v}_9},\overline{v_{12}{v}_{13}},\overline{v_{14}{v}_{16}},\overline{v_{17}{v}_{20}}$ in Figure 1b, which is a T-connected component that must be regarded as a local structure. In particular, a free vertex (e.g., $v_{21}$,$v_{22}$,$v_{23}$) is a single T-connected component. Based on this definition, the entire T-mesh can be decomposed into multiple different T-connected components without intersections (as illustrated by the independently enclosed dotted regions in Figure 1b).

2.2. Mixed-Smoothness Spline Spaces over T-Meshes

We define the spaces of piecewise polynomial functions on a T-mesh, with bounded degrees and given smoothness. Given a T-mesh $\mathcal{T}$, let $\mathcal{F}$ denote all the cells in $\mathcal{T}$, $\Omega$ denote the region occupied by all the cells in $\mathcal{T}$ and $\tau$ denote the maximal interior segments of a general planar T-mesh $\mathcal{T}$.

Definition 1.

The map $\mathbf{r}:\tau \to \mathbb{N}$ is referred to as a smoothness distribution on a T-mesh $\mathcal{T}$.

Using this notation, we can define the mixed-smoothness spline space $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ that forms the object of our study. The goal of this paper is to analyze the dimension of the space of bi-degree splines $(m,n)$ with smoothness $\mathbf{r}$ on a T-mesh $\mathcal{T}$. From the definition of $\mathbf{r}$ and the following definition, it will be clear that we are interested in obtaining highly local control over the smoothness of splines in $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$.

Definition 2.

Given a T-mesh $\mathcal{T}$, bi-degree $(m,n)$, and smoothness distribution $\mathbf{r}$, we define the mixed-smoothness spline space $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ as

$$S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right):=\left\{s(x,y)\left|{}_{\varphi }\in {\mathbb{P}}_{m,n},\forall \varphi \in \mathcal{F}\left|s(x,y)\in C^{\mathbf{r}\left(\tau \right)}(\Omega )smoothacross\tau \right.\right.\right\}$$

where ${\mathbb{P}}_{m,n}$ is the space of all bi-degree polynomials $(m,n)$, $\mathbf{r}\left(\tau \right)$ is the corresponding smoothness order for the interior segment τ, and $C^{\mathbf{r}\left(\tau \right)}(\Omega )$ is the space consisting of all bivariate functions which are continuous on Ω with $\mathbf{r}\left(\tau \right)$ continuity along corresponding interior segment τ.

Denote $v_{i,j}$ by each interior vertex located at $(x_i,y_j)$. For convenience, we will define the smoothness map $\mathbf{r}$ on interior segments of $\mathcal{T}$ as follows: for any vertical interior segment $\tau :x=x_i$ (resp. horizontal interior segment $\tau :y=y_j$), $\mathbf{r}\left(\tau \right)={\mathbf{r}}_h\left(x_i\right)$ (resp. $\mathbf{r}\left(\tau \right)={\mathbf{r}}_v\left(y_j\right)$). We will also define the horizontal and vertical smoothness at interior vertices as follows: for any $v_{i,j}$, ${\mathbf{r}}_h\left(v_{i,j}\right)={\mathbf{r}}_h\left(x_i\right)$ and ${\mathbf{r}}_v\left(v_{i,j}\right)={\mathbf{r}}_v\left(y_j\right)$.

3. A Sufficient Condition for Stable Dimension Formula for Mixed-Smoothness Spline Spaces

In this section, we will use the smoothing cofactor-conformality method to study the dimension of $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$. We then derive a sufficient condition to guarantee the dimensional stability of $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ when the desired order of smoothness is constrained along each interior segment. We omit the relevant proofs of the following lemmas and theorem, as their derivations are analogous to those in [14].

3.1. Two Types of Conformality Conditions Along T-Segments

Based on the smoothing cofactor-conformality method, there exists the corresponding smoothing cofactor $p_i(x,y)\in {\mathbb{P}}_{m,n-{\mathbf{r}}_v\left(y_j\right)-1}$ across each horizontal grid segment and $q_j(x,y)\in {\mathbb{P}}_{m-{\mathbf{r}}_h\left(x_i\right)-1,n}$ across each vertical grid segment.

As shown in Figure 2a, for each interior vertex $(x_i,y_j)$ denoted by $v_{i,j}$, the conformality condition is

$$(p_i-p_{i-1}){(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}+(q_{j-1}-q_j){(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1}=0.$$

(1)

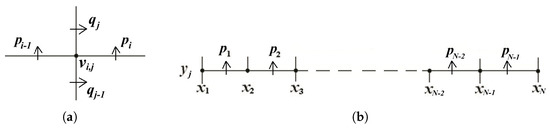
Figure 2. (a) The smoothing cofactors around $v_{i,j}$. (b) The smoothing cofactors along a horizontal T-segment.

Notice that if $v_{i,j}$ is a T-junction, one of the smoothing cofactors vanishes. Since ${(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1}$ and ${(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}$ are prime to each other, there exist $t_i(x,y),t_i(x,y)\in {\mathbb{P}}_{m-{\mathbf{r}}_h\left(x_i\right)-1,n-{\mathbf{r}}_v\left(y_j\right)-1}$ such that

$$p_i-p_{i-1}=t_i{(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1},q_{j-1}-q_j=t_j{(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}.$$

(2)

Substituting (2) into (1), it follows that

$$(t_i(x,y)+t_j(x,y)){(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1}{(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}\equiv 0.$$

(3)

Thus,

$$t_i(x,y)\equiv t_j(x,y)=:d_{i,j}(x,y)\in P_{m-{\mathbf{r}}_h\left(x_i\right)-1,n-{\mathbf{r}}_v\left(y_j\right)-1},$$

(4)

where $d_{i,j}(x,y)\in {\mathbb{P}}_{m-{\mathbf{r}}_h\left(x_i\right)-1,n-{\mathbf{r}}_v\left(y_j\right)-1}$ is regarded as the conformality cofactor at the interior vertex $v_{i,j}$, where ${\mathbb{P}}_{m-{\mathbf{r}}_h\left(x_i\right)-1,n-{\mathbf{r}}_v\left(y_j\right)-1}$ is the bi-degree polynomial space. Therefore, we find quantity relations between smoothing cofactors

$$p_i-p_{i-1}\equiv d_{i,j}(x,y){(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1},$$

(5)

and

$$q_j-q_{j-1}\equiv d_{i,j}(x,y){(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}.$$

(6)

For a horizontal T-segment containing N interior vertices, the corresponding smoothing cofactors $p_i(i=1,\dots ,N-1)$ are shown in Figure 2b. Based on the results in [14], N conformality conditions at each vertex $v_{i,j}$ are established:

$$\begin{array}{ccc}\hfill p_1& \equiv & d_{1,j}(x,y){(x-x_1)}^{{\mathbf{r}}_h\left(x_1\right)+1},\hfill \\ \hfill p_2-p_1& \equiv & d_{2,j}(x,y){(x-x_2)}^{{\mathbf{r}}_h\left(x_2\right)+1},\hfill \\ & \dots & \\ \hfill p_{N-1}-p_{N-2}& \equiv & d_{N-1,j}(x,y){(x-x_{N-1})}^{{\mathbf{r}}_h\left(x_{N-1}\right)+1},\hfill \\ \hfill -p_{N-1}& \equiv & d_{N,j}(x,y){(x-x_N)}^{{\mathbf{r}}_h\left(x_N\right)+1}.\hfill \end{array}$$

By summing the above equations, we derive the conformality condition along the horizontal T-segment

$$\sum _{i=1}^N{d}_{i,j}(x,y){(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1}\equiv 0.$$

(7)

Similarly, the conformality condition along the vertical T-segment is

$$\sum _{j=1}^N{d}_{i,j}(x,y){(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}\equiv 0,$$

(8)

where N denotes the number of interior vertices on the vertical T-segment.

Equations (7) and (8) are the first and second types of conformality conditions. The global conformality conditions of a T-connected component are composed of two types of conformality equation along all T-segments, and the corresponding conformality conditions of different T-connected components can be solved individually.

3.2. The Dimensions of the Two Types of Conformality Conditions

Lemma 1.

Let $d_{i,j}(x,y)\in {\mathbb{P}}_{m-{\mathbf{r}}_h\left(x_i\right)-1,n-{\mathbf{r}}_v\left(y_j\right)-1}$. The dimension of the solution space of the linear systems

$$\sum _{i=1}^N{d}_{i,j}(x,y){(x-x_i)}^{{\mathbf{r}}_h\left(x_i\right)+1}\equiv 0$$

is $di{m}_1\left(N\right)=(n-{\mathbf{r}}_v\left(y_j\right))({\displaystyle \sum _{i=1}^N}(m-{\mathbf{r}}_h\left(x_i\right))-(m+1){)}_{+}$, where $x_{+}=max(x,0)$. The dimension of the solution space of the linear systems

$$\sum _{j=1}^N{d}_{i,j}(x,y){(y-y_j)}^{{\mathbf{r}}_v\left(y_j\right)+1}\equiv 0$$

is $di{m}_2\left(N\right)=(m-{\mathbf{r}}_h\left(x_i\right))({\displaystyle \sum _{j=1}^N}(n-{\mathbf{r}}_v\left(y_j\right))-(n+1){)}_{+}.$

3.3. The Dimensions of the Spline Spaces $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ on T-Mesh

Lemma 2.

Given a T-mesh $\mathcal{T}$, let $\mathbf{r}$ be a smoothness distribution on $\mathcal{T}$, $C^h$ be interior horizontal cross-cuts, $C^v$ be interior vertical cross-cuts and ${\mathcal{T}}_k(k=1,\dots ,T)$ be T-connected components. Then

$$\begin{array}{cc}\hfill dim{S}_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)& =(m+1)(n+1)+\sum _{\tau \in C^h}(m+1)(n-\mathbf{r}(\tau \left)\right)\hfill \\ \hfill & +\sum _{\tau \in C^v}(n+1)(m-\mathbf{r}(\tau \left)\right)+\sum _{k=1}^{T}dim{\mathcal{T}}_k,\hfill \end{array}$$

(9)

where dim${\mathcal{T}}_k$ denotes the dimension of the global conformality conditions for the k-th T-connected component.

Lemma 3.

Let ${\mathcal{T}}_k$ be the k-th T-connected component, $T^{h,k}$ be its horizontal T-segments, $T^{v,k}$ be its vertical T-segments of ${\mathcal{T}}_k$ and $V^k$ be all the interior vertices of ${\mathcal{T}}_k$, with each interior vertex $v_{i,j}$ located at $(x_i,y_j)$. The j-th T-segment ${\tau }_j$ contains $h_j$ vertices including $h_j^{\left(1\right)}$ mono-vertices and $h_j^{\left(2\right)}$ multi-vertices except for two end vertices ($h_j=h_j^{\left(1\right)}+h_j^{\left(2\right)}+2$). Suppose $h_j^{\left(1\right)}+1\ge M_j$ if ${\tau }_j$ is a horizontal T-segment, and $h_j^{\left(1\right)}+1\ge N_j$ if ${\tau }_j$ is a vertical T-segment; then

$$\begin{array}{ccc}\hfill dim{\mathcal{T}}_k& =& \sum _{v_{i,j}\in V^k}(m-{\mathbf{r}}_h\left(x_i\right))(n-{\mathbf{r}}_v\left(y_j\right))-\sum _{\tau \in T^{h,k}}(m+1)(n-\mathbf{r}\left(\tau \right))\hfill \\ & & -\sum _{\tau \in T^{v,k}}(m-\mathbf{r}\left(\tau \right))(n+1),\hfill \end{array}$$

(10)

where $M_j$ and $N_j$ are two thresholds and $M_j={\displaystyle \frac{{\displaystyle \sum _{v_{i,j}\in {\tau }_j}}{\mathbf{r}}_h\left(x_i\right)+1}{m}}$, $N_j={\displaystyle \frac{{\displaystyle \sum _{v_{i,j}\in {\tau }_j}}{\mathbf{r}}_v\left(y_j\right)+1}{n}}$. In particular, for a free vertex $v_{i,j}$ at $(x_i,y_j)$, $dim{v}_{i,j}=(m-{\mathbf{r}}_h\left(x_i\right))(n-{\mathbf{r}}_v\left(y_j\right))$.

Subsequently, we present the following dimension result of $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ via the smoothing cofactor method.

Theorem 1.

Given a T-mesh $\mathcal{T}$, let $\mathbf{r}$ be a smoothness distribution on $\mathcal{T}$, $C^h$ be interior horizontal cross-cuts, $C^v$ be interior vertical cross-cuts, $T^h$ be horizontal T-segments, $T^v$ be vertical T-segments and V be all of the interior vertices in $\mathcal{T}$, with each interior vertex $v_{i,j}$ located at $(x_i,y_j)$. The j-th T-segment ${\tau }_j$ contains $h_j^{\left(1\right)}$ mono-vertices except for two end vertices. Suppose $h_j^{\left(1\right)}+1\ge M_j$ if ${\tau }_j$ is a horizontal T-segment, and $h_j^{\left(1\right)}+1\ge N_j$ if ${\tau }_j$ is a vertical T-segment. Then

$$\begin{array}{cc}\hfill dim{S}_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)& =(m+1)(n+1)+\sum _{v_{i,j}\in V}(m-{\mathbf{r}}_h\left(x_i\right))(n-{\mathbf{r}}_v\left(y_j\right))\hfill \\ \hfill & +(m+1)[\sum _{\tau \in C^h}(n-\mathbf{r}\left(\tau \right))-\sum _{\tau \in T^h}(n-\mathbf{r}\left(\tau \right))]\hfill \\ \hfill & +(n+1)[\sum _{\tau \in C^v}(m-\mathbf{r}\left(\tau \right))-\sum _{\tau \in T^v}(m-\mathbf{r}\left(\tau \right))],\hfill \end{array}$$

(11)

where $M_j$ and $N_j$ are two thresholds and $M_j={\displaystyle \frac{{\displaystyle \sum _{v_{i,j}\in {\tau }_j}}{\mathbf{r}}_h\left(x_i\right)+1}{m}}$, $N_j={\displaystyle \frac{{\displaystyle \sum _{v_{i,j}\in {\tau }_j}}{\mathbf{r}}_v\left(y_j\right)+1}{n}}$. The summation over $C^h$ represents the sum of the "degrees of freedom" or "smoothness deficits" contributed by every interior horizontal cross-cut τ in the partition $\mathcal{T}$, and the definitions of the other summation terms are analogous.

4. Dimension Instability in Mixed-Smoothness Spline Spaces over Certain T-Meshes

This section provides examples of instable dimensions in mixed-smoothness spline spaces defined over proper T-meshes. We first review results on the dimension singularity of $S(2,2,1,1,{\mathcal{T}}_1)$. Next, we discuss the instability of dimensions in spline spaces $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ over certain T-meshes. We demonstrate that this instability and structural degeneration relate to a geometric property called the singularity factor.

4.1. The Dimension Singularity Condition of $S(2,2,1,1,{\mathcal{T}}_1)$

Guo et al. [23] established a necessary and sufficient condition for dimension singularity in $S(2,2,1,1,{\mathcal{T}}_1)$ over the T-mesh ${\mathcal{T}}_1$ containing a T-cycle (shown in Figure 3a).

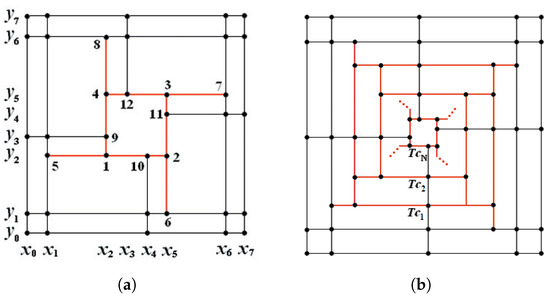
Figure 3. (a) A T-mesh ${\mathcal{T}}_1$ containing a T-cycle (highlighted in red). (b) A T-mesh ${\mathcal{T}}_N$ containing an N-nested T-cycle (highlighted in red).

Theorem 2

([23]). The necessary and sufficient condition of singularity of $dimS(2,2,1,1,{\mathcal{T}}_1)$ is $G_{st}=1$, where $G_{st}={\displaystyle \frac{s_{5,1}{s}_{5,4}}{s_{2,1}{s}_{2,4}}}{\displaystyle \frac{s_{2,6}{s}_{2,3}}{s_{5,6}{s}_{5,3}}}{\displaystyle \frac{t_{5,1}{t}_{5,4}}{t_{2,1}{t}_{2,4}}}{\displaystyle \frac{t_{2,6}{t}_{2,3}}{t_{5,6}{t}_{5,3}}},$ $s_{i,j}=x_i-x_j$, $t_{i,j}=y_i-y_j.$ If $G_{st}=1$, the dimension of $S(2,2,1,1,{\mathcal{T}}_1)$ is 30; otherwise the dimension of $S(2,2,1,1,{\mathcal{T}}_1)$ is 29.

Since dimension instability depends on the value of $G_{st}$, we define this number as the singularity factor for the T-cycle. This is also a geometric condition. For the case of an N-nested T-cycle, as shown in Figure 3b, there exists a corresponding singularity factor for each simple T-cycle, denoted by $a_i(i=1,\dots ,N)$. Li and Wang [24] proved that the dimension of $S(2,2,1,1,{\mathcal{T}}_N)$ is unstable when $N=2,3$ due to different values of the singularity factors $a_i$.

4.2. The Dimension Instability of Mixed-Smoothness Spline Space over a T-Mesh Containing a T-Cycle

Example 1.

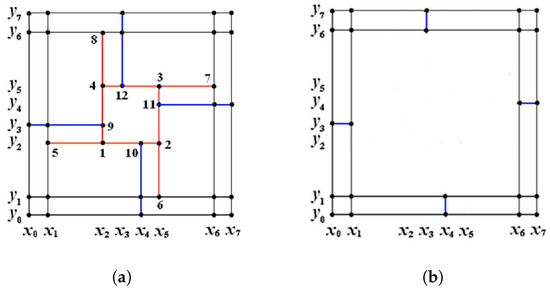
Consider the space of bi-cubic splines $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)$ over the T-mesh ${\mathcal{T}}_1$ with smoothness distribution $\mathbf{r}$ shown in Figure 4a. Let $\mathit{x}={\left(x_i\right)}_{i=0}^7$ and $\mathit{y}={\left(y_i\right)}_{y=0}^7$ be two ascending sequences. The T-cycle $T{c}_1$ in ${\mathcal{T}}_1$ consists of four T-segments: $e_1=\overline{v_5{v}_2}$, $e_2=\overline{v_6{v}_3}$, $e_3=\overline{v_7{v}_4}$ and $e_4=\overline{v_8{v}_1}$. For $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)$, the singularity factor $a_1$ for $T{c}_1$ is

$$a_1={\displaystyle \frac{s_{5,1}{s}_{5,4}^2}{s_{2,1}{s}_{2,4}^2}}{\displaystyle \frac{s_{2,6}{s}_{2,3}^2}{s_{5,6}{s}_{5,3}^2}}{\displaystyle \frac{t_{5,1}{t}_{5,4}^2}{t_{2,1}{t}_{2,4}^2}}{\displaystyle \frac{t_{2,6}{t}_{2,3}^2}{t_{5,6}{t}_{5,3}^2}}.$$

(12)

Figure 4. (a) T-mesh ${\mathcal{T}}_1$ (same as Figure 3a) with smoothness distribution $\mathbf{r}$: smoothness 1 for blue interior segments and smoothness 2 for other interior segments (red and black). (b) The degeneration of T-mesh ${\mathcal{T}}_1$.

Theorem 3.

The dimension of spline space $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)$ over T-mesh ${\mathcal{T}}_1$ shown in Figure 4a is unstable.

$$dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)=\left\{\begin{array}{c}44,if{a}_1\ne 1\left(T{c}_{1}degeneratesawayfrom{\mathcal{T}}_1\right)\hfill \\ 45,if{a}_1=1\left(Nonedegeneration\right)\hfill \end{array}\right.$$

where $a_1$ is defined by (12). The degeneration of the T-mesh is shown in Figure 4b.

Proof. 

See Appendix A. □

Theorem 4.

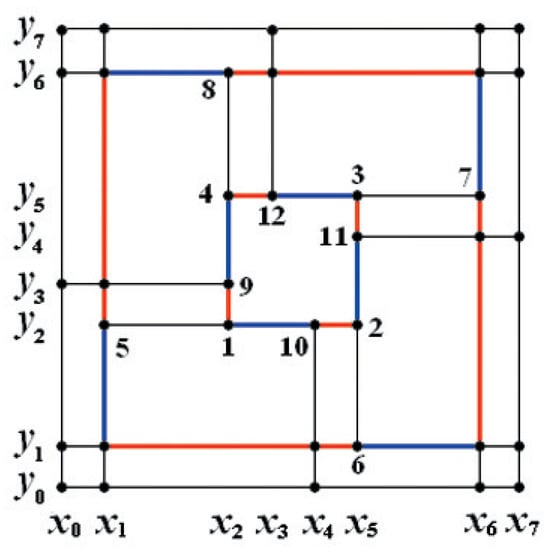
The necessary and sufficient condition for the singularity of $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)$ is that the product of the ratio of the red to blue segment lengths in the outer ring and the square of the ratio of the red to blue segment lengths in the inner ring equals 1 in Figure 5.

Figure 5. The two rings composed of alternating red and blue segments in ${\mathcal{T}}_1$.

We see that dimension instability and structural degeneration are related to the singularity factor $a_1$. Numerical examples for different cases are given below.

• Let $(x_0,x_1,\dots ,x_7)=(0,{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},6)$ and $(y_0,$ $y_1,\dots ,y_7)=(0,1,2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},6)$ in Figure 4a. Through computation, $a_1\ne 1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)=44$ and the inner T-cycle $T{c}_1$ degenerates away from ${\mathcal{T}}_1$.
• Let $(x_0,x_1,\dots ,x_7)=(0,{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},6)$ and $(y_0,$ $y_1,\dots ,y_7)=(0,{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},6)$ in Figure 4a. Through computation, $a_1=1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_1\right)=45$ and ${\mathcal{T}}_1$ is non-degenerate.

As an extension of the structure of ${\mathcal{T}}_1$, we next introduce a T-mesh containing a simple T-cycle that exhibits dimension instability in the mixed-smoothness spline space.

4.3. The Dimension Instability of Mixed-Smoothness Spline Space over a T-Mesh Containing a Simple T-Cycle

Example 2.

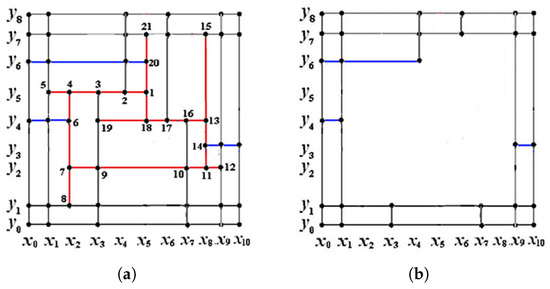
Consider the spline space $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}^{\prime }\right)$ over the T-mesh ${\mathcal{T}}^{\prime }$ with smoothness distribution $\mathbf{r}$ shown in Figure 6a. There is a simple T-cycle $T_s$ in ${\mathcal{T}}^{\prime }$, which consists of six T-segments: $e_1=\overline{v_5{v}_1}$, $e_2=\overline{v_4{v}_8}$, $e_3=\overline{v_7{v}_{12}}$, $e_4=\overline{v_{11}{v}_{15}}$, $e_5=\overline{v_{19}{v}_{13}}$, $e_6=\overline{v_{21}{v}_{18}}$. For $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}^{\prime }\right)$, the singularity factor $a_1^{\prime }$ for $T_s$ is

$$a_1^{\prime }={\displaystyle \frac{t_{4,6}^2{t}_{4,7}}{t_{5,6}^2{t}_{5,7}}}{\displaystyle \frac{s_{7,8}{s}_{6,8}{s}_{3,8}}{s_{5,7}{s}_{5,6}{s}_{3,5}}}{\displaystyle \frac{t_{2,3}^2{t}_{2,7}}{t_{3,4}^2{t}_{4,7}}}{\displaystyle \frac{s_{2,9}{s}_{2,7}{s}_{2,3}}{s_{7,8}{s}_{3,8}{s}_{8,9}}}{\displaystyle \frac{t_{4,5}^2{t}_{1,5}}{t_{2,4}^2{t}_{1,2}}}{\displaystyle \frac{s_{4,5}{s}_{3,5}{s}_{1,5}}{s_{2,4}{s}_{2,3}{s}_{1,2}}}.$$

(13)

Figure 6. (a) T-mesh ${\mathcal{T}}^{\prime }$ with smoothness distribution $\mathbf{r}$: smoothness 1 for blue interior segments and smoothness 2 for other interior segments (red and black). (b) The degeneration of T-mesh ${\mathcal{T}}^{\prime }$.

Theorem 5.

The dimension of spline space $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}^{\prime }\right)$ over T-mesh ${\mathcal{T}}^{\prime }$ shown in Figure 6a is unstable.

$$dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}^{\prime }\right)=\left\{\begin{array}{c}48,if{a}_1^{\prime }\ne 1\left(T_{s}degeneratesawayfrom{\mathcal{T}}^{\prime }\right)\hfill \\ 49,if{a}_1^{\prime }=1\left(Nonedegeneration\right)\hfill \end{array}\right.$$

where $a_1^{\prime }$ is defined by (13). The degeneration of the T-mesh is shown in Figure 6b.

Proof. 

See Appendix B. □

We give the following numerical examples for two different cases.

• Let $(x_0,x_1,\dots ,x_{10})=(1,2,{\displaystyle \frac{11}{4}},3,{\displaystyle \frac{15}{4}},4,5,8,9,{\displaystyle \frac{1367}{148}},10)$ and $(y_0,y_1,\dots ,y_8)=(0,{\displaystyle \frac{29}{38}},1,2,8,{\displaystyle \frac{17}{2}},{\displaystyle \frac{397}{50}}+{\displaystyle \frac{\sqrt{21}}{25}},{\displaystyle \frac{47}{5}},10)$ in Figure 6a. Through computation, $a_1^{\prime }\ne 1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}^{\prime }\right)=48$ and the inner T-cycle $T_s$ degenerates away from ${\mathcal{T}}^{\prime }$.
• Let $(x_0,x_1,\dots ,x_{10})=(1,{\displaystyle \frac{5}{2}},{\displaystyle \frac{11}{4}},3,{\displaystyle \frac{15}{4}},4,5,8,9,{\displaystyle \frac{1367}{148}},10)$ and $(y_0,y_1,\dots ,y_8)=(0,{\displaystyle \frac{29}{38}},1,2,8,{\displaystyle \frac{17}{2}},{\displaystyle \frac{397}{50}}+{\displaystyle \frac{\sqrt{21}}{25}},{\displaystyle \frac{47}{5}},10)$ in Figure 6a. Through computation, $a_1^{\prime }=1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}^{\prime }\right)=49$ and ${\mathcal{T}}^{\prime }$ is non-degenerate.

4.4. The Dimension Instability of Mixed-Smoothness Spline Space over a T-Mesh Containing a Two-Nested T-Cycle

Example 3.

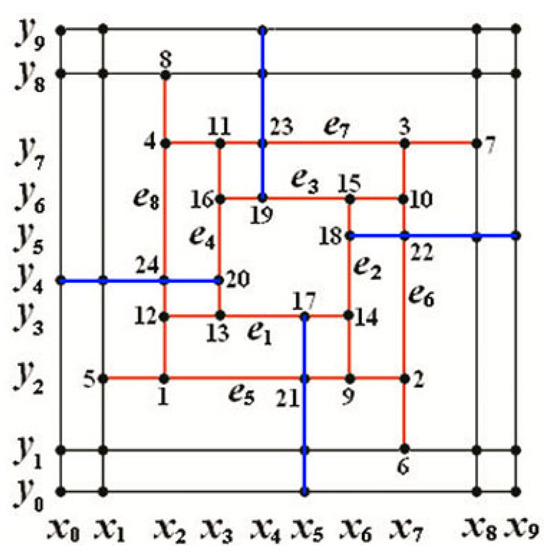
We now consider the spline space $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)$ over the T-mesh ${\mathcal{T}}_2$ containing a two-nested T-cycle, with its smoothness distribution $\mathbf{r}$ as shown in Figure 7. Let $\mathit{x}={\left(x_i\right)}_{i=0}^9$ and $\mathit{y}={\left(y_i\right)}_{y=0}^9$ be two ascending sequences. There are two T-cycles, $T{c}_1$ and $T{c}_2$, where $T{c}_1=\{e_5=\overline{v_5{v}_2},e_6=\overline{v_6{v}_3},e_7=\overline{v_7{v}_4},e_8=\overline{v_8{v}_1}\}$, $T{c}_2=\{e_1=\overline{v_{12}{v}_{14}},e_2=\overline{v_9{v}_{15}},e_3=\overline{v_{10}{v}_{16}},e_4=\overline{v_{11}{v}_{13}}\}$. For $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)$, the two singularity factors $a_1$ and $a_2$ for $T{c}_1$ and $T{c}_2$ are

$$a_1={\displaystyle \frac{s_{5,7}^2{s}_{1,7}}{s_{2,5}^2{s}_{1,2}}}{\displaystyle \frac{t_{5,7}^2{t}_{1,7}}{t_{2,5}^2{t}_{1,2}}}{\displaystyle \frac{s_{2,4}^2{s}_{2,8}}{s_{4,7}^2{s}_{7,8}}}{\displaystyle \frac{t_{2,4}^2{t}_{2,8}}{t_{4,7}^2{t}_{7,8}}},$$

(14)

$$a_2={\displaystyle \frac{s_{5,6}^2{s}_{2,6}}{s_{3,5}^2{s}_{2,3}}}{\displaystyle \frac{t_{5,6}^2{t}_{2,6}}{t_{3,5}^2{t}_{2,3}}}{\displaystyle \frac{s_{3,4}^2{s}_{3,7}}{s_{4,6}^2{s}_{6,7}}}{\displaystyle \frac{t_{3,4}^2{t}_{3,7}}{t_{4,6}^2{t}_{6,7}}}.$$

(15)

Figure 7. T-mesh ${\mathcal{T}}_2$ containing a 2-nested T-cycle with smoothness distribution $\mathbf{r}$: smoothness 1 for blue interior segments and smoothness 2 for other interior segments (red and black).

Theorem 6.

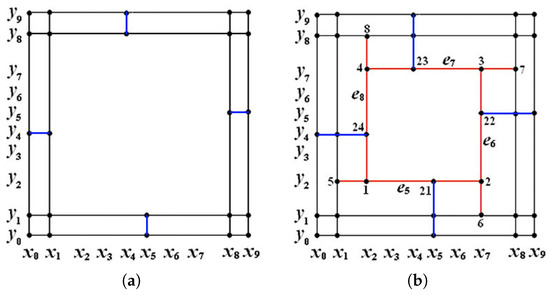
The dimension of spline space $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)$ over T-mesh ${\mathcal{T}}_2$ shown in Figure 7 is unstable.

$$\begin{array}{cc}\hfill & dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)=\hfill \\ \hfill & \left\{\begin{array}{cc}& 44,if{a}_1\ne 1and{a}_2\ne 1\left(BothT{c}_{1}andT{c}_{2}degenerateawayfrom{\mathcal{T}}_2\right),\hfill \\ \hfill & 45,if{a}_1=1and\forall a_2\left(T{c}_{2}degeneratesawayfrom{\mathcal{T}}_2\right),\hfill \\ \hfill & 45,if{a}_1\ne 1and{a}_2=1\left(Nonedegeneration\right).\hfill \end{array}\right.\hfill \end{array}$$

where $a_1$ and $a_2$ are defined by (14) and (15). The T-mesh’s degeneration for two different cases is shown in Figure 8.

Figure 8. The degeneration of T-mesh ${\mathcal{T}}_2$: (a) both T-cycles are degenerate; (b) the inner T-cycle is degenerate (the remaining T-cycle is highlighted in red).

Proof. 

See Appendix C. □

We see that dimension instability and structural degeneration relate to the singularity factor value of each T-cycle. We provide four numerical examples for different cases.

• Let $(x_0,x_1,\dots ,x_9)=(-2,1,{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},{\displaystyle \frac{11}{3}},{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ and $(y_0,$ $y_1,\dots ,y_9)=(-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ in Figure 7. Through computation, $a_1\ne 1$ and $a_2\ne 1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)=44$ and two T-cycles degenerate away from ${\mathcal{T}}_2$.
• Let $(x_0,x_1,\dots ,x_9)=(-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},{\displaystyle \frac{11}{3}},{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ and $(y_0,$ $y_1,\dots ,y_9)=(-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ in Figure 7. Through computation, $a_1=1$ and $a_2\ne 1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)=45$ and the inner T-cycle $T{c}_2$ degenerates away from ${\mathcal{T}}_2$.
• Let $(x_0,x_1,\dots ,x_9)=(-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ and $(y_0,$ $y_1,\dots ,y_9)=(-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ in Figure 7. Through computation, $a_1=1$ and $a_2=1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)=45$ and the inner T-cycle $T{c}_2$ degenerates away from ${\mathcal{T}}_2$.
• Let $(x_0,x_1,\dots ,x_9)=(-2,-{\displaystyle \frac{5}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ and $(y_0,$ $y_1,\dots ,y_9)=(-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},8)$ in Figure 7. Through computation, $a_1\ne 1$ and $a_2=1$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_2\right)=45$ and ${\mathcal{T}}_2$ is non-degenerate.

4.5. The Dimension Instability of Mixed-Smoothness Spline Spaces over a T-Mesh Containing a Three-Nested T-Cycle

Example 4.

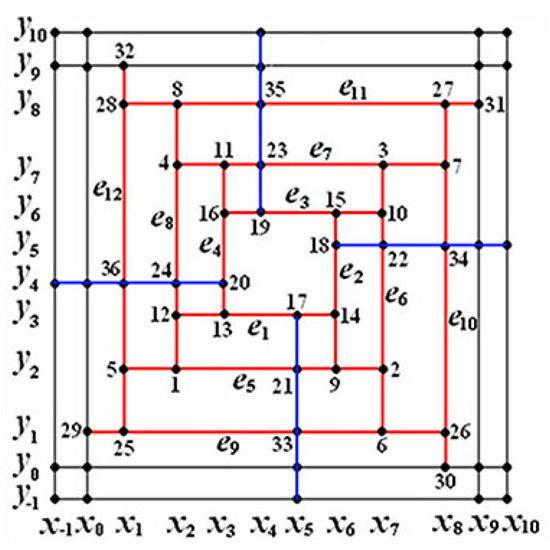
Figure 9 shows a T-mesh containing a three-nested T-cycle ${\mathcal{T}}_3$, formed by adding a new T-cycle outside the previously mentioned two-nested T-cycle in ${\mathcal{T}}_2$. We rename the three T-cycles as follows:

$$T{c}_1=\{e_9=\overline{v_{29}{v}_{26}},e_{10}=\overline{v_{30}{v}_{27}},e_{11}=\overline{v_{31}{v}_{28}},e_{12}=\overline{v_{32}{v}_{25}}\},$$

$$T{c}_2=\{e_5=\overline{v_5{v}_2},e_6=\overline{v_6{v}_3},e_7=\overline{v_7{v}_4},e_8=\overline{v_8{v}_1}\},$$

$$T{c}_3=\{e_1=\overline{v_{12}{v}_{14}},e_2=\overline{v_9{v}_{15}},e_3=\overline{v_{10}{v}_{16}},e_4=\overline{v_{11}{v}_{13}}\}.$$

For the spline space of $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)$, the three singularity factors $a_1$, $a_2$ and $a_3$ for $T{c}_1$,$T{c}_2$ and $T{c}_3$ are

$$a_1={\displaystyle \frac{s_{5,8}^2{s}_{0,8}}{s_{1,5}^2{s}_{0,1}}}{\displaystyle \frac{t_{5,8}^2{t}_{0,8}}{t_{1,5}^2{t}_{0,1}}}{\displaystyle \frac{s_{1,4}^2{s}_{1,9}}{s_{4,8}^2{s}_{8,9}}}{\displaystyle \frac{t_{1,4}^2{t}_{1,9}}{t_{4,8}^2{t}_{8,9}}},$$

(16)

$$a_2={\displaystyle \frac{s_{5,7}^2{s}_{1,7}}{s_{2,5}^2{s}_{1,2}}}{\displaystyle \frac{t_{5,7}^2{t}_{1,7}}{t_{2,5}^2{t}_{1,2}}}{\displaystyle \frac{s_{2,4}^2{s}_{2,8}}{s_{4,7}^2{s}_{7,8}}}{\displaystyle \frac{t_{2,4}^2{t}_{2,8}}{t_{4,7}^2{t}_{7,8}}},$$

(17)

$$a_3={\displaystyle \frac{s_{5,6}^2{s}_{2,6}}{s_{3,5}^2{s}_{2,3}}}{\displaystyle \frac{t_{5,6}^2{t}_{2,6}}{t_{3,5}^2{t}_{2,3}}}{\displaystyle \frac{s_{3,4}^2{s}_{3,7}}{s_{4,6}^2{s}_{6,7}}}{\displaystyle \frac{t_{3,4}^2{t}_{3,7}}{t_{4,6}^2{t}_{6,7}}}.$$

(18)

Figure 9. A T-mesh ${\mathcal{T}}_3$ containing a 3-nested T-cycle with smoothness distribution $\mathbf{r}$: smoothness 1 for blue interior segments and smoothness 2 for other interior segments (red and black).

Conjecture 1.

The dimension of spline space $S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)$ over the T-mesh ${\mathcal{T}}_3$ shown in Figure 9 is unstable.

$$\begin{array}{cc}\hfill & S_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=\hfill \\ \hfill & \left\{\begin{array}{cc}& 44,if{a}_1\ne 1,a_2\ne 1and{a}_3\ne 1(AllT{c}_1,T{c}_{2}andT{c}_{3}degenerateawayfrom{\mathcal{T}}_3),\hfill \\ \hfill & 45,if{a}_1=1,\forall a_{2}and\forall a_3\left(BothT{c}_{2}andT{c}_{3}degenerateawayfrom{\mathcal{T}}_3\right),\hfill \\ \hfill & 45,if{a}_1\ne 1,a_2=1and\forall a_3\left(T{c}_{3}degeneratesawayfrom{\mathcal{T}}_3\right),\hfill \\ \hfill & 45,if{a}_1\ne 1,a_2\ne 1and{a}_3=1\left(Nonedegeneration\right).\hfill \end{array}\right.\hfill \end{array}$$

where $a_1$, $a_2$ and $a_3$ are defined by (16), (17) and (18). The T-mesh’s degeneration in three different cases is shown in Figure 10.

Figure 10. The degeneration of T-mesh ${\mathcal{T}}_3$: (a) The T-cycles are completely degenerate. (b) The inner T-cycles $T{c}_2$ and $T{c}_3$ are degenerate(the remaining T-cycle is highlighted in red). (c) The innermost T-cycle $T{c}_3$ is degenerate(the remaining nested T-cycle is highlighted in red).

Analysis. See Appendix D.

We provide numerical examples for various degeneration cases of the T-mesh containing a three-nested T-cycle, as detailed below.

• Let $(x_{-1},x_0,\dots ,x_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},3,4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1\ne 1$, $a_2\ne 1$ and $a_3\ne 1$, $b_1=-0.6227$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=44$ and three T-cycles degenerate away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,5,{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1=1$, $a_2\ne 1$ and $a_3\ne 1$, $b_1=-0.6343$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, both $T{c}_2$ and $T{c}_3$ degenerate away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},{\displaystyle \frac{11}{3}},{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1=1$, $a_2=1$ and $a_3\ne 1$, $b_1=-0.4082$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, both $T{c}_2$ and $T{c}_3$ degenerate away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1=1$, $a_2=1$ and $a_3=1$, $b_1=-0.4082$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, both $T{c}_2$ and $T{c}_3$ degenerate away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-5,-4,1,4,5,7,11,13,14,16,28,30)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-5,-4,1,4,5,7,11,13,14,16,28,30)$ in Figure 9. Through computation, $a_1=1$, $a_2\ne 1$ and $a_3=1$, $b_1=-1.3777$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, both $T{c}_2$ and $T{c}_3$ degenerate away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-4,-3,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},{\displaystyle \frac{7}{3}},{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1\ne 1$, $a_2=1$ and $a_3\ne 1$, $b_1=-1.7699$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, $T{c}_3$ degenerates away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-3,-2,-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1\ne 1$, $a_2=1$ and $a_3=1$, $b_1=-3.9650$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, $T{c}_3$ degenerates away from ${\mathcal{T}}_3$.
• Let $(x_{-1},x_0,\dots ,x_{10})=(-30,-{\displaystyle \frac{76}{3}},0,{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ and $(y_{-1},$ $y_0,\dots ,y_{10})=(-30,-{\displaystyle \frac{76}{3}},-{\displaystyle \frac{4}{3}},{\displaystyle \frac{4}{3}},2,{\displaystyle \frac{8}{3}},{\displaystyle \frac{10}{3}},4,{\displaystyle \frac{14}{3}},{\displaystyle \frac{22}{3}},{\displaystyle \frac{94}{3}},35)$ in Figure 9. Through computation, $a_1\ne 1$, $a_2\ne 1$ and $a_3=1$, $b_1=-0.8464$; hence, $dim{S}_{3,3}^{\mathbf{r}}\left({\mathcal{T}}_3\right)=45$, ${\mathcal{T}}_3$ is non-degenerate.

5. Conclusions

In this paper, we analyse the dimensions of the spline space $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$ that are piecewise bi-degree polynomials $(m,n)$ with smoothness $\mathbf{r}$ across interior segments of a general planar T-mesh $\mathcal{T}$, where $\mathbf{r}$ denotes a smoothness distribution on $\mathcal{T}$. We establish a sufficient condition to guarantee the dimensional stability of $S_{m,n}^{\mathbf{r}}\left(\mathcal{T}\right)$. Furthermore, we study dimension instability in spline spaces with mixed smoothness over specific T-meshes, including T-cycle, simple T-cycle, and two- and three-nested T-cycles. The results show that dimension instability and structural degeneration relate to a geometric property defined by a singularity factor. In the future, we will discuss dimension instability and structural degeneration for more spline spaces.