The Instability in the Dimensions of Polynomial Splines of Mixed Smoothness over T-Meshes
Abstract
1. Introduction
2. Preliminaries
2.1. T-Meshes
2.2. Mixed-Smoothness Spline Spaces over T-Meshes
3. A Sufficient Condition for Stable Dimension Formula for Mixed-Smoothness Spline Spaces
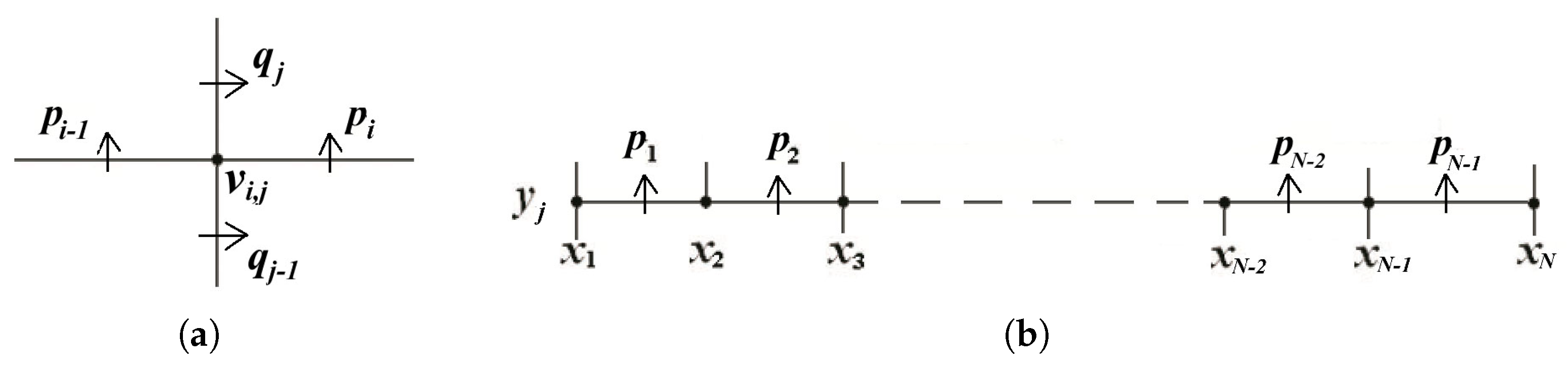
3.1. Two Types of Conformality Conditions Along T-Segments
3.2. The Dimensions of the Two Types of Conformality Conditions
3.3. The Dimensions of the Spline Spaces on T-Mesh
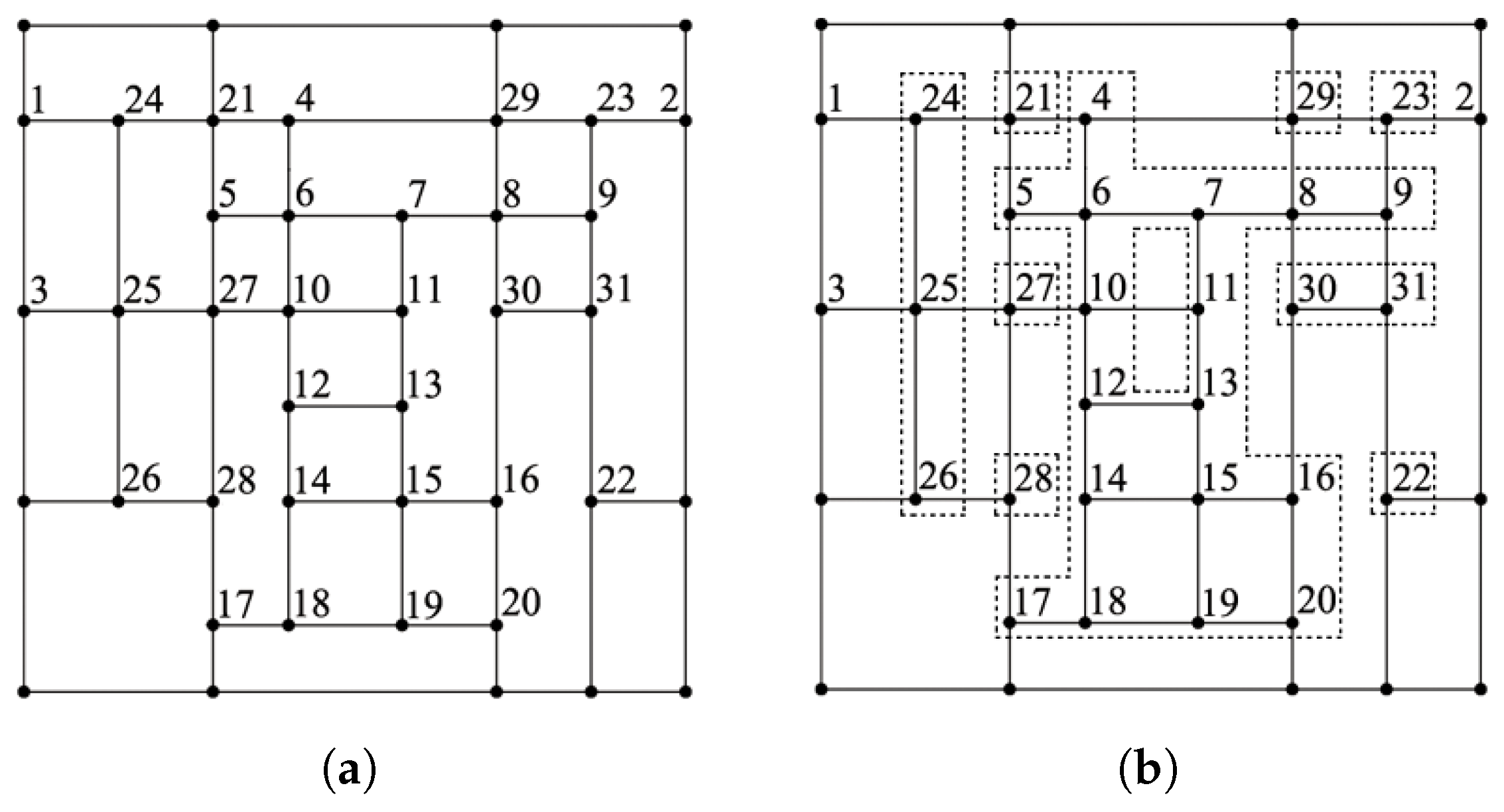
4. Dimension Instability in Mixed-Smoothness Spline Spaces over Certain T-Meshes
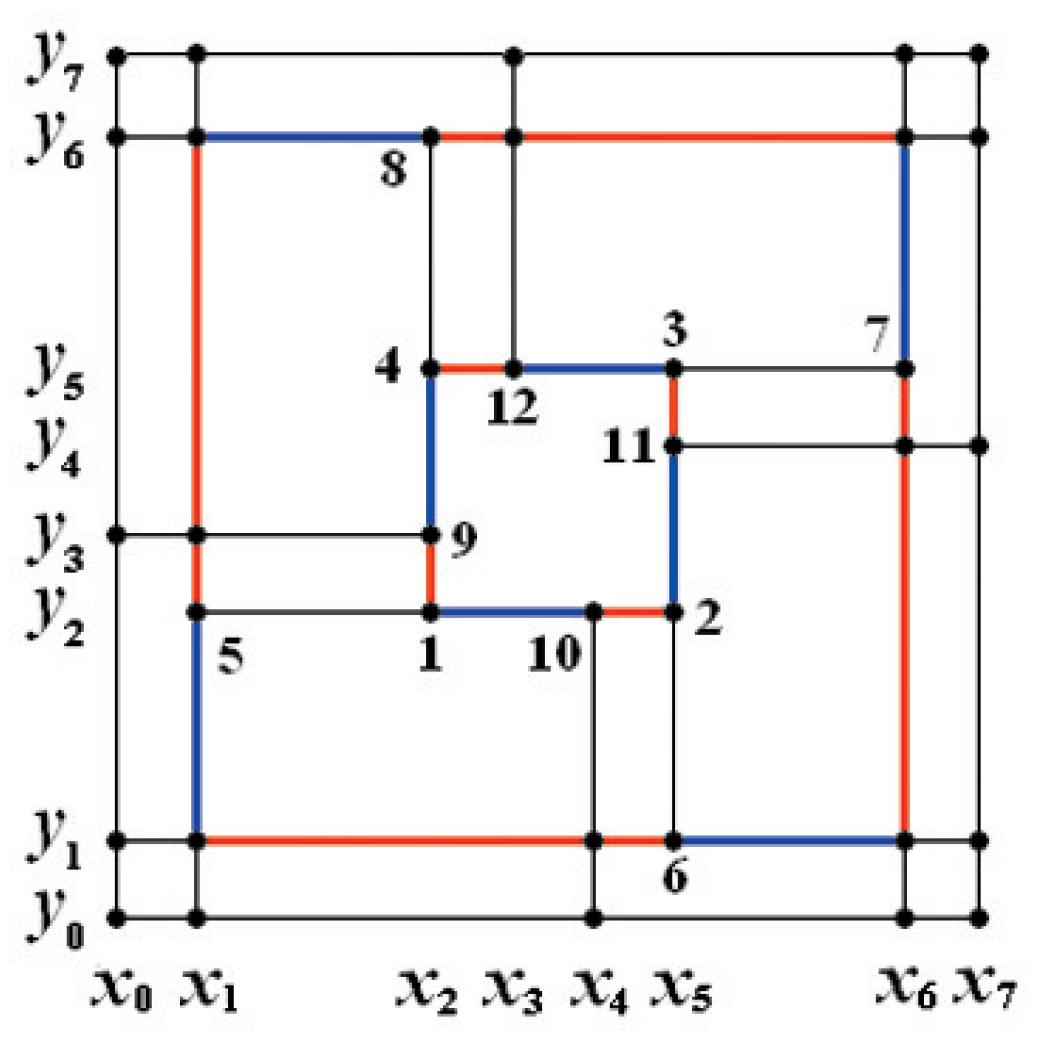
4.1. The Dimension Singularity Condition of
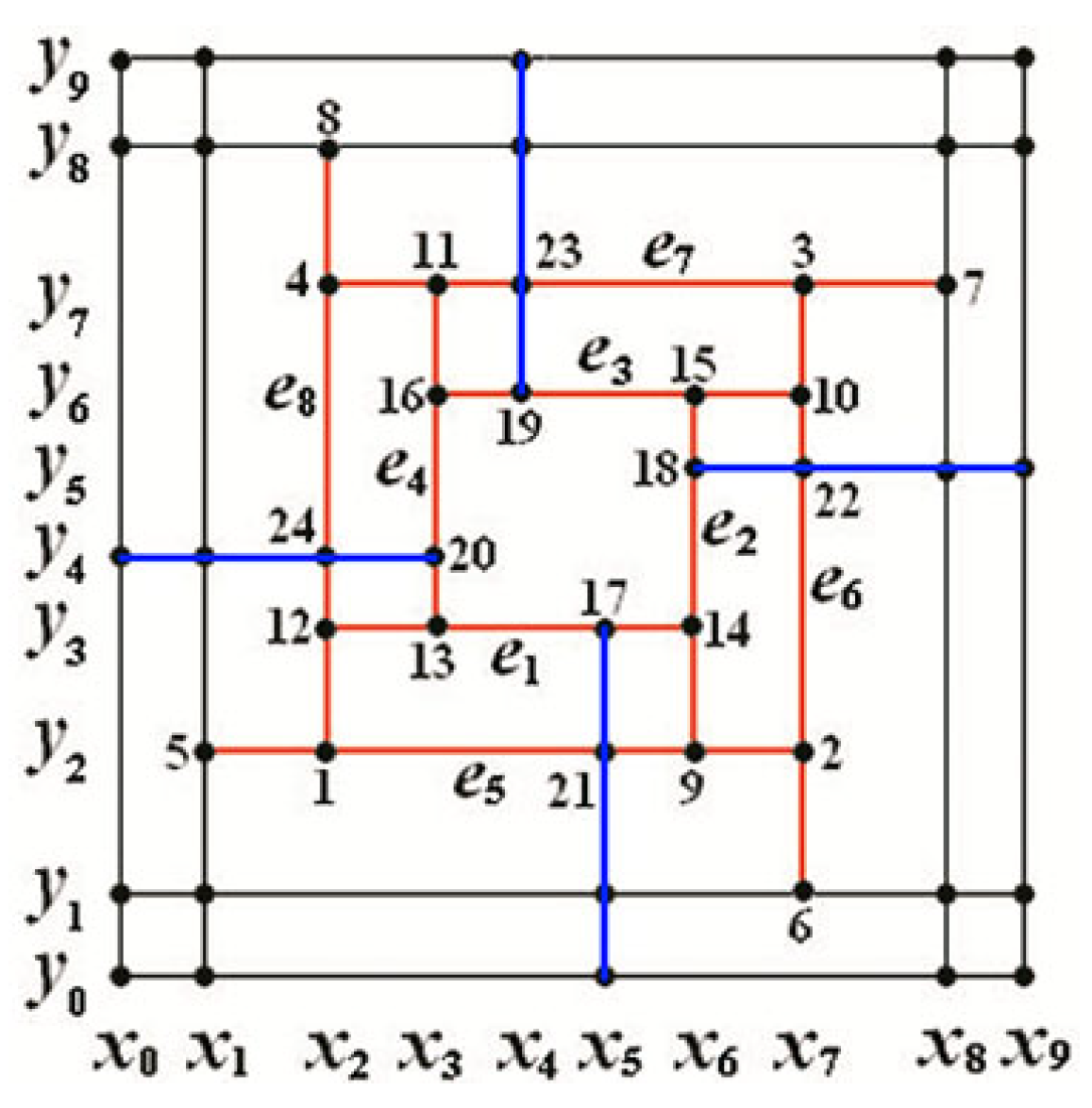
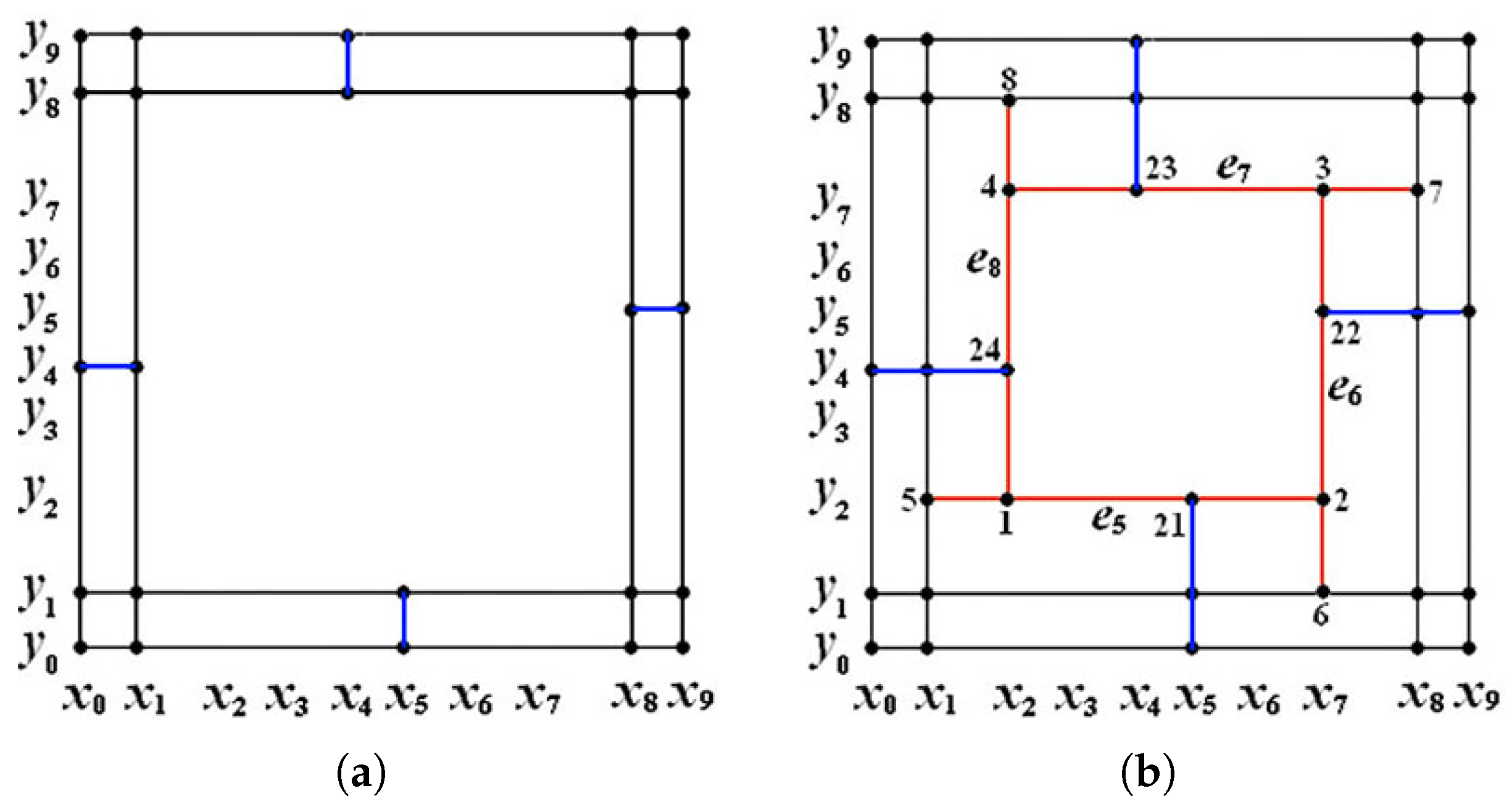
4.2. The Dimension Instability of Mixed-Smoothness Spline Space over a T-Mesh Containing a T-Cycle
- Let and in Figure 4a. Through computation, ; hence, and the inner T-cycle degenerates away from .
- Let and in Figure 4a. Through computation, ; hence, and is non-degenerate.
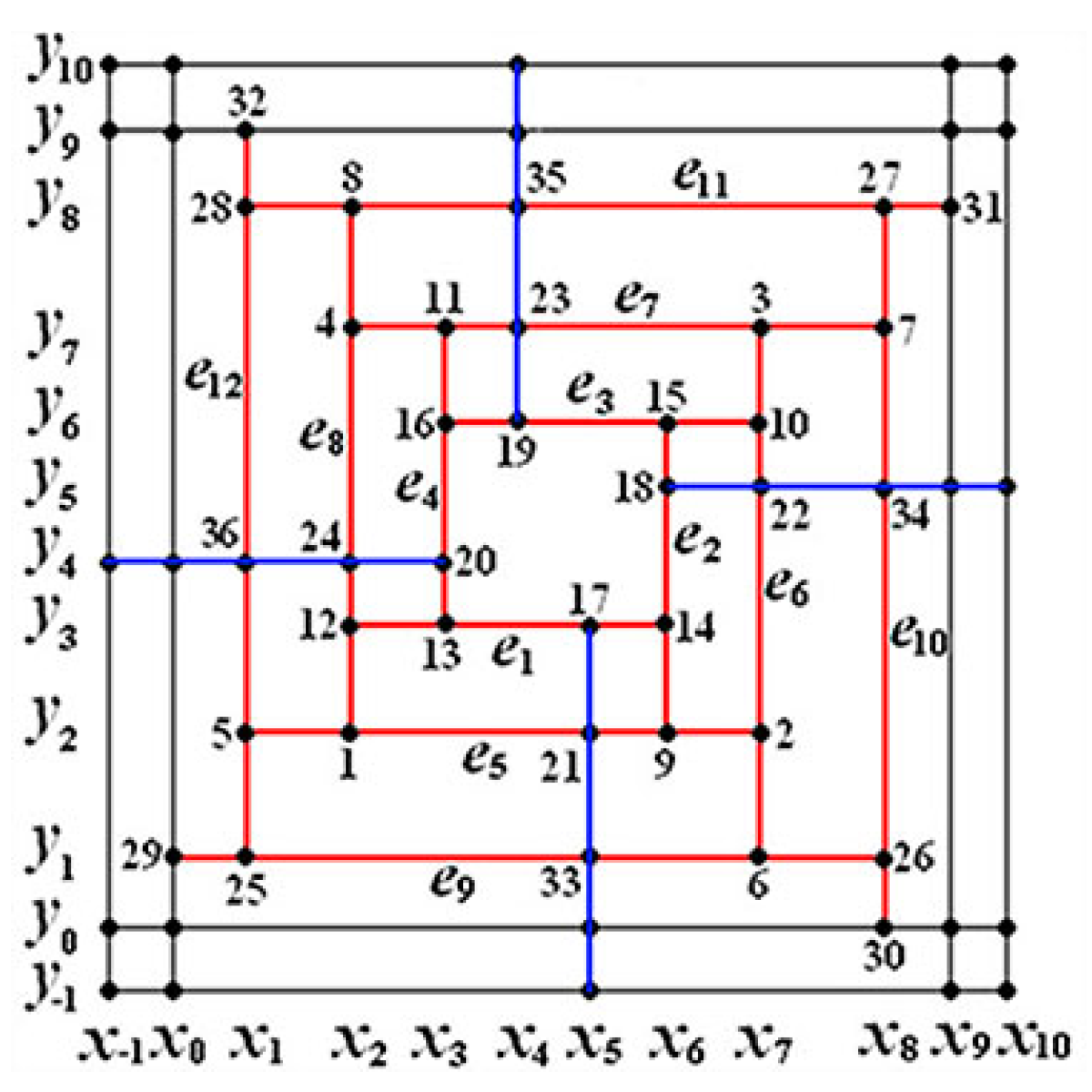
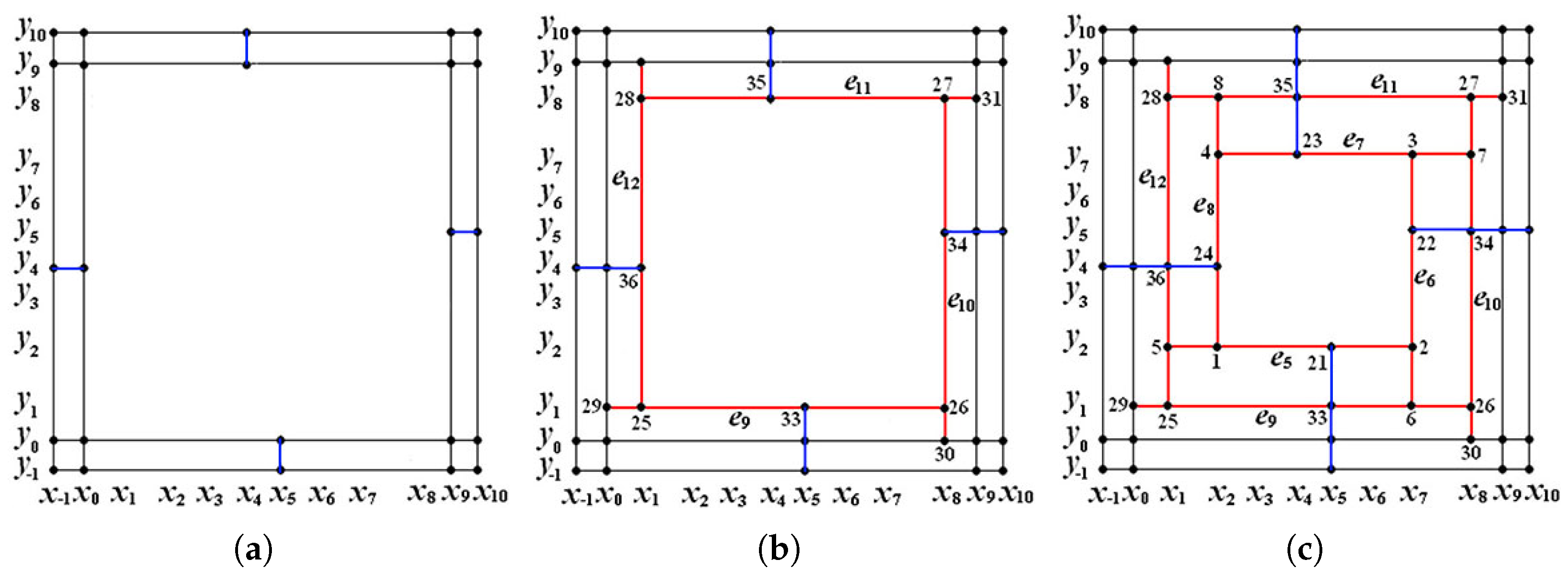
4.3. The Dimension Instability of Mixed-Smoothness Spline Space over a T-Mesh Containing a Simple T-Cycle
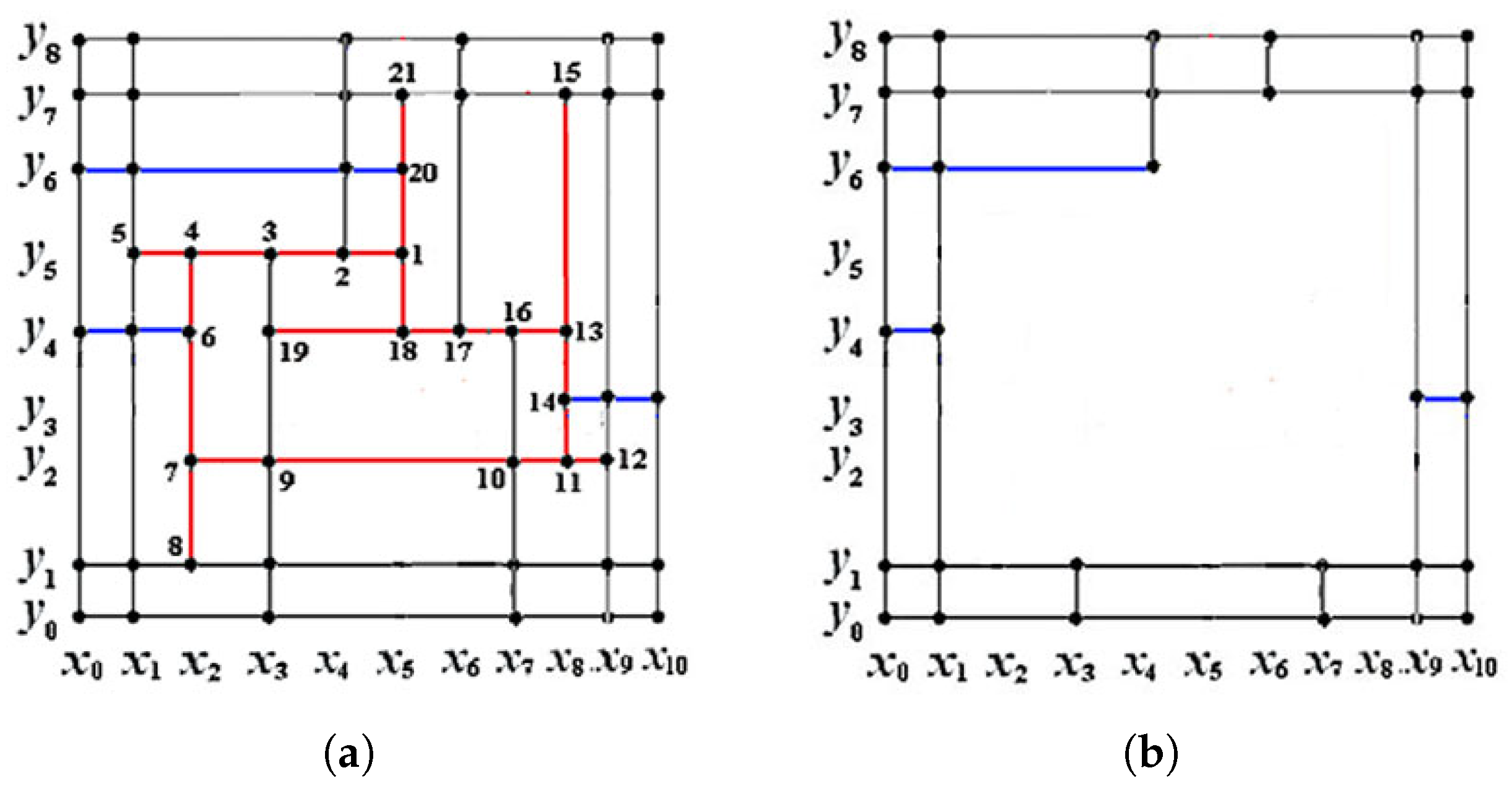
4.4. The Dimension Instability of Mixed-Smoothness Spline Space over a T-Mesh Containing a Two-Nested T-Cycle
- Let and in Figure 7. Through computation, and ; hence, and two T-cycles degenerate away from .
- Let and in Figure 7. Through computation, and ; hence, and the inner T-cycle degenerates away from .
- Let and in Figure 7. Through computation, and ; hence, and the inner T-cycle degenerates away from .
- Let and in Figure 7. Through computation, and ; hence, and is non-degenerate.
4.5. The Dimension Instability of Mixed-Smoothness Spline Spaces over a T-Mesh Containing a Three-Nested T-Cycle
- Let and in Figure 9. Through computation, , and , ; hence, and three T-cycles degenerate away from .
- Let and in Figure 9. Through computation, , and , ; hence, , both and degenerate away from .
- Let and in Figure 9. Through computation, , and , ; hence, , both and degenerate away from .
- Let and in Figure 9. Through computation, , and , ; hence, , both and degenerate away from .
- Let and in Figure 9. Through computation, , and , ; hence, , both and degenerate away from .
- Let and in Figure 9. Through computation, , and , ; hence, , degenerates away from .
- Let and in Figure 9. Through computation, , and , ; hence, , degenerates away from .
- Let and in Figure 9. Through computation, , and , ; hence, , is non-degenerate.
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
- If , then is a free variable, and the dimension of the T-connected component containing a two-nested T-cycle is 1.
- If , then , i.e., is also degenerate. The dimension of the T-connected component containing a two-nested T-cycle is 0.
Appendix D
References
- Ayman-Mursaleen, M. Quadratic function preserving wavelet type Baskakov operators for enhanced function approximation. Comp. Appl. Math. 2025, 44, 395. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Jha, N.K. Szász-integral operators linking general-Appell polynomials and approximation. AIMS Math. 2025, 10, 13836–13854. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Zheng, J.M.; Bakenov, A.; Nasri, A. T-splines and T-NURCCs. ACM Trans. Graph. 2003, 22, 477–484. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Cardon, D.L.; Finnigan, G.T.; North, N.S.; Zheng, J.M.; Lyche, T. T-spline simplification and local refinement. ACM Trans. Graph. 2004, 23, 276–283. [Google Scholar] [CrossRef]
- Li, X.; Zheng, J.M.; Sederberg, T.W.; Hughes, T.J.R.; Scott, M.A. On linear independence of T-spline blending functions. Comput. Aided Geom. Des. 2012, 29, 63–76. [Google Scholar] [CrossRef]
- Scott, M.A.; Li, X.; Sederberg, T.W.; Hughes, T.J.R. Local refinement of analysis-suitable T-splines. Comput. Methods Appl. Mech. Eng. 2012, 213–216, 206–222. [Google Scholar] [CrossRef]
- Pan, M.D.; Zou, R.J.; Jüttler, B. Algorithms and data structures for Cs-smooth RMB-splines of Degree 2s+1. Comput. Aided Geom. Des. 2024, 114, 102389. [Google Scholar] [CrossRef]
- Groiss, L.; Jüttler, B.; Pan, M.D. Local linear independence of bilinear (and higher degree) B-splines on hierarchical T-meshes. Comput. Aided Geom. Des. 2023, 103, 102190. [Google Scholar] [CrossRef]
- Groiss, L.; Jüttler, B.; Pan, M.D. On Tensor-Product Bases of PHT-Spline Spaces. In Proceedings of the INdAM Meeting: Approximation Theory and Numerical Analysis Meet Algebra, Geometry, Topology; Springer Nature: Singapore, 2022; Volume 60, pp. 181–203. [Google Scholar] [CrossRef]
- Deng, J.S.; Chen, F.L.; Feng, Y.Y. Dimensions of spline spaces over T-meshes. J. Comput. Appl. Math. 2006, 194, 267–283. [Google Scholar] [CrossRef]
- Huang, Z.J.; Deng, J.S.; Feng, Y.Y.; Chen, F.L. New proof of dimension formula of spline spaces over T-meshes via smoothing cofactors. J. Comput. Math. 2006, 24, 501–514. Available online: https://computmath.cjoe.ac.cn/jcm/CN/Y2006/V24/I4/501 (accessed on 2 September 2025).
- Wang, R.H. The structural characterization and interpolation for multivariate splines. Acta Math. Sinica 1975, 18, 91–106. [Google Scholar]
- Wang, R.H. Multivariate Spline Functions and Their Applications. Springer: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Li, C.J.; Wang, R.H.; Zhang, F. Improvement on the dimensions of spline spaces on T-mesh. J. Inf. Comput. Sci. 2006, 3, 235–244. Available online: https://www.researchgate.net/publication/228706959 (accessed on 2 September 2025).
- Li, C.J.; Chen, J. On the dimensions of bivariate spline spaces and the stability of the dimensions. J. Comput. Appl. Math. 2011, 236, 765–774. [Google Scholar] [CrossRef]
- Mourrain, B. On the dimension of spline spaces on planar T-meshes. Math. Comput. 2014, 83, 847–871. [Google Scholar] [CrossRef]
- Li, X.; Deng, J.S. On the dimension of spline spaces over T-meshes with smoothing cofactor-conformality method. Comput. Aided Geom. Des. 2016, 41, 76–86. [Google Scholar] [CrossRef]
- Shi, X.Q. The singularity of Morgan-Scott triangulation. Comput. Aided Geom. Des. 1991, 8, 201–206. [Google Scholar] [CrossRef]
- Diener, D. Instability in the dimension of spaces of bivariate piecewise polynomials of degree 2r and smoothness order r. SIAM J. Numer. Anal. 1990, 2, 543–551. [Google Scholar] [CrossRef]
- Du, H.; Shi, X.Q.; Wang, R.H. A geometric approach to (ΔMS). J. Syst. Sci. Complex. 2002, 15, 202–204. Available online: https://sysmath.cjoe.ac.cn/jssc/EN/Y2002/V15/I2/202 (accessed on 2 September 2025).
- Li, X.; Chen, F.L. On the instability in the dimension of splines spaces over T-meshes. Comput. Aided Geom. Des. 2011, 28, 420–426. [Google Scholar] [CrossRef]
- Berdinsky, D.; Oh, M.; Kim, T.; Mourrain, B. On the problem of instability in the dimension of a spline space over a T-mesh. Comput. Graph. 2012, 36, 507–513. [Google Scholar] [CrossRef]
- Guo, Q.J.; Wang, R.H.; Li, C.J. On the problem of instability in the dimensions of spline spaces over T-meshes with T-cycles. J. Comput. Math. 2015, 33, 248–262. [Google Scholar] [CrossRef]
- Li, C.J.; Wang, P.X. The instablility in the dimensions of spline spaces over T-meshes with Nested T-cycles. Numer. Math. Theor. Meth. Appl. 2019, 12, 187–211. [Google Scholar] [CrossRef]
- Toshniwal, D.; Villamizar, N. Dimension of polynomial splines of mixed smoothness on T-meshes. Comput. Aided Geom. Des. 2020, 80, 101880. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P. The Instability in the Dimensions of Polynomial Splines of Mixed Smoothness over T-Meshes. Mathematics 2025, 13, 2886. https://doi.org/10.3390/math13172886
Wang P. The Instability in the Dimensions of Polynomial Splines of Mixed Smoothness over T-Meshes. Mathematics. 2025; 13(17):2886. https://doi.org/10.3390/math13172886
Chicago/Turabian StyleWang, Pengxiao. 2025. "The Instability in the Dimensions of Polynomial Splines of Mixed Smoothness over T-Meshes" Mathematics 13, no. 17: 2886. https://doi.org/10.3390/math13172886
APA StyleWang, P. (2025). The Instability in the Dimensions of Polynomial Splines of Mixed Smoothness over T-Meshes. Mathematics, 13(17), 2886. https://doi.org/10.3390/math13172886





