Abstract
The security of video data requires cryptographic techniques that are resilient to both classical and quantum threats. This study presents an encryption framework based on association schemes and algebraic combinatorial tools that enable systematic and secure data transformations. In the classical setting, video encryption is achieved through random matrix transformations applied to the relations of an association scheme, producing secure and imperceptible ciphertext. Experimental evaluations, including statistical and error analyses, confirm the robustness and efficiency of the proposed method. We extend the framework to quantum cryptography by exploring unitary encryption operators derived from the Bose–Mesner algebra of association schemes. These operators are used to encrypt quantum-encoded multimedia data. The results demonstrate the potential of association schemes to support secure multimedia encryption in both classical and quantum domains.
MSC:
05E30; 94A60; 81P94; 94A08
1. Introduction
In today’s rapidly evolving digital landscape, the widespread adoption of video across domains such as pay television, video surveillance, video-on-demand (VOD), and conferencing platforms highlights the pressing need for robust security mechanisms. The open nature of transmission channels poses significant threats to the confidentiality and integrity of video data [1,2]. Additionally, new environments such as multi-UAV systems further necessitate secure, scalable encryption schemes [3].
The literature has explored several techniques aimed at securing two-dimensional data through various transformations, including optical, chaotic, and scrambling-based approaches [4,5,6,7,8,9]. Traditionally, video security can be achieved through three main techniques: video encryption (cryptography), video watermarking, and video steganography [10,11,12,13,14,15,16,17]. Cryptography stands out due to its ability to offer high confidentiality through mathematically driven key-based transformations. Within this space, algebraic combinatorics, specifically association schemes, offer a powerful foundation for constructing structured and efficient encryption algorithms. Multiple recent schemes have been developed for the secure transmission of video data, focusing on improving encryption speed, compression compatibility, and cryptographic strength [18].
Recent research into multimedia security has explored increasingly sophisticated techniques for robust content protection. Zhang et al. [19] proposed a frequency-domain, attention-guided, adaptive, robust, watermarking model that enhances resistance to diverse attacks while maintaining visual quality. In another direction, a visually meaningful triple-image encryption algorithm based on 2D compressive sensing and multi-region embedding [20] demonstrated how high-capacity multi-image encryption can be combined with visually meaningful outputs. These emerging approaches align with the present study’s aim of leveraging algebraic structures, particularly association schemes, for the development of classical and quantum cryptographic models tailored to secure multimedia transmission.
Association schemes, originally formalized by Bose and Shimamoto [21], are algebraic structures that describe relationships within a finite set through a partition of its Cartesian square. These schemes are widely used in coding theory, group theory, and design theory due to their strong combinatorial regularity and algebraic symmetry [22,23]. In particular, symmetric and commutative association schemes exhibit desirable properties that make them suitable for secure transformations. A complete exposition of definitions, algebraic properties, and examples of association schemes can be found in [22,23].
Sabharwal et al. recently introduced non-symmetric commutative association schemes for product groups such as and demonstrated their utility in securing image and text data via algebraic ciphers [24,25]. These schemes provide algebraic flexibility and cryptographic strength for multidimensional data structures.
Motivated by the versatility and strong algebraic foundation of association schemes, this work develops a dual cryptographic model operating in both classical and quantum settings. In the classical framework, we apply a Random Matrix Transformation on Association Schemes (RMTAS), where structured random matrices act on scheme relations over to realize systematic, key-driven pixel transformations for video encryption. In the quantum framework, we exploit the Bose–Mesner algebra of a symmetric association scheme to construct unitary encryption operators that act on quantum-encoded multimedia states. This approach is inspired by recent work by Chan and Martin [26], who demonstrated how association schemes can be applied in quantum information theory, particularly in problems such as the quantum isomorphism of graphs. By formulating both models within a unified algebraic framework, the study highlights the scalability of association schemes across computational paradigms and their potential as a mathematical bridge between current and quantum-secure cryptographic systems.
In this study, Section 2 presents the proposed classical cryptographic framework using association schemes and random matrix transformations. Section 3 reports the experimental results for the classical scheme, followed by detailed error analysis in Section 4. Section 5 provides a comparative evaluation with existing techniques. Section 6 introduces the quantum cipher construction, outlining the quantum encoding model and the unitary operator derived from the Bose–Mesner algebra. Finally, Section 7 concludes this study and discusses future research directions.
2. Proposed Approach for Secure Video Transmission
Cryptography is the process of protecting sensitive information and communications through encryption and decryption. During encryption, information is converted into ciphertext using an encryption key, making it unintelligible to unauthorized individuals. In this study, we propose a technique for securing color video data using association schemes.
Our approach involves first encrypting the original video data using random matrix transformation for the relations of an association scheme over , resulting in an initial encrypted video. This video is then further scrambled using the Arnold transformation, which enhances security by making data more resistant to statistical and structural attacks. This layered encryption technique effectively safeguards the video content against unauthorized access. The decryption process follows a similar strategy, enabling the recovery of the original video frames.
2.1. Random Matrix Transformation on Association Schemes (RMTAS)
Let be the RMT parameters, be the relation index in the association scheme, and n be the number of permissible symbols (including alphabetical letters, digits, and special characters). The value of is preferably chosen to be between 1 and .
The RMT uses thetransformation matrix
which is applied to the relation of the association scheme over , as described in Theorem 3 of [24]. Applying the RMT to involves multiplying the above matrix by the column vector formed by the base-n digits of each trigraph. The transformation is performed for every trigraph in the data, producing encrypted trigraphs that represent the ciphertext.
For decryption, let . Apply the same RMT to the relation and then apply the relation to each encrypted trigraph. This process reconstructs the original plaintext.
2.2. Encryption and Decryption of Colored Video Using RMTAS and Arnold Transformation
We begin by encrypting the original data, which are in the form of a colored video, using random matrix transformation for an association scheme over . Let R, G, and B be matrices over , representing the red, green, and blue pixel values of a video frame, respectively. Now, consider a single matrix M over . Each element of matrix M is a 3-tuple , where , , and are the entries of R, G, and B, respectively.
Let be the encryption keys shared with the receiver. Here, and d are used as the RMT parameters to form the transformation matrix, which is then applied to the relations of the association scheme over (see Theorem 3 of [24]) relative to key . This results in a new set of relations. By applying the selected relation to each element , we compute , the encrypted pixel in matrix C. Using , we determine the value of , the element of matrix C. Here, each element of C represents the encrypted pixel value.
In the final step, the Arnold transformationor cat map, introduced by V. Arnold [27], is iteratively applied times to scramble the encrypted data. The number of iterations acts as part of the decryption key. The procedure used to generate the final encrypted video using this approach is outlined in Algorithm 1.
A similar procedure is followed to recover the video during decryption, as shown in Algorithm 2. The inverse Arnold transformation is applied times to unscramble the frames. Then, the decryption key l is computed from using the association scheme. The original video is retrieved by applying the inverse of the RMT to relation .
| Algorithm 1 The encryption of colored video using RMTAS and the Arnold transformation |
| Require: Original video A, encryption keys Ensure: Encrypted video E
|
| Algorithm 2 The decryption of colored video using RMTAS and the Arnold transformation |
| Require: Encrypted video E, encryption keys Ensure: Decrypted video D
|
3. Experimental Results
This section provides a comprehensive evaluation of the proposed classical video encryption method using association schemes and random matrix transformations (RMTAS). This analysis was based on computer simulations and experimental results focused on the secure transmission of colored video, particularly emphasizing statistical performance metrics. The simulations were implemented in MATLAB R2021b in a Windows 11 environment and executed on a laptop equipped with a 12th Gen Intel® Core™ i7-1255U CPU @ 1.70 GHz with 16 GB RAM(Intel Corporation, Santa Clara, CA, USA).
For evaluation, three distinct color videos, namely Akiyo, Coastguard, and Foreman (see Figure 1a,d,g), were chosen. These videos underwent encryption utilizing RMTAS and the Arnold transformation (see Figure 1b,e,h). Notably, the recovered data (see Figure 1c,f,i) showed no noticeable distortion, confirming the reversibility of the transformations.

Figure 1.
Original, encrypted, and decrypted videos for the test sequences: (a–c) Akiyo: (a) original, (b) encrypted, (c) decrypted; (d–f) Coastguard: (d) original, (e) encrypted, (f) decrypted; (g–i) Foreman: (g) original, (h) encrypted, (i) decrypted.
This analysis included an assessment of the peak signal-to-noise ratio (PSNR), mean square error (MSE), histogram analysis, pixel intensity correlation graphs, correlation coefficient (CC), unified average changing intensity (UACI), and number of pixel change rate (NPCR) to evaluate the cryptosystem’s robustness. The choice of these metrics reflects the dual goals of the RMTAS and Arnold transformation scheme: achieving strongconfusion of pixel values (reflected in high NPCR and UACI) and strongdiffusion of spatial information (reflected in low correlation and uniform histograms). Theoretically, the algebraic mapping of RMTAS ensures each pixel’s RGB value is transformed in a key-dependent and non-linear way, while the Arnold transformation scrambles positions, producing statistical uniformity and resistance to both statistical and differential attacks.
3.1. Histogram Analysis
A histogram analysis was conducted to compare the original, encrypted, and decrypted versions of the selected videos, providing insight into the effectiveness of the encryption scheme. Figure 2, Figure 3 and Figure 4 demonstrate that the histograms of the encrypted videos exhibit a significantly altered distribution of pixel intensities compared to the original. This altered distribution is theoretically expected because RMTAS applies transformations derived from association schemes that uniformly permute pixel values across the full range . This uniform distribution prevents leakage of statistical patterns, while the Arnold transformation disrupts spatial structure, reinforcing histogram uniformity.

Figure 2.
Histogram analysis of ‘Akiyo’: (a) original frame, (b) encrypted frame, (c) decrypted frame.

Figure 3.
Histogram analysis of ‘Coastguard’: (a) original frame, (b) encrypted frame, (c) decrypted frame.

Figure 4.
Histogram analysis of ‘Foreman’: (a) original frame, (b) encrypted frame, (c) decrypted frame.
After decryption, the histograms of the recovered videos closely match those of the original, confirming lossless recovery due to the bijective nature of both RMTAS and the Arnold transformation.
3.2. Pixel Intensity
Pixel intensity measures the brightness or color value of pixels within encrypted or decrypted video frames. Figure 5, Figure 6 and Figure 7 illustrate that the encrypted frames have pixel intensity distributions drastically different from the original frames, a direct consequence of the confusion stage of RMTAS and the diffusion stage of the Arnold transformation. These changes ensure that even partial pixel value guesses are useless without spatial context, which is also scrambled.

Figure 5.
Pixel intensity of ‘Akiyo’: (a) original frame, (b) encrypted frame, (c) decrypted frame.

Figure 6.
Pixel intensity of ‘Coastguard’: (a) original frame, (b) encrypted frame, (c) decrypted frame.

Figure 7.
Pixel intensity of ‘Foreman’: (a) original frame, (b) encrypted frame, (c) decrypted frame.
4. Error Analysis
The analysis of the original, encrypted, and decrypted videos for the selected test cases is shown in Table 1 and Table 2.

Table 1.
Error analysis of original and encrypted videos.

Table 2.
Error analysis of original and decrypted videos.
The high NPCR values (around 99%) and UACI values (around 0.33) demonstrate the scheme’s strong sensitivity to changes in the input data. In practice, altering a single pixel in the original video triggers widespread changes in the encrypted output. Low correlation coefficients (close to 0) indicate that adjacent pixel dependencies in the original frames are destroyed, consistent with the goal of defeating statistical attacks. The high PSNR and zero MAE for the decrypted videos confirm the reversibility of the scheme, which follows from the invertible nature of both RMTAS and the periodic Arnold transformation. The histogram uniformity and high diffusion make the cipher robust against chosen-plaintext and known-plaintext attacks.
These theoretical properties align with the statistical observations, demonstrating that the performance metrics are not arbitrary but are a direct consequence of the cryptosystem’s algebraic and scrambling design. The formulas for these metrics are given below.
Themean absolute error (MAE) for videos measures the average absolute difference between the corresponding pixel values of two videos across all frames and color channels. The formula is given as
where F is the total number of frames, H and W are the height and width of the frames, and c represents the color channels (red, green, blue).
Themean square error (MSE) is a basic measure used to gauge differences between two images or video frames. It calculates the average squared difference of corresponding pixels:
In the context of encrypted and decrypted videos, the MSE helps to assess how accurately data are retrieved.
Thepeak signal-to-noise ratio (PSNR) is a widely used metric for evaluating the quality of reconstructed images and videos compared to their original versions. It quantifies the difference between the original and processed content, with higher values indicating better quality. The PSNR is defined by the following formula:
where MAX is the maximum possible pixel value of the image (e.g., 255 for an 8-bit image) and MSE (the mean squared error) is the average squared difference between the original and processed images.
Thecorrelation coefficient (CC) measures the strength and direction of the linear relationship between two variables, such as pixel intensities in video frames:
Thenumber of pixel change rate (NPCR) quantifies the difference between two video frames based on the percentage of pixels that change their values. It is calculated using the following formula:
where m and n are the dimensions of the frames.
Theunified average changing intensity (UACI) measures the average intensity difference between corresponding pixels of two images or video frames. It is calculated using the following formula:
Here, m and n denote the dimensions of the images or frames, while and represent pixel intensities from the original and processed images, respectively. In video analysis, the UACI provides valuable insights into the average pixel intensity changes between frames.
5. Comparative Analysis
To evaluate the performance of the proposed classical video encryption method using association schemes and random matrix transformations, we compared it with existing techniques, including those devised by Hosny et al. [1], Kotel et al. [28], Elkamchouchi et al. [29], Cheng et al. [16], and Hafsa et al. [15]. Using the standard ‘Foreman’ test video, we assessed performance using metrics such as the PSNR, MAE, NPCR, UACI, and correlation coefficient, as shown in Table 3.

Table 3.
A comparison of encryption techniques.
The results demonstrate that the proposed method achieves high NPCR (greater than 99%) and UACI values (approximately 0.33), indicating strong resistance to differential attacks and ensuring that small changes in the plaintext propagate widely in the ciphertext. The low CC values (close to 0) confirm that spatial correlations between adjacent pixels are effectively removed. These outcomes are expected from the design: the RMTAS algebraically transforms pixel values in a key-dependent, non-linear way, while the Arnold transformation disperses pixel positions across the frame, jointly ensuring confusion and diffusion.
In terms of the PSNR, the decrypted video achieves values comparable to or better than those of other methods, reflecting the lossless nature of the encryption–decryption process. This stems from the invertibility of both the association scheme mapping and the Arnold transform. MAE values are near zero for decrypted videos, further confirming error-free reconstruction.
Overall, the combination of algebraic structure from association schemes and spatial scrambling yields a cipher that maintains competitive performance with state-of-the-art methods while providing a mathematically rigorous framework suitable for extension into quantum encryption models.
6. Proposed Quantum Cipher Framework
In this section, we describe the theoretical foundation and model of the proposed quantum cipher designed for image and video encryption. The scheme integrates the algebraic structure of association schemes into the construction of quantum encryption operators. The framework consists of three key components, quantum data encoding, unitary encryption using association scheme-derived operators, and decryption using inverse unitary operations, as shown in Figure 8.
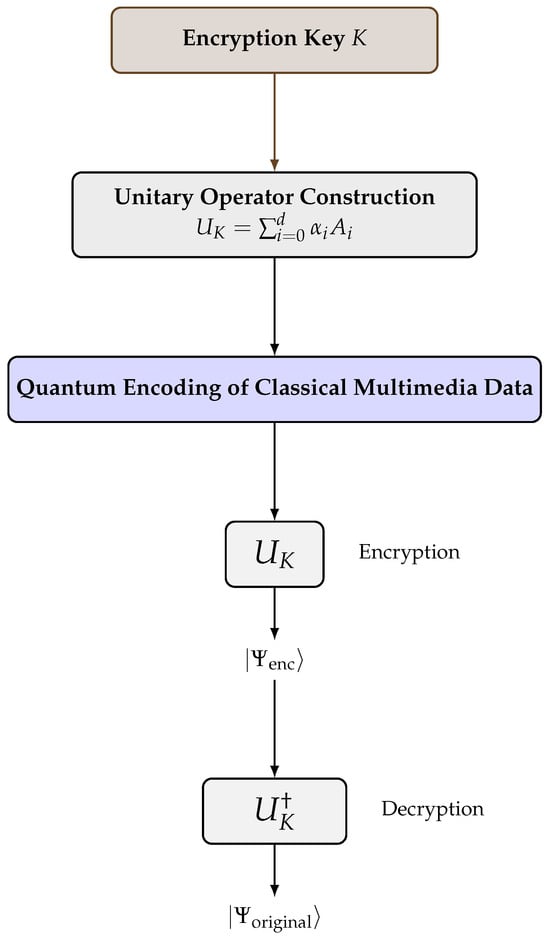
Figure 8.
Quantum cipher framework based on association schemes. The classical encryption key K defines the coefficients for constructing the unitary operator , which acts on quantum-encoded multimedia data for encryption. Decryption is achieved using .
6.1. Quantum Encoding of Classical Multimedia Data
Classical image or video data are first mapped into quantum states. A grayscale image of dimensions with 8-bit pixels is represented by a quantum state encoded over qubits. For RGB images, each pixel consists of three values , requiring 24 qubits per pixel.
The encoded quantum image is given as
where is the intensity or RGB value of the i-th pixel and N is the total number of pixels. Each is a computational basis state in a qubit register.
For video encryption, the sequence of frames is treated as a temporal quantum register:
6.2. Construction of Unitary Operator from Association Schemes
Let be the adjacency matrices of a symmetric association scheme defined over a finite set X, such that each is a real symmetric matrix satisfying . These matrices form the basis for the Bose–Mesner algebra , a commutative algebra with dimensions .
We define the quantum encryption operator as
where are coefficients derived from the classical encryption key K, chosen so that is unitary (see Figure 9). The unitarity condition can be ensured through normalization or algebraic constraints on the .
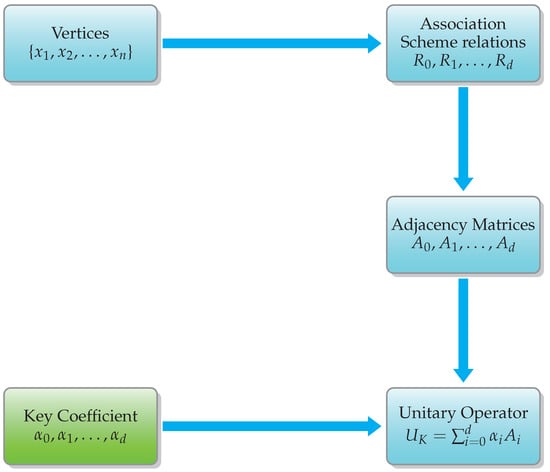
Figure 9.
A block diagram for the construction of the unitary encryption operator from an association scheme.
In the proposed quantum cipher, the encryption key K is a classical key that determines the structure of the unitary encryption operator . Specifically, K encodes the set of coefficients used in the Bose–Mesner algebra expansion above, where are the adjacency matrices of the association scheme. These coefficients are derived from the shared secret key material and are chosen to satisfy the unitarity condition, ensuring that is reversible. The same key K allows the legitimate receiver to reconstruct and recover the original quantum-encoded data.
This unitary operator acts on the encoded quantum image or video state as follows:
6.3. Decryption Process
Since is unitary, decryption is straightforward:
Thus, anyone with access to the shared classical key K, as well as knowledge of the association scheme structure, can reconstruct and recover the original data.
7. Conclusions and Future Research
This study presents a secure video encryption technique based on association schemes, combining random matrix transformations and Arnold scrambling. The experimental results confirm the method’s robustness through statistical and error analyses, while comparisons with existing techniques highlight its effectiveness and structural advantages. A quantum extension using unitary operators derived from association schemes has also been proposed, offering a foundation for quantum-secure multimedia encryption. Future research will focus on implementing the proposed quantum model using simulation tools such as Qiskit. This will be further extended by integrating quantum key distribution and error correction techniques to enhance security in next-generation communication systems.
Author Contributions
Conceptualization, R.K.S., A.S. and P.Y.; Methodology, R.K.S., A.S. and P.Y.; Software, A.S.; Validation, R.K.S., A.S. and P.Y.; Formal analysis, R.K.S., A.S. and P.Y.; Investigation, A.S.; Resources, A.S.; Data curation, A.S.; Writing—original draft, A.S.; Writing—review & editing, R.K.S. and P.Y.; Visualization, R.K.S., A.S. and P.Y.; Supervision, R.K.S. and P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hosny, K.M.; Zaki, M.A.; Lashin, N.A.; Hamza, H.M. Fast colored video encryption using block scrambling and multi-key generation. Vis. Comput. 2023, 39, 6041–6072. [Google Scholar] [CrossRef]
- von Solms, R.; van Niekerk, J. From information security to cyber security. Comput. Secur. 2013, 38, 97–102. [Google Scholar] [CrossRef]
- Wen, C.; Chen, G.; Gu, X.; Wang, W. Joint optimization of communication rates for multi-UAV relay systems. Complex Intell. Syst. 2025, 11, 1–27. [Google Scholar] [CrossRef]
- Arora, A.; Sharma, R.K. Cryptanalysis and enhancement of image encryption scheme based on word-oriented feed back shift register. Multimed. Tools Appl. 2022, 81, 16679–16705. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, L.; Liu, T.; Chen, H.; Li, P.; Lin, C.; Liu, S. Color image encryption by using Arnold transform and color-blend operation in discrete cosine transform domains. Opt. Commun. 2011, 284, 123–128. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, Q.; Xu, L.; Ahmad, M.A.; Liu, S. Double image encryption by using iterative random binary encoding in gyrator domains. Opt. Express 2010, 18, 12033–12043. [Google Scholar] [CrossRef]
- Abuturab, M.R. Securing color information using Arnold transform in gyrator transform domain. Opt. Lasers Eng. 2012, 50, 772–779. [Google Scholar] [CrossRef]
- Luo, Y.; Yu, J.; Lai, W.; Liu, L. A novel chaotic image encryption algorithm based on improved baker map and logistic map. Multimed. Tools Appl. 2019, 78, 22023–22043. [Google Scholar] [CrossRef]
- Hayat, U.; Azam, N.A. A novel image encryption scheme based on an elliptic curve. Signal Process. 2019, 155, 391–402. [Google Scholar] [CrossRef]
- Liu, F.; Koenig, H. A survey of video encryption algorithms. Comput. Secur. 2010, 29, 3–15. [Google Scholar] [CrossRef]
- El-Shafai, W.; Mesrega, A.K.; Ahmed, H.E.H.; El-Bahnasawy, N.A.; Abd El-Samie, F.E. An efficient multimedia compression-encryption scheme using latin squares for securing Internet-of-things networks. J. Inf. Secur. Appl. 2022, 64, 103039. [Google Scholar] [CrossRef]
- Gupta, G.; Gupta, V.; Chandra, M. An efficient video watermarking based security model. Microsyst. Technol. 2018, 24, 2539–2548. [Google Scholar] [CrossRef]
- Asikuzzaman, M.; Pickering, M.R. An overview of digital video watermarking. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2131–2153. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Y.; Zhao, H.; Liu, S. Video steganography: A review. Neurocomputing 2019, 335, 238–250. [Google Scholar] [CrossRef]
- Hafsa, A.; Fradi, M.; Sghaier, A.; Malek, J.; Machhout, M. Real-time video security system using chaos-improved advanced encryption standard (IAES). Multimed. Tools Appl. 2022, 81, 2275–2298. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, L.; Ao, N.; Han, Q. A selective video encryption scheme based on coding characteristics. Symmetry 2020, 12, 332. [Google Scholar] [CrossRef]
- Hadj Brahim, A.; Ali Pacha, A.; Hadj Said, N. An image encryption scheme based on a modified AES algorithm by using a variable S-box. J. Opt. 2024, 53, 1170–1185. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, L.; Chen, J. An efficient video slice encryption scheme and its application. Cybersecurity 2025, 8, 40. [Google Scholar] [CrossRef]
- Zhang, H.; Kone, M.; Ma, X.; Zhou, N. Frequency-domain attention-guided adaptive robust watermarking model. J. Frankl. Inst. 2025, 362, 107511. [Google Scholar] [CrossRef]
- Hu, L.; Chen, M.; Wang, M.; Zhou, N. Visually meaningful triple images encryption algorithm based on 2D compressive sensing and multi-region embedding. Knowl.-Based Syst. 2025, 324, 113804. [Google Scholar] [CrossRef]
- Bose, R.C.; Shimamoto, T. Classification and analysis of partially balanced incomplete block designs with two associate classes. J. Am. Stat. Assoc. 1952, 47, 151–184. [Google Scholar] [CrossRef]
- Bannai, E.; Bannai, E.; Bannai, H. Uniqueness of certain association schemes. Eur. J. Comb. 2008, 29, 1379–1395. [Google Scholar] [CrossRef][Green Version]
- Zieschang, P.H. An Algebraic Approach to Association Schemes; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sabharwal, A.; Yadav, P.; Sharma, R. Association Schemes for Some Finite Group Rings II. Commun. Appl. Nonlinear Anal. 2024, 31, 392–402. [Google Scholar] [CrossRef]
- Sabharwal, A.; Yadav, P.; Sharma, R. Association schemes in encrypting two dimensional data. J. Discret. Math. Sci. Cryptogr. 2025, 28, 161–183. [Google Scholar] [CrossRef]
- Chan, A.; Martin, W.J. Quantum isomorphism of graphs from association schemes. J. Comb. Theory Ser. B 2024, 164, 340–363. [Google Scholar] [CrossRef]
- Arnold, V.I.; Avez, A. Ergodic Problems of Classical Mechanics; W.A. Benjamin: New York, NY, USA, 1968; Volume 9. [Google Scholar]
- Kotel, S.; Zeghid, M.; Baganne, A.; Saidani, T.; Daradkeh, Y.I.; Rached, T. FPGA-based real-time implementation of AES algorithm for video encryption. In Recent Advances in Telecommunications, Informatics and Educational Technologies; WSEAS Press: Athens, Greece, 2014; pp. 27–36. [Google Scholar]
- Elkamchouchi, H.; Salama, W.M.; Abouelseoud, Y. New video encryption schemes based on chaotic maps. IET Image Process. 2020, 14, 397–406. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).