A New Topp–Leone Odd Weibull Flexible-G Family of Distributions with Applications
Abstract
1. Introduction
1.1. Background
1.2. Motivational Example: Failure Time Data
2. The New Family and Properties
2.1. Topp–Leone Odd Weibull Flexible-G Family
2.2. Properties
- (i)
- Set .
- (ii)
- Solve for s, using the Newton Raphson algorithm, the non-linear equation .
3. Special Models
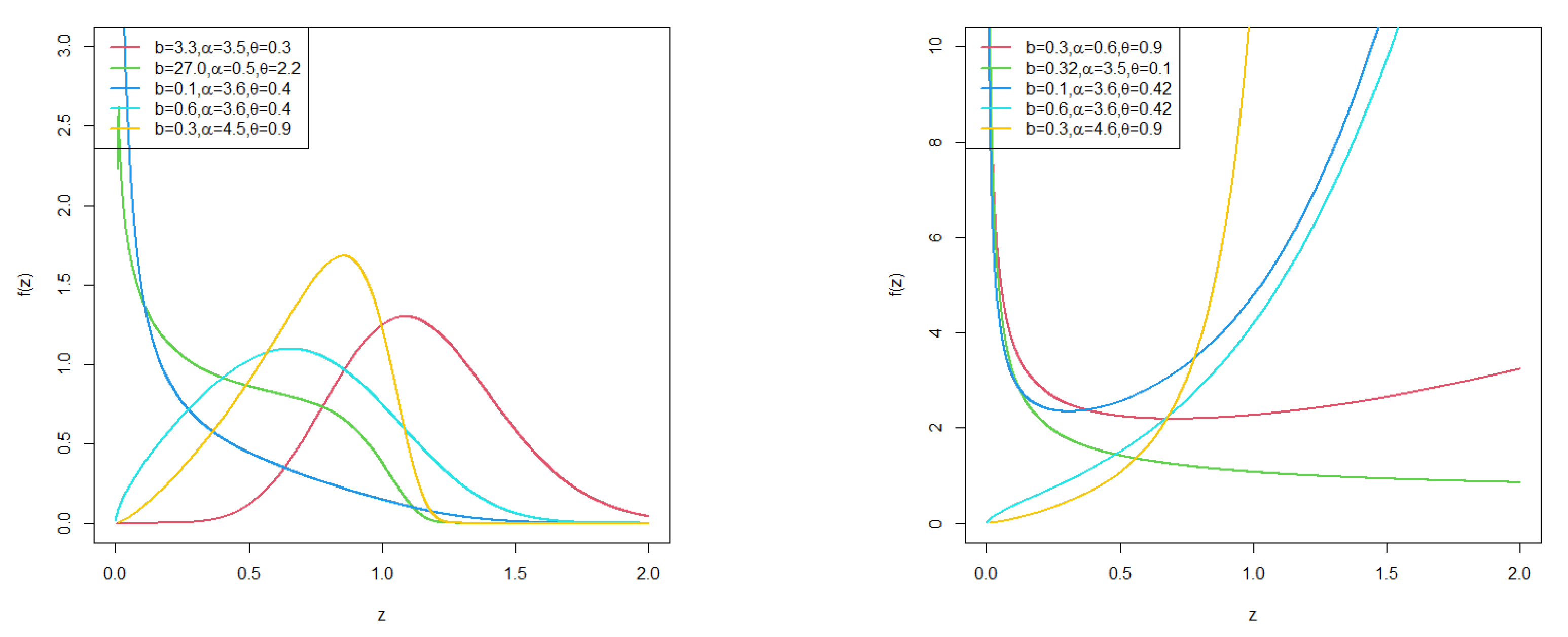
3.1. TL-OWF-W Distribution
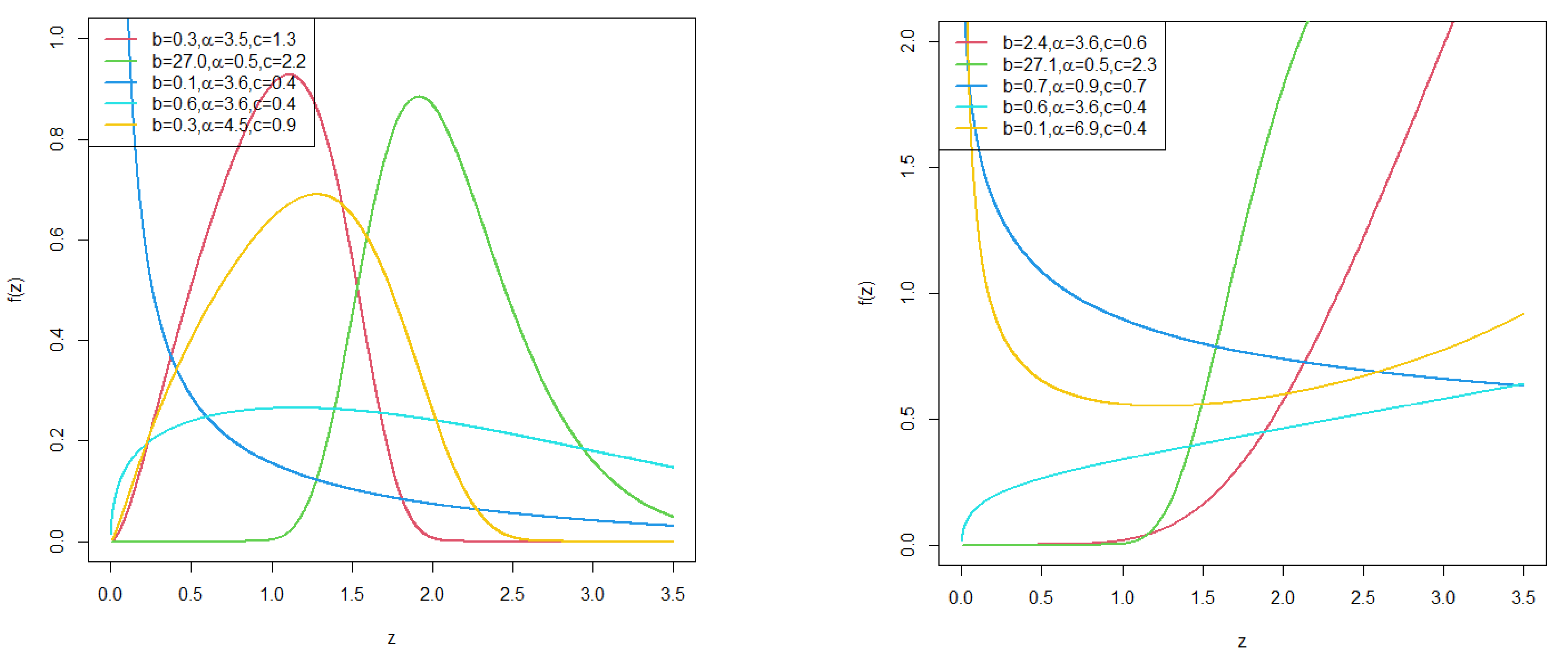
3.2. TL-OWF-LLoG Distribution
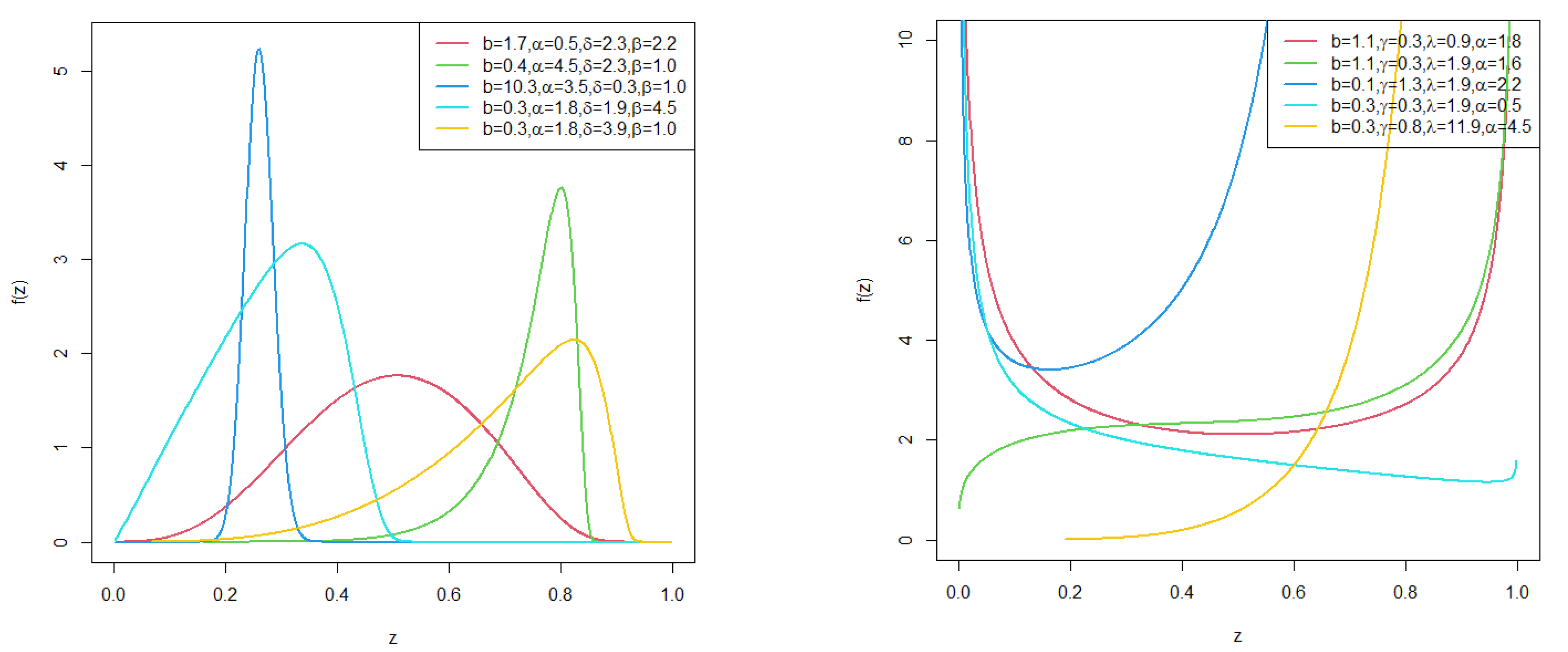
3.3. TL-OWF-Kum Distribution
4. Maximum Likelihood Estimation and Simulation Study
Maximum Likelihood Estimation
5. Simulation Study
6. Applications
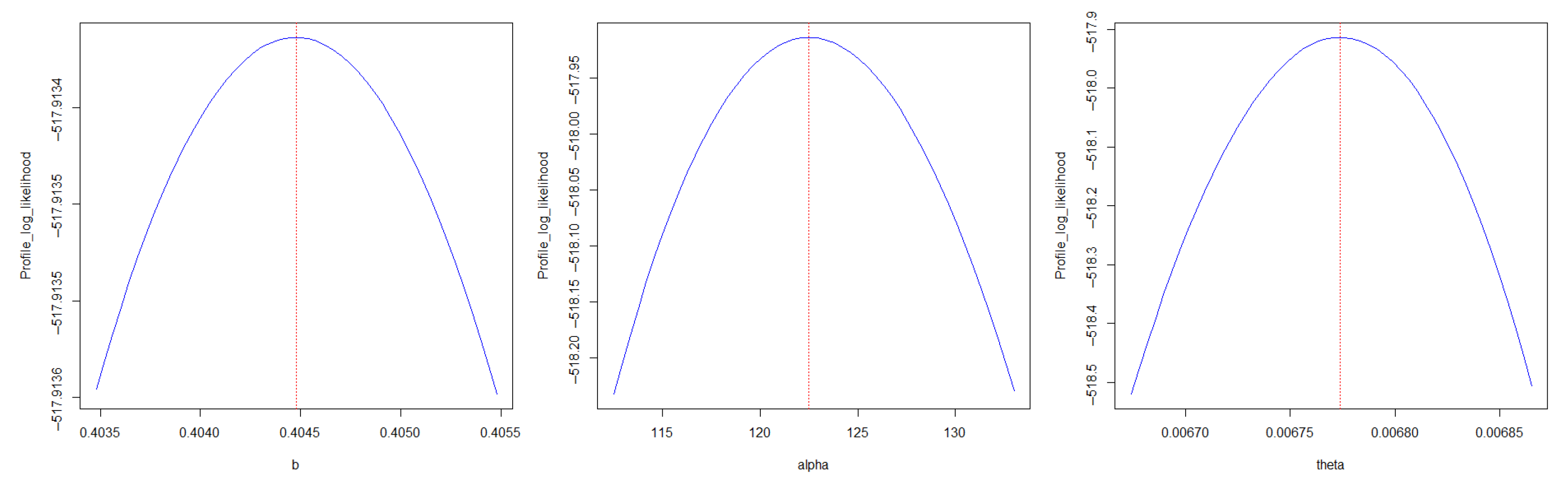
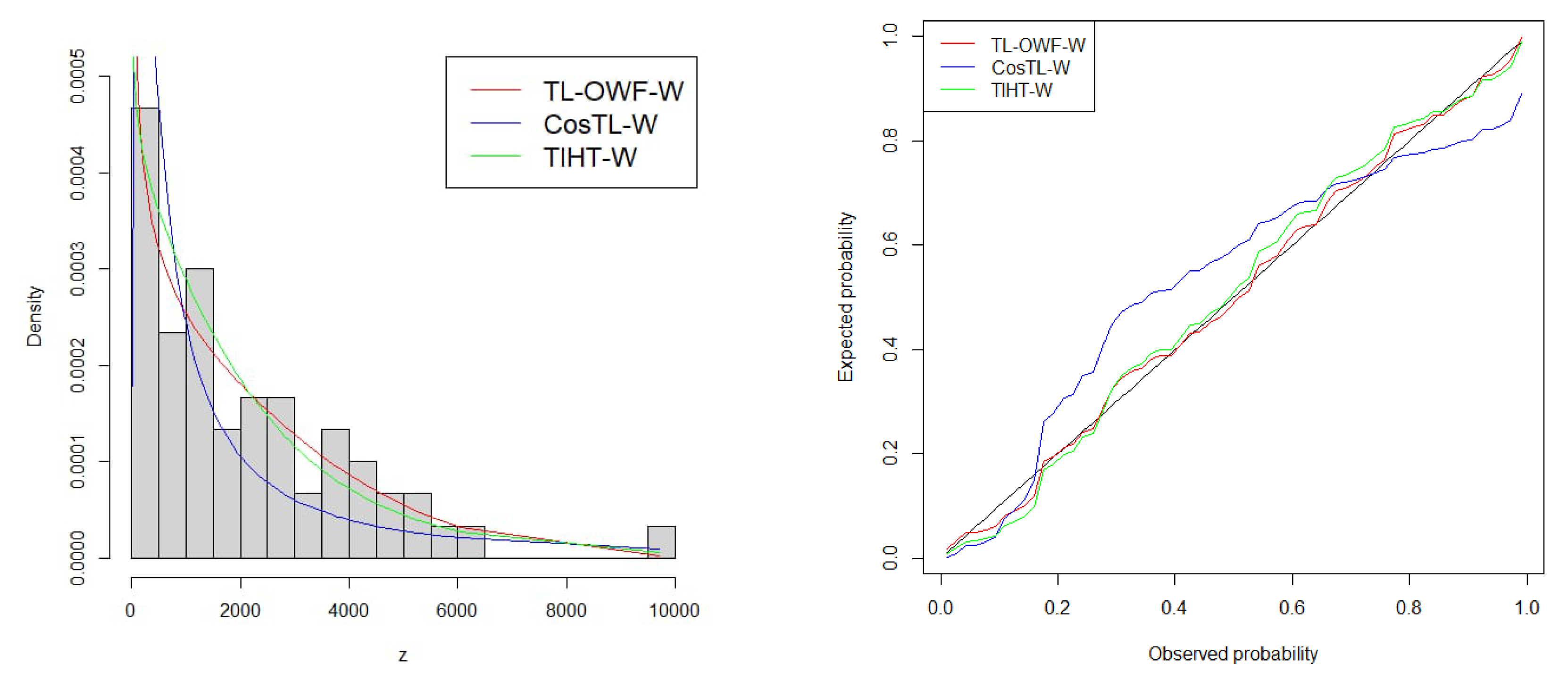
6.1. Failure Time Data
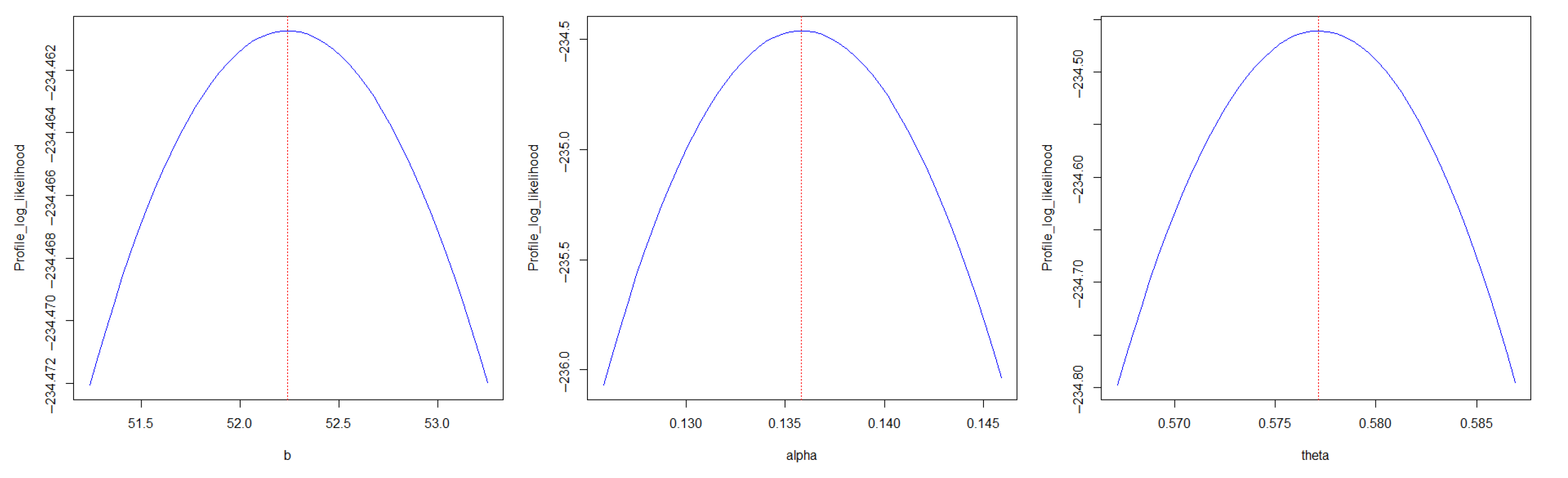
6.2. COVID-19 Dataset
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Datasets
Appendix A.1.1. Failure Time Data
Appendix A.1.2. Italy’s COVID-19 Data
References
- Cordeiro, G.M.; Alizadeh, M.; Ortega, E.M.M. The Exponentiated Half-Logistic Family of Distributions: Properties and Applications. J. Probab. Stat. 2014, 2014, 864396. [Google Scholar] [CrossRef]
- Tahir, M.H.; Hussain, M.A.; Cordeiro, G.M. A New Flexible Generalized Family for Constructing Many Families of Distributions. J. Appl. Stat. 2022, 49, 1625–1635. [Google Scholar] [CrossRef] [PubMed]
- Topp, C.W.; Leone, F.C. A Family of J-Shaped Frequency Functions. J. Am. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Al-Shomrani, A.; Arif, O.; Shawky, A.; Hanif, S.; Shahbaz, M.Q. The Topp–Leone Family of Distributions: Some Properties and Application. Pak. J. Stat. Oper. Res. 2016, 12, 443–451. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A New Method for Generating Families of Continuous Distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Rezaei, S.; Sadr, B.B.; Alizadeh, M.; Nadarajah, S. Topp–Leone Generated Family of Distributions: Properties and applications. Commun. Stat.-Theory Methods 2017, 46, 2893–2909. [Google Scholar] [CrossRef]
- Brito, E.; Cordeiro, G.M.; Yousof, H.M.; Alizadeh, M.; Silva, G.O. The Topp–Leone Odd Log-Logistic Family of Distributions. J. Stat. Comput. Simul. 2017, 87, 3040–3058. [Google Scholar] [CrossRef]
- Reyad, H.M.; Othman, S.A. The Topp–Leone Burr-XII Distribution: Properties and Applications. Br. J. Math. Comput. Sci. 2017, 21, 1–15. [Google Scholar] [CrossRef]
- Yousof, H.M.; Alizadeh, M.; Jahansshahi, S.M.A.; Ramires, T.G.; Ghosh, I.; Hamedani, G.G. The Transmuted Topp–Leone G Family of Distributions: Theory, Characterizations and Applications. J. Data Sci. 2017, 15, 723–740. [Google Scholar] [CrossRef]
- Reyad, H.M.; Alizadeh, M.; Jamal, F.; Othman, S.; Hamedani, G.G. The Exponentiated Generalized Topp Leone-G Family of Distributions: Properties and Applications. Pak. J. Stat. Oper. Res. 2019, XV, 1–24. [Google Scholar] [CrossRef]
- Ekemezie, D.N.; Anyiam, K.E.; Kayid, M.; Balogun, O.S.; Obulezi, J.O. DUS Topp–Leone-G Family of Distributions: Baseline Extension, Properties, Estimation, Simulation and Useful Applications. Entropy 2024, 26, 973. [Google Scholar] [CrossRef] [PubMed]
- Cordeiro, G.M.; Ortega, E.M.M.; Cunha, D.C.C. The Exponentiated Generalized Class of Distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling Failure Time Data by Lehman Alternatives. Commun. Stat. Theory Methods 1999, 27, 887–904. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A New Method for Adding Parameters to a Family of Distributions With Application to the Exponential and Weibull Families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Shaw, W.T.; Buckley, I.R. The Alchemy of Probability Distributions: Beyond Gram-Charlier Expansions, and a Skew-Kurtotic-Normal Distribution from a Rank Transmutation Map. 2007. Available online: https://ideas.repec.org/s/arx/papers.html (accessed on 1 September 2025).
- Ferreira, A.A.; Cordeiro, G.M. The Flexible Generalized Gamma Distribution With Applications to COVID-19 Data. Rev. Colomb. Estadística-Appl. Stat. 2024, 47, 453–473. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Biazatti, E.C.; Ortega, E.M.M.; De Lima, M.D.S.; De Santana, L.H. The Weibull Flexible Generalized Family of Bimodal Distributions: Properties, Simulation, Regression Models, and Applications. Chil. J. Stat. 2024, 15, 27–43. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G Family of Probability Distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2003. [Google Scholar]
- Apostol, T.M. 1974. Mathematical Analysis, Reading, Mass; Addison-Wesley: London, ON, Canada, 1974. [Google Scholar]
- Henningsen, A.; Toomet, O. maxLik: A Package for Maximum Likelihood Estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Chamunorwa, S.; Oluyede, B.; Makubate, B.; Chipepa, F. The Exponentiated Odd Weibull-Topp–Leone-G Family of Distributions: Model, Properties and Applications. Pak. J. Stat. 2021, 37, 143–158. [Google Scholar]
- Tuoyo, D.O.; Opone, F.C.; Ekhosuehi, N. The Topp–Leone Weibull Distribution: Its Propertis and Application. Earthline J. Math. Sci. 2021, 7, 381–401. [Google Scholar] [CrossRef]
- Nanga, S.; Nasiru, S.; Dioggban, J. Cosine Topp–Leone Family of Distributions: Properties and Regression. Res. Math. 2023, 10, 2208935. [Google Scholar] [CrossRef]
- Korkmaz, M.C.; Yousof, H.M.; Hamedani, G.G. The Exponential Lindley Odd Log-Logistic-G Family: Properties, Characterizations and Applications. J. Stat. Theory Appl. 2018, 17, 554–571. [Google Scholar] [CrossRef]
- Zhao, W.; Khosa, S.K.; Ahmad, Z.; Aslam, M.; Afify, A.Z. Type-I Heavy-Tailed Family with Applications in Medicine, Engineering and Insurance. PLoS ONE 2020, 15, 63–79. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, M.; Cordeiro, G.M.; Nascimento, A.D.C.; Lima, M.C.S.; Ortega, E.M.M. Odd-Burr Generalized Family of Distributions with Some Applications. J. Stat. Simul. 2017, 87, 367–389. [Google Scholar] [CrossRef]
- Charumbira, W.F.; Oluyede, B.; Chipepa, F. The New Topp–Leone Exponentiated Half Logistic-Gompertz-G Family of Distributions with Applications. Stat. Optim. Inf. Comput. 2025, 14, 486–515. [Google Scholar] [CrossRef]
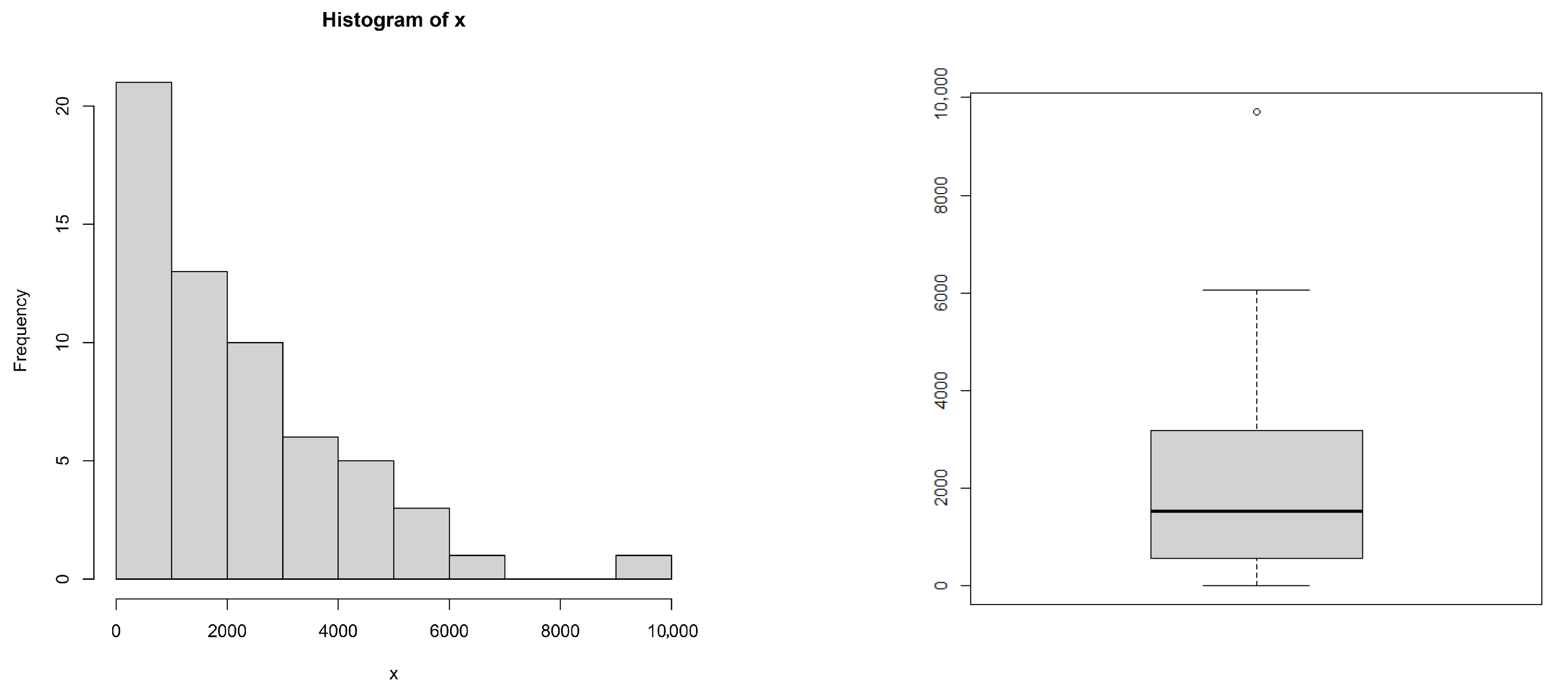

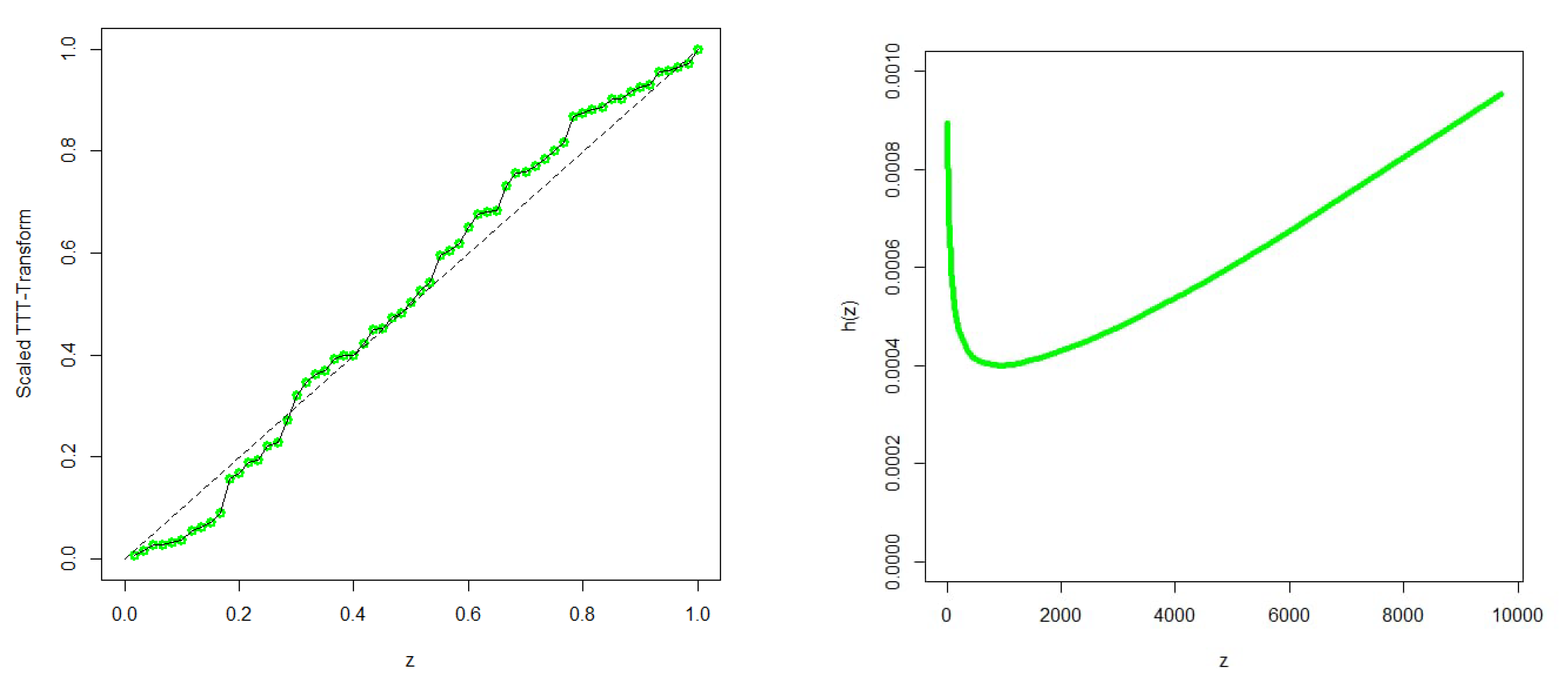
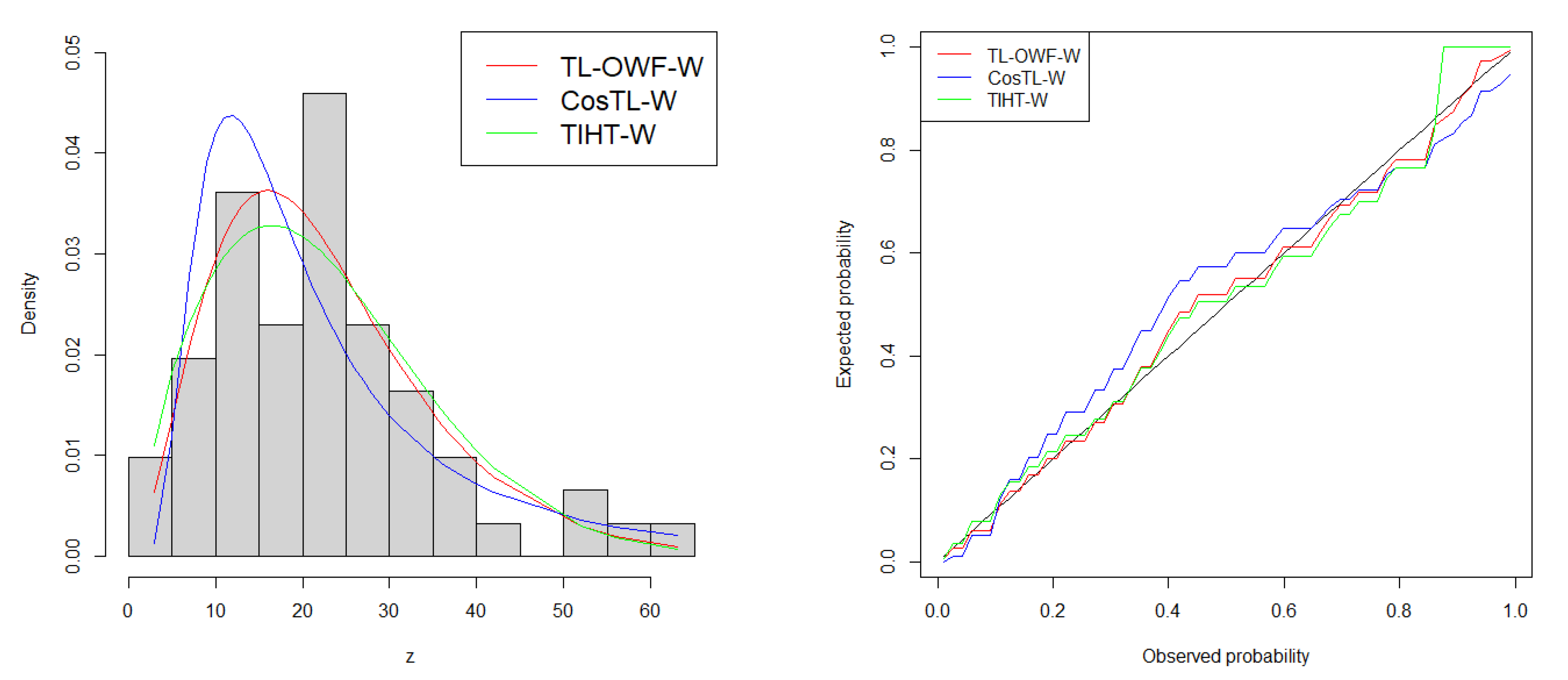
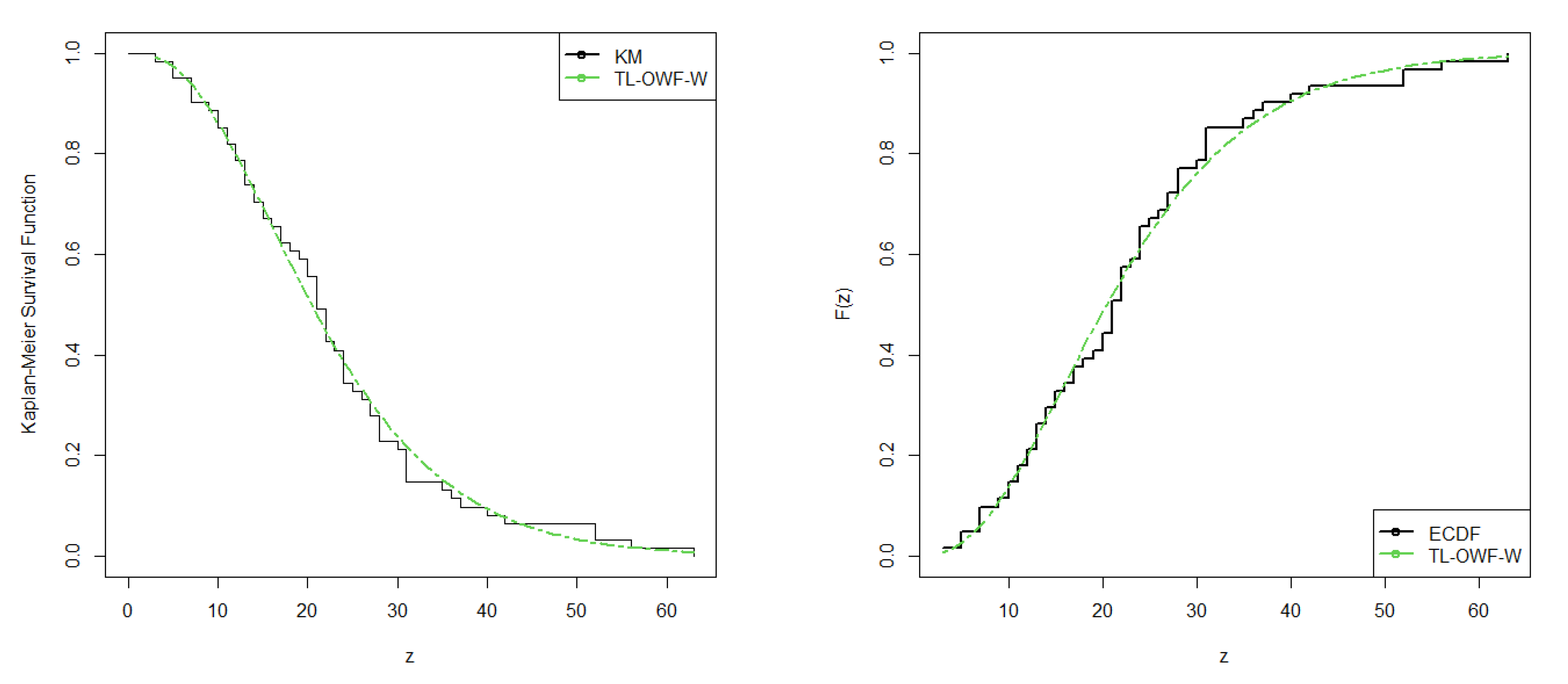
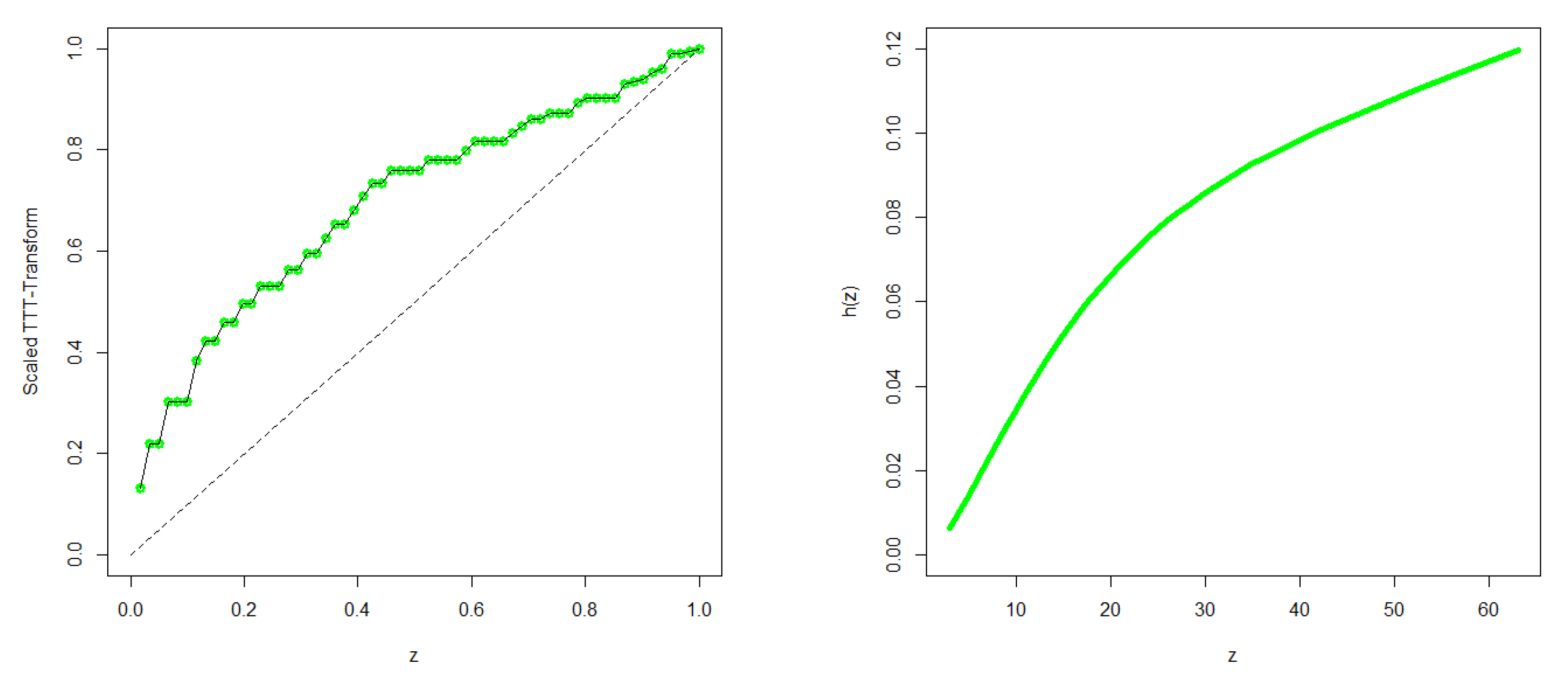
| Minimum | Maximum | Mean | Median | SD | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| 14.0 | 9701.0 | 2114.8 | 1527.5 | 1925.15 | 1.30 | 2.21 |
| u | (1.5,1.5,0.1) | (0.5,1,0.5) | (1.5,0.5,1.5) | (0.5,1.5,0.9) | (1.1,1.1,0.3) |
|---|---|---|---|---|---|
| 0.1 | 0.0018 | 0.0028 | 0.316 | 0.0989 | 0.0194 |
| 0.2 | 0.0114 | 0.0131 | 0.436 | 0.1844 | 0.0576 |
| 0.3 | 0.0367 | 0.0343 | 0.5286 | 0.2761 | 0.1136 |
| 0.4 | 0.0909 | 0.072 | 0.6086 | 0.3789 | 0.1909 |
| 0.5 | 0.1977 | 0.1355 | 0.682 | 0.4978 | 0.2958 |
| 0.6 | 0.4044 | 0.2411 | 0.7528 | 0.6399 | 0.4397 |
| 0.7 | 0.8185 | 0.4202 | 0.8246 | 0.8173 | 0.6449 |
| 0.8 | 1.7394 | 0.7454 | 0.9028 | 1.0557 | 0.9625 |
| 0.9 | 4.4318 | 1.4521 | 1.0006 | 1.4306 | 1.5591 |
| (1,1,1) | (1,1,0.5) | ||||||
| Paramater | Mean | RMSE | Abias | Mean | RMSE | Abias | |
| b | 25 | 2.4695 | 4.2455 | 1.4695 | 2.3462 | 3.8320 | 1.3462 |
| 50 | 1.9971 | 2.9784 | 0.9971 | 1.9541 | 3.2334 | 0.9541 | |
| 100 | 1.6885 | 2.1400 | 0.6885 | 1.6746 | 2.0814 | 0.6746 | |
| 200 | 1.4653 | 1.5408 | 0.4653 | 1.5216 | 1.6470 | 0.5216 | |
| 400 | 1.2217 | 0.9878 | 0.2217 | 1.1337 | 0.9359 | 0.1337 | |
| 25 | 1.0660 | 0.6004 | 0.0660 | 1.0673 | 0.5994 | 0.0673 | |
| 50 | 1.0196 | 0.4422 | 0.0196 | 1.0158 | 0.4286 | 0.0158 | |
| 100 | 0.9875 | 0.3435 | −0.0125 | 0.9871 | 0.3437 | −0.0129 | |
| 200 | 0.9904 | 0.2747 | −0.0096 | 0.9834 | 0.2846 | −0.0166 | |
| 400 | 1.0040 | 0.2101 | 0.0040 | 1.0232 | 0.2112 | 0.0232 | |
| 25 | 2.3467 | 2.5729 | 1.3467 | 1.2189 | 1.3567 | 0.7189 | |
| 50 | 1.8462 | 1.7927 | 0.8462 | 0.9978 | 0.9888 | 0.4978 | |
| 100 | 1.6409 | 1.4990 | 0.6409 | 0.8287 | 0.7496 | 0.3287 | |
| 200 | 1.4361 | 1.1494 | 0.4361 | 0.7287 | 0.5936 | 0.2287 | |
| 400 | 1.3338 | 0.9087 | 0.3338 | 0.7067 | 0.4769 | 0.2067 | |
| (0.5,0.5,0.9) | (0.5,0.5,1.1) | ||||||
| Paramater | Mean | RMSE | Abias | Mean | RMSE | Abias | |
| b | 25 | 1.3910 | 2.4397 | 0.8910 | 1.6203 | 2.5932 | 1.1203 |
| 50 | 1.0187 | 1.5717 | 0.5187 | 1.2257 | 1.8290 | 0.7257 | |
| 100 | 0.7861 | 0.9416 | 0.2861 | 1.1348 | 1.4951 | 0.6348 | |
| 200 | 0.7813 | 0.9283 | 0.2813 | 0.8345 | 0.8907 | 0.3345 | |
| 400 | 0.5476 | 0.2822 | 0.0476 | 0.6208 | 0.3821 | 0.1208 | |
| 25 | 0.5058 | 0.3051 | 0.0058 | 0.5076 | 0.3271 | 0.0676 | |
| 50 | 0.5279 | 0.2052 | 0.0279 | 0.4870 | 0.1995 | −0.0613 | |
| 100 | 0.5213 | 0.1546 | 0.0213 | 0.4839 | 0.1511 | −0.0161 | |
| 200 | 0.5328 | 0.1202 | 0.0328 | 0.5073 | 0.1053 | 0.0073 | |
| 400 | 0.5331 | 0.0756 | 0.0331 | 0.5210 | 0.0753 | 0.0021 | |
| 25 | 1.1957 | 0.8036 | 0.2957 | 1.3701 | 0.9775 | 0.2701 | |
| 50 | 1.0191 | 0.5815 | 0.1191 | 1.1514 | 0.6808 | 0.0951 | |
| 100 | 1.0054 | 0.5003 | 0.1054 | 1.0083 | 0.5731 | −0.0917 | |
| 200 | 0.9353 | 0.4186 | 0.0353 | 1.0232 | 0.4662 | −0.0768 | |
| 400 | 0.9755 | 0.3743 | 0.0755 | 1.0700 | 0.3738 | −0.0300 |
| (0.5,0.9,0.5) | (0.5,0.9,0.9) | ||||||
| Paramater | Mean | RMSE | Abias | Mean | RMSE | Abias | |
| b | 25 | 1.4583 | 3.1130 | 0.9583 | 1.8625 | 3.4889 | 1.3625 |
| 50 | 0.6873 | 1.6004 | 0.1873 | 1.3102 | 2.3183 | 0.8102 | |
| 100 | 0.5552 | 1.2547 | 0.0552 | 1.0050 | 1.4338 | 0.5050 | |
| 200 | 0.4053 | 0.6547 | −0.0547 | 0.8468 | 1.0522 | 0.3468 | |
| 400 | 0.4502 | 0.0609 | −0.0498 | 0.6271 | 0.5429 | 0.1271 | |
| 25 | 0.9938 | 0.5332 | 0.1938 | 0.9187 | 0.5132 | 0.0387 | |
| 50 | 1.0051 | 0.3607 | 0.1051 | 0.8998 | 0.3524 | −0.0302 | |
| 100 | 0.9871 | 0.2734 | 0.0871 | 0.8771 | 0.2595 | −0.0229 | |
| 200 | 1.0724 | 0.2354 | 0.0724 | 0.8791 | 0.2038 | −0.0209 | |
| 400 | 1.0102 | 0.1429 | 0.0102 | 0.9040 | 0.1382 | 0.0040 | |
| 25 | 0.8969 | 0.7228 | 0.3969 | 1.3258 | 1.1247 | 0.4258 | |
| 50 | 0.8401 | 0.5558 | 0.3501 | 1.1396 | 0.7960 | 0.2396 | |
| 100 | 0.8908 | 0.5488 | 0.3490 | 1.0318 | 0.6472 | 0.1318 | |
| 200 | 0.8486 | 0.4788 | 0.3486 | 0.9847 | 0.5393 | 0.0847 | |
| 400 | 0.5125 | 0.0335 | 0.0125 | 0.9971 | 0.4287 | 0.0971 | |
| (0.5,0.5,1) | (0.5,1.0,0.9) | ||||||
| Paramater | Mean | RMSE | Abias | Mean | RMSE | Abias | |
| b | 25 | 1.4079 | 2.2828 | 0.9079 | 1.6534 | 3.1737 | 1.1534 |
| 50 | 1.1854 | 1.8470 | 0.6854 | 1.1606 | 2.0469 | 0.6606 | |
| 100 | 0.9558 | 1.2172 | 0.4558 | 0.9854 | 1.4278 | 0.4854 | |
| 200 | 0.8059 | 0.8661 | 0.3059 | 0.8542 | 1.1024 | 0.3542 | |
| 400 | 0.5933 | 0.3817 | 0.0933 | 0.6235 | 0.5690 | 0.1235 | |
| 25 | 0.4870 | 0.3185 | −0.0130 | 1.0623 | 0.5402 | 0.0623 | |
| 50 | 0.5052 | 0.2224 | 0.0052 | 1.0108 | 0.3781 | 0.0108 | |
| 100 | 0.5045 | 0.1498 | 0.0045 | 0.9812 | 0.2879 | −0.0107 | |
| 200 | 0.5163 | 0.1146 | 0.0036 | 0.9792 | 0.2314 | −0.0106 | |
| 400 | 0.5316 | 0.0818 | 0.0032 | 1.0063 | 0.1574 | 0.0063 | |
| 25 | 1.3113 | 0.8669 | 0.3113 | 1.3852 | 1.1802 | 0.4852 | |
| 50 | 1.1082 | 0.6429 | 0.1082 | 1.2111 | 0.8577 | 0.3111 | |
| 100 | 1.0053 | 0.5226 | 0.0053 | 1.0851 | 0.6876 | 0.1851 | |
| 200 | 0.9493 | 0.4174 | −0.0507 | 1.0180 | 0.5705 | 0.1180 | |
| 400 | 1.0247 | 0.3684 | 0.0247 | 1.0240 | 0.4579 | 0.1240 |
| Estimates | Statistics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | b | −2log(L) | AIC | CAIC | BIC | K−S | p-Value | |||||
| TL-OWF-W | 0.4045 | 1.2249 | 6.7739 | 1035.8270 | 1041.8270 | 1042.2550 | 1048.1100 | 0.0220 | 0.2022 | 0.048 | 0.9974 | |
| (5.6736 ) | (2.3747 ) | (9.4765 ) | ||||||||||
| b | ||||||||||||
| TL-W | 1.1951 | 0.1366 | 1064.3390 | 1068.3390 | 1068.5490 | 1072.5270 | 0.4770 | 2.7835 | 0.1735 | 0.0476 | ||
| (25.0670) | (6.7652 ) | |||||||||||
| b | ||||||||||||
| CosTL-W | 59.5913 | 0.1319 | 1065.8710 | 1069.8710 | 1070.0810 | 1074.0600 | 0.4989 | 2.9015 | 0.1716 | 0.0516 | ||
| (12.0503) | (0.0068) | |||||||||||
| TIHT-W | 0.9061 | 0.6968 | 0.0017 | 1038.2230 | 1044.2230 | 1044.6510 | 1050.5060 | 0.0604 | 0.4467 | 0.0693 | 0.9163 | |
| (0.1364) | (0.3324) | (0.0026) | ||||||||||
| k | ||||||||||||
| OBIII-W | 0.0481 | 6.0431 | 0.518921 | 1043.7600 | 1049.7600 | 1050.1880 | 1056.043 | 0.0755 | 0.5799 | 0.0681 | 0.9255 | |
| (0.0404) | (1.5194) | (0.0969) | ||||||||||
| b | c | |||||||||||
| EOW-TL-LLoG | 0.2037 | 46.3545 | 4.2572 | 0.2313 | 1036.1490 | 1044.1490 | 1044.8760 | 1052.526 | 0.0567 | 0.3958 | 0.0893 | 0.6918 |
| (0.0798) | (0.0194) | (1.3416) | (0.0051) | |||||||||
| b | ||||||||||||
| TL-EHL-Gom-W | 3.0060 | 0.3589 | 3.8490 | 9.4391 | 1062.0970 | 1070.0970 | 1070.8240 | 1078.4740 | 0.4452 | 2.6160 | 0.1706 | 0.0537 |
| (6.0992 ) | (0.3353) | (9.6480 ) | (2.9173 ) | |||||||||
| EL-OLL-W | 5.3598 | 1.0072 | 6.0844 | 0.8941 | 1037.8680 | 1045.8680 | 1046.5950 | 1054.2450 | 0.0563 | 0.4198 | 0.0680 | 0.9262 |
| (1.4388 ) | (1.7684 ) | (1.2674 ) | (9.6488 ) |
| Estimates | Statistics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | b | −2log(L) | AIC | CAIC | BIC | K−S | p-Value | |||||
| TL-OWF-W | 52.2406 | 0.1358 | 0.5772 | 468.9215 | 474.9215 | 475.3425 | 481.2541 | 0.0433 | 0.2629 | 0.0757 | 0.8757 | |
| (15.4731) | (0.0620) | (0.1176) | ||||||||||
| b | ||||||||||||
| TL-W | 1.1951 | 0.1366 | 1064.3390 | 1068.3390 | 1068.5490 | 1072.5270 | 0.4770 | 2.7835 | 0.1735 | 0.04762 | ||
| (25.0670) | (6.7652 ) | |||||||||||
| b | ||||||||||||
| CosTL-W | 64.4954 | 0.3190 | 480.2325 | 484.2325 | 484.4394 | 488.4543 | 0.2136 | 1.2269 | 0.1362 | 0.2075 | ||
| (13.3887) | (0.0163) | |||||||||||
| TIHT-W | 1.8370 | 0.0025 | 1.0819 | 469.0900 | 475.0900 | 475.5111 | 481.4227 | 2.0642 | 11.1937 | 0.1312 | 0.2449 | |
| (0.1971) | (0.0022) | (0.5944) | ||||||||||
| k | ||||||||||||
| OBIII-W | 0.2172 | 9.8007 | 0.8269 | 469.4335 | 475.4335 | 475.8545 | 481.7661 | 0.042 | 0.2450 | 0.0837 | 0.7867 | |
| (0.1438) | (3.75) | (0.1680) | ||||||||||
| b | c | |||||||||||
| EOW-TL-LLoG | 1.2889 | 24.5939 | 1.2906 | 0.5252 | 469.4652 | 477.4652 | 478.1795 | 485.9087 | 0.0591 | 0.3401 | 0.0989 | 0.5895 |
| (0.7040) | (12.4521) | (0.4312) | (0.0914) | |||||||||
| b | ||||||||||||
| TL-EHL-Gom-W | 3.5953 | 0.3577 | 3.6141 | 0.2268 | 477.4705 | 485.4705 | 486.1847 | 493.9140 | 0.1766 | 1.0081 | 0.1345 | 0.2196 |
| (3.0615 ) | (0.3809) | (1.0098 ) | (7.9494 ) | |||||||||
| EL-OLL-W | 1.7323 | 2.4672 | 2.4042 | 1.9037 | 470.5295 | 478.5295 | 479.2438 | 486.973 | 0.0526 | 0.3738 | 0.0886 | 0.724 |
| (0.70660) | (4.1880 ) | (2.2550 ) | (0.18324) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chipepa, F.; Abdelwahab, M.M.; Charumbira, W.F.; Hasaballah, M.M. A New Topp–Leone Odd Weibull Flexible-G Family of Distributions with Applications. Mathematics 2025, 13, 2866. https://doi.org/10.3390/math13172866
Chipepa F, Abdelwahab MM, Charumbira WF, Hasaballah MM. A New Topp–Leone Odd Weibull Flexible-G Family of Distributions with Applications. Mathematics. 2025; 13(17):2866. https://doi.org/10.3390/math13172866
Chicago/Turabian StyleChipepa, Fastel, Mahmoud M. Abdelwahab, Wellington Fredrick Charumbira, and Mustafa M. Hasaballah. 2025. "A New Topp–Leone Odd Weibull Flexible-G Family of Distributions with Applications" Mathematics 13, no. 17: 2866. https://doi.org/10.3390/math13172866
APA StyleChipepa, F., Abdelwahab, M. M., Charumbira, W. F., & Hasaballah, M. M. (2025). A New Topp–Leone Odd Weibull Flexible-G Family of Distributions with Applications. Mathematics, 13(17), 2866. https://doi.org/10.3390/math13172866







