Evolutionary Sampling for Knowledge Distillation in Multi-Agent Reinforcement Learning

Abstract

The Centralized Teacher with Decentralized Student (CTDS) framework is a multi-agent reinforcement learning (MARL) approach that utilizes knowledge distillation within the Centralized Training with Decentralized Execution (CTDE) paradigm. In this framework, a teacher module learns optimal Q-values using global observations and distills this knowledge to a student module that operates with only local information. However, CTDS has limitations including inefficient knowledge distillation processes and performance gaps between teacher and student modules. This paper proposes the evolutionary sampling method that employs genetic algorithms to optimize selective knowledge distillation in CTDS frameworks. Our approach utilizes a selective sampling strategy that focuses on samples with large Q-value differences between teacher and student models. The genetic algorithm optimizes adaptive sampling ratios through evolutionary processes, where the chromosome represent sampling ratio sequences. This evolutionary optimization discovers optimal adaptive sampling sequences that minimize teacher–student performance gaps. Experimental validation in the $StarCraft$ Multi-Agent Challenge (SMAC) environment confirms that our method achieved superior performance compared to the existing CTDS methods. This approach addresses the inefficiency in knowledge distillation and performance gap issues while improving overall performance through the genetic algorithm.

1. Introduction

Multi-agent reinforcement learning (MARL) has demonstrated significant applicability in various domains, such as robotics [1], energy and power grid management [2,3], drone path optimization [4], and autonomous driving [5]. However, MARL faces several critical challenges in achieving effective cooperation among multiple agents. First, the partial observability problem restricts each agent to limited local observations, preventing access to the global state and hindering optimal decision-making [6]. Second, scalability issues arise as the joint state–action space expands exponentially with the increasing number of agents, leading to significantly increased computational complexity [7]. Third, non-stationarity arises when agents simultaneously learn and update their policies, causing each agent’s environment to change continuously and thereby hindering stable learning [8]. To address these challenges, the Centralized Training with Decentralized Execution (CTDE) paradigm has been proposed [9,10]. CTDE is designed to enable decentralized execution using only local observations while having access to global information during training.

A limitation of existing CTDE methods is that they do not fully exploit the available global information during training. Existing CTDE algorithms such as VDN [11], QMIX [12], and QPLEX [13] restrict individual Q-value estimation to local observations even during training and only utilize global information through mixing networks for value combination. This constraint significantly hinders the agents’ ability to learn effective cooperation patterns and limits their potential performance. To address this limitation, the Centralized Teacher with Decentralized Student (CTDS) framework has been proposed, introducing a novel teacher–student architecture [14]. The teacher module learns optimal Q-values utilizing global observations, while the student module learns to approximate the teacher’s Q-values using only local information through knowledge distillation. Through this approach, the student module can indirectly learn global information from the teacher module via knowledge distillation despite using only partial observations, thereby acquiring implicit cooperation patterns among agents.

However, CTDS faces two major limitations that hinder optimal performance. First, inefficiency in the knowledge distillation process occurs when the student module attempts to indiscriminately learn all Q-values from the teacher module, resulting in ineffective knowledge distillation by learning unnecessary or low-importance information. Second, performance gap issues arise where the student module fails to match the teacher module’s performance. The knowledge distillation approach that uniformly utilizes all data makes it difficult for the student to effectively mimic the complex Q-value patterns learned by the teacher, limiting practical effectiveness. To address these problems, we need novel Q-value selection strategies that enable effective knowledge distillation and reduce the performance gap between student and teacher, along with methods to optimize these strategies. Genetic algorithms offer significant advantages as optimization methods for such complex selection problems [15]. First, they can find global optimal solutions in complex search spaces, overcoming the limitations of gradient-based methods that often get trapped in local optima. Second, through population-based approaches, they can simultaneously explore multiple candidate solutions while maintaining diversity in the solution set, which is particularly beneficial for optimizing Q-value selection strategies that require exploration of diverse selection patterns. Similar selective optimization principles have been successfully applied across diverse domains, including computational efficiency enhancement in computer vision and frequency domain processing, demonstrating the broader applicability of such approaches [16,17].

In this study, we propose the evolutionary sampling method, a genetic-algorithm-based selective knowledge distillation approach. Instead of uniformly distilling all knowledge, this approach employs a selective sampling strategy that focuses on samples with large Q-value differences between teacher and student models. Specifically, we utilize only the top percentage of samples with the largest Q-value differences between teacher and student in each batch for knowledge distillation. This enables the student to prioritize learning from challenging samples where it struggles to match the teacher. Additionally, genetic algorithms are used to optimize the adaptive sampling ratio. The chromosomes in the genetic algorithm represent sampling ratio sequences throughout the learning process, evolving through generations via selection, crossover, and mutation operations. Through this evolutionary process, the chromosome population gradually converges toward sampling strategies that exhibit better performance. Finally, the evolution process discovers optimal adaptive sampling sequences that minimize the teacher–student performance gap.

We validated the proposed method in the StarCraft Multi-Agent Challenge (SMAC) environment, known as one of the most challenging environments in reinforcement learning. SMAC provides an ideal benchmark environment for validating MARL algorithm performance by offering multiple scenarios that require real-time strategy game complexity, partial observability, and cooperation among various units [18]. We validated the proposed method in the SMAC environment. Our experiments demonstrate performance improvements compared to existing CTDS. This validates that the genetic-algorithm-based selective knowledge distillation framework can effectively overcome CTDS limitations through sampling sequence optimization.

The main contributions of this paper are as follows. First, we propose an evolutionary sampling strategy that employs genetic algorithms to optimize knowledge distillation sequences in the CTDS framework, overcoming the limitations of static sampling methods. Second, we demonstrate superior performance compared to baseline CTDE algorithms and the original CTDS across multiple challenging multi-agent environments including SMAC and Combat scenarios. Third, we introduce a selective knowledge distillation approach that focuses on samples with large Q-value differences between teacher and student models, enabling more efficient knowledge transfer compared to the indiscriminate learning approach of existing CTDS methods.

This paper is organized as follows. Section 2 reviews related work. Section 3 describes the proposed evolutionary sampling methodology. Section 4 presents experimental results and performance analysis. Section 5 discusses conclusions and future research directions.

2. Related Work

2.1. Centralized Training Decentralized Execution

Multi-agent reinforcement learning (MARL) primarily employs the Centralized Training with Decentralized Execution (CTDE) paradigm. An intuitive approach is to adopt the Decentralized Training with Decentralized Execution (DTDE) paradigm, where each agent learns independently based solely on its local observations during both training and execution phases. Independent Q-Learning (IQL) represents a typical DTDE algorithm, where agents treat other agents as part of the environment and learn individual policies without explicit coordination mechanisms [19]. However, this approach struggles to learn effective coordination strategies in multi-agent environments.

To address these limitations of DTDE approaches, the Centralized Training with Decentralized Execution (CTDE) paradigm was developed. CTDE is a framework designed to learn cooperation patterns between agents by utilizing global information during training while enabling each agent to perform decentralized execution using only local observation information during execution. Value-based CTDE methods focus on mixing networks that combine local agent Q-values to approximate the joint action–value function. These methods are designed to satisfy the Individual-Global-Max (IGM) principle, which requires that the optimal joint action derived from the centralized Q-value function matches the combination of individual optimal actions from each agent [20].

VDN was an early study in this field that proposed the simplest form of value decomposition [11]. Under the assumption that all agents contribute equally to team reward, it represents the central Q-value function as a simple sum of individual Q-values. However, this simple combination approach shows limitations in adequately modeling complex inter-agent interactions. QMIX emerged to overcome VDN’s representational limitations [12]. It introduced a nonlinear mixing network that dynamically assigns different weights to each agent’s Q-values according to the global state. Using hypernetworks to generate state-dependent weights and ensuring the IGM principle through monotonicity constraints, QMIX can represent complex cooperation relationships between agents much better than VDN. However, it still has limitations in that the representable function class remains restricted due to monotonicity constraints. QPLEX was developed to address the representational limitations caused by QMIX’s monotonicity constraints [13]. It proposes a new approach that represents the central Q-value as a combination of the sum of individual Q-values and an advantage function. Through a duplex dueling network structure, the advantage function is designed to become zero only when all agents select optimal actions. This decomposition method can represent a complete function class that satisfies the IGM principle, providing theoretically stronger representational power. A common limitation that appears throughout the development of these algorithms is that all methods restrict individual Q-value learning to local observations even during training for decentralized execution. This creates an information gap where global information available during the training phase is not fully utilized.

2.2. Centralized Teacher, Decentralized Student

CTDS was proposed to address the information utilization inefficiency of existing value-based CTDE algorithms [14]. CTDS resolves the information gap between training and execution phases through a teacher–student learning structure. As illustrated in Figure 1, this framework consists of two independent networks: a teacher module and a student module.

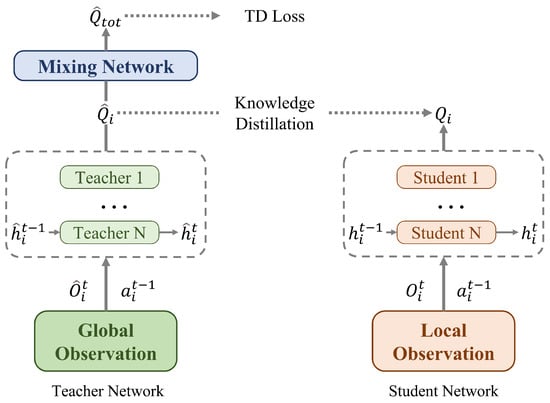
Figure 1. Centralized teacher decentralized student framework overview.

The teacher module learns Q-values for each agent by receiving global information as input. It consists of a Q-network and a mixing network similar to existing CTDE methods. The teacher module’s Q-network takes centralized observation ${\widehat{o}}_i^t$, last action $a_i^{t-1}$, and last hidden state ${\widehat{h}}_i^{t-1}$ as inputs to output individual Q-values ${\widehat{Q}}_i({\widehat{\tau }}_i,a_i^t)$. The mixing network combines these individual Q-values into centralized Q-values ${\widehat{Q}}_{tot}$ using global state information. The teacher module is trained through TD error.

The student module is designed for decentralized execution and uses only local observation information. It has a simpler architecture compared to the teacher module, containing only a Q-network without a mixing network. It takes partial observation $o_i^t$, last action $a_i^{t-1}$, and last hidden state $h_i^{t-1}$ as inputs. The network processes these inputs through MLP and GRU modules to generate individual Q-values $Q_i({\tau }_i,a_i^t)$. Importantly, the student module learns the teacher module’s knowledge without accessing any global information, satisfying the requirements for decentralized execution. During training, both teacher and student module parameters are updated simultaneously. The teacher module is optimized through TD loss, while the student module learns via MSE loss. This parallel training enables the student to distill knowledge from the teacher while maintaining its ability to operate with limited local information during execution.

Knowledge distillation is the key component connecting the teacher and student modules. It is implemented using mean-squared error (MSE) loss:

$$L_{MSE}=\sum _{i=1}^n\sum _{a_i\in A}{\left({\widehat{Q}}_i({\widehat{\tau }}_i,a_i)-Q_i({\tau }_i,a_i)\right)}^2$$

(1)

where $Q_i({\tau }_i,a_i)$ represents the Q-value (action–value function), defined as the expected cumulative reward an agent can obtain by taking action $a_i$ in state ${\tau }_i$ and following a particular policy thereafter:

$$Q^{\pi }({\tau }_i,a_i)=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_{t+1}\mid {\tau }_0={\tau }_i,a_0=a_i,\pi \right]$$

(2)

where $\pi$ is the policy, $\gamma$ is the discount factor, and $r_{t+1}$ is the reward received at time step $t+1$.

This loss function ensures the student module mimics the teacher module’s Q-values for all possible actions. During training, the teacher module interacts with the environment based on centralized observations using the $ϵ$-greedy policy. The parameters of both teacher and student modules are updated simultaneously through TD loss and MSE loss respectively.

However, existing CTDS performs learning with equal weights for all Q-value differences during the knowledge distillation process. This can cause inefficient knowledge distillation by equally including samples with low information content in learning. Additionally, it uses a fixed distillation strategy throughout the learning process, failing to consider characteristics specific to different learning stages. Performance gap issues persist where the student module cannot sufficiently approach the teacher module’s performance. Particularly in environments requiring complex cooperation patterns, the limitation becomes apparent that simple uniform learning approaches cannot effectively distill the sophisticated knowledge learned by the teacher.

2.3. StarCraft II

StarCraft  II is considered a representative challenge in reinforcement learning research. It is recognized as one of the most complex and difficult benchmarks in multi-agent reinforcement learning environments [21]. This real-time strategy game presents several fundamental challenges simultaneously. First, as a multi-agent cooperation problem, players must control hundreds of units. Each unit must cooperate to achieve common goals while simultaneously engaging in high-level strategic competition against opposing players. Second, as an imperfect information game, the map is partially observed through local cameras. Players must actively move to gather information, and fog-of-war in unvisited areas requires active exploration to assess enemy states. Third, the extensive action space presents approximately 10²⁶ possible action combinations at each step. Various unit and building types each have unique actions, providing nearly infinite action possibilities. Fourth, the real-time game characteristics require long-term planning capabilities. Unlike turn-based games like Go, this game proceeds for thousands of timesteps, with some games lasting over an hour. This creates reward delay problems where initial choices or actions are reflected as rewards only hundreds of steps later.

The StarCraft Multi-Agent Challenge (SMAC) is a standardized environment utilizing Starcraft  II’s complexity for multi-agent reinforcement learning research [18,22]. SMAC is an environment specifically designed for cooperative multi-agent reinforcement learning, providing micromanagement scenarios suitable for research purposes while maintaining the original game’s complexity. In this environment, agents perform battles against enemy units, with each agent controlling individual units and aiming for overall team victory. This rigorously evaluates algorithms’ generalization capabilities and adaptability. Particularly, scenarios like MMM2, 9m_vs_11m are known as high-difficulty maps requiring handling of extremely disadvantageous numerical inferiority of complex unit combinations. These combined characteristics make StarCraft II an ideal environment for simulating complex real-world multi-agent problems. It provides an appropriate testbed for validating the effectiveness of the evolutionary sampling framework proposed in this study.

2.4. Evolutionary Algorithms

Evolutionary algorithms have demonstrated substantial effectiveness in adaptive sampling and optimization problems across various reinforcement learning research areas. Studies have shown that evolutionary population methods can significantly improve reinforcement learning performance by optimizing both hyperparameters and action selection strategies simultaneously [23]. The combination of genetic algorithms’ global search capabilities with reinforcement learning’s policy optimization enables rapid convergence and improved generalization performance in sparse reward environments [24]. Multi-agent evolutionary reinforcement learning frameworks address coordination challenges by connecting reinforcement learning with evolutionary algorithms, demonstrating improved cooperation in social dilemma scenarios [25].

Recent research has explored genetic-based action sequence optimization to address the inherent greedy nature of reinforcement learning, where individual actions seeking optimal immediate rewards do not guarantee total reward maximization [26]. Integrated approaches combining genetic operations with Monte Carlo tree search have been developed to address the “penny-wise and pound-foolish” problem in reinforcement learning [27]. The theoretical foundation for evolutionary approaches in adaptive sampling stems from their ability to maintain population diversity while pursuing optimization objectives. Unlike gradient-based methods that can become trapped in local optima, evolutionary algorithms maintain multiple candidate solutions simultaneously, making them particularly suitable for adaptive sampling problems where optimal strategies may vary across different learning stages.

3. Method

3.1. Evolutionary Sampling Framework

The evolutionary sampling framework combines genetic algorithm optimization with the Centralized Teacher with Decentralized Student (CTDS) approach to address the optimal sampling strategy selection problem in multi-agent reinforcement learning. As shown in Figure 2, our framework consists of two main components: a genetic-algorithm-based optimization module and a CTDS-based evaluation module.

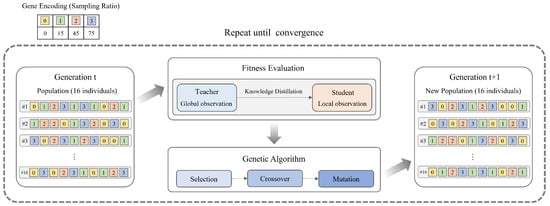
Figure 2. Evolutionary sampling framework overview.

The overall framework operates through generational evolution of the genetic algorithm. In the initial generation (Generation t), a population of 16 individuals is created, where each individual is represented by a chromosome encoding different sampling rate sequences. Each chromosome contains gene values from $\{0, 1, 2, 3\}$, corresponding to sampling rates $\{0.0, 0.15, 0.45, 0.75\}$, respectively. During the fitness evaluation phase, the sampling strategy defined by each chromosome is applied to the CTDS framework to measure performance. CTDS employs a structure where the teacher module leverages global observation information to learn optimal Q-values, while the student module distills the teacher’s knowledge using only local observation information. According to the sampling rate provided by the genetic algorithm, only the top percentage of samples with large Q-value differences between teacher and student participate in the knowledge distillation process. To prevent redundant evaluations and improve experimental efficiency, we adopt a first-visit approach where each unique chromosome is evaluated only once. Specifically, even if multiple chromosomes with identical genes exist across generations, that chromosome is evaluated only at its first appearance, and subsequent instances share the same result. This approach contributes to ensuring consistency and stability in evaluation. After fitness evaluation is completed, the genetic algorithm’s selection, crossover, and mutation operations generate a new population for the next generation (Generation $t+1$). This process repeats until a convergence condition is satisfied, where the majority of the population converges to identical chromosomes, ultimately discovering the most effective sampling strategy. The core contribution of our framework lies in enabling the genetic algorithm to dynamically optimize the sampling strategy used in CTDS’s knowledge distillation process, thereby overcoming the limitations of fixed sampling approaches and enabling adaptive knowledge distillation tailored to different learning stages.

3.2. Selective Knowledge Distillation

The original CTDS employs an indiscriminate learning approach where the student module learns from all Q-values of the teacher module. While it attempts to minimize Q-value differences between teacher and student across all training samples, this approach can lead to inefficient knowledge distillation. Specifically, the student module continues learning from samples where it already mimics the teacher well, resulting in inefficiency, while reducing focus on samples that truly require important learning.

Our selective knowledge distillation method addresses these limitations by introducing a Q-value-difference-based sample selection strategy. The core idea is that samples with large Q-value discrepancies between teacher and student networks provide more valuable learning signals for knowledge distillation. A larger Q-value difference indicates that the student module is not properly following the teacher module’s knowledge, and focused learning on such samples can improve the student module’s performance. In knowledge distillation, the student must effectively learn from the teacher. Q-value differences represent the learning gap between them—large differences indicate samples requiring focused learning, while small differences represent well-learned samples where repeated training is inefficient. This selective approach improves learning efficiency by concentrating resources on samples with large Q-value differences, enabling faster performance gap reduction compared to uniform learning. To address potential overfitting to difficult samples and early training instability, our genetic algorithm incorporates adaptive mechanisms. Population diversity explores various sampling strategies, while gene value 0.0 enables balanced learning when needed.

Formally, given the teacher network’s Q-values ${\widehat{Q}}_i({\widehat{\tau }}_i,·)$ and student network’s Q-values $Q_i({\tau }_i,·)$ for agent i, where a represents an action in the action space $\mathcal{A}$ denoting the set of all possible actions available to the agents, we define the Q-value difference at timestep t in batch b as follows:

$$\begin{array}{cc}\hfill \Delta Q_{b,t}& =\sum _{i=1}^N\sum _{a\in \mathcal{A}}{\left({\widehat{Q}}_i({\widehat{\tau }}_{i,t},a)-Q_i({\tau }_{i,t},a)\right)}^2\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathcal{D}}_{KD}& =\left\{(b,t)\in \mathcal{D}\mid \Delta Q_{b,t}\ge Q_p(\Delta Q)\right\}\hfill \end{array}$$

(4)

where $\Delta Q_{b,t}$ represents the sum of squared Q-value differences across all actions between teacher and student networks at timestep t of batch b. ${\mathcal{D}}_{KD}$ is the set of selected (batch, time) pairs for selective knowledge distillation, containing only samples with Q-value differences above the top percentile threshold across the entire batch. The selective sampling method computes Q-value differences in each training batch and establishes a percentile-based threshold accordingly. Based on the current sampling rate, only samples showing Q-value differences in the top percentile within the batch are considered important learning targets. This percentile-based selection approach dynamically selects learning targets by considering the relative importance of samples within the batch, unlike simple fixed thresholds. Only the selected samples participate in the knowledge distillation process, enabling the student network to learn intensively from experiences that require the most learning.

3.3. Genetic-Algorithm-Based Optimization

The genetic algorithm component optimizes sampling rate sequences through evolutionary computation principles. As presented in Algorithm 1, the optimization process discovers effective sampling strategies through chromosome encoding, fitness evaluation, and genetic operations.

Algorithm 1 Evolutionary Sampling Framework

1: Input: Plain CTDS algorithm, population size N, gene values $V=\{0.0, 0.15, 0.45, 0.75\}$, chromosome length L, mutation rate $\mu$, convergence threshold $\theta$  2: Output: $\text{best\_chromosome}$  3: Initialize population $P=\{C_1,C_2,\dots ,C_N\}$  4: $generation\leftarrow 0$, $\text{best\_chromosome}\leftarrow \mathtt{None}$  5: while convergence rate $<\theta$ do  6:       for each chromosome $C_i$ in P do  7:          $\text{sampling\_sequence}\leftarrow \mathtt{DecodeToSamplingRatio}(C_i,V)$  8:          $fitness\left[i\right]\leftarrow \mathtt{FitnessCalculation}(C_i,\text{sampling\_sequence})$  9:       end for 10:      $P_{selection}\leftarrow \mathtt{TournamentSelection}(P,fitness)$ 11:      $P_{crossover}\leftarrow \mathtt{UniformCrossover}\left(P_{selection}\right)$ 12:      $P_{mutation}\leftarrow \mathtt{Mutation}(P_{crossover},\mu )$ 13:      $P\leftarrow P_{mutation}$ 14:      $generation\leftarrow generation+1$ 15: end while 16: return $\text{best\_chromosome}$   ▹ chromosome with highest fitness in final generation

3.3.1. Chromosome Encoding

Each chromosome represents a sampling rate sequence to be used during the learning process. A chromosome is encoded as $C=[g_1,g_2,\dots ,g_L]$, where each gene $g_i$ represents a specific sampling rate value with $g_i\in \{0.0, 0.15, 0.45, 0.75\}$. Each gene corresponds to the sampling intensity applied in different intervals of the training process. For example, chromosome $[0.15, 0.75, 0.0, 0.45]$ means selecting the top 0.15 proportion of samples in the first interval, 0.75 proportion in the second interval, no sampling in the third interval, and 0.45 proportion in the fourth interval. While continuous values or finer-grained discrete values could potentially yield superior optimization results, the computational complexity would increase exponentially with the resolution of the search space. To address this computational challenge while maintaining effective optimization capability, we selected four representative values that can capture significant variations in sampling intensity. These discrete values provide sufficient diversity to explore different sampling strategies while keeping the genetic algorithm computationally tractable. The selected gene values represent various sampling intensities: 0.0 indicates no sampling (using all samples), 0.15 represents weak sampling, 0.45 represents moderate sampling, and 0.75 represents strong sampling. Specifically, we placed two values (0.15 and 0.45) within the 0.0–0.5 range to capture subtle differences in weak sampling regions where small variations can significantly impact performance. Additionally, we selected 0.75 as an appropriate level of strong sampling rather than excessive values (0.8, 0.9) to maintain a practical sampling range. These values are spaced to provide meaningful differences that can induce distinct learning patterns. These diverse combinations of sampling rates enable the discovery of optimal knowledge distillation strategies by appropriately placing weak or strong selective learning throughout episodes.

3.3.2. Fitness Function

We propose a novel Gaussian-based fitness function specifically designed for evaluating chromosomes in our evolutionary sampling framework for the CTDS paradigm. The fitness function evaluates the effectiveness of each chromosome by measuring the performance improvement achieved through the corresponding sampling strategy. This proposed fitness function simultaneously considers both the absolute performance of the student model and the performance similarity between teacher and student models, addressing the unique requirements of optimizing selective knowledge distillation. For each chromosome $C_i$, the fitness is calculated as

$$\mathrm{Fitness}(T,S)=S\times e^{-{\displaystyle \frac{{\left(\frac{T-S}{max(T,S)}\right)}^2}{2{\sigma }^2}}}$$

(5)

where T is the teacher win rate, S is the student win rate, and $\sigma$ is the sensitivity parameter of the Gaussian function set to 0.3. This fitness function consists of two main components: First, the student performance term S represents the absolute performance of the student model, where higher student performance leads to higher overall fitness. This directly drives improvement in the student model’s actual execution performance. Second, the Gaussian similarity term measures the performance gap between teacher and student models, designed to ensure the student effectively follows the teacher. By multiplying these two terms, our fitness function simultaneously optimizes both the student’s absolute performance and the teacher–student performance alignment, ensuring that high fitness is achieved only when both objectives are satisfied. The key goal is to prevent the performance gap between the student and teacher from widening. The Gaussian function achieves its maximum value of 1 when the performance difference is zero ($T=S$), approaches 1 as the performance difference decreases, and approaches 0 as the difference increases. Importantly, this value never becomes exactly 0, preventing extremely low fitness values or incomparable situations and providing stable, comparable evaluations for all sampling strategies. This design responds smoothly to small performance differences while applying stronger penalties to large differences, assigning high fitness to sampling strategies that achieve effective knowledge distillation.

3.3.3. Genetic Operations

Genetic operations consist of three main operations that evolve sampling strategies: selection, crossover, and mutation. In the selection phase, we employ tournament selection to identify individuals with high fitness, where the individual with the highest fitness among randomly selected candidates in each tournament is chosen as a parent for the next generation. In the crossover phase, we apply uniform crossover, exchanging genes between two parents only at even-indexed positions. This maintains structural stability while ensuring diversity in sampling strategies across learning intervals. In the mutation phase, we apply mutation to each gene with low probability to maintain diversity in the search space. When mutation occurs, the current gene value is replaced with a randomly selected value from the other possible values. The convergence condition is met when 90% or more of the population shares identical chromosomes. This convergence threshold ensures sufficient exploration, and when convergence is achieved, the converged chromosome from the final generation is adopted as the optimal sampling strategy.

4. Experiments

4.1. Experimental Setup

We validated our proposed method in two multi-agent environments: StarCraft Multi-Agent Challenge (SMAC) SC 2.3.1 and Combat grid-world environment. SMAC is a partially observable multi-agent environment where each agent can only acquire information within a limited sight range. The game rules are as follows: each agent can choose one of three actions (move, attack, or stop) at every timestep, with a cool-down period applied after attacking. The move and attack actions require agents to select specific target coordinates from the game map, creating a large discrete action space that poses significant challenges for multi-agent coordination. Agents must learn sophisticated cooperation strategies to win battles against enemy units, and episodes terminate when all enemy units are eliminated or the time limit is reached. The environment provides shaped rewards to facilitate learning, calculated by combining damage dealt to enemies, damage received, unit kills, and final battle outcomes. We conducted experiments on three scenarios: 5m_vs_6m (5 Marines vs. 6 Marines), 9m_vs_11m (9 Marines vs. 11 Marines), and MMM2 (1 Medivac, 2 Marauders, and 7 Marines). These scenarios have different complexity levels and numbers of agents, making them suitable for evaluating the generalization capability of our proposed method. Combat is a grid-world environment where two teams of agents engage in tactical combat. Each agent has health points and can move in four directions, attack enemies within range, or remain idle. The environment enforces a cool-down mechanism where agents cannot attack immediately after performing an attack. Episodes terminate when one team is eliminated or the maximum episode length is reached. The environment features partial observability and provides shaped rewards based on battle outcomes and strategic play.

All experiments were performed on Ubuntu 24.04.1 with NVIDIA GeForce RTX 4090 GPU and Intel Xeon Gold 6138 CPU. Each method was repeated with seven different seeds to calculate mean and standard deviation. The combination of MARL and genetic algorithm optimization presents significant computational challenges as both approaches are inherently computationally expensive. Our evolutionary approach requires additional computational resources due to the genetic algorithm optimization process. Specifically, our method executed the CTDS algorithm between 176 to 240 times across 11–15 generations with a population size of 16 to discover optimal sampling strategies. While this results in higher computational cost compared to standard CTDS, the performance improvements justify this additional expense. In terms of GPU memory usage, all baseline algorithms consumed approximately 2.4–2.5 GB, demonstrating comparable resource requirements for the core learning process. Despite these challenges, our study achieved meaningful optimization results even with a population size limited to 16 individuals in a resource-constrained environment, demonstrating the practical feasibility of our approach. The reinforcement learning hyperparameters used for our experiments are presented in Table 1. All agents use 64-dimensional RNN hidden states and were trained for 2 million steps with a learning rate of 0.0005. The batch size was set to 32, and a replay buffer of size 5000 was used. The target network was updated every 200 episodes, and the $ϵ$ value in the $ϵ$-greedy exploration strategy started at 1.0 and decreased linearly to 0.05 over 50,000 steps. In the CTDS framework, the teacher model earns individual Q-values using global observation information, while the student model receives knowledge distillation from the teacher using only local observation information. For CTDS experiments, we used a QMIX-based mixing network with 32-dimensional mixing embedding. Similarly, for our evolutionary sampling method experiments, we also employed a QMIX-based mixing network architecture. We selected QMIX as the base mixing network because it demonstrates superior performance in challenging scenarios such as MMM2 and 9m_vs_11m, making it an appropriate foundation for validating our genetic-algorithm-based optimization approach.

Table 1. Reinforcement learning hyperparameters.

Parameter	Value
Learning Rate	0.0005
Batch Size	32
Buffer Size	5000
Target Update Interval	200 episodes
Total Training Steps	2,000,000
Epsilon Start	1.0
Epsilon Finish	0.05
Epsilon Anneal Time	50,000 steps
Discount Factor (γ)	0.99
RNN Hidden Dimension	64
Mixing Embed Dimension	32

We optimized sampling sequences using the genetic algorithm hyperparameters specified in Table 2. The population size was set to 16, with each chromosome consisting of 10 genes. Each gene can have one of the values $\{0.0, 0.15, 0.45, 0.75\}$, which serves as the criterion for selecting top percentile samples during the knowledge distillation process. The mutation rate was set to 0.005, and the termination condition was set when 90% or more of the population converged to identical chromosomes within a generation. Percentile values are updated every 200,000 steps, and tournament selection (size 2) and uniform crossover are used to generate the next generation population.

Table 2. Genetic algorithm hyperparameters.

Parameter	Value
Population Size	16
Chromosome Size	10
Gene Values	{0.0, 0.15, 0.45, 0.75}
Mutation Rate	0.005
Convergence Threshold	0.9
P Update Interval	200,000 steps
Tournament Size	2
Selection Method	Tournament
Crossover Type	Uniform

4.2. Performance Evaluation

We compare our proposed evolutionary sampling method against five baseline approaches: IQL, VDN, QMIX, QPLEX, and CTDS. Table 3 presents the overall performance across all scenarios. In the table, IQL represents a DTDE algorithm where agents learn and execute independently. VDN, QMIX, and QPLEX represent existing CTDE algorithms. Teacher and student represent the two components of the CTDS framework applied to both CTDS and our evolutionary sampling method. ES (evolutionary sampling) represents our proposed method optimized with a genetic algorithm. The experimental results demonstrate that evolutionary sampling achieves superior performance across all scenarios.

Table 3. Win rate comparison across SMAC scenarios.

Algorithm		5m vs. 6m	9m vs. 11m	MMM2
IQL		$15.1\pm 3.3$	$0.0\pm 0.1$	$0.2\pm 0.4$
VDN		$33.5\pm 4.6$	$1.2\pm 0.5$	$6.6\pm 6.8$
QMIX		$30.9\pm 2.6$	$2.2\pm 1.7$	$37.3\pm 29.1$
QPLEX		$27.0\pm 3.9$	$1.8\pm 0.8$	$41.5\pm 13.7$
CTDS	Teacher	$63.3\pm 10.9$	$11.6\pm 7.0$	$60.3\pm 14.0$
	Student	$57.8\pm 13.5$	$15.6\pm 7.8$	$56.7\pm 13.0$
ES	Teacher	$\mathbf{69.6}\pm \mathbf{6.0}$	$\mathbf{18.3}\pm \mathbf{7.2}$	$\mathbf{77.7}\pm \mathbf{19.3}$
	Student	$\mathbf{70.1}\pm \mathbf{9.6}$	$\mathbf{20.5}\pm \mathbf{12.6}$	$\mathbf{69.6}\pm \mathbf{30.9}$

In the 5m_vs_6m scenario, our evolutionary sampling method achieved improved performance over baseline approaches. The teacher model reached a 69.6% win rate compared to the CTDS teacher’s 63.3%, while the student model achieved 70.1% compared to the CTDS student’s 57.8%. In the 9m_vs_11m scenario, which presents increased complexity due to larger unit asymmetry, our evolutionary sampling method achieved higher performance than the CTDS baseline. The teacher model achieved an 18.3% win rate compared to the CTDS teacher’s 11.6%, while the student model reached 20.5% compared to the CTDS student’s 15.6%. Similarly, in the $MMM2$ scenario, our method demonstrated performance gains with the teacher achieving 77.7%, while the CTDS teacher achieved 60.3%, and the student reached 69.6%, while the CTDS student achieved 56.7%. Particularly noteworthy is that the student model in the evolutionary sampling demonstrated performance comparable to the teacher model and in some cases, even achieved superior results. In the 5m_vs_6m scenario, the student achieved 70.1%, while the teacher achieved 69.6%, showing competitive performance levels. These results indicate that our approach enables more efficient sampling strategies compared to the existing CTDS framework. We attribute this improvement to our evolutionary algorithm’s ability to optimize sampling sequences, which provide more effective knowledge distillation processes. The genetic-algorithm-optimized sampling sequences enable both teacher and student models to achieve enhanced performance through more strategic and efficient sampling patterns, demonstrating the effectiveness of our proposed evolutionary approach in improving the overall CTDS framework.

Figure 3 demonstrates the effectiveness of knowledge distillation in our evolutionary sampling framework. The y-axis represents the teacher–student performance gap, calculated as the absolute difference between teacher and student win rates. This metric represents the efficiency of knowledge distillation. Lower median values indicate better knowledge distillation as they demonstrate that the student model successfully mimics the teacher’s performance with minimal gap. Our evolutionary approach demonstrates superior knowledge distillation effectiveness across most scenarios. In the 5m vs. 6m and MMM2 scenarios, our method achieves substantially lower median performance gaps compared to the baseline CTDS method. While the 9m vs. 11m scenario shows a slightly higher median gap for our approach, the overall performance across the three scenarios demonstrates the effectiveness of our knowledge distillation framework. These results demonstrate that our fitness function, which explicitly incorporates knowledge distillation objectives, successfully guides the evolutionary process to reduce the performance discrepancy between teacher and student models.

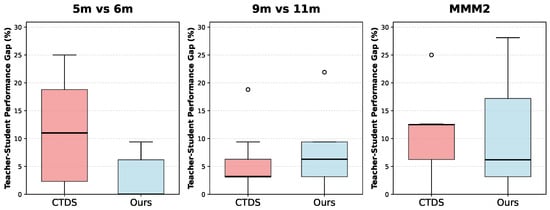
Figure 3. Knowledge distillation effectiveness across SMAC scenarios. Lower teacher-student performance gaps indicate better knowledge distillation.

We evaluate our ES method on the Combat scenario using return mean as the performance metric. The genetic algorithm optimization proceeded for 13 generations to find the optimal sampling sequence. The final optimized sequence discovered by GA is $[0.75, 0.15, 0.45, 0.75, 0.0, 0.75, 0.45, 0.0, 0.0, 0.75]$, which represents the percentile thresholds for selective sampling at different training stages. Table 4 presents the experimental results on the Combat environment. Our proposed ES method achieves superior performance compared to all baseline algorithms. The ES teacher network reaches a return mean of $-9.19\pm 0.39$, while the ES student network achieves $-9.73\pm 0.58$. These results significantly outperform traditional CTDE and CTDS algorithms. Compared to CTDS, our ES method shows substantial improvements. The ES teacher network outperforms CTDS teacher by approximately 1.6 points, while the ES student network surpasses CTDS student by about 0.9 points. This demonstrates that our GA-optimized sampling sequences effectively enhance learning performance across different network architectures. The results validate that genetic algorithm optimization successfully identifies effective sampling patterns that adapt to the specific characteristics of the Combat environment, leading to more efficient learning and superior final performance.

Table 4. Return mean comparison in Combat environment.

Algorithm		Return Mean
VDN		$-10.59\pm 0.29$
QMIX		$-10.48\pm 0.42$
QPLEX		$-10.64\pm 0.36$
CTDS	Teacher	$-10.81\pm 0.41$
	Student	$-10.65\pm 0.53$
ES	Teacher	$-\mathbf{9.19}\pm \mathbf{0.39}$
	Student	$-\mathbf{9.73}\pm \mathbf{0.58}$

4.3. Genetic Algorithm Analysis

This section analyzes the genetic algorithm’s convergence characteristics and optimization process. Figure 4 illustrates the evolution of average fitness across generations and the convergence percentage of the population. The left column shows the improvement in average fitness over generations, while the right column displays the percentage of individuals with identical chromosomes in the population. The red dashed line indicates the convergence threshold of 90%. The optimal sampling sequences presented below are derived from the best chromosomes in the final generation.

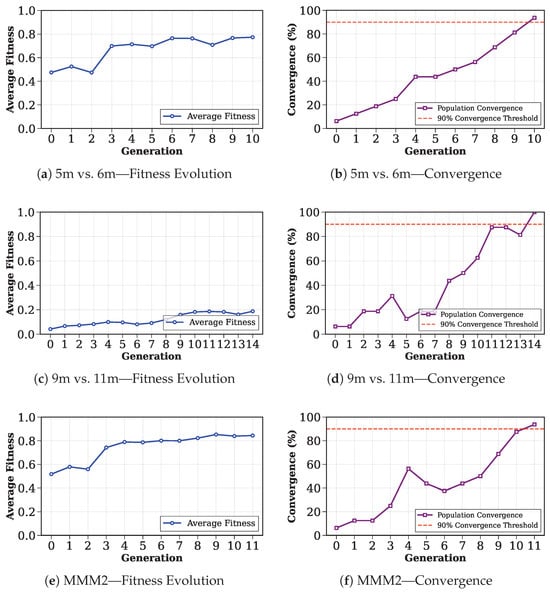
Figure 4. Genetic Algorithm analysis across different SMAC scenarios.

In the 5m_vs_6m scenario, the genetic algorithm satisfied the convergence condition within 11 generations. The average fitness improved from an initial value of 0.47 to a final value of 0.77, representing an improvement of approximately 0.29. The optimal sampling sequence derived at convergence was $[0.0, 0.45, 0.0, 0.45, 0.15, 0.75, 0.0, 0.75, 0.0, 0.45]$. This demonstrates enhanced performance compared to the initial search space and indicates successful evolution of the sampling strategy. For the MMM2 scenario, the algorithm required 12 generations to reach convergence. Starting from an initial fitness of 0.51, the population evolved to achieve a final average fitness of 0.84, marking a 0.32 improvement. The best chromosome was $[0.75, 0.0, 0.15, 0.15, 0.75, 0.75, 0.15, 0.15, 0.15, 0.45]$. These results confirm the genetic algorithm’s ability to successfully navigate the complex search space and converge to high-quality solutions even in challenging scenarios. For the 9m_vs_11m scenario, the genetic algorithm converged after 15 generations. The average fitness evolved from an initial value of 0.041 to a final value of 0.188, showing an improvement of 0.146. This scenario demonstrated the most challenging optimization problem among the three tested scenarios, as evidenced by the lower initial fitness values and extended convergence period. The optimal chromosome discovered was $[0.75, 0.45, 0.45, 0.15, 0.75, 0.75, 0.75, 0.15, 0.45, 0.0]$.

To validate the specialization of our evolutionary sampling sequences, we conducted cross-scenario validation experiments. Table 5 presents the performance of optimal sequences when applied across different scenarios. Each row represents the test scenario where the sequence was validated, while each column indicates the source scenario from which the optimal sequence was derived. The results demonstrate that each evolutionary sampling sequence achieves superior performance in its corresponding target scenario. For instance, the 5m_vs_6m-optimized sequence performs best in its original scenario but shows reduced performance when applied to other scenarios. Similarly, both the 9m_vs_11m sequence and MMM2 sequence demonstrate superior performance in their respective original scenarios compared to cross-scenario applications. This scenario-specific optimization validates that our genetic algorithm successfully discovers specialized sampling strategies rather than generic solutions. The performance degradation observed in cross-scenario validations confirms that each evolutionary chromosome encodes domain-specific knowledge tailored to the unique characteristics of its target scenario.

Table 5. Performance of optimal sequences across different scenarios.

Scenario		5m vs. 6m	9m vs. 11m	MMM2
5m vs. 6m	Teacher	$\mathbf{69.6}\pm \mathbf{6.0}$	$61.2\pm 7.3$	$61.2\pm 8.7$
	Student	$\mathbf{70.1}\pm \mathbf{9.6}$	$62.1\pm 7.4$	$56.2\pm 17.0$
9m vs. 11m	Teacher	$12.9\pm 9.9$	$\mathbf{18.3}\pm \mathbf{7.2}$	$12.9\pm 8.9$
	Student	$15.2\pm 8.3$	$\mathbf{20.5}\pm \mathbf{12.6}$	$13.4\pm 5.2$
MMM2	Teacher	$67.4\pm 33.8$	$69.6\pm 13.8$	$\mathbf{77.7}\pm \mathbf{19.3}$
	Student	$59.4\pm 32.1$	$62.9\pm 17.0$	$\mathbf{69.6}\pm \mathbf{30.9}$

Rows represent the test scenario where the sequence was evaluated, and columns represent the source scenario where the optimal sequence was found.

5. Ablation Study

To demonstrate the effectiveness of genetic-algorithm-optimized sampling sequences, we conduct an ablation study comparing our GA-based approach against fixed sampling ratios. This experiment aims to show that simply using fixed sampling ratios is not effective and that finding optimal sampling sequences through genetic algorithms is necessary for superior performance. The fixed sampling methods represent our selective sampling approach with static ratios, where the top percentile of experiences are consistently selected throughout training without optimization. Unlike our proposed GA-based method, which finds optimal sampling sequences, these fixed approaches maintain constant sampling percentages regardless of training dynamics. Table 6 presents the results on the SMAC scenario 5m vs. 6m. ES (evolutionary sampling) achieves the highest performance for both teacher (69.6 ± 6.0%) and student (70.1 ± 9.6%) networks. ES consistently shows superior performance compared to all fixed sampling ratios. The results demonstrate that genetic-algorithm-optimized sampling sequences provide superior and more stable performance compared to static fixed ratios. This validates that our approach effectively identifies optimal sampling sequences that fixed-ratio methods cannot achieve.

Table 6. Performance comparison between genetic algorithm and fixed sampling approaches.

Algorithm	Teacher	Student
Fixed—10%	$67.5\pm 6.1$	$61.2\pm 10.9$
Fixed—20%	$65.0\pm 15.1$	$41.3\pm 27.6$
Fixed—30%	$63.3\pm 9.9$	$52.8\pm 14.9$
Fixed—40%	$66.3\pm 12.0$	$58.7\pm 12.4$
Fixed—50%	$61.3\pm 8.7$	$64.4\pm 13.3$
CTDS	$63.3\pm 10.9$	$57.8\pm 13.5$
ES	$\mathbf{69.6}\pm \mathbf{6.0}$	$\mathbf{70.1}\pm \mathbf{9.6}$

6. Conclusions

We propose the evolutionary sampling method, a genetic-algorithm-based approach for optimizing selective knowledge distillation in multi-agent reinforcement learning. Our method addresses the key limitations of existing CTDS frameworks through genetic algorithm optimization of sampling strategies. The proposed approach combines genetic algorithms with the CTDS paradigm to discover optimal sampling sequences. Instead of uniform knowledge distillation, our method employs selective sampling that focuses on samples with large Q-value differences between teacher and student models. The genetic algorithm evolves sampling rate chromosomes through tournament selection, uniform crossover, and mutation operations to discover optimal adaptive sampling patterns. Experimental validation demonstrates that our method achieved superior performance compared to baseline CTDE algorithms and the original CTDS framework. Our approach contributes to the multi-agent reinforcement learning field by introducing a novel method for optimizing knowledge distillation processes. The integration of evolutionary computation with CTDS provides a principled framework for addressing sampling strategy optimization problems. Future research directions include exploring larger population sizes and investigating the application of our evolutionary sampling framework to other multi-agent environments.