Estimating Skewness and Kurtosis for Asymmetric Heavy-Tailed Data: A Regression Approach
Abstract
1. Introduction
2. Existing Estimators
- The mean: .
- The variance: .
- The skewness (third standardized central moment): .
- The kurtosis (fourth standardized central moment): .
2.1. L-Moments
2.2. Quantile-Based Methods
2.3. Other Quantile-Based Skewness Estimators
2.4. Medcouple Skewness Estimator
2.5. Modal Skewness Estimator
2.6. Hogg’s Kurtosis Estimator
2.7. Discussion
3. Proposed Method
3.1. Cornish–Fisher Expansion
3.2. Proposed Regression Approach
| Algorithm 1 Proposed Estimatior of Skewness and Kurtosis |
Require: Sample data
|
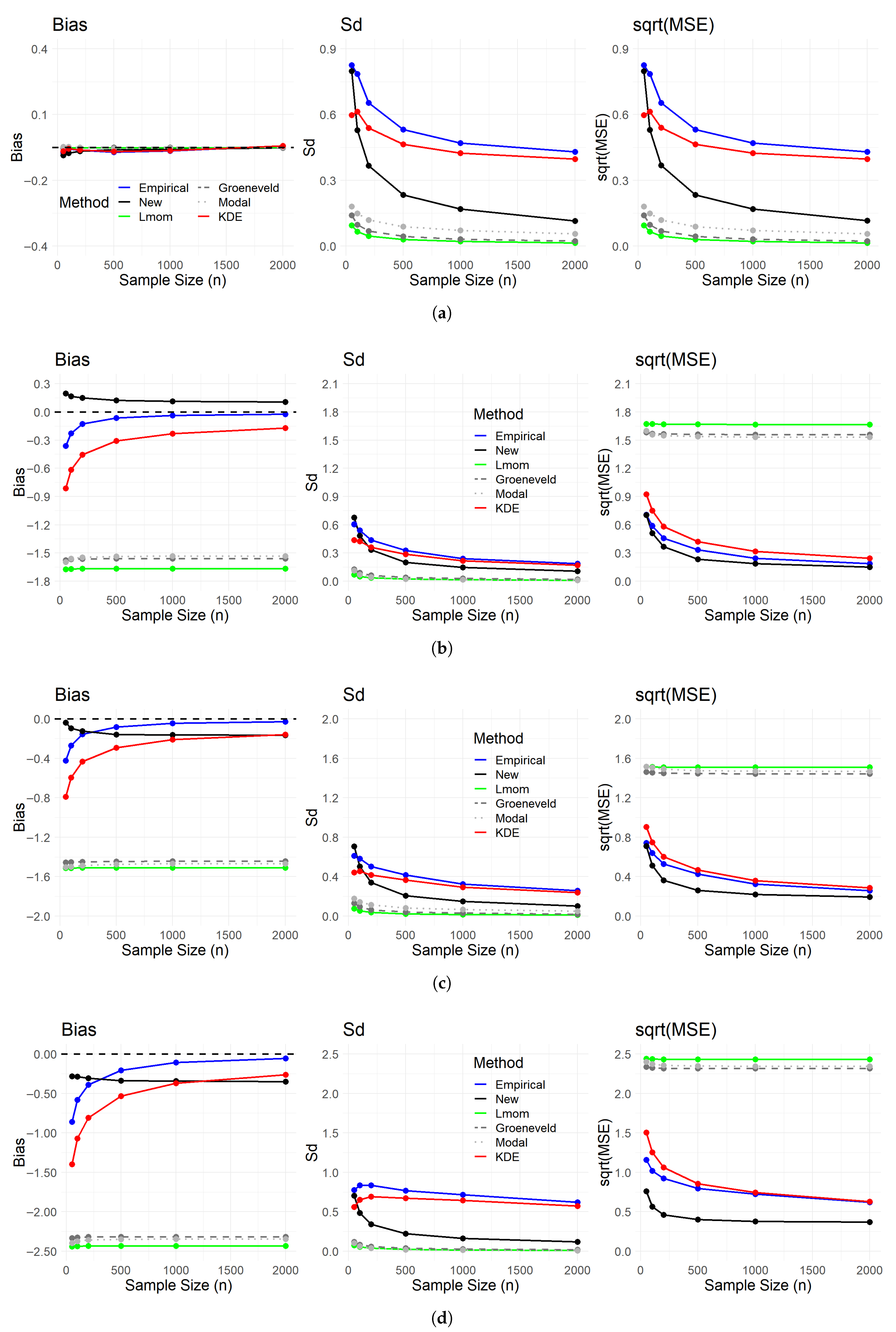
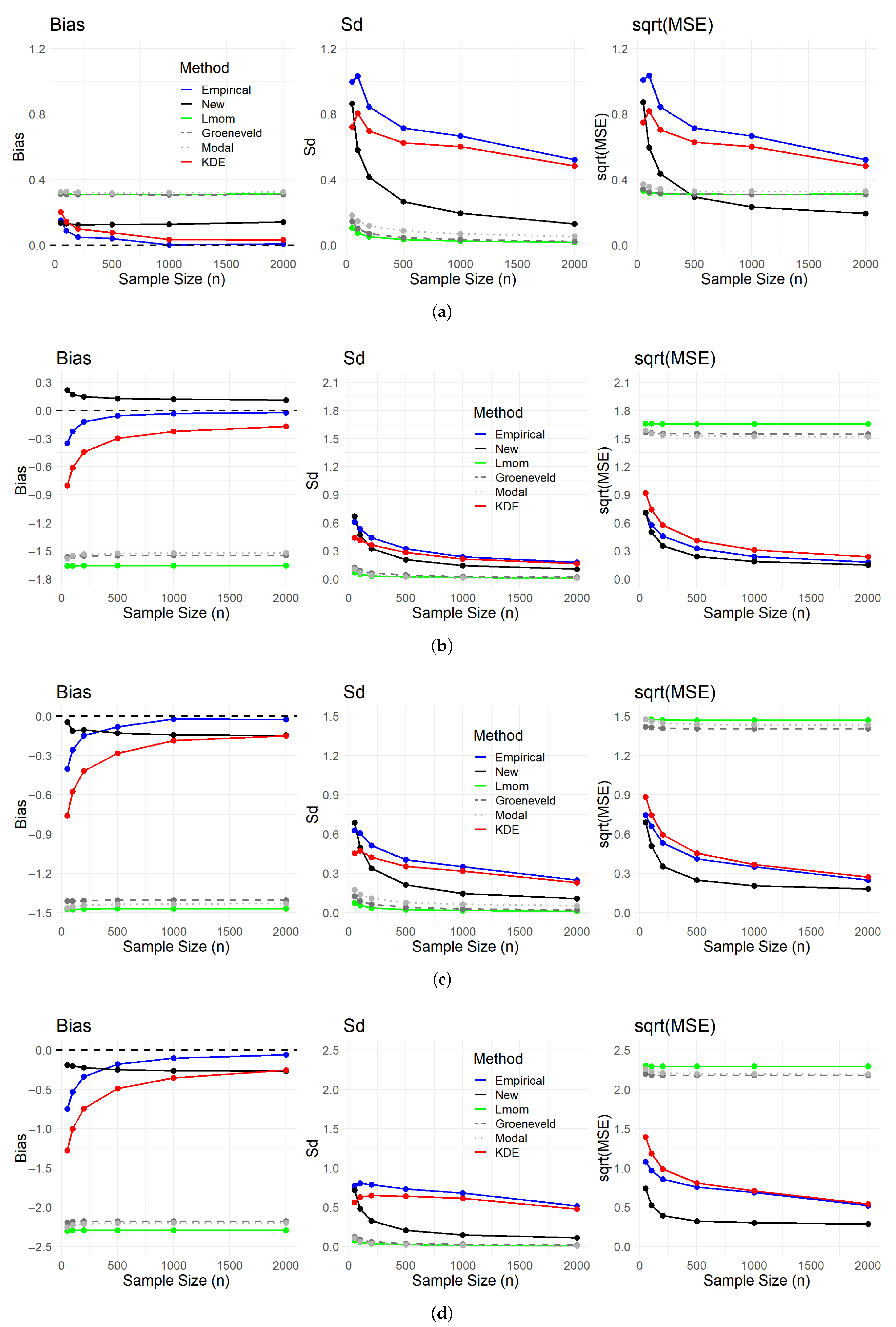
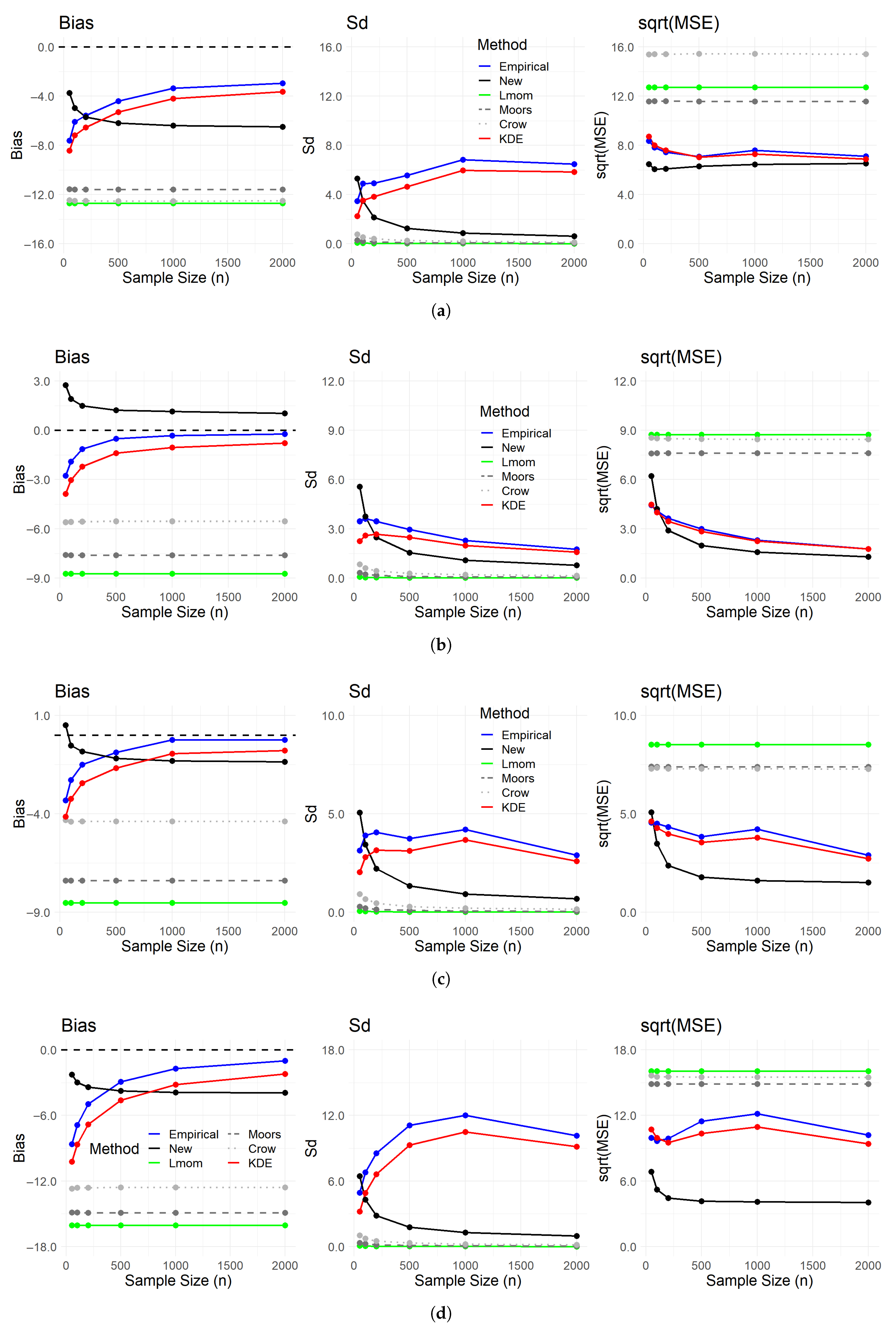
4. Numerical Study
4.1. First Simulation Study
- Skewness estimation methods:
- 1.
- Empirical: The sample-based skewness estimator computed directly from the data.
- 2.
- New: The newly proposed skewness estimator in this study.
- 3.
- Lmom: The L-moments-based skewness estimator defined in (1).
- 4.
- TL: The trimmed L-moments-based skewness estimator excluding the smallest and largest observations.
- 5.
- Bowley: The quantile-based skewness measure, defined in (2), using the 25th, 50th, and 75th percentiles.
- 6.
- Groeneveld: The symmetry-based skewness measure using median deviations defined in (3).
- 7.
- Pearson: The skewness coefficient based on the mean–median difference defined in (5).
- 8.
- MC: The Medcouple skewness estimator in (7).
- 9.
- Modal: The mode-based skewness measure in (8).
- 10.
- KDE: The skewness estimator from the Gaussian KDE.
- Kurtosis estimation methods:
- 1.
- Empirical: The sample-based kurtosis estimator computed directly from the data.
- 2.
- New: The newly proposed kurtosis estimator in this study.
- 3.
- Lmom: The L-moments-based kurtosis estimator, defined using L-kurtosis in (1).
- 4.
- TL: The trimmed L-moments-based kurtosis estimator excluding the smallest and largest observations.
- 5.
- Moors: The octile-based kurtosis measure defined in (6).
- 6.
- Hogg: The quantile-based kurtosis coefficient defined in (9).
- 7.
- Crow: The quantile-based kurtosis estimator in (4).
- 8.
- KDE: The kurtosis estimator from the Gaussian KDE.
4.2. Second Simulation Study
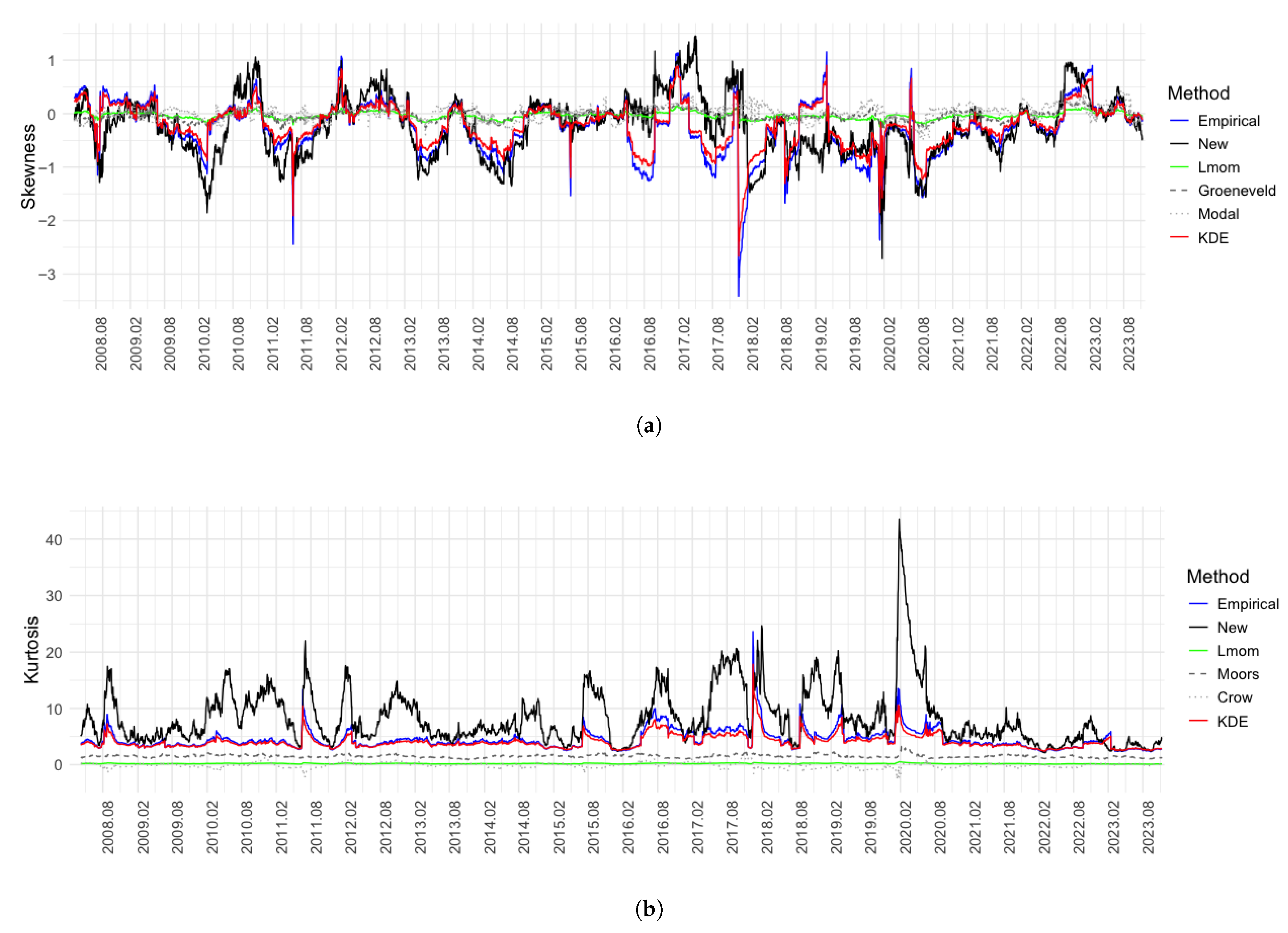
4.3. Analysis of Real Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- , Student’s t-distribution with degrees of freedom , has a density ofThe scaled t-distribution, denoted by X, is a location-scale transformation of the standard Student’s t-distribution. That is, , so that
- has a density of
- has a density of
- has a density, for , of
References
- Harvey, C.R.; Siddique, A. Conditional skewness in asset pricing tests. J. Financ. 2000, 55, 1263–1295. [Google Scholar] [CrossRef]
- Hwang, S.; Satchell, S.E. Modelling emerging market risk premia using higher moments. Int. J. Financ. Econ. 1999, 4, 271–296. [Google Scholar] [CrossRef]
- Jorion, P. On jump processes in the foreign exchange and stock markets. Rev. Financ. Stud. 1988, 1, 427–445. [Google Scholar] [CrossRef]
- Sandström, A. Solvency II: Calibration for skewness. Scand. Actuar. J. 2007, 126–134. [Google Scholar] [CrossRef]
- Brys, G.; Hubert, M.; Struyf, A. A comparison of some new measures of skewness. In Developments in Robust Statistics: International Conference on Robust Statistics 2001; Springer: Berlin/Heidelberg, Germany, 2003; pp. 98–113. [Google Scholar]
- Bates, D.S. Jumps and stochastic volatility: Exchange rate processes implicit in deutsche mark options. Rev. Financ. Stud. 1996, 9, 69–107. [Google Scholar] [CrossRef]
- Bonato, M. Robust estimation of skewness and kurtosis in distributions with infinite higher moments. Financ. Res. Lett. 2011, 8, 77–87. [Google Scholar] [CrossRef]
- Kim, T.-H.; White, H. On more robust estimation of skewness and kurtosis. Financ. Res. Lett. 2004, 1, 56–73. [Google Scholar] [CrossRef]
- Bastianin, A. Robust measures of skewness and kurtosis for macroeconomic and financial time series. Appl. Econ. 2020, 52, 637–670. [Google Scholar] [CrossRef]
- Groeneveld, R.A.; Meeden, G. Measuring skewness and kurtosis. J. R. Stat. Soc. Ser. D Stat. 1984, 33, 391–399. [Google Scholar] [CrossRef]
- Klugman, S.A.; Panjer, H.H.; Willmot, G.E. Loss Models, 3rd ed.; John Wiley: New York, NY, USA, 2008. [Google Scholar]
- Sandström, A. Handbook of Solvency for Actuaries and Risk Managers: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- van Broekhoven, H. Market value of liabilities mortality risk: A practical model. North Am. Actuar. J. 2002, 6, 95–106. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B Stat. Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Zhao, Y.-G.; Tong, M.-N.; Lu, Z.-H.; Xu, J. Monotonic expression of polynomial normal transformation based on the first four L-moments. J. Eng. Mech. 2020, 146, 06020003. [Google Scholar] [CrossRef]
- Elamir, E.A.H.; Seheult, A.H. Trimmed L-moments. Comput. Stat. Data Anal. 2003, 43, 299–314. [Google Scholar] [CrossRef]
- Bowley, A.L. Elements of Statistics; P. S. King & Son: London, UK, 1926. [Google Scholar]
- Crow, E.L.; Siddiqui, M.M. Robust estimation of location. J. Am. Stat. Assoc. 1967, 62, 353–389. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics; Griffin: London, UK, 1977; Volume 1. [Google Scholar]
- Moors, J.J.A. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. D (Stat.) 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Brys, G.; Hubert, M.; Struyf, A. A robust measure of skewness. J. Comput. Graph. Stat. 2004, 13, 996–1017. [Google Scholar] [CrossRef]
- Bickel, D.R. Robust estimators of the mode and skewness of continuous data. Comput. Stat. Data Anal. 2002, 39, 153–163. [Google Scholar] [CrossRef]
- Hogg, R.V. More light on the kurtosis and related statistics. J. Am. Stat. Assoc. 1972, 67, 422–424. [Google Scholar] [CrossRef]
- Hogg, R.V. Adaptive robust procedures: A partial review and some suggestions for future applications and theory. J. Am. Stat. Assoc. 1974, 69, 909–923. [Google Scholar] [CrossRef]
- Cornish, E.A.; Fisher, R.A. Moments and cumulants in the specification of distributions. Rev. L’Inst. Int. Stat. 1938, 5, 307–320. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Multivariate Distributions, Volume 1: Models and Applications; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Aboura, S.; Maillard, D. Option pricing under skewness and kurtosis using a Cornish–Fisher expansion. J. Futur. Mark. 2016, 36, 1194–1209. [Google Scholar] [CrossRef]
- Ruiz-Rodriguez, F.J.; Hernández, J.C.; Jurado, F. Probabilistic load flow for photovoltaic distributed generation using the Cornish–Fisher expansion. Electr. Power Syst. Res. 2012, 89, 129–138. [Google Scholar] [CrossRef]
- Zangari, P. A VaR methodology for portfolios that include options. RiskMetrics Monit. 1996, 1, 4–12. [Google Scholar]
- Zhao, Y.-G.; Lu, Z.-H. Cubic normal distribution and its significance in structural reliability. Struct. Eng. Mech. 2008, 28, 263–280. [Google Scholar] [CrossRef]
- Amédée-Manesme, C.-O.; Barthélemy, F.; Maillard, D. Computation of the corrected Cornish–Fisher expansion using the response surface methodology: Application to VaR and CVaR. Ann. Oper. Res. 2019, 281, 423–453. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Kim, J.H.T. A new skewness adjustment for Solvency II SCR standard formula. Scand. Actuar. J. 2025, in press. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Vol. 38, Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Jondeau, E.; Poon, S.-H.; Rockinger, M. Financial Modeling Under Non-Gaussian Distributions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Hardy, M. Investment Guarantees; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Frühwirth-Schnatter, S. Finite Mixture and Markov Switching Models; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]

| Distribution | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|
| (scaled) | 9.556 | 127.86 | 0 | 9 |
| 1 | 1 | 2 | 9 | |
| 3.08 | 2.69 | 1.75 | 8.898 | |
| 2.22 | 6.17 | 2.811 | 17.829 |
| Sample Size (n) | Time (Seconds) |
|---|---|
| 50 | 1.86 |
| 100 | 2.43 |
| 200 | 3.67 |
| 500 | 6.79 |
| 1000 | 11.96 |
| 2000 | 23.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.H.T.; Kim, H. Estimating Skewness and Kurtosis for Asymmetric Heavy-Tailed Data: A Regression Approach. Mathematics 2025, 13, 2694. https://doi.org/10.3390/math13162694
Kim JHT, Kim H. Estimating Skewness and Kurtosis for Asymmetric Heavy-Tailed Data: A Regression Approach. Mathematics. 2025; 13(16):2694. https://doi.org/10.3390/math13162694
Chicago/Turabian StyleKim, Joseph H. T., and Heejin Kim. 2025. "Estimating Skewness and Kurtosis for Asymmetric Heavy-Tailed Data: A Regression Approach" Mathematics 13, no. 16: 2694. https://doi.org/10.3390/math13162694
APA StyleKim, J. H. T., & Kim, H. (2025). Estimating Skewness and Kurtosis for Asymmetric Heavy-Tailed Data: A Regression Approach. Mathematics, 13(16), 2694. https://doi.org/10.3390/math13162694





