Abstract
This study presents a novel analytical–numerical framework for investigating the torsional divergence of composite sandwich structures composed of carbon fiber-reinforced skins and an AIREX foam core. A divergence differential equation is derived and modified to accommodate the anisotropic behavior of composite materials through an equivalent shear modulus, extending classical formulations originally developed for isotropic structures. The resulting equation is solved using the Galerkin method, yielding structural section rotations as a continuous function along the wing span. These torsional modes are then applied as boundary inputs in a high-fidelity finite element model of the composite fin to determine stress distributions across the structure. The method enables evaluation of not only in-plane (membrane) stresses, but also out-of-plane responses such as interlaminar stresses and local core-skin interactions critical for assessing failure modes in sandwich composites. This integrated workflow links analytical aeroelastic modeling with detailed structural analysis, offering valuable insights into the interplay between global torsional stability and local stress behavior in laminated composite systems.
Keywords:
torsional divergence; composite sandwich structures; equivalent shear modulus; Galerkin method; aeroelastic stability MSC:
70-10
1. Introduction
Aeroelastic phenomena are inherently complex, arising from the dynamic interplay among aerodynamic loads, structural deformation, and inertial effects. When not properly accounted for during the design phase of aerospace structures, these interactions can lead to catastrophic outcomes, including uncontrolled oscillations, structural divergence, and ultimate failure. The consequences of aeroelastic instabilities are well-documented and have historically had serious implications in both experimental and operational flight scenarios []. Despite advances in testing methods, physical validation of such phenomena remains expensive, time-consuming, and potentially hazardous. This underscores the critical role of reliable and mathematically rigorous modeling frameworks in the early stages of structural design.
Among the most critical aeroelastic instabilities is torsional divergence, a static instability driven by excessive aerodynamic moment relative to torsional stiffness. This phenomenon is especially significant in high aspect-ratio wings and lightweight configurations, where the torsional rigidity of structural members is inherently low. The increasing reliance on laminated composites and sandwich architectures particularly carbon fiber-reinforced laminates with polymeric foam cores such as AIREX has introduced additional layers of complexity due to anisotropic stiffness and interlaminar effects. AIREX® refers to a proprietary family of closed-cell polymeric foam cores developed by 3A Composites, widely used in aerospace sandwich structures. These materials offer an excellent balance of stiffness, low density, and thermal stability, making them particularly suitable for lightweight fin and panel applications under demanding mechanical and environmental conditions. In such systems, conventional divergence models derived under isotropic assumptions fail to capture the true mechanical response [].
To address this limitation, the present study introduces a generalized analytical–numerical framework capable of capturing torsional divergence behavior in composite sandwich structures. The analysis begins with a derivation of the divergence differential equation from torsional moment equilibrium in a simplified 3D wing configuration. To extend this classical formulation to orthotropic materials, an equivalent shear modulus is introduced, accommodating the direction-dependent stiffness of composite laminates. This technique aligns with ongoing efforts in the literature to adapt continuum theory to anisotropic structural elements [].
The resulting governing equation is solved using the Galerkin method, a weighted-residual approach known for its accuracy and adaptability in complex structural problems []. Galerkin-type formulations, including both continuous and discontinuous variants, have proven particularly effective when applied to composite structures [], and serve here to extract closed-form spanwise rotation functions that describe the structural twist under aerodynamic loading.
These analytical solutions are then transferred into a high-fidelity finite element model of a composite fin, where they are applied as boundary-driven inputs. This enables the detailed evaluation of both in-plane and interlaminar stress development across the laminate and core layers, bridging the gap between global aeroelastic instability prediction and local structural response [].
The remainder of the paper is organized as follows. A detailed derivation of the torsional divergence equation is presented, including the formulation of the equivalent shear modulus for orthotropic materials. This is followed by a description of the Galerkin-based solution technique and its implementation for the given wing geometry. A subsequent section introduces the finite element model, including material definitions, boundary conditions, and the integration of analytical torsional deformation. The paper concludes with a discussion of the resulting stress distributions and a reflection on the implications for the aeroelastic design of composite sandwich structures.
Recent studies have explored various hybrid modeling strategies to reconcile global aeroelastic predictions with localized stress phenomena, yet few have demonstrated a fully integrated workflow that preserves analytical tractability while enabling detailed numerical interrogation. The present framework distinguishes itself by maintaining closed-form control over torsional deformation inputs, thereby avoiding the need for iterative coupling between aerodynamic and structural solvers. This not only streamlines the analysis but also enhances reproducibility and interpretability key attributes for certification-oriented design environments. Furthermore, by embedding the analytical twist profile directly into the finite element boundary conditions, the method facilitates a direct mapping of aeroelastic instability onto stress-critical regions, offering a novel pathway for early-stage structural optimization in composite sandwich configurations [,,,].
2. Materials and Methods
In this section, we establish the mathematical foundation for analyzing torsional divergence in composite sandwich structures. The governing differential equation is derived by enforcing torsional moment equilibrium on a representative three-dimensional wing-like structure with spanwise-varying geometric and stiffness properties. The model explicitly captures variations in chord length and torsional rigidity along the wing span, consistent with real-world composite configurations. Material anisotropy is accounted for through the introduction of an equivalent shear modulus, enabling the orthotropic behavior of laminated skins to be expressed in a homogenized yet physically accurate form. The formulation assumes linear elastic behavior and employs a quasi-steady aerodynamic loading model suitable for subsonic flight conditions, in which the pitching moment is linearly dependent on local twist.
The resulting span-dependent torsional stiffness incorporates contributions from both the laminate skins and the compliant foam core using laminate theory and shear mechanics. This enhanced formulation yields a differential equation suitable for analytical and numerical treatment, enabling accurate prediction of the structural twist leading up to torsional divergence.
2.1. Development of the Aeroelastic Divergence Equation for Anisotropic Wings
Building on the foundational assumptions outlined above, the derivation begins by considering an idealized structural model, as illustrated schematically in Figure 1, that captures the torsional moments, aerodynamic forces, and geometric parameters acting on an infinitesimal wing element of length dy along the spanwise coordinate y. This differential element serves as the basis for formulating the torsional equilibrium equation that governs the onset of divergence in composite wing structures with spanwise-varying stiffness and geometry.
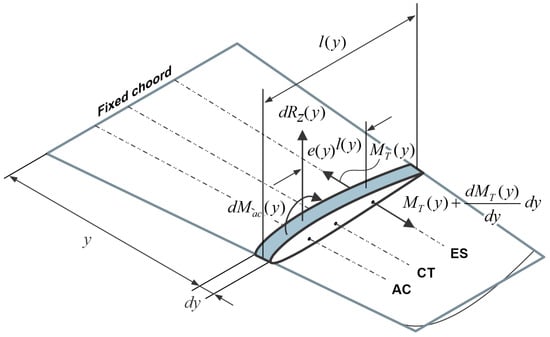
Figure 1.
Torsional Divergence model of the wing structure showing torsional moments MT(y), aerodynamic forces RZ(y), Aerodynamic moment Mac(y) and geometric parameters l(y) chord length, ES shear center location, AC aerodynamic center location, e(y) shear center to aerodynamic center relative distance acting on an infinitesimal spanwise element dy.
As shown schematically in Figure 1, consider an infinitesimal span element of the wing located at position y (measured from the fixed wing end), with local chord length l(y) and width dy. The aerodynamic lift that acts on this element can be represented as a force over the area l(y)dy and generates an aerodynamic pitching moment dMac(y) about the elastic axis (ES) due to the offset between the elastic and aerodynamic centers (AC).
In addition, the structural response includes internal torsional moments. On the inboard face of the element, the torsional moment is denoted by , and on the outboard face by which can be expanded by a Taylor series as:
The first-order expansion is typically sufficient in structural mechanics to analyze the equilibrium of a differential element under torsional loading, and Equation (1) can be written as:
By writing the moment equilibrium equation about the elastic axis and accounting for all forces and moments acting on the infinitesimal wing element, the following relationship can be established:
At this point, it is important to emphasize that the choice of aerodynamic theory significantly influences the form and validity of the resulting divergence equation. Depending on the flight regime and structural response timescales, one may adopt subsonic, transonic, supersonic, or even unsteady aerodynamic models. In this work, a linear subsonic aerodynamic theory is employed, which assumes inviscid, incompressible, and quasi-steady flow conditions. This approach is widely accepted for slender wings operating at low angles of attack and Mach numbers typically below 0.7–0.8, where compressibility effects remain modest and linearization remains valid []. The aerodynamic force and moment expressions derived under this assumption will be substituted into the moment equilibrium equation to obtain the governing differential equation for torsional divergence.
For a differential element at position y, under quasi-steady subsonic flow, the aerodynamic lift force per unit span can be expressed as:
The aerodynamic pitching moment about the elastic axis with assumed offset from the aerodynamic center by a distance is then:
In previous equations (Equations (4) and (5)), V is the linear flight speed, ρ is the air density at the flight altitude, Cz(y) is the local lift coefficient, Cmac is the constant aerodynamic moment coefficient about the aerodynamic center, αa is the angle of attack and θ(y) is the local twist angle.
To complete the formulation, the structural torsional moment must now be expressed in terms of the local twist angle []. Under linear elastic behavior and assuming Saint-Venant torsion, the relationship between torsional moment MT(y), torsional stiffness GeqJ(y), and the rate of twist is given by:
In this formulation, the shear modulus G is denoted as Geq to emphasize that an equivalent shear modulus is used, capturing the homogenized behavior of the orthotropic composite laminate and core combination. The method for determining Geq will be presented in a subsequent section. The term J(y) represents the torsional constant, which depends on the local cross-sectional geometry of the wing and accounts for the distribution of shear stresses under Saint-Venant torsion [,].
By substituting the expressions for the aerodynamic force and pitching moment (Equations (4) and (5)), along with the torsional moment–twist rate relation (Equation (6)), into the moment equilibrium equation (Equation (3)), one obtains the following second-order differential equation governing the torsional behavior of the wing (Appendix A.1):
This torsional divergence equation (Equation (7)) represents the equilibrium of moments acting about the elastic axis on a differential spanwise segment of the three-dimensional wing. Mathematically, it takes the form of a nonhomogeneous second-order differential equation with variable coefficients, reflecting the coupled aero-structural behavior across the span.
The governing differential equation for torsional divergence, expressed in terms of grouped spanwise-varying coefficients, takes the form:
In the previous equation (Equation (8)), A(y) is the torsional stiffness coefficient, B(y) represents the spatial gradient of torsional stiffness, C(y) is the aerodynamic coupling coefficient and D(y) is a forcing term due to external aerodynamic loading.
To explicitly incorporate anisotropic composite behavior into this framework, the Classical Laminate Theory (CLT) is employed. Unlike traditional aeroelastic analyses which typically assume isotropic or simplified stiffness representations, this new formulation directly integrates the laminated face sheets and foam core response via the laminate compliance matrix This allows the structural stiffness contributions from the laminated face and the core to be reflected through the compliance matrix (ABD) []. The general relation between force-moment (N, M) resultants and mid-plane strains/curvatures (ε, ϰ) is the following:
In the previous equation (Equation (9)), A is the extensional stiffness matrix, B is the bending-extension matrix, and D is the bending stiffness matrix that includes torsional resistance required by the divergence equation.
It is worth noting that the stiffness components within the ABD matrix, along with their inverse counterparts used in compliance-based formulations, are not arbitrary values but are derived systematically from the underlying laminate architecture. Their magnitudes depend on the mechanical properties of the fiber and matrix phases, the relative volume fractions, and the orientation of fibers within each ply. These effective properties can be rigorously evaluated using well-established micromechanics theories, which provide the necessary link between the material’s microstructure and the macroscopic response incorporated into the aeroelastic model.
Based on this multiscale formulation, the equivalent shear modulus that governs torsional response is defined by the following expression (Appendix A.2):
Here, d66(y) is the bending compliance component associated with twist curvature. It corresponds to the sixth diagonal element of the inverse of the D matrix. This value describes the amount of twist per unit applied moment and captures the directional stiffness behavior of the laminate in a simplified, homogenized form. Since the full laminate stiffness depends on constituent materials, fiber angles, and stacking, the compliance term d66 naturally reflects all those properties through Classical Laminate Theory. This definition allows us to express the coefficients of the governing torsional divergence equation directly in terms of Geq (y).
The explicit formulas for all these coefficients are given as:
This reformulation yields a second-order, nonhomogeneous differential equation with variable coefficients, which generally does not admit a closed-form analytical solution. In the remainder of this work, a methodology will be presented to calculate the equivalent shear modulus Geq for composite sandwich sections, followed by application of the Galerkin method to obtain the approximate distribution of the twist angle θ as a function of the span coordinate. This paves the way toward finite element implementation and detailed structural response analysis.
2.2. Galerkin-Based Approximate Solution to the Divergence Equation
As established in the previous section, the governing divergence equation for the composite fin structure, including its span-varying stiffness and aerodynamic coupling, takes the form summarized in Equations (7)–(11). These expressions incorporate an equivalent shear modulus Geq derived from the laminate compliance term d66, in turn linking micromechanical anisotropy with global torsional stiffness.
To obtain an approximate solution for the twist distribution θ(y) along the fin span, we now introduce a Galerkin-based approach. This method is particularly suited to problems involving spatially variable coefficients and structural constraints, such as those present in the clamped carbon-Airex fin configuration addressed here.
As with any second-order differential equation, a complete solution to the divergence model requires the specification of appropriate boundary conditions. These reflect the physical constraints of the system and are essential to ensure the uniqueness and consistency of the solution.
The corresponding boundary conditions for the fin configuration analyzed in this study are illustrated schematically in Figure 2.
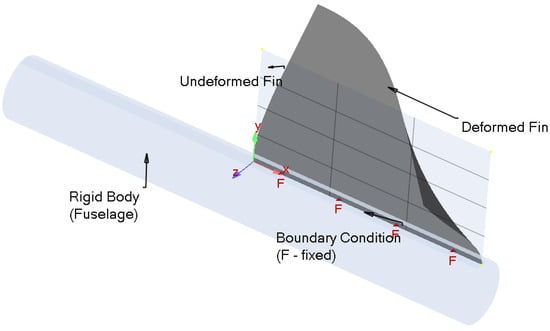
Figure 2.
Boundary condition setup for the torsional divergence problem.
Hence, the mathematical formulation of the boundary conditions corresponding to this structural configuration is presented in Equation (12):
Depicted in Figure 2 is a fin that is rigidly clamped at its root to the missile fuselage and free at the tip. This physical arrangement imposes two boundary conditions: one essential and one natural. The enforced fixed constraint at the clamped root represents an essential (Dirichlet-type) condition that must be built directly into the trial space. In contrast, the zero-torque condition at the free tip corresponds to a natural (Neumann-type) condition. Within the weak (variational) form adopted by the Galerkin method, this natural boundary condition emerges automatically through integration by parts and therefore does not require explicit imposition.
To proceed with the Galerkin formulation for the composite missile fin, we approximate the twist distribution θ(y) using a finite series expansion. This representation ensures that the solution space adheres to the essential boundary constraint at the clamped root while allowing flexibility to capture the twist behavior along the span. Accordingly, the twist field is expressed as:
where Ai are the unknown modal coefficients, and ϕi(y) are the admissible basis (trial) functions. For this problem, we select functions that satisfy the essential boundary condition (Equation (12)). In order to construct a Galerkin approximation that respects the physical and mathematical requirements of the torsional divergence problem, we define a finite set of smooth, linearly independent basis functions as:
The parameter ymax denotes the spanwise length of the lifting surface and thus coincides with the upper bound of the computational domain y ∈ [0, ymax]. The introduction of ymax serves several critical purposes:
- By normalizing the coordinate through the dimensionless ratio y/ymax, the basis functions remain scale-free; consequently, the same analytical expression is applicable to any wingspan by simply substituting the appropriate value of ymax.
- At the root, each ϕi satisfies the essential (geometric) boundary condition because ϕi(0) = 0 for all i, thus guaranteeing zero twist at the clamped root without any additional constraints.
- As y → ymax, the term (1 − y/ymax) tends to zero and the expression in parentheses approaches unity, ensuring ϕi(y) → 1. This end behavior provides the flexibility required to represent the twist distribution near the free tip while still allowing the natural boundary condition θ′(ymax) = 0 to be weakly enforced through the weighted residual statement.
- The exponent (i + 1) introduces progressively higher-order shape features with increasing i, enabling systematic enrichment of the approximation by simply adding basis functions.
- Finally, the closed algebraic form of ϕi(y) produces analytic first and second derivatives that are straightforward to differentiate and integrate, facilitating both the assembly of the Galerkin stiffness matrix
Collectively, these properties make the set {ϕi(y)} an efficient and physically consistent trial space: the essential boundary condition is embedded by construction, the basis spans the entire physical domain, and the resulting integrals are amenable to high-accuracy numerical quadrature. Substituting the approximate form of θ(y) into the governing divergence equation yields a nonzero residual:
The Galerkin method enforces that this residual be orthogonal to every basis function in the trial space, leading to the weighted integral condition.
This variational statement ensures that the governing equation is satisfied in a global, averaged sense across the domain. Applying this condition to the residual expression leads to a linear system of the form:
where K and f denote the stiffness matrix and load vector, respectively, as defined previously. Solving this system provides the modal amplitudes ai, which in turn define the approximate twist distribution θ(y) across the span of the fin. This solution characterizes the aeroelastic response in terms of divergence onset and spatial twist behavior. In the subsequent chapters, this spanwise twist profile will be applied as a sectional boundary condition in a finite element stress model, enabling detailed investigation of internal forces and local material responses within the composite sandwich architecture.
In the Galerkin-based formulation, the essential boundary condition at the clamped root is directly imposed through the construction of trial functions that satisfy zero twist and slope. At the free tip, however, the Neumann boundary condition representing the absence of applied moment and shear force is not explicitly enforced. Instead, it emerges naturally from the variational structure of the weak form. This behavior aligns with the physical intuition of the problem: the missile fin, modeled as a cantilevered sandwich structure subjected to aerodynamic loading, twists most significantly near the unconstrained tip. The lack of external torques and the form of the weighting functions result in vanishing boundary contributions at the free end, effectively capturing its unrestrained motion. This natural enforcement was confirmed via both analytical reasoning and numerical observation of shear and moment distributions near the tip.
The Galerkin approach provides an approximate yet efficient means of computing the twist field under prescribed aerodynamic loading. As the freestream velocity increases, the aerodynamic moments captured by the coefficient functions may lead to a progressive reduction in the effective torsional stiffness of the fin. Divergence occurs when the structure becomes statically unstable specifically, when the torsional restoring forces are no longer sufficient to counteract the aerodynamic moment. Physically, this corresponds to a scenario in which the twist angle grows without bound:
In the Galerkin approximation, this unbounded behavior arises when the stiffness matrix K becomes singular, and the governing system admits a nontrivial solution even in the absence of forcing:
This condition defines the divergence speed as the lowest freestream velocity at which the system loses uniqueness and torsional instability ensues. The corresponding mode shape, while unbounded in amplitude, reveals the characteristic distribution of twist at the onset of instability. This shape will serve as an input in the following chapter, where sectional twist fields are used as boundary conditions in a finite element stress analysis to assess the resulting material and structural responses.
3. Results and Analysis
To validate the methodology developed in this paper, we used a real composite structure of a missile fin as an example case study (Figure 3). The fin consists of carbon fiber face sheets bonded to an Airex foam core, forming a lightweight yet structurally efficient sandwich construction. Although this study focuses on a missile fin configuration, the same analysis flow is applicable to wings, control surfaces, and other composite aerodynamic structures subjected to high loads and torsional effects.

Figure 3.
Photograph of the analyzed composite missile fin, featuring carbon fiber face sheets and an Airex foam core.
The analytical approach to composite structures provides valuable fundamental insights into stress distribution and deformation behavior. However, for complex geometries such as a trapezoidal, non-symmetric fin with enforced rotation, analytical solutions alone may have limitations in capturing shear coupling effects, localized stress peaks, and interface interactions. The methodology developed here overcomes these constraints by combining analytical models with finite element analysis (FEA), allowing for a more complete evaluation of stress distributions, interfacial traction behavior, and failure mechanisms.
By integrating FEA with first-principles analytical calculations, stress components can be extracted with high fidelity across all structural regions, including face sheets, core, and interface layers. Based on these results, a deeper and more precise insight into structural integrity, load transfer efficiency, and failure initiation can be sought, ensuring that localized effects are properly accounted for.
The structural configuration analyzed in this study is presented in the following figure, showing an actual composite missile fin, which consists of carbon fiber face sheets bonded to an Airex foam core. This image provides direct visual confirmation of the geometry and material composition used in the finite element simulations.
The geometrical characteristics of the analyzed structure are presented in the following table (Table 1):

Table 1.
Geometric and material structural characteristics.
3.1. FEA Model Configuration
The top and bottom carbon fiber face sheets are modeled using laminate plate elements, following NASTRAN’s composite element formulation, which is based on the Mindlin–Reissner plate theory. This theory accounts for transverse shear deformation, allowing for more accurate modeling of bending, membrane, and shear behavior in fiber-reinforced composites especially in moderately thick laminates. These elements accurately represent multi-layered orthotropic laminates, with each ply defined by its specific orientation, material properties, and thickness. Each node includes six degrees of freedom three translational and three rotational allowing precise modeling of membrane, bending, and shear behavior typical of fiber-reinforced composites.
The internal Airex foam core is modeled using solid brick (continuum) elements, characterized by three translational degrees of freedom per node. These elements are well-suited for capturing through-thickness deformation and stress distribution across the foam volume, ensuring proper simulation of its shear transfer and out-of-plane response.
Since solid elements lack rotational degrees of freedom, a direct nodal connection between the core and laminate plate elements is not kinematically compatible. To ensure structural continuity, a glued (tie) connection is implemented at the bonded interface. This constraint enforces displacement compatibility by mapping translational degrees of freedom across the contact region. While rotational DOFs are not directly connected, their influence is inherently captured through laminate bending stiffness and shear deformation, enabling efficient load transfer and a cohesive structural response.
To apply the enforced rotation loads derived from analytical solutions, RBE2 elements are used to connect sectional nodes, ensuring smooth load transmission without inducing localized stress concentrations at the loading points.
RBE2 elements are rigid body constraints that enforce kinematic coupling by linking dependent nodes to a single master node, effectively distributing the applied rotation across a section rather than at a single point. This strategy prevents artificial stiffness variation and avoids high-stress gradients that could otherwise occur at direct force application sites.
By utilizing RBE2 elements, rotational loading is applied in a uniform manner, preserving the overall stiffness characteristics of the structure while ensuring that load transfer remains consistent across the laminate face sheets and core interface. This approach maintains structural fidelity in the finite element model, allowing realistic evaluation of composite behavior under torsional conditions.
An overview of the finite element model, including mesh transitions, element assignments, and interface constraints, is presented in Figure 4.
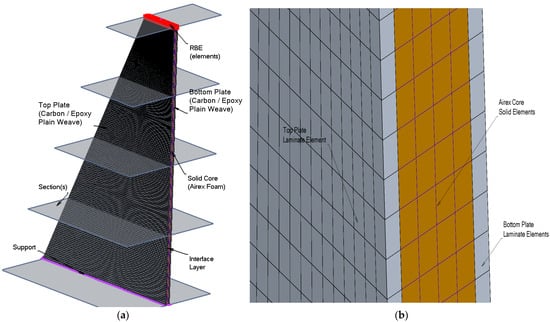
Figure 4.
(a) Computational model of the missile fin, with laminated plate elements for the carbon face sheets and solid elements for the Airex foam core. (b) Analyzed fin, finite element model, enlarged cross section (Carbon/Epoxy face sheets and Airex core).
3.2. Material Properties
To ensure accurate finite element analysis, the mechanical properties of the materials used in the composite missile fin are defined precisely (Table 2 and Table 3). The carbon fiber face sheets and Airex foam core are modeled with their respective elastic constants, strength parameters, and density, which directly influence stress distribution, failure behavior, and load transfer. These material properties govern the structural integrity of the laminated composite and its bonded interface, providing a basis for stress and deformation predictions in the FEA model.

Table 2.
Face sheets material structural characteristics (AGP3705H/3501-6).

Table 3.
Foam core material structural characteristics. (Airex C70.55).
3.3. Loading and Boundary Conditions
To simulate aeroelastic divergence-induced deformation, the root of the fin is modeled as a rigid connection, all translational and rotational degrees of freedom are fixed. Loading is introduced as prescribed torsional displacements (sectional twist) about the elastic axis at five discrete spanwise locations, derived from the analytical divergence solution (Figure 5). These kinematic inputs emulate the aerodynamic-induced twist experienced in subsonic flight and serve as boundary conditions to drive the internal deformation and stress field.
Figure 5.
(a) Spanwise twist distribution θ(y) obtained from the analytic solution corresponding to the analyzed carbon/Airex composite fin configuration. The solution corresponds to the estimated subsonic divergence speed, beyond which θ(y) → ∞; (b) geometry of the trapezoidal composite fin used in the finite element model. Sectional twist values extracted from the analytic solution are imposed at five discrete spanwise locations as rotational boundary conditions. (Finite elements not shown for clarity, and are presented in Figure 4).
This strategy ensures that the FEA model reflects the structural response under realistic flight-induced aeroelastic loading, directly linking the previously derived analytical formulation to a detailed numerical stress prediction.
3.4. Post-Processing and Results Interpretation
Following simulation, post-processing is conducted to extract key mechanical responses that reveal the aeroelastic behavior and structural integrity of the analyzed carbon/Airex sandwich fin. The imposed rotational boundary conditions, derived from the Galerkin solution, serve as the primary input driving internal stress development and deformation patterns. The results focus on critical load-bearing components of the sandwich architecture, offering insight into stiffness, failure margins, and load transfer mechanisms under divergence-induced torsional loading.
3.4.1. Shear Stress Evaluation in Foam Core
One of the primary concerns in sandwich composite structures subjected to torsional loading is the development of interlaminar shear stress within the lightweight foam core. Due to its relatively low shear modulus, the core such as Airex C70.55 is particularly susceptible to excessive shear deformation, which may lead to core crushing, local instability, or delamination at the face/core interface.
This shear stress component becomes especially critical under divergence-like conditions, where twist-induced loads are transferred from the stiff carbon/epoxy face sheets into the core. The spatial distribution of this stress provides insight into both the efficacy of load transfer and the core’s ability to constrain torsional warping of the structure.
In this paper, the notation used for principal stresses extracted from solid elements (e.g., in the foam core) uses the superscript “(p)” which denotes principal values. This distinction is necessary because conventional symbols σ1, σ2, and τ12 are reserved for composite stress components of the lamina aligned with the local material coordinate system (fiber, transverse and in-plane shear, respectively). Without this clarification, overlapping symbols for laminate and solid mechanics stress components may lead to confusion when interpreting stress states and failure indices across different parts of the fin.
In the present study, shear stresses in the core were evaluated using the SOLID MAX SHEAR STRESS of the NASTRAN solver. This value is derived from the principal stress state and represents the highest magnitude of shear stress at a given point in the core. Principal stresses are obtained by solving the eigenvalue problem of the full 3D stress tensor:
The maximum shear stress is then computed as
To evaluate structural integrity, the following shear failure index is computed:
Here, τallow is the shear strength of the Airex foam core, and SFI is the Shear failure index. A SFI value that exceeds unity indicates critical conditions such as the initiation of core crushing or delamination. In contrast to the Von Mises criterion which combines all stress components into an equivalent scalar measure and is best suited for isotropic ductile materials the maximum shear stress criterion directly targets the governing failure mechanism in foam cores. Provides a more conservative and physically appropriate estimate of core integrity.
Figure 6 presents a cross-sectional view of the fin highlighting the distribution of the core shear stress in five span sections. The results demonstrate the shear transfer behavior and help identify potential failure-prone regions under torsional loading.
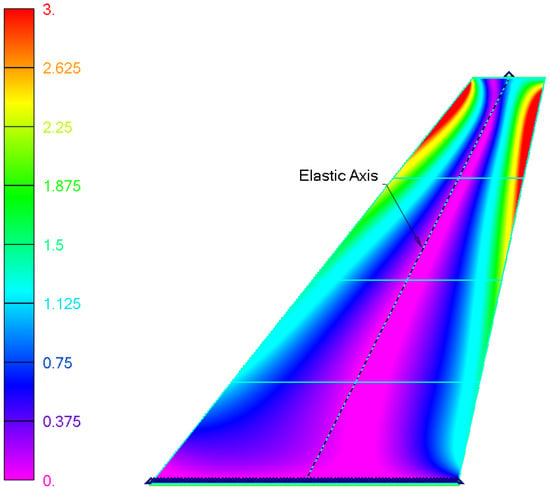
Figure 6.
Distribution of solid shear stress [GPa] within the core of the composite fin, extracted from the finite element model under divergence-induced torsional loading.
3.4.2. Interface Bond Analysis Using Total Glue Traction
The durability of a sandwich composite under torsional loading depends heavily on the bond quality between face sheets and core. In the present model, this interface is represented using cohesive constraints, and the integrity of the bond is evaluated using Total Glue Traction a scalar field derived from normal and shear tractions acting across the adhesive layer.
Post-processing of the simulation reveals the traction distribution along the face/core interface at one of the five spanwise twist sections. Regions of elevated total traction indicate high energy transfer zones and potential sites of adhesive degradation or delamination onset. The traction magnitude reflects localized force transmission across the adhesive plane and is particularly sensitive to twist gradient, geometry, and restraint conditions and is defined as:
where Tn is the traction normal to the bonding interface, and TS, Tt are the two orthogonal shear tractions in the tangential plane.
The following figure (Figure 7) illustrates this behavior through a color-mapped representation of Total Glue Traction at the selected interface section, highlighting stress localization patterns under divergence-induced torsional loading.
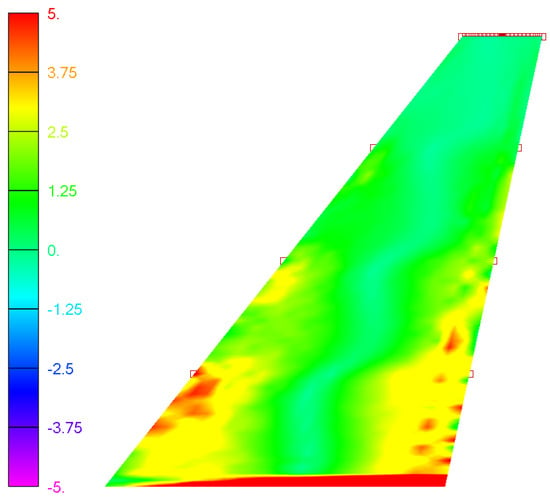
Figure 7.
Total Glue Traction distribution (units [MPa]) at face/core interface section, obtained from the finite element simulation under imposed torsional loading. The plot reveals localized traction concentrations near the spanwise extremities, indicating potential initiation zones for adhesive degradation due to high interfacial stress transfer.
3.4.3. Face Sheet Stress Evaluation
In the composite sandwich fin structure (Figure 3), the face sheets act as the primary load-bearing elements, responsible for carrying the in-plane stresses resulting from applied load. Hence, evaluating their behavior at the ply level is essential for understanding material performance and identifying potential failure modes under divergence-like conditions. This level of analysis enables detection of localized stress concentrations, ply–matrix interactions, and interlaminar shear effects, which are critical for predicting fiber rupture, matrix cracking, or delamination especially in sandwich structures subjected to complex loading such as aerodynamic divergence analyzed in this paper.
The analysis begins with a detailed assessment of in-plane stress components in the most critically loaded ply of the laminate. Specifically, the fiber-direction stress σ1 indicates axial tension or compression along the primary reinforcement path, while the transverse stress σ2 captures matrix-dominated behavior perpendicular to the fibers. In addition, the in-plane shear stress τ12 is evaluated to characterize the torsion-driven shear transfer within the ply, which plays a key role in fiber–matrix interaction and potential delamination. These stress components are sensitive to fiber orientation, boundary conditions, and the imposed twist profile. Figure 8 presents the spatial distribution of all three in-plane stress fields for the face sheet lamina which sustains the highest load.
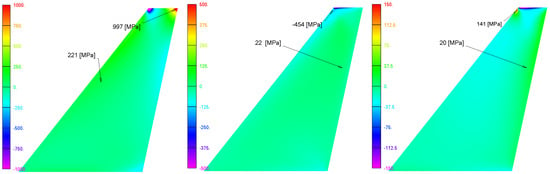
Figure 8.
(left) Fiber-direction normal stress σ1 (middle) transverse normal stress σ2, (right) in plane shear stress τ12 plotted across the most highly loaded face sheet ply.
To support the failure analysis, the finite element–extracted stress values for the most critically loaded lamina are summarized in Table 4. The table presents the in-plane normal stresses in the fiber direction σ1 transverse direction σ2, and the in-plane shear stress τ12 for two distinct regions of the composite face sheet: (i) the majority of the fin surface (approximately 95% of the area), where stress levels remain within typical operational bounds, and (ii) a localized high-stress zone near the fin tip, where elevated values are observed due to geometric tapering and stress concentration effects. These representative stress components are used in subsequent sections to calculate various ply-level failure indices.

Table 4.
Finite element-derived in-plane stress components in the most critically loaded ply of the face sheet for two distinct regions: the global 95% fin area and a localized high-stress zone near the tip.
Based on the computed in-plane stress fields presented in Figure 8 the structural integrity of the carbon fiber face sheets is evaluated using four established failure criteria: Tsai–Wu, Hashin, and Maximum Strain. Each criterion captures different aspects of composite failure behavior, ranging from interactive multiaxial stress effects to mode-specific damage mechanisms such as fiber rupture, matrix cracking, or shear-driven delamination. The application of multiple criteria enables a more robust and comparative assessment of ply-level performance under torsional loading [].
The Tsai-Wu failure criterion is a widely used interactive quadratic theory for predicting failure in anisotropic composite materials. It accounts for the combined effects of normal and shear stresses and is particularly suited for laminates subjected to multiaxial loading. Unlike maximum stress or strain criteria, Tsai–Wu incorporates interaction terms between stress components, allowing it to capture more complex failure behavior.
The general form of the Tsai–Wu criterion is expressed as:
where Fi and Fij are the material strength coefficients generally determined by means of experimentation or derived analytically from the ply’s unidirectional strength properties using the following expressions:
For the composite system analyzed in this study (AGP3705H/3501-6), the relevant strength values used in the Tsai–Wu formulation are listed in Table 2. Beyond computing a single scalar failure index, the Tsai–Wu criterion also permits decomposition into individual component-based contributions, allowing identification of which stress modes most significantly influence the failure potential. These decomposed failure indices are defined in Equation (27).
This decomposition is particularly valuable, as it highlights the relative influence of fiber-dominated stresses (tension or compression), matrix-driven transverse stresses, and in-plane shear on the overall failure risk. Such insight enables more targeted design optimization and ply tailoring by focusing on the most critical stress components affecting laminate integrity.
The Hashin failure criterion is a physically based failure model for fiber-reinforced composite materials that distinguishes between different failure modes: fiber tension, fiber compression, matrix tension, and matrix compression. This makes it particularly useful for predicting the initiation of damage in unidirectional composite laminae [,].
The Maximum Strain Criterion is a simple and intuitive failure theory for composite laminae that assumes failure occurs when any of the principal strain components exceeds its corresponding allowable limit. Specifically, failure is predicted when the longitudinal strain (ε1), transverse strain (ε2), or in-plane shear strain (γ12) exceeds the ultimate strain values in tension or compression. This criterion does not account for interactions between stress components and is therefore conservative [,,].
The computed failure indices for the most critically loaded ply, based on the Tsai–Wu, Maximum Strain, and Hashin criteria, are summarized in Table 5. This table presents the individual component-based indices such as fiber failure, matrix failure, and shear failure alongside the combined failure measures for two representative load cases. The comparison facilitates a comprehensive understanding of the different failure modes and their relative severity under the applied stress states []. These numerical results form the basis for subsequent discussion and visualization through the failure envelopes.

Table 5.
Summary of calculated failure indices for the critical ply under two load cases, using Tsai–Wu, Maximum Strain, and Hashin criteria.
Following the numerical assessment of all failure indices, it is valuable to visualize the interaction between in-plane stress components using a failure envelope representation. In this work, failure envelopes are constructed for the Tsai–Wu, Maximum Strain, and Hashin criteria to provide a comparative graphical overview of the allowable stress domain for the most critically loaded lamina.
To enable clear visualization in the (σ1, σ2) plane, the in-plane shear stress τ12 is set to zero. This assumption allows the construction of a two-dimensional cross-section through the full three-dimensional failure surface defined by each criterion. While all three failure theories inherently depend on the combined effects of σ1, σ2, and τ12, fixing τ12 = 0 isolates the influence of axial and transverse normal stresses, resulting in a meaningful and interpretable envelope [].
The resulting failure envelopes for all three criteria are shown in Figure 9 where both investigated cases are overlaid for reference.
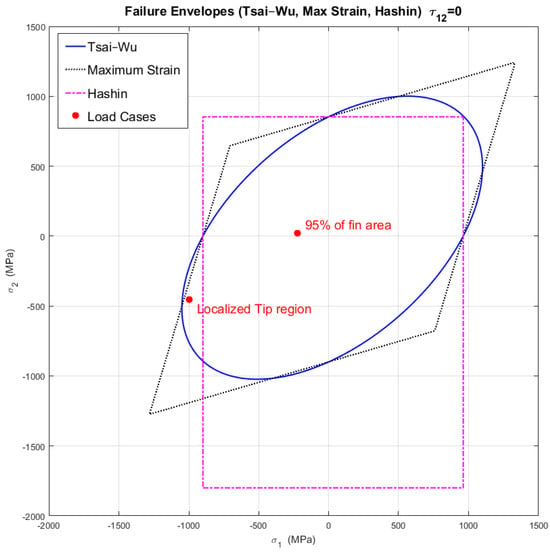
Figure 9.
Failure envelope.
3.4.4. Compressive Instability of Face Sheets in Foam-Core Sandwich Fins
To evaluate the risk of local instability in composite sandwich structures, it is essential to compare the in-plane compressive stress in the face sheets against the critical wrinkling stress predicted by analytical models, such as those of Hoff and Allen [,]. In this context, finite element analysis (FEA) serves as the primary tool for extracting localized stress data within the structure. This section outlines how stress data from FEA are interpreted and used in conjunction with wrinkling models to assess the integrity of the face sheets.
Wrinkling refers to the local buckling of a compressed face sheet supported by a soft core. The most relevant stress is the in-plane compressive stress in the fiber direction, typically denoted σ1. This stress represents the axial load carried by the face sheet along the primary reinforcement direction.
Hoff’s model is based on the analogy of a thin plate (the face sheet) resting on a continuous elastic foundation (the core). The critical wrinkling stress is given by
where σcr is critical wrinkling stress in the face sheet, Df is flexural rigidity of the face sheet, k is Winkler modulus of the core, Gc is the shear modulus of the core and tc is the core thickness.
Allen’s model simplifies the wrinkling analysis by treating the face sheet as a membrane rather than a bending plate. The critical wrinkling stress according to this model is given in the following form:
Plantema proposed a more conservative and realistic estimate by including both the shear and compressive moduli of the core, along with a correction for Poisson effects []:
All the classical wrinkling criteria Hoff’s, Allen’s, and Plantema’s have been incorporated into a single composite expression for the minimum critical wrinkling stress, σcrmin. This value is defined as the lowest predicted wrinkling stress among the three analytical models, ensuring a conservative estimate of face sheet instability (Table 6). The design requirement then enforces that σcrmin does not exceed the maximum allowable wrinkling stress, σ1 max, obtained from detailed finite element analysis (FEA). This unified approach facilitates robust and reliable sandwich panel design by combining theoretical and numerical assessments in one governing inequality:

Table 6.
Estimated critical wrinkling stresses in the face sheet of the sandwich fin using Hoff and Allen models based on analytical expressions and representative material properties.
3.4.5. Global Deformation Field and Displacement Patterns
Although the primary focus of this study is the internal stress distribution and failure potential of the composite structure under torsional loading, it is equally important to examine the resulting global deformation field particularly in the context of aeroelastic performance and aerodynamic interaction.
The figure below (Figure 10) illustrates the deformed shape of the composite fin under the imposed twist load, with color contours representing the magnitude of total displacement. The displacement values include contributions from both in-plane distortion and out-of-plane warping, captured from the post-processing of the finite element solution.
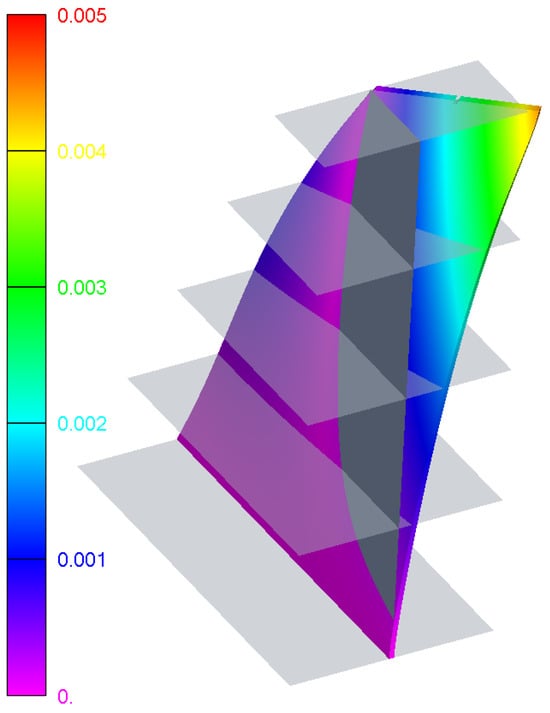
Figure 10.
Deformed shape of the composite fin under torsional loading, with color contours indicating total displacement magnitude. The visualization confirms expected twist behavior and highlights the spatial variation of deformation relevant to aerodynamic surface shaping.
While displacement results remain secondary in the context of stress and failure assessment, they provide critical insight into how the structure may interact with surrounding flow, especially near divergence onset. Excessive deflection could trigger nonlinear aeroelastic effects or compromise structural/aerodynamic coupling, which will be explored further in the Discussion.
4. Discussion
The cornerstone of this investigation is the analytical torsional-divergence equation, which we have rigorously extended to accommodate the orthotropic stiffness of composite laminates. By embedding the direction-dependent elastic moduli of the AGP3705H/3501-6 system into the classical divergence formulation, we derive a modified boundary-value problem whose eigenvalues predict the onset of divergence under torsional loading. This problem is solved via a Galerkin’s approach: for our trapezoidal fin geometry we introduce a bespoke basis function that captures the spanwise variation in cross-section and fiber orientation. Thanks to this tailored trial function, convergence is attained with very few terms and hence minimal computational effort yet yields accurate critical-load estimates.
Moreover, the Galerkin’s solution directly provides the sectional rotation profile along the span, which we then impose as boundary conditions in the subsequent FEA model. These rotation fields govern the finite-element stress distributions, so their fidelity is crucial to accurate stress-field results. The analyst can choose the number of spanwise sections at which to extract these rotations: increasing the section count refines the boundary condition interpolation and improves stress accuracy up to a clear convergence point, beyond which further subdivision yields negligible change. It is important to emphasize, however, that when applying this methodology to different fin planforms or composite layouts, the choice of Galerkin’s basis and the discretization into sections must be re-examined to ensure both convergence and solution fidelity.
With the divergence-driven sectional rotations now embedded as boundary conditions in the FEA model, the finite-element solution yields the in-plane stress distributions across the face-sheet plies. Simultaneously, the solid stress state within the foam core and the interfacial stresses in the bonding layer reflecting its stiffness and thickness characteristics are captured to evaluate core integrity and bond performance. In the sections that follow, we will dissect each stress field individually: face-sheet normal and shear stresses, core compressive and shear stresses, and bond-layer peel and shear. For each field, critical regions will be identified, underlying causes of stress concentrations examined, and potential mitigation strategies outlined to enhance overall laminate robustness.
4.1. Analysis of Shear Stresses in the Core
Analysis of the Airex 70.55 core shear stresses (Figure 8) reveals a complex distribution ranging from 0.1 MPa in low-load regions to peaks of 3.4 MPa near the leading edge, trailing edge, and fin tip. Given the core’s nominal shear yield strength of 0.85 MPa (Table 3), the Maximum Shear failure index reaches approximately 4.0 in those high-stress zones well above the failure threshold and indicative of core yielding under extreme torsional-divergence loading (θ → ∞, corresponding to 134.85 m/s). Without design adjustments, the foam core would undergo shear failure at the fin extremities under limit-load conditions. Potential mitigation strategies include local core reinforcement, selection of a higher-grade foam with increased shear strength, or tuning face-sheet stiffness through fiber-orientation adjustments. If face-sheet tuning is selected, appropriate optimization techniques such as genetic algorithms, gradient-based layup optimization, or surrogate modeling should be employed. In this study, we use a recommended layup drawn from similar sandwich-structure designs as a first approximation in the preliminary design stage [].
However, substituting a higher-grade Airex core inevitably increases the local density, altering the fin’s mass distribution and inertial properties. Such a shift can move the aircraft’s center of gravity and modify dynamic stability characteristics, potentially affecting flutter margins and control responses. Therefore, if a denser foam is chosen to improve shear capacity, a comprehensive stability and aeroelastic reassessment must be performed recomputing mass properties, inertia tensors, and flight-worthiness criteria to ensure that structural gains do not inadvertently compromise overall performance.
Analysis of the Airex 70.55 core shear stresses (Figure 8) reveals a complex distribution ranging from 0.1 MPa in low-load regions to peaks of 3.4 MPa near the leading edge, trailing edge, and fin tip. Given the core’s nominal shear yield strength of 0.85 MPa (Table 3), the Maximum Shear failure index reaches approximately 4.0 in those high-stress zones well above the failure threshold and indicative of core yielding under extreme torsional-divergence loading (θ → ∞, corresponding to 134.85 m/s). Without design adjustments, the foam core would undergo shear failure at the fin extremities under limit-load conditions.
Potential mitigation strategies include local core reinforcement, selection of a higher-grade foam with increased shear strength, or tuning face-sheet stiffness through fiber-orientation adjustments. If face-sheet tuning is selected, appropriate optimization techniques such as genetic algorithms, gradient-based layup optimization, or surrogate modeling should be employed. In this study, we use a recommended layup drawn from similar sandwich-structure designs as a first approximation in the preliminary design stage.
However, if no upgrades to the core or face sheets are implemented, the only remaining option is to prescribe a lower maximum flight speed to satisfy the torsional-divergence limit. The analytical–numerical methodology developed in this paper can then be deployed to recompute the critical divergence speed for the complete fin assembly, ensuring the operational envelope remains within safe structural margins.
4.2. Analysis of the Adhesive Interface
The adhesive interface is evaluated using the total glue traction output from cohesive-zone elements, defined as the combined magnitude of local peel (normal) and shear tractions at the bond line. This single scalar measure identifies where the adhesive experiences the highest demands under torsional-divergence loading.
In our trapezoidal fin configuration, no regions exceed the allowable limit, as shown in Figure 7. Computed total glue traction values range from 1.22 MPa to 4.49 MPa, which lies well below the epoxy adhesives reported in literature the in-plane shear strength of approximately 12 MPa for Airex-to-carbon bonding (manufacturer’s datasheet). This nearly 3:1 safety margin confirms that the bond line maintains integrity under limit-load torsional stresses.
It is important to recognize that directly comparing the total traction magnitude to a single shear-strength value is an approximation. Total glue traction combines peel and shear components into one metric; when peel tractions are negligible, the total value effectively equals the shear component and the shear-strength comparison is valid. In cases where both peel and shear are significant, a combined-mode failure criterion should be applied, in which each traction component is normalized by its respective allowable strength (peel or shear) and their contributions summed to assess debonding risk. Given the relatively high safety margin (approximately 3:1) in this study, validating bond integrity through comparison of total traction to the shear-strength remains justified.
In this study, cohesive-element results indicate minimal peel loading, so benchmarking total traction against the 12 MPa shear limit is justified. The highest demands occur near the fin root and the edges areas that could benefit from targeted enhancements such as local adhesive thickening, use of tougher adhesive formulations, or incorporation of mechanical fasteners.
Overall, the current bond design exhibits a comfortable margin against debonding under torsional-divergence conditions. For a more rigorous mixed-mode assessment in future work, we recommend extracting peel and shear tractions separately and applying a combined-mode evaluation to ensure both failure modes are accurately captured.
4.3. Analysis of the Stresses in Face Sheet(s)
The face sheet stress calculations presented in this study are representative of approximately 95% of the composite fin’s surface, where the in-plane stresses remain well within the allowable limits. However, a distinct localized region near the tip of the fin exhibits a sudden and disproportionate increase in stress, with computed values reaching up to 2000 MPa, far exceeding the tensile strength of the face sheet material. This abrupt stress amplification near the tip is a common and well-documented phenomenon in swept and tapered lifting surfaces and may be attributed to several factors, as discussed below.
The fin geometry is trapezoidal with a high sweep angle and taper ratio. As the chord length narrows towards the tip, the effective cross-sectional area decreases, leading to elevated stress under constant or smoothly varying loading. This geometric constraint inherently causes an increase in local stress intensity.
Near the tip, structural continuity is lost, and the available path for load transmission becomes restricted. This can lead to edge effects and shear-lag phenomena, particularly under torsional or bending loads, resulting in non-uniform stress distributions and local amplifications [].
Finite element models can exhibit artificially high stress gradients near sharp geometric transitions if the mesh is not sufficiently refined. Without local mesh convergence verification, the high stresses may partly reflect discretization effects rather than actual physical behavior.
4.4. Analysis of the Imposed Constraints
Artificial constraints or local interactions with adjacent structural features at the tip (such as bonded interfaces, rigid elements, or mass attachments) may introduce non-physical stress concentrations. These effects should be carefully evaluated and validated to determine if they contribute significantly to the stress amplification.
From an engineering perspective, the elevated stresses near the fin tip may not indicate immediate material failure, but they should not be dismissed without further assessment. While such regions may be structurally less critical or non-load-bearing, they often require specific design attention, such as:
- Local reinforcement: Adding extra plies, tapered laminates, or tip caps to reduce stress.
- Mesh refinement: Performing a local mesh convergence study to ensure numerical accuracy.
- Experimental validation: Applying strain gauges or full-field techniques such as Digital Image Correlation (DIC) in the tip region.
- Load redistribution: Reassessing boundary conditions or local constraint definitions that may artificially concentrate load.
- Substructuring (submodeling): isolate the high-stress tip region into a detailed submodel, apply the global FEA’s sectional-rotation boundary conditions, refine the mesh and represent each ply explicitly, then re-evaluate stresses to distinguish true hot-spots from numerical artifacts and guide precise local reinforcement.
Compressive instability or wrinkling of the carbon/epoxy face sheets was assessed by comparing the peak compressive fiber-direction stress (σ1) from the FEA with critical buckling stresses predicted by Hoff, Allen, and Plantema models. Both Hoff’s wrinkling formula and Allen’s shear-supported buckling criterion yield critical stresses well above the observed σ1, indicating a comfortable safety margin under torsional-divergence loading. In contrast, Plantema’s approach predicts a critical stress that lies at or below the laminate’s actual compressive demand, classifying the design as unstable and demonstrating its reputation for being overly conservative.
To guard against face-sheet wrinkling in service, we recommend:
- Increasing the core’s shear modulus (e.g., selecting a higher-stiffness foam) to better support the face sheets in compression.
- Adjusting face-sheet ply architecture thicker plies, higher-modulus fibers, or optimized fiber angles to boost local compressive stiffness.
- Ensuring flawless adhesive bonding and smooth ply terminations to eliminate delamination or free-edge effects that exacerbate wrinkling.
- Introducing targeted stiffeners or inserts at the high-stress tip region, possibly evaluated through submodeling, to suppress local buckle formation.
Implementing these measures and validating them with refined substructuring analyses or small-scale wrinkling tests will help ensure the face sheets remain stable throughout the revised operational envelope.
4.5. Discussion Summary
In closing, this discussion has demonstrated how extending the classical torsional-divergence formulation to orthotropic laminates and solving it efficiently via a tailored Galerkin approach yields accurate sectional-rotation boundary conditions that directly inform FEA stress analyses. Core shear evaluation revealed critical yielding near the fin extremities, driving either material upgrades or a reduction in allowable flight speed; interface bond checks confirmed a healthy safety margin under predominantly shear loading; and face-sheet assessments, including wrinkling predictions, isolated a small high-stress tip zone warranting substructuring, ply-tuning, or local reinforcements. Taken together, these insights form a coherent, multi-scale verification strategy for foam-core sandwich fins under torsional-divergence loads. Future work should validate these findings through targeted experiments, refine mixed-mode bond-line criteria, and integrate aeroelastic stability analyses to ensure the design meets both structural and flight-worthiness requirements.
5. Conclusions
The classical torsional-divergence formulation has been extended to include orthotropic composite stiffness directly in the eigenvalue problem, and a tailored Galerkin method achieves rapid convergence. Sectional-rotation boundary conditions derived from this analytical model are applied seamlessly in the FEA environment, resolving the full stress–strain field across the foam-core sandwich fin. Embedding anisotropy and coupling those rotations with actual stress outputs bridges the gap between theory and simulation, providing deeper insight into structural behavior under torsional loads.
Although the analytical equation despite its rigorous theoretical underpinnings tends to overestimate divergence speed, embedding anisotropy in the eigenvalue problem corrects this bias. The integrated workflow yields accurate divergence estimates without resorting to specialized aeroelastic fluid–structure interaction modules, which are optional, resource-intensive, and costly.
This methodology supports a multi-scale verification strategy: core shear-yielding zones are identified; mixed-mode bond-line integrity is confirmed via total-traction checks; face-sheet hot spots are isolated and examined through substructuring; and laminate compressive instability is assessed against established wrinkling criteria. Collectively, these elements form a coherent framework for preliminary design and validation of composite sandwich fins.
Future work will focus on extending the core torsional divergence framework to encompass supersonic and hypersonic aerodynamic regimes, where classical subsonic assumptions no longer apply. This transition will necessitate the incorporation of high-speed flow theories including piston theory, shock-expansion models, or nonlinear compressible formulations to account for the increased sensitivity of aeroelastic behavior at high Mach numbers.
Additionally, broadening the applicability of the Galerkin method to non-trapezoidal fin geometries, such as swept, tapered, or curved planforms, presents both mathematical and computational challenges. Developing custom trial functions tailored to irregular boundaries and geometric asymmetries will be essential for preserving solution accuracy and maintaining boundary compatibility.
By uniting theoretical rigor, numerical precision, and experimental validation, this research lays the groundwork for safer, lighter, and more efficient aerospace structures.
Author Contributions
Conceptualization, M.D.; methodology, M.D., M.P. and D.S.; validation, M.D., M.P. and D.S.; formal analysis, M.D.; investigation, M.D.; resources, M.T. and J.B.; data curation, M.T. and J.B.; writing—original draft preparation, M.D., writing—review and editing, M.D.; visualization, M.T. and J.B.; supervision, M.D., M.P. and D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interests.
Appendix A
Appendix A.1
The starting point in the mathematical formulation of the divergence problem is to express the torsional moment equilibrium condition around the elastic axis of the considered structure element. This moment equilibrium equation is expressed as follows:
In the previous moment equilibrium equation is the torsion moment at span location y, whereas the term is the torsion moment gradient. Terms, are differential aerodynamic force and moment about aerodynamic center (ac) acting on a structural differential element analyzed. Terms e(y) and l(y) are structure geometric characteristics, where e(y) is the relative distance between shear and aerodynamic centers, and l(y) is the chord length.
In this analysis, subsonic axial flow is assumed, according to known subsonic aerodynamic theories, are given in the following form:
In the previous equations for subsonic aerodynamic force and a moment, ρ is the fluid (air) density at the analyzed flight altitude, V is the flight speed, is the cross section (airfoil) lift gradient and the term is the sum of angle of attack (AOA) and the twist angle at the location y; is the moment coefficient.
It is worth noting that for other flow conditions appropriate aerodynamic theories should be used like hypersonic, supersonic and transonic.
For subsonic flow conditions, substituting the expressions for aerodynamic force and moment into the equilibrium equation directly leads to the following relation, capturing the torsional response under these flow conditions.
Continuing the formulation, the relationship between the torsional moment (MT), twist angle (θ), shear modulus (G) and torsional constant (J) is established in the following form:
Which by differentiation leads to the expression:
By incorporating all previous formulations, the moment equilibrium about the shear center accounting for all forces acting on the differential structural element is expressed in its final mathematical form:
By performing this analytical derivation, a second-order, linear, non-homogeneous ordinary differential equation with variable coefficients is obtained. This equation governs the twist angle as a function of aerodynamic loading, inertial effects, structural stiffness, and flight speed. The variable coefficients reflect the spatial dependence of geometric and material properties along the structure, ensuring an accurate representation of the aeroelastic response. This formulation serves as the foundation for determining the aeroelastic divergence speed of the orthotropic structure.
Appendix A.2
In CLPT (Classical Laminate Plate Theory), the relationship between the in-plane force resultants N, bending moment resultants M, mid-plane strains κ, and curvatures κ is given by:
where:
- N = [Nx, Ny, Nxy]T: in-plane force resultants;
- M = [Mx, My, Mxy]T: bending moment resultants;
- ε0= [ε0x, ε0y, γ0xy]T: mid-plane strains;
- κ = [κx, κy, κxy]T: mid-plane curvatures;
- A, B, D: extensional, coupling, and bending stiffness submatrices.
To extract curvatures and strains from the applied loads, we invert the stiffness relation:
Here, d = [D*ij] represents the bending compliance submatrix of the inverse ABD matrix. Of particular interest is the term D*66, which relates the twisting moment Mxy to the resulting curvature κxy:
From thin plate theory, the relation between the applied twisting moment Mxy and the curvature κxy is:
where D66 is the twisting stiffness coefficient from the bending stiffness matrix D. The classical relation between D66 and the shear modulus Gxy for a homogeneous plate is:
Considering the inverse relation from the inverse matrix:
Comparing both expressions for Mxy, we obtain:
References
- Abdalsalam, A.A.H.A. Aeroelastic Structural Analysis to Calculate Symmetrical Divergence Modes of an Aircraft Wing Using Aerodynamic Lifting Line Theory. Eng. Technol. J. 2024, 9, 5313–5320. [Google Scholar] [CrossRef]
- Rajasekaran, S. Torsion Analysis of Functionally Graded Iso/Orthotropic Sections Using Differential Quadrature and pb2-Rayleigh Ritz Methods. J. Inst. Eng. India Ser. A 2024, 105, 875–912. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and Transversal Stiffness of Orthotropic Sandwich Panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef] [PubMed]
- Wieners, C. Galerkin Methods. In Encyclopedia of Applied and Computational Mathematics; Engquist, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Ismail, S.O.; Eyvazinejad Firouzsalari, S.; Naseem, S.; Oladapo, B.I. Investigation into high-speed impact response of composite sandwich structures. J. Compos. Mater. 2025, 59, 1521–1531. [Google Scholar] [CrossRef]
- Cabral, P.H.; do Prado, A.P.; Carrera, E.; Pagani, A.; Sánchez-Majano, A.R.; Enea, M. Aeroelastic Tailoring Based on Virtually-Generated Allowable and High-Order Finite Elements for Improved Composite Wing Design. In Proceedings of the ICAS 2024 Proceedings, Florence, Italy, 9–13 September 2024; p. 0167. [Google Scholar]
- Drela, M.; Hall, D.; Selig, M. Hybrid Shell Model for Aeroelastic Modeling. In Proceedings of the AIAA SciTech 2019 AIAA 2019-2227, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Pan, Y.; Zhang, H.; Li, Q. Structural and Aeroelastic Optimization of a Large Aircraft Wing. In Proceedings of the 33rd International Council of the Aeronautical Sciences (ICAS), Florence, Italy, 9–13 September 2024. [Google Scholar]
- Sadiq, M.; Kovács, T. Optimization of Composite Sandwich Structures: A Review. Machines 2025, 13, 536. [Google Scholar] [CrossRef]
- Irisarri, F.X.; Renart, J.; Sarrado, C.; Costa, J.; Guillamet, G. A General Optimization Strategy for Composite Sandwich Structures. Struct. Multidiscip. Optim. 2021, 63, 1451–1467. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Rajagopalan, K. Torsion of Thin-Walled Structures. In St. Venant Torsion; Springer: Singapore, 2022; pp. 1–28. [Google Scholar]
- Gebre, T.H.; Galishnikova, V.V. The Impact of Section Properties on Thin-Walled Beam Sections with Restrained Torsion. J. Phys. Conf. Ser. 2020, 1687, 012020. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O. Engineering Mechanics of Composite Materials; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Wan, L.; Ullah, Z.; Yang, D.; Falzon, B.G. Comprehensive Inter-Fibre Failure Analysis and Failure Criteria Comparison for Composite Materials Using Micromechanical Modelling Under Biaxial Loading. J. Compos. Mater. 2023, 57, 2919–2932. [Google Scholar] [CrossRef]
- Hyer, M.W.; White, S.R. Stress Analysis of Fiber-Reinforced Composite Materials, Updated ed.; DEStech Publications: Lancaster, PA, USA, 2009. [Google Scholar]
- Osswald, T.A.; Hernández-Ortiz, J.P.; Gómez, C. A Strength Tensor Based Failure Criterion with Stress Interactions. Polym. Compos. 2020, 41, 2620–2631. [Google Scholar] [CrossRef]
- Wan, L.; Ullah, Z.; Yang, D.; Falzon, B.G. Progressive Failure Analysis of CFRP Composite Laminates Under Uniaxial Tension Using a Discrete Element Method. J. Compos. Mater. 2021, 55, 489–507. [Google Scholar] [CrossRef]
- De Baere, I.; Vanpaepeghem, C.; Van heeder, J.; Sundararaman, M.; Van Paepeghem, Y. An Enhanced Progressive Damage Model for Laminated Fiber-Reinforced Composites Using the 3D Hashin Failure Criterion: A Multi-Level Analysis and Validation. Materials 2024, 17, 5176. [Google Scholar]
- Hu, H.; Wei, Q.; Liu, B.; Liu, Y.; Hu, N.; Ma, Q.; Wang, C. Progressive Damage Behavior Analysis and Comparison with 2D/3D Hashin Failure Models on Carbon Fibre—Reinforced Aluminium Laminates. Polymers 2022, 14, 2946. [Google Scholar] [CrossRef] [PubMed]
- Elalfy, M.H.; Abdalla, M.M.; Abuelfoutouh, N. Numerical Generation of Omnistrain Failure Envelopes. J. Compos. Mater. 2023, 57, 4603–4614. [Google Scholar] [CrossRef]
- Pozorski, Z.; Pozorska, J. Influence of the Heterogeneity of the Core Material on the Local Instability of a Sandwich Panel. Materials 2022, 15, 6687. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Liu, S. New method for predicting the wrinkling stress in sandwich panels. Arch. Appl. Mech. 2025, 95, 4. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).