Abstract
Analytical solutions for the complex-valued nonlinear Gerdjikov–Ivanov (GI) equation have been studied extensively using integrability-based methods. In contrast, numerical and semi-analytical exploration remains relatively underdeveloped. Thus, the present study deploys both the traditional Adomian decomposition method (ADM) and its improved version (IADM) to explore the computational relevance of the GI equation to shock waves against a benchmark exact soliton solution. The findings indicate that both methods are effective in addressing the GI equation, with the improved method demonstrating an enhancement in the stability of the convergence under specific conditions. This work offers the first systematic semi-analytic and numerical evaluation of the GI equation, introducing practical implementation guidelines.
Keywords:
Gerdjikov–Ivanov equation; nonlinear Schrödinger’s equation; shock waves; decomposition methods; nonlinear optics; optical communications MSC:
35N05
1. Introduction
A substantial amount of research has been conducted over a considerable period of time on soliton molecules in optical fibers, metamaterials, and photonic crystal fibers (PCFs) [1]. Telecommunications advancements require a thorough understanding of soliton propagation in various waveguide structures and are governed by dissimilar nonlinear evolution equations [2,3,4,5]. Indeed, among the most outstanding models are two very important equations: the nonlinear Schrodinger equations (NLSEs) and the derivative NLSEs (DNLSEs) [6,7,8]. The DNLSEs can restore higher-order nonlinear effects in optical systems [9,10]. In addition, when accounting for higher-order nonlinear effects, the DNLSEs are regarded as a long-wave, small-amplitude model applicable in a wide array of disciplines, including quantum field theory and short light pulses [11,12]. Moreover, the categories of DNLSEs are referred to as DNLSE I, DNLSE II, and DNLSE III, respectively [13]. Moreover, the immense practical application of these systems has led to their massive development of analytical methods and a limited number of numerical methods in recent decades. Notably, DNLSE III corresponds to the Gerdjikov–Ivanov (GI) equation, which serves as the core focus of this study due to its rich structure and relevance in nonlinear wave analysis. GI equation has widespread applications in integrable systems, nonlinear optics, fluid dynamics, and quantum field theory [14,15].
In recent years, significant attention has been directed toward semi-analytic methods for solving nonlinear Schrödinger-type equations, particularly using the Adomian decomposition method (ADM) and its variants. Kapoor et al. (2022) [16] introduced the Shehu transform-based ADM (STADM) to derive analytical series solutions for multiple forms of the time fractional Schrödinger equation, demonstrating convergence without requiring discretization.
Similarly, El-Ajou et al. (2024) [17] applied an enhanced residual power series method, comparing it to the ADM, homotopy perturbation, homotopy analysis, and variational iteration techniques to solve time fractional Schrödinger equations. They showed that series-based approaches—including the ADM—remain competitive in terms of the simplicity and accuracy when benchmarked against multiple semi-analytic methods.
Although most recent ADM-based work focuses on fractional or generalized NLSEs, very few studies have extended these methods to DNLSEs such as the Gerdjikov–Ivanov equation.
In addition, the recent literature confirms that while the Gerdjikov–Ivanov (GI) equation has been thoroughly examined using integrability-based methods [18,19,20]—such as Darboux transformations, Riemann–Hilbert frameworks, and extended algebraic techniques—there is a notable absence of studies applying the Adomian decomposition method (ADM) or its improved variant (IADM) directly to GI equation or benchmarked against analytic soliton structures.
The present study is motivated precisely by this observation, which presents a numerical perspective for solving the GI equation, benchmarked against an exact one-soliton solution via Kudryshov’s method. The intended method is based upon the application of the classical Adomian decomposition method (ADM) [21,22], together with its enhanced version, the improved Adomian decomposition method (IADM) [23,24]. Certainly, the choice of ADM-based schemes for tackling the GI equation is associated with their high efficacy in effectively handling functional and integral problems.
In the same vein, the arrangement of the present study is as follows. Section 2 provides some preambles on the governing equation, Section 3 presents the outlines of the adopted decomposition methods, Section 4 supplies the numerical results and graphical representations, while Section 5 presents some concluding notes.
2. Governing Equation
The Gerdjikov–Ivanov equation arises naturally within the framework of derivative NLSE hierarchies, and its similarity reductions using Wronskian or affine Lie methods have been studied [25,26].
The dimensionless form of the governing GI equation reads as follows [27,28]:
where is the one-dimensional complex wave profile, together with its conjugate. To break down the equation, the second-order dispersion term has the coefficient , while and are non-zero constants for the quintic nonlinearity term and for the self-phase modulation and the derivative nonlinearity term, respectively; in addition, is the known imaginary number.
3. Methodology
This section provides the outlines of the steps of the deployed ADM and IADM for solving the leading GI equation. Certainly, these methods possess various recompenses, including high-precision approximations to the exact analytical solution—when it exists—without resorting to perturbation, discretization, or linearization.
3.1. Adomian Decomposition Method
The present subsection provides a complete description of the ADM for the GI equation. This method was discovered by George Adomian [21,22,29] while tackling some functional equations. Remarkably, the purported Adomian polynomials are used to approximate the involved nonlinear terms arising from the equations, in the case of differential and integral equations. In addition, this method has undergone several improvements, including the IADM [23,24,30], among others.
Begin by re-expressing the partial differential equation in Equation (1) as follows:
where is a differential operator, which includes both nonlinear and linear terms. Hence, representing Equation (1) through operator form as
where is a higher-order linear differential operator defined as is a linear operator in , which is the variable of the coefficient in Equation (1)—namely, , and is a nonlinear operator, and is a nonhomogeneous term; in this particular case, based on the GI equation in Equation (1), is equal to zero. Thus, rewrite Equation (3) with respect to the linear operator to get
Accordingly, application of the inversion operator to Equation (4) gives the following:
Note that only the first term is computed to get the solution term on the left-hand side and moving the other terms to the right-hand side. Simplify Equation (5) as follows:
with as the initial condition as a result of applying the inversion operator. Recall, the solution function is decomposed through the ADM procedure as a series in the following form:
Moreover, the nonlinear term is broken down using an infinite series of polynomials, referred as Adomian polynomials, as follows [21,22,29]:
Accordingly, the explicit expression for the nonlinear term in the latter formula is plainly obtained from Equation (6) as follows:
Next, utilize Equations (7) and (8) in Equation (6) to get
Further rewrite to form the recurrence relation. Thus, the resulting ADM scheme for the governing GI equation is obtained from the latter equation as follows:
Finally, upon using Equations (11) and (12), obtain the resultant approximate ADM solution for Equation (6) as follows:
With
In this regard, we have established a systematic approach for applying the ADM to the GI equation, demonstrating how the decomposition leads to manageable terms for computation with efficiency in generating a series solution.
3.2. Improved Adomian Decomposition Method
The method of the IADM [23,24,30] is introduced as an enhancement, designed to address some of the limitations associated with its forerunner. Thus, the present subsection provides an outline of the IADM when used on the leading GI equation.
To start, transform the complex-valued function in Equation (1) into the sum of real-valued functions and as follows:
Thus, upon substituting Equation (15) into Equation (1), obtain the following system of equations:
where
are the related initial conditions that arise from the real and imaginary parts of the imposed initial condition in Equation (40). Moreover, based on the traditional ADM process [21,22,29], the solution for the system in Equations (16) and (17) is decomposed into an infinite summation as follows:
with to be obtained recursively. Thus, perform one further re-write Equations (16) and (17) using the operator as follows:
Accordingly, carrying out the inversion process using the operator on Equations (22) and (23), obtain
Simplify them as follows:
Further, when indicating the nonlinear terms in Equations (26) and (27) as
they tend to serve as the related Adomian polynomials in two-system equations. Thus, substituting Equations (20), (21), (28) and (29) into Equations (26) and (27) gives
where and are Adomian polynomials computed accordingly from Equation (8). Furthermore, with the help of the ADM procedure, the improved recurrent scheme for the GI equation is thus acquired through Equations (30) and (31) as follows:
In the same manner as in the previous subsection, obtain the resultant approximate IADM solution from Equations (16), (17) and Equations from (32)–(35), as
with
4. Results and Graphical Illustrations
This section presents the graphical and numerical validation of the proposed ADM and IADM schemes using relevant initial conditions and exact analytical solutions for the GI equation, as outlined in [31]. Numerical simulations and visualizations are conducted using Maple 2024, which facilitates symbolic computation and high-precision plotting.
To validate the efficiency of the ADM and IADM, the following exact solution for the GI equation is adopted as a benchmark in the analysis:
where and are non-zero constant parameters. Note that the initial condition is
Take into consideration the set of the solution
Table 1 presents the parameter values used in the numerical simulations. These values are determined through multiple preliminary iterations and subsequently held fixed to ensure consistent and valid comparisons for the ADM and IADM through the benchmarked exact solution.

Table 1.
Reveals the parameter values used in the resulting simulations via the Adomian decomposition method (ADM) and the iterative Adomian decomposition method (IADM), benchmarked against the exact solution via Kudryashov’s method for the Gerdjikov–Ivanov (GI) equation.
Table 2 reports the resulting absolute errors from the numerical simulations, for the temporal variable at with the spatial variable at and . The corresponding numerical values are provided in Appendix A. These variations are indicative of similar behavior throughout the whole domains and thus suffice to validate the proposed methods. Utilize the absolute error, defined as , where and denote the approximate and exact solutions, respectively. This pointwise absolute error is commonly employed in numerical analysis for assessing the local accuracy [32].

Table 2.
Presents the absolute errors at specific temporal and spatial values the Adomian decomposition method (ADM) and the iterative Adomian decomposition method (IADM), benchmarked against the exact solution via Kudryashov’s method for the Gerdjikov–Ivanov (GI) equation.
Figure 1 and Figure 2 present graphical illustrations of the ADM and IADM solutions against the exact solution across time variations. In each figure,
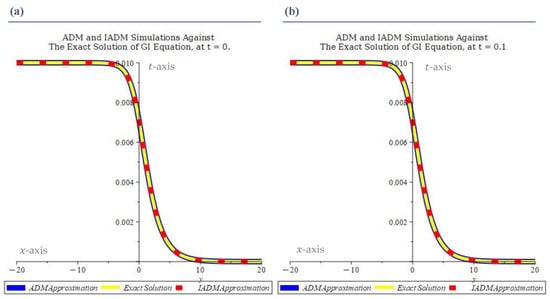
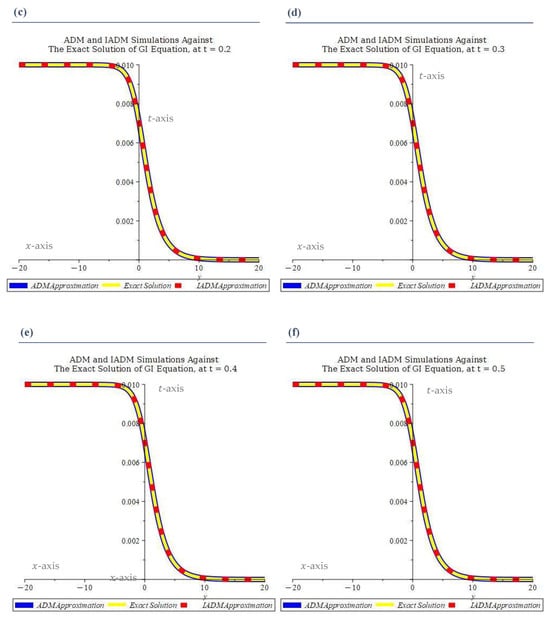
Figure 1.
(a–f) reveal the comparisons of the exact solution, via Kudryashov’s method, and the numerical solutions obtained via the Adomian decomposition method (ADM) and the iterative Adomian decomposition method (IADM) for the Gerdjikov–Ivanov (GI) equation. At
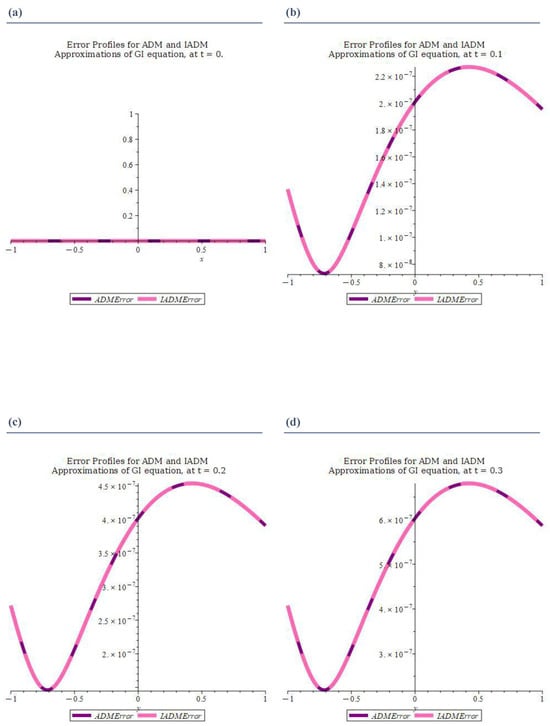
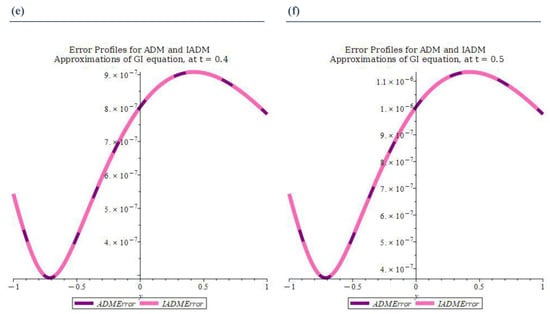
Figure 2.
(a–f) present the error profiles of the Adomian decomposition method (ADM) and the iterative Adomian decomposition method (IADM) for the Gerdjikov–Ivanov (GI) equation. At , over the spatial domain .
- the exact solution is plotted as a solid yellow line,
- the ADM approximations are shown with a blue line,
- the IADM approximations are denoted by a red dotted curve.
This color-coded distinction allows the clearest visual differentiation of each method’s performance relative to the exact solution.
The ADM and the IADM are applied to the GI equation and compared with Kudryashov’s exact solution for . The numerical results show excellent agreement between the numerical and exact profiles, with the curves being visually indistinguishable at all the tested times.
As demonstrated in Table 2, the improved ADM (IADM) consistently delivers significantly lower pointwise absolute errors compared to the classical ADM—particularly evident at (), where the ADM’s error spikes, while the IADM maintains accuracy. This supports prior theoretical expectations that a convergence control parameter accelerates series decay and extends convergence regions, enhancing the numerical stability in challenging regimes [33].
The graphical comparisons confirm that both the ADM and IADM preserve similar behavior of maintaining tight alignment with the exact solution profile. Moreover, the error profiles indicate that both methods achieve high accuracy, with maximum absolute errors typically in the order of or smaller.
For , the errors vanish as expected due to the exact initial condition matching. The peak errors occur at intermediate times () and align with regions of steep gradients in the exact solution, reflecting local truncation effects. Across all the cases, the IADM yields slightly smaller errors than the ADM, particularly for mid-range , while requiring comparable computational effort. The error distributions remain smooth and symmetric, with no evidence of spurious oscillations or boundary-related growth.
These results confirm that the ADM and IADM are both robust and accurate for solving higher-order nonlinear dispersive equations, with the IADM offering a marginal accuracy improvement. Both methods preserve the stability over the spatial and temporal ranges considered, supporting their suitability for long-time wave propagation simulations. The demonstrated agreement with the exact solution validates these approaches as reliable semi-analytical tools for the GI equation and related nonlinear systems.
5. Conclusions
The Gerdjikov–Ivanov (GI) equation is a prominent derivative nonlinear Schrödinger model exhibiting strong nonlinearity and rich wave dynamics, such as shock and soliton structures. Its nonlinear nature poses significant analytical and computational challenges. The Adomian decomposition method (ADM) addresses this by decomposing the solution into an infinite series and handling nonlinear terms via Adomian polynomials. This technique avoids linearization and often yields rapidly converging semi-analytic solutions under appropriate initial and boundary conditions, with minimal computational cost. In contrast, its improved version (IADM) enhances the numerical stability, especially in problems with strong nonlinearity or complex boundary conditions.
In this study, both the ADM and IADM are applied to the GI equation. While the ADM provides a straightforward, efficient approximation framework, the IADM refines it to achieve faster convergence and higher accuracy. Importantly, both methods retain the equation’s inherent nonlinear structure without recourse to perturbation or discretization. Combined, the ADM and IADM form a versatile and robust toolkit for semi-analytical resolution of nonlinear PDEs—including the GI equation. As a future direction, we intend to implement a finite difference scheme to provide a comparative numerical study that further validates and benchmarks the performance of the proposed ADM and IADM approaches. Moreover, the extension to the 2D Gerdjikov–Ivanov equation represents an important direction that we aim to pursue in upcoming work.
Author Contributions
F.A., A.S.H.F., A.A.A. (A. A. AlQarni), A.A.A. (A. A. Alshaery) and H.O.B.: conceptualization, methodology, writing—original draft preparation, data curation, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Numerical results for specific values of the exact solution and the ADM and IADM numerical approximations.
Table A1.
Numerical results for specific values of the exact solution and the ADM and IADM numerical approximations.
| Exact Value | ADM Approximation | IADM Approximation | ||
|---|---|---|---|---|
Note: Values are shown to 12 significant digits for clarity; original data contained greater precision.
References
- Singh, P.; Senthilnathan, K. Evolution of a solitary wave: Optical soliton, soliton molecule and soliton crystal. Discov. Appl. Sci. 2024, 6, 464. [Google Scholar] [CrossRef]
- Samina, S.; Munawar, M.; Ansari, A.R.; Jhangeer, A.; Wali, S. Nonlinear optical dynamics and complex wave structures in nonlinear dispersive media. Sci. Rep. 2025, 15, 15562. [Google Scholar] [CrossRef] [PubMed]
- Jandieri, V.; Khomeriki, R.; Berakdar, J.; Erni, D. Theory of soliton propagation in nonlinear photonic crystal waveguides. Opt. Express 2019, 27, 29558–29566. [Google Scholar] [CrossRef] [PubMed]
- Ostrovskaya, E.A.; Kivshar, Y.S. Nonlinear theory of soliton-induced waveguides. Opt. Lett. 1998, 23, 1268–1270. [Google Scholar] [CrossRef] [PubMed]
- Zayed, E.M.E.; Alurrfi, K.A.E. Solitons and other solutions for two nonlinear Schrödinger equations using the new mapping method. Optik 2017, 144, 132–148. [Google Scholar] [CrossRef]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann. Phys. 2015, 361, 490–500. [Google Scholar] [CrossRef]
- Wang, M.M.; Chen, Y. Dynamic behaviors of general n-solitons for the nonlocal generalized nonlinear Schrödinger equation. Nonlinear Dyn. 2021, 104, 2621–2638. [Google Scholar] [CrossRef]
- Younis, M.; Rehman, H.U.; Tahir, F. Optical Gaussons and dark solitons in directional couplers with spatiotemporal dispersion. Opt. Quantum Electron. 2018, 50, 422. [Google Scholar]
- Al-Shareef, A.; Al Qarni, A.A.; Al-Mohalbadi, S.; Bakodah, H.O. Soliton solutions and numerical treatment of the nonlinear Schrodinger’s equation using modified Adomian decomposition method. J. Appl. Math. Phys. 2016, 4, 2215–2232. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Xu, S.; Wu, Z.; He, J. The hierarchy of higher order solutions of the derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1706–1722. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Tuszynski, J.A. Exact solutions of the multidimensional derivative nonlinear Schrodinger equation for many-body systems of criticality. J. Phys. A 1990, 23, 1171–1196. [Google Scholar] [CrossRef]
- Zhou, H.J.; Chen, Y. Breathers and rogue waves on the double-periodic background for the reverse-space-time derivative nonlinear Schrödinger equation. Nonlinear Dyn. 2021, 6, 3437–3451. [Google Scholar] [CrossRef]
- Yıldırım, Y.; Biswas, A.; Asma, M.; Ekici, M.; Ntsime, B.P.; Zayed, E.M.E.; Moshokoa, S.P.; Alzahrani, A.K.; Belic, M.R. Optical soliton perturbation with Chen–Lee–Liu equation. Optik 2020, 220, 165177. [Google Scholar] [CrossRef]
- Kadkhoda, N.; Jafari, H. Analytical solutions of the Gerdjikov–Ivanov equation by using exp(−φ(ξ))-expansion method. Optik 2017, 139, 72–76. [Google Scholar] [CrossRef]
- Yang, J.; Jin, M.; Xin, X. Nonlocal symmetry and exact solutions of the (2+1)-dimensional Gerdjikov–Ivanov equation. Opt. Quantum Electron. 2024, 56, 707. [Google Scholar] [CrossRef]
- Kapoor, M.; Shah, N.A.; Weera, W. Analytical solution of time-fractional Schrödinger equations via Shehu Adomian Decomposition Method. AIMS Math. 2022, 7, 19562–19596. [Google Scholar] [CrossRef]
- El-Ajou, A.; Saadeh, R.; Dunia, M.A.; Qazza, A.; Al-Zhour, Z. A new approach in handling one-dimensional time-fractional Schrödinger equations. AIMS Math. 2024, 9, 10536–10560. [Google Scholar] [CrossRef]
- Biswas, A.; Yildirim, Y.; Yasar, E.; Babatin, M.M. Conservation laws for Gerdjikov–Ivanov equation in fiber optics and PCF. Optik 2017, 148, 209–214. Available online: http://refhub.elsevier.com/S0030-4026(17)31727-8/sbref0005 (accessed on 1 January 2025).
- Dai, H.H.; Fan, E.G. Variable separation and algebro-geometric solutions of the Gerdjikov–Ivanov equation. Chaos Solitons Fractals 2004, 22, 93–101. Available online: http://refhub.elsevier.com/S0030-4026(17)31727-8/sbref0015 (accessed on 20 July 2025). [CrossRef]
- Triki, H.; Alqahtani, R.T.; Zhou, Q.; Biswas, A. New envelope solitons for Gerdjikov-Ivanov model. Superlattices Microstruct. 2017, 111, 326–334. Available online: http://refhub.elsevier.com/S0030-4026(17)31727-8/sbref0055 (accessed on 20 July 2025). [CrossRef]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Okeke, A.A.; Tumba, P.; Gambo, J.J. The Use of Adomian Decomposition Method in Solving Second Order Autonomous and Non-autonomous Ordinary Differential Equations. Int. J. Math. Stat. Invent. 2019, 7, 2321–4759. [Google Scholar]
- Abassy, T.A. Improved Adomian decomposition method. Comput. Math. Appl. 2010, 59, 42–54. [Google Scholar] [CrossRef]
- Banaja, M.A.; Qarni, A.; Bakodah, H.; Zhou, Q.; Moshokoa, S.P.; Biswas, A. The investigate of optical solitons in cascaded system by improved Adomian decomposition scheme. Optik 2017, 130, 1107–1114. [Google Scholar] [CrossRef]
- Saburo, K.; Tetsuya, K. Solutions of a derivative nonlinear Schrödinger hierarchy and its similarity reduction. Glasgow Math. J. 2005, 47, 99–107. [Google Scholar]
- Guo, L.; Zhang, Y.; Xu, S. The higher order Rogu’e Wave solutions of the Gerdjikov–Ivanov equation. Phys. Scr. 2014, 89, 240. [Google Scholar] [CrossRef]
- Yilmaz, H. Exact solutions of the Gerdjikov-Ivanov equation using Darboux transformations. J. Nonlinear Math. Phys. 2015, 22, 32–46. Available online: https://link.springer.com/article/10.1080/14029251.2015.996438 (accessed on 1 January 2025). [CrossRef]
- Zheng, L.X.; Yong, L.X.; Ying, Z.L.; Liang, Z.J. Exact solutions of Gerdjikov-Ivanov equation. Acta Phys. Sin. 2008, 51, 2031–2034. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method, with a Preface by Yves Cherruault, Fundamental Theories of Physics; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1994; Volume 1. [Google Scholar]
- Bakodah, H.O.; Al Qarni, A.; Banaja, M.; Zhou, Q.; Moshokoa, S.P.; Biswas, A. Bright and dark thirring optical solitons with improved Adomian decomposition method. Optik 2017, 130, 1115–1123. [Google Scholar] [CrossRef]
- Althrwi, F.; A Alshaery, A.; O Bakodah, H.; Nuruddeen, R.I. Supplementary optical solitonic expressions for Gerdjikov-Ivanov equations with three Kudryashov-based methods. Commun. Theor. Phys. 2024, 76, 125001. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Parabolic and Hyperbolic Initial Boundary Value Problems. In Numerical Mathematics; Springer: New York, NY, USA, 2007; pp. 581–626. [Google Scholar]
- Abdelrazec, A.; Pelinovsky, D. Convergence of the Adomian decomposition method for initial-value problems. Numer. Methods Partial Differ. Equ. 2009, 27, 749–766. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).