Abstract
Dempster–Shafer theory (DST), a generalization of probability theory, is well suited for managing uncertainty and integrating information from diverse sources. In recent years, DST has gained attention in cybersecurity research. However, despite the growing interest, there is still a lack of systematic comparisons of DST implementation strategies for malware detection. In this paper, we present a comprehensive evaluation of DST-based ensemble mechanisms for malware detection, addressing critical methodological questions regarding optimal mass function construction and combination rules. Our systematic analysis was tested with 630,504 benign and malicious samples collected from four public datasets (BODMAS, DREBIN, AndroZoo, and BMPD) to train malware detection models. We explored three approaches for converting classifier outputs into probability mass functions: global confidence using fixed values derived from performance metrics, class-specific confidence with separate values for each class, and computationally optimized confidence values. The results establish that all approaches yield comparable performance, although fixed values offer significant computational and interpretability advantages. Additionally, we introduced a novel linear combination rule for evidence fusion, which delivers results on par with conventional DST rules while enhancing interpretability. Our experiments show consistently low false positive rates—ranging from 0.16% to 3.19%. This comprehensive study provides the first systematic methodology comparison for DST-based malware detection, establishing evidence-based guidelines for practitioners on optimal implementation strategies.
Keywords:
malware detection; Dempster–Shafer theory; ensemble learning; classifier fusion; machine learning; uncertainty quantification MSC:
68T05; 68T01; 68M25
1. Introduction
Malicious software poses a severe threat to the security of digital systems [1], with consequences that extend far beyond technical damages. These attacks can compromise sensitive data, disrupt critical operations, and result in substantial financial losses. For example, MKS Instruments reported losses exceeding USD 200 million in February 2023 following a ransomware attack [2]. Such incidents highlight the need for robust preventive measures, particularly in malware detection, which remains a significant challenge.
Traditional detection methods struggle to keep up with the sophistication of modern malware and the sheer volume of new threats [3]. Conventional approaches to malware detection are not well equipped to handle new or obfuscated threats [4], and signature-based systems are increasingly outpaced by zero-day and polymorphic threats [5]. Therefore, advanced machine learning methods have gained popularity among security experts [6]. Recently, researchers have explored adaptive methods using machine learning as a potential solution [7].
Among the vast number of machine learning tools and techniques, ensemble methods are particularly promising for malware detection because of their ability to combine multiple algorithms, often resulting in improved prediction performance [8]. Our empirical findings [9] corroborate these observations, demonstrating that ensemble techniques consistently outperform individual classifiers in malware detection, particularly when addressing novel and sophisticated threats.
The Dempster–Shafer theory (DST), also known as evidence theory or the theory of belief functions, is a framework for reasoning with uncertainty [10] that generalizes probability theory by allowing the allocation of probability mass to subsets of a domain rather than just individual elements. Unlike traditional probability theory, DST admits belief allocation over sets of hypotheses, making it particularly useful when dealing with conflicting or ambiguous evidence [11,12]. The ability of DST to handle uncertainty and incorporate classifier reliability is highly appealing for malware detection, where different classifiers may provide contradictory evidence based on various aspects of a file or its behavior [13]. In DST formalism, degrees of belief are represented as mass functions, with probability values assigned to sets of possibilities rather than single events, naturally encoding evidence in favor of propositions.
A critical challenge when applying DST to malware detection is transforming classifier outputs into mass functions that properly represent degrees of belief while avoiding computational issues, such as division by zero, in Dempster’s combination rule [14]. Generally, the implementation of combination rules requires careful adjustment of the classifier output using confidence values that reflect the reliability of each classifier. However, systematic studies comparing different mass function construction approaches and their impact on detection performance are lacking in the literature. To address these challenges, this study makes four key methodological contributions.
- Systematic DST methodology comparison: We provide the first comprehensive evaluation of three mass function construction approaches for malware detection, demonstrating that all three approaches achieve equivalent performance, with fixed methods offering significant computational advantages for operational deployment.
- Novel interpretable linear combination rule: We introduce a weighted linear combination approach for DST evidence fusion that assigns optimized coefficients to individual mass function components, achieving performance comparable to traditional DST combination rules while providing enhanced interpretability.
- Evidence-based implementation guidelines: We establish practical recommendations for DST deployment in malware detection, including the identification of Matthews Correlation Coefficient (MCC) as a sufficient primary performance metric and computational trade-off analysis between different combination strategies.
- Multi-dataset validation: We demonstrate the robustness and generalizability of DST-based approaches across four diverse public datasets (630,504 samples total), achieving consistent performance with MCC scores ranging from 0.78 to 0.99 and maintaining low false positive rates between 0.16% and 3.19%.
Our experimental validation encompassed 630,504 samples across four public datasets (BODMAS, DREBIN, AndroZoo, and BMPD), implementing DST fusion with the three best-performing base classifiers (Random Forest, Stacking, and Bagging) selected from seven candidates. We evaluated nine combination rules and three mass function construction methods, with our novel linear combination approach providing enhanced interpretability while maintaining performance parity with traditional DST rules.
The remainder of this paper is organized as follows: Section 2 reviews related studies on malware detection and DST applications. Section 3 describes the theoretical foundations of the proposed method. Section 4 details the experimental setup, including the datasets and their implementation. Section 5 presents our results and discusses their implications, including the limitations and practical considerations. Finally, Section 6 concludes the paper and suggests directions for future research.
2. Related Work
Malware analysis can be conducted in various ways [15], including static [16] and dynamic analyses [17,18]. Each of these methods employs different features to perform its tasks. The choice of method is guided by specific circumstances and available data. For simple file scanning, static analysis may be the most efficient option because it does not require file execution. In contrast, in dynamic analysis, collecting data from a running executable may offer deeper insights into questionable executables, actual behavior, and potential malicious intent.
Its capacity to learn generalized patterns that enable the identification of previously unseen threats [19,20] has allowed machine learning to emerge as a prominent alternative for developing malware detection systems. Our prior research [9] proved that ensemble methods consistently outperform individual classifiers, confirming the findings of other researchers in this field [21,22].
The inherent uncertainty in malware detection, arising from polymorphic malware, adversarial samples, and evolving attack vectors, has motivated researchers to explore uncertainty-aware approaches [23]. The DST has emerged as a prominent framework that offers a mathematical foundation for reasoning under uncertainty and evidence combination.
2.1. Dempster–Shafer Theory in Malware Detection
The Dempster–Shafer theory [24] provides a mathematical framework for evidence combination and uncertainty quantification, making it valuable for malware detection in the presence of conflicting evidence. The application of DST involves three key steps: defining mass functions, selecting combination rules, and establishing decision criteria.
- Mass Function Construction: Previous studies have employed different approaches for creating mass functions. Wang et al. [25] used classifier outputs weighted by confusion matrix results, while Ahmadi et al. [26] used feature importance scores. Recent advances have used DST in distributed intrusion detection systems [27] and integrated them with deep learning architectures for enhanced uncertainty quantification [28]. However, no systematic comparison exists between global confidence (single value per classifier), class-specific confidence (separate values per class), and computationally optimized confidence approaches for mass function construction, which represents a critical gap in the literature that we address in this study.
- Combination Rules and Decision Criteria: Most malware detection studies using DST rely on Dempster’s original combination rule [25,29]. Alternative rules proposed for handling conflicting evidence include Yager’s rule [30], Dubois and Prade’s rule [31], and Murphy’s averaging approach [32], which we have tested. Recent DST applications include distributed attack prevention in cloud federations [27] and intrusion detection in ad hoc networks [33]. However, these applications have not been systematically evaluated for malware detection. Moreover, existing combination rules follow traditional DST formulations without exploring interpretable linear weighting approaches that could provide explicit insights into the contributions of classifiers. While most studies use maximum belief as the decision criterion, comprehensive comparisons of different decision approaches in malware detection contexts are limited to date.
2.2. Alternative Uncertainty-Aware Approaches in Cybersecurity
Beyond the DST, other mathematical frameworks have been explored for handling uncertainty in malware detection and cybersecurity applications, each offering unique advantages for different aspects of uncertainty management.
- Fuzzy Logic Systems: Fuzzy logic has been applied to cybersecurity due to their ability to handle gradual transitions between benign and malicious behaviors. In intrusion detection systems, Moudni et al. [34] developed a fuzzy-based approach to detect black hole attacks in mobile ad hoc networks, demonstrating the effectiveness of fuzzy inference in network security. For malware classification, Atacak [35] proposed a fuzzy logic-based dynamic ensemble model that combined machine learning classifiers using a Mamdani-type fuzzy inference system, achieving a high accuracy of 99.33% on the DREBIN dataset. This approach selectively routes classifier outputs based on their performance for positive and negative instances, demonstrating how fuzzy reasoning can optimize ensemble decision-making in uncertain cybersecurity environments.
- Bayesian Approaches: Bayesian networks have shown promise in cybersecurity threat assessment and malware analysis. Yang et al. [36] proposed Bayesian autoencoders for uncertainty quantification in cybersecurity anomaly detection, demonstrating improved trustworthiness of anomaly predictions on the UNSW-NB15 and CIC-IDS-2017 datasets. Previously, Pappaterra and Flammini [37] developed Bayesian networks for the online detection of cybersecurity threats by translating the attack trees into probabilistic detection models. All these approaches demonstrate the potential of probabilistic methods to manage uncertainties in cybersecurity.
- Hybrid Approaches: Several studies have explored combinations of uncertainty frameworks. For instance, Denoeux et al. [28] proposed an evidential deep learning classifier that combined DST with convolutional neural networks for set-valued classification, achieving improved accuracy and cautious decision-making capabilities. Similarly, the integration of DST with deep learning for threat detection has demonstrated superior performance compared with traditional baseline methods in cybersecurity applications.
Systematic comparisons of different uncertainty-handling frameworks, such as DST, fuzzy logic, and Bayesian approaches, in malware detection contexts remain limited, representing an important area for future studies.
2.3. Performance Evaluation and Datasets
A significant limitation of malware detection research is the lack of comparative evaluations across several public datasets. Most studies use proprietary datasets [29] or rely on a single public dataset [26,35], making it difficult to assess their generalizability to other datasets. Moreover, few studies have systematically compared DST-based approaches with traditional ensemble methods using comprehensive evaluation metrics beyond accuracy and F1-score.
The choice of evaluation metrics is particularly important for DST-based methods. While Atacak [35] reported high performance using traditional metrics, a comprehensive evaluation of DST approaches requires metrics that can assess the uncertainty quantification quality, which is rarely reported in the malware detection literature. Additionally, the identification of sufficient performance metrics for comparing different DST implementation strategies remains an open question.
The lack of standardized evaluation protocols across multiple datasets and the limited adoption of uncertainty-aware metrics represent significant barriers to the advancement of DST-based malware detection research.
3. Methodology
This section describes our approach to malware detection using ensemble methods based on the Dempster–Shafer theory (DST). We focus on the development of methods for mass function construction and the implementation of combination rules that can effectively handle uncertainty and conflicting evidence.
3.1. Theoretical Framework
DST provides a mathematical framework for reasoning under uncertainty and offers several advantages over traditional probability theory: an explicit representation of uncertainty, combination of evidence without requiring prior probabilities, and ability to handle conflicting information. These characteristics make DST particularly suitable for malware detection, where different classifiers may provide conflicting results.
In DST, for a frame of discernment , a mass function m assigns belief over subsets of , where
Throughout our implementation, we assume that , which means that no belief is assigned to the empty set. This is a common assumption in standard DST applications, although some advanced combination rules may allow non-zero values for the empty set to represent conflicting evidence.
The belief function represents the total committed belief to A, whereas the plausibility function represents the extent to which evidence fails to refute A.
3.2. Mass Function Construction Approaches
We propose and compare three principal approaches for mass function construction, addressing the critical challenge of transforming classifier outputs into appropriate DST mass functions.
3.2.1. Fixed Confidence Values
We investigated two fixed confidence strategies that used performance-based measures to adjust the classifier’s outputs.
Global Confidence per Classifier:
We assign a single confidence measure to each classifier i based on its performance. Global confidence is computed as the average of four key performance metrics:
For the predicted probabilities and , the mass functions are constructed as
Class-Specific Confidence:
We assign separate confidence values and for each class based on the per-class F1-scores:
The mass functions are constructed as follows:
3.2.2. Optimized Confidence Values
In our third approach, we investigated whether fixed confidence values could be improved by computational optimization. We employed a hybrid optimization method combining a random search with L-BFGS-B (limited-memory Broyden–Fletcher–Goldfarb–Shanno with bounds) to find confidence values that maximize the balanced accuracy on a validation set.
The optimization process involves two phases: First, the global exploration phase uses a random search to generate multiple sets of confidence values within feasible bounds and evaluates each configuration using balanced accuracy to identify promising regions of the parameter space. Second, the local refinement phase applies L-BFGS-B optimization to fine-tune the most promising configurations found during the random search phase, leveraging the gradient information for efficient convergence to local optima.
This hybrid approach balances global exploration with local exploitation, effectively handling the bounded optimization problem while avoiding convergence to poor local optima that purely gradient-based methods may encounter.
3.3. Novel Linear Combination Rule
We propose a novel linear combination method that assigns optimized weights to each mass function component before combining the evidence from multiple classifiers. Unlike traditional DST combination rules that apply fixed mathematical operations, our approach learns optimal weighting coefficients that maximize the classification performance on validation data. This method provides both computational flexibility and enhanced interpretability through explicit component weighting, allowing security practitioners to understand how different types of evidence contribute to the final decisions.
Unlike traditional weighted voting, which combines final classifier predictions, our linear combination approach operates within the DST framework by assigning optimized weights to individual mass function components (benign, malicious, and uncertainty masses) before evidence fusion. This enables a more granular control over how different types of evidence contribute to the final belief structure, preserving the uncertainty quantification capabilities inherent in the DST while optimizing the combination process.
The linear combination process operates by assigning six distinct weight parameters – to different components of the mass functions. For two classifiers with mass functions and , our method computes the combined mass function according to the following procedure (Algorithm 1), where .
| Algorithm 1 Linear Combination Rule |
| Require: Mass functions , from two classifiers Require: Optimized weights Ensure: Combined mass function
|
The weight optimization process employs a hybrid approach that combines a random search with Sequential Least Squares Programming (SLSQP) to maximize the balanced accuracy of the validation data. This two-stage optimization begins with a random exploration of the parameter space to identify promising regions, followed by gradient-based refinement using SLSQP to converge on optimal weight values.
The normalization step in line 6 of the algorithm ensures that the resulting mass function satisfies the fundamental DST constraint that all mass assignments are summed to unity. This step is critical for maintaining the mathematical validity of the belief structure while preserving the relative importance of the relationships established by the optimized weights.
For scenarios involving more than two classifiers, we extended this pairwise combination approach sequentially. The algorithm processes classifiers iteratively, first combining the initial two classifiers using the optimized weights and then incorporating additional classifiers one at a time using the same linear combination procedure.
3.4. Computational Efficiency and Scalability Framework
Our linear combination approach supports arbitrary ensemble sizes using sequential pairwise optimization. The method combines classifiers iteratively: first, optimizing six parameters for an initial pair, and then optimizing six additional parameters to integrate each subsequent classifier with the existing combination.
This design maintains fixed optimization subproblems, regardless of the ensemble size. For n classifiers, the approach requires sequential optimizations, each in a 6-dimensional space, rather than joint optimization in space, where complexity grows exponentially with dimensionality [38].
Traditional DST combination rules exhibit exponential time complexity , where N = represents the sum of elements across all evidence sources, and are proven to be #P-complete [39]. Our sequential approach addresses these computational challenges through fixed 6-dimensional optimization problems, regardless of the ensemble size.
Each optimized combination becomes a reusable building block containing consolidated mass functions from the previous decisions. Adding a new classifier requires the optimization of six parameters to combine it with the existing results while preserving all previous computational work. Algorithm 2 details the incremental integration process.
The modular structure enables practical deployment scenarios in which classifier ensembles evolve over time using standard 6-dimensional optimization algorithms, regardless of the ensemble size. The optimization of alpha coefficients can be performed using various numerical methods, depending on the computational requirements and deployment constraints. Our implementation employs Sequential Least Squares Programming (SLSQP) with random initialization owing to its effectiveness with bounded optimization problems, although alternative approaches, including evolutionary algorithms or Bayesian optimization, could provide different performance characteristics within the same framework.
| Algorithm 2 Scalable Classifier Integration Framework |
| Require: Existing combined result with optimized mass functions Require: New classifier with probability outputs , Ensure: Updated combined result with optimized weights
|
3.5. Traditional Combination Rules
To compare our novel linear combination approach, we implemented nine traditional DST combination rules, as shown in Figure 1, which represent different strategies for handling conflicting evidence and uncertainty in fusion scenarios.
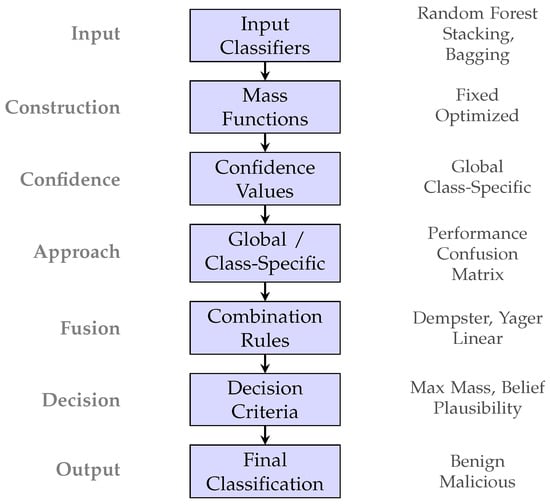
Figure 1.
Overview of the DST-based malware detection framework showing the complete pipeline from input classifiers to final classification decision.
Dempster’s rule is the foundational combination method in DST and operates as a normalized conjunctive rule that proportionally redistributes conflicting evidence among the remaining focal elements. This rule assumes that the sources are independent and reliable, making it particularly effective when classifiers provide complementary rather than contradictory evidence. However, Dempster’s rule can produce counterintuitive results when sources exhibit high levels of conflict.
Yager’s rule addresses the limitation of Dempster’s approach by explicitly handling conflicting beliefs through assignment to uncertainty, rather than redistribution. When the evidence sources disagree significantly, Yager’s rule assigns the conflicting mass to the complete frame of discernment , effectively representing the system’s uncertainty regarding the correct classification. This conservative approach prevents the amplification of conflicts that can occur using Dempster’s rule.
Dubois and Prade’s rule provides a hybrid approach that combines aspects of both conjunctive and disjunctive combination strategies. This method attempts to balance the strengths of different combination philosophies by applying conjunctive operations when the sources agree and disjunctive operations when they conflict. The resulting combination preserves more information about source disagreements while still producing clear classifications.
The Proportional Conflict Redistribution rules, specifically PCR5 and PCR6, represent advanced approaches that redistribute conflicting evidence proportionally based on the individual masses of competing hypotheses. PCR5 redistributes the conflict only to elements involved in the conflict, whereas PCR6 extends this redistribution to all focal elements. These rules aim to provide a more nuanced handling of conflicting evidence compared to simple normalization or assignment to uncertainty.
Zhang’s rule incorporates the concept of distance between focal elements when combining evidence, providing a mathematically sophisticated approach that considers the semantic relationships between different hypotheses. This rule is particularly useful when the frame of discernment has an inherent structure or when certain combinations of evidence are more plausible than others based on domain knowledge.
3.6. Decision Criteria
To make final classifications based on the combined evidence from DST fusion, we implemented four distinct decision criteria that transformed the resulting mass functions into concrete classification decisions. Each criterion represents a different interpretation of how to extract actionable decisions from the belief structures.
The maximum mass criterion selects the hypothesis with the highest mass value directly assigned to it, representing the most straightforward approach to decision-making in DST. This criterion focuses exclusively on direct evidence supporting each hypothesis without considering the broader belief structure. Although computationally simple, this approach may not fully utilize the rich uncertainty information encoded in the mass function.
The maximum belief criterion considers all evidence that supports a particular hypothesis, including the mass assigned to subsets containing that hypothesis. This approach computes the belief function for each singleton hypothesis and selects that with the highest total supporting evidence. By aggregating all supporting masses, this criterion provides a more comprehensive view of the accumulated evidence favoring each classification option.
The maximum plausibility criterion adopts a complementary perspective by considering all evidence that does not contradict the hypothesis. The plausibility function measures the extent to which the evidence fails to refute each hypothesis, effectively capturing the absence of contradictory evidence. This criterion is particularly useful in scenarios in which the absence of negative evidence is as important as the presence of positive evidence.
The maximum pignistic probability criterion transforms the belief structure into a classical probability distribution using Smets’ pignistic transformation. This approach distributes the uncertainty mass proportionally among all singleton hypotheses, creating a probability distribution that can be interpreted using the traditional probabilistic decision theory. Pignistic transformation provides a bridge between the DST framework and conventional probabilistic reasoning, making it particularly suitable for integration with existing probabilistic systems and scenarios requiring strict probabilistic interpretations of the results.
3.7. Framework Overview
Figure 1 presents a comprehensive overview of the proposed DST-based malware detection framework. The framework processes input from three base classifiers (Random Forest, Stacking, and Bagging) through several stages: mass function construction using either fixed or optimized confidence values with global or class-specific approaches, evidence fusion using traditional DST rules or our novel linear combination method, and final decision-making through four different criteria.
4. Experimental Setup
This section describes our comprehensive experimental framework for evaluating DST-based malware detection approaches, including dataset characteristics, baseline classifier evaluation, and implementation details of our proposed method.
4.1. Datasets and Experimental Design
We utilized four public datasets with diverse characteristics to ensure a robust evaluation of our DST-based approach. Table 1 presents the key characteristics of each dataset, demonstrating significant variation in size, class distribution, and feature representation.

Table 1.
Dataset characteristics used in the experimental evaluation.
The datasets represent different aspects of the malware detection challenge and provide diverse evaluation scenarios for the model. BODMAS provides a balanced distribution of high-dimensional features, making it suitable for testing classifier performance under moderate complexity conditions. DREBIN presents a significant class imbalance (95.69% benign samples), which tests the robustness of fusion approaches under the extreme distribution skew commonly found in real-world deployments. AndroZoo offers the largest sample size (347,444 samples) with the most diverse malware families and variants, creating the most challenging classification scenario that reflects the operational complexity. BMPD features an inverted class distribution (74.44% malware) with moderate dimensionality, providing a contrasting evaluation context to other datasets.
Importantly, these four datasets are completely independent, with no known relationships in terms of collection methodologies, temporal periods, or feature engineering approaches. BODMAS focuses on PE malware with engineered features, DREBIN uses Android permissions and API calls, AndroZoo provides raw APK files from diverse sources, and BMPD contains Windows PE files with basic statistical features. This independence strengthens the validity of our transferability results, as a successful coefficient transfer across unrelated datasets suggests genuine generalizability rather than dataset-specific overfitting.
Our preprocessing pipeline included feature normalization to the range and 5-fold stratified cross-validation to maintain the class balance in each fold. To ensure reproducibility, we employed fixed random seeds in all experiments. Stratified cross-validation ensures that each fold maintains the original class distribution, which is particularly important for the highly imbalanced DREBIN dataset.
4.2. Baseline Classifier Evaluation and Selection
We implemented seven classifiers using scikit-learn 1.1.2 with default parameters to establish performance baselines: Random Forest, Decision Tree, Multilayer Perceptron (MLP), Support Vector Classifier (SVC), Gradient Boosting, Bagging, and Stacking. Our selection strategy prioritized reliable base classifiers over compensating for poor individual classifier performance, as our focus was on evaluating the effectiveness of DST fusion rather than classifier optimization. The use of default parameters ensured a fair comparison across methods while maintaining the computational feasibility for large-scale experimentation.
Each classifier was trained using probability calibration (CalibratedClassifierCV with 5-fold cross-validation and the sigmoid method in scikit-learn 1.1.2) to ensure reliable probability outputs that were suitable for DST mass function construction. The calibration process is critical for converting classifier outputs into meaningful belief assignments.
Based on consistent performance across datasets, particularly the Matthews Correlation Coefficient (MCC) scores, we selected the three best-performing methods for DST-based fusion. This selection was driven by empirical results rather than theoretical considerations. Stacking achieved an MCC range of 0.7799–0.9898, demonstrating superior meta-learning capabilities that effectively combine multiple base learners. Random Forest achieved an MCC range of 0.7800–0.9889, providing robust ensemble performance through bootstrap aggregation and random feature selection. Bagging achieved an MCC range of 0.7745–0.9885, offering complementary variance reduction properties through bootstrap sampling.
The classifiers that were excluded showed significant performance limitations that would compromise fusion effectiveness. The MLP showed inconsistent performance across datasets (MCC range 0.4766–0.9888), indicating sensitivity to dataset characteristics and training conditions. The SVC showed inconsistent performance across datasets (MCC range 0.0000–0.9739), with particularly weak results on AndroZoo and DREBIN, likely due to scaling issues with large datasets and class imbalance sensitivity. These performance issues would introduce noise into the fusion process rather than contributing meaningful evidence for malware detection.
4.3. DST Implementation Details
Our implementation encompasses the three distinct approaches for mass function construction described in Section 3.2.1 and Section 3.2.2, nine traditional combination rules, and our novel linear combination method presented in Section 3.3.
4.3.1. Parameter Optimization Framework
For our novel linear combination approach, we selected the BMPD dataset as the reference for parameter optimization because of its moderate size (19,612 samples), reasonable computational requirements, and inverse class distribution that provides good training diversity. The coefficients were optimized using Sequential Least Squares Programming (SLSQP) with bounds for each parameter.
The optimization process on BMPD yielded transferable parameters that were fixed to the other datasets without reoptimization. This transfer learning approach tests whether the classifier relationships captured by the linear combination method represent generalizable patterns in malware detection across different data distributions and characteristics.
4.3.2. Combination Rules and Decision Criteria
We implemented nine traditional DST combination rules for comparison: Dempster’s rule, Yager’s rule, Dubois and Prade’s rule, Zhang’s rule, PCR5, PCR6, conjunctive rule, disjunctive rule, and Murphy’s rule. Each rule represents a different strategy for handling conflicting evidence and uncertainty in the fusion of multiple classifiers.
For decision-making, we evaluated four criteria: maximum mass, maximum belief, maximum plausibility, and maximum pignistic probability. These criteria transform the combined mass functions into final classification decisions using different interpretations of the evidence structure.
4.4. Performance Evaluation Framework
We employed multiple metrics specifically chosen to address the class imbalance inherent to malware detection. The Matthews Correlation Coefficient (MCC) serves as our primary metric because it provides a balanced assessment for imbalanced datasets and accounts for true and false positives and negatives across both classes. Balanced accuracy computes the average of malware and benign recall, ensuring equal treatment of both classes, regardless of their frequency in the dataset. Precision and recall were calculated separately for each class to assess specific performance characteristics and identify potential bias toward majority or minority classes. The F1-score provides the harmonic mean of precision and recall for overall performance assessment while being more robust to class imbalance than simple accuracy.
Our experimental validation used 5-fold stratified cross-validation with consistent, random seed values to ensure reproducibility. Stratification maintains the original class distributions in each fold, which is essential for reliable performance estimation on imbalanced datasets such as DREBIN.
4.5. Computational Environment
All experiments were conducted using parallel processing with 16 CPU cores to handle the computational demands of parameter optimization and large-scale dataset processing. The parallel implementation distributed classifier training, mass function construction, and combination rule evaluation across multiple cores while maintaining result consistency through controlled random seeding.
The computational setup enabled the efficient processing of the largest dataset (AndroZoo with 347,444 samples), while supporting the intensive parameter optimization required for confidence values and -coefficient tuning on the BMPD reference dataset.
5. Results and Discussion
This section presents and analyzes the results of our DST-based malware detection approach across multiple datasets. We first established baseline performance with traditional classifiers, then systematically evaluated our three mass function construction approaches, compared the combination rules, and analyzed our novel linear combination method while discussing its implications, strengths, and limitations.
5.1. Baseline Performance Analysis
We first evaluated the individual classifiers and traditional ensemble methods to establish the performance baselines. Table 2 presents the Matthews Correlation Coefficient (MCC) results for all datasets.

Table 2.
Baseline performance comparison (MCC).
These results revealed significant performance variations between the datasets and classifiers, confirming the dataset-specific analysis presented in Section 4.1. The AndroZoo dataset consistently produced the lowest MCC scores across all classifiers, reflecting the challenging nature of this large-scale, diverse dataset with raw APK features and a broad temporal range. Stacking consistently achieved the highest performance (MCC scores 0.7799–0.9898), particularly for datasets with balanced class distributions, demonstrating the effectiveness of meta-learning approaches in malware detection.
The highly imbalanced DREBIN dataset (95.69% benign) challenged many classifiers, with the SVC exhibiting particularly poor performance (MCC: 0.2746). Based on these findings, we selected Stacking, Random Forest, and Bagging as our base classifiers for DST-based fusion owing to their consistently strong and complementary performance characteristics.
Statistical Significance Analysis
Given the small variance observed in our cross-validation results (typically ±0.001–0.003 MCC), the performance differences between the DST methods and traditional ensemble approaches fall within the statistical error margins. This confirms that DST and traditional ensemble methods achieve equivalent performance, supporting our main finding that the value of DST lies in interpretability and uncertainty quantification rather than performance improvements. The consistently low variance across all datasets demonstrates the reliability and stability of our experimental framework.
The negligible performance differences (within 0.002 MCC difference for mass function approaches and within 0.003 MCC for combination rules) indicate that the theoretical distinctions between various DST implementations become less relevant when base classifiers exhibit high agreement. This finding has practical implications for deployment scenarios, as it allows practitioners to select simpler approaches based on computational efficiency rather than pursuing marginal performance improvements through complex optimization procedures.
5.2. Mass Function Construction Analysis
We systematically compared three approaches for mass function construction: global, class-specific, and optimized confidence.
5.2.1. Fixed Confidence Approaches Comparison
Table 3 presents a performance comparison between the global and class-specific confidence approaches across datasets using Dempster’s rule and maximum belief as the decision criterion.

Table 3.
Comparison of fixed mass function construction approaches (MCC).
The results demonstrated negligible performance differences between the global and class-specific approaches (within 0.002 MCC difference). For BODMAS and BMPD, the approaches yielded identical MCC scores, whereas for DREBIN and AndroZoo, the global approach performed marginally better but within statistical error margins. This finding suggests that the simpler global confidence approach provides equivalent effectiveness with reduced computational complexity.
5.2.2. Optimized Confidence Values Analysis
We also evaluated the computationally optimized confidence values using our hybrid random search with the L-BFGS-B method. However, the performance improvements were negligible (within 0.001 MCC difference) compared with fixed-confidence approaches across all datasets. This finding challenges the common assumption that parameter optimization necessarily leads to better performance in fusion-based systems and has important implications for practical deployment, particularly in resource-constrained environments where computational efficiency is critical.
One of our most significant findings is that fixed confidence values perform as effectively as optimized values, offering substantial computational advantages without compromising the detection performance. This result establishes evidence-based guidelines for practitioners choosing between computational complexity and performance in operational malware detection systems.
5.3. Combination Rules Evaluation
We evaluated nine DST combination rules across all datasets, with maximum belief as the decision criterion and a global confidence adjustment. Table 4 presents the MCC scores of the representative subset.

Table 4.
Performance comparison of different ombination rules (MCC).
Most combination rules achieved similar performances, with differences generally within the standard deviation ranges. This similarity stems from the high agreement between the selected base classifiers, as evidenced by their consistent performance rankings across the datasets in Table 2. Dempster’s rule was the most consistent performer in all datasets. PCR6 was the only rule that showed significant performance degradation on the BODMAS and BMPD datasets, likely because of its handling of conflicting evidence in scenarios with a high classifier agreement.
Interestingly, all four decision criteria (maximum mass, maximum belief, maximum plausibility, and maximum pignistic probability) yield identical results across all datasets and combination rules. This suggests that the base classifiers provided clear distinctions between malware and benign samples with minimal uncertainty, rendering the theoretical differences between the decision criteria irrelevant in this experimental context.
The similar performance across various combination rules indicates that the theoretical differences in handling conflicting evidence become less relevant when the base classifiers show high agreement. This suggests that in operational settings, simpler rules, such as Dempster’s, can be preferred for their computational efficiency without compromising detection effectiveness. The primary value of DST in such scenarios lies in providing systematic uncertainty quantification and interpretable evidence combination rather than improving the performance of individual classifiers.
5.4. Linear Combination Approach Analysis
We evaluated our proposed linear combination approach, which assigns optimized weights to each component of the mass function. The coefficients were optimized on the BMPD dataset and transferred to other datasets without reoptimization to assess their transferability and generalization capabilities.
5.4.1. Optimized Alpha Coefficients
Table 5 presents the optimized coefficients from the BMPD dataset, which show the learned relationships among the classifiers.

Table 5.
Optimized alpha coefficients from the BMPD dataset.
The coefficients reveal interpretable patterns that provide insights into the classifier’s behavior and contributions. Higher weights for the Stacking classifier (, ) in Stage 1 for class-specific decisions (benign: 0.6295; malicious: 0.6082) reflect its superior meta-learning capabilities, as demonstrated in the baseline performance analysis. Bagging receives a higher weight for uncertainty handling ( = 0.6074), which aligns with its variance reduction properties through bootstrap sampling. In Stage 2, the pattern shifted toward more balanced contributions between the combined evidence and Random Forest, indicating adaptive weighting based on the combination context.
5.4.2. Transferability and Performance Analysis
Table 6 demonstrates the successful transfer of the BMPD-optimized coefficients to other datasets without reoptimization.

Table 6.
Linear combination performance with transferred alpha values.
The successful transfer of coefficients demonstrates that our linear combination approach captures generalizable relationships between classifiers that remain valid across different malware detection scenarios. Notably, the performance on BODMAS (MCC: 0.9898) slightly exceeded that of the optimization dataset BMPD (MCC: 0.9729), indicating robust generalization capabilities of the model.
Alpha coefficients provide clear insights into classifier relationships, supporting security analysts in understanding decision-making processes. The higher weights assigned to Stacking for class-specific decisions reflect its superior meta-learning capabilities, whereas Bagging’s contribution to uncertainty handling aligns with its variance reduction properties. This transparency supports incident investigations and system improvements in operational environments where understanding why a particular decision was made is as important as the decision itself.
5.5. Comparative Analysis and False Positive Rates
Table 7 presents a comprehensive comparison between our linear combination approach, traditional DST (Dempster’s rule), and the best individual classifier (i.e., Stacking).

Table 7.
Performance comparison: linear combination vs. traditional DST vs. best individual method (MCC).
The performance differences between the methods were minimal, with MCC score variations typically within 0.003. Although the absolute performance improvements are modest, the main advantages of DST-based approaches lie in their interpretability, uncertainty quantification, and systematic evidence combination, rather than pure performance gains.
False positive rate (FPR) analysis revealed consistently low rates across all approaches, which is critical for operational malware detection systems. Table 8 presents the FPR results for the DST-based approaches.

Table 8.
False positive rates across datasets.
All configurations maintained low false positive rates, with BODMAS and DREBIN achieving particularly impressive results (0.24% and 0.16%, respectively). Even on the more challenging AndroZoo and BMPD datasets, the FPR remained below 3.2%, which is acceptable for operational deployment, where false positives can lead to significant disruption and resource wastage.
5.6. Practical Implications and Guidelines
Our evaluation provides practical guidelines for implementing DST-based malware detection systems. Fixed confidence values using the global approach offer an effective balance between computational efficiency and detection performance, eliminating the need for complex optimization procedures. This finding is critical for operational deployment, where computational resources are limited.
Traditional DST combination rules perform similarly in malware detection contexts, suggesting that practitioners can choose simpler approaches, such as Dempster’s rule, without sacrificing effectiveness. This is because our selected base classifiers show high agreement, reducing conflicting evidence that would highlight the advantages of sophisticated combination rules.
Our linear combination approach offers enhanced interpretability through explicit weighting, while maintaining performance equivalent to that of traditional DST methods. The successful transfer of coefficients across datasets shows that these relationships capture fundamental patterns in classifier interactions that generalize beyond specific data distributions.
For instance, in a scenario where Random Forest indicates benign (confidence 0.7) while Stacking suggests malicious (confidence 0.8), DST provides systematic uncertainty quantification rather than arbitrary tie-breaking, enabling security analysts to flag samples for manual review. The coefficients provide insights into classifier relationships: higher weights for Stacking reflect its meta-learning capabilities, whereas Bagging’s contribution to uncertainty handling aligns with its variance reduction properties.
Similarly, in enterprise environments requiring decision auditability, the DST’s explicit weighting enables security teams to document why specific classifications were made, thereby supporting compliance requirements and incident response procedures.
Based on our findings, we recommend using fixed global confidence values for computational efficiency, applying Dempster’s rule for consistent performance, and considering linear combinations when interpretability is prioritized. The Matthews Correlation Coefficient serves as a sufficient primary evaluation metric. DST-based fusion is deployed when uncertainty quantification and transparent decision-making are more valuable than marginal performance gains.
The consistently low false positive rates achieved (0.16% to 3.19%) support the operational viability of DST-based approaches in production environments where the misclassification of legitimate software can significantly impact system usability and user trust.
5.7. Limitations and Future Work
Despite these results, our approach has several important limitations that warrant careful consideration in future studies. The relatively small performance improvements over traditional ensemble methods suggest that DST’s primary value lies in uncertainty quantification and interpretability rather than detection accuracy. The architectural similarity among our selected classifiers represents a conscious methodological choice to isolate DST fusion effects under controlled conditions but limits our understanding of how DST performs with more diverse algorithmic perspectives, such as deep neural networks or different kernel-based approaches. This evaluation across diverse algorithmic paradigms represents an important step toward extending our systematic DST methodology.
Transferability analysis across four independent datasets provided initial validation; however, several challenges remain unaddressed. Temporal drift, where malware evolution may invalidate confidence relationships learned from older datasets, represents a critical operational concern. Feature engineering differences require validation between static and dynamic analysis features, and class distribution sensitivity, where extreme imbalances may require confidence value recalibration, highlighting the need for adaptive mechanisms in production deployments.
Perhaps most importantly, our binary classification framework represents a foundational step toward multi-class malware family detection, where the potential of DST-based fusion may be realized. Multi-class scenarios with n families require the management of subsets, creating computational and methodological challenges that make domain-specific knowledge critical. For example, evidence fusion for conflicts between {ransomware, trojan} and {adware} and {benign} requires specialized handling that cannot be addressed by our generic binary approach. With five malware families, the framework must manage possible evidence combinations; with ten families, this explodes to subsets, making our current generic approach insufficient and family-specific optimization essential.
We acknowledge that adversarial robustness is a significant limitation of the current study. Our research focused on fusion methodology evaluation using clean datasets and did not include an adversarial robustness assessment. This represents an important gap because adversarial examples can potentially exploit fusion mechanisms by targeting multiple classifiers simultaneously, and evasion techniques may manipulate the confidence relationships on which our approach relies. Future research should investigate the adversarial robustness of DST fusion compared to individual classifiers and the uncertainty behavior when classifiers face adversarial samples.
Future work should investigate alternative uncertainty frameworks beyond the DST, such as fuzzy logic or probabilistic graphical models, which could provide different perspectives on handling evidence combinations in malware detection contexts. A comparative evaluation of uncertainty frameworks (DST, fuzzy logic, and Bayesian approaches) represents a natural progression from our systematic DST foundation, enabling comprehensive uncertainty quantification analysis in cybersecurity applications. Additionally, a comprehensive computational complexity analysis comparing DST-based approaches with recent deep learning-based malware detection techniques would provide valuable insights for practitioners choosing between different methodological approaches.
Recent advances in uncertainty quantification from other domains, such as Bayesian optimization techniques demonstrated in structural engineering applications [40], may offer transferable insights for improving DST parameter optimization efficiency and interpretability analysis of classifier contributions in cybersecurity. Specifically, Tree-structured Parzen Estimator (TPE) approaches could enhance our coefficient optimization beyond SLSQP methods, while SHAP-based analysis techniques could provide deeper insights into individual classifier contribution patterns and decision-making transparency in operational environments.
A systematic evaluation of DST-based approaches with more diverse classifier architectures, including convolutional neural networks, transformers, and deep clustering methods, represents another important direction. Such diversity could reveal whether DST’s theoretical advantages become more pronounced when combining fundamentally different algorithmic perspectives, potentially unlocking performance gains that our current ensemble-focused evaluation could not demonstrate. This comprehensive approach would establish whether the modest improvements observed with ensemble methods represent DST’s fundamental limitations or simply reflect the high agreement among classifiers that are architecturally similar.
5.8. Summary
Our DST-based fusion approach demonstrated effective malware detection across diverse datasets, establishing several key findings that advance the understanding of evidence combinations in cybersecurity applications. The analysis revealed that fixed confidence values perform equivalently to computationally expensive optimized approaches, providing significant computational savings without sacrificing detection efficacy. This finding challenges the conventional assumptions regarding the necessity of parameter optimization in fusion systems and establishes practical guidelines for resource-constrained deployment scenarios.
Traditional combination rules achieve remarkably similar performances in malware detection contexts, with differences typically falling within the statistical error margins. This suggests that the theoretical distinctions between various DST rules become less relevant when the base classifiers exhibit high agreement, allowing practitioners to select simpler approaches based on computational efficiency rather than theoretical sophistication.
Our novel linear combination method provides enhanced interpretability while maintaining performance parity with established DST approaches. The successful transfer of coefficients from the BMPD to other datasets demonstrates that this method captures generalizable classifier relationships that remain valid across different malware detection scenarios. The interpretable nature of these coefficients offers valuable insights into the contributions of the classifier and system behavior for security practitioners.
The consistently low false positive rates achieved across all datasets (ranging from 0.16% to 3.19%) support the operational viability of DST-based approaches in production environments where the misclassification of legitimate software can significantly impact system usability and user trust. These results, combined with the systematic uncertainty handling provided by DST frameworks, offer valuable advantages for security practitioners requiring transparent and explainable malware detection systems, even when absolute performance improvements over individual classifiers remain modest.
6. Conclusions
This study investigated the application of Dempster–Shafer theory for malware detection, focusing on optimal methods for mass function construction and developing a novel linear combination approach. Through experimentation across four diverse public datasets, we provide the first systematic methodology for evaluating DST-based fusion approaches, establishing evidence-based guidelines for practitioners.
Our research makes several contributions to the field of malware detection. We provided the first systematic comparison of three mass function construction approaches—global confidence, class-specific confidence, and computationally optimized confidence values—demonstrating that fixed confidence values perform as effectively as optimized ones while offering computational advantages. We developed a novel linear combination approach that achieves performance comparable to traditional DST rules while providing enhanced interpretability through explicit -weighting. The transfer of optimized coefficients across datasets demonstrates that our approach captures generalizable classifier relationships that remain valid across various malware detection scenarios.
Our methodology evaluation established that most DST combination rules achieved similar performance, with Matthews Correlation Coefficient scores ranging from 0.78 to 0.99. This analysis revealed that the theoretical differences between combination rules become less relevant when the base classifiers exhibit high agreement, allowing practitioners to prioritize computational efficiency over theoretical sophistication.
Although DST-based methods show only modest improvements over traditional ensemble approaches, their main advantages lie in interpretability, uncertainty quantification, and systematic evidence combination, rather than performance gains. These characteristics are particularly valuable in operational cybersecurity environments, where understanding system decisions and managing uncertainty are as important as the raw detection performance.
This study provides a methodological basis for multi-class malware family detection, where DST’s potential of DST may be realized. Multi-class scenarios require the management of complex evidence combinations, making domain-specific knowledge and diverse classifier architectures important for future implementations.
Future research should investigate adversarial robustness and evaluate diverse classifier architectures to determine whether DST’s theoretical advantages become more pronounced with fundamentally different algorithmic perspectives. The transferability analysis across independent datasets validated our methodology before addressing the complexity of specialized implementations.
This study establishes a systematic framework that enables future comprehensive comparative studies across uncertainty frameworks and diverse classifier architectures.
In conclusion, our methodology evaluation provides the research community with evidence-based guidelines for implementing DST in malware detection. The transferability of our linear combination approach and the equivalence of fixed and optimized confidence values offer practical advantages that extend beyond theoretical contributions, providing actionable insights for real-world applications and establishing the basis for future specialized fusion techniques that can address the complexity of multi-class malware family detection.
Author Contributions
Conceptualization, P.G. and C.G.-S.; methodology, P.G.; software, P.G.; validation, P.G., S.Y.E. and C.G.-S. and formal analysis, P.G.; investigation, P.G.; resources, C.G.-S. and M.A.P.; data curation, P.G.; writing—original draft preparation, P.G.; writing—review and editing, S.Y.E., C.G.-S. and M.A.P.; visualization, P.G.; supervision, C.G.-S. and M.A.P.; project administration, C.G.-S., P.G. and C.G.-S.; funding acquisition: P.G., C.G.-S. and M.A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Vicerrectoría de Investigación y Doctorados de la Universidad San Sebastián—Fondo USS-FIN-25-APCS-34; by Universidad del Bío-Bío, Chile, under grant INN I+D 23-53 and DIUBB 2130253 IF/R; and partially by the authors’ personal funds. Marco A. Palomino thanks The University of Aberdeen for supporting his participation in this work.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in this study are publicly available: BODMAS [41], DREBIN [42], AndroZoo [43], and BMPD [44]. The code implementing the DST-based fusion methods will be made available upon publication to ensure reproducibility of the results.
Acknowledgments
The authors thank the organizations that provided the public datasets used in this research. We also acknowledge the computational resources provided by Universidad San Sebastián and Universidad del Bío-Bío. We are grateful to José Pino and Nelson Baloian from DCC, Universidad de Chile for introducing us to Dempster-Shafer theory, which became foundational to this research.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DST | Dempster–Shafer Theory |
| MCC | Matthews Correlation Coefficient |
| BPA | Basic Probability Assignment |
| ML | Machine Learning |
| FPR | False Positive Rate |
| API | Application Programming Interface |
| CNN | Convolutional Neural Network |
References
- Death, D. Information Security Handbook: Develop a Threat Model and Incident Response Strategy to Build a Strong Information Security Framework; Packt Publishing: New York, NY, USA, 2017. [Google Scholar]
- Helyome, K. Ransomware Attacks in Manufacturing and What Business Leaders Fear Most. 2023. Available online: https://blogs.blackberry.com/en/2023/03/ransomware-attacks-in-manufacturing-and-what-business-leaders-fear-most (accessed on 15 March 2025).
- James, N. 30+ Malware Statistics You Need to Know in 2023. Astra Security Blog. 2023. Available online: https://www.getastra.com/blog/security-audit/malware-statistics/ (accessed on 15 July 2023).
- Menzli, A. Building Trust in Machine Learning Malware Detectors Can We Trust the Decision Made by the ML Systems? Data Science, Medium. 2020. Available online: https://medium.com/data-science/building-trust-in-machine-learning-malware-detectors-d01f3b8592fc (accessed on 15 July 2023).
- Egele, M.; Scholte, T.; Kirda, E.; Kruegel, C. A survey on automated dynamic malware-analysis techniques and tools. ACM Comput. Surv. 2008, 44, 1–42. [Google Scholar] [CrossRef]
- Akhtar, M.; Tao, F. Malware Analysis and Detection Using Machine Learning Algorithms. Symmetry 2022, 14, 2304. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Mohandes, M.; Deriche, M.; Aliyu, S.O. Classifiers Combination Techniques: A Comprehensive Review. IEEE Access 2018, 6, 19626–19639. [Google Scholar] [CrossRef]
- Galdames, P.; Gutiérrez-Soto, C.; Palomino, M. Ensembling Machine Learning Models for Malware Detection. In Proceedings of the 4-th Workshop on Collaborative Technologies and Data Science in Smart City Applications (CODASSCA 2024): From Data to Information and Knowledge, Yerevan, Armenia, 3–6 October 2024; pp. 47–60. [Google Scholar]
- Dempster, A. The Dempster–Shafer Calculus for Statisticians. Int. J. Approx. Reason. 2008, 48, 365–377. [Google Scholar] [CrossRef]
- Saha, S.; Saha, S. A novel approach to classify edible oil using multiple classifier fusion based on spectral data. In Proceedings of the International Conference on Intelligent Control Power Instrumentation (ICICPI), Kolkata, India, 21–23 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 108–113. [Google Scholar]
- Mohandes, M.; Deriche, M. Arabic sign language recognition by decisions fusion using Dempster–Shafer theory of evidence. In Proceedings of the IEEE Computing, Communications and IT Applications Conference, Hong Kong, China, 1–4 April 2013; pp. 90–94. [Google Scholar]
- Moosavian, A.; Khazaee, M.; Najafi, G.; Kettner, M.; Mamat, R. Spark plug fault recognition based on sensor fusion and classifier combination using Dempster–Shafer evidence theory. Appl. Acoust. 2015, 93, 120–129. [Google Scholar] [CrossRef]
- Shafer, G. Dempster’s Rule of Combination. Int. J. Approx. Reason. 2016, 79, 26–40. [Google Scholar] [CrossRef]
- Gržinić, T.; González, E.B. Methods for Automatic Malware Analysis and Classification: A Survey. Int. J. Inf. Comput. Secur. 2022, 17, 179–203. [Google Scholar] [CrossRef]
- Baker del Aguila, R.; Contreras Pérez, C.D.; Silva-Trujillo, A.G.; Cuevas-Tello, J.C.; Nunez-Varela, J. Static Malware Analysis Using Low-Parameter Machine Learning Models. Computers 2024, 13, 59. [Google Scholar] [CrossRef]
- Li, C.; Cheng, Z.; Zhu, H.; Wang, L.; Lv, Q.; Wang, Y.; Li, N.; Sun, D. DMalNet: Dynamic malware analysis based on API feature engineering and graph learning. Comput. Secur. 2022, 122, 102872. [Google Scholar] [CrossRef]
- Yong Wong, M.; Landen, M.; Antonakakis, M.; Blough, D.M.; Redmiles, E.M.; Ahamad, M. An Inside Look into the Practice of Malware Analysis. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, 15–19 November 2021; pp. 3053–3069. [Google Scholar]
- Brown, A.; Gupta, M.; Abdelsalam, M. Automated Machine Learning for Deep Learning Based Malware Detection. Comput. Secur. 2024, 137, 103582. [Google Scholar] [CrossRef]
- Xie, W.; Xu, S.; Zou, S.; Xi, J. A System-Call Behavior Language System for Malware Detection Using a Sensitivity-Based LSTM Model. In Proceedings of the 3rd International Conference on Computer Science and Software Engineering, Beijing, China, 22–24 May 2020; pp. 112–118. [Google Scholar]
- Feng, P.; Ma, J.; Sun, C.; Xu, X.; Ma, Y.A. Novel Dynamic Android Malware Detection System with Ensemble Learning. IEEE Access 2018, 6, 30996–31011. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Wang, X.; Liu, J.; Zhang, X. Detecting Android malicious apps and categorizing benign apps with ensemble of classifiers. Futur. Gener. Comput. Syst 2018, 78, 987–994. [Google Scholar] [CrossRef]
- Singh, J.; Singh, J. A Survey on Machine Learning-Based Malware Detection in Executable Files. J. Syst. Archit. 2021, 112, 101861. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Wang, X.; Zhang, D.; Su, X.; Li, W. Mlifdect: Android malware detection based on parallel machine learning and information fusion. Secur. Commun. Netw. 2017, 2017, 6451260. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ulyanov, D.; Semenov, S.; Trofimov, M.; Giacinto, G. Novel feature extraction, selection and fusion for effective malware family classification. In Proceedings of the Sixth ACM Conference on Data and Application Security and Privacy, New Orleans, LA, USA, 9–11 March 2016; pp. 183–194. [Google Scholar]
- MacDermott, A.; Shi, Q.; Kifayat, K. Distributed Attack Prevention Using Dempster-Shafer Theory of Evidence. In Intelligent Computing Methodologies, Proceedings of the 13th International Conference, ICIC 2017, Liverpool, UK, 7–10 August 2017; Springer: Cham, Switzerland, 2017; Lecture Notes in Computer Science; Volume 10363, pp. 203–212. [Google Scholar] [CrossRef]
- Tong, Z.; Xu, P.; Denœux, T. An evidential classifier based on Dempster-Shafer theory and deep learning. Neurocomputing 2021, 450, 275–293. [Google Scholar] [CrossRef]
- Du, Y.; Wang, X.; Wang, J. A static Android malicious code detection method based on multi-source fusion. Secur. Commun. Netw. 2015, 8, 3238–3246. [Google Scholar] [CrossRef]
- Yager, R.R. On the Dempster-Shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Representation and combination of uncertainty with belief functions and possibility measures. Comput. Intell. 1988, 4, 244–264. [Google Scholar] [CrossRef]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Chen, T.M.; Venkataramanan, V. Dempster-Shafer theory for intrusion detection in ad hoc networks. IEEE Internet Comput. 2005, 9, 35–41. [Google Scholar] [CrossRef]
- Moudni, H.; Er-rouidi, M.; Mouncif, H.; El Hadadi, B. Black Hole attack Detection using Fuzzy based Intrusion Detection Systems in MANET. Procedia Comput. Sci. 2019, 151, 1176–1181. [Google Scholar] [CrossRef]
- Atacak, I. An Ensemble Approach Based on Fuzzy Logic Using Machine Learning Classifiers for Android Malware Detection. Appl. Sci. 2023, 13, 1484. [Google Scholar] [CrossRef]
- Yang, T.; Qiao, Y.; Lee, B. Towards trustworthy cybersecurity operations using Bayesian Deep Learning to improve uncertainty quantification of anomaly detection. Comput. Secur. 2024, 144, 103909. [Google Scholar] [CrossRef]
- Pappaterra, M.J.; Flammini, F. Bayesian Networks for Online Cybersecurity Threat Detection. In Machine Intelligence and Big Data Analytics for Cybersecurity Applications; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Benalla, M.; Achchab, B.; Hrimech, H. On the computational complexity of Dempster’s Rule of combination, a parallel computing approach. J. Comput. Sci. 2021, 50, 101283. [Google Scholar] [CrossRef]
- Wan, S.; Li, S.; Chen, Z.; Tang, Y. An ultrasonic-AI hybrid approach for predicting void defects in concrete-filled steel tubes via enhanced XGBoost with Bayesian optimization. Case Stud. Constr. Mater. 2025, 22, e04359. [Google Scholar] [CrossRef]
- Yang, L.; Ciptadi, A.; Laziuk, I.; Ahmadzadeh, A.; Wang, G. BODMAS: An Open Dataset for Learning based Temporal Analysis of PE Malware. In Proceedings of the 2021 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 27 May 2021; pp. 78–84. [Google Scholar]
- Arp, D.; Spreitzenbarth, M.; Hubner, M.; Gascon, H.; Rieck, K. DREBIN: Effective and Explainable Detection of Android Malware in Your Pocket. In Proceedings of the 21st Annual Network and Distributed System Security Symposium, NDSS 2014, San Diego, CA, USA, 23–26 February 2014; The Internet Society: Reston, VA, USA, 2014; pp. 23–26. [Google Scholar]
- Allix, K.; Bissyandé, T.F.; Klein, J.; Le Traon, Y. AndroZoo: Collecting Millions of Android Apps for the Research Community. In Proceedings of the 13th International Conference on Mining Software Repositories, Austin, TX, USA, 14–15 May 2016; pp. 468–471. [Google Scholar]
- Mauricio. Benign & Malicious PE Files. Kaggle Data 2018, V1. Available online: https://www.kaggle.com/datasets/amauricio/pe-files-malwares (accessed on 30 November 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).