A Study of Periodicities in a One-Dimensional Piecewise Smooth Discontinuous Map

Abstract

In this study, we investigate the nonlinear dynamical behavior of a one-dimensional linear piecewise-smooth discontinuous (LPSD) map with a negative slope, motivated by its occurrence in systems exhibiting discontinuities, such as power electronic converters. The objective of the proposed research is to develop an analytical approach. Analytical conditions are derived for the existence of stable period-1 and period-2 orbits within the third quadrant of the parameter space defined by slope coefficients $a<0$ and $b<0$. The coexistence of multiple attractors is demonstrated. We also show that a novel class of orbits exists in which both points lie entirely in either the left or right domain. These orbits are shown to eventually exhibit periodic behavior, and a closed-form expression is derived to compute the number of iterations required for a trajectory to converge to such orbits. This method also enhances the ease of analyzing system stability by mapping the state–variable dynamics using a non-smooth discontinuous map. The analytical findings are validated using bifurcation diagrams, cobweb plots, and basin of attraction visualizations.

1. Introduction

Piecewise-smooth (PWS) systems have become of interest in recent decades for their dynamics associated with a wide range of applications in engineering, economics, biology, physics, and other fields. There are numerous practical systems that are governed by the dynamics of piecewise smooth systems. Some of them are DC motor drives, switching circuits, power systems [1,2,3,4,5,6], pulses width modulators [7,8], Tantalus and impact oscillators [9,10], hybrid systems, and in financial markets [11,12,13,14]. The interest in piecewise smooth systems is due to a special bifurcation phenomenon that occurs only in non-smooth dynamical systems. This is termed the border collision bifurcation (BCB) [15] and was first reported by M. Feigin [16]. There is a large body of work on smooth systems [17,18,19]. For more than a decade, the focus has been on piecewise smooth discontinuous maps. The results for one-dimensional maps [20,21,22], two-dimensional maps [4,23], three-dimensional maps [24,25], n-dimensional maps [26], linear discontinuous maps as well as co-dimension maps [27,28] have been reported by various authors.

The PWS discontinuous maps must be analyzed, as there is a wide range of phenomena that can occur; some are stable and unstable periodic orbits, which are admissible or non-admissible and converge to unstable periodic or leading to chaotic orbits [29]. Furthermore, atypical orbits are discussed in [30]. The stable periodic orbits are structured in a particular manner in 1D piecewise smooth discontinuous maps which constitute period adding cascades [31]. BCB curves are analyzed numerically, analytically, or by simplified method, i.e., a map replacement technique proposed by Leonav [32,33,34]. The approach is then simplified and extended to discuss the analytical results and characterization of stable [20], unstable [21], and periodic orbits of the 1D map. This work is helpful in knowing the exact number of distinct periodic orbits at a given cardinality. In the previous work, slopes in the map were assumed to be positive and respective results are proven.

In power electronics, non-smooth maps are particularly relevant for analyzing switched-mode converters (viz. buck, boost, and hybrid inverters) that operate with discontinuous control laws, such as pulse-width modulation (PWM) or hysteresis-based switching [35,36,37]. For instance, the dynamics of grid-tied inverters under maximum power point tracking (MPPT) are often demonstrated as linear piecewise-smooth discontinuous (LPSD) maps due to abrupt transitions between operating modes [38,39]. Recent studies have leveraged PWS theory to predict chaotic oscillations and stabilize DC–DC converters in photovoltaic (PV) systems, while demonstrating its utility in mitigating subharmonic instabilities in wind energy inverters [40,41,42]. Although significant progress has been made in the theoretical and applied analysis of PWS maps, a critical gap remains in leveraging this framework for the sustainable design of power converters, particularly in regimes characterized by negative slopes, which are commonly encountered in applications such as bidirectional power flow in battery-integrated systems. The existing body of work predominantly addresses positive-slope dynamics, while the nonlinear behavior of negative-slope LPSD maps remains comparatively underexplored, despite their relevance in systems involving regenerative braking and grid-following inverters. Furthermore, analytical tools for the rapid stability assessment of such maps under disturbances remain limited. Atypical orbit types—such as continuum period-2 solutions—are not well characterized.

In the design of power electronic converters, system parameters—such as input voltage, inductor, or capacitor value, and load range—are typically selected to ensure stable operation and avoid undesirable behaviors like sub-harmonic oscillations or chaotic dynamics. However, determining the exact regions in the parameter space where these nonlinear phenomena emerge remains a challenge. Such regions are often identified through empirical methods, including laboratory experiments or detailed time-domain simulations. Bifurcation theory offers a systematic and analytical framework for addressing this issue by elaborating the boundaries of stable periodic operation, particularly the period-1 regime. This is achieved by constructing a discontinuous map, which involves sampling the system state at discrete intervals synchronized with the switching clock. The stability of period-1 orbit is maintained as long as the eigenvalues of the associated return map lie within the unit circle in the complex plane. This paper presents a PWS map resembling the mathematical model of non-smooth systems. In this paper, we carry out a detailed analysis of stable and unstable periodic orbits that can appear in 1D piecewise smooth discontinuous maps when slopes in the map are negative, by focusing on phenomena which are new and interesting. The main objective of the paper is to give assertive mathematical insights into the 1D PWS map, which has not been done previously. Furthermore, the proposed approach will help in designing the sustainable power converters that can operate under the dynamic conditions.

This paper is organized as follows. In Section 2, one-dimensional map definition and related terms are provided. Section 3 reviews region P, and the results are discussed. Also, some typical phenomena for particular parameter boundary values ($a=b=-1$) are considered in Section 4, which have not been discussed earlier in the analysis using numerical simulations. Furthermore, Section 5, Section 6, Section 7 and Section 8 discuss the results and analyses of other boundary line and unstable region cases. The analyzed work is summarized in Section 9.

2. Definition of the 1-$\mathit{D}$ Map

The 1-D linear piecewise-smooth discontinuous map is [29]:

$$x_{n+1}=f(x_n,a,b,\mu ,\ell )=\left\{\begin{array}{ccc}a{x}_n+\mu ,\hfill & & x_n\le 0\hfill \\ b{x}_n+\mu +\ell ,\hfill & & x_n>0\hfill \end{array}\right.$$

(1)

Figure 1 illustrates the map (1), with $a,b\in (0,1)$, $\ell >0$ and $-l<\mu <0$.

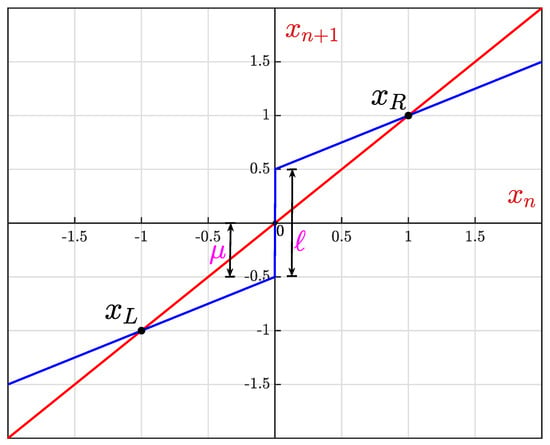
Figure 1. General one-dimensional map with $a,b\in (0,1)$, positive ℓ and $-\ell <\mu ⩽0$.

Here, ‘a’, ‘b’ and ‘$\mu$’ are parameters, whlie jump discontinuity is denoted by ‘ℓ’. The map has $\mathcal{L}:=(-\infty ,0]$ (the closed left half plane) and $\mathcal{R}:=(0,\infty )$ (the open right half plane). Given a particular sequence of points ${\left\{x_n\right\}}_{n\ge 0}$ through which the system evolves, one can convert this into a sequence of $\mathcal{L}s$ and $\mathcal{R}s$ by indicating which of the two sets ($\mathcal{L}$ or $\mathcal{R}$) the each point belongs to. Clearly, a periodic orbit corresponds to a string $\mathcal{L}s$ and $\mathcal{R}s$ that repeats indefinitely. We call this repeating string, a pattern, and denote it by $\sigma$. The length of the string $\sigma$ is denoted by $\left|\sigma \right|$ and gives the number of symbols in the pattern, i.e., the period of the orbit. ${\mathcal{P}}_{\sigma }$ denotes the interval of the parameter $\mu$ for which pattern $\sigma$ exists. We denote the sum of geometric series $1+k+k^2+\dots +k^n$ by $S_n^k$. The basic notions of 1-D PWS map are discussed in the literature [20,43].

The parameters ‘a’ and ‘b’ can take either positive or negative values, and they divide the $ab$-plane into four quadrants, as depicted in Figure 2 and characterized in [22]. Stable–unstable periodic orbits and chaotic orbits are discussed in detail for quadrants for which a and b are both positive values [20,21]. Results based on different parameter values are illustrated in [44], where it is shown that the dynamics of the attractor and Poincaré rotation on the unit circle behave alike. Furthermore, conditions on the parameters are obtained that exhibit the topological attractor. In this work, we make an attempt to investigate all possible orbits and characterize the map for the quadrant in which both parameters have negative values. The quadrant III is again subdivided into four regions and three boundary cases, based on values of a and b as follows. For region P, $a,b\in (0,-1)$, region Q takes $a,b\in (-\infty ,-1)$. Previous work has shown that regions R and S are equivalent, where one parameter belongs to $(0,-1)$ and the other is less than $-1$ and vice versa. The boundaries $PR(a=-1,b\in (0,-1\left)\right)$, $QR(a\in (-\infty ,-1),b=-1)$ and boundary point $O(a=b=-1)$ are analyzed in this work.

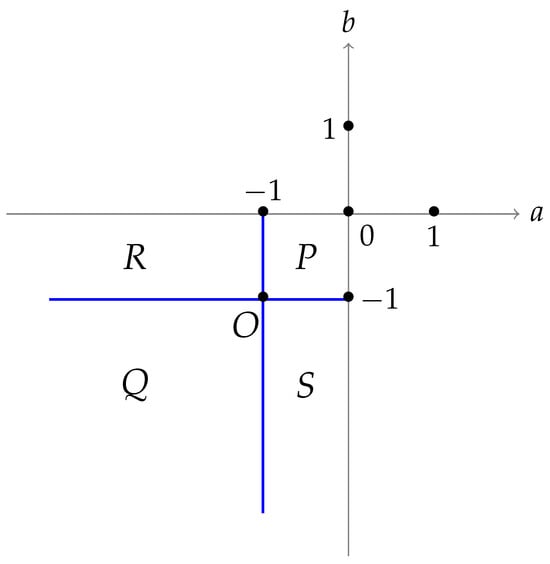
Figure 2. The parameter $ab$-plane with four quadrants.

3. Region $\mathit{P}$ $(\mathit{a},\mathit{b}\in (-\mathbf{1},\mathbf{0}\left)\right)$

In this region, the parameters a and b both are in the range of $(-1,0)$, so the slope of the map is always less than 1. For this region, we show that a stable period-2 orbit coexists with a stable fixed point. All the possible scenarios with positive ℓ and $\mu$ are depicted in Figure 3.

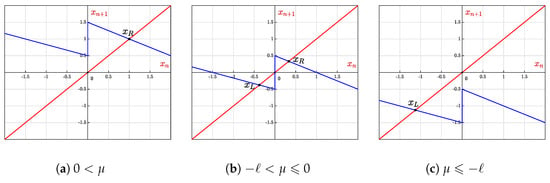
Figure 3. Graph of map for $a,b\in (-1,0)$ and $\ell >0$.

Let us begin by assuming $\ell >0$ in map (1). Three scenarios are illustrated, as shown in Figure 3.

3.1. Scenario $P.1$: $(\ell >0,\mu >0)$

For $\mu >0$, from the map it is clear that there exists a stable fixed point in the right-half plane. The location of the fixed point can be obtained from map (1) as,

$$x_R={\displaystyle \frac{\mu +\ell }{1-b}}$$

It is observed in Figure 3a. In this scenario, every point in $\mathcal{L}$ will immediately move to $\mathcal{R}$ under the action of map (1); furthermore, every point in $\mathcal{R}$ will eventually move towards $x_R$. Therefore, any point $x\in (-\infty ,+\infty )$ will converge to $x_R$. Thus, $x_R$ is a global attractor.

3.2. Scenario $P.2$: $(\ell >0,\mu ⩽-\ell )$

When $\mu ⩽-\ell$, there exists one stable fixed point in the left half-plane as shown in Figure 3b, given by,

$$x_L={\displaystyle \frac{\mu }{1-a}}$$

This is also a global attractor.

3.3. Scenario $P.3$: $(\ell >0,-\ell <\mu ⩽0)$

For $-\ell <\mu ⩽0$, there are two stable fixed points on either side of the discontinuity, as shown in Figure 3c. The basin of attraction (BoA) for these two fixed points is shown in Figure 4a. The region of convergence for $x_L$ when $x_0⩽0$ is given by ranges:

$$\begin{array}{c}\hfill \left[-{\displaystyle \frac{\mu }{a}}-{\displaystyle \frac{\mu +\ell }{ab}}\left(1-\sum _{k=1}^N{\displaystyle \frac{1}{a^k{b}^k}}+\sum _{k=1}^{N-1}{\displaystyle \frac{1}{a^k{b}^k}}\right)\right.,\\ \hfill \left.-{\displaystyle \frac{\mu }{a}}-{\displaystyle \frac{\mu +\ell }{ab}}\left(1-\sum _{k=1}^{N-1}{\displaystyle \frac{1}{a^k{b}^k}}+\sum _{k=1}^{N-1}{\displaystyle \frac{1}{a^k{b}^k}}\right)\right]\end{array}$$

and $\left[-{\displaystyle \frac{\mu }{a}},0\right]$.

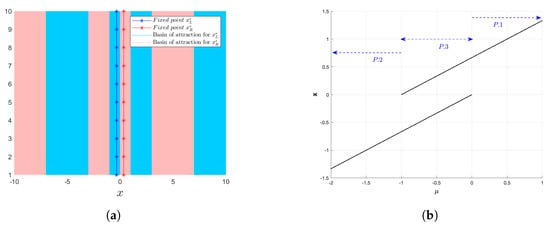
Figure 4. Basin of attraction of region $P.3$ and bifurcation diagram for region $P(a,b\in (-1,0\left)\right)$. (a) With $\ell =1$, $\mu =-{\displaystyle \frac{1}{2}}$, $a=b=-{\displaystyle \frac{1}{2}}$, $x_L$ at $-{\displaystyle \frac{1}{3}}$ and $x_R$ at ${\displaystyle \frac{1}{3}}$. (b) With $\ell =1$ and $a=b=-{\displaystyle \frac{1}{2}}$, and $\mu \in (-2,1)$.

For $x_0>0$ the range for BoA is given as,

$$\begin{array}{c}\hfill \left[-{\displaystyle \frac{\mu +\ell }{b}}\left(1-\sum _{k=1}^{N-1}{\displaystyle \frac{1}{a^k{b}^{k-1}}}+\sum _{k=1}^{N-1}{\displaystyle \frac{1}{a^k{b}^k}}\right)\right.,\\ \hfill \left.-{\displaystyle \frac{\mu +\ell }{b}}\left(1-\sum _{k=1}^N{\displaystyle \frac{1}{a^k{b}^{k-1}}}+\sum _{k=1}^{N-1}{\displaystyle \frac{1}{a^k{b}^k}}\right)\right]\end{array}$$

Consequently, any $x_0$ other than the above range will attract towards $x_R$. Therefore, there is no possibility of orbits.

Figure 4b shows the bifurcation diagram for scenarios 1, 2 and 3 of region P. The preliminary investigation is validated by this diagram. From the above discussion, it is clear that there is no possibility of periodic orbits in any of the three scenarios.

Now, consider a negative length of discontinuity, $\ell <0$, and the corresponding maps are shown in Figure 5.

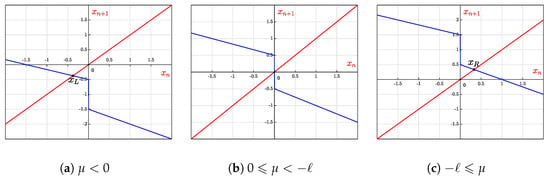
Figure 5. Graph of map for $a,b\in (0,-1)$ and $\ell <0$.

3.4. Scenario $P.4$: $(\ell <0,\mu <0)$

When $\mu <0$, there exists a stable fixed point in the left half-plane for $x_0\in (-{\displaystyle \frac{\mu }{a}},0)$ that exhibits periodic orbits except for this range. The range of these periodic cycles is computed as follows:

$$\left({\displaystyle \frac{(b+1)\mu +\ell }{1-ab}},a{\displaystyle \frac{(b+1)\mu +\ell }{1-ab}}+\mu \right)$$

(2)

3.5. Scenario $P.5$: $(\ell <0,-\ell ⩽\mu )$

For $-\ell ⩽\mu$, there exists one stable fixed point in the right half-plane for $x_0\in (0,-{\displaystyle \frac{\mu +\ell }{b}})$ and periodic orbits are present with the range given by (2) elsewhere.

3.6. Scenario $P.6$: $(\ell <0,0⩽\mu <-\ell )$

For $0⩽\mu <-\ell$, there are no fixed points, but this case is significant in characterizing and analyzing the systems.

The scenario with no fixed points (scenario $P.6$) is analyzed as it is considered the most interesting among the six scenarios listed above, given that it contains no fixed point.

3.7. Analysis

In this section, we show that periodic orbits of any period $n\ge 2$ exist. Furthermore, we provide a complete characterization of these orbits with respect to distinct patterns that they exhibit and their ranges of existence. Orbits of period-n can have various distinct patterns of length n. The paper [20] demonstrated the same using a different approach that only requires the application of map (1). For scenario $P.6$, the cobweb plot shows that any point in the space will repeat and form a periodic orbit as shown in Figure 6.

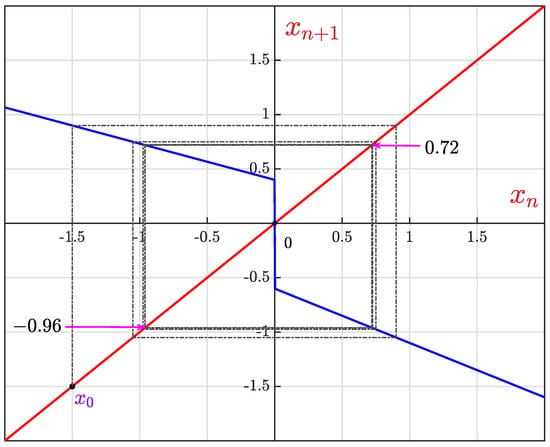
Figure 6. Cobweb plot for scenario $P.6$.

Lemma 1.

In scenario P.6, no admissible pattern other than period-2 orbit exists, i.e., $\mathcal{L}$$\mathcal{R}$ is the only admissible pattern for $0⩽\mu <-\ell$ in region P.

Proof. 

Let us start assuming that the pattern is $\mathcal{L}$$\mathcal{R}$. Using map (1), the inequalities are

$$\begin{array}{ccc}\hfill x_0& ⩽& 0\hfill \\ \hfill x_1& =& a{x}_0+\mu \hfill \\ \hfill x_2=x_0& =& b{x}_1+\mu +\ell \hfill \\ \hfill \mathrm{Simplifying}\mathrm{for}{x}_0\\ \hfill x_0⩽0& \Rightarrow & {\displaystyle \frac{(b+1)\mu +\ell }{1-ab}}\le 0\hfill \\ \hfill \mathrm{gives}\mu & ⩽& {\displaystyle \frac{-\ell }{b+1}}\hfill \end{array}$$

Considering $\ell =-1$ without loss of generality, this gives ${\mu }^{upper}$ as

$$\mu ⩽{\displaystyle \frac{1}{b+1}}$$

Similarly, putting $x_0$ in $x_1$, gives ${\mu }^{lower}$

$$\mu >{\displaystyle \frac{a}{a+1}}$$

Thus, the range of existence is,

$${\mathcal{P}}_{\supset }=\left({\displaystyle \frac{a}{a+1}},{\displaystyle \frac{1}{b+1}}\right]$$

(3)

To show that this pattern is admissible,

$${\mathcal{P}}_{\supset }\ne \varphi \mathrm{i}.\mathrm{e}.,{\displaystyle \frac{a}{a+1}}<{\displaystyle \frac{1}{b+1}}.$$

Cross multiplying and simplifying, we get $1-ab>0$ This is true $\forall a,b\in (-1,0)$. The same is verified from the cobweb plot shown in Figure 6. On the contrary, a pattern other than $\mathcal{L}$$\mathcal{R}$ gives ${\mathcal{P}}_{\supset }$$=\varphi$. □

Corollary 1.

For map (1), with $a,b\in (-1,0),\ell <0,0⩽\mu <-\ell$, the interval

$$\mathcal{I}=\left\{x:(\mu +\ell )⩽x_n⩽\mu \right\}$$

is not invariant.

Proof. 

From Lemma 1, it is proved that $\mathcal{L}$$\mathcal{R}$ orbit is the only admissible pattern in scenario $P.6$. Any $0<x_0⩽\mu$, we have

$$\begin{array}{ccc}\hfill x_1=& b{x}_0+\mu +\ell & ⩽0\Rightarrow x_1<(\mu +\ell )\hfill \\ \hfill x_2=& a{x}_1+\mu & >0\Rightarrow x_2⩾\mu \hfill \end{array}$$

Similarly, it is calculated that, for $(\mu +\ell )⩽x_0<0$, we get $x_1⩾\mu$ and $x_2<(\mu +\ell )$. Therefore, the interval $\mathcal{I}=\left\{x:(\mu +\ell )⩽x_n⩽\mu \right\}$ is not invariant or any $x_0\in (\mu +\ell ,\mu )$ repelled this interval and forms a period-2 orbit with repeating points at

$$\left({\displaystyle \frac{(b+1)\mu +\ell }{1-ab}},a{\displaystyle \frac{(b+1)\mu +\ell }{1-ab}}+\mu \right)$$

Thus, the corollary is proved. □

Example 1.

For $a=-{\displaystyle \frac{1}{3}},b=-{\displaystyle \frac{1}{2}},\mu ={\displaystyle \frac{2}{5}}\&\ell =-1$, then $(x_0,x_1)=(0.72,-0.96)$ and $(-0.96,0.72)$ periodic orbit points shown in Figure 6.

Lemma 2.

In scenarios $P.4$ and $P.5$, an admissible pattern contains a period-2 orbit and a fixed point that coexist.

Proof. 

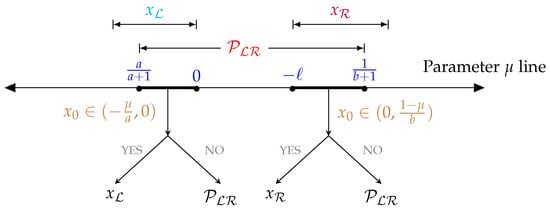
In scenario $P.4$, range of $\mu$ for a fixed point is ${\mathcal{P}}_{\mathcal{L}}=\left(-\infty ,0\right]$ as $x_L$ and $\mu$ has to be less than 0. In scenario $P.5$, range of $\mu$ for a fixed point is ${\mathcal{P}}_{\mathcal{R}}=\left(0,\infty \right]$ as $x_R$ has to be greater than 0 and $\mu >1$. In scenario $P.6$, ${\mathcal{P}}_{\mathcal{LR}}=\left({\displaystyle \frac{a}{1+a}},{\displaystyle \frac{1}{1+b}}\right]$ when ${\displaystyle \frac{a}{1+a}}<0$ and ${\displaystyle \frac{1}{1+b}}>1$. This is a non-empty intersection of the range of $\mu$, illustrated in Figure 7. □

Figure 7. Range of existence for periodic orbit and stable fixed points corresponding to pattern $\mathcal{L}$$\mathcal{R}$ and $x_{\mathcal{L}}$ or $x_{\mathcal{R}}$ the parameter line $\mu$ when they are overlapping.

Example 2.

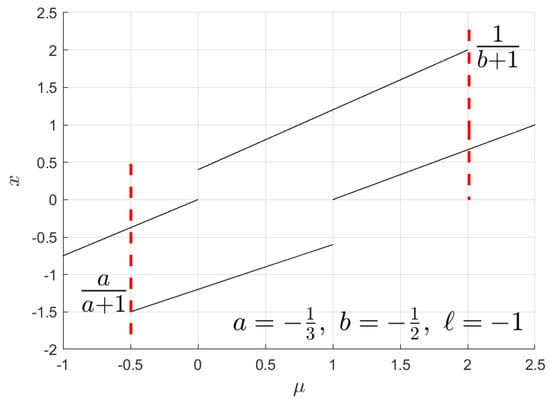
For $a=-{\displaystyle \frac{1}{3}},b=-{\displaystyle \frac{1}{2}}\&\ell =-1$ gives ${\mathcal{P}}_{\mathcal{LR}}=\left(-0.5,2\right]$. The corresponding plot is shown in Figure 8.

Figure 8. Intersection of range of $\mu$ in $P.4$ to $P.6$ cases.

4. Boundary Point $\mathit{O}$ $(\mathit{a}=\mathit{b}=-\mathbf{1})$

This is a very special case, as it is the boundary point for all regions and lines.

In this case, $a=b=-1$ and three scenarios are observed for each with $\ell >0$ and $\ell <0$.

4.1. Scenario $O.1$: $(\ell >0,\mu >0)$

For $\mu >0$, from the map it is clear that there exists a stable fixed point in the right-half plane. The location of the fixed point can be obtained from map (1) as

$$x_R={\displaystyle \frac{\mu +\ell }{1-b}}$$

It is a stable attractor, only for points ${\displaystyle \frac{\mu +\ell }{2}}\pm \mathbb{W}\ell$, where $\mathbb{W}$ is a whole number, and the remaining points form orbits of period-2 of type $\mathcal{R}$$\mathcal{R}$.

4.2. Scenario $O.2$: $(\ell >0,\mu ⩽-\ell )$

For $\mu ⩽-\ell$, one stable fixed point in the left half-plane given by $x_L={\displaystyle \frac{\mu }{1-a}}={\displaystyle \frac{\mu }{2}}$ is present and is a stable attractor, only for points ${\displaystyle \frac{\mu }{2}}\pm \mathbb{W}\ell$. All other initial points form period-2 orbits of type $\mathcal{L}$$\mathcal{L}$.

4.3. Scenario $O.3$: $(\ell >0,-\ell <\mu ⩽0)$

For $-\ell <\mu ⩽0$, there exist two stable fixed points on either side of the discontinuity, as shown in Figure 9. Fixed points $x_L$ and $x_R$ are stable attractor only for points $\left({\displaystyle \frac{\mu +\ell }{2}}\pm \mathbb{W}\ell \right)$ and $\left({\displaystyle \frac{\mu }{2}}\pm \mathbb{W}\ell \right)$, respectively.

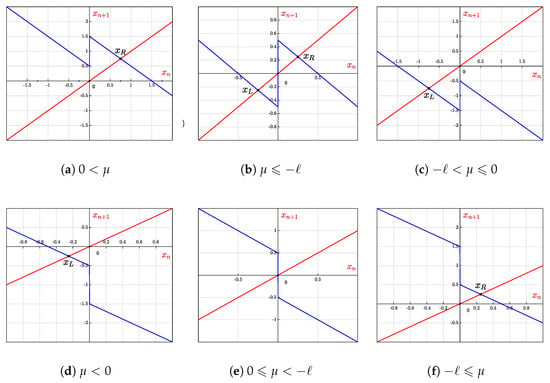
Figure 9. Graph of map for boundary point O, i.e., $a=b=-1$ for $\ell >0$ and $\ell <0$.

4.4. Scenario $O.4$: $(\ell <0,\mu <0)$

For $\mu <0$, there exists a stable fixed point $x_L$ and points $x_0\in \left[\mu ,0\right]$, form period-2 $\mathcal{L}$$\mathcal{L}$ orbit. All other points move away and form unstable orbits.

4.5. Scenario $O.5$: $(\ell <0,0⩽\mu <-\ell )$

For $0⩽\mu <-\ell$, there are no fixed points, and any initial point diverges to $\pm \infty$.

4.6. Scenario $O.6$: $(\ell <0,-\ell ⩽\mu )$

For $-\ell ⩽\mu$, there exists a stable fixed point $x_R$ and points in $x_0\in (0,(\mu +\ell ))$ form $\mathcal{R}$$\mathcal{R}$ periodic orbit, and all other points except for this range lead to instability.

4.7. Analysis

For $a=b=-1$

$$\begin{array}{c}\hfill x_{n+1}=\left\{\begin{array}{cccc}a{x}_n+\mu \hfill & =-x_n+\mu \hfill & \mathrm{for}& x_n⩽0\hfill \\ b{x}_n+\mu +\ell \hfill & =-x_n+\mu +\ell \hfill & \mathrm{for}& x_n>0\hfill \end{array}\right.\end{array}$$

(4)

4.7.1. $O.1:a=-1,b=-1,\mu >0,\ell >0$

Proposition 1.

The boundary point O with a positive length of discontinuity; only $\mathcal{R}$$\mathcal{R}$ orbits are admissible when $\mu >0$.

Proof. 

With both $\ell \&\mu$ positive, there exists a fixed point in $\mathcal{R}$ given by $x_R={\displaystyle \frac{\mu +\ell }{1-b}}$, for $b=-1$, $x_R={\displaystyle \frac{\mu +\ell }{2}}$.

Since the magnitudes of slopes of a and b are equal to 1, any $x_0\in \left(-\infty ,\infty \right)$ keeps oscillating around the $x_R$. A detailed analysis is given below considering all possible $x_0$ ranges in accordance with $\mu \&\ell$.

Orbits for Different Initial Conditions

Using map (4), the following analysis is carried out,

$\mathrm{For}-\ell ⩽x_0<0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell >0\hfill \\ \hfill x_3& =& -x_2+\mu +\ell =-x_0+\mu =x_1>0\hfill \\ \hfill x_4& =& -x_3+\mu +\ell =x_0+\ell =x_2>0\hfill \end{array}$$

This condition illustrates that $x_1$ and $x_2$ repeat alternately, forming a period-2 orbit. Furthermore, the repeating points of these $\mathcal{R}$$\mathcal{R}$ orbits are $(x_0+\ell ,-x_0+\mu )$. This is illustrated in Figure 10 with initial condition $x_{0_1}=-0.4$ with a black color plot and $\mathcal{R}$$\mathcal{R}$ orbit settles at points $(0.6,1)$.

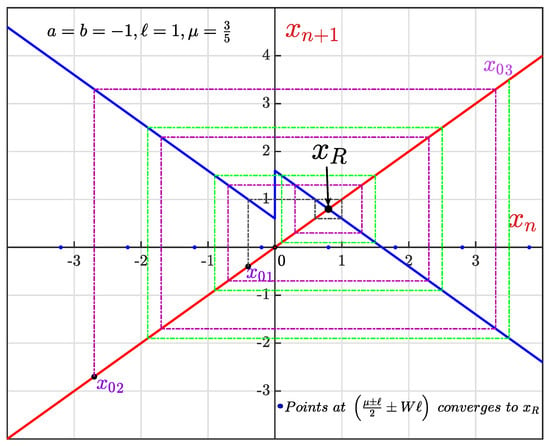
Figure 10. Cobweb plot for $\mu >0\&\ell >0$ with different initial conditions.

$\mathrm{For}{x}_0<-\ell$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell <0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on}& \mathrm{with}\mathcal{L}\mathcal{R}\mathrm{pattern}\mathrm{till}0<x_n<(\mu +\ell )\hfill \\ \hfill x_{n+1}& =& -x_n+\mu +\ell >0\hfill \\ \hfill x_{n+2}& =& -x_{n+1}+\mu +\ell =x_n>0\hfill \\ \hfill x_{n+3}& =& -x_{n+2}+\mu +\ell =-x_n+\mu +\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on}& \hfill \\ & \mathrm{with}& \mathcal{R}\mathcal{R}\mathrm{pattern}\mathrm{with}\mathrm{points}(-x_n+\mu +\ell ,x_n).\hfill \end{array}$$

This case is represented by a magenta color line in Figure 10, where $x_{0_2}=-2.7$ and $x_n=1.3$, so repeating points are at $(0.3,1.3)$.

$\mathrm{For}{x}_0>0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell <0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0-\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on}& \mathrm{with}\mathcal{L}\mathcal{R}\mathrm{pattern}\mathrm{till}0<x_n⩽(\mu +\ell )\hfill \\ \hfill x_{n+1}& =& -x_n+\mu +\ell >0\hfill \\ \hfill x_{n+2}& =& -x_{n+1}+\mu +\ell =x_n>0\hfill \\ \hfill x_{n+3}& =& -x_{n+2}+\mu +\ell =-x_n+\mu +\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on}& \hfill \\ & \mathrm{with}& \mathcal{R}\mathcal{R}\mathrm{orbit}\mathrm{fixed}\mathrm{points}(-x_n+\mu +\ell ,x_n).\hfill \end{array}$$

The green color lines shown in Figure 10 elaborate this case, where $x_{0_3}=3.5$, then $x_n=1.5$ and the period-2 orbit is formed at $(0.1,1.5)$.

Number of Iterations

The number of iterations or steps required to go into periodic orbit $\mathcal{R}$$\mathcal{R}$ is calculated as follows, for $a=b=-1,\ell >0,\mu \in (0,\infty )$:

$\mathrm{For}{x}_0\le 0$

Consider $x_0\in \left(-n\ell ,-(n-1)\ell \right]$, where $n\in \mathbb{N}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell <0\hfill \\ \hfill x_3& =& -x_2+\mu =-x_0-\ell +\mu >0\hfill \\ \hfill x_4& =& -x_3+\mu +\ell =x_0+2\ell <0\hfill \\ \hfill x_5& =& -x_4+\mu =-x_0-2\ell +\mu >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction}\mathrm{we}\mathrm{can}\mathrm{write}\hfill \\ \hfill x_{2n-1}& =& -x_0-(n-1)\ell +\mu >0\hfill \\ \hfill x_{2n}& =& -x_0+n\ell >0(\because x_0<n\ell )\hfill \\ \hfill x_{2n+1}& =& -x_0-(n-1)\ell +\mu >0\hfill \end{array}$$

Here, it is a period-2 orbit of type $\mathcal{R}$$\mathcal{R}$ with fixed points at

$$(x_0+n\ell ,-x_0+\mu -(n-1)\ell )$$

and it takes $2n$ steps to become periodic. In the aforementioned examples $x_{0_1}=-0.4\Rightarrow n=1$ and $x_{0_2}=-2.7\Rightarrow n=3$ takes 2^nd and 6^th steps, respectively, to enter the $\mathcal{R}$$\mathcal{R}$ orbit.

$\mathrm{For}{x}_0>0$

Consider $x_0\in \left((n-1)\ell +\mu ,n\ell +\mu \right]$, where $n\in \mathbb{N}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell <0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0-\ell >0\hfill \\ \hfill x_3& =& -x_2+\mu +\ell =-x_0+\mu +2\ell <0\hfill \\ \hfill x_4& =& -x_3+\mu =x_0-2\ell >0\hfill \\ \hfill x_5& =& -x_4+\mu +\ell =-x_0+\mu +3\ell <0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction}\mathrm{we}\mathrm{can}\mathrm{write}\hfill \\ \hfill x_{2n-3}& =& <0\hfill \\ \hfill x_{2n-2}& =& x_0-(n-1)\ell >0\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu +n\ell >0(\because x_0<(\mu +n\ell ))\hfill \\ \hfill x_{2n}& =& x_0-(n-1)\ell >0\hfill \end{array}$$

Thus, it is a period-2 orbit of type $\mathcal{R}$$\mathcal{R}$ with fixed points at

$$(x_0-(n-1)\ell ,-x_0+\mu +n\ell )$$

and it becomes periodic after $(2n-2)$ iterations. For $x_{0_3}=3.2\Rightarrow n=3$ it becomes periodic after 4th iteration i.e., 5th iteration is in periodic orbit. □

4.7.2. $O.2:a=-1,b=-1,\mu ⩽-\ell ,\ell >0$

Proposition 2.

In boundary point O with $\ell >0$ and $\mu ⩽-\ell$, only $\mathcal{L}$$\mathcal{L}$ orbits exists.

Proof. 

The fixed point in this scenario ($\ell >0,\mu ⩽-\ell$) is $x_L={\displaystyle \frac{\mu }{1-a}}$ for $a=-1$, $x_L={\displaystyle \frac{\mu }{2}}$. Similar to the proof of Proposition 1, any $x_0\in \left(-\infty ,\infty \right)$ will form a period-2 orbit with both periodic points being negative, forming $\mathcal{L}$$\mathcal{L}$ orbit. For different $x_0$, the detailed analysis, including the number of iterations required to go into $\mathcal{L}$$\mathcal{L}$ orbit, is illustrated below.

Orbits for Different Initial Conditions

Using (4) for the following analysis,

$\mathrm{For}\mu <x_0<0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu ⩽0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0⩽0\hfill \end{array}$$

For this condition, there will be always a period-2 $\mathcal{L}$$\mathcal{L}$ orbit with fixed points at $(x_0,-x_0+\mu )$ that is in periodic orbit from the initial step. An initial condition $x_{0_1}=-0.5$ and the evolution of its path are depicted in Figure 11 with a black color plot. $\mathrm{For}{x}_0<\mu$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell ⩽0\hfill \\ \hfill x_3& =& -x_2+\mu =-x_0-\ell +\mu >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{with}\mathcal{L}\mathcal{R}\mathrm{pattern}\mathrm{till}\mu <x_n<0\hfill \\ \hfill x_{n+1}& =& -x_n+\mu <0\hfill \\ \hfill x_{n+2}& =& -x_n<0\hfill \end{array}$$

So on, with periodic orbit $\mathcal{L}$$\mathcal{L}$, and fixed points are at $(x_n,-x_n+\mu )$. This scenario is illustrated with an example as $x_{0_2}=-2.5$ and the corresponding plot is shown in the magenta color in Figure 11.

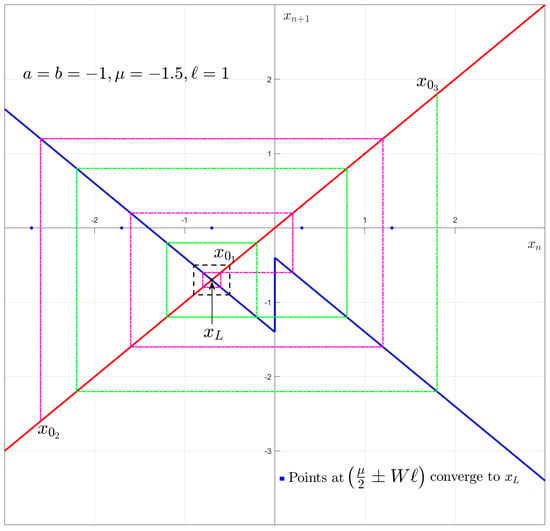
Figure 11. Cobweb plot for $\mu ⩽-\ell \&\ell >0$ with different initial conditions.

$\mathrm{For}{x}_0>0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell <0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0-\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on}& \mathrm{with}\mathcal{L}\mathcal{R}\mathrm{pattern}\mathrm{till}{x}_{n-1}<\left(\mu \right)\hfill \\ \hfill x_n& =& -x_{n-1}+\mu <0\hfill \\ \hfill x_{n+1}& =& -x_n+\mu =x_{n-1}<0\hfill \\ & \mathrm{so}\mathrm{on}& \hfill \\ & \mathrm{with}& \mathcal{L}\mathcal{L}\mathrm{orbit}\mathrm{fixed}\mathrm{points}(x_{n-1},-x_{n-1}+\mu ).\hfill \end{array}$$

This case is shown in Figure 11 with a green color plot, where $x_{0_3}=1.8$.

Number of Iterations

The number of iterations or steps required to go into periodic orbit $\mathcal{R}$$\mathcal{R}$ is calculated as follows for $a=b=-1,\ell >0,\mu \in (0,\infty )$:

$\mathrm{For}{x}_0⩽0$

Consider, $x_0\in \left[-n\ell +\mu ,-(n-1)\ell +\mu \right)$, where $n\in \mathbb{W}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell <0\hfill \\ \hfill x_3& =& -x_2+\mu =-x_0+\mu -\ell >0\hfill \\ \hfill x_4& =& -x_3+\mu +\ell =x_0+2\ell <0\hfill \\ \hfill x_5& =& -x_4+\mu =-x_0+\mu -2\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction},\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu -(n-1)\ell >0\hfill \\ \hfill x_{2n}& =& x_0+n\ell <0\hfill \\ \hfill x_{2n+1}& =& -x_0+\mu -n\ell <0(\because -x_0<n\ell -\mu )\hfill \\ \hfill x_{2n+2}& =& x_0+n\ell <0\hfill \end{array}$$

Thus, there is a period-2 $\mathcal{L}$$\mathcal{L}$ orbit with fixed points at $(x_0+n\ell ,-x_0+\mu -n\ell )$; after $2n$ iterations it becomes periodic. Applying this to $x_{0_1}=-0.5$ and $x_{0_2}=-2.5$, the map dynamics goes into periodicity after 0th and 4th iterations, respectively.

$\mathrm{For}{x}_0>0$

Consider, $x_0\in \left[(n-1)\ell ,n\ell \right)$, where $n\in \mathbb{N}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell <0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0-\ell >0\hfill \\ \hfill x_3& =& -x_2+\mu +\ell =-x_0+\mu +2\ell <0\hfill \\ \hfill x_4& =& -x_3+\mu =x_0-2\ell >0\hfill \\ \hfill x_5& =& -x_4+\mu +\ell =-x_0+\mu +3\ell <0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction}\mathrm{we}\mathrm{can}\mathrm{write}\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu +n\ell <0\hfill \\ \hfill x_{2n}& =& x_0-n\ell <0(\because x_0<n\ell )\hfill \end{array}$$

Thus, a period-2 orbit of type $\mathcal{L}$$\mathcal{L}$ exists with fixed points at $(x_0-n\ell ,-x_0+\mu +n\ell )$ and it becomes periodic after $(2n-1)$ iterations. For $x_{0_3}=1.8$, $n=2$, so after 3rd iteration it goes into $\mathcal{L}$$\mathcal{L}$ orbit. □

4.7.3. $O.3:a=-1,b=-1,-\ell <\mu ⩽0,\ell >0$

Proposition 3.

The boundary point O with $\ell >0$ and $-\ell <\mu ⩽0$ exhibits $\mathcal{L}$$\mathcal{L}$ as well as $\mathcal{R}$$\mathcal{R}$ orbits.

Proof. 

The map (4) has two fixed points $(x_L,x_R)$ with the conditions of $\ell >0$ and $-\ell <\mu ⩽0$. Here, for any $x_0$ based on Propositions 1 & 2, only either $\mathcal{L}$$\mathcal{L}$ or $\mathcal{R}$$\mathcal{R}$ orbits are possible and are proved in the below analysis.

Orbits and Number of Iterations

Map (4) is used for the following analysis,

$\mathrm{For}{x}_0⩽0$:

Consider, $x_0\in \left[-n\ell +\mu ,-(n-1)\ell +\mu \right)$, where $n\in \mathbb{N}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell <0\hfill \\ \hfill x_3& =& -x_2+\mu =-x_0+\mu -\ell >0\hfill \\ \hfill x_4& =& -x_3+\mu +\ell =x_0+2\ell <0\hfill \\ \hfill x_5& =& -x_4+\mu =-x_0+\mu -2\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction},\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu -(n-1)\ell >0\hfill \\ \hfill x_{2n}& =& x_0+n\ell \hfill \end{array}$$

1.

Now, if $x_{2n}=x_0+n\ell >0$, then

$x_{2n+1}=-x_0+\mu -(n-1)\ell >0$

Thus, forming periodic orbit $\mathcal{R}$$\mathcal{R}$ with fixed points at

$$(-x_0+\mu -(n-1)\ell ,x_0+n\ell )$$

it becomes periodic after $(2n-1)$ steps. For example, $x_{0_2}=-1.6$ gives $n=2$ and goes into $\mathcal{R}$$\mathcal{R}$ orbit after three iterations.

2.

Now, if $x_{2n}=x_0+n\ell ⩽0$, then

$x_{2n+1}=-x_0+\mu -n\ell <0(\because -x_0<(n\ell -\mu ))$ and

$x_{2n+2}=x_0+n\ell$.

Thus, it forms a $\mathcal{L}$$\mathcal{L}$ periodic orbit with fixed points at

$$(x_0+n\ell ,-x_0+\mu +n\ell )$$

and it becomes periodic after $2n$ iterations. Consider that $x_{0_1}=-3.4$ gives $n=3$ and forms $\mathcal{L}$$\mathcal{L}$ orbit after six iterations.

These cases are demonstrated in Figure 12.

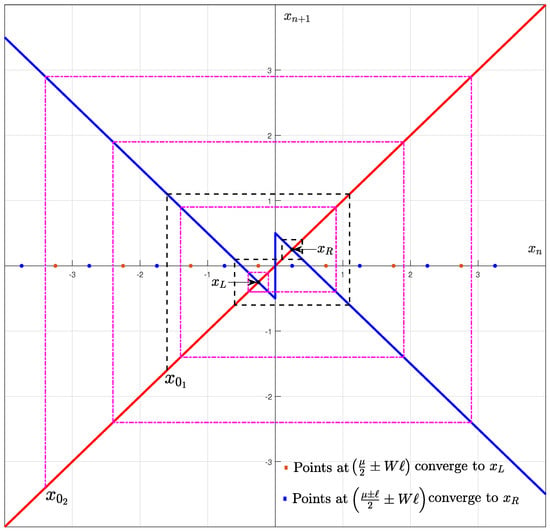
Figure 12. Occurrence of period-2 orbits of type $\mathcal{L}$$\mathcal{L}$ and $\mathcal{R}$$\mathcal{R}$ for different $x_0<0$.

$\mathrm{For}{x}_0>0$:

Consider $x_0\in \left[(n-1)\ell ,n\ell \right)$, where $n\in \mathbb{N}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell <0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0-\ell >0\hfill \\ \hfill x_3& =& -x_2+\mu +\ell =-x_0+\mu +2\ell <0\hfill \\ \hfill x_4& =& -x_3+\mu =x_0-2\ell >0\hfill \\ \hfill x_5& =& -x_4+\mu +\ell =-x_0+\mu +3\ell <0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction},\hfill \\ \hfill x_{2n-2}& =& x_0-(n-1)\ell >0\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu +n\ell \hfill \end{array}$$

1.

Now, if $x_{2n-1}=-x_0+\mu +n\ell >0$, then

$x_{2n}=x_0-(n-1)\ell >0$

Thus. there will be $\mathcal{R}$$\mathcal{R}$ periodic orbit with fixed points at

$$(x_0-(n-1)\ell ,-x_0+\mu +n\ell )$$

and it becomes periodic after $(2n-2)$ steps. Let $x_{0_1}=1.1$, then $n=2$, so it goes into a periodic orbit after two steps.

2.

Now if $x_{2n-1}=-x_0+\mu +n\ell ⩽0$, then

$x_{2n}=x_0-n\ell <0(\because x_0<n\ell )$ and

$x_{2n+1}=-x_0+\mu +n\ell <0$.

Thus, it forms $\mathcal{L}$$\mathcal{L}$ periodic orbit with fixed points at $(-x_0+\mu +n\ell ,x_0-n\ell )$ and it becomes periodic after $(2n-1)$ iterations. Say $x_{0_2}=2.9$, then $n=3$, so it forms $\mathcal{L}$$\mathcal{L}$ orbit after five steps. These cases are shown in the Figure 13.

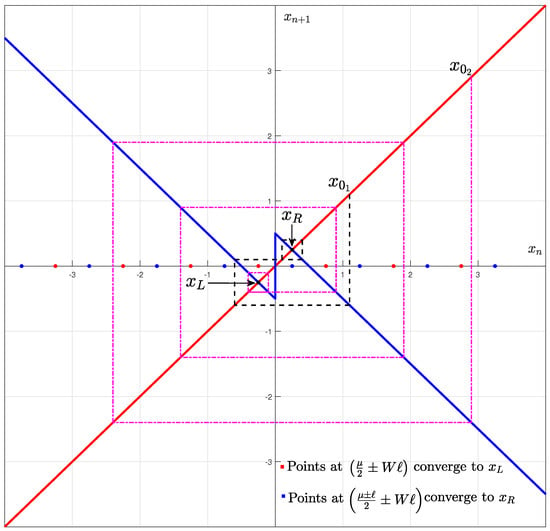Figure 13. Occurrence of period-2 orbits of type $\mathcal{L}$$\mathcal{L}$ and $\mathcal{R}$$\mathcal{R}$ for different $x_0>0$.

□

Lemma 3. 

The only admissible patterns for the boundary point O scenario with positive length of discontinuity (ℓ) are $\mathcal{L}$$\mathcal{L}$ or $\mathcal{R}$$\mathcal{R}$.

Proof. 

The boundary point scenario has a magnitude of both slopes ($a\&b$) equal to one, so for any fixed point ($x_L,x_R$), the map dynamics takes any initial point into oscillatory mode, specifically a period-2 orbit. Based on the values of parameters $\mu \&\ell$, these period-2 oscillations go into $\mathcal{L}$$\mathcal{L}$ or $\mathcal{R}$$\mathcal{R}$ patterns. These period-2 orbits are neither asymptotically stable nor unstable. Hence, this scenario is equivalent to period-2, which is explained in [30] in the boundary point $a=b=1.$ These admissible orbits are proved in Propositions 1–3 by considering all possible variations. □

Lemma 4. 

Under the action of map (4), any initial point moves towards infinity except a certain range of initial conditions depending on μ, when $\ell <0$.

Proof. 

Any fixed point ($x_L,x_R$) under the action of map (4) with $\ell <0$ acts similarly to an unstable fixed point, as both slopes of the map go away from the fixed points. Moreover, there is no common portion of slopes during the next iterations, as can be seen in Figure 9d–f. The detailed analysis and proof for different values of $\mu$ and $x_0$ are discussed below.

4.7.4. $O.4:a=-1,b=-1,\ell <0,\mu <0$

Consider $x_0\in \left[-{\displaystyle \frac{\mu }{a}},0\right]$ i.e., $x_0\in \left[\mu ,0\right]$

$x_1=-x_0+\mu \le 0(\because x_0⩽\mu )$

$x_2=-x_1+\mu =x_0⩽0$

Thus, it forms a period-2 $\mathcal{L}$$\mathcal{L}$ orbit with fixed points at $(x_0,-x_0+\mu )$ and is periodic from the initial step.

Here, except $x_0\in \left[\mu ,0\right]$ all other points are unstable, and it can be shown as:

For $x_0\in (-\infty ,\mu )$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& -x_1+\mu +\ell =x_0+\ell <0\hfill \\ \hfill x_3& =& -x_2+\mu =-x_0+\mu -\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction},\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu -(n-1)\ell >0\hfill \\ \hfill x_{2n}& =& x_0+n\ell <0\hfill \\ \hfill x_{2n+1}& =& -x_0+\mu -n\ell >0\hfill \\ & \mathrm{so}\mathrm{on},\end{array}$$

This $\mathcal{L}$$\mathcal{R}$ sequence continues and the points eventually move to $\pm \infty$ as $n\to \infty$.

For $x_0>0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell <0\hfill \\ \hfill x_2& =& -x_1+\mu =x_0-\ell >0\hfill \\ \hfill x_3& =& -x_2+\mu +\ell =-x_0+\mu +2\ell <0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction}\mathrm{we}\mathrm{write},\hfill \\ \hfill x_{2n-1}& =& -x_0+\mu +n\ell <0\hfill \\ \hfill x_{2n}& =& x_0-n\ell >0\hfill \\ \hfill x_{2n+1}& =& -x_0+\mu -n\ell <0\hfill \end{array}$$

As $n\to \infty$, the points go to $\pm \infty$, leading to instability.

4.7.5. $O.5:a=-1,b=-1,\ell <0,0⩽\mu <-\ell$

Here, any $x_0\in (-\infty ,+\infty )$ forms unstable sequences and under the action of the map, any initial point moves towards infinity.

4.7.6. $O.6:a=-1,b=-1,\ell <0,-\ell ⩽\mu$

Consider $x_0\in \left(0,(\mu +\ell )\right)>0$

$x_1=-x_0+\mu +\ell >0(\because x_0⩽(\mu +\ell ))$

$x_2=-x_1+\mu +\ell =x_0>0$

Thus, it forms a $\mathcal{R}$$\mathcal{R}$ periodic orbit with fixed points as $(x_0,-x_0+\mu +\ell )$ and is periodic from initial iteration.

Here, except for $x_0\in \left(0,(\mu +\ell )\right)>0$, all other points are unstable and can be proved as above. □

5. Boundary Line $\mathit{PR}$: $(\mathit{a}=-\mathbf{1},\mathit{b}\in (-\mathbf{1},\mathbf{0}\left)\right)$

The boundary line case observes three scenarios when $\ell >0.$

5.1. Scenario $PR.1$: $(\ell >0,\mu >0)$

For $\mu >0$, from the map it is clear that there exists a stable fixed point $x_R$, which is a global attractor.

5.2. Scenario $PR.2$: $(\ell >0,\mu ⩽-\ell )$

For $\mu ⩽-\ell$, one stable fixed point in the left half plane and it is given by $x_L={\displaystyle \frac{\mu }{1-a}}$. Which is a global attractor forming periodic orbit-2 of type $\mathcal{L}$$\mathcal{L}$.

5.3. Scenario $PR.3$: $(\ell >0,-\ell <\mu ⩽0)$

For $-\ell <\mu ⩽0$, since two stable fixed points, on either side of the discontinuity as shown in Figure 14. Here, either points attract towards $x_R$ or forms a periodic orbit around $x_L$. For $\ell <0$, following cases are seen:

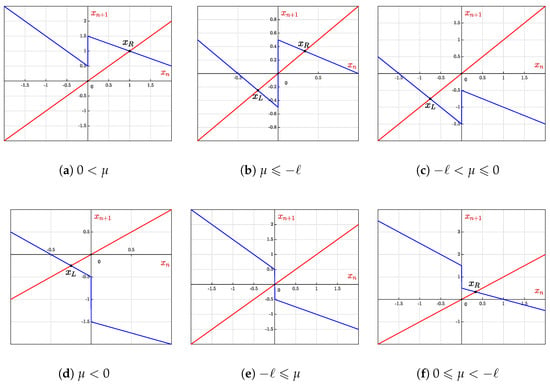
Figure 14. Graph of map for boundary line $PR$, i.e., $a=-1,b\in (-1,0)$ for $\ell >0$ and $\ell <0$.

5.4. Scenario $PR.4$: $(\ell <0,\mu <0)$

For $\mu <0$, there is a stable fixed point $x_L$ that acts as an attractor for $x_0\in [\mu ,0]$, forming a period-2 orbit of type $\mathcal{L}$$\mathcal{L}$, all other points form a periodic orbit $\mathcal{L}$$\mathcal{R}$.

5.5. Scenario $PR.5$: $(\ell <0,-\ell ⩽\mu )$

For $-\ell ⩽\mu$, there exists one stable fixed point $x_R$ which is attractor for $x_0\in \left(0,{\displaystyle \frac{-(\mu -\ell )}{b}}\right)$. Otherwise, there will be a $\mathcal{L}$$\mathcal{R}$ periodic orbit.

5.6. Scenario $PR.6$: $(\ell <0,0⩽\mu <-\ell )$

For $0⩽\mu <-\ell$, there are no fixed points, and a periodic orbit $\mathcal{L}$$\mathcal{R}$ is formed.

5.7. Analysis of Boundary Line $PR$

The analysis of boundary line $PR$ is carried out based on the map, where $a=-1,b\in (-1,0)$

$$\begin{array}{c}\hfill x_{n+1}=\left\{\begin{array}{cccc}a{x}_n+\mu \hfill & =-x_n+\mu \hfill & \mathrm{for}& x_n⩽0\hfill \\ b{x}_n+\mu +\ell \hfill & =b{x}_n+\mu +\ell \hfill & \mathrm{for}& x_n>0\hfill \end{array}\right.\end{array}$$

(5)

5.7.1. $PR.1$

From map (5), for $\mu >0$ and $\ell >0$, it is seen that there exists a stable fixed point $x_R$ in right half plane. As the magnitude of $b<1$, any point on x will attract towards $x_R$, so it is a global attractor.

5.7.2. $PR.2$

In this case, $\ell >0$ and $\mu ⩽-\ell$. There exists a stable fixed point $x_L$ and period-2 orbits around it. The fixed points for this $\mathcal{L}$$\mathcal{L}$ orbit are found as follows:

$\mathrm{For}{x}_0⩽0$. Consider,

$$x_0\in \left(-\sum _{k=1}^n{\left(-{\displaystyle \frac{\ell }{b}}\right)}^k+\mu ,-\sum _{k=1}^{n-1}{\left(-{\displaystyle \frac{\ell }{b}}\right)}^k+\mu \right)$$

where $n\in \mathbb{N}$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_2& =& b{x}_1+\mu +\ell =-b{x}_0+b\mu +\mu +\ell ⩽0\hfill \\ \hfill x_3& =& -x_2+\mu =b{x}_0-b\mu -\ell >0\hfill \\ \hfill x_4& =& b{x}_3+\mu +\ell =b^2{x}_0-b^2\mu +\mu -(b-1)\ell ⩽0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{with}\mathcal{L}\mathcal{R}\mathrm{pattern}\hfill \\ \hfill x_{2n-1}& =& {(-b)}^{n-1}(-x_0+\mu )-\sum _{k=1}^{n-1}{(-b)}^{k-1}\ell >0\hfill \\ \hfill x_{2n}& =& -{(-b)}^n(-x_0+\mu )+\mu +\sum _{k=1}^n{(-b)}^{k-1}\ell ⩽0\hfill \\ \hfill x_{2n+1}& =& {(-b)}^n(-x_0+\mu )-\sum _{k=1}^n{(-b)}^{k-1}\ell ⩽0,\hfill \\ & \mathrm{for},& {(-b)}^n(-x_0+\mu )⩽\sum _{k=1}^n{(-b)}^{k-1}\ell \hfill \end{array}$$

So, with periodic orbit $\mathcal{L}$$\mathcal{L}$ with fixed points as $(x_{2n},x_{2n+1})$, it becomes periodic after $(2n-1)$ iterations.

$\mathrm{For}{x}_0>0$. Consider

$$x_0\in \left(-\sum _{k=1}^n{\left(-{\displaystyle \frac{\ell }{b}}\right)}^k,-\sum _{k=1}^{n-1}{\left(-{\displaystyle \frac{\ell }{b}}\right)}^k\right),\mathrm{where}n\in \mathbb{N}$$

$$\begin{array}{ccc}\hfill x_1& =& b{x}_0+\mu +\ell ⩽0\hfill \\ \hfill x_2& =& -x_1+\mu =-b{x}_0-\ell >0\hfill \\ \hfill x_3& =& b{x}_2+\mu +\ell =-b^2{x}_0+\mu -(b-1)\ell ⩽0\hfill \\ \hfill x_4& =& -x_3+\mu =b^2{x}_0+(b-1)\ell >0\hfill \\ & ⋮& \hfill \\ & \mathrm{so}\mathrm{on},& \mathrm{from}\mathrm{induction}\hfill \\ \hfill x_{2n-1}& =& -{(-b)}^n{x}_0+\mu +\sum _{k=1}^n{(-b)}^{k-1}\ell ⩽0\hfill \\ \hfill x_{2n}& =& {(-b)}^n{x}_0-\sum _{k=1}^n{(-b)}^{k-1}\ell ⩽0,\hfill \\ & \mathrm{for},& {(-b)}^n{x}_0⩽\sum _{k=1}^n{(-b)}^{k-1}\ell \hfill \end{array}$$

Thus, there exists a period-2 orbit of type $\mathcal{L}$$\mathcal{L}$ with points $(x_{2n-1},x_{2n})$; it becomes periodic after $(2n-1)$ steps.

5.7.3. $PR.3$

In this scenario, both $x_L$ and $x_R$ exist. All points $x_0\in (\mu ,0)$ form period-2 orbits around $x_L$ and others either form period-2 orbits or attract towards $x_R$. This can be seen in Figure 15.

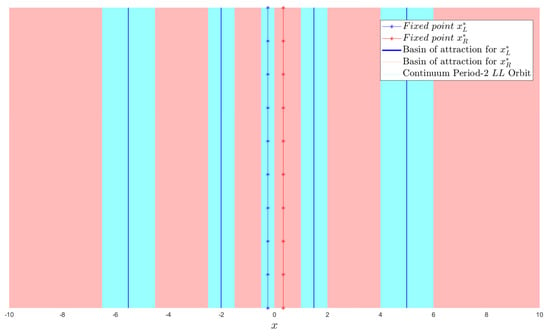
Figure 15. Basin of attraction of boundary line PR with $a=-1,b=-0.5,\ell =1,\mu =-0.5$.

$\mathrm{For}{x}_0⩽0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu +\ell \le 0\mathrm{if}-x_0<-\mu \hfill \\ \hfill \therefore x_{0_{LL}}& =& [\mu ,0]\hfill \\ \hfill \mathrm{if}{x}_1& >& 0,\mathrm{then}\hfill \\ \hfill x_2& =& -x_1+\mu =-b{x}_0+b\mu +\mu +\ell \le 0\hfill \\ & \Rightarrow & x_0\le \mu +{\displaystyle \frac{\mu +\ell }{b}}\hfill \\ \hfill x_3& =& b{x}_0-b\mu -\ell \le 0\mathrm{if}-b{x}_0<(b\mu +\ell )\hfill \\ & \Rightarrow & x_0\le \mu +{\displaystyle \frac{\ell }{b}}\hfill \\ \hfill \therefore x_{0_{LL}}& =& \left(\mu +{\displaystyle \frac{\ell }{b}},\mu +{\displaystyle \frac{\mu +\ell }{b}}\right)\hfill \\ \hfill \mathrm{if}{x}_3& >& 0,\mathrm{then}\hfill \\ \hfill x_4& =& b{x}_3+\mu +\ell =b^2{x}_0-b^2\mu +\mu -(b-1)\ell \le 0\hfill \\ & \Rightarrow & x_0\le \mu +{\displaystyle \frac{\ell }{b}}-{\displaystyle \frac{\mu +\ell }{b^2}}\hfill \\ \hfill x_5& =& -x_4+\mu =-b^2{x}_0+b^2\mu +(b-1)\ell \le 0\hfill \\ & \mathrm{if}& -b^2{x}_0\le -b^2\mu -b\ell +\ell \hfill \\ & \Rightarrow & x_0\le \mu +{\displaystyle \frac{\ell }{b}}-{\displaystyle \frac{\ell }{b^2}}\hfill \\ \hfill \therefore x_{0_{LL}}& =& \left(\mu +{\displaystyle \frac{\ell }{b}}-{\displaystyle \frac{\ell }{b^2}},\mu +{\displaystyle \frac{\ell }{b}}-{\displaystyle \frac{\mu +\ell }{b^2}}\right)\hfill \end{array}$$

from induction, we write a range for a period-2 orbit of type $\mathcal{L}$$\mathcal{L}$ for $x\le 0$,

$$\left(\mu -\sum _{k=1}^n{\displaystyle \frac{\ell }{{(-b)}^k}},\mu -\sum _{k=1}^{n-1}{\displaystyle \frac{\ell }{{(-b)}^k}}-{\displaystyle \frac{(\mu +\ell )}{{(-b)}^n}}\right)(\mu ,0)$$

where $n\in \mathbb{N}$.

All other points except for the above range attract towards $x_R$.

$\mathrm{For}{x}_0>0$

$x_1=b{x}_0+\mu +\ell \le 0$ if $b{x}_0\le -(\mu +\ell )$ $\therefore x_0\le -{\displaystyle \frac{(\mu +\ell )}{b}}$

$x_2=-x_1+\mu =-b{x}_0-\ell \le 0$ if $-b{x}_0\le \ell \therefore x_0\le -{\displaystyle \frac{\ell }{b}}$

Thus,

$$x_{0_{LL}}\in \left(-{\displaystyle \frac{(\mu +\ell )}{b}},-{\displaystyle \frac{\ell }{b}}\right)$$

if $x_2>0$ then,

$x_3=-b^2{x}_0+\mu -(b-1)\ell \le 0\therefore x_0\le {\displaystyle \frac{(\mu +\ell )}{b^2}}-{\displaystyle \frac{\ell }{b}}$

$x_4=b^2{x}_0+(b-1)\ell \le$ if $b^2{x}_0\le -(b-1)\ell \therefore x_0\le {\displaystyle \frac{\ell }{b^2}}-{\displaystyle \frac{\ell }{b}}$

$$\therefore x_{0_{LL}}\in \left({\displaystyle \frac{(\mu +\ell )}{b^2}}-{\displaystyle \frac{\ell }{b}},{\displaystyle \frac{\ell }{b^2}}-{\displaystyle \frac{\ell }{b}}\right)$$

Similar to induction, we write

$$\left({\displaystyle \frac{(\mu +\ell )}{{(-b)}^n}}+\sum _{k=1}^{n-1}{\displaystyle \frac{\ell }{{(-b)}^k}},\sum _{k=1}^n{\displaystyle \frac{\ell }{{(-b)}^k}}\right)$$

where $n\in \mathbb{N}$.

The points other than the above range move towards the stable fixed point $x_R$.

Proposition 4.

Only admissible patterns in the boundary line $PR$ with positive length of discontinuity are fixed point (period-1) and period-2 ($\mathcal{L}$$\mathcal{L}$) solutions.

Proof. 

The boundary line $PR$ has $b\in (-1,0)$, therefore, the fixed point in $\mathcal{R}$ is going to be a stable attractor, which is seen in the above analysis when $\ell >0\&\mu >0$. Thus, any initial point $x_0\in \left(-\infty ,\infty \right)$ attracts to $x_R$, making it a global attractor and exhibiting a fixed point or period-1 solution. However, for $\ell >0,\mu ⩽-\ell$, the fixed point $x_L$ is neither stable nor unstable due to the slope $a=-1$. So, any point $x_0$ keep oscillating around $x_L$ forming orbits of period-2 ($\mathcal{L}$$\mathcal{L}$). Furthermore, when $-\ell <\mu ⩽0$, both $x_L$ and $x_R$ are present; therefore, a certain range of initial points attract towards $x_R$, and the remaining points form $\mathcal{L}$$\mathcal{L}$ orbits. □

5.7.4. $PR.4$

In this case, when $x_0\in [\mu ,0]$ then $x_1=-x_0+\mu \le 0$, forming the period-2 orbit of type $\mathcal{L}$$\mathcal{L}$ with fixed points $(x_0,-x_0+\mu )$.

For all other points, there will be a period-2 $\mathcal{L}$$\mathcal{R}$ orbit as the magnitude of slope is either 1 or less than 1.

$\therefore x_0=x_2=-x_1+\mu =-b{x}_0+b\mu +\mu +\ell ⩽0$

$\therefore x_0={\displaystyle \frac{(b+1)\mu +\ell }{1+b}}⩽0$ and

$x_1=-x_0+\mu =-{\displaystyle \frac{(b+1)\mu +\ell }{1+b}}+\mu >0$. Thus, the fixed points of $\mathcal{L}$$\mathcal{R}$ orbit are:

$$(x_0,x_1)=\left({\displaystyle \frac{(b+1)\mu +\ell }{1+b}},-{\displaystyle \frac{(b+1)\mu +\ell }{1+b}}+\mu \right)$$

Considering $\ell =-1$ without loss of generality,

$x_0={\displaystyle \frac{(b+1)\mu -1}{1+b}}\le 0\Rightarrow \mu ⩽{\displaystyle \frac{1}{1+b}}$.

It can be observed from the bifurcation diagram in Figure 16 that $\mu$ exceeds the range for case $PR.4$ and enters into the range of $\mu$ for cases $PR.5$ and $PR.6$.

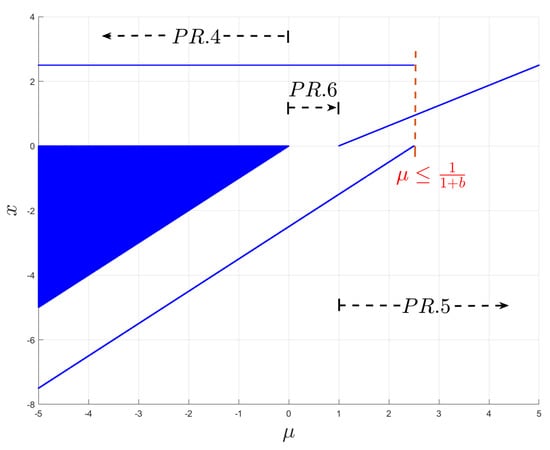
Figure 16. Bifurcation diagram showing scenarios $PR.4,PR.5$ & $PR.6$ with $a=-1,b=-{\displaystyle \frac{3}{5}}\&\ell =-1$.

5.7.5. $PR.5$

In this scenario ($\ell <0,-\ell ⩽\mu$), there is a stable fixed point $x_R$. Moreover, when $\mu ⩽-{\displaystyle \frac{\ell }{1+b}}$, it will have either period-1 or period-2 solutions. The period-1 solution occurs only when $x_0\in \left(0,-{\displaystyle \frac{\mu +\ell }{b}}\right)$, and all other initial points exhibit a period-2 $\mathcal{L}$$\mathcal{R}$ orbit. Furthermore, when $\mu >-{\displaystyle \frac{\ell }{1+b}}$, then any initial point $x_0$ will attract towards the fixed points $x_R$. This is evident in the bifurcation diagram shown in Figure 16.

The $\mathcal{L}$$\mathcal{R}$ orbit periodic points are calculated as follows, when

$$\mu ⩽-{\displaystyle \frac{\ell }{1+b}}\mathrm{and}{x}_0\notin \left(0,-{\displaystyle \frac{\mu +\ell }{b}}\right).$$

$\mathrm{For}{x}_0⩽0$

$$\begin{array}{ccc}\hfill x_1& =& -x_0+\mu >0\hfill \\ \hfill x_0=x_2& =& b{x}_1+\mu +\ell ⩽0\hfill \\ \hfill \therefore x_0& =& -b{x}_0+b\mu +\mu +\ell \hfill \\ \hfill \therefore x_0& =& {\displaystyle \frac{(b+1)\mu +\ell }{(1+b)}}⩽0\hfill \\ \hfill \mathrm{and}{x}_1& =& -x_0+\mu \Rightarrow x_1={\displaystyle \frac{-\ell }{(1+b)}}>0\hfill \end{array}$$

$\mathrm{For}{x}_0⩾{\displaystyle \frac{-(\mu +\ell )}{b}}$

$$\begin{array}{ccc}\hfill x_1& =& b{x}_0+\mu +\ell ⩽0\hfill \\ \hfill x_0=x_2& =& -x_1+\mu >0\hfill \\ \hfill \therefore x_0& =& {\displaystyle \frac{-\ell }{(1+b)}}>0\hfill \\ \hfill \mathrm{and}{x}_1& =& b{x}_0+\mu +\ell \Rightarrow x_1={\displaystyle \frac{(b+1)\mu +\ell }{(1+b)}}⩽0\hfill \end{array}$$

Thus, the fixed points for $\mathcal{L}$$\mathcal{R}$ orbit are

$$\left({\displaystyle \frac{(b+1)\mu +\ell }{(1+b)}},{\displaystyle \frac{-\ell }{(1+b)}}\right)$$

5.7.6. $PR.6$

In this case, there is no fixed point on either side, and the map slope magnitudes are also $⩽1$, so it forms a period-2 $\mathcal{L}$$\mathcal{R}$ orbit with fixed points given by (6).

Proposition 5.

The $PR$ line with negative ℓ exhibits fixed point and period-2 solutions.

Proof. 

The fixed point in $\mathcal{L}$ makes the $x_0\in \left[\mu ,0\right]$ points to oscillate within $\mathcal{L}$ forming $\mathcal{L}$$\mathcal{L}$ orbit and all other points form period-2 ($\mathcal{L}$$\mathcal{R}$) orbit, when $\mu <0$. When $-\ell ⩽\mu$, due to $x_R$ either a fixed point solution or $\mathcal{L}$$\mathcal{R}$ orbit are admissible for different initial points. When $0⩽\mu <-\ell$ and $\ell <0$, there is no fixed point in $\mathcal{L}$ or $\mathcal{R}$. Therefore, any initial point keeps oscillating between the left and right regions, making it a period-2 $\mathcal{L}$$\mathcal{R}$ orbit. □

Lemma 5.

Period-1 and period-2 ($\mathcal{L}$$\mathcal{L}$ &∖or $\mathcal{L}$$\mathcal{R}$) are the only admissible patterns in boundary line $PR$.

Proof. 

The proof follows from Propositions 4 & 5. We illustrate the results of Lemma 5 in Figure 15 and Figure 16. □

6. Region $\mathit{R}$: $(\mathit{a}<-\mathbf{1},\mathit{b}\in (-\mathbf{1},\mathbf{0}\left)\right)$

The maps for this region are shown in Figure 17 with variations in parameters ℓ and $\mu$. Here, the fixed point in $\mathcal{R}$ is stable and the one in $\mathcal{L}$ is unstable. In this work, the analysis of this region is carried out considering the magnitude of slope as less than one ($K(=a^n{b}^m)<\left|1\right|$). When $K>\left|1\right|$, then any $x_0$ will move to infinity except a certain range of initial values.

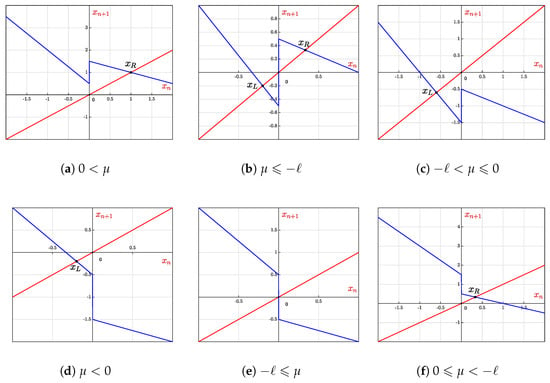
Figure 17. Graph of map for region R, i.e., $a<-1,b\in (-1,0)$ for $\ell >0$ and $\ell <0$.

6.1. Scenario $R.1$: $(\ell >0,\mu >0)$

The parameter $\mu >0$ with $\ell >0$ resembles that there is a stable fixed point $x_R$ which is a global attractor. Under the action of map, any $x_0\in \mathbb{R}$ will converge to $x_R$.

6.2. Scenario $R.2$: $(\ell >0,\mu ⩽-\ell )$

When $\ell >0$ and $\mu ⩽-\ell$, there is an unstable fixed point $x_L$, so any $x_0$ will be repelled out. Here, as $\mu <-\ell$, and at $x_n=\mu$

$$\begin{array}{ccc}\hfill x_n& =& \mu <0\hfill \\ \hfill x_{n+1}& =& a{x}_n+\mu =a\mu +\mu =(a+1)\mu >0\hfill \\ \hfill \therefore x_{n+2}& =& b{x}_{n+1}+\mu +\mu +\ell =b(a+1)\mu +\mu +\ell <0\hfill \\ & \Rightarrow & (ab+b+1)\mu +\ell <0\hfill \\ \hfill \therefore \mu & <& -{\displaystyle \frac{\ell }{(ab+b+1)}}\hfill \end{array}$$

Therefore,

$$\mu <max\left(-\ell ,-{\displaystyle \frac{\ell }{(ab+b+1)}}\right)\Rightarrow \mu <-{\displaystyle \frac{\ell }{(ab+b+1)}}$$

(6)

Similarly, with $x_n=(\mu +\ell )$, we have

$$\begin{array}{cc}\hfill a{x}_n+\mu & =a(\mu +\ell )+\mu =(a+1)\mu +a\ell >0\hfill \\ \hfill \therefore \mu & >-{\displaystyle \frac{a\ell }{(a+1)}}\hfill \end{array}$$

(7)

The relations (6), (7) gives range of $\mu$ for which trajectories are quasi-periodic in nature i.e.

$$\mu \in \left(-{\displaystyle \frac{a\ell }{a+1}},-{\displaystyle \frac{\ell }{ab+b+1}}\right)$$

(8)

Moreover, these quasi-periodic orbits are bounded within range $\left(\mu ,(a+1)\mu \right)$. Furthermore, to verify the quasi-periodicity nature of the orbits, the Lyapunov exponent is calculated, which comes out to be less than zero.

When $\mu ⩽-{\displaystyle \frac{a\ell }{a+1}}$, then only $\mathcal{L}$$\mathcal{R}$ orbit is possible with fixed points at

$$(x_{P_L},x_{P_R})=\left({\displaystyle \frac{(b+1)\mu +\ell }{1-ab}},a{\displaystyle \frac{(b+1)\mu +\ell }{1-ab}}+\mu \right)$$

(9)

The bifurcation diagram in Figure 18 demonstrates that there exist period-1, period-2, quasi-periodic orbits and chaos for $\ell >0$.

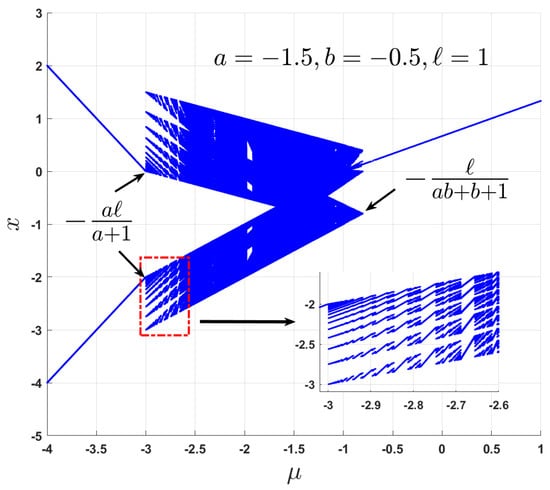
Figure 18. Bifurcation diagram showing period-1 & -2, quasi-periodic orbits and chaos for region R with $\ell >0$ cases.

6.3. Scenario $R.3$: $(\ell >0,-\ell <\mu ⩽0)$

Stable ($x_R$) and unstable ($x_L$) fixed points both exists in this scenario $(-\ell <\mu ⩽0)$. Therefore, whenever $K<1$, then $x_R$ is a global attractor, and the same can be seen in Figure 18.

For the above three cases, the Lyapunov exponent (LE) plot is shown in Figure 19 for the piecewise smooth map along with the bifurcation diagram to provide a clearer dynamical interpretation of the observed orbit transitions.

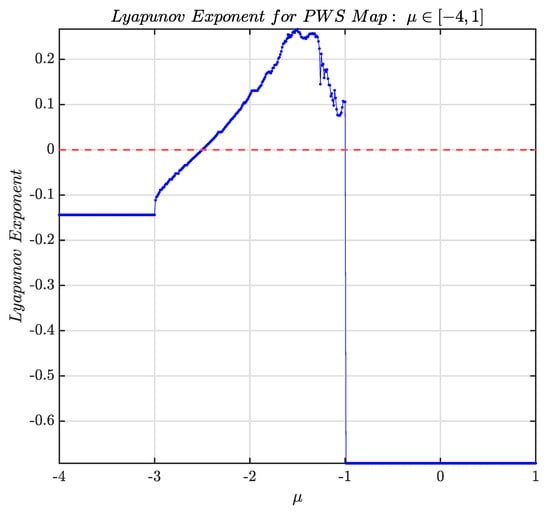
Figure 19. Lyapunov exponent (LE) for $\mu \in [-4,1]$.

The LE plot clearly distinguishes regions of:

1.

Negative LE: indicating stable periodic orbits (period-2);

2.

Near-zero LE: suggesting quasi-periodic orbits;

3.

Positive LE: confirming the presence of chaos.

6.4. Scenario $R.4$: $(\ell <0,\mu <0)$

With a negative length of discontinuity and $\mu <0$, an unstable fixed point is present and, under the action of map (1), every point moves in $\mathcal{L}$ and $\mathcal{R}$ forming $\mathcal{L}$$\mathcal{R}$ orbit with fixed points given by Equation (9), when $x⩽0$ and for $x>0$, these are given as:

$$(x_{P_R},x_{P_L})=\left({\displaystyle \frac{(a+1)\mu +a\ell }{1-ab}},b{\displaystyle \frac{(a+1)\mu +a\ell }{1-ab}}+\mu +\ell \right)$$

(10)

6.5. Scenario $R.5$: $(\ell <0,-\ell ⩽\mu )$

In this case $\ell <0,-\ell ⩽\mu$, fixed point $x_R$ is a stable attractor for the basin $\left(0,-{\displaystyle \frac{(\mu +\ell )}{b}}\right)$.

Lemma 6.

Period-2 orbit and period-1 solution coexist with $\mu ⩽-{\displaystyle \frac{\ell }{b+1}}$.

Proof. 

The magnitude of slope in $\mathcal{R}$ is less than one, so any point within the

$$\left(0,-{\displaystyle \frac{(\mu +\ell )}{b}}\right)$$

will attract to the stable fixed point $x_R$ irrespective of $\mu$.

Whenever $x_0$ is outside the above basin, it will oscillate between $\mathcal{L}$ and $\mathcal{R}$. Consider,

$$\begin{array}{ccc}\hfill x_0& =& 0\hfill \\ \hfill x_1& =& \mu >0\hfill \\ \hfill x_2& =& (b+1)\mu +\ell ⩽0\mathrm{if}(b+1)\mu ⩽-\ell \hfill \\ \hfill \therefore \mu & ⩽& -{\displaystyle \frac{\ell }{b+1}}\Rightarrow \mathrm{period}-2\left(\mathcal{L}\mathcal{R}\right)\mathrm{orbit}\hfill \end{array}$$

Otherwise, $x_2>0$ and further states move towards $x_R$. Therefore, period-1 & -2 coexist when $\mu ⩽-{\displaystyle \frac{\ell }{b+1}}$. It is illustrated in Figure 20. □

Figure 20. Bifurcation diagram for case R.5.

6.6. Scenario $R.6$: $(\ell <0,0⩽\mu <-\ell )$

In this case, there is no fixed point and the state keeps hopping between left and right regions at points given by (9) or (10).

7. Region $\mathit{Q}$: $(\mathit{a}<-\mathbf{1};\mathit{b}<-\mathbf{1})$

This is the unstable region as both a and b are less than $-1$, so in all cases where fixed points present, they repel the states.

7.1. Scenario $Q.1:(\ell >0,\mu >0)$

$\ell >0,\mu >0$: Here, a fixed point in $\mathcal{R}$ is present. As both slopes are negative, the map exhibits chaotic ${\mathcal{LR}}^{\mathrm{m}}$ orbits within a certain range of $x_0$. Although these orbits are bounded, the Lyapunov exponent is greater than zero. Consider,

$$\begin{array}{ccc}\hfill x_0& ⩽& 0\hfill \\ \hfill x_1& =& a{x}_0+\mu >0\hfill \\ \hfill x_0=x_2& =& ab{x}_0+(b+1)\mu +\ell ⩽0\hfill \end{array}$$

The lower limit on $x_0$ for the orbit to be stable is

$${\displaystyle \frac{(b+1)\mu +\ell }{1-ab}}⩽x_0<0$$

Similarly, for

$$\begin{array}{ccc}\hfill x_0& >& 0\hfill \\ \hfill x_1& =& b{x}_0+\mu +\ell ⩽0\hfill \\ \hfill x_0=x_2& =& ab{x}_0+(a+1)\mu +a\ell >0\hfill \end{array}$$

The upper bound on $x_0$ for the orbit to be stable is

$$0<x_0<{\displaystyle \frac{(a+1)\mu +a\ell }{1-ab}}$$

Therefore for $\mu >0$ the orbit exists $iff$

$${\displaystyle \frac{(b+1)\mu +\ell }{1-ab}}⩽x_0<{\displaystyle \frac{(a+1)\mu +a\ell }{1-ab}}$$

(11)

At steady state, these orbits are constrained within:

$$\begin{array}{ccc}\hfill x_n& ⩽& (\mu +\ell )>0\hfill \\ \hfill \mathrm{at}{x}_n& =& (\mu +\ell )\hfill \\ \hfill x_{n+1}& =& b{x}_n+\mu +\ell =b(\mu +\ell )+\mu +\ell ⩽0\hfill \\ & =& (b+1)(\mu +\ell )⩽0\hfill \\ \hfill \therefore x_n& \in & \left((b+1)(\mu +\ell ),(\mu +\ell )\right)\hfill \end{array}$$

7.2. Scenario $Q.2:(\ell >0,\mu ⩽-\ell )$

With $\mu ⩽-\ell$, chaotic orbits if $x_0$ is in the range given by (11). These orbits are constrained within:

$$\begin{array}{ccc}\hfill x_n& >& \mu ⩽0\hfill \\ \hfill \mathrm{at}{x}_n& =& \mu \hfill \\ \hfill x_{n+1}& =& a{x}_n+\mu =a\left(\mu \right)+\mu >0\hfill \\ & =& (a+1)\mu >0\hfill \\ \hfill \therefore x_n& \in & \left(\mu ,(a+1)\mu \right)\hfill \end{array}$$

7.3. Scenario $Q.3:(\ell >0,-\ell <\mu ⩽0)$

Both fixed points are present and a chaotic orbit is exhibited if $x_0$ is within the range given by (11) and the chaotic orbit is constrained in

$$(a+1)\mu <x_n<(b+1)(\mu +\ell )$$

Theorem 1.

For all $a,b<-1$, $\mathcal{L}$-prime (${\mathcal{L}}^{\mathrm{n}}\mathcal{R}$) and $\mathcal{R}$-prime (${\mathcal{LR}}^{\mathrm{m}}$) patterns are admissible only for positive even n and m, respectively.

Proof. 

The range of existence for ${\mathcal{L}}^{\mathrm{n}}\mathcal{R}$ is given as

$${\mathcal{P}}_{{\mathcal{L}}^{\mathrm{n}}\mathcal{R}}=\left(-{\displaystyle \frac{a^n\ell }{S_n^a}},-{\displaystyle \frac{a^{n-1}\ell }{a^{n-1}b+S_{n-1}^a}}\right]$$

(12)

To show that ${\mathcal{P}}_{{\mathcal{L}}^{\mathrm{n}}\mathcal{R}}$ is admissible, we show that ${\mathcal{P}}_{{\mathcal{L}}^{\mathrm{n}}\mathcal{R}}$$\ne \varphi$

$$\begin{array}{cc}\hfill \therefore & {\displaystyle \frac{-a^n\ell }{S_n^a}}<{\displaystyle \frac{-a^{n-1}\ell }{a^{n-1}b+S_{n-1}^a}}\hfill \\ & -a^n\ell (a^{n-1}b+S_{n-1}^a)<-a^{n-1}\ell S_n^a\hfill \\ & \mathrm{Simplifying},a^{n-1}(a^{n}b-1)<0\hfill \\ & (a^{n}b-1)<0\mathrm{is}\mathrm{true}\iff n\mathrm{is}\mathrm{even}.\hfill \\ & \mathrm{For}\mathrm{odd}n,(a^{n}b-1)>0,\mathrm{so}\mathrm{it}\mathrm{is}\mathrm{not}\mathrm{admissible}.\hfill \end{array}$$

Similarly, for ${\mathcal{LR}}^{\mathrm{m}}$, the range of existence is

$${\mathcal{P}}_{{\mathcal{LR}}^{\mathrm{m}}}=\left(-{\displaystyle \frac{(a{b}^{m-1}+S_{m-2}^b)\ell }{a{b}^{m-1}+S_{m-1}^b}},-{\displaystyle \frac{S_{m-1}^b\ell }{S_m^b}}\right]$$

(13)

To show this range is admissible for even m, we show ${\mathcal{P}}_{{\mathcal{LR}}^{\mathrm{m}}}\ne \varphi$

$$\begin{array}{cc}\hfill \therefore & -{\displaystyle \frac{(a{b}^{m-1}+S_{m-2}^b)\ell }{a{b}^{m-1}+S_{m-1}^b}}<-{\displaystyle \frac{S_{m-1}^b\ell }{S_m^b}}\hfill \\ & S_m^b(a{b}^{m-1}+S_{m-2}^b)<S_{m-1}^b(a{b}^{m-1}+S_{m-1}^b)\hfill \\ & \mathrm{Simplifying},b^{m-1}(a{b}^m-1)<0\hfill \\ & (a{b}^m-1)<0\mathrm{is}\mathrm{true}\iff m\mathrm{is}\mathrm{even}.\hfill \\ & \mathrm{For}\mathrm{odd}m,(a{b}^m-1)>0,\mathrm{so}\mathrm{not}\mathrm{admissible}.\hfill \end{array}$$

□

7.4. Scenario $Q.4:(\ell <0,\mu <0)$; $Q.5:(\ell <0,-\ell ⩽\mu )$ and $Q.6:(\ell <0,0⩽\mu <-\ell )$

These scenarios present unstable action with a negative length of discontinuity. Under the action of map (1), any initial point $x_0$ moves to infinity.

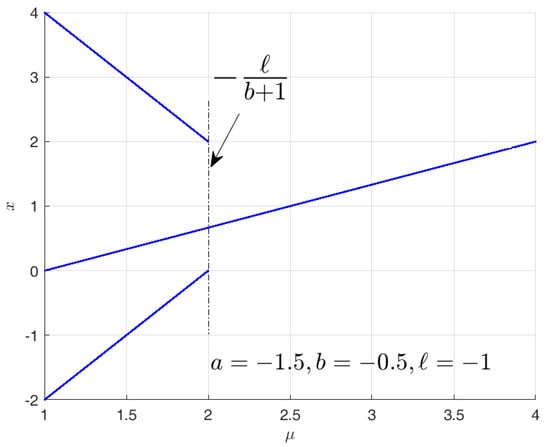
8. Boundary Line $\mathit{QR}$: $(\mathit{a}<-\mathbf{1},\mathit{b}=-\mathbf{1})$

This boundary line explores stable and unstable dynamics with parameter values $a<-1,b=-1$.

With positive length of discontinuity ($\ell >0$), the following three cases are present.

8.1. Scenario $QR.1:(\ell >0,\mu >0)$

For $\ell >0,\mu >0$ there exists a fixed point $x_R$ and as the magnitude of the slope is greater than 1, it will have period-2 ($\mathcal{R}$$\mathcal{R}$) orbits within the following range of $x_0$,

$$x_0\in \left({\displaystyle \frac{\ell }{a+1}},{\displaystyle \frac{(a+1)\mu +a\ell }{a+1}}\right)$$

(14)

8.2. Scenario $QR.2:(\ell >0,\mu ⩽-\ell )$

For $\ell >0,\mu ⩽-\ell$, an unstable fixed point $x_L$ is present. It exhibits the ${\mathcal{L}}^{\mathrm{n}}\mathcal{R}$ orbits if and only if $x_0$ is in the range given by Equation (14). The remaining are chaotic orbits, as these are bounded and have positive Lyapunov exponent.

8.3. Scenario $QR.3:(\ell >0,-\ell <\mu ⩽0)$

For $\ell >0,-\ell <\mu ⩽0$, both the fixed points $x_L$ and $x_R$ are present. The map exhibits $\mathcal{R}$$\mathcal{R}$ orbits within the $x_0$ range of Equation (14). Otherwise, these lead to infinity.

8.4. Scenario $QR.4:(\ell <0,\mu <0)$; $QR.5:(\ell <0,-\ell ⩽\mu )$ and $QR.6:(\ell <0,0⩽\mu <-\ell )$:

The negative length of discontinuity will lead to instability for any $\mu$ except when $x_0\in \left(0,\mu +\ell \right)$ in the case $-\ell ⩽\mu$ where it forms $\mathcal{R}$$\mathcal{R}$ orbits with periodic points $(x_0,-x_0+\mu +\ell )$.

9. Conclusions

This work presents a comprehensive analytical study of a one-dimensional linear piecewise-smooth discontinuous map with both slope parameters negative, thereby exploring the dynamical regimes situated in the third quadrant of the parameter space. The bifurcation behavior and orbit structures of the map were systematically analyzed by varying the parameters $\mu$ and ℓ, under the constraint that the absolute values of the slopes remain less than or equal to one. Special emphasis was placed on identifying the parameter conditions that lead to stable periodic orbits, especially period-2 and period-2 orbits of types ($\mathcal{L}$$\mathcal{L}$ or $\mathcal{R}$$\mathcal{R}$), which emerge as characteristic features in this quadrant. Distinct dynamical phenomena, including coexisting attractors, periodic and quasi-periodic behavior, as well as chaotic regimes in a couple of scenarios, were observed and mathematically characterized. In particular, the study established closed-form expressions to determine the number of iterations required for a trajectory to settle into periodic orbits. Boundary cases, including switching manifolds and the critical intersections of phase space partitions, were addressed to gain insight into transitions between qualitatively different dynamics.

The theoretical analysis was rigorously validated using numerical tools such as bifurcation diagrams, cobweb plots, and basin of attraction visualizations. The outcomes of this investigation provide a useful framework for the robust or sustainable design and stability assessment of power electronic converters, especially when integrated into renewable energy systems where discontinuities and non-smooth behaviors are inherent. Overall, this study contributes to a foundational understanding of discontinuous dynamical systems and their application to sustainable energy conversion technologies. Further, these converters can be modelled and analyzed in two-dimensions or n-dimensions.