Abstract
The berth allocation and crane assignment problem (BACAP) is a key challenge in port logistics, particularly under dynamic and uncertain vessel arrival conditions. To address the limitations of existing methods in handling large-scale and high-disturbance scenarios, this paper proposes a novel optimization framework: Ternary Historical Memory-based Robust Clustered Particle Swarm Optimization (THM-RCPSO). In this method, the initial particle swarm is divided into multiple clusters, each conducting local searches to identify regional optima. These clusters then exchange information to iteratively refine the global best solution. A ternary historical memory mechanism further enhances the optimization by recording and comparing the best solutions from three different strategies, ensuring guidance from historical performance during exploration. Experimental evaluations on 25 dynamic BACAP benchmark instances show that THM-RCPSO achieves the lowest average vessel dwell time in 22 out of 25 cases, with the lowest overall average rank among five tested algorithms. Specifically, it demonstrates significant advantages on large-scale instances with 150 vessels, where it consistently outperforms competing methods such as HRBA, ACO, and GAMCS in both solution quality and robustness. These results confirm THM-RCPSO’s strong capability in solving dynamic and large-scale DBACAP scenarios with high disturbance levels.
Keywords:
berth allocation and crane assignment; robust optimization; swarm intelligence; ternary historical memory MSC:
62F35
1. Introduction
In the context of globalization, international trade has become one of the key drivers of economic growth for countries around the world [1]. Among various modes of transportation, international maritime shipping stands out as the backbone of global economic activity due to its large cargo capacity and low cost [2]. Statistics show that over 80% of global trade by volume is carried out through maritime transport, with nearly every industry relying on shipping for the transportation of goods—ranging from raw materials to finished products, from food to electronics [3]. Ports, as critical nodes in the maritime transport chain, perform essential functions such as cargo loading and unloading, storage, inspection, and quarantine. The efficiency of port operations directly affects transportation costs and delivery times. To improve port operation efficiency, it is crucial to allocate berth and crane resources in a rational manner. As a result, the berth allocation and crane assignment problem (BACAP) has been proposed [4].
In BACAP, the term berth refers to the position within the port where a vessel can dock, while quay crane (QC) refers to the container cranes located at the port’s quay, typically installed along the dock to load and unload containers. BACAP aims to allocate berth and crane resources rationally in order to minimize the vessels’ stay and waiting times at the port. Figure 1 provides a schematic of BACAP, where a. represents the minimum safety distance between vessels; b. represents the minimum safety distance between QCs. Each time a vessel finishes unloading, it will depart. c. represents the vessel allocation process; d. represents the QC allocation process; e. represents the vessels waiting to dock have been assigned both a berth and a QC. Once a QC completes its current task, it can immediately be reassigned to another vessel that requires its service.
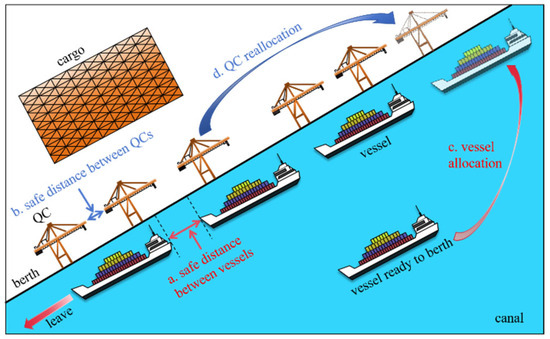
Figure 1.
Schematic of BACAP.
Early studies on BACAP mostly assumed a static condition, where vessel arrival times and cargo volumes were known and fixed [5]. Researchers applied algorithms based on Linear Programming (LP) [6] and Integer Programming (IP) [7] to solve such problems. However, LP and IP are only suitable for small to medium-sized port problems. With economic growth and the increasing demand at ports [8], these algorithms can no longer meet the requirements. As a result, heuristic methods have been used to solve the problem, as these algorithms are better suited for large-scale, complex port environments. For example, Imai et al. [9] used Genetic Algorithms (GAs) to obtain fitness values for chromosomes by scheduling QC transfers between berths. Li et al. [10] combined the simulated annealing (SA) algorithm to design an enhanced Quantum Annealing algorithm (EQA) with strong global search capability. Krimi et al. [11] integrated the Tabu Search (TS) algorithm. All these studies achieved good results under static assumptions.
However, due to various uncertain factors such as weather, shipping conditions, and customs processes, vessel arrival times and cargo volumes are often difficult to predict accurately [12], making the solution methods developed under static conditions unable to meet the demand. For example, delays in vessel arrival times may disrupt the original work schedule, leading to frequent adjustments in QC assignments and affecting the overall operational efficiency of the port. Therefore, researchers have shifted focus to solving the BACAP under dynamic conditions, taking into account the impact of uncontrollable factors, such as climate, on vessel arrival times and cargo volumes [13,14]. However, most heuristic algorithms do not fully consider the influence of these factors on the overall allocation plan, and under conditions of frequent resource conflicts, they often get trapped in local optima. Although many methods exist to optimize these algorithms, the time cost required can significantly increase [15,16].
In recent years, with the work of Monaco et al. [17] combining Differential Evolution (DE) and Robust Optimization (RO) to solve BACAP, the use of RO to address the dynamic berth allocation and crane assignment problem (DBACAP) has gradually become the focus of research. RO aims to generate more adaptable solutions by simulating the impact of uncertain factors under different scenarios [18,19]. Specifically, within a limited time window, RO can reduce the need for frequent resource adjustments by tolerating a certain range of changes, thus achieving efficient and stable allocation [20]. Imai et al. [21] proposed a berth allocation scheme based on GA to address berth demands with service priorities, but it did not consider QC allocation simultaneously. Zhu and Lim [22] designed a simulated annealing algorithm with effective neighborhood search for solving large-scale dynamic scenarios, but they overlooked constraints such as port length and the safety distance between vessels. Zou et al. [23] combined Particle Swarm Optimization (PSO) with an intra-layer and inter-layer competition mechanism to solve this problem, but they did not simulate multiple scenarios to handle uncertain situations. Wang R. et al. [24] proposed an improved Ant Colony System (ACS) algorithm to solve it, but did not adequately address the global optimality of the solution.
In this paper, we make efforts to address the robustness issue of the large-scale DBACAP under the uncertainty of vessel arrival times.
1.1. Berth Allocation and Crane Assignment Problem
BACAP is a core issue in port management, aiming to maximize the loading and unloading efficiency of vessels and minimize their waiting time by finding reasonable berth and crane allocation solutions. Before BACAP was proposed, the earliest issue encountered in port management was the berth allocation problem (BAP) [25,26], which has been extensively studied for small, medium, and large-scale instances [27,28,29]. Furthermore, early considerations of berth allocation were discrete, known as discrete berth allocation problem (DBAP), where fixed docking locations were preassigned [30], until researchers introduced continuous berth conditions, known as continuous berth allocation problem (CBAP), where vessels could dock at any available position [31]. However, in BAP, only factors such as vessel arrival times, berth locations, and berth capacity were considered, and QC allocation was not addressed in detail. With the increasing demand for terminal services, port managers began to focus on the scheduling of QCs, and the crane assignment problem (CAP) gradually came into the spotlight [32,33,34]. Soon, some researchers combined BAP and CAP in the hope of improving port operational efficiency by considering both berth and crane assignments, leading to the emergence of BACAP, which quickly garnered significant attention [35,36,37]. We summarize some methods for solving BACAP in Table 1.

Table 1.
Literature description of methods for solving BACAP.
However, when we consider external factors, such as adverse weather conditions causing vessels to arrive later than scheduled, or customs inspections leading to changes in cargo volume, the performance of the above algorithms significantly deteriorates. Therefore, a solution is urgently needed for DBACAP.
1.2. Berth Allocation Model Based on Robust Optimization
As the uncertainty during a vessel’s voyage increases [38], factors such as adverse weather, crew conditions, and customs processes directly affect the vessel’s arrival time, cargo volume, and operational requirements. Traditional BACAP have gradually revealed many shortcomings. The optimal solutions proposed under fixed conditions cannot adapt to such random fluctuations, leading to a deterioration in the robustness of the model. The uncertainty of vessel arrival times can cause port congestion and delays in unloading processes, which have a decisive impact on port resource scheduling. As a result, it is often a focal point of research [39].
For example, Zhen and Chang [40] proposed a bi-objective robust optimization model, Lu et al. [41] incorporated the uncertainty of vessel arrival times and container handling times into the scheduling considerations, Iris et al. [42] developed a recoverable robust optimization method, Bin et al. [43] introduced buffer time as a robustness indicator, Yang et al. [44] developed a feedforward-feedback dynamic berth allocation method, Wu and Miao [45] used berth areas and relative sequences as new scheduling variables, and Du et al. [46] proposed a feedback-based robust berth allocation model. We summarize some methods for solving DBACAP in Table 2.

Table 2.
Literature description of methods for solving DBACAP.
However, most existing algorithms can only achieve optimal results when the disturbance in vessel arrival times is slight (within 10%), and as the number of vessels increases, the performance of these algorithms gradually deteriorates.
1.3. Contribution of This Work
Existing robust optimization algorithms for vessel berth allocation typically consider only small disturbances in vessel arrival times, limiting their applicability in real-world, large-scale, high-disturbance scenarios. To address this, we propose a ternary historical memory-based robust optimization framework (THM-RCPSO) for solving the dynamic berth allocation and crane assignment problem (DBACAP) under such challenging conditions.
Our main contributions are summarized as follows:
- (1)
- Improved PSO algorithm incorporating ternary historical memory: We enhance the traditional Particle Swarm Optimization (PSO) by integrating gradient descent and Lévy flight strategies with certain probabilities. This yields three local optima, each stored in historical memory and compared to guide the swarm toward the global optimum. Gradient descent accelerates local convergence, while Lévy flight promotes global exploration. This balance significantly improves convergence speed, solution accuracy, and robustness against multimodal optimization challenges, outperforming conventional PSO methods [7,8,9,10].
- (2)
- Cluster-based strategy for robust optimization in BACAP: We introduce a clustering mechanism that divides the particle swarm into multiple smaller clusters. Each cluster performs independent local searches to identify local optima, followed by inter-cluster competition and information exchange to update the global best solution continuously. This approach mitigates the premature convergence issues and high time complexity typical of gradient-based methods [40,42,46], enabling more thorough exploration of the search space. The clustering mechanism also reduces computational complexity by limiting search scope within smaller groups.
- (3)
- Robustness under large-scale and high-disturbance environments: Our framework explicitly models significant disturbances in vessel arrival times through multiple simulated scenarios, ensuring the generated berth and crane allocation plans maintain high performance and stability under uncertainty.
2. Materials and Methods
In this section, we first introduce DBACAP, followed by the symbols used in this paper, and finally, we present the mathematical model for solving this problem.
2.1. Problem Statements
In DBACAP, the planned arrival time, cargo volume, berth length, and number of QCs for each vessel are provided to the decision-maker. However, the actual arrival time of the vessel will fluctuate around the planned arrival time. When making the plan, the decision-maker needs to take this fluctuation into account and ensure that the waiting time for an available berth is minimized, while ensuring that each vessel can dock and unload normally. Of course, when the number of QCs required for a vessel’s operation decreases as the unloading process nears completion, QCs can be reallocated from one vessel to another. Before mathematically modeling DBACAP, we make the following assumptions:
- (1)
- A certain safety distance must be maintained between vessels and between QCs to ensure operational safety. Vessels and QCs cannot approach each other closer than the set minimum safety distance.
- (2)
- Berths are continuous, meaning vessels can dock at any position, not necessarily at discrete, fixed docking locations.
- (3)
- When the loading and unloading of a vessel is nearing completion and the number of required QCs decreases, excess QCs may be reassigned to other vessels to improve crane utilization.
- (4)
- All QCs have the same operational efficiency, meaning they can handle the same amount of cargo in the same amount of time.
- (5)
- All QCs can move and operate normally.
- (6)
- The cost of QC movement is ignored.
2.2. Notations
| Set of ships, , where is the total number of ships. | |
| Set of cranes, , where is the total number of cranes. | |
| Total length of the port’s berths. | |
| Set of time moments, representing the set of moments involved in solving the problem, with being a specific time point. | |
| Planned arrival time of ship . | |
| Actual arrival time of ship . | |
| Departure time of ship . | |
| Length of ship . | |
| Cargo volume of ship . | |
| Crane efficiency, representing the amount of cargo that can be handled per hour by a crane. | |
| Continuous variable representing the berth position of ship . | |
| Number of cranes assigned to ship . | |
| Safety distance ratio between ships. | |
| Safety distance between cranes. | |
| Binary variable indicating whether crane is operating for ship at time . | |
| Binary variable indicating whether ship is docked at a berth at time . | |
| Learning rate for berth position gradient update. | |
| Learning rate for crane assignment gradient update. |
2.3. Mathematical Models
Our optimization objective is to minimize the expected total stay time of all vessels at the port, while considering the uncertainty in the vessels’ arrival times. First, we introduce a Gaussian disturbance based on the vessel’s length to simulate the uncertainty in the arrival time. The arrival time of the vessel is modeled with a Gaussian disturbance as follows:
where is an adjustment factor that represents the impact of the vessel’s length on the disturbance of the arrival time.
Since the arrival time is random, we take the expectation of the objective function:
where is the set of decision variables, including berth positions and the number of cranes assigned.
Berth position constraint:
QC operation position constraint:
Vessel loading and unloading operation constraint:
Vessel departure time constraint:
Safety distance between QCs:
Safety distance between vessels:
Operational load constraint:
Vessel docking constraint:
QC operation constraint:
3. Proposed Algorithm
A large number of experiments have shown that existing robust optimization algorithms for DBACAP can achieve good results when the vessel arrival time disturbance is small, and the number of vessels is limited. However, when the disturbance in vessel arrival times increases or the number of vessels grows, these algorithms exhibit significant drawbacks. To improve the optimization performance of DBACAP under large-scale and high-disturbance conditions, we propose a THM-RCPSO algorithm to enhance the performance of swarm optimization algorithms under uncertainty. Additionally, we address the issue of local convergence by introducing a clustering mechanism to balance the search within the population. Finally, under the clustering framework, we also design a restart strategy to ensure that each exploration position is sufficiently distant from the previous optimal solution.
In the following chapters, we first provide a comprehensive overview of the overall framework, and then sequentially introduce the encoding method, the robust optimization framework, the clustering method, and the ternary historical memory-based particle swarm optimization strategy used in this paper.
3.1. Overall Framwork
Before presenting the model framework, let us ask the readers to consider the following scenario: Suppose the arrival time of a single vessel fluctuates. Specifically, assume that the vessel arrives 10 min later than planned. This change could lead to two different outcomes: Through local adjustments to the berth location and crane allocation, the vessel could still dock and unload normally without affecting the schedule of other vessels or their resource allocation; or, the vessel could not dock and unload as planned, disrupting the schedules of subsequent vessels. We refer to the first scenario as the vessel’s arrival time fluctuation being within the robust region, as shown in Figure 2a, and the second scenario as the arrival time fluctuation being outside the robust region, as shown in Figure 2b. The model proposed in this paper aims to identify such a robust region, where, regardless of how much the vessel arrival time fluctuates, the berth and crane allocation schemes will remain valid.
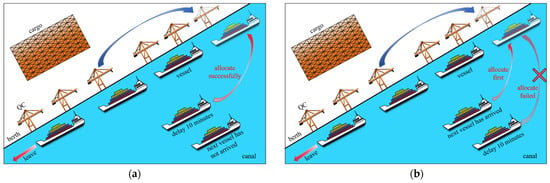
Figure 2.
Diagram of robust region when only a single vessel experiences fluctuations: (a) allocate successfully; (b) allocate failed.
Algorithm 1 presents the overall framework of THM-RCPSO. Before presenting the details of the framework process, the algorithm’s encoding scheme is introduced.
Determining the particle encoding method is a prerequisite for the implementation of the algorithm. We encode each particle as a vector containing elements. This encoding method combines two key decision variables: the vessel’s berth position and the number of cranes allocated. Specifically, assuming there are vessels in the port that need to be allocated berths and cranes, the encoding of each particle can be represented as a dimensional vector. The first elements represent the berth position of each vessel, and the last elements represent the number of cranes allocated to each vessel. Figure 3 illustrates the particle encoding method.
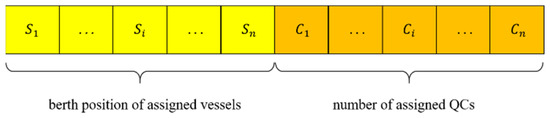
Figure 3.
Encoding method.
The specific formula is as follows:
The details of THM-RCPSO are as follows. First, we initialize the particle swarm and perform clustering (line 1). Then, we evaluate the fitness of the particles and perform iterative optimization using the robust optimization framework (line 2–line 14). In each iteration, we cluster the particles in each cluster to find the local optimum (line 5–line 8). Next, we compute the robust fitness value (line 9) and position changes (line 11) for each cluster, and check for convergence (line 12). The solving process of THM-RCPSO is shown in Figure 4.
| Algorithm 1 THM-RCPSO |
|
| Algorithm 2 Clustered PSO |
|
| Algorithm 3 RobustFitness |
|
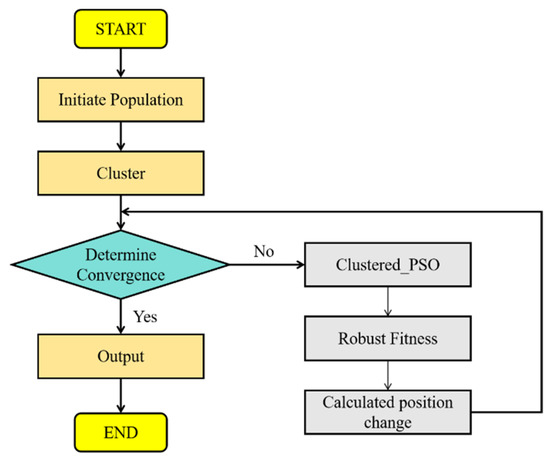
Figure 4.
Solving process of THM-RCPSO.
3.2. Local Search
To improve the stability of DBACAP, enhance the sufficiency of the search, and reduce its complexity, we propose the THM-RCPSO algorithm. It consists of two main components: local search and particle swarm optimization, as shown in Figure 5. First, the particle swarm is clustered, followed by a local search within each cluster. Then, the ternary historical memory mechanism is utilized to enhance exploration within the population, while robust optimization ensures the stability of the solutions. The detailed steps of the THM-RCPSO algorithm are described below.
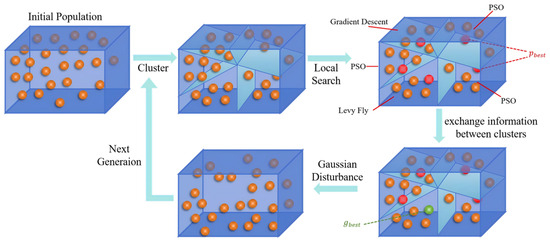
Figure 5.
Illustration of THM-RCPSO Algorithm.
During the iterative process, each particle swarm gradually approaches a local optimal solution. When the particle swarm is close to a local optimum, gradient descent and Lévy flight are applied for search optimization with a certain probability.
Using gradient descent allows particles to quickly approach the robust region, accelerating convergence and ensuring that local solutions within each cluster remain stable in the robust region. Randomly, 20% of the particles are selected for gradient descent optimization. The execution process of gradient descent is illustrated in Figure 6.
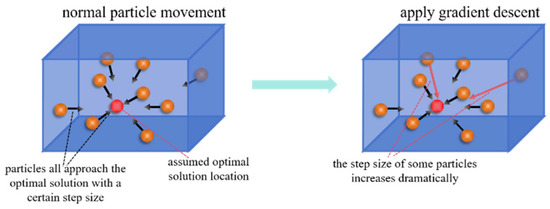
Figure 6.
Execution process of gradient descent.
The berth position is updated as follows:
The QC is updated as follows:
The Lévy flight strategy is employed to explore a larger solution space, preventing the particle swarm from getting trapped in local optima and enhancing global search capability. By utilizing Lévy flight, particles can escape local regions and explore more potential solutions, thereby improving the overall robustness of the solution.
Among the particles not selected for gradient descent, 20% are randomly chosen for Lévy flight optimization. The execution process of Lévy flight is illustrated in Figure 7.
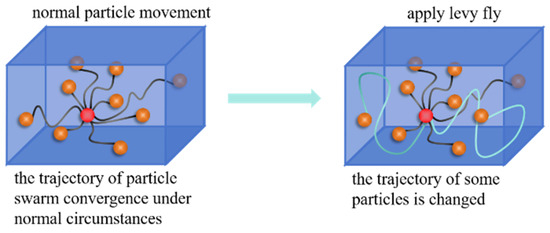
Figure 7.
Execution process of Lévy flight.
The berth position is updated as follows:
The QC is updated as follows:
The step size and are generated based on the Lévy distribution:
is the exponent parameter of the Lévy distribution, typically in the range of (0, 2]. is the scaling factor that controls the size of the steps.
3.3. THM-RCPSO Algiorithm
To improve search efficiency and avoid getting trapped in local optima, this paper proposes a Clustered Particle Swarm Optimization (Clustered PSO) strategy. We divide the initial particle swarm evenly into multiple clusters. Each cluster independently performs local search to find the optimal solution, and then, through information exchange and competition between clusters, updates the global optimal solution.
As shown in Algorithm 2, we employ the following method for clustering: The entire particle swarm is divided evenly into clusters, with each cluster containing particles.
Each particle within a cluster performs a search using the standard PSO algorithm, and this results in obtaining local best information (). The fitness function can be calculated based on (3).
The particle position update formula is:
The particle velocity update formula is:
To ensure the validity of berth positions and quay crane allocations, the dimensions of the particles must be constrained within given upper and lower bounds:
The distance between particles and within a cluster can be defined as:
when is smaller than a predefined threshold, the particles are considered to be in the same cluster.
When a cluster does not update near the local optimal solution for a long time, or when the convergence speed slows down, the algorithm will trigger a restart mechanism to reinitialize the particle swarm of that cluster. The restart trigger conditions are as follows:
In addition, as shown in Algorithm 3, during the local search for each cluster, considering the simulation of the uncertainty in the vessel’s arrival time, we generate multiple disturbance scenarios based on (1) and (2), and evaluate the adaptability of the solution for each scenario. This ensures the validity of the berth and quay crane allocation scheme under different disturbance conditions, in order to find the robust region.
The ternary historical memory mechanism is one of the key innovations of this algorithm. Its overall framework is shown in Algorithm 4. Section 3.2 explains two local search optimization strategies, both of which are executed with a certain probability in the algorithm. Therefore, our algorithm will produce three local optimal solutions: obtained by directly using the traditional PSO; obtained by using the gradient descent strategy; and obtained by using the Lévy flight strategy. The global optimal solution can be obtained by the following formula:
Our robust clustering mechanism divides the initial particle swarm into multiple clusters, each performing independent local searches. This approach enhances the algorithm’s ability to explore diverse regions of the solution space, avoiding premature convergence and improving robustness. Particles are grouped into clusters based on their Euclidean distance in the solution space. Specifically, if the distance between two particles is less than 10% of the maximum possible distance between particles, they are assigned to the same cluster. The number of clusters is fixed at five in our experiments. This value was chosen based on preliminary tests, which showed that five clusters provide a good balance between exploration and exploitation. The effectiveness of the robust clustering mechanism is demonstrated by the experimental results presented in Section 4.
| Algorithm 4 OptimizeBestSolution |
|
3.4. Theoretical Analysis of Robustness
To theoretically support the effectiveness of the proposed THM-RCPSO framework, we highlight how the ternary historical memory mechanism contributes to improved robustness. Traditional PSO often suffers from premature convergence or slow adaptation in dynamic environments due to reliance on limited memory (i.e., personal and global best). In contrast, our method introduces a threefold memory design that enhances both exploration and exploitation capacities across different temporal and spatial scales: 1. The personal historical memory retains the particle’s elite states over time, allowing reactivation of high-quality solutions that may become relevant again in dynamic settings. 2. The neighborhood memory facilitates local cooperation, enabling faster adaptation to changes in specific regions of the search space. 3. The global memory provides access to globally diverse elite positions, improving the swarm’s ability to avoid stagnation and escape from local optima.
This division of memory sources effectively decouples local search from global search and reduces the variance of convergence paths. By aggregating guidance from multiple perspectives, particles are less sensitive to noise, disruptions, or abrupt landscape shifts. The adaptive combination of these memories also serves as a stabilizing mechanism, maintaining performance even when the optimization landscape is subject to frequent changes.
The robustness of the THM-RCPSO framework is supported by both theoretical analysis and experimental validation. The ternary historical memory mechanism ensures that the algorithm retains information from multiple optimization strategies, enabling it to dynamically adjust the search direction and avoid local optima. This mechanism is particularly effective in multimodal problems, where traditional methods often fail to explore the entire solution space. Furthermore, the clustering mechanism divides the particle swarm into multiple clusters, each performing independent local searches. This approach not only improves search efficiency but also ensures that the algorithm can handle large-scale problems with high disturbance levels. Experimental results on 25 test instances in next section demonstrate that THM-RCPSO consistently outperforms other robust algorithms in terms of both solution quality and stability, further validating its robustness.
4. Numerical Experiments
In this section, we tested the performance of THM-RCPSO on a set of BACAP test cases to demonstrate its capabilities. First, we introduced the data for the test cases. Next, we described the experimental design, including THM-RCPSO and several comparison algorithms. Then, we presented and analyzed the results of all the experiments.
4.1. Case Generation
We selected a BACAP dataset containing 25 test cases, and Table 3 presents the specifications of each case in the dataset. These cases cover a wide range of scales and configurations of port operations, designed to simulate various real-world scenarios. The dataset includes the following details:

Table 3.
Specifications of each case in BACAP dataset.
Number of vessels: The dataset includes cases with 30, 50, 100, 150, and 200 vessels, with five cases for each vessel count.
Number of cranes: The number of available cranes for each group of five cases is set to 30, 50, 50, 70, and 70, respectively.
Vessel length and cargo volume: The length of vessels ranges from 50 to 400 m, and the cargo handling capacity ranges from 800 to 12,000 units, ensuring a realistic representation of port operations.
This diversified test scenario design aims to comprehensively evaluate the performance of the algorithm under different conditions, including small-scale, medium-scale, and large-scale problems. By incorporating varying vessel counts, crane configurations, and cargo volumes, the dataset effectively reflects the complexity and diversity of real-world port operations. The total length of the port’s quay is 3000 m.
4.2. Comparison Algorithms
To demonstrate the superiority of THM-RCPSO’s performance, we selected four classical DBACAP solutions as benchmark comparisons. These include: an Ant Colony Optimization-based discrete berth allocation model (ACO) [43], a feedforward–feedback dynamic berth allocation model (HRBA) [44], a robust scheduling method using simulation-generated feedforward plans (GAMCS) [45], and a feedback-program-based robust berth allocation model (FPA-RBAP) [46]. In order to make these algorithms applicable to the test cases we designed, we made appropriate adjustments to their encoding methods and constraints, which are described as follows:
- (1)
- ACO: ACO algorithm gradually updates information to select the optimal berth allocation scheme, excelling in small-scale dynamic optimization problems. Since this algorithm only considers berth allocation and does not include crane resource allocation, we added crane numbers and related constraints to the original encoding.
- (2)
- HRBA: HRBA model addresses uncertainty by constructing a linear allocation scheme. It not only considers continuous updates to the optimal solution but also adjusts the positions of historical solutions. This algorithm is well-suited to handle optimization problems with small-scale disturbances.
- (3)
- GAMCS: GAMCS introduces the concept of berth regions and relative order, applying simulation-generated feedforward plans to improve convergence speed. To adapt this algorithm to our case’s specific needs, we adjusted the allocation rules for berths and cranes in its constraint conditions.
- (4)
- FPA-RBAP: FPA-RBAP combines simulated annealing, feedback adjustments, and buffer adjustments based on inconsistent costs. This method performs well in robust optimization for large-scale datasets but often incurs higher time costs.
The running parameters for all algorithms are shown in Table 4. For each test case, each algorithm is independently run 25 times to ensure the stability of the statistical data. We use the mean and standard deviation as performance indicators, measuring the average fitness of each algorithm and calculating its standard deviation. In the tests, the algorithm stops iterating when the change in fitness value is less than 1 × 10−3 or when the maximum number of iterations (, where is the number of vessels) is reached.

Table 4.
Dataset parameters for all algorithms.
4.3. Results Display
Table 5 presents the experimental results of all comparison algorithms, with the optimal solution for each test case highlighted in bold. From these results, the superior performance of the proposed THM-RCPSO algorithm is clearly evident. It consistently achieves lower average vessel dwell times and standard deviations compared to the other algorithms. This advantage becomes particularly pronounced in large-scale instances involving 150 vessels (C16–C25), underscoring THM-RCPSO’s strong capability in handling dynamic and large-scale DBACAP scenarios with high disturbance levels.

Table 5.
Experimental results for all comparison algorithms.
To enhance the clarity of the comparative analysis, we added an Average Rank row to Table 5. The ranks were calculated by sorting each algorithm’s performance in every test case (excluding standard deviation) and assigning a score from 1 (best) to 5 (worst). The final average rank results clearly demonstrate the overall superiority of THM-RCPSO, which consistently ranks first across all 25 instances. It is followed by HRBA, ACO, and FPA-RBPA, while GAMCS performs the worst overall. This ranking provides an intuitive and comprehensive perspective on algorithm performance across diverse problem scales.
Moreover, the comparative performance of HRBA reveals its strength in terms of solution stability, as indicated by its relatively low standard deviations across several instances. This suggests that preserving historical solutions during iterative optimization contributes to robustness in dynamic environments. The direct comparison between THM-RCPSO and HRBA further validates the effectiveness of the ternary historical memory mechanism embedded in our framework.
In addition, the results demonstrate that THM-RCPSO significantly outperforms GAMCS, highlighting the limited effectiveness of feedforward planning in this context when compared to historical memory-guided search strategies. Similarly, when compared with ACO and FPA-RBPA, THM-RCPSO exhibits a more robust and consistent optimization performance across both small- and large-scale DBACAP instances, reaffirming the practical value of its robust clustered swarm structure.
4.4. Statistical Analysis
To validate the superiority of THM-RCPSO, we performed a Friedman Test to compare its performance with other algorithms (ACO, HRBA, GAMCS, and FPA-RBPA) across 25 test instances.
The Friedman Test is used to compare the performance of multiple algorithms across multiple test instances. It ranks the performance of each algorithm on each test instance and then evaluates whether the differences in rankings are statistically significant. The test is based on the following steps:
First, for each test instance, rank the algorithms based on their performance. The best-performing algorithm receives a rank of 1, the second-best receives a rank of 2, and so on. Then, calculate the average rank of each algorithm across all test instances. Finally compute the Friedman statistic using the following formula:
where is the number of test instances. is the number of algorithms. is the average rank of the -th algorithm.
Based on the data in Table 5, we calculated the average rankings of each algorithm across the 25 test instances. The results are as follows: THM-RCPSO: 1.2, HRBA: 2.1, ACO: 3.0, GAMCS: 3.8, FPA-RBPA: 4.9.
With four degrees of freedom (since = 5), the critical value for a significance level of 0.05 is 9.49. Since the Friedman statistic (15.67) exceeds the critical value, we conclude that there are statistically significant differences in performance among the algorithms.
5. Discussion
In this section, we first discuss the differences between THM-RCPSO and some commonly used robust optimizers, and theoretically prove its superiority. Then, we use ablation experiments to demonstrate the effectiveness of the proposed three-term historical memory method in robust optimization. Finally, we analyze the combined effects of the gradient descent ratio and Lévy flight ratio on the performance of THM-RCPSO. All experiments in this section use the same cases and settings as those in Section 4.
5.1. Comparative Analysis
Currently, the mainstream robust optimizers mostly combine heuristic algorithms to address the resulting robust berth scheduling problems [47,48]. For example, RBSHO [49] uses a bi-objective optimization approach, applying simulation to assess the proposed berth scheduling strategy and comparing it with the three commonly used vessel service strategies under uncertain conditions. RBAP [50] integrates simulated annealing and branch-and-bound algorithms to construct a robust berth scheduling model. Additionally, some researchers have developed deep extensions based on PSO, such as PSO-TBIR [51], which introduces a time-buffer insertion algorithm, incorporating the adaptive search process of time buffers into PSO.
However, the direction explored by THM-RCPSO differs from theirs. Based on PSO, we divide the particles into multiple clusters through a clustering strategy. Each cluster performs independent local searches, and the inter-cluster competition mechanism prevents resource waste in clusters that have already converged. In complex, high-dimensional DBACAP problems, this allows for more effective coverage of the search space. Additionally, the algorithm retains historical memory, exploring future solutions while not abandoning the best historical solutions. Therefore, whether in terms of vertical or horizontal performance, THM-RCPSO demonstrates superior performance.
5.2. Ablation Study
In this section, we conduct an ablation study to evaluate the effectiveness of the core components of THM-RCPSO, including the clustering mechanism and the ternary historical memory strategy. We compare four algorithmic variants: the complete THM-RCPSO, No-Cluster (without particle clustering), No-Memory (with the historical memory mechanism disabled), and the canonical PSO algorithm as a baseline. The experiments are performed on the same 25 benchmark test cases and under identical disturbance settings as described earlier. Each algorithm is independently run 25 times per case, and the mean and standard deviation of the vessel dwell times are reported. The final column in Table 6 shows the performance gain (or loss) of THM-RCPSO relative to the other variants, using GAP percentage to quantify improvements, calculated as the relative difference from the baseline solution.

Table 6.
Ablation study of No-Cluster, No-Memory, and Complete THM-RCPSO based on original algorithms.
From Table 6, it is evident that THM-RCPSO performs well in both small-scale and large-scale DBACAP scenarios, thanks to the clustering mechanism. Specifically, THM-RCPSO achieved the best performance in test cases C1, C4, C5, C21, C22, C24, and C25. Among these, the improvement reached 3.97% in the C1 case and 3.29% in the C25 case. The reasons for this can be analyzed as follows: In small-scale scenarios, the intra-cluster and inter-cluster competition mechanisms help slow down the convergence speed of the particle swarm, allowing for more thorough exploration. In large-scale scenarios, clustering effectively addresses the multi-modal nature of the problem and prevents the exploration from being too localized. In medium-sized cases, these characteristics are not as apparent but still provide some benefit, likely because the swarm size is moderate, and the three-way historical memory algorithm alone can maintain a good exploration effect.
Secondly, for the ternary historical memory-based algorithm, the optimization performance is particularly significant in large-scale cases. Specifically, test cases C21–C25 exhibit superior results. The reason behind this is that in large-scale populations, the number of particles in each cluster increases, providing more samples and optimization space for the execution of the ternary historical memory-based algorithm. In each iteration, a certain percentage of particles are selected for Lévy flight and gradient descent strategies with a certain probability, allowing the algorithm to achieve a better balance between exploration and exploitation. THM-RCPSO can dynamically adjust its search direction. This strategy is particularly effective in multi-modal problems, as it helps the algorithm switch between different solution regions, increasing the probability of finding the global optimum.
5.3. Parameter Analysis
In THM-RCPSO, two key parameters are involved: the adjustment coefficient , which influences the impact of ship length on port arrival time perturbations, and the probability , which determines the likelihood of selecting Lévy flight or gradient descent during local exploration. In this section, we conduct tests on five representative scenarios, namely C5, C10, C15, C20, and C25, using different combinations of {,} to analyze their joint effects. Specifically, ∈ {0.05, 0.1, 0.15, 0.2, 0.25, 0.3} and ∈ {0.05, 0.1, 0.15, 0.2, 0.25, 0.3}.
Figure 8 presents a 3D surface plot illustrating the performance of THM-RCPSO under different {,} combinations, where darker colors indicate better results (lower evaluation values). The results clearly show that and significantly impact THM-RCPSO’s effectiveness. In particular, the optimal setting {,} = {0.2, 0.2} yields the best performance across tested scenarios, suggesting that appropriate tuning of these parameters is crucial for balancing exploration and exploitation and improving solution quality.
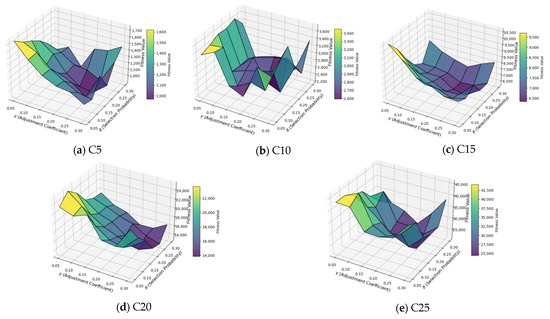
Figure 8.
Impact of different and combinations on performance of THM-RCPSO.
Other parameters related to the PSO framework and gradient descent, such as the inertia weight , learning coefficients and , and gradient descent learning rates and , were set following standard practices and preliminary validations. Specifically, decreases linearly from 0.9 to 0.4 over iterations to balance global and local search; and are both set to 2.05, consistent with canonical PSO settings, ensuring balanced influence from personal and global best positions. Parameters and were empirically set to 0.01, providing a good trade-off between convergence speed and stability, and gradient descent is applied with 20% probability to maintain global exploration capabilities. Given these parameters follow well-established guidelines and showed stable performance in preliminary tests, a more comprehensive sensitivity analysis was focused on and .
Parameter selection was conducted via grid search combined with cross-validation to identify the optimal settings.
6. Conclusions
In this paper, we designed the THM-RCPSO model to solve the DBACAP. First, we established a mathematical model for this problem, which considers uncertainties in vessel arrival times and crane assignments. Then, we designed a robust optimization framework based on three-memory history to evaluate the fitness and iteratively optimize the particle swarm. Furthermore, during each iteration, we perform clustering and local search for each cluster of particles to find local optimal solutions. In the experiments, we conducted comparative tests on 25 BACAP cases. The experimental results show that THM-RCPSO outperforms ACO, HRBA, GAMCS, and FPA-RBPA. Finally, we analyzed the theory and parameters of THM-RCPSO for solving dynamic BACAP and conducted ablation studies to demonstrate the effectiveness of three-memory history in large-scale cases.
While the THM-RCPSO method demonstrates strong performance in DBACAP, it does have some limitations. The performance of THM-RCPSO can be influenced by the initial distribution of particles in the solution space. If the initial particles are concentrated in a suboptimal region, the algorithm may require more iterations to converge to the global optimum. THM-RCPSO relies on several parameters, which need to be carefully tuned for optimal performance.
In future work, we will continue to study solutions for BACAP under various uncertainties. Additionally, we will explore applying THM-RCPSO to optimize and solve other large-scale problems, such as power grid optimization scheduling [52], cloud resource allocation, load balancing [53], etc.
Author Contributions
Conceptualization, R.W.; Methodology, R.W.; Software, R.W.; Validation, S.M. and Y.S.; Formal analysis, S.M.; Investigation, S.M.; Data curation, Y.S.; Writing—original draft, R.W.; Writing—review & editing, R.W., S.M. and Y.S.; Visualization, S.M. and Y.S.; Supervision, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in https://github.com/EvoNexusX/BACAP-cases (accessed on 28 September 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, Z.; Li, Y.; Chau, S.N.; Dietz, T.; Li, C.; Wan, L.; Zhang, J.; Zhang, L.; Li, Y.; Chung, M.G.; et al. Impacts of international trade on global sustainable development. Nat. Sustain. 2020, 3, 964–971. [Google Scholar] [CrossRef]
- Cullinane, K.; Haralambides, H. Global trends in maritime and port economics: The COVID-19 pandemic and beyond. Marit. Econ. Logist. 2021, 23, 369. [Google Scholar] [CrossRef]
- Clark, X.; Dollar, D.; Micco, A. Port efficiency, maritime transport costs, and bilateral trade. J. Dev. Econ. 2004, 75, 417–450. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated berth allocation and quay crane assignment problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Golias, M.M.; Saharidis, G.K.; Boile, M.; Theofanis, S.; Ierapetritou, M.G. The berth allocation problem: Optimizing vessel arrival time. Marit. Econ. Logist. 2009, 11, 358–377. [Google Scholar] [CrossRef]
- Ünal, Y.Z.; Uysal, Ö. A new mixed integer programming model for curriculum balancing: Application to a Turkish university. Eur. J. Oper. Res. 2014, 238, 339–347. [Google Scholar] [CrossRef]
- Gkolias, M.D. The Discrete and Continuous Berth Allocation Problem: Models and Algorithms. Ph.D. thesis, Rutgers University, New Brunswick, NJ, USA, 2007. [Google Scholar]
- Song, L.; van Geenhuizen, M. Port infrastructure investment and regional economic growth in China: Panel evidence in port regions and provinces. Transp. Policy 2014, 36, 173–183. [Google Scholar] [CrossRef]
- Imai, A.; Chen, H.C.; Nishimura, E.; Papadimitriou, S. The simultaneous berth and quay crane allocation problem. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 900–920. [Google Scholar] [CrossRef]
- Li, Z.; Li, S. An Integrated Model and Enhanced Quantum Annealing Algorithm for Berth Allocation and Quay Crane Scheduling Problem. EasyChair Preprint 5595, 2021. 9 p. Available online: https://easychair.org/publications/preprint/w59D (accessed on 1 August 2025).
- Krimi, I.; Todosijević, R.; Benmansour, R.; Ratli, M.; El Cadi, A.A.; Aloullal, A. Modelling and solving the multi-quays berth allocation and crane assignment problem with availability constraints. J. Glob. Optim. 2020, 78, 349–373. [Google Scholar] [CrossRef]
- Elmi, Z.; Singh, P.; Meriga, V.K.; Goniewicz, K.; Borowska-Stefańska, M.; Wiśniewski, S.; Dulebenets, M.A. Uncertainties in liner shipping and ship schedule recovery: A state-of-the-art review. J. Mar. Sci. Eng. 2022, 10, 563. [Google Scholar] [CrossRef]
- Correcher, J.F.; Alvarez-Valdes, R.; Tamarit, J.M. New exact methods for the time-invariant berth allocation and quay crane assignment problem. Eur. J. Oper. Res. 2019, 275, 80–92. [Google Scholar] [CrossRef]
- Ksciuk, J.; Kuhlemann, S.; Tierney, K.; Koberstein, A. Uncertainty in maritime ship routing and scheduling: A Literature review. Eur. J. Oper. Res. 2023, 308, 499–524. [Google Scholar] [CrossRef]
- Luo, W.; Xu, P.; Yang, S.; Shi, Y. Benchmark for CEC 2024 Competition on Multiparty Multiobjective Optimization. arXiv 2024, arXiv:2402.02033. [Google Scholar] [CrossRef]
- Yang, Q.; Qiao, Z.Y.; Xu, P.; Lin, X.; Gao, X.-D.; Wang, Z.-J.; Lu, Z.-Y.; Jeon, S.-W.; Zhang, J. Triple competitive differential evolution for global numerical optimization. Swarm Evol. Comput. 2024, 84, 101450. [Google Scholar] [CrossRef]
- Monaco, M.F.; Sammarra, M. The berth allocation problem: A strong formulation solved by a Lagrangean approach. Transp. Sci. 2007, 41, 265–280. [Google Scholar] [CrossRef]
- Shang, X.T.; Cao, J.X.; Ren, J. A robust optimization approach to the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 44–65. [Google Scholar] [CrossRef]
- Wang, C.; Miao, L.; Zhang, C.; Wu, T.; Liang, Z. Robust optimization for the integrated berth allocation and quay crane assignment problem. Nav. Res. Logist. (NRL) 2024, 71, 452–476. [Google Scholar] [CrossRef]
- Fabozzi, F.J.; Kolm, P.N.; Pachamanova, D.A.; Focardi, S.M. Robust Portfolio Optimization and Management; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Imai, A.; Nishimura, E.; Papadimitriou, S. Berth allocation with service priority. Transp. Res. Part B Methodol. 2003, 37, 437–457. [Google Scholar] [CrossRef]
- Zhu, Y.; Lim, A. Crane scheduling with non-crossing constraint. J. Oper. Res. Soc. 2006, 57, 1464–1471. [Google Scholar] [CrossRef]
- Zou, Y.; Xu, P.; Dai, H.; Song, H.; Luo, W. Swarm Optimization with Intra-and Inter-Hierarchical Competition for Large-Scale Berth Allocation and Crane Assignment. IEEE Trans. Emerg. Top. Comput. Intell. 2025, 9, 1307–1321. [Google Scholar] [CrossRef]
- Wang, R.; Ji, F.; Jiang, Y.; Wu, S.-H.; Kwong, S.; Zhang, J.; Zhan, Z.-H. An adaptive ant colony system based on variable range receding horizon control for berth allocation problem. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21675–21686. [Google Scholar] [CrossRef]
- Guan, Y.; Cheung, R.K. The berth allocation problem: Models and solution methods. OR Spectr. 2004, 26, 75–92. [Google Scholar] [CrossRef]
- Ting, C.J.; Wu, K.C.; Chou, H. Particle swarm optimization algorithm for the berth allocation problem. Expert Syst. Appl. 2014, 41, 1543–1550. [Google Scholar] [CrossRef]
- Lee, D.H.; Chen, J.H.; Cao, J.X. The continuous berth allocation problem: A greedy randomized adaptive search solution. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 1017–1029. [Google Scholar] [CrossRef]
- Pang, K.W.; Liu, J. An integrated model for ship routing with transshipment and berth allocation. IIE Trans. 2014, 46, 1357–1370. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, Z.; Li, R. A collaborative berth allocation problem with multiple ports based on genetic algorithm. J. Coast. Res. 2015, 73, 290–297. [Google Scholar] [CrossRef]
- Buhrkal, K.; Zuglian, S.; Ropke, S.; Larsen, J.; Lusby, R. Models for the discrete berth allocation problem: A computational comparison. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 461–473. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y. A dynamic continuous berth allocation method based on genetic algorithm. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; IEEE: Washington, DC, USA, 2017; pp. 770–773. [Google Scholar]
- Diabat, A.; Theodorou, E. An integrated quay crane assignment and scheduling problem. Comput. Ind. Eng. 2014, 73, 115–123. [Google Scholar] [CrossRef]
- Fu, Y.M.; Diabat, A.; Tsai, I.T. A multi-vessel quay crane assignment and scheduling problem: Formulation and heuristic solution approach. Expert Syst. Appl. 2014, 41, 6959–6965. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Makui, A.; Salahi, S.; Bazzazi, M.; Taheri, F. An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports. Comput. Ind. Eng. 2009, 56, 241–248. [Google Scholar] [CrossRef]
- Vacca, I.; Salani, M.; Bierlaire, M. An exact algorithm for the integrated planning of berth allocation and quay crane assignment. Transp. Sci. 2013, 47, 148–161. [Google Scholar] [CrossRef]
- Raa, B.; Dullaert, W.; Van Schaeren, R. An enriched model for the integrated berth allocation and quay crane assignment problem. Expert Syst. Appl. 2011, 38, 14136–14147. [Google Scholar] [CrossRef]
- Rodriguez-Molins, M.; Salido, M.A.; Barber, F. A GRASP-based metaheuristic for the Berth Allocation Problem and the Quay Crane Assignment Problem by managing vessel cargo holds. Appl. Intell. 2014, 40, 273–290. [Google Scholar] [CrossRef]
- Fan, H.; Jia, H.; He, X.; Lyu, J. Navigating uncertainty: A dynamic Bayesian network-based risk assessment framework for maritime trade routes. Reliab. Eng. Syst. Saf. 2024, 250, 110311. [Google Scholar] [CrossRef]
- Li, M.; Xie, C.; Li, X.; Karoonsoontawong, A.; Ge, Y.-E. Robust liner ship routing and scheduling schemes under uncertain weather and ocean conditions. Transp. Res. Part C Emerg. Technol. 2022, 137, 103593. [Google Scholar] [CrossRef]
- Zhen, L.; Chang, D.F. A bi-objective model for robust berth allocation scheduling. Comput. Ind. Eng. 2012, 63, 262–273. [Google Scholar] [CrossRef]
- Lu, Z.; Xi, L. A proactive approach for simultaneous berth and quay crane scheduling problem with stochastic arrival and handling time. Eur. J. Oper. Res. 2010, 207, 1327–1340. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Sun, B.; Sun, J.; Liu, F.; Yang, P.; Han, M.; Feng, M. On robust discrete berth allocation based on ant colony algorithm. In Proceedings of the 29th Chinese Control Conference, Chongqing, China, 28–30 May 2017. [Google Scholar]
- Yang, P.; Cai, L.; Guo, W.; Li, W. A Proactive-Reactive Approach for Dynamic Hybrid Berth Allocation Problem Considering Vessels Arrival Delay. In Proceedings of the 2023 IEEE Symposium Series on Computational Intelligence (SSCI), Mexico City, Mexico, 5–8 December 2023; pp. 1753–1758. [Google Scholar] [CrossRef]
- Wu, Y.; Miao, L. A Robust Scheduling Model for Continuous Berth Allocation Problem Under Uncertainty. In Proceedings of the 2020 5th International Conference on Electromechanical Control Technology and Transportation (ICECTT), Nanchang, China, 15–17 May 2020; pp. 43–49. [Google Scholar] [CrossRef]
- Du, Y.; Xu, Y.; Chen, Q. A feedback procedure for robust berth allocation with stochastic vessel delays. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 2210–2215. [Google Scholar] [CrossRef]
- Xu, P.; Luo, W.; Lin, X.; Zhang, J.; Wang, X. A large-scale continuous optimization benchmark suite with versatile coupled heterogeneous modules. Swarm Evol. Comput. 2023, 78, 101280. [Google Scholar] [CrossRef]
- Xu, P.; Luo, W.; Lin, X.; Qiao, Y.; Zhu, T. Hybrid of PSO and CMA-ES for global optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; IEEE: Washington, DC, USA, 2019; pp. 27–33. [Google Scholar]
- Golias, M.; Portal, I.; Konur, D.; Kaisar, E.; Kolomvos, G. Robust berth scheduling at marine container terminals via hierarchical optimization. Comput. Oper. Res. 2014, 41, 412–422. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Q.; Quan, X. Robust berth scheduling with uncertain vessel delay and handling time. Ann. Oper. Res. 2012, 192, 123–140. [Google Scholar] [CrossRef]
- Park, H.J.; Cho, S.W.; Lee, C. Particle swarm optimization algorithm with time buffer insertion for robust berth scheduling. Comput. Ind. Eng. 2021, 160, 107585. [Google Scholar] [CrossRef]
- Sobu, A.; Wu, G. Optimal operation planning method for isolated micro grid considering uncertainties of renewable power generations and load demand. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January 2012; IEEE: Washington, DC, USA, 2012; pp. 1–6. [Google Scholar]
- Mousavi, S.; Mosavi, A.; Varkonyi-Koczy, A.R. A load balancing algorithm for resource allocation in cloud computing. In Recent Advances in Technology Research and Education, Proceedings of the 16th International Conference on Global Research and Education Inter-Academia 2017, Iași, Romania, 25–28 September 2017; Springer International Publishing: Cham, Switzerland, 2018; pp. 289–296. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).