Abstract
In this work, line defects in two-dimensional dodecagonal quasicrystals are investigated. Using the ten-dimensional framework of the integral formalism of two-dimensional quasicrystals, the closed-form solutions for the displacement fields and stress functions of line defects, which are dislocations and line forces, in two-dimensional dodecagonal quasicrystals of Laue class 18 are derived. In dodecagonal quasicrystals, the phonon and phason fields are decoupled. The three phonon displacement components, two phason displacement components, three phonon stress functions and two phason stress functions of a straight dislocation and a line force are computed for a two-dimensional dodecagonal quasicrystals of Laue class 18. The self-energies of a straight dislocation and a line force are given. Moreover, the two-dimensional Green tensor is derived for two-dimensional dodecagonal quasicrystals of Laue class 18 within the framework of the integral formalism.
Keywords:
line defects; dislocations; line forces; generalized elasticity; integral formalism; quasicrystals MSC:
52C23; 74Bxx; 74E10; 35Qxx
1. Introduction
Quasicrystals are an important class of novel materials discovered by Shechtman et al. [1]. In 2011, Daniel Shechtman was awarded the Nobel Prize in Chemistry for the discovery of quasicrystals. This discovery was revolutionary because it revealed a new type of solid material with atomic structures that were previously thought to be impossible. Quasicrystals belong to aperiodic crystals and possess long-range orientational order but no translational symmetry in the quasiperiodic directions. Therefore, a quasicrystal is a solid material whose atomic structure is ordered but not periodic. Quasicrystals can be described mathematically by projecting a higher-dimensional periodic lattice (like 4D, 5D or 6D hyperspace) onto the three-dimensional space (physical or parallel space). This projection creates a structure that looks ordered, often with symmetries forbidden in ‘traditional’ crystals (like 5-fold or 10-fold symmetry), but lacks translational symmetry. Quasicrystals can exhibit crystallographic point groups consisting of only crystallographically allowable symmetry operations and non-crystallographic point groups containing crystallographically ‘forbidden’ symmetries, such as 5-fold, 8-fold, 10-fold or 12-fold rotational symmetry (see, e.g., [2,3,4,5]). Quasicrystals have been found in various metal alloys, such as aluminum-manganese, and also occur naturally (e.g., in some meteorites). They possess unusual properties like low thermal conductivity, high hardness and low friction [3].
In quasicrystals, there are two elementary excitations: phonons and phasons [6,7]. Phonons are vibrations of atoms around their equilibrium positions, such as standard lattice vibrations. Phasons are additional degrees of freedom that correspond to atomic rearrangements or ‘shifts’ in the structure in the quasiperiodic directions. These shifts do not correspond to physical displacement of atoms in three-dimensional physical space like phonons do, but rather to changes in the relative arrangement of tiles or atoms, preserving overall order. Phasons can cause tile flips or rearrangements in the quasicrystal structure. Thus, phasons in quasicrystals are internal degrees of freedom that arise because the structure is quasiperiodic. There are three types of quasicrystals: one-, two- and three-dimensional quasicrystals. In one-dimensional quasicrystals, there is a quasiperiodic arrangement of atoms in one direction, usually in -direction, and a regular periodic arrangement of atoms in the plane perpendicular to this direction that is in the -plane. Two-dimensional quasicrystals are quasiperiodic in the -plane, but periodic in the -direction. A three-dimensional quasicrystal is a structure that exhibits order without periodicity in all three spatial dimensions.
Dislocations in quasicrystals are topological line defects like in ‘traditional’ crystals, but their nature is more complex due to the aperiodic structure and the presence of phason degrees of freedom. A dislocation in a quasicrystal corresponds to a dislocation in the higher-dimensional space (hyperspace), which has both a phonon component (displacement in physical or parallel space) and a phason component (displacement in the perpendicular space). The topological charge of a dislocation in a quasicrystal is the so-called generalized Burgers vector which is a vector in the higher-dimensional space (hyperspace) with a phonon part in physical or parallel space and phason part in the perpendicular space (see, e.g., [5,7,8,9,10,11,12,13,14,15]). Dislocations influence mechanical strength, diffusion and plastic deformation of quasicrystals. The theory of generalized elasticity of quasicrystals was developed by Ding et al. [16]. The basic key equations of dislocations in quasicrystals were given by Ding et al. [17,18] and Lazar and Agiasofitou [19]. Ding et al. [20] have extended the integral formalism [21,22,23] for the displacement field of a dislocation in quasicrystals (see also [2,13]). Ding et al. [20] derived the integral formalism using the Stroh formalism for quasicrystals, but without giving an application of it. The integral formalism is a powerful technique for the numerical and analytical calculations of the elastic fields caused by line defects (see [23]). Lazar [24] has derived the extended integral formalism of line defects (straight dislocations and line forces) for the displacement fields and stress functions for quasicrystals in a straightforward manner without an unnecessary detour via the Stroh formalism. Therefore, the integral formalism is an advanced analytical method adapted to quasicrystals from anisotropic elasticity. It solves a matrix partial differential equation of first order, resulting in logarithmic and angular terms typical for dislocations. As a first application of the integral formalism given in [24], analytical solutions of line defects in one-dimensional hexagonal quasicrystals of Laue class 10 were calculated for the first time in Lazar [25] using the integral formalism.
Two-dimensional quasicrystals are an important class of quasicrystals. A two-dimensional quasicrystal is defined as a three-dimensional body which is quasiperiodic in the -plane (basal plane) and periodic in the -direction. Two-dimensional quasicrystals possess 18 Laue classes with 57 point groups, namely 10 Laue classes with 31 crystallographic point groups and 8 Laue classes with 26 non-crystallographic point groups (pentagonal, octagonal, decagonal, dodecagonal systems) [5,26,27]. Quasicrystals with non-crystallographic point groups have crystallographically ‘forbidden’ symmetries. These are rotations of order different from 1, 2, 3, 4 and 6, for instance, rotations of order 5, 8, 10 and 12. In particular, two-dimensional dodecagonal quasicrystals (Laue classes 17 and 18) are quasicrystals where the phonons and phasons are decoupled [26,28], making them an ideal platform for studying the physics of phasons without the direct influence of phonons. The first (metastable) dodecagonal phase has been discovered by Ishimasa et al. [29] in the system Ni–Cr. A two-dimensional dodecagonal quasicrystal with a 12-fold rotation axis has been found in rapidly solidified and alloys by means of transmission electron microscopy in Chen et al. [30]. Further representatives of two-dimensional dodecagonal quasicrystals have been uncovered in the systems Bi–Mn [31] and Ta–Te [32,33]. Theoretical aspects of the 12-fold symmetry in two-dimensional dodecagonal quasicrystals can be found in Yang and Wei [34], Gähler [35] and Socolar [36]. The subject of two-dimensional dodecagonal quasicrystals is an interesting and important on-going research topic (see, e.g., [37,38,39,40,41]).
Furthermore, there is a strong interest in the study of dislocations in two-dimensional quasicrystals (see, e.g., [5]). Dislocations in pentagonal quasicrystals were studied by Levine et al. [7]. Using the technique of Green functions, De and Pelcovits [42] have computed the displacement fields induced by straight dislocations in pentagonal quasicrystals, Ding et al. [18] have computed the displacement fields induced by straight dislocations in decagonal quasicrystals of Laue class 14 and Yang et al. [43] have computed the displacement fields induced by straight dislocations in dodecagonal quasicrystals of Laue class 18. Using the generalized Eshelby method, Qin et al. [44] have computed the displacement fields induced by straight dislocations in decagonal, octagonal and dodecagonal quasicrystals. The elastic fields of a straight dislocation in a decagonal quasicrystal of Laue class 13 have been calculated by Li et al. [45]. Barak and Lifshitz [46] numerically studied the dislocation motion in a dodecagonal quasicrystal model. Dislocations were also observed in transmission electron microscopy (TEM) images of dodecagonal quasicrystals [47].
In this work, we use, for the first time, the integral formalism for two-dimensional quasicrystals, which is mathematically more complicated than that for one-dimensional quasicrystals (see [25]). As a second application of the integral formalism given in [24], exact closed-form solutions of line defects in two-dimensional quasicrystals are derived using the integral formalism. In particular, the closed-form expressions for the displacement fields and stress functions of line defects in two-dimensional dodecagonal quasicrystals of Laue class 18 where the defect line is parallel to the periodic direction are the goal of the present work. In addition, the two-dimensional Green tensor of a two-dimensional dodecagonal quasicrystal of Laue class 18 is derived within the framework of the integral formalism.
2. Generalized Elasticity of Two-Dimensional Quasicrystals
A two-dimensional quasicrystal can be obtained by projecting a five-dimensional periodic structure onto the three-dimensional physical space. The five-dimensional hyperspace can be decomposed into the direct sum of two orthogonal subspaces,
where is the three-dimensional physical or parallel space of the phonon fields and is the two-dimensional perpendicular space of the phason field with quasiperiodicity in the -plane. Throughout the text, phonon fields will be denoted by and phason fields by . Note that the phonon and phason fields depend on the so-called material space coordinates . Indices in the parallel space are denoted by small Latin letters with . Indices in the perpendicular space are denoted by small Greek letters with .
In the generalized elasticity theory of two-dimensional quasicrystals, the (elastic) phonon and phason distortion tensors, and , are defined as the gradients of the phonon displacement vector and the phason displacement vector , respectively,
Here, describes the displacement field in the parallel space , and describes the displacement field in the perpendicular space . The phonon displacement field is a three-dimensional vector in , while the phason displacement field is a two-dimensional vector in . For crystallographic symmetries and , both transform according to a vector-like representation, but for non-crystallographic symmetries transforms according to the vector-like representation and transforms according to another non-vector-like representation (see [26,27,48]).
The constitutive relations for a two-dimensional quasicrystal are given by
where and are the phonon and phason stress tensors. is the tensor of the elastic moduli of phonons, is the tensor of the elastic moduli of phasons and is the tensor of the elastic moduli of the phonon–phason coupling.
Using the hyperspace notation of two-dimensional quasicrystals [19], the phonon and phason fields can be unified in the corresponding extended fields in the hyperspace and the components of the extended fields will be denoted by capital letters, e.g., . In such a hyperspace notation, we have the extended displacement vector :
the extended elastic distortion tensor :
the extended stress tensor :
and the tensor of the extended elastic moduli :
In matrix form, Equation (9) reads as
The extended stress tensor (8) can be written in terms of an extended stress function tensor :
with
where and are the phonon and phason stress function tensors. Here, denotes the three-dimensional Levi-Civita tensor.
3. Integral Formalism for Two-Dimensional Quasicrystals
For the technical details of the integral formalism of quasicrystals, we refer to Lazar [24,25].
We choose an orthogonal coordinate system in the parallel space with a unit vector in the -direction and a unit vector in the -direction (, ) and the notation
which is a matrix in the hyperspace. In the integral formalism of two-dimensional quasicrystals, the characteristic blocks of the constitutive tensor are given by
The 10-vector of the extended displacement vector and the extended stress function vector reads as
where and the matrix , being the fundamental elasticity matrix for two-dimensional quasicrystals, is defined by its blocks
In the integral formalism, we can choose two orthogonal unit vectors and which are orthogonal to such that forms a right-handed Cartesian basis in . This basis is rotated around by an angle against another fixed basis in such that
It yields and . The matrix is defined by the contraction of the elastic constants with orthogonal unit vectors and according to Equation (13). Since the vectors and are turned against the , coordinate system by an angle , now the matrix depends on the angle (see [24]).
4. Line Defects in Two-Dimensional Quasicrystals
Now, we consider a line defect in a two-dimensional quasicrystal, namely a straight dislocation with extended Burgers vector and a line force with extended strength in a two-dimensional quasicrystal located at the origin of the coordinate system. The defect line runs along the axis which is parallel to the periodic direction.
In the integral formalism, the 10-vector of the extended displacement vector and the extended stress function vector for a straight dislocation with extended Burgers vector and a line force with extended strength in a two-dimensional quasicrystal reads (see [24])
with the extended Burgers vector of a straight dislocation in a two-dimensional quasicrystal
and the extended body force vector of a line force in a two-dimensional quasicrystal
Hence, for two-dimensional quasicrystals, and due to . There is no screw dislocation component of the phason part of a straight dislocation in a two-dimensional quasicrystal if the dislocation line is along the axis .
Equation (24) consists of four pieces, which are 5-vectors in the five-dimensional hyperspace (see [24]), namely the extended displacement vector of a straight dislocation with extended Burgers vector
the extended displacement vector of a line force with extended strength
the extended stress function vector of a straight dislocation with extended Burgers vector
and the extended stress function vector of a line force with extended strength
Moreover, the elastic self-energy of a straight dislocation per unit length is given by (see [24])
where and R are the inner and outer cutoff radii, and the elastic self-energy of a line force per unit length is given by (see [24])
5. Line Defects in Two-Dimensional Dodecagonal Quasicrystals of Laue Class 18
Dodecagonal quasicrystals are quasicrystals with non-crystallographic symmetry, namely a 12-fold symmetry axis. In particular, we consider two-dimensional dodecagonal quasicrystals of Laue class 18. Laue class 18 consists of the following non-crystallographic point groups [5,26]: , 1222, and . Laue class 18 is the Laue class with the highest symmetry for two-dimensional quasicrystals. We consider a line defect in a two-dimensional dodecagonal quasicrystal of Laue class 18 with a defect line parallel to the periodic direction (-axis) of the dodecagonal quasicrystal.
A two-dimensional dodecagonal quasicrystal of Laue class 18 (see [26,28,43]), with -axis chosen in the periodic direction and the -plane being the quasiperiodic plane, is characterized by five elastic moduli of phonons
four elastic moduli of phasons
and zero elastic moduli of phonon–phason coupling
Equation (38) means that phonons and phasons are decoupled in two-dimensional dodecagonal quasicrystals of Laue class 18. From the group theoretical point of view, the irreducible pieces of the phonon distortion tensor and the irreducible pieces of the phason distortion tensor transform under different irreducible representations and hence no phonon–phason coupling between the phonon distortion and phason distortion occurs (see [28,49]).
The conditions of positive definiteness for the elastic constants of two-dimensional dodecagonal quasicrystal of Laue class 18 to ensure positive elastic energy density (elastic stability) are given by [50]
For a two-dimensional dodecagonal quasicrystal of Laue class 18, Equations (14)–(16) reduce to
For generalized plane strain, only three elastic moduli of phonons , , , , and three elastic moduli of phasons , , , are relevant. In order to keep equations as simple as possible, we may use instead of in the formulas. For plane strain, there are only two elastic moduli of phonons (no ) and three elastic moduli of phasons. The number of the elastic moduli of phonons is the same as for isotropic solids. Therefore, in the -plane (basal plane), the 12-fold symmetry forces the tensor of the elastic moduli of phonons to be isotropic, whereas it does not impose enough constraints to make the tensor of the elastic moduli of phasons isotropic (see also [49,51]).
The four blocks of the matrix read
and
where
The angular behaviour of the matrices , and is obtained by the transformations
where
is the corresponding rotation matrix in the hyperspace where is the rotation angle about the -axis in the parallel space and is the rotation angle in the perpendicular space . For two-dimensional dodecagonal quasicrystals, there is the following special relation of the rotation angles (see [52]):
which is used in Equations (49)–(51) with Equation (52).
Carrying out the integrations explicitly, we obtain
where
where
and
where
5.1. Extended Displacement Vector of a Straight Dislocation
Now, substituting Equations (54), (62), (68) and (69) into Equation (30), the extended displacement vector of a straight dislocation with extended Burgers vector reads in matrix form
where
The five components of Equation (70) read explicitly
with . Equations (72) and (73) are the phonon displacement components of an edge dislocation with Burgers vector components and . Equation (74) is the phonon displacement component of a screw dislocation with Burgers vector component . Equations (75) and (76) are the phason displacement components of an edge dislocation with Burgers vector components and . As already mentioned in Section 4, there is no screw dislocation component of the phason part. It is interesting to note that the phonon components (72) and (73) and the phason components (75) and (76) have a similar mathematical form but with different pre-factors of the elastic constants. For the phonon components (72) and (73), the two elastic constants of phonons and contribute, while for the phason components (75) and (76), the three elastic constants of phasons , and contribute. The displacement components of a straight dislocation in two-dimensional dodecagonal quasicrystal of Laue class 18, Equations (72)–(76), are in agreement with the expressions for the phonon and phason displacement fields given by Yang et al. [43] using the technique of Green functions and by Qin et al. [44] using the generalized Eshelby method. The only difference is an irrelevant constant displacement in Equations (73) and (76), leading to instead of in [43]. The phonon displacement fields (72)–(74) take the same form as in hexagonal crystals. The isotropic limit of the phonon displacement fields (72) and (73) can be found in [25]. The contours of the extended displacement field components of an edge dislocation with extended Burgers vector are shown in Figure 1. In Figure 1a,c, the jump of the phonon field and the phason field can be seen. Figure 1b,d show the typical contours of the phonon field and the phason field depending on the elastic constants.
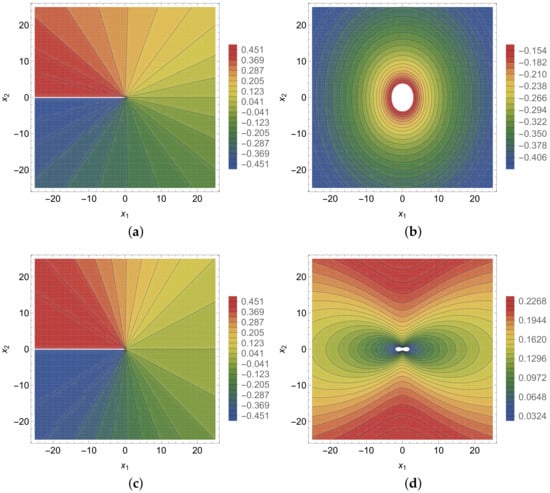
Figure 1.
Extended displacement field components of an edge dislocation with extended Burgers vector : (a) , (b) , (c) , (d) . Elastic constants are taken as , , , and (see [28]).
5.2. Extended Displacement Vector of a Line Force
If we substitute Equations (54), (62), (67) and (69) into Equation (31), then the extended displacement vector of a line force with extended strength reads in matrix form
and the five components of Equation (77) read explicitly
Equations (78)–(82) are the displacement components of a line force with strength components , , , and . The phonon components (78) and (79) and the phason components (81) and (82) have a similar mathematical form but with different pre-factors of the elastic constants. For the phonon components (78)–(80), the three elastic constants of phonons , and contribute, while for the phason components (81) and (82), the three elastic constants of phasons , and contribute. The phonon displacement fields (78)–(80) take the same form as in hexagonal crystals. The isotropic limit of the phonon displacement fields (78)–(80) has been given in [25].
5.3. Extended Stress Function Vector of a Straight Dislocation
Substituting Equations (59), (62), (68) and (69) into Equation (32), the extended stress function vector of a straight dislocation with extended Burgers vector reads in matrix form
where
The five components of Equation (83) read explicitly
Equations (85) and (86) are the phonon stress function components of an edge dislocation with Burgers vector components and . Equation (87) is the phonon stress function component of a screw dislocation with Burgers vector component . Equations (88) and (89) are the phason stress function components of an edge dislocation with Burgers vector components and . The phonon components (85) and (86) and the phason components (88) and (89) have a similar mathematical form but with different pre-factors of the elastic constants. For the phonon components (85)–(87), the three elastic constants of phonons , and contribute, while for the phason components (88) and (89), the three elastic constants of phasons , and contribute. The phonon stress functions (85)–(87) take the same form as in hexagonal crystals. The isotropic limit of the phonon stress functions (85)–(87) can be found in [25]. It is interesting to note the similarity between the displacements of a line force (78)–(82) and the stress functions of a dislocation (85)–(89).
5.4. Extended Stress Function Vector of a Line Force
Now, if we substitute Equations (59), (62), (67) and (69) into Equation (33), then the extended stress function vector of a line force with extended strength reads in matrix form
and the five components of Equation (90) read explicitly
Equations (91)–(95) are the stress functions of a line force with strength components , , , and . The phonon components (91) and (92) and the phason components (94) and (95) have a similar mathematical form but with different pre-factors of the elastic constants. For the phonon components (91) and (92), the two elastic constants of phonons and contribute, while for the phason components (94) and (95), the three elastic constants of phasons , and contribute. The phonon stress functions (91)–(93) take the same form as in hexagonal crystals. The isotropic limit of the phonon stress functions (85) and (86) has been given in [25]. It is interesting to note the similarity between the displacements of a dislocation (72)–(76) and the stress functions of a line force (91)–(95).
5.5. Self-Energy of a Line Defect
6. Green Tensor in the Integral Formalism
In the framework of the integral formalism, the displacement field of a line force, Equations (78)–(82), gives the two-dimensional Green tensor for quasicrystals in the hyperspace, namely
with
For generalized plane strain, the non-vanishing components of the two-dimensional Green tensor for two-dimensional dodecagonal quasicrystal of Laue class 18 read
The phonon components (102)–(105) take the same form as for hexagonal crystals. For plane strain, a corresponding two-dimensional Green tensor for two-dimensional dodecagonal quasicrystals has been given by Ding et al. [18]. The phonon components (102)–(104) and the phason components (106)–(108) have a similar mathematical form but with different pre-factors of the elastic constants. The phonon components of the Green tensor (102)–(105), are plotted in Figure 2. The phason components of the Green tensor (106)–(107), are plotted in Figure 3.
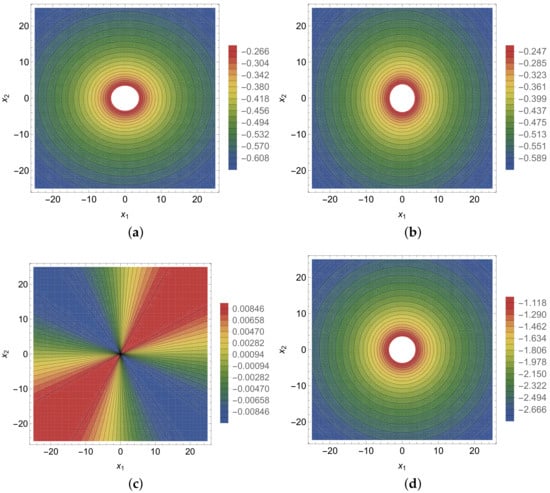
Figure 2.
Phonon components of the Green tensor: (a) , (b) , (c) and (d) . Phonon elastic constants are taken as , and (see [28]).
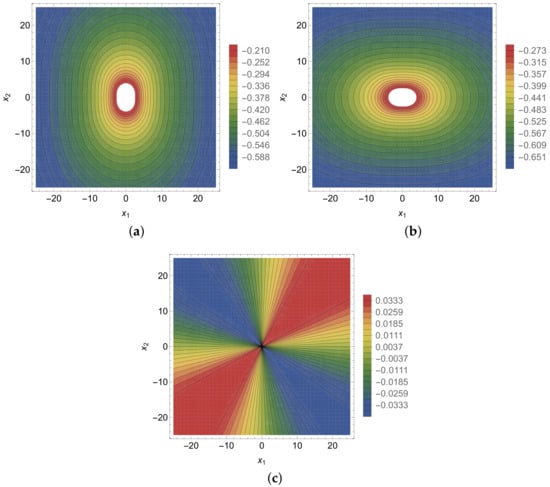
Figure 3.
Phason components of the Green tensor: (a) , (b) and (c) . Phason elastic constants are taken as , and (see [28]).
7. Conclusions
Using the ten-dimensional integral formalism for two-dimensional quasicrystals, we have derived exact analytical solutions of the displacement fields and stress functions of line defects, namely straight dislocations and line forces, parallel to the periodic direction in a two-dimensional dodecagonal quasicrystal of Laue class 18. Since the phonon–phason coupling is zero for two-dimensional dodecagonal quasicrystals, the displacement fields and the stress functions of straight dislocations and line forces can be dived into two independent parts, namely the phonon fields which take the same form as in hexagonal crystals and the phason fields which are more anisotropic. In addition, we have calculated the self-energy of a straight dislocation and the self-energy of a line force. The two-dimensional Green tensor of a two-dimensional dodecagonal quasicrystal of Laue class 18 has been derived within the framework of the integral formalism.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft, Grant Number LA1974/5-1.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Markus Lazar gratefully acknowledges the grant from the Deutsche Forschungsgemeinschaft (Grant number LA1974/5-1). The author wishes to thank Eleni Agiasofitou for their many useful and stimulating discussions on the fascinating subject of quasicrystals, in particular to point out the special role of dodecagonal quasicrystals.
Conflicts of Interest
The author declares no conflict of interest.
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.-W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Ding, D.-H. Symmetry groups, physical property tensors, elasticity and dislocations in quasicrystals. Rep. Prog. Phys. 2000, 63, 1–39. [Google Scholar] [CrossRef]
- Maciá-Barber, E. Quasicrystals: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Maciá, E. Alloy quasicrystals: Perspectives and some open questions at forty years. Symmetry 2023, 15, 2139. [Google Scholar] [CrossRef]
- Fan, T.Y. Mathematical Theory of Elasticity of Quasicrystals and Its Applications; Science Press and Springer Science+Business Media Singapore: Beijing, China, 2011. [Google Scholar]
- Bak, P. Symmetry, stability, and elastic properties of icosahedral incommensurate crystals. Phys. Rev. B 1985, 32, 5764–5772. [Google Scholar] [CrossRef] [PubMed]
- Levine, D.; Lubensky, T.C.; Ostlund, S.; Ramaswamy, S.; Steinhardt, P.J.; Toner, J. Elasticity and dislocations in pentagonal and icosahedral quasicrystals. Phys. Rev. Lett. 1985, 54, 1520–1523. [Google Scholar] [CrossRef] [PubMed]
- Socolar, J.E.S.; Lubensky, T.C.; Steinhardt, P.J. Phonons, phasons, and dislocations in quasicrystals. Phys. Rev. B 1986, 34, 3345–3360. [Google Scholar] [CrossRef] [PubMed]
- Lubensky, T.C.; Ramaswamy, S.; Toner, J. Dislocation motion in quasicrystals and implications for macroscopic properties. Phys. Rev. B 1986, 33, 7715–7719. [Google Scholar] [CrossRef]
- Edagawa, K. Dislocations in quasicrystals. Mater. Sci. Eng. A 2001, 309–310, 528–538. [Google Scholar] [CrossRef]
- Edagawa, K.; Takeuchi, S. Elasticity, dislocation and their motion in quasicrystals. In Dislocations in Solids; Nabarro, F.R.N., Hirth, J.P., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2007; Volume 13, pp. 365–417. [Google Scholar]
- Kleman, M. Phasons and the plastic deformation of quasicrystals. Eur. Phys. J. B 2003, 31, 315–325. [Google Scholar] [CrossRef]
- Wang, R.; Hu, C. Dislocations in quasicrystals. In Intermetallic Compounds—Principles and Practice: Progress; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2002; Volume 3, pp. 379–402. [Google Scholar]
- Feuerbacher, M. Dislocations in icosahedral quasicrystals. Chem. Soc. Rev. 2012, 41, 6745–6759. [Google Scholar] [CrossRef]
- Janot, G. Quasicrystals: A Primer, 2nd ed.; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Ding, D.-H.; Wang, W.; Hu, C.; Yang, R. Generalized elasticity theory of quasicrystals. Phys. Rev. B 1993, 48, 7003–7010. [Google Scholar] [CrossRef]
- Ding, D.; Yang, W.; Hu, C.; Wang, R. Linear elasticity theory of quasicrystals and defects in quasicrystals. In Materials Science Forum; Trans Tech Publications, Ltd.: Baech, Switzerland, 1994; Volumes 150–151, pp. 345–354. [Google Scholar]
- Ding, D.-H.; Wang, R.; Yang, W.; Hu, C. General expressions for the elastic displacement fields induced by dislocations in quasicrystals. J. Phys. Condens. Matter 1995, 7, 5423–5436. [Google Scholar] [CrossRef]
- Lazar, M.; Agiasofitou, E. Fundamentals in generalized elasticity and dislocation theory of quasicrystals: Green tensor, dislocation key-formulas and dislocation loops. Philos. Mag. 2014, 94, 4080–4101. [Google Scholar] [CrossRef]
- Ding, D.-H.; Wang, R.; Yang, W.; Hu, C.; Qin, Y. Elasticity theory of straight dislocations in quasicrystals. Philos. Mag. Lett. 1995, 72, 353–359. [Google Scholar] [CrossRef]
- Barnett, D.M.; Lothe, J. Synthesis of the sextic and the integral formalism for dislocations, Green’s function and structure waves in anisotropic elastic solids. Phys. Norv. 1973, 7, 13–19. [Google Scholar]
- Asaro, R.J.; Hirth, J.P.; Barnett, D.M.; Lothe, J. A further synthesis of sextic and integral theories for dislocations and line forces in anisotropic media. Phys. Status Solidi (b) 1973, 60, 261–271. [Google Scholar] [CrossRef]
- Ting, T.C.T. Anisotropic Elasticity; Oxford Science Publishers: Oxford, UK, 1996. [Google Scholar]
- Lazar, M. Line defects in quasicrystals. Crystals 2025, 15, 275. [Google Scholar] [CrossRef]
- Lazar, M. Line defects in one-dimensional hexagonal quasicrystals. Mathematics 2025, 13, 1493. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yang, W.; Ding, D. Point groups and elastic properties of two-dimensional quasicrystals. Acta Cryst. A 1996, 52, 251–256. [Google Scholar] [CrossRef]
- Grimmer, H. Elastic properties of two-dimensional quasicrystals. Acta Cryst. A 2008, 64, 459–464. [Google Scholar] [CrossRef]
- Lei, J.; Wang, R.; Hu, C.; Ding, D.-H. Diffuse scattering from dodecagonal quasicrystals. Eur. Phys. J. B 2000, 13, 21–30. [Google Scholar] [CrossRef]
- Ishimasa, T.; Nissen, H.U.; Fukano, Y. New ordered state between crystalline and amorphous in Ni–Cr particles. Phys. Rev. Lett. 1988, 55, 511–513. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Li, D.X.; Kuo, K.H. New type of two-dimensional quasicrystal with twelvefold rotational symmetry. Phys. Rev. Lett. 1988, 60, 1645–1648. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Yamada, T.; Taniguchi, Y. Long-period tetragonal lattice formation by solid-state alloying at the interfaces of Bi–Mn double-layer thin films. Acta Cryst. B 1989, 45, 40–45. [Google Scholar] [CrossRef]
- Conrad, M.; Krumeich, F.; Harbrecht, B. A dodecagonal quasicrystalline chalcogenide. Angew. Chem. Int. Ed. 1998, 37, 1383–1386. [Google Scholar] [CrossRef]
- Krumeich, F.; Conrad, M.; Nissen, H.U.; Harbrecht, B. The mesoscopic structure of disordered dodecagonal tantalum telluride: A high-resolution transmission electron microscopy study. Philos. Mag. Lett. 1998, 78, 357–367. [Google Scholar] [CrossRef]
- Yang, Q.B.; Wei, W.D. Description of the dodecagonal quasicrystal by a projection method. Phys. Rev. Lett. 1987, 58, 1020–1023. [Google Scholar] [CrossRef]
- Gähler, F. Crystallography of Dodecagonal Quasicrystals. In Quasicrystalline Materials; Janot, C., Dubois, J.M., Eds.; World Scientific: Singapore, 1988; pp. 272–284. [Google Scholar]
- Socolar, J.E.S. Simple octagonal and dodecagonal quasicrystals. Phys. Rev. B 1989, 39, 10519–10551. [Google Scholar] [CrossRef]
- Steurer, W. Twenty years of structure research on quasicrystals. Part I. Pentagonal, octagonal, decagonal and dodecagonal quasicrystals. Z. Kristallogr.-Cryst. Mater. 2004, 219, 391–446. [Google Scholar] [CrossRef]
- Krumeich, F.; Müller, E.; Wepf, R.A.; Conrad, M.; Reich, C.; Harbrecht, B.; Nesper, R. The structure of dodecagonal (Ta,V)1.6Te imaged by phase-contrast scanning transmission electron microscopy. J. Solid State Chem. 2012, 194, 106–112. [Google Scholar] [CrossRef]
- Förster, S.; Meinel, K.; Hammer, R.; Trautmann, M.; Widdra, W. Quasicrystalline structure formation in a classical crystalline thin-film system. Nature 2013, 502, 215–218. [Google Scholar] [CrossRef]
- Schenk, S.; Krahn, O.; Cockayne, E.; Meyerheim, H.L.; de Boissieu, M.; Förster, S.; Widdra, W. 2D honeycomb transformation into dodecagonal quasicrystals driven by electrostatic forces. Nat. Commun. 2022, 13, 7542. [Google Scholar] [CrossRef]
- Tokumoto, Y.; Hamano, K.; Nakagawa, S.; Kamimura, Y.; Suzuki, S.; Tamura, R.; Edagawa, K. Superconductivity in a van der Waals layered quasicrystal. Nat. Commun. 2024, 15, 1529. [Google Scholar] [CrossRef]
- De, P.; Pelcovits, R.A. Linear elasticity theory of pentagonal quasicrystals. Phys. Rev. B 1987, 35, 8609–8620. [Google Scholar] [CrossRef]
- Yang, W.; Lei, J.; Ding, D.-H.; Yang, R.; Hu, C. Elastic displacement fields induced by dislocations in dodecagonal quasicrystals. Phys. Lett. A 1995, 200, 177–183. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, R.; Ding, D.; Lei, J. Analytical expressions of the elastic displacement fields induced by straight dislocations in decagonal, octagonal and dodecagonal quasicrystals. J. Phys. Condens. Matter 1996, 9, 859–872. [Google Scholar] [CrossRef]
- Li, X.F.; Duan, X.Y.; Fan, T.Y.; Sun, Y.F. Elastic fields of a straight dislocation in a decagonal quasicrystal. J. Phys. Condens. Matter 1999, 11, 703–711. [Google Scholar] [CrossRef]
- Barak, G.; Lifshitz, R. Dislocation dynamics in a dodecagonal quasiperiodic structure. Philos. Mag. 2006, 86, 1059–1064. [Google Scholar] [CrossRef]
- Korkidi, L.; Barkan, K.; Lifshitz, R. Analysis of dislocations in quasicrystals composed of self-assembled nanoparticles. In Aperiodic Crystals; Schmid, S., Withers, R., Lifshitz, R., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 117–124. [Google Scholar]
- Lazar, M.; Agiasofitou, E. Eshelbian mechanics of novel materials: Quasicrystals. J. Micromech. Mol. Phys. 2016, 1, 1640008. [Google Scholar] [CrossRef]
- Hu, C.-Z.; Ding, D.-H.; Yang, W.-G. Expression of the elastic energy in two-dimensional quasicrystals. Acta Phys. Sin. (Overseas Ed.) 1993, 2, 42–47. [Google Scholar]
- Wang, J.; Zhang, R.; Ding, D.-H.; Wang, R. Positive-definite conditions of elastic constants of two-dimensional quasicrystals with noncrystallographic symmetries. Acta Cryst. A 1999, 55, 558–560. [Google Scholar] [CrossRef]
- Gong, P.; Hu, C.-Z.; Zhou, X.; Miao, L.; Wang, X. Isotropic and anisotropic properties of quasicrystals. Eur. Phys. J. B 2006, 52, 477–481. [Google Scholar] [CrossRef]
- Yang, W.; Wang, R.; Ding, D.-H.; Hu, C. Group-theoretical derivation of quadratic elastic invariants of two-dimensional quasicrystals of rank five and rank seven. J. Phys. Condens. Matter 1995, 7, 7099–7112. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).