Abstract
Secure autonomous secret key distillation (SKD) systems traditionally depend on external common randomness (CR) sources, which often suffer from instability and limited reliability over long-term operation. In this work, we propose a novel SKD architecture that synthesizes CR by combining a keystream of a shared-key keystream generator with locally generated binary Bernoulli noise. This construction emulates the statistical properties of the classical Maurer satellite scenario while enabling deterministic control over key parameters such as bit error rate, entropy, and leakage rate (LR). We derive a closed-form lower bound on the equivocation of the shared-secret key from the viewpoint of an adversary with access to public reconciliation data. This allows us to define an admissible operational region in which the system guarantees long-term secrecy through periodic key refreshes, without relying on advantage distillation. We integrate the Winnow protocol as the information reconciliation mechanism, optimized for short block lengths (), and analyze its performance in terms of efficiency, LR, and final key disagreement rate (KDR). The proposed system operates in two modes: ideal secrecy, achieving secret key rates up to 22% under stringent constraints (KDR < 10−5, LR < 10−10), and perfect secrecy mode, which approximately halves the key rate. Notably, these security guarantees are achieved autonomously, without reliance on advantage distillation or external CR sources. Theoretical findings are further supported by experimental verification demonstrating the practical viability of the proposed system under realistic conditions. This study introduces, for the first time, an autonomous CR-based SKD system with provable security performance independent of communication channels or external randomness, thus enhancing the practical viability of secure key distribution schemes.
Keywords:
common randomness; secret key distillaton; information reconciliation; secret key equivocation; keystream generator; ideal secrecy; perfect secrecy MSC:
94A60; 94A62
1. Introduction
This paper addresses the design and synthesis of artificial sources of common randomness (CR) suitable for autonomous secret key distillation (SKD) by public discussions. The proposed CR source is based on a shared-key keystream generator , combined with locally injected Bernoulli noise. This construction ensures equivalence with the classical Maurer satellite scenario [1] while affording precise and deterministic control over critical parameters, including key disagreement rate (KDR), secret key rate, and information leakage rate (LR). To fulfill these requirements, the synthesized CR source is required to satisfy the following conditions:
- General Accessibility: Both parties (Alice and Bob) can implement and observe the CR source efficiently.
- Integrity: An adversary (Eve) cannot influence or manipulate the generation parameters of the CR source.
- Optimality: The CR synthesis mechanism must be designed to maximize the achievable secrecy capacity of the SKD system, thereby operating at theoretical efficiency bounds.
- Key Security: The integration of the CR source with the SKD protocol must ensure provably secure key generation with rigorously bounded information LR, under the assumption that the adversary employs an optimal inference strategy based on complete knowledge of the public discussion and system specifications.
A key contribution of this work is the derivation of a closed-form lower bound on the equivocation of the secret key , ensuring provable secrecy even in the presence of public reconciliation data. This analytical result facilitates the rigorous characterization of an admissible operational region wherein long-term secrecy can be maintained through periodic key refresh without relying on traditional advantage distillation (AD) techniques.
The remainder of this paper is organized as follows:
Section 2 provides an overview of related works and discusses the key contributions and innovations of this study.
Section 3 presents the overall system architecture, detailing each component and their interactions within the SKD framework.
Section 4 provides an information-theoretic analysis of the proposed CR source, including the derivation of equivocation bounds and operation constraints.
Section 5 describes the design and performance analysis of the optimized CR KSG and Winnow reconciliation protocol with emphasis on secrecy performance and implementation feasibility.
Section 6 introduces two system operating modes of SKD based on CR KSG and Winnow reconciliation protocol: ideal secure and perfect secure mode.
Section 7 presents a computational complexity analysis of the proposed system and highlights its advantages compared to traditional SKD systems that rely on natural sources of common randomness.
Section 8 presents experimental verification to validate the theoretical analysis developed in Section 4, Section 5 and Section 6.
Section 9 provides security analysis and discusses practical considerations, implementation trade-offs, and design guidelines for deployment in real-world settings.
Section 10 concludes the paper with a summary of results and directions for future research.
2. Related Works and Contributions
The foundation of secret key agreement from correlated random sources was laid by works of Csiszár & Körner [2], Ahlswede & Csiszár [3], and Maurer [1], who introduced the satellite scenario to formalize secrecy generation in the presence of an eavesdropper. This model has since inspired significant research, particularly in quantum key distribution (QKD) and physical layer security, where the main sources of CR are different observable and measurable characteristics of the wireless communication channels between legitimate parties [4,5,6,7,8,9,10,11].
A principal limitation of secret key extraction from wireless channels lies in its strong dependence on channel dynamics and fluctuations, which significantly constrains the achievable secret key rate. Under conditions of frequent fading or deliberate jamming by an adversary, the volume of extractable secret key material typically becomes negligible, thereby rendering practical deployment infeasible [8,12].
Subsequent research has broadened the applicability of SKD beyond the physical layer, incorporating diverse CR source models, including those based on biometric signals [13,14,15,16]. However, a critical limitation of biometric signals as CR sources stems from the intrinsically bounded entropy of biometric patterns. In operational contexts requiring continuous and reliable real-time secret key generation, such sources are generally unsuitable or restricted to a limited subset of communication modalities—most notably, voice-based systems [16].
Artificial generation of common randomness via pseudorandom constructs has also been investigated, yet with limited attention to closed-form entropy analysis or integration with adaptive SKD protocols [12,17]. Notably, prior designs often depend on unstable or external entropy sources with inconsistent long-term performance.
Recent surveys have comprehensively analyzed key agreement and authentication protocols in IoT environments [18] and the use of intelligent reflecting surfaces to enhance physical layer secret key generation [19], emphasizing the practical challenges of secure key establishment under varying physical conditions. In parallel, advances in quantum information processing and integrated photonic platforms have led to high-performance heterodyne receivers supporting secure quantum random number generation and continuous-variable quantum key distribution (CV-QKD) with high secret key rates [20]. Techniques for establishing common randomness through round-trip travel times in packet data networks have been explored as a novel frontier in physical layer security, enabling secrecy level adaptation based on the similarity of common randomness [21]. Furthermore, random modulation has been utilized to enhance secret key generation over atmospheric optical channels, demonstrating practical improvements in the robustness and efficiency of key distribution schemes [22]. These developments collectively underscore the growing interest in autonomous and adaptable secret key generation mechanisms across classical, quantum, and hybrid environments, aligning with the motivation of the present study to design a scalable SKD system with bounded leakage and autonomous operation.
More recently, equivocation-based analysis, following Shannon’s original concept of ideal secrecy, has been used to evaluate the robustness of cryptographic protocols against adversaries observing public exchanges [23]. However, existing systems rarely incorporate mechanisms to ensure a quantifiable lower bound on equivocation over time.
This paper addresses these gaps by proposing a theoretically grounded and practically implementable system for CR synthesis based on deterministic keystream generators. It further integrates a high-efficiency, short-block Winnow protocol for reconciliation, optimized for minimal communication overhead and robustness under constrained bit error rate (BER) conditions.
Contributions and Innovations of This Work
This work introduces a structured approach for synthesizing artificial CR sources using a shared-key KSG and local pure randomness injection. The novelty of this system lies in its ability to deterministically emulate the statistical behavior of naturally correlated sources while enabling precise control over security-relevant parameters. The core innovations of the proposed architecture include:
- A formal mathematical framework for generating cryptographically secure common randomness from a deterministic keystream generator, enabling predictable system behavior.
- A tunable and transformable CR source that statistically mimics Maurer’s satellite model, but with enhanced control over secrecy capacity, KDR, and LR.
- Closed-form analytical expressions for bounding the equivocation of the secret key under conditions of full public discussion information (Theorem 1).
- A fully autonomous SKD system architecture, capable of internal key refreshing and separation of reusable versus system-maintenance keys (Theorem 2–4).
- Integration and optimization of the Winnow protocol for highly efficient reconciliation over short block lengths (e.g., ), resulting in low KDR and LR along with minimal communication overhead (Theorem 5 and 6).
- Identification of two system operating modes—ideal secrecy and perfect secrecy—in relation to system parameters, and determination of the maximum secret key generation rate in both modes (Theorem 7).
- Elimination of the AD phase without degrading secrecy performance, thereby simplifying protocol design and reducing complexity.
- Practical guidelines for system parameterization to maximize the achievable secrecy rate, while ensuring sustained key confidentiality through equivocation management.
3. System Architecture
Figure 1 shows the general architecture of the proposed autonomous system for secret key distillation based on public discussion.
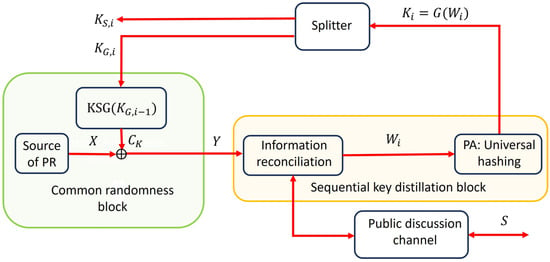
Figure 1.
Autonomous SKD systems that employ a synthetic source of CR based on a shared-key keystream generator and local pure randomness.
The system consists of three subsystems:
- A CR block, which functions as a source of common randomness;
- A SKD block, which performs information reconciliation (IR) and privacy amplification (PA);
- A Splitter, which divides the distilled secret key into two parts, , used for refreshing the secret key , and , intended for further cryptographic use. The lengths of and can be arbitrary, provided that their total length satisfies , and are typically chosen according to the system’s operational requirements.
In each operation cycle of the system, the CR block generates the output sequence by performing a bitwise modulo-2 addition (XOR) of the sequences and , i.e.,
Remark 1.
If Alice and Bob have a pre-shared secret key , they can generate their local sequences and
The probability of disagreement between those sequences, i.e., the BER is
where denotes binary convolution
If is adopted, then it follows:
The inverse relation also follows, which will be of interest in the subsequent discussion
Therefore, the proposed CR source can be considered as a variant of Maurer’s satellite scenario, where by controlling the parameter , any desired BER between Alice’s and Bob’s sequences can be achived; see Figure 2.
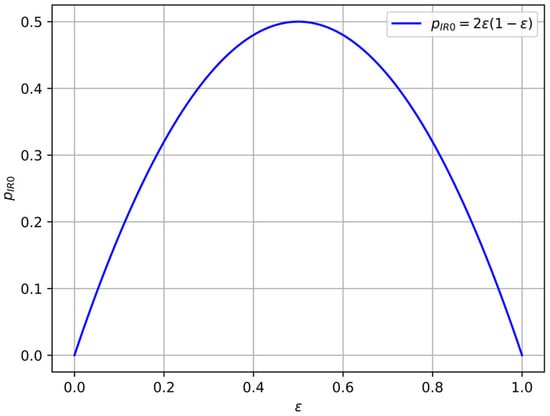
Figure 2.
Dependence (6) of the initial BER between Alice’s and Bob’s sequences on the parameter of the local source of pure randomness whose probability distribution is .
It should be noted that such precise control of the correlation properties of sequences generated in Maurer’s satellite scenario is practically impossible to achieve [11]. Moreover, if Eve does not possess the secret key , then the error probability between her sequence and Alice’s sequence is
given that
where denotes the keystream generated by the key stream generator , with Eve’s secret key Condition (9) is a mandatory property of any secure cryptographic and is closely related to the so-called avalanche effect; see [24,25]. Similarly, we obtain
Figure 3 illustrates the equivalent Maurer satellite scenario, where functions as a satellite, broadcasting the keystream . To this signal, binary additive noises are superimposed at Alice’s, Bob’s, and Eve’s channels. In the case of Alice’s and Bob’s channels, these noises correspond to sequences generated by local sources of pure randomness distributed according to Eve’s optimal strategy for selecting the sequence is
which is structurally identical to Alice’s and Bob’s sequences and , but generated with her own encryption key . Then, Eve’s equivalent binary noise relative to the satellite signal is given by
which has a Bernoulli distribution with parameter given by
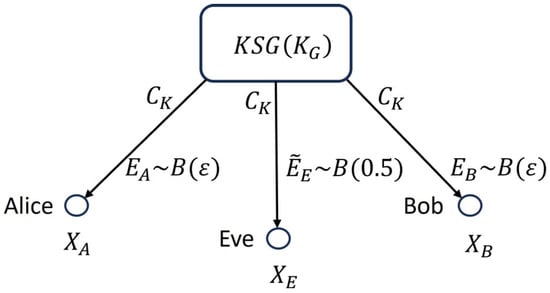
Figure 3.
Equivalent Maurer satellite scenario representation within the proposed SKD system. The satellite represents the shared-key keystream generator , which broadcasts the keystream . Independent binary additive noises , , and (locally generated binary Bernoulli sequences) are added on Alice’s, Bob’s, and Eve’s channels, respectively, illustrating how the system enables controlled correlation between legitimate parties while preserving secrecy against an adversary without the secret key .
Remark 2.
In the analyses presented, see (8)–(14), we have, among other considerations, employed the well-known result that the modulo-two sums of a binary sequence distributed as with an independent sequence distributed as , for any results in a sequence that remains distributed as . This result is a classical property in information theory, particularly within the analysis of the Binary Symmetric Channel (BSC), where it is well known that if the channel input is uniformly distributed (i.e., each bit is ) and the channel noise is an independent random variable, the channel output remains uniformly distributed regardless of the parameter . This property ensures that an adversary observing the output gains no information about the input, which underlies the statement that the “most secure change” of a sequence is achieved when each bit changes with probability 0.5. Although this property is often considered folklore, it is systematically presented in standard references such as [26,27,28]. Additionally, we would like to point out that this result aligns with the random-in/random-out property of non-expanding ciphers, as discussed by Massey [29], where it is shown that the cascade of a binary symmetric source (BSS), corresponding to a source, with a non-expanding cipher (such as additive stream ciphers or block ciphers) yields an output that is also a BSS, regardless of the secret key distribution. This implies that the ciphertext sequence is statistically independent of the secret key, guaranteeing that no information about the key can be obtained from the ciphertext alone, no matter how much ciphertext is observed by an adversary. This further supports the security principle that the highest level of uncertainty—and thus security—is achieved when bit changes occur with probability 0.5.
It is well known that, in the case of the satellite scenario (see [1]), the secrecy capacity, thus the maximum length of a secret key that can be distilled in the presence of an eavesdropper, is
where denotes the mutual information between and , while denotes this mutual information conditioned by . Taking into account (8) and (10), we conclude that Eve’s sequence is independent of Alice and Bob sequence and , which reduces (15) to
The advantage of the SKD strategy, which consists of applying PA to the result of the IR protocol, lies in achieving all secret key rates below the secrecy capacity , as well as its explicit practical implementation [1].
In the SKD block, a suitably chosen IR algorithm is first applied, whose primary function is to eliminate differences between Alice’s and Bob’s sequences by exchanging various types of parity information over the available public authenticated channel [1,4,30]. As a result of this phase, Alice and Bob share identical sequences with high probability (see Figure 1). In the final phase of the SKD protocol, PA is performed by Alice and Bob agreeing over the public channel on the choice of a compression function , to distill from a shorter string about which Eve has only a negligible amount of information [31,32]. As a rule, it is achieved by applying a suitable hash function from the class of universal hash functions [1,33,34]. Universality means that for any two different inputs, the chance they collide (hash to the same output) is at most . From Theorem 3 and Corollary 4 in [35], it follows that if the hash output length is at most the Rényi entropy of order 2 of the input minus a small security parameter, then the output is nearly indistinguishable from uniform. Moreover, if Eve holds some side information about the reconciled sequence (the input to the hash function) after the IR phase, then her information about the hash output becomes negligibly small, provided her conditional Rényi entropy of order 2 is greater than the hash output length minus a small security parameter.
In the splitter block, from the distilled key , the key is selected to refresh the secret key of , resulting in the updated , while the remaining part, , is reserved for subsequent use. From the system’s end-use perspective, the generation rate of usable secret keys is equal to the generation rate of .
The refresh rate of , is chosen such that Eve’s equivocation
never falls below a predetermined margin for every operation cycle , where denotes the total information that Eve obtains by observing the public channel during the execution of the SKD protocol for the -th block cycle.
Summary of Assumptions Made in the Design of Proposed System
Finally, let us summarize the assumptions made in the design of the proposed autonomous SKD systems from Figure 1. The proposed architecture operates under the following assumptions:
- Pre-shared secret key is available to Alice and Bob for initializing the keystream generator and is refreshed securely in each cycle.
- Both parties have trusted local sources of true randomness generating Bernoulli-distributed sequences with a tunable parameter , enabling precise control over the BER in the system, thus emulating a synthetic Maurer satellite scenario.
- The keystream generator satisfies the avalanche criterion, ensuring that without knowledge of , the keystream appears statistically indistinguishable from a Bernoulli sequence to an adversary.
- An authenticated public channel is available for IR and PA, assumed to be observable but not modifiable by an adversary.
- Eve is assumed to have unlimited computational power (information-theoretic security model) and complete access to the public channel, but no access to or the synchronized keystream.
- The system assumes the use of efficient IR protocols capable of reconciling Alice’s and Bob’s sequences to enable secret key rates approaching the secrecy capacity.
- PA is performed using universal hash functions, assuming sufficiently high conditional Rényi-2 entropy (or Shannon equivocation) of the reconciled sequences with respect to Eve’s view to ensure negligible leakage.
- Security is guaranteed cycle-by-cycle, with the refreshed secret key satisfying conditions (17), maintaining a controlled secrecy margin against any information Eve may have acquired through public communications
These assumptions ensure that the architecture enables autonomous secret key distillation while maintaining forward secrecy under practical, information-theoretic security constraints.
4. Information-Theoretic Analysis of the Source of Common Randomness Based on KSG(KG)
Theorem 1.
Let the set of information available to Eve over the public channel during the execution of the IR phase of an SKD protocol be denoted as , , where
Let denote the binary vector—mask associated with each , of the form
Then, the lower bound on the equivocation of the secret key of , based on observations from the public channel, is given by
where is the parameter of the Bernoulli distribution , of the random variable , and denotes the binary entropy function
Proof of Theorem 1.
According to [36], for every symmetric cipher system , where is the secret key, is the message, and is the ciphertext, the following holds
Based on Equation (18), it follows that
Therefore, the observations on the public channel can be regarded as the ciphertext of an equivalent cipher system , given that each sequence is generated by the corresponding using the same secret key The entropy of the equivalent plaintext is given by
Namely, Equation (25) directly follows from the fact that is the sum of i.i.d. random variables distributed according to ; see for example proofs in [37,38].
If the observations on the public channel are considered as the ciphertext of the cipher system , then the following equalities hold
The sum of these equations results in
Given that are mutually independent, the following holds
which, by substitution into (27), gives
Bearing in mind that the entropy satisfies the inequality , we obtain
which proves the claim (20) of the theorem. This completes the proof. □
Remark 3.
To assist the reader, we emphasize that Theorem 1 provides a lower bound on the uncertainty (equivocation) that an eavesdropper retains about the secret key even after observing all public communication. This result is crucial, as it ensures that the secret key maintains a provable level of secrecy regardless of public leakage. The bound directly quantifies how the entropy of the key is preserved, depending on the properties of the system’s injected randomness and the structure of the reconciliation masks.
Remark 4.
then, based on the observations , , from the public channel during the execution of the given IR protocol, Eve cannot reduce the initial uncertainty of the key below , where .
Knowing the lower bound of the equivocation of the secret key allows us to formulate conditions under which this bound never falls below a predetermined threshold . According to (20), if the following condition is satisfied:
Definition 1.
where is the security margin, is the length of initial Alice and Bob strings before starting IR protocol, while is so-called data remaining efficiency, defined as the ratio of the length of reconciliated sequences after completion of the IR protocol and the length of initial sequences, i.e.,
The admissible region of the system operation shown in Figure 1 is defined by the following constraints:
The denotes the so-called innovative or fresh entropy [38].
For the considered system, IE is actually the amount of entropy introduced into the system by the local source of randomness.
Condition (32) ensures the selection of the lower bound of the equivocation of the keys , as given by (33). Condition (34) guarantees the autonomy of the system in maintaining this lower bound. This is achieved through regular refreshing of the keys after each block of newly generated sequences of length , during which the system simultaneously distills keys for independent use. Condition (35) establishes a relation between the length of the distilled keys , the security margin , which reflects the compression rate of the PA block, and the length of the reconciled sequences resulting from the IR phase [1,35]. Condition (36) imposes the constraint on the length of the distilled keys and the amount of innovative entropy introduced in each system cycle. Through condition (37), the KDR is controlled. Typical values for range from 30 to 40, while is on the order of .
Remark 5.
The admissible region can also be defined using quantities normalized by the length , which allows clearer interpretation and visualization. Let us introduce the following notation for the normalized quantities of interest
These can now be interpreted as the corresponding rates. The corresponding definition of the normalized admissible region is given by the following set of constraints
It is particularly convenient to represent the admissible region in the coordinates (see Figure 4) where denotes the initial BER, , between Alice’s and Bob’s sequence at the beginning of the IR protocol. Theorem 2 provides the lower and upper bounds of the admissible region in coordinates in the general case.
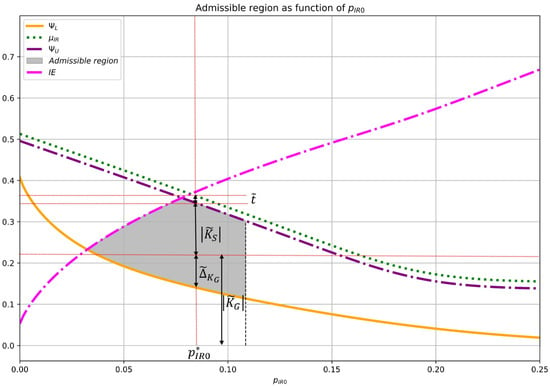
Figure 4.
Normalized admissible region as a function of the initial bit error rate between Alice and Bob’s sequence at the start of the IR protocol. The figure highlights the optimal operating point and the corresponding maximum achievable values for , , , and security margin . The yellow line represents the lower bound on Eve’s equivocation about the secret key when she has access to all information available over the public channel. The green dotted line indicates the remaining data efficiency of the IR protocol, as defined in (38), and also serves as the upper bound for the secret key distillation capacity of the CR SKD system; see (48). Taking into account the security margin , which ensures the predetermined key leakage level, this upper bound is reduced by , as shown by the purple dotted line. Finally, the admissible region is further constrained by the condition that the input innovative entropy (magenta dotted line) must exceed the entropy of the distilled keys in each operational cycle of the system.
Theorem 2.
and lower bound
where is data remaining efficiency of the applied IR protocol.
Let the set of information available to Eve over the public channel during the IR phase of a given SKD protocol be denoted by , , where each is given by equation (18), and denotes the binary mask vector associated with each , as defined in equation (19). Let denote the initial sequence length and the initial BER between Alice’s and Bob’s sequences. Then, the admissible region is bounded with upper
Proof of Theorem 2.
For each fixed , the upper bound corresponds with the maximum achievable rate of the distilled key, i.e.,
Based on constraints (43) and (44), we conclude that the following must hold simultaneously
from which it follows that
The lower bound is equal to the minimum achievable rate of the distilled key that guarantees system autonomy and the specified lower bound on the secret key equivocation (41) for a given , i.e.,
From (42) and (31), after normalizing by , we obtain
given that
The right side of equation (52) reaches its minimum value for and , giving
Taking into account (25) and (7), we find that
which into (54), results in (47). This completes the proof of the theorem. □
Based on Theorem 2, it immediately follows that for a given , where the maximum rate of distilled keys is
For a fixed , given the condition (42), the maximum rate of the usable component of the distilled keys is given by
The maximum possible equivocation for additionally fixed , given the condition (52), is
By combining (57) and (58), we obtain an alternative expression
Finally, from (57) and (57), it follows that
Figure 4 illustrates the relationships and interdependencies among the quantities ,,, and for an arbitrarily chosen , given by relations (56–60). Since it makes sense to consider only the maximum values for the quantities , and , in the following text they will be denoted without explicitly indicating that these are maximum values.
Based on (60), we can formulate the following theorem.
Theorem 3.
The maximum distillation rate of secret keys for further use is achieved at given by
Remark 6.
Theorem 3 identifies the optimal operating point of the system in terms of the initial bit error rate at which the maximum usable key rate is achieved. This result is significant for system designers, as it provides a clear criterion for tuning the parameters to maximize secure key output. Figure 4 now illustrates this optimal point and its associated values for all critical quantities.
For the autonomy of the proposed system, it is crucial that the successively generated keys are mutually independent.
Theorem 4.
where is the length of the block of sequence over which the IR protocol is executed, and is its data remaining efficiency given by (38).
Let a sequence of distilled keys , , be generated during the autonomous operation of the system shown in Figure 1. Then, it holds that
Proof of Theorem 4.
By applying the chain rule for entropy, it can be written
Since , and . The same joint entropy can be written in another way
given that and . By equating the right sides of the equations (64) and (65), we obtain
Since , from (66) it follows
According to Theorem 3 [32], the following holds
where the compression function
is a member of a universal class of hash functions [35], while denotes the second order Renyi entropy [31]. Since the random variables , , and , form a Markov chain, i.e., , it holds that
Thus, based on (67)–(70)
Considering that , , and , we finally obtain
which completes the proof. □
Remark 7.
Based on Theorem 4, we conclude that the secret keys generated by the CR KSG system have maximum entropy and are mutually independent. This property fully justifies expression (36) for the innovative entropy, which includes not only of a component originating from the local true random number generator but also of an additional component derived from the distillation of secret keys in the previous cycle of the system.
Remark 8.
In practical implementation, we fix the security margin t, affecting the compression rate of the hash function G, at t = 34 based on the leakage bound in Equation (62) of Theorem 4, which states that the key leakage is bounded by . This choice ensures that the leakage remains below while maintaining computational efficiency within the SKD system.
The specific shape of the admissible region depends on the choice of the IR protocol. In the following chapter, the admissible region will be analyzed in detail for the case when the IR protocol is based on the Winnow protocol [39].
5. Optimal SKD System Based on CR KSG and Winnow IR Protocol
According to Theorem 1, the crucial influence on the shape of the admissible region comes from the parity bit structure that Alice and Bob send over the public channel, i.e., the structure of the entire set of masks , , where . We denote by the CR KSG system in which the Winnow protocol is used for the IR phase of the SKD protocol. The choice of this IR protocol is based on its efficiency in the case of a small initial error between Alice’s and Bob’s sequences. Recall that in the CR KSG system , and according to (7) equivalently the parameter , are system design choices. Therefore, properly chosen will enable this protocol to correct errors efficiently and quickly with minimal communication while simultaneously preventing information leakage to Eve (so-called privacy maintenance) [39,40,41]. The Winnow protocol begins by dividing the initial sequences into data blocks of length . The choice of this length has been the subject of intensive analysis over the past two decades, predominantly within QKD algorithms. Reference [39] demonstrates that the Winnow protocol with shorter block lengths, especially for , is more efficient at error correction than with longer block lengths. Therefore, in the following, we adopt this value as a fixed parameter of the system. A detailed explanation of the protocol steps is provided below (Algorithms 1 and 2).
| Algorithm 1. The Winnow protocol |
| 1: Alice and Bob permute their initial key strings according to the negotiated rule and divide the permuted key strings into blocks of length , . |
| 2: Alice and Bob calculate the parity of each N-bit block. |
| 3: Alice and Bob compare their block parity pair. If the block parity pair is accordant error-correcting operation is not performed but the first bit of the block is discarded for privacy maintenance. Otherwise, an odd number of errors exist in the N-bit block, and the first bit of the block is discarded for privacy maintenance. Then, an error-correcting operation is performed with the Hamming algorithm for the remaining N-1 bits. |
| 4: Steps 1–3 are performed iteratively until the predetermined number of iterations are reached. |
| Algorithm 2. Hamming algorithm |
| a: Let be Alice’s (N-1)-bit string and be Bob’s (N-1)-bit string. Alice and Bob calculate r-bit syndromes and ,, and on their (N-1)-bit blocks, respectively, where is the Hamming check matrix. |
| b: Alice transmits to Bob, and errors are only discovered if the syndrome difference, , is non-zero, where . Bob corrects errors. |
| c: Finally, r bits are deleted from each block to prevent the potential loss of privacy to Eve due to the public transmission of Alice’s syndrome. |
The following theorem provides explicit expressions for the upper and lower bounds of the admissible region of , thereby enabling the optimal synthesis of the corresponding SKD system.
Theorem 5.
where is the data remaining efficiency of the Winnow protocol, and denotes the initial BER between Alice’s and Bob’s sequences. The variable denotes the number of parity blocks of length sent by Alice, while represents the number of her transmitted syndromes from the (7,4) Hamming error-correcting code.
The upper and lower bounds of the region , which corresponds to the system with the Winnow IR protocol, are given by the following expressions
Proof of Theorem 5.
During the execution of the Winnow protocol, two classes of parity bits are transmitted over the public channel
The class is computed for each block and exchanged with the other party. In terms of Theorem 1, all masks corresponding to this class have a fixed length of 8 and contain eight ones, i.e.,
The class is computed for each block in which Alice’s and Bob’s parity bits differ. The matrix is the parity-check matrix of the (7,4) Hamming error-correcting code, so is a three-bit syndrome of this code [42]. By examining the structure of the matrix , we observe that each row contains exactly four ones, which implies that the masks in this class satisfy the following property
Therefore, the sum in the expression for the lower bound (47) in Theorem 2 can be split into two terms: one corresponding to the parity bits from class and the other corresponding to the parity bits from class . Based on (77), we have and for classes and , respectively. Since , for all , we finally obtain
The factor of 2 in the first term arises from the fact that, in addition to Alice, Bob also sends his parity bits from class . By substituting (79) into (47), we obtain the statement (74) for the lower bound. The upper bound (73) follows directly from (46) by instantiating the general remaining data efficiency with , which corresponds to the Winnow protocol. This completes the proof of the theorem. □
In [40], a complete algorithm is presented for calculating , , , , and , where denotes the BER between Alice’s and Bob’s sequences at the end of the protocol. Figure 5, Figure 6 and Figure 7 show how these quantities vary as functions of , with the number of parity bits normalized with respect to the initial sequence length
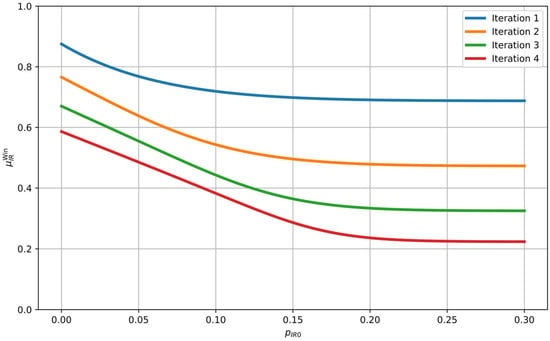
Figure 5.
Evolution of over four iterations of the Winnow protocol.
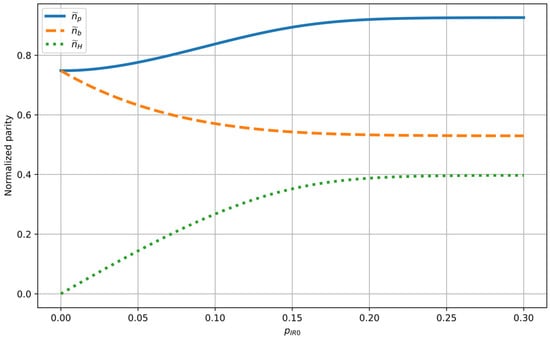
Figure 6.
Variation of normalized values , , and , as functions of after four iterations of the Winnow protocol.
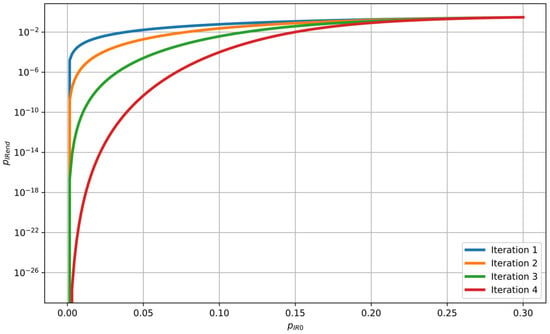
Figure 7.
Variation of the final BER between Alice’s and Bob’s sequences after the first four iterations of the Winnow protocol.
Remark 9.
The Winnow protocol iteratively applies the basic operations of dividing strings into blocks, exchanging block parity bits, computing and sending (7,4) Hamming code syndromes, performing error correction, and discarding a corresponding number of bits to maintain privacy. As the number of iterations increases, the value of decreases for every , as shown in Figure 5, thereby reducing the key distillation rate of the system. On the other hand, according to Figure 7, a smaller number of iterations increases for each , effectively reducing the key distillation rate. Therefore, selecting the number of iterations is a trade-off between these two opposing effects and is typically determined through experimental evaluation of the system. Our choice of a maximum of four iterations () has been practically confirmed as the optimal solution.
In Figure 8 (middle), the admissible region for the key distillation rate of the system is shown, with Winnow protocol parameters , , and an upper bound on the KDR .
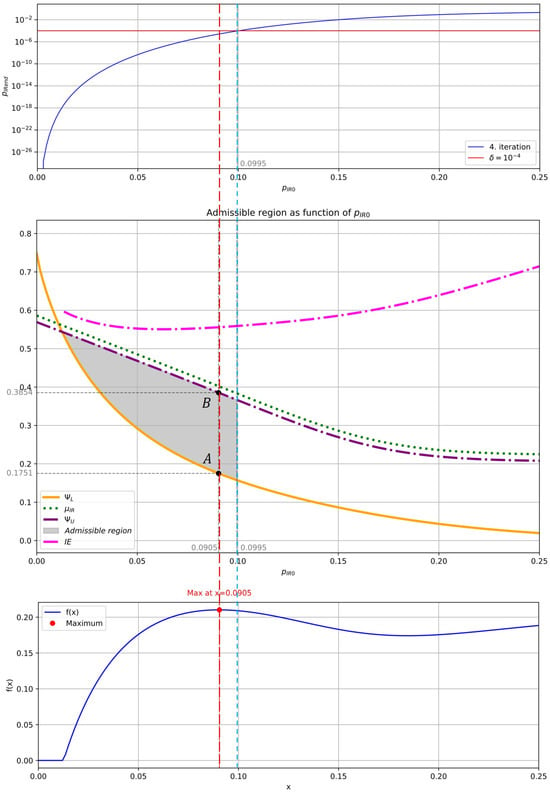
Figure 8.
Correspondence between the parameters and (top). Admissible region for the key distillation rate system, with Winnow protocol parameters , , and an upper bound on the KDR of (middle). The function and its maximum , achieved at , corresponding to (bottom).
In Figure 8 (top), the correspondence between the parameter and is shown, which determines the upper bound of the admissible region along the axis. Taking into account relation (7), the corresponding parameter is .
Based on Theorem 3, it follows that the maximum value of , regardless of the choice of , is achieved by finding the maximum of the function
Due to the highly complex analytical expressions for and , this maximum can be obtained numerically. Figure 8 (bottom) shows the function and its maximum , which is achieved at , corresponding to . Figure 8 (middle) shows points and on and , respectively, for the value. The coordinates of these points are
where and denote
The value , indicates an extremely low probability of KDR.
Remark 10.
and based on Equations (59) and (39), we obtain
where the constants and are given in Equation (83). For sufficiently large and sufficiently small r, from (84) we conclude that the asymptotic value of the maximal effective secrecy capacity is equal to = 0.2272, or 22.72%.
From Equation (60) and the definition of normalized values given in (39), we obtain
The effective secrecy capacity (84) can also be expressed in terms of , by substituting (85) into (84), which gives
The synthesis of the optimal system begins with the selection of the parameter and , which according to (87) uniquely determine the secrecy capacity ; see Figure 9.
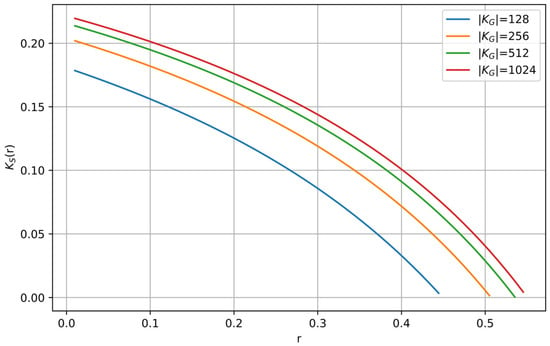
Figure 9.
The effective secrecy capacity given in (87) as a function of the parameter for various values of . The security margin is fixed at 34, according to explanation given in Remark 8.
The selection of the secret key length can be made based on various practical considerations. For example, if a standard KSG is used, such as AES, DES, or 3DES, which typically comes with predefined key lengths [41], then one of the available options is chosen.
This value uniquely determines the base block length , according to (85). Figure 10 shows the functions , for several typical values of .
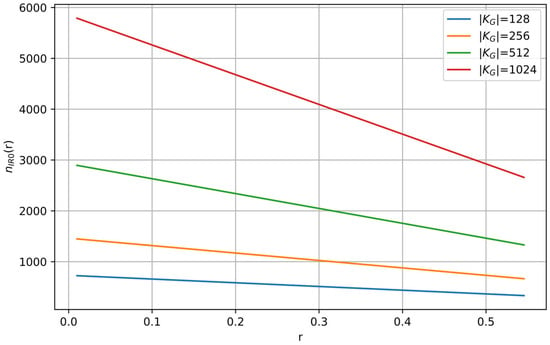
Figure 10.
Initial data block length given in (85) as a function of for various values of .
Example 1.

If we choose and , the resulting effective secrecy rate is , which is achieved by selecting a base block length of . In this case, the lower bound on equivocation is . The compression parameter is, as before, fixed at which ensures a leakage rate below , see Remark 8. Table 1 provides an overview of the values of and for typical values of , while maintaining the equivocation lower bound at a constant value of .

Table 1.
Maximum effective secret key rate and the corresponding base block length , for typical values of key length and a fixed security margin .
6. From Ideal Security Towards Perfect Security by SKD Based on CR KSG and Winnow IR Protocol
The security of the proposed SKD based on the CR KSG relies on the ideality of the KSG in the Shannon sense [36]. In Shannon’s definition of an ideal system, it is important that the key equivocation is not reduced to zero with an unlimited increase in the available ciphertext [36].
An extension of the original Shannon concept to the so-called Ideally Secret Autonomous Robust (ISAR) ciphering system was introduced in [23]. According to Definition 3, in [23], the ISAR ciphering system can maintain minimal key equivocation at a predefined value , independently of the message’s probability distribution and without an additional secret key distribution system.
Remark 11.
According to Theorem 1, common randomness block of proposed SKD based on CR KSG is an ISAR ciphering system, in which the ciphertext consists of all parity bits transmitted over the public channel. Therefore, an attack on the system aimed at reconstructing the key faces an uncertainty on the order of . In other words, the cryptanalyst is presented with equally probable hypothesis for the key .
Figure 11 illustrates an extension of the basic CR SKD System from Figure 1 to a system whose ultimate purpose is the generation of secret keys for the Vernam cipher [43], which is used to encrypt an independent message source . An intriguing question is whether and under what conditions this system can achieve perfect secrecy. To answer this question, it is necessary to prove the following theorem.
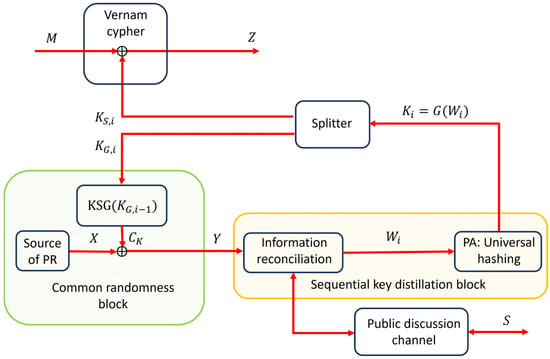
Figure 11.
Perfectly secure system based on SKD by CR KSG and Winnow IR protocol.
Theorem 6.
For the CR SKD system the following holds
Proof.
The information from the public channel, , available to Eve, is always in the form of parity bits given by
where are the bits of the mask vector associated with , as indicated in Theorem 1, Formulas (18) and (19). After transmitting the bit , Alice discards one bit from a known position within the current block of length , as a result of which Equation (90) is transformed into equation
Equation (91) can also be written in the following equivalent form
Since , knowing the parity bit does not provide any information about of the remaining bits. After the completion of the IR protocol, the sequence consists only of the bits that remain after the exclusion of the bits at positions . Eve gains no additional knowledge about their values, even though all parity bits transmitted over the public channel are available to her. Hence, , which is precisely the first claim of this theorem.
To prove statement (89), let us recall that for the conditional Rényi entropy of order two and the corresponding Shannon entropy, the following inequality holds
where equality is achieved only when , which is when the sequence has maximum entropy. Given that each bit in is of the form , , we conclude that , and therefore, from (93), it follows that
which completes the proof of the theorem. □
Remark 12.
Based on Corollary 5 [35], Theorems 4 and 6, it follows that
where is the compression rate of the applied universal hash function . In other words, Eve’s information about given and can be made arbitrarily small.
Theorem 7.
The system shown in Figure 11 is perfectly secret if
up to an error smaller than where t is the security margin defining the compression rate of the applied universal hash function G. The maximum effective secrecy rate, is given by
Proof.
A necessary and sufficient condition for perfect secrecy is that the eavesdropper’s observations do not change their uncertainty about the applied secret keys, that is, the following must hold
Note that the condition for perfect secrecy (98) involves the complete set of observations available to the attacker, not only the ciphertext , but also all the information from the public channel during the execution of the associated SKD protocol.
The relationship between , , and is defined by the Vernam cipher.
where and is independent of . It follows that is independent of , that is,
Based on (95), from (100) it follows that
which means that Eve’s entropy about the secret key is close to maximum, or in other words
with accuracy . This proves that the condition for perfect secrecy (98) holds with respect to the secret key .
On the other hand, since the CR block is an ISAR cryptosystem, it holds that
From (102) and (103), it follows that in the case when
the attacker gains no advantage in reconstructing compared to reconstructing since due to (103) and (104), they face a set of equally likely alternatives of the same cardinality , meaning that simultaneously the following holds
with accuracy . This completes the proof of the theorem. □
Remark 13.
where the constants and are given by (83), see
Figure 12. For sufficiently large , from (106), we conclude that the asymptotic value of the maximal effective secrecy capacity is equal to = 0.1136, or 11.36%.
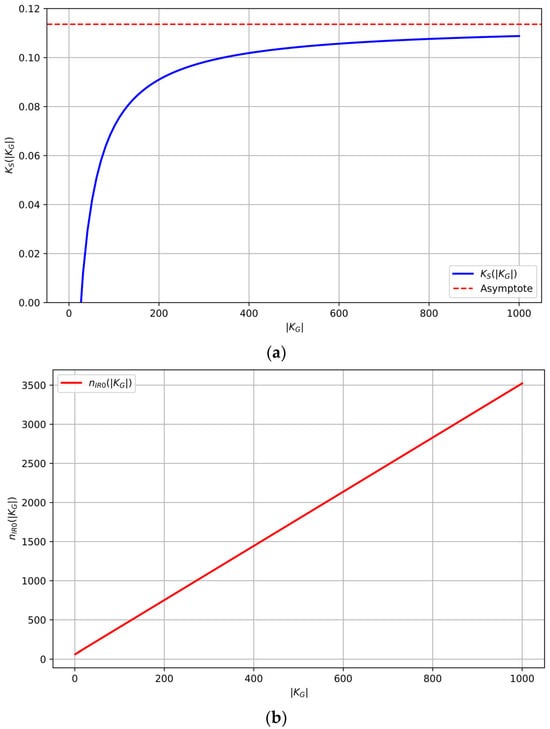
Starting from (84) and (85), we can derive expressions that relate the maximum and the length of the basic block with and the security margin

Figure 12.
(a) Maximum effective secrecy capacity as a function of the secret key length (top). The asymptotic value is also shown. (b) Required basic data block length as a function of the secret key length . The security margin defining the compression rate of the applied universal hash function G is fixed at .
The synthesis is straightforward and consists first of selecting and , which then uniquely determine . Note from Figure 12a, that once , we enter the saturation region where does not increase by more than 10%. Table 2 provides an overview of these values for standard settings.

Table 2.
Maximum effective rate of secret key generation and the corresponding basic block length , for typical key lengths and a security margin .
Example 2.
By selecting the optimal parameters , , , , we synthesized a perfectly secret autonomous encryption system capable of protecting an information source with a rate up to , with , and a key leakage rate .
The selection of the system’s operational mode fundamentally depends on the operational environment and the prioritized security requirements. If it is assessed that the adversary does not possess computational capabilities sufficient to feasibly analyze all hypotheses regarding the applied secret key within an acceptable timeframe, then the ideal security mode, with the corresponding equivocation bound on the secret keys, becomes the logical choice. Here, the acceptable analysis time is practically defined by the period during which the protected information retains its relevance. However, if the system is required to provide forward secrecy and ensure the impossibility of decryption regardless of the adversary’s computational resources, including quantum computing, then the perfect secrecy mode should be selected. The trade-off in this case is a reduction in the secret key distillation rate. In the subsequent Example 3, we present two practical scenarios in which each operational mode offers distinct advantages.
Example 3.
Mode Selection for Secure Communications.
Consider a secure messaging system in a high-latency environment (e.g., satellite communication). The system requires key updates every 60 s and operates with a constrained public channel. In this context, the ideal secrecy mode is appropriate—it enables higher secret key rates by tolerating a strictly bounded (but non-zero) leakage rate, ensuring timely key availability.
In contrast, a critical infrastructure application (e.g., defense-grade secure storage) may prioritize zero leakage over key throughput. For such use cases, the perfect secrecy mode is preferred, despite halving the key rate, as it guarantees zero information disclosure to an adversary even under full public observation.
Summary of Additional Assumptions Made in in the Design of Proposed Perfectly Secure System
For clarity, let us summarize the assumptions made in the design of the proposed autonomous perfectly secure system from Figure 11. In addition to the assumptions outlined for system from Figure 1, (see Section “Summary of Assumptions Made in the Design of Proposed System”), the system in Figure 11 assumes:
- The secret key output from the SKD system is used for encryption of an independent message source under the Vernam cipher, requiring statistical independence between and .
- The distilled key is uniformly distributed , ensuring maximum entropy, and its length is dimensioned to match the secrecy margin, i.e., , maintaining effective secrecy when used for encryption.
- The Winnow IR protocol is implemented with puncturing, ensuring that the leakage of parity bits over the public channel does not reduce the entropy of the reconciled sequence, satisfying .
- The system operates with sufficient block lengths and a chosen compression rate to achieve the perfect secrecy region within a negligible error, ensuring that holds to within an error bounded by , where is the compression rate of the universal hash function.
- The CR SKD block is assumed to function as an ISAR cryptosystem, maintaining the secrecy margin on the key even under unlimited ciphertext exposure, with .
- The authenticated but public communication channel remains assumed secure against injection or modification by the adversary, consistent with the assumptions made for system from Figure 1.
These additional assumptions collectively enable the system to transition from ideal secrecy to practical perfect secrecy in the Shannon sense, ensuring the effective and autonomous generation of secure keys for Vernam encryption under practical conditions.
7. Computational Complexity and Overhead Analysis
The proposed autonomous SKD system based on a synthetic CR source using a shared-key keystream generator and local pure randomness achieves bounded, predictable computational complexity and communication overhead per cycle, which is critical for deployment in embedded and resource-constrained environments.
7.1. CR Generation Phase
The CR block performs bitwise modulo-2 addition (XOR) between the local Bernoulli-generated sequence and the keystream from , see (1), requiring n XOR operations per data block of length . The generation of involves calls to a local random number generator (RNG), while the satisfies the avalanche criterion and typically requires a fixed, small number of operations per bit depending on the implementation. Table 3 provides a structured comparison of widely used that can be employed within SKD systems, focusing on their operational complexity, memory footprint, and throughput performance under practical conditions.

Table 3.
Comparison of stream cipher keystream generators for SKD systems.
The table includes:
- AES in CTR/OFB mode, representing a high-security, block-cipher-based KSG with higher per-bit cost in pure software but highly efficient under AES-NI [44,45,46].
- Lightweight stream ciphers (Grain v1 [47,48], Trivium [48,49]), illustrating extremely low per-bit complexity and minimal memory requirements suitable for resource-constrained SKD embedded implementations with minimal RAM and low power.
- ChaCha20 [50,51] and HC-128 [48,52], demonstrating high throughput and balanced security for SKD systems eliminating the need for hardware accelerators.
Based on these findings, we conclude that for autonomous SKD with :
- AES remains suitable when hardware AES-NI support is available, ensuring low latency and secure keystream generation.
- Grain/Trivium may be preferable in microcontroller-based SKD nodes due to minimal computational complexity and energy usage.
7.2. Comparative Operational Complexity per Secret Key Bit in SKD Systems
When comparing SKD architectures, the supreme criterion for practical viability is the operational complexity per distilled secret key bit under equivalent security guarantees. To enable a fair and insightful comparison, consider:
- System A: A classical SKD system based on natural CR sources (e.g., wireless fading, biometric signals) requiring an AD phase to reduce Eve’s correlation while increasing Alice-Bob correlation.
- System B (Proposed): An autonomous SKD system using a synthetic CR source created by combining a local Bernoulli random sequence with a keystream from a shared-key generator, . This architecture completely removes the need for AD, operating with maximum intrinsic correlation and maximum second-order Rényi entropy.
The AD phase in System A requires exponentially more initial raw data to achieve the same final block length at the end of IR phase, particularly under high initial Eve–Alice correlations, see [1,40]. The produced sequence has reduced second-order Rényi entropy, necessitating greater compression during PA to meet security parameters. System A typically undergoes a compression , [53] where, due to residual correlation with Eve side information leading to a significantly lower yield of distilled secret bits per cycle.
In contrast, System B ensures that the second-order Rényi entropy equals the maximal Shannon entropy for the reconciled sequence. This allows the PA step to operate with minimal compression , where is a fixed security margin independent of data block of length .
As a result, for a reasonably large , the final distilled secret key length is close in System B but can be dramatically smaller in System A.
Given that both systems have similar complexity in IR (Winnow: )) and PA (Toeplitz universal hash: , see [54,55]) the effective per-distilled-bit complexity for System A becomes significantly higher due to the necessity of AD, and reduced output length after PA.
In contrast, System B requires only the additional cost of generating the keystream using , which can be efficiently implemented with ~1–15 operations per generated keystream bit depending on the chosen KSG (AES, Grain, Trivium, etc.) and minimal additional RAM and energy overhead, see Table 3.
Moreover, this advantage increases for System B as the initial Eve–Alice correlation in System A increases, further reducing System A’s efficiency. Thus, the proposed architecture not only simplifies the protocol stack by eliminating the AD phase but also maximizes the effective key rate while minimizing operational and communication overheads, achieving superior efficiency for secure autonomous SKD in practical deployments.
8. Experimental Verification
To confirm the theoretical analysis presented in Section 4, Section 5 and Section 6, we conducted 1000 repeated simulations of the proposed CR-based SKD system operating in perfect secrecy mode with a basic data block length of bits per run.
Figure 13 shows the empirical spread of the measured all four system parameter curves (yellow, pink, red, green), displaying the one-sigma confidence regions around each curve. The results show excellent agreement between the simulated and theoretical predictions from Figure 8, confirming the accuracy of the analytical model under perfect secrecy constraints.
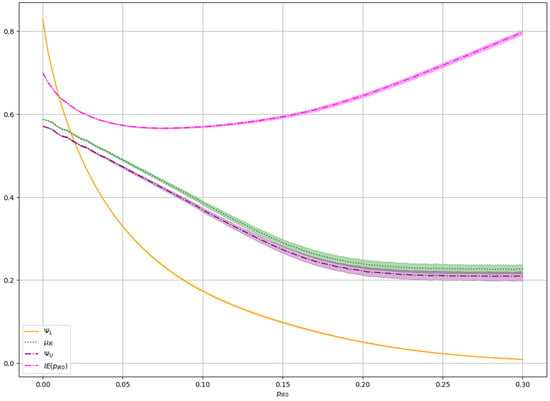
Figure 13.
Empirical one-sigma spread of the measured secret key rates under perfect secrecy mode across 1000 simulation runs of the proposed CR-based SKD system with bits. The yellow lines represent the lower bound on Eve’s equivocation. The green lines are the remaining data efficiency of the IR protocol. The upper bound reduced by security margin is shown by the purple lines. The input innovative entropy is represented by magenta lines.
Figure 14 presents the histogram of the generated perfectly secret key lengths across all simulation runs (solid line), with the vertical dashed line indicating the theoretically expected value calculated using Equations (106) and (107). Due to the low variance observed in the simulations, we conclude that the experimental and theoretical results for the perfect secret key rate exhibit exceptional agreement. The expected theoretical value for the distilled secret key rate was computed as: , confirming the system’s ability to consistently generate secret keys at the predicted rate while maintaining perfect secrecy.
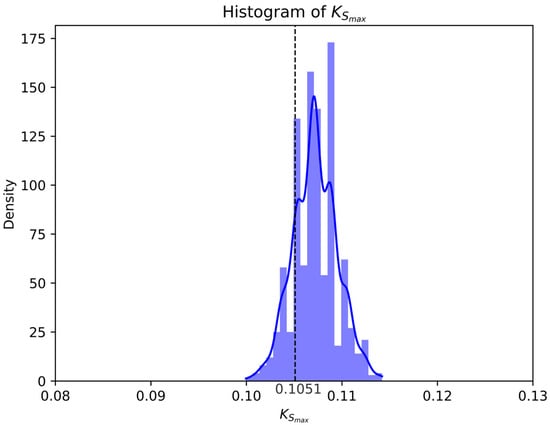
Figure 14.
Histogram of the generated perfectly secret key lengths across 1000 simulation runs (solid line). The vertical dashed line marks the theoretically expected value of the secret key rate . The low variance demonstrates the exceptional agreement between experimental and theoretical results.
The yellow, purple, magenta, and green curves represent different system parameter configurations. The excellent agreement with theoretical predictions from Figure 8 validates the analytical model.
9. Security Analysis and Practical Consideration
Generic attacks on SKD systems are based on optimal eavesdropper strategies for estimating the sequence . Based on Theorem 6, we conclude that the proposed system is resistant to this type of attack. However, strategies for reconstructing the secret key are the most critical for this class of systems. If Eve is able to reconstruct , she obtains the same keystream as Alice and Bob. In that case, Eve’s optimal strategy consists of generating her own local binary noise and tracking all steps of the IR and PA protocols executed by Alice and Bob [1]. In that case, based on Equation (15), we obtain that the secrecy capacity is
given that
and assuming that the AD protocol is not applied, which could otherwise shift the advantage to Alice and Bob over Eve. This type of attack is prevented in the CR KSG system by continuously maintaining the equivocation above a predefined threshold . In practical terms, this means that in every operational cycle, the adversary is faced with equally likely hypotheses about the key , making the system ideally secure in the Shannon sense. As shown in Remark 10, within this mode of operation, referred to as the ideal security regime, it is possible to select appropriate parameters to ensure a desired trade-off between the secret key distillation rate and the lower bound on the key equivocation.
In Section 5, Theorem 7 demonstrates how the CR KSG system transitions into the regime of perfect secrecy by equalizing the equivocations of the distilled keys and the KSG secret key. When this regime is compared to the ideal security regime, it becomes evident that the cost of achieving perfect secrecy is a reduction in the effective secret key distillation rate.
Remark 14.
The distribution of the initial value can be carried out in several ways depending on the security environment of the system. (a) Within well-organized permanent protection systems, the policy of using cryptographic keys can ensure that previously distributed keys are never exhausted to the end. A predefined remainder can be saved for the initial and the start of the autonomous CR KSG system. (b) In other cases, can be distilled by a previous independent stage of SKD based on biometric sources of CR, such as, e.g., EEG or voice [13,14,56].
The proposed autonomous SKD system can always be implemented in practice, provided that the parties involved in the protocol have access to a public authenticated channel with sufficient capacity. To quantify this requirement, we introduce a measure of the load of the public channel per distilled secret key bit
or taking into account (85), we can express in equivalent form
Figure 15 shows the dependence given by (111) for different values of , when the system operates in the ideal secrecy mode. In the case of perfect secrecy, based on (106), we obtain the following dependence
which is shown in Figure 16.
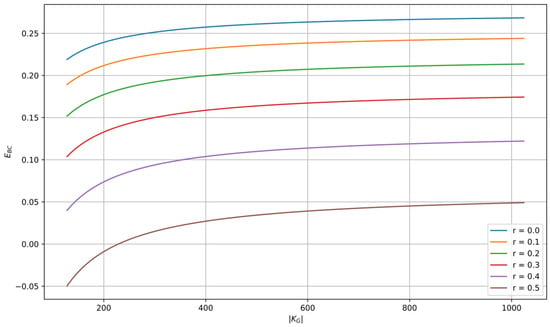
Figure 15.
Dependence of the public channel load measure on for different values of in the ideal security operating mode.
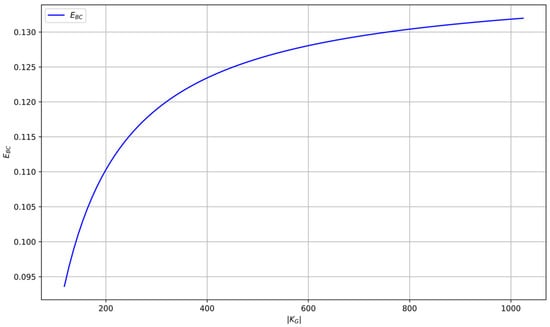
Figure 16.
Dependence of the public channel load measure on in the perfect security operating mode.
Based on these dependencies, we can conclude that in the perfect secrecy operating mode, for , this ratio is not less than 1/8. In other words, for the online operation of an autonomous, perfectly secret CR KSG system, the public channel must support transmission speeds approximately eight times greater than the rate of the information source being protected. From Figure 15, we observe that for the same values of , and a secret key equivocation of approximately 128 bits , this requirement is significantly lower, just around 5 times. In the era of modern telecommunications and the internet, this demand does not pose a serious challenge. In offline operation mode, the limitation of the transmission speed over the public channel only affects the time needed to distill the required amount of secret keys.
The practical application of autonomous CR KSG systems encompasses a wide range of scenarios, from commercial to strategic uses for the security of critical infrastructure, diplomatic correspondence, and cover communications during military operations. Since specialized and complex cryptographic key generation and distribution systems are typically developed at strategic levels, autonomous CR KSG systems are ideal as backup systems that can assume their function in the event of failure, compromise, or destruction of the primary systems.
In military applications, these systems become especially attractive due to the widespread availability of mobile internet, such as Starlink. In the event of disruption of standard secure communication links, which are critical for the successful conduct of military or special operations, autonomous CR KSG systems can take over the role of generating and distributing cryptographic keys. For example, the war in Ukraine has demonstrated that the ubiquity of the Starlink system potentially enables perfectly secure communication with central or regional commands even in conditions where military units are completely isolated or surrounded, despite not having been previously supplied with cryptographic keys or having exhausted them entirely.
Limitation of Proposed Systems
While the proposed architectures aim to achieve practical perfect secrecy in the Shannon sense, several limitations merit discussion.
- The systems rely on the availability of trusted, high-quality local randomness sources, whose continuous entropy guarantees and unbiased generation are critical but challenging in practice.
- The requirement for a pre-shared secret key , while refreshed autonomously, necessitates an initial secure distribution step.
- The models assume an authenticated public channel immune to modification, requiring additional mechanisms and key resources for robust authentication.
- While the ISAR framework provides theoretical secrecy under unlimited ciphertext observation, practical implementations may face side-channel or physical security challenges affecting effective secrecy.
- Finite block lengths introduce deviations from asymptotic secrecy rates, with practical IR errors and compression factors impacting performance.
- Achieving low BER regimes to maximize secrecy rates may incur latency and throughput trade-offs, particularly for large block operations.
- While information-theoretic security is computation-independent, practical implementations of , Winnow IR, and universal hashing must be carefully designed to avoid vulnerabilities and inefficiencies.
- The proposed models focus on message secrecy and do not inherently address traffic analysis resistance, which remains an open area for further development.
Addressing these limitations represents important directions for advancing autonomous, practically secure key distillation and encryption systems.
10. Conclusions
This paper introduces a new SKD paradigm using synthetic CR based on KSG with shared secret key and locally generated binary Bernoulli noise. We have shown that the introduced source of CR meets all the requirements mentioned in the introduction of the paper: general accessibility, integrity, optimality, and key security.
This paradigm offers a comprehensive approach to secure key distribution, combining theoretical rigor with practical applicability. The proposed design has been both theoretically analyzed and practically validated, demonstrating the following key features:
- Parameter-controlled equivocation: The system allows for adjustable equivocation levels, enabling fine-tuning of security parameters to meet specific requirements.
- High-efficiency Winnow-based reconciliation: By implementing the Winnow protocol, the design achieves efficient error reconciliation with reduced communication overhead, enhancing overall system performance.
- Autonomous key refresh: The architecture supports automatic key renewal processes, ensuring sustained security without manual intervention.
- Secure operation without AD: The system maintains robust security standards without relying on AD techniques, simplifying the implementation.
- Explicit optimal design: The framework is explicitly optimized to maximize the secrecy capacity of distilled keys while minimizing potential information leakage to eavesdroppers.
- Dual modes of operation: The system can operate in two distinct modes—ideal and perfect secrecy—providing flexibility to adapt to various security scenarios.
Based on the experimental verification, the proposed SKD system reliably achieves secret key rates close to the theoretical secrecy capacity while maintaining low BER and high collision entropy. The consistent high levels of entropy across repeated simulations confirm that the system remains secure against passive eavesdroppers even under finite-length conditions, thus making it suitable for practical lightweight secure communication systems.
As a direction for future work, we aim to extend the current framework to support adaptive SKD systems that dynamically adjust key generation parameters in response to real-time system conditions, such as varying bit error rates and entropy availability. Another promising direction involves exploring hardware implementations of the proposed architecture under resource-constrained settings, including IoT and edge computing environments. Additionally, integrating post-quantum primitives with the CR KSG model could enhance resilience against future quantum adversaries while maintaining the system’s autonomous operation and bounded leakage guarantees.
Finally, we note that proposed general system design is readily applicable to other information reconciliation protocols, including those based on BCH, LDPC, and Polar Codes (PC) [57], with the potential to extend the optimization methodologies demonstrated here using the Winnow protocol.
Author Contributions
Conceptualization, D.C. and M.M.; methodology, D.C. and M.M.; software, J.R., N.L., T.U. and M.V.; validation, M.M., J.R., N.L., T.U. and M.V.; formal analysis, D.C. and M.M.; investigation, D.C., M.M., J.R. and N.L.; resources, J.R. and M.V.; data curation, D.C., J.R., N.L., T.U. and M.V.; writing—original draft preparation, D.C.; writing—review and editing, M.M. and J.R.; visualization, M.M. and J.R.; supervision, M.M. and M.V.; project administration, D.C., J.R. and N.L.; funding acquisition, D.C., M.M., T.U. and M.V. All authors have read and agreed to the published version of the manuscript.
Funding
The research is funded by the Vlatacom Institute of High Technologies under Project #164 EEG_Keys.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations and notations are used in this manuscript:
| KSG | Key Stream Generator |
| CR | Common Randomness |
| SKD | Secret Key Distillation |
| QKD | Quantum Key Distribution |
| AD | Advantage Distillation |
| IR | Information Reconciliation |
| PA | Privacy Amplification |
| LR | Leakage Rate |
| KDR | Key Disagreement Rate |
| BER | Bit Error Rate |
| IE | Innovative Entropy |
| AES | Advanced Encryption Standard |
| DES | Data Encryption Standard |
| 3DES | Triple Data Encryption Standard |
| BCH | Bose–Chaudhuri–Hocquenghem |
| PC | Polar Codes |
| LDPC | Low-Density Parity-Check |
| ISAR | Ideally Secret Autonomous Robust |
| RNG | Random Number Generator |
| RAM | Random Access Memory |
| CTR/OFB | Counter/Output Feedback mode |
| AES-NI | Advanced Encryption Standard—New Instructions |
| Notations | |
| Part of distilled secret key used for refreshing | |
| Block length of Winnow protocol | |
| Distilled secret key | |
| Part of secret key used for encryption | |
| Random sequence | |
| Running key (or keystream) | |
| Parameter of the Bernoulli distribution | |
| Secrecy capacity | |
| Total information that Eve obtains by observing the public channel during the execution of the SKD protocol | |
| equivocation margin | |
| Number of total information that Eve obtains by observing the public channel during the execution of the SKD protocol | |
| Equivalent keystream | |
| Equivalent plaintext | |
| Security margin | |
| Length of initial Alice and Bob strings before starting IR protocol | |
| Data remaining efficiency | |
| Length of reconciliated sequences after completion of the IR protocol | |
| Admissible region | |
| Normalized variable | |
| Upper bound of admissible region | |
| Lower bound of admissible region | |
| Initial BER between Alice’s and Bob’s sequence | |
| Sequence after IR protocol | |
| sent by Alice | |
| Number of transmitted syndromes by Alice | |
| Class of parity bits representing syndrome | |
| BER between Alice’s and Bob’s sequences at the end of the IR protocol | |
| Universal hash function | |
| Ciphertext | |
References
- Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Csiszar, I.; Korner, J. Broadcast channels with confidential messages. IEEE Trans. Inform. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszar, I. Common randomness in information theory and cryptography. Part I: Secret sharing. IEEE Trans. Inf. Theory 1993, 39, 1121–1132. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dusek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Wang, Q.; Zhang, J.; Ng, S.X.; Hanzo, L. The evolution of quantum key distribution networks: On the road to the qinternet. IEEE Commun. Surv. Tutor. 2022, 24, 839–894. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Zhang, J.; Duong, T.Q.; Marshall, A.; Woods, R. Key generation from wireless channels: A review. IEEE Access 2016, 4, 614–626. [Google Scholar] [CrossRef]
- Li, G.; Sun, C.; Zhang, J.; Jorswieck, E.; Xiao, B.; Hu, A. Physical layer key generation in 5G and beyond wireless communications: Challenges and opportunities. Entropy 2019, 21, 497. [Google Scholar] [CrossRef]
- Zhang, J.; Duong, T.Q.; Woods, R.; Marshall, A. Securing wireless communications of the Internet of Things from the physical layer, an overview. Entropy 2017, 19, 420. [Google Scholar] [CrossRef]
- Jost, D.; Maurer, U.; Ribeiro, J.L. Information-theoretic secret-key agreement: The asymptotically tight relation between the secret-key rate and the channel quality ratio. In Theory of Cryptography, TCC 2018; Beimel, A., Dziembowski, S., Eds.; Springer: Cham, Switzerland, 2018; Volume 11239. [Google Scholar] [CrossRef]
- Alwazani, H.; Chaaban, A. Disruptive RIS for Enhancing Key Generation and Secret Transmission in Low-Entropy Environments. arXiv 2024, arXiv:2409.15303. [Google Scholar] [CrossRef]
- Radomirović, J.; Milosavljević, M.; Kovačević, B.; Jovanović, M. Secret key distillation with speech input and deep neural network-controlled privacy amplification. Mathematics 2023, 11, 1524. [Google Scholar] [CrossRef]
- Galis, M.; Milosavljević, M.; Jevremović, A.; Banjac, Z.; Makarov, A.; Radomirović, J. Secret-key agreement by asynchronous EEG over authenticated public channels. Entropy 2021, 23, 1327. [Google Scholar] [CrossRef] [PubMed]
- Pourbemany, J.; Zhu, Y.; Bettati, R. Survey of wearable devices pairing based on biometric signals. arXiv 2021, arXiv:2107.11685v1. [Google Scholar] [CrossRef]
- Radomirović, J.; Milosavljević, M.; Čubrilović, S.; Kuzmanović, Z.; Perić, M.; Banjac, Z.; Perić, D. A Class of Perfectly Secret Autonomous Low-Bit-Rate Voice Communication Systems. Symmetry 2025, 17, 365. [Google Scholar] [CrossRef]
- Tomaru, T. Secret key generation from channel noise with the help of a common key. arXiv 2018, arXiv:1803.05090. [Google Scholar] [CrossRef]
- Szymoniak, S.; Kesar, S. Key Agreement and Authentication Protocols in the Internet of Things: A Survey. Appl. Sci. 2023, 13, 404. [Google Scholar] [CrossRef]
- Xia, E.; Hu, B.-J.; Shen, Q. A Survey of Physical Layer Secret Key Generation Enhanced by Intelligent Reflecting Surface. Electronics 2024, 13, 258. [Google Scholar] [CrossRef]
- Peri, A.; Gualandi, G.; Bertapelle, T.; Sabatini, M.; Corrielli, G.; Piétri, Y.; Avesani, M. High-Performance Heterodyne Receiver for Quantum Information Processing in a Laser Written Integrated Photonic Platform. arXiv 2025, arXiv:2506.08924. [Google Scholar] [CrossRef]
- Khandani, A.K. Looping for Encryption Key Generation Over the Internet: A New Frontier in Physical Layer Security. In Proceedings of the 2023 Biennial Symposium on Communications (BSC), Montreal, QC, Canada, 4–7 July 2023; pp. 59–64. [Google Scholar] [CrossRef]
- Chen, C.; Li, Q. Enhanced secret-key generation from atmospheric optical channels with the use of random modulation. Opt. Express 2022, 30, 45862–45882. [Google Scholar] [CrossRef] [PubMed]
- Milosavljević, M.; Radomirović, J.; Unkašević, T.; Božilović, B. One class of ideally secret autonomous symmetric ciphering systems based on wiretap polar codes. Mathematics 2024, 12, 3724. [Google Scholar] [CrossRef]
- Barker, E.; Kelsey, J. NIST Special Publication 800-90A Revision 1. In Recommendation for Random Number Generation Using Deterministic Random Bit Generators; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2014. [Google Scholar] [CrossRef]
- Menezes, A.J.; van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; Wiley: New York, NY, USA, 1968. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Massey, J.L. Some Applications of Source Coding in Cryptography. Eur. Trans. Telecommun. 1994, 5, 421–429. [Google Scholar] [CrossRef]
- Brassard, G.; Salvail, L. Secret-key reconciliation by public discussion. In Advances in Cryptology—EUROCRYPT’93; Springer: Berlin/Heidelberg, Germany, 1994; pp. 410–423. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; Wiley: Hoboken, NJ, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Carter, J.L.; Wegman, M.N. Universal classes of hash functions. J. Comput. Syst. Sci. 1979, 18, 143–154. [Google Scholar] [CrossRef]
- Hannusch, C.; Horváth, G. Properties of hash functions based on Gluškov product of automata. J. Autom. Lang. Comb. 2021, 26, 55–65. [Google Scholar] [CrossRef]
- Clermont, S.; Düzlü, S.; Janson, C.; Porzenheim, L.; Struck, P. Lattice-based sanitizable signature schemes: Chameleon hash functions and more. Lect. Notes Comput. Sci. 2025, 15577, 278–311. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Maurer, U.M. Generalized privacy amplification. IEEE Trans. Inf. Theory 1995, 41, 1915–1923. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Gallager, R.G. Low-Density Parity-Check Codes; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar] [CrossRef]
- NIST. Fresh Entropy. Available online: https://csrc.nist.gov/glossary/term/fresh_entropy (accessed on 1 May 2025).
- Buttler, W.T.; Lamoreaux, S.K.; Torgerson, J.R.; Nickel, G.H.; Donahue, C.H.; Peterson, C.G. Fast, efficient error reconciliation for quantum cryptography. Phys. Rev. A 2003, 67, 052303. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Lv, Q.; Ye, X.; Luo, Y.; You, L. Analysis of the information theoretically secret key agreement by public discussion. Secur. Commun. Netw. 2015, 8, 2507–2523. [Google Scholar] [CrossRef]
- Luo, Y.; Cheng, X.; Mao, H.-K.; Li, Q. An overview of postprocessing in quantum key distribution. Mathematics 2024, 12, 2243. [Google Scholar] [CrossRef]
- Hamming, R.W. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Vernam, G.S. Secret Signaling System. U.S. Patent 1,310,719, 22 July 1919. [Google Scholar]
- Daemen, J.; Rijmen, V. The Design of Rijndael: AES—The Advanced Encryption Standard; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Gueron, S. Intel AES New Instructions Set. In Intel White Paper; Mobility Group, Israel Development Center: Tel Aviv-Yafo, Israel, 2010. [Google Scholar]
- Biryukov, A.; Khovratovich, D.; Nikolić, I. Distinguisher and Related-Key Attack on the Full AES-256. In Advances in Cryptology—CRYPTO 2009; Halevi, S., Ed.; LNCS; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5677, pp. 231–249. [Google Scholar] [CrossRef]
- Hell, M.; Johansson, T.; Meier, W. Grain: A stream cipher for constrained environments. Int. J. Wirel. Mob. Comput. 2005, 2, 86–93. [Google Scholar] [CrossRef]
- Canteaut, A.; Carpov, S.; Fontaine, C.; Lepoint, T.; Naya-Plasencia, M.; Paillier, P.; Sirdey, R. Evaluation of stream ciphers: Status 2008. In eSTREAM Final Report; ECRYPT: Westlake Village, CA, USA, 2008. [Google Scholar]
- De Cannière, C.; Preneel, B. Trivium—Specifications. eSTREAM, ECRYPT Stream Cipher Project, Report 2005/030, 2005. Available online: http://www.ecrypt.eu.org/stream (accessed on 20 July 2025).
- Bernstein, D.J. ChaCha, a variant of Salsa20. In Proceedings of the SASC 2008, Lausanne, Switzerland, 13–14 February 2008; pp. 3–5. [Google Scholar]
- Robshaw, M.J.B.; Billet, O. New Stream Cipher Designs: The eSTREAM Finalists; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Wu, H. The Stream Cipher HC-128. In New Stream Cipher Designs; Robshaw, M., Billet, O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4986, pp. 39–47. [Google Scholar] [CrossRef]
- Radomirović, J.; Milosavljević, M.; Kovačević, B.; Jovanović, M. Privacy Amplification Strategies in Sequential Secret Key Distillation Protocols Based on Machine Learning. Symmetry 2022, 14, 2028. [Google Scholar] [CrossRef]
- Tsurumaru, T.; Hayashi, M. Dual universality of hash functions and its applications to quantum cryptography. IEEE Trans. Inf. Theory 2013, 59, 4700–4717. [Google Scholar] [CrossRef]
- Hayashi, M.; Tsurumaru, T. More efficient privacy amplification with less random seeds via dual universal hash function. IEEE Trans. Inf. Theory 2016, 62, 2213–2232. [Google Scholar] [CrossRef]
- Milosaljević, M.; Adamović, S.; Jevremovic, A.; Antonijević, M. Secret key agreement by public discussion from EEG signals of participants. In Proceedings of the 5th International Conference on Electrical, Electronic and Computing Engineering, IcETRAN, Palić, Serbia, 11–14 June 2018; pp. 1256–1259. [Google Scholar]
- Lin, S.; Costello, D.J. Error Control Coding, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).