Swap Test-Based Quantum Protocol for Private Array Equality Comparison

Abstract

Private array equality comparison (PAEC) aims to evaluate whether two arrays are equal while maintaining the confidentiality of their elements. Current private comparison protocols predominantly focus on determining the relationships of secret integers, lacking exploration of array comparisons. To address this issue, we propose a swap test-based quantum protocol for PAEC, which satisfies both functionality and security requirements using the principles of quantum mechanics. This protocol introduces a semi-honest third party (TP) that acts as a medium for generating Bell states as quantum resources and distributes the first and second qubits of these Bell states to the respective participants. They encode their array elements into the received qubits by performing rotation operations. These encoded qubits are sent to TP to derive the comparison results. To verify the feasibility of the proposed protocol, we construct a quantum circuit and conduct simulations on the IBM quantum platform. Security analysis further indicates that our protocol is resistant to various quantum attacks from outsider eavesdroppers and attempts by curious participants.

1. Introduction

Quantum information science has advanced significantly in recent decades, with quantum cryptography emerging as a pivotal field. By exploiting quantum mechanical principles, such as superposition and entanglement, quantum cryptography achieves security guarantees unattainable by classical methods reliant on computational complexity. The field originated with Bennett and Brassard’s BB84 protocol [1], the first quantum cryptographic scheme proven unconditionally secure. Since then, numerous protocols integrating quantum mechanics with cryptographic primitives have been developed to counter threats from quantum computing, including quantum key distribution [2,3,4], quantum key agreement [5,6], quantum private set intersection [7,8,9], and quantum secure direct communication [10,11,12,13].

Secure multiparty computation (MPC) is a vital cryptographic framework that facilitates collaborative computation among multiple parties while ensuring the privacy of their private inputs [14]. The “millionaires’ problem” [15] serves as a foundational MPC protocol, allowing two parties to compare wealth without disclosing their exact amounts. Boudot et al. [16] extended this to equality checks, enabling parties to verify if their inputs match while preserving secrecy. While early works focus on two-party scenarios, Lo [17] highlighted inherent security limitations in such settings, advocating for the involvement of a semi-honest third party (TP) to enhance security.

Traditional private comparison methods often rely on computational hardness assumptions, such as integer factorization—fundamental to public-key cryptosystems like RSA—and discrete logarithms, which underpin many cryptographic protocols. However, these foundations face significant threats from quantum algorithms: Shor algorithm [18] and Grover algorithm [19]. Shor algorithm solves integer factorization and discrete logarithm problems in polynomial time, posing a risk to public-key cryptosystems and potentially rendering them obsolete. Grover algorithm effectively halves the key lengths of symmetric-key cryptography, compromising security through accelerated search capabilities. These vulnerabilities highlight the urgent need for quantum-resistant cryptographic solutions in the post-quantum era. As quantum computing advances, developing secure protocols that can withstand these threats becomes increasingly critical.

To counter the threats posed by quantum computing, quantum private comparison (QPC) protocols have been developed by integrating classical comparison techniques with principles of quantum mechanics. These protocols offer enhanced security guarantees, ensuring the confidentiality of private inputs even against adversaries with quantum computational capabilities. Yang and Wen [20] introduced the first QPC protocol, utilizing Einstein–Podolsky–Rosen (EPR) pairs as quantum resources and employing a one-way hash function to securely verify the equality of two integers. Subsequent protocols have leveraged various quantum states (e.g., single photons [21,22], entangled states [23,24,25,26,27,28], cluster states [29,30,31,32], and d-level quantum states [33,34]) to enhance functionality and security. Wu and Zhao [35] expanded QPC to enable size relationship comparisons using d-dimensional Bell states. Lang [36] introduced quantum private magnitude comparison (QPMC), which allows for determining the larger of two inputs. Huang et al. [37] enhanced scalability by employing swap tests to compare single-qubit quantum states. Additionally, semi-quantum private comparison (SQPC) [38,39,40,41,42,43] protocols have been proposed to achieve private comparison functionality while alleviating the current shortage of quantum resources and avoiding the high costs associated with using complete quantum equipment. Despite the various QPC protocols proposed, most focus on determining the relationships of secret integers and lack exploration into array comparisons. Designing a private array equality comparison (PAEC) scheme remains a challenging issue.

The swap test [44] is a pivotal quantum subroutine used to measure the overlap between two quantum states, providing a means to determine their similarity without fully collapsing the states. Its unique properties make it a cornerstone in various quantum communication and computing applications, such as quantum signature [45], quantum-enhanced neural network [46,47], and the blind millionaire’s problem [48]. The versatility of the swap test highlights its importance in addressing complex cryptographic and computational challenges in the quantum realm.

To address the limitation of existing QPC protocols, which are confined to comparing single integers, we propose the first swap test-based quantum protocol for PAEC. This approach allows for the comparison of arrays while maintaining confidentiality and robustness against various attacks. The key contributions of the protocol are as follows.

(1)

We propose a swap test-based quantum protocol for PAEC, in which two participants encode their array elements into qubits received from a semi-honest TP by performing rotation operations. They then return the encoded states to TP to derive the results without revealing any array elements.

(2)

The proposed protocol utilizes near-term feasible quantum technologies, including Bell states, rotation operations, and swap tests, as core components, which are easier to simulate on quantum platforms. To verify the feasibility of the proposed protocol, we simulate it using the IBM Quantum Composer.

(3)

Due to the use of decoy photon insertion for eavesdropping detection and rotation operations to obfuscate encoded information, the protocol exhibits robustness against quantum attacks from outsider eavesdroppers and attempts by curious participants.

(4)

Unlike existing QPC schemes that are typically limited to single-integer comparisons, the proposed protocol enables comparisons of two arrays.

The rest of this paper is organized as follows. Section 2 reviews the concepts of rotation operation and the swap test. Section 3 details the design of the proposed protocol, outlining its framework and operational steps. Section 4 presents the simulation experiment, demonstrating the protocol’s feasibility and performance on a quantum computing platform. Section 5 offers a comprehensive analysis, including correctness, security, and fairness. Section 6 contains a comparison of the proposed protocol with existing QPC protocols, highlighting its advantages and enhancements. Section 7 concludes the work.

2. Preliminaries

2.1. Rotation Operation

The rotation operation around the y-axis [49] can be written as

$$R_y\left(\theta \right)=\left(\begin{array}{cc}\cos \left({\displaystyle \frac{\theta }{2}}\right)& -\sin \left({\displaystyle \frac{\theta }{2}}\right)\\ \sin \left({\displaystyle \frac{\theta }{2}}\right)& \cos \left({\displaystyle \frac{\theta }{2}}\right)\end{array}\right)$$

(1)

This operation is a unitary transform that satisfies the following relation:

$${R_y}^{†}\left(\theta \right)R_y\left(\theta \right)=R_y\left(-\theta \right)R_y\left(\theta \right)=I$$

(2)

Here, I represents the identity matrix and the parameter $\theta$ can be viewed as an encryption key.

When applying $R_y\left(\theta \right)$ to the quantum states $\left|0\right.〉$ and $\left|1\right.〉$, we obtain the following results:

$$R_y\left(\theta \right)\left|0\right.〉=\cos \left({\displaystyle \frac{\theta }{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\theta }{2}}\right)\left|1\right.〉$$

(3)

$$R_y\left(\theta \right)\left|0\right.〉=\cos \left({\displaystyle \frac{\theta }{2}}\right)\left|1\right.〉-\sin \left({\displaystyle \frac{\theta }{2}}\right)\left|0\right.〉$$

(4)

Therefore, the transformation of the quantum states $\left|0\right.〉$ and $\left|1\right.〉$ into superposition states through the rotation operation $R_y\left(\theta \right)$ serves as an effective encryption mechanism. Without knowledge of the angle $\theta$, it is impossible to recover the original states $\left|0\right.〉$ and $\left|1\right.〉$.

The recovery of the original quantum states is accomplished by executing $R_y\left(-\theta \right)$ on the resulting states. The recovery process is as follows.

$$R_y\left(-\theta \right)\left(\cos \left({\displaystyle \frac{\theta }{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{\theta }{2}}\right)\left|1\right.〉\right)=R_y\left(-\theta \right)R_y\left(\theta \right)\left|0\right.〉=\left|0\right.〉$$

(5)

$$R_y\left(-\theta \right)\left(\cos \left({\displaystyle \frac{\theta }{2}}\right)\left|1\right.〉-\sin \left({\displaystyle \frac{\theta }{2}}\right)\left|0\right.〉\right)=R_y\left(-\theta \right)R_y\left(\theta \right)\left|1\right.〉=\left|1\right.〉$$

(6)

2.2. Swap Test

The swap test [44] is a quantum circuit designed to evaluate the similarity between two quantum states of identical dimensionality, which is shown in Figure 1. Its core is to estimate the modulus squared of the inner product ${\left|\langle {\psi }_1|{\psi }_2\rangle \right|}^2$ between two quantum states $\left|{\psi }_1\right.〉$ and $\left|{\psi }_2\right.〉$. An ancillary qubit is introduced into the circuit, which plays a crucial role in measuring the similarity between the states and the measurement outcome of the ancilla qubit provides the probability related to the inner product of the two states.

A schematic representation of the swap test’s quantum circuit typically includes the following:

• Input states: Two quantum states $\left|{\psi }_1\right.〉$ and $\left|{\psi }_2\right.〉$.
• Ancillary qubit: Initialized to $\left|0\right.〉$.
• Hadamard gate: Applied to the ancillary qubit to create a superposition.
• Controlled-SWAP gate: The states $\left|{\psi }_1\right.〉$ and $\left|{\psi }_2\right.〉$ interact with the ancillary qubit via a controlled-SWAP operation.
• Measurement: The ancillary qubit is measured to determine the probability of being in state $\left|0\right.〉$ or $\left|1\right.〉$.

By conducting a swap test on two quantum states $\left|{\psi }_1\right.〉$ and $\left|{\psi }_2\right.〉$, the probability of the ancillary qubit being in state $\left|0\right.〉$ or $\left|1\right.〉$ are expressed as follows:

$$P\left(\left|0\right.〉\right)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\left|〈{\psi }_1|{\psi }_2〉\right|}^2$$

(7)

$$P\left(\left|1\right.〉\right)={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈{\psi }_1|{\psi }_2〉\right|}^2$$

(8)

Therefore, we can derive that

$${\left|〈{\psi }_1|{\psi }_2〉\right|}^2=2P\left(\left|0\right.〉\right)-1 \mathrm{or} {\left|〈{\psi }_1|{\psi }_2〉\right|}^2=1-2P\left(\left|1\right.〉\right)$$

(9)

Theorem 1.

When performing the swap test on two quantum states $\left|{\psi }_1\right.〉=\mathit{cos}({\alpha }_1)\left|0\right.〉+\mathit{sin}({\alpha }_1)\left|1\right.〉$ and $\left|{\psi }_2\right.〉=\mathit{cos}({\alpha }_2)\left|0\right.〉+\mathit{sin}({\alpha }_2)\left|1\right.〉$, where ${\alpha }_1,{\alpha }_2\in \left.[0,\pi \right)$, the modulus squared of the inner product ${\left|{\psi }_1|{\psi }_2\right|}^2$ is ${\mathit{cos}}^2\left({\alpha }_1-{\alpha }_2\right)$.

Proof. 

The inner product ${\psi }_1|{\psi }_2$ is computed as follows:

$$\begin{array}{l}〈{\psi }_1|{\psi }_2〉=\left(\cos \left({\alpha }_1\right)\left.〈0\right|+\sin \left({\alpha }_1\right)\left.〈1\right|\right)\left(\cos \left({\alpha }_2\right)\left|0\right.〉+\sin \left({\alpha }_2\right)\left|1\right.〉\right)\\ =\cos \left({\alpha }_1\right)\cos \left({\alpha }_2\right)〈0|0〉+\cos \left({\alpha }_1\right)\sin \left({\alpha }_2\right)〈0|1〉\\ +\sin \left({\alpha }_1\right)\cos \left({\alpha }_2\right)〈1|0〉+\sin \left({\alpha }_1\right)\sin \left({\alpha }_2\right)〈1|1〉\\ =\cos \left({\alpha }_1\right)\cos \left({\alpha }_2\right)+\sin \left({\alpha }_1\right)\sin \left({\alpha }_2\right)\\ =\cos \left({\alpha }_1-{\alpha }_2\right)\end{array}$$

(10)

Combined Equations (8) and (10), we deduce that:

$$\begin{array}{l}P\left(\left|1\right.〉\right)={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈{\psi }_1|{\psi }_2〉\right|}^2\\ ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\alpha }_1-{\alpha }_2\right)\end{array}$$

(11)

Therefore, the modulus squared of the inner product ${\left|\langle {\psi }_1|{\psi }_2\rangle \right|}^2$ is given by

$$\begin{array}{l}{\left|〈{\psi }_1|{\psi }_2〉\right|}^2=1-2P\left(\left|1\right.〉\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}=1-2\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\alpha }_1-{\alpha }_2\right)\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}={\cos }^2\left({\alpha }_1-{\alpha }_2\right)\end{array}$$

(12)

□

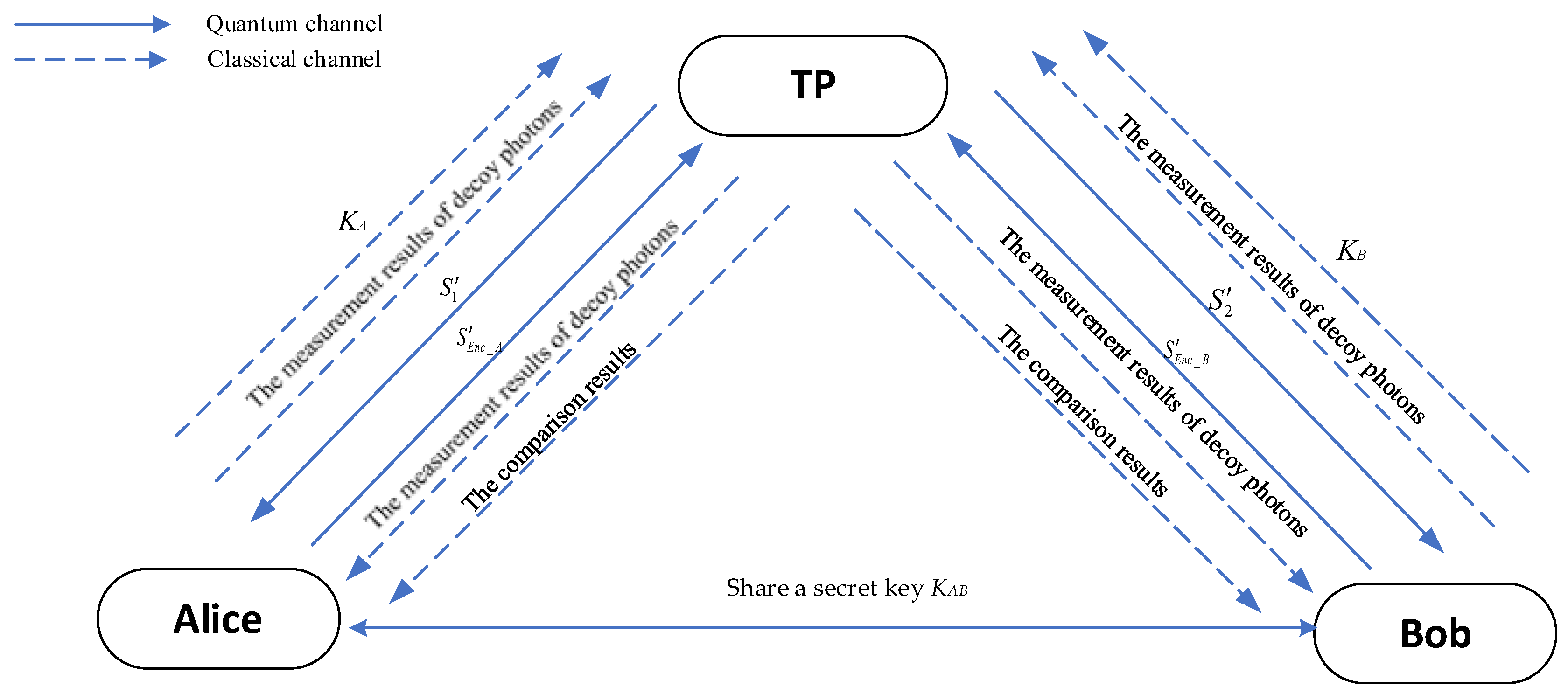
3. Design of the Proposed Protocol

The proposed protocol is designed to securely determine the equality of two arrays A and B, owned by distinct parties, Alice and Bob, with the assistance of a semi-honest third party (TP). The two arrays are defined as $A=\left(a_0,a_1,\dots ,a_{L-1}\right)$ and $B=\left(b_0,b_1,\dots ,b_{L-1}\right)$. Both arrays must have the same length L, which is known to TP. TP prepares L Bell states as quantum resources and announces the comparison result to both Alice and Bob. As a semi-honest participant, TP follows the protocol without colluding with either party.

The proposed protocol must guarantee the following properties:

• Correctness: If both Alice and Bob input their arrays honestly and comply with the protocol, TP will accurately announce the comparison result.
• Security: The arrays A and B remain confidential from both other participants and potential attackers, ensuring the confidentiality of the participants’ inputs.
• Fairness: Each party receives the comparison result simultaneously, preventing any asymmetric information advantages.

The protocol assumes lossless and noiseless quantum channels. Classical channels between the participants are authenticated to prevent unauthorized access. However, in practical scenarios, quantum error-correcting codes [50] can be implemented to detect and correct errors induced by noise. Before the protocol begins, it is assumed that Alice and Bob share a secret key $K_{AB}=\left({\theta }_0^{AB},{\theta }_1^{AB},\dots ,{\theta }_{L-1}^{AB}\right)$ using a quantum key distribution protocol. This key facilitates secure communications and operations within the protocol. A detailed outline of the steps is as follows, and the diagram is shown in Figure 2.

Step 1: Preparation byTP

(1)

TP prepares L Bell states in the state $\left|{\varphi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.〉+\left|11\right.〉\right)$ and organizes the first and second particles into two quantum sequences $S_1$ and $S_2$, respectively.

(2)

To mitigate eavesdropping risks, TP prepares $2\delta$ decoy photons from the set $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉={\displaystyle \frac{\left|0\right.〉+\left|1\right.〉}{\sqrt{2}}},\left|-\right.〉={\displaystyle \frac{\left|0\right.〉-\left|1\right.〉}{\sqrt{2}}}\right\}$, inserts $\delta$ decoy photons into $S_1$ to create ${S^{\prime }}_1$, and inserts another $\delta$ decoy photons into $S_2$ to create ${S^{\prime }}_2$.

(3)

TP records the positions and states of the decoy photons, and sends ${S^{\prime }}_1$ and ${S^{\prime }}_2$ to Alice and Bob via quantum channels, respectively.

Step 2. Confirmation and Measurement of Decoy Photons

(1)

Upon receiving ${S^{\prime }}_1$ and ${S^{\prime }}_2$, Alice and Bob send confirmation information to TP via an authenticated classical channel.

(2)

TP announces the positions and measurement bases for the decoy photons. If the decoy photon is in states $\left|0\right.〉$ or $\left|1\right.〉$, the Z basis is used; otherwise, the X basis is applied.

(3)

Alice and Bob measure the decoy photons and send results back to TP, which computes the error rate. If the error rate exceeds a predefined threshold (τ = 2∼8.9%) depending on the channel situation [51,52], the protocol is aborted and restarted.

Step 3. Encoding and Encrypting Arrays

(1)

Alice and Bob remove the decoy photons from ${S^{\prime }}_1$ and ${S^{\prime }}_2$ to recover $S_1$ and $S_2$, respectively.

(2)

Alice encodes each element $a_i$ in array A as ${\theta }_i^A={\displaystyle \frac{\pi }{a_i}}$ (notably, if $a_i=0$, then ${\theta }_i^A=0$). Bob encodes each element $b_i$ in array B using the same method.

(3)

Alice applies $R_y\left({\theta }_i^A+{\theta }_i^{AB}\right)$ to the $i$-th qubit in $S_1$, and Bob applies $R_y\left({\theta }_i^B+{\theta }_i^{AB}\right)$ to the $i$-th qubit in $S_2$, generating sequences $S_A$ and $S_B$, respectively.

(4)

Alice generates an encrypted key $K_A=\left({\theta }_0^{Enc\_A},{\theta }_1^{Enc\_A},\dots ,{\theta }_L^{Enc\_A}\right)$, and Bob generates $K_B=\left({\theta }_0^{Enc\_B},{\theta }_1^{Enc\_B},\dots ,{\theta }_L^{Enc\_B}\right)$.

(5)

Alice and Bob apply the rotation operations $R_y\left({\theta }_i^{Enc\_A}\right)$ and $R_y\left({\theta }_i^{Enc\_B}\right)$ to the i-th qubit in $S_A$ and $S_B$, resulting in encrypted sequences $S_{Enc\_A}$ and $S_{Enc\_B}$, respectively.

(6)

Both Alice and Bob prepare $\delta$ decoy photons and insert them into their respective encrypted sequences, forming ${S^{\prime }}_{Enc\_A}$ and ${S^{\prime }}_{Enc\_B}$, and send these to TP via quantum channels.

Step 4. Eavesdropping Detection

(1)

When TP receives ${S^{\prime }}_{Enc\_A}$ and ${S^{\prime }}_{Enc\_B}$, he interacts with Alice and Bob to check for eavesdropping.

(2)

Alice and Bob compute the error rate as in Step 2. If the error rate is acceptable, they publish their secret keys $K_A$ and $K_B$ to TP.

Step 5. Recovery and Comparison

(1)

TP removes decoy photons from ${S^{\prime }}_{Enc\_A}$ and ${S^{\prime }}_{Enc\_B}$ to recover $S_{Enc\_A}$ and $S_{Enc\_B}$, respectively.

(2)

TP applies $R_y\left(-{\theta }_i^{Enc\_A}\right)$ and $R_y\left(-{\theta }_i^{Enc\_B}\right)$ to the i-th qubit in $S_{Enc\_A}$ and $S_{Enc\_B}$, respectively, to obtain sequences $S_A$ and $S_B$.

(3)

TP conducts swap tests on each i-th qubit in sequences $S_A$ and $S_B$.

(4)

TP measures the ancilla qubits from the swap tests to obtain measurement results.

Step 6: Final Result Announcement

(1)

By performing the above steps $\lambda$ times, TP collects multiple measurement results.

(2)

If any measurement result indicates |1⟩, the arrays A and B are not identical. If all results indicate |0⟩, the arrays are the same.

(3)

TP announces the result to Alice and Bob simultaneously.

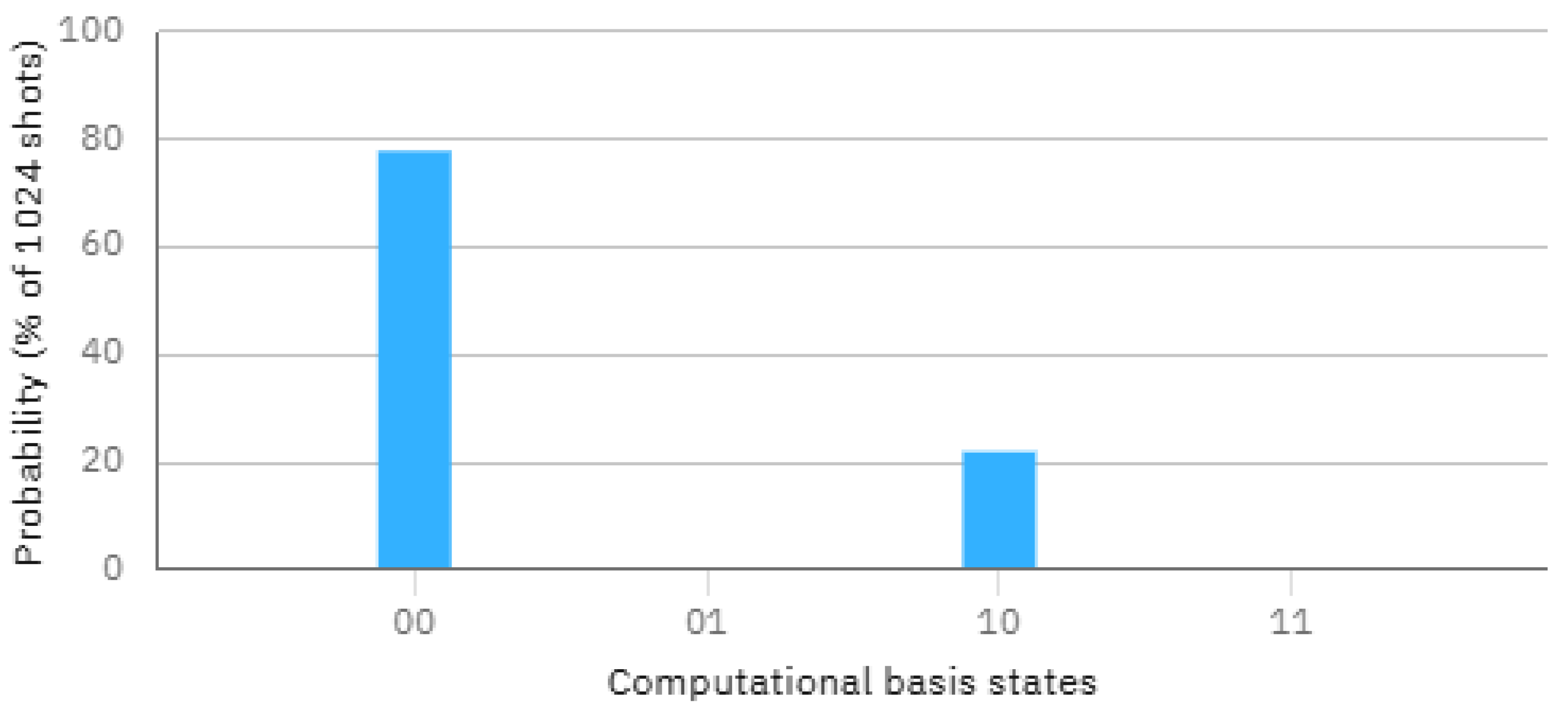
4. Simulation

Consider a case where Alice and Bob wish to determine whether their arrays $A=\left[3,6\right]$ and $B=\left[3,2\right]$ are identical without revealing any elements. Suppose that they share a secret key $K_{AB}=\left({\displaystyle \frac{\pi }{3}}, {\displaystyle \frac{3\pi }{4}}\right)$ in advance. Since both the lengths of arrays A and B are 2, TP prepares 2 Bell states in the state $\left|{\varphi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.〉+\left|11\right.〉\right)$. TP organizes the first and second particles into quantum sequences $S_1$ and $S_2$.

For simplification, we do not take the eavesdropping detection process into account. Alice encodes her array A as angles ${\theta }^A=\left[{\displaystyle \frac{\pi }{3}},{\displaystyle \frac{\pi }{6}}\right]$ and Bob encodes his array B as angles ${\theta }^B=\left[{\displaystyle \frac{\pi }{3}},{\displaystyle \frac{\pi }{2}}\right]$, respectively. Alice applies $R_y\left({\displaystyle \frac{\pi }{3}}+{\displaystyle \frac{\pi }{3}}\right)$ and $R_y\left({\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{3\pi }{4}}\right)$ to the qubits in $S_1$, generating sequence $S_A$. Bob applies $R_y\left({\displaystyle \frac{\pi }{3}}+{\displaystyle \frac{\pi }{3}}\right)$ and $R_y\left({\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{3\pi }{4}}\right)$ to the qubits in $S_2$, generating sequence $S_B$. The encrypted keys generated by Alice and Bob are assumed to be $K_A=\left({\displaystyle \frac{4\pi }{5}}, {\displaystyle \frac{5\pi }{6}}\right)$ and $K_B=\left({\displaystyle \frac{5\pi }{8}}, {\displaystyle \frac{\pi }{7}}\right)$, respectively. Alice applies $R_y\left({\displaystyle \frac{4\pi }{5}}\right)$ and $R_y\left({\displaystyle \frac{5\pi }{6}}\right)$ to the qubits in $S_A$, generating sequence $S_{Enc\_A}$. Bob applies $R_y\left({\displaystyle \frac{5\pi }{8}}\right)$ and $R_y\left({\displaystyle \frac{\pi }{7}}\right)$ to the qubits in $S_B$, producing sequence $S_{Enc\_B}$.

Disregard eavesdropping detection for simplification. When receiving $K_A$ and $K_B$, TP applies $R_y\left(-{\displaystyle \frac{4\pi }{5}}\right)$ and $R_y\left(-{\displaystyle \frac{5\pi }{6}}\right)$ to qubits in $S_{Enc\_A}$ to obtain $S_A$, and applies $R_y\left(-{\displaystyle \frac{5\pi }{8}}\right)$ and $R_y\left(-{\displaystyle \frac{\pi }{7}}\right)$ to obtain $S_B$. TP performs swap tests on the first and second qubits of $S_A$ and $S_B$, measuring the ancilla qubits to obtain the measurement results.

To validate the feasibility of the proposed protocol using this case, we construct a quantum circuit and simulate it using the IBM Quantum Composer. The IBM Quantum Composer is a user-friendly graphical tool designed for constructing and executing quantum circuits. Users can easily build quantum circuits by dragging and dropping various quantum operations (including single-qubit gates, controlled-qubit gates, and measurement operations) onto a canvas. When simulating this protocol, eavesdropping detection, a separate procedure for identifying eavesdropping rather than for encoding information, is excluded from the simulation. The quantum circuit for comparing arrays A and B is shown in Figure 3, and the measurement results displayed in the form of histograms after executing the quantum circuit are shown in Figure 4.

Based on the measurement results shown in Figure 4, we conclude that the measurement result of q[0] is in the state $\left|0\right.〉$, while the measurement results of q[1] can be either $\left|0\right.〉$ or $\left|1\right.〉$. According to the proposed scheme, if any measurement result indicates the state $\left|1\right.〉$, it confirms that the arrays A and B are not identical. Since the measurement results of q[1] include the state $\left|1\right.〉$, we conclude that the arrays A and B are indeed not identical. This simulation illustrates the feasibility of the proposed protocol by providing a concrete example on a quantum computing platform.

5. Analysis

5.1. Correctness

Let $P\left(\left|1\right.〉\right)$ denote the probability of measuring the ancilla qubit in state $\left|1\right.〉$. When conducting swap tests on each i-th qubit in sequences $S_A$ and $S_B$, the probability that the i-th ancilla qubit is in the state $\left|1\right.〉$ can be expressed as

$$\begin{array}{ll}{P}_i\left(\left|1\right.〉\right)& ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈\left(\cos \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left.〈0\right|+\sin \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left.〈1\right|\right)|\cos \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left|0\right.〉+\sin \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left|1\right.〉〉\right|}^2\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\left|\cos \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\cos \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)+\sin \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\sin \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\right|\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|\cos \left({\displaystyle \frac{{\theta }_i^A}{2}}-{\displaystyle \frac{{\theta }_i^B}{2}}\right)\right|}^2={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\displaystyle \frac{{\theta }_i^A}{2}}-{\displaystyle \frac{{\theta }_i^B}{2}}\right)\end{array}$$

(13)

$$\begin{array}{ll}{P}_i\left(\left|1\right.〉\right)& ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|〈\left(-\sin \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left.〈0\right|+\cos \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left.〈1\right|\right)|-\sin \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left|0\right.〉+\cos \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\left|1\right.〉〉\right|}^2\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\left|\left(-\sin \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\right)\left(-\sin \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\right)+\cos \left({\displaystyle \frac{{\theta }_i^A}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\cos \left({\displaystyle \frac{{\theta }_i^B}{2}}+{\displaystyle \frac{{\theta }_i^{AB}}{2}}\right)\right|\\ & ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\left|\cos \left({\displaystyle \frac{{\theta }_i^A}{2}}-{\displaystyle \frac{{\theta }_i^B}{2}}\right)\right|}^2={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}{\cos }^2\left({\displaystyle \frac{{\theta }_i^A}{2}}-{\displaystyle \frac{{\theta }_i^B}{2}}\right)\end{array}$$

(14)

Based on Equations (13) and (14), we conclude that the ancilla qubit yields the state $\left|1\right.〉$ with a probability of 0 if and only if the angles ${\theta }_i^A$ and ${\theta }_i^B$ are identical. That is, $P\left(\left|1\right.〉\right)=0$ if and only if ${\theta }_i^A={\theta }_i^B$. In other words, if any measurement result of the ancilla qubit indicates the state $\left|1\right.〉$, it indicates that the arrays A and B are not identical. Conversely, if all measurement results yield the state $\left|0\right.〉$, it confirms that the arrays A and B are the same.

5.2. Security

Eavesdroppers may attempt to intercept the quantum sequences transmitted between Alice, Bob, and TP, or use Trojan horse methods to gain access to the quantum systems and deduce information about the inputs. Additionally, participating entities, such as TP, could potentially exploit information from the protocol to infer the inputs of Alice and Bob. To counter these threats, decoy photons are employed to detect eavesdropping attempts. By inserting decoy photons into the quantum sequences, the sender can monitor for discrepancies in measurement outcomes. An elevated error rate in measurements indicates potential eavesdropping, prompting the protocol to abort if necessary. The secret keys are used to encrypt the quantum states, ensuring that even if the quantum sequences are intercepted, the actual information remains concealed from eavesdroppers. Furthermore, the use of rotation operations based on the secret keys adds another layer of security, making it difficult for attackers to deduce the original input values. The combined use of decoy photons and secret key encryption maintains the confidentiality of the arrays A and B. Below, we will provide a concrete analysis regarding the confidentiality of the arrays A and B.

5.2.1. Outside Attacks

In the context of the proposed protocol, an external attacker, often referred to as Eve, may attempt various quantum-based attacks to extract the arrays A and B. These attacks include intercept-measure-resend, entangle-measure, and Trojan horse attacks.

Case I. Intercept-measure-resend attack

Eve intercepts the quantum sequences ${S^{\prime }}_{Enc\_A}$ and ${S^{\prime }}_{Enc\_B}$ that contain encoded private information sent from Alice and Bob to TP. She measures these sequences using randomly chosen measurement bases (either Z-basis or X-basis). Based on her measurement results ($\mathrm{e}.\mathrm{g}., \left|0\right.〉,\left|1\right.〉,\left|+\right.〉={\displaystyle \frac{\left|0\right.〉+\left|1\right.〉}{\sqrt{2}}},\left|-\right.〉={\displaystyle \frac{\left|0\right.〉-\left|1\right.〉}{\sqrt{2}}}$), Eve prepares and sends two fake sequences to TP. However, decoy photons are inserted at random positions within the quantum sequences specifically to detect eavesdropping. Eve cannot differentiate between the actual target states and the decoy photons when she intercepts the sequences. If Eve measures a decoy photon using an incorrect basis (e.g., measuring a decoy in the X-basis when it was prepared in the Z-basis), the measurement results will be $\left|+\right.〉$ or $\left|-\right.〉$, leading to an increased error rate. For a decoy photon prepared in the Z-basis (e.g., $\left|0\right.〉$), if she uses the Z-basis, she may obtain the correct result $\left|0\right.〉$. If she uses the X-basis, she has a 50% chance of getting the correct result. In the X-basis, measuring $\left|0\right.〉$ gives outcomes $\left|+\right.〉$ or $\left|-\right.〉$, and measuring $\left|1\right.〉$ also results in $\left|+\right.〉$ or $\left|-\right.〉$). Therefore, the probability that Eve gets the correct result and passes the eavesdropping detection for a single decoy photon is calculated as follows:

$$P\left(\mathrm{pass} \mathrm{for} \mathrm{a} \mathrm{decoy} \mathrm{photon}\right)={\displaystyle \frac{1}{2}}\times 1+{\displaystyle \frac{1}{2}}\times {\displaystyle \frac{1}{2}}={\displaystyle \frac{3}{4}}$$

(15)

For $\delta$ decoy photons, the probability that Eve passes the eavesdropping detection becomes

$$P\left(\mathrm{pass} \mathrm{for} \delta \mathrm{decoy} \mathrm{photon}\right)=1-{\left({\displaystyle \frac{3}{4}}\right)}^{\delta }$$

(16)

When $\delta =20$, $P\left(\mathrm{pass} \mathrm{for} 20 \mathrm{decoy} \mathrm{photons}\right)=1-{\left({\displaystyle \frac{3}{4}}\right)}^{20}=0.9968$. As $\delta$ increases, this probability approaches 1, indicating that Eve’s behavior will likely be detected during the eavesdropping detection process.

Case II. Entangle-measure attack

In the entangle-measure attack, Eve applies a special unitary transformation U to entangle the intercepted states with the ancilla qubits. The goal is to create a situation where she can infer the target states by measuring the ancilla qubits. The transformation U acts on the intercepted qubits in states such as $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$ along with the ancilla states $\left|a_i\right.〉$. The operation can be represented as follows:

$$U\left|0\right.〉\left|a_i\right.〉=u_{00}\left|0\right.〉\left|a_{00}\right.〉+u_{01}\left|1\right.〉\left|a_{01}\right.〉$$

(17)

$$U\left|1\right.〉\left|a_i\right.〉=u_{10}\left|0\right.〉\left|a_{10}\right.〉+u_{11}\left|1\right.〉\left|a_{11}\right.〉$$

(18)

$$\begin{array}{l}U\left|+\right.〉\left|a_i\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(U\left|0\right.〉\left|a_i\right.〉+U\left|1\right.〉\left|a_i\right.〉\right)\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{1}{\sqrt{2}}}\left(u_{00}\left|0\right.〉\left|a_{00}\right.〉+u_{01}\left|1\right.〉\left|a_{01}\right.〉+u_{10}\left|0\right.〉\left|a_{10}\right.〉+u_{11}\left|1\right.〉\left|a_{11}\right.〉\right)\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(u_{00}\left|a_{00}\right.〉+u_{01}\left|a_{01}\right.〉+u_{10}\left|a_{10}\right.〉+u_{11}\left|a_{11}\right.〉\right)\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(u_{00}\left|a_{00}\right.〉-u_{01}\left|a_{01}\right.〉+u_{10}\left|a_{10}\right.〉-u_{11}\left|a_{11}\right.〉\right)\end{array}$$

(19)

$$\begin{array}{l}U\left|-\right.〉\left|a_i\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(U\left|0\right.〉\left|a_i\right.〉-U\left|1\right.〉\left|a_i\right.〉\right)\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{1}{\sqrt{2}}}\left(u_{00}\left|0\right.〉\left|a_{00}\right.〉+u_{01}\left|1\right.〉\left|a_{01}\right.〉-u_{10}\left|0\right.〉\left|a_{10}\right.〉-u_{11}\left|1\right.〉\left|a_{11}\right.〉\right)\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(u_{00}\left|a_{00}\right.〉+u_{01}\left|a_{01}\right.〉-u_{10}\left|a_{10}\right.〉-u_{11}\left|a_{11}\right.〉\right)\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(u_{00}\left|a_{00}\right.〉-u_{01}\left|a_{01}\right.〉-u_{10}\left|a_{10}\right.〉+u_{11}\left|a_{11}\right.〉\right)\end{array}$$

(20)

where $\left\{\left|a_{00}\right.〉,\left|a_{01}\right.〉,\left|a_{10}\right.〉,\left|a_{11}\right.〉\right\}$ are four pure states determined by the operation U and the parameters satisfy the following:

$${\left|u_{10}\right|}^2+{\left|u_{11}\right|}^2=1$$

(21)

$${\left|u_{00}\right|}^2+{\left|u_{01}\right|}^2=1$$

(22)

To avoid detection during eavesdropping, the following conditions must be met.

$$u_{01}=0,u_{10}=0$$

(23)

$$u_{00}\left|a_{00}\right.〉=u_{11}\left|a_{11}\right.〉$$

(24)

Substituting the results from Equations (23) and (24) into Equations (17)–(20), we derive the following:

$$U\left|0\right.〉\left|a_i\right.〉=u_{00}\left|0\right.〉\left|a_{00}\right.〉$$

(25)

$$U\left|1\right.〉\left|a_i\right.〉=u_{11}\left|1\right.〉\left|a_{11}\right.〉=u_{00}\left|1\right.〉\left|a_{00}\right.〉$$

(26)

$$U\left|+\right.〉\left|a_i\right.〉={\displaystyle \frac{1}{2}}\left|+\right.〉\left(u_{00}\left|a_{00}\right.〉+u_{11}\left|a_{11}\right.〉\right)=u_{00}\left|+\right.〉\left|a_{00}\right.〉=u_{11}\left|+\right.〉\left|a_{11}\right.〉$$

(27)

$$U\left|-\right.〉\left|a_i\right.〉={\displaystyle \frac{1}{2}}\left|-\right.〉\left(u_{00}\left|a_{00}\right.〉+u_{11}\left|a_{11}\right.〉\right)=u_{00}\left|-\right.〉\left|a_{00}\right.〉=u_{11}\left|-\right.〉\left|a_{11}\right.〉$$

(28)

Based on Equations (25)–(28), we conclude that no entanglement exists between the intercepted qubits and the ancilla states. If Eve measures the ancilla qubits and obtains the result $\left|a_{00}\right.〉$, she still cannot determine the states of the intercepted qubits, which could be $\left|0\right.〉$ or $\left|1\right.〉$. Similarly, if Eve measures the ancilla qubits and obtains the result $\left|a_{11}\right.〉$, she remains unable to infer the states of the intercepted qubits, which could be $\left|+\right.〉$ or $\left|-\right.〉$. Consequently, the entangle-measure attack does not succeed.

Case III. Trojan horse attacks

Trojan horse attacks pose a significant threat to quantum communication protocols, particularly those utilizing bidirectional quantum channels. These attacks include two categories: delay-photon and invisible photon attacks [53]. Given that the proposed protocol utilizes Bell states as information carriers transmitted between TP, Alice, and Bob, it is inherently vulnerable to these Trojan horse attacks. However, by implementing wavelength quantum filters and photon number splitters, the scheme can maintain its confidentiality and integrity against these attacks. Such measures ensure that only legitimate photons are transmitted, effectively securing the communication against potential eavesdropping.

5.2.2. Participant Attacks

The proposed protocol effectively secures the confidentiality of arrays A and B against potential threats from TP, Alice, and Bob. Below are detailed analyses of how the protocol addresses these threats.

Case I. Security Against TP’s Threat

TP is considered semi-honest, meaning it follows the protocol without colluding with either participant. However, it has access to the initial quantum sequences $S_1$ and $S_2$ as well as the final sequences $S_A$ and $S_B$. The sequences $S_A$ and $S_B$ are generated by applying rotation operations $R_y\left({\theta }_i^A+{\theta }_i^{AB}\right)$ and $R_y\left({\theta }_i^B+{\theta }_i^{AB}\right)$ to the i-th qubit in $S_1$ and $S_2$, and the angles ${\theta }_i^A$ and ${\theta }_i^B$ are derived from the elements $a_i$ and $b_i$ in arrays A and B. However, the angle ${\theta }_i^{AB}$ is shared between Alice and Bob but remains unknown to TP. Without knowledge of ${\theta }_i^{AB}$, TP cannot access the angles ${\theta }_i^A$ and ${\theta }_i^B$ due to the quantum indeterminacy. Even if TP measures sequences $S_A$ and $S_B$, the results will only yield the measurement outcomes of $\left|0\right.〉$ or $\left|1\right.〉$, without revealing the specifics of the rotation angles. Therefore, the arrays A and B remain confidential from TP, demonstrating the scheme’s security against threats from TP.

Case II. Security Against Alice’s or Bob’s Threat

Both participants have analogous roles. In this scenario, we assume Alice attempts to extract Bob’s array B. The i-th element in Bob’s array B is encoded into the angle ${\theta }_i^B$, used to transform the i-th qubit in sequence $S_2$. The sequence $S_B$ is then encrypted using $R_y\left({\theta }_i^{Enc\_B}\right)$ to the i-th qubit in $S_B$, and the encrypted sequence $S_{Enc\_B}$ includes decoy photons, resulting in a modified sequence ${S^{\prime }}_{Enc\_B}$ sent to TP. Although Alice can measure the sequence $S_1$ to know the corresponding qubits in $S_2$ due to entanglement (for example, if Alice’s measurement result is $\left|0\right.〉$, then Bob’s measurement result must also be $\left|0\right.〉$, owing to the entanglement correlation in Bell states), she cannot determine the target states in $S_{Enc\_B}$. If Alice intercepts ${S^{\prime }}_{Enc\_B}$ and tries to resend a fake sequence, this behavior will be detected, leading to an aborted protocol. Even if Alice discards the decoy photons to access $S_{Enc\_B}$ and measures $S_{Enc\_B}$ to obtain the measurement results $\left|0\right.〉$ or $\left|1\right.〉$, she cannot deduce ${\theta }_i^B$ without also knowing ${\theta }_i^{Enc\_B}$. The angle ${\theta }_i^{Enc\_B}$ is only announced if the eavesdropping detection is passed—something Alice cannot achieve if she attempts to tamper with the sequences. The quantum nature of the sequences ensures that Alice cannot ascertain any information about $S_B$ without also knowing ${\theta }_i^{Enc\_B}$. Thus, the array B remains undisclosed to her. A similar argument holds for Bob regarding Alice’s array A. Therefore, our protocol is secure against threats from either Alice or Bob.

5.3. Fairness

The introduction of a third party (TP) in the proposed protocol plays a crucial role in ensuring the fairness of the protocol while determining the equality of the arrays A and B. TP measures the ancilla qubits resulting from the swap tests conducted between the sequences $S_A$ and $S_B$, and analyzes the measurement results from the ancilla qubits. If any result indicates the state $\left|1\right.〉$, it signifies that the arrays are not identical. If all results indicate $\left|0\right.〉$, it confirms that the arrays are the same. After obtaining the measurement results, TP announces the comparison outcome to both Alice and Bob at the same time. This simultaneous announcement prevents either participant from gaining any advantage over the other, ensuring that both parties have equal access to the results.

6. Comparison

The proposed protocol presents several advantages over existing QPC schemes. Below, we compare our protocol with previous QPC schemes in terms of quantum resources, unitary operation, entanglement swapping operation, quantum measurement, and comparison object (

Table 1. A comparison between the proposed protocol and previous schemes.

Protocol	Quantum Resources	Unitary Operation	Entanglement Swapping Operation	Quantum Measurement	Comparison Object
Ref. [25]	2L Bell states	No	Yes	GHZ-basis	Binary representation of integer
Ref. [26]	L + 4m χ-type entangled states	Yes	Yes	Joint	Binary representation of integer
Ref. [31]	2L Four-qubit cluster state and extended Bell state	No	Yes	Bell basis and extended Bell basis	Binary representation of integer
Ref. [33]	(1 + δ) d-level Bell state	Yes	Yes	d-level Bell basis	Integer
Ref. [34]	2L d-level Bell state	No	No	d-level single-particle	Integer
Ours	2λL Bell states	Yes	No	Single-particle (Z basis)	Array

).

(1)

Unlike existing QPC schemes [25,26,31,33,34] that are typically limited to single-integer comparisons, the proposed protocol enables comparisons of two arrays. This scalability makes it more suitable for practical applications.

(2)

The proposed protocol utilizes Bell states, rotation operations, and swap tests, avoiding the need for entanglement swapping [25,26,31,33] and d-level quantum states [33,34]. This simplification reduces the operational complexity of the protocol and enhances its compatibility with current quantum technologies, facilitating implementation.

(3)

The proposed protocol employs single-particle measurements rather than Bell-basis measurements [31], joint measurements [26], or d-level quantum state measurements [33,34]. Single-particle measurements require base vector projection of a single quantum state (e.g., Z-basis, X-basis), without the need for multi-particle cooperative operations. In contrast, joint measurements necessitate multi-particle interference, which is hindered by imperfections in light sources. Additionally, d-dimensional quantum state measurements require the design of d orthogonal basis vectors, and high-dimensional control is vulnerable to decoherence effects. For instance, in remote state preparation, d-level Bell state measurement demands customized quantum gates and entanglement sources, with experimental difficulty increasing exponentially with d. This approach reduces the measurement requirements, making the protocol more practical and easier to implement.

7. Conclusions

In this paper, we introduce the first swap test-based quantum protocol specifically designed for private array equality comparison. Participants encode their array elements into rotation angles of operations performed on shared Bell states, which are encrypted before being transmitted to the TP. TP decrypts the received states and conducts swap tests on two particles of the Bell states to derive the results of the array comparison. Due to the utilization of decoy photon technology for detecting eavesdropping and the rotation operations used for encoding and encrypting quantum information, the proposed protocol is resilient against both external eavesdroppers and internal threats. By announcing the results simultaneously, the protocol ensures fairness, preventing any participant from gaining an advantage over the other. Unlike existing QPC schemes that focus on single-integer comparisons, our protocol supports array comparisons, making it more applicable to real-world scenarios. The elimination of entanglement swapping and d-level quantum states simplifies the protocol, relying on components (Bell states, rotation operations, swap tests) that are compatible with current quantum technologies. Future research will focus on adapting the protocol to function efficiently in noisy quantum environments and exploring semi-quantum architectures that can reduce quantum resource demands while maintaining the security of the protocol.