Abstract
For a vertex subset S of a graph if each vertex of G is either in S or adjacent to some vertex in then S is a dominating set of Let S be a dominating set of a graph If each vertex v not in S has a neighbor u in S such that is also a dominating set of then S is a secure dominating set of If each vertex u in S has a neighbor v not in S such that is also a dominating set of G, then S is a co-secure dominating set of G. The minimum cardinality of a secure (resp. co-secure) dominating set of G is the secure (resp. co-secure) domination number of Arumugam et al. proposed the questions to characterize a graph G such that the co-secure domination number of G equals the independence number and the secure domination number of G, respectively. Inspired by those questions, in this paper, we obtain two classes of claw-free graphs such that the co-secure domination number equal the independence number and the secure domination number. Our results provide some theoretical basis of claw-free graphs for networks.
Keywords:
co-secure dominating set; secure dominating set; co-secure domination number; secure domination number MSC:
05C69
1. Introduction
We consider only simple and undirected graphs in this paper. For notation and terminology not defined in this paper, readers are referred to [1]. For a graph G and we use to denote the subgraph of G induced by S. Let denote the set of all the neighbors of v in and moreover, we set and for simplicity. Let For a graph if a subgraph of a graph G is isomorphic to then let A complete graph consisting of n vertices is denoted by and a complete bipartite graph consisting of two vertex-disjoint independent is denoted by where and We use to denote the vertex set where S is a vertex subset of G.
Given a graph a graph G is H-free if G contains no induced subgraph isomorphic to A claw is a graph isomorphic to Let such that if a subgraph H consisting of in G is isomorphic to a claw. Let denote the graph obtained by deleting an edge of For a positive integer we use and to denote a cycle, and a path of order k, respectively. A bull is a graph (see Figure 1) obtained by joining two isolated vertices to two distinct vertices of a triangle, respectively. We use to denote a subgraph H of G isomorphic to a bull, which consists of such that and A is a graph (see Figure 1) obtained by identifying an end of a path of length 2 to a vertex of a triangle. In this paper, we use to denote a subgraph H of G isomorphic to , which consists of such that and For two graphs and the join of and denoted by is a graph with vertex set and edge set Let denote the independence number of a graph G.
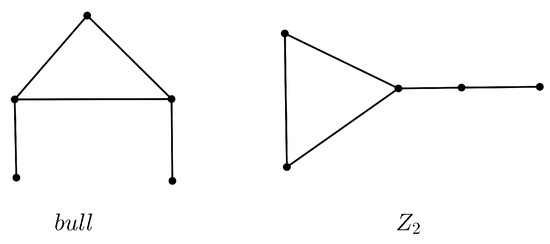
Figure 1.
Two forbidden induced subgraphs in this paper.
If every vertex of a graph G is in S or adjacent to some vertex in then S is called a dominating set of Let S be a dominating set of a graph G. If for every vertex S contains a neighbor of denoted by such that is also a dominating set of then S is called a secure dominating set of S is called a co-secure dominating set of G if for every vertex v in there is a neighbor of v in denoted by such that is also a dominating set of The minimum cardinality of a co-secure dominating set (resp. secure dominating set) of G is the called the co-secure (resp. secure) domination number of We use and to denote the co-secure domination number and secure domination number of , respectively.
Let S be a dominating set of a graph For a vertex if u has an exactly one neighbor in S, denoted by then u is called an external private neighbor of v with respect to For a vertex let is an external private neighbor of v with respect to S and and is a dominating set of G
In [2], Cockayne et al. proposed the concepts of a secure dominating set and secure domination number; moreover, they also determined the exact values of the secure domination number of paths, cycles, and complete multipartite graphs. Araki and Yumoto [3] proved that the secure domination number of a maximal outerplane graph of n vertices is at most Degawa and Saito [4] gave that the secure domination number of every -free graph is no larger than its independence number. The secure domination number of Cartesian products of small graphs with paths, cycles, and some other graph classes were given in [5]. For the bounds of the secure domination number of more classes of graphs, the readers are referred to [6,7,8].
Arumugan et al. introduced the concept of co-secure domination in [9]. They also obtained the co-secure domination number of paths and cycles, and the sharp upper and lower bounds of some graphs; moreover, they proposed that the problem to determine the co-secure domination number of a graph is NP-complete even if it is a bipartite, chordal or planar graph. Joseph and Sangeetha [10] obtained the co-secure domination number of Friendship graphs, Jahangir graphs, and Helm graphs; they also studied a family of trees such that the co-secure domination number equals the secure domination number. Pothuvath et al. [11] gave the bounds of domination number and co-secure domination number for jump graphs. We summarize the results on the parameter in the bound of co-secure domination number in Table 1.

Table 1.
Parameter in the bounds of the secure domination number of a graph G.
Finding the minimum dominating set (MDS) and co-secure dominating set (MCSDS) are NP-complete. However, MCSDS is practically harder due to the co-secure constraint, which introduces combinatorial challenges. The co-secure condition (the “swap” for every in a dominating set S) forces solutions to be larger and more structured. Specifically, algorithms must consider larger sets S, and the number of candidate sets grows exponentially with size (e.g., from for MDS to for larger c in MCSDS).
Arumugan et al. [9] gave the bounds of the co-secure domination number by independence number, and secure domination number, as follows.
Theorem 1
([9]). If G is a non-trivial graph, then
Theorem 2
([9]). If G is a graph and then
Moreover, in [9], Arumugan et al. proposed the following two problems.
Problem 1
([9]). Characterize graphs G with
Problem 2
([9]). Characterize graphs G with
There is very little research on Problems 1 and 2. We think the dense graphs may satisfy the characterization by the structural analysis. Claw-free graphs can be utilized to design deadlock-free routing algorithms in the context of supercomputer networks and distributed systems, because their structure can avoid complex dependencies that may lead to deadlocks. -free graphs are useful for creating low-diameter and fault-tolerant network topologies, as their restricted path structure helps minimize communication latency and improve robustness. Inspired by the significant application value of -free graphs and the above open problems, in this paper, we characterize the co-secure domination number of -free graphs.
Notice that if a graph G contains an isolate vertex v, then v is in every dominating set of By the definition, for a co-secure dominating set S of a graph each vertex in S has a neighbor in which implies that G contains no isolated vertex. Thus, if G contains a co-secure dominating set.
2. Characterization of Claw-Free Graphs with
In this section, we characterize the claw-free graphs G with Firstly, we obtain the following preliminaries.
Lemma 1.
Let G be a non-trivial claw-free graph such that G contains exactly one vertex of degree Then
Proof.
Let v be the only one vertex of G of degree Then, G is not a complete graph, and hence, Moreover, each vertex of G is in , which implies since G is claw-free. Suppose and is a minimum co-secure dominating set of Then, there is a vertex y in such that is dominating set of which implies a contradiction. Thus, Assume are two nonadjacent vertices of G. We claim that is a co-secure dominating set of G, and then, S is a minimum co-secure dominating set of G by Since S is a maximum independent set of and hence, S is a dominating set of Clearly, since each vertex of G is adjacent to v and Thus, is a dominating set of G for each It follows that S is a minimum co-secure dominating set of G and then □
Let be the family of claw-free graphs G of such that G is not complete, and G contains at least two vertices of degree (see Figure 2). It is easy to verify that and Thus, by Lemma 1, if G contains a vertex of degree and In Theorem 4 of [12], we prove that every -free graph G with and contains a minimum co-secure dominating set that is a maximum independent set of i.e., . However, there is a -free graph G with such that . In this paper, we give the following result, which is more precise.
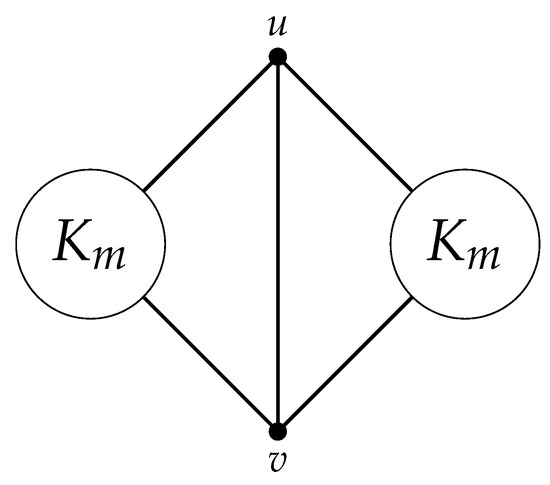
Figure 2.
A -free graph G with and .
Theorem 3.
Let G be a -free graph with and Then, G contains a minimum co-secure dominating set that is a maximum independent set of
Assume that and is a 5-cycle. Let G be the graph (see Figure 3) obtained by joining each vertex in to every vertex in of Clearly, G is -free, but not -free. Thus, there is a -free graph that is not -free. Conversely, there is a -free graph that is not -free; for example, is a -free graph, but not -free.
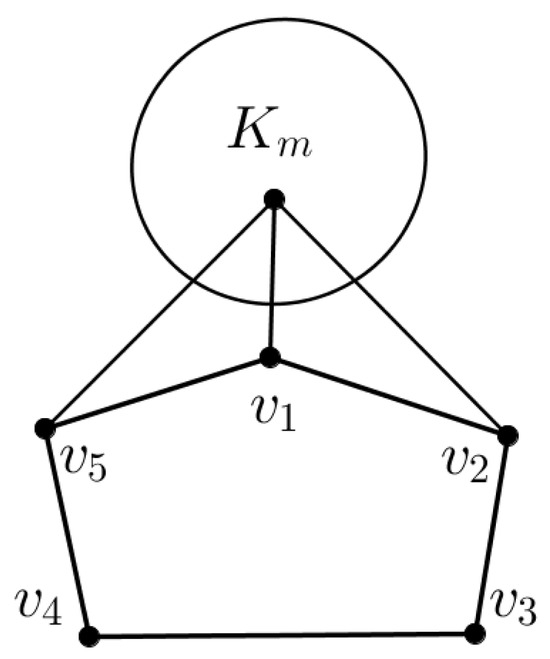
Figure 3.
A -free graph but not -free.
In the following, we give the relation between the co-secure domination number and independence number of -free graphs.
Theorem 4.
Let G be a -free graph such that and Then, G contains a minimum co-secure dominating set that is a maximum independent set of G.
Proof.
Since for a disconnected graph, its co-secure domination number is the sum of the co-secure domination number of all the components, and hence, it suffices to consider G is connected in the following proof. If G is complete, then we are done. Thus, we assume that G is a connected and non-complete graph. Then, which implies that by . We take a minimum co-secure dominating set S of G such that contains the minimum number of edges. We have by . In the following proof, firstly, we prove that S is an independent set, and then, we claim that S is a maximum independent set of G. □
We need the following result to prove S is an independent set of G.
Claim 1.
if and
Proof.
Suppose to the contrary that there is a vertex such that and Let such that We claim that is a clique. Otherwise, contains two non-adjacent vertices. Let such that Since and we have It follows that a contradiction. Thus, is a clique.
Let and . Since is a clique, we have and hence, is a dominating set of G with By contains fewer edges than Thus, is not a co-secure dominating set of G by the choice of Clearly, Then, there is vertex such that and contains two nonadjacent vertices with We have by
Suppose Then, by and a contradiction. Thus, Without loss of generality, assume that and Then, Recall that Suppose Then, by which implies a contradiction. Thus, and then, a contradiction. The claim is true. □
Next, we prove S is an independent set.
Claim 2.
S is an independent set.
Proof.
Suppose to the contrary that S is not an independent set. Let be in S such that and set By Claim 1, and hence, is a dominating set of Since and S is a minimum co-secure dominating set of is not a co-secure dominating set of Thus, there is a vertex such that and contains two nonadjacent vertices with
Suppose Then, we have or by and which implies by for each We have by Claim 1, and hence, each vertex in is adjacent to Then, a contradiction to Thus,
Without loss of generality, assume and Then, which implies since by Claim 1. Thus, by It follows that a contradiction. Thus, S is an independent set of G. □
If there is a minimum co-secure dominating set of G that is a maximum independent set of G, then we are done. Suppose on the contrary, that every minimum co-secure dominating set of G is not a maximum independent set of G. Let be a maximum independent set of G. Subject to the original assumption that S is a minimum co-secure dominating set of G such that contains the minimum number of edges; we choose S such that is maximum. S is an independent set of G by Claim 2, but it is not a maximum independent set of G. Then, and
Claim 3.
If and for some vertex then
Proof.
Let and such that Suppose to the contrary that Let Then, we obtain that by Thus, is a dominating set of and is an independent set of G by We have by and and hence, Then, by the choice of is not a co-secure dominating set of G. Clearly, It follows that there is a vertex such that and contains two non-adjacent vertices with .
By and we have We claim that For otherwise, and then, , a contradiction. Without loss of generality, assume and . Then, and Clearly, by Thus, a contradiction. It follows that □
Claim 4.
If then for any vertex y in
Proof.
Let and . Suppose to the contrary that Then, by Claim 3, Thus, there is a vertex such that Since S is a co-secure dominating set of Let . Then, We claim that Suppose on the contrary, for some vertex Then, by and hence, a contradiction. Thus,
We claim that Note that since S is an independent set of G. Suppose to the contrary that there is a vertex We have since G is claw-free and S is an independent set. Let Clearly, and by We have or by and We claim that , for otherwise, a contradiction. Without loss of generality, assume It follows that a contradiction. Thus,
Since and G is connected, contains a vertex adjacent to some vertex in that has a neighbor in by Let such that By we have that We claim that Suppose on the contrary that Then, by and It follows that a contradiction. Thus, which implies Similarly, and We have for otherwise, a contradiction. We obtain that or by and Moreover, we have for otherwise, a contradiction. Without loss of generality, assume that Then, , and hence, a contradiction. Thus, for any vertex □
Claim 5.
There are two vertices in such that moreover,
Proof.
Since S is a dominating set of G and is an independent set of G, each vertex in is adjacent to some vertex in Moreover, there are at least two vertices in that have a common neighbor in S by Let and Since is an independent set with we have By Claim 4, and hence, Moreover, since G is claw-free and S is an independent set of G.
Suppose on the contrary that . Let and Clearly, and Thus, a contradiction. It follows that x and y have two common neighbors in □
Now, let us complete the proof of Theorem 4. By Claim 5, let be in and such that Since are in and is an independent set, we have Let We have is an independent set of G since S is an independent set of and For each vertex we have or by and Thus, is a dominating set with By and we have Thus, Then, by the choice of we have is not a co-secure dominating set of G. Thus, there is a vertex x in such that We claim that
Suppose on the contrary that and There are two non-adjacent vertices in such that by Without loss of generality, assume Then, or since each vertex in is adjacent to or Thus, by a contradiction to It follows that Without loss of generality, assume that Then, by By and we have or Without loss of generality, assume that Then, we have for otherwise, a contradiction. Thus, by a contradiction. Thus, Theorem 4 is true.
By Theorem 4, we obtain the following result, which characterizes a -free graph G with
Corollary 1.
Let G be a -free graph such that and Then,
A cograph is a graph that contains no induced subgraph isomorphic to Obviously, a cograph is -free. Then, by Theorem 4, we can obtain the following result.
Corollary 2.
Let G be a -free cograph with and Then
3. Characterization of Claw-Free Graphs G with
According to Problem 2 in Section 1, we characterize the claw-free graph G with in this section. By Theorem 2, for a graph G, if the minimum degree of G is at least 2, then For a claw-free graph, we can obtain the following result, in which the minimum degree can be decreased to 1. We will apply this result to the proof of the main result in this section.
Theorem 5.
If G is a claw-free graph and , then
Proof.
It suffices to prove that there is a minimum secure dominating set of G such that it is also a co-secure domination set of G. If G is disconnected, then the minimum secure (resp. co-secure) domination number is the sum of the minimum secure (resp. co-secure) domination number of each component in G. Thus, without loss of generality, we assume that G is a connected claw-free graph. If G is complete, then we are done. Thus, we assume G is not complete. We prove the theorem by reduction to absurdity. Suppose to the contrary that each minimum secure dominating set of G is not a co-secure domination set of G. Firstly, we have the following result. □
Claim 6.
There is a vertex v in S such that all the neighbors of v are in S for every minimum secure dominating set S of G.
Proof.
Suppose to the contrary that there is a minimum secure dominating set S of G such that each vertex in S has at least one neighbor in Since S is not a co-secure dominating set of G, there is a vertex such that
If then each vertex in is in a contradiction. Thus, Since S is a secure dominating set, is a clique, which implies a contradiction. Thus, the claim is true. □
In the following proof, let S be a minimum secure dominating set of G such that contains the minimum number of edges among all the minimum secure dominating sets of By Claim 6, let such that Since contains at least one edge. Then, Let Then, is a dominating set of G by Clearly, By the minimality of is not a secure dominating set of G. Thus, there is a vertex x in such that for each neighbor y of x in By it is easy to verify that v is the exactly one vertex in such that for every neighbor y of v in Thus, there is a vertex in that is non-adjacent to v for each neighbor y of v in
Let and such that Clearly, We claim that is a clique. For two distinct vertices we have by and hence, by Thus, is a clique.
Let Since is a clique, is a dominating set of G with Moreover, for each vertex x in with and for each vertex in Thus, for each vertex for some neighbor of x in if . Furthermore, it is easy to verify that and It follows that is a secure dominating set of Clearly, contains fewer edges than a contradiction. Thus, G contains a minimum secure dominating set that is also a co-secure dominating set of i.e.,
Theorem 6.
If G is a -free graph with and then
Proof.
By Theorem 5, it suffices to prove that If G is complete, then we are done. We assume that G is not complete. Then, by Without loss of generality, assume that G is connected. In the following, we will prove that G contains a minimum co-secure dominating set that is also a secure dominating set, and hence, □
Note that by Thus, by Theorem 4, let S be a minimum co-secure dominating set of G such that S is a maximum independent set of G. If S is also a secure dominating set of then we are done. Thus, we assume that S is not a secure dominating set of Notice that . Firstly, we have the following result.
Claim 7.
is a clique if for a vertex
Proof.
Suppose to the contrary that and contains two distinct non-adjacent vertices . Clearly, is non-adjacent to any vertex in by for each . Let Then, is an independent set of G with a contradiction to the choice that S is a maximum independent set of G. Thus, the claim is true. □
Since S is not a secure dominating set of in the following proof, let such that for each neighbor y of x in By Claim 7, if for some vertex then a contradiction. Thus,
Let . Then, and contains at least one vertex that is non-adjacent to x by for each Let such that for each By and we have Since S is an independent set of G, we have . Thus, by
We claim that for each vertex u in Note that since S is an independent set of G. Without loss of generality, suppose to the contrary that such that Since S is an independent set of G and G is claw-free, we have and which implies Thus, We have by which implies a contradiction. It follows that for each vertex u in
Since and G is connected, there is a vertex in adjacent to some vertex in that has a neighbor in by for each vertex u in
Without loss of generality, assume that such that Then, and by for each vertex u in We have for otherwise, by a contradiction. It follows that We have by and Moreover, we have by and It follows that a contradiction. Thus, Theorem 6 is true.
Note that is necessary in Theorem 6. Let and be three vertex-disjoint graphs such that and is a 5-cycle, where . Let G be a graph (see Figure 4) obtained by joining every vertex in to each vertex of and joining every vertex in to each vertex in of Clearly, G is a -free graph with It is easy to verify that and
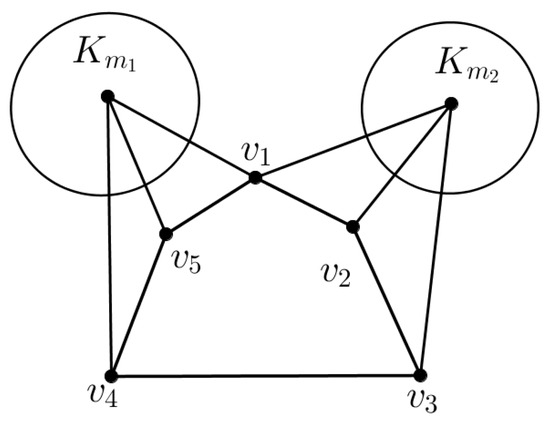
Figure 4.
A -free graph G such that and .
It is obvious that for each graph G in Thus, by Corollary 1 and Theorem 6, we can obtain the following result.
Corollary 3.
Let G be a -free graph with and Then,
In the following, we characterize the relationship between the co-secure domination number and secure domination number of -free graphs.
Theorem 7.
If G is a -free graph with and then
Proof.
If G is complete, then we are done. Thus, we assume G is not complete, and then, by By Theorem 2, it suffices to prove that As in the proof of Theorem 6, assume G is connected, and in the following proof, we show that G contains a minimum co-secure dominating set S such that S is also a secure dominating set of G.
By Theorem 3, let S be a minimum co-secure dominating set of G such that S is a maximum independent set of G. Then by . If S is a secure dominating set of then we are done. Suppose to the contrary that S is not a secure dominating set of Let x be in such that for each neighbor y of x in As in the proof of Claim 7 of Theorem 6, we can also obtain that is a clique, and then if for a vertex Thus, and contains a vertex that is non-adjacent to x for each neighbor y of x in
Let and such that for each
We claim that for each vertex u in . Without loss of generality, suppose on the contrary that such that by . Since G is claw-free and S is an independent set, we have and . Thus, and Moreover, by and . By and we have or Suppose . Then, by a contradiction. Thus, and then, It follows that a contradiction. Thus, for each vertex u in .
Since G is connected and we have contains a vertex adjacent to some vertex in that has a neighbor in since G is connected. Without loss of generality, let such that Then, by for each vertex u in . We have for otherwise, a contradiction. Thus,
We have that for otherwise a contradiction. Moreover, we have for otherwise a contradiction.
Since and let Then, or by and We have by for each vertex u in .
We claim that Otherwise, by and . Then, we have for otherwise a contradiction. Thus, by and It follows that a contradiction. Thus, and then,
We have by and Thus, , a contradiction. Thus, the theorem is true. □
In the following, we construct a -free G with such that and which shows that is necessary in Theorem 7. Let and be two complete graphs of order respectively, such that and Assume that such that Let Suppose that H is a graph obtained by joining every vertex of to each vertex in except of and of Let G be the graph (see Figure 5) with such that u is adjacent to each vertex in of and v is adjacent to each vertex in of
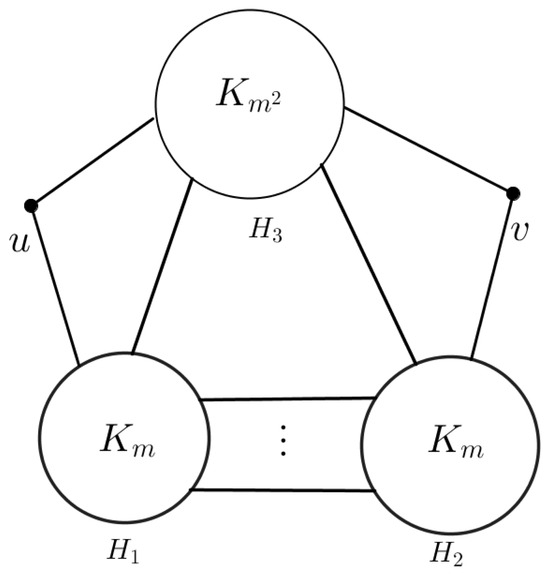
Figure 5.
A -free graph G with such that and .
By Theorem 3 and Theorem 7, we can obtain the following results.
Corollary 4.
Let G be a -free graph with and Then,
Corollary 5.
Let G be a 3-connected -free graph and Then,
4. Conclusions
Co-secure dominating sets can be applied to wireless sensor networks, network security, combinatorial optimization problems, and other fields. Claw-free graphs are beneficial for designing deadlock-free routing algorithms and simplifying communication protocols in supercomputer networks. Moreover, inspired by Arumugam et al.’s [9] questions on the co-secure domination number, in this paper, we characterize two classes of claw-free graphs such that their co-secure domination numbers equal the independence number and the secure domination number. The research on degree conditions of graphs are always the focus problems in graph theory, and the minimum degree affects the bound of co-secure domination number. Thus, we propose the question: What is the minimum degree such that if G is claw-free, then ?
Author Contributions
Conceptualization, Y.Z. and J.Z.; methodology, X.C., J.Z. and S.J.; validation, X.C. and S.J.; writing—original draft preparation, X.C.; writing—review and editing, Y.Z. and S.J.; project administration, L.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Foundation of China (Grant No. 11901268, No. 12131013) and the Fundamental Research Funds for the Universities of Liaoning Province (Grant No. LJ212410165065).
Data Availability Statement
No data, models, or code were generated or used during the study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bondy, J.; Murty, U. Graph Theory with Applications; American Elsevier: New York, NY, USA, 1976. [Google Scholar]
- Cockayne, E.; Grobler, P.; Gründlingh, W.; Munganga, J.; Vuuren, J. Protection of a graph. Util. Math. 2005, 67, 19–32. [Google Scholar]
- Araki, T.; Yumoto, I. On the secure domination numbers of maximal outerplanar graphs. Discrete Appl. Math. 2018, 236, 23–29. [Google Scholar] [CrossRef]
- Degawa, S.; Saito, A. A note on secure domination in C5-free graphs. Discrete Appl. Math. 2023, 333, 82–83. [Google Scholar] [CrossRef]
- Haythorpe, M.; Newcombe, A. The secure domination number of Cartesian products of small graphs with paths and cycles. Discrete Appl. Math. 2022, 309, 32–45. [Google Scholar] [CrossRef]
- Cockayne, E.; Favaron, O.; Mynhardt, C. Secure domination, weak Roman domination and forbidden subgraphs. Bull. Inst. Comb. Appl. 2003, 39, 87–100. [Google Scholar]
- Manjusha, P.; Chithra, M.R. Co-secure domination in mycielski graph. J. Comb. Math. Comb. Comput. 2020, 113, 289–297. [Google Scholar]
- Merouane, H.; Chellali, M. On secure domination in graphs. Inform. Process. Lett. 2015, 115, 786–790. [Google Scholar] [CrossRef]
- Arumugan, S.; Ebadi, K.; Manrique, M. Co-secure and secure domination in graphs. Util. Math. 2014, 94, 167–182. [Google Scholar]
- Joseph, A.; Sangeetha, V. Bounds on co-secure domination in graphs. Int. J. Math. Trends Technol. 2018, 55, 158–164. [Google Scholar] [CrossRef]
- Pothuvath, M.; Iyer, R.R.; Asiri, A.; Somasundaram, K. Co-secure domination in jump graphs for enhanced security. Mathematics 2024, 12, 3077. [Google Scholar] [CrossRef]
- Cui, J.; Li, T.; Zhang, J.; Chen, X.; Xiong, L. Co-secure domination number in some graphs. Axioms 2025, 14, 10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).