CIRGNN: Leveraging Cross-Chart Relationships with a Graph Neural Network for Stock Price Prediction
Abstract
1. Introduction
- A new framework is proposed to fully employ both technical charts and technical indicators for predicting stock price.
- Our methods involve exploring the relationship between technical charts and indicators, overcoming the limitation of relying solely on specific charts in deep learning.
- Our framework outperforms the baseline methods in prediction accuracy. We also attain the utmost excess return in the actual stock market.
2. Related Work
2.1. Technical Charts
2.2. Graph Learning for Stock Prediction
3. Method
3.1. Problem Definition
3.2. Visual Graph Algorithm
3.3. Adaptive Relationship Graph Learning Layer
3.4. Graph Neural Network
3.5. Prediction Module
4. Experiments
4.1. Data
4.2. Comparison Methods
- VAR: The first baseline method employs a VAR model with two-dimensional input data [28].
- ARIMA: The second baseline method involves the utilization of an ARIMA model, which relies on historical price data as its foundation for forecasting future stock prices [28].
- SVM: The third baseline method involves an SVM utilizing two-dimensional input data [28].
- LSTM: The fourth baseline method entails a fundamental LSTM network designed to forecast future stock prices, relying on historical price data as its basis [29].
- CNN: The fifth baseline method entails a fundamental convolution neural network designed to forecast future stock prices, relying on historical price data as its basis [28].
- MTGNN: The sixth baseline method is the novel Multivariate Time-Series Forecasting with Graph Neural Networks (MTGNN). MTGNN automatically extracts the relations among indicators, capturing the spatial and temporal dependencies inherent in the stock data [22].
- Chart-GCN: The seventh baseline method involves extracting a key point sequence from the stock price series. Subsequently, it transforms the input sequence into a graph and utilizes a graph convolutional network to effectively mine information from the technical chart of closing price for stock price prediction [7].
- iTransformer: The last baseline method is a recently proposed Transformer-based model designed for time-series forecasting. Unlike conventional approaches that apply attention over temporal tokens, iTransformer inverts the input dimensions and embeds the entire sequence of time points for an individual variable as a token, allowing attention to be applied across variate tokens. This design enables the model to explicitly capture complex cross-variable dependencies for improved forecasting performance [30].
4.3. Parameter Setting
4.4. Results
5. Discussion
5.1. Ablation
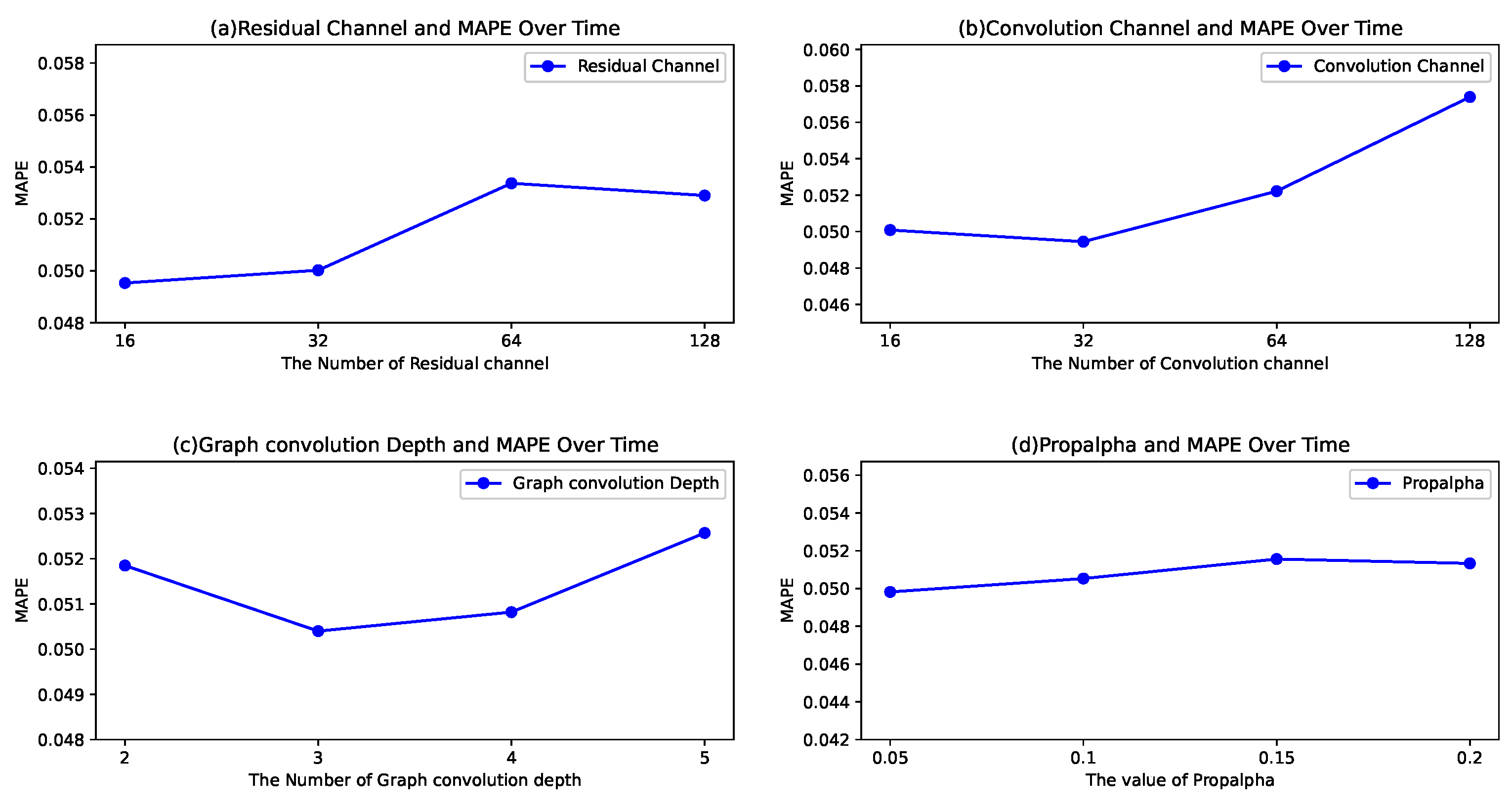
5.2. Parameter Sensitivity Analysis
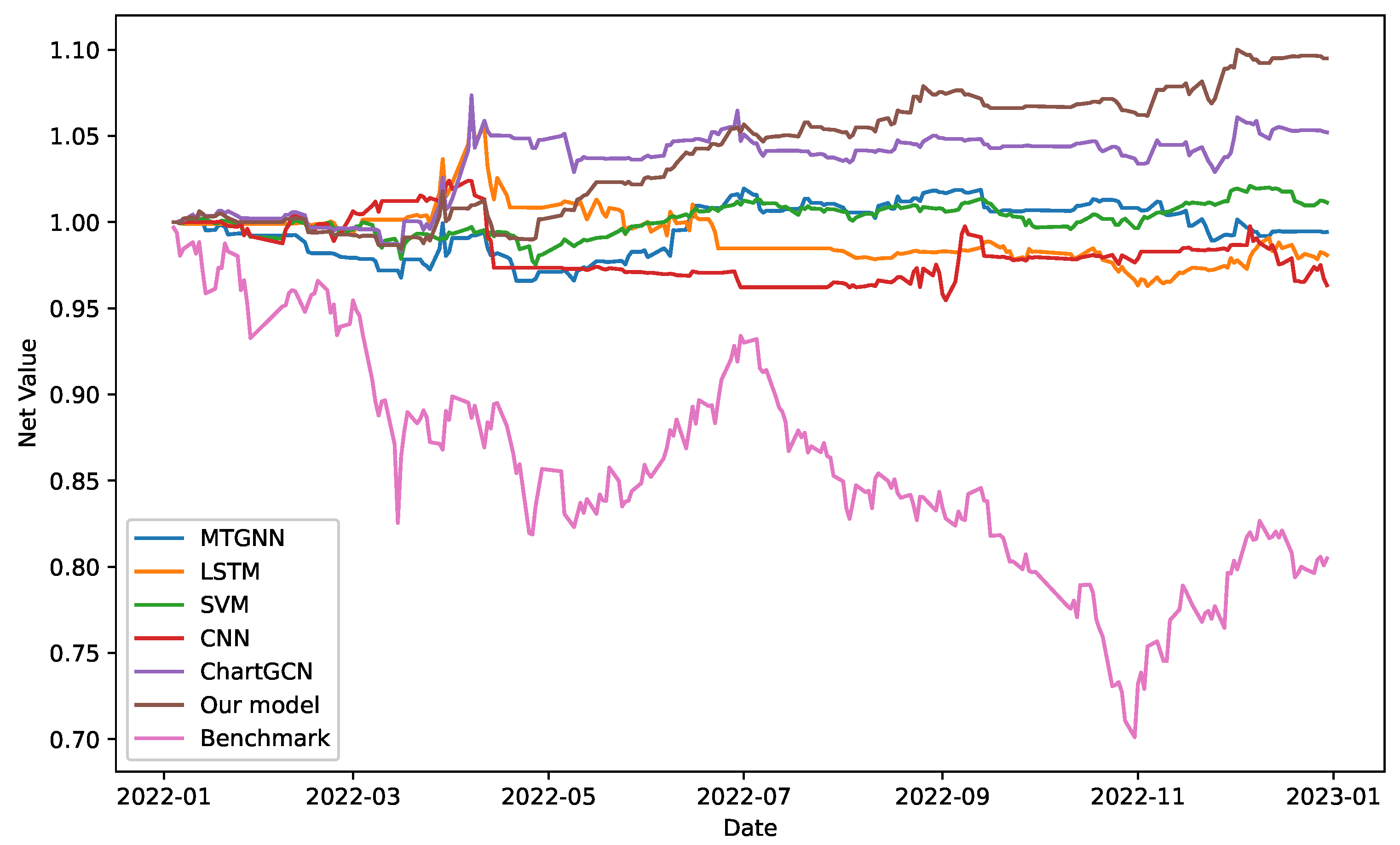
5.3. Trading Simulation
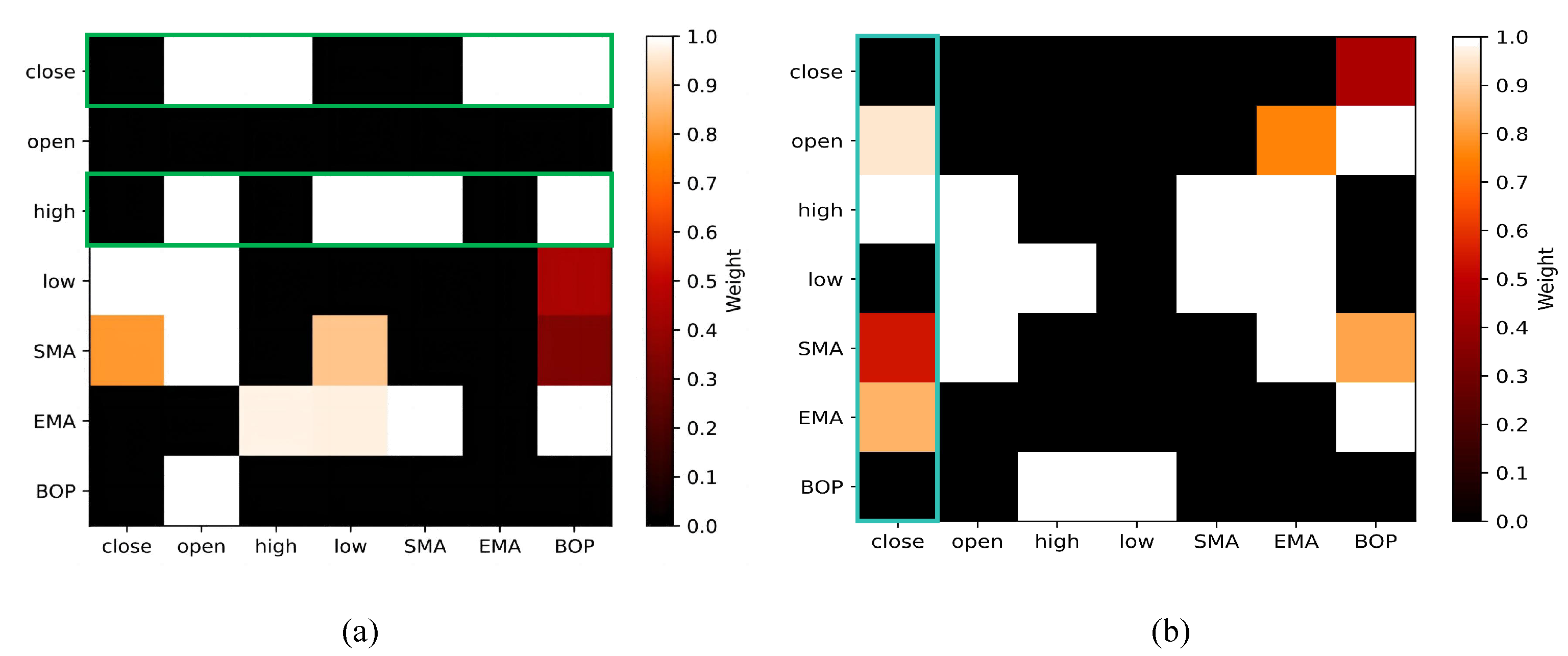
5.4. Interpretability of the Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takata, M.; Kidoguchi, N.; Chiyonobu, M. Stock recommendation methods for stability. J. Supercomput. 2024, 80, 12091–12101. [Google Scholar] [CrossRef]
- Lee, M.C.; Chang, J.W.; Hung, J.C.; Chen, B.L. Exploring the effectiveness of deep neural networks with technical analysis applied to stock market prediction. Comput. Sci. Inf. Syst. 2021, 18, 401–418. [Google Scholar] [CrossRef]
- Leigh, W.; Modani, N.; Purvis, R.; Roberts, T. Stock market trading rule discovery using technical charting heuristics. Expert Syst. Appl. 2002, 23, 155–159. [Google Scholar] [CrossRef]
- Agrawal, M.; Shukla, P.K.; Nair, R.; Nayyar, A.; Masud, M. Stock Prediction Based on Technical Indicators Using Deep Learning Model. Comput. Mater. Contin. 2022, 70, 287–304. [Google Scholar] [CrossRef]
- Tsinaslanidis, P.E. Subsequence dynamic time warping for charting: Bullish and bearish class predictions for NYSE stocks. Expert Syst. Appl. 2018, 94, 193–204. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wu, L.H.; Wu, L.C. An integrative extraction approach for index-tracking portfolio construction and forecasting under a deep learning framework. J. Supercomput. 2024, 80, 2047–2066. [Google Scholar] [CrossRef]
- Li, S.; Wu, J.; Jiang, X.; Xu, K. Chart GCN: Learning chart information with a graph convolutional network for stock movement prediction. Knowl.-Based Syst. 2022, 248, 108842. [Google Scholar] [CrossRef]
- Wu, J.; Xu, K.; Chen, X.; Li, S.; Zhao, J. Price graphs: Utilizing the structural information of financial time series for stock prediction. Inf. Sci. 2022, 588, 405–424. [Google Scholar] [CrossRef]
- Dahlquist, J.R.; Kirkpatrick, C.D., II. Technical Analysis: The Complete Resource for Financial Market Technicians; FT Press: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. A systematic review of fundamental and technical analysis of stock market predictions. Artif. Intell. Rev. 2020, 53, 3007–3057. [Google Scholar] [CrossRef]
- Dumiter, F.C.; Turcaș, F.M. Charts Used in Technical Analysis. In Technical Analysis Applications: A Practical and Empirical Stock Market Guide; Springer: Berlin/Heidelberg, Germany, 2023; pp. 71–89. [Google Scholar]
- Jiang, W.; Luo, J. Graph neural network for traffic forecasting: A survey. Expert Syst. Appl. 2022, 207, 117921. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef]
- He, Q.Q.; Siu, S.W.I.; Si, Y.W. Instance-based deep transfer learning with attention for stock movement prediction. Appl. Intell. 2023, 53, 6887–6908. [Google Scholar] [CrossRef]
- Cervelló-Royo, R.; Guijarro, F.; Michniuk, K. Stock market trading rule based on pattern recognition and technical analysis: Forecasting the DJIA index with intraday data. Expert Syst. Appl. 2015, 42, 5963–5975. [Google Scholar] [CrossRef]
- Tsinaslanidis, P.; Guijarro, F. What makes trading strategies based on chart pattern recognition profitable? Expert Syst. 2021, 38, e12596. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; PMLR: Cambridge, MA, USA, 2017; pp. 1263–1272. [Google Scholar]
- Xiao, T.; Chen, Z.; Wang, D.; Wang, S. Learning how to propagate messages in graph neural networks. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, 14–18 August 2021; pp. 1894–1903. [Google Scholar]
- Liao, L.; Hu, Z.; Zheng, Y.; Bi, S.; Zou, F.; Qiu, H.; Zhang, M. An improved dynamic Chebyshev graph convolution network for traffic flow prediction with spatial-temporal attention. Appl. Intell. 2022, 52, 16104–16116. [Google Scholar] [CrossRef]
- Han, H.; Xie, L.; Chen, S.; Xu, H. Stock trend prediction based on industry relationships driven hypergraph attention networks. Appl. Intell. 2023, 53, 29448–29464. [Google Scholar] [CrossRef]
- Cheng, D.; Yang, F.; Xiang, S.; Liu, J. Financial time series forecasting with multi-modality graph neural network. Pattern Recognit. 2022, 121, 108218. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Wu, L.; Cui, P.; Pei, J.; Zhao, L.; Guo, X. Graph neural networks: Foundation, frontiers and applications. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 4840–4841. [Google Scholar]
- Li, S.; Liu, Y.; Chen, X.; Wu, J.; Xu, K. Forecasting turning points in stock price by integrating chart similarity and multipersistence. IEEE Trans. Knowl. Data Eng. 2024, 36, 8251–8266. [Google Scholar] [CrossRef]
- Shynkevich, Y.; McGinnity, T.M.; Coleman, S.A.; Belatreche, A.; Li, Y. Forecasting price movements using technical indicators: Investigating the impact of varying input window length. Neurocomputing 2017, 264, 71–88. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, S.; Yang, H.; Wu, H. Stock trend prediction using candlestick charting and ensemble machine learning techniques with a novelty feature engineering scheme. IEEE Access 2021, 9, 101433–101446. [Google Scholar] [CrossRef]
- Shah, J.; Vaidya, D.; Shah, M. A comprehensive review on multiple hybrid deep learning approaches for stock prediction. Intell. Syst. Appl. 2022, 16, 200111. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Kundu, R.; Chattopadhyay, S.; Nag, S.; Navarro, M.A.; Oliva, D. Prism refraction search: A novel physics-based metaheuristic algorithm. J. Supercomput. 2024, 80, 10746–10795. [Google Scholar] [CrossRef]

| Indicator Name | Formula |
|---|---|
| Simple n-day Moving Average (SMA) | |
| Exponential n-day Moving Average (EMA) | |
| Momentum | |
| Larry Williams R% | |
| Balance of Power (BOP) |
| Model | SSE | DJIA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAPE | MAE | RMSE | RAE | RSE | MAPE | MAE | RMSE | RAE | RSE | |
| VAR | 0.4809 | 14.6583 | 17.4545 | 2.6931 | 9.6259 | 0.4061 | 42.5859 | 55.7185 | 2.2829 | 27.5177 |
| ARIMA | 0.3223 | 15.2649 | 17.8768 | 1.4139 | 2.3091 | 0.2721 | 44.3484 | 57.0665 | 1.1985 | 6.6011 |
| SVM | 0.2726 | 27.4281 | 29.6670 | 1.5620 | 3.5046 | 0.2302 | 79.6855 | 94.7032 | 1.3241 | 10.0186 |
| LSTM | 0.0694 (±0.0063) | 3.4587 (±1.1209) | 4.6312 (±1.3033) | 0.5691 (±0.0545) | 1.4955 (±0.1312) | 0.0568 (±0.0064) | 16.2183 (±2.3334) | 23.8613 (±6.2842) | 0.4671 (±0.0349) | 4.1402 (±0.9055) |
| CNN | 0.0997 (±0.0091) | 3.4818 (±1.1672) | 4.6466 (±1.3421) | 0.5793 (±0.0573) | 0.7702 (±0.0691) | 0.0815 (±0.0089) | 16.3270 (±2.4102) | 23.9411 (±6.4381) | 0.4756 (±0.0355) | 2.1322 (±0.4663) |
| MTGNN | 0.0509 (±0.0051) | 3.5443 (±1.1038) | 4.7731 (±1.3891) | 0.0531 (±0.0048) | 0.4255 (±0.0359) | 0.0419 (±0.0047) | 10.0474 (±1.4127) | 14.8673 (±3.8642) | 0.0439 (±0.0033) | 1.1869 (±0.2734) |
| Chart-GCN | 0.0521 (±0.0044) | 3.8005 (±1.2685) | 5.052 (±1.3874) | 0.0549 (±0.0056) | 0.4378 (±0.0397) | 0.0429 (±0.0048) | 10.7738 (±1.5501) | 15.7378 (±4.2156) | 0.0454 (±0.0034) | 1.2211 (±0.2518) |
| iTransformer | 0.0514 (±0.0047) | 2.8577 (±0.9261) | 4.1553 (±1.1694) | 0.5267 (±0.0505) | 0.5852 (±0.0513) | 0.0479 (±0.0054) | 10.2965 (±1.4814) | 15.5281 (±4.0895) | 0.4441 (±0.0332) | 0.4938 (±0.1080) |
| Our model | 0.0473 * (±0.0037) | 1.7952 * (±0.5818) | 2.3348 * (±0.6571) | 0.0477 * (±0.0043) | 0.2784 * (±0.0244) | 0.0383 * (±0.0039) | 7.9971 * (±1.1506) | 11.4282 * (±3.0098) | 0.0372 * (±0.0028) | 0.7322 (±0.1601) |
| Model | SSE | DJIA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAPE | MAE | RMSE | RAE | RSE | MAPE | MAE | RMSE | RAE | RSE | |
| CIRGNN-1 | 0.0529 | 1.8701 | 2.5110 | 0.0538 | 0.3122 | 0.0488 | 9.9069 | 13.4727 | 0.0470 | 0.8703 |
| CIRGNN-2 | 0.0502 | 1.8511 | 2.4254 | 0.0509 | 0.2914 | 0.0438 | 8.9417 | 12.5743 | 0.0421 | 0.8148 |
| CIRGNN-3 | 0.0520 | 1.8850 | 2.4515 | 0.0501 | 0.2923 | 0.0402 | 8.3970 | 11.9996 | 0.0391 | 0.7688 |
| CIRGNN | 0.0473 | 1.7952 | 2.3348 | 0.0477 | 0.2784 | 0.0383 | 7.9971 | 11.4282 | 0.0372 | 0.7322 |
| Model | Annualized Return | Sharpe Ratio | Alpha | Beta | Max Drawdown | Information Ratio |
|---|---|---|---|---|---|---|
| SVM | −0.0224 | −1.5315 | −0.0200 | 0.1076 | 0.0280 | −0.0350 |
| LSTM | −0.0385 | −0.4000 | −0.0345 | 0.1151 | 0.1502 | −0.1184 |
| CNN | −0.0410 | −0.3728 | −0.0159 | 0.2089 | 0.1696 | 0.0097 |
| MTGNN | −0.0374 | −0.6151 | −0.0350 | 0.1080 | 0.0749 | −0.1779 |
| ChartGCN | 0.0514 | 0.3123 | 0.0654 | 0.1595 | 0.0685 | 0.7884 |
| CIRGNN | 0.1000 | 0.9647 | 0.1015 | 0.1037 | 0.0468 | 1.5757 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Gao, H.; Huang, J.; Liu, Y.; Li, S. CIRGNN: Leveraging Cross-Chart Relationships with a Graph Neural Network for Stock Price Prediction. Mathematics 2025, 13, 2402. https://doi.org/10.3390/math13152402
Jia S, Gao H, Huang J, Liu Y, Li S. CIRGNN: Leveraging Cross-Chart Relationships with a Graph Neural Network for Stock Price Prediction. Mathematics. 2025; 13(15):2402. https://doi.org/10.3390/math13152402
Chicago/Turabian StyleJia, Shanghui, Han Gao, Jiaming Huang, Yingke Liu, and Shangzhe Li. 2025. "CIRGNN: Leveraging Cross-Chart Relationships with a Graph Neural Network for Stock Price Prediction" Mathematics 13, no. 15: 2402. https://doi.org/10.3390/math13152402
APA StyleJia, S., Gao, H., Huang, J., Liu, Y., & Li, S. (2025). CIRGNN: Leveraging Cross-Chart Relationships with a Graph Neural Network for Stock Price Prediction. Mathematics, 13(15), 2402. https://doi.org/10.3390/math13152402





