Abstract
This study presents a graph knowledge-enhanced iterated greedy algorithm that incorporates dual directional decoding strategies, disjunctive graphs, neighborhood structures, and a rapid evaluation method to demonstrate its superior performance for the hybrid flowshop scheduling problem (HFSP). The proposed algorithm addresses the trade-off between the finite solution space corresponding to solution representation and the search space for the optimal solution, as well as constructs a decision mechanism to determine which search operator should be used in different search stages to minimize the occurrence of futile searching and the low computational efficiency caused by individuals conducting unordered neighborhood searches. The algorithm employs dual decoding with a novel disturbance operation to generate initial solutions and expand the search space. The derivation of the critical path and the design of neighborhood structures based on it provide a clear direction for identifying and prioritizing operations that have a significant impact on the objective. The use of a disjunctive graph provides a clear depiction of the detailed changes in the job sequence both before and after the neighborhood searches, providing a comprehensive view of the operational sequence transformations. By integrating the rapid evaluation technique, it becomes feasible to identify promising regions within a constrained timeframe. The numerical evaluation with well-known benchmarks verifies that the performance of the graph knowledge-enhanced algorithm is superior to that of a prior algorithm, and seeks new best solutions for 183 hard instances.
Keywords:
hybrid flow-shop scheduling problem; iterated greedy algorithm; critical paths; neighborhood structure; rapid evaluation method MSC:
90B99
1. Introduction
Shop scheduling involves creating a rational problem model and developing scheduling optimization methods aimed at enhancing manufacturing efficiency and reducing production costs, which are crucial for modern manufacturing systems. The hybrid flowshop scheduling problem (HFSP) is a prevalent issue within the realm of shop scheduling. Initially introduced by Salvador in the context of synthetic fiber processing [1], the HFSP has since been a subject of interest. In a hybrid flow shop, there are multiple machines available for at least one stage of the process. This setup integrates the two fundamental models of flow shop [2] and parallel machine problems to effectively boost productivity. However, this complex shop model introduces a higher level of complexity and difficulty in decision-making compared to the simpler models. The HFSP continues to be a focus of research due to its extensive practical applications within industrial production systems [3], as shown in Figure 1. Industrial processes such as automotive welding are typical examples of hybrid flowshop processes.
Figure 1.
Schematic diagram of the welding process flow.
In an HFSP, there is a set J with n jobs and a set M of m stages, where each stage i is composed of identical parallel machines, . All jobs are required to complete the same series of processes on m stages. Figure 2 illustrates a hybrid flowshop layout. The HFSP then consists in finding a schedule (i.e., a set of starting times for each job on each machine) that minimizes the makespan or maximum completion time among the jobs, i.e., . means higher machine utilization, lower inventory of Work-In-Process, and higher customer satisfaction. This study aims to optimize the by determining the processing sequence of jobs and machine allocation at each stage.
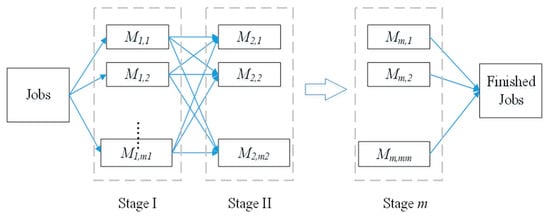
Figure 2.
A schematic diagram of a hybrid flow shop with N jobs and M stages.
The HFSP is recognized as a strongly NP-hard problem due to its intricate nature [4]; traditional exact methods are only capable of yielding optimal solutions for a limited number of small-scale issues. These methods prove to be ineffective when scaled up [5]. Approximate algorithms are always used to address this complex optimization problem, while they also struggle to find optimal solutions for certain hard instances, often due to a lack of knowledge-driven learning strategies [3,4,5]. On the one hand, the representation of solutions, as one of the cores of approximate algorithms, has its limitations. The commonly used single-stage encoding based on job sequences (which provides the job sequence for the first stage, with the jobs in subsequent stages being sorted according to scheduling variables based on certain rules) and complete encoding (which determines the machine assignment and the processing order between all operations to represent all solutions), respectively, have the problems of narrowing the algorithm’s search space and having low search efficiency in large-scale issues [6]. Therefore, this study applies an initial solution generation method using dual permutation-based encoding and a novel perturbation strategy in the decoding process to expand the search space.
On the other hand, these algorithms often employ random neighborhood search operators, such as multi-point random insertion and two-point random swapping or mutation. Random and unstructured movements fail to achieve efficient neighborhood search [7]. It is worth noting that single-stage encoding cannot intuitively represent the operation movement of the neighborhood search because changing the job sequence in the initial stage will alter the sequences in other stages. Therefore, this encoding method cannot fully depict the sequence after the move. This study aims to optimize the by determining the processing sequence of jobs and machine allocation at each stage. Therefore, this study combines the complete encoding method of the disjunctive graph model and designs a graph knowledge-enhanced strategy to mine domain knowledge of the HFSP, which in turn guides the design of efficient neighborhood search operators.
This study introduces a knowledge-driven enhanced iterative greedy algorithm tailored for the HFSP. The IG algorithm, a prominent metaheuristic, has demonstrated robust performance in addressing a variety of scheduling challenges, including HFSP [8], the flowshop scheduling problem [9], and the distributed scheduling problem [10]. The IG algorithm presented in this paper incorporates a local search that leverages a knowledge-driven neighborhood structure to produce new feasible solutions.
To assess the quality of a neighborhood solution, it is necessary to re-decode the new scheduling plan to obtain the fitness value of the neighborhood solution. However, a neighborhood move only adjusts a small portion of the operations on certain machines, and the processing order on most machines remains unchanged. Decoding the entire schedule multiple times would consume a significant amount of computational time. There is a dearth of research on rapid evaluation methods for neighborhood solutions. This study proposes a novel rapid evaluation method designed to locate promising areas within a limited timeframe. Current research on the aforementioned key issues is very limited. Therefore, this study aims to design a novel scheduling method capable of tackling certain hard instances present in existing benchmarks. The main contributions of this study can be summarized as follows:
- An initial solution generation method that utilizes dual permutation-based encoding and a decoding technique with a novel perturbation strategy to broaden the search space.
- A graph knowledge-enhanced IG algorithm with a knowledge-based neighborhood structure and rapid evaluation method for solving the HFSP.
- The proposed graph knowledge-enhanced IG algorithm seeks new best solutions for 183 hard instances.
The structure of this paper is organized as follows. Section 2 summarizes recent literature about the HFSP. Section 3 describes the details of the enhanced IG algorithm. Section 4 investigates the effectiveness of the dual directional decoding strategy and knowledge-based neighborhood search strategy, and verifies the performance of IG. Finally, Section 5 gives the conclusion and future work.
2. Related Work
In the HFSP and its variants, many scheduling methods have been developed, which can be broadly categorized into exact methods, scheduling rules, metaheuristic algorithms, and learning-based algorithms. Initially, research efforts were concentrated on exact methods for tackling small-scale HFSPs using traditional mathematical programming techniques and their subsequent algorithmic derivations. For instance, He et al. [11] proposed a polynomial-time algorithm for the two-stage HFSP with machine constraints of batch processing. Sun et al. [12] propose a branch-and-bound method and mathematical programming for minimizing makespan. As the scale of the problem increases, the complexity of the problem increases exponentially, resulting in a dramatic increase in the search space. This has prompted researchers to develop scheduling rules that assign jobs to machines in a rational manner at each stage, yielding feasible solutions. Examples of such rules include the Johnson rule, the Nawaz-Enscore-Ham method, the shortest processing time rule, and the first available machine approach. Paterina et al. [13] designed machine selection rules based on the identification of bottleneck phases.
Distinct from the previous two methods, the metaheuristic algorithm integrates stochastic factors and utilizes them to perform multiple iterations and guided searches on the problem solution, which makes the algorithm produce a better solution in multiple iterations. Metaheuristic algorithms are praised for their simplicity and efficacy, prompting extensive research on their design and enhancement. Scholars have dedicated efforts to this field, with applications that span a wide array of practical uses in various industries, as well as serving as a benchmark for solution updates [8]. Lin et al. [14] proposed an improved simulated annealing algorithm with a chaos-enhanced annealing mechanism to solve the Jose benchmark instances and successfully updated 137 of 240 problems. Fan et al. [5] combined forward and backward decoding methods to expand the search space, and applied a disjunctive graph to represent each solution, which clearly shows its critical path. Huang et al. [15] applied discrete differential evolution with two-stage stochastic programming to solve the HFSP. Safari et al. [16] designed the leader and follower agents to decompose the HFSP and afterwards, the optimal solution is obtained by a co-evolutionary genetic algorithm for each sub-problem; the effects of the designed methods are validated on the tire manufacturing industry. For the HFSP with reentrant constraints and limited buffer, Lin et al. [17] proposed a hybrid harmony search and GA to minimize the makespan and flowtime. Ozsoydan and Sagir [18] solved an HFSP with machine setup times under a learning IG algorithm. Luan et al. [19] proposed a low-carbon HFSP and discrete whale optimization algorithm to minimize completion time cost and energy consumption cost. Some of the metaheuristic algorithms for solving distributed HFSP include IG [20,21], GA [22], the artificial bee colony algorithm [23,24], the nested variable neighborhood descent algorithm [25], and so on.
The efficacy of metaheuristic algorithms hinges on solution representation and neighborhood search. Early encoding methods, such as permutation-based encoding in the first stage, confined search within the limited solution space, potentially excluding optimal solutions. With AI advancements, learning-based algorithms have been applied to the HFSP [26], integrating agent systems and machine learning. Li et al. [27] proposed a bilevel scheduler with a constrained Markov decision process for initial global sequence identification and partial sequence refinements through Deep Q and graph pointer networks.
In recent years, HFSP research has increasingly integrated graph structures and learning algorithms, showing promising prospects. Wang et al. [28] proposed a mandatory operation acceleration mechanism in graph space, which reduces insertion positions by analyzing critical paths in the graph, thereby significantly lowering the computational cost of neighborhood search. This provides a theoretical foundation for designing efficient graph-guided search strategies. In the field of reinforcement learning, Liu et al. [29] proposed a PPO-GAT algorithm, combining graph attention networks with a difference reward mechanism to effectively handle delayed optimization in dynamic HFSP scenarios. Furthermore, Wan et al. [30] and Huang et al. [31], respectively, introduced a multi-agent graph reinforcement learning model and a multiexpert graph neural network approach, both enhancing the representational capacity and generalization ability in complex scheduling states.
Although these studies have made considerable progress in intelligent decision-making and scheduling modeling, they often suffer from uncontrollable structural operations and weak interpretability in the search process. In contrast, this study proposes a graph-augmented iterative greedy algorithm that leverages graph-based neighborhood perturbation and fast evaluation strategies, aiming to improve both the interpretability and efficiency of the search process, thereby addressing key limitations in existing literature.
The IG algorithm, with its flexibility in accommodating various scheduling problem constraints, has been further developed. Pan et al. [32] considered the due windows constraint and proposed a hybrid IG and greedy local search algorithm through an optimal idle time insertion operator to balance the earliness and tardiness. Öztop et al. [33] proposed four different IG algorithms to optimize the total flow time by combining the variable batch insertion heuristic. To clarify the research progress in this field, this paper provides a comparative summary of relevant literature in Table 1.

Table 1.
Literature Summary.
Through the evolution of algorithms, this paper concludes that the IG algorithm demonstrates significant advantages in solving the HFSP, yet there are also shortcomings in its design that require attention. However, despite its effectiveness, the algorithm still has areas that can be improved upon: (1) it lacks domain-specific knowledge of the problem, leading to a heavy reliance on specialized local searches; (2) there is no memory storage structure within the IG, meaning that a vast number of historical solutions are discarded during the evolution of the solution; and (3) the number of heuristic methods is relatively limited, which leads to a lack of diversity in the solutions. Therefore, this paper seeks to address the deficiencies in the current literature regarding IG algorithm design.
3. The Enhanced IG Algorithm for the HFSP
This section encompasses nine distinct parts, delving into the operational design under the IG algorithm framework. It highlights the representation of problem solutions, the derivation of critical paths for the HFSP, and the crafting of neighborhood structures predicated on these critical paths.
3.1. The Encoding and Decoding Disruption Mechanism
The enhanced IG algorithm employs a permutation-based encoding method. The encoding method is one of the core aspects of algorithm design. An excellent encoding scheme effectively covers the solution space, ensuring the search efficiency of the algorithm. Encoding based on job sequences has been proven to be the most optimal. In this section, the encoded vector, comprised of real numbers, signifies the job sequence at the initial stage. Subsequent stages of job sequencing and machine scheduling are determined based on this encoded vector. The job sequence is governed by the First Come First Served (FCFS) rule, while the First Available Machine (FAM) rule dictates the machine assignment. The rigidity of the FCFS and FAM decoding rules confines the search within a restricted space.
To transcend this limitation and enhance diversity in scheduling schemes, this paper introduces a decoding perturbation mechanism that probabilistically adjusts the job sequence of the current stage for refinement. The fine-tuning operation consists of two steps: The initial step involves arranging a group of jobs in non-descending order according to their completion times from the previous stage. In the second step, the completion times of two consecutive jobs are compared to determine whether their positions need to be swapped.
Furthermore, to fully improve the quality of the solution, this section also applies a hybrid approach combining forward and backward decoding techniques. This technique employs two distinct decoding approaches. In forward decoding, jobs are scheduled for the earliest possible start times, with the encoding vector dictating the initial job sequence. Subsequent stages adhere to the FCFS rule, scheduling new job sequences based on the release order from the previous stage. Machine allocation follows the FAM rule. Conversely, backward decoding schedules jobs for the latest possible start times, with the encoding vector representing the final stage job sequence. Remaining stages schedule jobs based on the start times of the following phase, with machine allocation also adhering to the FAM rule. In the proposed enhanced IG algorithm, an initial solution is randomly generated to optimize the utilization of the designed local search. This solution is decoded using a hybrid forward and backward decoding technique, further enhanced by a decoding perturbation mechanism.
3.2. Scheduling Scheme of HFSP Represented by a Disjunctive Graph
The permutation-based encoding method is unable to express such movements intuitively, as alterations to the initial job sequence will result in changes to the subsequent stages. Consequently, the encoding method cannot fully represent these sequences after the movements have occurred. This paper proposes the use of a disjunctive graph as a means of representing the scheduling plans for the HFSP, as this allows for the depiction of such plans in a manner that is both concise and accurate.
A disjunctive graph consists of a set of nodes and a set of arcs. A node represents an operation, and an arc indicates the relationship between two adjacent operations within a given job, or two consecutive operations on the same machine. This work introduces a pair of dummy nodes, which are defined as follows: Obegin and Oend represent the beginning and end of the schedule, respectively. If an operation is the first operation for a job or machine, its predecessor should be the dummy node Obegin. The node Oend can be connected to the current operation without a subsequent job or machine operation. In Figure 3, the Gantt chart on the left (a) and the disjunctive graph on the right (b) represent two different ways of presenting a solution for the 5 × 3 scale instance. Within the Gantt chart, the red solid line signifies a critical path. The disjunctive graph of a solution, where connecting arcs link two consecutive operations of the same job, and separating arcs match two consecutive operations processed on the same machine. The red solid arcs represent the three adjacent operations of Jobs. The green dashed arcs indicate two consecutive operations on the same machine, with the arrow pointing to indicate the order of operations on the same machine.
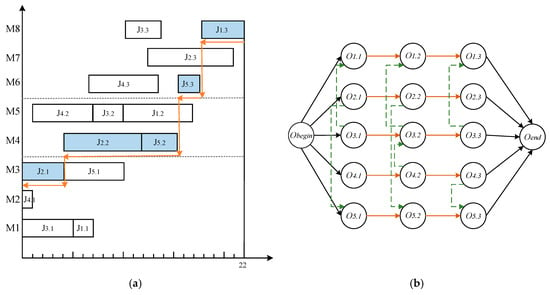
Figure 3.
Two ways of presenting a solution for the 5 × 3 scale instance. (a) The Gantt chart; (b) The disjunctive graph.
In the disjunctive diagram, the longest distance between operations Oi,j and Oh,g is denoted as L(Oi,j, Oh,g), and hence, the makespan can be expressed as L(Obegin, Oend). To clearly delineate the proposed neighborhood structure based on the disjunctive graph, the head length and tail length of operation Oi,j are defined as and , respectively. The recursive computation for these lengths is detailed in Equations (1) to (2), where and denote the job predecessor operation and machine predecessor operation of the operation Oi,j, and and denote the job successor operation and machine successor operation of the operation Oi,j, respectively.
3.3. The Critical Path of HFSP and Its Neighborhood Structure
The critical path is the longest in the disjunctive graph from the Obegin to Oend, and operations included in the critical path are defined as critical operations. This paper constructs two theorems and their proofs are shown as follows:
Theorem 1.
The sum of the head length, tail length, and processing time of the operations on the critical path is equal to the longest path, i.e., , where Oi,j is a critical operation and is the processing time of Oi,j.
Proof.
Assume Oi,j is any operation on the critical path; then the critical path is the longest path in the disjunctive graph from the head node Obegin to the tail node Oend, and the length of the critical path is . Operation Oi,j on the critical path, so the length of the longest path from the head node to the tail node passing through Oi,j is . is the longest distance from the head node to Oi,j; is the longest distance from Oi,j to the tail node, which means is the length of the longest path from the head node to the tail node passing through Oi,j, i.e., Cmax. □
Theorem 2.
From the perspective of disjunctive graphs, if the disjunctive graph length from a non-first operation in any critical path block to the end of the entire sequence is greater than or equal to the disjunctive graph length from the last operation in that critical path block to the end of the entire sequence, then inserting this operation after the last operation for processing will not improve the solution.
Proof.
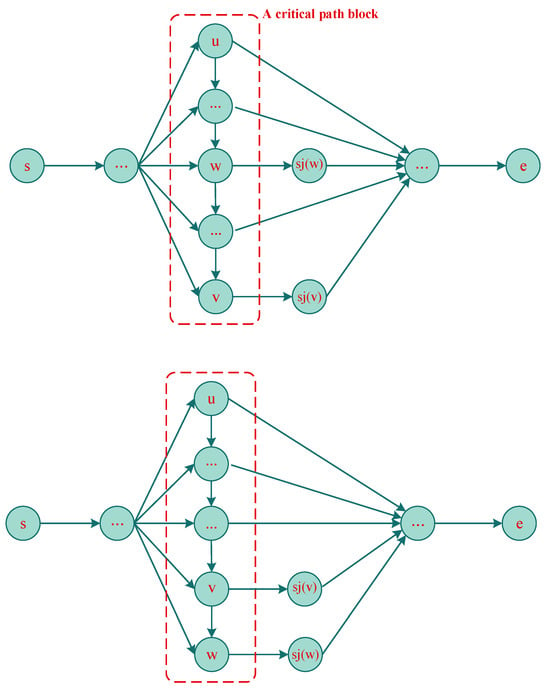
As shown in Figure 4, let operations u and v be within a certain critical path block, with u being the first operation in the block and v being the last operation. Let w be an operation between u and v; js(w) is the successor of operation w on the same job; js(v) is the successor of operation v on the same job; mp(w) is the predecessor of operation w on the same machine; and ms(w) is the successor of operation w on the same machine. Let L[u,v] denote the disjunctive graph length from operation u to operation v. If the processing order of operations is not changed, the total completion time is C = L[s,mp(w)] + L[w,v] + L[sj(v),e]. When operation w is inserted after operation v for processing, the total completion time is given by C* = max{L[s,mp(w)] + L[ms(w),w] + L[sj(w),e], L[s,mp(w)] + L[ms(w),v] + L[sj(v),e]}. It is easy to see that the disjunctive graph length L[w,v] when the processing sequence is not changed is equal to the disjunctive graph length L[ms(w),w] after changing the processing sequence, i.e., L[w,v] = L[ms(w),w]. When the disjunctive graph length from the successor of a non-first operation in the critical path block to the end of the entire sequence is greater than or equal to the disjunctive graph length from the successor of the last operation in that critical path block to the end of the entire sequence, i.e., .

Figure 4.
Diagram illustrating the critical path involving key blocks.
Therefore, , and , therefore . Theorem 2 is thus proven. □
3.4. The Local Search Based on the Critical Path
This section introduces two neighborhood structures, N7 [34] and k-insertion [35], which are proposed to address the flexible job shop scheduling problem (FJSP). These structures are categorized under insertion operations and have demonstrated significant efficacy across various algorithmic approaches. Based on the N7 and k-insertion, three critical path-based neighborhood structures are used randomly. The selected neighborhood structure is used to perform a neighborhood search on the current solution, and the best solution in the neighborhood solutions is selected. If the solution is better than the current solution, then the search proceeds to the next stage and continues. The pseudo code is shown in Algorithm 1.
| Algorithm 1. The proposed local search |
| Input: Current solution π Output: Improved solution π* 1: getCriticalPath(π*);// Get critical path of current solution 2: do { 3: switch (rand(1, 4)) { 4: case (1): //Randomly select one neighborhood operation 5: choose one of {N7, k-insertion, k-swap}; 6: update π*; // Apply selected neighborhood operation to update solution 7: break; 8: case (2): // Randomly select two neighborhood operations 9: choose two of {N7, k-insertion, k-swap}; 10: update π*; // Apply two neighborhood operations sequentially 11: break; 12: case (3): // Randomly select three neighborhood operations 13: choose three of {N7, k-insertion, k-swap}; 14: update π*; // Apply all three neighborhood operations sequentially 15: break; 16: } 17: } while (!terminationCondition); // Repeat until termination condition is met 18: return π*; |
3.5. The Two-Step Insertion Neighborhood Operation
Both N7 and k-insertion utilize a one-step insertion operation on the current solution to produce a neighboring solution, subsequently selecting the optimal solution for the subsequent insertion step. However, due to the predefined decoding rules, this one-step insertion operation restricts the potential for a suboptimal solution to evolve into a superior one after the next insertion. To overcome this limitation, this paper extends the one-step operation to a two-step operation. This approach accepts initially inferior neighborhood solutions that may improve in the second step. A novel neighborhood structure incorporating a two-step neighborhood operation is thus designed.
As depicted in Figure 5, the job swap between machines within the same stage exemplifies the two-step neighborhood operation. It is crucial to emphasize that the stage decoding rule of the HFSP ensures that movement operations do not result in infeasible solutions. The newly proposed neighborhood structure maintains the feasibility of movement operations for the HFSP.
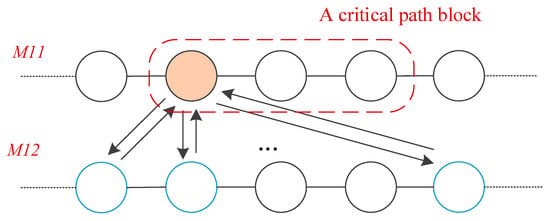
Figure 5.
The proposed two-step neighborhood operation.
A 5 × 3 instance is given to demonstrate the efficacy of the proposed neighborhood structure. Table 2 gives the processing information of the 5 × 3 instance. A feasible solution to this instance is optimized by the two-step neighborhood operation. The initial job sequence for the first stage is denoted as {J3,1, J5,1, J2,1, J4,1, J1,1}. The Gantt chart is generated by decoding rules, as shown in the left diagram of Figure 6. A new solution is obtained by exchanging the J4,1 on machine M4 with J5,1 on machine M3, and the Gantt chart is depicted in the right diagram of Figure 4. Upon comparing, it is observed that the objective value has improved from 26 to 22, showing the optimization achieved through the two-step neighborhood operation.

Table 2.
Processing time of the 5 × 3 instance.
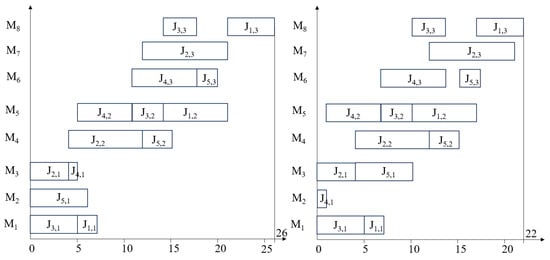
Figure 6.
Makespan with two-step insertion neighborhood operation.
3.6. The Destruction and Construction
The process of destruction can be categorized into two primary types: single-point and multi-point destruction. Single-point destruction involves the removal of a randomly selected job sequence position within the encoding vector. In contrast, multi-point destruction entails the random selection of multiple, non-repeating positions in the encoding vector for deletion. Following the application of either destruction method, a destroyed job sequence and a list of all deleted jobs are created. Subsequently, a construction operation is executed through greedy insertion, where the deleted jobs are individually inserted into the optimal position within the current destroyed job sequence.
The single-point destruction and construction speeds up the search, but the consistent search reduces the probability of finding the optimal solution. The multi-point destruction increases the search time of construction when the number of deleted jobs is too high. Therefore, the proposed enhanced IG algorithm selects the number of deleted jobs dynamically within a certain range. The operation is shown in Algorithm 2.
| Algorithm 2. Destruction and construction |
|
Input: Current solution π, destruction size x Output: Reconstructed solution π* 1: for i = 0 to x do // Destruction phase: remove x jobs 2: place = rand(0, length of Seq); // Randomly select removal position 3: Seq -> erase(Seq_place); // Remove job from current sequence 4: Del_Seq -> insert(Seq_place); // Add removed job to deletion list 5: End for 6: π*->Seq = Del_Seq; / Update current sequence to post-destruction sequence 7: for i = 0 to x do // Construction phase: reinsert deleted jobs 8: job = Del_Seq_i; //Get the i-th deleted job 9: π*1->Seq = insert job to the first of π*->Seq;// Insert job at beginning as baseline 10: for j = 1 to (length of π*->Seq) do // Try all possible insertion positions 11: π*2->Seq = insert job to the j-th place of π*->Seq; // Insert at j-th position 12: if (makespan(π*2) < makespan(π*1))// Compare makespan values 13: π*1 = π*2 // Update to better solution 14: end if 15: end for 16: π* = π*1// Confirm best insertion position for current job 17: end for 18: π = π*; // Update final solution 19: return π; // Return reconstructed solution |
3.7. The Update Mechanism of Poor-Quality Solutions
Since the IG algorithm is a greedy local search algorithm, the proposed enhanced IG algorithm introduces a simulated annealing strategy to prevent the algorithm from falling into a local optimum. Some of the poor-quality solutions are accepted with a certain probability to avoid a local optimum. The acceptance rule depends on the probability value g(x), which is calculated as follows:
The current solution and neighborhood solution are denoted by and , respectively. The fitness value is calculated by Equation (1). If the value of is less than a random number between [0, 1], then is replaced with ; otherwise, it is not replaced.
3.8. A Novel Rapid Evaluation Method
The quality of a neighborhood solution is ascertained through re-decoding the new scheduling scheme. However, a neighborhood search typically modifies only the local job sequence on a few machines, leaving the majority of job sequences unchanged. Conducting numerous neighborhood searches with full decoding can be computationally expensive. While there is a fast approximate evaluation method for the FJSP that can effectively assess the quality of neighborhood solutions, it does not guarantee 100% accuracy and is not directly applicable to the proposed two-step neighborhood structure of the critical path. Consequently, this paper introduces a rapid evaluation method for neighborhood solutions, leveraging the stage-based decoding rule of the HFSP.
The rapid evaluation method divides the scheduling into three parts. If the current neighborhood operation is for stage a, then from 0 to the a stage is the first part, a is the second part, and from the a stage to the s stage is the third part. Before the neighborhood operation, the starting time and completion time of each operation O are denoted by s and t, respectively. After the neighborhood operation, the starting time and completion time are denoted by s− and t−, respectively. The machine predecessor and successor of operation are expressed as MP and MS. Pij represents the processing time of job j at stage i. After performing a neighborhood move, the second part will adjust part of the job sequence on machines and the job sequence will remain unchanged in the first and the second parts. The first part always satisfies s = s−, and the second part always satisfies t = t−.
There is always a critical path through the operation Oa j from the beginning to the end of the process, so
where,
And then,
When the number of stages is zero, s = 0; When the number of stages is S, t = 0. This evaluation obtains the longest path from the beginning to the end of processing. In other words, the proposed method is equal to the actual objective value through full decoding. The conventional evaluation method requires recalculating all jobs across S stages, resulting in a time complexity of O(n×S). In contrast, the proposed rapid evaluation method divides the scheduling process into three parts: the first part remains unchanged and requires no recalculation; the second part involves only the re-evaluation of jobs affected by the neighborhood operation at stage a; and the third part is updated recursively based on the results of the second part. This approach reduces the overall computational complexity to O(2n), and it can be further reduced when applied to single-machine job sequences. The proposed method maintains 100% accuracy by preserving the complete temporal dependencies in the schedule while avoiding redundant computations. By adopting this stage-wise local update strategy, the computational efficiency is significantly improved. As the number of stages increases, the acceleration ratio can reach approximately S/2, enabling the evaluation of a larger number of neighborhood solutions within a limited time and facilitating more effective exploration of promising search regions. The detailed procedure of this method is presented in Algorithm 3.
| Algorithm 3. Rapid Evaluation Method |
| Input: Solution π, changed stage a Output: Updated makespan 1: affected_ops = GetAffectedOperations(move, stage_a); // Identify operations in stage a 2: s_new = π->start_times; // Copy current start times 3: t_new = π->completion_times; // Copy current completion times 4: // Part 1: stages 0 to (a-1) remain unchanged (s = s−) 5: // Part 3: stages (a+1) to S remain unchanged (t = t−) 6: for each operation O[i,a] in affected_ops do // Part 2: update stage a only 7: job_pred_time = t_new[i][a − 1] + P[i][a − 1]; // Job predecessor constraint 8: machine_pred = GetMachinePredecessor(O[i,a], move); // Get machine predecessor 9: if (machine_pred ≠ NULL) 10: machine_pred_time = t_new[machine_pred] + P[machine_pred]; 11: else machine_pred_time = 0; 12: end if 13: s_new[i][a] = max(job_pred_time, machine_pred_time); // Equation (5) 14: t_new[i][a] = s_new[i][a] + P[i][a]; // Update completion time (6) 15: end for 16: new_makespan = 0; // Initialize makespan calculation 17: for each job j ∈ J do // Apply Equation (7) 18: path_length = s_new[j][a] + P[j][a] + max(t_new[j][a+1] + P[j][a+1], t_new[machine_successor]); 19: new_makespan = max(new_makespan, path_length); // Update maximum 20: end for 21: return new_makespan; |
3.9. Procedure of the Graph Knowledge-Enhanced IG Algorithm
The essence of the enhanced IG algorithm lies in conducting a methodical and sustained exploration of the neighborhood solution within the solution space. The proposed IG algorithm is structured around four distinct phases: initialization, destruction, construction, and local search. The process begins with the generation of an initial solution, which then undergoes a series of searches through the destruction and construction phases, steering towards more promising regions within the solution space. To balance exploration and exploitation during the search process, the total runtime is divided into two phases by introducing a strategy-switching threshold at 30% of the total StopTime. In the first phase (0–30% of runtime), the algorithm emphasizes global exploration using destruction and reconstruction operations to enhance solution diversity. After this point, the search intensifies through critical-path-based neighborhood structures, focusing on local exploitation and fine-tuning of promising areas. The choice of 0.3 *StopTime follows a widely used empirical rule in metaheuristic design, where a 30/70 runtime allocation is commonly adopted to achieve a practical trade-off between diversification and intensification. The destruction and construction process introduces a disturbance to the current solution. As the algorithm approaches convergence, local search is initiated during the iterations to broaden the search space and facilitate further enhancements. These phases are iteratively executed until the termination criterion is satisfied. The workflow of the enhanced IG algorithm is depicted in Figure 7.
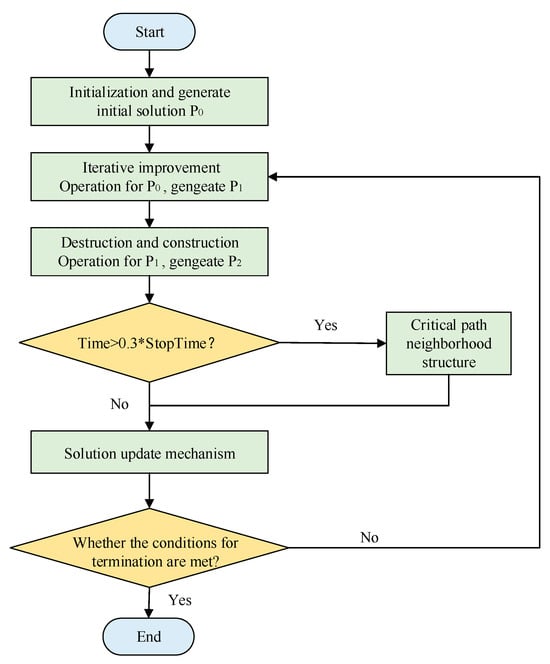
Figure 7.
Flowchart of the graph knowledge-enhanced IG algorithm.
4. Experimental Study
To test the proposed enhanced IG algorithm, three groups of experiments are shown, including Calier 77 instances [36], Liao 10 instances [37], and 240 small-scale instances [8]. These benchmarks and results were adopted from other published papers. Before the start of the three experiments, we needed to carry out the parameter experiment of the enhanced IG algorithm. The proposed enhanced IG algorithm is implemented in C++(Visual studio 2019) on a computer with an Inter(R) Core i7 processor, 3.5 GHz, RAM 32 GB, and tested on three types of HFSP benchmarks. To evaluate the quality of the solutions, the relative percent deviation (DEV) is adopted for each instance of the HFSP.
where LB means the low bound of each instance.
4.1. Evaluation of the Rapid Evaluation Methods
To test the effectiveness of the rapid evaluation methods, the comparative experiments are designed to compare the enhanced IG algorithm without the rapid evaluation method through 24 small-scale instances and 24 large-scale instances. A total of 48 different instances are generated with n {10, 20, 30, 40, 60, 80, 100, 120}, and s {5, 10, 15, 20, 30, 40}. The number of machines and processing times of machines per stage are uniformly distributed according to [1, 3] and [1, 30], respectively. Each instance runs five times for forward decoding and backward decoding independently. The proposed evaluation strategy and full decoding method are run 20 times for each instance. Each time it executes 100,000 times. The full decoding is used to compare the longest time-consuming part in the rapid evaluation, which is a situation where all calculations are performed on the second part of the job. Figure 8a,b show the average of 10 run times for rapid evaluation and full decoding, and the horizontal and vertical axes, respectively, indicate the number of stages and the time required for one decoding.
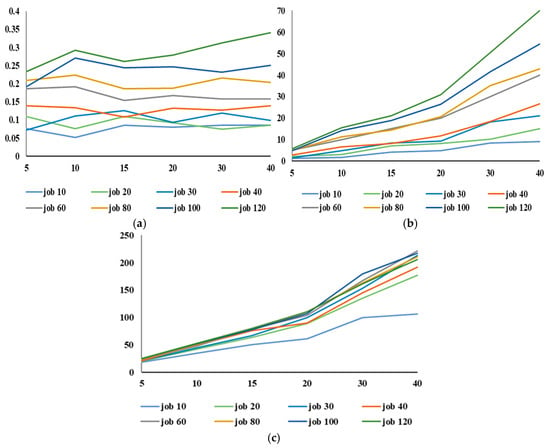
Figure 8.
(a) The results of the rapid evaluation; (b) The results of the full decoding; (c) The ratio of the full decoding to rapid evaluation.
The experimental results show that the computational speed of rapid evaluation is faster than that of the full decoding method. When the number of jobs is constant, the computational speed of the rapid evaluation is not affected by the change in the number of stages, while the running time of the full decoding method increases with the increase in the number of stages. In Figure 8c, the horizontal axis represents the number of processing stages, and the vertical axis represents the ratio of the full decoding time to the rapid evaluation time. When the number of stages increases, the computational time for rapid evaluation is much smaller than that for full decoding. As the number of stages increases, the proposed method becomes more effective.
4.2. Experiment 1—Carlier Benchmark
Experiment 1 contains 77 instances, which were adopted from the well-known Carlier benchmark, in which the problem size and No. of all instances can be identified by its name. “j10c5a2” means 10 jobs, 5 stages, and the second instance. The proposed enhanced IG algorithm is compared with algorithms, which have achieved good results in the literature: the branch-and-bound (B&B) algorithm [38], the artificial immune system (AIS) algorithm [39], the particle swarm optimization (PSO) algorithm [37], and LABC [40]. These algorithms used 1600s as the StopTime. The StopTime of the enhanced IG algorithm is reduced to 60s with limited computational costs, and the optimal solution is recorded by 20 independently run times. In Table 3, experimental results show that the enhanced IG algorithm obtains optimal solutions for the given 77 instances, such as the good results of “j10c10c” (114), “j10c10a4” (119), and “j10c10e6” (105). In terms of the deviation of the values obtained by these algorithms, the deviation between the proposed enhanced IG algorithm and the lower bound is merely 1.49%; however, the lowest deviation of the four compared algorithms is 1.54%. In terms of the running time to obtain the optimal solution, the average time of the proposed algorithm is only 0.08 for all 77 instances, while the lowest average time of the other compared algorithms is 0.33. It can be seen from the experimental results that the proposed enhanced IG algorithm has better search speed and efficiency.

Table 3.
Computational results of the Carlier benchmark.
4.3. Experiment 2—Liao Benchmark
Regarding the well-known Liao benchmark, the termination condition is 1600s, and each instance is run 10 times to record the optimal solution and the time taken to obtain the optimal solution. Table 4 compares the experimental results of the proposed enhanced IG algorithm with the current superior algorithms: PSO [37], LABC [40], IBBO [41], and IGT [33]. The “MINC” and “MINT” in the table indicate the minimum makespan of all results and the corresponding run time. Among the whole of 10 instances, the proposed enhanced IG algorithm and IGT can obtain the best solution in 9 instances, LABC can obtain 2 instances, while PSO and IBBO merely obtain 1 instance. The proposed enhanced IG algorithm obtains the new optimal solution (571) of “j30c5e10”. About the deviation of the values, the deviation between the proposed enhanced IG algorithm and the lower bound is merely 0.02%; however, the lowest deviation of the four comparing algorithms is 0.04%. It is verified that the introduced critical path can improve the quality of the algorithm.

Table 4.
Computational results of Liao benchmark.
4.4. Experiment 3—Jose Benchmark
The 240 instances are adopted from the Jose benchmark [8], where n {10, 15, 20, 25, 30, 35}, and s {5, 10, 15, 20}. The name of each instance indicates the scale of the problem. Notably, “10 × 5 × 1” means the first problem with 10 jobs and 5 stages. Fernandez and Framinan [8] used an IG algorithm to solve these 240 instances and set an upper bound with the designed StopTime = 50 × (the number of jobs^3) × (the number of stages). In this paper, the termination time is reduced by 25 times (StopTime = 2 × (job number^3) × (stage number)). The optimal solution and its running time are recorded by running 10 times independently. The results are compared with the given upper bound, and related comparison results are shown in Table 5. The proposed enhanced IG algorithm obtains 182 new upper bounds and the same upper bounds for the other 42 instances. Computational results prove that the proposed strategies and IG algorithm can effectively improve the solution quality compared to the given IG algorithm [8].

Table 5.
Computational results of Jose benchmark.
5. Conclusions and Future Work
This paper presents a graph knowledge-enhanced IG algorithm that integrates a critical path analysis and rapid evaluation technique to address the high-frequency scheduling problem—HFSP. An initial solution generation method that utilizes dual permutation-based encoding and a decoding technique with a novel perturbation strategy to broaden the search space. The integration of critical path analysis provides the algorithm with a strategic advantage in identifying and prioritizing tasks that have the most significant impact on the overall schedule. Coupled with the rapid evaluation technique, the algorithm can quickly discard infeasible or suboptimal solutions, thus accelerating the convergence towards an optimal or near-optimal schedule. Experimental evaluation demonstrates that the proposed algorithm surpasses the performance of existing algorithms when applied to the HFSP. The proposed graph knowledge-enhanced IG algorithm seeks new best solutions for 183 hard instances.
This study still has several limitations. The proposed algorithm involves multiple parameters that require manual tuning and lacks adaptive control mechanisms. As the problem scale increases, memory consumption grows significantly, and its effectiveness on ultra-large-scale instances remains underexplored. Moreover, the method is specifically designed for the hybrid flowshop scheduling problem, and its generalizability to other domains has not yet been examined. The objective function focuses solely on makespan minimization, without considering multi-objective scenarios such as energy consumption or tardiness penalties. Additionally, the model assumes a static scheduling environment, ignoring dynamic job arrivals, machine breakdowns, and other real-world uncertainties. Integration with manufacturing execution systems (MES) also presents certain practical challenges.
Future research could be extended in several directions, including automated algorithmic framework construction, incorporation of self-learning mechanisms, and the development of hybrid neighborhood structures driven by both knowledge and data. Furthermore, the proposed method has the potential for adaptation to other complex scheduling and optimization problems, such as flexible job shop scheduling, cloud task scheduling, and logistics distribution optimization.
Author Contributions
Conceptualization, Y.W.; Methodology, L.Z.; Software, Z.Z.; Formal analysis, Y.W.; Writing—original draft, Y.L.; Writing—review & editing, B.Z. and K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Project supported by Hubei Provincial Natural Science Foundation Youth Project (Grant No.2023AFB088); Education Department’s Social Science Research Youth Project (Grant No.24Q121); National Science Foundation of China (Grant No.62303204); National Natural Science Foundation of China (Grant No. 52475524, 62303358); and Natural Science Foundation of Shandong Province (Grant No. ZR2024MF054, ZR2021QF036).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Michaels, S. A Solution to a Special Class of Flow Shop Scheduling Problems. In Proceedings of the International Conference on Flow Shop Scheduling; Springer: Berlin/Heidelberg, Germany, 1973; pp. 83–91. [Google Scholar]
- Xu, J.Y.; Lin, W.C.; Chang, Y.W.; Chung, Y.H.; Chen, J.H.; Wu, C.C. A Two-Machine Learning Date Flow-Shop Scheduling Problem with Heuristics and Population-Based GA to Minimize the Makespan. Mathematics 2023, 11, 4060. [Google Scholar] [CrossRef]
- Zhang, B.; Meng, L.L.; Lu, C.; Li, J.Q. Real-time data-driven automatic design of multi-objective evolutionary algorithm: A case study on production scheduling. Appl. Soft Comput. 2023, 138, 110187. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman and Company: New York, NY, USA, 1979. [Google Scholar]
- Fan, J.; Li, Y.L.; Xie, J.; Zhang, C.J.; Shen, W.M.; Gao, L. A hybrid evolutionary algorithm using two solution representations for hybrid flow-shop scheduling problem. IEEE Trans. Cybern. 2023, 53, 1752–1764. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Viagas, V.; Pérez-González, P.; Framinan, J.M. Efficiency of the Solution Representations for the Hybrid Flow Shop Scheduling Problem with Makespan Objective. Comput. Oper. Res. 2019, 109, 77–88. [Google Scholar] [CrossRef]
- Ruiz, R.; Vázquez-Rodríguez, J.A. The Hybrid Flow Shop Scheduling Problem. Eur. J. Oper. Res. 2010, 205, 1–18. [Google Scholar] [CrossRef]
- Victor, F.V.; Framinan, J.M. Design of a Testbed for Hybrid Flow Shop Scheduling with Identical Machines. Comput. Ind. Eng. 2020, 141, 106288. [Google Scholar] [CrossRef]
- Rubén, R.; Stützle, T. A Simple and Effective Iterated Greedy Algorithm for the Permutation Flowshop Scheduling Problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Shao, W.S.; Shao, Z.S.; Pi, D.C. Modeling and Multi-Neighborhood Iterated Greedy Algorithm for Distributed Hybrid Flow Shop Scheduling Problem. Knowl.-Based Syst. 2020, 194, 105527. [Google Scholar] [CrossRef]
- He, L.M.; Sun, S.J.; Luo, R.Z. A Hybrid Two-Stage Flowshop Scheduling Problem. Asia-Pac. J. Oper. Res. 2007, 24, 45–56. [Google Scholar] [CrossRef]
- Sun, Z.W.; Lv, D.Y.; Wei, C.M.; Wang, J.B. Flow Shop Scheduling with Shortening Jobs for Makespan Minimization. Mathematics 2025, 13, 363. [Google Scholar] [CrossRef]
- Paternina, A.; Carlos, D.; Jairo, R.M.; Milton, J.; Maria, C.H. Scheduling Jobs on a K-Stage Flexible Flow-Shop. Ann. Oper. Res. 2007, 164, 29–40. [Google Scholar] [CrossRef]
- Lin, S.W.; Cheng, C.Y.; Pourya, P.; Ying, K.C.; Lee, C.H. New Benchmark Algorithm for Hybrid Flowshop Scheduling with Identical Machines. Expert Syst. Appl. 2021, 183, 115422. [Google Scholar] [CrossRef]
- Huang, Y.P.; Deng, L.B.; Wang, J.L.; Qiu, W.W.; Liu, J.F. Modelling and Solution for Hybrid Flow-Shop Scheduling Problem by Two-Stage Stochastic Programming. Expert Syst. Appl. 2023, 233, 120846. [Google Scholar] [CrossRef]
- Safari, G.; Ashkan, H.; Hiva, M.; Mohammad, K. Competitive Scheduling in a Hybrid Flow Shop Problem Using Multi-Leader-Multi-Follower Game: A Case Study from Iran. Expert Syst. Appl. 2022, 195, 116584. [Google Scholar] [CrossRef]
- Lin, C.C.; Liu, W.Y.; Chen, Y.H. Considering Stockers in Reentrant Hybrid Flow Shop Scheduling with Limited Buffer Capacity. Comput. Ind. Eng. 2020, 139, 106154. [Google Scholar] [CrossRef]
- Ozsoydan, F.B.; Müjgan, S. Iterated Greedy Algorithms Enhanced by Hyper-Heuristic Based Learning for Hybrid Flexible Flowshop Scheduling Problem with Sequence Dependent Setup Times: A Case Study at a Manufacturing Plant. Comput. Oper. Res. 2021, 125, 105044. [Google Scholar] [CrossRef]
- Luan, F.; Cai, Z.Y.; Wu, S.Q.; Liu, S.Q.; He, Y.X. Optimizing the Low-Carbon Flexible Job Shop Scheduling Problem with Discrete Whale Optimization Algorithm. Mathematics 2019, 7, 688. [Google Scholar] [CrossRef]
- Ying, K.C.; Lin, S.W. Minimizing Makespan for the Distributed Hybrid Flowshop Scheduling Problem with Multiprocessor Task. Expert Syst. Appl. 2018, 92, 132–141. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, L. An Iterated Greedy Algorithm for Distributed Hybrid Flowshop Scheduling Problem with Total Tardiness Minimization. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering, Vancouver, BC, Canada, 22–26 August 2019; pp. 350–355. [Google Scholar]
- Cui, H.H.; Li, X.Y.; Gao, L. An Improved Multi-Population Genetic Algorithm with a Greedy Job Insertion Inter-Factory Neighborhood Structure for Distributed Heterogeneous Hybrid Flow Shop Scheduling Problem. Expert Syst. Appl. 2023, 222, 119805. [Google Scholar] [CrossRef]
- Li, Y.L.; Li, X.Y.; Gao, L.; Zhang, B.; Pan, Q.K.; Tasgetiren, M.F. A Discrete Artificial Bee Colony Algorithm for Distributed Hybrid Flowshop Scheduling Problem with Sequence-Dependent Setup Times. Int. J. Prod. Res. 2020, 59, 3880–3899. [Google Scholar] [CrossRef]
- Li, M.; Wang, G.G.; Yu, H.L. Sorting-Based Discrete Artificial Bee Colony Algorithm for Solving Fuzzy Hybrid Flow Shop Green Scheduling Problem. Mathematics 2021, 9, 2250. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, C.; Meng, L.L.; Han, Y.Y.; Sang, H.Y.; Jiang, X.C. Reconfigurable distributed flowshop group scheduling with a nested variable neighborhood descent algorithm. Expert Syst. Appl. 2023, 217, 119548. [Google Scholar] [CrossRef]
- Jia, Y.H.; Qi, Y.; Wang, H.F. Q-Learning Driven Multi-Population Memetic Algorithm for Distributed Three-Stage Assembly Hybrid Flow Shop Scheduling with Flexible Preventive Maintenance. Expert Syst. Appl. 2023, 232, 120837. [Google Scholar] [CrossRef]
- Li, L.K.; Fu, X.J.; Zhen, H.L.; Yuan, M.X.; Wang, J.; Lu, J.W.; Tong, X.L.; Zeng, J.; Schnieders, D. Bilevel Learning for Large-Scale Flexible Flow Shop Scheduling. Comput. Ind. Eng. 2022, 168, 108140. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Y.; Li, H.; Li, J.; Gao, K.; Liu, Y. Theoretical Analysis and Implementation of Mandatory Operations-Based Accelerated Search in Graph Space for Hybrid Flow Shop Scheduling. Expert Syst. Appl. 2024, 257, 125026. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, J.; Shen, W. A Deep Reinforcement Learning Approach with Graph Attention Network and Multi-Signal Differential Reward for Dynamic Hybrid Flow Shop Scheduling Problem. J. Manuf. Syst. 2025, 80, 643–661. [Google Scholar] [CrossRef]
- Wan, L.; Fu, L.; Li, C.; Li, K. An Effective Multi-Agent-Based Graph Reinforcement Learning Method for Solving Flexible Job Shop Scheduling Problem. Eng. Appl. Artif. Intell. 2025, 139, 109557. [Google Scholar] [CrossRef]
- Huang, D.; Zhao, H.; Tian, W.; Chen, K. A Deep Reinforcement Learning Method Based on a Multiexpert Graph Neural Network for Flexible Job Shop Scheduling. Comput. Ind. Eng. 2025, 200, 110768. [Google Scholar] [CrossRef]
- Pan, Q.K.; Ruiz, R.; Pedro, A.F. Iterated Search Methods for Earliness and Tardiness Minimization in Hybrid Flowshops with Due Windows. Comput. Oper. Res. 2017, 80, 50–60. [Google Scholar] [CrossRef]
- Öztop, H.; Tasgetiren, M.F.; Deniz, T.E.; Pan, Q.K. Metaheuristic Algorithms for the Hybrid Flowshop Scheduling Problem. Comput. Oper. Res. 2019, 111, 177–196. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Li, P.G.; Guan, Z.L.; Rao, Y.Q. A Tabu Search Algorithm with a New Neighborhood Structure for the Job Shop Scheduling Problem. Comput. Oper. Res. 2007, 34, 3229–3242. [Google Scholar] [CrossRef]
- Mastrolilli, M.; Luca, M.G. Effective Neighbourhood Functions for the Flexible Job Shop Problem. J. Sched. 2000, 3, 3–20. [Google Scholar] [CrossRef]
- Carlier, J.; Néron, E. An Exact Method for Solving the Multi-Processor Flow-Shop. RAIRO-Oper. Res. 2000, 34, 1–25. [Google Scholar] [CrossRef]
- Liao, C.J.; Evi, T.; Chung, T.P. An Approach Using Particle Swarm Optimization and Bottleneck Heuristic to Solve Hybrid Flow Shop Scheduling Problem. Appl. Soft Comput. 2012, 12, 1755–1764. [Google Scholar] [CrossRef]
- Neron, E.; Baptiste, P.; Gupta, J.N.D. Solving hybrid flow shop problem using energetic reasoning and global operations. Omega-Int. J. Manag. Sci. 2001, 29, 501–511. [Google Scholar] [CrossRef]
- Engin, O.; Doyen, A. A new approach to solve hybrid flow shop scheduling problems by artificial immune system. Future Gener. Comput. Syst. 2004, 20, 1083–1095. [Google Scholar] [CrossRef]
- Li, J.Q.; Han, Y.Q. A hybrid multi-objective artificial bee colony algorithm for flexible task scheduling problems in cloud computing system. Clust. Comput.-J. Netw. Softw. Tools Appl. 2019, 23, 2483–2499. [Google Scholar] [CrossRef]
- Li, Z.P.; Gu, X.S. Improved Biogeography-based Optimization Algorithm used in Solving Hybrid Flow Shop Scheduling Problem. CIESC J. 2016, 67, 751–757. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).