Abstract
In this paper, a novel mathematical formalization of Crisp-Set Qualitative Comparative Analysis (csQCA) that enables a rigorous connection with a specific class of association rule mining (ARM) problems is proposed. Although these two methodologies are frequently used to identify logical patterns in binary datasets, they originate from different traditions. While csQCA is rooted in set theory and Boolean logic and is primarily applied in the social sciences to model causal complexity, ARM originates from data mining and is widely used to discover frequent co-occurrences among items. In this study, we establish a formal mathematical equivalence between csQCA configurations and a subclass of association rules, including both positive and negative conditions. Moreover, we propose a minimization procedure for association rules that mirrors the Quine–McCluskey reduction method employed in csQCA. We demonstrate the consistency of the results obtained using both methodologies through two examples (a small-N study on internet shutdowns in Sub-Saharan Africa and a large-N analysis of immigration attitudes in Europe) and some numerical experiments. However, it is also clear that ARM offers improved scalability and robustness in high-dimensional contexts. Overall, these findings provide researchers with valuable theoretical and practical guidance when choosing between these approaches in qualitative data analysis.
Keywords:
qualitative comparative analysis; association rule mining; Boolean logic; causal inference MSC:
68Txx; 91Fxx; 00A06
1. Introduction
While Qualitative Comparative Analysis (QCA) and association rule mining (ARM) are both widely used techniques for uncovering logical patterns in general datasets, they originate from distinct research traditions. QCA, especially in its Crisp-Set form (csQCA), was developed by Charles Ragin in the 1980s [] as a set-theoretic method for analyzing causal complexity in small- to medium-sized case studies, particularly in the social sciences. It enables researchers to identify configurations of causal conditions that are necessary or sufficient for a given outcome, emphasizing multiple factors’ interplay and conjunctural nature []. This method is particularly valuable for its ability to handle causal complexity and its focus on identifying patterns between cases rather than isolating individual variables []. A standard solution configuration in a QCA problem is characterized by a causal relationship of the form “If this combination of factors is given, then this outcome occurs”.
In contrast, ARM emerged from the field of data mining and was initially used in market basket analysis to discover frequent item co-occurrences in transactional databases []. The technique identifies rules of the form “if items A and B occur, then item C also occurs,” using metrics such as support and confidence to evaluate the strength and reliability of such patterns. Over the years, ARM has been applied in diverse fields, including marketing, bioinformatics, healthcare, and finance, due to its scalability and computational efficiency.
Despite the conceptual similarities between csQCA and ARM—with both generating if–then rules from binary data using Boolean logic—their methodological foundations and evaluation strategies differ substantially. Surprisingly, few studies have formally examined their theoretical relationship, and even fewer have attempted to unify their respective solution processes. This lack of integration represents a gap in the literature, especially as researchers increasingly turn to hybrid or comparative methodological approaches.
This study aims to bridge this gap by establishing a formal equivalence between csQCA configurations and a subset of association rules that include both positive and negative conditions. We show that any csQCA problem can be reformulated as an ARM problem under a specific encoding of presence and absence conditions. Moreover, we prove that the key evaluation metrics in csQCA—consistency and coverage—are mathematically equivalent to the support and confidence measures used in ARM.
The contributions of this paper are threefold. First, we propose a mathematical framework for csQCA that facilitates precise mapping to association rule structures. Second, we introduce a theorem that enables the minimization of association rules similarly to the Quine–McCluskey logic minimization procedure employed in csQCA, enabling the identification of reduced rule sets without relying on exponentially large truth tables. Third, we illustrate our theoretical findings through two comparative applications: a small-N study on internet shutdowns during African elections and a large-N analysis of opposition to immigration in Europe.
Through formally connecting csQCA and ARM, we provide researchers with a deeper understanding of the conditions under which these methods yield similar or complementary insights. Our findings also demonstrate the advantages of ARM in terms of robustness and scalability, particularly in high-dimensional datasets. This opens up new opportunities for researchers to integrate or select between these approaches more effectively, depending on the nature and size of their empirical data.
The remainder of this paper is structured as follows: In Section 2, we provide a brief review of the relevant literature on csQCA and association rule mining (ARM). Section 3 presents our main theoretical contributions: we introduce a new mathematical formalization of csQCA (Section 3.1), outline the ARM framework (Section 3.2), and prove an equivalence theorem linking csQCA configurations to a specific class of association rules (Section 3.3). We also propose an ARM minimization procedure analogous to the Quine–McCluskey reduction used in csQCA (Section 3.4). Section 4 illustrates these ideas through two empirical applications (a small-N study on internet shutdowns and a large-N analysis of immigration attitudes) and a numerical computational experiment. Section 5 discusses the theoretical and practical implications of the results. Finally, in Section 6, we provide some conclusions and directions for future research.
2. Literature Review
In recent times, researchers from different areas of knowledge have opted for the use of configurational comparative methods. Configurational methods propose different types of solutions and new ways of approaching problems [,]. The increasing adoption of these methodologies by researchers is justified by the fact that they provide powerful methodological tools to find frequent patterns in datasets. Therefore, some of these tools focus on inferring cases as condition configurations and using truth tables [], such as the Qualitative Comparative Analysis (QCA) technique, and although the data configuration in the association rule mining (ARM) algorithms presents a truth table structure, the solution search process is based on solution metrics of interest [] (i.e., a solution may be prevalent but not interesting). Similarly, there have been doubts about the best solution for each type of research problem [].
The Crisp-Set QCA (csQCA) methodology is used in social research to analyze and identify combinations of causal conditions that lead to a specific outcome. It combines qualitative and quantitative techniques to examine complex patterns and identify causal configurations that can explain social phenomena []. Meanwhile, the ARM methodology is widely used to discover interesting patterns in datasets. These patterns are expressed as association rules that indicate the relationship between different elements in a set of transactions [].
In the last 30 years, numerous papers have been published in different areas of knowledge using both methodologies [,,,,,,,]. These methodologies have accentuated applications in several fields, such as engineering, mathematics, medicine, computer science, administration and management, political science, economics, finance, biology, and education [,].
Many authors have advocated for the use of configurational methods instead of classical statistical methods [,,]. These researchers argue that configurational theory is fundamentally grounded in the assumption that combinations of initial variables can lead to the same outcome. Consequently, the relationship between an outcome and its preconditions is often more asymmetric than symmetric. For instance, different groups of customers may choose to fly with a particular airline, considering different variables or attributes. However, certain customers may decide not to fly with an airline until a specific condition is met, even if the provided condition alone does not result in the intended use. Such asymmetric relationships and combinatorial complexities cannot be modeled using conventional regression-based methods.
According to [], a configuration is a specific set of causal variables that interact, producing a desired outcome. However, using data analysis techniques that focus on causal configurations helped estimate the causal contribution of various configurations/combinations to achieve the expected outcome.
Table 1 presents studies by various authors that aim to compare or integrate different methodologies, elucidating the parallels, distinctions, strengths, and weaknesses of classical statistical techniques compared to emerging configurational methods. Notable examples within these studies include the examination of QCA versus linear regression models (LRMs) [,,], AR versus LRMs [,], QCA versus Structural Equation Models (SEMs) [], and AR versus SEMs []. This table furnishes a concise summary of the most significant investigations comparing configurational methods and classical statistical approaches.

Table 1.
An overview of selected studies comparing or combining QCA, association rules (ARs), Logistic Regression Models (LRM), and Structural Equation Modeling (SEM).
In recent years, there has been an effort to integrate QCA with computational or rule-based approaches, and the following studies were identified through an extensive review of the literature. One study proposed a hybrid model that combines QCA with Support Vector Machines (SVMs), utilizing various kernels and ensemble techniques (Bagging, Random Subspace, and AdaBoost) to analyze passenger resistance to biometric e-gates at airports []. This approach integrated QCA’s configurational logic with the predictive capabilities of machine learning algorithms. A further study introduced a Bayesian rule-based model as a quantitative alternative to QCA, capturing complex causal relationships through probabilistic logic []. The integration of QCA with process tracking has been explored to strengthen causal inference in case-based research. In this approach, conservative QCA solutions provide a foundation for more in-depth research []. Simultaneously, the development of the scpQCA method is proposed []. The scpQCA method constitutes an extension of multi-value QCA (mvQCA) grounded in set-covering principles. The objective of the method’s development scpQCA is to overcome the typical limitations of mvQCA, such as low coverage and limited interpretability. More recently, a 2025 investigation applied QCA within an explanatory sequential mixed-methods design, integrating quantitative and qualitative analyses to examine family-related factors influencing the outcomes of parenting programs [].
In addition to using Crisp-Set QCA, other variants, such as fsQCA and mvQCA, have been used in various domains. This case study employed fsQCA to identify configurations that contribute to adherence to development timelines in Product Lifecycle Management (PLM) co-development projects []. In a similar study, fsQCA was applied to assess stakeholder satisfaction in public participation processes under the EU Water Framework Directive []. In corporate governance, fsQCA was used to examine the interactive effects of good governance practices and CEO profiles on ESG performance []. These studies underline the adaptability of fsQCA in managing intricate causal relationships across diverse contexts.
Notwithstanding these advances, the existing literature contains no study formally establishing mathematical equivalence between csQCA and ARM. To the best of our knowledge, there has been no prior attempt to implement a direct one-to-one transformation between csQCA configurational solutions and association rules encompassing both presence and absence conditions or to provide formal proofs of equivalence between key evaluation metrics, including consistency and coverage in QCA and support and confidence in ARM. This study is the first systematic attempt to formally integrate csQCA and ARM, thereby providing a coherent theoretical model and substantial computational advantages, including scalability, interpretability, and applicability to high-dimensional contexts. These advantages are supported by empirical applications involving both small-N and large-N datasets.
3. Materials and Methods
3.1. QCA
QCA is a prominent methodology based on solid foundations in set theory. The first version [] presented a binary system called Crisp Sets (csQCA), which was eventually extended to Fuzzy Sets (fsQCA) and multivalued variants, known as mvQCA [].
QCA conceptualizes causal relationships between social phenomena as established relationships. This perspective enables the analysis of causal complexity by constructing and examining arguments about the necessity and/or sufficiency of causal conditions —combinations of attributes theoretically relevant to the study—for a given causal outcome [].
In this section, we present a novel mathematical formalization of the Crisp-Set Qualitative Comparative Analysis (csQCA) methodology. While csQCA is typically described in set-theoretic and logical terms, our objective here is to provide a precise formal framework that will allow us, in the following sections, to establish a rigorous correspondence between csQCA and a specific class of association rule mining (ARM) problems.
This formalization will serve as the foundational structure for proving a theoretical equivalence between csQCA solution configurations and association rules, including both positive and negative conditions.
Definition 1.
A csQCA model is a tern , where is a set of n variables; R is an outcome or response variable (i.e., another variable, such that ); and M is the sample dataset, which is an matrix of the form
where , for all , where 1 indicates the presence and 0 indicates the absence of each condition/variable and the outcome.
Each row of the matrix M represents a sample case and is denoted by
where is the antecedent vector, and is the consequent (or outcome) value.
Definition 2.
We say that a csQCA dataset M is consistent if, for any given two cases, and , if ; then, necessarily, . This means that there are no contradictions among the sample cases.
Definition 3.
A configuration of order k () is a pair , where with and .
Definition 4.
A case is compatible with the configuration if
Definition 5.
A configuration is conducive to the outcome R if there exists at least a case compatible with for which .
Remark 1.
It is important to note that all possible n-configurations (conducive or non-conducive to the outcome R) can be written as a truth table with rows. Each row of the truth table corresponds to a specific combination of conditions, and collectively, all the rows display the possible logical combinations of conditions using the logical AND operation. These configurations are observed in one or more cases (the rows of the matrix M), and sufficiency is determined by the association of these cases with the outcome R [].
An important aspect of QCA analysis is the reducibility or minimization of configurations. This is particularly essential because it enables the simplification of complex configurations into more parsimonious and interpretable expressions without losing their explanatory power. This process relies on a fundamental property of set theory . In other words, when a condition A leads to an outcome both in the presence (B) and in the absence (∼B) of another condition, the influence of B becomes irrelevant and can be eliminated. Thus, minimization identifies and removes such redundancies across cases, producing a simpler and more general causal model that still accurately captures the empirical patterns observed. Next, we define the concept of minimizable configurations within the framework of our mathematical formalization.
Definition 6.
where is the p-th vector of the canonical base (i.e., .
Two configurations of order k, and , can be minimized (or reduced) to a configuration of order if
- Both are conducive to the outcome R;
- ;
- There exists a such that
In that case, and can be reduced to the -configuration , where
and
If two configurations cannot be minimized, we say they are irreducible.
The objective in csQCA is to obtain all irreducible configurations leading to a certain outcome. That is, we can define the solution set of a csQCA problem as follows:
Definition 7.
The solutions of the csQCA model are given by
where each set is the family of all irreducible configurations of order k ( may be void) conducible to the outcome R; that is, is given by
where
- is conducible to outcome R for all .
- and are irreducible with .
In csQCA, evaluating the reliability and relevance of causal configurations requires the use of classical metrics, namely, consistency and coverage. These metrics help to determine the strength and explanatory power of the identified patterns. Consistency measures the degree to which cases supporting a given configuration also exhibit the outcome, ensuring that the solution is logically coherent with the dataset. That is,
Definition 8.
Given a configuration , with , then the consistency of the configuration is defined as
where
That is, represents the number of cases in the sample dataset compatible with the configuration , regardless of the outcome of the case; on the other hand, is the number of cases in the sample dataset compatible with for which the outcome is positive.
However, coverage assesses how much of the observed outcome is explained by a specific configuration, providing insight into the generalizability of the findings, as described in the following definition.
Definition 9.
The coverage of a causal configuration is defined as the proportion of cases with a positive outcome compatible with the given configuration. That is,
where is defined above, and is the number of cases in the sample dataset for which the result is 1, i.e.,
A high-consistency configuration indicates a strong causal link, while high coverage suggests that the configuration accounts for a significant portion of the cases with the outcome.
A configuration is compatible with the sample dataset M if it is compatible with at least one case of the sample dataset. Otherwise, we say that the configuration and the sample dataset are incompatible.
We obviously have that, given a configuration ,
- 1.
- If is compatible with M, then .
- 2.
- If is conducive to the outcome R, and the sample dataset M is consistent (there are no contradictions), then .
The procedure for finding the solution set is based on the Boolean minimization algorithm developed in the 1950s by Quiney and McCluskey in the context of electronic circuit optimization [,,]. This procedure is a top–bottom algorithm that starts with the maximal configurations—that is, the configurations of order n (where n is the number of variables in the set )—and then, for each size k, it finds the configurations of order k reducible to configurations of order . The procedure stops once the configurations of order 1 are reached, or at a certain step, the configurations of order k are the empty set.
The computation of csQCA solutions relies on analyzing truth tables, which systematically enumerate all possible configurations of causal conditions. Although this approach ensures a comprehensive evaluation of causal relationships, it also presents a significant computational challenge. As the number of possible configurations grows exponentially with the number of variables (specifically, as for n binary variables), analyzing large datasets with numerous causal conditions becomes increasingly infeasible. This combinatorial explosion can lead to excessive processing times and computational limitations, especially in cases where the dataset includes dozens of variables.
3.2. Association Rules Mining Model
Association rule mining (ARM), formalized by Agrawal et al. (1993) [], is a data-driven methodology designed to identify frequent item sets and extract meaningful if–then rules from transactional datasets. These rules, often expressed as , reveal co-occurrence patterns where the presence of item set X implies the presence of item set Y, quantified by metrics such as support (the frequency of co-occurrence) and confidence (conditional probability). Originally developed for market basket analysis, ARM has evolved into a cornerstone technique for exploratory data mining in diverse domains, including retail, healthcare, and bioinformatics [,].
The widespread adoption of ARM in recent decades stems from its algorithmic efficiency in handling large-scale datasets. Central to this is the Apriori algorithm [], which employs a breadth-first search strategy to iteratively generate candidate item sets and prune those failing to meet user-defined minimum support thresholds. By leveraging the downward closure property (subsets of frequent item sets are themselves frequent), Apriori reduces computational complexity, enabling scalable pattern discovery even in high-dimensional datasets [].
Mathematically, ARM operates on a transactional database T, where each transaction is represented by a binary vector encoding the presence (1) or absence (0) of items from a universal set I. More precisely, let be a universal set of items, and let be a transactional database where each transaction . Then, we have the following:
Definition 10.
An association rule [] is an implication of the form
This rule indicates that the occurrence of item set X in a transaction implies the occurrence of item set Y in the same transaction; that is, for every transaction ,
Analogously to csQCA problems, extracting meaningful association rules relies on quantitative criteria to evaluate their statistical significance and practical relevance. Two fundamental metrics serve as critical filters to distinguish robust patterns from spurious correlations: support and confidence. Support ensures that rules reflect frequently observed co-occurrences, while confidence measures the reliability of the implication. Mathematically,
Definition 11.
Given an association rule , we define
- Support: The proportion of transactions in T containing both X and Y:
- Confidence: The conditional probability that a transaction containing X also contains Y:
These metrics enable researchers to prioritize rules that are both prevalent in the dataset and probabilistically robust, thereby balancing generality and predictive strength. By setting thresholds for these values, practitioners can systematically discard trivial or coincidental associations, focusing instead on actionable insights with empirical validity.
In an association rule , X is the antecedent (left-hand side, LHS), and Y is the consequent (right-hand side, RHS).
Definition 12.
The rule is considered strong or interesting if it satisfies user-defined thresholds for both support (frequency) and confidence (reliability), commonly referred to as minimum support and minimum confidence.
In practice, identifying interesting rules (those satisfying minimum support and confidence thresholds) relies on efficient algorithms capable of handling large datasets. One of the most widely used methods for this purpose is the Apriori algorithm, which systematically uncovers frequent item sets that serve as the foundation for generating such rules.
The Apriori algorithm is a foundational technique in association rule mining (ARM) used to discover frequent item sets and generate association rules from large datasets. It operates by systematically identifying item sets whose frequency exceeds a predefined minimum support threshold. From these frequent item sets, association rules are generated, provided their confidence surpasses a user-specified minimum level—thus ensuring both frequency and reliability.
The algorithm proceeds iteratively: it begins with 1 item set and expands to larger item sets by joining previously discovered frequent item sets. To maintain computational efficiency, Apriori leverages the downward closure property, which states that if an item set is frequent, then all of its subsets must also be frequent. Conversely, if an item set is infrequent, all of its supersets can be safely pruned from further consideration.
Despite its effectiveness, the Apriori algorithm can become computationally expensive with large datasets due to the generation of numerous candidate item sets. To address this, several alternative algorithms have been developed to enhance efficiency and scalability. Notable alternatives include the following:
- FP-Growth (Frequent Pattern Growth), which eliminates the need for candidate generation by using a compact tree structure to store transactions [].
- ECLAT (Equivalence Class Clustering and bottom-up Lattice Traversal), which relies on a depth-first search strategy and intersection operations to find frequent item sets [].
- CHARM (Closed Association Rule Mining), which focuses on discovering closed item sets to reduce redundancy [].
- RARM (Rapid Association Rule Mining), optimized for high-dimensional datasets by leveraging specialized data structures [].
These advanced algorithms offer performance improvements over Apriori, particularly in handling large-scale and high-dimensional data scenarios.
3.3. The Equivalence Theorem
Having established the mathematical formalization of the two techniques—csQCA and AR—we now show that any csQCA problem can be reformulated as a certain type of association rule mining problem. In particular, we use the so-called negative association rules, which capture relationships involving the absence of an item [,].
Let us consider a csQCA model , with and , for and . Then, we define the following AR problem:
- The item set is , with items.
- The transaction database is , where the transaction is related to the csQCA case in the following way: , whereThus, each transaction can be regarded as a collection of n elements, which are either the variables or their negation , together with the presence of the outcome R or its absence r.
Remark 2.
It is important to note that, although there are items in I, the conditions imposed on the set of transactions T greatly limit the range of possibilities: first, all transactions are of length ; second, no transaction can contain a variable and its negation ( and or R and r).
Now, we need to establish the relationship between the k-configurations in the csQCA model and the association rules in the AR model.
Let be a k-configuration conducive to the outcome R. Let us assume that the set ; then, is equivalent to the association rule , where
is
Remark 3.
We use to denote mapping between the csQCA k-configurations and the association rules; that is,
Similarly, abusing the notation, we write to denote the element-wise transformation of the configurations defining (see Definition 7).
With this relationship between k-configurations and association rules, it is obvious that we have established a one-to-one correspondence between the cases described in the dataset matrix M and the set of transactions T. Moreover, we verify that if the case is compatible with the configuration , then is straightforward. That is, the antecedent of the association rule associated with is included in the transaction associated with the case .
However, it is important to note that in a csQCA problem, it is sufficient that there is a case in M compatible with a given k-configuration for it to be incorporated into the solution set. Still, in an association rule problem, only the interesting rules are considered in the solution set, and those depend on the scores of support and confidence. Therefore, we need to compare the metrics in QCA and ARM.
Given the consistency and coverage definitions (Equations (3) and (5)) and the above definition of the item and transaction sets, it is clear that
Therefore, given a k-configuration and its equivalent association rule , we first see that the quantity is directly related to the support of the rule . In particular,
where m denotes the number of rows (cases) in the sample data matrix M. In addition, there is a direct relationship between the consistency of the configuration and the confidence of the equivalent rule; that is,
On the other hand, the consistency can be regarded as the confidence of the necessary condition for the outcome; that is,
With these considerations in mind, the following theorem relates the solutions of a csQCA problem to the mining of a certain type of association rules.
Theorem 1.
Let be a csQCA model, and let be the association rule mining problem defined above in this section. Then,
where denotes the set of all interesting rules with minimum support and confidence thresholds given by
Proof.
Let , and is its equivalent association rule. Since the configuration is conducible to outcome R, there exists at least one case such that , and for all . Therefore, . Then, from Equation (7),
On the other hand, if the csQCA model is consistent, then , so from (8), .
Hence, association rule is an interesting association rule with the thresholds
so , and then . □
Remark 4.
It is important to note that of the two thresholds set in the theorem, the first is set to such that it is sufficient for one case to exist for it to be included in the solution set of the csQCA problem. The second is 1 because it is assumed that the matrix M is consistent and, therefore, there are no contradictions.
These two conditions, which may seem very restrictive initially, have been commonly used in csQCA since its origin. If, for some reason, a larger number of repetitions were required in the csQCA problem for a case to be considered conducive to the result, it would suffice to change the minsupp threshold accordingly.
Likewise, although not common in csQCA practice, if a certain degree of inconsistency in the cases was allowed, it would be sufficient to lower the confidence threshold to the desired consistency value.
3.4. Reducible Association Rules
One of the main issues with association rules is the number of solutions they generate. Khedr et al., 2012 [], state that many solutions generated by association rule algorithms may be redundant and irrelevant. Therefore, reducing the number of rules is one of the primary objectives of research on association rule extraction. With this in mind, the main goal of this section is to devise an association rule minimization algorithm for later comparison with the solutions produced by the QCA algorithms.
In the particular case of association rules stemming from a QCA problem, such as those defined in the previous section, we demonstrate a result below that will allow us to simplify association rules simply and efficiently, yielding the same results as the Quine–McCluskey reduction seen for csQCA.
Theorem 2.
Let and be two interesting association rules such that their corresponding k-configurations, and , are reducible to the -configuration . Then, the association rule corresponding to the reduced configuration is also an interesting rule.
Proof.
If and are interesting rules, then both rules meet the minimum support and minimum confidence criteria:
Let denote the association rule corresponding to the configuration (i.e., )). To prove that is also an interesting rule, we need to show that this rule also verifies the minimum support and confidence criteria.
Since and are reducible to the -configuration , according to Definition 6, we can consider, without any loss of generalization, that , and there exists a variable that we may assume is , such that
and
Moreover, since the variable is the only one in which the configurations and differ, we may assume that, for example,
After these considerations, the association rules related to these configurations, , , and , are given by
where
for . Thus, and .
Now, we show that any transaction containing either contains or ; that is,
For this purpose, we use the double inclusion method.
- ⊆
- Let ; then, from Remark 2, we know that all transactions have the length and that they contain each variable once, either in its affirmative () or negative () form. Therefore, since , it is ensured that eitherIn either case, .
- ⊇
- Let . If , then , and if , then . In either case, , and therefore, .
Moreover, it is trivial that and are disjoint sets as, if a transaction contains , then it contains the affirmative variable and, thus, cannot contain . Therefore,
Analogously, it can also be shown that
Therefore,
and
We are now in a position to prove that is an interesting rule. From Equations (10) and (11), it is obvious that
On the other hand, considering the algebraic property that states that if and , then
and if we assume, without any loss of generalization, that , then from (12),
Thus,
and, from (10), we can conclude that
and, therefore, is an interesting rule. □
This result allows us to obtain a method to minimize association rules in the Quine–McCluskey sense, but with the advantage of not needing to use truth tables (whose size grows exponentially with the number of variables). The Apriori method provides a list of interesting association rules that we know contain all the solutions to the csQCA problem. Now, as we know from Theorem 2, if two interesting rules are reducible, their reduction is also interesting and, therefore, it will already be in the list. Hence, we only have to eliminate reducible rules from the list.
4. Examples
4.1. Internet Blockades in Election Times
In this initial example, the csQCA and ARM methodologies are illustrated using a case study derived from [], who analyzed the presence or absence of Internet shutdowns during electoral periods, including the days preceding the elections, the election day itself, and the subsequent days. The data used, as presented in Table 2, were obtained from a comparative study encompassing 33 countries within the Sub-Saharan African region (treated as cases/transactions). Consequently, for educational purposes, this study explores three causal conditions (ISP, AT, and EV) alongside an outcome (IS).

Table 2.
A summary of cases and variables.
4.1.1. csQCA Approach
Following the notation introduced in Section 3.1, the csQCA model is given by , where
- is the variable set. More precisely, ISP refers to “State-Owned Internet Service Providers” (ISPs). These ISPs play a crucial role, especially in contexts where the government has direct control over the telecommunications infrastructure, such as the national Internet backbone, allowing it to exert significant influence over Internet access and availability. AT is the variable “Autocracy”. It is used to categorize the political regime of a country, distinguishing between “1” if the regime is an autocracy and “0” if it is a democracy. EV refers to the occurrence of violence associated with the electoral process.
- . The outcome variable is “Internet Shutdown”.
- M is the data matrix given in Table 2.
Table 3 presents the truth table for the occurrence of Internet shutdowns. In the present study, with three causal conditions (variables) considered, there are theoretically possible configurations across the 33 cases examined. While all eight of these configurations appear in the empirical data, achieving such empirical completeness is not typical. When certain configurations lack empirical representation, it results in limited diversity, a frequently encountered constraint in small- and medium-scale comparative studies.

Table 3.
Truth table for the outcome “Internet Shutdown”.
Next, we perform the so-called sufficiency analysis, whose central objective is to evaluate all possible combinations of causal conditions and identify which constitute consistent subsets of the outcome []. In this situation, the configuration is considered sufficient for the outcome (IS) []. Analyzing Table 3, we can observe four 3-configurations conducive to the IS outcome; namely,
In this small-size example, it is easy to see that all 3-configurations are reducible to three 2-configurations. In particular,
Since the 2-configurations obtained are no longer reducible, the solution set of the QCA problem is
To interpret the solution obtained, we follow the standard notation in QCA, in which variables are denoted in upper and lower case to indicate the presence and absence of a causal condition, respectively. The symbol “*” is used to aggregate variables, and the “+” sign denotes the union of configurations.
Hence, with this notation, the 2-configurations obtained can be written as
and therefore, the minimization of the truth table for the Internet shutdown leads to the following solution:
In summary, three solutions for Internet shutdowns during recent elections in Sub-Saharan African (SSA) countries were identified. In the first scenario, the ISP ownership is not public, and significant incidents of electoral violence occurred. In the second scenario, an autocratic state that holds majority ownership of Internet service providers (ISPs) initiates a disruption of the Internet service during elections. Finally, the combination of an authoritarian regime with episodes of electoral violence also led to disruptions in Internet access, regardless of public or private ISP ownership.
Regarding the metrics, it is worth noting that, as shown in Table 4, all three solution configurations have a consistency of 1, as there are no contradictory cases. The coverage of the cases is , , and , showing that when an Internet service disruption occurs, the second causal configuration () is the most frequent (examples of this can be observed in events in 2015 (Ethiopia, Togo, and Burundi) and 2016 (Gabon, Ghana, and Chad).

Table 4.
A table of solutions with consistency and coverage.
4.1.2. Positive and Negative Association Rule Solution
From the viewpoint of association rule mining, for this problem, we define the set of items as
and the set of transactions T is defined by the rows in Table 2. For example, row 1, corresponding to the 2015 electoral process in Benin, indicates the transaction .
The Apriori algorithm for mining positive and negative boolean association rules follows four main steps [].
- (a)
- Generate Candidate Item Sets as Subsets of the Universal Item Set I given in (13): Start with individual items (1 item set), then iteratively combine frequent item sets from the previous step to form larger candidate item sets (k item sets).
- (b)
- Prune Using Minimum Support: Eliminate candidates that do not meet a user-defined minimum support threshold (frequency in the dataset). This relies on the Apriori principle: any subset of a frequent item set must itself be frequent.
- (c)
- Repeat: Continue to generate and prune item sets of increasing size until no new frequent item sets are found.
- (d)
- Form Association Rules: From the final frequent item sets, generate rules (e.g., X → Y) and filter them using a minimum confidence threshold (how often Y appears when X is present).
If denotes the candidate item set of length k, then it can be shown that, if there are n variables and an outcome, then the number of items in (taking into account that cannot contain a variable and its negation) is given by
Therefore, in this example, , , , and .
As previously stated, Apriori is a bottom-up algorithm that starts with the smallest sets and increases in size, eliminating combinations that do not exceed a minimum support threshold. In our case, and following Theorem 1, the minimum support threshold is
It is important to note that association rule mining does not initially consider some items as antecedents and others as consequents in the same way that QCA separates the antecedent variables and the outcome to be analyzed. Consequently, the preliminary step involves extracting the item sets containing the response variable ‘’, as well as analyzing which of these item sets meet the minimum support and confidence conditions.
Table 5 shows the item sets that have passed the minimum support threshold, the association rule they define, and the confidence of the rule. Association rules that have confidence 1 are highlighted in boldface.

Table 5.
The association rules leading to the outcome “IS” and meeting the minimum support condition.
Given the results shown in Table 5, the set of interesting association rules leading to the outcome “Internet Shutdown” is formed by the following rules:
It is evident that a relationship can be established between the causal configurations of the QCA problem and the association rules obtained. Indeed, recalling the definition of the operator in Remark 3,
Consequently, the solution set of the QCA problem is contained in AR. Furthermore, it should be noted that the set AR encompasses both the initial and the minimized causal configurations. To obtain the same result, it suffices to determine , , and from among the rules and whether they can be obtained by minimizing the rules . It is clear that this is the case, and that if we were to complete this minimization, we would obtain the same set of solutions.
4.2. Opposition to Immigration in Europe
In the following case study, we show how the association rule methodology can also be used efficiently when the number of cases is larger. To achieve this, we adapt the data from [] to present another comparison between QCA and association rules. These data consist of a robust sample of 2223 calibrated observations from a study investigating opposition to immigration in Europe. The original data were collected using a 10-point ordinal scale, which allowed participants to express their levels of agreement and disagreement on the issue of immigration. This dataset covers a total of six variables, five of which represent potential conditioning factors: 1—low education [LOWEDU], 2—preference for cultural unity [UNITY], 3—a lack of immigrant friends [NOFRIEND], 4—perceived economic threat [THREAT], and 5—gender [MAN]. In addition to these, there is an outcome variable called [OPPOSITION]. Table 6 summarizes the sample used in this study, highlighting the frequencies corresponding to each possible combination of participants’ responses. Because we have five independent variables and two answer options (yes or no) for each, there are 32 possible combinations of answers, as shown in Table 6. For example, in the first line of the table, we see that 22 individuals responded negatively to the first variable and affirmatively to the remaining four variables.

Table 6.
Summary data for case study 2: opposition to immigration.
4.2.1. csQCA Solution
In this context, we present the solutions obtained with the csQCA algorithm to analyze opposition to immigration in Europe. Using the statistical programming language R (v. 4.3.0) [] and the QCA package (v. 3.23) [], we found that these solutions comprise four causal combinations that lead to the analyzed phenomenon:
- 1.
- LOWEDU * UNITY.
- 2.
- LOWEDU * NOFRIEND * THREAT.
- 3.
- LOWEDU * NOFRIEND * MAN.
- 4.
- UNITY * NOFRIEND * THREAT * MAN.
It can be seen that the most concise solution, characterized by the smallest number of causal conditions, is the first, comprising just two conditions: low schooling and preference for cultural unity. On the other hand, the solution with the greatest number of causal conditions is the fourth, which comprises four different causal variables.
4.2.2. Positive and Negative Association Rule Solution
Next, we transform the csQCA problem into a binary association rule mining problem, as was accomplished in the previous section. To achieve this goal, the item set was constructed, which contains 12 elements (5 variables and 1 outcome and its negations). The list of transactions T was obtained from the truth table given in Table 6, and the arules package [,] was used to determine the interesting association rules, i.e., those with a support higher than 0.0004 (≈1/2263) and a confidence of 1.
Table 7 shows the solution set of association rules derived from the proposed problem, together with the corresponding metrics. A total of 39 rules were generated, organized in increasing order of complexity. The least complex rule combines just two variables, while the most complex rules combine five different variables.

Table 7.
Association rules with 100% confidence () implying {OPPOSITION}.
However, thanks to Theorem 2, we know that if two interesting association rules are reducible, then the reduced rule is also interesting. This insight enables a very simple minimization procedure: we can eliminate from the list all rules for which there exists another that differs from it in only one bit. For example, rules 2 and 7, 3 and 6, and 4 and 5 are all reducible to rule 1. Similarly, all rules of length 5 (i.e., rules 28 to 39) are reducible to rules with a length of 4, which are already present in the list, and so on.
After filtering out all reducible rules, the remaining rules are as follows:
- 1.
- Rule 1: LOWEDU * UNITY.
- 2.
- Rule 8: LOWEDU * MAN * NOFRIEND.
- 3.
- Rule 9: LOWEDU * NOFRIEND * THREAT.
- 4.
- Rule 15: MAN * NOFRIEND * THREAT * UNITY.
These coincide with the solution obtained for the csQCA problem in the previous subsection.
4.3. Numerical Experiments
The computational cost of a truth table analysis and Quine-McCluskey minimization has been widely discussed in the QCA literature. It is well established that QCA studies typically involve a limited number of variables (rarely exceeding ten) and a relatively small number of cases (often only in the tens). Examples involving hundreds or thousands of cases—such as that shown in the earlier example—are exceptionally rare.
Initially, QCA analysis methods were especially applicable to studies with an intermediate number of cases (between 10 and 50 []). Over the years, several researchers have developed studies handling thousands of cases for different purposes [,,]. In fact, in theory, the sample size is only limited by hardware and software limitations, and not necessarily by the limitation imposed by the methodology itself.
We conducted a series of numerical experiments to illustrate the practical differences between csQCA and association rule mining, focusing particularly on computational feasibility. These experiments simulate problems with varying numbers of variables and cases, allowing for a systematic comparison of the scalability and efficiency of both approaches. For each scenario, we randomly generated consistent data tables (i.e., without contradictions) with a fixed number of variables and cases. Each experiment was repeated five times, and we recorded the mean computation time and memory usage for the csQCA algorithm (implemented via the QCA R package []), the Apriori rule mining algorithm (using the arules R package [,]), and a custom implementation of an association rule minimization algorithm in R. All computations were conducted on a 13th Gen Intel(R) Core(TM) i7-1360P (2.20 GHz) with 16 GB of RAM and no use of GPU acceleration. The code for this experiment is available at the GitHub repository https://github.com/rbensua/csQCAARM/ (accessed on 30 April 2025).
In the first experiment, we set a small number of variables (five variables) and varied the number of cases from 5 to 10,000. The results shown in Figure 1 show that csQCA required almost a thousand times greater memory usage than Apriori. The minimization of association rules, on the other hand, required only about 300 Kb, regardless of the number of cases.
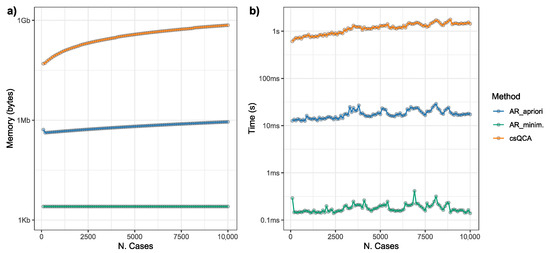
Figure 1.
A comparison between csQCA and AR mining memory usage (a) and computation time (b) as the number of cases in the dataset increases. In both plots the scale in the y-axis is logatithmic. The number of variables was fixed at 5.
In the second experiment, we set the number of cases at 60 and varied the number of variables from 5 to 21. The results, shown in Figure 2, reveal that with both csQCA and AR, the memory usage and processing times both increase exponentially with the number of variables (note the logarithmic scales). However, within the range of a typical csQCA problem (5–15 variables), ARM memory usage—when both finding the rules via the Apriori algorithm and the minimization procedure—is significantly lower than that of csQCA. For a larger number of variables, the memory usage of Apriori rapidly increases (which is a well-known issue in association rule mining). Regarding computation times, AR algorithms performed significantly better than csQCA, which rapidly faces severe computational limitations as the number of variables increases (struggling to find solutions when dealing with more than 20 variables, as also noted by []). In the second experiment, we fixed the number of cases at 60 and varied the number of variables from 5 to 21. The results, shown in Figure 2, indicate that both the csQCA and AR methods exhibit exponential increases in memory usage and processing time as the number of variables grows (note the logarithmic scales on both axes).
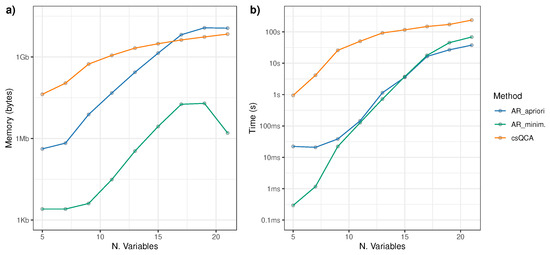
Figure 2.
Comparison between csQCA and AR mining memory usage (a) and computation time (b) as the number of variables (conditions) increases. In both plots the scale in the y-axis is logatithmic. The number of cases was fixed at 60.
Within the typical range of csQCA applications (5–15 variables), both AR steps (rule generation via the Apriori algorithm and the subsequent minimization procedure) use significantly less memory than csQCA. However, for larger numbers of variables, the memory usage of Apriori increases rapidly, which is a well-known limitation in association rule mining, giving values of the same order of magnitude as csQCA.
Regarding computation time, both AR algorithms also outperform csQCA. The csQCA computation times are in the range of [0.9 s–236 s], while the AR times combined are in the range of [0.02 s–105.7 s]. In this regard, csQCA shows a steep increase in processing time and becomes computationally infeasible for more than 20 variables, which is consistent with the findings of [].
Remark 5.
It is important to mention that although the solutions obtained with csQCA and ARM were exactly the same in the examples seen in the previous sections, in the numerical experiments, this was not the case. Obviously, according to Theorem 1, the solutions of csQCA were included in the list of interesting and irreducible rules of ARM, but ARM found more rules. This discrepancy arises from differences in the minimization algorithms used. In csQCA, the Quine–McCluskey algorithm follows a top-down approach, meaning that smaller configurations are always derived as simplifications of larger ones. In contrast, ARM starts by generating all potentially interesting rules and then eliminates those that are reducible. As a result, csQCA cannot produce configurations that do not originate from the minimization of more complex rules. We did not include the full list of solutions in the numerical experiments because, in higher-dimensionality cases, the number of resulting rules reached tens of millions.
5. Discussion
At first glance, both Qualitative Comparative Analysis (QCA) and association rule mining rest on case-based, Boolean “if–then” logic and seek to identify patterns of conditions or attributes that co-occur or link to a particular outcome [,]. However, their goals diverge: QCA explicitly engages with causal complexity, enabling multiple intersecting pathways to an outcome, whereas association rules capture statistical co-occurrence without implying causation [,].
The Quine–McCluskey minimization algorithm, which was originally devised to optimize logic circuits in electrical engineering [], is applied by QCA in all its variants. This algorithm is employed to reduce complex configurations of conditions into simpler expressions. In contrast, the process of association rule mining starts with the enumeration of frequent item sets, subsequently leading to the derivation of rules based on support and confidence thresholds (see []).
Despite these conceptual and procedural differences, both techniques face the same combinatorial explosion: the search space for all possible condition combinations grows exponentially with the number of distinct attributes or conditions [,]. Furthermore, there is a formal parallel in the way rules are interpreted. In association rule mining, an implication is deemed strong if X satisfies a minimum frequency threshold, and every transaction containing X also includes Y []. Similarly, in QCA, the set of conditions X is considered necessary for outcome Y precisely when across the observed cases [], which may be regarded as an alternative formulation of the same concept.
This study provides a detailed comparative analysis of the solutions obtained using the association rule and Configurational Comparative Analysis (csQCA) methodologies.
Considering the evidence presented, the following key points emerge:
- 1.
- A one-to-one relationship can be established between a csQCA problem and a particular type of positive and negative binary association rule mining problem (Theorem 1). To our knowledge, this relationship has not been explored previously.
- 2.
- All the solutions generated by the csQCA algorithm were previously captured by the association rule mining algorithm. In other words, the emerging solution set from association rules acts as a superset of the emerging solutions from the csQCA approach. In this way, association rules show greater potential to generate a broader spectrum of solutions compared to the csQCA methodology.
- 3.
- The procedure used for obtaining solutions is completely different. While csQCA follows a top-down approach, in which the most complex solutions are obtained first, and, from the Quine–McCluskey minimization, simpler irreducible solutions are found, in ARM, a bottom-up approach is used (Apriori algorithm), starting with the simplest solutions and obtaining increasingly complex solutions.However, the Apriori algorithm does not simplify reducible solutions, since the objective for which it is designed is to obtain all frequent configurations. Despite this, we showed that it is not necessary to perform a Quine–McCluskey minimization since, as shown in Theorem 2, if two interesting rules are reducible, their reduction is also an interesting rule; thus, it is enough to filter and eliminate the reducible rules.
- 4.
- QCA originated in the context of social science research, where, traditionally, datasets have been relatively small in order to facilitate the extraction of interpretable solutions. In contrast, association rule mining emerged from the need to identify patterns within large-scale databases. As a result, the algorithms developed for ARM are specifically designed to operate efficiently on large datasets. Given the relationship established between QCA and association rule mining, this connection yields the possibility of using ARM techniques to obtain QCA-like solutions even when large datasets are involved, overcoming the traditional computational limitations of QCA.
- 5.
- Furthermore, it is important to emphasize that the solutions obtained through both methodologies exhibit identical robustness metrics, with confidence in association rule mining corresponding directly to consistency in csQCA. Additionally, all identified solutions adhere to an “if–then” structure, reinforcing their logical interpretability. Finally, both approaches are fundamentally grounded in set theory.
In this study, we show that association rules (ARs) produce solutions equivalent to those of csQCA. In contexts of limited data diversity, csQCA typically yields fewer solutions than ARs. However, the methods differ significantly. csQCA targets a single predefined outcome [], while ARs can identify multiple outcomes and their complements [], with outcomes either predefined or data-driven.
Both methods structure solutions as “if–then” statements joined by disjunctive (OR) operators []; however, only csQCA suggests causality, whereas AR identifies associations without causal claims []. Conditional elements must be selected in advance: causal conditions in csQCA [] and items in AR []. Both approaches rely on Boolean structures and allow negative terms. Conjunctive (AND) combinations express conjunctural causality in csQCA [], while in ARs, item sets are connected similarly but without causal interpretation, which must be inferred by the researcher.
Combinatorial generation also differs: csQCA yields combinations [], whereas AR initially generates possibilities, usually filtered down to [].
6. Conclusions
In this study, we explored the theoretical and practical connections between Crisp-Set Qualitative Comparative Analysis (csQCA) and association rule mining (ARM). Using a formal mathematical framework, we demonstrated that every csQCA problem can be represented as a specific ARM problem involving positive and negative rules. By uncovering the internal mechanics of csQCA through this mathematical lens, we pave the way for a deeper understanding of its computational properties and compatibility with ARM approaches.
We showed that key QCA concepts such as consistency and coverage naturally correspond to ARM metrics such as confidence and lift. This equivalence was further supported by two illustrative applications: a small-N case on Internet shutdowns in Africa and a large-N dataset on immigration attitudes in Europe.
One of the key advantages of ARM—particularly in large datasets—lies in its computational efficiency and the ability to uncover a broader set of relevant rules, including those missed by traditional QCA algorithms. We proposed a minimization algorithm for association rules that mimics the Quine–McCluskey approach in csQCA, thus avoiding the need to construct large truth tables.
These findings provide a foundation for researchers to select between csQCA and ARM based on sample size, computational constraints, and research goals. Future research could extend this comparison to Fuzzy-Set QCA and explore the integration of AR-based methods into mixed-method research designs.
Author Contributions
Conceptualization, A.D.L., R.B. and M.d.C.B.; methodology, A.D.L. and M.d.C.B.; software, A.D.L. and R.B.; validation, A.D.L. and R.B.; formal analysis, R.B. and M.d.C.B.; investigation, A.D.L.; data curation, A.D.L.; writing—original draft preparation, A.D.L.; writing—review and editing, R.B. and M.d.C.B.; supervision, R.B. and M.d.C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets used in this study are included in this article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QCA | Qualitative Comparative Analysis. |
| csQCA | Crisp-Set QCA. |
| fsQCA | Fuzzy-Set QCA. |
| AR | Association rule. |
| ARM | Association rule mining. |
References
- Ragin, C.C. The Comparative Method: Moving Beyond Qualitative and Quantitative Strategies; University of California Press: Oakland, CA, USA, 1987. [Google Scholar]
- Pagliarin, S.; La Mendola, S.; Vis, B. The “qualitative” in qualitative comparative analysis (QCA): Research moves, case-intimacy and face-to-face interviews. Qual. Quant. 2023, 57, 489–507. [Google Scholar] [CrossRef]
- Hanckel, B.; Petticrew, M.; Thomas, J.; Green, J. The use of Qualitative Comparative Analysis (QCA) to address causality in complex systems: A systematic review of research on public health interventions. BMC Public Health 2021, 21, 877. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, R.; Imieliński, T.; Swami, A. Mining association rules between sets of items in large databases. In Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 25–28 May 1993; Association for Computing Machinery: New York, NY, USA, 1993. SIGMOD ’93. pp. 207–216. [Google Scholar] [CrossRef]
- Schneider, C.Q.; Wagemann, C. Set-Theoretic Methods for the Social Sciences: A Guide to Qualitative Comparative Analysis; Strategies for Social Inquiry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Swiatczak, M.D. Different algorithms, different models. Qual. Quant. 2022, 56, 1913–1937. [Google Scholar] [CrossRef]
- Ragin, C.C.; Sonnett, J. Between Complexity and Parsimony: Limited Diversity, Counterfactual Cases, and Comparative Analysis. In Vergleichen in der Politikwissenschaft; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2005; pp. 180–197. [Google Scholar] [CrossRef]
- Duşa, A. QCA with R. A Comprehensive Resource; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Ragin, C.; Rihoux, B. Qualitative comparative analysis (CQA): State of the art and prospects. Qual. Multi-Method Res. 2004, 2, 3–13. [Google Scholar] [CrossRef]
- De Cock, M.; Cornelis, C.; Kerre, E. Elicitation of fuzzy association rules from positive and negative examples. Fuzzy Sets Syst. 2005, 149, 73–85. [Google Scholar] [CrossRef]
- Muyeba, M.; Khan, M.S.; Coenen, F. A Framework for Mining Fuzzy Association Rules from Composite Items. In Proceedings of the New Frontiers in Applied Data Mining, Bangkok, Thailand, 27–30 April 2010; Chawla, S., Washio, T., Minato, S.i., Tsumoto, S., Onoda, T., Yamada, S., Inokuchi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 62–74. [Google Scholar]
- Korhonen-Kurki, K.; Jenniver Sehring, M.B.; Gregorio, M.D. Enabling factors for establishing REDD+ in a context of weak governance. Clim. Policy 2014, 14, 167–186. [Google Scholar] [CrossRef]
- Aversa, P.; Furnari, S.; Haefliger, S. Business model configurations and performance: A qualitative comparative analysis in Formula One racing, 2005–2013. Ind. Corp. Change 2015, 24, 655–676. [Google Scholar] [CrossRef]
- Kumar, S.; Sahoo, S.; Lim, W.M.; Kraus, S.; Bamel, U. Fuzzy-set qualitative comparative analysis (fsQCA) in business and management research: A contemporary overview. Technol. Forecast. Soc. Change 2022, 178, 121599. [Google Scholar] [CrossRef]
- Mangalampalli, A.; Pudi, V. Fuzzy association rule mining algorithm for fast and efficient performance on very large datasets. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju Island, Republic of Korea, 20–24 August 2009; pp. 1163–1168. [Google Scholar] [CrossRef]
- Ho, G.; Ip, W.; Wu, C.; Tse, Y. Using a fuzzy association rule mining approach to identify the financial data association. Expert Syst. Appl. 2012, 39, 9054–9063. [Google Scholar] [CrossRef]
- Chien, B.C.; Cheng, M.C. A color image segmentation approach based on fuzzy similarity measure. In Proceedings of the 2002 IEEE World Congress on Computational Intelligence, 2002 IEEE International Conference on Fuzzy Systems, FUZZ-IEEE’02. Proceedings (Cat. No.02CH37291), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 449–454. [Google Scholar] [CrossRef]
- Tan, P.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Always Learning, Pearson: London, UK, 2014. [Google Scholar]
- Ragin, C.C.; Shulman, D.; Weinberg, A.S.; Gran, B.K. Complexity, Generality, and Qualitative Comparative Analysis. Field Methods 2003, 15, 323–340. [Google Scholar] [CrossRef]
- Fiss, P.C. A Set-Theoretic Approach to Organizational Configurations. Acad. Manag. Rev. 2007, 32, 1180–1198. [Google Scholar] [CrossRef]
- Woodside, A.G. Moving beyond multiple regression analysis to algorithms: Calling for adoption of a paradigm shift from symmetric to asymmetric thinking in data analysis and crafting theory. J. Bus. Res. 2013, 66, 463–472. [Google Scholar] [CrossRef]
- Rihoux, B.; Ragin, C. Configurational Comparative Methods: Qualitative Comparative Analysis (QCA) and Related Techniques; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2009. [Google Scholar] [CrossRef]
- Vis, B. The Comparative Advantages of fsQCA and Regression Analysis for Moderately Large-N Analyses. Sociol. Methods Res. 2012, 40, 168–198. [Google Scholar] [CrossRef]
- Seawright, J. Qualitative Comparative Analysis vis-A-vis Regression. Stud. Comp. Int. Dev. 2005, 40, 3–26. [Google Scholar] [CrossRef]
- Buxton, E.K.; Vohra, S.; Guo, Y.; Fogleman, A.; Patel, R. Pediatric population health analysis of southern and central Illinois region: A cross sectional retrospective study using association rule mining and multiple logistic regression. Comput. Methods Programs Biomed. 2019, 178, 145–153. [Google Scholar] [CrossRef]
- Changpetch, P.; Lin, D.K. Model selection for logistic regression via association rules analysis. J. Stat. Comput. Simul. 2013, 83, 1415–1428. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, C. User acceptance of information feed advertising: A hybrid method based on sem and qca. Future Internet 2020, 12, 209. [Google Scholar] [CrossRef]
- Mguirris, I.; Amdouni, H.; Gammoudi, M.M. A new validation method of fuzzy association rules based on the Structural Equation Modeling. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; pp. 624–633. [Google Scholar] [CrossRef]
- Kim, C.; Costello, F.J.; Lee, K.C. Integrating Qualitative Comparative Analysis and Support Vector Machine Methods to Reduce Passengers’ Resistance to Biometric E-Gates for Sustainable Airport Operations. Sustainability 2019, 11, 5349. [Google Scholar] [CrossRef]
- Chiu, A.; Xu, Y. Bayesian Rule Set: A Quantitative Alternative to Qualitative Comparative Analysis. J. Politics 2023, 85, 280–295. [Google Scholar] [CrossRef]
- Álamos Concha, P.; Pattyn, V.; Rihoux, B.; Schalembier, B.; Beach, D.; Cambré, B. Conservative solutions for progress: On solution types when combining QCA with in-depth Process-Tracing. Qual. Quant. 2022, 56, 1965–1997. [Google Scholar] [CrossRef]
- Fu, M. scpQCA: Enhancing mvQCA Applications through Set-Covering-Based QCA Method. arXiv 2024. [Google Scholar] [CrossRef]
- Ljungstrom, B.M.; Denk, T.; Sarenmalm, E.K.; Axberg, U. Use of qualitative comparative analysis (QCA) in an explanatory sequential mixed methods design to explore combinations of family factors that could have an impact on the outcome of a parent training program. Child. Youth Serv. Rev. 2025, 170, 108120. [Google Scholar] [CrossRef]
- Merminod, V.; Rowe, F. Identification de configurations par la méthode Fuzzy set Qualitative Comparative Analysis: Illustration par la contribution de la technologie PLM au respect du temps de développement. SystèMes D’Inf. Manag. 2018, 23, 71–97. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Merigo, J.M.; Xu, Y. Application of Fuzzy Set/Qualitative Comparative Analysis to Public Participation Projects in Support of the EU Water Framework Directive. Water Environ. Res. 2018, 90, 73–82. [Google Scholar] [CrossRef]
- Shalahuddin, M.; Sunindyo, W.; Effendi, M.; Surendro, K. Fuzzy-set qualitative comparative analysis (fsQCA) for validating causal relationships in system dynamics models. Eng. Rep. 2024, 6, e12855. [Google Scholar] [CrossRef]
- Greckhamer, T.; Misangyi, V.F.; Fiss, P.C. The Two QCAs: From a Small-N to a Large-N Set Theoretic Approach. In Configurational Theory and Methods in Organizational Research; Research in the Sociology of Organizations; Emerald Group Publishing Limited: Leeds, UK, 2013; Volume 38, pp. 49–75. [Google Scholar] [CrossRef]
- Oana, I.E.; Schneider, C.Q.; Thomann, E. Qualitative Comparative Analysis Using R: A Beginner’s Guide; Methods for Social Inquiry, Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- McCluskey, E.J. Minimization of Boolean functions. Bell Syst. Tech. J. 1956, 35, 1417–1444. [Google Scholar] [CrossRef]
- Quine, W.V. The Problem of Simplifying Truth Functions. Am. Math. Mon. 1952, 59, 521–531. [Google Scholar] [CrossRef]
- Quine, W.V. A Way to Simplify Truth Functions. Am. Math. Mon. 1955, 62, 627–631. [Google Scholar] [CrossRef]
- Hegland, M. Algorithms for Association Rules. In Advanced Lectures on Machine Learning: Machine Learning Summer School 2002 Canberra, Australia, February 11–22, 2002 Revised Lectures; Springer: Berlin/Heidelberg, Germany, 2003; pp. 226–234. [Google Scholar] [CrossRef]
- Hegland, M. The Apriori Algorithm—A Tutorial. In Mathematics and Computation in Imaging Science and Information Processing; World Scientific Publishing Co.: Singapore, 2007; pp. 209–262. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Yin, Y. Mining frequent patterns without candidate generation. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; Association for Computing Machinery: New York, NY, USA, 2000. SIGMOD ’00. pp. 1–12. [Google Scholar] [CrossRef]
- Zaki, M. Scalable algorithms for association mining. IEEE Trans. Knowl. Data Eng. 2000, 12, 372–390. [Google Scholar] [CrossRef]
- Zaki, M.J.; Hsiao, C.J. CHARM: An Efficient Algorithm for Closed Itemset Mining. In Proceedings of the 2002 SIAM International Conference on Data Mining (SDM), Arlington, VA, USA, 11–13 April 2002; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002; pp. 457–473. [Google Scholar] [CrossRef]
- Das, A.; Ng, W.K.; Woon, Y.K. Rapid association rule mining. In Proceedings of the Tenth International Conference on Information and Knowledge Management, Atlanta, GA, USA, 5–10 November 2001; Association for Computing Machinery: New York, NY, USA, 2001. CIKM ’01. pp. 474–481. [Google Scholar] [CrossRef]
- Savasere, A.; Navathe, S.; Omiecinski, E. Mining for Strong Negative Associations in a Large Database of Customer Transactions. In Proceedings of the 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, Australia, 8–12 April 2013; IEEE Computer Society: Los Alamitos, CA, USA, 1998; p. 494. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, C.; Zhang, S. Efficient Mining of Both Positive and Negative Association Rules. ACM Trans. Inf. Syst. 2004, 22, 381–405. [Google Scholar] [CrossRef]
- Khedr, A.; Ramadan, R.; Abdel-Mageid, S. Qmr: Quine-mccluskey for rule minimization in rule-based systems. Int. J. Intell. Comput. Inf. Sci. 2012, preprint. [Google Scholar]
- Freyburg, T.; Garbe, L. Authoritarian Practices in the Digital Age| Blocking the Bottleneck: Internet Shutdowns and Ownership at Election Times in Sub-Saharan Africa. Int. J. Commun. 2018, 12, 21. [Google Scholar]
- Cornelis, C.; Yan, P.; Zhang, X.; Chen, G. Mining Positive and Negative Association Rules from Large Databases. In Proceedings of the 2006 IEEE Conference on Cybernetics and Intelligent Systems, Taipei, Taiwan, 8–11 October 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Emmenegger, P.; Schraff, D.; Walter, A. QCA, the Truth Table Analysis and Large-N Survey Data: The Benefits of Calibration and the Importance of Robustness Tests. In Proceedings of the 2nd International QCA Expert Workshop, Zurich, Switzerland, 5–7 November 2014. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Hahsler, M.; Gruen, B.; Hornik, K. Arules—A Computational Environment for Mining Association Rules and Frequent Item Sets. J. Stat. Softw. 2005, 14, 1–25. [Google Scholar] [CrossRef]
- Hahsler, M.; Chelluboina, S.; Hornik, K.; Buchta, C. The arules R-Package Ecosystem: Analyzing Interesting Patterns from Large Transaction Datasets. J. Mach. Learn. Res. 2011, 12, 1977–1981. [Google Scholar]
- Mendel, J.M.; Korjani, M.M. Theoretical aspects of Fuzzy Set Qualitative Comparative Analysis (fsQCA). Inf. Sci. 2013, 237, 137–161. [Google Scholar] [CrossRef]
- Agrawal, A.; Knoeber, C.R. Firm Performance and Mechanisms to Control Agency Problems between Managers and Shareholders. J. Financ. Quant. Anal. 1996, 31, 377–397. [Google Scholar] [CrossRef]
- Ragin, C.C. Redesigning Social Inquiry; University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).