Quantitative Recurrence Properties in Some Irregular Sets for Beta Dynamical Systems

Abstract

Let $\beta >1$ be a real number and $T_{\beta }x=\beta x\left(mod1\right)$. This paper is concerned with the quantitative recurrence properties of the system $([0,1],T_{\beta })$ in some (refined) irregular sets. Specifically, let ${\alpha }_1,{\alpha }_2>0$ and $\psi :\mathbb{N}\to (0,1)$ be a positive function; we define the set $E_{{\alpha }_1,{\alpha }_2}^{\beta }=\left\{x\in [0,1):\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_1,\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_2\right\},$ and calculate the Hausdorff dimension of the set $E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right):=\left\{x\in E_{{\alpha }_1,{\alpha }_2}^{\beta }:|T_{\beta }^{n}x-x|<\psi \left(n\right)i.m.n\in \mathbb{N}\right\},$ where $i.m.$ stands for infinitely many. Consequently, the Hausdorff dimension of the set ${\widehat{E}}^{\beta }\left(\psi \right)=\left\{x\in [0,1):\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )\mathrm{does}\mathrm{not}\mathrm{exist}, |T_{\beta }^{n}x-x|<\psi \left(n\right)i.m.n\in \mathbb{N}\right\}$ is also determined.

1. Introduction

The quantitative recurrence property has been a hot research topic in recent years in ergodic theory and dynamical systems; it focuses on the size of the set of points in a dynamical system with a given recurrence rates from the perspective of fractal geometry. Previous research mainly focused on the quantitative recurrence property in the entire phase space, with less attention given to the study of quantitative recurrence in subsets of the phase space. This motivated us to investigate the quantitative recurrence of beta dynamical systems on certain irregular subsets.

Quantitative recurrence originates from the classical Poincaré recurrence theorem. Let $(X,\mathcal{B},\mu ,T)$ be a finite measure-preserving dynamical system with $(X,d)$ being a separate metric space. The Poincaré recurrence theorem tells us that for $\mu$-almost, every $x\in X$ is recurrent in the sense that

$$\underset{n\to \infty }{lim\; inf}d(T^{n}x,x)=0.$$

(1)

That is to say, for $\mu$-almost every $x\in X$, the orbit ${\left\{T^{n}x\right\}}_{n\ge 0}$ returns to shrinking neighborhoods of the initial point x infinitely often.

However, the result (1) is qualitative in nature and says nothing about the rate at which a generic orbit returns back to the initial point or in what manner the neighborhoods of the start point can shrink. This has motivated many authors to investigate the so-called quantitative recurrence properties. Boshernitzan [1] first established a relationship between the rate at which the orbit of a generic point returns to its neighborhood and the Hausdorff measure of the phase space X (see [2] for further results), providing a new perspective for understanding the recurrence properties of dynamical systems in a quantitative manner. Later, Barreira and Saussol [3] found that the orbit recurrence rate is related to the local dimension. Fernández, Melián, and Pestana [4] related the quantitative recurrence properties of inner functions to their mixing property. Tan and Wang [5] studied the quantitative recurrence properties of general beta dynamical systems from the perspective of fractal geometry. Related work for homogeneous self-similar sets and self-conformal sets can be found in [6,7] and references therein.

Let $\beta >1$ be a real number and the $\beta$-transformation $T_{\beta }$ be given by

$$T_{\beta }:[0,1]\to [0,1],x\to \beta x-\lfloor \beta x\rfloor ,$$

where $\lfloor x\rfloor$ denotes the integral part of x. In this paper, we study the quantitative recurrence properties of some irregular sets associated with the beta dynamical system $([0,1],T_{\beta })$ for general $\beta >1$. To begin with, we recall that every $x\in [0,1]$ can be uniquely expanded into a finite or infinite series

$$x={\displaystyle \frac{{\epsilon }_1(x,\beta )}{\beta }}+\cdots +{\displaystyle \frac{{\epsilon }_n(x,\beta )}{{\beta }^n}}+\cdots .$$

(2)

where ${\epsilon }_n(x,\beta )=\lfloor \beta T_{\beta }^{n-1}\left(x\right)\rfloor$ for all $n\ge 1$. The series (2) is called the $\beta$-expansion of x, which was introduced by Rényi [8], and ${\left\{{\epsilon }_n(x,\beta )\right\}}_{n\ge 1}$ denotes the sequence of digits of x (see Section 2 for more details).

Let $S_n(x,\beta )={\sum }_{k=1}^n{\epsilon }_k(x,\beta )$ be the sum of the first n digits in the $\beta$-expansion of x, which is an ergodic sum ${\sum }_{k=0}^{n-1}\phi \left(T_{\beta }^{k}x\right)$ with $\phi \left(x\right)={\epsilon }_1(x,\beta )$, the first digit in the $\beta$-expansion of x. It is well known that $T_{\beta }$ is invariant and ergodic with respect to the Parry measure ${\nu }_{\beta }$ [9], which is equivalent to the Lebesgue measure. The Birkhoff ergodic theorem implies that ${lim}_{n\to \infty }{\displaystyle \frac{1}{n}}{S}_n(x,\beta )$ exists and is equal to $\int {\epsilon }_1(x,\beta )d{\nu }_{\beta }\left(x\right)$ for ${\nu }_{\beta }$-almost every $x\in [0,1]$.

Furthermore, for $\beta >1$, define

$$\Lambda \left(\beta \right)=\underset{x\in [0,1]}{sup}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta ).$$

Again, by the Birkhoff ergodic theorem, for every $\alpha \in [0,\Lambda (\beta \left)\right]$, there exists $x\in [0,1]$ such that ${lim}_{n\to \infty }{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha$ (see [10,11]). Multifractal analysis related to $S_n(x,\beta )$ was first performed by Besicovitch [12] for $\beta =2$ and Eggleston [13] for general integer bases. From the perspective of multifractal analysis, it is also interesting to study the following irregular set

$${\widehat{E}}_{\beta }=\left\{x\in [0,1]:\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )<\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )\right\},$$

(3)

or the refined irregular set

$$E_{{\alpha }_1,{\alpha }_2}^{\beta }=\left\{x\in [0,1):\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_1,\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_2\right\},$$

(4)

where $0\le {\alpha }_1\le {\alpha }_2\le \Lambda \left(\beta \right)$. It was proved that ${\widehat{E}}_{\beta }$ has full Hausdorff dimension [14]. The Hausdorff dimension of $E_{{\alpha }_1,{\alpha }_2}^{\beta }$ depends on the dimensional quantity $h^{\beta }\left(\alpha \right)$ defined in [11] (see Section 2.3 or [15] for more details). Specifically, for $\beta >1$, $\alpha \in [0,\Lambda (\beta \left)\right]$ and $\delta >0$, define the set $H^{\beta }(\alpha ,n,\delta )$ as:

$$H^{\beta }(\alpha ,n,\delta )=\left\{({\epsilon }_1,\dots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n:\alpha -\delta <{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\epsilon }_i<\alpha +\delta \right\},$$

and let $h^{\beta }(\alpha ,n,\delta )=\#H^{\beta }(\alpha ,n,\delta )$, where ${\Sigma }_{\beta }^n$ denotes the set of $\beta$-admissible sequences of length n (see Definition 2.1). Define the function $h^{\beta }\left(\alpha \right)$ as:

$$\begin{array}{cc}\hfill h^{\beta }\left(\alpha \right)& =\underset{\delta \to 0}{lim}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{log{h}^{\beta }(\alpha ,n,\delta )}{nlog\beta }}.\hfill \end{array}$$

Using this quantity, Li and Li [15] determined the Hausdorff dimension of $E_{{\alpha }_1,{\alpha }_2}^{\beta }$.

Theorem 1

(see [15]). Let $\beta >1$ be a real number and $0\le {\alpha }_1\le {\alpha }_2\le \Lambda \left(\beta \right)$, we have

$${dim}_{\mathrm{H}}{E}_{{\alpha }_1,{\alpha }_2}^{\beta }=min\left\{h^{\beta }\left({\alpha }_1\right),h^{\beta }\left({\alpha }_2\right)\right\}.$$

In particular, for any $\alpha \in [0,\Lambda (\beta \left)\right]$, we have

$${dim}_{\mathrm{H}}\{x\in [0,1]:\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha \}=h^{\beta }\left(\alpha \right).$$

(5)

The main purpose of this paper is to investigate the quantitative recurrence properties of the beta dynamical system in the refined irregular set $E_{{\alpha }_1,{\alpha }_2}^{\beta }$. Define the recurrence set by

$$R_{\beta }\left(\psi \right):=\left\{x\in [0,1]:|T_{\beta }^{n}x-x|<\psi \left(n\right)\mathrm{for}\mathrm{infinitely}\mathrm{many}n\in \mathbb{N}\right\},$$

(6)

for general beta dynamical systems, where $\psi :\mathbb{N}\to (0,1)$ is a positive function. Set ${\displaystyle a=\underset{n\to \infty }{lim\; inf}-\frac{1}{n}{log}_{\beta }\psi \left(n\right)}$ in the sequel of this paper. We remark that the recurrence set $R_{\beta }\left(\psi \right)$ shares a similar flavor with the shrinking target set, which was first studied by Hill and Velani [16] (see [17] and references therein for some recent developments). Compared with the extensive developments of the shrinking target problems, the study of recurrence sets lagged behind for several years. Motivated by the work of Boshernitzan [1], Tan and Wang [5], we calculate the Hausdorff dimension of $R_{\beta }\left(\psi \right)$.

Theorem 2

(see [5]). For any $\beta >1$, we have

$${dim}_{\mathrm{H}}{R}_{\beta }\left(\psi \right)={\displaystyle \frac{1}{1+a}}.$$

Theorem 2 determines the Hausdorff dimension of the recurrence set for beta dynamical systems. However, it does not tell us anything about the recurrence properties in any subsets of the unit interval. In this paper, we remedy this by studying the intersection of the refined irregular set $E_{{\alpha }_1,{\alpha }_2}^{\beta }$ and the recurrence set $R_{\beta }\left(\psi \right)$. Specifically, let

$$E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right):=\left\{x\in E_{{\alpha }_1,{\alpha }_2}^{\beta }:|T_{\beta }^{n}x-x|<\psi \left(n\right)\mathrm{for}\mathrm{infinitely}\mathrm{many}n\in \mathbb{N}\right\}.$$

(7)

One of our motivations is to investigate in what manner two types of dynamical behaviors intersect with each other. In particular, we aim to see whether the asymptotic behavior of the first n digit in the $\beta$-expansion of x and the rate of recurrence of the orbit ${\left\{T_{\beta }^n\right\}}_{n\ge 1}$ are independent or not. Our main result reveals that the two types of dynamical properties of $T_{\beta }$ are independent in the sense that the Hausdorff dimension of the intersection $E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)$ is equal to the product of the Hausdorff dimensions of $E_{{\alpha }_1,{\alpha }_2}^{\beta }$ and $R_{\beta }\left(\psi \right)$.

Theorem 3.

Let $\beta >1$, $0\le {\alpha }_1\le {\alpha }_2\le \Lambda \left(\beta \right)$ and $\psi :\mathbb{N}\to (0,1)$, we have

$${dim}_{\mathrm{H}}{E}_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)={\displaystyle \frac{min\{h^{\beta }\left({\alpha }_1\right),h^{\beta }\left({\alpha }_2\right)\}}{1+a}}.$$

In particular, for any $\alpha \in [0,\Lambda (\beta \left)\right]$, we have

$${dim}_{\mathrm{H}}\left\{x\in [0,1]:\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha ,|T_{\beta }^{n}x-x|<\psi \left(n\right)i.m.n\in \mathbb{N}\right\}={\displaystyle \frac{h^{\beta }\left(\alpha \right)}{1+a}},$$

(8)

where $i.m.$ stands for infinitely many.

Although the explicit formula of $h^{\beta }\left(\alpha \right)$ is lacking for general $\beta >1$, we have the explicit values for some specific $\beta >1$ (see Examples 3 and 4). Therefore, Theorem 3 gives the following examples.

Example 1.

Let $\beta =2$, $0\le {\alpha }_1\le {\alpha }_2\le 1$ and $\psi :\mathbb{N}\to (0,1)$. Then,

$${dim}_H{E}_{{\alpha }_1,{\alpha }_2}^2\left(\psi \right)={\displaystyle \frac{min\left\{logf\left({\alpha }_1\right),logf\left({\alpha }_2\right)\right\}}{(1+a)log2}},\mathit{where}f\left(\alpha \right)={\displaystyle \frac{1}{{\alpha }^{\alpha }{(1-\alpha )}^{1-\alpha }}}.$$

Example 2.

Let $\beta ={\displaystyle \frac{1+\sqrt{5}}{2}}$, and $0\le {\alpha }_1\le {\alpha }_2\le 1$ and $\psi :\mathbb{N}\to (0,1)$. Then,

$${dim}_H{E}_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)={\displaystyle \frac{min\left\{logg\left({\alpha }_1\right),logg\left({\alpha }_2\right)\right\}}{(1+a)log\beta }},\mathit{where}g\left(\alpha \right)={\displaystyle \frac{{(1-\alpha )}^{1-\alpha }}{{\alpha }^{\alpha }{(1-2\alpha )}^{1-2\alpha }}}.$$

Recently, Shi et al. [18] have determined the Hausdorff dimension of the intersection of the so-called Besicovitch–Eggleston set (see [12,13]) and the recurrence set under the $\times b$ map on the unit interval, where $b\ge 2$ is an integer. Their result is in the flavor of (8). We remark that our result is slightly more general. On one hand, the $\beta$-transformation might not be Markov for some $\beta >1$, which is quite different from the $\times b$ map; on the other hand, different from the set considered in [18], the limsup and liminf of the quantity ${\displaystyle \frac{1}{n}}{S}_n(x,\beta )$ are not equal for $x\in E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)$ with ${\alpha }_1\ne {\alpha }_2$, which causes additional difficulty.

As a consequence of Theorem 3, we also determine the Hausdorff dimension of the intersection of the irregular set ${\widehat{E}}_{\beta }$ and the recurrence set $R_{\beta }\left(\psi \right)$. Write

$${\widehat{E}}^{\beta }\left(\psi \right)=\left\{x\in {\widehat{E}}^{\beta }:|T_{\beta }^{n}x-x|<\psi \left(n\right)\mathrm{for}\mathrm{infinitely}\mathrm{many}n\in \mathbb{N}\right\}.$$

Theorem 4.

Let $\beta >1$ be a real number, we have

$${dim}_{\mathrm{H}}{\widehat{E}}^{\beta }\left(\psi \right)={\displaystyle \frac{1}{1+a}}.$$

For a topological mixing subshift of finite type over a finite alphabet, Zhao [19] established a similar result as in Theorem 4, corresponding to the case where $\beta >1$ is a Parry number. However, their methods cannot be applied to general beta dynamical systems.

The novelty of our proof lies in constructing an appropriate Cantor subset. When constructing the Cantor set, we need to balance the upper and lower limits and construct a set in which the points satisfy the given recurrence rate through alternating selection of words step-by-step. For general $\beta >1$, the corresponding $\beta$-dynamical system is non-Markov. Therefore, in constructing Cantor subsets, free concatenation of selected words is not allowed. We first proved the results for Parry number $\beta >1$ and then completed the proof using approximation techniques.

It is plausible that our method could be applied to study the dynamical systems $(X,T)$ with a certain form of weak specification property (see [14] for more details) or some piecewise monotonic maps on the unit intervals $[0,1]$. However, to tackle higher-dimensional dynamical systems, for instance, the automorphisms on the d-dimensional torus, new methods are needed.

2. Preliminaries

2.1. $\beta$-Expansion

Let $\beta >1$ and define the $\beta$-transformation on $[0,1]$ by $T_{\beta }\left(x\right)=\beta x-\lfloor \beta x\rfloor$. The system $\left([0,1],T_{\beta }\right)$ is called the beta dynamical system. Taking ${\epsilon }_n(x,\beta )=\lfloor \beta T_{\beta }^{n-1}\left(x\right)\rfloor$ recursively for all $n\ge 1$, every $x\in [0,1]$ can be uniquely expressed as a finite or infinite series

$$x={\displaystyle \frac{{\epsilon }_1(x,\beta )}{\beta }}+\cdots +{\displaystyle \frac{{\epsilon }_n(x,\beta )}{{\beta }^n}}+\cdots ,$$

which is called the $\beta$-expansion of x and ${\left\{{\epsilon }_n(x,\beta )\right\}}_{n\ge 1}$ is called the sequence of digits of x. We also write $\epsilon (x,\beta )=({\epsilon }_1(x,\beta ),\cdots ,{\epsilon }_1(x,\beta ),˯)$ as the $\beta$-expansion of x. Clearly, ${\epsilon }_n(x,\beta )\in {\mathcal{A}}_{\beta }$ for any $n\ge 1$, where ${\mathcal{A}}_{\beta }=\{0,1,\cdots ,\beta -1\}$ if $\beta \in \mathbb{N}$, and ${\mathcal{A}}_{\beta }=\{0,1,\cdots ,\lfloor \beta \rfloor \}$ if $\beta \notin \mathbb{N}$.

Definition 1.

A finite sequence $({\epsilon }_1,\cdots ,{\epsilon }_n)$ is called β-admissible if there exists $x\in [0,1]$ such that ${\epsilon }_k(x,\beta )={\epsilon }_k$ for all $1\le k\le n$. An infinite sequence $\epsilon =({\epsilon }_1,\cdots ,{\epsilon }_n,\cdots )\in {\mathcal{A}}_{\beta }^{\mathbb{N}}$ is called β-admissible if $({\epsilon }_1,\cdots ,{\epsilon }_k)$ is β-admissible for all $k\ge 1$. Denote by ${\Sigma }_{\beta }^n$ the set of all β-admissible sequences with length n and ${\Sigma }_{\beta }$ the set of all infinite β-admissible sequences.

We endow ${\mathcal{A}}_{\beta }^{\mathbb{N}}$ with the product topology and the shift operator

$$\sigma :({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n\cdots )\to ({\epsilon }_2,{\epsilon }_3,\cdots ,{\epsilon }_{n+1}\cdots ).$$

The closure of ${\Sigma }_{\beta }$ under the product topology in ${\mathcal{A}}_{\beta }^{\mathbb{N}}$ is called the $\beta$-shift $S_{\beta }$. The lexicographical order ${<}_{\mathrm{lex}}$ on ${\mathcal{A}}_{\beta }^{\mathbb{N}}$ is defined as follows: for $\epsilon ,{\epsilon }^{\prime }\in {\mathcal{A}}_{\beta }^{\mathbb{N}}$, $\epsilon {<}_{\mathrm{lex}}{\epsilon }^{\prime }$ if, and only if, there exists $k\ge 1$ such that ${\epsilon }_j={\epsilon }_j^{\prime }$ for all $1\le j<k$ and ${\epsilon }_k<{\epsilon }_k^{\prime }$. And $\epsilon {\le }_{\mathrm{lex}}{\epsilon }^{\prime }$ means $\epsilon {<}_{\mathrm{lex}}{\epsilon }^{\prime }$ or $\epsilon ={\epsilon }^{\prime }$. This lexicographical order can be extended to finite sequences by identifying $({\epsilon }_1,\cdots ,{\epsilon }_n)$ with the infinite sequence $({\epsilon }_1,\cdots ,{\epsilon }_n,0,0,\cdots )$.

The $\beta$-expansion of 1 is crucial in characterizing ${\Sigma }_{\beta }$ and $S_{\beta }$; this is called Parry’s criterion [9]. If $\epsilon (1,\beta )$ is finite, that is, $\epsilon (1,\beta )=({\epsilon }_1(1,\beta ),\cdots ,{\epsilon }_m(1,\beta ))$, then $\beta$ is called a Parry number. In such a case, we put

$${\epsilon }^{*}(1,\beta )={({\epsilon }_1(1,\beta ),\cdots ,{\epsilon }_{m-1}(1,\beta ),{\epsilon }_m(1,\beta )-1)}^{\infty },$$

where ${\omega }^{\infty }$ denotes the periodic sequence $(\omega ,\omega ,\cdots )$. If $\beta$ is not a Parry number, we also denote the $\beta$-expansion of 1 by ${\epsilon }^{*}(1,\beta )=({\epsilon }_1^{*}(1,\beta ),{\epsilon }_2^{*}(1,\beta ),\cdots )$.

Theorem 5

(Parry [9]). Let $\beta >1$ and $\epsilon \in {\mathcal{A}}_{\beta }^{\mathbb{N}}$, then

(1) $\epsilon \in {\Sigma }_{\beta }$ if, and only if, ${\sigma }^k\epsilon {\le }_{\mathrm{lex}}({\epsilon }_1^{*}(1,\beta ),{\epsilon }_2^{*}(1,\beta ),\cdots ),\forall k\ge 0$;

(2) the sequence $({\epsilon }_1^{*}(1,\beta ),{\epsilon }_2^{*}(1,\beta ),\cdots )$ of the β-expansion of 1 is monotone with respect to β. Therefore, for any $1<{\beta }_1<{\beta }_2$, we have ${\Sigma }_{{\beta }_1}\subset {\Sigma }_{{\beta }_2}$ and ${\Sigma }_{{\beta }_1}^n\subset {\Sigma }_{{\beta }_2}^n$.

Rényi [8] showed that

$${\beta }^n\le \#{\Sigma }_{\beta }^n\le {\displaystyle \frac{{\beta }^{n+1}}{\beta -1}},\forall n\ge 1,$$

where # denotes the cardinality of a finite set. Thus, the topological entropy of $\left([0,1],T_{\beta }\right)$ is equal to $log\beta$. Moreover, there exists a unique $T_{\beta }$-invariant measure ${\nu }_{\beta }$ equivalent to the Lebesgue measure, that is, the Parry measure [9], whose density function is given by $d{\nu }_{\beta }={\sum }_{k:T_{\beta }^{k}1\ge x}{\beta }^{-n}dx$.

For any $\beta$-admissible sequence $({\epsilon }_1,\cdots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n$, the set

$$I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right):=\left\{x\in [0,1):{\epsilon }_k(x,\beta )={\epsilon }_k,1\le k\le n\right\}$$

is called a n-th basic interval with respect to base $\beta$. We use $I_{n,\beta }\left(x\right)$ to denote the n-th basic interval containing x (with respect to base $\beta$).

By the algorithm of $\beta$-expansion, any n-th basic interval is an interval whose length is less than ${\beta }^{-n}$. We call $I_{n,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n)$ a full interval if the image of it under the iteration $T_{\beta }^n$ is the unit interval $[0,1]$. Clearly, the length of a n-th full interval with respect to base $\beta$ is ${\beta }^{-n}$. When $\beta \notin \mathbb{N}$, not every basic interval is full. Indeed, the existence of a non-full interval is the main obstacle to determining the metric properties of general $\beta$-expansions (see [20,21]).

For $\beta >1$ and $n\ge 0$, let

$$l_n\left(\beta \right):=sup\{k\ge 0:{\epsilon }_{n+j}^{*}(1,\beta )=0\mathrm{for}\mathrm{all}1\le j\le k\},$$

that is, the maximal length of the string of 0’s following ${\epsilon }_n^{*}(1,\beta )$. The following criterion of full intervals is useful.

Proposition 1

(see [20,21]). For $n\ge 1$, let $\epsilon \in {\Sigma }_{\beta }^n$, then

(1) the basic interval $I_{n+l_n\left(\beta \right)+1,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n,0^{l_n\left(\beta \right)+1})$ is full;

(2) if $I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)$ is full, then $I_{n+k,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n,0^k)$ is full for any $k\ge 1$;

(3) if $I_{n,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n)$, then for any ${\epsilon }^{\prime }\in {\Sigma }_{\beta }^m$, we have

$$|I_{n+m,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n,{\epsilon }_1^{\prime },\cdots ,{\epsilon }_m^{\prime })|={\beta }^{-n}|I_{m,\beta }({\epsilon }_1^{\prime },\cdots ,{\epsilon }_m^{\prime })|.$$

Remark 1

(see [21]). Let $\beta >1$ be a Parry number; then, there exists $N>0$ such that $I_{n+N,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n,0^N)$ is full for any $({\epsilon }_1,\cdots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n$.

2.2. Approximation from Below

To obtain the dimensional results in general $\beta$-expansions, it is useful to apply an approximation method from below for $\beta$-shifts (see [5,15] and references therein for more details). We first define the projection ${\pi }_{\beta }$ from ${\Sigma }_{\beta }$ to $[0,1]$ by

$${\pi }_{\beta }\left(\epsilon \right)=\sum _{k=1}^{\infty }{\displaystyle \frac{{\epsilon }_k}{{\beta }^k}},\forall \epsilon \in {\Sigma }_{\beta }.$$

It is well known that ${\pi }_{\beta }$ is Lipschitz, i.e., $|{\pi }_{\beta }\left(\epsilon \right)-{\pi }_{\beta }\left({\epsilon }^{\prime }\right)|\le d(\epsilon ,{\epsilon }^{\prime })$ for any $\epsilon ,{\epsilon }^{\prime }\in {\Sigma }_{\beta }$, where d is the metric on ${\Sigma }_{\beta }$ defined by $d(\epsilon ,{\epsilon }^{\prime })={\beta }^{-min\left\{k\ge 0:{\epsilon }_{k+1}\ne {\epsilon }_{k+1}^{\prime }\right\}}$.

Let $1<{\beta }^{\prime }<\beta$, since ${\Sigma }_{\beta }^{\prime }\subset {\Sigma }_{\beta }$, we know that $G_{\beta }^{{\beta }^{\prime }}:={\pi }_{\beta }\left({\Sigma }_{{\beta }^{\prime }}\right)$ is a Cantor subset of ${\pi }_{\beta }\left({\Sigma }_{\beta }\right)=[0,1]$. Define the function $g:G_{\beta }^{{\beta }^{\prime }}\to [0,1]$ by $g\left(x\right)={\pi }_{{\beta }^{\prime }}\left(\epsilon (x,\beta )\right)$.

Proposition 2

(see [22]). (1) For any $x\in G_{\beta }^{{\beta }^{\prime }}$, we have $\epsilon (g\left(x\right),{\beta }^{\prime })=\epsilon (x,\beta )$.

(2) The function g is bijective, strictly increasing and continuous on $G_{\beta }^{{\beta }^{\prime }}$.

(3) If ${\beta }^{\prime }$ be a Parry number, write $N=max\{l_n\left({\beta }^{\prime }\right):n\ge 1\}$; then, g is Hölder continuous on $G_{\beta }^{{\beta }^{\prime }}$. Moreover,

$$|g\left(x\right)-g\left(y\right)|\le 2{\beta }^{\prime N+1}{|x-y|}^{{\displaystyle \frac{log{\beta }^{\prime }}{log\beta }}},\forall x,y\in G_{\beta }^{{\beta }^{\prime }}.$$

Now, we shall construct a sequence of Parry numbers ${\beta }_k$ approximating $\beta$ from below. Recall that the $\beta$-expansion of 1 is ${\epsilon }^{*}(1,\beta )=({\epsilon }_1^{*}(1,\beta ),{\epsilon }_2^{*}(1,\beta ),\cdots )$. For each $k\in \mathbb{N}$ with ${\epsilon }_k^{*}(1,\beta )\ge 1$, define ${\beta }_k$ to be the unique positive solution of the equation

$$1={\displaystyle \frac{{\epsilon }_1^{*}(1,\beta )}{{\beta }_k}}+{\displaystyle \frac{{\epsilon }_2^{*}(1,\beta )}{{\beta }_k^2}}+\cdots +{\displaystyle \frac{{\epsilon }_k^{*}(1,\beta )}{{\beta }_k^k}}.$$

Clearly, ${\beta }_k$ is strictly increasing and ${lim}_{k\to \infty }{\beta }_k=\beta$. Thus, ${\Sigma }_{{\beta }_k}$ increases to ${\Sigma }_{\beta }$.

By the criterion of full intervals (Proposition 1), we have

Proposition 3

(see [11]). For any $\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\in {\sum }_{{\beta }_k}^n$, the basic interval $I_{n+k,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n,0^k)$ is full. Thus,

$${\displaystyle \frac{1}{{\beta }^{n+k}}}\le \left|I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right|\le {\displaystyle \frac{1}{{\beta }^n}}.$$

2.3. Auxiliary Results

Let $S_n(x,\beta )={\sum }_{k=1}^n{\epsilon }_k(x,\beta )$ denote the sum of the first n digits in the $\beta$-expansion of $x\in [0,1]$. We are concerned with the asymptotic properties of ${\displaystyle \frac{1}{n}}{S}_n(x,\beta )$. Set

$$\Lambda \left(\beta \right)=\underset{x\in [0,1]}{sup}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{S_n(x,\beta )}{n}}.$$

As a consequence of the Birkhoff ergodic theorem, for every $\alpha \in [0,\Lambda (\beta \left)\right]$, there exists $x\in [0,1]$ such that ${lim}_{n\to \infty }{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha$. Moreover, by Parry’s criterion (Theorem 5), $\Lambda \left(\beta \right)$ is determined by the $\beta$-expansion of 1. In particular, when $\beta$ is a Parry number, that is, ${\epsilon }^{*}(1,\beta )={({\epsilon }_1(1,\beta ),\cdots ,{\epsilon }_{m-1}(1,\beta ),{\epsilon }_m(1,\beta )-1)}^{\infty }$, then,

$$\Lambda \left(\beta \right)={\displaystyle \frac{{\sum }_{j=1}^m{\epsilon }_j(1,\beta )-1}{m}}.$$

Let $0\le \alpha \le \Lambda \left(\beta \right),n\in \mathbb{N}$ and $\delta >0$, denote

$$H^{\beta }(\alpha ,n,\delta )=\left\{({\epsilon }_1,\cdots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n:\alpha -\delta <{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\epsilon }_i<\alpha +\delta \right\}.$$

(9)

and

$$h^{\beta }(\alpha ,n,\delta )=\#H^{\beta }(\alpha ,n,\delta ).$$

The following dimensional quantity was introduced in [11] (see also [15]), and was used to estimate the Hausdorff dimension of level sets related to the Birkhoff average.

$$h^{\beta }\left(\alpha \right):=\underset{\delta \to 0}{lim}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{log{h}^{\beta }(\alpha ,n,\delta )}{nlog\beta }},$$

(10)

In general, we do not know the explicit formulas of $h^{\beta }\left(\alpha \right)$ except for some special $\beta$. The next two examples are borrowed from [15]; we include them for the readers’ convenience.

Example 3.

When $\beta =2$, it is easy to see that $\Lambda \left(2\right)=1$.

$$h^{\beta }(\alpha ,n,\delta )=\sum _{j=\left[n\right(\alpha -\delta \left)\right]+1}^{\left[n\right(\alpha +\delta \left)\right]}{C}_j^n,$$

where $C_j^n$ denotes the binomial coefficient “n choose j”, by Stirling’s formula,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{log{C}_j^n}{nlog2}}={\displaystyle \frac{-\alpha log\alpha -(1-\alpha )log(1-\alpha )}{log2}},$$

where $j=\left[n\right(\alpha -\delta \left)\right]+1,\dots ,\left[n\right(\alpha +\delta \left)\right]$. Hence,

$$\begin{array}{cc}\hfill h^2\left(\alpha \right)& =\underset{\delta \to 0}{lim}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{log{\sum }_{j=\left[n\right(\alpha -\delta \left)\right]+1}^{\left[n\right(\alpha +\delta \left)\right]}{C}_j^n}{nlog2}}\hfill \\ & ={\displaystyle \frac{-\alpha log\alpha -(1-\alpha )log(1-\alpha )}{log2}},\forall \alpha \in [0,1].\hfill \end{array}$$

Example 4.

When $\beta >1$ is the root of the equation ${\beta }^2-\beta -1=0$, we have $\epsilon (1,\beta )={\left(10\right)}^{\infty }$; hence, $\Lambda \left(\beta \right)=1/2$. In this case,

$$h^{\beta }(\alpha ,n,\delta )=\sum _{j=\left[n\right(\alpha -\delta \left)\right]+1}^{\left[n\right(\alpha +\delta \left)\right]}{C}_j^{n-j-2},$$

by Stirling’s formula,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{log{C}_{j-2}^{n-j-2}}{nlog\beta }}={\displaystyle \frac{-\alpha log\alpha +(1-\alpha )log(1-\alpha )-(1-2\alpha )log(1-2\alpha )}{log\beta }},$$

where $j=\left[n\right(\alpha -\delta \left)\right]+1,\dots ,\left[n\right(\alpha +\delta \left)\right]$. Hence,

$$h^{\beta }\left(\alpha \right)={\displaystyle \frac{-\alpha log\alpha +(1-\alpha )log(1-\alpha )-(1-2\alpha )log(1-2\alpha )}{log\beta }}\forall \alpha \in [0,1/2].$$

Figure 1 and Figure 2 are the graphs of $h^{\beta }\left(\alpha \right)$ for $\beta =2$ and $\beta =={\displaystyle \frac{1+\sqrt{5}}{2}}$ respectively.

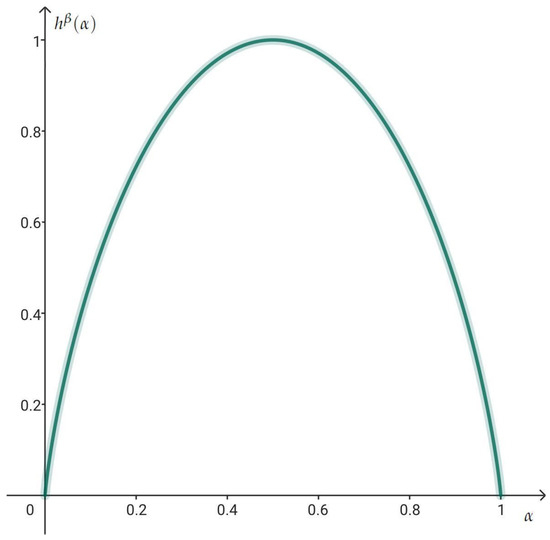
Figure 1. The graph of $h^{\beta }\left(\alpha \right)$ for $\beta =2$.

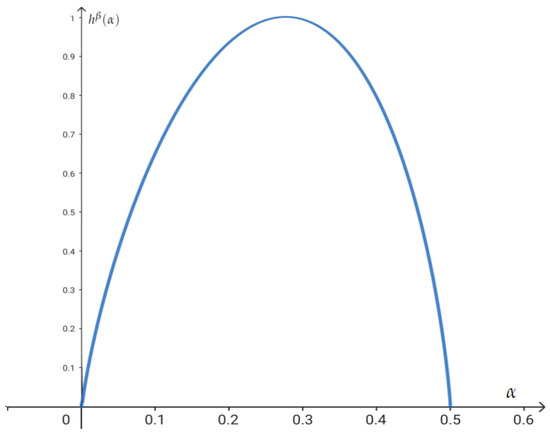
Figure 2. The graph of $h^{\beta }\left(\alpha \right)$ for $\beta ={\displaystyle \frac{1+\sqrt{5}}{2}}$.

Lemma 1

(see [15]). Let β be a Parry number; then, the function $h^{\beta }\left(\alpha \right)$ is concave and continuous on the interval $(0,\Lambda (\beta \left)\right)$.

The following mass distribution principle is useful in obtaining the lower bound of the Hausdorff dimension.

Proposition 4

(see [23]). Let F be a Borel set in ${\mathbb{R}}^n$ and μ be a Borel measure in ${\mathbb{R}}^n$ with $\mu \left(F\right)>0$. If for any $x\in F$, we have

$$\underset{r\to \infty }{lim\; inf}{\displaystyle \frac{log\mu \left(B\right(x,r\left)\right)}{logr}}\ge s,$$

then ${dim}_{\mathrm{H}}F\ge s$.

3. Proofs of the Main Results

3.1. Proof of Theorem 3

It suffices to consider the case when $a<\infty$; otherwise it follows directly from Theorem 2. We first show Theorem 3 for Parry numbers; the desired result for general $\beta >1$ follows by applying the approximation methods described in Section 2.2.

• Upper bound.

The upper bound is obtained by considering the natural coverings. For $\alpha \in [0,\Lambda (\beta \left)\right]$, denote

$$E_{\alpha }=\left\{x\in [0,1):\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha \right\}$$

and

$$E^{\alpha }=\left\{x\in [0,1):\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha \right\}.$$

For any $\delta >0$ and $0\le \alpha \le \Lambda \left(\beta \right)$, let $\epsilon =({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n)\in H^{\beta }(\alpha ,n,\delta )$, and define the n-th order basic interval

$$I_n\left(\epsilon \right):=\{x\in [0,1):x_1\left(x\right)={\epsilon }_1,\dots ,x_n\left(x\right)={\epsilon }_n\}.$$

It follows that

$$\begin{array}{cc}& \left\{x\in [0,1):\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha \right\}\hfill \\ & =\left\{x\in [0,1):\begin{array}{cc}& \forall \delta >0,\exists N>0s.t.\forall n\ge N,{\displaystyle \frac{1}{n}}{S}_n(x,\beta )>\alpha -\delta ,\hfill \\ & \mathrm{and}\exists i.m.n\mathrm{such}\mathrm{that}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )<\alpha +\delta \hfill \end{array}\right\}\hfill \\ & =\bigcap _{\delta >0}\bigcap _{N=1}^{\infty }\bigcup _{n=N}^{\infty }\left\{x\in [0,1):\alpha -\delta <{\displaystyle \frac{1}{n}}{S}_n(x,\beta )<\alpha +\delta \right\},\hfill \end{array}$$

we can obtain

$$E_{\alpha }=\bigcap _{\delta >0}\bigcap _{N=1}^{\infty }\bigcup _{n=N}^{\infty }\bigcup _{\epsilon \in H^{\beta }(\alpha ,n,\delta )}{I}_n\left(\epsilon \right),$$

where “i.m.” stands for “infinitely many”. Similarly, we can obtain

$$E^{\alpha }=\bigcap _{\delta >0}\bigcap _{N=1}^{\infty }\bigcup _{n=N}^{\infty }\bigcup _{\epsilon \in H^{\beta }(\alpha ,n,\delta )}{I}_n\left(\epsilon \right).$$

For any $\epsilon =({\epsilon }_1,\cdots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n$, set

$$J_{n,\beta }\left(\epsilon \right):=\left\{x\in I_{n,\beta }\left(\epsilon \right):|T_{\beta }^{n}x-x|<\psi \left(n\right)\right\},$$

where $\psi \left(n\right)$ is a positive real-valued function. Define

$$E_{\alpha }\left(\psi \right)=\left\{x\in [0,1]:\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha \right\}\cap R_{\beta }\left(\psi \right)$$

and

$$E^{\alpha }\left(\psi \right)=\left\{x\in [0,1]:\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\alpha \right\}\cap R_{\beta }\left(\psi \right).$$

For any $\epsilon =({\epsilon }_1,\cdots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n$, set

$$J_{n,\beta }\left(\epsilon \right):=\left\{x\in I_{n,\beta }\left(\epsilon \right):|T_{\beta }^{n}x-x|<\psi \left(n\right)\right\}.$$

Clearly, for any $\delta >0$,

$$E_{\alpha }\left(\psi \right),E^{\alpha }\left(\psi \right)\subset \bigcap _{N\ge 1}\bigcup _{n\ge N}\bigcup _{\epsilon \in H^{\beta }(\alpha ,n,\delta )}{J}_{n,\beta }\left(\epsilon \right).$$

(11)

Now, we bound the length of $J_{n,\beta }\left(\epsilon \right)$ from above. For each $x\in J_{n,\beta }\left(\epsilon \right)$, we have

$$x={\displaystyle \frac{{\epsilon }_1}{\beta }}+{\displaystyle \frac{{\epsilon }_2}{{\beta }^2}}+\cdots +{\displaystyle \frac{{\epsilon }_n+T_{\beta }^{n}x}{{\beta }^n}}$$

and

$$|T_{\beta }^{n}x-x|=|{\displaystyle \frac{{\epsilon }_1}{\beta }}+{\displaystyle \frac{{\epsilon }_2}{{\beta }^2}}+\cdots +{\displaystyle \frac{{\epsilon }_n+T_{\beta }^{n}x}{{\beta }^n}}-T_{\beta }^{n}x|<\psi \left(n\right).$$

Thus, for any $x_1,x_2\in J_{n,\beta }\left(\epsilon \right)$, we have $|T_{\beta }^n{x}_1-T_{\beta }^n{x}_2| ={\beta }^n|x_1-x_2|$ and

$$|T_{\beta }^n{x}_1-T_{\beta }^n{x}_2| - |x_1-x_2| \le |T_{\beta }^n{x}_1-x_1| + |T_{\beta }^n{x}_2-x_2| \le 2\psi \left(n\right).$$

Therefore,

$$|J_{n,\beta }\left(\epsilon \right)|\le {\displaystyle \frac{2\psi \left(n\right)}{{\beta }^n-1}}\le {\displaystyle \frac{4\psi \left(n\right)}{{\beta }^n}}.$$

By the definition of $h^{\beta }\left(\alpha \right)$ and a, for arbitrarily small $\eta >0$, there exists $\delta >0$ and $N\in \mathbb{N}$ such that for all $n\ge N$,

$$h^{\beta }(n,\alpha ,\delta )<{\beta }^{n(h^{\beta }\left(\alpha \right)+\eta )}\mathrm{and}\psi \left(n\right)\le {\beta }^{-n(a-\eta )}.$$

Put $s={\displaystyle \frac{h^{\beta }\left(\alpha \right)+2\eta }{1+a-\eta }}$, by (11), we have

$$\begin{array}{cc}\hfill {\mathcal{H}}^s\left(E^{\alpha }\left(\psi \right)\right)& \le \underset{N\to \infty }{lim\; inf}\sum _{n=N}^{\infty }\sum _{\epsilon \in H^{\beta }(\alpha ,n,\delta )}{\left|J_{n,\beta }\left(\epsilon \right)\right|}^s\hfill \\ \hfill & \le \underset{N\to \infty }{lim\; inf}\sum _{n=N}^{\infty }{\beta }^{n(h^{\beta }\left(\alpha \right)+\eta )}{\left(4{\beta }^{-n(a+1-\eta )}\right)}^s\hfill \\ \hfill & \le \underset{N\to \infty }{lim}\sum _{n=N}^{\infty }{4}^s{\beta }^{-n\eta }<\infty .\hfill \end{array}$$

As a result,

$${dim}_{\mathrm{H}}{E}^{\alpha }\left(\psi \right)\le {\displaystyle \frac{h^{\beta }\left(\alpha \right)+2\eta }{1+a-\eta }}.$$

Since $\eta$ is arbitrarily small, we have ${dim}_{\mathrm{H}}{E}^{\alpha }\left(\psi \right)\le {\displaystyle \frac{h^{\beta }\left(\alpha \right)}{1+a}}$. Similarly, ${dim}_{\mathrm{H}}{E}_{\alpha }\left(\psi \right)\le {\displaystyle \frac{h^{\beta }\left(\alpha \right)}{1+a}}$. Observe that $E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)=E^{{\alpha }_2}\left(\psi \right)\cap E_{{\alpha }_1}\left(\psi \right)$; we conclude that

$${dim}_{\mathrm{H}}{E}_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\le {\displaystyle \frac{min\{h^{\beta }\left({\alpha }_1\right),h^{\beta }\left({\alpha }_2\right)\}}{1+a}}.$$

• Lower bound.

We first suppose that $\beta >1$ is a Parry number. By Remark 1, there exists $N>0$ such that $I_{n+N,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n,0^N)$ is full for any $({\epsilon }_1,\cdots ,{\epsilon }_n)\in {\Sigma }_{\beta }^n$. In the sequel, we fix such a N. For $0\le \alpha \le \Lambda \left(\beta \right),\delta >0$ and $n>N$, define

$$H_N^{\beta }(\alpha ,n,\delta )=\left\{({\epsilon }_1,\cdots ,{\epsilon }_{n-N},0^N):({\epsilon }_1,\cdots ,{\epsilon }_{n-N})\in {\Sigma }_{\beta }^{n-N}\mathrm{and}\alpha -\delta <{\displaystyle \frac{1}{n}}\sum _{i=1}^{n-N}{\epsilon }_i<\alpha +\delta \right\}$$

and

$$h_N^{\beta }(\alpha ,n,\delta )=\#H_N^{\beta }(\alpha ,n,\delta ).$$

Lemma 2.

For fixed $N>0$, we have

$$h^{\beta }\left(\alpha \right)=\underset{\delta \to 0}{lim}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{log{h}_N^{\beta }(\alpha ,n,\delta )}{nlog\beta }}.$$

(12)

Proof. 

Evidently, $H_N^{\beta }(\alpha ,n,\delta )\subseteq H^{\beta }(\alpha ,n,\delta )$. Hence,

$$h_N^{\beta }(\alpha ,n,\delta )\le h^{\beta }(\alpha ,n,\delta )$$

(13)

For sufficiently small $\delta >0$ and large $n>N$, we shall show

$$h_N^{\beta }(\alpha ,n,2\delta )\ge h^{\beta }(\alpha ,n-N,\delta ).$$

(14)

To prove this, it suffices to show that, for each $({\epsilon }_1,\cdots ,{\epsilon }_{n-N})$ in $H^{\beta }(\alpha ,n-N,\delta )$, we have $({\epsilon }_1,\cdots ,{\epsilon }_{n-N},0^N)\in H_N^{\beta }(\alpha ,n,2\delta )$. Indeed,

$$(n-N)(\alpha -\delta )<\sum _{i=1}^{n-N}{\epsilon }_i<(n-N)(\alpha +\delta ),$$

Dividing both sides by n gives

$${\displaystyle \frac{n-N}{n}}(\alpha -\delta )<{\displaystyle \frac{1}{n}}\sum _{i=1}^{n-N}{\epsilon }_i<{\displaystyle \frac{n-N}{n}}(\alpha +\delta ).$$

For sufficiently small $\delta >0$ and large $n>N$, we obtain

$$\alpha -2\delta <{\displaystyle \frac{1}{n}}\sum _{i=1}^{n-N}{\epsilon }_i<\alpha +2\delta .$$

This proves (14). Since N is fixed, (13) and (14) together with the definition of $h^{\beta }\left(\alpha \right)$ yield (12). □

Let $\beta >1$ be a Parry number, and let N be the fixed constant as above. By Lemma 2, for any $\eta >0$, there exist $\delta >0$ and $M_0\in \mathbb{N}$ such that for all $n\ge M_0$, we have

$$h_N^{\beta }(\alpha ,n,\delta )\ge n(1-\eta )h^{\beta }\left(\alpha \right)log\beta .$$

(15)

For each $k\ge 1$, let $M_k=M_0+k$. We take a sufficiently sparse sequence ${\left\{n_k\right\}}_{k\ge 1}$ such that

$$\underset{k\to \infty }{lim}{\displaystyle \frac{-{log}_{\beta }\psi \left(n_k\right)}{n_k}}=\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{-{log}_{\beta }\psi \left(n\right)}{n}}.$$

(16)

We shall construct a Cantor subset of $E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)$, among which the point x will realize the event $|T_{\beta }^{n}x-x|<\psi \left(n\right)$ infinitely many times along the sequence ${\left\{n_k\right\}}_{k\ge 1}$.

To begin with, write $n_1=(l_1+1)M_1+c_1,$ where $l_1\ge 1,0\le c_1<M_1$. Let $t_1\in \mathbb{N}$ be such that

$${\beta }^{-t_1}<\psi \left(n_1\right)\le {\beta }^{-t_1+1}.$$

Define $r_1$ to be the rational number satisfying $n_1{r}_1=n_1+t_1$. Now, we choose a sparse subsequence of ${\left\{n_k\right\}}_{k\ge 1}$ recursively in the following way: for each $j\ge 2$, choose $n_j\in {\left\{n_k\right\}}_{k\ge 1}$ such that

$$n_j=n_{j-1}+t_{j-1}+(l_j+1)M_j+c_j+N,$$

where $l_j\ge 1$ and $0\le c_j<M_j$. Define integer $t_j$ and rational number $r_j$, which satisfy

$${\beta }^{-t_j}<\psi \left(n_j\right)\le {\beta }^{-t_j+1}\mathrm{and}{n}_j{r}_j=n_j+t_j.$$

Now, we have obtained a subsequence of ${\left\{n_k\right\}}_{k\ge 1}$, still denoted by ${\left\{n_k\right\}}_{k\ge 1}$, which satisfy

$$\underset{k\to \infty }{lim}{\displaystyle \frac{n_{k-1}+t_{k-1}}{n_k}}=0\mathrm{and}\underset{k\to \infty }{lim}{\displaystyle \frac{M_k}{n_{k-1}+t_{k-1}}}=0.$$

(17)

Now, we are ready to construct a Cantor subset ${\mathbb{F}}_{\infty }\subset E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)$.

• Step 1. Level 1 and 2 of the Cantor subset.

By the definition of $H_N^{\beta }(\alpha ,n,\delta )$, the choice of $n_1$ and $t_1$, and Proposition 1, for any ${\omega }_1^{\left(1\right)},\dots ,{\omega }_{l_1}^{\left(1\right)}\in H_N^{\beta }({\alpha }_1,M_1,\delta )$ and ${\nu }^{\left(1\right)}\in H_N^{\beta }({\alpha }_1,M_1+c_1,\delta )$, we can obtain a full interval

$$I_{n_1+t_1,\beta }\left({\left({\omega }_1^{\left(1\right)},\cdots ,{\omega }_{l_1}^{\left(1\right)},{\nu }^{\left(1\right)}\right)}^{r_1}\right).$$

Then, we define the first level of the Cantor set as

$${\mathbb{F}}_1=\bigcup I_{n_1+t_1,\beta }\left({\left({\omega }_1^{\left(1\right)},\dots ,{\omega }_{l_1}^{\left(1\right)},{\nu }^{\left(1\right)}\right)}^{r_1}\right),$$

where the union is taken over all finite sequences ${\omega }_i^{\left(1\right)}\in H_N^{\beta }({\alpha }_1,M_1,\delta )$ for each $1\le i\le l_1$, and over all finite sequences ${\nu }^{\left(1\right)}\in H_N^{\beta }({\alpha }_1,M_1+c_1,\delta )$.

By construction, for all basic intervals $I_{n_1+t_1,\beta }$ in ${\mathbb{F}}_1$, both $T_{\beta }^{n_1}x$ and x are in $I_{n_1+t_{1,\beta }}$. Thus, the first $t_1$-digits in their $\beta$-expansions are the same, which implies

$$|T_{\beta }^{n_1}x-x|\le {\beta }^{-t_1}<\psi \left(n_1\right).$$

For each basic interval $J_1$ in ${\mathbb{F}}_1$, we will construct a subset of $J_1$, denoted by ${\mathbb{F}}_2\left(J_1\right)$. Note that each $J_1\in {\mathbb{F}}_1$ has the form $I_{n_1+t_1,\beta }\left({\left({\omega }_1^{\left(1\right)},{\omega }_2^{\left(1\right)},\dots ,{\omega }_{l_1}^{\left(1\right)},{\nu }^{\left(1\right)}\right)}^{r_1}\right)$; define

$${\mathbb{F}}_2\left(J_1\right)=\bigcup I_{n_2+t_2,\beta }\left({\left({\left({\omega }_1^{\left(1\right)},{\omega }_2^{\left(1\right)},\cdots ,{\omega }_{l_1}^{\left(1\right)},{\nu }^{\left(1\right)}\right)}^{r_1},0^N,{\omega }_1^{\left(2\right)},{\omega }_2^{\left(2\right)},\cdots ,{\omega }_{l_2}^{\left(2\right)},{\nu }^{\left(2\right)}\right)}^{r_2}\right),$$

where the union is taken over all finite sequences ${\omega }_i^{\left(2\right)}\in H_N^{\beta }({\alpha }_2,M_2,\delta )$ for each $1\le i\le l_2$, and over all finite sequences ${\nu }^{\left(2\right)}\in H_N^{\beta }({\alpha }_2,M_2+c_2,\delta )$. Let

$${\mathbb{F}}_2=\bigcup _{J_1\in {\mathbb{F}}_1}{\mathbb{F}}_2\left(J_1\right).$$

By construction, for all basic intervals $I_{n_2+t_2,\beta }$ in ${\mathbb{F}}_2$, both $T_{\beta }^{n_2}x$ and x are in $I_{n_2+t_{2,\beta }}$. Thus, the first $t_2$-digits in their $\beta$-expansions are the same, which implies

$$|T_{\beta }^{n_2}x-x|\le {\beta }^{-t_2}<\psi \left(n_2\right).$$

• Step 2. Inductions

Assume that the k-level ${\mathbb{F}}_k$ has been constructed. Note that each element $J_k$ of ${\mathbb{F}}_k$ is a $n_k+t_k$-th basic interval, which has the form

$$J_k=I_{n_k+t_k,\beta }\left({\left({\zeta }^{(k-1)},0^N,{\omega }_1^{\left(k\right)},{\omega }_2^{\left(k\right)},\cdots ,{\omega }_{l_k}^{\left(k\right)},{\nu }^{\left(k\right)}\right)}^{r_k}\right),$$

where ${\zeta }^{\left(0\right)}$ stands for the empty word; if k is odd, then ${\omega }_i^{\left(k\right)}\in H_N^{\beta }({\alpha }_1,M_k,\delta )$ for each $1\le i\le l_k$, and ${\nu }^{\left(k\right)}\in H_N^{\beta }({\alpha }_1,M_k+c_k,\delta )$; otherwise, we take ${\omega }_i^{\left(k\right)}\in H_N^{\beta }({\alpha }_2,M_k,\delta )$ for each $1\le i\le l_k$, and ${\nu }^{\left(k\right)}\in H_N^{\beta }({\alpha }_2,M_k+c_k,\delta )$. For each $J_k\in {\mathbb{F}}_k$, define

$${\mathbb{F}}_{k+1}\left(J_k\right)=\bigcup I_{n_{k+1}+t_{k+1},\beta }\left({\left({\zeta }^{\left(k\right)},0^N,{\omega }_1^{(k+1)},{\omega }_2^{(k+1)},\cdots ,{\omega }_{l_1}^{(k+1)},{\nu }^{(k+1)}\right)}^{k_{k+1}}\right)$$

where the choice of the finite sequences in the union depends on k: if k is even, then ${\omega }_i^{(k+1)}\in H_N^{\beta }({\alpha }_1,M_{k+1},\delta )$ for each $1\le i\le l_{k+1}$, and ${\nu }^{(k+1)}\in H_N^{\beta }({\alpha }_1,M_{k+1}+c_{k+1},\delta )$; otherwise, we take ${\omega }_i^{(k+1)}\in H_N^{\beta }({\alpha }_2,M_{k+1},\delta )$ for each $1\le i\le l_{k+1}$, and ${\nu }^{(k+1)}\in H_N^{\beta }({\alpha }_2,M_{k+1}+c_{k+1},\delta )$.

Notice that the common prefix corresponding to the set of basic intervals in ${\mathbb{F}}_{k+1}$ is ${\zeta }^{\left(k\right)}$, which means that ${\mathbb{F}}_{k+1}$ is a subset of ${\mathbb{F}}_k$. By construction, for any basic interval $I_{n_k+t_k,\beta }\in {\mathbb{F}}_k$ and any $x\in I_{n_k+t_k,\beta }$, $T^{n_k}x$ and x share the first $t_k$ digits in their $\beta$-expansions. As a result,

$$|T_{\beta }^{n_k}x-x|\le {\beta }^{-t_k}<\psi \left(n_k\right).$$

Repeating the above steps, we obtain a nested sequence ${\left\{{\mathbb{F}}_k\right\}}_{k\ge 1}$, each of which is the union of some basic intervals. The Cantor subset is defined as

$${\mathbb{F}}_{\infty }=\bigcap _{k=1}^{\infty }{\mathbb{F}}_k.$$

• Step 3. ${\mathbb{F}}_{\infty }\subset E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)$.

It is easy to see that ${\mathbb{F}}_{\infty }\subset R_{\beta }\left(\psi \right)$. Now, we shall prove that, for any $x\in {\mathbb{F}}_{\infty }$,

$$\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_1\mathrm{and}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_2.$$

(18)

From the choice of ${\left\{n_k\right\}}_{k\ge 1}$, and noting that

$$n_{k-1}=o\left(n_k\right),M_k\to \infty ,M_k=o\left(n_k\right)\mathrm{and}{l}_k=o\left(n_k\right),$$

it is plausible that the desired result in (18) holds. Now, we check it in detail. By construction, each $x\in {\mathbb{F}}_{\infty }$ can be expressed as

$$x=\left({\left({\zeta }^{(k-2)},0^N,{\omega }_1^{(k-1)},\cdots ,{\omega }_{l_{k-1}}^{(k-1)},{\nu }^{(k-1)}\right)}^{r_{k-1}},0^N,{\omega }_1^{\left(k\right)},\cdots ,{\omega }_{l_k}^{\left(k\right)},{\nu }^{\left(k\right)},\cdots \right).$$

We only discuss the case when k is even; the case when k is odd is similar. By the definition of $H_N^{\beta }(\alpha ,n,\delta )$, we have

$$\begin{array}{cc}\hfill S_{n_{k-1}}(x,\beta )& \le |{\zeta }^{(k-2)}|\beta +l_{k-1}\left(M_{k-1}-N\right)({\alpha }_1+\delta )+\left(M_{k-1}+c_{k-1}-N\right)({\alpha }_1+\delta )\hfill \\ \hfill & \le (n_{k-2}+t_{k-2})\beta +l_{k-1}{M}_{k-1}({\alpha }_1+\delta )+\left(M_{k-1}+c_{k-1}\right)({\alpha }_1+\delta )\hfill \\ \hfill & \le n_{k-1}({\alpha }_1+\delta )+o\left(n_{k-1}\right).\hfill \end{array}$$

(19)

On the other hand, by the selection of $\left\{n_k\right\}$, we have $l_{k-1}{M}_{k-1}({\alpha }_1-\delta )+o\left(n_{k-1}\right)=n_{k-1}({\alpha }_1-\delta )+o\left(n_{k-1}\right)$. Thus,

$$\begin{array}{cc}\hfill S_{n_{k-1}}(x,\beta )& \ge l_{k-1}(M_{k-1}-N)({\alpha }_1-\delta )+\left(M_{k-1}+c_{k-1}-N\right)({\alpha }_1-\delta )\hfill \\ \hfill & \ge n_{k-1}({\alpha }_1-\delta )+o\left(n_{k-1}\right).\hfill \end{array}$$

(20)

Combining (19) and (20), we arrive at

$$\underset{k\to \infty }{lim}{\displaystyle \frac{1}{n_{k-1}}}{S}_{n_{k-1}}(x,\beta )={\alpha }_1.$$

Similarly, we can show

$$\underset{k\to \infty }{lim}{\displaystyle \frac{1}{n_k}}{S}_{n_k}(x,\beta )={\alpha }_2.$$

For a general integer n, if there exists k even such at $n_{k-1}+t_{k-1}\le n<n_k+t_k$, then

• Case 1. $n=n_{k-1}+t_{k-1}$, we write $n=⌊r_{k-1}⌋n_{k-1}+j$.

(1) If $0\le j\le n_{k-2}+t_{k-2}$, by the periodicity of the $\beta$-expansion of x, we have

$$\begin{array}{cc}\hfill S_n(x,\beta )& \le \lfloor r_{k-1}\rfloor S_{n_{k-1}}(x,\beta )+(n_{k-2}+t_{k-2})\beta \hfill \\ \hfill & \le \lfloor r_{k-1}\rfloor (n_{k-1}({\alpha }_1+\delta )+o\left(n_{k-1}\right))+(n_{k-2}+t_{k-2})\beta \hfill \\ \hfill & =n({\alpha }_1+\delta )-j({\alpha }_1+\delta )+o\left(\lfloor r_{k-1}\rfloor n_{k-1}\right)\hfill \\ \hfill & =n({\alpha }_1+\delta )+o\left(\lfloor r_{k-1}\rfloor n_{k-1}\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill S_n(x,\beta )& \ge \lfloor r_{k-1}\rfloor S_{n_{k-1}}(x,\beta )\hfill \\ \hfill & \ge \lfloor r_{k-1}\rfloor (n_{k-1}({\alpha }_1-\delta )+o\left(n_{k-1}\right))\hfill \\ \hfill & =n({\alpha }_1-\delta )-j({\alpha }_1-\delta )+o\left(\lfloor r_{k-1}\rfloor n_{k-1}\right)\hfill \\ \hfill & =n({\alpha }_1-\delta )+o\left(\lfloor r_{k-1}\rfloor n_{k-1}\right).\hfill \end{array}$$

(2) If $j\ge n_{k-2}+t_{k-2}$, then

$$\begin{array}{cc}\hfill S_n(x,\beta )& \le \lfloor r_{k-1}\rfloor S_{n_{k-1}}(x,\beta )+(n_{k-2}+t_{k-2})\beta +\left({\displaystyle \frac{j}{M_{k-1}}}+2\right)(M_{k-1}-N)({\alpha }_1+\delta )\hfill \\ \hfill & \le \lfloor r_{k-1}\rfloor (n_{k-1}({\alpha }_1+\delta )+o\left(n_{k-1}\right))+j({\alpha }_1+\delta )+o\left(n_{k-1}\right)\hfill \\ \hfill & =n({\alpha }_1+\delta )+o\left(\lfloor r_{k-1}\rfloor n_{k-1}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill S_n(x,\beta )& \ge \lfloor r_{k-1}\rfloor S_{n_{k-1}}(x,\beta )+\left({\displaystyle \frac{j-(n_{k-2}+t_{k-2})-N}{M_{k-1}}}-2\right)(M_k-N)({\alpha }_1-\delta )\hfill \\ \hfill & \ge \lfloor r_{k-1}\rfloor (n_{k-1}({\alpha }_1-\delta )+o\left(n_{k-1}\right))+j({\alpha }_2-\delta )-(n_{k-2}+t_{k-2})({\alpha }_2-\delta )\hfill \\ \hfill & -N({\alpha }_2-\delta )-{\displaystyle \frac{Nj}{M_{k-1}}}({\alpha }_1-\delta )\hfill \\ \hfill & =n({\alpha }_1-\delta )+o\left(\lfloor r_{k-1}\rfloor n_{k-1}\right),\hfill \end{array}$$

where the last equality holds since $M_k\to \infty$. Hence,

$$\underset{k\to \infty }{lim}{\displaystyle \frac{1}{n_{k-1}+t_{k-1}}}{S}_{n_{k-1}+t_{k-1}}(x,\beta )={\alpha }_1.$$

(21)

• Case 2. $n_{k-1}+t_{k-1}<n\le n_k$, write $n=n_{k-1}+t_{k-1}+l{M}_k+j+N$, where $l,j\in \mathbb{N}$, $0\le l\le l_k+1$ and $0\le j\le M_k$. From the above calculations, we get

$$\begin{array}{cc}\hfill S_n(x,\beta )& \le S_{n_{k-1}+t_{k-1}}(x,\beta )+l{M}_k({\alpha }_2+\delta )+2M_k\beta \hfill \\ \hfill & \le (n_{k-1}+t_{k-1})({\alpha }_1+\delta )+o(n_{k-1}+t_{k-1})+l{M}_k({\alpha }_2+\delta )+2M_k\beta \hfill \\ \hfill & \le ({\alpha }_2+\delta )+o(n_{k-1}+t_{k-1})\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill S_n(x,\beta )& \ge S_{n_{k-1}+t_{k-1}}(x,\beta )+l(M_k-N)({\alpha }_2-\delta )\hfill \\ \hfill & \ge (n_{k-1}+t_{k-1})({\alpha }_1-\delta )+o(n_{k-1}+t_{k-1})+l{M}_k({\alpha }_1-\delta )+N({\alpha }_1-\delta )\hfill \\ \hfill & +j({\alpha }_1-\delta )-((l+1)N-j)({\alpha }_2-\delta )\hfill \\ \hfill & =n({\alpha }_1-\delta )+o(n_{k-1}+t_{k-1}).\hfill \end{array}$$

Hence, for $n_{k-1}+t_{k-1}<n\le n_k$, we have

$${\alpha }_1\le \underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )\le \underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )\le {\alpha }_2.$$

(22)

• Case 3. $n_k<n<n_k+t_k$, write $n=l{n}_k+j$, where $1\le l\le \lfloor r_k\rfloor ,0\le j<n_k$. We assume that $j\ge n_{k-1}+t_{k-1}$; otherwise, j would be very small and would not affect the limit. We can write $n={ln}_k+n_{k-1}+t_{k-1}+\widehat{l}{M}_k+\widehat{j}$, then,

$$\begin{array}{cc}\hfill S_n(x,\beta )& \le l{S}_{n_k}(x,\beta )+(n_{k-1}+t_{k-1})\beta +\widehat{l}{M}_k({\alpha }_2+\delta )+2M_k\beta \hfill \\ \hfill & \le l(n_k({\alpha }_2+\delta )+o\left(n_k\right))+(n_{k-1}+t_{k-1})\beta +\widehat{l}{M}_k({\alpha }_2+\delta )+2M_k\beta \hfill \\ \hfill & =n({\alpha }_2+\delta )+o\left(l{n}_k\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill S_n(x,\beta )& \ge l{S}_{n_k}(x,\beta )+\widehat{l}(M_k-N)({\alpha }_2-\delta )\hfill \\ \hfill & \ge l(n_k({\alpha }_2-\delta )+o\left(n_k\right))+\widehat{l}(M_k-N)({\alpha }_2-\delta )\hfill \\ \hfill & =n({\alpha }_2+\delta )+o\left(l{n}_k\right).\hfill \end{array}$$

Hence, for $n_k<n<n_k+t_k$, we have

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_2$$

(23)

To sum up, now we see that for any $x\in {\mathbb{F}}_{\infty }$, (18) holds. Therefore, the Cantor set ${\mathbb{F}}_{\infty }$ is a subset of $E_{{\alpha }_1{\alpha }_2}^{\beta }\left(\psi \right)$.

• Step 4. Mass distribution on ${\mathbb{F}}_{\infty }$.

We construct a mass distribution $\mu$ on ${\mathbb{F}}_{\infty }$, and then estimte its local dimension in the next step. Let $J_k$ be a generic interval in ${\mathbb{F}}_k$ and $J_{k-1}$ be its mother interval. When k is even, the measure of $J_k$ is defined as

$$\begin{array}{cc}\hfill \mu \left(J_k\right)& ={\displaystyle \frac{1}{\#\mathbb{F}\left(J_k\right)}}\mu \left(J_{k-1}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{{\left(\#H_N^{\beta }({\alpha }_2,M_{k+1},\delta )\right)}^{l_k}\left(\#H_N^{\beta }({\alpha }_2,M_{k+1}+c_{k+1},\delta )\right)}}\mu \left(J_{k-1}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{{\left(h_N^{\beta }({\alpha }_2,M_{k+1},\delta )\right)}^{l_k}\left(h_N^{\beta }({\alpha }_2,M_{k+1}+c_{k+1},\delta )\right)}}\mu \left(J_{k-1}\right).\hfill \end{array}$$

(24)

That is, the mass on $J_{k-1}$ is distributed uniformly to its offspring. When k is odd, in the above equations, ${\alpha }_2$ will be replaced by ${\alpha }_1$.

For any $n\ge 1$ and a n-th basic interval $I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)$ with $I_{n,\beta }\cap {\mathbb{F}}_{\infty }\ne \varnothing$, let k be the integer such that $n_{k-1}+t_{k-1}<n\le n_k+t_k$; here, by convention $n_0=t_0=0$. We still consider the case when k is even; the odd case is similar. Define

$$\mu \left(I_{n,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n)\right)=\sum _{J_k\subset I_{n,\beta }}\mu \left(J_k\right),$$

where the summation is taken over all basic intervals $J_k\in {\mathbb{F}}_k$ contained in $I_{n,\beta }$. Now, we estimate the measure $\mu \left(I_{n,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n)\right)$.

(1) If $n_{k-1}+t_{k-1}<n\le n_{k-1}+t_{k-1}+N$, then

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)=\mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right).$$

(2) If $n_{k-1}+t_{k-1}+N<n\le n_k$, let $n=n_{k-1}+t_{k-1}+l{M}_k+i+N$,

• when $0\le l\le l_k$ and $i=0$,

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)=\mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right){\displaystyle \frac{1}{{\left(h_N^{\beta }\left({\alpha }_2,M_k,\delta \right)\right)}^l}}.$$

• when $0\le l\le l_k$ and $i\ne 0$,

$$\mu \left(I_{n,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n\right))\le \mu \left(I_{n_{k-1}+t_{k-1}+l{M}_k+N,\beta }({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}+l{M}_k+N})\right).$$

• when $l=l_k+1$ and $0\le i\le c_k$,

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)\le \mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right){\displaystyle \frac{1}{{\left(h_N^{\beta }\left({\alpha }_2,M_k,\delta \right)\right)}^{l_k}}}.$$

(3) If $n_k<n\le n_k+t_k$, then

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)=\mu \left(I_{n_k+t_k,\beta }\left({({\epsilon }_1,\cdots ,{\epsilon }_{n_k})}^{r_k}\right)\right).$$

• Step 5. Local dimension of $\mu$.

Firstly, we estimate the local dimension of $\mu$. By the definitions of $t_k$ and a, combining (17), we have

$$\underset{k\to \infty }{lim}{\displaystyle \frac{t_k}{n_k}}=a\mathrm{and}\underset{k\to \infty }{lim}{\displaystyle \frac{t_1+\cdots +t_{k-1}}{n_k}}=0.$$

(25)

Pick a sufficiently large $k_0$ such that for any $k\ge k_0$,

$${\displaystyle \frac{n_k-\left(t_1+\cdots +t_{k-1}\right)-kN}{n_k+t_k}}\ge {\displaystyle \frac{1-\eta }{1+a}}.$$

(26)

For any $n>n_{k_0}+t_{k_0}$, let $k\ge k_0$ be such that $n_{k-1}+t_{k-1}<n\le n_k+t_k$. By (15) and (24), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{-log\mu \left(J_k\right)}{n_k+t_k}}& ={\displaystyle \frac{{\sum }_{j=1}^k\left(l_{j}log{h}_N^{\beta }\left({\alpha }_2,M_j,\delta \right)+log{h}_N^{\beta }\left({\alpha }_2,M_j+c_j,\delta \right)\right)}{n_k+t_k}}\hfill \\ \hfill & \ge {\displaystyle \frac{n_k-\left(t_1+\cdots +t_{k-1}\right)-kN}{n_k+t_k}}(1-\eta )h^{\beta }\left({\alpha }_2\right)log\beta \hfill \\ \hfill & \ge {\displaystyle \frac{{(1-\eta )}^2{h}^{\beta }\left({\alpha }_2\right)log\beta }{1+a}}.\hfill \end{array}$$

Write $s_0={\displaystyle \frac{{(1-\eta )}^2{h}^{\beta }\left({\alpha }_2\right)}{1+a}}$. For general $n\ge 1$, we have

(1) If $n_{k-1}+t_{k-1}<n\le n_{k-1}+t_{k-1}+N$, then we have

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)=\mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right),$$

it follows that

$${\displaystyle \frac{-log\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)}{n}}\ge {\displaystyle \frac{-log\mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right)}{n_{k-1}+t_{k-1}+N}}\ge s_{0}log\beta .$$

(2) If $n_{k-1}+t_{k-1}+N<n\le n_k$, let $n=n_{k-1}+t_{k-1}+l{M}_k+i+N$,

• when $0\le l\le l_k$ and $i=0$, we have

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)=\mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right){\displaystyle \frac{1}{{\left(h_N^{\beta }\left({\alpha }_2,M_k,\delta \right)\right)}^l}}.$$

Thus,

$$\begin{array}{cc}& {\displaystyle \frac{-log\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)}{n}}\hfill \\ \hfill \ge & {\displaystyle \frac{-log\mu \left(I_{n_{k-1}+t_{k-1},\beta }({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}})\right)+(1-\eta )l{M}_k{h}^{\beta }\left({\alpha }_2\right)log\beta }{n_{k-1}+t_{k-1}+l{M}_k}}\hfill \\ \hfill \ge & min\left\{{\displaystyle \frac{-log\mu \left(I_{n_{k-1}+t_{k-1},\beta }\right)}{n_{k-1}+t_{k-1}}},(1-\eta )h^{\beta }\left({\alpha }_2\right)log\beta \right\}\ge s_{0}log\beta .\hfill \end{array}$$

• when $0\le l\le l_k$ and $i\ne 0$, we have

$$\mu \left(I_{n,\beta }({\epsilon }_1,\cdots ,{\epsilon }_n)\right)\le \mu \left(I_{n_{k-1}+t_{k-1}+M_k+N,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}+M_k+N}\right)\right).$$

Thus,

$$\begin{array}{cc}& {\displaystyle \frac{-log\mu \left(I_{n,\beta }({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n)\right)}{n}}\hfill \\ \hfill \ge & {\displaystyle \frac{-log\mu \left(I_{n_{k-1}+t_{k-1}+l{M}_k+N,\beta }\right)}{n_{k-1}+t_{k-1}+l{M}_k+N}}·{\displaystyle \frac{n_{k-1}+t_{k-1}+l{M}_k+N}{n}}\hfill \\ \hfill \ge & {\displaystyle \frac{{(1-\eta )}^2{h}^{\beta }\left({\alpha }_2\right)log\beta }{1+a}}\left(1-{\displaystyle \frac{i}{n}}\right)\ge s_{0}log\beta .\hfill \end{array}$$

• When $l=l_k+1$ and $0\le i\le c_k$, we have

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)\le \mu \left(I_{n_{k-1}+t_{k-1},\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}}\right)\right){\displaystyle \frac{1}{{\left(h_N^{\beta }\left({\alpha }_2,M_k,\delta \right)\right)}^{l_k}}}.$$

Thus,

$$\begin{array}{cc}& {\displaystyle \frac{-log\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)}{n}}\hfill \\ \hfill \ge & {\displaystyle \frac{-log\mu \left(I_{n_{k-1}+t_{k-1},\beta }({\epsilon }_1,\cdots ,{\epsilon }_{n_{k-1}+t_{k-1}})\right)+(1-\eta )l_k{M}_k{h}^{\beta }\left({\alpha }_2\right)log\beta }{n_{k-1}+t_{k-1}+l_k{M}_k+M_k+c_k+N}}\hfill \\ \hfill \ge & min\left\{{\displaystyle \frac{-log\mu \left(I_{n_{k-1}+t_{k-1},\beta }\right)}{n_{k-1}+t_{k-1}+N}},{\displaystyle \frac{(1-\eta )h^{\beta }\left({\alpha }_2\right)log\beta }{1+2/l_k}}\right\}\hfill \\ \hfill \ge & {\displaystyle \frac{{(1-\eta )}^2{h}^{\beta }\left({\alpha }_2\right)log\beta }{1+a}}\ge s_{0}log\beta .\hfill \end{array}$$

(3) If $n_k<n\le n_k+t_k$, then

$$\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)=\mu \left(I_{n_k+t_k,\beta }\left({({\epsilon }_1,\cdots ,{\epsilon }_{n_k})}^{r_k}\right)\right).$$

Hence,

$${\displaystyle \frac{-log\mu \left(I_{n,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)\right)}{n}}\ge {\displaystyle \frac{-log\mu \left(I_{n_k+t_k,\beta }\left({\epsilon }_1,\cdots ,{\epsilon }_{n_k+t_k}\right)\right)}{n_k+t_k}}\ge {\displaystyle \frac{{(1-\eta )}^2{h}^{\beta }\left({\alpha }_2\right)log\beta }{1+a}}.$$

Now, we consider the ball $B(x,r)$ for any $x\in {\mathbb{F}}_{\infty }$ and $r>0$, we calculate the $\mu$ measure of the ball $B(x,r)$. Let $n\in \mathbb{N}$ be such that

$$|I_{n+1}\left(x\right)|\le r<|I_n\left(x\right)|.$$

Since $B(x,r)$ can intersect at most $4{\beta }^N$n-th order basic intervals, it follows that

$$r\ge |I_{n+1}\left(x\right)|\ge {\displaystyle \frac{1}{{\beta }^{N+1}}}\left|I_n\left(x\right)\right|.$$

From the three cases (1)–(3), it follows that

$${\displaystyle \frac{-log\mu \left(B\right(x,r\left)\right)}{logr}}\ge {\displaystyle \frac{{(1-\eta )}^2{h}^{\beta }\left({\alpha }_2\right)}{1+a}}.$$

Applying Proposition 4 and letting $\eta$ tend to zero, we have

$${dim}_{\mathrm{H}}{\mathbb{F}}_{\infty }\ge {\displaystyle \frac{h^{\beta }\left({\alpha }_2\right)}{1+a}},$$

(27)

Similarly, we have

$${dim}_{\mathrm{H}}{\mathbb{F}}_{\infty }\ge {\displaystyle \frac{h^{\beta }\left({\alpha }_1\right)}{1+a}}.$$

(28)

From (27) and (28), we get

$${dim}_H{E}_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\ge {dim}_H{\mathbb{F}}_{\infty }\ge {\displaystyle \frac{min\left\{h^{\beta }\left({\alpha }_1\right),h^{\beta }\left({\alpha }_2\right)\right\}}{1+a}}.$$

(29)

• Step 6. Approximating $\beta >1$ by Parry numbers.

For a general $\beta >1$ which is not a Parry number. Let ${\left\{{\beta }_k\right\}}_{k\ge 1}$ be a strictly increasing sequence of Parry numbers with ${lim}_{k\to \infty }{\beta }_k=\beta$. For any $k\ge 1$, we have ${\Sigma }_{{\beta }_k}\subset {\Sigma }_{\beta }$. Let $G_{\beta }^{{\beta }_k}={\pi }_{\beta }\left({\Sigma }_{{\beta }_k}\right)$, define the function $g:G_{\beta }^{{\beta }_k}\to [0,1]$ by

$$g\left(x\right)={\pi }_{{\beta }_k}\left(\epsilon (x,\beta )\right).$$

Lemma 3.

For the above $G_{\beta }^{{\beta }_k}$, we have

$$g\left(E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\cap G_{\beta }^{{\beta }_k}\right)\supset E_{{\alpha }_1,{\alpha }_2}^{{\beta }_k}\left(\tilde{\psi }\right).$$

where $\tilde{\psi }\left(n\right)={\left(\psi \left(n\right)\right)}^{log{\beta }_k/log\beta }$.

Proof. 

For any $x\in E_{{\alpha }_1,{\alpha }_2}^{{\beta }_k}\left(\tilde{\psi }\right)$, we have

$$\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n\left(x,{\beta }_k\right)={\alpha }_1\mathrm{and}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n\left(x,{\beta }_k\right)={\alpha }_2.$$

and $|T_{{\beta }_k}^{n}x-x|<\tilde{\psi }\left(n\right)$ happens infinitely many times. From the definition of $G_{\beta }^{{\beta }_k}$ and g, we know that

$$\epsilon (g\left(x\right),{\beta }_k)=\epsilon (x,\beta ),\forall x\in G_{\beta }^{{\beta }_k}.$$

(30)

For any $x\in E_{{\alpha }_1,{\alpha }_2}^{{\beta }_k}\left(\tilde{\psi }\right)$, let $y={\pi }_{\beta }\left(\epsilon (x,{\beta }_k)\right)$, we will show that $g\left(y\right)=x$. Indeed, by (30), it is easy to see

$$\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{1}{n}}{S}_n(y,\beta )={\alpha }_1\mathrm{and}\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{1}{n}}{S}_n(y,\beta )={\alpha }_2.$$

(31)

Since $|T_{{\beta }_k}^{n}x-x|<\tilde{\psi }\left(n\right)$ happens infinitely many times, there exist two sequences $\left\{n_j\right\}$ and $\left\{t_j\right\}$ such that $|T_{{\beta }_k}^{n_j}x-x|<\tilde{\psi }\left(n_j\right)$ and ${{\beta }_k}^{-t_j-1}<\tilde{\psi }\left(n_j\right)\le {{\beta }_k}^{-t_j}$. This means that $T_{{\beta }_k}^{n_j}$ and x are in the same $t_j$-th basic interval, denoted by $|I_{t_j,{\beta }_k}({\epsilon }_1,\cdots ,{\epsilon }_{t_j})|$. Since $\epsilon (x,{\beta }_k)=\epsilon (y,\beta )$, $T_{\beta }^{n_j}y$ and y are also in the $t_j$-th basic interval $|I_{t_j,\beta }({\epsilon }_1,\cdots ,{\epsilon }_{t_j})|$. Hence,

$$\begin{array}{cc}\hfill |T_{\beta }^{n_j}y-y|& \le |I_{t_j,\beta }({\epsilon }_1,\cdots ,{\epsilon }_{t_j})|\le {\beta }^{-t_j}={\left({\beta }_k^{-t_j}\right)}^{{\displaystyle \frac{log\beta }{log{\beta }_k}}}\hfill \\ \hfill & <{\left(\tilde{\psi }\left(n_j\right)\right)}^{{\displaystyle \frac{log\beta }{log{\beta }_k}}}=\psi \left(n_j\right).\hfill \end{array}$$

(32)

Combining (31) and (32), we have $y\in E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)$. Therefore, for any $x\in E_{{\alpha }_1,{\alpha }_2}^{{\beta }_k}\left(\tilde{\psi }\right)$, there exists $y\in E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\cap G_{\beta }^{{\beta }_k}$ such that $g\left(y\right)=x$. That is,

$$E_{{\alpha }_1,{\alpha }_2}^{{\beta }_k}\left(\tilde{\psi }\right)\subseteq g\left(E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\cap G_{\beta }^{{\beta }_k}\right).$$

The proof is complete. □

Applying the previous result (29) for Parry numbers and Lemma 3, and noting that ${\displaystyle \underset{n\to \infty }{lim\; inf}\frac{-{log}_{\beta }\psi \left(n\right)}{n}=\underset{n\to \infty }{lim\; inf}\frac{-{log}_{{\beta }_k}\tilde{\psi }\left(n\right)}{n}}$, we have

$$\begin{array}{cc}\hfill {dim}_{\mathrm{H}}{E}_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)& \ge {dim}_{\mathrm{H}}\left(E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\cap G_{\beta }^{{\beta }_k}\right)\hfill \\ \hfill & \ge {\displaystyle \frac{log{\beta }_k}{log\beta }}{dim}_{\mathrm{H}}\left(g\left(E_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\cap G_{\beta }^{{\beta }_k}\right)\right)\hfill \\ \hfill & \ge {\displaystyle \frac{log{\beta }_k}{log\beta }}{dim}_{\mathrm{H}}{E}_{{\alpha }_1,{\alpha }_2}^{{\beta }_k}\left(\tilde{\psi }\right)\ge {\displaystyle \frac{log{\beta }_k}{log\beta }}·{\displaystyle \frac{min\{h^{\beta }\left({\alpha }_1\right),h^{\beta }\left({\alpha }_2\right)\}}{1+a}}.\hfill \end{array}$$

Letting $k\to \infty$, we obtain

$${dim}_{\mathrm{H}}{E}_{{\alpha }_1,{\alpha }_2}^{\beta }\left(\psi \right)\ge {\displaystyle \frac{min\{h^{\beta }\left({\alpha }_1\right),h^{\beta }\left({\alpha }_2\right)\}}{1+a}}.$$

3.2. Proof of Theorem 4

Recall that there exists a unique $T_{\beta }$-invariant and ergodic measure ${\nu }_{\beta }$ equivalent to the Lebesgue measure. By the Birkhoff ergodic theorem, for ${\nu }_{\beta }$-almost every $x\in [0,1]$, we have:

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )=\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\sum _{k=0}^{n-1}{\epsilon }_1(T_{\beta }^{k}x,\beta )={\alpha }_0$$

for ${\nu }_{\beta }$-a.e. $x\in [0,1]$, where ${\alpha }_0=\int {\epsilon }_1(x,\beta )d{\nu }_{\beta }$.

Combining (5), we have

$${dim}_{\mathrm{H}}\left\{x\in [0,1]:\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}{S}_n(x,\beta )={\alpha }_0\right\}=h^{\beta }\left({\alpha }_0\right)=1.$$

Clearly, ${max}_{\alpha }{h}^{\beta }\left(\alpha \right)=1$. Now, we proceed to prove Theorem 4. Firstly, consider the case where $\beta$ is a Parry number. Let $\left\{{\alpha }_n\right\}$ be a strictly increasing sequence that approaches ${\alpha }_0$; then, we have

$$E_{{\alpha }_n,{\alpha }_0}^{\beta }\left(\psi \right)\subset {\widehat{E}}_{\beta }\left(\psi \right).$$

By Theorem 3, we have

$${dim}_{\mathrm{H}}{\widehat{E}}_{\beta }\left(\psi \right)\ge {dim}_{\mathrm{H}}{E}_{{\alpha }_n,{\alpha }_0}^{\beta }\left(\psi \right)={\displaystyle \frac{h^{\beta }\left({\alpha }_n\right)}{1+a}}.$$

Since $h^{\beta }\left(\alpha \right)$ is continuous (see Lemma 1), combining (8), we see that

$${dim}_{\mathrm{H}}{\widehat{E}}_{\beta }\left(\psi \right)\ge \underset{n\to \infty }{lim}{\displaystyle \frac{h^{\beta }\left({\alpha }_n\right)}{1+a}}={\displaystyle \frac{h^{\beta }\left({\alpha }_0\right)}{1+a}}={\displaystyle \frac{1}{1+a}}.$$

For the upper bound, we note that ${\widehat{E}}_{\beta }\left(\psi \right)\subset R_{\beta }\left(\psi \right)$, by Theorem 2,

$${dim}_{\mathrm{H}}{\widehat{E}}_{\beta }\left(\psi \right)\le {dim}_{\mathrm{H}}{R}_{\beta }\left(\psi \right)={\displaystyle \frac{1}{1+a}}.$$

Hence,

$${dim}_{\mathrm{H}}{\widehat{E}}_{\beta }\left(\psi \right)={\displaystyle \frac{1}{1+a}}.$$

The case for a general $\beta >1$ follows by applying the approximation argument as in the proof of Theorem 3.

4. Conclusions and Further Questions

We study the quantitative recurrence property of the $\beta$-dynamical system $([0,1),T_{\beta })$ on the set where ${lim}_{n\to \infty }{\displaystyle \frac{1}{n}}{S}_n(x,\beta )$ does not exist, and obtain the dimension of the relevant set. The results indicate that the Hausdorff dimension of the intersection of the recurrence set and the irregular set equals to the product of their Hausdorff dimensions. A similar phenomenon is present in the classical Diophantine approximation (see [24]). This research deepens our understanding of $\beta$-expansions and the orbit distributions of $\beta$-dynamical systems from the fractal perspective.

The main result of this paper may be generalized in three directions:

(1)

For the $\beta$-dynamical system $([0,1),T_{\beta })$, our methods can be extended to study the more general ergodic average ${\displaystyle \frac{1}{n}}{S}_n\varphi \left(x\right)$, where $\varphi :[0,1]\to {\mathbb{R}}^d$ is an integrable vector-valued function.

(2)

Let f and $\varphi$ be continuous functions defined on $[0,1]$. The local Birkhoff level set $E_{\varphi }\left(f\right)$ is defined as follows:

$$E_{\phi }\left(f\right)=\left\{x\in [0,1]:\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\sum _{j=0}^{n-1}\varphi \left(T_{\beta }^{j}x\right)=f\left(x\right)\right\}.$$

We can estimate the Hausdorff dimension of the intersection of $E_{\phi }\left(f\right)$ and the recurrence set $R_{\beta }\left(\psi \right)$.

(3)

The $\beta$-dynamical system $([0,1),T_{\beta })$ can be extended to the dynamical system $(X,T)$ with a certain form of weak specification property (see [14] for more details). We can also consider piecewise monotonic maps on the interval $[0,1]$, such as the Manneville–Pomeau map or the Gauss map. Unlike beta dynamical systems, these maps either lack uniform hyperbolicity or have infinitely many branches, which may cause new difficulty.