Modeling the Phylogenetic Rates of Continuous Trait Evolution: An Autoregressive–Moving-Average Model Approach

Abstract

The rates of continuous evolution plays a crucial role in understanding the pace at which species evolve. Various statistical models have been developed to estimate the rates of continuous trait evolution for a group of related species evolving along a phylogenetic tree. Existing models often assume the independence of the rate parameters; however, this assumption may not account for scenarios where the rate of continuous trait evolution correlates with its evolutionary history. We propose using the autoregressive–moving-average (ARMA) model for modeling the rate of continuous trait evolution along the tree, hypothesizing that rates between two successive generations (ancestor–descendant) are time-dependent and correlated along the tree. We denote PhyRateARMA$(p,q)$ as a phylogenetic rate-of-continuous-trait-evolution ARMA(p,q) model in our framework. Our algorithm begins by utilizing the tree and trait data to estimate the rates on each branch, followed by implementing the ARMA process to infer the relationships between successive rates. We apply our innovation to analyze the primate body mass dataset and plant genome size dataset and test for the autoregressive effect of the rates of continuous evolution along the tree.

1. Introduction

In evolution, studying the heritable characteristics of the biological population is helpful for understanding the diversity between species on our planet Earth [1]. Macroevolution is expected to occur when selection acts on a trait that has a heritable basis of phenotypic variation. During the evolutionary process, speciation results in new species, and the comparison of traits (e.g., height, weight, size, etc.) among a group of related species can be performed by studying the speed of changes in their characteristics over successive generations [2].

Although one subgroup of species evolved at a faster rate and resulted in a larger variation in the trait, the other subgroup of species evolved at a relatively lower rate and produced a moderate variation of the trait. When evolutionary processes such as natural selection (including sexual selection) and genetic drift act on this variation, certain characteristics become more common or rare within a population [3]. For example, Darwin finches are a group of about 18 species of dull-colored passerine birds on the Galápagos islands [4]. They are well known for their remarkable diversity in the form, size, and function of the beak, which is highly adaptable to different food sources [5]. Another example is angiosperms, which survive and thrive successfully on our planet. The evolution of fruits is one of the most important characteristics, as fruits not only provide a food source for other species, but also protect seeds and contribute to seed dispersal [6]. The survival and success of fruits require adaptation to their environment. For example, while dragon fruit (Selenicereus) endures temperatures of up to 40 °C (104 °F) for survival, watermelon (Citrullus lanatus) needs temperatures higher than about 25 °C (77 °F) to thrive. Studying the reproducible properties by the rates of continuous evolution to the resistance of temperature would help us shed light on the evolution of angiosperms themselves and understand their ecological implications.

The rates of continuous evolution is a measurement of the change in an evolutionary lineage over time and can be defined as the ratio of the character displacement over a certain time interval. The rate of change between two samples is defined using three quantities [7]: the proportional difference between the sample means, the pooled standard deviation of the samples, and the time interval between the samples. For example, suppose that a character has been measured twice, $t_1$ and $t_2$, where $t_1$ and $t_2$ are expressed as the time before the present in millions of years. The time interval between the two samples can be written as $dt=t_1-t_2$, which is 1 million years if $t_1=6.27$ and $t_2=5.27$. The average value of the character is defined as $x_1$ in the previous sample and $x_2$ in the later sample. Let $y_{t_i}=log\left(x_{t_i}\right),i=1,2$ be the natural logarithm, taking into account $x_{t_1}$ and $x_{t_2}$. Then, the evolutionary rate ($\sigma$) can be defined as in Equation (1):

$$\sigma =(y_{t_2}-y_{t_1})/(t_2-t_1).$$

(1)

Next, multiplying the time difference $t_2-t_1$ on both sides of Equation (1) produces the character difference within a time unit $y_{t_2}-y_{t_1}=\sigma (t_2-t_1).$ Conceptually consider that the character change occurred in infinitesimal time and denote the character displacement by $d{y}_t={lim}_{t_1\to t_2}(y_{t_2}-y_{t_1})={lim}_{t_1\to t_2}\sigma (t_2-t_1)$; then, we have the differential equation $d{y}_t=\sigma dt$. Given $y\left(0\right)=y_0$, the solution is $y_t=y_0+\sigma t$, which shows that $y_t$ increased with time t. Unfortunately, this may not be an appropriate model for describing character change in the evolutionary perspective. Instead, one may consider that the variation in the character change adopts a certain dynamic. For example, if one considers that the variation in the character change is proportional to time, then a stochastic variable $W_t$ can be introduced, where $W_t$ is a Brownian motion (BM) process with an independent Gaussian distributed increment, and $d{W}_t=W_{t+dt}-W_t$ is a normal distributed random variable with mean 0 and variance $dt$ (i.e., $d{W}_t\sim \mathcal{N}(0,dt)$). Thus, the displacement of the continuous trait variable $y_t$ (=$log{x}_t$) solves the stochastic differential equation shown in Equation (2):

$$d{y}_t=\sigma d{W}_t.$$

(2)

Given $y\left(0\right)=y_0$, integrate both sides of Equation (2), and then one has

$$y_t=y_0+\sigma W_t,$$

(3)

where $W_0=0$, and $W_t\sim \mathcal{N}(0,t)$.

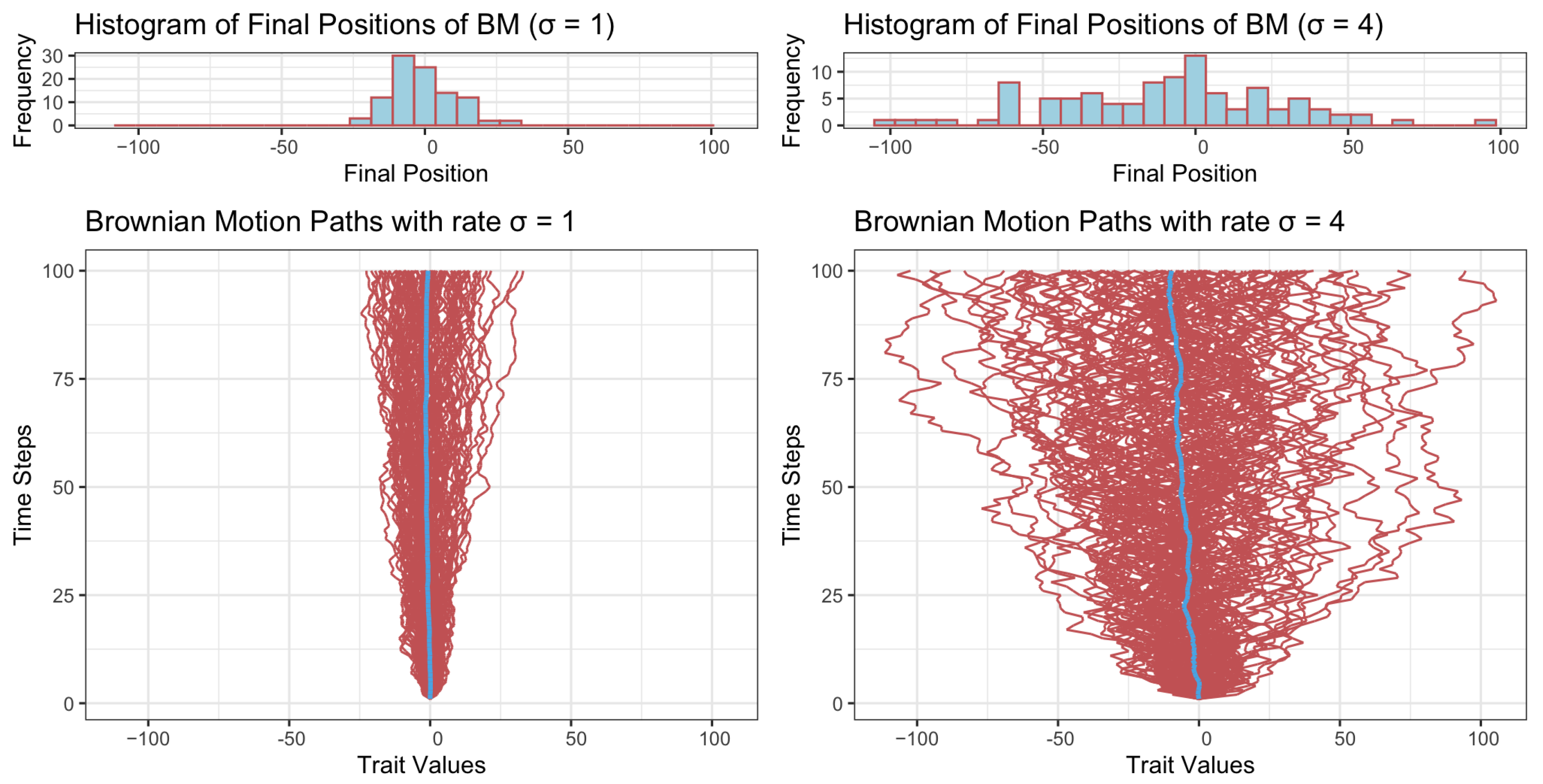
Given the initial value $y_0$, Equation (3) describes the dynamic of the trait variable $y_t$ at time t pending the rate parameter $\sigma$. Figure 1 presents one hundred trajectories generated using rates $\sigma =1$ (bottom left) and $\sigma =4$ (bottom right), respectively. It can be seen straightforwardly that while a smaller rate ($\sigma =1$) yields a narrower range of character value, the larger rate ($\sigma =4$) yields a wider range of character value.

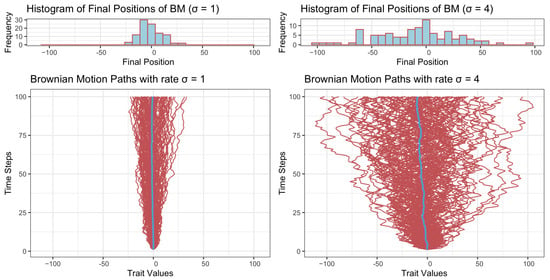
Figure 1. Trait values under Brownian motion dynamics with two different rates (left: $\sigma =1$, right: $\sigma =4$). Histograms in the top row represent the distribution of final positions, showing greater spread with higher $\sigma$. The bottom row illustrates 100 trajectories in red over time and the mean trajectory in blue, with higher $\sigma$ resulting in more dispersed paths. The time span is set to 100.

For a group of n related species, denote $y_{i,t},i=1,2,\cdots ,n$ as the trait variable for the ith species. Then, we can apply the Brownian motion with the rate parameter to explore the dynamic of the trait along the evolutionary history using a phylgoenetic tree $\mathcal{T}$ that represents the relatedness between species. In particular, the estimation of the evolution rate $\sigma$ can be performed using phylogenetic comparative methods (PCMs) [8,9,10].

There are models created on the basis of Equation (3) by considering that the constant-rate BM model may not be well addressed for the evolution in many scenarios [11,12,13,14,15]. Such models come with the assumption that the evolution of a species changes over time, wherethe rates of continuous trait evolution can be modeled as either constants or stochastic variables along times (branch lengths). The trait variable $y_t$ adopts the following dynamics:

$$y_t=\mu +{\sigma }_t{W}_t,$$

(4)

where ${\sigma }_t$ can be constant (i.e., ${\sigma }_t=\sigma ,t>0$) [16], piecewise constant (i.e., ${\sigma }_t={\sigma }_i,{\gamma }_{i-1}\le t\le {\gamma }_i$, where ${\gamma }_i$ and ${\gamma }_{i-1}$ are the successive time regimes) [11] or a random variable modeled by another pertinent process (i.e., ${\sigma }_t\sim \mathcal{D}\left(t\right)$ where $\mathcal{D}\left(t\right)$ is a distribution function for the stochastic variable) [17,18].

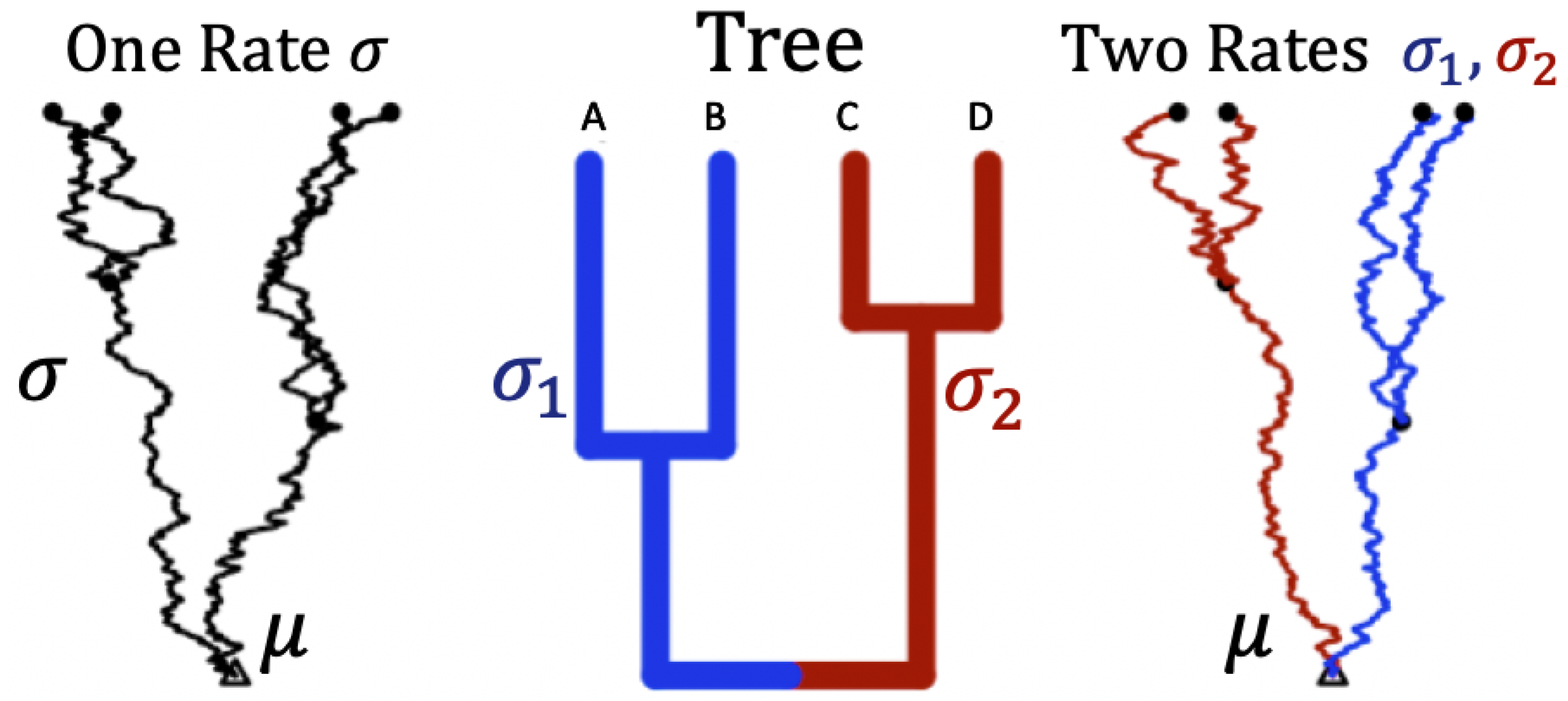
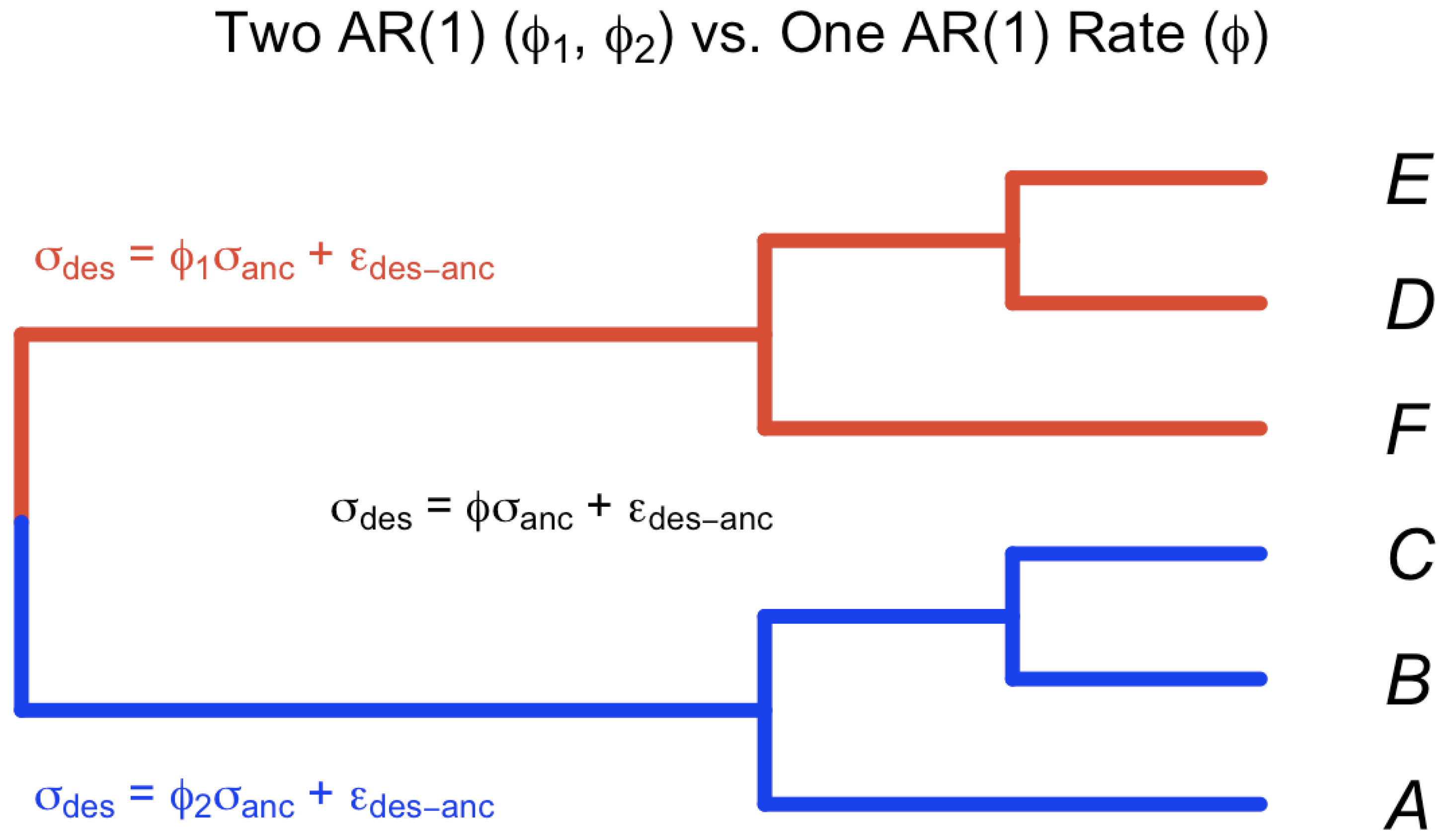
A hypothetical tree of four species $A,B,C,D$ and the corresponding simulation of the trajectories $y_{i,t}$ using Brownian motion along a rooted phylogenetic tree under two different rates is shown in Figure 2.

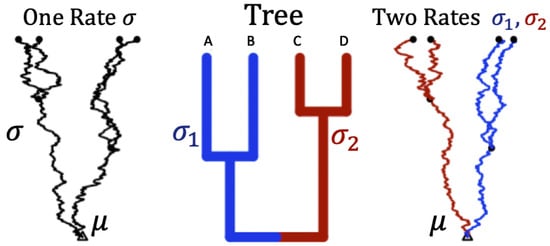
Figure 2. Trajectories of trait evolution for 4 species $A,B,C,D$ along a rooted phylogenetic tree. Middle panel: A rooted phylogenetic tree with four taxa $A,B,C,D$. Left panel: A set of four dependent trajectories along the tree using a single rate (${\sigma }_t=\sigma$ on all branches). Right panel: A set of four dependent trajectories along the tree using two rates (${\sigma }_t={\sigma }_1$ on the blue branches, and ${\sigma }_t={\sigma }_2$ on the red branches). $\mu$ is the root status denoted as a parameter of interest (analogous to $y_0$).

These models have been broadly applied in many studies. For example, in the evolution of the morphology of the world’s largest flowers (Raffkesianeae: up to 1 m in diameter), the authors of [19] found that the enormous flowers evolved from ancestors with tiny flowers. In the study of the evolution of the size of the plant genome, the authors of [20] found that the woody lineages had a stochastic motion rate that was nearly five times slower than the rate of the herbaceous lineages. Although the existing framework has produced rate models, none consider a scenario in which the rate is treated as a time-correlated stochastic variable, which could potentially enhance the study of rate evolution. This highlights the need for our work to apply a time series model [21,22]. Specifically, this approach aims to answer the following key question:

Are the evolutionary rates of biological traits statistically independent, or are they believed to be phylogenetically serially autocorrelated?

Note that in modeling the rates of continuous evolution, it is essential to consider its dynamic nature, as the rate can fluctuate, increase, or decrease over time as well as vary gradually and stochastically across a clade. Refs. [18,23,24], rather than remain constant. Consider that the implementation of the time-correlated rate evolution ${\sigma }_t$ could possibly provide an alternative to reveal embedded information about species evolution; in this work, we intend to expand the model $y_t=\mu +{\sigma }_t{W}_t$ in Equation (4) within the framework of correlated rate evolution (${\sigma }_t=g\left({\sigma }_s\right|\Theta )$ for $s<t$, where $\Theta$ is a parameter vector) to model the trait evolution for phylogenetic comparative analysis. In particular, we use the autoregressive–moving-average (ARMA) time series model that has been widely applied in econometrics to model the rate parameter [25,26]. The description of the methods can be found in Section 2. The simulations are detailed in Section 3. Empirical analyses are presented in Section 4. The discussions and conclusions are covered in Section 5.

2. Methods

2.1. Trait Evolution with Time-Correlated Rate

We describe our procedure as follows. In Section 2.1.1, we adopt phylogenetic ridge regression [27] to perform the analysis using the phylogenetic tree and trait data as input to obtain rate estimates. In Section 2.1.2, we perform a phylogenetic rate ARMA(p,q) regression, where the rate estimates are incorporated along the tree using a traversal algorithm, treating the data as time series.

The combination of ridge regression and ARMA models allows us to address the challenges of estimating evolutionary rates by leveraging their respective strengths. Specifically, ridge regression is employed to obtain reliable and stable estimates of evolutionary rates, even in scenarios where multicollinearity may arise in the data. Meanwhile, the ARMA model is used to capture the series-correlated rate dynamics, incorporating the dependency structure dictated by the phylogenetic tree topology.

2.1.1. Step 1: Phylogenetic Ridge Regression

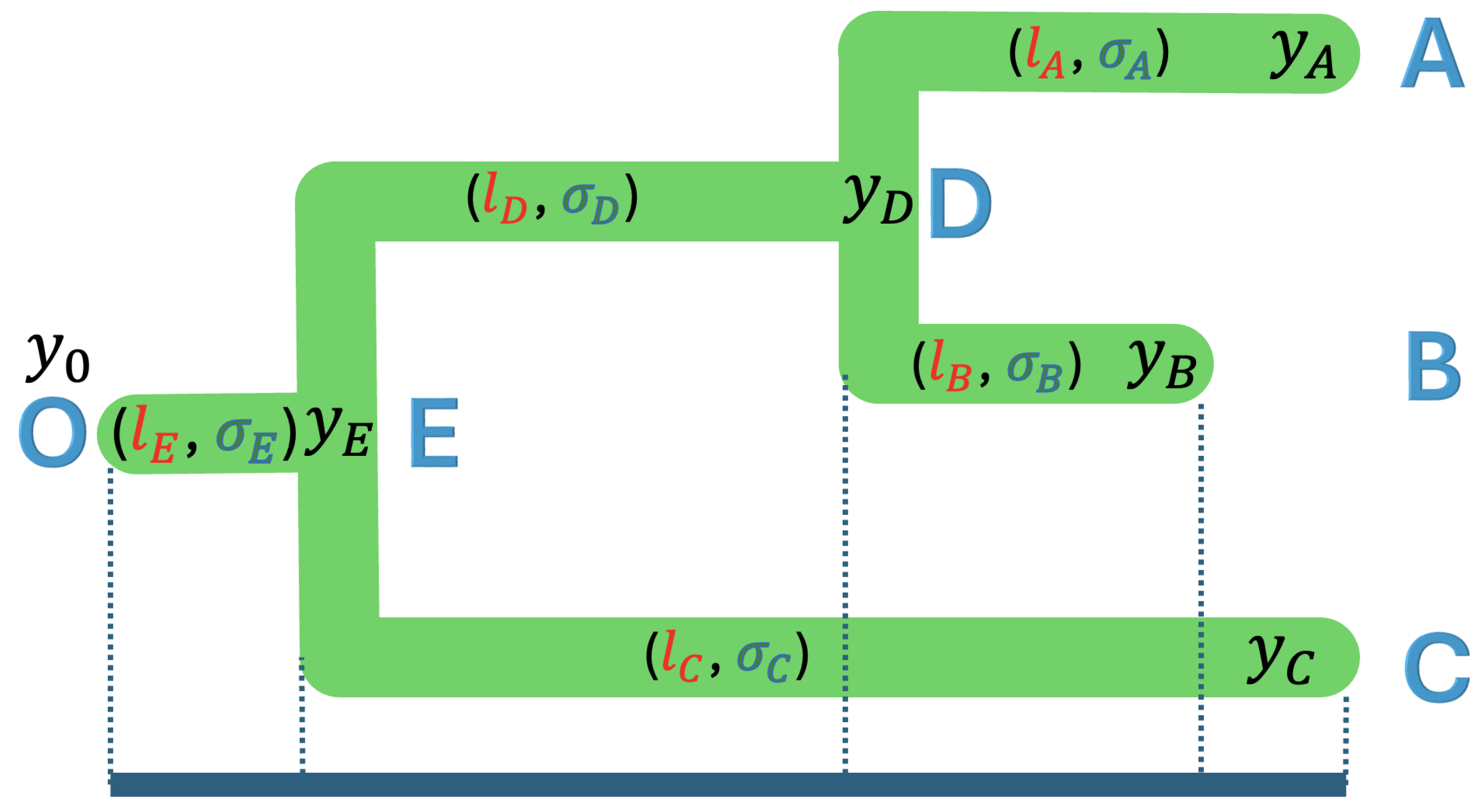
Given the tree with the topology and branch lengths, one should assume that the observed trait values are a linear combination of past values, time has elapsed, and the rate of continuous trait evolution changes. To illustrate, we used a case of a 3-taxon tree as shown in Figure 3, where the extant species A, B, and C, and the fossil species D, E, and O have trait values of $(y_A,y_B,y_C)$ and $(y_D,y_E,y_0)$. These trait values can be expressed as a linear combination of the time elapsed and the rates of continuous evolution, as shown in Equation (5):

$$\begin{array}{cc}\hfill y_A& =y_0+l_A{\sigma }_A+l_D{\sigma }_D+l_E{\sigma }_E,\hfill \\ \hfill y_B& =y_0+l_B{\sigma }_B+l_D{\sigma }_D+l_E{\sigma }_E,\hfill \\ \hfill y_C& =y_0+l_C{\sigma }_C+l_E{\sigma }_E,\hfill \\ \hfill y_D& =y_0+l_D{\sigma }_D+l_E{\sigma }_E,\hfill \\ \hfill y_E& =y_0+l_E{\sigma }_E.\hfill \end{array}$$

(5)

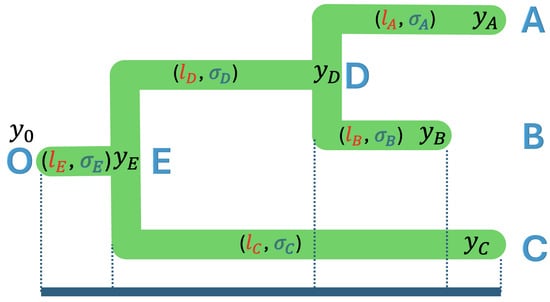
Figure 3. A rooted phylogenetic tree of three taxa with tip nodes A, B, and C; internal nodes D and E; and root node O, where the branch lengths are $l_A$, $l_B$, $l_C$, $l_D$, and $l_E$, and the rate variables are ${\sigma }_A$, ${\sigma }_B$, ${\sigma }_C$, ${\sigma }_D$, and ${\sigma }_E$.

One can formulate into the system of linear equation using Equation (6):

$$\left[\begin{array}{c}{y}_A\\ y_B\\ y_C\\ y_D\\ y_E\end{array}\right]=\left[\begin{array}{c}{y}_0\\ y_0\\ y_0\\ y_0\\ y_0\end{array}\right]+\left[\begin{array}{ccccc}{l}_A& 0& 0& l_D& l_E\\ 0& l_B& 0& l_D& l_E\\ 0& 0& l_C& l_D& l_E\\ 0& 0& 0& l_D& l_E\\ 0& 0& 0& l_D& l_E\end{array}\right]\left[\begin{array}{c}{\sigma }_A\\ {\sigma }_B\\ {\sigma }_C\\ {\sigma }_D\\ {\sigma }_E\end{array}\right].$$

(6)

Given the empirical data where the tip values are $y_A$, $y_B$, and $y_C$, and that the ancestral values $y_4$ and $y_5$ may be known through fossil records or remain unknown, and assuming the currently provided data, $\mathit{y}=(y_A,y_B,y_C)$, and the phylogenetic tree $\mathcal{T}$ with a given set of known branch lengths, set $\{l_A,l_B,l_C,l_D,l_E\}$, then the tip states $(y_A,y_B,y_C)$ can be written into a matrix form as Equation (7):

$$\left[\begin{array}{c}{y}_A\\ y_B\\ y_C\end{array}\right]=\left[\begin{array}{c}{y}_0\\ y_0\\ y_0\end{array}\right]+\left[\begin{array}{ccccc}{l}_A& 0& 0& l_D& l_E\\ 0& l_B& 0& l_D& l_E\\ 0& 0& l_C& 0& l_E\end{array}\right]\left[\begin{array}{c}{\sigma }_A\\ {\sigma }_B\\ {\sigma }_C\\ {\sigma }_D\\ {\sigma }_E\end{array}\right],$$

(7)

where L is the design matrix corresponding to species with the associated branch from the root of the tree, as shown in Figure 3, and ${({\sigma }_A,{\sigma }_B,{\sigma }_C,{\sigma }_D,{\sigma }_E)}^t$ represents the rate vector. Equation (7) can be reformulated and written as Equation (8):

$$\widehat{\mathit{y}}=L\widehat{\Sigma },$$

(8)

where the estimates for the rate vector $\Sigma ={({\sigma }_A,{\sigma }_B,{\sigma }_C,{\sigma }_D,{\sigma }_E)}^t$ can be obtained [27] in Equation (9):

$$\widehat{\Sigma }=\underset{\Sigma }{argmin}\sum _i{(y_i-{(L\Sigma )}_i)}^2+\lambda \sum _j{\Sigma }_j^2,$$

(9)

which can be written as

$$\widehat{\Sigma }={(L^{T}L+\lambda I)}^{-1}{L}^T\mathit{y}.$$

(10)

In general, given the tip data $\mathit{y}=\{y_1,y_2,\cdots ,y_n\}\in {\mathcal{R}}^n$ and tree topology $\mathcal{T}$ of n taxa with the branch-length set $\mathcal{B}=\{l_{j_1},l_{j_2},\cdots ,l_{j_m}\}$, where $(j_1,j_2,\cdots ,j_m):=\mathcal{J}$ is the internal node index set with the corresponding ancestral–descendant relationship delineated by the tree topology, we use the R package rrphylo (version 2.8.1) [28] to perform the analysis for the estimation of phenotypic evolutionary rates ${\left\{{\sigma }_{j_s}\right\}}_{j_s\in \mathcal{J}}$ using Equation (10), adopting the leave-one-out cross-validation (LOOCV) to search for the optimal $\lambda$. In this method, each observation is removed one at a time, and the remaining data are used to make predictions. The error for the excluded observation is calculated, and this process is repeated for all observations. The total LOOCV error is computed for various $\lambda$ values, and the $\lambda$ with the smallest error is selected as the best regularization parameter, improving model performance [27].

2.1.2. Step 2: Phylogenetic ARMA(p,q) Rates Model for Continuous Trait Evolution

Next, we implemented the ARMA model for studying the rates ${\left\{{\sigma }_{j_s}\right\}}_{j_s\in \mathcal{J}}$. Given tree topology $\mathcal{T}$ of n taxa, with tip node $\mathit{y}=\{y_1,y_2,\cdots ,y_n\}\in {\mathcal{R}}^n$ and internal node index set $\mathcal{J}=(j_1,j_2,\cdots ,j_m)$, and the corresponding branch length set $\mathcal{B}=\{l_{j_1},l_{j_2},\cdots ,l_{j_m}\}$ with the ancestral–descedant relationship delineated by the tree topology, by utilizing phylogenetic ridge regression in Equation (10), one can obtain a set of estimated rates ${\Sigma }_{\mathcal{J}}={\left\{{\sigma }_{j_s}\right\}}_{s=1}^m$, where index $j_s$ corresponds to the internal index. Then, the phylogenetic ARMA(p,q) rates model for continuous trait evolution, defined by a mixture of phylogenetic autoregressive (AR) and phylogenetic moving average (MA) models, is given by Equation (11):

$${\sigma }_{j_s}=\sum _{i=1}^p{\varphi }_i{\sigma }_{j_{s-i}}+\sum _{j=1}^q{\theta }_j{ϵ}_{j_{s-j}}+{ϵ}_{j_s},$$

(11)

where ${\sigma }_{j_s}$ represents the time series at time $j_s$, ${\varphi }_i$ are coefficients for the AR terms, ${\theta }_j$ are coefficients for the MA terms, and ${ϵ}_{j_s}$ denotes the white noise error terms following a normal distribution with mean zero and variable proportional to the branch length $j_s$ as shown in Equation (12):

$${ϵ}_{j_s}\sim \mathcal{N}(0,{\tau }^2{l}_{j_s}).$$

(12)

For a phylogenetic ARMA (1, 1) rate model, we denote ${\sigma }_{\mathrm{des}}={\sigma }_{j_s}$ as the descendent (${\sigma }_{j_s}$) and ${\sigma }_{\mathrm{anc}}={\sigma }_{j_{s-1}}$ as the ancestor; thus, the model in Equation (11) can be represented as in Equation (13):

$${\sigma }_{\mathrm{des}}=\varphi {\sigma }_{\mathrm{anc}}+\theta {ϵ}_{\mathrm{anc}}+{ϵ}_{\mathrm{des}},\mathrm{where}{ϵ}_{\mathrm{des}}\sim \mathcal{N}(0,{\tau }^2{l}_{\mathrm{des}}).$$

(13)

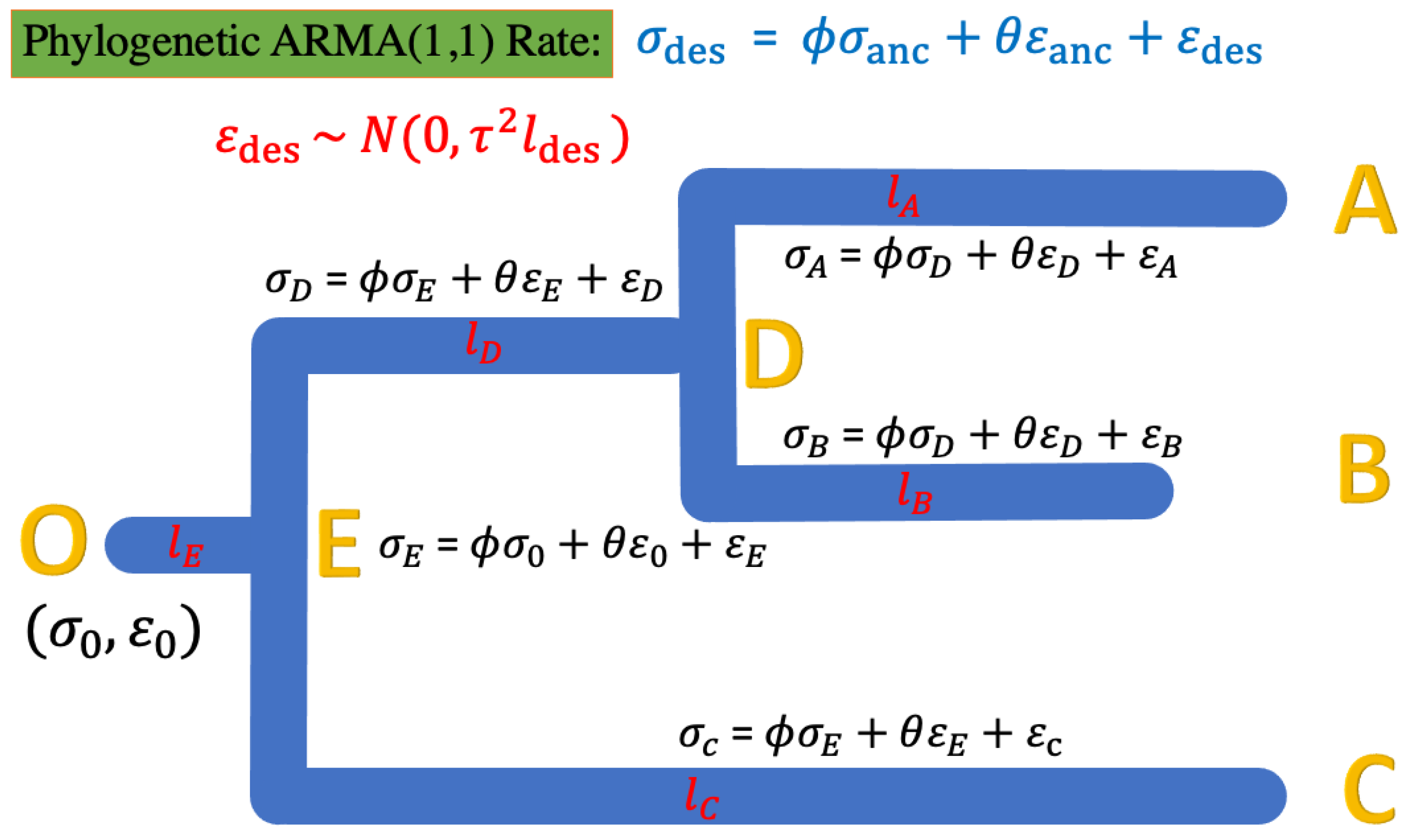
A model example of the 3-taxon case is shown in Figure 4.

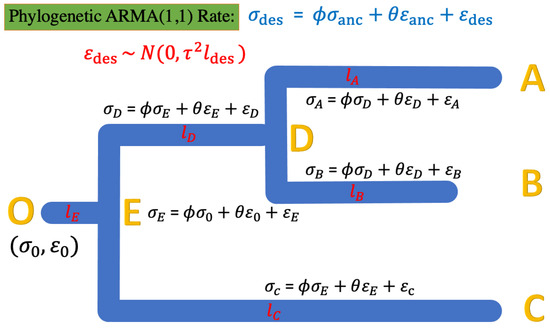
Figure 4. The phylogenetic ARMA$(1,1)$ rate model for the rates of continuous evolution along the studied tree. The root status O starts with ${\sigma }_0$, and along the tree is the error of the rate estimate. The ARMA rates are bound to the tree topology’s ancestral–descendant relationship. For instance, the rate ${\sigma }_A$ at tip node A has the relationship with the ancestor node D of ${\sigma }_A=\varphi {\sigma }_A+\theta {\sigma }_D+{ϵ}_A$, where ${ϵ}_A\sim \mathcal{N}(0,{\tau }^2{l}_A)$, while the rate ${\sigma }_D$ at internal node D has the relationship with the ancestor node E of ${\sigma }_E=\varphi {\sigma }_E+\theta {\sigma }_0+{ϵ}_D$, where ${ϵ}_D\sim \mathcal{N}(0,{\tau }^2{l}_D)$.

We are interested in the joint distribution $L(\Theta |\mathit{y},\mathit{\sigma },\mathit{ϵ},\mathcal{T})$, where $\Theta$ is the parameter vector (i.e., $\Theta =({\left\{{\varphi }_i\right\}}_{i=1}^p,{\left\{{\theta }_j\right\}}_{j=1}^q,\tau )$ for the PhyRateARMA $(p,q)$ model. On a specific branch $s\in \mathcal{J}$ with branch length $l_s$, we assume that error ${ϵ}_{j_s}$ follows a normal distribution with mean conditioning on the ancestor and variance with branch length $l_{j_s}$. The logarithmic likelihood on a branch is a one-dimensional ARMA $(p,q)$ that has likelihood in Equation (14):

$$logL(\Theta |\mathit{y},{\sigma }_{j_s},{ϵ}_{j_s},\mathcal{T})={\displaystyle \frac{1}{2}}\left(-log\left(2\pi \right)-log\left({\tau }^2{l}_{js}\right)-{\displaystyle \frac{{ϵ}_{js}^2}{{\tau }^2{l}_{js}}}\right).$$

(14)

Assuming that the branches are independent [24,29], the full log-likelihood given the tree $\mathcal{T}$ and trait $\mathit{y}$, $\mathit{\sigma }={\left\{{\sigma }_s\right\}}_{s\in \mathcal{J}},\mathit{ϵ}={\left\{{ϵ}_s\right\}}_{s\in \mathcal{J}}$ can be written as

$$logL(\Theta |\mathit{y},\mathit{\sigma },\mathit{ϵ},\mathcal{T})=logL(\Theta |{ϵ}_0,{\sigma }_0,\mathcal{T})+\sum _{s\in \mathcal{J}}logL(\Theta |\mathit{y},{\sigma }_s,{ϵ}_s,\mathcal{T}),$$

(15)

where ${ϵ}_0$ is the residual at the root, and the product operator $s\in \mathcal{J}$ follows the corresponding tree topology $\mathcal{T}$.

To perform model inference on parameter estimation, given the trait vector $\mathit{y}={(y_1,y_2,\cdots ,y_n)}^t$ on the tip and a phylogenetic tree $\mathcal{T}$ with the known branch-length set $\mathcal{B}$, where $l_0=0$ is the branch length of the root node and each branch is $l_{js}$, use $\mathit{y}$ and the tree $\mathcal{T}$ to obtain the rate estimates at the root ${\sigma }_0$ from the Brownian motion model [12]:

$${\sigma }_0=\sqrt{{(\mathit{y}-\widehat{\mu }\mathbf{1})}^t{\mathit{C}}^{-1}(\mathit{y}-\widehat{\mu }\mathbf{1})/n},$$

(16)

where the matrix $\mathit{C}$ is the phylogenetic similarity matrix, in which the element $c_{ij}$ measures the shared branch length between species i and j on the tree $\mathcal{T}$ [30]. $\widehat{\mu }=\left(\mathbf{1}{\mathit{C}}^{-1}\mathit{y}\right)/\left({\mathbf{1}}^t{\mathit{C}}^{-1}\mathbf{1}\right)$ is the MLE for the ancestral at the root under the Brownian motion model, and $\mathbf{1}={(1,1,\cdots ,1)}^t$ is vectors of 1s. Then, we used the maximum likelihood approach for parameter estimation and inference. Refer to Appendix A.2 for our expression and parameter estimation of a first few orders of the PhyRateARMA($(p,q)$) model.

For empirical analysis, we analyzed the data using the model up to the order $p=2,q=2$. For model selection, the Akaike information criterion $AIC=2k-logL$, its sample size correction version $AICc=AIC+2k(k+1)/(n-k-1)$ [31], and the weighted parameter were calculated using the equation $w_k=exp\left(-0.5\times \Delta {\mathrm{AIC}}_k\right)/{\sum }_{k=1}^{K}exp\left(-0.5\times \Delta {\mathrm{AIC}}_k\right)$, where $w_i$ is the weight for the models i and $\Delta {\mathrm{AIC}}_i={\mathrm{AIC}}_i-{min}_i\left\{{\mathrm{AIC}}_i\right\}$. The weighted parameter estimate $\tilde{\xi }$ was calculated as $\tilde{\xi }={\sum }_{k=1}^K{w}_i\times {\widehat{\xi }}_k$. Here, ${\widehat{\xi }}_i$ represents the MLE from model i. This method incorporates uncertainty in the selection of the model by averaging parameters based on AIC weights [32].

2.2. Testing of PhyRateAR(1) Effect

We conducted inference to test for the existence of the autoregressive effect. This is equivalent to testing whether $\varphi =0$, as shown in Section 2.2.1. Additionally, we investigated whether the autoregressive effect varies across different clades of the tree. For this, we posed the null hypothesis $H_0:{\varphi }_1={\varphi }_2$, which is discussed in Section 2.2.2.

2.2.1. Test of Correlated Rate Evolution

Given the PhyRateAR(1) process, ${\sigma }_{j_s}=\varphi {\sigma }_{j_s-1}+{ϵ}_{j_s}$, where ${ϵ}_{j_s}\sim \mathcal{N}(0,{\tau }^2{l}_{j_s})$ is white noise, the asymptotic variance of the MLE $\widehat{\varphi }$ is $\mathrm{Var}\left(\widehat{\varphi }\right)={\tau }^2/{\sum }_{j_s\in \mathcal{J}}{\sigma }_{j_s}^2$. The null hypothesis is given by $H_0:\varphi ={\varphi }_0$, where ${\varphi }_0$ is a hypothesized value. The alternative hypothesis for a two-sided test is $H_1:\varphi \ne {\varphi }_0$. We set ${\varphi }_0=0$ to test for the PhyRateAR(1) effect. To perform the test, first fit an PhyRateAR(1) model to the data and obtain the estimate $\widehat{\varphi }$ of $\varphi$ and its standard error $\mathrm{SE}\left(\widehat{\varphi }\right)$. The test statistic is then calculated as

$$t={\displaystyle \frac{\widehat{\varphi }-{\varphi }_0}{\mathrm{SE}\left(\widehat{\varphi }\right)}}.$$

(17)

This test statistic is compared with the critical value of the t distribution with $n-1$ degrees of freedom, where n is the sample size. The standard deviation estimate can be derived from the Hessian matrix obtained during the optimization process, which is then used to conduct hypothesis testing.

In the context of hypothesis testing for a phylogenetic rate model in an PhyRateAR(1) model, the process begins by establishing the null hypothesis, $H_0:\varphi ={\varphi }_0$, where ${\varphi }_0$ represents a specific hypothesized value. The alternative hypothesis for a two-sided test is $H_1:\varphi \ne {\varphi }_0$. The methodology for testing these hypotheses involves several steps: (i) Firstly, an PhyRateAR(1) model is fitted to the data. From this model, the estimate $\widehat{\varphi }$ of $\varphi$ and its standard error $SE\left(\widehat{\varphi }\right)$ are obtained. (ii) The next step involves calculating the test statistic using the formula $t={\displaystyle \frac{\widehat{\varphi }-{\varphi }_0}{SE\left(\widehat{\varphi }\right)}}$. (iii) Finally, this test statistic is compared against the critical value from the t-distribution, which is determined by the sample size $J=\left|\mathcal{J}\right|$, where $\left|\mathcal{J}\right|$ is the number of the branches of the tree and corresponds to $J-1$ degrees of freedom.

This comprehensive method is essential to determine whether the hypothesized value ${\varphi }_0$ is a plausible value for $\varphi$ in the PhyRateAR(1) model.

2.2.2. Testing Heterogeneity Rates on Subclades

We consider whether heterogeneity autoregressive effect exists on the two subclades, as shown in Figure 5.

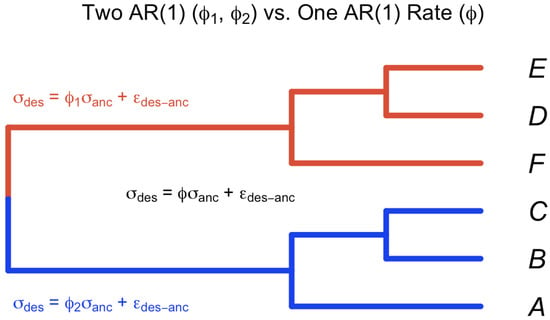
Figure 5. Test heterogeneity rates for trait evolution on the two subclades of the tree with tips $A,B,C,D,E,F$. Evaluate the model with two $\varphi$’s (${\varphi }_1,{\varphi }_2$) vs. a single $\varphi$.

The null Hypothesis ($H_0$) poses that a single tree with n taxa uses one parameter $\varphi$, while the alternative Hypothesis ($H_a$) states that two autoregressive parameters, ${\varphi }_1$ and ${\varphi }_2$, would be more appropriate when the tree is divided into two subtrees from the root and the parameters are estimated independently.

The null hypothesis in the likelihood ratio test states that the simpler model (in this case, the single combined tree) is sufficient to explain the variability in the data. The alternative hypothesis suggests that dividing the tree into two subtrees provides a better fit. The likelihood ratio test (LRT) statistic is computed as

$$\mathrm{LRT}=-2\left(log{L}_{H_0}-log{L}_{H_a}\right),$$

(18)

where $log{L}_{H_0}$ is the log-likelihood under the null hypothesis and $log{L}_{H_a}$ is the log-likelihood under the alternative hypothesis. The test statistic follows a chi-squared distribution with the degrees of freedom $df=1$.

The procedure in our framework is summarized in Algorithm 1.

Algorithm 1 Procedure of PhyRateARMA(p,q) Model Data Analysis

1: Input: a phylogenetic tree $\mathcal{T}$ with m branch lengthes $\mathcal{B}=\{l_{j_1},l_{j_2},\cdots ,l_{j_m}\}$, and quantitative trait values $\mathit{y}={(y_1,y_2,\cdots ,y_n)}^t$ of n taxa. 2: Output: estimated rates of continuous evolution ${\Sigma }_{\mathcal{J}}={\left\{{\tilde{\sigma }}_{j_s}\right\}}_{s=1}^m$, the parameter estimates ($\widehat{\varphi }s$, $\widehat{\theta }$s, ${\widehat{\tau }}^2$), the AICc values, the test statistics t-value for $H_0:\varphi =0$, and ${\chi }_2$-value for $H_0:{\varphi }_1={\varphi }_2$ and their corresponding p values. 3: Apply the phylogenetic ridge regression using the tree $\mathcal{T}$, branch lengths $\mathcal{B}$, and trait value $\mathit{y}$ using Equation (10) to obtain the rate estimates ${\left\{{\tilde{\sigma }}_{j_s}\right\}}_{s=1}^m$. 4: Use ${\left\{{\tilde{\sigma }}_{j_s}\right\}}_{s=1}^m$ as input and apply the tree traveral algorithm on the tree $\mathcal{T}$ to fit the PhyRateARMA(p,q) model. 5: Evaluate the AICc to compare the PhyRateARMA($p,q$) model, and compute the Akaike weight and the weighted estimate. 6: Test of the significance of the PhyRateAR(1) relationship in the two scenarios: Test of correlated rate evolution $H_0:\varphi =0$. Testing heterogeneity of PhyRateAR(1) on two subclades $H_0:{\varphi }_1={\varphi }_2$. 7: Return the results.

3. Simulation

We assessed the performance of the model using simulation. Two types of trees, a balanced tree and a birth-and-death tree, were used for the assessment, each with sizes of 16, 32, 64, and 128, respectively. The initial samples were drawn from an independent normal distribution. The initial estimate for ${\sigma }_0$ by applying the formula in Equation (16) at the root was estimated by the Brownian motion model using the R package geiger (version 2.0.11) [33]. For each type of tree and for each taxa, a million replicates of the sample were generated to assess performance of the model.

Let the tree $\mathcal{T}$ have m branches, with each branch representing a transition between an ancestral node $j_s-1$ and a descendant node $j_s$. The tree is traversed in postorder (from root to tips), and the trait values for each node are computed based on the following AR(1) process.

For each branch, the evolutionary rate at the descendant node $j_s$ is determined by the rate at its ancestor $j_s-1$, with some noise (innovation) added. The autoregressive equation is shown in Equation (19):

$${\sigma }_{j_s}=\varphi {\sigma }_{j_s-1}+{ϵ}_{j_s}$$

(19)

Initially, the rate value at the root node is set to zero: ${\sigma }_0=0$.

After simulating the rates using Equation (19) for all nodes in the tree, the final trait values at the tree tips (taxa) are computed by accumulating the rates along the path from the root to each tip.

Let $\mathcal{J}$ denote the set of nodes from the root to tip j, and ${\ell }_{j_s}$ denote the branch length leading to node $j_s$. The trait value at each tip j is

$$y_j=\sum _{j_s\in \mathcal{J}}{\sigma }_{j_s}{\ell }_{j_s}$$

(20)

where $y_j$ is the final accumulated trait value at tip j.

The final output consists of two arrays: (1) the array of simulated evolutionary rates for each node, $\mathit{\sigma }$, and (2) the trait values at the tree tips $\mathit{y}$, summarized by the following Equation (21):

$$\begin{array}{cc}\hfill {\sigma }_{j_s}& =\varphi {\sigma }_{j_{s-1}}+{ϵ}_{j_s},ϵ\sim \mathcal{N}(0,{\tau }^2{l}_{j_s}),\hfill \\ \hfill y_j& =\sum _{j_{s\in \mathcal{J}}}{\sigma }_{j_s}{\ell }_{j_s}.\hfill \end{array}$$

(21)

This simulation captures the evolutionary rate changes along a phylogeny under an AR(1) model, accounting for both ancestral states and random innovation at each branch. We implemented the corresponding method and script in R software (version 4.4.2) [34], naming the function simulate_trait_data_given_phi (refer to Appendix A.1.1 for the programming script), which simulates the trait evolution process along a phylogenetic tree using an autoregressive process (AR(1)) for the rates of continuous trait evolution. The simulation setup is shown in Algorithm 2.

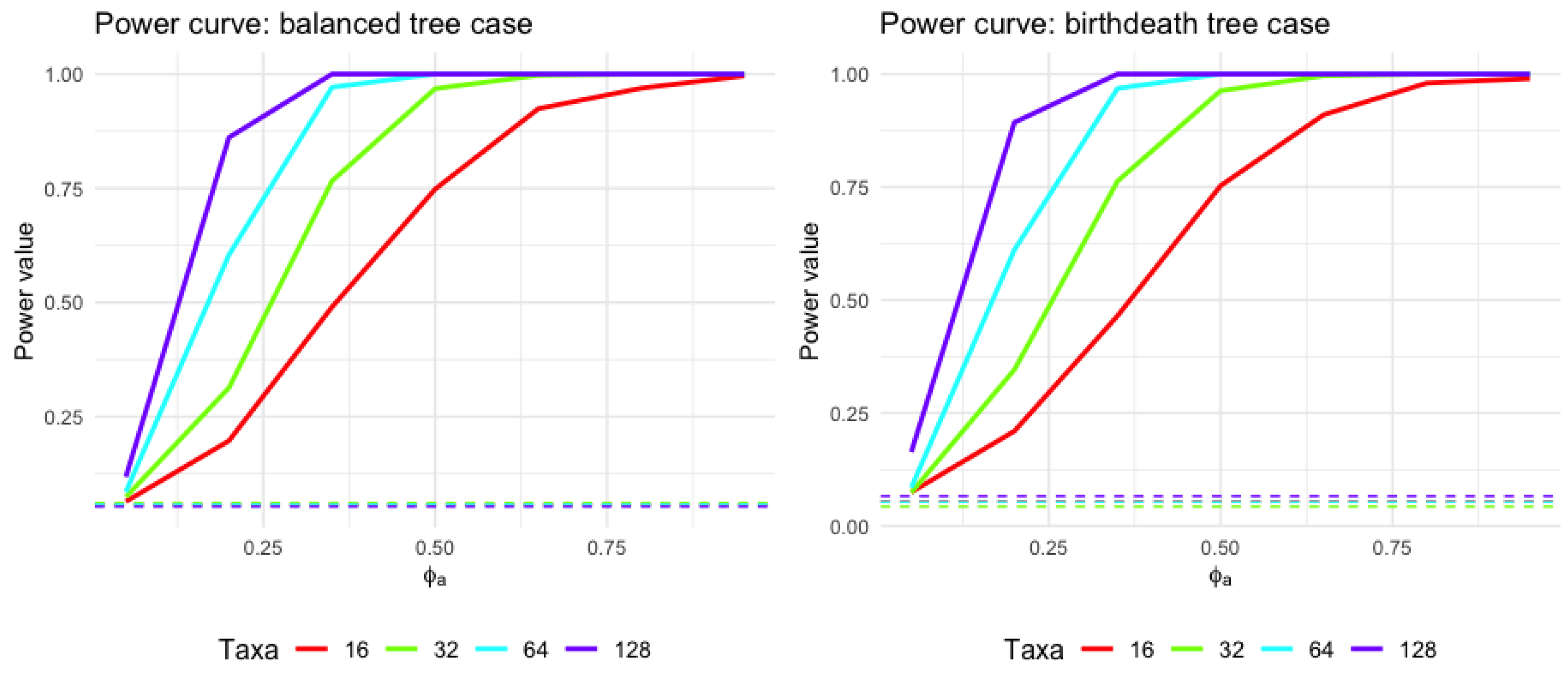
Figure 6 and Table 1 show how the statistical power to detect an effect changes with different values of ${\varphi }_a$ and different taxon levels.

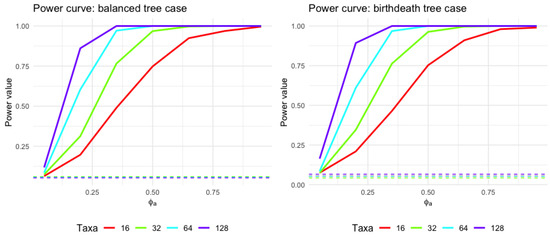
Figure 6. Power curve for varying taxon levels (using balanced tree and birth–death tree cases as demonstration). The horizontal axis represents an adjusted value of a parameter called ${\varphi }_a$, ranging from 0 to near 1. The vertical axis depicts the statistical power, indicating the probability of rejecting a null hypothesis when an alternative is true; a range from 0 suggests no detection ability, while 1 signifies certain detection. The four curves represent different taxon counts $(16,32,64,128)$, which could indicate distinct sample sizes or biological classifications. The horizontal lines present the type I error rate using level $0.05$.

Table 1. The type I error (T1 err) rate and the power of tree AR(1) rate on the null $H_0:\varphi =0$ using 2 types of trees and 4 taxon sizes. The alternative ${\varphi }_a$ are set to values of $0.05,0.2,0.35,0.5,0.65,0.8,$ and $0.95$, respectively. A total of 1000 replicates are used and the significance level $\alpha$ is set to $0.05$.

Tree Type	Taxa	T1 err	0.05	0.20	0.35	0.50	0.65	0.80	0.95
Balanced	16	0.066	0.050	0.211	0.481	0.746	0.924	0.970	0.991
	32	0.041	0.084	0.355	0.792	0.965	0.997	1.000	1.000
	64	0.043	0.081	0.616	0.970	1.000	1.000	1.000	1.000
	128	0.055	0.124	0.903	1.000	1.000	1.000	1.000	1.000
Birth–Death	16	0.058	0.064	0.197	0.490	0.748	0.924	0.969	0.996
	32	0.061	0.074	0.313	0.766	0.968	0.997	1.000	1.000
	64	0.057	0.085	0.604	0.971	1.000	1.000	1.000	1.000
	128	0.053	0.118	0.861	1.000	1.000	1.000	1.000	1.000

From Figure 6 and Table 1, one can envision that the power of the test changes depending on the number of taxa. Generally, as the number of taxa increases, the power also increases. Next, for all taxon levels, as ${\varphi }_a$ increases, the power of the test also increases. This could mean that as the parameter ${\varphi }_a$ increases, the ability to detect an effect or a difference becomes stronger. Third, all curves converge or come closer together at higher values of ${\varphi }_a$, indicating that the power could be more consistent between different levels of taxa at these higher values. This simulation provides the evidence that our methods fit the statistical properties as expected in the performance of evaluating the statistical power and type I error. Results using the coalescent tree and pure birth tree are similar, and readers can refer to the online appendix link in Appendix A.1.2.

Algorithm 2 Estimating Type I Error and Power with PhyRateAR(1) rate Model

1: Input: tree type {balanced, birth death }, taxa size $\{16,32,64,128\}$, simulations 1000, $\alpha =0.05$, ${\varphi }_0=0$, ${\sigma }_0=1$, ${\varphi }_a=\{0.05,0.10,0.15,\cdots ,0.95,1\}$. 2: Output: Type I error and power for each taxon size. 3: for each tree type do 4:     Generate tree $\mathcal{T}$ with branch length set $\mathcal{B}={\left\{l_{j_s}\right\}}_{j_s\in \mathcal{J}}$ 5:     for each taxa do 6:         Initialize Type I Error $T_1=0$                                                                                                                                                                                                                                                 ▹Estimate Type I Error 7:         for $i=1\mathrm{to}\mathrm{sims}$ do 8:            Use Equation (21) with $\varphi ={\varphi }_0$ to simulate trait data y 9:            Use Equation (10) to obtain rate estimates ${\left\{{\tilde{\sigma }}_{j_s}\right\}}_{j_s\in \mathcal{J}}$ 10:            Optimize the negative log-likelihood (15) to estimate $\widehat{\varphi },\widehat{\theta },\widehat{\tau }$. 11:            Use Equation (17) to test $\varphi =0$ using MLE, SE, and p-value. 12:            if $p<\alpha$ then 13:                $T_1=T_1+1$ 14:            end if 15:         end for 16:         Store $T_1$ for this tree and taxa size                                                                                                                                                                                                                                                 ▹Estimate Power 17:         for each ${\varphi }_a$ do 18:            Initialize power pow $=0$ 19:            for $i=1\mathrm{to}\mathrm{sims}$ do 20:                Use Equation (21) with $\varphi ={\varphi }_a$ to simulate trait data y 21:                Use Equation (10) to obtain rate estimates ${\left\{{\tilde{\sigma }}_{j_s}\right\}}_{j_s\in \mathcal{J}}$ 22:                Optimize Equation (15) to obtain MLEs $\widehat{\varphi },\widehat{\theta },\widehat{\tau }$. 23:                Use Equation (17) to test $\varphi =0$ with MLE, standard error, and p-value. 24:                if $p<\alpha$ then 25:                    pow= pow $+1$ 26:                end if 27:            end for 28:            Store pow for this tree and taxa size 29:         end for 30:     end for 31: end for 32: Return$T_1,pow$

4. Empirical Analysis

4.1. Genome Size Rate Evolution in Herbaticus and Woody Plant

We collected and analyzed datasets on the genome size in pg of herbaticus and woody plant. The primary data source is [35], from whichwe included 35 herbaticus and 33 woody species in this study. The main objective was to test whether there is a time series relationship in the evolutionary rate of these plants’ genome sizes.

Figure 7 shows the phylgoenetic tree for herbaticus, woody, and their joint tree.

Figure 7. Left: Herbaticus tree. Right: Woody species Middle: Combined herbaticus and woody species. The herbaticus and woody trees were obtained using TimeTree [36], where species names are entered and the system generates the tree in Newick format. The combined tree was obtained using R ape package (version 5.8-1) function bind.tree by applying the molecular dating with a penalized likelihood approach [29] for branch-length estimation. This was performed using the R ape package (version 5.8-1) function chronopl, taking the herbaticus tree and woody tree as input.

4.1.1. Genome Size: Combined Herbaticus and Woody Species

Table 2 presents the parameter estimates for various autoregressive (PhyRateAR) and autoregressive–moving-average (PhyRateARMA) models. PhyRateARMA(1,1) has a ${\varphi }_1$ value of $-0.600$ and a ${\theta }_1$ value of $0.738$, indicating a moderate correlation between consecutive rates of evolution, with a residual variance of ${\tau }^2=4.663$. The weighted estimates combine values across the models, with ${\varphi }_1=-0.050$, ${\theta }_1=0.202$, and ${\tau }^2=4.722$, providing a comprehensive view of the underlying evolutionary process.

Table 2. MLE parameter estimated for the 68 combined species of herbaticus (35) and woody (33) species.

	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$0.095$				$4.732$
PhyRateAR(2)	$0.108$	$-0.083$			$4.748$
PhyRateARMA(1,1)	$-0.600$		$0.738$		$4.663$
PhyRateARMA(2,1)	$-0.046$	$-0.554$	$0.738$		$4.663$
PhyRateARMA(2,2)	$-0.769$	$0.168$	$0.869$	$-0.131$	$4.663$
Weighted Estimate	$-0.050$	$-0.079$	$0.202$	$-0.003$	$4.722$

Using the phylogenetic PhyRateARMA(1,1) rate model described in Equation (13), the equation for ${\sigma }_{\mathrm{des}}$ demonstrates how the descendant’s rates of continuous evolution is influenced by multiple factors. In the weighted estimate, the AR(1) estimate ${\varphi }_1$ indicates that −5.0% of the ancestor’s evolutionary rate (${\sigma }_{\mathrm{anc}}$) is carried over to the descendant, reflecting a weak and inverse correlation between the two rates. The MA(1) estimate ${\theta }_1$, with a coefficient of $0.202$, adjusts for the random variation (or noise) in the ancestor’s rate. This positive value suggests that random fluctuations in the ancestor’s rate have a small reinforcing effect on the descendant. Finally, ${ϵ}_{\mathrm{des}}$, with variance proportional to ${\tau }^2=4.722$, represents the new random variation specific to the descendant. The weighted estimates offer a balanced perspective on how both inherited traits and random fluctuations shape evolutionary changes across generations.

In Table 3, PhyRateAR(2) ranks first with the lowest AICc value of $537.870$ and the highest Akaike weight ($w=0.530$), indicating the best fit among the models. PhyRateAR(1) follows with an AICc of $539.850$ and a weight of $0.2$, suggesting a close fit but slightly less optimal than PhyRateAR(2). PhyRateARMA(1,1) ranks third with an AICc of $540.070$ and a weight of $0.180$. Models PhyRateARMA(2,1) and PhyRateARMA(2,2) show considerably lower Akaike weights, indicating that increasing model complexity beyond PhyRateAR(2) does not significantly improve the fit.

Table 3. Model information for the combined herbaticus and 88 woody primate species.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(2)	3	$-265.940$	$537.870$	$0.530$	1st
PhyRateAR(1)	2	$-267.920$	$539.850$	$0.200$	2nd
PhyRateARMA(1,1)	3	$-267.040$	$540.070$	$0.180$	3rd
PhyRateARMA(2,1)	4	$-267.040$	$542.070$	$0.070$	4th
PhyRateARMA(2,2)	5	$-267.040$	$544.070$	$0.020$	5th

4.1.2. Genome Size: Herbaticus Species

The parameter estimates in Table 4 for the herbaticus models show that PhyRateAR(1) has a ${\varphi }_1$ value of $0.470$ with residual variance ${\tau }^2=0.009$, indicating a moderate influence from the previous rates of continuous evolution. PhyRateAR(2) introduces a second autoregressive term (${\varphi }_2=-0.019$) and maintains a similar variance of ${\tau }^2=0.009$. The PhyRateARMA(1,1) model has ${\varphi }_1=0.491$ and ${\theta }_1=-0.024$, with the same variance of ${\tau }^2=0.009$. More complex models, such as PhyRateARMA(2,1) and PhyRateARMA(2,2), show mixed ${\varphi }_1$ and ${\theta }_1$ values, but they maintain the same low variance of ${\tau }^2=0.009$.

Table 4. Herbaticus species model parameter estimates.

	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$0.470$				$0.009$
PhyRateAR(2)	$0.451$	$-0.019$			$0.009$
PhyRateARMA(1,1)	$0.491$		$-0.024$		$0.009$
PhyRateARMA(2,1)	$0.167$	$0.163$	$0.150$		$0.009$
PhyRateARMA(2,2)	$-0.128$	$0.609$	$0.476$	$-0.480$	$0.009$
Weighted Estimate	$0.427$	$0.030$	$0.021$	$-0.014$	$0.009$

The weighted estimate balances these models, showing ${\varphi }_1=0.427$, ${\theta }_1=0.021$, and ${\tau }^2=0.009$. This suggests that the descendant’s rates of continuous evolution is influenced by $42.7$% of the ancestor’s rate, with a small adjustment of $2.1$% due to noise from the ancestor, all within a low variance process.

In Table 5, PhyRateAR(1) ranks first with the lowest AICc value of $-110.550$ and the highest Akaike weight ($w=0.610$), making it the best-fitting model for the herbaticus data. PhyRateARMA(1,1) follows in second place with an AICc of $-108.550$ and a weight of $0.220$, while PhyRateAR(2) ranks fourth with an AICc of $-105.690$ and a weight of $0.050$. More complex models like PhyRateARMA(2,1) and PhyRateARMA(2,2) have even lower Akaike weights, indicating that they provide little additional explanatory power compared to simpler models.

Table 5. Herbaticus species model results.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(1)	2	$57.270$	$-110.550$	$0.610$	$1\mathrm{st}$
PhyRateARMA(1,1)	3	$57.270$	$-108.550$	$0.220$	$2\mathrm{nd}$
PhyRateARMA(2,1)	4	$57.250$	$-106.500$	$0.080$	$3\mathrm{rd}$
PhyRateAR(2)	3	$55.840$	$-105.690$	$0.050$	$4\mathrm{th}$
PhyRateARMA(2,2)	5	$57.270$	$-104.550$	$0.030$	$5\mathrm{th}$

4.1.3. Genome Size: Woody Species

The parameter estimates in Table 6 for the woody models indicate that PhyRateAR(1) has a ${\varphi }_1$ value of $-0.013$ and a residual variance of ${\tau }^2=0.002$, suggesting a very weak negative influence from the previous rates of continuous evolution. PhyRateAR(2) introduces a second autoregressive term (${\varphi }_2=-0.302$) and slightly increases the variance to ${\tau }^2=0.003$. PhyRateARMA(1,1) shows stronger dependence with ${\varphi }_1=0.359$ and ${\theta }_1=-0.446$, while maintaining a variance of ${\tau }^2=0.002$.

Table 6. Woody species model parameter estimates.

	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$-0.013$				$0.002$
PhyRateAR(2)	$-0.017$	$-0.302$			$0.003$
PhyRateARMA(2,1)	$-0.269$	$-0.315$	$0.283$		$0.003$
PhyRateARMA(1,1)	$0.359$		$-0.446$		$0.002$
PhyRateARMA(2,2)	$-0.223$	$-0.714$	$0.207$	$0.450$	$0.002$
Weighted Estimate	$0.023$	$-0.010$	$-0.044$	$0.005$	$0.002$

The weighted estimate balances the models, with ${\varphi }_1=0.023$, ${\theta }_1=-0.044$, and ${\tau }^2=0.002$. This suggests that the descendant’s rate is slightly positively influenced by the ancestor’s rate ($2.3$%) but is slightly negatively impacted by the noise ($-4.4$%), with very low overall variance ($0.002$), indicating minimal change between generations.

In Table 7, PhyRateAR(1) ranks first with the lowest AICc value of $-192.770$ and the highest Akaike weight ($w=0.860$), indicating that it is the best-fitting model for the woody data. PhyRateARMA(1,1) ranks second with an AICc of $-188.710$ and a much smaller weight ($w=0.110$), while PhyRateAR(2) ranks last with an AICc of $-180.880$ and no Akaike weight ($w=0.000$). More complex models, such as PhyRateARMA(2,1) and PhyRateARMA(2,2), also have minimal Akaike weights ($w=0.010$), suggesting that they provide little additional explanatory power and overcomplicate the fit for the woody data.

Table 7. Woody species model results.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(1)	2	$98.390$	$-192.770$	$0.860$	$1\mathrm{st}$
PhyRateARMA(1,1)	3	$97.360$	$-188.710$	$0.110$	$2\mathrm{nd}$
PhyRateARMA(2,2)	5	$97.160$	$-184.310$	$0.010$	$3\mathrm{rd}$
PhyRateARMA(2,1)	4	$95.960$	$-183.910$	$0.010$	$4\mathrm{th}$
PhyRateAR(2)	3	$93.440$	$-180.880$	$0.010$	$5\mathrm{th}$

From above, one may foresee that the woody primate and the herbaticus genome size possess different autoregressive effects for the rates of evolution, and we present the test we conducted in the following sections.

4.1.4. Testing Autocorrelation Rate

Interpretation of PhyRateAR(1) Test Results

Table 8 shows the PhyRateAR(1) test result.

Table 8. $H_0:\varphi =0$, $H_a:\varphi \ne 0$.

Tree Case	z-val	p-val	Significant?
combined tree	$1.119$	$0.263$	N
herbaticus tree	$5.100$	$0.000$	Y
woody tree	$-0.121$	$0.903$	N

Table 8 presents the results of the PhyRateAR(1) test under the null hypothesis $H_0:\varphi =0$ (no autocorrelation) and the alternative hypothesis $H_a:\varphi \ne 0$. The herbaticus tree shows a significant positive autocorrelation with a large z-value of 5.100 and a p-value of 0.000, strongly rejecting the null hypothesis. This suggests a significant effect of the previous rates of continuous evolution on the current rate in the herbaticus dataset.

In contrast, the woody tree shows no significant autocorrelation, with z values of $-0.121$; and p values of $0.903$ indicate that the null hypothesis cannot be rejected for these datasets, suggesting that there is no significant relationship between the past and current rates of evolution in the woody trees. This may due to the fact that the woody tree has slower rates (5 times slower than the herbaticus tree [20]).

The combined tree shows no significant autocorrelation, with z-values of $1.119$, and p-values of $0.263$. The result suggests that there is no significant relationship between the past and current rates of evolution in the combined trees.

Testing Heterogeneity Rates on Subclades

Table 9 presents the results of the heterogeneity test in evolutionary rates across the herbaticus, woody, and combined (dino) subclades using various autoregressive models (PhyRateAR(1), PhyRateAR(2), PhyRateARMA(1,1), PhyRateARMA(2,1), PhyRateARMA(2,2)). The log-likelihood values for the herbaticus ($log{L}_{\mathrm{di}}$), woody ($log{L}_{\mathrm{no}}$), and combined ($log{L}_{\mathrm{dino}}$) datasets are provided, along with the chi-squared statistic and p-values.

Table 9. Testing heterogeneity rates on subclades. $H_0$: ${\varphi }_1={\varphi }_2$, $H_a$: ${\varphi }_1\ne {\varphi }_2$.

Model	$log\mathit{L}$_di	$log\mathit{L}$_no	$log\mathit{L}$_dino	${\mathrm{LRT}}_{{\mathit{\chi }}^2}$	p-val	Significant?
PhyRateAR(1)	$57.27$	$98.39$	$-267.92$	$847.16$	$0.00$	Y
PhyRateAR(2)	$55.84$	$93.44$	$-265.94$	$830.44$	$0.00$	Y
PhyRateARMA(1,1)	$57.27$	$97.36$	$-267.04$	$843.34$	$0.00$	Y
PhyRateARMA(2,1)	$57.25$	$95.96$	$-267.04$	$840.50$	$0.00$	Y
PhyRateARMA(2,2)	$57.27$	$97.16$	$-267.04$	$842.94$	$0.00$	Y

All models yield highly significant results (p-values = 0.00), indicating strong evidence for rate heterogeneity between the subclades. The highest chi-squared statistic is observed for PhyRateAR(1) (847.16), suggesting that it explains the greatest amount of variance in the data compared to the other models.

4.2. Body Mass Rate Evolution in Diurnal and Nocturnal Primates

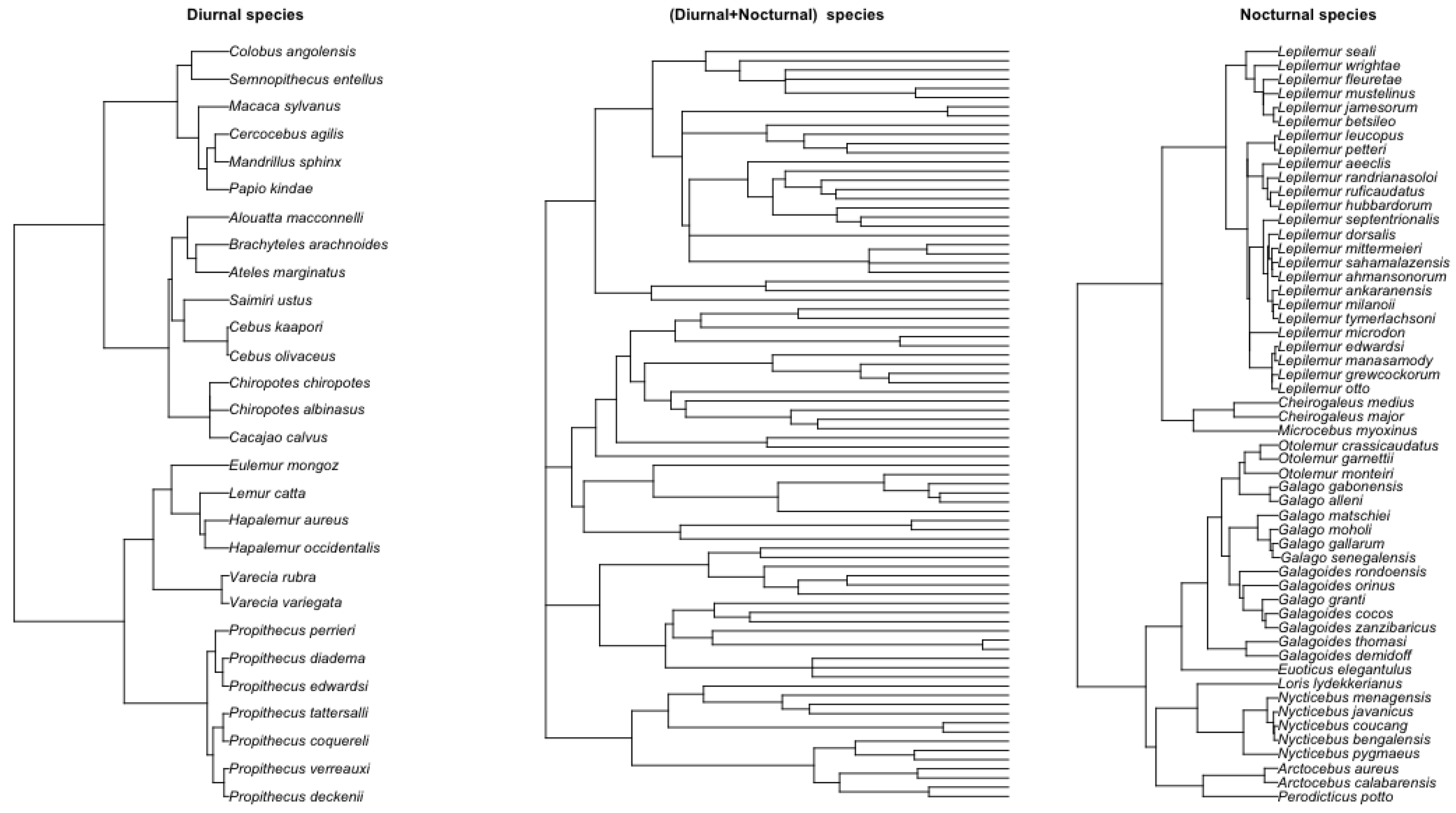
We collected and analyzed datasets on the body weights of male and female primates. The primary data sources are from [37] and Animal Diversity Web [38], which include diurnal and nocturnal male and female primates. The phylogenetic tree of 88 primate species was obtained from [37,39]. Figure 8 shows the phylogenetic tree for nocturnal, diurnal, and their joint tree. The main objective was to test whether there is a time series relationship in the evolutionary rate of these primates’ body weights. The original dataset contained 88 primate species, 34 diurnal species, and 54 nocturnal species. Body weight for males, females, or combined was collected. We present the combined analysis of male and female primate data below. For the male-only and female-only analysis cases, see Appendix A.1.2. Note here that we expanded the analysis from [40], where a smaller dataset of the primate was analyzed under the PhyRateAR(1) and PhyRateARMA(1,1) models.

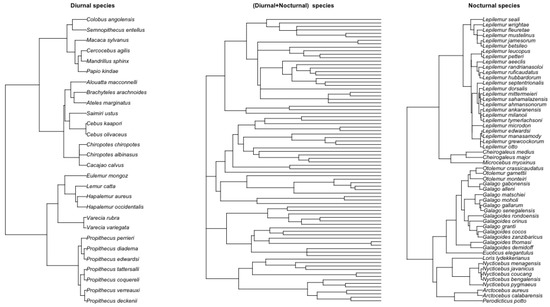
Figure 8. Left: Tree with 54 nocturnal primates. Right: Tree with 28 diurnal primates. Middle: Combined phylogenetic tree of 88 primate species.

4.2.1. Body Mass: Combined Diurnal and Nocturnal Species

Table 10 presents the parameter estimates for various phylogenetic autoregressive–moving-average (PhyRateARMA) and autoregressive (PhyRateAR) models. PhyRateARMA(1,1) shows the highest ${\varphi }_1$ value of $0.875$ and ${\theta }_1$ of $-0.652$, indicating a significant correlation between consecutive rates of evolution, with residual variance ${\tau }^2=1.103$. The weighted estimates combine the values across the models, with ${\varphi }_1=0.779$, ${\theta }_1=-0.566$, and $\tau =1.109$ providing a balanced view of the underlying process.

Table 10. MLE parameter estimated for the 88 combined diurnal and nocturnal primate species.

	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$0.372$				$1.170$
PhyRateAR(2)	$0.336$	$0.063$			$1.169$
PhyRateARMA(1,1)	$0.875$		$-0.652$		$1.103$
PhyRateARMA(2,1)	$0.784$	$0.091$	$-0.652$		$1.103$
PhyRateARMA(2,2)	$0.468$	$0.406$	$-0.225$	$-0.427$	$1.103$
Weighted Estimate	$0.779$	$0.057$	$-0.566$	$-0.034$	$1.109$

Using the PhyRateARMA(1,1) rate model in Equation (13), and as the equation for ${\sigma }_{\mathrm{des}}$ shows how the descendant’s rates of continuous evolution is determined by a combination of factors, in the weighted estimate the AR(1) estimate ${\varphi }_1$ suggests that 77.9% of the ancestor’s evolutionary rate (${\sigma }_{\mathrm{anc}}$) carries over to the descendant, indicating a strong correlation between the two rates. The MA(1) estimate ${\theta }_1$, which has a coefficient of $-0.566$, adjusts for the random variation (or noise) in the ancestor’s rate. This negative value means that random fluctuations in the ancestor’s rate are counterbalanced, effectively reducing the influence of ancestor-specific randomness on the descendant. Finally, ${ϵ}_{\mathrm{des}}$ has variance proportional to ${\tau }^2=1.109$, representing the new random variation specific to the descendant. The weighted estimates provide a balanced view of the process by combining these terms, giving insight into how both inherited traits and random fluctuations influence evolutionary changes across generations.

In Table 11, PhyRateARMA(1,1) ranks first with the lowest AICc value of $417.080$ and the highest Akaike weight ($w=0.610$), indicating the best fit among the models. PhyRateARMA(2,1) and PhyRateARMA(2,2) follow, but with considerably lower Akaike weights, suggesting that increasing model complexity beyond PhyRateARMA (1,1) does not produce substantial fit improvements. PhyRateAR(1) ranks the lowest, highlighting its reduced explanatory power compared to more complex models.

Table 11. Model information for the 88 combined diurnal and nocturnal primate species.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateARMA(1)	3	$-205.540$	$417.080$	$0.610$	1st
PhyRateARMA(2,1)	4	$-205.540$	$419.080$	$0.230$	2nd
PhyRateARMA(2,2)	5	$-205.540$	$421.080$	$0.080$	3rd
PhyRateAR(2)	3	$-208.060$	$422.120$	$0.050$	4th
PhyRateAR(1)	2	$-209.640$	$423.280$	$0.030$	5th

4.2.2. Body Mass: Diurnal Species

The parameter estimates in Table 12 for the diurnal models show that PhyRateAR(1) has a ${\varphi }_1$ value of $0.422$ with residual variance ${\tau }^2=0.129$, indicating a moderate level of influence from the previous rates of continuous evolution. PhyRateAR(2) introduces a second autoregressive term (${\varphi }_2=-0.206$) and slightly increases the variance to ${\tau }^2=0.131$. PhyRateARMA(1,1) and more complex models, such as PhyRateARMA(2,1) and PhyRateARMA(2,2), demonstrate negative ${\varphi }_1$ and ${\theta }_1$ values, but these more complex models have similar or slightly lower variances (${\tau }^2=0.127$). The weighted estimate shows that the descendant’s rate is influenced by ${\varphi }_1=26.0$% of the ancestor’s rate, with a positive adjustment of ${\theta }_1=22.2$% from the ancestor’s noise, while the process has a relatively low variance of $0.127$.

Table 12. Diurnal species model parameter estimates.

	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$0.422$				$0.129$
PhyRateAR(2)	$0.526$	$-0.206$			$0.131$
PhyRateARMA(1,1)	$-0.138$		$0.730$		$0.127$
PhyRateARMA(2,1)	$-0.004$	$-0.134$	$0.730$		$0.127$
PhyRateARMA(2,2)	$-0.008$	$-0.130$	$-0.128$	$0.858$	$0.127$
Weighted Estimate	$0.260$	$-0.050$	$0.222$	$0.026$	$0.127$

In Table 13, PhyRateAR(1) is the first with the lowest AICc value of $45.680$ and the highest Akaike weight ($w=0.480$), making it the best-fitting model for the diurnal data. PhyRateARMA(1,1) ranks second with an AICc of $47.170$ and a lower weight ($w=0.230$), followed by PhyRateAR(2) with an AICc of $47.710$ ($w=0.170$). More complex models such as PhyRateARMA(2,1) and PhyRateARMA(2,2) rank lowest, with minimal Akaike weights, indicating that they provide little additional explanatory power.

Table 13. Diurnal species model results.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(1)	2	$-20.840$	$45.680$	$0.480$	1st
PhyRateARMA(1,1)	3	$-20.580$	$47.170$	$0.230$	2nd
PhyRateAR(2)	3	$-20.850$	$47.710$	$0.170$	3rd
PhyRateARMA(2,1)	4	$-20.580$	$49.170$	$0.080$	4th
PhyRateARMA(2,2)	5	$-20.580$	$51.170$	$0.030$	5th

4.2.3. Body Mass: Nocturnal species

The parameter estimates in Table 14 for the nocturnal models indicate that PhyRateAR(1) has a ${\varphi }_1$ value of $-0.213$ and a residual variance of ${\tau }^2=0.003$, suggesting a weak negative influence from the previous rates of continuous evolution. PhyRateAR(2) introduces a second autoregressive term (${\varphi }_2=-0.080$) and slightly increases the variance to ${\tau }^2=0.004$. PhyRateARMA (1,1) has larger ${\varphi }_1=0.593$ and ${\theta }_1=-0.901$, with a similar variance of ${\tau }^2=0.004$, indicating a stronger dependency on the autoregressive and moving average terms. The weighted estimate shows a balance between models with ${\varphi }_1=-0.181$, ${\theta }_1=-0.037$, and ${\tau }^2=0.003$. The weighted estimate indicates that the descendant’s rate is slightly negatively influenced by the ancestor’s rate (${\varphi }_1=-18.1$%) and its noise (${\theta }_1=-3.7$%), with very low overall variance ($0.003$), suggesting minimal change between generations.

Table 14. Nocturnal species model parameter estimates.

	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$-0.213$				$0.003$
PhyRateAR(2)	$-0.230$	$-0.080$			$0.004$
PhyRateARMA(1,1)	$0.593$		$-0.901$		$0.004$
PhyRateARMA(2,1)	$0.647$	$0.075$	$-1.000$		$0.004$
PhyRateARMA(2,2)	$-0.107$	$0.610$	$-0.243$	$-0.757$	0.004
Weighted Estimate	$-0.181$	$-0.002$	$-0.037$	$0.000$	$0.003$

In Table 15, PhyRateAR (1) is the first with the lowest AICc value of $-255.450$ and the highest Akaike weight ($w=0.930$), indicating that it is the best-fitting model for nocturnal data. PhyRateAR(2) and PhyRateARMA(1,1) rank much lower, with AICc values of $-248.710$ and $-248.690$, respectively, both having a very small Akaike weight ($w=0.030$). More complex models such as PhyRateARMA(2,1) and PhyRateARMA(2,2) rank lowest, with minimal Akaike weights, indicating they add little explanatory power and overcomplicate the fit for the nocturnal data.

Table 15. Nocturnal species model results.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(1)	2	$129.730$	$-255.450$	$0.930$	1st
PhyRateAR(2)	3	$127.350$	$-248.710$	$0.030$	2nd
PhyRateARMA(1,1)	3	$127.340$	$-248.690$	$0.030$	3th
PhyRateARMA(2,1)	4	$127.290$	$-246.580$	$0.010$	4th
PhyRateARMA(2,2)	5	$123.660$	$-237.320$	$0.000$	5th

From the above results, one may foresee that the nocturnal primate and the diurnal primate body masses possess different autoregressive effects for the rates of the evolution, and we provide the test results in the following sections.

4.2.4. Testing Autocorrelation Rate

Interpretation of PhyRateAR(1) Test Results

Table 16 shows the PhyRateAR(1) test result.

Table 16. $H_0:\varphi =0$, $H_a:\varphi \ne 0$.

Tree Case	z-val	p-val	Significant?
Diurnal tree	$4.237$	$0.000$	Y
Nocturnal tree	$-2.763$	$0.006$	Y
Combined tree	$4.229$	$0.000$	Y

Table 16 presents the results of the PhyRateAR(1) test under the null hypothesis $H_0:\varphi =0$ (no autocorrelation) and the alternative hypothesis $H_a:\varphi \ne 0$. The combined tree and the diurnal tree show significant positive autocorrelation with large z-values ($4.229$ and $4.237$, respectively) and p values of $0.000$, indicating a strong rejection of the null hypothesis. This suggests a significant effect of the previous evolution rate on the current rate in these datasets.

Interestingly, the nocturnal tree exhibits a significant negative autocorrelation with a z value of $-2.763$ and a p value of $0.006$. Despite the negative z-value, the small p-value suggests a significant relationship. This indicates that while each tree shows a significant effect, the nocturnal tree behaves differently from the combined and diurnal trees, potentially indicating unique evolutionary dynamics in nocturnal species.

Testing Heterogeity Rates on Subclades

Table 17 presents the results of the test of heterogeneity in evolutionary rates in the diurnal, nocturnal, and combined (dino) subclades using various autoregressive models (PhyRateAR(1), PhyRateAR(2), PhyRateARMA(1,1), PhyRateARMA(2,1), PhyRateARMA(2,2)). The log-likelihood values for the diurnal ($logL$_di), nocturnal ($logL$_no), and combined ($logL$_dino) data are shown, along with the chi-squared statistic and p-values. All models show highly significant results (p-values = 0.00), indicating strong evidence for rate heterogeneity between subclades. The chi-squared statistic is the highest for PhyRateAR(1) ($637.06$), suggesting that it explains the greatest amount of variance in the data compared to the other models.

Table 17. Testing heterogeneity rates on subclade. $H_0$: one ${\varphi }_1={\varphi }_2$, $H_a$: ${\varphi }_1\ne {\varphi }_2$.

Model	$log\mathit{L}$_di	$log\mathit{L}$_no	$log\mathit{L}$_dino	${\mathrm{LRT}}_{{\mathit{\chi }}^2}$	p-val	Significant?
PhyRateAR(1)	$-20.84$	$129.73$	$-209.64$	$637.06$	$0.00$	Y
PhyRateAR(2)	$-20.85$	$127.35$	$-208.06$	$629.12$	$0.00$	Y
PhyRateARMA(1,1)	$-20.58$	$127.34$	$-205.54$	$624.60$	$0.00$	Y
PhyRateARMA(2,1)	$-20.58$	$127.29$	$-205.54$	$624.50$	$0.00$	Y
PhyRateARMA(2,2)	$-20.58$	$123.66$	$-205.54$	$617.24$	$0.00$	Y

5. Discussion and Conclusions

This study introduces the first model developed for evolutionary rate estimation using the ARMA model. We first assumed that species evolve along a phylogenetic tree, with time length, evolutionary rate, and trait values expressed as a linear combination. Using the given trait values and branch lengths of the phylogenetic tree, we applied ridge regression and used the R package RRphylo to estimate the evolutionary rate. Next, we modeled the evolutionary rate using the PhyRateARMA(p,q) models, fitting these models to ancestral trait values, and then applied these models to estimate present-day trait values.

In the empirical analysis, we tested whether the rates of continuous trait evolution exhibited time series correlation. In the plant dataset, which combines herbaticus and woody genome sizes, the results did not show an autoregressive effect relationship. However, in the diurnal and nocturnal population dataset, which combines male and female primate body masses, the results indicated an autoregressive effect in the separate analyses of diurnal and nocturnal populations, suggesting a time-series relationship. To observe the evolutionary dynamics, the branches might have different autoregressive coefficients ($\varphi$). These branches can be analyzed to understand how differences between them affect the overall model. Further analysis could deepen the exploration of the effects of this statistical model in the biological context, providing a more comprehensive scientific explanation to more precisely understand and interpret evolutionary processes and phylogenetic patterns in biological systems.

Several methods estimate autoregressive (AR) and moving average (MA) model parameters. Maximum Likelihood Estimation (MLE) assumes normally distributed errors, while Least Squares focuses on AR parameters. The Yule-Walker Equations and Burg’s method enhance AR estimation, but the Innovations Algorithm handles both AR and MA. Bayesian Estimation uses priors and MCMC [41], while bootstrapping evaluates differences in PhyRateAR(1) parameters by resampling and comparing empirical distributions of $\Delta \varphi$. Recent applications of machine learning (ML) in related fields, such as molecular evolution [42,43], demonstrate the potential to enhance phylogenetic analyses and inference. Developing such approaches for trait evolution could open new avenues for addressing unresolved questions and refining our understanding of evolutionary processes. Advanced approaches, such as a PhyRateARMA framework, could leverage ML to better account for structural dependencies in phylogenetic trees and manage conditional heterogeneity in evolutionary processes. Inspired by the use of ARMA/GARCH models in other domains [22]. These advancements would provide a promising direction for future studies, extending the utility and applicability of evolutionary rate models.

Proposed research could extend the phylogenetic autoregressive-moving-average model by examining how regional factors like vaccination rates or population density influence SARS-CoV-2 mutation rates and traits like transmissibility. For land mammals, the model could assess changes in diet breadth, climate niche, and range size over time, incorporating phylogenetic data to study species’ responses to environmental pressures. Additionally, exploring how latitude impacts elevation across biomes and under human activities like deforestation would provide deeper insights into climate-related changes, broadening the model’s applicability.

A.1. Code and Scripts

Script and data can be accessed through the following link https://tonyjhwueng.info/phyarmarate (accessed on 28 December 2024).

A.1.1. Model Script

• Main empirical analysis: https://tonyjhwueng.info/phyarmarate/mainPhyarima.R (accessed on 28 December 2024).
• Model PhyRateARMA(p,q): https://tonyjhwueng.info/phyarmarate/testphyloratesV3.r (accessed on 28 December 2024).

A.1.2. Figures and Table

• Figure 1: https://tonyjhwueng.info/phyarmarate/twosigbmv4.html (accessed on 28 December 2024).
• Figure 2: https://tonyjhwueng.info/phyarmarate/4spetreemap.html (accessed on 28 December 2024).
• Figure 3: https://tonyjhwueng.info/phyarmarate/yLs.pptx (accessed on 28 December 2024).
• Figure 4: https://tonyjhwueng.info/phyarmarate/armarate2.pptx (accessed on 28 December 2024).
• Figure 5: https://tonyjhwueng.info/phyarmarate/tworatetree.html (accessed on 28 December 2024).
• Figure 6, Table 1: https://tonyjhwueng.info/phyarmarate/onerateT1powerSummarizer.html (accessed on 28 December 2024).
• Section 4.1, Figure 7 and Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9: https://tonyjhwueng.info/phyarmarate/plantWoHeGsize.html (accessed on 28 December 2024).
• Section 4.2, Figure 8 and Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16 and Table 17: https://tonyjhwueng.info/phyarmarate/primateDiNoBodyMass.html (accessed on 28 December 2024).
• Additional:

  –

  Male primates: https://tonyjhwueng.info/phyarmarate/primateDiNoBodyMassMale.html (accessed on 28 December 2024).

  –

  Female primates: https://tonyjhwueng.info/phyarmarate/primateDiNoBodyMassFemale.html (accessed on 28 December 2024).

• Appendix A.3: https://tonyjhwueng.info/phyarmarate/TestPhyArimaExample.html (accessed on 28 December 2024).

A.2. Phylogenetic ARMA(p,q) Model for Rate Evolution

Given tree topology $\mathcal{T}$ of n taxa, with tip node $\mathit{y}=(y_1,y_2,\cdots ,y_n)$ and internal node $\mathcal{J}=(j_1,j_2,\cdots ,j_m)$, and the corresponding branch-length set $\mathcal{B}=\{l_{j_1},l_{j_2},\cdots ,l_{j_m}\}$ with the ancestral-descendant relationship and fitting RRphylo [28], one can obtain a set of estimated rates ${\Sigma }_{\mathcal{J}}={\left\{{\sigma }_{j_s}\right\}}_{s=1}^m$ for the tree. The phylogenetic ARMA($p,q$) model of rates is a mixture of phylogenetic autoregressive (AR) and phylogenetic moving average (MA) models given by the following equation:

$${\sigma }_{j_s}=c+\sum _{i=1}^p{\varphi }_i{\sigma }_{j_{s-i}}+\sum _{j=1}^q{\theta }_j{ϵ}_{j_{s-j}}+{ϵ}_{j_s},\mathrm{where}{ϵ}_{j_s}\sim \mathcal{N}(0,{\tau }^2{l}_{j_s})$$

(A1)

where ${\sigma }_{j_s}$ represents the time series at time $j_s$, c is a constant, ${\varphi }_i$ are coefficients for the AR terms, ${\theta }_j$ are coefficients for the MA terms, and ${ϵ}_{j_s}$ denotes the white noise error terms with mean 0 and variance ${\tau }^2{l}_{j_s}$.

A.2.1. PhyRateAR(1) Model

The PhyRateAR(1) model for rates of continuous trait evolution along the phylogenetic tree is written as

$${\sigma }_{j_s}=\varphi {\sigma }_{j_s^{\prime }}+{ϵ}_{j_s},$$

(A2)

where nodes $j_s,j_s^{\prime }\in \mathcal{J}$ possess ancestral-descendant relationship, and ${ϵ}_{j_s}\sim \mathcal{N}(0,{\tau }^2{l}_{j_s}).$

The negative log-likelihood is

$$L(\varphi ,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})={\displaystyle \frac{m}{2}}log\left(2\pi \right)+{\displaystyle \frac{m}{2}}log\left({\tau }^2\right)+{\displaystyle \frac{1}{2{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }}\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }})}^2,$$

(A3)

where $m=\left|\mathcal{J}\right|$ is the number of branches, and ${\sigma }_{j_s}$ and ${\sigma }_{j_s^{\prime }}$ are the two successive rates along the branch lengths $l_{j_s}$ and $l_{j_s^{\prime }}$, respectively.

To find the maximum likelihood estimates of $\varphi$ and ${\tau }^2$ for the PhyRateAR(1) rate process, we aim to minimize the negative log-likelihood. This requires setting the derivatives of the negative log-likelihood with respect to $\varphi$ and ${\tau }^2$ to zero and solving these equations for the parameters.

The first-order conditions for the derivatives are $-L_{\varphi }=0$ and $-L_{{\tau }^2}=0.$ For $\varphi$, the derivative simplifies to

$$-L_{\varphi }=-{\displaystyle \frac{1}{{\tau }^2}}\sum _{({\sigma }_{j_s},{\sigma }_{j_s^{\prime }})\in {\Sigma }_{\mathcal{J}}}({\sigma }_{j_s^{\prime }}{\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}^2)=0,$$

(A4)

which leads to

$$\widehat{\varphi }={\displaystyle \frac{{\sum }_{({\sigma }_{j_s},{\sigma }_{j_s^{\prime }})\in {\Sigma }_{\mathcal{J}}}{\sigma }_{j_s^{\prime }}{\sigma }_{j_s}}{{\sum }_{({\sigma }_{j_s},{\sigma }_{j_s^{\prime }})\in {\Sigma }_{\mathcal{J}}}{\sigma }_{j_s^{\prime }}^2}}.$$

(A5)

For ${\tau }^2$, the derivative is

$$-L_{{\tau }^2}={\displaystyle \frac{m}{2{\tau }^2}}-{\displaystyle \frac{1}{2{\left({\tau }^2\right)}^2}}\sum _{({\sigma }_{j_s},{\sigma }_{j_s^{\prime }})\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }})}^2=0,$$

(A6)

leading to

$${\widehat{\tau }}^2={\displaystyle \frac{1}{m}}\sum _{({\sigma }_{j_s},{\sigma }_{j_s^{\prime }})\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }})}^2.$$

(A7)

These formulations allow us to estimate the parameters that best fit our PhyloRateAR(1) model based on the observed evolutionary rates along a phylogenetic tree.

A.2.2. PhyRateAR(2) Model

The PhyRateAR(2) model for rates of continuous trait evolution along the phylogenetic tree is written as

$${\sigma }_{j_s}={\varphi }_1{\sigma }_{j_s^{\prime }}+{\varphi }_2{\sigma }_{j_s^{″}}+{ϵ}_{j_s},$$

(A8)

where ${\sigma }_{j_s^{″}}$ is the rate on the next down successive branch.

Given a phylogenetic lineage with rates ${\left\{{\sigma }_{j_s}\right\}}_{s=1}^m$, the likelihood function for the PhyRateAR(2) model parameters ${\varphi }_1,{\varphi }_2$ and ${\tau }^2$ is

$$L({\varphi }_1,{\varphi }_2,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})=\prod _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }},{\sigma }_{j_s^{″}}\in {\Sigma }_{\mathcal{J}}}{\displaystyle \frac{1}{\sqrt{2\pi {\tau }^2}}}exp\left(-{\displaystyle \frac{{({\sigma }_{j_s}-{\varphi }_1{\sigma }_{j_s^{\prime }}-{\varphi }_2{\sigma }_{j_s^{″}})}^2}{2{\tau }^2}}\right)$$

(A9)

The log-likelihood function simplifies to

$$logL({\varphi }_1,{\varphi }_2,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})=-{\displaystyle \frac{m-2}{2}}log\left(2\pi {\tau }^2\right)-{\displaystyle \frac{1}{2{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }},{\sigma }_{j_s^{″}}\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-{\varphi }_1{\sigma }_{j_s^{\prime }}-{\varphi }_2{\sigma }_{j_s^{″}})}^2$$

(A10)

To find the maximum likelihood estimates (MLEs) for ${\varphi }_1$, ${\varphi }_2$, and ${\tau }^2$, the log-likelihood function’s partial derivatives are taken with respect to each parameter, set to zero, and solved for these parameters.

The equations for partial derivatives are

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial {\varphi }_1}}L({\varphi }_1,{\varphi }_2,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})& ={\displaystyle \frac{-1}{{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }},{\sigma }_{j_s^{″}}\in {\Sigma }_{\mathcal{J}}}({\sigma }_{j_s}-{\varphi }_1{\sigma }_{j_s^{\prime }}-{\varphi }_2{\sigma }_{j_s^{″}}){\sigma }_{j_s^{\prime }},\hfill \end{array}$$

(A11)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial {\varphi }_2}}logL({\varphi }_1,{\varphi }_2,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})& ={\displaystyle \frac{-1}{{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }},{\sigma }_{j_s^{″}}\in {\Sigma }_{\mathcal{J}}}({\sigma }_{j_s}-{\varphi }_1{\sigma }_{j_s^{\prime }}-{\varphi }_2{\sigma }_{j_s^{″}}){\sigma }_{j_s^{″}},\hfill \end{array}$$

(A12)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial {\tau }^2}}logL({\varphi }_1,{\varphi }_2,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})& =-{\displaystyle \frac{m-2}{2{\tau }^2}}+{\displaystyle \frac{1}{2{\left({\tau }^2\right)}^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }},{\sigma }_{j_s^{″}}\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-{\varphi }_1{\sigma }_{j_s^{\prime }}-{\varphi }_2{\sigma }_{j_s^{″}})}^2.\hfill \end{array}$$

(A13)

Solving these equations provides the MLEs for ${\varphi }_1$, ${\varphi }_2$, and ${\tau }^2$ in a phylogenetic context.

A.2.3. PhyRateARMA(1,1) Model

The PhyRateARMA(1,1) model for rates of continuous trait evolution along the phylogenetic tree is written as

$${\sigma }_{j_s}={\varphi }_1{\sigma }_{j_s^{\prime }}+{ϵ}_{j_s^{\prime }}+{\theta }_1{ϵ}_{j_s^{″}},$$

(A14)

where ${ϵ}_{j_s^{″}}$ represents the corresponding white noise error terms with variance ${\tau }^2{l}_{j_s^{″}}$ associated with the noise of the evolutionary process.

The likelihood function for the PhyRateARMA(1, 1) process, assuming that the errors are normally distributed, is given by the product of the probability densities of the innovations ${\eta }_t$, which are the one-step forecast errors:

$$\begin{array}{cc}\hfill L(\varphi ,\theta ,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})& =\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }}\in {\Sigma }_{\mathcal{J}}}{\displaystyle \frac{1}{\sqrt{2\pi {\tau }^2}}}exp\left(-{\displaystyle \frac{{({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}-\theta {\epsilon }_{j_s^{\prime }})}^2}{2{\tau }^2}}\right),\hfill \end{array}$$

(A15)

$$\begin{array}{cc}\hfill logL(\varphi ,\theta ,{\tau }^2|\mathcal{T},{\Sigma }_{\mathcal{J}})& =-{\displaystyle \frac{m-1}{2}}log\left(2\pi \right)-{\displaystyle \frac{m-1}{2}}log\left({\tau }^2\right)-{\displaystyle \frac{1}{2{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }}\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}-\theta {\epsilon }_{j_s^{\prime }})}^2.\hfill \end{array}$$

(A16)

The MLEs for $\varphi$, $\theta$, and ${\tau }^2$ are found by taking the partial derivatives of the log-likelihood function with respect to these parameters and setting them to zero:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial logL}{\partial \varphi }}& =-{\displaystyle \frac{1}{{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }}\in {\Sigma }_{\mathcal{J}}}({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}-\theta {\epsilon }_{j_s^{\prime }}){\sigma }_{j_s^{\prime }}=0,\hfill \end{array}$$

(A17)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial logL}{\partial \theta }}& =-{\displaystyle \frac{1}{{\tau }^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }}\in {\Sigma }_{\mathcal{J}}}({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}-\theta {\epsilon }_{j_s^{\prime }}){\epsilon }_{j_s^{\prime }}=0,\hfill \end{array}$$

(A18)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial logL}{\partial {\tau }^2}}& =-{\displaystyle \frac{m-1}{2{\tau }^2}}+{\displaystyle \frac{1}{2{\left({\tau }^2\right)}^2}}\sum _{{\sigma }_{j_s},{\sigma }_{j_s^{\prime }}\in {\Sigma }_{\mathcal{J}}}{({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}-\theta {\epsilon }_{j_s^{\prime }})}^2=0.\hfill \end{array}$$

(A19)

These equations generally require numerical optimization to solve because the innovations ${({\sigma }_{j_s}-\varphi {\sigma }_{j_s^{\prime }}-\theta {\epsilon }_{j_s^{\prime }})}^2$ depend on both $\varphi$ and $\theta$ in a nonlinear way. To estimate the parameters $\varphi$ and $\theta$, we use iterative numerical optimization methods that handle nonlinearity. Specifically, we apply the L-BFGS-B method [44] by initializing with a starting point and boundary constraints, to maximize the likelihood function. the R software package stats::optim (version 3.6.2) [34].

A.2.4. PhyRateARMA(2,2) Model

The PhyRateARMA(2,2) model for rates of continuous trait evolution along the phylogenetic tree is written as

$${\sigma }_{j_s}={\varphi }_1{\sigma }_{j_s^{\prime }}+{\varphi }_2{\sigma }_{j_{s^{″}}}+{\theta }_1{ϵ}_{j_s^{\prime }}+{\theta }_2{ϵ}_{j_{s^{″}}}+{ϵ}_{j_s},$$

(A20)

where ${\sigma }_{j_s}$ represents the time series at time $j_s$; c is a constant; ${\varphi }_1,{\varphi }_2$ are coefficients for the AR terms; ${\theta }_1,{\theta }_2$ are coefficients for the MA terms; and ${ϵ}_{j_s}$ denotes the white noise error terms.

Similar to PhyRateARMA(1,1), to estimate the parameters $({\varphi }_1,{\varphi }_2)$, $({\theta }_1,{\theta }_2)$, and $\tau$, we again apply the L-BFGS-B method [44] to maximize the likelihood function performed by the R software package stats::optim (version 3.6.2) [34].

A.3. Test Example

Figure A1:

Figure A1. A rooted phylogenetic tree $\mathcal{T}$ of 8 taxa.

Trait values are listed in Table A1.

Table A1. Trait values.

y1	y2	y3	y4	y5	y6	y7	y8
$-0.03$	$-0.09$	$-0.45$	$-0.85$	$-0.51$	$-0.05$	$-1.31$	$-0.57$

Table A1. Trait values.

y1	y2	y3	y4	y5	y6	y7	y8
$-0.03$	$-0.09$	$-0.45$	$-0.85$	$-0.51$	$-0.05$	$-1.31$	$-0.57$

Table A2. Edge lengths obtained by tree $\mathcal{T}$ with branch lengths using R ape package (version 5.8.1) [45].

eg1	eg2	eg3	eg4	eg5	eg6	eg7
$0.143$	$0.143$	$0.143$	$0.143$	$0.286$	$0.286$	$0.143$
eg8	eg9	eg10	eg11	eg12	eeg13	eeg14
$0.143$	$0.143$	$0.143$	$0.143$	$0.286$	$0.286$	$0.571$

Table A2. Edge lengths obtained by tree $\mathcal{T}$ with branch lengths using R ape package (version 5.8.1) [45].

eg1	eg2	eg3	eg4	eg5	eg6	eg7
$0.143$	$0.143$	$0.143$	$0.143$	$0.286$	$0.286$	$0.143$
eg8	eg9	eg10	eg11	eg12	eeg13	eeg14
$0.143$	$0.143$	$0.143$	$0.143$	$0.286$	$0.286$	$0.571$

Use Equation (10) (and package RRphylo) to obtain rate estimate $\left\{{\sigma }_{j_s}\right\}$ in Table A3.

Table A3. Rate estimates $\left\{{\sigma }_{j_s}\right\}$ (here denote as ${\mathrm{nd}}_j$ corresponding to the tree $\mathcal{T}$ in Figure A1 from rrphylo.

nd1	nd2	nd3	nd4	nd5	nd6	nd7	nd8
$-0.320$	$-0.034$	0.053	$-0.070$	$-1.247$	$-0.178$	$-0.445$	$0.003$
nd9	nd10	nd11	nd12	nd13	nd14	nd15
$0.023$	$-0.041$	$0.006$	$-0.062$	$-0.027$	$-0.054$	$-0.168$

Table A3. Rate estimates $\left\{{\sigma }_{j_s}\right\}$ (here denote as ${\mathrm{nd}}_j$ corresponding to the tree $\mathcal{T}$ in Figure A1 from rrphylo.

nd1	nd2	nd3	nd4	nd5	nd6	nd7	nd8
$-0.320$	$-0.034$	0.053	$-0.070$	$-1.247$	$-0.178$	$-0.445$	$0.003$
nd9	nd10	nd11	nd12	nd13	nd14	nd15
$0.023$	$-0.041$	$0.006$	$-0.062$	$-0.027$	$-0.054$	$-0.168$

Table A4. Maximum likelihood for parameter estimates under each model.

Model	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$0.296$				$0.130$
PhyRateAR(2)	$0.303$	$-0.017$			$0.141$
PhyRateARMA(1,1)	$0.582$		$-0.396$		$0.125$
PhyRateARMA(2,1)	$-0.087$	0.669	$-0.396$		$0.125$
PhyRateARMA(2,2)	$-0.046$	$0.629$	$-0.120$	$-0.276$	$0.125$
Weighted Estimate	$0.322$	$0.070$	$-0.126$	$-0.008$	$0.130$

Table A4. Maximum likelihood for parameter estimates under each model.

Model	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\tau }}^2$
PhyRateAR(1)	$0.296$				$0.130$
PhyRateAR(2)	$0.303$	$-0.017$			$0.141$
PhyRateARMA(1,1)	$0.582$		$-0.396$		$0.125$
PhyRateARMA(2,1)	$-0.087$	0.669	$-0.396$		$0.125$
PhyRateARMA(2,2)	$-0.046$	$0.629$	$-0.120$	$-0.276$	$0.125$
Weighted Estimate	$0.322$	$0.070$	$-0.126$	$-0.008$	$0.130$

Table A5. Model output: k number of parameters; AICc weight w.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(1)	2	$8.66$	$-13.33$	$0.60$	1st
PhyRateARMA(1,1)	3	$8.67$	$-11.33$	$0.22$	2nd
PhyRateARMA(2,1)	4	$8.67$	$-9.33$	$0.08$	3th
PhyRateAR(2)	3	$7.52$	$-9.04$	$0.07$	4th
PhyRateARMA(2,2)	5	$8.67$	$-7.33$	$0.03$	5th

Table A5. Model output: k number of parameters; AICc weight w.

Model	k	$log\mathit{L}$	$\mathit{AICc}$	w	Rank
PhyRateAR(1)	2	$8.66$	$-13.33$	$0.60$	1st
PhyRateARMA(1,1)	3	$8.67$	$-11.33$	$0.22$	2nd
PhyRateARMA(2,1)	4	$8.67$	$-9.33$	$0.08$	3th
PhyRateAR(2)	3	$7.52$	$-9.04$	$0.07$	4th
PhyRateARMA(2,2)	5	$8.67$	$-7.33$	$0.03$	5th

A.4. Trait Dataset for Empirical Analysis

For plant data and primate data, the tree files in Newick format, as well as the trait dataset in csv files, can be accessed at https://tonyjhwueng.info/phyarmarate/dataset (accessed on 28 December 2024).