Adaptive Control for Multi-Agent Systems Governed by Fractional-Order Space-Varying Partial Integro-Differential Equations
Abstract
1. Introduction
2. Problem Formulation
3. Consensus of Leaderless Fractional-Order SVPIDE-Based MASs
4. Consensus of the Leader-Following Fractional-Order SVPIDE-Based MASs
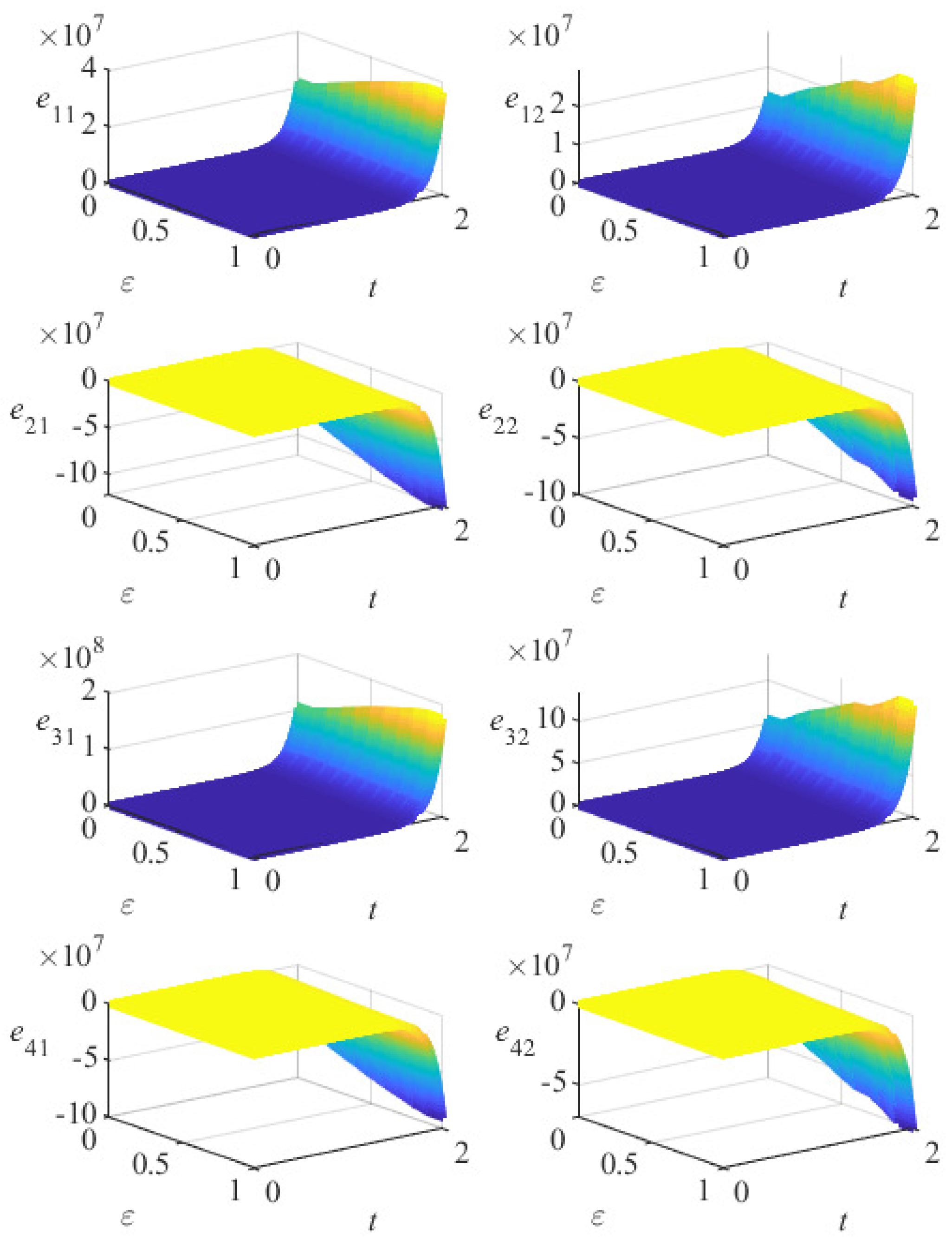
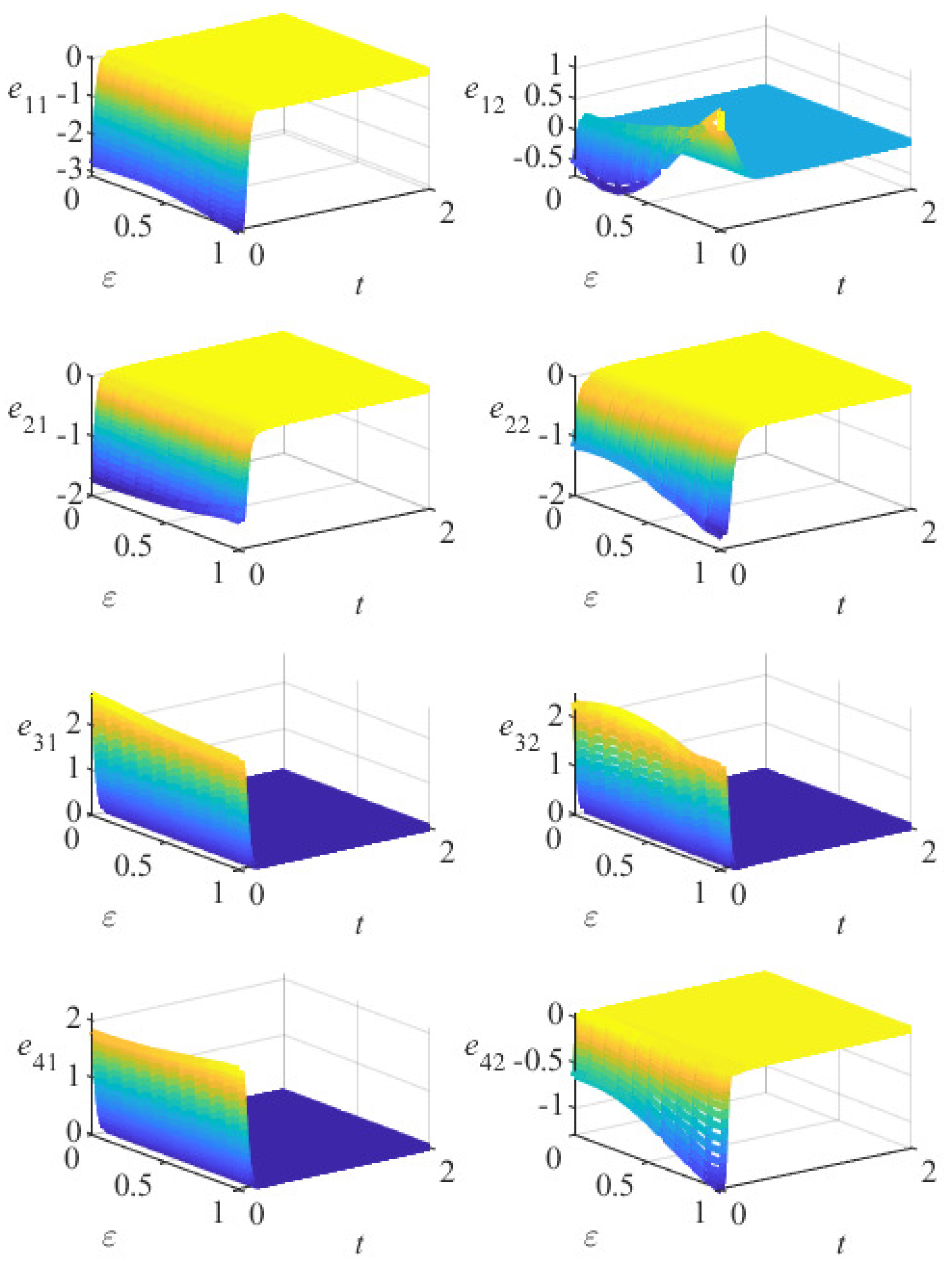
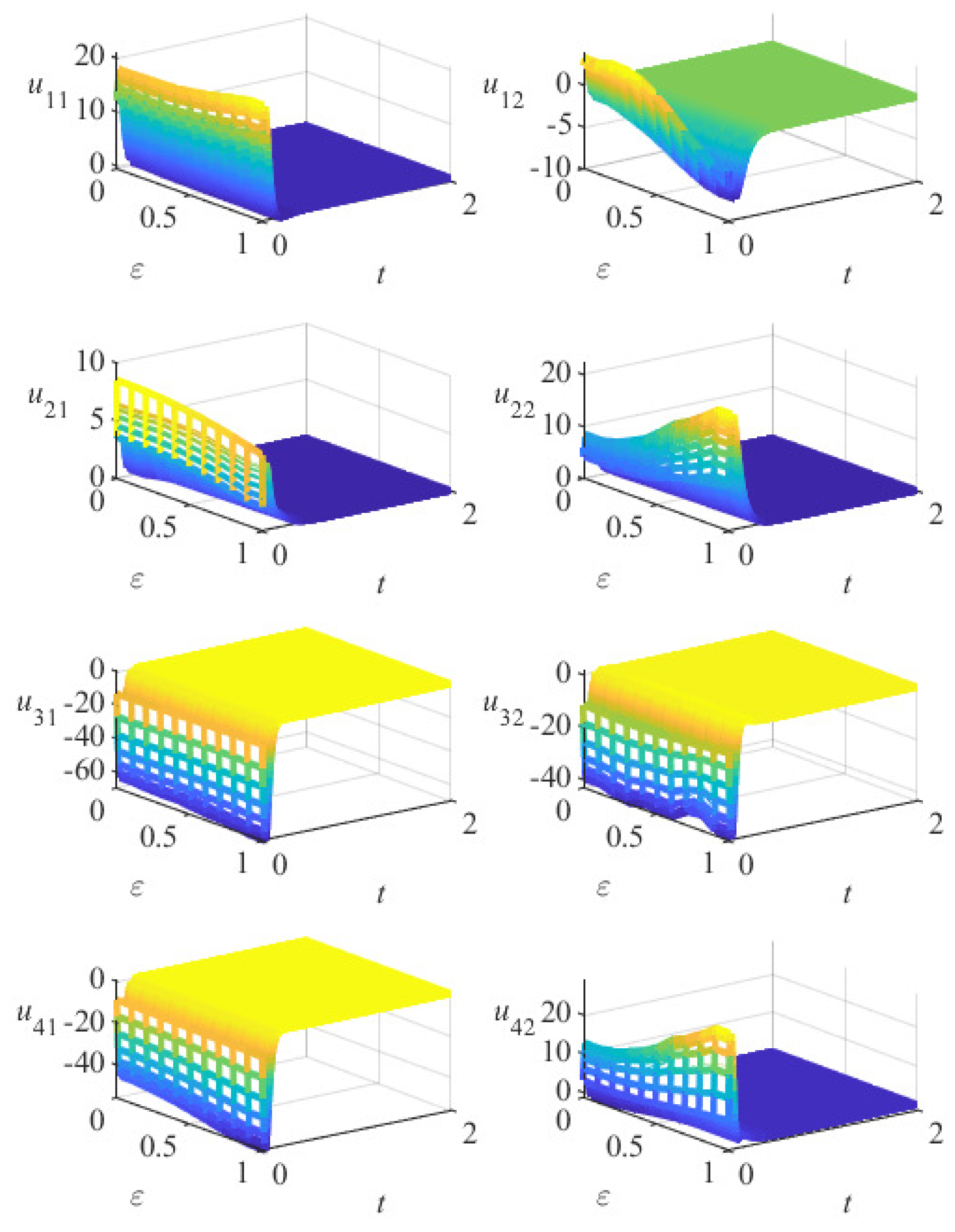
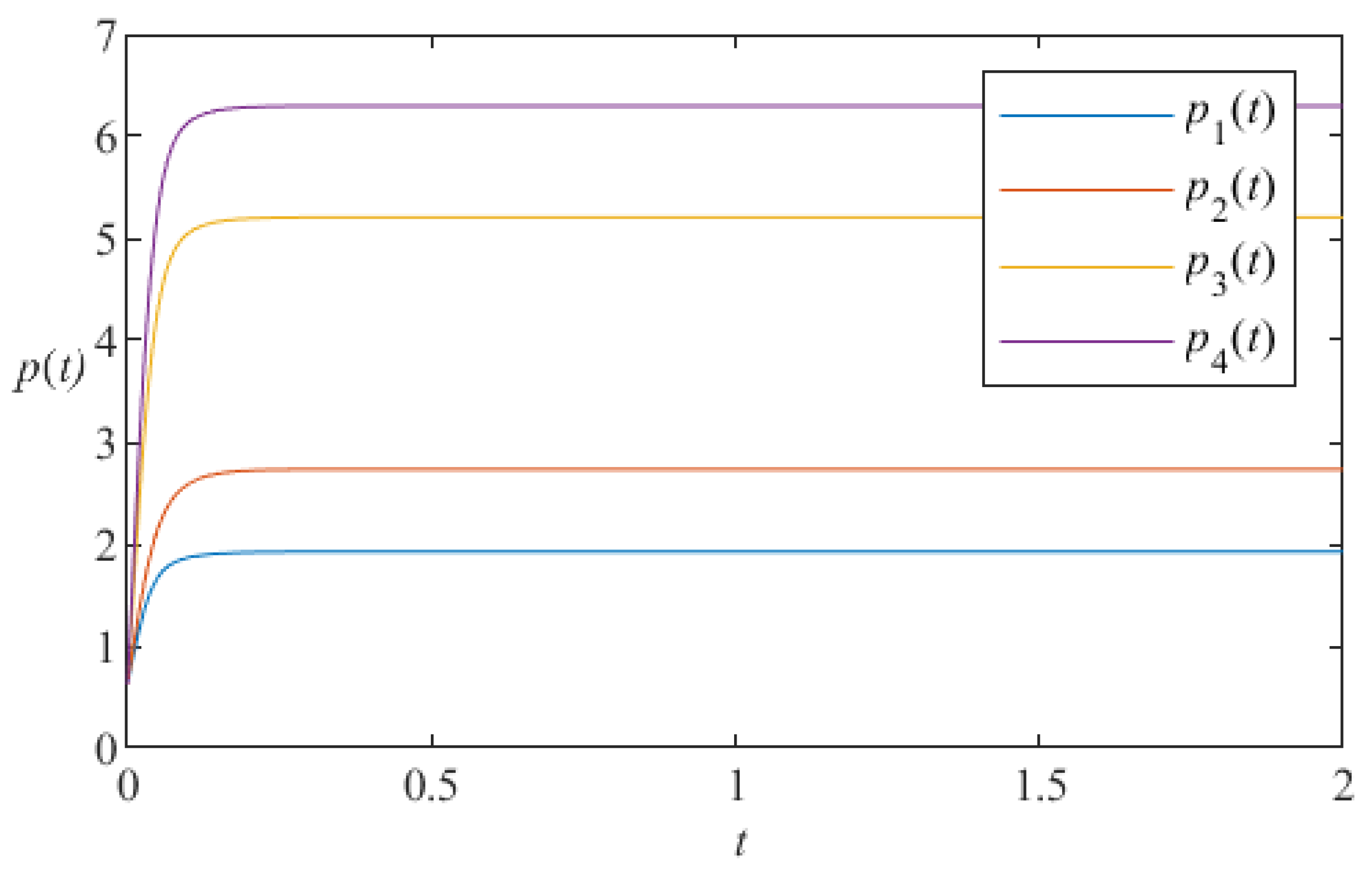
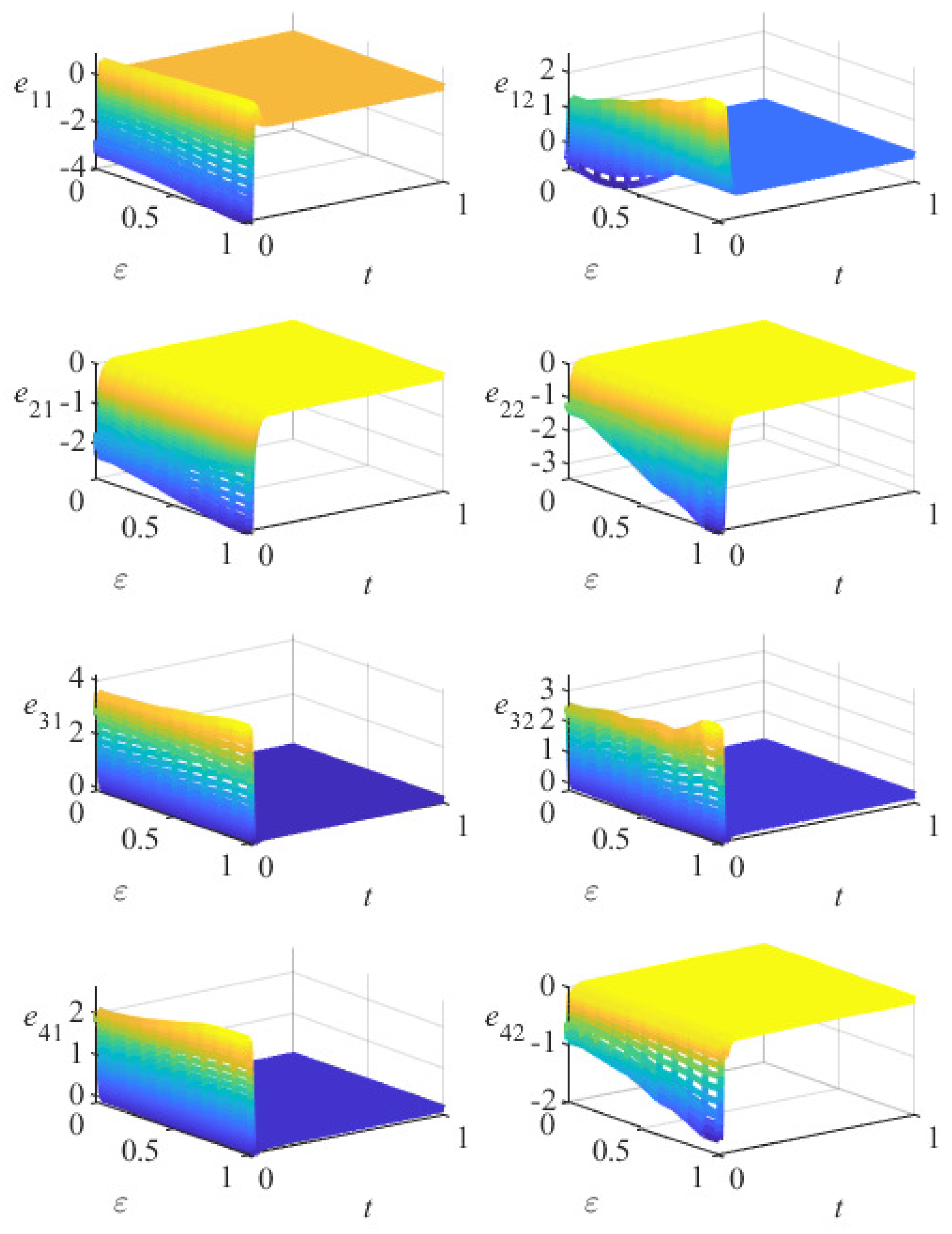
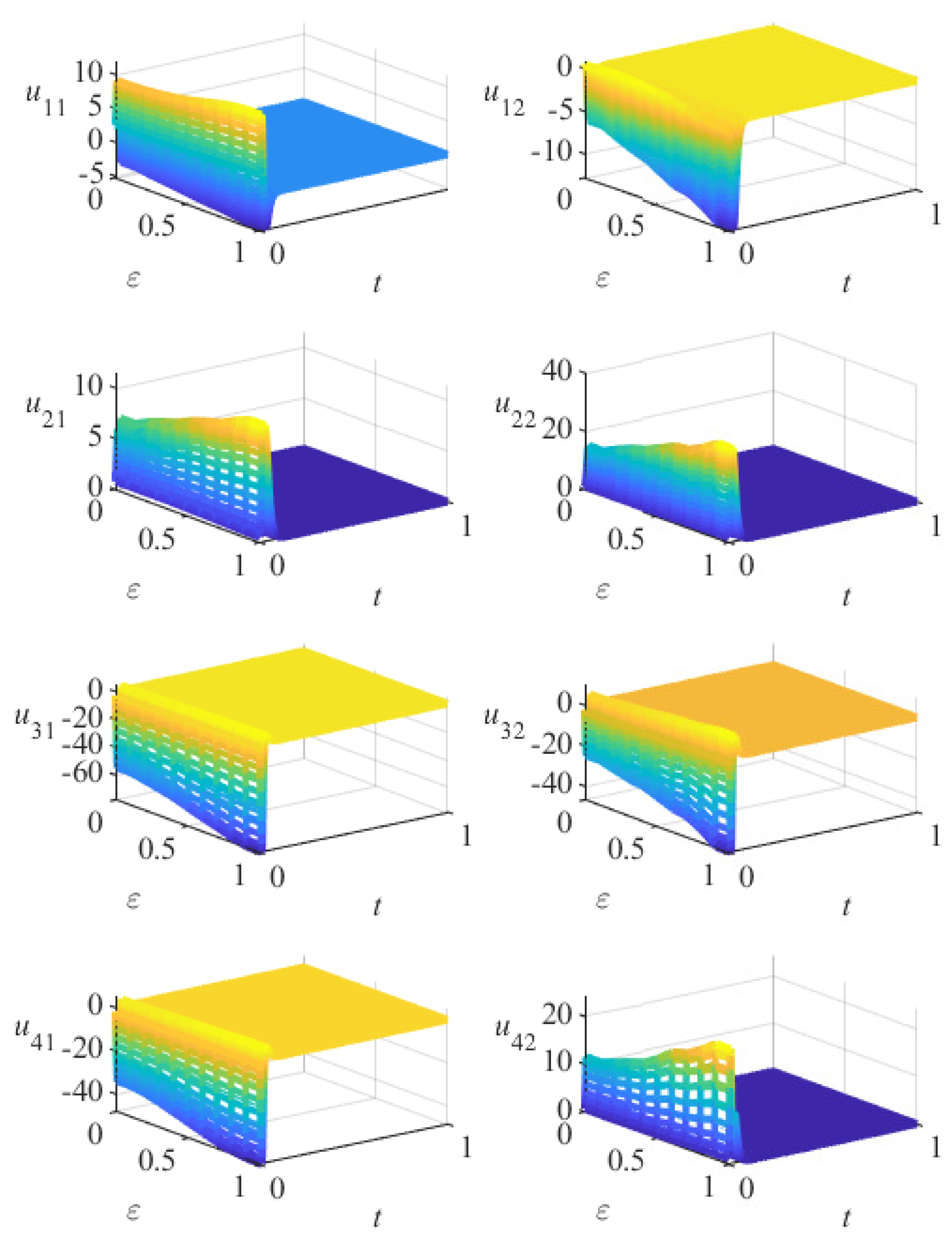
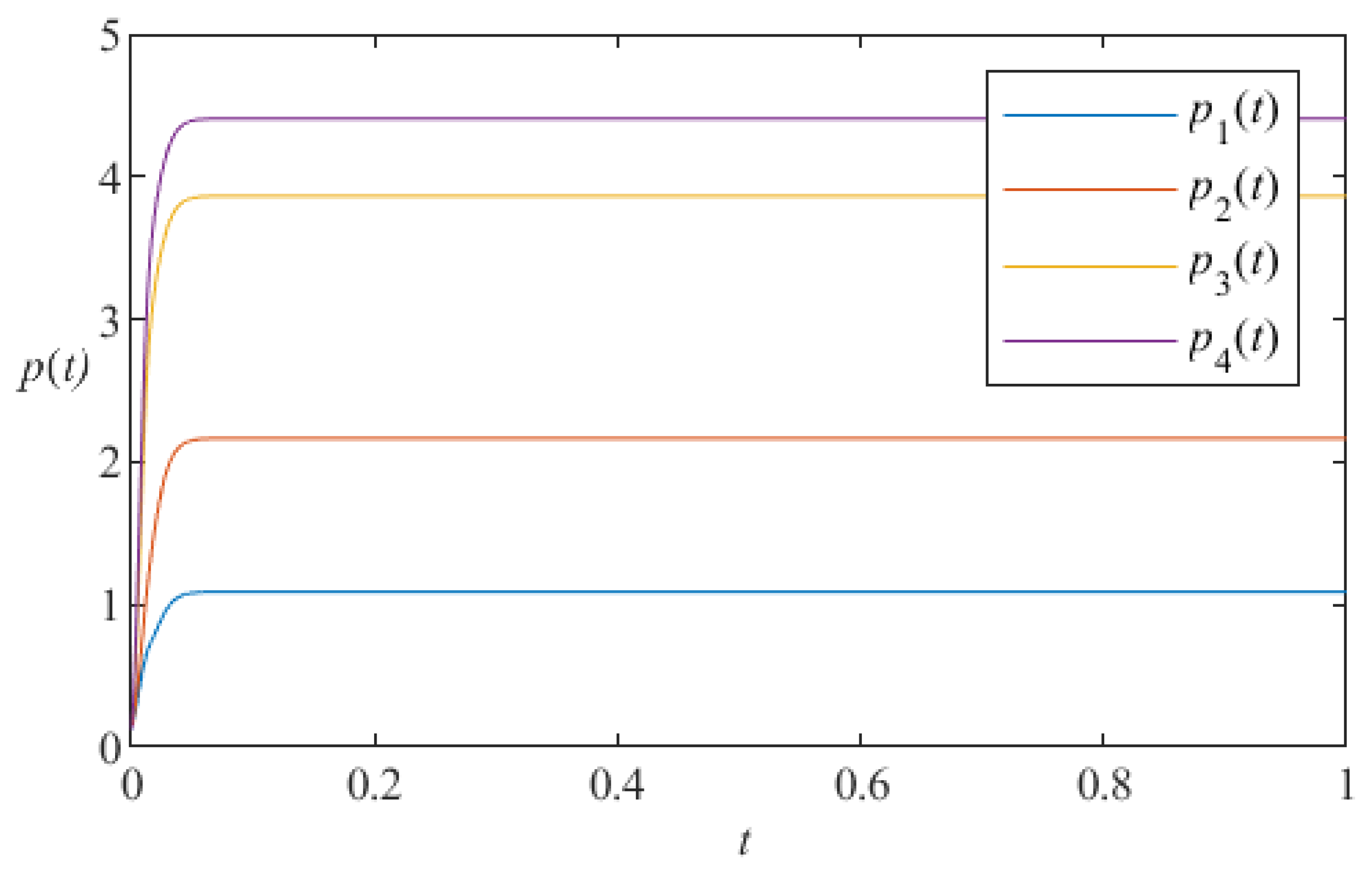
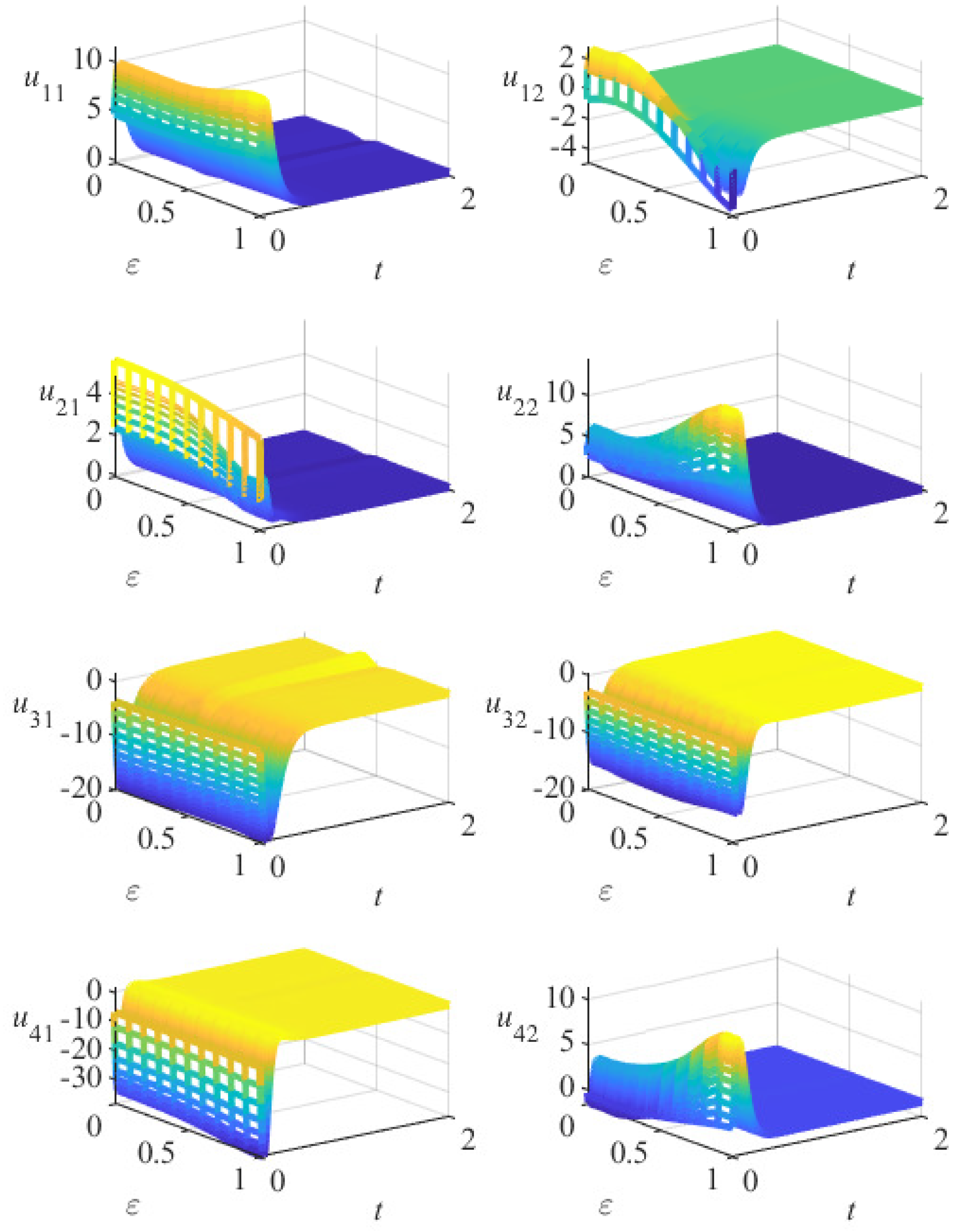
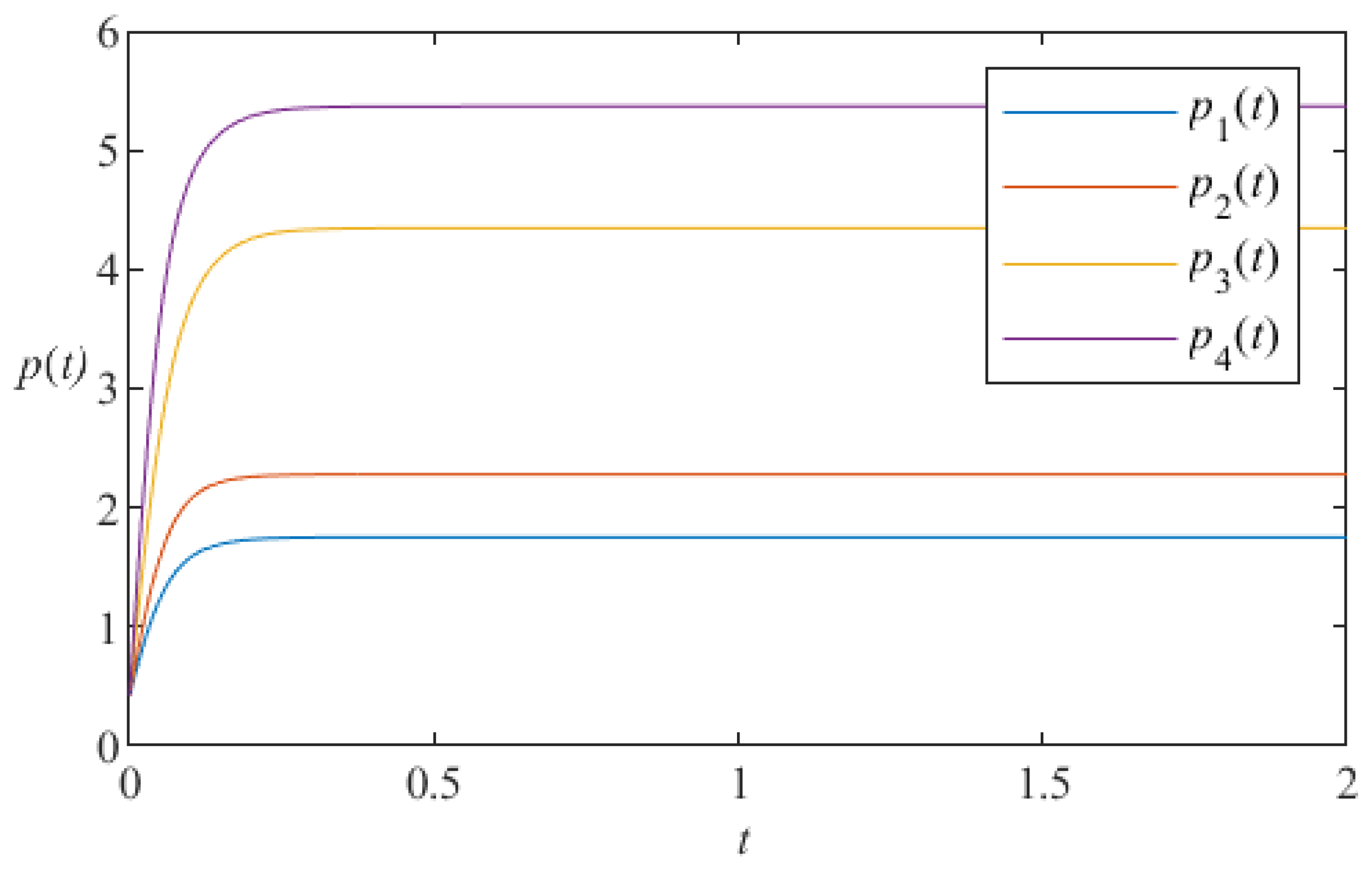
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, L.; Jian, L. Distributed Disturbance Observer-Based Containment Control of Multi-Agent Systems with Event-Triggered Communications. Mathematics 2024, 12, 3117. [Google Scholar] [CrossRef]
- Hou, Z.; Zhou, Z.; Yuan, H.; Wang, W.; Wang, J.; Xu, Z. Adaptive event-triggered consensus of multi-agent systems in sense of asymptotic convergence. Sensors 2024, 24, 339. [Google Scholar] [CrossRef] [PubMed]
- Joshi, N.; Mehta, A. Distributed discrete-time exponential sliding mode consensus protocol for discrete multi-agent system comprise of multiple robotic arms. ISA Trans. 2024, 148, 412–421. [Google Scholar] [CrossRef] [PubMed]
- Bretas, A.M.; Mendes, A.; Jackson, M.; Clement, R.; Sanhueza, C.; Chalup, S. A decentralised multi-agent system for rail freight traffic management. Ann. Oper. Res. 2023, 320, 631–661. [Google Scholar] [CrossRef]
- Binyamin, S.S.; Ben Slama, S. Multi-agent systems for resource allocation and scheduling in a smart grid. Sensors 2022, 22, 8099. [Google Scholar] [CrossRef] [PubMed]
- Gherairi, S. Design and implementation of an intelligent energy management system for smart home utilizing a multi-agent system. Ain Shams Eng. J. 2023, 14, 101897. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, L.; Yuan, Q.; Long, Y.; Ren, H. Distributed consensus estimation for networked multi-sensor systems under hybrid attacks and missing measurements. Sensors 2024, 24, 4071. [Google Scholar] [CrossRef]
- Nanda, P.; Patnaik, S. A multi-agent coalition-based approach for order fulfilment in e-commerce. Decis. Anal. J. 2023, 7, 100227. [Google Scholar] [CrossRef]
- Goswami, P.; Mukherjee, A.; Sarkar, B.; Yang, L. Multi-agent-based smart power management for remote health monitoring. Neural Comput. Appl. 2023, 35, 22771–22780. [Google Scholar] [CrossRef]
- Wu, J.; Yu, Y.; Ren, G. Leader-following formation control for discrete-time fractional stochastic multi-agent systems by event-triggered strategy. Fractal Fract. 2024, 8, 246. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; He, Z.; Li, Z.; Zhang, Q.; Ding, Z. A survey of multi-agent systems on distributed formation control. Unmanned Syst. 2024, 12, 913–926. [Google Scholar] [CrossRef]
- He, W.; He, X.; Zou, M.; Li, H. PDE model-based boundary control design for a flexible robotic manipulator with input backlash. IEEE Trans. Control Syst. Technol. 2018, 27, 790–797. [Google Scholar] [CrossRef]
- Wang, J.W.; Wang, J.M. Spatiotemporal adaptive state feedback control of a linear parabolic partial differential equation. Int. J. Robust Nonlinear Control 2023, 33, 3850–3873. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Y.; Wang, J.W.; Li, H.X. Backstepping-based distributed abnormality localization for linear parabolic distributed parameter systems. Automatica 2022, 135, 109930. [Google Scholar] [CrossRef]
- Wang, J.W.; Feng, Y.; Dubljevic, S.; Lam, H.K. Spatiotemporal fuzzy-observer-based feedback control for networked parabolic PDE systems. IEEE Trans. Fuzzy Syst. 2024, 32, 2625–2638. [Google Scholar] [CrossRef]
- Wang, X.; Wu, H.; Cao, J.; Li, X. Dynamic event-triggered boundary control for exponential consensus of multi-agent systems of impulsive PDEs with switching topology. Inf. Sci. 2024, 655, 119901. [Google Scholar] [CrossRef]
- Dai, J.; Yang, C.; Yan, X.; Wang, J.; Zhu, K.; Yang, C. Leaderless consensus control of nonlinear PIDE-type multi-agent systems with time delays. IEEE Access 2022, 10, 21211–21218. [Google Scholar] [CrossRef]
- Yang, C.; Huang, T.; Zhang, A.; Qiu, J.; Cao, J.; Alsaadi, F.E. Output consensus of multiagent systems based on PDEs with input constraint: A boundary control approach. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 370–377. [Google Scholar] [CrossRef]
- Ferrari-Trecate, G.; Buffa, A.; Gati, M. Analysis of coordination in multi-agent systems through partial difference equations. IEEE Trans. Autom. Control 2006, 51, 1058–1063. [Google Scholar] [CrossRef]
- Qi, J.; Vazquez, R.; Krstic, M. Multi-agent deployment in 3-D via PDE control. IEEE Trans. Autom. Control 2014, 60, 891–906. [Google Scholar] [CrossRef]
- Man, J.; Sheng, Y.; Chen, C.; Zeng, Z. PDE-based finite-time deployment of heterogeneous multi-agent systems subject to multiple asynchronous semi-Markov chains. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 71, 885–897. [Google Scholar] [CrossRef]
- Wang, X.; Huang, N. Finite-time consensus of multi-agent systems driven by hyperbolic partial differential equations via boundary control. Appl. Math. Mech. 2021, 42, 1799–1816. [Google Scholar] [CrossRef]
- Wan, X.; Yan, X.; Li, Z.; Qiu, J.; Yang, C. Consensus of multi-agent system with reaction-diffusion terms and time delays via output-feedback adaptive boundary control. Int. J. Adapt. Control Signal Process. 2024, 38, 3361–3380. [Google Scholar] [CrossRef]
- Li, L.; Liu, J. Consensus tracking control and vibration suppression for nonlinear mobile flexible manipulator multi-agent systems based on PDE model. Nonlinear Dyn. 2023, 111, 3345–3359. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, A.; Chen, X.; Chen, X.; Qiu, J. Stability and stabilization of a delayed PIDE system via SPID control. Neural Comput. Appl. 2017, 28, 4139–4145. [Google Scholar] [CrossRef]
- Gabriel, J.; Deutscher, J. Robust cooperative output regulation for networks of hyperbolic PIDE–ODE systems. IEEE Trans. Autom. Control 2023, 69, 888–903. [Google Scholar] [CrossRef]
- Koochakzadeh, A.; Naderi Soorki, M.; Azizi, A.; Mohammadsharifi, K.; Riazat, M. Delay-dependent stability region for the distributed coordination of delayed fractional-order multi-agent systems. Mathematics 2023, 11, 1267. [Google Scholar] [CrossRef]
- Yan, X.; Yang, C.; Cao, J.; Korovin, I.; Gorbachev, S.; Gorbacheva, N. Boundary consensus control strategies for fractional-order multi-agent systems with reaction-diffusion terms. Inf. Sci. 2022, 616, 461–473. [Google Scholar] [CrossRef]
- Yan, X.; Li, K.; Zhuang, J.; Yang, C.; Cao, J. Boundary control strategies for consensus of fractional-order multi-agent systems based on coupling PDE-ODEs. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 2179–2183. [Google Scholar] [CrossRef]
- Yan, X.; Li, K.; Yang, C.; Zhuang, J.; Cao, J. Consensus of fractional-order multi-agent systems via observer-based boundary control. IEEE Trans. Netw. Sci. Eng. 2024, 11, 3370–3382. [Google Scholar] [CrossRef]
- Yang, J.; Fečkan, M.; Wang, J. Consensus of linear conformable fractional order multi-agent systems with impulsive control protocols. Asian J. Control 2023, 25, 314–324. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, H.; Cao, J. Event-triggered boundary consensus control for multi-agent systems of fractional reaction–diffusion PDEs. Commun. Nonlinear Sci. Numer. Simul. 2023, 127, 107538. [Google Scholar] [CrossRef]
- Wang, Z.P.; Wu, H.N.; Wang, X.H. Sampled-data fuzzy control with space-varying gains for nonlinear time-delay parabolic PDE systems. Fuzzy Sets Syst. 2020, 392, 170–194. [Google Scholar] [CrossRef]
- Bouklata, A.; Giri, F.; Krstic, M.; Brouri, A.; Chaoui, F. Parameter identification of linear systems with heat sensors subject to unknown space-varying parameters. Syst. Control Lett. 2024, 192, 105890. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, J.; He, H. Exponential synchronization for a class of complex spatio-temporal networks with space-varying coefficients. Neurocomputing 2015, 151, 401–407. [Google Scholar] [CrossRef]
- Wang, J.W. Spatial domain decomposition approach to dynamic compensator design for linear space-varying parabolic MIMO PDEs. IET Control Theory Appl. 2020, 14, 39–51. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Yang, Y.; Li, N. Observer-based consensus of fractional order parabolic PDEs agents on directed networks via boundary communication. Chaos Solitons Fractals 2023, 170, 113332. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H. Bipartite consensus for multi-agent networks of fractional diffusion PDEs via aperiodically intermittent boundary control. Math. Biosci. Eng. 2023, 20, 12649–12665. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Tversky, A.; Gati, I. Similarity, separability, and the triangle inequality. Psychol. Rev. 1982, 89, 123. [Google Scholar] [CrossRef]
- Wang, J.W.; Wu, H.N. Some extended Wirtinger’s inequalities and distributed proportional-spatial integral control of distributed parameter systems with multi-time delays. J. Frankl. Inst. 2015, 352, 4423–4445. [Google Scholar] [CrossRef]
- Li, Y.X.; Wang, Q.Y.; Tong, S. Fuzzy adaptive fault-tolerant control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1372–1379. [Google Scholar] [CrossRef]
- Gong, P.; Lan, W.; Han, Q.L. Robust adaptive fault-tolerant consensus control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2020, 117, 109011. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, F.; Che, W.W. Distributed adaptive fuzzy fault-tolerant control for multi-agent systems with node faults and denial-of-service attacks. Inf. Sci. 2023, 631, 385–395. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, S.; Ahn, C.K.; Xie, Y. Adaptive neural consensus for fractional-order multi-agent systems with faults and delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7873–7886. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, S. Event-triggered fuzzy adaptive output feedback containment fault-tolerant control for nonlinear multi-agent systems against actuator faults. Eur. J. Control 2023, 75, 100887. [Google Scholar] [CrossRef]
- Shanmugam, L.; Mani, P.; Rajan, R.; Joo, Y.H. Adaptive synchronization of reaction–diffusion neural networks and its application to secure communication. IEEE Trans. Cybern. 2018, 50, 911–922. [Google Scholar] [CrossRef] [PubMed]
- Hui, M.; Liu, X.; Zhu, S.; Cao, J. Event-triggered impulsive cluster synchronization of coupled reaction-diffusion neural networks and its application to image encryption. Neural Netw. 2024, 170, 46–54. [Google Scholar] [CrossRef]
- Kowsalya, P.; Kathiresan, S.; Kashkynbayev, A.; Rakkiyappan, R. Fixed-time synchronization of delayed multiple inertial neural network with reaction-diffusion terms under cyber–physical attacks using distributed control and its application to multi-image encryption. Neural Netw. 2024, 180, 106743. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wen, Y.; Zhao, B.; Yang, C. Adaptive Control for Multi-Agent Systems Governed by Fractional-Order Space-Varying Partial Integro-Differential Equations. Mathematics 2025, 13, 112. https://doi.org/10.3390/math13010112
Liu Z, Wen Y, Zhao B, Yang C. Adaptive Control for Multi-Agent Systems Governed by Fractional-Order Space-Varying Partial Integro-Differential Equations. Mathematics. 2025; 13(1):112. https://doi.org/10.3390/math13010112
Chicago/Turabian StyleLiu, Zhen, Yingying Wen, Bin Zhao, and Chengdong Yang. 2025. "Adaptive Control for Multi-Agent Systems Governed by Fractional-Order Space-Varying Partial Integro-Differential Equations" Mathematics 13, no. 1: 112. https://doi.org/10.3390/math13010112
APA StyleLiu, Z., Wen, Y., Zhao, B., & Yang, C. (2025). Adaptive Control for Multi-Agent Systems Governed by Fractional-Order Space-Varying Partial Integro-Differential Equations. Mathematics, 13(1), 112. https://doi.org/10.3390/math13010112







