Towards a Generalized Cayley–Dickson Construction through Involutive Dimagmas

Abstract

A generalized construction procedure for algebraic number systems is hereby presented. This procedure offers an efficient representation and computation method for complex numbers, quaternions, and other algebraic structures. The construction method is then illustrated across a range of examples. In particular, the novel developments reported herein provide a generalized form of the Cayley–Dickson construction through involutive dimagmas, thereby allowing for the treatment of more general spaces other than vector spaces, which underlie the associated algebra structure.

1. Introduction

The Cayley–Dickson construction is a powerful algebraic tool that generates a sequence of number systems, known as the Cayley–Dickson algebras. These algebras extend the real numbers to more complex structures, incorporating properties such as addition, multiplication, and conjugation. Originally introduced in 1845 by the mathematician Arthur Cayley [1], and later analyzed by Leonard Eugene Dickson in 1919 [2], the Cayley–Dickson construction has found significant applications in various branches of mathematics, including algebra, analysis, and geometry [3,4,5,6,7,8,9,10,11,12,13,14] along with mathematical physical applications [15,16,17,18,19,20,21,22,23,24,25,26,27,28].

Notwithstanding their significant advances and breadth of applications, Cayley–Dickson constructions exhibit a number of important limitations pertaining to restrictions in the construction procedure and the loss of relevant properties in the algebras being generated as the construction unfolds. Regarding the construction procedure, classically it entails dimensionality doubling, thereby being limited to generating algebras the dimension of which is a power of 2. As for properties being lost upon the iterative steps of the classical construction, commutativity and associativity are examples of said properties. In fact, while commutativity still holds as the dimension of the algebra increases to 2 dimensions (complex numbers), it is lost in the second step of the construction namely at 4 dimensions (quaternions), followed by loss of associativity in the third step as the dimension further doubles to 8 (octonions). By further iterating to 16 dimensions, the resulting algebra (sedenions) features the loss of additional relevant properties. Moreover, as the dimensionality increases and the aforementioned relevant properties are lost in the process, further consequences emerge such as the loss of division algebra properties. In fact, while complex numbers and quaternions form division algebras, wherein every non-zero element has a multiplicative inverse, higher-dimensional algebras generated by the Cayley–Dickson construction no longer ensure that this property holds. For instance, sedenions are no longer division algebras.

In the present study, a new generalization of the Cayley–Dickson construction is proposed that extends the original construction to a broader class of number systems. By relaxing certain constraints imposed by the traditional construction, such as the dimensionality doubling and the classical iterative nature of the construction, new possibilities are explored, further expanding the scope of algebraic structures that can be generated.

The key motivation behind this investigation is to provide a systematic framework for studying and understanding a more diverse range of algebraic systems. By developing and leveraging a generalized Cayley–Dickson construction, the present study aims to uncover novel properties and structures that arise when extending the real numbers to higher dimensions. Additionally, it is anticipated that the construction will shed light on the connections between previously disparate algebraic systems and reveal underlying patterns and symmetries.

The significance of the proposed generalized construction lies in its potential to enrich our understanding of mathematical structures and open up new avenues for research in various domains. By extending the reach of the Cayley–Dickson construction beyond the traditional boundaries, the present study seeks to contribute to the advancement of algebraic theory and its applications in diverse scientific fields.

In the subsequent sections of this paper, the necessary background will be provided on the original Cayley–Dickson construction, followed by the formalization of the generalized approach and the illustration of its application through concrete examples, along with the analysis of algebraic, geometric, and analytical implications of the generated structures. Finally, potential future directions for research and applications will be discussed, along with the broader impact of this generalized construction in mathematics.

2. The Classical Construction

The Cayley–Dickson construction is a mathematical process used to construct a sequence of algebras with more complex properties from a given algebra. The construction starts with a given algebra, often the real numbers or the complex numbers, and defines a new algebra based on the original one. This process involves doubling the dimension of the original algebra by introducing new elements and defining new multiplication rules.

Specifically, for a given algebra with dimension n, the Cayley–Dickson construction defines a new algebra with dimension $2n$. This is achieved by extending the original algebra with new elements called “imaginary units” that satisfy certain multiplication rules.

In each step of the Cayley–Dickson construction, the new algebra inherits the addition and scalar multiplication properties of the original algebra. However, the multiplication operation is modified to incorporate the properties of the new imaginary units.

More specifically, Let $K=(K,0,1,+,·)$ be a field and let $A=(A,0,1,+,·)$ be a K-algebra with an involution $\overline{\left(\right)}:A\to A$ with $\overline{x·y}=\overline{y}·\overline{x}$ and $\overline{x+y}=\overline{x}+\overline{y}$. The Cayley–Dickson construction considers an algebra structure on the set $A\times A$ with involution ${(a_1,a_2)}^{*}=(\overline{a_1},-a_2)$ and product

$$(a_1,a_2)·(b_1,b_2)=(a_1{b}_1-\overline{b_2}{a}_2,a_2\overline{b_1}+b_2{a}_1).$$

(1)

The Cayley–Dickson construction can be iterated multiple times to create a sequence of algebras, known as Cayley–Dickson algebras. These algebras possess interesting properties, such as division algebras for complex numbers and quaternions. However, at each step, some of the properties of the original algebra are lost, such as commutativity and associativity of multiplication, as noted in the introduction.

In essence, the construction process starts with an algebraic system of the form $A=(A,0,1,+,-,·,{\left(\right)}^{*})$. From there, a new algebraic system is constructed on the product $A\times A$ with component-wise addition and subtraction, with $(0,0)$ as the neutral element for addition and $(1,0)$ as the neutral element for multiplication, whereas conjugation is defined as $\overline{(a_1,a_2)}=(a_1^{*},-a_2)$ and multiplication as

$$(a_1,a_2)·(b_1,b_2)=(a_1{b}_1-{b_2}^{*}{a}_2,a_2{b_1}^{*}+b_2{a}_1).$$

(2)

This suggests that scalar multiplication is not involved and that the associativity conditions on addition and multiplication can be relaxed from the beginning. This will be addressed in the following section.

Overall, the Cayley–Dickson construction provides a powerful and systematic way to generate new and increasingly complex algebras from a given starting point, leading to the exploration of non-commutative and non-associative algebraic structures.

3. A Generalized Construction of Arbitrary Dimension through Involutive Magmas

Generalizations of Cayley–Dickson algebras have been considered in the literature, such as in [29] where the involution involves multiplication by an arbitrary scalar rather than specifically by $-1$, whilst retaining the conjugation procedure unchanged. However, in such generalized cases, the key dimensionality requirement holds that all algebras entail dimensions in powers of 2. The present study relaxes that requirement to obtain a broader class of generality. In fact, here algebras whose dimensions are not necessarily powers of 2 are considered for broader generality. In doing so, a broader construction shall emerge that is not necessarily iterative. Moreover, even in the particular (iterative) cases where the dimension comes in powers of 2, a 4-tensor action can be defined by the user at each step, i.e., without needing to be prescribed a priory by the construction process.

By reinstating the constraints associated with the earlier generalizations of the Cayley–Dickson construction and the original construction itself, the known prior cases are recovered.

The proposed construction is formulated as follows. As observed in the previous section, the vector space part of the algebra structure does not play a significant role in it. Therefore, the new construction is no longer restricted to being based on vector spaces. This provides yet another generalized feature relative to the classical construction. Instead of classical algebras, a magma structure $(X,+)$, a dimagma $(B,+,·)$ shall be considered, along with two connecting maps between them. With this established as a base structure, it is now possible to form the category whose objects are all algebras generated by a 4-tensor action.

Let $X=(X,+)$ be a magma, i.e., a set equipped with a binary operation and $B=(B,+,·)$ a dimagma, i.e., a set equipped with two independent binary operations over the same set. Suppose that X and B are connected via two maps given by:

$$X\underset{h}{\overset{t}{\rightleftarrows }}B$$

(3)

Here no assumption is made that the two maps would preserve any of the magma structures involved.

A 4-tensor-action structure on X is hereby defined as the following representation of four tensor action operations defined on the set X given by:

$$\begin{array}{c}\hfill x{\otimes }_1{x}^{\prime }\end{array}$$

(4)

$$\begin{array}{c}\hfill x{\otimes }_2{b}^{\prime }\end{array}$$

(5)

$$\begin{array}{c}\hfill b{\otimes }_3{x}^{\prime }\end{array}$$

(6)

$$\begin{array}{c}\hfill b{\otimes }_4{b}^{\prime }\end{array}$$

(7)

for every $x,x^{\prime }\in X$ and $b,b^{\prime }\in B$. In order to simplify the notation, the subscripts in the symbol ⊗ will be omitted, since ambiguity and misinterpretation are unlikely to emerge. In doing so, the 4-tensor-action structure is rewritten as:

$$\begin{array}{c}\hfill x\otimes x^{\prime }\end{array}$$

(8)

$$\begin{array}{c}\hfill x\otimes b^{\prime }\end{array}$$

(9)

$$\begin{array}{c}\hfill b\otimes x^{\prime }\end{array}$$

(10)

$$\begin{array}{c}\hfill b\otimes b^{\prime }\end{array}$$

(11)

With this, a dimagma structure is defined on the set $X\times B$ as follows (note that the use of parenthesis cannot be avoided!):

$$\begin{array}{cc}\hfill (x,b)+(x^{\prime },b^{\prime })=& ((x+t\left(b\right))+(x^{\prime }+t\left(b^{\prime }\right)),\hfill \\ & (h\left(x\right)+b)+(h\left(x^{\prime }\right)+b^{\prime }))\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill (x,b)·(x^{\prime },b^{\prime })=& \left(\right((x\otimes x^{\prime }+t(h\left(x\right)·h\left(x^{\prime }\right)))\hfill \\ \hfill +& (x\otimes b^{\prime }+t(h\left(x\right)·b^{\prime })))\hfill \\ \hfill +& ((b\otimes x^{\prime }+t(b·h\left(x^{\prime }\right)))\hfill \\ \hfill +& (b\otimes b^{\prime }+t(b·b^{\prime }))),\hfill \\ \hfill & ((h(x\otimes x^{\prime })+h\left(x\right)·h\left(x^{\prime }\right))\hfill \\ \hfill +& (h(x\otimes b^{\prime })+h\left(x\right)·b^{\prime }))\hfill \\ \hfill +& ((h(b\otimes x^{\prime })+b·h\left(x^{\prime }\right))\hfill \\ \hfill +& (h(b\otimes b^{\prime })+b·b^{\prime })\left)\right).\hfill \end{array}$$

(13)

In order to make the product operation more explicit, it can be presented as:

$$(x,b)·(x^{\prime },b^{\prime })=(u(x,b,x^{\prime },b^{\prime }),v(x,b,x^{\prime },b^{\prime }))$$

(14)

where u and v are defined as

$$\begin{array}{cc}\hfill u& =((x\otimes x^{\prime }+t(h\left(x\right)·h\left(x^{\prime }\right)))\hfill \\ \hfill & +(x\otimes b^{\prime }+t(h\left(x\right)·b^{\prime })))\hfill \\ \hfill & +((b\otimes x^{\prime }+t(b·h\left(x^{\prime }\right)))\hfill \\ \hfill & +(b\otimes b^{\prime }+t(b·b^{\prime })))\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill v& =((h(x\otimes x^{\prime })+h\left(x\right)·h\left(x^{\prime }\right))\hfill \\ \hfill & +(h(x\otimes b^{\prime })+h\left(x\right)·b^{\prime }))\hfill \\ \hfill & +((h(b\otimes x^{\prime })+b·h\left(x^{\prime }\right))\hfill \\ \hfill & +(h(b\otimes b^{\prime })+b·b^{\prime })).\hfill \end{array}$$

(16)

The proposed algebra structure on the set $X\times B$ is motivated by the notion of a semibiproduct extension (see, e.g., [30]) of the underlying dimagma $B=(B,+,·)$ over the magma $(X,+)$ in order to produce a diagram of the form

$$X\underset{\langle t,1\rangle }{\overset{{\pi }_X}{\rightleftarrows }}X\times B\underset{\langle h,1\rangle }{\overset{{\pi }_B}{\rightleftarrows }}B$$

(17)

where the maps t and h are the connecting maps between X and B. The magma $(X,+)$ becomes a dimagma with the first component of the 4-action tensor, whereas the three other components of the 4-tensor action give the · operation on the set $X\times B$. The + operation on $X\times B$ is not the expected component-wise operation due to the lack of associativity of the magmas $(X,+)$ and $(B,+)$.

These developments can be seen as a generalization of the Cayley–Dickson construction in the sense that it is no longer limited to having the algebra generation restricted to doubling the dimension of the algebra (e.g., Real, Complex, Quaternions, Octonions, Sedenions). This further allows us to explore algebras with dimensions other than powers of 2 (i.e., other than $2^k$), thereby paving the way for a richer diversity of generated structures and associated properties.

As mentioned above, the other aspects in which the proposed construction is more general than Cayley–Dickson constructions and than their traditional generalizations, entails being released from the requirement of anchoring onto vector spaces, along with having the flexibility to provide various 4-tensor actions as the construction unfolds, be it through automatic or user-defined procedures, rather than having a prescribed invariant.

While these additional features hold inherent theoretical value by endowing further flexibility to algebraic constructions, they also entail relevant practical value. In fact, these generalized features of the new construction enable an abstract algebraic articulation with the synergistic dynamic theory of complex coevolutionary systems [31], which furthers the analysis and model design of complex coevolutionary systems where the system dynamics take place not in a classical vector space, but rather in a generalized operator space, and where classical structural-functional invariants and symmetries are no longer required to hold, thereby allowing for coevolutionary actions as the constructions unfold. This entails added value both in the mathematical physics of far-from-equilibrium coevolutionary phenomena, and in critically relevant applications such as hydro-meteorological modeling under structural-functional climatic coevolution [32].

The proposed construction further enables a systematic study of all possible 4-tensor action structures as above, for each fixed $(X,+)$ and $(B,+,·)$ with fixed h and t. This shall provide added value in building abstract algebraic treatments to scenario pool generation of structural-functional configurations across physical science and engineering applications, such as when designing structure-of-structures in system-of-systems.

Moreover, it does so by considering all possible subsets $R\subseteq X\times B$ which are closed under the two magma operations + and · defined on $X\times B$ and which contain the pairs $(x,h(x\left)\right)$ and $\left(t\right(b),b)$ for all $x\in X$ and $b\in B$. This will be conducted in a follow-up study.

4. Illustrative Examples

4.1. The Example of the Cayley–Dickson Construction

An illustrative case of the generalization laid out in the previous section is hereby presented. Given an algebra $(A,0,1,+,-,·,\overline{\left(\right)})$ let $X=B=A$ and take $t\left(b\right)=-b$, $h\left(x\right)=\overline{x}$ for every $x,b\in A$. Moreover, set:

$$\begin{array}{cc}\hfill x+x^{\prime }\mathrm{and}b+b^{\prime }& \mathrm{as}\mathrm{the}\mathrm{addition}\mathrm{in}A\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill b·b\mathrm{and}x\otimes x^{\prime }& \mathrm{as}\mathrm{the}\mathrm{product}\mathrm{in}A\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill x\otimes b^{\prime }& =0\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill b\otimes x^{\prime }& =\overline{b}\overline{x^{\prime }}-x^{\prime }\overline{b}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill b\otimes b^{\prime }& =b{b}^{\prime }-b^{\prime }\overline{b}\hfill \end{array}$$

(22)

noting that Equations (19)–(22) comprise an implementation of the 4-tensor-action defined in the previous section.

It is readily checked that the formula (14) for the product in $A\times A$ is the same as the one in the Cayley–Dickson construction [1,2]. It is further observed that the addition is no longer the usual component-wise addition as it would be expected in the Cayley–Dickson case. The present case yields:

$$(x,b)+(x^{\prime },b^{\prime })=((x-b)+(x^{\prime }-b^{\prime }),(\overline{x}+b)+(\overline{x^{\prime }}+b^{\prime })).$$

(23)

This new operation for the sum shall require a physical and geometrical interpretation, which will be developed in a follow-up study. Moreover, it may be relevant to investigate the case where X is the set of real numbers and B is the set of complex numbers (or vice versa), in order to explore the possibility of defining a meaningful product operation in ${\mathbb{R}}^3$ other than the usual cross product. For instance, a higher-order product operation can be considered admitting more than two input arguments. In this sense, since the additive structure is not required to be associative, there is still potential for development towards fulfilling the original dream of Hamilton in having a way to multiply triplets (see, e.g., [33]).

A caveat of not being in the context of vector spaces would be to risk losing the notion of scalar. However, this can be avoided by noting that the notion of a norm, such as $n\left(x\right)=x\overline{x}$, instead of being specifically required to be a scalar, is more generally required to be a central element in the algebra in the sense that it commutes with every other element (see, e.g., [34]).

4.2. Possible Different Ways to Multiply Vectors

Another example pertains to the illustration of the proposed general construction in the case where X and B need not be the same. This yields the possibility of having different formulas for multiplying vectors with the potential to be used in physical applications.

For that purpose, consider $X={\mathbb{R}}^3$ and $B=\mathbb{R}$ where $x\otimes x^{\prime }$ is the usual vector product and $x\otimes b^{\prime }$ and $b\otimes x^{\prime }$ are the usual scalar product. Next, take the map t to be such that $t\left(b\right)=0$ for every $b\in \mathbb{R}$ and $h\left(x\right)$ to be the norm of the vector $x\in {\mathbb{R}}^3$. In this case, the formula (14) becomes:

$$\begin{array}{cc}\hfill (x,b)·(x^{\prime },b^{\prime })=& (x\otimes x^{\prime }+x\otimes b^{\prime }+b\otimes x^{\prime },\hfill \\ \hfill & h\left(x\right)h\left(x^{\prime }\right)(1+sin\left(\theta \right))+\hfill \\ \hfill & 2(b^{\prime }h\left(x\right)+bh\left(x^{\prime }\right))+b{b}^{\prime })\hfill \end{array}$$

(24)

which can be compared to the usual quaternion multiplication:

$$\begin{array}{cc}\hfill (x,b)·(x^{\prime },b^{\prime })=& (x\otimes x^{\prime }+x\otimes b^{\prime }+b\otimes x^{\prime },\hfill \\ \hfill & -h\left(x\right)h\left(x^{\prime }\right)cos\left(\theta \right)+b{b}^{\prime })\hfill \end{array}$$

(25)

where $\theta$ is the angle between the two vectors x and $x^{\prime }$, in the sense that the vector operations coincide whereas the scalar operations differ. The difference between (24) and (25) is therefore only manifested in the second argument of the rhs, yielding:

$$\begin{array}{c}\hfill h\left(x\right)h\left(x^{\prime }\right)(1+cos\left(\theta \right)+sin\left(\theta \right))+2(b^{\prime }h\left(x\right)+bh\left(x^{\prime }\right)).\end{array}$$

(26)

In particular, when $\theta =0$ or $\theta =\frac{\pi }{2}$ the first term becomes $2h\left(x\right)h\left(x^{\prime }\right)$, whereas when $\theta =-\frac{\pi }{2}$ or $\theta =\pi$ the first term becomes 0.

4.3. An Example with $X={\mathbb{C}}^{*}\times {\mathbb{C}}^{*}$ and $B={\mathbb{C}}^{*}$

As another illustrative example of the proposed general construction, consider ${\mathbb{C}}^{*}$ to be the set of non-zero complex numbers, in such a way that $X={\mathbb{C}}^{*}\times {\mathbb{C}}^{*}$ and $B={\mathbb{C}}^{*}$. The elements in X are given by pairs $x=(m,v)$ where $m,v\in {\mathbb{C}}^{*}$ whereas the elements in $B={\mathbb{C}}^{*}$ are denoted by p. The notation is motivated by intuition in relativistic kinematics where there is an inherent kinematic phase component to a theoretical “mass” and a duality between kinematic “mass” and “momentum”. The maps $t:X\to B$ and $h:B\to X$ are defined by $t(m,v)=mv$ and $h\left(p\right)=\left(\frac{p^2}{k^2},k\right)$ where k is a fixed constant.

The 4-tensor action structure is hereby given by:

$$\begin{array}{c}\hfill x\otimes x^{\prime }=(m,v)\otimes (m^{\prime },v^{\prime })=(m{m}^{\prime },v+v^{\prime })\end{array}$$

(27)

$$\begin{array}{c}\hfill x\otimes b^{\prime }=(m,v)\otimes p^{\prime }=\left(m\frac{p^{\prime }}{v},v+\frac{p^{\prime }}{m}\right)\end{array}$$

(28)

$$\begin{array}{c}\hfill b\otimes x^{\prime }=p\otimes (m^{\prime },v^{\prime })=\left(\frac{p}{v}{m}^{\prime },\frac{p}{m^{\prime }}+v^{\prime }\right)\end{array}$$

(29)

$$\begin{array}{c}\hfill b\otimes b^{\prime }=p\otimes p^{\prime }=\left(\frac{p{p}^{\prime }}{k(p+p^{\prime })},\frac{k(p+p^{\prime })}{p{p}^{\prime }}\right).\end{array}$$

(30)

Moreover, the + operation on X is defined as:

$$\begin{array}{c}\hfill (m,v)+(m^{\prime },v^{\prime })=\left(m+m^{\prime },\frac{v+v^{\prime }}{2}\right)\end{array}$$

(31)

whereas the + and · operations on B are given, respectively, by the formulas $\frac{p+p^{\prime }}{2}$ and $p{p}^{\prime }$.

The resulting algebra in $X\times B={\mathbb{C}}^{*}\times {\mathbb{C}}^{*}\times {\mathbb{C}}^{*}$ can then be trivially obtained by applying this structure onto Equation (14).

4.4. A Simple Example from an Arbitrary Category Illustrated with the Unit Interval

The present example examines how to generate an underlying algebra A considered in the illustrative case of generating algebras through an iterative procedure akin to that in the classical Cayley–Dickson construction. For that purpose, consider the unit interval $I=[0,1]$ in the category of sets. Note, however, that the proposed approach is also valid in any category with products and coproducts, with a selected object I playing the role of the unit interval. The essential structure of the unit interval is as follows. There is an involution, namely $t\mapsto 1-t$, there is an addition, namely $\frac{t+s}{2}$, and the usual multiplication $ts$ for any two elements $t,s\in I$ (see, e.g., [35] for more details).

The proposed algebra shall consist of triplets $(X,f,\phi )$, where f is a function from X to I and $\phi$ is an endomap of X. Such an object is hereby called an I-link (see, e.g., [36]). Given two such I-links $(X,f,\phi )$ and $(Y,g,\psi )$, the following addition and multiplication operations are defined:

$$\begin{array}{c}\hfill (X,f,\phi )+(Y,g,\psi )=(X+Y,[f,g],\phi +\psi )\end{array}$$

(32)

$$\begin{array}{c}\hfill (X,f,\phi )·(Y,g,\psi )=(X\times Y,f\ast g,\phi \times \psi )\end{array}$$

(33)

where $[f,g]:X+Y\to I$ is the unique map such that $[f,g]{\iota }_X=f$ and $[f,g]{\iota }_Y=g$, which stems from the universal property of coproduct as illustrated below:

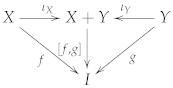
Similarly, $\phi +\psi$ and $\phi \times \psi$ are induced as well. The map $f\ast g$ is defined as follows

$$(f\ast g)(x,y)=\sum _n\sum _m\frac{f\left({\phi }^n\left(x\right)\right)·g\left({\psi }^m\left(y\right)\right)}{f\left({\phi }^n\left(x\right)\right)+g\left({\psi }^m\left(y\right)\right)}$$

(34)

with $n,m$ assuming all values in ${\mathbb{N}}_0$ and considering ${\phi }^0=1_X$ and ${\psi }^0=1_Y$.

If restricting to the case in which $\phi$ is a bijection, then $n,m$ can vary over the range of the integers $\mathbb{Z}$, rather than over just the ${\mathbb{N}}_0$. In that case a conjugate can be defined as ${(f,\phi )}^{*}=(\overline{f},{\phi }^{-1})$ with $\overline{f}\left(t\right)=1-f\left(t\right)$, for all $t\in I$.

With this, the iterative process can be enacted akin to the classical Cayley–Dickson procedure.

4.5. Partitions of the Complex Plane

A diversity of examples can be generated with arbitrary 4-tensor actions on the algebra whose elements are functions $f:\mathbb{C}\to \mathbb{Z}$. For instance, a specific example can be considered by taking the component-wise addition:

$$(f+g)\left(x\right)=f\left(x\right)+g\left(x\right)$$

(35)

along with a simple formula for the product, such as:

$$(f·g)\left(x\right)=max\left(f\right(x),g(x\left)\right).$$

(36)

The present example has a clear geometrical interpretation in the sense that a function $f:\mathbb{C}\to \mathbb{Z}$ can be seen as a partition of the complex plane into level regions giving rise to a wide range of potential future applications. These include, but are not limited to, a diversity of fields ranging from information physical nonlinear statistical mechanics [37] to non-harmonic spectral and hyper-spectral analysis in information-theoretic geophysical sciences [38].

Moreover, the definition of the 4-tensor action can be defined as an ad-hoc formula capturing a collective interference pattern among the structure of the level regions with the latter being interpreted as propagating wave fronts in physical or spectral domains. Given the abstract algebraic focus of the present short communication, we defer detailed physically based investigations to a follow-up study.

The proposed functions $f:\mathbb{C}\to \mathbb{Z}$ can be restricted to the bounded case. In other words, the existence of $N\ge 0$ for which $f\left(x\right)\le N$ is required for all $x\in \mathbb{C}$. The smallest such N is denoted as $max\left(f\right)$. In this case an involution operation can be defined as:

$$\overline{f}\left(x\right)=max\left(f\right)-f\left(x\right).$$

(37)

A particular iterative Cayley–Dickson construction can then ensue starting with the initial structure $(A,+,·,\overline{\left(\right)})$.

This is one way to proceed. Another possibility would be to consider all possible 4-tensor action structures and substructures and explore their properties.

5. Discussion and Conclusions

The categorical constructions introduced in the present study generate an algebra $(A,+,·,{\left(\right)}^{*})$ endowed with properties deemed more general than those underlying the Cayley–Dickson construction. Two core generalization aspects pertain, on one hand, not being restricted to operating with vector spaces, and on the other hand allowing for dimensionalities other than natural powers of 2 in the construction of said algebras. The missing operation of subtraction can be seen as a property of whether the equation $a+x=b$ has solution $x=b-a$.

Relative to the generalization provided in [39], the approach proposed in the present study differs by providing the added value of not requiring an iterative procedure for our construction, though such a procedure can still be admitted as a particular case. Moreover, the dimensionality of the proposed construction is not required to entail a power of 2, thereby further providing a broader set of possible constructions than those admitted by the aforementioned prior efforts.

Aside from the inherent theoretical value, these developments further provide relevance to improved scalability, computational complexity, and efficiency of the proposed construction. In fact, it provides pathways for improved operational implementations for the following reasons: Firstly, by not being limited to dimensional configurations in powers of 2, it can construct non-binary systems, e.g., as simple as a ternary system that reaches higher orders of complexity in information structuring and treatment with much lower input requirements, given the richer diversity of configuration generation possibilities enabled by said ternary construct (see, e.g., [40]). Secondly, by not requiring an iterative procedure in the construction, a higher-order application can forego lengthy iterative approaches by replacing them with a block tensor action, e.g., the proposed 4-tensor action that provides a richer structure in a block operation instead of requiring a lengthy binary power iteration loop to provide a comparable level of richness in structure and function in the algebraic construction. This thus allows for algebraic structures with high-order structural complexity to be generated with a lower number of computational steps as the practical case of a single non-iterative block tensor action replacing strenuous classical structural iterations in the traditional Cayley–Dickson approach.

Notwithstanding the practical relevance and operational added value of the proposed generalized construction, the main focus of the present short communication pertains to the presentation of the key concepts pertaining to the proposed abstract algebraic construction. As a theoretical construct that can actually be analytically explored, this first study is not bound to scalability and complexity considerations arising in technological implementations. Even so, the aforementioned added value and relevance to those regards shall be further explored in follow-up developments geared towards a diversity of applications across the complex system sciences and information technologies.

All in all, the present contribution has introduced a generalization of a Cayley–Dickson construction methodology, discussed its key differences relative to the traditional construction and prior generalization efforts, and further illustrated its applicability by constructing higher-dimensional algebras. Moreover, this study equips researchers and practitioners with the tools to build further constructions such as those considered in the illustrative cases making use of features brought up in the present generalization.

In future works, it will be interesting to investigate the algebraic properties of these extended number systems, such as associativity, commutativity, and the existence of inverses. It will also be worthwhile to explore how these new structures relate to existing algebraic systems and investigate their geometric interpretations when applicable. Finally, the additional properties and insights brought out by the theoretical developments shall further broaden the breadth and depth of applications to a wide range of challenges encompassing all areas where characterizing, encoding, and processing information is pivotal to efficient analytics, model design, and operational implementation in science and engineering.