Two Approximation Formulas for Gamma Function with Monotonic Remainders

Abstract

In this paper, two new approximation formulas with monotonic remainders for the gamma function have been presented. Also, we present some numerical comparisons between our new approximation formulas and some known ones, which demonstrate the superiority of our results.

1. Introduction

The ordinary Euler gamma function is defined as follows [1]:

$$\Gamma \left(r\right)={\int }_0^{\infty }{e}^{-t}{t}^{r-1}dt, r>0$$

(1)

or by

$$\Gamma \left(r\right)=\underset{n\to \infty }{lim}\frac{n!n^r}{r(r+1)(r+2)\dots (r+n)}, r\in \mathbb{R}-\{0,-1,-2,\dots \}.$$

(2)

The derivative of $ln\Gamma \left(r\right)$, denoted by $\psi \left(r\right)=\frac{{\Gamma }^{\prime }\left(r\right)}{\Gamma \left(r\right)}$, is called the digamma function and the derivatives ${\psi }^{\left(n\right)}\left(r\right)$ for $n\ge 0$ are referred to as the polygamma functions. For more information about gamma function and polygamma functions see [2,3,4,5,6], as well as the closely linked references therein, for further details.

Many disciplines of mathematics and other fields of research make substantial use of the Gamma function $\Gamma \left(r\right)$, which generalises the factorial function $n!=\Gamma (n+1)$. In numerical techniques and algorithms, when exact assessments are computationally costly, gamma function approximations are essential and functions involving the Gamma function can be efficiently computed with the use of approximations [7]. Gamma function approximations are widely used in engineering and physics for the analysis of systems that show exponential decay, such as radioactive decay, fluid dynamics, and signal processing [8]. Also, Gamma function and its approximations are used in machine learning and pattern recognition in various algorithms, such as those involving probabilistic models, maximum likelihood estimation, and Bayesian inference [9].

Numerous studies concentrate on developing more precise estimates for the gamma function. Here are some of the approximate formulas most commonly used for the gamma function with bounds for their remainder functions:

Stirling’s approximation formula (see [10,11,12])

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^{r}exp\left(\frac{{\sigma }_1\left(r\right)}{12r}\right),$$

where

$$0<{\sigma }_1\left(r\right)<1, r>0.$$

Ramanujan’s approximation formula (see [13,14,15])

$$\Gamma (r+1)=\sqrt{\pi }{\left(\frac{r}{e}\right)}^r\sqrt[6]{8r^3+4r^2+r+{\sigma }_2\left(r\right)},$$

where

$$\frac{1}{100}<{\sigma }_2\left(r\right)<\frac{1}{30}, r>0.$$

Burnside’s approximation formula (see [16,17,18])

$$\Gamma (r+1)=\sqrt{2\pi }{\left(\frac{r+\frac{1}{2}}{e}\right)}^{r+\frac{1}{2}}exp\left({\sigma }_3\left(r\right)\right),$$

where

$$ln\sqrt{\frac{e}{\pi }}<{\sigma }_3\left(r\right)<0, r>0.$$

Gosper’s approximation formula (see [19,20,21])

$$\Gamma (r+1)=\sqrt{2\pi }{\left(\frac{r}{e}\right)}^r{\left(r+\frac{1}{6}\right)}^{1/2} {\sigma }_4\left(r\right),$$

where

$$1<{\sigma }_4\left(r\right)<\sqrt{\frac{3e^2}{7\pi }}, r\ge 1.$$

Windschitl’s approximation formula (see [22,23,24])

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(rsinh\left(\frac{1}{r}\right)\right)}^{r/2}exp\left(\frac{{\sigma }_5\left(r\right)}{r^5}\right),$$

where

$$0<{\sigma }_5\left(r\right)<\frac{1}{1620}, r>0.$$

Nemes’s approximation formula (see [25,26,27])

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(1+\frac{1}{12r^2-{\sigma }_6\left(r\right)}\right)}^r,$$

where

$$\frac{1}{10}<{\sigma }_6\left(r\right)<\frac{1}{9}, r\ge 4.$$

C.-P. Chen’s approximation formula (see [28])

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{1}{12r^3+\frac{24r}{7}-\frac{1}{2}}+1\right)}^{r^2+\frac{53}{210}}\left(\frac{{\sigma }_7\left(r\right)}{r^9}-\frac{2117}{5080320r^7}+1\right),$$

where

$$0<{\sigma }_7\left(r\right)<\frac{1892069}{2347107840}, r\ge 2.$$

Yang and Tian’s approximation formula (see [29])

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(rsinh\left(\frac{1}{r}\right)\right)}^{r/2}exp\left(\frac{7}{324r^3\left(35r^2+33\right)}\right){\sigma }_8\left(r\right),$$

where

$$1<{\sigma }_8\left(r\right)<\frac{exp\left(\frac{33041}{22032}\right)}{\sqrt{\left(e^2-1\right)\pi }}, r\ge 1.$$

Mahmoud and Almuashi’s approximation formula (see [30,31])

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}\left(1+\frac{{\sigma }_9\left(r\right)}{r^5}\right),$$

where

$$0<{\sigma }_9\left(r\right)<\frac{461}{907200}, r\ge 1.$$

The goal of this study is to introduce two new approximation formulas for the gamma function with monotonic remainders in light of Mahmoud and Almuashi’s results. We also offer some numerical comparisons to show how our results outperform some of the formulas listed above.

2. Main Results

Theorem 1.

The remainder function ${\theta }_1\left(r\right)$ defined from

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}exp\left(\frac{1}{r^7}\left(\frac{461}{907200}{r}^2+{\theta }_1\left(r\right)\right)\right), r\ge 1$$

is strictly decreasing with the sharp constant

$$-\frac{5197}{9072000}<{\theta }_1\left(r\right)\le ln\sqrt{\frac{57}{134\pi }exp\left(\frac{906739}{453600}\right)}, r\ge 1.$$

Proof. 

For $r>1$, we have

$${\theta }_1\left(r\right)=-\frac{1}{2}{r}^7\left(ln\left(2\pi \right)-2ln\left(exp\left(r-\frac{461}{907200r^5}\right){\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{-\frac{r}{2}}{r}^{-r-\frac{1}{2}}\Gamma (r+1)\right)\right)$$

and hence

$$\begin{array}{ccc}\hfill {\theta }_1^{\prime }\left(r\right)& & =7r^7+r^7\psi (r+1)-\frac{r^6}{2}-\frac{7}{2}{r}^{6}ln\left(2\right)-\frac{7}{2}{r}^{6}ln\left(\pi \right)-\frac{1}{2}(16r+7)r^{6}ln\left(r\right)\hfill \\ & & +7r^{6}ln(\Gamma (r+1))-4r^{7}ln\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)+\frac{200r^9}{1200r^4+80r^2-7}-\frac{461r}{453600}.\hfill \end{array}$$

Now, consider the two functions

$$\begin{array}{ccc}\hfill H_1\left(r\right)& =& \frac{d}{dr}\left(\frac{1}{r^6}\frac{d{\theta }_1\left(r\right)}{dr}\right)\hfill \\ & =& -\frac{461}{453600r^5}-4rln\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)+\frac{200r^3}{1200r^4+80r^2-7}+7r-8rln\left(r\right)-\frac{7}{2}ln\left(2\pi r\right)\hfill \\ & & +r\psi (r+1)+7ln\Gamma (r+1)-\frac{1}{2},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill H_2\left(r\right)& =& H_1\left(r\right)-H_1(r+1)\hfill \\ & =& \frac{461}{90720r^6}+\frac{7}{20r^2-1}+\frac{49}{60r^2+7}+\frac{98}{{\left(60r^2+7\right)}^2}-\frac{2}{{\left(1-20r^2\right)}^2}-\frac{7}{2r}\hfill \\ & & -\frac{7}{2(r+1)}-\frac{461}{90720{(r+1)}^6}-\frac{7}{20r(r+2)+19}+\frac{2}{{(20r(r+2)+19)}^2}\hfill \\ & & -\frac{49}{60r(r+2)+67}-\frac{98}{{(60r(r+2)+67)}^2}-8lnr+8ln(r+1)\hfill \\ & & +4ln\left(\frac{10}{60r(r+2)+57}+1\right)-4ln\left(\frac{10}{60r^2-3}+1\right)-{\psi }^{\prime }(r+1).\hfill \end{array}$$

Using the recurrence formula (see [1])

$$\psi (r+1)=\frac{1}{r}+\psi \left(r\right),$$

(3)

then we have

$$\frac{d}{dr}\left[H_2\left(r\right)-H_2(r+1)\right]=\frac{H_3\left(r\right)}{H_4\left(r\right)},$$

where

$$\begin{array}{c}{H}_3(r+1)=\hfill \\ -7.78127\times {10}^{32}{r}^{44}-6.84751\times {10}^{34}{r}^{43}-2.93473\times {10}^{36}{r}^{42}-8.1629\times {10}^{37}{r}^{41}\hfill \\ -1.65674\times {10}^{39}{r}^{40}-2.6155\times {10}^{40}{r}^{39}-3.34341\times {10}^{41}{r}^{38}-3.55706\times {10}^{42}{r}^{37}\hfill \\ -3.21293\times {10}^{43}{r}^{36}-2.50108\times {10}^{44}{r}^{35}-1.69753\times {10}^{45}{r}^{34}-1.01383\times {10}^{46}{r}^{33}\hfill \\ -5.36771\times {10}^{46}{r}^{32}-2.53456\times {10}^{47}{r}^{31}-1.07262\times {10}^{48}{r}^{30}-4.08484\times {10}^{48}{r}^{29}\hfill \\ -1.40453\times {10}^{49}{r}^{28}-4.37204\times {10}^{49}{r}^{27}-1.23474\times {10}^{50}{r}^{26}-3.16911\times {10}^{50}{r}^{25}\hfill \\ -7.40155\times {10}^{50}{r}^{24}-1.57439\times {10}^{51}{r}^{23}-3.05161\times {10}^{51}{r}^{22}-5.39063\times {10}^{51}{r}^{21}\hfill \\ -8.67673\times {10}^{51}{r}^{20}-1.27186\times {10}^{52}{r}^{19}-1.69626\times {10}^{52}{r}^{18}-2.05563\times {10}^{52}{r}^{17}\hfill \\ -2.25965\times {10}^{52}{r}^{16}-2.24814\times {10}^{52}{r}^{15}-2.01885\times {10}^{52}{r}^{14}-1.6309\times {10}^{52}{r}^{13}\hfill \\ -1.18036\times {10}^{52}{r}^{12}-7.61567\times {10}^{51}{r}^{11}-4.35389\times {10}^{51}{r}^{10}-2.18922\times {10}^{51}{r}^9\hfill \\ -9.59241\times {10}^{50}{r}^8-3.62017\times {10}^{50}{r}^7-1.15922\times {10}^{50}{r}^6-3.08733\times {10}^{49}{r}^5\hfill \\ -6.65309\times {10}^{48}{r}^4-1.11436\times {10}^{48}{r}^3-1.36085\times {10}^{47}{r}^2-1.07762\times {10}^{46}r\hfill \\ -4.15224\times {10}^{44}<0, r>0\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill H_4(r+1)=& & 7560{(r+1)}^7{(r+2)}^7{(r+3)}^7{\left(20r^2+40r+19\right)}^3{\left(20r^2+80r+79\right)}^3\hfill \\ & & {\left(20r^2+120r+179\right)}^3{\left(60r^2+120r+67\right)}^3{\left(60r^2+240r+247\right)}^3\hfill \\ & & {\left(60r^2+360r+547\right)}^3>0, r>0.\hfill \end{array}$$

Then, the function $H_2\left(r\right)-H_2(r+1)$ is strictly decreasing for $r\ge 1$.

Using the derivative of the asymptotic formula (see [14])

$$\psi \left(r\right)\sim lnr-\frac{1}{r}-\sum _{s=1}^{\infty }\frac{B_s}{s{r}^s}, r\to \infty$$

(4)

where $B_s$ are the Bernoulli numbers generated by [1]

$$\sum _{s=0}^{\infty }\frac{B_s}{s!}{r}^s=\frac{r}{e^r-1}=1-\frac{r}{2}+\sum _{s=1}^{\infty }\frac{B_{2s}}{\left(2s\right)!}{r}^{2s}, \left|r\right|<2\pi ,$$

(5)

we get

$$H_2\left(r\right)-H_2(r+1)\sim \frac{1436249}{864000r^{12}}-\frac{1436249}{72000r^{13}}+\frac{563824855621}{4082400000r^{14}}+\dots , r\to \infty$$

and ${lim}_{r\to \infty }\left[H_2\left(r\right)-H_2(r+1)\right]=0$. Therefore, the function $H_2\left(r\right)-H_2(r+1)$ is positive for $r\ge 1$.

Hence,

$$H_2\left(r\right)>H_2(r+1), r\ge 1$$

and then

$$H_2\left(r\right)>H_2(r+1)>H_2(r+2)>\cdots >H_2(r+n), r\ge 1.$$

Again, using the derivative of the asymptotic Formula (4), we obtain

$$H_2\left(r\right)\sim \frac{1436249}{9504000r^{11}}-\frac{1436249}{1728000r^{12}}+\frac{15339610187}{6633900000r^{13}}+\dots , r\to \infty$$

and hence, ${lim}_{n\to \infty }{H}_2(r+n)=0$. Then $H_2\left(r\right)=H_1\left(r\right)-H_1(r+1)>0$ for $r\ge 1$, and therefore we have

$$H_1\left(r\right)>H_1(r+1)>H_1(r+2)>\cdots >H_1(r+n), r\ge 1.$$

Using the asymptotic Formula (4) and the asymptotic series, known as Stirling’s series [14],

$$ln\Gamma \left(r\right)\sim (r-1/2)lnr-r+ln\sqrt{2\pi }+\sum _{s=1}^{\infty }\frac{B_s}{2s(2s-1)r^{2s-1}}, r\to \infty$$

(6)

we get

$$H_1\left(r\right)\sim \frac{1436249}{95040000r^{10}}-\frac{26863154077}{318427200000r^{12}}+\frac{326590926551}{653184000000r^{14}}+\dots , r\to \infty$$

and ${lim}_{n\to \infty }{H}_1(r+n)=0$. Hence $H_1\left(r\right)=\frac{d}{dr}\left(\frac{1}{r^6}\frac{d{\theta }_1\left(r\right)}{dr}\right)>0$ for $r\ge 1$ and then the function $\frac{1}{r^6}\frac{d{\theta }_1\left(r\right)}{dr}$ is strictly increasing for $r\ge 1$. Using the two the asymptotic Formulas (4) and (6), we have

$$\frac{d{\theta }_1\left(r\right)}{dr}\sim -\frac{1436249}{855360000r^3}+\frac{26863154077}{3502699200000r^5}-\frac{326590926551}{8491392000000r^7}+\dots , r\to \infty$$

we have ${lim}_{r\to \infty }\frac{1}{r^6}\frac{d{\theta }_1\left(r\right)}{dr}=0$. Then $\frac{1}{r^6}\frac{d{\theta }_1\left(r\right)}{dr}<0$ for $r\ge 1$ or ${\theta }_1\left(r\right)$ is decreasing function for $r\ge 1$.

Using the asymptotic Formula (6), we have

$${\theta }_1\left(r\right)\sim -\frac{5197}{9072000}+\frac{1436249}{1710720000r^2}-\frac{26863154077}{14010796800000r^4}+\dots , r\to \infty$$

which gives ${lim}_{r\to \infty }{\theta }_1\left(r\right)=-\frac{5197}{9072000}$ and the function ${\theta }_1\left(r\right)$ satisfies

$$-\frac{5197}{9072000}<{\theta }_1\left(r\right)\le {\theta }_1\left(1\right), r\ge 1$$

with sharp constants. □

Using the bounds of the function ${\theta }_1\left(r\right)$ in Theorem 1, we get the following result:

Corollary 1.

The following inequality holds for $r\ge 1$

$$exp\left(\frac{1}{r^7}\left(\frac{461}{907200}{r}^2+c_1\right)\right)<\frac{\Gamma (r+1)}{\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}}<exp\left(\frac{1}{r^7}\left(\frac{461}{907200}{r}^2+c_2\right)\right)$$

(7)

with sharp constants

$$c_1=\underset{r\to \infty }{lim}{\theta }_1\left(r\right)=-\frac{5197}{9072000}\approx -0.000572862$$

and

$$c_2={\theta }_1\left(1\right)=ln\sqrt{\frac{57}{134\pi }exp\left(\frac{906739}{453600}\right)}\approx -0.000267366.$$

Theorem 2.

The remainder function ${\theta }_2\left(r\right)$ defined from

$$\Gamma (r+1)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}exp\left(\frac{461}{907200r^3\left(r^2+\frac{5197}{4610}\right)}+\frac{{\theta }_2\left(r\right)}{r^9}\right), r\ge 1$$

is strictly increasing with sharp constants

$$\sqrt{\frac{57}{134\pi }exp\left(\frac{889478519}{444845520}\right)}<{\theta }_2\left(r\right)<\frac{213922547}{1104098688000}, r\ge 1.$$

Proof. 

For $r>1$, we have

$${\theta }_2\left(r\right)=-\frac{1}{2}{r}^9\left(ln\left(2\pi \right)-2ln\left(exp\left(r-\frac{461}{907200r^3\left(r^2+\frac{5197}{4610}\right)}\right){\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{-\frac{r}{2}}{r}^{-r-\frac{1}{2}}\Gamma (r+1)\right)\right)$$

and hence

$$\begin{array}{cc}\hfill {\theta }_2^{\prime }\left(r\right)& =9r^9-10r^{9}ln\left(r\right)+r^9\psi (r+1)-\frac{r^8}{2}-\frac{9}{2}{r}^{8}ln\left(2\pi r\right)+9r^{8}ln(\Gamma (r+1))\hfill \\ & -\frac{5197r}{4536000{\left(\frac{5197}{4610r^2}+1\right)}^2}-5r^{9}ln\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)-\frac{212521r^5}{22680\left(4610r^2+5197\right)}\hfill \\ & +\frac{200r^{11}}{1200r^4+80r^2-7}.\hfill \end{array}$$

Consider the two functions

$$\begin{array}{ccc}\hfill K_1\left(r\right)& =& \frac{d}{dr}\left(\frac{1}{r^8}\frac{d{\theta }_2\left(r\right)}{dr}\right)\hfill \\ & =& -5rln\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)-\frac{5197}{4536000{\left(\frac{5197}{4610r^2}+1\right)}^2{r}^7}-\frac{212521}{22680r^3\left(4610r^2+5197\right)}-\frac{1}{2}\hfill \\ & +& \frac{200r^3}{1200r^4+80r^2-7}+9r-10rln\left(r\right)-\frac{9}{2}ln\left(2\pi r\right)+r\psi (r+1)+9ln\Gamma (r+1),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill K_2\left(r\right)& =& K_1\left(r\right)-K_1(r+1)\hfill \\ & =& \frac{212521}{26192880r^4}-\frac{97972181}{30627989406r^2}+\frac{9}{20r^2-1}+\frac{63}{60r^2+7}+\frac{98}{{\left(60r^2+7\right)}^2}\hfill \\ & & +\frac{225825877205}{15313994703\left(4610r^2+5197\right)}-\frac{1129129386025}{11786796{\left(4610r^2+5197\right)}^2}-\frac{2}{{\left(1-20r^2\right)}^2}\hfill \\ & & -\frac{225825877205}{567{\left(4610r^2+5197\right)}^3}-5ln\left(\frac{10}{60r^2-3}+1\right)-\frac{9}{2r}-\frac{9}{2(r+1)}\hfill \\ & & +\frac{97972181}{30627989406{(r+1)}^2}-\frac{212521}{26192880{(r+1)}^4}-\frac{9}{20r(r+2)+19}\hfill \\ & & -\frac{63}{60r(r+2)+67}-\frac{98}{{(60r(r+2)+67)}^2}-\frac{225825877205}{15313994703\left(4610r\right(r+2)+9807)}\hfill \\ & & +\frac{1129129386025}{11786796{(4610r(r+2)+9807)}^2}+\frac{225825877205}{567{(4610r(r+2)+9807)}^3}-10ln\left(r\right)\hfill \\ & & +10ln(r+1)+5ln\left(\frac{10}{60r(r+2)+57}+1\right)+\frac{2}{{(20r(r+2)+19)}^2}-{\psi }^{\prime }(r+1).\hfill \end{array}$$

Using the recurrence Formula (3), then we have

$$\frac{d}{dr}\left[K_2\left(r\right)-K_2(r+1)\right]=\frac{K_3\left(r\right)}{K_4\left(r\right)},$$

where

$$\begin{array}{c}{K}_3(r+1)=\hfill \\ 5.1341\times {10}^{76}{r}^{60}+6.16092\times {10}^{78}{r}^{59}+3.63085\times {10}^{80}{r}^{58}+1.40077\times {10}^{82}{r}^{57}\hfill \\ +3.97869\times {10}^{83}{r}^{56}+8.87201\times {10}^{84}{r}^{55}+1.61734\times {10}^{86}{r}^{54}+2.47835\times {10}^{87}{r}^{53}\hfill \\ +3.25771\times {10}^{88}{r}^{52}+3.73018\times {10}^{89}{r}^{51}+3.7657\times {10}^{90}{r}^{50}+3.38418\times {10}^{91}{r}^{49}\hfill \\ +2.72884\times {10}^{92}{r}^{48}+1.98729\times {10}^{93}{r}^{47}+1.31427\times {10}^{94}{r}^{46}+7.92993\times {10}^{94}{r}^{45}\hfill \\ +4.38263\times {10}^{95}{r}^{44}+2.22618\times {10}^{96}{r}^{43}+1.04236\times {10}^{97}{r}^{42}+4.51033\times {10}^{97}{r}^{41}\hfill \\ +1.8075\times {10}^{98}{r}^{40}+6.72121\times {10}^{98}{r}^{39}+2.32284\times {10}^{99}{r}^{38}+7.47125\times {10}^{99}{r}^{37}\hfill \\ +2.23912\times {10}^{100}{r}^{36}+6.25886\times {10}^{100}{r}^{35}+1.63302\times {10}^{101}{r}^{34}+3.97955\times {10}^{101}{r}^{33}\hfill \\ +9.06207\times {10}^{101}{r}^{32}+1.92888\times {10}^{102}{r}^{31}+3.83831\times {10}^{102}{r}^{30}+7.14059\times {10}^{102}{r}^{29}\hfill \\ +1.24174\times {10}^{103}{r}^{28}+2.01795\times {10}^{103}{r}^{27}+3.06324\times {10}^{103}{r}^{26}+4.34098\times {10}^{103}{r}^{25}\hfill \\ +5.73855\times {10}^{103}{r}^{24}+7.07001\times {10}^{103}{r}^{23}+8.10872\times {10}^{103}{r}^{22}+8.64618\times {10}^{103}{r}^{21}\hfill \\ +8.55775\times {10}^{103}{r}^{20}+7.84827\times {10}^{103}{r}^{19}+6.65518\times {10}^{103}{r}^{18}+5.20555\times {10}^{103}{r}^{17}\hfill \\ +3.74528\times {10}^{103}{r}^{16}+2.47066\times {10}^{103}{r}^{15}+1.48877\times {10}^{103}{r}^{14}+8.15907\times {10}^{102}{r}^{13}\hfill \\ +4.04608\times {10}^{102}{r}^{12}+1.80466\times {10}^{102}{r}^{11}+7.18795\times {10}^{101}{r}^{10}+2.53455\times {10}^{101}{r}^9\hfill \\ +7.82839\times {10}^{100}{r}^8+2.09009\times {10}^{100}{r}^7+4.74271\times {10}^{99}{r}^6+8.94464\times {10}^{98}{r}^5\hfill \\ +1.3598\times {10}^{98}{r}^4+1.59388\times {10}^{97}{r}^3+1.34296\times {10}^{96}{r}^2+7.1649\times {10}^{94}r\hfill \\ +1.78658\times {10}^{93}>0, r>0\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill K_4(r+1)=& 1890{(r+1)}^5{(r+2)}^5{(r+3)}^5{\left(20r^2+40r+19\right)}^3{\left(20r^2+80r+79\right)}^3\hfill \\ & {\left(20r^2+120r+179\right)}^3{\left(60r^2+120r+67\right)}^3{\left(60r^2+240r+247\right)}^3\hfill \\ & {\left(4610r^2+18440r+23637\right)}^4{\left(4610r^2+27660r+46687\right)}^4\hfill \\ & {\left(60r^2+360r+547\right)}^3{\left(4610r^2+9220r+9807\right)}^4>0, r>0.\hfill \end{array}$$

Then, the function $K_2\left(r\right)-K_2(r+1)$ is strictly increasing for $r\ge 1$.

Using the asymptotic Formula (4), we get

$$K_2\left(r\right)-K_2(r+1)\sim -\frac{708238139903501}{173519146080000r^{14}}+\frac{708238139903501}{12394224720000r^{15}}+\dots , r\to \infty$$

and ${lim}_{r\to \infty }\left[K_2\left(r\right)-K_2(r+1)\right]=0$. Therefore, the function $K_2\left(r\right)-K_2(r+1)$ is negative for $r\ge 1$. Hence,

$$K_2\left(r\right)<K_2(r+1), r\ge 1$$

and then

$$K_2\left(r\right)<K_2(r+1)<K_2(r+2)<\cdots <K_2(r+n), r\ge 1.$$

Again, using the derivative of the asymptotic Formula (4), we obtain

$$K_2\left(r\right)\sim -\frac{708238139903501}{2255748899040000r^{13}}+\frac{708238139903501}{347038292160000r^{14}}+\dots , r\to \infty$$

and hence, ${lim}_{n\to \infty }{K}_2(r+n)=0$. Then, $K_2\left(r\right)=K_1\left(r\right)-K_1(r+1)<0$ for $r\ge 1$, and therefore we have

$$K_1\left(r\right)<K_1(r+1)<K_1(r+2)<\cdots <K_1(r+n), r\ge 1.$$

Using the two asymptotic Formulas (4) and (6), we have

$$K_1\left(r\right)\sim -\frac{708238139903501}{27068986788480000r^{12}}+\frac{5580017896128641687}{19198158322291200000r^{14}}+\dots , r\to \infty$$

and ${lim}_{n\to \infty }{K}_1(r+n)=0$. Hence, $K_1\left(r\right)=\frac{d}{dr}\left(\frac{1}{r^8}\frac{d{\theta }_2\left(r\right)}{dr}\right)<0$ for $r\ge 1$ and then the function $\frac{1}{r^8}\frac{d{\theta }_2\left(r\right)}{dr}$ is strictly decreasing for $r\ge 1$. Using the two asymptotic Formulas (4) and (6), we get

$$\frac{d{\theta }_2\left(r\right)}{dr}\sim \frac{708238139903501}{297758854673280000r^3}-\frac{5580017896128641687}{249576058189785600000r^5}+\dots , r\to \infty$$

and ${lim}_{r\to \infty }\frac{1}{r^8}\frac{d{\theta }_2\left(r\right)}{dr}=0$. Then $\frac{1}{r^8}\frac{d{\theta }_2\left(r\right)}{dr}>0$ for $r\ge 1$ or ${\theta }_2\left(r\right)$ is increasing function for $r\ge 1$.

Using the asymptotic Formula (6), we obtain

$${\theta }_2\left(r\right)\sim \frac{213922547}{1104098688000}-\frac{708238139903501}{595517709346560000r^2}+\frac{5580017896128641687}{998304232759142400000r^4}+\dots , r\to \infty .$$

Then, ${lim}_{r\to \infty }{\theta }_2\left(r\right)=\frac{213922547}{1104098688000}$ and the function ${\theta }_2\left(r\right)$ satisfies

$${\theta }_2\left(1\right)<{\theta }_2\left(r\right)<\frac{213922547}{1104098688000}, r\ge 1$$

with sharp constants. □

Using the bounds of the function ${\theta }_2\left(r\right)$ in Theorem 2, we get the following result:

Corollary 2.

The following inequality holds for $r\ge 1$

$$exp\left(\frac{461}{907200r^3\left(r^2+\frac{5197}{4610}\right)}+\frac{c_3}{r^9}\right)<\frac{\Gamma (r+1)}{\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}}<exp\left(\frac{461}{907200r^3\left(r^2+\frac{5197}{4610}\right)}+\frac{c_4}{r^9}\right)$$

(8)

with sharp constants

$$c_3={\theta }_2\left(1\right)=ln\sqrt{\frac{57}{134\pi }exp\left(\frac{889478519}{444845520}\right)}\approx 1.92045\times {10}^{-6}$$

and

$$c_4=\underset{r\to \infty }{lim}{\theta }_2\left(r\right)=\frac{213922547}{1104098688000}\approx 0.000193753.$$

3. Numerical Comparisons of Some Gamma Function Approximation Formulas

In this section, we contrast the numerical performance of a number of gamma function approximation formulas with our new formulations. Firstly, we will compare the following lower approximation formulas [13,21,23,28,29]:

$$\begin{array}{cc}{L}_1\left(r\right)=\sqrt{\pi }{\left(\frac{r}{e}\right)}^r\sqrt[6]{8r^3+4r^2+r+\frac{e^6}{{\pi }^3}-13}, r\ge 1\hfill & (\mathit{Ramanujan})\hfill \\ L_2\left(r\right)=\sqrt{2\pi }{\left(\frac{r}{e}\right)}^r{\left(r+\frac{1}{6}\right)}^{1/2}, r\ge 1\hfill & (\mathit{Gosper})\hfill \\ L_3\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(rsinh\left(\frac{1}{r}\right)\right)}^{r/2}, r>0\hfill & (\mathit{Windschitl})\hfill \\ L_4\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{1}{12r^3+\frac{24r}{7}-\frac{1}{2}}+1\right)}^{r^2+\frac{53}{210}}\left(-\frac{2117}{5080320r^7}+1\right), r\ge 2\hfill & (\mathit{Chen})\hfill \\ L_5\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(rsinh\left(\frac{1}{r}\right)\right)}^{r/2}exp\left(\frac{7}{324r^3\left(35r^2+33\right)}\right), r\ge 1\hfill & (\mathit{Yang} \mathit{and} \mathit{Tian})\hfill \end{array}$$

with our new lower approximation formula

$$L_6\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}exp\left(\frac{c_3}{r^9}+\frac{461}{907200r^3\left(r^2+\frac{5197}{4610}\right)}\right) r\ge 1$$

From the graphs in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, we can see that our new approximation $L_6$ is better than the approximations $L_1,L_2,L_3,L_4$, and $L_5$ for larger values of r as lower bounds of the function $\Gamma (r+1)$ for $r\ge 1$.

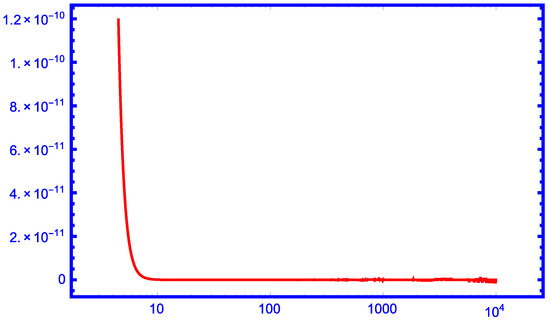
Figure 1. The function $\frac{L_6\left(r\right)-L_5\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,{10}^4]$.

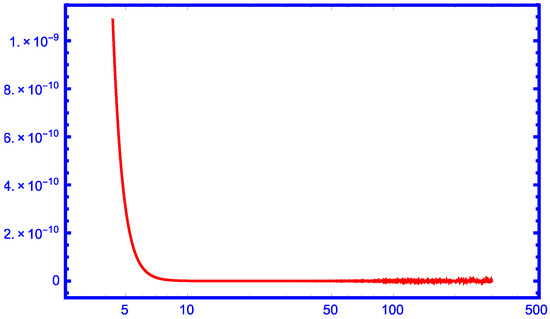
Figure 2. The function $\frac{L_6\left(r\right)-L_4\left(r\right)}{\Gamma (r+1)}$ for $r\in [2,300]$.

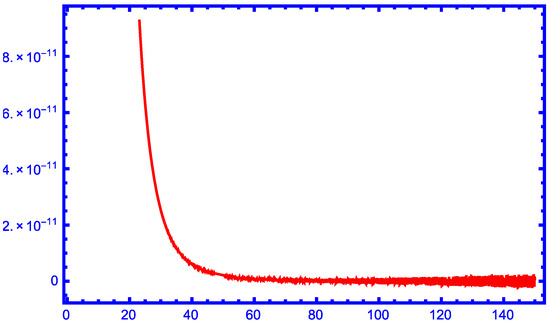
Figure 3. The function $\frac{L_4\left(r\right)-L_3\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,150]$.

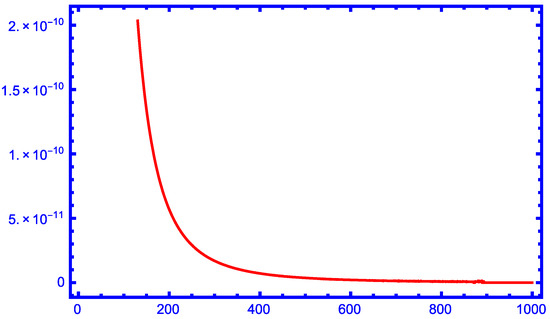
Figure 4. The function $\frac{L_3\left(r\right)-L_1\left(r\right)}{\Gamma (r+1)}$ for $r\in [3,{10}^3]$.

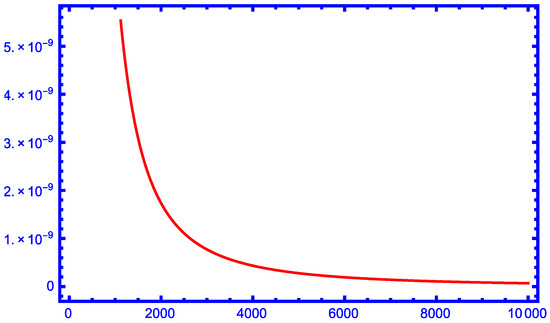
Figure 5. The function $\frac{L_1\left(r\right)-L_2\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,{10}^4]$.

Secondly, we will compare the following upper approximation formulas [13,21,23,28,29]:

$$\begin{array}{cc}{U}_1\left(r\right)=\sqrt{\pi }{\left(\frac{r}{e}\right)}^r\sqrt[6]{8r^3+4r^2+r+\frac{1}{30}}, r\ge 1\hfill & (\mathit{Ramanujan})\hfill \\ U_2\left(r\right)=\sqrt{2\pi }{\left(\frac{r}{e}\right)}^r{\left(r+\frac{1}{6}\right)}^{1/2}\sqrt{\frac{3e^2}{7\pi }}, r\ge 1\hfill & (\mathit{Gosper})\hfill \\ U_3\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r\left(\frac{1}{1620r^5}+1\right){\left(rsinh\left(\frac{1}{r}\right)\right)}^{r/2}, r>0\hfill & (\mathit{Windschitl})\hfill \\ U_4\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{1}{12r^3+\frac{24r}{7}-\frac{1}{2}}+1\right)}^{r^2+\frac{53}{210}}\left(\frac{c_5}{r^9}-\frac{2117}{5080320r^7}+1\right), r\ge 2\hfill & (\mathit{Chen})\hfill \\ U_5\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(rsinh\left(\frac{1}{r}\right)\right)}^{r/2}exp\left(\frac{7}{324r^3\left(35r^2+33\right)}\right)\frac{exp\left(\frac{33041}{22032}\right)}{\sqrt{\left(e^2-1\right)\pi }}, r\ge 1\hfill & (\mathit{Yang} \mathit{and} \mathit{Tian})\hfill \end{array}$$

where $c_5=\frac{1892069}{2347107840}$, with our new upper approximation formula

$$U_6\left(r\right)=\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r{\left(\frac{r^2+\frac{7}{60}}{r^2-\frac{1}{20}}\right)}^{r/2}exp\left(\frac{c_4}{r^9}+\frac{461}{907200\left(\frac{5197}{4610r^2}+1\right)r^5}\right), r\ge 1.$$

From the graphs in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, we can see that our new approximation $U_6$ is better than the approximations $U_1,U_2,U_3,U_4$, and $U_5$ for larger values of r as upper bounds of the function $\Gamma (r+1)$ for $r\ge 1$.

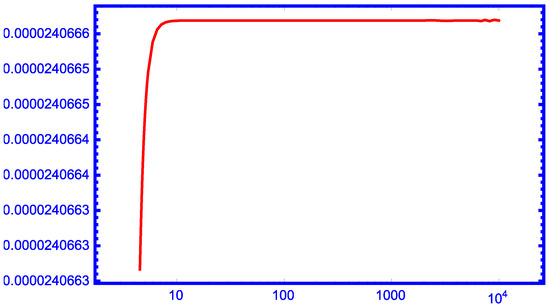
Figure 6. The function $\frac{U_5\left(r\right)-U_6\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,{10}^4]$.

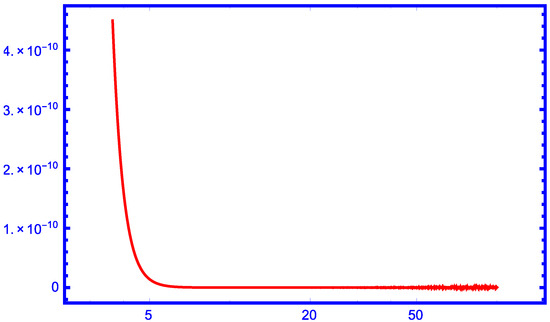
Figure 7. The function $\frac{U_4\left(r\right)-U_6\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,{10}^2]$.

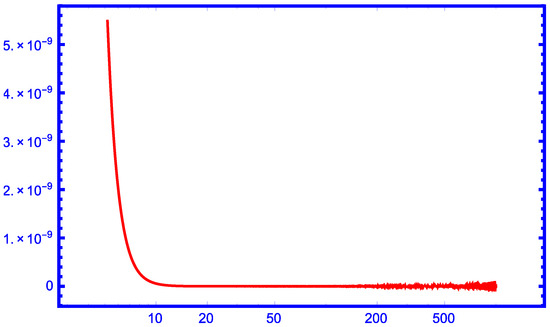
Figure 8. The function $\frac{U_3\left(r\right)-U_4\left(r\right)}{\Gamma (r+1)}$ for $r\in [2,{10}^3]$.

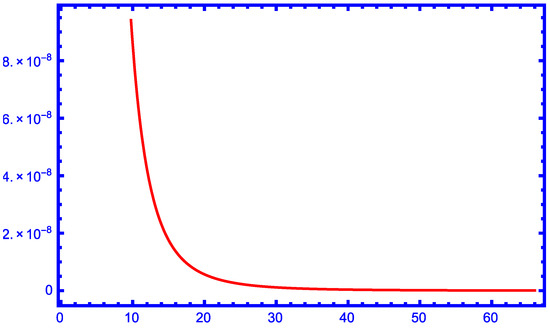
Figure 9. The function $\frac{U_1\left(r\right)-U_3\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,66]$.

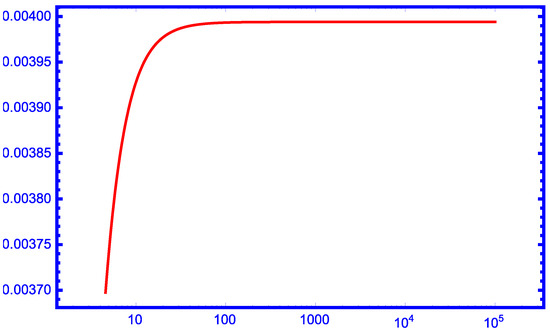
Figure 10. The function $\frac{U_2\left(r\right)-U_1\left(r\right)}{\Gamma (r+1)}$ for $r\in [1,{10}^4]$.

Using the asymptotic Laplace’s formula (see [32])

$$\frac{\Gamma (r+1)}{\sqrt{2\pi r}{\left(\frac{r}{e}\right)}^r}\sim 1+\frac{1}{12r}+\frac{1}{288r^2}-\frac{139}{51840r^3}-\frac{571}{2488320r^4}+\frac{163879}{209018880r^5}, r\to \infty$$

we obtain the following behaviour of the above mentioned bounds:

$$\begin{array}{ccc}\hfill \Gamma (r+1)& =& L_1\left(r\right)\left[1+O\left(r^{-3}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& L_2\left(r\right)\left[1+O\left(r^{-2}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& L_3\left(r\right)\left[1+O\left(r^{-5}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& L_4\left(r\right)\left[1+O\left(r^{-9}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& L_5\left(r\right)\left[1+O\left(r^{-9}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& L_6\left(r\right)\left[1+O\left(r^{-9}\right)\right], r\to \infty \hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \Gamma (r+1)& =& U_1\left(r\right)\left[1+O\left(r^{-4}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& U_3\left(r\right)\left[1+O\left(r^{-7}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& U_4\left(r\right)\left[1+O\left(r^{-7}\right)\right], r\to \infty \hfill \\ \hfill \Gamma (r+1)& =& U_6\left(r\right)\left[1+O\left(r^{-11}\right)\right], r\to \infty .\hfill \end{array}$$

Therefore, the faster asymptotic formula in the above-mentioned formulas will be $U_6\left(r\right)$ with a rate of convergence like $\frac{1}{r^{11}}$.

Our new bounds are, of course, superior to those in [31], which deduced from the bounds of the remainder function ${\sigma }_9\left(r\right)$. Also, even though the bounds in [30] are superior to our new bounds, what strengthens our results and gives them an advantage is proving that the remainders ${\theta }_1\left(r\right)$ and ${\theta }_2\left(r\right)$ are monotonic and bounded in the new approximation formulas, which was not discussed in [30].

4. Discussion

We have provided an explanation of the importance of gamma function approximations and some of their applications in some sciences. Theorems (1) and (2) outline the key findings of this paper. In more concrete terms, using the formula presented by Mahmoud and Almuashi, we provided two new approximation formulas for the Gamma function that are numerically more precise than some previously mentioned formulas. Additionally, these formulas have monotonic and bounded remainder functions, which are important in practical calculations because they provide measures of how accurate the approximations are and produce new inequalities of $\Gamma \left(r\right)$. Finally, we have shown the rate of convergence of some approximation formulas for large values of r to facilitate comparisons with the new formulas deduced in this work.