Dynamics of a Stochastic SEIR Epidemic Model with Vertical Transmission and Standard Incidence

Abstract

A stochastic SEIR epidemic model with standard incidence and vertical transmission was developed in this work. The primary goal of this study was to determine whether stochastic environmental disturbances affect dynamic features of the epidemic model. The existence, uniqueness, and boundedness of global positive solutions are stated. A threshold was determined for the extinction of the infectious disease. After that, the existence and uniqueness of an ergodic stationary distribution were verified by determining the correct Lyapunov function. Ultimately, theoretical outcomes of numerical simulations are shown.

1. Introduction

As a huge challenge throughout human history, infectious diseases have always been evolving and endangering human life. Since ancient times, scientists have been committed to studying the transmission mechanisms and effective response strategies of infectious diseases. With the continuous development of science and technology, our understanding of different fields has greatly deepened [1,2]. Among these developments, biological mathematical models play an important role in infectious disease research [1,3,4]. Since the proposal of the basic SIR (susceptible–infected–recovered) epidemic model by Kermack and McKendrick [1], various biological mathematical models have been established and analyzed, such as SIS, SIR, and SIRS [3,4,5,6,7,8,9,10,11]. Different infectious diseases have different characteristics, for example, infected individuals in a latent period before infection, so scholars introduced an exposed (E) class to study hepatitis B, AIDS, and so on. The SEIR epidemic model has been established and extensively studied [12,13,14].

In addition, the above mentioned diseases have a vertical transmission characteristic; with infected mothers infecting their unborn or newborn babies, and their descendants may be infected or susceptible [15,16]. Therefore, many scholars have studied infectious diseases with vertical transmission by establishing corresponding biological models [15,17,18]. Based on the SEIR epidemic model with vertical transmission proposed by Li et al. [15], we constructed a subsequent deterministic model:

$$\left\{\begin{array}{c}{\displaystyle \dot{S}\left(t\right)=\Lambda -\frac{\beta S\left(t\right)I\left(t\right)}{N}+qbE\left(t\right)+qbI\left(t\right)+bS\left(t\right)+bR\left(t\right)-dS\left(t\right)-\omega S\left(t\right),}\hfill \\ {\displaystyle \dot{E}\left(t\right)=\frac{\beta S\left(t\right)I\left(t\right)}{N}+pbE\left(t\right)+pbI\left(t\right)-\left(d+\omega +ϵ\right)E\left(t\right),}\hfill \\ {\displaystyle \dot{I}\left(t\right)=ϵE\left(t\right)-\left(\gamma +d+\omega +\alpha \right)I\left(t\right),}\hfill \\ {\displaystyle \dot{R}\left(t\right)=\gamma I\left(t\right)-\left(d+\omega \right)R\left(t\right),}\hfill \end{array}\right.$$

(1)

in which the numbers of susceptible, exposed (in the latent period), infectious, and recovered individuals are indicated by $S\left(t\right)$, $E\left(t\right)$, $I\left(t\right)$, and $R\left(t\right)$, respectively. $N\left(t\right)$ = $S\left(t\right)$+ $E\left(t\right)$+ $I\left(t\right)$ + $R\left(t\right)$ denotes the overall number of population individuals. The definitions in the following Table 1 apply to the parameters in model (1). All parameter values are non-negative.

Table 1. Biological significance of each parameter.

Parameters	Biological Significance
$\Lambda$	The recruitment rate of susceptible individuals corresponding to immigration.
$\beta$	The disease transmission rate.
b	The birth rate.
d	The natural mortality rate.
$\omega$	The population output rate that corresponds to emigration.
$ϵ$	The rate at which those who are exposed become infectious.
$\alpha$	The mortality rate associated with the disease.
$\gamma$	The rate of recovery for those who carry the infection.
p (0 < p < 1)	The proportion of exposed individuals in babies of exposed or infected individuals.
q = $1-p$	The proportion of susceptible individuals in babies of exposed or infected individuals.

Meanwhile, in the real world, the transmission of infectious illnesses is often influenced by numerous random factors, such as climate change, social dynamics, and population mobility. These random factors can have a significant impact on the transmission of infectious illnesses, sometimes even leading to disease outbreaks and large-scale transmission. Therefore, studying the effect of random disturbances on the transmission of infectious illnesses has become an important research direction. Like Jiang et al. [10] and Qi et al. [19], many authors have studied how random factors affect the dynamics of infectious diseases [20,21,22,23,24,25]. However, the dynamic research on SEIR epidemic models with vertical transmission and random disturbances seems to be limited. The research motivation of this study is to reveal how environmental disturbances affect the dynamic behavior of systems (1).

In this paper, we presume a positive proportional relationship between stochastic white noise and different populations (S-E-I-R). Hence, we derive the subsequent stochastic model:

$$\left\{\begin{array}{cc}\hfill \mathrm{d}S\left(t\right)=& \left(\Lambda -\frac{\beta S\left(t\right)I\left(t\right)}{N}+qbE\left(t\right)+qbI\left(t\right)+bS\left(t\right)+bR\left(t\right)-dS\left(t\right)-\omega S\left(t\right)\right)\mathrm{d}t\hfill \\ & +{\sigma }_{1}S\left(t\right)\mathrm{d}{B}_1\left(t\right),\hfill \\ \hfill \mathrm{d}E\left(t\right)=& \left(\frac{\beta S\left(t\right)I\left(t\right)}{N}+pbE\left(t\right)+pbI\left(t\right)-\left(d+\omega +ϵ\right)E\left(t\right)\right)\mathrm{d}t+{\sigma }_{2}E\left(t\right)\mathrm{d}{B}_2\left(t\right),\hfill \\ \hfill \mathrm{d}I\left(t\right)=& \left(ϵE\left(t\right)-\left(\gamma +d+\omega +\alpha \right)I\left(t\right)\right)\mathrm{d}t+{\sigma }_{3}I\left(t\right)\mathrm{d}{B}_3\left(t\right),\hfill \\ \hfill \mathrm{d}R\left(t\right)=& \left(\gamma I\left(t\right)-\left(d+\omega \right)R\left(t\right)\right)\mathrm{d}t+{\sigma }_{4}R\left(t\right)\mathrm{d}{B}_4\left(t\right),\hfill \end{array}\right.$$

(2)

in which the normal Brownian motion $B_i\left(t\right)$ is independent and $B_i\left(0\right)=0$, ${\sigma }_i>0$ expresses the white noise intensity for different populations (S-E-I-R). The above i equals 1, 2, 3, and 4.

Remark 1.

We presume that the vertical infection rates of E (exposed) and I (infected) are the same in this study, 0 < p < 1, 0 < q < 1, and when they are different, further discussion is given.

The remainder of the paper is organized as follows. In Section 2 and Section 3, we examine the existence, uniqueness, and boundedness of global positive solutions. In Section 4, the threshold criterion for the extinction of a disease can be found. In Section 5, it is determined that an ergodic stationary distribution exists and is unique. Ultimately, Section 6 presents numerical simulations and conclusions.

2. Existence of the Unique Global Positive Solution

In this section, the unique global positive solution of system (2) is proven to exist. First, we briefly introduce the subsequent lemma.

Lemma 1

([26]). (Itô formula) For a detailed explanation about Itô formula, please refer to [26]. These are the primary formulas that are applied.

$$\mathrm{d}V(x\left(t\right),t)=V_t(x\left(t\right),t)+V_x(x\left(t\right),t)f\left(t\right)+\frac{1}{2}\mathrm{trace}\left[g^T\left(t\right)V_{xx}(x\left(t\right),t)g\left(t\right)\right]\mathrm{d}t+V_x(x\left(t\right),t)g\left(t\right)dB\left(t\right),$$

then by the diffusion operator $LV$: ${\mathbb{R}}^n\times {\mathbb{R}}_{+}\to \mathbb{R}$

$$LV(x,t)=V_t(x,t)+V_x(x,t)f\left(t\right)+\frac{1}{2}\mathrm{trace}\left[g^T\left(t\right)V_{xx}(x,t)g\left(t\right)\right],$$

another expression for the Itô formula is

$$\mathrm{d}V(x\left(t\right),t)=LV(x\left(t\right),t)\mathrm{d}t+V_x(x\left(t\right),t)g\left(t\right)dB\left(t\right).$$

Next, we demonstrate that there is a unique global solution for the stochastic system (2).

Theorem 1.

For any initial condition $(S\left(0\right),E\left(0\right),I\left(0\right),R\left(0\right))\in {\mathbb{R}}_{+}^4$, there is a unique global positive solution $\left(S\right(t),E(t),I(t),R(t\left)\right)$ for system (2) which will be maintained in ${\mathbb{R}}_{+}^4$ with probability one.

Proof. 

Considering the subsequent non-negative $C^2$-function P:

$$P(S,E,I,R)=S-1-lnS+E-1-lnE+I-1-lnI+R-1-lnR.$$

Applying Itô’s formula results in

$$\begin{array}{c}\hfill \mathrm{d}P=LP\mathrm{d}t+{\sigma }_1(S-1)\mathrm{d}{B}_1\left(t\right)+{\sigma }_2(E-1)\mathrm{d}{B}_2\left(t\right)+{\sigma }_3(I-1)\mathrm{d}{B}_3\left(t\right)+{\sigma }_4(R-1)\mathrm{d}{B}_4\left(t\right),\end{array}$$

in which

$$\begin{array}{ccc}\hfill LP& =& \left(1-\frac{1}{S}\right)\left(\Lambda -\frac{\beta SI}{N}+qbE+qbI+bS+bR-dS-\omega S\right)+\frac{{\sigma }_1^2}{2}\hfill \\ & & +\left(1-\frac{1}{E}\right)\left(\frac{\beta SI}{N}+pbE+pbI-\left(d+\omega +ϵ\right)E\right)+\frac{{\sigma }_2^2}{2}\hfill \\ & & +\left(1-\frac{1}{I}\right)\left(ϵE-\left(\gamma +d+\omega +\alpha \right)I\right)+\frac{{\sigma }_3^2}{2}+\left(1-\frac{1}{R}\right)\left(\gamma I-\left(d+\omega \right)R\right)+\frac{{\sigma }_4^2}{2}\hfill \\ & =& \Lambda -\left(d+\omega -b\right)\left(S+E+I+R\right)-\alpha I-\frac{\Lambda }{S}+\frac{\beta I}{N}-\frac{qbE}{S}-\frac{qbI}{S}\hfill \\ & & -\frac{bR}{S}-b+d+\omega +\frac{{\sigma }_1^2}{2}-\frac{\beta SI}{EN}-pb-\frac{pbI}{E}+d+\omega +ϵ+\frac{{\sigma }_2^2}{2}\hfill \\ & & -\frac{ϵE}{I}+\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}-\frac{\gamma I}{R}+d+\omega +\frac{{\sigma }_4^2}{2}\hfill \\ & \le & \Lambda +\beta +4d+4\omega +ϵ+\gamma +\alpha +\frac{{\sigma }_1^2}{2}+\frac{{\sigma }_2^2}{2}+\frac{{\sigma }_3^2}{2}+\frac{{\sigma }_4^2}{2}:=K,\hfill \end{array}$$

where the constant K is positive. The approach of proof is the same as in [27], and the remainder proof is omitted. □

3. Boundedness

The solutions to system (2) are shown to be bounded in this section.

Theorem 2.

For any initial condition $(S\left(0\right),E\left(0\right),I\left(0\right),R\left(0\right))\in {\mathbb{R}}_{+}^4$, the solution $\left(S\right(t),E(t),I(t),R(t\left)\right)$ satisfies

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}(S\left(t\right),E\left(t\right),I\left(t\right),R\left(t\right))\le \frac{\Lambda }{d+\omega -b}.a.s.\end{array}$$

(3)

Proof. 

By adding and solving the four equations of (2),

$$\begin{array}{ccc}\hfill S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)& =& \frac{\Lambda }{d+\omega -b}+[S\left(0\right)+E\left(0\right)+I\left(0\right)+R\left(0\right)\hfill \\ & & -\frac{\Lambda }{d+\omega -b}]e^{-\left(d+\omega -b\right)t}-\alpha {\int }_0^t{e}^{-\left(d+\omega -b\right)(t-u)}I\left(u\right)\mathrm{d}u+M\left(t\right)\hfill \\ & \le & \frac{\Lambda }{d+\omega -b}+M\left(t\right)+[S\left(0\right)+E\left(0\right)+I\left(0\right)+R\left(0\right)\hfill \\ & & -\frac{\Lambda }{d+\omega -b}]e^{-\left(d+\omega -b\right)t},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill M\left(t\right)& =& {\sigma }_1{\int }_0^t{e}^{-\left(d+\omega -b\right)(t-u)}S\left(u\right)\mathrm{d}{B}_1\left(u\right)\hfill \\ & & +{\sigma }_2{\int }_0^t{e}^{-\left(d+\omega -b\right)(t-u)}E\left(u\right)\mathrm{d}{B}_2\left(u\right)\hfill \\ & & +{\sigma }_3{\int }_0^t{e}^{-\left(d+\omega -b\right)(t-u)}I\left(u\right)\mathrm{d}{B}_3\left(u\right)\hfill \\ & & +{\sigma }_4{\int }_0^t{e}^{-\left(d+\omega -b\right)(t-u)}R\left(u\right)\mathrm{d}{B}_4\left(u\right).\hfill \end{array}$$

Given $M\left(t\right)$ is considered a continuous local martingale and $M\left(0\right)=0$, let

$$\begin{array}{ccc}\hfill X\left(0\right)& =& S\left(0\right)+E\left(0\right)+I\left(0\right)+R\left(0\right),\hfill \\ \hfill U\left(t\right)& =& X\left(0\right)(1-e^{-\left(d+\omega -b\right)t}),\hfill \\ \hfill A\left(t\right)& =& \frac{\Lambda }{d+\omega -b}(1-e^{-\left(d+\omega -b\right)t}),\hfill \\ \hfill X\left(t\right)& =& X\left(0\right)-U\left(t\right)+A\left(t\right)+M\left(t\right).\hfill \end{array}$$

With (4), one obtains

$$\begin{array}{c}\hfill S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)\le X\left(t\right).a.s.\end{array}$$

$A\left(t\right)$ and $U\left(t\right)$ appear to be continuous adaptive rising processes when $t\ge 0$, with $A\left(0\right)=U\left(0\right)=0$. Consequently, $\underset{t\to \infty }{lim}A\left(t\right)=\frac{\Lambda }{d+\omega -b}<\infty$. From Lemma 2.1 in [28] results in, $\underset{t\to \infty }{lim}X\left(t\right)<\infty ,a.s.$ and $\underset{t\to \infty }{lim\; sup}(S\left(t\right),E\left(t\right),I\left(t\right),R\left(t\right))\le \frac{\Lambda }{d+\omega -b}.a.s.$ Above, the proof is finished. □

4. Extinction

The primary focus of this section is to discuss the threshold of (2) for the extinction of disease.

Lemma 2.

The solution of system (2) with initial condition $\left(S\right(0),E(0),I(0),R(0\left)\right)$ can be represented as $\left(S\right(t),E(t),I(t),R(t\left)\right)$; then

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}(S\left(t\right)+E\left(t\right)+\left(t\right)+R\left(t\right))<\infty ,a.s.\end{array}$$

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\frac{S\left(t\right)}{t}=0,\underset{t\to \infty }{lim}\frac{E\left(t\right)}{t}=0,\underset{t\to \infty }{lim}\frac{I\left(t\right)}{t}=0,\underset{t\to \infty }{lim}\frac{R\left(t\right)}{t}=0,a.s.\end{array}$$

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}\frac{lnS\left(t\right)}{t}=0,\underset{t\to \infty }{lim\; sup}\frac{lnE\left(t\right)}{t}=0,\underset{t\to \infty }{lim\; sup}\frac{lnI\left(t\right)}{t}=0,\underset{t\to \infty }{lim\; sup}\frac{lnR\left(t\right)}{t}=0.a.s.\end{array}$$

Moreover,

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}S\left(n\right)\mathrm{d}{B}_1\left(n\right)=0,\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}E\left(n\right)\mathrm{d}{B}_2\left(n\right)=0,\\ \hfill \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}I\left(n\right)\mathrm{d}{B}_3\left(n\right)=0,\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}R\left(n\right)\mathrm{d}{B}_4\left(n\right)=0.a.s.\end{array}$$

Proof. 

According to Theorem 2, we can obtain

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}(S\left(t\right),E\left(t\right),I\left(t\right),R\left(t\right))\le \frac{\Lambda }{d+\omega -b}<\infty .a.s.\end{array}$$

(5)

Hence, we can easily obtain

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\frac{S\left(t\right)}{t}=0,\underset{t\to \infty }{lim}\frac{E\left(t\right)}{t}=0,\underset{t\to \infty }{lim}\frac{I\left(t\right)}{t}=0,\underset{t\to \infty }{lim}\frac{R\left(t\right)}{t}=0.a.s.\end{array}$$

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}\frac{lnS\left(t\right)}{t}=0,\underset{t\to \infty }{lim\; sup}\frac{lnE\left(t\right)}{t}=0,\underset{t\to \infty }{lim\; sup}\frac{lnI\left(t\right)}{t}=0,\underset{t\to \infty }{lim\; sup}\frac{lnR\left(t\right)}{t}=0.a.s.\end{array}$$

Let

$$\begin{array}{c}\hfill M_1={\int }_0^{t}S\left(n\right)\mathrm{d}{B}_1\left(n\right), M_2={\int }_0^{t}E\left(n\right)\mathrm{d}{B}_2\left(n\right), M_3={\int }_0^{t}I\left(n\right)\mathrm{d}{B}_3\left(n\right), M_4={\int }_0^{t}R\left(n\right)\mathrm{d}{B}_4\left(n\right).\end{array}$$

From the quadratic variations such that

$$\begin{array}{c}\hfill ⟨M_1,M_1⟩={\int }_0^t{S}^2\left(n\right)\mathrm{d}{B}_1\left(n\right)\le \left(\underset{t\ge 0}{sup}{S}^2\left(t\right)\right)t.\end{array}$$

With the large number theorem for the martingale (see Lemma 3.1 in [29]) and (5), one has

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}S\left(n\right)\mathrm{d}{B}_1\left(n\right)=0.a.s.\end{array}$$

Similarly, other equations can also be obtained. In summary, the proof has been completed. □

A parameter is defined

$$R_0^e=\frac{2\beta ϵ\left(\omega +d+ϵ\right)+2pb{\left(\omega +d+ϵ\right)}^2-2ϵpb\left(\omega +d+ϵ\right)}{\left[{\left(\omega +d+ϵ\right)}^2+\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)\wedge \frac{{ϵ}^2{\sigma }_2^2}{2}\right]},$$

where $\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)\wedge \frac{{ϵ}^2{\sigma }_2^2}{2}=min\left\{\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2},\frac{{ϵ}^2{\sigma }_2^2}{2}\right\}$.

Theorem 3.

The solution of system (2) with initial condition $(S\left(0\right),E\left(0\right),I\left(0\right),R\left(0\right))\in {\mathbb{R}}_{+}^4$ is denoted by $\left(S\right(t),E(t),I(t),R(t\left)\right)$. If $R_0^e<1$ holds, then $\underset{t\to \infty }{lim\; sup}\frac{\ln (ϵE+(d+\omega +ϵ\left)I\right)}{t}<0$,a.s. which suggests that the illness becomes extinct.

Proof. 

A $C^2$-function V is constructed:

$$\begin{array}{ccc}\hfill V& =& ϵE+(d+\omega +ϵ)I,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill LlnV& =& \frac{1}{V}\left[ϵ\left(\frac{\beta SI}{N}+pbE+pbI-\left(d+\omega +ϵ\right)E\right)+(d+\omega +ϵ)\left(ϵE-\left(\gamma +d+\omega +\alpha \right)I\right)\right]\hfill \\ & & -\frac{{ϵ}^2{\sigma }_2^2{E}^2+{\left(d+\omega +ϵ\right)}^2{\sigma }_3^2{I}^2}{2V^2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{d}lnV& =& LlnV\mathrm{d}t+\frac{ϵ{\sigma }_{2}E}{V}\mathrm{d}{B}_2\left(t\right)+\frac{\left(d+\omega +ϵ\right){\sigma }_{3}I}{V}\mathrm{d}{B}_3\left(t\right)\hfill \\ & =& [\frac{\frac{ϵ\beta SI}{S+E+R+I}+ϵpbE+ϵpbI-\left(d+\omega +ϵ\right)\left(\gamma +d+\omega +\alpha \right)I}{ϵE+(d+\omega +ϵ)I}\hfill \\ & & -\frac{{ϵ}^2{\sigma }_2^2{E}^2+{\left(d+\omega +ϵ\right)}^2{\sigma }_3^2{I}^2}{2{\left[ϵE+(d+\omega +ϵ)I\right]}^2}]\mathrm{d}t\hfill \\ & & +\frac{ϵ{\sigma }_{2}E}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_2\left(t\right)+\frac{\left(d+\omega +ϵ\right){\sigma }_{3}I}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_3\left(t\right)\hfill \\ & \le & \left(\frac{ϵ\beta }{d+\omega +ϵ}+pb+\frac{ϵpb}{d+\omega +ϵ}\right)\mathrm{d}t\hfill \\ & & -\frac{1}{{\left[ϵE+(d+\omega +ϵ)I\right]}^2}\{\left[{(d+\omega +ϵ)}^2\left(\gamma +d+\omega +\alpha \right)+\frac{1}{2}{(d+\omega +ϵ)}^2{\sigma }_3^2\right]I^2\hfill \\ & & +\frac{1}{2}{ϵ}^2{\sigma }_2^2{E}^2\}\mathrm{d}t+\frac{ϵ{\sigma }_{2}E}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_2\left(t\right)+\frac{\left(d+\omega +ϵ\right){\sigma }_{3}I}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_3\left(t\right)\hfill \\ & \le & \left(\frac{ϵ\beta }{d+\omega +ϵ}+pb+\frac{ϵpb}{d+\omega +ϵ}\right)\mathrm{d}t\hfill \\ & & -\frac{1}{{(d+\omega +ϵ)}^2{(E+I)}^2}\left[{(d+\omega +ϵ)}^2\left(\gamma +d+\omega +\alpha +\frac{1}{2}{\sigma }_3^2\right)I^2+\frac{1}{2}{ϵ}^2{\sigma }_2^2{E}^2\right]\mathrm{d}t\hfill \\ & & +\frac{ϵ{\sigma }_{2}E}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_2\left(t\right)+\frac{\left(d+\omega +ϵ\right){\sigma }_{3}I}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_3\left(t\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill \\ & \le & \left(\frac{ϵ\beta }{d+\omega +ϵ}+pb+\frac{ϵpb}{d+\omega +ϵ}\right)\mathrm{d}t\hfill \\ & & -\frac{1}{2{(d+\omega +ϵ)}^2(I^2+E^2)}\left\{\left[{\left(d+\omega +ϵ\right)}^2\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)\wedge \frac{{ϵ}^2{\sigma }_2^2}{2}\right](I^2+E^2)\right\}\mathrm{d}t\hfill \\ & & +\frac{ϵ{\sigma }_{2}E}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_2\left(t\right)+\frac{\left(d+\omega +ϵ\right){\sigma }_{3}I}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_3\left(t\right)\hfill \\ & =& \left(\frac{ϵ\beta }{d+\omega +ϵ}+pb+\frac{ϵpb}{d+\omega +ϵ}\right)\mathrm{d}t-\frac{1}{2{(d+\omega +ϵ)}^2}[{\left(d+\omega +ϵ\right)}^2\hfill \\ & & \left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)\wedge \frac{{ϵ}^2{\sigma }_2^2}{2}]\mathrm{d}t+\frac{ϵ{\sigma }_{2}E}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_2\left(t\right)\hfill \\ & & +\frac{\left(d+\omega +ϵ\right){\sigma }_{3}I}{ϵE+(d+\omega +ϵ)I}\mathrm{d}{B}_3\left(t\right).\hfill \end{array}$$

(6)

By dividing both sides by t after integrating (6) from 0 to t, we derive

$$\begin{array}{ccc}\hfill \frac{lnV\left(t\right)}{t}-\frac{\ln V\left(0\right)}{t}& \le & \frac{ϵ}{d+\omega +\beta ϵ}+pb+\frac{ϵpb}{d+\omega +ϵ}\hfill \\ & & -\frac{1}{2{(d+\omega +ϵ)}^2}\left[{\left(d+\omega +ϵ\right)}^2\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)\wedge \frac{{ϵ}^2{\sigma }_2^2}{2}\right]\hfill \\ & & +\frac{ϵ{\sigma }_2}{t}{\int }_0^t\frac{E\left(s\right)}{ϵE\left(s\right)+(d+\omega +ϵ)I\left(s\right)}\mathrm{d}{B}_2\left(s\right)\hfill \\ & & +\frac{\left(d+\omega +ϵ\right){\sigma }_3}{t}{\int }_0^t\frac{I\left(s\right)}{ϵE\left(s\right)+(d+\omega +ϵ)I\left(s\right)}\mathrm{d}{B}_3\left(s\right).\hfill \end{array}$$

(7)

By taking the superior limit on either side of (7), we may obtain that by combining Lemma 2 with $R_0^e<1$,

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim\; sup}\frac{\ln (ϵE+(d+\omega +ϵ\left)I\right)}{t}& \le & \frac{1}{2{(d+\omega +ϵ)}^2}[{\left(d+\omega +ϵ\right)}^2\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)\hfill \\ & & \wedge \frac{{ϵ}^2{\sigma }_2^2}{2}](R_0^e-1)\hfill \\ & & <0,a.s.\hfill \end{array}$$

which means $\underset{t\to \infty }{lim}E\left(t\right)=0$, $\underset{t\to \infty }{lim}I\left(t\right)=0$.a.s. This shows that the illness will eventually disappear. $\underset{t\to \infty }{lim}R\left(t\right)=0$. a.s. can also be easily obtained from system (2). Thus, the proof is completed. □

5. Stationary Distribution and Ergodicity

We verify in this section that system (2) exists as an ergodic stationary distribution by applying Theorem 4 and Assumption (B) [30], which indirectly reflects the persistence of the disease.

A parameter is defined

$$R_0^s=\frac{\left(d+\omega -b\right)\beta ϵ}{\left(\omega +d-b+\frac{{\sigma }_1^2}{2}\right)\left(\omega +d+ϵ-pb+\frac{{\sigma }_2^2}{2}\right)\left(\gamma +\omega +d+\alpha +\frac{{\sigma }_3^2}{2}\right)}.$$

Theorem 4.

There exists a unique ergodic stationary distribution $\pi (·)$ for system (2) if $R_0^s>1$.

Proof. 

Let $\widehat{M}=\min \left\{{\sigma }_1^2{S}^2,{\sigma }_2^2{E}^2,{\sigma }_3^2{I}^2,{\sigma }_4^2{R}^2\right\}$.

The following is the diffusion matrix of System (2)

$$C=\left(\begin{array}{cccc}{\sigma }_1^2{S}^2& 0& 0& 0\\ 0& {\sigma }_2^2{E}^2& 0& 0\\ 0& 0& {\sigma }_3^2{I}^2& 0\\ 0& 0& 0& {\sigma }_4^2{R}^2\end{array}\right),$$

$\eta =({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)\in {\mathbb{R}}^4$, given any $(S,E,I,R)\in D_r$, then

$$\sum _{i,j=1}^4{c}_{ij}\left(x\right){\eta }_i{\eta }_j={\sigma }_1^2{S}^2{\eta }_1^2+{\sigma }_2^2{E}^2{\eta }_2^2+{\sigma }_3^2{I}^2{\eta }_3^2+{\sigma }_4^2{R}^2{\eta }_4^2\ge \widehat{M}{\left|\eta \right|}^2,$$

where $D_r=\left[\frac{1}{r},r\right]\times \left[\frac{1}{r},r\right]\times \left[\frac{1}{r},r\right]\times \left[\frac{1}{r},r\right]$, with $r>1$ being a sufficiently large constant.

Thus, the condition (B.1) of Assumption (B) [30] is proved. Next, we define a $C^2$-function $Z:{\mathbb{R}}_{+}^4\to {\mathbb{R}}_{+}:$

$$\begin{array}{ccc}\hfill Z(S,E,I,R)& =& M\left(-a_{1}lnS-a_{2}lnE-a_{3}lnI+S+E+I+R\right)+\frac{1}{\delta +1}{(S+E+I+R)}^{\delta +1}\hfill \\ & & -lnS-lnE-lnR+\left(S+E+I+R\right)\hfill \\ & =& M{V}_1+V_2+V_3,\hfill \end{array}$$

where

$$a_1=\frac{\Lambda \beta ϵ\left(d+\omega -b\right)}{{\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right)}^2\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right)\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)},$$

$$a_2=\frac{\Lambda \beta ϵ\left(d+\omega -b\right)}{\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right){\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right)}^2\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)},$$

$$a_3=\frac{\Lambda \beta ϵ\left(d+\omega -b\right)}{\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right)\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right){\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)}^2},$$

the constant $\delta >0$ is small enough to ensure

$$(d+\omega -b)-\frac{1}{2}\delta \left({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\right)>0.$$

In addition to being a sufficiently large positive constant, M also meets the following requirement

$$\begin{array}{c}\hfill -MY+C\le -2,\end{array}$$

where

$$Y=\Lambda \left(R_0^s-1\right)>0,$$

and

$$\begin{array}{ccc}\hfill C& =& \underset{(S,E,I,R)\in R_{+}^4}{sup}\{\Lambda +\beta +3d+3\omega +ϵ+\frac{1}{2}\left({\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2\right)\hfill \\ & & +G-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})\}.\hfill \end{array}$$

It is worth noting that $a_1$, $a_2$, $a_3$, Y, and C are derived from the subsequent proof process.

Clearly,

$$\underset{n\to \infty ,(S,E,I,R)\in {\mathbb{R}}_{+}^4\setminus U_r}{lim\; inf}Z(S,E,I,R)=+\infty ,$$

in which $U_r=\left(\frac{1}{r},r\right)\times \left(\frac{1}{r},r\right)\times \left(\frac{1}{r},r\right)\times \left(\frac{1}{r},r\right)$. There exists a minimum $Z(S_0,E_0,I_0,R_0)$ at ${\mathbb{R}}_{+}^4$ since $Z(S,E,I,R)$ is continuous on ${\mathbb{R}}_{+}^4$.

The $C^2$-function is defined: ${\mathbb{R}}_{+}^4\to {\mathbb{R}}_{+},$

$$\tilde{Z}=Z(S,E,I,R)-Z(S_0,E_0,I_0,R_0).$$

According to Itô’s formula,

$$\begin{array}{ccc}\hfill L{V}_1& =& -\frac{a_1}{S}\left(\Lambda -\frac{\beta SI}{N}+qbE+qbI+bS+bR-dS-\omega S\right)+\frac{a_1{\sigma }_1^2}{2}\hfill \\ & & -\frac{a_2}{E}\left(\frac{\beta SI}{N}+pbE+pbI-\left(d+\omega +ϵ\right)E\right)+\frac{a_2{\sigma }_2^2}{2}\hfill \\ & & -\frac{a_3}{I}\left(ϵE-\left(\gamma +d+\omega +\alpha \right)I\right)+\frac{a_3{\sigma }_3^2}{2}+\Lambda -\left(d+\omega -b\right)\left(S+E+I+R\right)-\alpha I\hfill \\ & \le & -\frac{a_1\Lambda }{S}+\frac{a_1\beta I}{S+E+I+R}+a_1\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right)\hfill \\ & & -\frac{a_2\beta SI}{E\left(S+E+I+R\right)}+a_2\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right)\hfill \\ & & -\frac{a_3ϵE}{I}+a_3\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)+\Lambda -\left(\omega +d-b\right)\left(S+E+I+R\right)\hfill \\ & \le & -4\sqrt[4]{a_1{a}_2{a}_3\Lambda \beta ϵ\left(d+\omega -b\right)}+a_1\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right)+a_2\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right)\hfill \\ & & +a_3\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)+\Lambda +\frac{a_1\beta I}{S+E+I+R}\hfill \\ & \le & -\frac{\left(d+\omega -b\right)\Lambda \beta ϵ}{\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right)\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right)\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)}+\Lambda \hfill \\ & & +\frac{a_1\beta I}{S+E+I+R}\hfill \\ & =& -\Lambda \left[\frac{\left(d+\omega -b\right)\beta ϵ}{\left(d+\omega -b+\frac{{\sigma }_1^2}{2}\right)\left(d+\omega +ϵ-pb+\frac{{\sigma }_2^2}{2}\right)\left(\gamma +d+\omega +\alpha +\frac{{\sigma }_3^2}{2}\right)}-1\right]\hfill \\ & & +\frac{a_1\beta I}{S+E+I+R}\hfill \\ & =& -Y+\frac{a_1\beta I}{S+E+I+R},\hfill \end{array}$$

where

$$Y=\Lambda \left(R_0^s-1\right)>0.$$

With Itô’s formula, we can furthermore obtain

$$\begin{array}{ccc}\hfill L{V}_2& =& {(S+E+I+R)}^{\delta }\left[\Lambda -\left(d+\omega -b\right)(S+E+I+R)-\alpha I\right]\hfill \\ & & +\frac{1}{2}\delta {(S+E+I+R)}^{\delta -1}\left({\sigma }_1^2{S}^2+{\sigma }_2^2{E}^2+{\sigma }_3^2{I}^2+{\sigma }_4^2{R}^2\right)\hfill \\ & \le & \Lambda {(S+E+I+R)}^{\delta }-\left(d+\omega -b\right){(S+E+I+R)}^{\delta +1}\hfill \\ & & +\frac{\delta }{2}\left({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\right){(S+E+I+R)}^{\delta +1}\hfill \\ & =& \Lambda {(S+E+I+R)}^{\delta }-m{(S+E+I+R)}^{\delta +1}\hfill \\ & \le & G-\frac{m}{2}{(S+E+I+R)}^{\delta +1}\hfill \\ & \le & G-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1}),\hfill \end{array}$$

let

$$\begin{array}{ccc}\hfill {\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2& =& max\left\{{\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2,{\sigma }_4^2\right\},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill m& =& \left(d+\omega -b\right)-\frac{\delta }{2}\left({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill G& =& \underset{(S,E,I,R)\in {\mathbb{R}}_{+}^4}{sup}\left\{\Lambda {(S+E+I+R)}^{\delta }-\frac{m}{2}{(S+E+I+R)}^{\delta +1}\right\}.\hfill \end{array}$$

Similarly,

$$\begin{array}{c}\hfill L(-lnS)=-\frac{1}{S}\left(\Lambda -\frac{\beta SI}{N}+qbE+qbI+bS+bR-dS-\omega S\right)+\frac{{\sigma }_1^2}{2},\end{array}$$

$$\begin{array}{c}\hfill L(-lnE)=-\frac{1}{E}\left(\frac{\beta SI}{N}+pbE+pbI-\left(d+\omega +ϵ\right)E\right)+\frac{{\sigma }_2^2}{2},\end{array}$$

$$\begin{array}{c}\hfill L(-lnR)=-\frac{1}{R}\left(\gamma I-\left(d+\omega \right)R\right)+\frac{{\sigma }_4^2}{2},\end{array}$$

$$\begin{array}{c}\hfill L(S+E+I+R)=\Lambda -\left(d+\omega -b\right)\left(S+E+I+R\right)-\alpha I,\end{array}$$

and

$$\begin{array}{ccc}\hfill L{V}_3& =& L(-lnS)+L(-lnE)+L(-lnR)+L(S+E+I+R)\hfill \\ & \le & -\frac{\Lambda }{S}-\frac{\beta SI}{EN}-\frac{\gamma R}{I}+\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}+\Lambda -\left(d+\omega -b\right)N.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill L\tilde{Z}(S,E,I,R)& \le & M\left(-Y+\frac{a_1\beta I}{S+E+I+R}\right)+G-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})-\frac{\Lambda }{S}\hfill \\ & & -\frac{\beta SI}{EN}-\frac{\gamma R}{I}+\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}+\Lambda -\left(d+\omega -b\right)N\hfill \\ & \le & -MY+\frac{M{a}_1\beta I}{S+E+I+R}-2\sqrt{\frac{\beta \left(d+\omega -b\right)SI}{E}}-\frac{\Lambda }{S}-\frac{\gamma R}{I}+G\hfill \\ & & -\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}.\hfill \end{array}$$

After, we define the bounded closed set that follows

$$U=\left\{(S,E,I,R)\in {\mathbb{R}}_{+}^4:\theta \le S\le \frac{1}{\theta },{\theta }^5\le E\le \frac{1}{{\theta }^5},{\theta }^2\le I\le \frac{1}{{\theta }^2},{\theta }^3\le R\le \frac{1}{{\theta }^3}\right\},$$

where $\theta >0$ is a sufficiently small number. Within ${\mathbb{R}}_{+}^4\setminus U$, we can select $\theta$ small enough so that

$$\begin{array}{c}\hfill -\frac{\Lambda }{\theta }+A\le -1,\end{array}$$

(8)

$$\begin{array}{c}\hfill \frac{-2\sqrt{\beta \left(d+\omega -b\right)}}{\theta }+A\le -1,\end{array}$$

(9)

$$\begin{array}{c}\hfill M{a}_1\beta \theta -MY+C\le -1,\end{array}$$

(10)

$$\begin{array}{c}\hfill -\frac{\gamma }{\theta }+A\le -1,\end{array}$$

(11)

$$\begin{array}{c}\hfill -\frac{m}{4}\frac{1}{{\theta }^{\delta +1}}+D\le -1,\end{array}$$

(12)

$$\begin{array}{c}\hfill -\frac{m}{4}\frac{1}{{\theta }^{5\left(\delta +1\right)}}+F\le -1,\end{array}$$

(13)

$$\begin{array}{c}\hfill -\frac{m}{4}\frac{1}{{\theta }^{2\left(\delta +1\right)}}+H\le -1,\end{array}$$

(14)

$$\begin{array}{c}\hfill -\frac{m}{4}\frac{1}{{\theta }^{3\left(\delta +1\right)}}+J\le -1,\end{array}$$

(15)

where A, C, D, F, H, and J are positive constants which can be determined from the later Equations (16), (18), (20), (21), (22), and (23), respectively. For ease of proof, eight domains are created by dividing ${\mathbb{R}}_{+}^4\setminus U$,

$$\begin{array}{cc}& U_1=\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,0<S<\theta \},\\ & U_2=\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,S>\theta ,0<E<{\theta }^5,I>{\theta }^2\},\\ & U_3=\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,S>\theta ,0<I<{\theta }^2\},\\ & U_4=\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,I>{\theta }^2,0<R<{\theta }^3\},\end{array}$$

$$\begin{array}{c}\\ & U_5=\left\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,S>\frac{1}{\theta }\right\},\\ & U_6=\left\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,E>\frac{1}{{\theta }^5}\right\},\\ & U_7=\left\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,I>\frac{1}{{\theta }^2}\right\},\\ & U_8=\left\{(S,E,I,R)\in {\mathbb{R}}_{+}^4,R>\frac{1}{{\theta }^3}\right\}.\end{array}$$

Next, we demonstrate that $L\tilde{Z}(S,E,I,R)\le -1$ in the eight mentioned domains, that is, in the ${\mathbb{R}}_{+}^4\setminus U$.

Case 1. In conjunction with (8) and $(S,E,I,R)\in U_1$, we have

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -\frac{\Lambda }{S}+\frac{M{a}_1\beta I}{S+E+I+R}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & -\frac{\Lambda }{\theta }+A\hfill \\ & \le & -1,\hfill \end{array}$$

(16)

where

$$\begin{array}{ccc}\hfill A& =& \underset{(S,E,I,R)\in {\mathbb{R}}_{+}^4}{sup}\{\frac{M{a}_1\beta I}{S+E+I+R}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\}.\hfill \end{array}$$

Case 2. Considering (9), if $(S,E,I,R)\in U_2$, one attains

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -2\sqrt{\frac{\beta \left(d+\omega -b\right)SI}{E}}+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & -\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})+G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & \frac{-2\sqrt{\beta \left(d+\omega -b\right)}}{\theta }+A\hfill \\ & \le & -1.\hfill \end{array}$$

(17)

Case 3. Combining (10) with $(S,E,I,R)\in U_3$, one has

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -MY+\frac{M{a}_1\beta I}{S}+G-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})\hfill \\ & & +\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & M{a}_1\beta \theta -MY+C\hfill \\ & \le & -1,\hfill \end{array}$$

(18)

where

$$\begin{array}{ccc}\hfill C& =& \underset{(S,E,I,R)\in R_{+}^4}{sup}\{\Lambda +\beta +3d+3\omega +ϵ+\frac{1}{2}\left({\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2\right)\hfill \\ & & +G-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})\}.\hfill \end{array}$$

Case 4. When $(S,E,I,R)\in U_4$, together with (11), this results in

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -\frac{\gamma R}{I}+\frac{M{a}_1\beta I}{S+E+I+R}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1}+R^{\delta +1})\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & -\frac{\gamma }{\theta }+A\hfill \\ & \le & -1.\hfill \end{array}$$

(19)

Case 5. Applying (12) if $(S,E,I,R)\in U_5$ has

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -\frac{m}{4}{S}^{\delta +1}-\frac{m}{4}{S}^{\delta +1}-\frac{m}{2}(E^{\delta +1}+I^{\delta +1}+R^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & -\frac{m}{4}\frac{1}{{\theta }^{\delta +1}}+D\hfill \\ & \le & -1,\hfill \end{array}$$

(20)

where

$$\begin{array}{ccc}\hfill D& =& \underset{(S,E,I,R)\in {\mathbb{R}}_{+}^4}{sup}\{-\frac{m}{4}{S}^{\delta +1}-\frac{m}{2}(E^{\delta +1}+I^{\delta +1}+R^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\}.\hfill \end{array}$$

Case 6. Given that $(S,E,I,R)\in U_6$, (13) implies that

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -\frac{m}{4}{E}^{\delta +1}-\frac{m}{4}{E}^{\delta +1}-\frac{m}{2}(S^{\delta +1}+I^{\delta +1}+R^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & -\frac{m}{4}\frac{1}{{\theta }^{5\left(\delta +1\right)}}+F\hfill \\ & \le & -1,\hfill \end{array}$$

(21)

where

$$\begin{array}{ccc}\hfill F& =& \underset{(S,E,I,R)\in {\mathbb{R}}_{+}^4}{sup}\{-\frac{m}{4}{E}^{\delta +1}-\frac{m}{2}(S^{\delta +1}+I^{\delta +1}+R^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\}.\hfill \end{array}$$

Case 7. Combining (14) with $(S,E,I,R)\in U_7$, one obtains

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -\frac{m}{4}{I}^{\delta +1}-\frac{m}{4}{I}^{\delta +1}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+R^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & -\frac{m}{4}\frac{1}{{\theta }^{2\left(\delta +1\right)}}+H\hfill \\ & \le & -1,\hfill \end{array}$$

(22)

where

$$\begin{array}{ccc}\hfill H& =& \underset{(S,E,I,R)\in {\mathbb{R}}_{+}^4}{sup}\{-\frac{m}{4}{I}^{\delta +1}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+R^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\}.\hfill \end{array}$$

Case 8. When $(S,E,I,R)\in U_8$, (15) implies that

$$\begin{array}{ccc}\hfill L\tilde{Z}& \le & -\frac{m}{4}{R}^{\delta +1}-\frac{m}{4}{R}^{\delta +1}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\hfill \\ & \le & -\frac{m}{4}\frac{1}{{\theta }^{3\left(\delta +1\right)}}+J\hfill \\ & \le & -1,\hfill \end{array}$$

(23)

where

$$\begin{array}{ccc}\hfill J& =& \underset{(S,E,I,R)\in {\mathbb{R}}_{+}^4}{sup}\{-\frac{m}{4}{R}^{\delta +1}-\frac{m}{2}(S^{\delta +1}+E^{\delta +1}+I^{\delta +1})+\frac{M{a}_1\beta I}{S+E+I+R}\hfill \\ & & +G+\Lambda +\beta +3d+3\omega +ϵ+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_4^2}{2}\}.\hfill \end{array}$$

Obviously, one can conclude that for a small enough $\theta$, through Equations (16)–(23),

$$L\tilde{Z}(S,E,I,R)\le -1,(S,E,I,R)\in {\mathbb{R}}_{+}^4\setminus U.$$

Hence, the requirement (B.2) of Assumption (B) from [30] holds. Theorem 4 is fully proved. □

6. Numerical Simulations and Conclusions

First, we assigned the following values to the parameters in the system (2),

$$\left(S\left(0\right),E\left(0\right),I\left(0\right),R\left(0\right)\right)=\left(10,3,3,4\right),$$

$$\Lambda =1.2, b=0.1, d=0.1, \omega =0.05, \beta =0.8,$$

$$\alpha =0.1, p=0.8, q=0.2, ϵ=0.7, \gamma =0.1.$$

Next, we conducted numerical simulations.

(1)

Let ${\sigma }_1$ = 0.1, ${\sigma }_2$ = 1.2, ${\sigma }_3$ = 1.2, and ${\sigma }_4$ = 0.1. The other parameter values are as described above, calculated as $R_0^e=0.0838<1$, which fulfills the requirement of Theorem 3 and verifies the conclusion of Theorem 3. Figure 1 provides a better explanation.

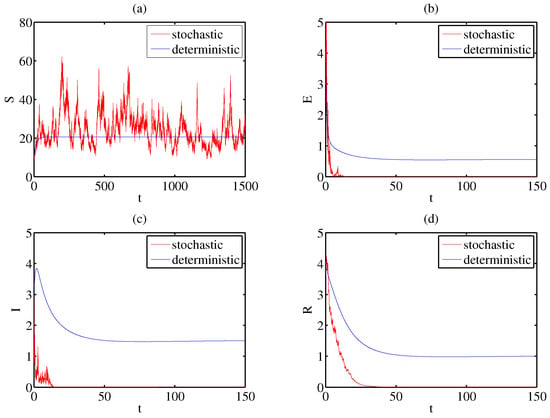Figure 1. (a–d): Extinction trend of System (2).

(2)

Let ${\sigma }_i=0.015$, where $i=1,2,3,4$. Computing that $R_0^s=2.0723>1$ satisfies the requirement of Theorem 4, and the system (2) supports an ergodic stationary distribution. The numerical simulation results are shown in Figure 2. This also indicates that the disease is prevalent in a stable state.

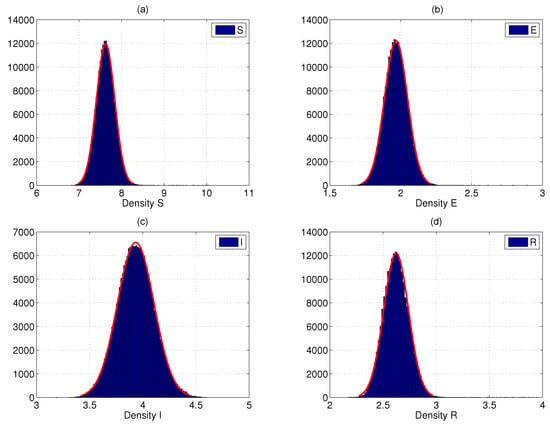
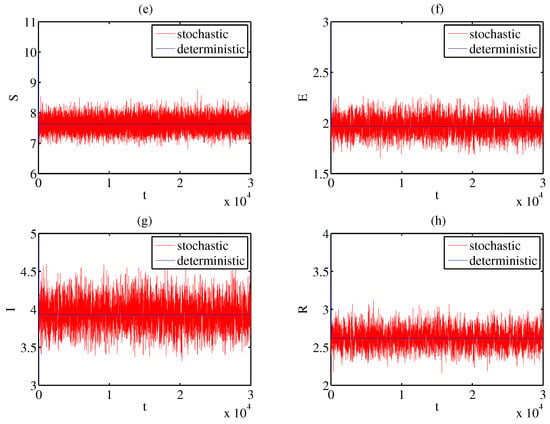Figure 2. (a–d): The density function of the solution. (e–h): The persistence of the system (2).

(3)

Due to the consideration of vertical transmission in this paper, the impact of parameter p on the system (2) is discussed. Figure 3 shows an inverse trend, where the larger the value of p, the smaller the value when it tends to stabilize. Therefore, by controlling the value of p, further exploration of the dynamic properties of disease transmission can be carried out in future work.

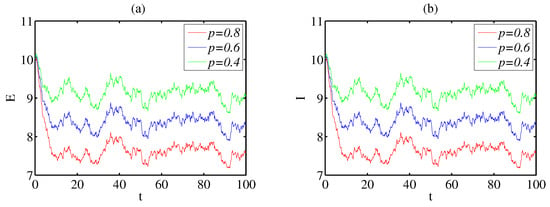Figure 3. (a,b): The impact of parameter p on the system (2).

Compared to other papers, this paper establishes a new stochastic SEIR epidemic model and explores how environmental disturbances affect the dynamic behavior of the system. First, the existence, uniqueness, and boundedness of global positive solutions are shown. Second, we demonstrate the threshold requirements for disease extinction and stationary distribution. The illness will go extinct if $R_0^e<1$, and the system (2) accords with a stationary distribution if $R_0^s>1$. By comparing the parameter values, as well as Figure 1 and Figure 2, the disease becomes extinct when white noise intensity is high and becomes prevalent when it is low. From this perspective, white noise can suppress the occurrence of diseases, indicating that the dynamics of the epidemic system are significantly impacted by random environmental disruptions. In addition, the random noise considered in this article is linear; therefore, in future work, the impact of nonlinear random noise on infectious disease dynamics will also be considered.