A Rate-Dependent Probabilistic Model of Hysteresis

Abstract

Instead of modelling an economic agent by a hysteron, we suggest a fluid–mechanical notion of rate-dependent hysteretic agents based on the theory of Poisson counters. It leads to a simple representation of assemblies of such agents. We discuss the properties of the new version of hysteresis and its advantages over classical models of hysteresis in economics.

1. Introduction

We start with a brief discussion of concepts connected with the notion of hysteresis; for a general treatment of systems with hysteresis please see [1,2,3] for a more mathematical approach. A detailed discussion of hysteresis in economics can be found in the review [4].

By hysteresis, one usually means some type of memory capacity in a system; there are many definitions and approaches to hysteresis in different areas, and even in any one particular area, as for example, in economics, there is no one accepted definition. The concept that is most often invoked when speaking about hysteresis is a (static) hysteresis loop, such as an S- or a Z-curve.

In engineering and control, the starting point of discussions of hysteresis is a hysteron, which is a two-state agent/black box, for which there exist two values, $\alpha$ and $\beta$, $\alpha <\beta$, of a control parameter s, such that if $s>\beta$, the hysteron is in state 1 and if $s<\alpha$, it is in state 0. For $s\in (\alpha ,\beta )$, the state of the hysteron depends on its history: one says that the hysteron remembers (some of) the past history of the values s has gone through. One can denote a hysteron by $F_{\alpha ,\beta }\left(s\right)$, which outputs 0 and 1 according to the rules explained above; see Figure 1 for illustration (note that the motion on horizontal segments is bi-directional). The state of the hysteron $F_{\alpha ,\beta }\left(s\right)$ is uniquely determined by the history of change of the control parameter s. Note that adjustment of the hysteron to the control parameter is instantaneous and synchronous. In such a case, we say that hysteresis is rate-independent: it is not important how fast s changes. If s stops changing, so does the state of the hysteron.

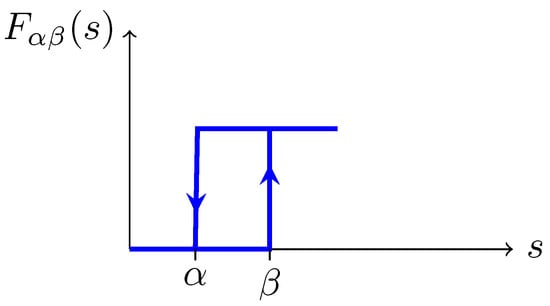
Figure 1. A hysteron.

The hysteron also provides a simple model of an economic agent. For example, in the theory of the firm [5], it may represent a firm that enters the market (goes into state 1) when the price for its product rises above $\beta$ and exits the markets when the price falls below $\alpha$ (goes into state 0). Here, it is assumed that the behaviour of single firm does not affect the price of the product. An important question that has to be addressed is why would an economic agent be hysteretic. A frequently mentioned reason is sunk costs, which is particularly obvious in the case of a firm. When the price determined by the market at large is high enough, it makes economic sense for an inactive firm to enter the market; this corresponds to $s=\beta$, but if then the price slips below $\beta$, it makes no sense for the firm to exit immediately as it has invested in plant, workforce, taxes—costs that cannot be easily recovered if at all. So, the firm will only exit the market when the price falls below the lower threshold value $\alpha$, when remaining in the market becomes unsustainable.

Another example from finance rather than economics is provided by the motivation underlying decisions to switch large investment portfolios. As has been noted, as in [6], there can be considerable pressure on fund managers who have been under-performing compared to their peers to ‘chase the average’ and shift their portfolio to better match their competitors. This also involves sunk costs, and such herding/imitation effects will be both hysteretic and rate-dependent.

By an assembly of hysterons, we mean a set of hysterons $F_{\alpha ,\beta }(·)$, where $\alpha$, $\beta$ belong to some set; $\Gamma$ is the region $\beta >\alpha$ in the $(\alpha ,\beta )$ plane distributed according to a density function $g(\alpha ,\beta )$.

An assembly of hysterons in economics would represent, e.g., the entire market for a product. This has proved to be a very fruitful idea. An extensive theory (see, e.g., [2]) has been developed by defining an aggregate quantity:

$$A\left(s\right)={\int }_{\Gamma }{F}_{\alpha ,\beta }\left(s\right)g(\alpha ,\beta )d\alpha d\beta .$$

As s courses adiabatically beyond the support of g, $A\left(s\right)$ describes a “hysteresis” loop. So, not only are the constituents of the assembly $F_{\alpha ,\beta }$ hysteretic (they only “remember” whether the last time s went beyond their particular values of $\alpha$ or $\beta$), but the whole assembly has memory that has been described by the staircase construction of Mayergoyz [2].

Hence, in the Mayergoyz picture of hysteresis (which in economics has been called strong hysteresis), there are hysteretic micro-agents that give rise to a hysteretic macro-assembly.

It is the heterogeneity of the agents expressed through the density function $g(\alpha ,\beta )$ that makes the behaviour of the assemblage interesting and suggestive in the explanation of economic phenomena. The adjustment of the system to the control parameter is instantaneous and synchronous. So, a property of the strong (Mayergoyz) hysteresis is that, just like a hysteron, it is rate-independent.

In many areas of economics (as in the theory of the firm mentioned above), it makes sense to assume that the state of the assemblage $A\left(s\right)$ does not determine the value of the control parameter s. The same assumption is made in micro-magnetics, where the orientation of spins does not influence the magnetic field they are subjected to.

The motivation for the present work is that we find a number of features of the accepted strong hysteresis framework in economics to be problematic. In particular, a hysteron with rigidly defined thresholds and rate-independence does not seem to offer a realistic picture of an economic agent. Furthermore, the decoupling of the control parameter from the functioning of an assemblage of hysteretic agents seems to us unrealistic (see also the recent preprint of Mayergoyz and Korman [7] where this point is made as well).

Hence, we pursue two goals:

(1) to construct a more sensible model of an economic agent than that afforded by a hysteron;

(2) to introduce feedback dynamics into the model of an assemblage of hysteretic agents.

The most obvious way dynamics can be introduced into hysteresis models is via price mechanisms: if a firm starts supplying a product to a market that is already served by other competing firms, the price will come down, and hence some firms will have to reconsider the profitability of staying in the market; in our present treatment, we prefer to deal with a supply–demand system directly, without introducing price mechanisms.

The structure of this paper is as follows: in Section 2, we present our new picture of a hysteretic economic agent and connect it with the hysteron; in Section 3, we show how to incorporate feedback into the dynamics of an assembly of such agents, and we conclude with remarks and suggestions for further work.

2. A Hysteretic Agent

We start by suggesting a different picture of a hysteretic agent, which makes probabilistic decisions. Thus, for a fixed value of the control parameter s, we modify both the hysteron picture and its interpretation.

In preparation for our definition, let us reconsider Figure 1. We can define the function

$$P_{01}^H\left(s\right)=\left\{\begin{array}{c}0\mathrm{if}s<\beta ,\hfill \\ 1\mathrm{if}\ge \beta \hfill \end{array}\right.\mathrm{and}{P}_{10}^H\left(s\right)=\left\{\begin{array}{c}0\mathrm{if}s>\alpha ,\hfill \\ 1\mathrm{if}\le \alpha .\hfill \end{array}\right.$$

(1)

as probabilities, respectively, that if a hysteron finds itself in state 0 (1), to move to state 1 (0). Note that a consequence of this interpretation is that $P_{01}^H\left(s\right)+P_{10}^H\left(s\right)=0$ for $s\in (\alpha ,\beta )$.

Definition 1.

We say that an agent is hysteretic if the probability $P_{01}\left(s\right)$ of an agent in state 0 to switch to state 1 is for every value of the control parameter s less than the probability $P_{11}\left(s\right)$ of an agent in state 1 to stay in that state, such that $P_{01}\left(s\right)+P_{10}\left(s\right)$ has a unique minimum, where $P_{10}\left(s\right)=1-P_{11}\left(s\right)$.

This situation shown in Figure 2.

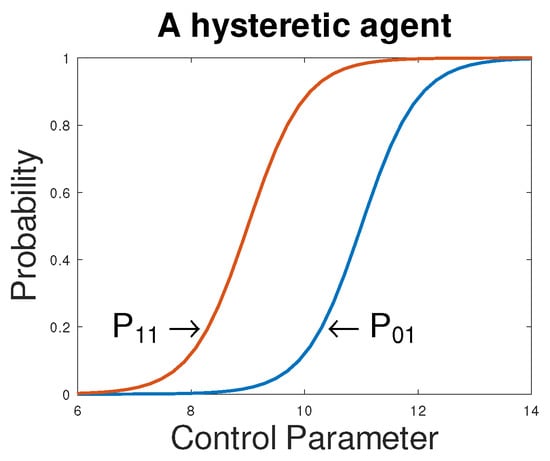
Figure 2. $P_{11}\left(s\right)$ and $P_{01}\left(s\right)$.

Since $P_{00}\left(s\right)+P_{01}\left(s\right)=1=P_{10}\left(s\right)+P_{11}\left(s\right)$, it immediately follows that for all s, $P_{10}\left(s\right)<P_{11}\left(s\right)$ as well. We define an anti-hysteretic agent to be one for which for all s, $P_{01}\left(s\right)>P_{11}\left(s\right)$ and $P_{01}\left(s\right)+P_{10}\left(s\right)$ has a unique maximum. Note that the area between the graphs of $P_{11}\left(s\right)$ and $P_{01}\left(s\right)$ is an appropriate measure of hysteresis.

Let us compare this notion to that of a hysteron. If in Figure 2, we choose for $P_{11}\left(s\right)$ and $P_{01}\left(s\right)$ discontinuous functions so that $P_{11}\left(s\right)=1-P_{10}^H\left(s\right)$ for $s<\alpha$ and $P_{11}\left(s\right)=1$ for $s\ge \alpha$ and $P_{01}\left(s\right)=P_{01}^H\left(s\right)$, where $P_{10}^H\left(s\right)$ and $P_{01}^H\left(s\right)$ are defined in (1); we recover the picture in Figure 1. The requirement for $P_{01}\left(s\right)+P_{10}\left(s\right)$ is to be consistent with the property of the hysteron that $P_{01}^H\left(s\right)+P_{10}^H\left(s\right)=0$ for $s\in (\alpha ,\beta )$. Therefore, our new picture of a hysteretic agent is a true generalisation of the hysteron one.

One can model such agents by Markov chains, as is performed in [8]; we follow the approach suggested by Brockett [9,10], by using Poisson counters which we will now introduce. We start by fixing the value of the control parameter s.

Consider an SDE for an unknown real-valued function $x\left(t\right)$ of the form

$$dx\left(t\right)=f\left(x\right(t),t)dt+g\left(x\right(t),t)dN\left(t\right),$$

(2)

where $N\left(t\right)$ is a Poisson counter. Of the function $f(x,t)$, we require Lipshitz continuity and at most linear growth in x, so that the existence and uniqueness of global solutions of the initial value problem $x^{\prime }=f(x,t)$, $x\left(t_0\right)=x_0$ are ensured, while of $g(x,t)$, we just require continuity in the first variable. Below, we omit the explicit dependence of x and counters on t.

Definition 2.

By a solution of (2) in the Itô sense, we mean a function $x(·)$, which satisfies $x^{\prime }=f(x,t)$ on an interval where N is constant, and if N jumps at some time $t_1$, we have

$$\underset{t\to t_1^{+}}{lim}x\left(t\right)=\underset{t\to t_1^{-}}{lim}x\left(t\right)+g(\underset{t\to t_1^{-}}{lim}x\left(t\right),t_1).$$

An agent that exists in states 0 and 1 can then be modelled by an SDE involving two Poisson counters: if the state variable is $x\left(t\right)$, then

$$dx=(1-x)d{N}_1-xd{N}_2,x\left(0\right)=x_0\in \{0,1\},$$

(3)

where the Poisson counters $N_1$ and $N_2$ have intensities ${\lambda }_{01}\left(s\right)$ and ${\lambda }_{10}\left(s\right)$, respectively, and where following Definition 1 we require ${\lambda }_{01}\left(s\right)+{\lambda }_{10}\left(s\right)$ to have a unique minimum (see Figure 3).

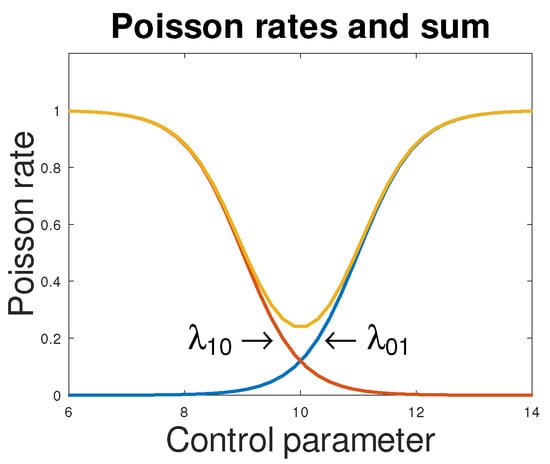
Figure 3. A hysteretic agent; the yellow curve is the sum of the intensities ${\lambda }_{01}\left(s\right)$ and ${\lambda }_{10}\left(s\right)$.

The situation for an anti-hysteretic agent is shown in Figure 4.

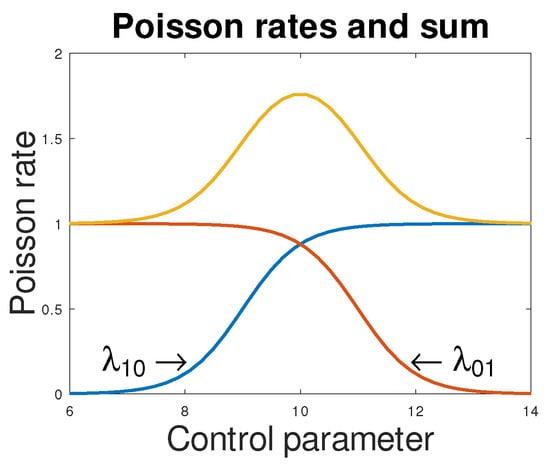
Figure 4. An anti-hysteretic agent; the yellow curve is the sum of the intensities ${\lambda }_{01}\left(s\right)$ and ${\lambda }_{10}\left(s\right)$.

In such an interpretation of a hysteron, for every value of s, ${\mathbb{E}}_s\left(x\right)$ is defined (and is an increasing function of s, as it is for an anti-hysteron); so, there is no “infinite duration” memory as in the classical hysteron. But note that

$${\displaystyle \frac{d{\mathbb{E}}_s\left(x\left(t\right)\right)}{dt}}={\lambda }_{01}\left(s\right)-({\lambda }_{01}\left(s\right)+{\lambda }_{10}\left(s\right)){\mathbb{E}}_s\left(x\left(t\right)\right),$$

so the rate of convergence to the stationary value of the expectation

$${\mathbb{E}}_s\left(x\right)={\displaystyle \frac{{\lambda }_{01}\left(s\right)}{{\lambda }_{01}\left(s\right)+{\lambda }_{10}\left(s\right)}}$$

is governed by $({\lambda }_{01}\left(s\right)+{\lambda }_{10}\left(s\right))$, which can be very small in the hysteretic case.

Another remark is that the steady rate of accrual of sunk costs, given by

$$C_s={\displaystyle \frac{{\lambda }_{10}\left(s\right){\lambda }_{01}\left(s\right)}{{\lambda }_{01}\left(s\right)+{\lambda }_{10}\left(s\right)}},$$

is clearly much larger in the anti-hysteretic case.

3. Feedback Dynamics

So far, we have dealt with a single agent transitioning between states 0 and 1 in accordance with Equation (3). Now, we want to derive equations for assemblies of such agents and introduce feedback into the dynamics.

In this work, we do not model price-making mechanisms and instead work directly with supply and demand. A simple fluid–mechanical analogy (which belongs to the class of “fluid queuing models” considered in other contexts by Brockett and co-authors [9,10]) for such a situation is as follows:

Assume we have a vessel that is filled with water at a constant rate $\alpha$. Suppose that the bottom of the vessel has a number M of pressure-sensitive valves that open or close depending on the height of the water $h\left(t\right)$. The rate at which a valve lets water through is r. We further assume that these valves are hysteretic in the sense defined above and would like to understand the dynamics of such a system.

More precisely, we have

$${\displaystyle \frac{dh}{dt}}=\alpha -rV\left(t\right),$$

(4)

where $V\left(t\right)$ is the number of valves open at time t. Each valve k is defined by a variable $x_k$, which takes the value 1 when it is open and 0 otherwise.

We can therefore rewrite (4) as

$$\left\{\begin{array}{cc}{\displaystyle \frac{dh}{dt}}=\alpha -r\sum _{k=1}^M{x}_k,\hfill & \\ d{x}_k=(1-x_k)d{N}_{1.k}-x_{k}d{N}_{2,k},k=1,2,\dots M,\hfill & \end{array}\right.$$

(5)

and now assume that the intensities ${\lambda }_{01,k}$ and ${\lambda }_{10,k}$ of the counters are functions of $h\left(t\right)$. (In the simulations below, we take the intensities ${\lambda }_{01,k}\left(h\right)$ and ${\lambda }_{10,k}\left(h\right)$ to be independent of k; we use shifted tanh functions for the intensities, such as

$${\lambda }_{01}\left(s\right)=1+tanh\left(\beta (s-P_1)\right)/2,{\lambda }_{10}\left(s\right)=1-(1+tanh\left(\beta (s-P_2)\right)/2),$$

for some values of $P_1$ and $P_2$).

The economics interpretation of (5) is that $h\left(t\right)$ is the (excess) demand for a commodity that appears at a constant rate $\alpha$ and is met at rate $r{\sum }_{k=1}^M{x}_k$; the higher the demand, the larger the size of the market will be (delimited a priori by M). We assume $\alpha -rM<0$.

The case $M=1$ can be fully analysed; this is the Dichotomous Markovian Noise (DMN) case considered, for example, in [11]. The trichotomous case $M=2$ is also known, but is not easy to deal with even without feedback. Analytically working out the Fokker–Planck equation for the $M>2$ case, even for the stationary solution, seems an open problem.

Going back to $M=1$, first note that without feedback, that is if the intensities ${\lambda }_{01}$ and ${\lambda }_{10}$ are constant, $h\left(t\right)\to \infty$ if $\alpha /r>{\lambda }_{01}/({\lambda }_{01}+{\lambda }_{10})$ and $h\left(t\right)\to 0$ if the opposite inequality holds.

Following the arguments of Horsthemke and Lefever [12] (Section 6,1), we can compute the stationary solution of the Fokker–Planck equation associated with $h\left(t\right)$.

Proposition 3.

The steady-state probability distribution function for the height has the density

$$p\left(x\right)=Cexp\left(-{\int }^x\left[{\displaystyle \frac{{\lambda }_{01}\left(s\right)}{\alpha }}+{\displaystyle \frac{{\lambda }_{10}\left(s\right)}{\alpha -r}}\right]ds\right),$$

where C is a normalisation constant.

Once that is known, we can check that

$${\displaystyle \frac{\alpha }{r}}={\displaystyle \frac{{\int }_0^{\infty }p\left(x\right){\lambda }_{01}\left(x\right)dx}{{\int }_0^{\infty }p\left(x\right)\left({\lambda }_{01}\left(x\right)+{\lambda }_{10}\left(x\right)\right)dx}},$$

and compute, for example, the rate of sunk cost accumulation,

$$C_s={\displaystyle \frac{\alpha }{r}}{\int }_0^{\infty }{\lambda }_{10}\left(x\right)p\left(x\right)dx.$$

The same computations can be performed for the anti-hysteretic case and, as expected, the rate of sunk costs accumulation is much higher in that case.

Note that to find $C_s$, we define a new variable $y\left(t\right)$ that satisfies

$$dy=xd{N}_2,$$

and take expectations to obtain

$${\displaystyle \frac{d\mathbb{E}\left(y\right)}{dt}}=\mathbb{E}\left(x\right)\mathbb{E}\left({\lambda }_{10}\left(h\right)\right).$$

The outstanding open question in the case $M=1$ is to analyse the time-dependent Fokker–Planck equation, and prove the existence of solutions and their convergence to the unique stationary solution $p\left(x\right)$.

As mentioned, deriving a Fokker–Planck equation for $M>1$ is a hard analytical problem. On the other hand, numerical simulation in the Poisson counter set-up is easy and the results are intuitive: the more valves there are, the smaller the variance (in fact, the mean field limit is very easy to analyse); the bigger the area of the hysteresis loop, the bigger the variance. In Figure 5 and Figure 6, we show the result of simulations for $M=15$ identical suppliers. Here, time is measured in the number of timesteps taken by the simulation.

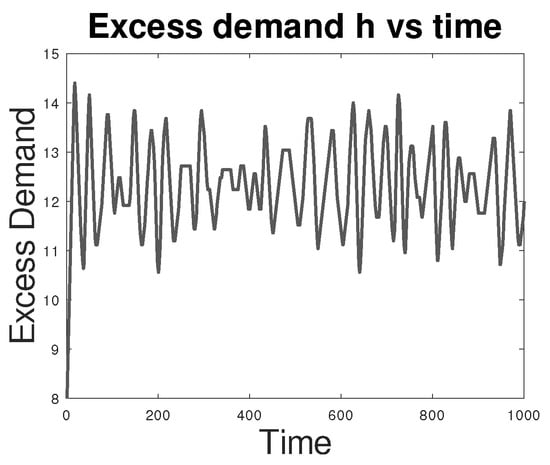
Figure 5. Excess demand vs. time for a system of 15 identical suppliers.

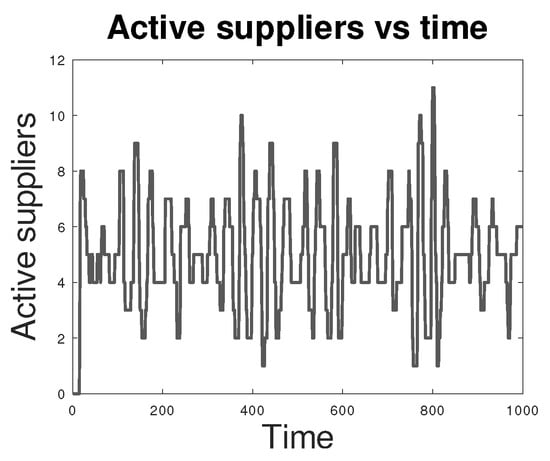
Figure 6. Number of active suppliers vs. time.

In the limit $M\to \infty$, keeping $\kappa :=rM$ constant, setting p to be the fraction of active suppliers, we have the system of ordinary differential equations (see [13] for background):

$$\left\{\begin{array}{cc}{\displaystyle \frac{dp}{dt}}=-p{\lambda }_{10}\left(h\right)+(1-p){\lambda }_{01}\left(h\right),\hfill & \\ {\displaystyle \frac{dh}{dt}}=\alpha -\kappa p,\hfill \end{array}\right.$$

(6)

Unlike the situation for finite M, we have

Proposition 4.

System (6) has a unique globally asymptotically stable equilibrium point.

Proof. 

By our blanket assumption, $\kappa >\alpha$; hence, any equilibrium point of (6) has to satisfy $p=p^{*}:=\alpha /\kappa <1$ and

$${\displaystyle \frac{{\lambda }_{10}\left(h\right)}{{\lambda }_{01}\left(h\right)}}={\displaystyle \frac{\kappa -\alpha }{\alpha }}>0.$$

(7)

Since ${\lambda }_{10}\left(h\right)$ is monotone decreasing in h and ${\lambda }_{01}\left(h\right)$ is monotone increasing in h, (7) has a unique (positive) solution, which we call $h^{*}$. Linearising (6) around the point $(p^{*},h^{*})$, we see that it is locally asymptotically stable; finally, using the Bendixson negative criterion [13] (p. 105) for (6) shows that the equilibrium point is globally asymptotically stable by the Poincaré–Bendixson theorem [13] (p. 383). □

4. Conclusions and Remarks

We have introduced a new model of a hysteretic agent and a simple way to incorporate feedback dynamics into an assemblage of such agents. We feel that the framework advocated here is more realistic in the economics context than the classical Preisach-based one; in particular, we have hysteresis without rate-independence.

The loss of rate-independence means that the behaviour of the hysteresis model now depends on the rate of change in the control parameter. If it changes adiabatically, then the only meaningful quantity is ${\mathbb{E}}_s$, which has no hysteresis, and “too fast” changes lead results that are hard to interpret.

Clearly, a lot remains to be achieved. Among the possible extensions to the model, we see the following:

• Make the rate of growth in excess demand ($\alpha$) stochastic.
• Characterise an $M>1$ system which is heterogeneous in intensities.
• Introduce price formation mechanisms.
• Model herding/imitation effects in financial markets.

As a final remark, note that in electrical engineering, hysteresis is not considered a positive feature of a power generation system and much effort is expended in reducing it. However, in economics, sunk costs necessitate the existence of hysteresis loops. Hence, in the exploitation of renewable natural resources, these should always be taken into account. An important project, therefore, is to understand the implications of hysteresis (in the framework we suggest) in cases where the dynamics without exploitation are non-linear and self-limiting.