Abstract
The crossing number of a graph G is the minimum number of edge crossings over all drawings of G in the plane. The main aim of this paper is to give the crossing numbers of the join products and for the connected graph obtained by removing one edge (incident with the dominating vertex) from the wheel on six vertices, and where and are paths and cycles on n vertices, respectively. Finally, we also introduce four new conjectures concerning crossing numbers of the join products of and with obtained by removing one edge (of both possible types) from the wheel on vertices.
MSC:
05C10; 05C38
1. Introduction
The crossing number is one of the basic parameters of a simple graph as it offers certain information about some complexity of the examined graph and, in many cases, determines the difficulty of drawing it [1]. Among the most popular areas in which the minimum number of crossings plays an important role is the implementation of VLSI layout. Integer linear programming can also be used to formulate some exact algorithms to find provably optimal crossing numbers. Implementations of QuickCross heuristics also allow one to find optimal or near-optimal embeddings of many graphs. Minimizing the number of crossovers also has a significant impact on visualizing and understanding complex data [2]. It is evident that drawings of graphs with a lower number of crossings help to create more efficient and of course more reliable (electrical) circuit designs [3]. There are many important graph algorithms defined only for planar graphs, i.e., with a drawing with no crossing edges. This is also one of the reasons why reducing the number of crossings on edges is a frequent problem in planar graph theory [4]. Graphs are also a suitable tool in cartography when depicting various geographical elements such as roads, rivers or political borders. In order to create clearer and more readable maps, any reduction in the number of edge crossings in considered drawings of graphs is highly desirable [5]. In contrast, from Garey and Johnson [6], it is well known that examining the number of crossings of simple graphs is an NP-complete problem. Despite this knowledge, many researchers try to solve this problem at least on some class of graphs. Such a summarization of the known values of crossing numbers for some graph classes has been published thanks to Clancy et al. [7].
Let G be a simple graph (without loops or multiple edges). We use and to denote the vertex set and the edge set of G, respectively. The used graph terminology is taken from the book [8]. The crossing number of graph G, denoted , is defined as the minimum possible number of edge crossings over all drawings of G in the plane (for the definition of a drawing see Klešč [9]). A drawing with a minimum number of crossings (an optimal drawing) is always a good drawing, meaning that no edge crosses itself, no two edges cross more than once, and no two edges incident with the same vertex cross. Let D be a good drawing of graph G. We denote the number of crossings in D by . Let and be edge-disjoint subgraphs of G. We denote the number of crossings between edges of and edges of by , and the number of crossings among edges of in D by . For any three mutually edge-disjoint subgraphs , , and of G by [9], the following equations hold:
In certain parts of the proofs, we make strong use of Kleitman’s result [10] on crossing numbers for complete bipartite graphs . He showed that
The join product of two graphs and , denoted , is obtained from vertex-disjoint copies of and by adding all edges between and . For and , the edge set of is the union of the disjoint edge sets of the graphs , , and the complete bipartite graph . Let and be the path and the cycle on n vertices, respectively, and let denote the discrete graph (sometimes called empty graph) on n vertices. For a relatively long time, the exact values of the crossing numbers of graphs on at most four vertices in the join product with paths and cycles have been known by Klešč [11,12], and Klešč and Schrötter [13]. Also for this reason, it is desirable to extend this knowledge to all graphs G of order five and six. Several results have already been obtained for and in the case of a connected graph G on five and six vertices [9,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Note that the issue of the Cartesian product and the strong product with paths was partially solved by Klešč et al. in [30,31].
In a good drawing D of some graph G, we say that a cycle Cseparates some two different vertices of the subgraph if they are contained in different components of , where means a two-dimensional space. This considered cycle C is said to be a separating cycle of graph G in D, see also Thomassen [32]. In the proofs of this paper, we often use the term “region” in nonplanar subdrawings as well. In that case, crossings are considered to be vertices of the “map”; see again Klešč [9].
Let be the connected graph obtained by removing one edge (incident with the dominating vertex) from the wheel on six vertices. This type of edge is referred to as in the following. For any , the crossing number of has recently been found by Berežný and Staš [15]. One of the main goals of this paper is to determine both crossing numbers of and described in Theorems 2 and 3, respectively. The paper concludes by giving some new conjectures concerning crossing numbers of the join products of and with obtained by removing one edge (of both possible types) from the wheel on vertices. Both conjectures about crossings numbers of have already been established in [15]. Of course, we also confirm the correctness of our new hypotheses for some smallest possible values of m and n by using several isomorphisms between graphs mentioned in the last part of Section 4.
2. The Crossing Numbers of
Let be the connected graph on six vertices obtained by removing one edge from the wheel , and let also . In the rest of the paper, let be the vertex notation of one vertex of degree four (the dominant vertex of ) in all assumed good subdrawings of . We denote a cycle induced on the five remaining vertices of with degrees two, three, three, three, and three by . Let also , , , , and be their vertex notation in the appropriate order of cycle with .
We consider the join product of with the discrete graph on n vertices. The graph consists of one copy of and n vertices . Any such vertex is adjacent with any vertex of . Let , , denote the subgraph induced by six edges incident with the vertex . Since is isomorphic to , we obtain
and for all good drawings D of , thanks to (1),
We denote the path induced on n vertices of not belonging to the subgraph by . The path contains n vertices and edges for . As , we have
for any good drawing D of . Determining the crossing numbers of will follow the result of given by Berežný and Staš [15].
Theorem 1
([15], Theorem 2.6). for .
First, let D be a good drawing of . The rotation of a vertex in the drawing D, as the cyclic permutation that records the (cyclic) counter-clockwise order in which the edges leave , has been defined by Hernández-Vélez et al. [33] or Woodall [34]. We use the notation if the counter-clockwise order the edges incident with the vertex is , , , , , and . We recall that a rotation is a cyclic permutation. For the purpose of a simpler description, we divide n subgraphs into three mutually disjoint sets of subgraphs depending on the number of crossings with graph . We denote the set of subgraphs for which and by and , respectively. Every other subgraph crosses at least twice in D. The idea of redistributing subgraphs into three mentioned sets is also preserved in all good drawings of (also for all drawings of in Section 3).
In Figure 1, the edges of cross each other
times, the graph is crossed once and twice by each subgraph , on the right side and , on the left side, respectively. The path contributes one crossing to , and so crossings appear among edges of in this drawing, that is, . The aim of Section 2 is to prove that the crossing number of is equal to this upper bound. In the following, we discuss all possible drawings of induced by any optimal drawing D of .
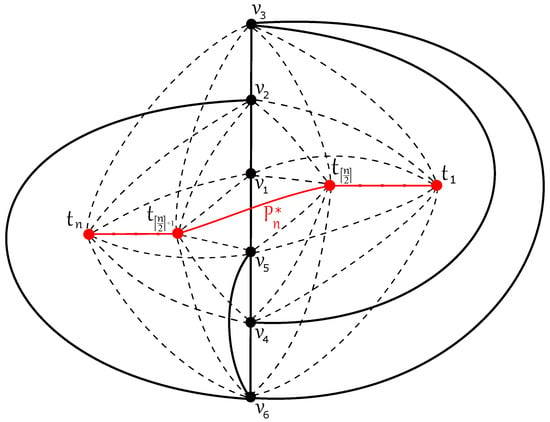
Figure 1.
The good drawing of with crossings.
Lemma 1.
The edges of do not cross each other in each optimal drawing D of the join product . Moreover, at least five vertices of must be located on the boundary of one region .
Proof.
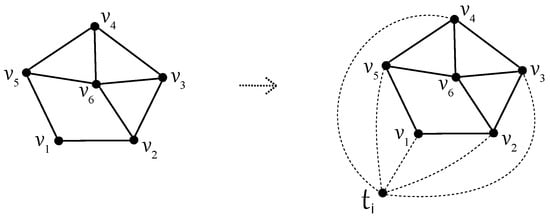
The first part can be easily verified because we can always redraw a crossing of two edges of trying to obtain a new good drawing of (with a change in the order of vertices but with a preservation of the incidence of all edges) with fewer edge crossings. This idea has already been presented for by Berežný and Staš [15]. There is only one planar drawing of (with respect to isomorphisms), see also Figure 2a. Now, assume an optimal drawing D of with the nonplanar subdrawing and at most four vertices of located on a boundary of each region. As the set is empty, thanks to (3) together with enforce more than crossings in D provided that
The drawing from Figure 1 giving the upper bound provides a contradiction with the optimality of D. □

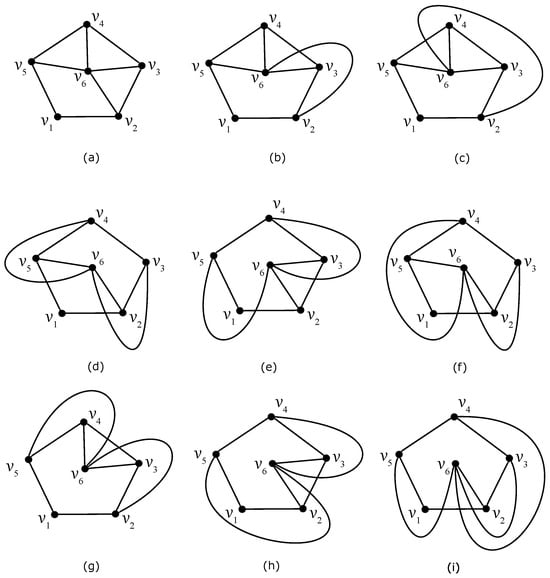
Figure 2.
Nine possible non-isomorphic drawings of the graph with no crossing among edges of and also with at least five vertices of located on a boundary of one region: (a) there is no crossing on edges of ; (b) the edge of is crossed once; (c) the edge of is crossed once; (d) each of the edges and of is crossed once; (e) each of the edges and of is crossed once; (f) the edge of is crossed twice; (g) the edge of is crossed twice; (h) the edge of is crossed twice; (i) the edge of is crossed three times.
Corollary 1.
In any optimal drawing D of , the set cannot be empty, that is, the subdrawing is isomorphic to one of the nine drawings illustrated in Figure 2.
Theorem 2.
for .
Proof.
The crossing number of must be at most using the drawing in Figure 1. We prove the reverse inequality by contradiction, and so let us suppose that there is an optimal drawing D of with
Since by Theorem 1, the edges of must be crossed exactly times, and no edge of the path is crossed in D. This also enforces that all vertices of must be placed in the same region of the considered good subdrawing of induced by D. Now, using Corollary 1, we show that a contradiction with assumption (6) can be obtained for all possibilities of obtaining a subgraph in D.
Let us first consider the subdrawing given in Figure 2a. As no face is incident with all six vertices of in , there is no way to obtain a subdrawing of for a subgraph . For , let be a subgraph from the nonempty set , that is, the vertex is placed in the pentagonal region of with the five vertices , , , , and of on its boundary and the edge crosses exactly once. There is only one possible subdrawing of without the edge , see also Figure 3.

Figure 3.
One possible subdrawing of obtained from Figure 2a for a .
Because all vertices of must be placed in the same region of , it is easily verified in all five possible regions on three vertices that the edges of are crossed at least four times by every other subgraph , . Together with at least one crossing on the edge , the subgraph must cross the edges of at least five times. Thus, by fixing the subgraph using (3), we obtain
The same result contrary to (6) can be achieved if we consider the subdrawing of induced by D presented in Figure 2b–f.
Let us now discuss the good subdrawing given in Figure 2g. Let the set be nonempty and , . The vertex must be located in the hexagonal region of with all six vertices of on its boundary, see also Figure 4.

Figure 4.
One possible subdrawing of obtained from Figure 2g for a .
Again one can easily verify over all six considered triangular regions that each subgraph , , must cross the edges of at least five times. Then, the same idea as in the previous case also confirms a contradiction with assumption (6) in D. If the set is empty, there are only two possibilities to obtain a subgraph , (the crossed edge of must be incident with a vertex of degree two). For both subdrawings, we obtain at least five crossings on edges of by each remaining subgraph , . Now, the same idea as in the first case again contradicts (6). The same result contrary to (6) can be achieved if we consider both subdrawings given in Figure 2h,i.
Because there is no optimal drawing D of with less than crossings, the proof of Theorem 2 is complete. □
To date, the crossing number of could only be given as a hypothesis. The next section is devoted to this open problem.
3. The Crossing Numbers of
Let be the vertex notation of the n-cycle for . The join product consists of one copy of graph , one copy of the cycle , and the edges joining each vertex of with each vertex of . Let denote the cycle as a subgraph of induced on the vertices of not belonging to the subgraph . The subdrawing induced by any good drawing D of represents some drawing of . For the vertices of graph , let denote the subgraph induced by n edges joining the vertex with n vertices of . The edges joining the vertices of with the vertices of form the complete bipartite graph , and so
for all good drawings D of . All three of the following statements concerning some restricted subdrawings of are unavoidable to prove the main theorem of Section 3.
Lemma 2
([11], Lemma 2.2). For and , let D be a good drawing of in which no edge of is crossed, and does not separate the other vertices of the graph. Then, for all , two different subgraphs and cross each other in D at least times.
Corollary 2
([35], Corollary 4). For and , let D be a good drawing of the join product in which the edges of do not cross each other and does not separate p vertices , . Let , , be the subgraphs induced on the edges incident with the vertices that do not cross . If k edges of some subgraph induced on the edges incident with the vertex , , cross the cycle , then the subgraph crosses each of the subgraphs at least times in D.
Lemma 3
([35], Lemma 1). For , let G be a graph of order m. In an optimal drawing of the join product , , the edges of do not cross each other.
The crossing numbers of and can be computed using the algorithm located at the website http://crossings.uos.de/ (accessed on 13 September 2024). This algorithm uses the ILP formulation based on Kuratowski subgraphs and thereby determines the crossing numbers of small undirected graphs; see also Chimani and Wiedera [36].
Lemma 4.
and .
The proof of Lemma 5 can be easily obtained according to the expected result of the main Theorem 3 of this section and using similar arguments as in the proof of Lemma 1.
Lemma 5.
For , the edges of do not cross each other in any optimal drawing D of . Moreover, if there are at most crossings ind D, then the subdrawing is isomorphic to one of the nine drawings illustrated in Figure 2.
Proof.
For , let D be an optimal drawing of . The edges of do not cross each other using arguments similar to the proof of Lemma 1. If both sets and are empty, then each subgraph crosses edges of at least twice. Assuming thanks to (3), we obtain a contradiction with at most
crossings in D. Since the subdrawing is planar or the set is nonempty, must be isomorphic to one of the nine drawings illustrated in Figure 2. □
Lemma 6.
For , let D be a good drawing of with the nonplanar subdrawing of induced by D and one region with all six vertices of located on its boundary. If all vertices are placed in such a region and at least one subgraph does not cross edges of , then there are at least crossings in D.
Proof.
By Lemma 5, we deal with possible subdrawings of induced by D in which the set is nonempty, i.e., there is a region of incident with all six vertices of . At first, we consider the subdrawing with the vertex notation given in Figure 2g. Let be a subgraph from the nonempty set , that is, the subgraph is represented by . Because all vertices of lie in the same region of , it is easy to verify over only all six possible regions of that the edges of must be crossed by each of the remaining subgraphs at least five times. Thus, by fixing the subgraph using (3), we obtain
Of course, the same idea of a fixation as in the previous case can be repeated for both possible remaining drawings of given in Figure 2h,i with and , respectively. □
Theorem 3.
for .
Proof.
The result of Theorem 3 holds for both and based on Lemma 4. The edge can be added into the drawing in Figure 1 in such a way that it completes the cycle on n vertices with exactly three additional crossings, i.e., of crosses three edges , , and of graph . Thus, , and let us suppose that there is an optimal drawing D of such that
In the rest of the proof, let . According to Theorem 1 and Lemma 3, there are at most three crossings on the edges of that do not cross each other, respectively. Now, three possible cases may occur:
Case 1: The edges of are crossed at most once. There are at least five different considered subgraphs and for , which cross each other at least times by Lemma 2. It means there are at least crossings in D, which confirms a contradiction with the assumption (7).
Case 2: There are just two crossings on the edges of . If or for exactly one , then the same idea as in Case 1 can be applied. Finally, let and for two distinct . Using Lemma 2 and Corollary 2 for , , , we have at least crossings in D which confirms a contradiction with assumption (7).
Case 3: The edges of are crossed just three times and we consider three subcases:
- (a)
- Let . If the cycle separates only one vertex of graph (vertex of degree three), then the same idea as in Case 1 can be also used. Now, let the cycle separate two vertices of graph . One vertex of degree two and his neighbor (vertex or ). Thanks to Lemma 2, together with three crossings on , we have crossings in D. We need a dispute between at least four more crossings. If , we have at least n more crossings, which contradicts the assumption (7). Finally, let . In this case, (see Figure 2), and by Lemma 6, there is at least one vertex located in a different region of , , such that . We also have a contradiction with the assumption (7).
- (b)
- Let , so for exactly one . If is not a separating cycle, then the same idea as in Case 1 can be again applied. Now, let be a separating cycle. It means cycle separates vertex . By Lemma 2, Corollary 2 for , , , together with three crossings on the edges of , we have at least crossings in D, which confirms a contradiction with the assumption (7).
- (c)
- Let (a case where is impossible because has no bridge). If for only one , then the same idea as in Case 1 can be again used. Let and for two distinct . Then, by Lemma 2, Corollary 2 for , , and , , , we have at least crossings in D, which confirms a contradiction with assumption (7). Finally, let , , and for three distinct . For such an index pair , the subgraph is isomorphic to . Assume vertices of incident with the edges of and which do not cross . Let us delete all edges of and which are not incident with these vertices. The resulting subgraph is homeomorphic to , and in its subdrawing induced by D, we obtain thanks to Lemma 2. This fact, together with Lemma 2, Corollary 2 for , , , and three crossings on , gives us crossings, which also contradicts assumption (7).
Because there is no optimal drawing D of with less than crossings, the proof of Theorem 3 is complete. □
4. Some Consequences of the Main Result
Each wheel on vertices consists of two edge-disjoint subgraphs and , that is, . We distinguish two types of edges of the wheel , i.e., let us denote by and any edge of and , respectively. First, we deal with the possibility of deleting one edge from the star of . Staš and Berežný [15] have already claimed the result for the join product with discrete graphs , i.e., for all natural numbers m at least four and n at least one, where by , we mean Zarankiewicz’s number [7]. For all integers and , conjectures regarding the crossing number of graphs with values were given thanks to Staš and Valiska [26]. Now, we are able to postulate the next conjecture.
Conjecture 1.
for all integers and .
For all integers , the upper bound for Conjecture 1 can be reached by removing the edge from the drawing in Figure 5, because is crossed by each subgraph on the left side exactly times. Note that for , the optimal drawing of with crossings cannot be obtained by removing the edge for n odd and at least three. This special situation is first caused by the fact that the wheel is isomorphic to the complete graph ; see also Klešč and Schrötter [13].
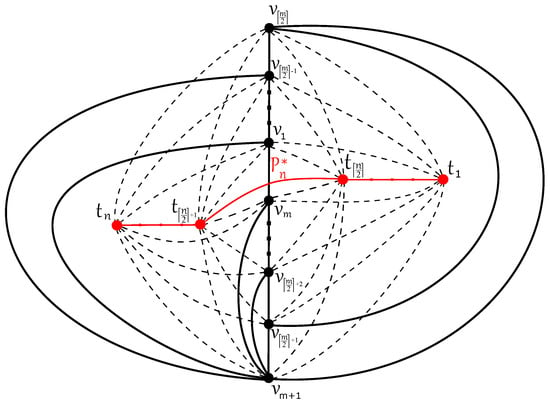
Figure 5.
The good drawing of with just crossings.
Recently, Su and Huang [27] proved Conjecture 1 for graph , and the validity for is also confirming by Theorem 2. On the other hand, graph contains a subgraph that is a subdivision of graph . Thus, . The crossing numbers of are already well known from Staš and Valiska [26].
Theorem 4
([26], Theorem 5.1). for all integers .
Based on the mentioned facts, we can justify further results for the join product of with the path on two vertices if m is at least four.
Corollary 3.
for all integers .
It is easy to see that Corollary 3 also confirms the validity of Conjecture 1 for . Similarly, we obtain the following conjecture.
Conjecture 2.
for all integers and .
For , the upper bound for Conjecture 2 can be reached by removing the edge from the drawing in Figure 5 and adding the new edge such that it completes the cycle on n vertices with exactly additional crossings. Recently, our Conjecture 2 was proved for graph by Staš [22]. Theorem 3 also confirms the validity of this conjecture for .
Now, let us turn to the possibility of deleting one edge from the cycle of . Staš and Berežný [15] already claimed the result for the join product with discrete graphs
for all integers and . On the assumption of Zarankiewicz’s conjecture saying that , they established the following:
Theorem 5
([15], Corollary 3.2). If Zarankiewicz’s conjecture is true, then
holds for all integers , .
We postulate the following conjecture.
Conjecture 3.
for all integers and .
For all , the upper bound for Conjecture 3 can be reached by removing the edge from the drawing in Figure 5 because is crossed by each subgraph on the right side exactly once. Similar to the previous case, consequently, by adding the edge with just additional crossings, we obtain the last conjecture.
Conjecture 4.
for all integers .
The exact values for the crossing numbers of the join products of , , and with paths and cycles were given by Klešč and Schrötter [13], Klešč [12], Staš [23], and Staš and Timková [24], respectively, and so the validity of both Conjectures 3 and 4 can be trivially verified for . On the other hand, the graph is isomorphic to because and . The crossing numbers of equal to were determined by Klešč [11] for any , with . Note that graphs and are isomorphic to each other for all integers m, n at least three due to and . Thus, the next results are obvious and confirming the validity of our Conjecture 3 for .
Corollary 4.
for .
Corollary 5.
for .
Corollary 6.
for .
Corollary 7.
for .
Moreover, graph is isomorphic to for all using and . The crossing numbers of the wheels on four, five, and six vertices in the join product with paths are also given by Klešč and Schrötter [13], Staš and Valiska [26], and Berežný and Staš [14], respectively. Thus, the next results are again obvious and confirm the validity of Conjecture 4 for .
Corollary 8.
for .
Corollary 9.
for .
Corollary 10.
for .
5. Conclusions
A thorough analysis of all possible drawings of a simple graph is one of the main tasks for successfully determining its crossing numbers in the join product with , and . This form of analysis tends to be much more demanding in cases with an increasing number of edges, especially if . A lot of drawings can also be solved by sorting them based on the existence or non-existence of a special (separating) subgraph; for more, see also [25].
Author Contributions
Conceptualization, M.S. and M.T.; methodology, M.S.; validation, M.S. and M.T.; formal analysis, M.S.; investigation, M.S. and M.T.; writing—original draft preparation, M.S. and M.T.; writing—review and editing, M.T.; visualization, M.T.; supervision, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Scientific Grant Agency (VEGA) under Contract 1/0413/22.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Schaefer, M. The Graph Crossing Number and its Variants: A Survey. Electron. J. Comb. 2013, 20, DS21. [Google Scholar] [CrossRef] [PubMed]
- Fridman, G.; Vasiliev, Y.; Puhkalo, V.; Ryzhov, V. A Mixed-Integer Program for Drawing Orthogonal Hyperedges in a Hierarchical Hypergraph. Mathematics 2022, 10, 689. [Google Scholar] [CrossRef]
- Nath, R.K.; Sen, B.; Sikdar, B.K. Optimal synthesis of QCA logic circuit eliminating wire-crossings. IET Circuits Devices Syst. 2017, 11, 201–208. [Google Scholar] [CrossRef]
- Gethner, E.; Hogben, L.; Lidicky, B.; Pfender, F.; Ruiz, A.; Young, M. On Crossing Numbers of Complete Tripartite and Balanced Complete Multipartite Graphs. J. Graph Theory 2017, 84, 552–565. [Google Scholar] [CrossRef]
- Jenny, B.; Stephen, D.M.; Muehlenhaus, I.; Marston, B.E.; Sharma, R.; Zhang, E.; Jenny, H. Design principles for origin-destination flow maps. Cartogr. Geogr. Inf. Sci. 2018, 45, 62–75. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Crossing number is NP-complete. SIAM J. Algebr. Discret. Methods 1983, 4, 312–316. [Google Scholar] [CrossRef]
- Clancy, K.; Haythorpe, M.; Newcombe, A. A survey of graphs with known or bounded crossing numbers. Australas. J. Comb. 2020, 78, 209–296. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Klešč, M. The crossing number of join of the special graph on six vertices with path and cycle. Discret. Math. 2010, 310, 1475–1481. [Google Scholar] [CrossRef]
- Kleitman, D.J. The crossing number of K5,n. J. Comb. Theory 1970, 9, 315–323. [Google Scholar] [CrossRef]
- Klešč, M. The join of graphs and crossing numbers. Electron. Notes Discret. Math. 2007, 28, 349–355. [Google Scholar] [CrossRef]
- Klešč, M. The crossing numbers of join of cycles with graphs of order four. In Proceedings of the Aplimat 2019: 18th Conference on Applied Mathematics, Bratislava, Slovakia, 5–7 February 2019; pp. 634–641. [Google Scholar]
- Klešč, M.; Schrötter, Š. The crossing numbers of join products of paths with graphs of order four. Discuss. Math. Graph Theory 2011, 31, 321–331. [Google Scholar] [CrossRef]
- Berežný, Š.; Staš, M. On the crossing number of the join of the wheel on six vertices with a path. Carpathian J. Math. 2022, 38, 337–346. [Google Scholar] [CrossRef]
- Berežný, Š.; Staš, M. Conjectures about wheels without one edge. Carpathian J. Math. 2025, 41, 45–55. [Google Scholar]
- Draženská, E. On the crossing number of join of graph of order six with path. In Proceedings of the CJS 2019: 22nd Czech-Japan Seminar on Data Analysis and Decision Making, Nový Světlov, Czech Republic, 25–28 September 2019; pp. 41–48. [Google Scholar]
- Draženská, E. Crossing numbers of join product of several graphs on 6 vertices with path using cyclic permutation. In Proceedings of the MME 2019: Proceedings of the 37th International Conference, České Budějovice, Czech Republic, 11–13 September 2019; pp. 457–463. [Google Scholar]
- Klešč, M.; Kravecová, D.; Petrillová, J. The crossing numbers of join of special graphs. Electr. Eng. Inform. 2011, 2, 522–527. [Google Scholar]
- Klešč, M.; Schrötter, Š. The crossing numbers of join of paths and cycles with two graphs of order five. In Lecture Notes in Computer Science: Mathematical Modeling and Computational Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7125, pp. 160–167. [Google Scholar]
- Klešč, M.; Valo, M. Minimum crossings in join of graphs with paths and cycles. Acta Electrotech. Inform. 2012, 12, 32–37. [Google Scholar] [CrossRef]
- Ouyang, Z.; Wang, J.; Huang, Y. The crossing number of join of the generalized Petersen graph P(3,1) with path and cycle. Discuss. Math. Graph Theory 2018, 38, 351–370. [Google Scholar]
- Staš, M. Join Products K2,3 + Cn. Mathematics 2020, 8, 925. [Google Scholar] [CrossRef]
- Staš, M. The Crossing Numbers of Join Products of Paths and Cycles with Four Graphs of Order Five. Mathematics 2021, 9, 1277. [Google Scholar] [CrossRef]
- Staš, M.; Timková, M. The crossing numbers of join products of seven graphs of order six with paths and cycles. Carpathian J. Math. 2023, 39, 727–743. [Google Scholar] [CrossRef]
- Staš, M.; Timková, M. The influence of separating cycles in drawings of K5∖e in the join product with paths and cycles. Math. Slovaca 2024, 74, 1089–1106. [Google Scholar] [CrossRef]
- Staš, M.; Valiska, J. On the crossing numbers of join products of W4 + Pn and W4 + Cn. Opusc. Math. 2021, 41, 95–112. [Google Scholar] [CrossRef]
- Su, Z.; Huang, Y. Crossing Number of K2,3 ∨ Pn. Appl. Math. China Ser. A 2012, 27, 488–492. [Google Scholar]
- Su, Z.; Huang, Y. Crossing Number of join of three 5-vertex graphs with Pn. Appl. Math. China 2014, 29, 245–252. [Google Scholar]
- Yue, W.; Huang, Y.; Ouyang, Z. On crossing numbers of join of W4 + Cn. Comp. Eng. Appl. 2014, 50, 79–84. [Google Scholar]
- Klešč, M.; Kravecová, D.; Petrillová, J. On the crossing numbers of Cartesian products of paths with special graphs. Carpathian J. Math. 2014, 30, 317–325. [Google Scholar] [CrossRef]
- Klešč, M.; Petrillová, J.; Valo, M. Minimal number of crossings in strong product of paths. Carpathian J. Math. 2013, 29, 27–32. [Google Scholar] [CrossRef]
- Thomassen, C. On separating cycles in graphs. Discret. Math. 1978, 22, 57–73. [Google Scholar] [CrossRef]
- Hernández-Vélez, C.; Medina, C.; Salazar, G. The optimal drawing of K5,n. Electron. J. Comb. 2014, 21, P4.1. [Google Scholar]
- Woodall, D.R. Cyclic-order graphs and Zarankiewicz’s crossing number conjecture. J. Graph Theory 1993, 17, 657–671. [Google Scholar] [CrossRef]
- Klešč, M.; Petrillová, J.; Valo, M. On the crossing numbers of Cartesian products of wheels and trees. Discuss. Math. Graph Theory 2017, 37, 399–413. [Google Scholar] [CrossRef]
- Chimani, M.; Wiedera, T. An ILP-based proof system for the crossing number problem. In Proceedings of the 24th Annual European Symposium on Algorithms (ESA 2016), Aarhus, Denmark, 22–24 August 2016; Volume 29, pp. 1–13. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).