Abstract
Let be the moduli space of -Higgs bundles over a compact Riemann surface X of genus . This admits a system called the Hitchin integrable system, induced by the Hitchin map, the fibers of which are Prym varieties. Moreover, the triality automorphism of acts on , and those Higgs bundles that admit a reduction in the structure group to are fixed points of this action. This defines a map of moduli spaces of Higgs bundles . In this work, the action of triality automorphism is extended to an action on the Hitchin integrable system associated with . In particular, it is checked that the map is restricted to a map at the level of the Prym varieties induced by the Hitchin map. Necessary and sufficient conditions are also provided for the Prym varieties associated with the moduli spaces of and -Higgs bundles to be disconnected. Finally, some consequences are drawn from the above results in relation to the geometry of the Prym varieties involved.
MSC:
14H60; 14H10; 57R57
1. Introduction
Let X be a compact Riemann surface of genus , and let G be a semi-simple complex Lie group with Lie algebra . A G-Higgs bundle over X is defined to be a pair , where E is a holomorphic principal G-bundle over X, and is a holomorphic global section of the adjoint bundle of E, , twisted by the canonical bundle, K. The section is called a Higgs field of the Higgs bundle. Suitable notions of stability and polystability can be given for G-Higgs bundles that extend what is given by Ramanathan [1,2] for principal G-bundles and for stable principal G-bundles in [3], obtaining that the moduli space of polystable G-Higgs bundles, , is a complex algebraic variety of dimension .
Higgs bundles were introduced by Hitchin in his groundbreaking 1987 paper [4] and possess a remarkable wealth of geometric structures, so they are of interest in many different areas and have been intensively studied. Indeed, G-Higgs bundles provide the framework for the extension of the theorem of Narasimhan and Seshadri [5], whose analog states that the moduli space of polystable G-Higgs bundles is isomorphic to the moduli space of reductive representations of the fundamental group in G [6,7,8,9,10]. In other directions, G-Higgs bundles are of interest in different areas of mathematics and physics, including gauge theory, mirror symmetry, Langlands duality, or symplectic, Kähler, and hyperkähler geometry [11,12,13].
Hitchin proved the existence of an integrable system in the moduli space of polystable G-Higgs bundles over an algebraic curve for any reductive complex Lie group, G [14]. A relevant and classical theorem by Chevalley [15] states that, for any complex reductive Lie group, G, with adjoint representation , the algebra of all Ad-invariant polynomials is finitely generated, and the degrees, (where ), of the elements of a basis of homogeneous polynomials are well-defined. Given any principal G-bundle, E, over X, an Ad-invariant (or G-invariant, or simply invariant) homogeneous polynomial p of degree d defines a map, , via the evaluation of p on the corresponding Higgs field , where ⊗ denotes the tensor product of bundles (and also a spectral curve, S, is induced by each G-Higgs bundle by taking the characteristic polynomial of the Higgs field through the adjoint representation, which is a cover of X, the fibers of which correspond to the eigenvalues of ). This can be computed using a basis of invariant polynomials to finally obtain a map.
This map, which is called a Hitchin map, is, indeed, proper. The space is an affine space called the base of the Hitchin map. For each stable and simple principal G-bundle, E (i.e., a stable principal G-bundle for which the only automorphisms are those induced by the action of the center of the structure group, G, which is a smooth point in the moduli space of principal G-bundles), the space is isomorphic, according to Serre duality, to , the cotangent bundle to the moduli space of stable and simple principal G-bundles at E. This cotangent bundle is naturally embedded in the moduli space of polystable G-Higgs bundles. Hitchin defined a global symplectic structure in that extends the natural symplectic structure of that cotangent space in a way that the Hitchin map defines an integrable system. The Hitchin fibration has proven to be an essential tool for understanding the Geometric Langlands program, as Kapustin and Witten [13] pointed out.
A fruitful way of studying the geometry of the moduli spaces of G-Higgs bundles is by describing the subvarieties and maps between these moduli spaces [16,17,18]. Specifically, given an automorphism of , a subvariety is naturally defined by taking the fixed points of that automorphism. It is then useful to study automorphisms of a finite order of . The case of involutions of the moduli space of -Higgs bundles was developed by García-Prada in [17], where he related Higgs bundles with representations of the fundamental group of the surface in the real forms of the group. A larger family of finite-order automorphisms is studied in [19] but in the context of orthogonal bundles over a curve. Moreover, the case of the involutions of induced by the action of outer automorphisms of order 2 of G has been studied in [18] and with different techniques for simple classical complex Lie groups in [20].
This paper is interested in Higgs bundles, the structure group of which is . This group is the only simple, complex Lie group that admits an outer automorphism of order 3, called triality automorphism. This unique fact makes the geometric structures related to this group (including -Higgs bundles) have both interesting and very specific geometric features, which usually require specific studies [21,22,23]. In particular, in the previous literature, it has been proved that triality automorphism acts on the moduli space , and its fixed points can be described as reductions in the structure group to the subgroups or of . This leads to the existence of two maps of algebraic varieties, and . In this work, the study of the first map, , is deepened. The way to carry out this deepening is through the study of the Hitchin integrable system associated with the two moduli spaces involved. Specifically, if B is the basis of the Hitchin map of and is the basis of the Hitchin map of , it is proved that the triality automorphism acts on B, that there exists a homomorphism compatible with the map between moduli spaces, and that the image of j is formed by fixed points of the action of the triality automorphism on B (Lemma 2). This allows us to state that the map between moduli spaces is restricted to maps between Prym varieties , where and and are the associated spectral curves. Following this, in this paper, the geometry of the Prym varieties involved is studied to the extent of providing necessary and sufficient conditions for these Prym varieties to be disjointed (Proposition 5).
Prym varieties play a key role in the study of the geometry of moduli spaces of Higgs bundles and G-Higgs bundles. In particular, the connection or disconnection of Prym varieties, understood as branched coverings, allows us to identify the irreducible components of the fibers of the moduli space. Not only this, but several authors have shown that the knowledge of the topology of Prym varieties helps to deepen the knowledge of the topology of moduli spaces of G-Higgs bundles [14,24] and to study the automorphisms of the moduli spaces of principal bundles [25].
As a consequence of the above results, sufficient conditions are provided for the two Prym varieties involved to be disjointed. Thus, the paper provides innovative results on the geometry of the map and also provides novel techniques for the mentioned geometry study (consisting specifically in studying the Hitchin integrable system). In particular, it is intended to provide tools to advance knowledge about the map and to be able (in the future )to prove properties such as, for example, whether it is injective, in the spirit of Serman [26].
In addition, the map has been considered because the preceding literature provides sufficient results on the Hitchin integrable system of [22] and on the relationship between -invariant polynomials and -invariant polynomials [27] to be able to carry out the analysis intended here. Indeed, Hitchin [22] deepened the study of the integrable system of the moduli space of -Higgs bundles because the special characteristics of the group make it of great interest in differential equations [28], geometry, and physics [16,29]. Thus, Hitchin [22] described the spectral curves, S, associated with the Hitchin fibration for the group and the associated Prym varieties. In particular, he proved the existence of an intermediate curve, C, such that the covering factors were found through C and an involution of S so that is given by those satisfying . He also proved that the -Higgs bundle can be reconstructed from the associated spectral curve. It has also been proved that every -invariant polynomial is also a -invariant polynomial fixed by the action of the triality automorphism [27].
In summary, the main results of this work are as follows. First, the existence of a map between the bases of the Hitchin map of and is proved, which commutes with the forgetful map and the image of which is composed of the fixed points of the -action on the base of the Hitchin map of (Proposition 1). Secondly, necessary and sufficient conditions are provided so that the characteristic polynomial of the Higgs field of a -Higgs bundle (Proposition 2) or of a -Higgs bundle (Proposition 3) admits irreducible factors of all possible degrees. Finally, the above results are used to give necessary and sufficient conditions for the Prym varieties of and to be disjointed (Proposition 5).
The article is organized in the following way. In Section 2, some foundations on the geometry of the Lie group and the triality automorphism are recalled. The action of the group of outer automorphisms of any semi-simple complex Lie group, G, on the moduli space of G-Higgs bundles over X, introduced in [16], is described and studied. The particular case of and the specific characteristics of the triality automorphism are also explained in a more detailed way. In Section 4, the action of the triality automorphism on the base and on the fibers of the Hitchin integrable system is constructed. Section 5 is devoted to providing the main geometric features of the Prym varieties coming from the Hitchin integrable system associated with . Finally, the main conclusions of the paper are drawn.
2. The Group Spin(8, ) and Triality Automorphism
In this section, some basics on the Lie group , its subgroups, and the triality automorphism are provided. Suitable references for this topic are [16,21,30]. The group is the only simple and simply connected complex Lie group of type . Its Lie algebra is , and its center is isomorphic to . It is, indeed, the double cover of the special orthogonal Lie group , and it can then be described as an extension of by :
Of course, the action of the group of automorphisms of leaves the center invariant; hence, there is a homomorphism of into the group of permutations of the set of central elements of order 2. The subgroup of inner automorphisms clearly acts trivially on Z; thus, this induces a homomorphism of the group of the outer automorphisms of into , which is actually an isomorphism. Recall that is the quotient of the group of automorphisms of by the normal subgroup of inner automorphisms. The triality automorphism is then a choice, , of an order 3 outer automorphism (the other outer automorphism of order 3 is ).
Since is the simply connected complex Lie group with Lie algebra of , there is an isomorphism of short exact sequences of the form
Given any complex Lie algebra , if , it is stated that if there exists such that [18]. Thus defined, is an equivalence relation such that the obvious map
is well-defined [18,21].
Notice that the order of an automorphism of clearly coincides with the order of its class modulo . Then, if denotes the subset of automorphisms of order 3 of and an analogous definition is given for and for , it is satisfied that
It is also clear that the automorphisms of order 3 are sent to elements of of order 3 or to the identity through the map defined in (4). This implies that is sent onto through the natural map; that is,
There are exactly two pre-images of the triality automorphism given by the map defined in (6) [18,21]. Then, there are two possibilities for the sub-algebra of the fixed points of an automorphism of order 3 of representing . Wolf and Gray [31] proved in Theorem 5.10 that these two different representatives of given by the map (6) have and as sub-algebras of fixed points (with simply connected subgroups and ), respectively.
3. The Action of the Triality Automorphism on the Moduli Space of Spin(8, )-Higgs Bundles
Let X be a compact Riemann surface of genus . A principal -bundle over X is a complex rank-8 and trivial determinant vector bundle equipped with a globally defined holomorphic non-degenerate symmetric bilinear form. The set of isomorphism classes of principal -bundles is parametrized by the cohomology set . A map, , is defined, which assigns to each principal -bundle E its second Stiefel-Whitney class, . The bundle E lifts to a principal -bundle over X if and only if , with two of such lifts differing in a line bundle of order 2. However, every principal -bundle admits an associated -bundle through the covering map defined in (2).
In the next definitions, the notions of Higgs bundles are specified for the structure groups and following the original notion of the G-Higgs bundle introduced by Hitchin [4]. Recall that, when given a semi-simple complex Lie group G, a G-Higgs bundle over X is a pair , where E is a principal G-bundle over X (i.e., a bundle over X, the fiber of which is G, so a right action of G on it is given) and is a holomorphic global section of , where is the vector bundle, the fiber of which is the Lie algebra of G induced by the adjoint action , where ⊗ denotes the tensor product, and K is the canonical line bundle over X. Depending on the specific form of the structure group, G-Higgs bundles may have particular interpretations, such as that given below for and .
Definition 1.
An -Higgs bundle over X is a pair where E is a principal -bundle over X with an associated bi-linear form, q, and is a complex vector bundle homomorphism preserving the bi-linear form, q, where K denotes the canonical bundle over X.
Definition 2.
A -Higgs bundle over X is a pair , where E is a principal -bundle over X and . Here, K is the canonical bundle over X, is the adjoint vector bundle of E, and is a vector bundle morphism preserving the bi-linear form with which the special orthogonal bundle associated with E is equipped.
For both principal -Higgs bundles and -Higgs bundles, the element is called a Higgs field, and it can be understood on each fiber of the orthogonal bundle E as an 8-dimensional complex matrix of the Lie algebra .
There are suitable notions of stability and polystability that allow us to construct the moduli space of G-Higgs bundles for any complex reductive Lie group G [32], which will be denoted by . These notions extend to the notions given by Ramanathan [1,2] to Higgs pairs for principal bundles and by Ramanan [33] for orthogonal and Spin bundles. The moduli space of -Higgs bundles over X is then the algebraic variety, which parameterizes isomorphism classes of polystable -bundles over X.
Given any -Higgs bundle , an automorphism of is an automorphism of the principal -bundle E such that the following diagram commutes:
that is, .
Consider now any semi-simple complex Lie group, G, with Lie algebra, . In [16,18], it is proved that the following defines an action of the group on the moduli space of G-Higgs bundles; if and , then is defined to be the G-Higgs bundle
where is an automorphism of G representing , and is the principal G-bundle, the total space of which is that of E, but it is equipped with the right action of G given by for and . It can be proved that this action preserves the stability and polystability of the G-Higgs bundles and that it does not depend on the choice of the representative A of since inner automorphisms act trivially on G-Higgs bundles [16,18].
Let be the triality automorphism, and let be a -Higgs bundle over X fixed by the action of . If is an automorphism of representing , then . A way to understand the action of the triality automorphism on the moduli space of -Higgs bundles is by attending to the action of triality on vector representations of the group. Bi-jective correspondence exists between the nodes of the Dynkin diagram of (Figure 1), its irreducible representations, which are 8-dimensional, and the nontrivial elements of its center [30]. Triality automorphism acts by permuting the three fundamental representations and the three nontrivial central elements of . At the level of vectorial forms of the principal -bundles, it should be recalled that the underlying vector bundle of every stable -bundle E through the homomorphism of groups admits a vector decomposition of the form for some rank 2 vector subbundles, e.g., , , , and , as proved in Proposition 2.3 of [21]. The action of the triality automorphism is enacted by fixing one of these vector sub-bundles and permuting the other three mentioned sub-bundles so that in a fixed point of the action of the triality automorphism, three of these vector sub-bundles are isomorphic. Thus, a -bundle, the underlying vector bundle of which is of the form for certain rank 2 stable vector bundles F and V over X is an example of a -bundle on which the triality acts trivially.
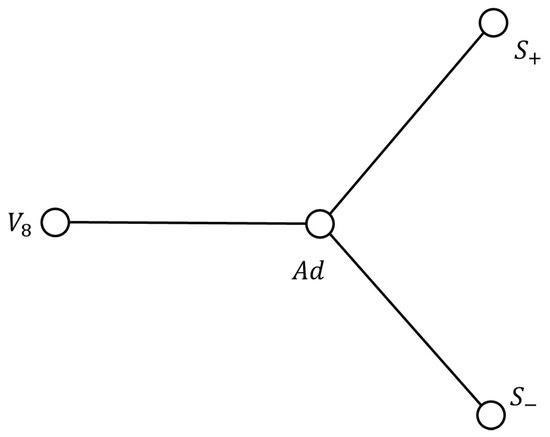
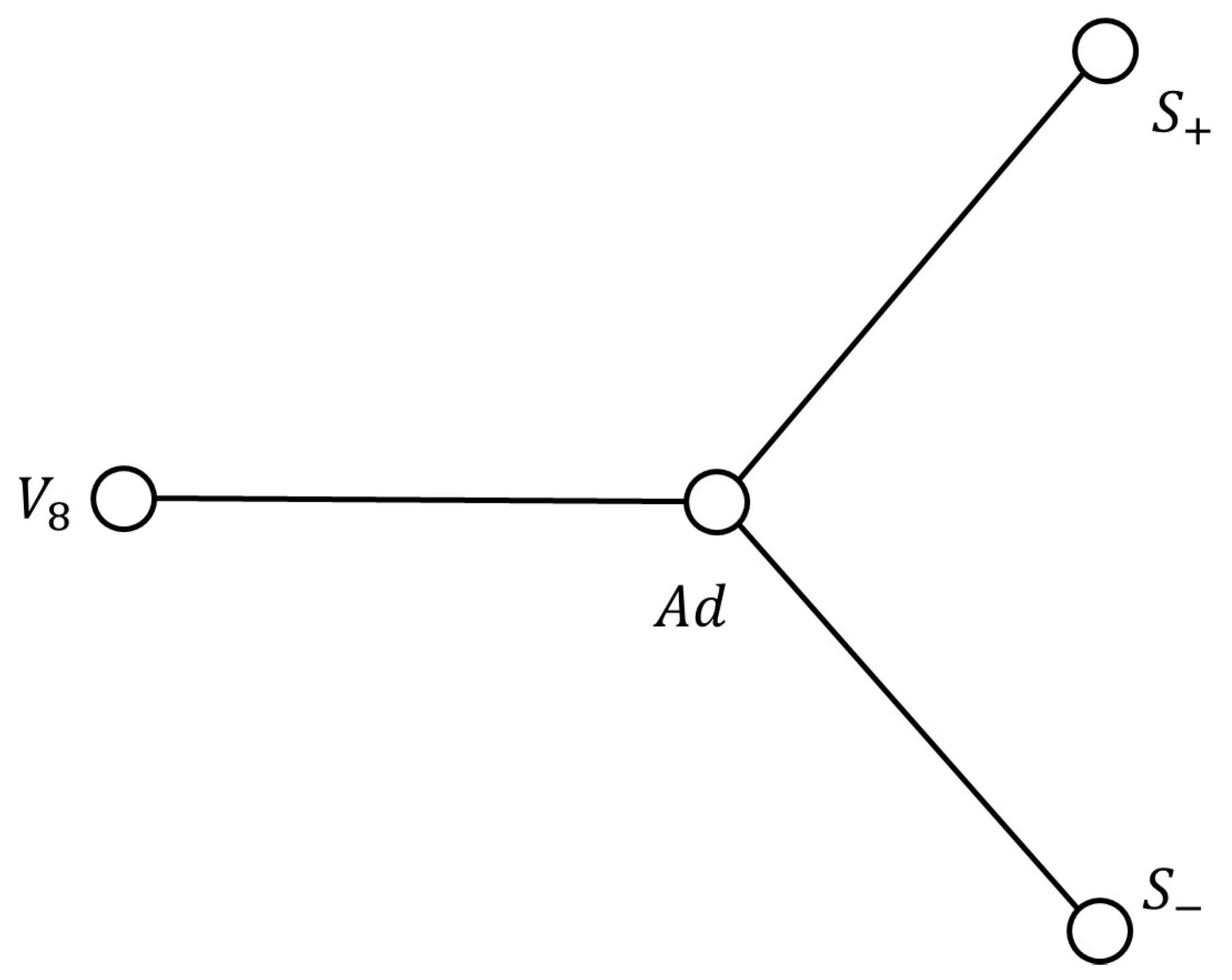
Figure 1.
Dynkin diagram of the simple Lie group , where the nodes of the diagram correspond to the vectorial representation and the spinor representations and of , corresponding to the two types of spinors in dimension 8, known as Weyl spinors (which are 8-dimensional and interchanged by the action of the triality automorphism) and the adjoint representation Ad (which is 28-dimensional and fixed by the action of triality) [30]. The figure is original and was made using Microsoft Word® v. 2409.
Recall that there are only two possibilities for the group of fixed points of A, depending on the lifting of the triality automorphism by the relation . These two possibilities are or , as proved in Theorem 5.10 of [31]. In [16,18], it is proved that the fixed points of the action of the triality automorphism on the moduli space of -Higgs bundles are those which admit a reduction in structure group to or . Then, there are maps and such that their images complete the subvariety of fixed points of the action of the triality automorphism. In this work, the study of map is deepened, taking advantage of the existence of results relating the invariant polynomials of and , which will be key in the study.
4. The Triality Automorphism and the Hitchin Integrable System
In the context of the moduli space of G-Higgs bundles over X for a semi-simple complex Lie group G, the Hitchin map projects over an affine space B called base, which parametrizes certain invariant polynomials (for the adjoint action of G) associated with the Higgs fields of the Higgs bundles [14]. Specifically, these invariant polynomials, when evaluated on a Higgs field , lead to global sections of the canonical line bundle K tensored with Casimir polynomials of the Lie algebra of G. This defines the Hitchin map . This map not only projects but transforms it in the integrable system of the induced fibration; thus, it is called a Hitchin integrable system. This system has some remarkable properties. Between them, the generic fiber of this fibration is an abelian variety called the Prym variety. This Hitchin system admits a natural symplectic structure from that of the cotangent bundle in a way that the Poisson bracket of the functions defined by the Hitchin map is zero. This is key for the system to be integrable in the sense of Liouville [14]. The study of this integrable system, particularly the geometry and topology of the Prym varieties, is key to addressing and studying problems concerning the topology of .
Given a finite covering, , of X, the Prym variety (or simply ) is the subgroup of the Jacobian of that parametrizes divisors on of zero norms, which is an abelian variety, with the norm being the map that moves the divisors on to the divisors on X. In the context of the moduli space of G-Higgs bundles over X, with G being a semi-simple complex Lie group acting as the structure group of the Higgs bundles, the Higgs field of each G-Higgs bundle induces a spectral covering of X, which is essentially the zero locus of the characteristic polynomial of the Higgs field, taken through the adjoint representation of G on its Lie algebra . Then, the associated Prym variety is given by the Prym variety of this spectral covering, which can be proved to be isomorphic to the fiber of the Hitchin map [14].
Specifically, let G be a semi-simple complex Lie group with Lie algebra , and let be the basis of the ring of invariant homogeneous polynomials of , where r is the rank of . The action of each polynomial on the Higgs field defines a map
where for . This map allows us to define the so-called Hitchin map,
where is the moduli space of G-Higgs bundles. The vector space
is called the base of the Hitchin map. In [14], it is proved that . If n is the dimension of , the Hitchin map induces n complex-valued functions defined on , where denotes the moduli space of stable and simple principal G-bundles, which is a dense open subset of the moduli space of principal G-bundles. The tangent space to at an element is isomorphic to , which coincides with according to Serre duality. Hitchin also proved that the n functions Poisson-commute with the canonical symplectic structure of the cotangent bundle as shown in Proposition 4.5 of [14]. This, then, defines a completely integrable system on [34].
As will be proved below, the group of outer automorphisms of G acts on the base of the Hitchin map so that this action is compatible with the action of on when G is simply connected, (which is the case of ).
Lemma 1.
Let G be a semi-simple and simply connected complex Lie group. Let f be an automorphism of the Lie algebra of G, and let p be an invariant homogeneous polynomial of G. Then, is also an invariant homogeneous polynomial of G.
Proof.
Since f is a linear map, it is clear that is a homogeneous polynomial. Therefore, it suffices to show that it is invariant.
Let be an automorphism of G such that (such automorphism exists because G is simply connected), and let . Then, for any ,
(where is defined as the inner automorphism induced by g, ), so is invariant, as desired. □
From this, the announced action of on the base, B, of the Hitchin map can be defined for a semi-simple and simply-connected complex Lie group, G. Hitchin [14] proved that the Hitchin map is surjective. Then, for each , there exists such that . If , it is defined
where is an automorphism of G representing .
Lemma 2.
Proof.
To check that the action given in (13) is well-defined, notice the following:
- It is clear from Lemma 1 that are invariant homogeneous polynomials of G.
- If f is an inner automorphism of G, then, since are invariant under this kind of automorphism, the action is trivial, so the above action descends to an action of .
- If and are polystable G-Higgs bundles over X such thatthen, since is a basis of invariant polynomials of G, for every invariant polynomial p of G, so, in particular,
The above three points lead to the conclusion that the action under consideration is well-defined.
Now, let . To check that the action of on the base of the Hitchin map is compatible with the action on , it suffices to show that
for all . Notice that
as it was intended to prove. □
Remark 1.
Since, according to Lemma 2, the action of an outer automorphism ρ on the base of the Hitchin map does not depend on the representative of ρ chosen in , if is an element if the base of the Hitchin map for some G-Higgs bundle, , it can be denoted
The above study will now be particularized to the case of and -Higgs bundles. The algebra of invariant polynomials of is generated by four invariant homogeneous polynomials
where for each i, and is the Pfaffian, so [14]. Indeed, as it can be found in [35],
Then, the base of the Hitchin map is
When given a quadruple , it induces the polynomial
in the sense that the characteristic polynomial of the Higgs field of any in the fiber of the Hitchin map at a is , where each or is a holomorphic global section of over X, and defines the Hitchin map .
The mentioned characteristic polynomial defines the spectral curve in the total space of the canonical bundle . Then, given any , it defines the equation of the corresponding spectral curve, which will be called as the divisor of a section of defined by the induced polynomial, where x is the tautological section of ; it is a single-valued eigenvalue of the Higgs field .
Consider now the Lie group , which is seen as a subgroup of . The algebra of invariant polynomials of is generated by using two polynomials, , of degrees 2 and 6, respectively.
Then, the base of the Hitchin map of the moduli space of -Higgs bundles is
and, given a pair , the induced invariant polynomial is ; therefore, by taking a common factor , it follows that the polynomial
is also -invariant [22,35].
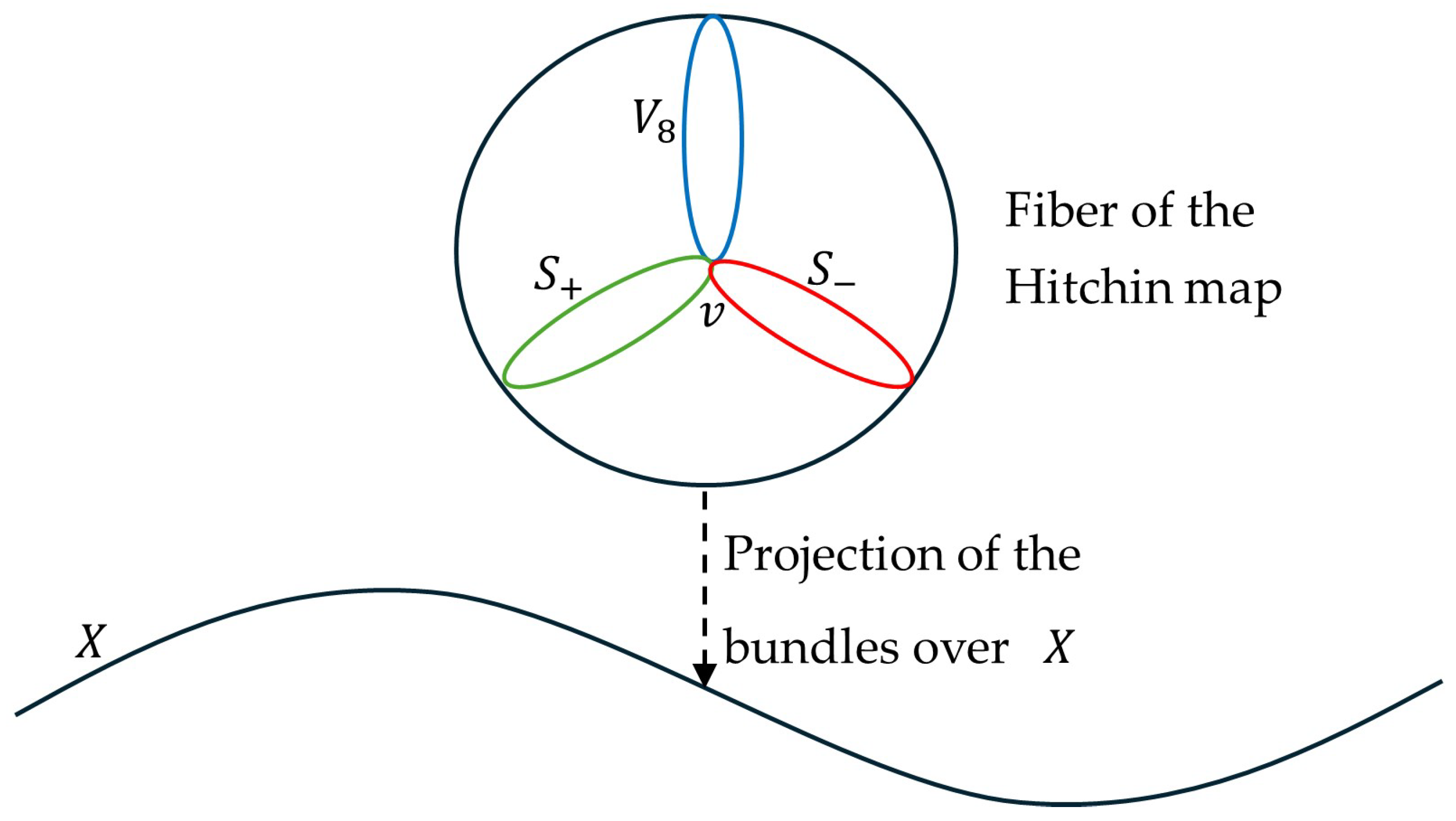
Roughly speaking, the triality automorphism of acts in each fiber of the Hitchin map by permuting the orbits corresponding to the three 8-dimensional irreducible representations of mentioned above (the vectorial version and the two spinor versions, positive and negative, corresponding to the Weyl spinors [30]). In Figure 2, a generic fiber of the mentioned Hitchin map of the moduli space of -Higgs bundles over the compact Riemann surface X is represented, and three orbits interchanged by the triality automorphisms are shown in a very simple and schematic way. The point called v in the intersection of the orbits represents a fixed point of the action of triality on the fiber.
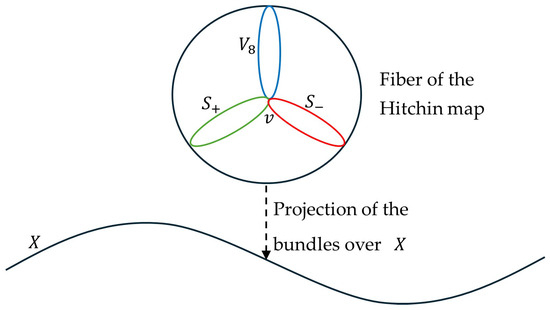
Figure 2.
Action of triality on a fiber of the Hitchin map of . In blue is an orbit corresponding to the irreducible vectorial representation of , and in red and green are orbits corresponding to the two spinor representations. These three orbits are interchanged by the action of triality. The figure is original and was made using Microsoft Word® v. 2409.
Some facts on spectral curves and Prym varieties associated with the moduli spaces and will be now recalled. Given a -Higgs bundle over X, the characteristic polynomial of the Higgs field defines an element, , so a spectral cover and an 8-sheeted covering map are defined, the fibers of which are identified using the eigenvalues of . A detailed construction of this curve can be found in [22,36,37]. There exists an exact sequence on the spectral curve
where E denotes both the principal -bundle and the orthogonal bundle that it induces ([22,36]). By dualizing Equation (26) and tensoring it with , the following is obtained:
Here, L is a line bundle that satisfies (as a vector bundle). It is constructed as the coker of , where x denotes the tautological global section of , and can be identified with the support of L. The covering map gives a norm map Nm defined by on divisor classes. The norm defines a map at the level of Jacobian varieties . Then, the Prym variety of the spectral curve is defined to be the connected component of the kernel of . This Prym variety is then an abelian subvariety of the Jacobian of the sectral curve . Observe that since takes values in , the opposite of an eigenvalue of is also an eigenvalue of , so an involution of is defined by a change in sign, and the eigenspace V of eigenvalue of is moved to for eigenvalue . Then, according to (26) and (27), so . This means that satisfies that is trivial (the choice of a square root of K is required here). Then, the Prym variety is the collection of those elements M of the Jacobian of such that is trivial. This is equivalent to stating that the desired Prym variety coincides with , with the last Prym variety being defined from the covering map . Notice that, given any , one has that , where , and since , then , as a consequence of (26) and (27); therefore, the special orthogonal bundle is obtained from the element of the Prym variety. Then, the fiber is a -sheeted covering of the Prym variety of (details on this construction can be found in [22]).
Now, consider the Lie group . The fundamental complex representation of has rank 7 and defines (in addition) an inclusion, . A holomorphic anti-symmetric 3-form can be defined in in a way that is the group of elements of , which preserves this 3-form [29]. For any -Higgs bundle over X, Hitchin [22] considered the spectral curve associated with it and constructed an intermediate curve, C, such that the covering map admits a factorization
and proved the existence of an involution of such that and represent the subspace of those for which is trivial. From this description, Hitchin [22] proved that the globally defined holomorphic anti-symmetric 2-form defined in E by its -structure can be reconstructed from the corresponding point of the Prym variety . In this way, it was proved that the fiber of the Hitchin map of is isomorphic to [22].
Notice that if is a -Higgs bundle, then when it is seen as a -Higgs bundle through the contention of groups , it satisfies the Pfaffian being 0. Then, if a is the -invariant polynomial and is the associated spectral curve, b is the -invariant polynomial, and is the associated spectral curve, the map is restricted to a map:
Proposition 1.
Let B and be the base of the Hitchin maps of and , as defined in (21) and (24), respectively. Then, there exists a map such that the diagram
is commutative, and is given by fixed points for the action of the triality automorphism of on B. Moreover, the generating homogeneous -invariant polynomials and can be described as
where are the generating homogeneous -invariant polynomials given in (21).
Proof.
The algebra of homogeneous -invariant polynomials is naturally embedded in the algebra of homogeneous polynomials of , which are invariant for the action of the subgroup , and there is also a surjective map of this sub-algebra on the algebra of homogeneous -invariant polynomials, as proved in Corollary 2.2.3 of [27] and in Propositions 4.2 and 4.3 of [35]. From this, the map, j, making the diagram above commutative is defined by the composition of the two maps described. It has also been proved that the image (according to j of the algebra of homogeneous -invariant polynomials) is exactly represented by the fixed points of the triality automorphism action on the algebra of homogeneous -invariant polynomials, as shown in Propositions 4.2 and 4.3 of [35]. Moreover, Hitchin proved that a matrix of the Lie algebra , when considered as a matrix of , has eigenvalues of such that , with the homogeneous invariant polynomials being and , which generates the algebra of invariant polynomials of , taking values of and , respectively [22,35]. From this, in Proposition 4.3 of [35], the explicit expressions for and of the statement are computed. □
Remark 2.
Notice that if , is the spectral curve of the -invariant polynomial induced by a, and if is the spectral curve associated with , where j is defined in Proposition 1, then the map is restricted to a map: . The image of represents the fixed points of the action of the triality automorphism on .
5. Connectedness Criteria for the Prym Varieties
In this section, the geometry of the Prym varieties and of and , respectively, will be studied, where are defined in (24). In particular, the necessary and sufficient conditions for the above Prym varieties to be disconnected will be established.
Lemma 3.
Let G be the complex simple Lie group or . Let be the moduli space of G-Higgs bundles over X and be the Hitchin map defined in (10), where B denotes the base of the Hitchin map. Let and let be the associated spectral curve. Then, admits a copy of X in it if and only if the polynomial defined in (22) or (25), respectively, induced by a admits a global linear factor.
Proof.
Consider the polynomial on t induced by a defined in (22) or (25), which will also be called a for simplicity. Let d be the degree of a. Suppose that a admits a linear factor, say , where and . Then, on a dense open subset U of X. The element defines an isomorphism
By taking the dual, it is induced as an isomorphism
Then, there exists a unique element such that . Since , this implies that for all . This, then, defines a morphism such that , where is the spectral covering. Therefore, is injective. Since X and are projective curves, extends to the desired morphism.
Reciprocally, suppose that is an inclusion of curves. It is then clear that is a linear factor of a. □
Proposition 2.
Let be the moduli space of -Higgs bundles over X, and let B be the base of the Hitchin map defined in (21). Let and let be the associated spectral curve. Let be the invariant polynomial defined by a, where and for all i. This polynomial will also be denoted by a. Then,
- 1.
- The polynomial induced by a admits a linear factor if and only if admits a copy of X, in the sense that X is a component of .
- 2.
- The polynomial induced by a admits an irreducible factor of order two if and only if there exist , , and such that the following identities in and , respectively, hold:
- 3.
- The polynomial induced by a admits an irreducible factor of order three if and only if there exist , , and such that the following identities in , and , respectively, hold:
- 4.
- The polynomial induced by a admits an irreducible factor of order four if and only if there exist , , , and such that the following identities in , , , and , respectively, hold:
Proof.
The first part is a consequence of Lemma 3. For the second part, notice that the polynomial induced by a admits a factor of degree 2 if and only if there exist elements for and for such that
This gives the following system of equations:
Since, according to the hypothesis, the factor is irreducible, it follows that . Therefore, from the first seven equations, it is obtained that the s are determined by the s, so the other two equations provide the necessary and sufficient conditions, which the s should satisfy for the existence of a solution. Straightforward computations show that these two conditions are those announced in the statement.
The third part is analogous to the case above when considering the system in for induced by the expression
where for . That is,
The s are determined by the s from the first six equations since it must be . Then, the necessary and sufficient conditions on the s for the existence of a solution are given by the last three equations. These conditions are those of the statement.
Finally, the fourth part is similar. It follows from the expression
which induces a system on the s with coefficients in s of the form
From the first five equations, the s can be expressed in terms of the s (notice that, in this case, it must be ), so the four conditions of the statement follow from the four last equations of the system. □
Consider now the moduli space of -Higgs bundles over X. From Lemma 3, similar computations to those made in Proposition 2 allow us to prove the following analogous result.
Proposition 3.
Let be the moduli space of -Higgs bundles over X, and let be the base of the Hitchin map of defined in (24). Let and be the induced spectral curve. Suppose that the invariant polynomial induced by a, which will be also called a, is , where for all . Then,
- 1.
- The polynomial induced by a admits a linear factor if and only if admits a copy of X in the sense that X is a component of .
- 2.
- The polynomial induced by a admits an irreducible factor of order two if and only if there exist , , and such that the following identities on and , respectively, hold:
- 3.
- The polynomial induced by a admits an irreducible factor of order three if and only if there exist , , , and such that the following identities on , and , respectively, hold:
Proof.
The first part is an immediate consequence of Lemma 3. For the second part, note that the polynomial induced by a admits a factor of degree two if and only if there exist elements for and for such that
This gives the following system of equations.
It must be , since, according to the hypothesis, the factor is irreducible. It is then clear that the s are determined by the s from the first five equations of this system, so the other two equations give the necessary and sufficient conditions, which the s should verify for the existence of a solution. Straightforward computations, then, readily show that these two conditions are those of the statement.
For the third part, notice that the condition for the polynomial induced by a to admit a degree three factor is the existence of elements for and for such that
from which a similar system of equations follows; thus, an analogous computation (to the above) leads to the expressions of the statement since it must be according to the irreducibility of . Specifically, the induced system is of the form
Here, it also must be , so the first four equations allow us to express the s in terms of the s. The rest of the three equations give the conditions announced. □
Corollary 1.3 of the work by Hausel and Pauly [38] is recalled here, as it will be useful in the study of the geometry of Prym varieties associated with the Hitchin system in the moduli spaces and . Although the findings in [38] work with the -case, the results that will be used here are directly applicable to the cases of interest in the present work since the representations that are considered allow us to interpret the curves as spectral curves associated with some -Higgs bundle, which admits an additional structure.
Proposition 4
([38], Corollary 1.3). Let be an n-sheeted spectral cover of the complex irreducible projective curve, X. The Prym variety is not connected if and only if there exists a prime number, d, with such that the spectral cover comes from a degree, , spectral cover over the étale Galois cover of degree, d, over X.
Consider the moduli space of -Higgs bundles over X. Let B be the base of the Hitchin map of , as defined in (21). In Proposition 4, Hausel and Pauly prove that the Prym variety of a given spectral curve with is connected if and only if the polynomial does not divide the polynomial defined by a in (22) whatever , , and d is a prime number that divides the degree of the cover, .
Similarly, if the moduli space of -Higgs bundles over X is considered and denotes the base of its Hitchin map defined in (24), Proposition 4 states that, for any with associated spectral curve , the Prym variety is connected if and only if for every , and every prime number d (such that d divides the degree of the cover ), the polynomial does not divide the polynomial defined by a in (25).
From Proposition 4 and the discussion above, one can prove the following result, which determines the condition of a Prym variety given by the groups or to be connected.
Proposition 5.
Let G be the complex simple Lie group or , and let be the moduli space of G-Higgs bundles over X. Let a be an element of the base of the associated Hitchin map. Then, the following is satisfied:
- 1.
- If and the invariant polynomial associated with a is with for and , then the Prym variety is not connected if and only if one of the following conditions holds:
- (a)
- contains a copy of X.
- (b)
- There exists a global section such that β is a solution of the polynomialwhich takes values in .
- 2.
- If and the invariant polynomial associated with a is with for , then the Prym variety is not connected if and only if one of the following conditions holds:
- (a)
- contains a copy of X.
- (b)
- There exists a global section such that β is a solution to the polynomialwhich takes values in .
- (c)
- , and there exists a global section such that β is a solution to the polynomialwhich takes values in .
Proof.
As a consequence of Proposition 4, in both cases, is disconnected if and only if there exists a polynomial of the form , with and , which divides the polynomial associated with a and such that d is a prime number that divides the degree of the polynomial associated with a. Consequently,
- If , the only possibility for d is since the degree of the polynomial associated with a is 8. There are two possibilities for the polynomial to have a factor of the form : first, the polynomial is reducible if and only if contains a copy of X, according to the first part of Proposition 2; secondly, the polynomial is irreducible if and only if satisfy the conditions of the second part of Proposition 2. Notice that since is supposed to be irreducible, both sections, and , should be non-zero. By taking in those expressions, it follows that is a solution to the polynomial , which takes values in .
- If , since the polynomial associated with a has a degree of 6, there are two possibilities for the degree, d:
- (a)
- If , the polynomial may be reducible or irreducible. It is reducible if and only if contains a copy of X, according to the first part of Proposition 3; it is irreducible if and only if satisfy the two conditions given in the second part of Proposition 3. Since is supposed to be irreducible, and are non-zero sections, and by taking in those expressions, it is deduced that is a solution to the polynomial , which takes values in .
- (b)
- If , then, as in the previous item, the polynomial may be reducible or irreducible. It is easily seen that the reducible case falls in the preceding case. It is irreducible if and only if satisfy the conditions given in the third part of Proposition 3. Since it should be and , by taking and to those expressions, it follows that and represent a solution to in .
□
Remark 3.
Proposition 5 gives the necessary and sufficient conditions for the elements for the base of the Hitchin map of for the Prym varieties and to be connected or disconnected, where j is the map defined in Proposition 1. Recall that these two Prym varieties are related to each other through the map , as defined in the Remark after Proposition 1. At the present moment, it is not easy (in the light of what has been proved) to give a simple criterion for deriving, for example, the connection of from the connection of . To illustrate this difficulty, consider criterion 2(c) of Proposition 5. In the case illustrated in that item, ; so, according to Proposition 1, the polynomial associated with is . Even if criterion 2(c) for the disconnection of (the existence of such that ) is satisfied, it is not possible to ensure that is disjointed because this would require the existence of such that . However, by taking the intersection of both criteria, it is possible to give a sufficient condition for the two Prym varieties to be disjointed, as is stated in the following result, which is an immediate consequence of Proposition 5.
Corollary 1.
Let be an element of the base of the Hitchin map of defined in (24), the associated polynomial of which is (that is, ). Then, if there exists such that , then the Prym varieties and are both disconnected, where j is defined in Proposition 1.
6. Conclusions
Let X be a compact Riemann surface of genus , and let and be the moduli spaces of and -Higgs bundles over X, respectively. It is known that there is a map of algebraic varieties , the image of which is composed of the fixed points of the action of the triality automorphism on . In this paper, it has been proven that acts on the base, B, of the Hitchin map given by the Hitchin integrable system associated with ; there exists a homomorphism , where is the base of the Hitchin map of ; the image of j is composed by using the fixed points of the action of . This led to the definition of maps between Prym varieties , where , given by the restriction of the map . As a way of studying the geometry of the maps (which, in turn, deepens the study of the geometry of the map ), the results on the geometry of the Prym varieties involved have been provided. In particular, the Prym varieties being disjointed has been characterized. As a consequence, sufficient conditions are provided for both Prym varieties, and , to be disjointed. All this contributes to a better understanding and deepening of the map and, therefore, of the geometry of the moduli spaces of the Higgs bundles involved. Specifically, the main implication of the present work is to provide criteria for deciding the connection or disconnection of Prym varieties of the two moduli spaces above, which, moreover, are related because there is an obvious homomorphism of one in the other. These findings allow us to deepen our knowledge of the topology of moduli spaces with structure groups and , which is key in the identification of irreducible components and the computation of Betti numbers and characteristic classes. Specifically, the disconnection of the Prym varieties implies the existence of a stratification in the corresponding fiber of the moduli space. This leads not only to the existence of different irreducible components but to the existence of non-isomorphic Higgs bundles with different geometric properties. In addition, when the Prym varieties are connected, the cohomology of the moduli space can be simplified, and it should also be easier to compute Betti numbers and other topological invariants. In mathematical physics, the connection or disconnection of the Prym varieties affects the way in which certain dualities, such as Langlands duality, act. Thus, the results provided here provide mathematical physicists with a suitable framework with which to study the mentioned dualities in the context of string theory.
Consequently, as a future line of research, the analysis of the topological invariants of both moduli spaces and, definitely, the discussion about whether the forgetful map is or is not injective and, in any case, the behavior of its image concerning the irreducible components of are proposed. Specifically, we propose explicitly computing the number of connected components of the considered Prym varieties, which is an open problem that may help to identify irreducible components in the fibers of the Hitchin map of the moduli spaces of and -Higgs bundles over a curve, X. We also propose proving whether the map above is injective and explicitly identifying the image of the homomorphism , where is the base of the Hitchin map of and B is the base of the Hitchin map of . These aims may make use of the results on connectedness of the Prym varieties provided here, and it would also be interesting to analyze the effect of the action of triality automorphism on certain subvarieties of , such as the Lagrangian subspaces that are defined as reductions in the real forms of the structure group coming from the action of involutions of , which are identified in [11]. All these are open problems related to the one addressed here that would strengthen the applications of the study to mirror symmetry and Langlands duality.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data associated with this research are contained in the paper.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Ramanathan, A. Moduli for principal bundles over algebraic curves. I. Proc. Indian Acad. Sci. Math. Sci. 1966, 106, 301–328. [Google Scholar] [CrossRef]
- Ramanathan, A. Moduli for principal bundles over algebraic curves. II. Proc. Indian Acad. Sci. Math. Sci. 1966, 106, 421–449. [Google Scholar] [CrossRef]
- Ramanathan, A. Stable principal bundles on a compact Riemann surface. Math. Ann. 1975, 213, 129–152. [Google Scholar] [CrossRef]
- Hitchin, N. The self-duality equations on a Riemann surface. Proc. Lond. Math. Soc. 1987, 55, 59–126. [Google Scholar] [CrossRef]
- Narasimhan, M.S.; Seshadri, C.S. Stable and unitary bundles on a compact Riemann surface. Ann. Math. 1965, 82, 540–564. [Google Scholar] [CrossRef]
- Corlette, K. Flat G-bundles with canonical metrics. J. Diff. Geom. 1988, 28, 361–382. [Google Scholar] [CrossRef]
- Donaldson, S.K. A new proof of a theorem of Narasimhan and Seshadri. J. Diff. Geom. 1983, 18, 269–277. [Google Scholar] [CrossRef]
- Simpson, C.T. Higgs Bundles and Local Systems. Publ. Math. L’IHES 1992, 75, 5–95. [Google Scholar] [CrossRef]
- Simpson, C.T. Moduli of representations of the fundamental group of a smooth projective variety I. Inst. Hautes Études Sci. Publ. Math. 1994, 79, 47–129. [Google Scholar] [CrossRef]
- Simpson, C.T. Moduli of representations of the fundamental group of a smooth projective variety II. Inst. Hautes Études Sci. Publ. Math. 1994, 80, 5–79. [Google Scholar] [CrossRef]
- Baraglia, D.; Schaposnik, L.P. Real structures on moduli spaces of Higgs bundles. Adv. Theor. Math. Phys. 2016, 20, 525–551. [Google Scholar] [CrossRef]
- Hausel, T.; Thaddeus, M. Mirror symmetry, Langlands duality, and the Hitchin system. Invent. Math. 2003, 153, 197–229. [Google Scholar] [CrossRef]
- Kapustin, A.; Witten, E. Electric-magnetic duality and the geometric Langlands program. Commun. Number Theory Phys. 2007, 1, 1–236. [Google Scholar] [CrossRef]
- Hitchin, N. Stable bundles and integrable systems. Duke Math. J. 1987, 54, 91–114. [Google Scholar] [CrossRef]
- Chevalley, C. Invariants of finite groups generated by reflections. Am. J. Math. 1955, 77, 778–782. [Google Scholar] [CrossRef]
- Antón-Sancho, Á. Automorphisms of order three of the moduli space of Spin-Higgs bundles. Hokkaido Math. J. 2018, 47, 387–426. [Google Scholar]
- García-Prada, O. Involutions of the moduli space of SL(n,)-Higgs bundles and real forms. In Vector Bundles and Low Codimensional Subvarieties: State of the Art and Recent Developments; Casnati, G., Catanese, F., Notari, R., Eds.; Quaderni di Matematica, 21; Dipartimento di Matematica, Seconda Università Napoli: Caserta, Italy, 2007; pp. 219–238. [Google Scholar]
- García-Prada, O.; Ramanan, S. Involutions and higher order automorphisms of Higgs bundle moduli spaces. Proc. Lond. Math. Soc. 2019, 119, 681–732. [Google Scholar] [CrossRef]
- Antón-Sancho, Á. Principal SO(2n,)-bundle fixed points over a compact Riemann surface. J. Math. Phys. Anal. Geom. 2024, 20, 139–152. [Google Scholar]
- Antón-Sancho, Á. Fixed points of involutions of G-Higgs bundle moduli spaces over a compact Riemann surface with classical complex structure group. Front. Math. 2024, 19, 1025–1039. [Google Scholar] [CrossRef]
- Antón-Sancho, Á. Triality and automorphisms of principal bundles moduli spaces. Adv. Geom. 2024, 24, 421–435. [Google Scholar]
- Hitchin, N. Langlands duality and G2-spectral curves. Q. J. Math. 2007, 58, 319–344. [Google Scholar] [CrossRef]
- Witt, F. Special metrics and triality. Adv. Math. 2008, 219, 1972–2005. [Google Scholar] [CrossRef]
- Migliorini, L.; Shende, V. A support theorem for Hilbert schemes of planar curves. J. Eur. Math. Soc. 2013, 15, 2353–2367. [Google Scholar] [CrossRef]
- Fringuelli, R. Automorphisms of moduli spaces of principal bundles over a smooth curve. Int. J. Math. 2024, 35, 2450036. [Google Scholar] [CrossRef]
- Serman, O. Moduli spaces of orthogonal and symplectic bundles over an algebraic curve. Compos. Math. 2008, 144, 721–733. [Google Scholar] [CrossRef]
- Beck, F.; Donagi, R.; Wendland, K. Folding of Hitchin systems and crepant resolutions. Int. Math. Res. Not. 2022, 2022, 8370–8419. [Google Scholar] [CrossRef]
- Beckers, J.; Hussin, V.; Winternitz, P. Complex parabolic subgroups of G2 and nonlinear differential equations. Lett. Math. Phys. 1986, 11, 81–86. [Google Scholar] [CrossRef]
- Bryant, R.L. Some remarks on G2-structures. In Proceedings of the Gökova Geometry-Topology Conference 2005, Gokova Bay, Turkey, 30 May–3 June 2005; pp. 75–109. [Google Scholar]
- Fulton, E.; Harris, J. Representation Theory: A First Course; GTM 129; Springer: New York, NY, USA, 1991. [Google Scholar]
- Wolf, J.A.; Gray, A. Homogeneous Spaces defined by Lie groups automorphisms. I. J. Differ. Geom. 1968, 2, 77–114. [Google Scholar]
- García-Prada, O.; Gothen, P.; Mundet, I. Higgs bundles and the surface group representations of surface groups in the real symplectic group. J. Topol. 2013, 6, 64–118. [Google Scholar] [CrossRef]
- Ramanan, S. Orthogonal and spin bundles over hyperelliptic curves. Proc. Indian Acad. Sci. Math. Sci. 1981, 90, 151–166. [Google Scholar] [CrossRef]
- Adler, M.; Van-Moerbeke, P. Completely integrable systems, Euclidean Lie algebras and curves. Adv. Math. 1980, 38, 267–317. [Google Scholar] [CrossRef]
- Schaposnik, L.P.; Schulz, S. Triality for homogeneous polynomials. SIGMA 2021, 17, 79. [Google Scholar] [CrossRef]
- Beauville, A.; Narasimhan, M.S.; Ramanan, S. Spectral curves and the generalised theta divisor. J. Reine Angew. Math. 1989, 398, 169–179. [Google Scholar]
- Donagi, R. Decomposition of spectral covers. Astérisque 1993, 218, 145–175. [Google Scholar]
- Hausel, T.; Pauly, C. Prym varieties of spectral covers. Geom. Topol. 2012, 16, 1609–1638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).