Abstract
This work employs the Extended Direct Algebraic Method (EDAM) to solve quadratic and cubic nonlinear Klein–Gordon Equations (KGEs), which are standard models in particle and quantum physics that describe the dynamics of scaler particles with spin zero in the framework of Einstein’s theory of relativity. By applying variables-based wave transformations, the targeted KGEs are converted into Nonlinear Ordinary Differential Equations (NODEs). The resultant NODEs are subsequently reduced to a set of nonlinear algebraic equations through the assumption of series-based solutions for them. New families of soliton solutions are obtained in the form of hyperbolic, trigonometric, exponential and rational functions when these systems are solved using Maple. A few soliton solutions are considered for certain values of the given parameters with the help of contour and 3D plots, which indicate that the solitons exist in the form of dark kink, hump kink, lump-like kink, bright kink and cuspon kink solitons. These soliton solutions are relevant to actual physics, for instance, in the context of particle physics and theories of quantum fields. These solutions are useful also for the enhancement of our understanding of the basic particle interactions and wave dynamics at all levels of physics, including but not limited to cosmology, compact matter physics and nonlinear optics.
Keywords:
Klein–Gordon equations; nonlinear partial differential equations; extended direct algebraic method; kink solitons; explicit solutions MSC:
33B15; 34A34; 35A20; 35A22; 44A10
1. Introduction
A more generalised form of the nonlinear Klein–Gordon Equation (KGE) with different nonlinearities can be articulated as follows:
where , is a constant and is a suitable nonlinear function that is frequently selected as the potential energy [1]. Choosing results in the generation of a number of equations that can be used to simulate a wide range of physical processes, from quantum physics to wave motion, including sine-Gordon, Landau–Ginzburg–Higgs, PHI-4 and reaction Duffing equations [2]. Kragh discusses the KGE’s inception, stating that prominent physicists such as Klein, Fock and Schrödinger were involved in revealing the connection between general relativity theory and some of the older forms of the KGE, which is one of the most significant equations, from which the canonical version of the nonlinear Schrödinger equation can be derived [3,4]. Galehouse [5] used suitable gauge transformations to obtain the KGE geometrically. Moreover, Schechter provided proof of the scattering theory for the more general form of the KGE [6]. The KGE’s equivalent theory is created by adhering to the traditional process comprising a comparable equation in a certain finite-energy normed Hilbert space that contains first-order time [7]. In this article, Weder also provided evidence for the invariance principle, interweaving relations and the existence and completeness of the wave operators. Thus, similar eigenfunction expansions can be applied to a certain field case in order to construct the spectral and scattering theory of the KGE, and the strong results are similar to the Schrödinger case [8]. Tsukanov discusses the translation motion of a KGE in an external field [9].
Since its introduction, the KGE has yielded a wide range of solutions that describe many physical phenomena, including kinks and solitary waves. Tariq et al., in [10], developed a new plethora of exact solutions such as bright and dark solitary wave solutions, kink solitary wave solutions, anti-kink solitary wave solutions, periodic solitary wave solutions and hyperbolic function solutions using the Sardar sub-equation and extended Fan sub-equation methods with stability analysis of the observed solutions. Onyenegecha constructed analytical solutions of a D-dimensional KGE with modified Mobius squared potential [11]. By using the reduced differential transform method, Belayeh et al. found approximate analytic solutions to a two-dimensional nonlinear KGE [12]. Ahmadov et al. used the Nikiforov–Uvarov method to construct analytical solutions for the KGE with combined exponential-type and ring-shaped potentials [13]. Abdeljabbar et al. explored bright and dark soliton solutions in the realm of quadratic KGEs [14]. Applying the extended first kind elliptic sub-equation approach, certain bell- and kink-type solitary wave solutions produced by applying some hyperbolic functions for the KGE were constructed [15]. Using the modified simple equation method, Akter and Akbar derived similar solutions [16]. Adomian applied the decomposition technique to the KGE’s initial boundary value problems [17]. Kudryavtsev [18] studied the interaction of two solitons that are weakly oscillatory, self-localised and damped for a specific form of the KGE. In addition to the analytical solutions previously outlined, a range of numerical techniques have been used to solve KGE-related problems. A few difficulties based on the KGE were resolved by Strauss and Vazquez [19] using the most straightforward central second difference approach. The energy-saving scheme is better suited to model the long-term behaviour of the solutions than the other two, according to the numerical integration of the problem using four explicit finite-difference methods [20]. Another way to solve the KGE numerically is via a collocation method based on radial basis functions of thin plate splines [21]. Integrated radial basis function network methods and multi-quadratic quasi-interpolation are used to approximate the solutions of the non-homogenous version of the KGE [22]. In order to generate numerical solutions of the KGE, classical polynomial cubic B-spline functions have also been adapted for the collocation method [23,24,25,26,27].
Motivated by the ongoing research on KGEs, in this work, we use the EDAM to construct and analyse new families of kink soliton solutions for two KGEs, i.e., the quadratic KGE and the cubic KGE. These models are articulated as follows:
a. When and are substituted into (1), where m and n are non-zero constants, then the quadratic KGE takes the following shape [28]:
b. When is substituted into (1), then the cubic KGE takes the following shape [29]:
KGEs are prominent models in particle and quantum physics which articulate the dynamics of scaler particles (particles with spin zero) in the context of special relativity. The unfinished task of the current study is to use the EDAM to generate kink soliton solutions for (2) and (3). The KGEs are converted into NODEs using variables-based wave transformation. From the resultant NODEs, numerous soliton solutions can be obtained by further reducing them into an assortment of nonlinear algebraic equations under the presumption that they have a series-based solution. With the use of illustrated contour and 3D graphs, the dynamics of a few soliton solutions are investigated for certain values of the supplied parameters. This shows that the solitons take on the structures of several kink wave types, including dark, hump, lump-like, bright and cuspon kink solitons. These graphics also confirm the presence of kink waves in both KGE models. The found soliton solutions have significant physical implications, especially in the context of quantum field theories and particle physics.
The format of the rest of the article is as follows: The Section 2 goes into further detail about the EDAM’s methodology. For its induction to the KGEs, we present Section 3. In Section 4, we provide illustrations of particular kink soliton solutions along with an explanation, while the Section 5 summarises our investigation.
2. The Working Methodology of EDAM
In this section, we present a general description of the EDAM [30,31,32]. Look into the general Nonlinear Partial Differential Equation (NPDE) in the following form:
where . In order to solve Equation (4), the following steps are followed:
Step 1. Equation (4) is first subjected to a variable transformation of the form = , where , which may be expressed in a many ways. This transformation converts (4) into an NODE with the following structure:
where .
Step 2. Next, we suppose the subsequent series-based solution for (5):
Here, symbolises parameters which need to be estimated, while satisfies the Ricatti equation of the following form:
where are constants.
Step 3. We obtain a positive integer N (as expressed in Equation (6)) whenever we try to find a homogeneous balance between the dominant nonlinear term and highest-order derivative in Equation (5). By using the ensuing formulae, we obtain the balance number N more precisely:
such that
where D shows the degree of and and r are positive integers.
Step 4. We then substitute (6) into (5) or integrate (5), developing the equation, and place all the terms in order of to form a polynomial in . When all the coefficients of the derived polynomial are set to zero, an algebraic system of equations for and other parameters are generated.
Step 5. Then, Maple is utilised to solve this system of nonlinear algebraic equations.
Step 6. The travelling wave solutions, which can be obtained from Equation (4), are found by solving for the unknown parameters and substituting the resultant solution into Equation (5) together with the appropriate solution from Equation (7). Using the general solution of Equation (7), we can generate the families of travelling soliton solutions shown below:
Family 1.
For and ,
and
Family 2.
For and ,
and
Family 3.
For and ,
and
Family 4.
For and ,
and
Family 5.
For and ,
and
Family 6.
For and ,
and
Family 7.
For ,
Family 8.
For , and (with ),
Family 9.
For ,
Family 10.
For ,
Family 11.
For , and ,
and
Family 12.
For , (with ) and ,
In the above solutions, .
3. Construction of Soliton Solutions for KGEs
In this section, we evaluate soliton solutions using the EDAM for the nonlinear KGEs.
3.1. Example 1
First, we evaluate soliton solutions for the quadratic KGE stated in (2) as follows:
Taking the travelling wave transformation of the form
where a and b denote non-zero constants, we obtain the following by the chain rule:
Equation (2) can be transformed into the following NODE:
To find the balance number N presented in (7), we balance the highest-order derivative term with the highest-power nonlinear term in the above equation, which determines . Thus, . Putting into (7), starting from , suggests the following closed-form solution for (10):
The arbitrary constants , and are placeholders that need to be found. A substitution of (11) with (10) yields an expression in . After gathering terms with the same powers of and equating the coefficients to zero, we obtain the following system of nonlinear algebraic equations:
and
When this system is solved using the Maple tool, it leads to the following three cases of solutions:
Case 1.
Case 2.
Case 3.
Considering Case 1 and utilizing Equations (11), (9) and the corresponding general solution of (7), we construct the ensuing families of soliton solutions for the quadratic KGE in (2):
Family 13.
For and ,
Family 14.
For and ,
Family 15.
For and ,
Family 16.
For and ,
Family 17.
For and ,
Family 18.
For and ,
Family 19.
For ,
Family 20.
For , and ,
In the above solutions, .
Considering Case 2 and utilizing Equations (11), (9) and the corresponding general solution of (7), we construct the ensuing families of soliton solutions for the quadratic KGE in (2):
Family 21.
For and ,
Family 22.
For and ,
Family 23.
For and ,
Family 24.
For and ,
Family 25.
For and ,
Family 26.
For and ,
Family 27.
For ,
Family 28.
For ,
Family 29.
For , and ,
and
Family 30.
For , (with ) and ,
In the above solutions, .
Considering Case 3 and utilizing Equations (11), (9) and the corresponding general solution of (7), we construct the ensuing families of soliton solutions for the quadratic KGE in (2):
Family 31.
For and ,
Family 32.
For and ,
Family 33.
For and ,
Family 34.
For and ,
Family 35.
For and ,
Family 36.
For and ,
Family 37.
For , and (with ),
Family 38.
For , and (with ),
Family 39.
For ,
Family 40.
For ,
Family 41.
For , and ,
and
Family 42.
For , (with ) and ,
In the above solutions, .
3.2. Example 2
Now, we evaluate the soliton solutions for the cubic KGE stated in (3) as follows:
Taking the travelling wave transformation of the form
where is a non-zero constant, we obtain the following by the chain rule:
The above transformation reduces (3) to the ensuing nonlinear NODE:
To find the balance number N presented in (7), we balance the highest-order derivative term with the highest-power nonlinear term in the above equation. Putting into (7), starting from , suggests the following closed-form solution for (121):
The arbitrary constants , and are placeholders that need to be found. The substitution of (122) into (121) yields an expression in . After gathering terms with the same powers of and equating the coefficients to zero, we obtain the following system of nonlinear algebraic equations:
and
When this system is solved using the Maple tool, it leads to the following two cases of solutions:
Case 4.
Case 5.
Considering Case 4 and utilizing Equations (120), (122) and the corresponding general solution of (7) we construct the ensuing families of soliton solutions for the cubic KGE in (3):
Family 43.
For and ,
Family 44.
For and ,
Family 45.
For and ,
Family 46.
For and ,
Family 47.
For and ,
Family 48.
For and ,
Family 49.
For , and ,
and
Family 50.
For , (with ) and ,
In the above solutions, .
Considering Case 5 and utilizing Equations (120), (122) and the corresponding general solution of (7) we construct the ensuing families of soliton solutions for the cubic KGE in (3):
Family 51.
For and ,
Family 52.
For and ,
Family 53.
For and ,
Family 54.
For and ,
Family 55.
For and ,
Family 56.
For and ,
Family 57.
For , and (with ),
In the above solutions, .
4. Discussion and Graphs
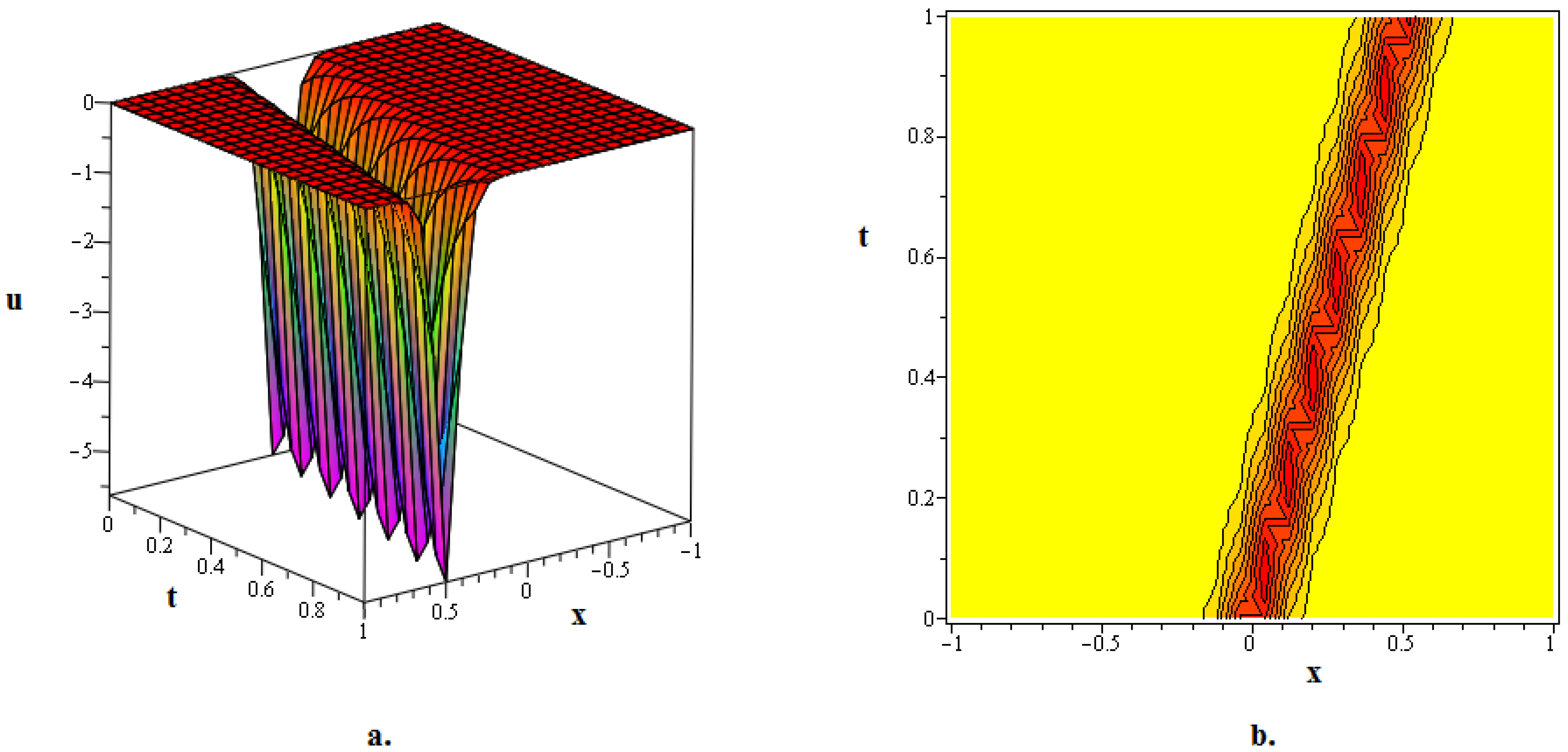
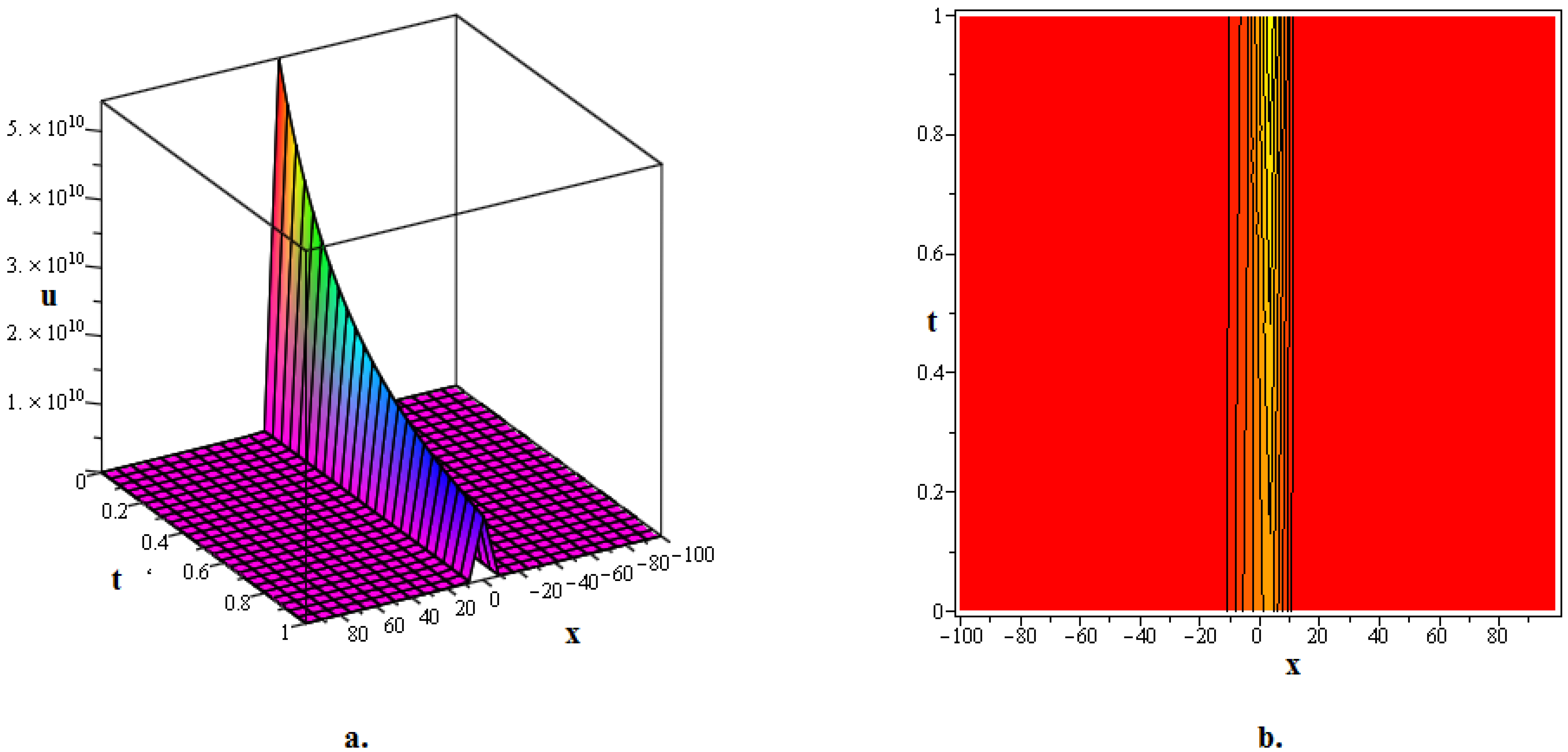
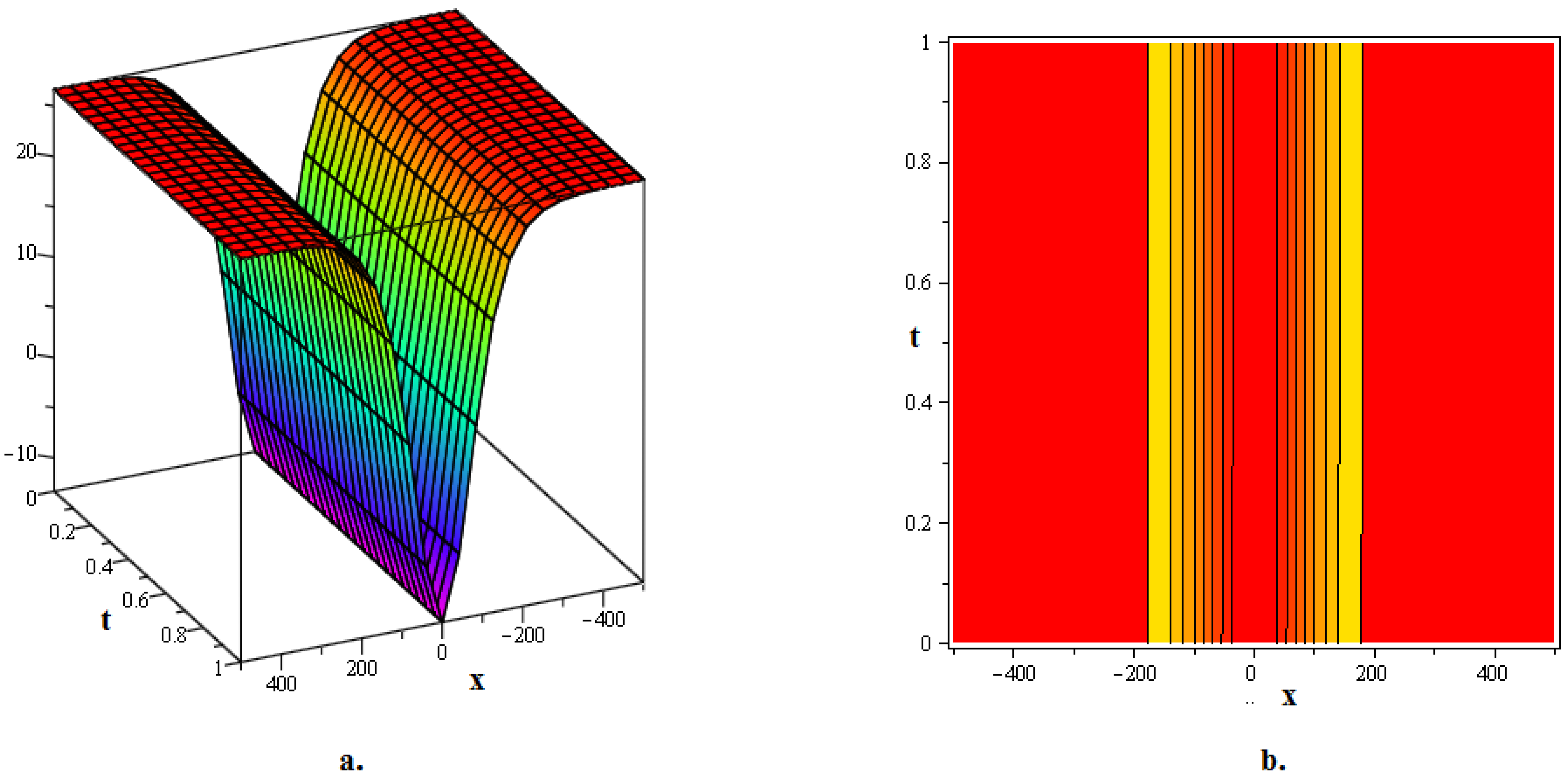
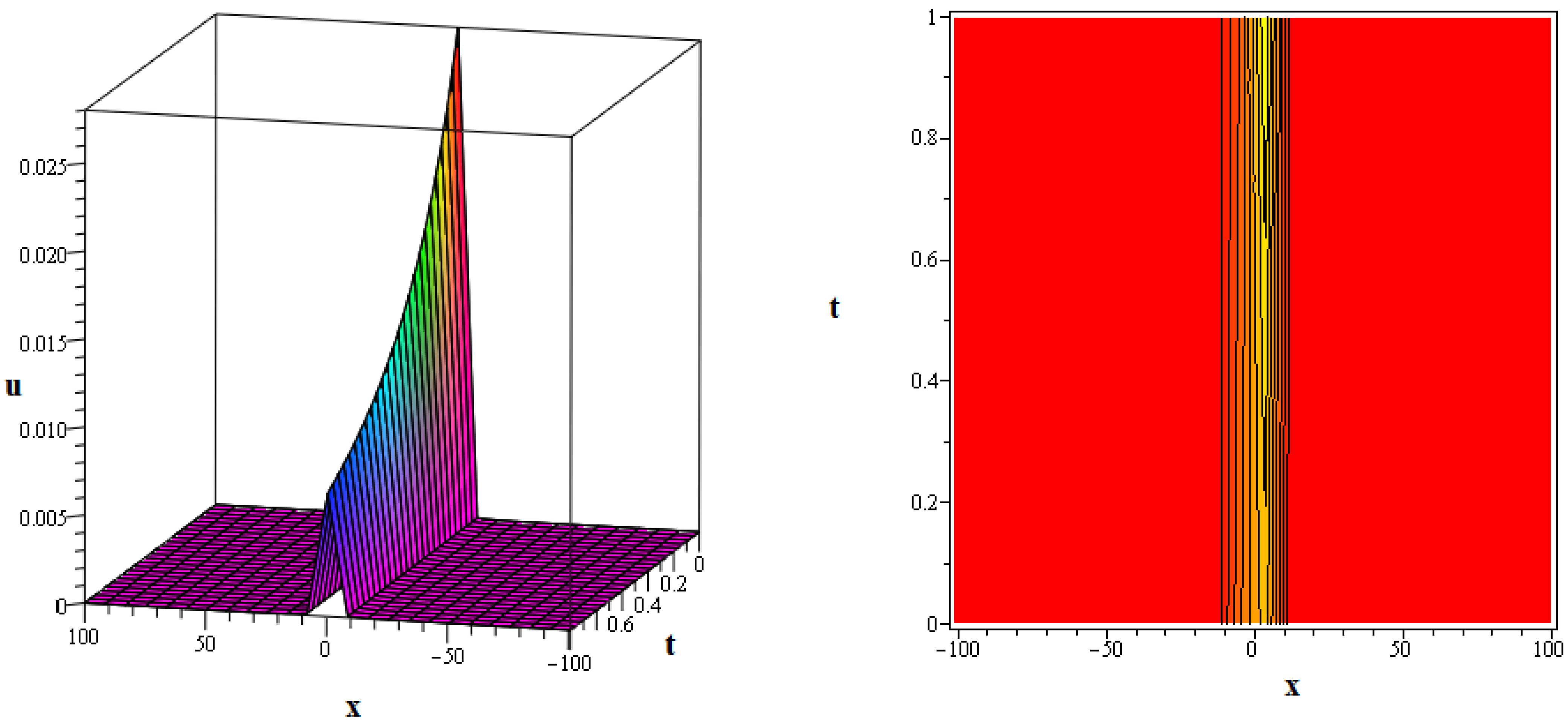
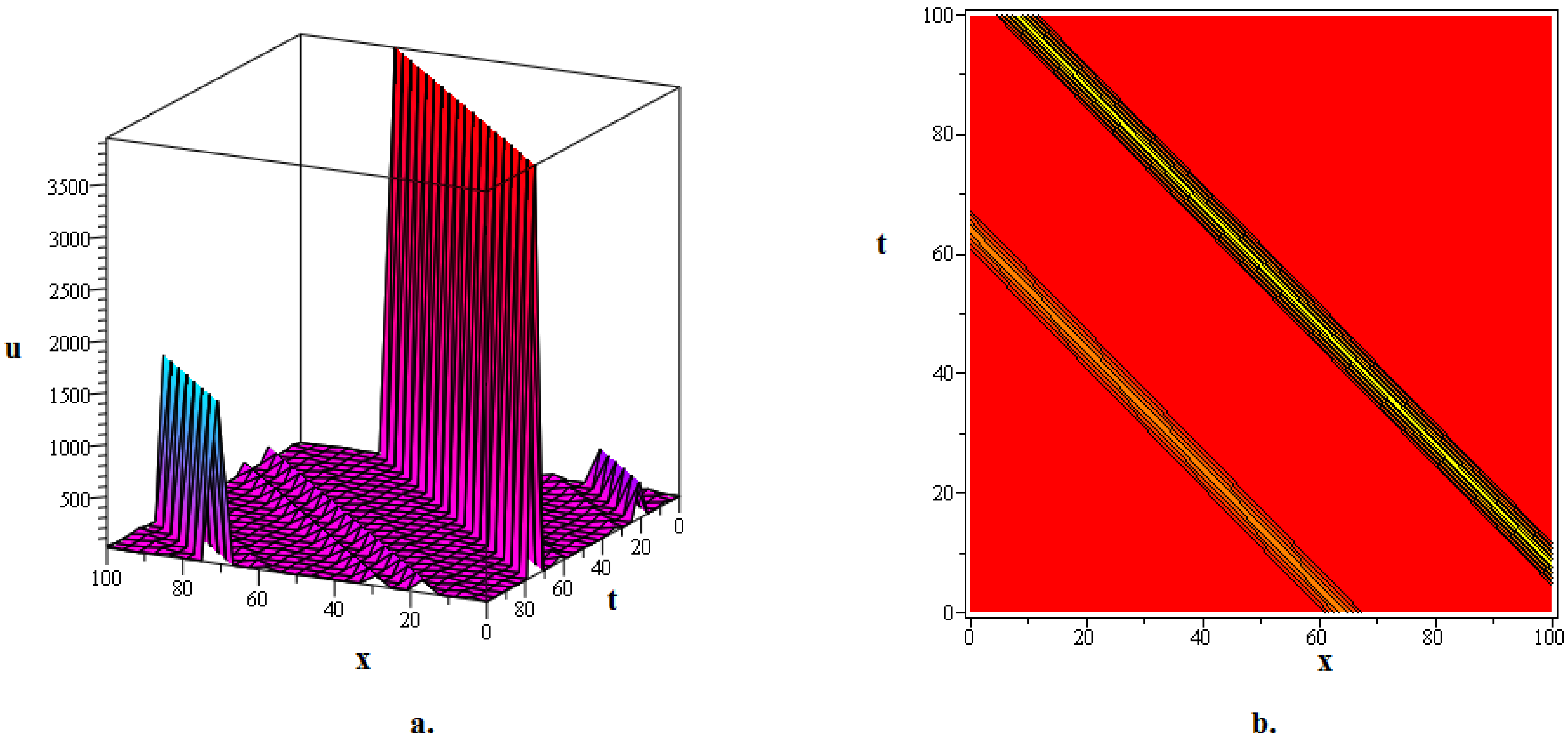
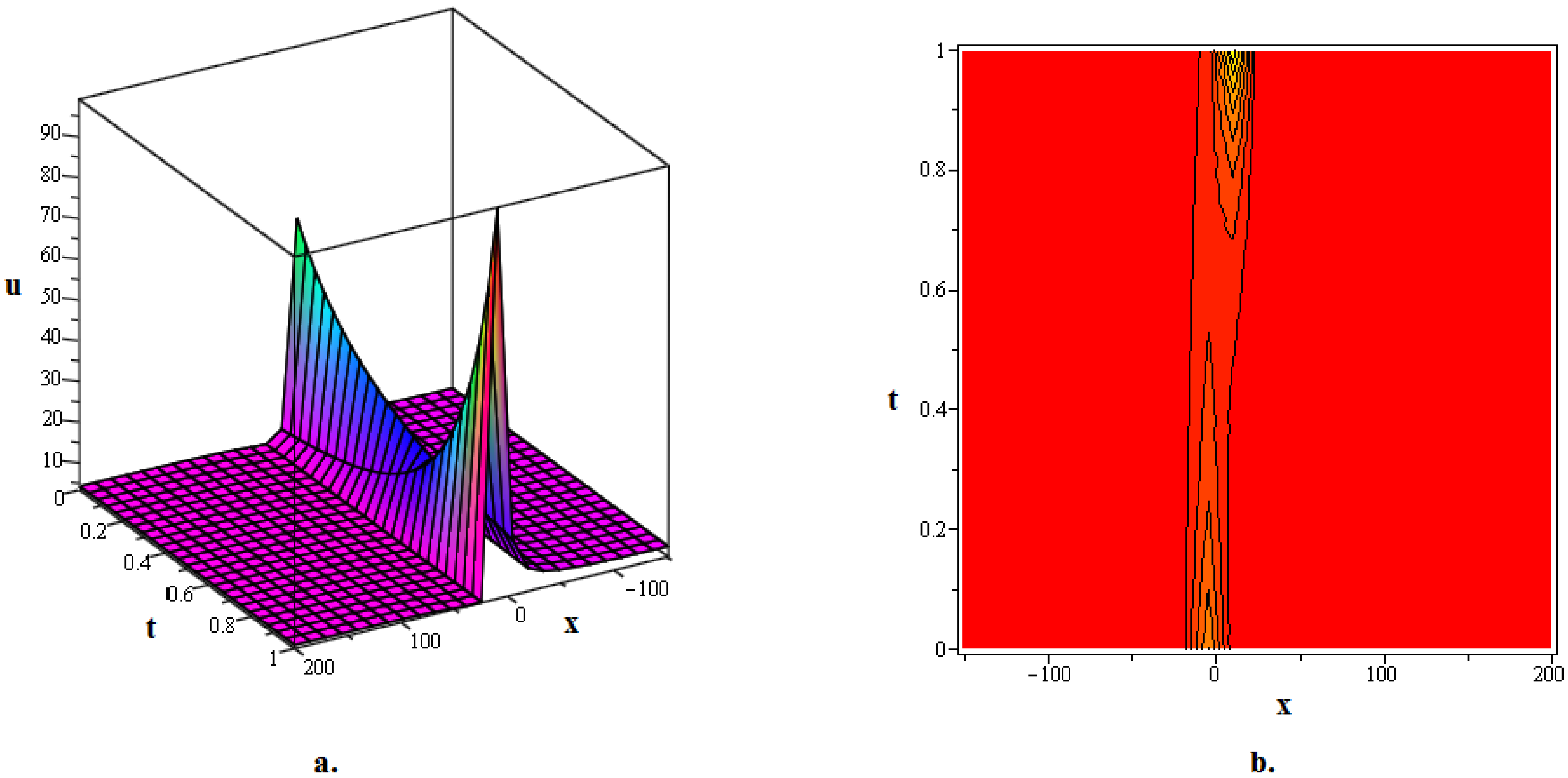
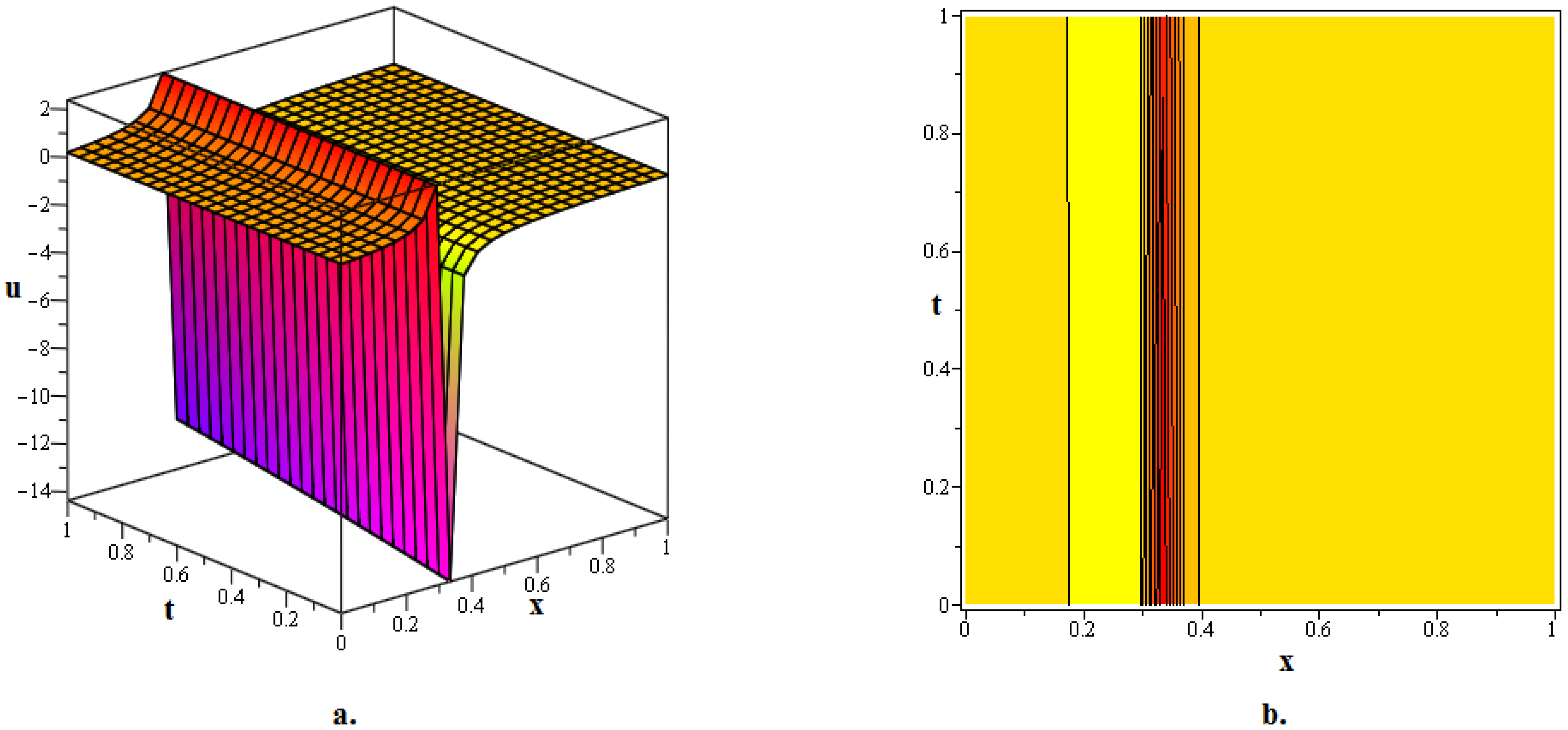
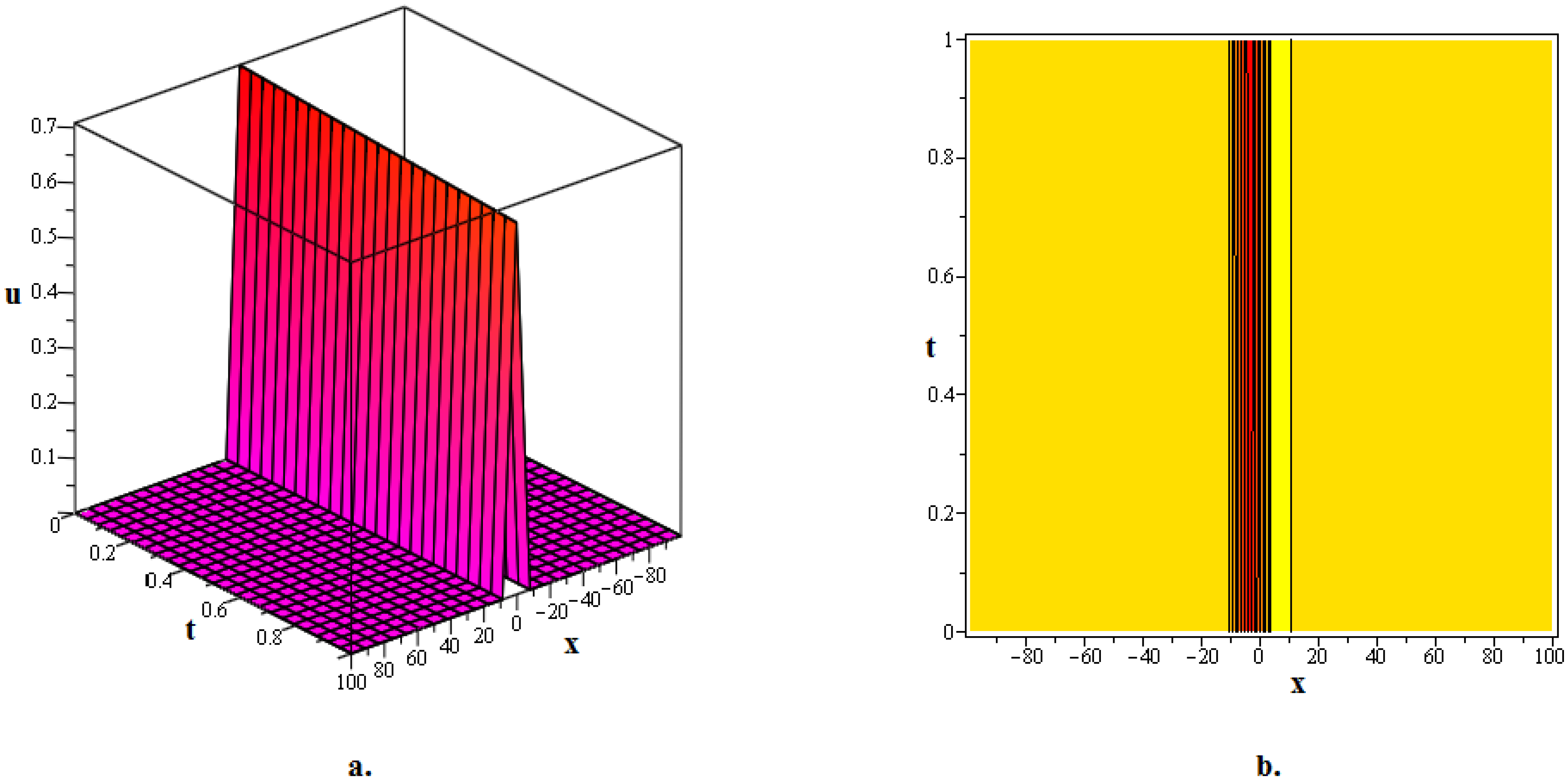
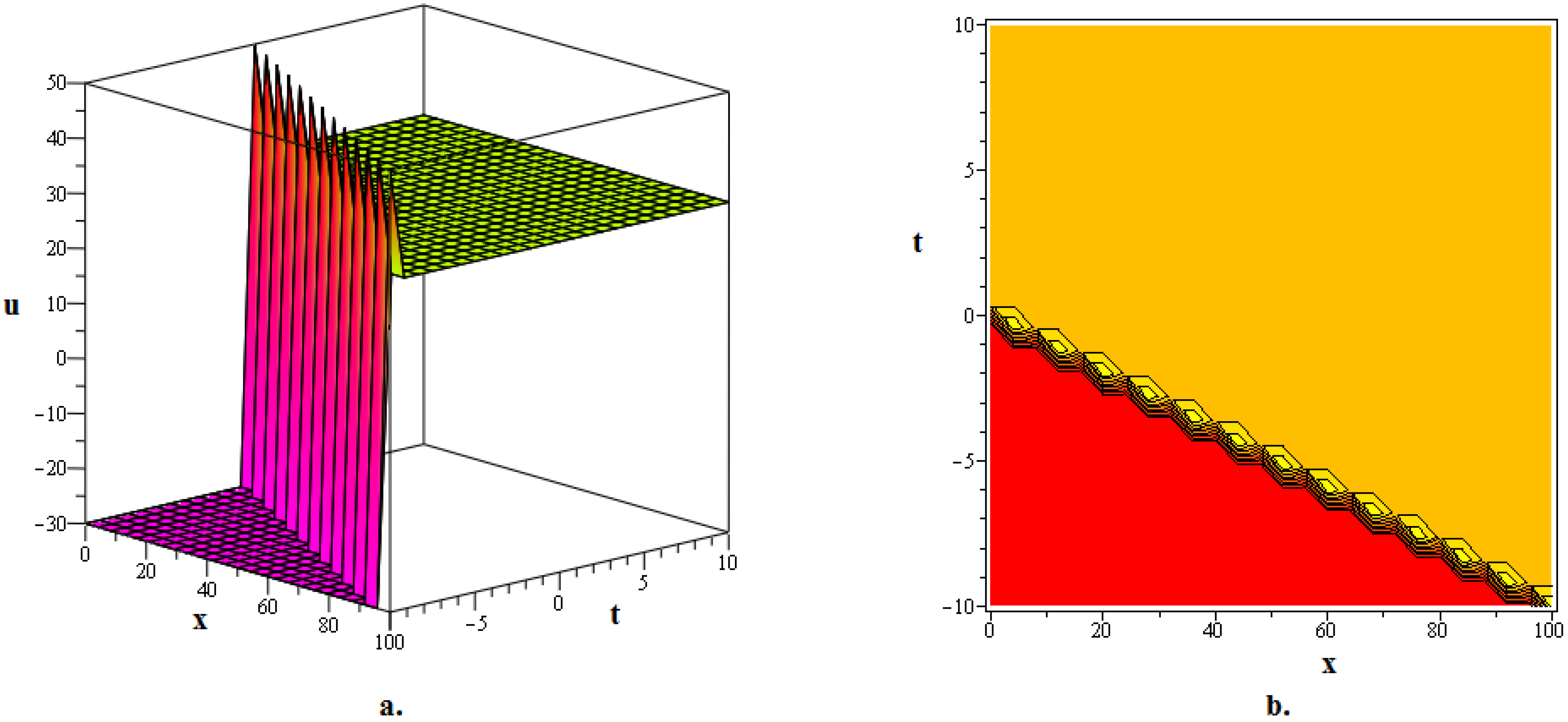
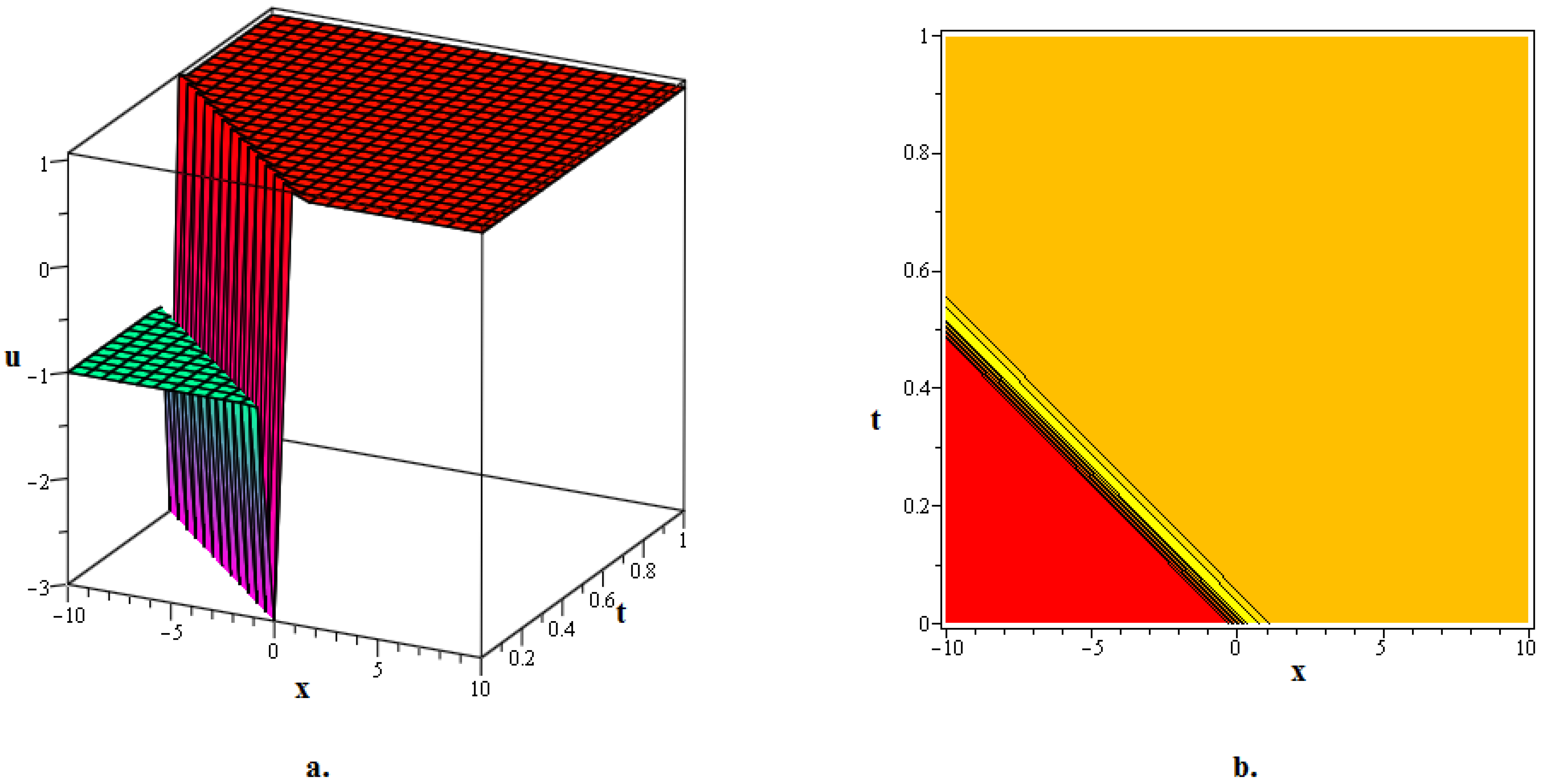
In this section, numerous kink soliton structures discovered in the framework of the two KGEs under investigation are visually displayed. Using the EDAM, we were able to identify and then demonstrate wave patterns in contour as well as in three-dimensional plots. The soliton solutions developed for the cubic and quadratic KGEs mostly include kink soliton profiles. When studying NPDEs associated with fluid dynamics, quantum field theory and optics, it is beneficial to examine solitons which are travelling waves that keep moving at a constant speed and formation. Such waveforms explain how scalar fields act within relativistic quantum physics when the KGEs are considered, like in vacuum state transition, kink solitons and sharp interfaces delineating fields with stable boundaries within scalar zones of different phases or amplitudes. By researching solitons to the KGEs, one is able to understand the basic characteristics of relativistic quantum mechanical systems and particles and the features of vacuums. Figure 1, The 3D and contour graphics of the bell-shaped dark soliton solution given in (20) are plotted for , , , , and . Figure 2, The 3D and contour graphics of the bright kink soliton solution given in (31) are plotted for , , , , and . Figure 3, The 3D and contour graphics of the bell-shaped kink soliton solution given in (62) are plotted for , , , , and . Figure 4, The 3D and contour graphics of the bright kink soliton solution given in (77) are plotted for , , , , and . Figure 5, The 3D and contour graphics of the bright kink soliton solution given in (92) are plotted for , , , , , , and . Kink soliton solutions, such as bright, dark, bell-shaped, cuspon and lump-like kink solutions, indicate different localised solutions or stimulations that result from nonlinear field concepts, corresponding to phenomena like topological deformity or particle-like structures in the context of KGEs and related fields like quantum field theory and quantum mechanics. Dark kinks show a localised dip in their profile, possibly signifying robust soliton-like features, whereas bright kinks show peaks or humps in their profile, possibly suggesting transitory or meta-stable excitations. Lump-type kinks compress on the field in pliable zones like lumps, whereas cuspon kinks have sharp cusp-like structures and frequently exhibit interesting dynamical behaviour. Bell-shaped kinks feature bell-like curves and can exhibit a range of behaviours depending on the circumstances. Such kinks are fascinating because of their ability to build robust or meta-stable localised frameworks, offer insight into the theory of field dynamics and play a role in breaking symmetry and phase shifts. Ultimately, these kinks will aid in our understanding of field theory, nonlinear interactions and the behaviour of physical systems in both the classical and quantum realms. Figure 6, The 3D and contour graphics of the twinning bright kink soliton solution given in (108) are plotted for . Figure 7, The 3D and contour graphics of the lump-like kink soliton solution given in (127) are plotted for , , , and . Figure 8, The 3D and contour graphics of the bright kink soliton solution given in (134) are plotted for , , , and . Figure 9, The 3D and contour graphics of the kink soliton solution given in (166) are plotted for , , , and . Figure 10, The 3D and contour graphics of the cuspon kink soliton solution given in (188) are plotted for , , , , .
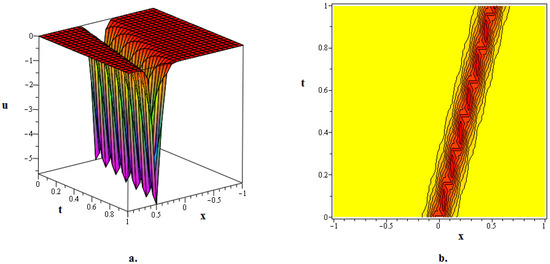
Figure 1.
The 3D and contour graphics of the bell-shaped dark soliton solution given in (20) are plotted for , , , , and .
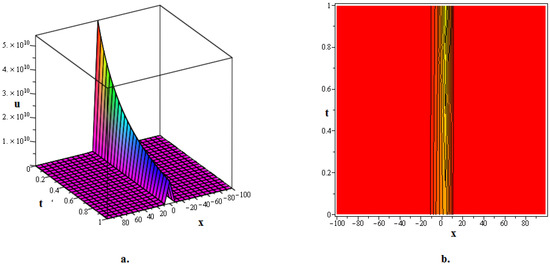
Figure 2.
The 3D and contour graphics of the bright kink soliton solution given in (31) are plotted for , , , , and .
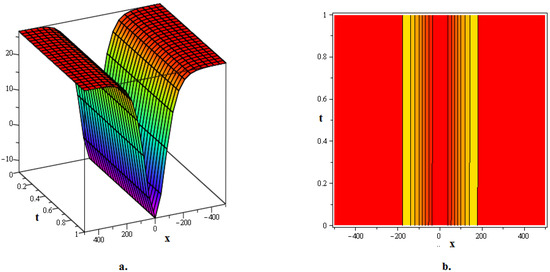
Figure 3.
The 3D and contour graphics of the bell-shaped kink soliton solution given in (62) are plotted for , , , , and .
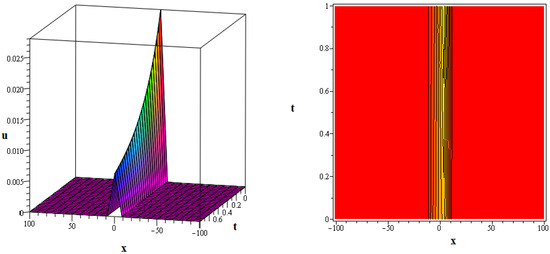
Figure 4.
The 3D and contour graphics of the bright kink soliton solution given in (77) are plotted for , , , , and .
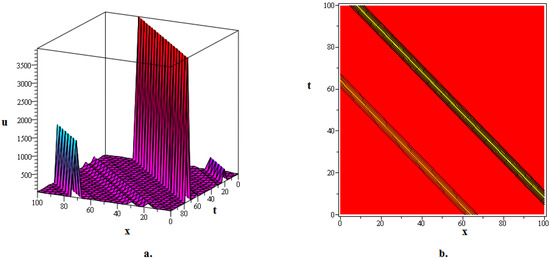
Figure 5.
The 3D and contour graphics of the bright kink soliton solution given in (92) are plotted for , , , , , , and .
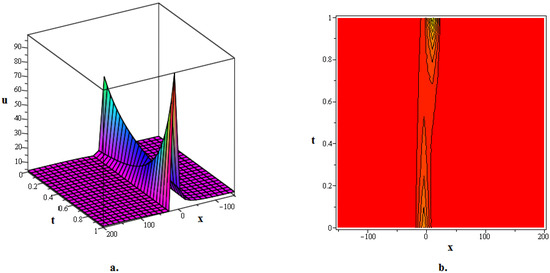
Figure 6.
The 3D and contour graphics of the twinning bright kink soliton solution given in (108) are plotted for .
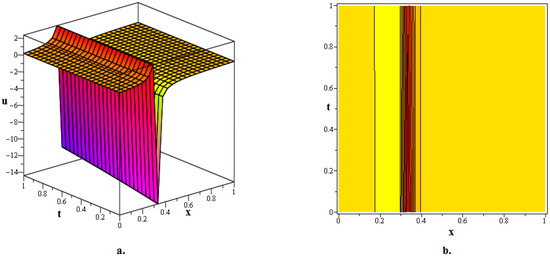
Figure 7.
The 3D and contour graphics of the lump-like kink soliton solution given in (127) are plotted for , , , and .
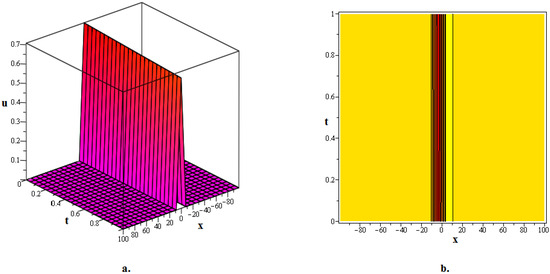
Figure 8.
The 3D and contour graphics of the bright kink soliton solution given in (134) are plotted for , , , and .
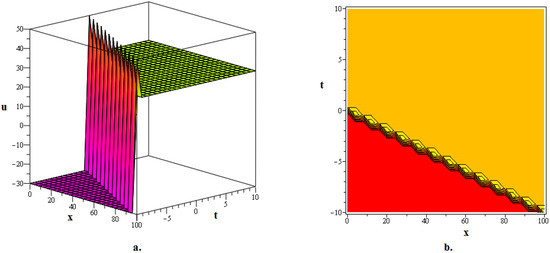
Figure 9.
The 3D and contour graphics of the kink soliton solution given in (166) are plotted for , , , and .
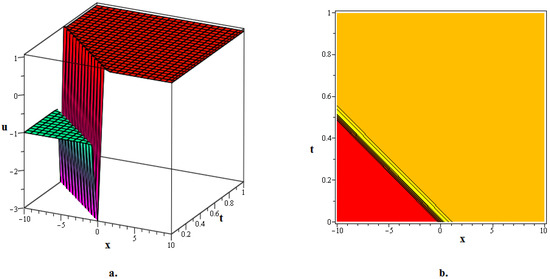
Figure 10.
The 3D and contour graphics of the cuspon kink soliton solution given in (188) are plotted for , , , , .
Furthermore, several analytical methods have been established in the literature to study soliton phenomena in nonlinear phenomena [33,34,35,36,37]. It is crucial to acknowledge that, while these approaches greatly advance our comprehension of soliton dynamics and assist in linking them to the theories that explain phenomena, they may also have limitations and shortcomings (like the seven common mistakes) [38,39]. Moreover, several methods of this kind depend on the Riccati equation [40,41]. A general class of exact solutions to the Riccati Equation (7) was systematically presented by [42]. Moreover, expression (6), for determining travelling waves, is precisely a rational function of the solution to the Riccati equation. Thus, the entire solution procedure of the study exemplifies the application of the transformed rational function method [43]. While there exist solitary solutions for the Riccati equation, these techniques are useful for examining soliton occurrences in nonlinear models [44]. Motivated by the above applications of the Riccati hypothesis, the present study used the EDAM, which incorporates the Riccati equation, to build and investigate soliton dynamics in two KGEs. This incorporation is helpful since it produces a large number of additional kink soliton solutions in five families of solutions, periodic, hyperbolic, rational, rational-hyperbolic and exponential, for the selected models. The solutions proposed here greatly expand our knowledge of soliton dynamics and allow us to relate the phenomena in the focused model to the underlying theories.
5. Conclusions
We employed the proposed EDAM to construct and analyse the transmission of kink solitons within the quadratic and cubic KGEs, two models that are frequently used in solid-state physics, nonlinear optics and quantum field theory. Several soliton solutions such as the dark kink, hump kink, lump-like kink, bright kink and cuspon kink soliton solutions were obtained in terms of trigonometric, hyperbolic, exponential and rational functions by converting the targeted models into NODEs under the circumstance where solutions are assumed to be of closed form. The contour and 3D plots helped us comprehend the behaviour of the transmitting soliton processes along with various kink soliton solutions. These graphs are directly linked to areas associated with the models discussed. As a result, these results enhanced our comprehension of nonlinear dynamics and temporal evolution processes and have implications for the comprehension of some related physical phenomena. While the EDAM contributed significantly to our comprehension of soliton dynamics and their linking with the targeted models, it is important to state that the proposed method fails when the greatest derivative and the nonlinear terms are not homogenously balanced. Despite this limitation, the present research demonstrates that the method employed in this study is very effective, adaptable and useful for nonlinear models across a variety of scientific fields. Furthermore, the future goal of this study is to delve into the stability analysis of solitons and the incorporation and impact of the fractional derivatives on solitons in the realm of targeted models.
Author Contributions
Conceptualization, S.A. and O.A.A.; methodology, M.A.; software, H.Z.; validation, M.M.A.-S.; formal analysis, S.A.; investigation, O.A.A.; resources, M.A.; data curation, H.Z.; writing—original draft preparation, M.M.A.-S. and S.A.; writing—review and editing, H.Z.; visualization, M.A.; supervision, O.A.A.; project administration, M.M.A.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the scientific research deanship at the University of Hail, Saudi Arabia, through project number (RG-23122).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Baloch, S.A.; Abbas, M.; Abdullah, F.A.; Rizvi, S.T.; Althobaiti, A.; Seadawy, A.R. Multiple Soliton Solutions of Generalized Reaction Duffing Model Arising in Various Mechanical Systems. Int. J. Theor. Phys. 2024, 63, 1–15. [Google Scholar] [CrossRef]
- Kragh, H. Equation with the many fathers. The Klein-Gordon equation in 1926. Am. J. Phys. 1984, 52, 1024–1033. [Google Scholar] [CrossRef]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011; Volume 47. [Google Scholar]
- Galehouse, D.C. Geometrical derivation of the Klein-Gordon equation. Int. J. Theor. Phys. 1981, 20, 457–479. [Google Scholar] [CrossRef]
- Schechter, M. The Klein-Gordon equation and scattering theory. Ann. Phys. 1976, 101, 601–609. [Google Scholar] [CrossRef]
- Weder, R.A. Scattering theory for the Klein-Gordon equation. J. Funct. Anal. 1978, 27, 100–117. [Google Scholar] [CrossRef][Green Version]
- Lundberg, L.E. Spectral and scattering theory for the Klein-Gordon equation. Commun. Math. Phys. 1973, 31, 243–257. [Google Scholar] [CrossRef]
- Tsukanov, V.D. Motion of a Klein-Gordon kink in an external field. Theor. Math. Phys. 1990, 84, 930–933. [Google Scholar] [CrossRef]
- Tariq, K.U.; Bekir, A.; Nisar, S.; Alp, M. Construction of new wave structures and stability analysis for the nonlinear Klein-Gordon equation. Phys. Scr. 2024, 99, 055220. [Google Scholar] [CrossRef]
- Onyenegecha, C.P.; Opara, A.I.; Njoku, I.J.; Udensi, S.C.; Ukewuihe, U.M.; Okereke, C.J.; Omame, A. Analytical solutions of D-dimensional Klein Gordon equation with modified Mobius squared potential. Results Phys. 2021, 25, 104144. [Google Scholar] [CrossRef]
- Belayeh, W.G.; Mussa, Y.O.; Gizaw, A.K. Approximate Analytic Solutions of Two-Dimensional Nonlinear Klein Gordon Equation by Using the Reduced Differential Transform Method. Math. Probl. Eng. 2020, 2020, 5753974. [Google Scholar] [CrossRef]
- Ahmadov, A.I.; Nagiyev, S.M.; Ikot, A.N.; Tarverdiyeva, V.A. Analytical solutions for the Klein Gordon equation with combined exponential type and ring-shaped potentials. Sci. Rep. 2024, 14, 5527. [Google Scholar] [CrossRef] [PubMed]
- Abdeljabbar, A.; Roshid, H.O.; Aldurayhim, A. Bright, dark, and rogue wave soliton solutions of the quadratic nonlinear Klein Gordon equation. Symmetry 2022, 14, 1223. [Google Scholar] [CrossRef]
- Huang, D.J.; Zhang, H.Q. The extended first kind elliptic sub-equation method and its application to the generalized reaction Duffing model. Phys. Lett. 2005, 344, 229–237. [Google Scholar] [CrossRef]
- Akter, J.; Akbar, M.A. Exact solutions to the Benney-Luke equation and the Phi-4 equations by using modified simple equation method. Results Phys. 2015, 5, 125–130. [Google Scholar] [CrossRef]
- Ebaid, A. Exact solutions for the generalized Klein-Gordon equation via a transformation and Exp-function method and comparison with Adomians method. J. Comput. Appl. Math. 2009, 223, 278–290. [Google Scholar] [CrossRef]
- Kudryavtsev, A.E. Solitonlike Solutions for a Higgs Scalar Field; Institute of Theoretical and Experimental Physics: Moscow, Russia, 1975. [Google Scholar]
- Strauss, W.; Vazquez, L. Numerical solution of a nonlinear Klein-Gordon equation. J. Comput. Phys. 1978, 28, 271–278. [Google Scholar] [CrossRef]
- Jiménez, S.; Vzquez, L. Analysis of four numerical schemes for a nonlinear Klein-Gordon equation. Appl. Math. Comput. 1990, 35, 61–94. [Google Scholar] [CrossRef]
- Dehghan, M.; Shokri, A. Numerical solution of the nonlinear Klein-Gordon equation using radial basis functions. J. Comput. Appl. Math. 2009, 230, 400–410. [Google Scholar] [CrossRef]
- Sarboland, M.; Aminataei, A. Numerical solution of the nonlinear Klein-Gordon equation using multiquadric quasi-interpolation scheme. Univers. J. Appl. Math. 2015, 3, 40–49. [Google Scholar] [CrossRef]
- Alsisi, A. Analytical and numerical solutions to the Klein Gordon model with cubic nonlinearity. Alex. Eng. J. 2024, 99, 31–37. [Google Scholar] [CrossRef]
- Nirmala, A.N.; Kumbinarasaiah, S. Numerical solution of nonlinear Hunter-Saxton equation, Benjamin-Bona Mahony equation, and Klein-Gordon equation using Hosoya polynomial method. Results Control. Optim. 2024, 14, 100388. [Google Scholar] [CrossRef]
- Denton, P.B. Techniques for solving static Klein-Gordon equation with self-interaction λϕ4 and arbitrary spherical source terms. Phys. Lett. B 2024, 855, 138860. [Google Scholar] [CrossRef]
- Bao, W.; Lu, Y.; Zhang, Z. Convergence Rates in the Nonrelativistic Limit of the Cubic Klein Gordon Equation. Siam J. Math. Anal. 2024, 56, 6822–6860. [Google Scholar] [CrossRef]
- Ali, I.; Ahmad, I. Applications of the nonlinear Klein/Sinh-Gordon equations in modern physics: A numerical study. Math. Model. Control. 2024, 4, 361–373. [Google Scholar] [CrossRef]
- Sadiya, U.; Inc, M.; Arefin, M.A.; Uddin, M.H. Consistent travelling waves solutions to the ar time fractional Klein-Gordon and Sine-Gordon equations through extended tanh-function approach. J. Taibah Univ. Sci. 2022, 16, 594–607. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.B.; Yousif, E.A. Solution of nonlinear space-time fractional differential equations using the fractional Riccati expansion method. Math. Probl. Eng. 2013, 2013, 846283. [Google Scholar] [CrossRef]
- Aldandani, M.; Altherwi, A.A.; Abushaega, M.M. Propagation patterns of dromion and other solitons in nonlinear Phi-Four (f 4) equation. Aims Math. 2024, 9, 19786–19811. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating symmetric soliton solutions for the fractional coupled konno-onno system using improved versions of a novel analytical technique. Mathematics 2023, 11, 2686. [Google Scholar] [CrossRef]
- Bilal, M.; Iqbal, J.; Ali, R.; Awwad, F.A.; Ismail, E.A. Exploring families of solitary wave solutions for the fractional coupled Higgs system using modified extended direct algebraic method. Fractal Fract. 2023, 7, 653. [Google Scholar] [CrossRef]
- Rizvi, S.T.; Ghafoor, S.; Seadawy, A.R.; Arnous, A.H.; AL, H. Exploration of solitons and analytical solutions by sub-ODE and variational integrators to Klein-Gordon model. Aims Math. 2024, 9, 21144–21176. [Google Scholar] [CrossRef]
- Díaz Palencia, J.L.; Roa González, J.; Sánchez Sánchez, A. Study of Solutions for a Degenerate Reaction Equation with a High Order Operator and Advection. Mathematics 2022, 10, 1729. [Google Scholar] [CrossRef]
- Ullah, I.; Shah, K.; Barak, S.; Abdeljawad, T. Pioneering the Plethora of Soliton for the (3+1)-Dimensional Fractional Heisenberg Ferromagnetic Spin Chain Equation. Phys. Scr. 2024, 99, 095229. [Google Scholar] [CrossRef]
- Ali, R.; Barak, S.; Altalbe, A. Analytical study of soliton dynamics in the realm of fractional extended shallow water wave equations. Phys. Scr. 2024, 99, 065235. [Google Scholar] [CrossRef]
- Ullah, I.; Shah, K.; Abdeljawad, T.; Alam, M.M.; Hendy, A.S.; Barak, S. Dynamics Behaviours of Kink Solitons in Conformable Kolmogorov-Petrovskii-Piskunov Equation. Qual. Theory Dyn. Syst. 2024, 23 (Suppl. 1), 268. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Seven common errors in finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3507–3529. [Google Scholar] [CrossRef]
- Navickas, Z.; Ragulskis, M. Comments on A new algorithm for automatic computation of solitary wave solutions to nonlinear partial differential equations based on the Exp-function method. Appl. Math. Comput. 2014, 243, 419–425. [Google Scholar] [CrossRef]
- Antonova, A.O.; Kudryashov, N.A. Generalization of the simplest equation method for nonlinear non-autonomous differential equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4037–4041. [Google Scholar] [CrossRef]
- Xiao, Y.; Barak, S.; Hleili, M.; Shah, K. Exploring the dynamical behaviour of optical solitons in integrable kairat-II and kairat-X equations. Phys. Scr. 2024, 99, 095261. [Google Scholar] [CrossRef]
- Ma, W.X.; Fuchssteiner, B. Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. Int. J. -Non-Linear Mech. 1996, 31, 329–338. [Google Scholar] [CrossRef]
- Ma, W.X.; Lee, J.H. A transformed rational function method and exact solutions to the 3+ 1 dimensional Jimbo-Miwa equation. Chaos Solitons Fractals 2009, 42, 1356–1363. [Google Scholar] [CrossRef]
- Navickas, Z.; Marcinkevicius, R.; Telksniene, I.; Telksnys, T.; Ragulskis, M. Structural stability of the hepatitis C model with the proliferation of infected and uninfected hepatocytes. Math. Comput. Model. Dyn. Syst. 2024, 30, 51–72. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).