Data Quality-Aware Client Selection in Heterogeneous Federated Learning

Abstract

Federated Learning (FL) enables decentralized data utilization while maintaining edge user privacy, but it faces challenges due to statistical heterogeneity. Existing approaches address client drift and data heterogeneity issues. However, real-world settings often involve low-quality data with noisy features, such as covariate drift or adversarial samples, which are usually ignored. Noisy samples significantly impact the global model’s accuracy and convergence rate. Assessing data quality and selectively aggregating updates from high-quality clients is crucial, but dynamically perceiving data quality without additional computations or data exchanges is challenging. In this paper, we introduce the FedDQA (Federated learning via Data Quality-Aware) (FedDQA) framework. We discover increased data noise leads to slower loss reduction during local model training. We propose a loss sharpness-based Data-Quality-Awareness (DQA) metric to differentiate between high-quality and low-quality data. Based on the DQA, we design a client selection algorithm that strategically selects participant clients to reduce the negative impact of noisy clients. Experiment results indicate that FedDQA significantly outperforms the baselines. Notably, it achieves up to a 4% increase in global model accuracy and demonstrates faster convergence rates.

1. Introduction

Federated Learning (FL) is a distributed machine learning approach that enables the utilization of decentralized data while maintaining user privacy in the nearby edge. Conventional FL downloads share global models to local clients, perform training on these models with the client’s unique data, upload the parameter updates, and then synthesize these updates server-side to refine the global model. Despite its promise, FL encounters significant obstacles stemming from statistical heterogeneity. This diversity in local datasets can precipitate skewed learning processes, where the resulting global model may exhibit suboptimal performance when generalized across the spectrum of client data distributions [1].

To tackle the challenges posed by statistical heterogeneity in federated learning, current approaches concentrate on issues of client drift and data heterogeneity, a consequence of the non-independent and identically distributed (non-IID) nature and imbalance of data across clients, including (1) creating a standard data sample set or using generative models to generate common data [2,3,4,5,6,7,8,9]; (2) training personalized local models tailored to the individual objectives of clients [10,11,12]; and (3) using external variables or partial training to bridge the differences between local and global models [13,14,15,16].

Despite the effectiveness of these existing methods in handling data heterogeneity, in real-world settings, the data can be unexpectedly diverse, containing low-quality data and extraneous elements outside the global model’s scope, which we refer to as noisy samples (Figure 1). Some studies have acknowledged the challenges posed by low-quality or noisy data, primarily focusing on label noise, such as [17,18,19,20]. In contrast, the issue of feature noise receives less consideration. For instance, in federated learning, malicious nodes may introduce adversarial examples detrimental to the training process, or some clients face covariate shifts due to environmental factors. As shown in Figure 1, the presence of noisy nodes not only substantially diminishes the accuracy of the global model ($61\%\to 58\%$) but also notably slows down its convergence rate (FedDQA, by selectively aggregating cleaner nodes, achieved a $60\%$ accuracy in just 10 rounds, whereas a random node selection strategy, which included a more significant number of noisy nodes, failed to reach $60\%$ accuracy even after 50 rounds).

Mitigating the impact of data heterogeneity caused by noisy datasets is crucial in federated learning. Assessing data quality and selectively aggregating updates from high-quality clients offers an intuitive solution to avoid the detrimental effects of noisy data on the global model. A straightforward approach to assessing client data quality is to evaluate each client’s local model using a clean, public dataset. However, this method requires a labeled dataset and consumes additional computational and bandwidth resources. Therefore, dynamically perceiving the quality of each client’s local data during the training process without introducing additional computations or data exchanges and selectively choosing high-quality participating clients is a highly challenging task.

In this paper, we introduce a Federatedlearning via Data Quality-Aware (FedDQA) framework. Through experimental analysis, we investigated the impact of local models on the global model in heterogeneous federated learning. A crucial discovery reveals that increased data noise leads to a slower loss reduction rate during the training process of local neural network models. The fluctuation of the loss function reflects the feature skew from the noisy data, which is formalized as loss sharpness. Based on this insight, we proposed a loss sharpness-based metric to differentiate between high-quality and low-quality data, called Data-Quality-Awareness (DQA) metrics. By strategically identifying the data noise level of the clients according to their DQA, such as light-noise, mixed-noise, and heavy-noise, the server utilizes data of superior quality for reducing the negative impact of noisy clients on the global model. In general, our approach makes the following contributions to the research on heterogeneous federated learning:

First, to the best of our knowledge, we are the first to investigate the feature noisy issue in heterogeneity federated learning. Through in-depth analysis, we discovered an inherent relationship between the loss values of local models and the level of data noise. Based on this insight, we designed a novel loss sharpness metric that dynamically perceives data quality during training.

Second, our proposed FedDQA framework senses the client’s data quality through the loss sharpness metric and strategically selects the participant client. The method can obtain perceptual results with fewer training rounds at the early stage of training and does not require the construction of any public datasets or data exchange.

Third, we conduct experiments on multiple datasets to validate the effectiveness of FedDQA. The results demonstrate that FedDQA achieves superior average accuracy by up to $4\%$ more than the baselines.

2. Related Works

2.1. Federated with Data Heterogeneity

Federated Learning (FL) has long been grappling with the issue of data heterogeneity, particularly in the context of non-independently and identically distributed (non-i.i.d) data. The prevalent aggregation technique, FedAVG [21], has demonstrated a performance degradation when applied to heterogeneous data across distinct local clients.

Investigations into non-i.i.d issues have primarily revolved around the skewness in label distribution, where non-i.i.d datasets are established by segregating an existing dataset based on labels [22]. Notable advancements have been made in addressing these limitations. For instance, FedProx [23] addressed data heterogeneity by allowing partial information aggregation and supplementing FedAVG with a proximal term. Additionally, FedMA [24] introduced an aggregation strategy for non-i.i.d data that disseminates the global model layer-wise. However, while numerous [25,26,27], these techniques often overlook the performance across diverse domains, focusing predominantly on developing an internal model.

Nevertheless, there has been a scarcity of solutions considering non-i.i.d issues stemming from feature shift, a common scenario in medical data collection from different instruments and natural images gathered in varying noisy environments. FedRobust [28] and SiloBN [29] represent recent attempts at addressing this problem, with the former assuming an affine distribution shift and the latter demonstrating improved robustness to data heterogeneity through local clients maintaining some untrainable batch normalization (BN) parameters. However, both approaches have their shortcomings. FedRobust’s effectiveness is hampered when the explicit affine transformation cannot be estimated. SiloBN, despite its empirical success, lacks a theoretical foundation. An alternative approach, FedBN [1], opts for strictly local retention of all BN parameters.

Recent studies have also explored unsupervised domain adaptation for target domain [30,31] and domain generalization on unseen domains [32]. However, these methods typically require exhaustive data collection in the target domains and make optimistic assumptions about performance on unknown domains.

2.2. Federated Client Selection

The objective of client selection in federated learning is to identify the most suitable clients for participation in each iterative cycle of the learning procedure. This crucial step is designed to effectively address and mitigate various challenges arising from heterogeneous conditions in the federated learning environment. Several client selection strategies have been developed in the literature to counteract the bias inherently introduced by non-IID.

One such approach is the experience-driven control framework, Favor [33], which innovatively recasts the problem of device selection for federated learning as a deep reinforcement learning problem. The aim is to cultivate an agent capable of learning an optimal selection policy. This methodology allows for actively selecting the most suitable subset of clients for participation in federated learning iterations, thereby improving model performance. In situations where the client data distribution is uneven, class imbalance can arise. Yang et al. [18] address this issue by developing an estimation scheme to discern the client class distribution. This is achieved by examining the gradient of client service updates while excluding the original data. In tandem with this, they designed a client selection algorithm geared towards minimum class imbalance, thereby enhancing global model convergence. FedCor [34] put forth a correlation-based client selection strategy. By utilizing a Gaussian process to model loss changes of clients, they select one client in each iteration to minimize the overall loss expectation. RIPFL [35] is an alternative perspective on client selection for collaborative training. The authors argue that beyond considering the individual characteristics of clients, it is vitally important to examine the synergy between clients. This holistic view can further optimize the collaboration among selected clients, enhancing the overall federated learning process.

3. Notations and Preliminaries

This section defines the data domain and model for heterogeneous federated learning.

3.1. General FL Framework

In the vanilla federated learning, the global objective across N clients is to obtain a global model ${\omega }^{*}$ training over the global dataset $\mathcal{D}={\bigcup }_{i\in \left[N\right]}{\mathcal{D}}_i$:

$${\omega }^{*}=arg\underset{w}{min}L\left(\omega \right)=\sum _{i=1}^N{\displaystyle \frac{\left|{\mathcal{D}}_i\right|}{\left|\mathcal{D}\right|}}{L}_i\left(\omega \right)=\sum _{i=1}^N{p}_i{L}_i\left(\omega \right)$$

(1)

where $\omega$ is the parameter of the global model, $L\left(\omega \right)$ is the empirical loss on the global dataset $\mathcal{D}$, each client i corresponds to a private training data ${\mathcal{D}}_i$ and a local model ${\omega }_i$. A sample-label pair is denoted as $(\mathbf{x},y)$ where $\mathbf{x}$ is the raw input data point and y is its label. $\left|{\mathcal{D}}_i\right|$ is the number of data samples on $\mathcal{D}$, $L_i\left(\omega \right)={\mathbb{E}}_{(\mathbf{x},y)\in D_i}l(\omega ;(\mathbf{x},y))$ is the local empirical loss on the dataset ${\mathcal{D}}_i$ of client i.

In light of privacy concerns and communication restrictions prevalent in the federated learning (FL) paradigm, algorithms often incorporate the presumption of partial client participation and execute localized model updates. Specifically, during the communication round t, a subset of clients, denoted as ${\mathcal{K}}_t$, is selected from the total client set N. The size of this subset, $|{\mathcal{K}}_t|=C$, is less than or equal to the total number of clients N.

Only the clients within ${\mathcal{K}}_t$ are chosen to receive the global model weights ${\omega }_t$ and independently conduct training iterations on their local datasets. Upon completion of local training, the server retrieves the updated models from the selected clients. It aggregates them, typically utilizing a weighted averaging approach [22], to derive the updated global model ${\omega }_{t+1}$.

This procedure can be formally articulated as follows:

$$\begin{array}{cc}\hfill {\omega }_i^{t+1}& ={\omega }^t-{\eta }_t\tilde{\nabla }{l}_i\left({\omega }^t\right)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\omega }^{t+1}& ={\displaystyle \frac{1}{C}}\sum _{i\in {\mathcal{K}}_t}{\omega }_i^{t+1}\hfill \\ \hfill & ={\omega }^t-{\displaystyle \frac{{\eta }_t}{C}}\sum _{i\in {\mathcal{K}}_t}\tilde{\nabla }{l}_i\left({\omega }^t\right),\hfill \end{array}$$

(3)

Here, ${\eta }_t$ represents the learning rate, and $\tilde{\nabla }{l}_i\left({\omega }^t\right)$ is interpreted as the equivalent cumulative gradient [28] in the t-th communication round. More precisely, for an arbitrary optimizer operating on client i, it generates $\Delta w_i^{t,e}=-\eta d_i^{t,e}$ as the local model update at the e-th epoch within the specific round. The cumulative gradient is subsequently computed as $\tilde{\nabla }{l}_i\left(w^t\right)={\sum }_e{d}_i^{t,e}$.

In the pursuit of preserving data privacy and preventing potential data leakage, every client must maintain the confidentiality of its raw data, refraining from sharing it with other clients. The Federated Averaging (FedAVG) algorithm, is a strategy proposed to facilitate cooperative global model training across multiple clients, orchestrated by a central server, while ensuring rigorous data privacy measures [21].

3.2. Heterogeneous Federated Learning

Data Heterogeneity: the data distribution of client i is denoted as $P_i$. For any client i and client j, the data heterogeneity refers to the $P_i\left(\mathbf{x}\right)\ne P_j\left(\mathbf{x}\right)$ while $P_i\left(y\right|\mathbf{x})=P_j\left(y\right|\mathbf{x})$.

Recent studies have demonstrated the existence of a divergence between the local model trained by each client on its dataset and the global model derived directly from the aggregated dataset [17,22]. If this inter-client drift is not addressed, the server is prone to producing a skewed aggregation of the global model. Federated learning faces the challenge of accommodating heterogeneous data distributions among clients. FedAVG suffers significantly degraded performance when facing non-independent and identically distributed (non-IID) data in federated settings. This underscores that neglecting local drift can lead the global model astray from the optimal solution.

Figure 2 provides a toy example where local divergence arising from disparate local data partitions can bias the aggregated outcome of FedAVG. We assume there is a non-linear transformation function f, for instance, $sigmoid$ activation layer in the model. There are three clients with local parameters named ${\theta }_1,{\theta }_2,{\theta }_3$. ${\omega }_c$ is the optimal model parameter, ${\omega }_{12}$ (${\omega }_{23}$) is the global model parameters aggregated by ${\theta }_1$ and ${\theta }_2$ (${\theta }_2$ and ${\theta }_3$) using FedAVG. x is the input data point, and the outputs on client 1 are $y_1=f({\theta }_1,x)$ and $y_2=f\left({\theta }_{2}x\right)$ on client 2. Although $f({\omega }_{12},x)\ne {\displaystyle \frac{y_1+y_2}{2}}\ne f({\omega }_c,x)$, the figure illustrates that compared to ${\omega }_{23}$, ${\omega }_{12}$ is closer to the optimal global model parameter.

Therefore, we can infer that the existence of data heterogeneity among clients can result in the deviation of aggregated global parameters from the optimal ones. However, the effect varies depending on the client selection strategy employed, indicating that different strategies may lead to different outcomes. For example, choosing ${\omega }_{12}$ may converge faster than ${\omega }_{23}$.

We choose the Emnist dataset [36] and the FedAVG method for a simple experiment to verify the impact of noisy clients in the federated aggregation. We split the training dataset into 20 parts in the form of independent homogeneous distributions. In the natural setting, clients do not undergo any additional processing. For the noisy setting, different levels of Gaussian noise $\Delta$ are added to each copy of the data and assigned to different clients i, totaling 20 clients. Specifically, $\Delta \sim N(\mu =0,{\sigma }^2)$, when $\sigma \sim i\times {\displaystyle \frac{1}{C}},i\in (1,|C\left|\right)$.

Suppose we know in advance how noisy the clients are in this experiment. Therefore, when performing federated learning, we adopt a different client selection strategy, where Top $k\%$ denotes the selection of the top $k\%$ of client IDs in each round of aggregation, and Random $k\%$ denotes the random selection; the experimental results are shown in Figure 2b. According to the experimental results, it can be seen that in the case of nature’s data distribution, the more clients are aggregated in each round, the better the generalization and eventually higher accuracy, while randomly selecting $50\%$ clients for aggregation in each round does not make much difference to the effect from the effect of aggregating the top $90\%$. However, for a noisy data environment, aggregating too many clients means aggregating to those heavily noisy clients, which results in lower accuracy. Random aggregation still cannot avoid aggregating to heavily noisy clients.

4. Loss Sharpness in Federated Learning

Suppose there exist data ${\mathcal{D}}_i$, a model inference process $f({\omega }_i,{\mathbf{x}}_i)=y_i^{\prime }$ for client i, where the model weights ${\omega }_i$ come from the supervised training process: $T\left({\mathcal{D}}_i\right)\to {\omega }_i$, then for this training process, there is a corresponding loss function: $l({\omega }_i;({\mathbf{x}}_i,y_i))\in R^{+}$, abbreviated as $l({\omega }_i,{\mathcal{D}}_i)$.

We let ${\mathcal{D}}_i$ be the IID testing dataset, and there is an inference accuracy $ACC({\omega }_i,{\mathcal{D}}_i)$:

$$ACC({\omega }_i,{\mathcal{D}}_i)={\displaystyle \frac{\left|\right\{({\mathbf{x}}_j,y_j)\in {\mathcal{D}}_i|f(\omega ,{\mathbf{x}}_j)=y_j\}|}{n}}$$

(4)

Assuming that there is noise $\Delta ={\left\{{\delta }_j\right\}}_{j=1}^n,{\delta }_j\sim R^{+}$, then the data ${\mathcal{D}}_i$ with noise can be expressed as ${\mathcal{D}}_i^{\prime }$:

$${\mathcal{D}}_i^{\prime }={\mathcal{D}}_i+\Delta =\{(\mathbf{x}+\delta ),y^{\prime }\}$$

(5)

For noisy data, there is a neural network model training process $T\left({\mathcal{D}}_i^{\prime }\right)\to {\omega }_i^{\prime }$ and a corresponding inference process $f({\omega }_i^{\prime },{\mathbf{x}}^{\prime })=y^{″}$.

As a supervised machine learning training process, the model parameters obtained from the training process are an abstraction of the training data space. An intuitive understanding is that the closer the feature distribution of the test dataset is to that of the training dataset, the higher the inference accuracy of the model. Conversely, a large amount of out-of-distribution data in the test data poses a challenge to model inference. However, the noisy data change the data feature distribution of the original dataset to a certain extent, i.e., feature skew occurs for the noisy data. For the original data $\mathbf{x}$, the inference results of the model $f({\omega }_i,\mathbf{x})$, which is trained with the same distribution of the data, are better than the model $f({\omega }_i^{\prime },\mathbf{x})$, which is trained with the noisy data, i.e., $ACC({\omega }_i^{\prime },\overline{{\mathcal{D}}_i})$ is better than the model $f({\omega }_i^{\prime },\mathbf{x})$ trained with the noisy data, i.e., $ACC({\omega }_i,\overline{{\mathcal{D}}_i})>ACC({\omega }_i^{\prime },\overline{{\mathcal{D}}_i})$. Similarly, for the model $f(\omega ,\mathbf{x})$, inference using data x with the same distribution yields better inference results than model inference $f({\omega }_i,{\mathbf{x}}^{\prime })$ using noisy data ${\mathbf{x}}^{\prime }$, i.e., $ACC({\omega }_i,\overline{{\mathcal{D}}_i})>ACC({\omega }_i,{\overline{{\mathcal{D}}_i}}^{\prime })$. To obtain better inference results in the natural data space, federated learning tends to select models obtained from clients’ training of data whose feature skew is less deviated.

The accuracy of the model inference is affected due to the noise that makes the original data feature skew. Since there is some positive correlation between test accuracy and loss function value, such a feature skew may also be reflected in the matter and volatility of the loss function. We verify such a phenomenon using a simple experiment, as shown in Figure 3. In the figure, the loss function values of different noisy data show other distribution characteristics during the training process compared with natural data.

In the following, we use formal definitions to describe this phenomenon. First, the loss function for one training epoch can be denoted as follows:

$$L_i({\omega }_i,{\mathcal{D}}_i)={\mathbb{E}}_{(\mathbf{x},y)\in D_i}l(\omega ;(\mathbf{x},y))$$

(6)

For the noisy data and the corresponding model, the value of the loss function is denoted as follows:

$$L_i({\omega }_i^{\prime },{\mathcal{D}}_i^{\prime })={\mathbb{E}}_{(\mathbf{x},y)\in D_i}l(\omega ;(\mathbf{x}+{\mathit{\delta }}^{\prime },y))$$

(7)

Assuming here that the loss function l measures the difference between the inference result and the actual value, then, when $f({\omega }_i,\mathbf{x})=y$, there is $l\left(f\right(\omega ,\mathbf{x}),y)\to 0$.

$$L_i({\omega }_i,{\mathcal{D}}_i)=\sim {\displaystyle \frac{1}{ACC({\omega }_i,{\overline{\mathcal{D}}}_i)}}$$

(8)

Then, for the training process of the model, there is

$$L_i({\omega }_i^{\prime },{\mathcal{D}}_i^{\prime })>L_i({\omega }_i^{\prime },{\mathcal{D}}_i)>L_i({\omega }_i,{\mathcal{D}}_i)$$

(9)

Let e epochs be trained at a time. The loss value of training is written as follows:

$${\mathcal{L}}_i=\{L_i^1,L_i^2,\dots ,L_i^e\}$$

(10)

We compute the mean value of the loss function variation process L as follows:

$$Mean\left({\mathcal{L}}_i\right)={\displaystyle \frac{1}{e}}\sum _{j=1}^e{L}_i^j$$

(11)

The standard deviation is

$$Std\left({\mathcal{L}}_i\right)=\sqrt{{\displaystyle \frac{1}{e}}{\displaystyle \sum _{j=1}^e}{(L_i^j-Mean\left({\mathcal{L}}_i\right))}^2}$$

(12)

When noise is added uniformly to all data, it is more difficult to perform accurate inference with noisy data than raw data. As a result, noisy data with lower inference accuracy may have a higher loss function mean. At the same time, the noisy data are less cohesive, which may lead to a slower model optimization process, i.e., having a lower loss function standard deviation. We describe this phenomenon using the coefficient of variation of loss, i.e., the sensation of loss sharpness:

$$\begin{array}{cc}\hfill CoV\left({\mathcal{L}}_i({\omega }_i,{\mathcal{D}}_i)\right)& ={\displaystyle \frac{Std\left({\mathcal{L}}_i({\omega }_i,{\mathcal{D}}_i)\right)}{Mean\left({\mathcal{L}}_i({\omega }_i,{\mathcal{D}}_i)\right)}}\hfill \\ \hfill & >{\displaystyle \frac{Std\left({\mathcal{L}}_i({\omega }_i^{\prime },{\mathcal{D}}_i^{\prime })\right)}{Mean\left({\mathcal{L}}_i({\omega }_i^{\prime },{\mathcal{D}}_i^{\prime })\right)}}\hfill \\ \hfill & =CoV\left({\mathcal{L}}_i({\omega }_i^{\prime },{\mathcal{D}}_i^{\prime })\right)\hfill \end{array}$$

(13)

Loss sharpness is a metric used to assess the quality of data on each client in federated learning by analyzing the variability of the loss function during local training. It is based on the observation that the rate and variability at which the loss decreases during training can indicate the presence of noise in the data. In federated learning, data quality is assessed across clients without requiring direct access to their datasets. It leverages the natural training dynamics of the model. High loss sharpness signifies that the model is effectively learning from clean, informative data, as evidenced by significant fluctuations and reductions in loss during training. However, low loss sharpness indicates potential issues with the data, such as noise or corruption, causing slow and steady loss reduction without substantial learning progress.

By incorporating loss sharpness into the client selection process, the FedDQA framework enhances the federated learning process by improving global model quality and prioritizing client updates with high-quality data, leading to a more accurate and generalizable global model. Furthermore, focusing on clients contributing valuable learning signals helps the global model converge more quickly. The metric relies solely on loss values available during standard training, avoiding the need for additional data exchange or computations.

5. FedDQA

The nature of the loss sharpness is only significant at the beginning of training. As updating proceeds, the coefficient of the loss is likely to gradually converge to a smooth state due to over-fitting, regardless of the data quality. In addition, for the federated learning process, the loss may re-emerge with large fluctuations after aggregation with the global model because of individualized differences. To better perceive the changes in the loss distribution at the beginning of training, we set the slow-start loss threshold $ϵ>0$. At the beginning of the updating, the federation system waits for the loss function value of all clients to be less than $ϵ$ to start model aggregation and federation learning. To avoid individual clients failing to reach the threshold for a long time, it is also agreed that federation learning should be started automatically after a specific time (training epochs). Then, for client k, there is a sequence of loss values when the threshold is reached:

$${\mathcal{L}}_i^{*}=\{L_i^1,\dots ,L_i^{\lambda }|L_i^{\lambda }\ge ϵ,L_i^{\lambda +1}<ϵ\}$$

(14)

At the same time, we calculate the number of epochs $\lambda$ at which the loss reaches the threshold $ϵ$ and the constants ${\mu }_1,{\mu }_2$ as additional constraints to amplify the volatility of the change in the loss to obtain the final DQA formula:

$$Q_i=({\displaystyle \frac{CoV\left({\mathcal{L}}_i^{*}\right)}{\lambda }}{)}^{{\mu }_1}\times {\mu }_2$$

(15)

In the federated learning process, client selection relates to the quality of the global model and affects the synchronization mechanism and network transmission. Due to network instability, client dropouts, etc., assuming all clients are synchronized for aggregation is unrealistic. Usually, some federated frameworks take a randomly selected set of clients for aggregation or randomly arrange some clients to drop out. When network resources are limited, choosing a limited number of high-quality clients also helps to save transmission resources and improve training efficiency. Here, we give the method of selection of clients based on the variation in loss sharpness. Suppose a set of clients $\mathcal{K}={\left\{c_i\right\}}_{i=1}^n$ exists. Then, the group of loss sharpness of $\mathcal{K}$ in the tth updating can be obtained according to:

$$Q_{\mathcal{K}}={\left\{Q_i\right\}}_{i=1}^n$$

(16)

where $Q_i$ is the DQA of client $c_i$. ordering $Q_{\mathcal{K}}$ yields:

$${\mathcal{Q}}_{\mathcal{K}}=<Q_u,Q_v,\dots >,Q_u\ge Q_v,u\in [1,n],v\in [1,n]$$

(17)

The server aggregates the clients based on the ${\mathcal{Q}}_{\mathcal{K}}$ order. In contrast, the number of clients participating in each round of aggregation can be dynamically decided in conjunction with the network environment.

The $Q_i^t$ computation occurs on the server side to save the client’s computational resources and standardize the metric. Clients only need to send the server the first round ($t=1$) of DQA value $Q_i^1$. This subsection describes a client selection process based on a dynamic threshold to make the client selection more flexible, as shown in Figure 4. The process is motivated by the consideration that not all low-quality clients are harmful. In general, mild noise does not harm the model’s knowledge acquisition and even helps increase the model’s generalization. Only those heavy noises have the potential to poison the model and impair the reasoning of the aggregated model. Therefore, we first sort ${\mathcal{Q}}_{\mathcal{K}}$ according to quality perception in the client selection. Different selection probabilities $P_i$ are assigned to clients with other degrees or types of noise, e.g., by posting a higher selection probability to clients with slight noise; such clients have a higher likelihood of being selected in the aggregation process. In addition, the computationally obtained data quality perception $Q_i$ will also be used as a weighting parameter in the computational process of model aggregation.

According to the above conventions, FedDQA can be described as Figure 4.

For local updating $F^L$, there are:

• L1: Local training. Train local model ${\omega }_k$ by $D_i$.
• L2: Data quality-aware with loss sharpness. Perceive client data quality during training and obtain the quality score $Q_i$.

Remote updating $F^R$, involves the following:

• R1: Client selection. Client selection using quality score ${\mathcal{Q}}_C\to {\mathcal{P}}_C$ to obtain a subset of users $\mathcal{K}$.
• R2: Model aggregation. A global model is aggregated based on client subset $\mathcal{K}$.
• R3: Global model broadcast. Distribute the global model parameters obtained from aggregation to clients for the next round of updating.

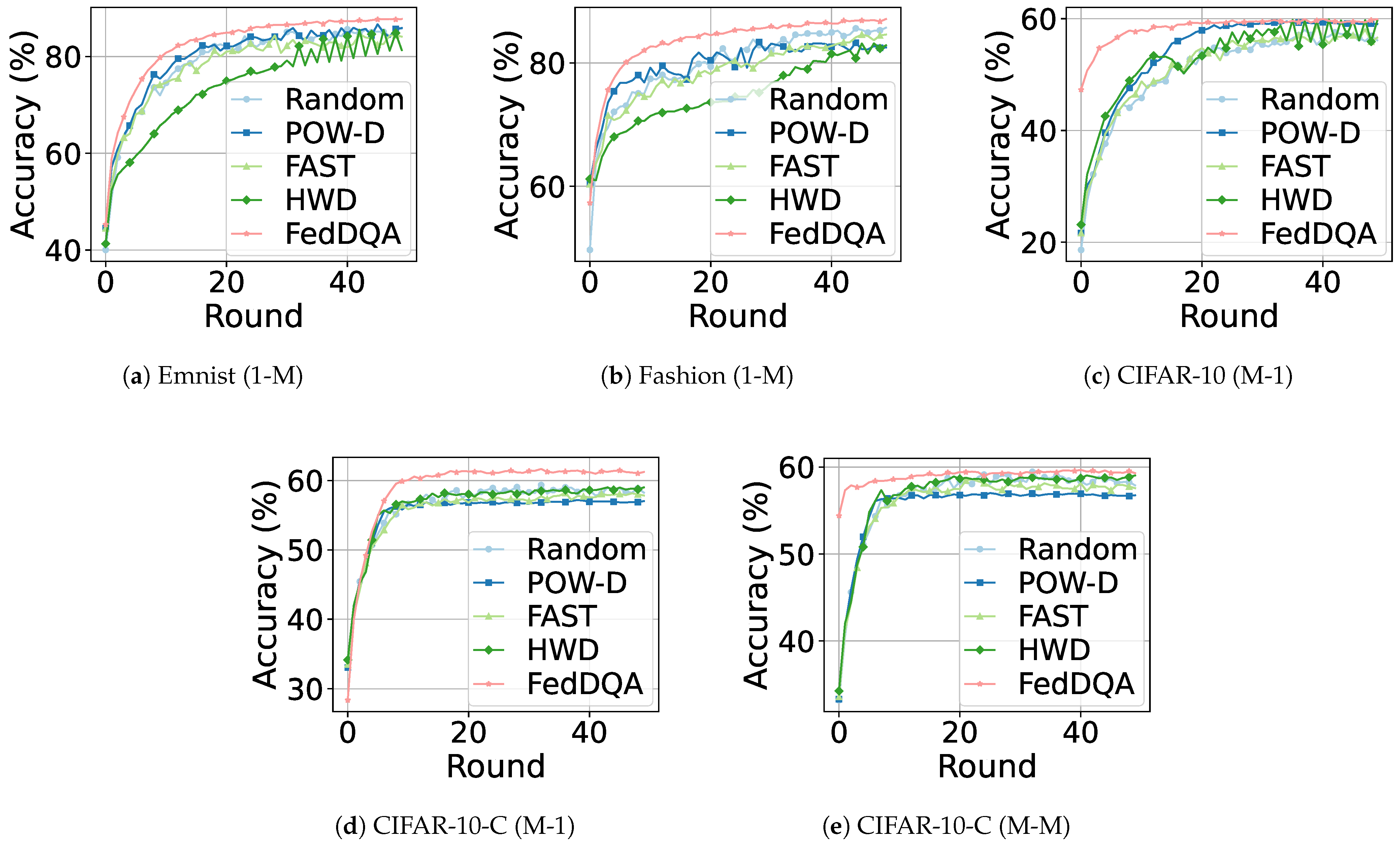
6. Performance Evaluation

6.1. Evaluation Setup

6.1.1. System Settings and Datasets

This section uses simulation experiments to validate the application of FedDQA based on loss sharpness-aware in noisy data space. First, for the system model, $n=20$ clients are used to participate in federated learning. A total of ${\displaystyle \frac{n}{2}}$ clients participate in model aggregation for each round of updating. Simultaneous updating mode is used, with 5 local and 50 global updating rounds. The datasets used are the grayscale image datasets Emnist (26 classes) [36] and Fashion (10 classes) [37], the color image dataset CIFAR-10 (10 classes) [38], and the noisy color image dataset CIFAR-10-C (10 classes) [39]. Among them, CIFAR-10-C contains 19 different kinds of noise data, namely: ‘gaussian_noise’, ‘shot_noise’, ‘speckle_noise’, ‘impulse_noise’, ‘defocus_blur’, ‘gaussian_blur’, ‘motion_blur’, ‘zoom_blur’, ‘snow’, ‘fog’, ‘brightness’, ‘contrast’, ‘elastic_transform’, ‘pixelate’, ‘jpeg_compression’, ‘spatter’, ‘saturate’, ‘frost’, ‘glass_blur’. Each noise corresponds to 1 to 5 noise levels. These datasets have many applications in federated learning and data noise studies [40,41].

For grayscale images, a simple 2-layer fully connected model is used. For color images, a 2-layer CNN model is used. These simple models are more suitable to be deployed in smart IoT devices or mobile devices. The learning rate is $0.1$, and the batch size is 10. Slow-start selection parameters for the FedDQA algorithm are as follow: $\beta =0.7, \lambda =2.0$. After slow-start client selection, FedDQA only needs to select the client in the $70\%$. Ideally, real-world scenarios with unstable network connections and device resource constraints make it challenging to maintain synchronized model aggregation over long periods. As analyzed in Section 3, aggregating low-quality local models can lead to slow or non-convergence of the global model. In our experiments, client selection strategies prioritize aggregating models trained on high-quality data, resulting in a biased and non-fair aggregation approach. To confirm that the global model is derived from clients with high-quality data, we use natural, noise-free test data for evaluation.

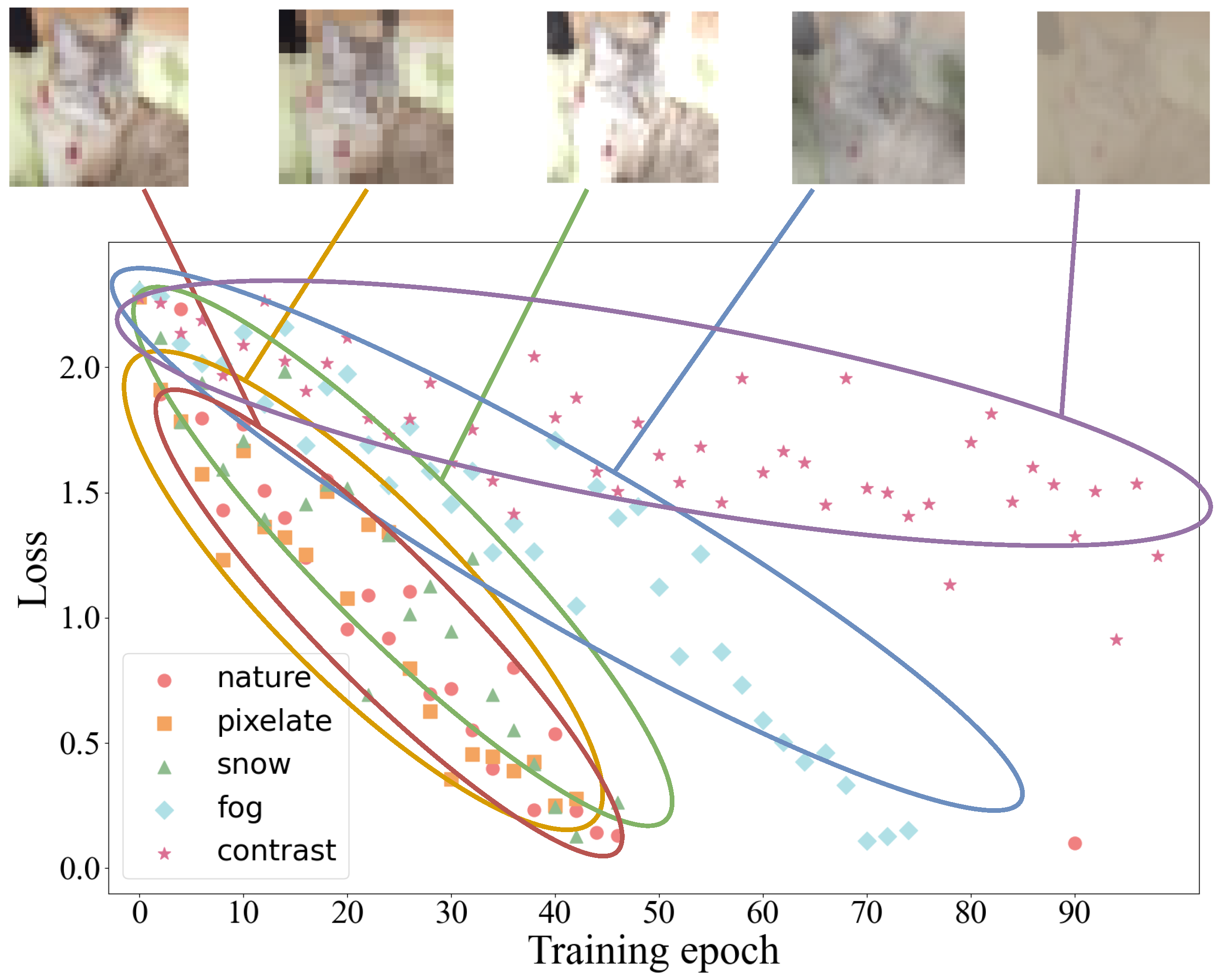
6.1.2. Noisy Environment Setup

In the noisy environment setup, we consider three noise scenarios as follows:

(1)

Single noise type and multiple noise levels (1-M). We choose the Emnist and Fashion datasets. We split the training dataset into n parts as independent homogeneous distributions and add different Gaussian noise $\Delta$ levels to each data part, assigning them to different clients i. Specifically, there are $\Delta \sim N(\mu =0,{\sigma }^2)$, when $\sigma \sim i\times {\displaystyle \frac{1}{C}},i\in (1,|C\left|\right)$.

(2)

Multiple noise types and single noise level (M-1). We choose the CIFAR-10 and CIFAR-10-C datasets. Among them, the noiseless natural data of client0 comes from the dataset CIFAR-10. client1∼client19 each comes with one different type of noise data, and the data come from 19 types of noise (level 5) in CIFAR-10-C.

(3)

Multiple noise types and noise levels (M-M). We choose the CIFAR-10 and CIFAR-10-C datasets. Among them, the noiseless natural data of client0 comes from the dataset CIFAR-10. client1∼client9 each carries a different type of noise data, and the data come from 9 types of noise in CIFAR-10-C (level 3). client10∼client19 each carries a different type of noise data from the FedDQA parameter $\lambda =1.0$.

6.1.3. Benchmark Algorithms

We chose a variety of user-selected methods combined with federated learning as a comparison experiment. The underlying federated learning method is FedAVG. Since loss sharpness is a simple data metric, the experiments mainly consider the effects of various independent factors [42] and do not select those that utilize a combination of factors for client selection.

(1)

Random: This method selects a subset of clients randomly within the available range, which has been widely used in many studies (e.g., [21,43,44]).

(2)

POW-D: This method prioritizes clients with lower local losses. The method considers that the smaller the local final loss, the better its training results. This is a biased client selection scheme proposed in study [45] and applied in study FedCor [34].

(3)

WGD: Weights Gradient Differences prioritizes the clients with the most significant parameter gradient of model updates. The method considers that the global model that receives more parameter updates during the local training process is considered to learn more; this metric has been applied in studies such as [23,46,47].

(4)

FAST: This method prioritizes the client with the fastest decreasing loss. The method considers that the faster the loss decreases during the local training process, the more content updates it has; this metric is applied in the study [48].

(5)

DQA: The method used in this paper.

6.1.4. Experimental Settings for Clients Selection

Considering that only those with heavy noise have the potential to poison the model, in the client selection process, we applied straightforward settings to classify clients into three subsets as follows: light-noise, mix-noise, and heavy-noise, based on the quality-aware ranking ${\overline{Q}}^C$, notated as ${\overline{C}}^l$, ${\overline{C}}^m$, ${\overline{C}}^h$. Light-noise clients are recommended to participate in model aggregation in this round, while heavy-noise clients are not advised to participate. For the vacancies that do not satisfy the number of candidate clients, a certain number of clients from mix-noise are randomly selected to participate in model aggregation. To distinguish three kinds of clients with different quality perceptions, we set two threshold parameters $(\alpha ,\beta )$, where $\alpha \in (0,1), \beta \in (0,1)$ are ranked according to the quality perceptions, and $P^l,P^m,P^h$ are the selected probability for each clients set. The specific process is shown in Algorithm 1.

Algorithm 1: Client selection with dynamic thresholds

Data: client set C, DQA ordered set ${\overline{Q}}^C$, thresholds parameters $\alpha , \beta$, client sub set size $\kappa$ Result: selected client sub set ${\overline{C}}^k$ $A=\alpha \times \left|C\right|$; $B=\beta \times \left|C\right|$; select ${\left\{c_i\right\}}_{i=0}^A\to {\overline{C}}^l$according to 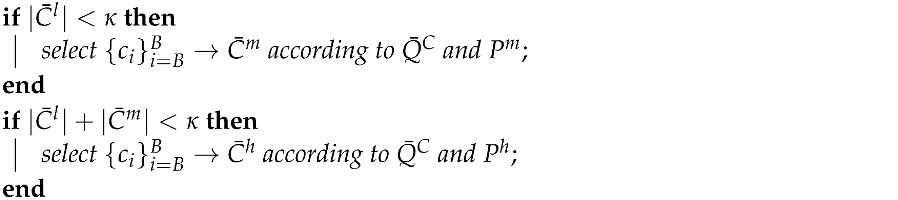${\overline{Q}}^C$and $P^l$; combine $({\overline{C}}^l,{\overline{C}}^m,{\overline{C}}^h)\to {\overline{C}}^k$

6.2. Effecient and Convergence Analysis

The FedDQA is designed to dynamically assess data quality based on loss sharpness during local training, allowing it to handle various types of noise in the data, not just simple Gaussian noise. In this subsection, we evaluate FedDQA’s performance in scenarios where the noise in the data is more complex by using the CIFAR-10-C dataset, which introduces a wide range of corruption types that simulate real-world noisy conditions.

In Figure 5, we observe that FedDQA can perceive the data quality better by slow-start client selection and loss sharpness computation compared to other factors of client selection. Combined with

Table 1. Classification accuracy (%) and corresponding standard deviations of FedDQA compared to other client selection methods on different datasets. Bold numbers have the highest accuracy.

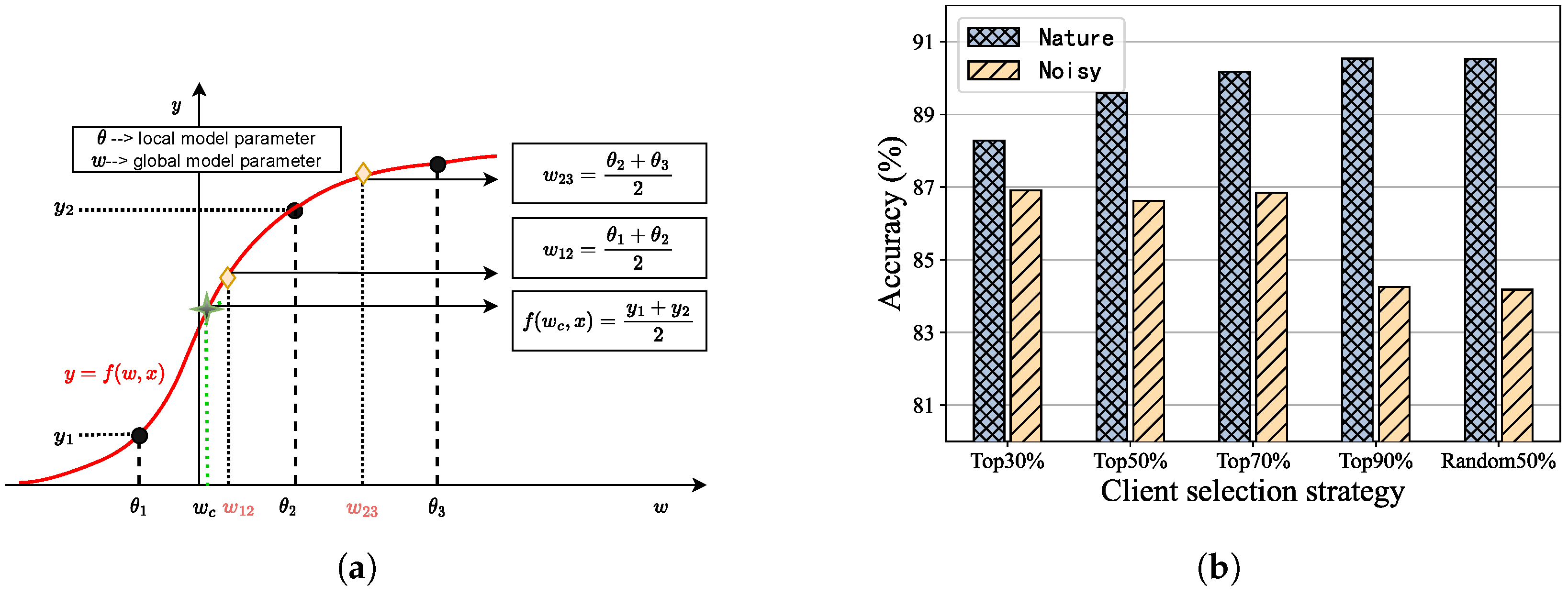
Dataset	Letters (1-M)	Fashion (1-M)	cifar-10 (M-1)	cifar-10-C (M-1)	cifar-10-C (M-M)
Random	85.37 ± 0.3	85.72 ± 0.01	57.11 ± 0.75	59.19 ± 0.66	59.02 ± 0.8
POW-D	86.08 ± 0.58	82.89 ± 0.3	59.5 ± 0.38	57.17 ± 0.48	57.25 ± 0.69
WGD	84.42 ± 2.2	83.22 ± 0.34	58.51 ± 1.64	59.44 ± 0.59	59.38 ± 0.3
FAST	83.92 ± 0.37	84.72 ± 0.23	58.03 ± 1.02	58.93 ± 0.81	58.76 ± 0.86
DQA	87.33 ± 0.34	86.88 ± 0.33	59.82 ± 0.15	60.24 ± 0.76	59.34 ± 0.07

, it can be seen that FedDQA can perceive the data quality stably under different environmental settings with multiple noise levels and multiple noise types. By aggregating more clients of high-quality data, the obtained global model performs even better on natural datasets. The experimental results demonstrate that FedDQA consistently obtains higher accuracy on different noise sets. This shows that FedDQA performs robustly in scenarios where the noise in the data is more complex than simple Gaussian noise. The experiments using the CIFAR-10-C dataset, including a diverse set of complex corruptions, demonstrate that FedDQA handles heterogeneous and complex noise conditions effectively.

6.3. Flexibility in Parameter Choices

To test the scalability of DQA, we evaluate the DQA accuracy at client choice by setting different parameters $\lambda$.

Table 2. Impact of slow-start metric $ϵ$ on results. Better accuracy can still be obtained using higher $ϵ$, which further proves that the loss sharpness phenomenon is evident at the beginning of training.

Metric $\mathit{ϵ}$	Emnist (1-M)	CIFAR-10-C (M-1)
0.1	86.93	60.24
0.5	87.18	59.84
1.0	87.75	59.32
1.5	87.96	59.65
2.0	87.75	61.23
Avg	87.51	60.06

shows the accuracy for the dataset Emnist and the CIFAR-10-C task when 50 rounds of training are performed using different $\lambda$. Expressly, we set a threshold for the parameter $\lambda$, train on the dataset using FedDQA, and evaluate the performance by using the accuracy. We can observe that when the threshold parameter $\lambda$ is varied, the accuracy rate does not change significantly. FedDQA achieves robust and consistent results across a range of parameter values, making it practical for real-world federated learning scenarios where exact parameter tuning may be challenging. This robustness ensures that FedDQA can be effectively applied without extensive parameter optimization, allowing for greater flexibility and ease of use in heterogeneous federated learning environments.

6.4. Impact of Feature Skew

In this subsection, we further discuss the impact of noisy clients. Noise is essentially a change to the data domain. In federated learning, the convergence of the global model is affected when the model obtained by training different environments is aggregated. Figure 6 shows the performance under different noisy clients when there are 20 clients in the dataset Emnist. We make the following main statements: First, our proposed FedDQA client selection method can outperform other benchmarks in most settings. For example, we can visualize that FedDQA can achieve $87\%$ accuracy after 50 training sessions when noisy clients = 19, but the accuracy is below $85\%$ in other benchmarks. Second, when noisy clients increase, the performance gap between FedDQA and other benchmarks becomes more evident. This means that FedDQA can have higher accuracy against different numbers of noisy clients, which is favorable for its practical application.

6.5. Conjunction with Popular Federal Learning Methods

In the personalized federated learning process, the data quality problem is usually regarded as a feature of skew of the data, i.e., client personalization. Usually, these methods achieve model optimization by adjusting the difference between the local model and the global model. However, the noise space remains challenging for these personalized federated learning methods. We select popular personalized federated learning methods as our basic experiments. Relevant methods include (1) FedAVG [21]: classical federated learning, model aggregation based on average model weights; (2) FedProx [23]: classical personalized federated learning, used to cope with statistical and system heterogeneity by parameterizing FedAVG; (3) Ditto [49]: federation learning approach focusing on improving fairness and robustness for heterogeneous clients.

The experimental results are shown in

Table 3. Comparison of accuracy (%) of popular personalized federated learning combined with FedDQA client selection methods under different CIFAR-10-C datasets. Bold results indicate higher accuracy, which was improved for all of these methods when combined with FedDQA.

Method	1-M	M-1	M-M
FedAVG	56.15	58.26	57.89
+Ours(FedDQA)	59.92	59.32	59.29
FedProx	55.34	57.9	57.43
+Ours(FedDQA)	60.59	59.84	60.23
Ditto	57.93	55.01	55.29
+Ours(FedDQA)	59.69	58.57	59.07

. The experimental results show that aggregation of the personalized federated learning model is more stable and obtains higher accuracy when combined with the DQA client selection method. For example, for a given dataset CIFAR-10-C (M-M), the accuracy can be improved from $57.89\%$ to $59.29\%$, $57.43\%$ to $60.23\%$, and $55.29\%$ to $59.07\%$ for FedAVG, FedProx, and Ditto methods combined with DQA.

7. Conclusions

In conclusion, our proposed FedDQA framework effectively addresses the challenges of feature noise in heterogeneous federated learning by dynamically assessing data quality through loss sharpness metrics during training. This strategic client selection mitigates the negative impact of noisy clients on the global model’s performance and convergence rate and enhances overall model accuracy without additional computations or data exchanges. Furthermore, FedDQA can be adapted for model heterogeneity by incorporating a model compatibility assessment. This could involve evaluating the alignment of local models with the global model in terms of architecture and parameters and adjusting the aggregation process to account for structural differences, possibly through model distillation techniques or layer-wise aggregation strategies. Regarding computational resource heterogeneity, FedDQA can be extended by integrating a resource-awareness component, such as training time per epoch, memory usage, or energy consumption in the client selection process.