Some Properties and Graphical Applications of a New Subclass of Harmonic Functions Defined by a Differential Inequality

Abstract

This paper establishes new results related to geometric function theory by presenting a new subclass of harmonic functions with complex values within the open unit disk, characterized by a second-order differential inequality. The investigation explores the bounds on the coefficients and estimates of the function growth. This paper also demonstrates that this subclass remains stable under the convolution operation applied to its members. In addition, in the last section, images of the unit disk under some functions of this class are given.

1. Introduction

Harmonic functions play a central role in mathematical analysis and applied mathematics due to their intriguing properties and widespread applications. Harmonic functions are solutions to Laplace’s equation, a second-order partial differential equation that emerges in various fields such as physics, engineering, and probability theory. The study of harmonic functions opens doors to exploring diverse mathematical phenomena, including conformal mappings, potential theory, and complex analysis. Their unique characteristic of being infinitely differentiable and satisfying the mean value property has made them a staple in the analysis of functions and solutions to differential equations.

In this research, we shift our focus to harmonic functions that are subject to additional constraints, specifically those defined by a second-order differential inequality. By incorporating a second-order differential inequality, we introduce new dynamics that broaden the traditional scope of harmonic functions, leading to intriguing insights and possibly to novel applications.

In this article, the exploration of certain properties of harmonic functions defined by a second-order differential inequality provides a good basis for deeper analysis. This study aims to investigate the new characteristics that emerge from these constraints and to expand our understanding of harmonic functions beyond the classical framework. Through a combination of theoretical derivations and practical examples, we will uncover the distinctive attributes and potential applications that arise from this area of research.

Consider $\Delta =\left\{\zeta \in \mathbb{C}:\left|\zeta \right|<1\right\}$ as the open unit disk in the complex plane $\mathbb{C}$. Let $\mathcal{H}$ denote the set comprising complex-valued harmonic functions f within $\Delta$. These functions are normalized such that $f\left(0\right)=0$ and $f_{\zeta }^{\prime }\left(0\right)=1$. Also, let ${\mathcal{H}}^0=\left\{f\in \mathcal{H}:f_{\overline{\zeta }}^{\prime }\left(0\right)=0\right\}.$ Every function $f\in {\mathcal{H}}^0$ has the canonical representation $f=h+\overline{g}$, where

$$h\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{ϵ=2}}{a}_{ϵ}{\zeta }^{ϵ},g\left(\zeta \right)=\stackrel{\infty }{\sum _{ϵ=2}}{b}_{ϵ}{\zeta }^{ϵ},$$

(1)

both h and g are analytic in $\Delta .$ $f=h+\overline{g}$ is locally univalent and sense-preserving in $\Delta$ if and only if $\left|g^{\prime }\left(\zeta \right)\right|<\left|h^{\prime }\left(\zeta \right)\right|$ in $\Delta$. Denote by ${\mathcal{SH}}^0$ the subclass of ${\mathcal{H}}^0$ that is univalent and sense-preserving in the open unit disk $\Delta$ (see [1,2]). When $g\left(\zeta \right)=0$, the traditional set $\mathcal{S}$ comprising analytic, univalent, and normalized functions within the unit disk $\Delta$ is a subset of ${\mathcal{SH}}^0$, similar to how the set $\mathcal{A}$ consisting of analytic and normalized functions in $\Delta$ is a subset of ${\mathcal{H}}^0$.

Let $\mathcal{K}$, ${\mathcal{S}}^{*}$, and $\mathcal{CK}$ denote the subsets of $\mathcal{S}$ that map $\Delta$ onto convex, starlike, and close-to-convex domains, respectively. Correspondingly, ${\mathcal{KH}}^0$, $\mathcal{S}{\mathcal{H}}^{*,0}$, and ${\mathcal{CKH}}^0$ represent the subsets of $\mathcal{S}{\mathcal{H}}^0$ mapping $\Delta$ onto their respective domains.

In 2013, Ponnusamy et al. [3] introduced a class:

$${\mathcal{PH}}^0=\left\{f\in {\mathcal{H}}^0:\mathrm{Re}\left(h^{\prime }\left(\zeta \right)\right)>\left|g^{\prime }\left(\zeta \right)\right|\mathrm{for}\zeta \in \Delta \right\}$$

and they proved that functions in ${\mathcal{PH}}^0$ are close-to-convex.

Recently, Ghosh and Vasudevarao [4] defined a class for $\zeta \in \Delta ,\gamma \ge 0$:

$${\mathcal{WH}}^0\left(\gamma \right)=\left\{f=h+\overline{g}\in {\mathcal{H}}^0:\mathrm{Re}\left(h^{\prime }\left(\zeta \right)+\gamma \zeta h^{″}\left(\zeta \right)\right)>\left|g^{\prime }\left(\zeta \right)+\gamma \zeta g^{″}\left(\zeta \right)\right|\right\}$$

and they investigated coefficient bounds, growth estimates, convolution, and radius of convexity for the partial sums of the members of their class.

Also, Rajbala and Prajapat [5] studied such properties of the class

$${\mathcal{WH}}^0\left(\gamma ,\lambda \right)=\left\{f=h+\overline{g}\in {\mathcal{H}}^0:\mathrm{Re}\left(h^{\prime }\left(\zeta \right)+\gamma \zeta h^{″}\left(\zeta \right)-\lambda \right)>\left|g^{\prime }\left(\zeta \right)+\gamma \zeta g^{″}\left(\zeta \right)\right|\right\}$$

where $\zeta \in \Delta ,\gamma \ge 0,0\le \lambda <1$.

In 2014, Nagpal and Ravichandran [6] studied a class ${\mathcal{WH}}^0(1,0)={\mathcal{WH}}^0$ of functions $f=h+\overline{g}\in {\mathcal{H}}^0$ satisfying the condition $\mathrm{Re}\left(h^{\prime }\left(\zeta \right)+\zeta h^{″}\left(\zeta \right)\right)>\left|g^{\prime }\left(\zeta \right)+\zeta g^{″}\left(\zeta \right)\right|$ for $\zeta \in \Delta$, which is a harmonic analogue of the class $\mathcal{W}$ defined by Chichra [7] consisting of the functions $h\in \mathcal{A}$ satisfying the condition $\mathrm{Re}\left(h^{\prime }\left(\zeta \right)+\zeta h^{″}\left(\zeta \right)\right)>0$ for $\zeta \in \Delta$. In 1977, Chichra [7] studied the class $\mathcal{G}\left(\delta \right)$ for some $\delta \ge 0,$ where $\mathcal{G}\left(\delta \right)$ consisting of the analytic function $h\left(\zeta \right)$ such that

$$\mathrm{Re}\left[(1-\delta ){\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)\right]>0$$

for $\left|\zeta \right|<1.$

Recently, Liu and Yang [8] defined a class:

$$\begin{array}{c}{\mathcal{G}}_{\mathcal{H}}^0(\delta ;r)=\left\{f=h+\overline{g}\in {\mathcal{H}}^0:\mathrm{Re}\left[(1-\delta ){\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)\right]\right.\\ \\ \left.>\left|(1-\delta ){\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)\right|\mathrm{for}\left|\zeta \right|<r\right\}\end{array}$$

where $\delta \ge 0,$ $0<r\le 1.$

Next, Çakmak and et al. [9] investigated some properties of the class

$${\mathcal{G}}_{\mathcal{H}}^0\left(\gamma ,\delta ,\lambda \right)=\left\{f=h+\overline{g}\in {\mathcal{H}}^0:\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)-\lambda \right]>\left|\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)\right|\right\}$$

where $\gamma \ge 0,\delta >0$ and $0\le \lambda <\gamma +\delta \le 1.$

Finally, Breaz et al. [10] defined a subclass:

$$\begin{array}{c}{\mathbb{W}}_H^0(\alpha ,\beta )=\left\{f=h+\overline{g}\in {\mathcal{H}}^0:\mathrm{Re}\left[(2\beta +1-\alpha ){\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+(\alpha -2\beta )h^{\prime }\left(\zeta \right)+\beta \zeta h^{″}\left(\zeta \right)\right]\right.\\ \\ \left.>\left|(2\beta +1-\alpha ){\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+(\alpha -2\beta )g^{\prime }\left(\zeta \right)+\beta \zeta g^{″}\left(\zeta \right)\right|\right\}\end{array}$$

where $\alpha \ge \beta \ge 0.$

Other interesting studies of harmonic mappings that inspired us in this work are [11,12,13,14,15]. In [11], new subclasses of harmonic functions are introduced for which coefficient inequality results and distortion bounds are obtained. An investigation is conducted on a subset of univalent, sense-preserving, complex-valued close-to-convex harmonic functions in the open unit disc in [12] and the coefficient and growth estimates are obtained, an area theorem is established, and boundary dynamics and convolution and convex combination features are examined. Other subclasses of harmonic functions are examined in the other papers listed above, concerning distortion limits and univalence conditions, extreme points, partial sum problems, and convolution-related properties.

For the study presented in this paper, the following class is considered.

Denote by ${\mathcal{BH}}^0(\gamma ,\delta )$ the class of functions $f=h+\overline{g}\in {\mathcal{H}}^0$ and satisfy

$$\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]>\left|\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)\right|$$

(2)

where $\delta \ge \gamma \ge 0$ and $\zeta \in \Delta .$

Let ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$ denote a class of functions $h\in \mathcal{A}$ such that

$$\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]>0\left(\delta \ge \gamma \ge 0\right).$$

Al-Refai [16], studied the inclusion properties of the class ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$.

In Section 2, we derive bounds for coefficients and estimates for growth and establish sufficient conditions for coefficients within the class ${\mathcal{BH}}^0(\gamma ,\delta )$. In Section 3, we demonstrate that the class maintains closure under convex combinations and convolution operations among its elements. Additionally, in Section 4, graphical representations of some function examples belonging to this class will be given.

2. The Sharp Coefficient Estimates and Growth Theorems of ${\mathcal{BH}}^{\mathbf{0}}(\mathbf{\gamma },\mathbf{\delta })$

In this section, we shall investigate the necessary and sufficient coefficient conditions and distortion bounds for functions belonging to the class ${\mathcal{BH}}^0(\gamma ,\delta ).$

Theorem 1.

The mapping $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta )$ if and only if ${\mathsf{Ϝ}}_{\mu }=h+\mu g\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for each μ such that $\left|\mu \right|=1.$

Proof. 

Suppose $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta ).$ For each $\left|\mu \right|=1,$

$$\begin{array}{cc}\hfill & \mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)+\mu g\left(\zeta \right)}{\zeta }}+\delta \left(h^{\prime }\left(\zeta \right)+\mu g^{\prime }\left(\zeta \right)\right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta \left(h^{″}\left(\zeta \right)+\mu g^{″}\left(\zeta \right)\right)\right]\hfill \\ \hfill & =\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]\hfill \\ \hfill & +\mathrm{Re}\left[\mu \left(\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)\right)\right]\hfill \\ \hfill & >\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]\hfill \\ \hfill & -\left|\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)\right|\hfill \\ \hfill & >0,\zeta \in \Delta .\hfill \end{array}$$

Thus, ${\mathsf{Ϝ}}_{\mu }\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for each $\mu \left(\left|\mu \right|=1\right).$ Conversely, let ${\mathsf{Ϝ}}_{\mu }=h+\mu g\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$, then,

$$\begin{array}{cc}& \mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]\hfill \\ \hfill >& \mathrm{Re}\left[-\mu \left(\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)\right)\right]\left(\zeta \in \Delta \right).\hfill \end{array}$$

(3)

Setting $C=\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)$, ${\alpha }_0=argC$. Therefore, $C=\left|C\right|e^{i{\alpha }_0}$. For each fixed $\zeta \in {\Delta }_r,r\in (0,1)$ and arbitrarily chosen complex number $\mu$ with $\left|\mu \right|=1,$ that is, $\mu =e^{i(\pi -{\alpha }_0)},$ (3) becomes

$$\begin{array}{ccc}& & \mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]\hfill \\ & >& -\mathrm{Re}\left[e^{i(\pi -{\alpha }_0)}C\right]=-\mathrm{Re}\left[e^{i\pi }\left|C\right|\right]=\left|C\right|\left(\zeta \in {\Delta }_r\right),\hfill \end{array}$$

and hence, $f\in {\mathcal{BH}}^0(\gamma ,\delta ).$ □

Theorem 2.

Let the function f be in the form (1) and $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta )$, then, for $ϵ\ge 2,$

$$\left|b_{ϵ}\right|\le {\displaystyle \frac{2(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}.$$

(4)

The result is sharp and equality holds for the function $f\left(\zeta \right)=\zeta +{\displaystyle \frac{2(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\overline{\zeta }}^{ϵ}.$

Proof. 

Suppose that $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta ).$ Using the series representation of $g\left(r{e}^{i\theta }\right),0\le r<1$ and $\theta \in \mathbb{R},$ we derive

$$\begin{array}{ccc}& & {\displaystyle \frac{2\gamma +2\delta ϵ+(\delta -\gamma )ϵ(ϵ-1)}{2}}\left|b_{ϵ}\right|r^{ϵ-1}\hfill \\ & \le & {\displaystyle \frac{1}{2\pi }}\underset{0}{\overset{2\pi }{\int }}\left|\gamma {\displaystyle \frac{g\left(r{e}^{i\theta }\right)}{r{e}^{i\theta }}}+\delta g^{\prime }\left(r{e}^{i\theta }\right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)r{e}^{i\theta }{g}^{″}\left(r{e}^{i\theta }\right)\right|d\theta \hfill \\ & <& {\displaystyle \frac{1}{2\pi }}\underset{0}{\overset{2\pi }{\int }}\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(r{e}^{i\theta }\right)}{r{e}^{i\theta }}}+\delta h^{\prime }\left(r{e}^{i\theta }\right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)r{e}^{i\theta }{h}^{″}\left(r{e}^{i\theta }\right)\right]d\theta \hfill \\ & =& {\displaystyle \frac{1}{2\pi }}\underset{0}{\overset{2\pi }{\int }}\mathrm{Re}\left[\delta +\gamma +{\displaystyle \frac{1}{2}}\sum _{ϵ=2}^{\infty }(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ]a_{ϵ}{r}^{ϵ-1}{e}^{i(ϵ-1)\theta }\right]d\theta \hfill \\ =& \delta +\gamma .\hfill \end{array}$$

Allowing $r\to 1^{-},$ we prove the result (4). Moreover, it can be easily seen that the equality is achieved for $f\left(\zeta \right)=\zeta +{\displaystyle \frac{2(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\overline{\zeta }}^{ϵ}$. □

Theorem 3.

Let the function f be in the form (1) and $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta )$. Then, for $ϵ\ge 2,$ we have

$$\begin{array}{c}\left(i\right)\left|a_{ϵ}\right|+\left|b_{ϵ}\right|\le {\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}},\hfill \\ \left(ii\right)\left|\left|a_{ϵ}\right|-\left|b_{ϵ}\right|\right|\le {\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}},\hfill \\ \left(iii\right)\left|a_{ϵ}\right|\le {\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}.\hfill \end{array}$$

All the results given in this theorem are certain and the equations are provided for the following function $f\left(\zeta \right)=\zeta +{\displaystyle \sum _{ϵ=2}^{\infty }}{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ}.$

Proof. 

$\left(i\right)$ Suppose that $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta ),$ then, from Theorem 1, ${\mathsf{Ϝ}}_{\mu }=h+\mu g\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for each $\mu$ $\left(\left|\mu \right|=1\right).$ Thus, for each $\left|\mu \right|=1,$ we have

$$\mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)+\mu g\left(\zeta \right)}{\zeta }}+\delta {(h\left(\zeta \right)+\mu g\left(\zeta \right))}^{\prime }+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {(h\left(\zeta \right)+\mu g\left(\zeta \right))}^{″}\right]>0$$

for $\zeta \in \Delta .$ Therefore, there exists an analytic function p of the form $p\left(\zeta \right)=1+{\displaystyle \sum _{ϵ=1}^{\infty }}{p}_{ϵ}{\zeta }^{ϵ}$ with a positive real part in $\Delta ,$ such that

$$\gamma {\displaystyle \frac{h\left(\zeta \right)+\mu g\left(\zeta \right)}{\zeta }}+\delta {(h\left(\zeta \right)+\mu g\left(\zeta \right))}^{\prime }+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {(h\left(\zeta \right)+\mu g\left(\zeta \right))}^{″}=(\delta +\gamma )p\left(\zeta \right).$$

(5)

Comparing coefficients on both sides of (5), we have

$$(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ](a_{ϵ}+\mu b_{ϵ})=2(\delta +\gamma )p_{ϵ-1}\mathrm{for}ϵ\ge 2.$$

Since $\left|p_{ϵ}\right|\le 2$ for $ϵ\ge 1,$ and $\mu$ $\left(\left|\mu \right|=1\right)$ is arbitrary, the proof of (i) is complete. By following the methods in proof (i), proof (ii) and proof (iii) are obtained. For $\Omega =2,3,\dots ,\infty$ the function $f\left(\zeta \right)=\zeta +$ ${\displaystyle \sum _{ϵ\in \Omega }}{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ}$ shows that all inequalities are sharp. □

Now, we give a sufficient condition for a function to be in the class ${\mathcal{BH}}^0(\gamma ,\delta ).$

Theorem 4.

Let $f=h+\overline{g}\in {\mathcal{H}}^0$ with

$$\sum _{ϵ\in \Omega }(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ]\left(\left|a_{ϵ}\right|+\left|b_{ϵ}\right|\right)\le 2(\delta +\gamma ),$$

(6)

then, $f\in {\mathcal{BH}}^0(\gamma ,\delta ).$

Proof. 

Suppose that $f=h+\overline{g}\in {\mathcal{H}}^0.$ Then, using (6),

$$\begin{array}{ccc}& & \mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]\hfill \\ & =& \mathrm{Re}\left[\delta +\gamma +{\displaystyle \frac{1}{2}}\sum _{ϵ\in \Omega }(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ]a_{ϵ}{\zeta }^{ϵ-1}\right]\hfill \\ & >& \delta +\gamma -{\displaystyle \frac{1}{2}}\sum _{ϵ\in \Omega }(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ]\left|a_{ϵ}\right|\hfill \\ & \ge & {\displaystyle \frac{1}{2}}\sum _{ϵ\in \Omega }(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ]\left|b_{ϵ}\right|\hfill \\ & >& {\displaystyle \frac{1}{2}}\left|\sum _{ϵ\in \Omega }(ϵ+1)[ϵ(\delta -\gamma )+2\gamma ]b_{ϵ}{\zeta }^{ϵ-1}\right|\hfill \\ & =& \left|\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)\right|.\hfill \end{array}$$

Hence, $f\in {\mathcal{BH}}^0(\gamma ,\delta ).$ □

Theorem 5.

Let $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta )$ for $\delta \ge \gamma \ge 0.$ Then,

$$\begin{array}{c}max\left\{0,\left|\zeta \right|-4(\delta +\gamma ){\displaystyle \sum _{ϵ\in \Omega }}{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}\right\}\\ \le \left|f\left(\zeta \right)\right|\le \left|\zeta \right|+4(\delta +\gamma ){\displaystyle \sum _{ϵ\in \Omega }}{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}.\end{array}$$

(7)

Inequalities are sharp for the function $f\left(\zeta \right)=\zeta +{\displaystyle \sum _{ϵ\in \Omega }}{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ}.$

Proof. 

Let $f=h+\overline{g}\in {\mathcal{BH}}^0(\gamma ,\delta ).$ Then, using Theorem 1, ${\mathsf{Ϝ}}_{\mu }=h+\mu g\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ and for each $\left|\mu \right|=1$, we have $\mathrm{Re}\left\{p\left(\zeta \right)\right\}>0$, where

$$p\left(\zeta \right)={\displaystyle \frac{\gamma \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }+\delta {\mathsf{Ϝ}}_{\mu }^{\prime }\left(\zeta \right)+\left(\frac{\delta -\gamma }{2}\right)\zeta {\mathsf{Ϝ}}_{\mu }^{″}\left(\zeta \right)}{\delta +\gamma }}.$$

Thus, we obtain

$${\displaystyle \frac{2\gamma }{\delta -\gamma }}{\left(\zeta {\mathsf{Ϝ}}_{\mu }\left(\zeta \right)\right)}^{\prime }+{\left({\zeta }^2{\mathsf{Ϝ}}_{\mu }^{\prime }\left(\zeta \right)\right)}^{\prime }={\displaystyle \frac{2(\gamma +\delta )}{\delta -\gamma }}\zeta p\left(\zeta \right)$$

and

$${\displaystyle \frac{2\gamma }{\delta -\gamma }}\zeta {\mathsf{Ϝ}}_{\mu }\left(\zeta \right)+{\zeta }^2{\mathsf{Ϝ}}_{\mu }^{\prime }\left(\zeta \right)={\displaystyle \frac{2(\gamma +\delta )}{\delta -\gamma }}\underset{0}{\overset{\zeta }{\int }}\zeta p\left(\zeta \right)d\zeta .$$

Making substitution $w=\zeta t$ and simplifying yields

$${\left[{\zeta }^{{\displaystyle \frac{2\gamma }{\delta -\gamma }}}{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)\right]}^{\prime }={\displaystyle \frac{2(\gamma +\delta )}{\delta -\gamma }}{\int }_0^1{\zeta }^{{\displaystyle \frac{2\gamma }{\delta -\gamma }}}tp\left(\zeta t\right)dt$$

(8)

and

$${\zeta }^{{\displaystyle \frac{2\gamma }{\delta -\gamma }}}{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)={\displaystyle \frac{2(\gamma +\delta )}{\delta -\gamma }}{\int }_0^{\zeta }{\int }_0^1{w}^{{\displaystyle \frac{2\gamma }{\delta -\gamma }}}tp\left(wt\right)dtdw.$$

Now, integrating (8) and making substitution $w=\zeta s^{{\displaystyle \frac{\delta -\gamma }{\delta +\gamma }}}$ produces

$${\displaystyle \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }}=2{\int }_0^1{\int }_0^{1}tp\left(\zeta t{s}^{{\displaystyle \frac{\delta -\gamma }{\delta +\gamma }}}\right)dtds.$$

On the other hand, since Re$\left\{p\right(\zeta \left)\right\}>0$, then $p\left(\zeta \right)\prec {\displaystyle \frac{1+\zeta }{1-\zeta }}$, where “≺” denotes subordination (see [2]). Let

$${\displaystyle \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }}=2{\int }_0^1{\int }_0^1{\displaystyle \frac{1+\zeta t{s}^{\frac{\delta -\gamma }{\delta +\gamma }}}{1-\zeta t{s}^{\frac{\delta -\gamma }{\delta +\gamma }}}}tdtds.$$

Thus, we obtain

$$\begin{array}{ccc}\hfill \left|{\displaystyle \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }}\right|& =& \left|2{\int }_0^1{\int }_0^1\left[t+2\sum _{ϵ=1}^{\infty }{t}^{ϵ+1}{s}^{ϵ\left({\displaystyle \frac{\delta -\gamma }{\delta +\gamma }}\right)}{\zeta }^{ϵ}\right]dtds\right|\hfill \\ & =& \left|2{\int }_0^1\left[{\displaystyle \frac{1}{2}}+2\sum _{ϵ=1}^{\infty }{\displaystyle \frac{s^{ϵ\left(\frac{\delta -\gamma }{\delta +\gamma }\right)}}{ϵ+2}}{\zeta }^{ϵ}\right]ds\right|\hfill \\ & =& \left|1+\sum _{ϵ\in \Omega }{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[(ϵ-1)(\delta -\gamma )+\delta +\gamma \right]}}{\zeta }^{ϵ-1}\right|\hfill \\ & \le & 1+\sum _{ϵ\in \Omega }{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\left|\zeta \right|}^{ϵ-1}\hfill \end{array}$$

and

$$\left|{\displaystyle \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }}\right|\ge 1-\sum _{ϵ\in \Omega }{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\left|\zeta \right|}^{ϵ-1}.$$

Since $\mu$ $\left(\left|\mu \right|=1\right)$ is arbitrary, we have

$$\begin{array}{ccc}& & max\left\{0,\left|\zeta \right|-4(\delta +\gamma )\sum _{ϵ\in \Omega }\frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}\right\}\hfill \\ & \le & \left|{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)\right|\le \left|\zeta \right|+4(\delta +\gamma )\sum _{ϵ\in \Omega }\frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]},\zeta \in \Delta .\hfill \end{array}$$

Since

$$\begin{array}{ccc}\hfill \left|{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)\right|& =& \left|h\left(\zeta \right)+\mu g\left(\zeta \right)\right|\hfill \\ & \le & \left|\zeta \right|+4(\delta +\gamma )\sum _{ϵ\in \Omega }{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)\right|& =& \left|h\left(\zeta \right)+\mu g\left(\zeta \right)\right|\hfill \\ & \ge & \left|\zeta \right|-4(\delta +\gamma )\sum _{ϵ\in \Omega }{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}},\hfill \end{array}$$

in particular, we have

$$\left|h\left(\zeta \right)\right|+\left|g\left(\zeta \right)\right|\le \left|\zeta \right|+4(\delta +\gamma )\sum _{ϵ\in \Omega }{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}$$

and

$$\left|h\left(\zeta \right)\right|-\left|g\left(\zeta \right)\right|\ge \left|\zeta \right|-4(\delta +\gamma )\sum _{ϵ\in \Omega }{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}.$$

Then,

$$\begin{array}{ccc}\hfill \left|f\left(\zeta \right)\right|& \le & \left|h\right(\zeta \left)\right|+\left|g\right(\zeta \left)\right|\hfill \\ & \le & \left|\zeta \right|+4(\delta +\gamma )\sum _{ϵ\in \Omega }{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|f\left(\zeta \right)\right|& \ge & \left|h\right(\zeta \left)\right|-\left|g\right(\zeta \left)\right|\hfill \\ & \ge & \left|\zeta \right|-4(\delta +\gamma )\sum _{ϵ\in \Omega }{\displaystyle \frac{{\left|\zeta \right|}^{ϵ}}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}.\hfill \end{array}$$

Since $\mu$ $\left(\left|\mu \right|=1\right)$ is arbitrary, we have (7). □

3. Convex Combinations and Convolutions

This section explores the properties of convex combinations and convolutions within the class ${\mathcal{BH}}^0(\gamma ,\delta )$ of harmonic mappings. Additionally, this section introduces the concept of the Hadamard product, a convolution of a harmonic function with an analytic function, and proves its closure property under certain conditions on the analytic function.

Overall, these results contribute to a deeper understanding of the structural properties of harmonic mappings in the class ${\mathcal{BH}}^0(\gamma ,\delta )$, providing foundational insights and analytical tools for further study.

Theorem 6.

The class ${\mathcal{BH}}^0(\gamma ,\delta )$ is closed under convex combinations.

Proof. 

Suppose $f_j=h_j+\overline{g_j}\in {\mathcal{BH}}^0(\gamma ,\delta )$ for $j=1,2,\dots ,m$ and ${\displaystyle \sum _{j=1}^m}{l}_j=1$ $(0\le l_j\le 1).$ The convex combination of functions $f_j$ $\left(j=1,2,\dots ,m\right)$ may be written as

$$f\left(\zeta \right)=\sum _{j=1}^m{l}_j{f}_j\left(\zeta \right)=h\left(\zeta \right)+\overline{g\left(\zeta \right)},$$

where

$$h\left(\zeta \right)=\sum _{j=1}^m{l}_j{h}_j\left(\zeta \right)\mathrm{and}g\left(\zeta \right)=\sum _{j=1}^m{l}_j{g}_j\left(\zeta \right).$$

Then, both h and g are analytic in $\Delta$ with $h\left(0\right)=g\left(0\right)=h^{\prime }\left(0\right)-1=g^{\prime }\left(0\right)=0$ and

$$\begin{array}{ccc}& & \mathrm{Re}\left[\gamma {\displaystyle \frac{h\left(\zeta \right)}{\zeta }}+\delta h^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h^{″}\left(\zeta \right)\right]\hfill \\ & =& \mathrm{Re}\left[\sum _{j=1}^m{l}_j\left(\gamma {\displaystyle \frac{h_j\left(\zeta \right)}{\zeta }}+\delta h_j^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta h_j^{″}\left(\zeta \right)\right)\right]\hfill \\ & >& \sum _{j=1}^m{l}_j\left|\gamma {\displaystyle \frac{g_j\left(\zeta \right)}{\zeta }}+\delta g_j^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g_j^{″}\left(\zeta \right)\right|\hfill \\ & \ge & \left|\gamma {\displaystyle \frac{g\left(\zeta \right)}{\zeta }}+\delta g^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta g^{″}\left(\zeta \right)\right|\hfill \end{array}$$

showing that $f\in {\mathcal{BH}}^0(\gamma ,\delta )$. □

A sequence ${\left\{{\lambda }_{ϵ}\right\}}_{ϵ=0}^{\infty }$ of non-negative real numbers is said to be a convex null sequence, if ${\lambda }_{ϵ}\to 0$ as $ϵ\to \infty$, and ${\lambda }_0-{\lambda }_1\ge {\lambda }_1-{\lambda }_2\ge {\lambda }_2-{\lambda }_3\ge \dots \ge {\lambda }_{ϵ-1}-{\lambda }_{ϵ}\ge \dots \ge 0.$ We shall require the following Lemma 1 and Lemma 2 to prove the results of the convolution.

Lemma 1

([17]). If ${\left\{{\lambda }_{ϵ}\right\}}_{ϵ=0}^{\infty }$ is a convex null sequence, then function

$$q\left(\zeta \right)={\displaystyle \frac{{\lambda }_0}{2}}+\sum _{ϵ=1}^{\infty }{\lambda }_{ϵ}{\zeta }^{ϵ}$$

is analytic and $\mathit{Re}\left[q\left(\zeta \right)\right]>0$ in $\Delta .$

Lemma 2

([18]). Let the function p be analytic in Δ with $p\left(0\right)=1$ and $\mathit{Re}\left[p\left(\zeta \right)\right]>1/2$ in $\Delta .$ Then, for any analytic function Ϝ in $\Delta ,$ the function $p\ast \mathsf{Ϝ}$ takes values in the convex hull of the image of Δ under $\mathsf{Ϝ}.$

Lemma 3.

Let $\mathsf{Ϝ}\in {\mathcal{B}}_1(\gamma ,\delta ,0;0),$ then $\mathit{Re}\left[{\displaystyle \frac{\mathsf{Ϝ}\left(\zeta \right)}{\zeta }}\right]>{\displaystyle \frac{1}{2}}.$

Proof. 

Suppose $\mathsf{Ϝ}\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ is given by $\mathsf{Ϝ}\left(\zeta \right)=\zeta +{\sum }_{ϵ=2}^{\infty }{A}_{ϵ}{\zeta }^{ϵ},$ then

$$\mathrm{Re}\left[1+\sum _{ϵ\in \Omega }{\displaystyle \frac{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}{2(\gamma +\delta )}}{A}_{ϵ}{\zeta }^{ϵ-1}\right]>0(\zeta \in \Delta ),$$

which is equivalent to $\mathrm{Re}\left[p\left(\zeta \right)\right]>{\displaystyle \frac{1}{2}}$ in $\Delta ,$ where

$$p\left(\zeta \right)=1+\sum _{ϵ\in \Omega }{\displaystyle \frac{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}{4(\gamma +\delta )}}{A}_{ϵ}{\zeta }^{ϵ-1}.$$

Now consider a sequence ${\left\{{\lambda }_{ϵ}\right\}}_{ϵ=0}^{\infty }$ defined by

$${\lambda }_0=2\mathrm{and}{\lambda }_{ϵ-1}={\displaystyle \frac{4(\gamma +\delta )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}\mathrm{for}ϵ\ge 2.$$

It can be easily seen that the sequence ${\left\{{\lambda }_{ϵ}\right\}}_{ϵ=0}^{\infty }$ is a convex null sequence. Using Lemma 1, this implies that the function

$$q\left(\zeta \right)=1+\sum _{ϵ\in \Omega }{\displaystyle \frac{4(\gamma +\delta )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ-1}$$

is analytic and $\mathrm{Re}\left[q\left(\zeta \right)\right]>0$ in $\Delta .$ Writing

$${\displaystyle \frac{\mathsf{Ϝ}\left(\zeta \right)}{\zeta }}=\mathfrak{p}\left(\zeta \right)\ast \left(1+\sum _{ϵ\in \Omega }{\displaystyle \frac{4(\gamma +\delta )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ-1}\right),$$

and making use of Lemma 2 shows that $\mathrm{Re}\left\{{\displaystyle \frac{\mathsf{Ϝ}\left(\zeta \right)}{\zeta }}\right\}>{\displaystyle \frac{1}{2}}$ for $\zeta \in \Delta .$ □

Lemma 4.

Let ${\mathsf{Ϝ}}_j\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for $j=1,2.$ Then, ${\mathsf{Ϝ}}_1\ast {\mathsf{Ϝ}}_2$∈${\mathcal{B}}_1(\gamma ,\delta ,0;0).$

Proof. 

Suppose ${\mathsf{Ϝ}}_1\left(\zeta \right)=\zeta +{\sum }_{ϵ\in \Omega }{A}_{ϵ}{\zeta }^{ϵ}$ and ${\mathsf{Ϝ}}_2\left(\zeta \right)=\zeta +{\sum }_{ϵ\in \Omega }{B}_{ϵ}{\zeta }^{ϵ}.$ Then, the convolution of ${\mathsf{Ϝ}}_1\left(\zeta \right)$ and ${\mathsf{Ϝ}}_2\left(\zeta \right)$ is defined by

$$\mathsf{Ϝ}\left(\zeta \right)=({\mathsf{Ϝ}}_1\ast {\mathsf{Ϝ}}_2)\left(\zeta \right)=\zeta +\sum _{ϵ=2}^{\infty }{A}_{ϵ}{B}_{ϵ}{\zeta }^{ϵ}.$$

Since ${\mathsf{Ϝ}}^{\prime }\left(\zeta \right)={\mathsf{Ϝ}}_1^{\prime }\left(\zeta \right)\ast {\displaystyle \frac{{\mathsf{Ϝ}}_2\left(\zeta \right)}{\zeta }}$, we then have

$$\begin{array}{c}\gamma {\displaystyle \frac{\mathsf{Ϝ}\left(\zeta \right)}{\zeta }}+\delta {\mathsf{Ϝ}}^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\mathsf{Ϝ}}^{″}\left(\zeta \right)\\ \\ =\left[\gamma {\displaystyle \frac{{\mathsf{Ϝ}}_1\left(\zeta \right)}{\zeta }}+\delta {\mathsf{Ϝ}}_1^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\mathsf{Ϝ}}_1^{″}\left(\zeta \right)\right]\ast {\displaystyle \frac{{\mathsf{Ϝ}}_2\left(\zeta \right)}{\zeta }}.\end{array}$$

(9)

Since ${\mathsf{Ϝ}}_1\in$ ${\mathcal{B}}_1(\gamma ,\delta ,0;0),$

$$\mathrm{Re}\left[\gamma {\displaystyle \frac{{\mathsf{Ϝ}}_1\left(\zeta \right)}{\zeta }}+\delta {\mathsf{Ϝ}}_1^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\mathsf{Ϝ}}_1^{″}\left(\zeta \right)\right]>0\left(\zeta \in \Delta \right)$$

and using Lemma 3, $\mathrm{Re}\left[{\displaystyle \frac{{\mathsf{Ϝ}}_2\left(\zeta \right)}{\zeta }}\right]>{\displaystyle \frac{1}{2}}$ in $\Delta .$ Now, applying Lemma 2 to (9) yields

$\mathrm{Re}\left[\gamma {\displaystyle \frac{\mathsf{Ϝ}\left(\zeta \right)}{\zeta }}+\delta {\mathsf{Ϝ}}^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\mathsf{Ϝ}}^{″}\left(\zeta \right)\right]>0$ in $\Delta .$ Thus, $\mathsf{Ϝ}={\mathsf{Ϝ}}_1\ast {\mathsf{Ϝ}}_2$∈${\mathcal{B}}_1(\gamma ,\delta ,0;0).$ □

Now, using Lemma 4, we prove that the class ${\mathcal{BH}}^0(\gamma ,\delta )$ is closed under convolutions of its members.

Theorem 7.

Let $f_j\in {\mathcal{BH}}^0(\gamma ,\delta )$ for $j=1,2.$ Then, $f_1\ast f_2$∈${\mathcal{BH}}^0(\gamma ,\delta ).$

Proof. 

Suppose $f_j=h_j+\overline{g_j}\in {\mathcal{BH}}^0(\gamma ,\delta )$ $(j=1,2)$. Then, the convolution of $f_1$ and $f_2$ is defined as $f_1\ast f_2=h_1\ast h_2+\overline{g_1\ast g_2}.$ In order to prove that $f_1\ast f_2$∈${\mathcal{BH}}^0(\gamma ,\delta ),$ we need to prove that ${\mathsf{Ϝ}}_{\mu }=h_1\ast h_2+\mu (g_1\ast g_2)\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for each $\mu$ $\left(\left|\mu \right|=1\right).$ By Lemma 4, the class ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$ is closed under convolutions for each $\mu$ $\left(\left|\mu \right|=1\right),$ $h_j+\mu g_j\in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for $j=1,2.$ Then, both ${\mathsf{Ϝ}}_1$ and ${\mathsf{Ϝ}}_2$ given by

$${\mathsf{Ϝ}}_1=(h_1-g_1)\ast (h_2-\mu g_2)\mathrm{and}{\mathsf{Ϝ}}_2=(h_1+g_1)\ast (h_2+\mu g_2),$$

belong to ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$. Since ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$ is closed under convex combinations, then the function

$${\mathsf{Ϝ}}_{\mu }={\displaystyle \frac{1}{2}}({\mathsf{Ϝ}}_1+{\mathsf{Ϝ}}_2)=h_1\ast h_2+\mu (g_1\ast g_2)$$

belongs to ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$. Hence, ${\mathcal{BH}}^0(\gamma ,\delta )$ is closed under convolution. □

Now, we consider the Hadamard product of a harmonic function with an analytic function, which is defined by Goodloe [19] as

$$f\tilde{\ast }\varphi =h\ast \varphi +\overline{g\ast \varphi },$$

where $f=h+\overline{g}$ is a harmonic function and $\varphi$ is an analytic function in $\Delta .$

Theorem 8.

Let $f\in$ ${\mathcal{BH}}^0(\gamma ,\delta )$ and $\varphi \in \mathcal{A}$ be such that $\mathit{Re}\left[{\displaystyle \frac{\varphi \left(\zeta \right)}{\zeta }}\right]>{\displaystyle \frac{1}{2}}$ for $\zeta \in \Delta ,$ then, $f\tilde{\ast }\varphi$∈${\mathcal{BH}}^0(\gamma ,\delta ).$

Proof. 

Suppose that $f=h+\overline{g}\in$ ${\mathcal{BH}}^0(\gamma ,\delta ),$ then, ${\mathsf{Ϝ}}_{\mu }=h+\mu g\in$ ${\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for each $\mu$ $\left(\left|\mu \right|=1\right).$ By Theorem 1, to show that $f\tilde{\ast }\varphi$∈${\mathcal{BH}}^0(\gamma ,\delta ),$ we need to show that $\Theta =h\ast \varphi +\mu (g\ast \varphi )$∈${\mathcal{B}}_1(\gamma ,\delta ,0;0)$ for each $\mu$ $\left(\left|\mu \right|=1\right).$ Write $\Theta$ as $\Theta ={\mathsf{Ϝ}}_{\mu }\ast \varphi ,$ and

$$\begin{array}{ccc}& & \gamma {\displaystyle \frac{\Theta \left(\zeta \right)}{\zeta }}+\delta {\Theta }^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\Theta }^{″}\left(\zeta \right)\hfill \\ & & \\ & =& \left(\gamma {\displaystyle \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }}+\delta {\mathsf{Ϝ}}_{\mu }^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\mathsf{Ϝ}}_{\mu }^{″}\left(\zeta \right)\right)\ast {\displaystyle \frac{\varphi \left(\zeta \right)}{\zeta }}.\hfill \end{array}$$

Since $\mathrm{Re}\left[{\displaystyle \frac{\varphi \left(\zeta \right)}{\zeta }}\right]>{\displaystyle \frac{1}{2}}$ and $\mathrm{Re}\left[\gamma {\displaystyle \frac{{\mathsf{Ϝ}}_{\mu }\left(\zeta \right)}{\zeta }}+\delta {\mathsf{Ϝ}}_{\mu }^{\prime }\left(\zeta \right)+\left({\displaystyle \frac{\delta -\gamma }{2}}\right)\zeta {\mathsf{Ϝ}}_{\mu }^{″}\left(\zeta \right)\right]>0$ in $\Delta ,$ Lemma 2 proves that $\Theta \in {\mathcal{B}}_1(\gamma ,\delta ,0;0)$. □

Corollary 1.

Let $f\in$ ${\mathcal{BH}}^0(\gamma ,\delta )$ and $\varphi \in \mathcal{K},$ then, $f\tilde{\ast }\varphi \in$ ${\mathcal{BH}}^0(\gamma ,\delta ).$

Proof. 

Suppose $\varphi \in \mathcal{K},$ then, $\mathrm{Re}\left[{\displaystyle \frac{\varphi \left(\zeta \right)}{\zeta }}\right]>{\displaystyle \frac{1}{2}}$ for $\zeta \in \Delta .$ As a corollary of Theorem 8, $f\tilde{\ast }\varphi$∈${\mathcal{BH}}^0(\gamma ,\delta ).$ □

4. Graphical Representation

Graphical representation is pivotal in understanding harmonic functions by providing visual insights into their behavior and properties. Graphical representations, such as plots and diagrams, offer a tangible way to grasp their oscillatory patterns, amplitude variations, and phase shifts. Visualizing graphs allows one to discern key features like nodes, antinodes, and resonance frequencies, which are crucial for analyzing phenomena ranging from acoustics to electromagnetic fields.

Harmonic functions, which satisfy Laplace’s equation and exhibit qualities such as periodicity and symmetry, can often be complex to comprehend through equations alone. Moreover, graphical representation facilitates the comparison of different harmonic functions, aiding in identifying similarities, differences, and underlying mathematical relationships. Thus, in the realm of harmonic functions, graphical representation serves as an indispensable tool for elucidating their intricate nature and enhancing conceptual understanding.

These visual tools not only aid in the comprehension of abstract concepts but also serve as powerful aids in educational settings. They help students and researchers alike to bridge the gap between theoretical formulations and practical understanding. By providing a concrete representation, graphical methods can illuminate subtle aspects of harmonic functions that might otherwise be overlooked. Hence, the use of graphical representation is essential in both learning and teaching environments for a more intuitive grasp of harmonic phenomena.

In this section, we will examine where the unit disk is mapped under these functions for the special values of the functions in this article.

Example 1.

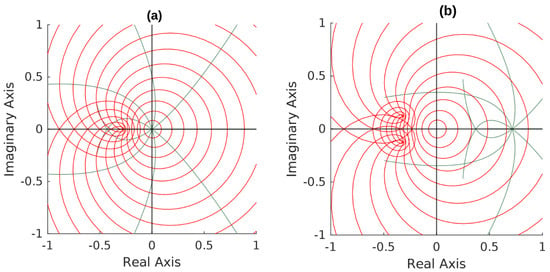
Consider the function $f\left(\zeta \right)=\zeta +{\displaystyle \frac{2(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\overline{\zeta }}^{ϵ}$ in Theorem 2. Let $ϵ=2,\delta =0.3$ and $\gamma =0.1$. Then, $f\left(\zeta \right)=\zeta +{\displaystyle \frac{4}{9}}{\overline{\zeta }}^2$.

With the help of Figure 1, it can be seen which region the unit disk transforms into under the function f. In general, these graphs provide a visual representation of the effect of the transformation on geometric shapes in the complex plane. Figure 1a shows the unit disk, while Figure 1b shows their transformed images, showing how the complex function changes the points on the unit disk.

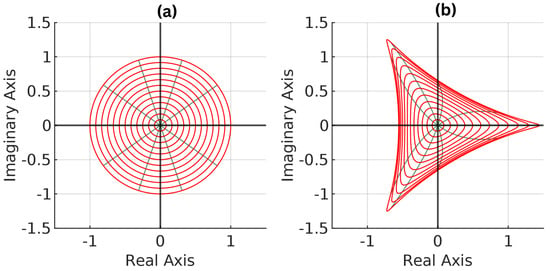
Figure 1. (a) shows the unit disk. (b) is the image of the unit disk under f.

In Figure 2, the 3D graph of the unit disk under the f function will be examined. To better understand the three-dimensional image to be drawn, we have drawn circles in different colors inside the unit disk. If we imagine that the circles of different colors we have drawn are filled with the same colors, we can find out in which region the f function transforms the different colors on the unit disk.

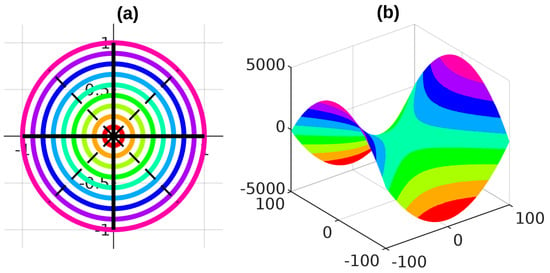
Figure 2. (a) shows the unit disk. (b) is 3D plot of the unit disk under f.

This example also shows us that ${\mathcal{BH}}^0(\gamma ,\delta )$ is a non-empty subclass of harmonic functions defined by a differential inequality.

Now, we will look at these applications for a different function and examine what the unit disk will look like under the new f function. As in Example 1, first, the image set under the given function and then the three-dimensional drawing of the unit disk will be given. In Example 1, we derived the function from Theorem 2; now, it will be derived from Theorem 3.

Example 2.

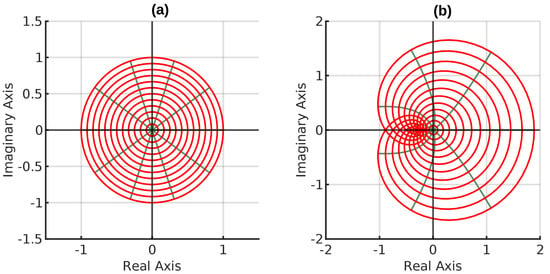
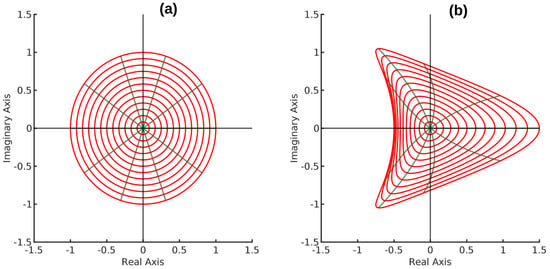
Consider the function $f\left(\zeta \right)=\zeta +{\displaystyle \sum _{ϵ\in \Omega }}{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ}$ in Theorem 3. Let $ϵ=2,\delta =0.3$ and $\gamma =0.1$. Then, $f\left(\zeta \right)=\zeta +{\displaystyle \frac{8}{9}}{\zeta }^2$. The region into which the function f used here transforms the unit disk is shown in Figure 3.

Figure 3. (a) shows the unit disk. (b) is the image of the unit disk under f.

We will now examine the 3D graph of the function $f\left(\zeta \right)=\zeta +{\displaystyle \frac{8}{9}}{\zeta }^2$ defined in Example 2 (Figure 4).

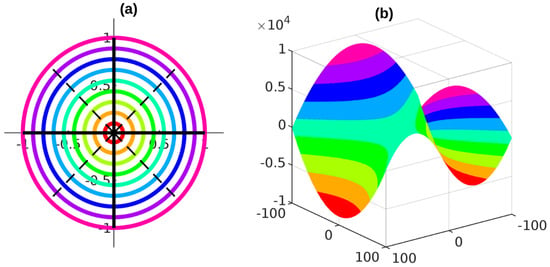
Figure 4. (a) shows the unit disk. (b) is 3D plot of the unit disk under f.

Example 3.

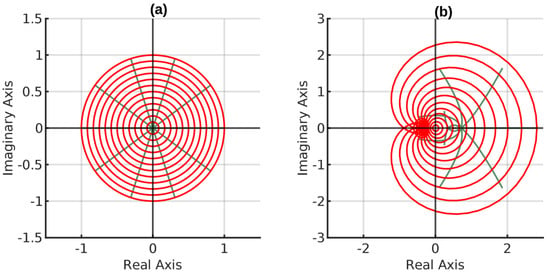
Consider the function $f\left(\zeta \right)=\zeta +{\displaystyle \sum _{ϵ\in \Omega }}{\displaystyle \frac{4(\delta +\gamma )}{(ϵ+1)\left[ϵ\right(\delta -\gamma )+2\gamma ]}}{\zeta }^{ϵ}$ in Theorem 3. Let $ϵ=3,\delta =0.015$ and $\gamma =0.01$. Then, $f\left(\zeta \right)=\zeta +{\displaystyle \frac{10}{9}}{\zeta }^2+{\displaystyle \frac{5}{7}}{\zeta }^3$. The region into which the function f used here transforms the unit disk is shown in Figure 5.

Figure 5. (a) shows the unit disk. (b) is the image of the unit disk under f.

Now, we will show what Figure 3b and Figure 5b look like up close for a better understanding. We have enlarged these plottings, and they are shown below (Figure 6).

Figure 6. A closer look at Figure 3b (a) and Figure 5b (b).

Example 4.

For $ϵ=2,\delta =0.3$, and $\gamma =0.1$, we can write $f\left(\zeta \right)=\zeta +{\displaystyle \frac{1}{6}}{\zeta }^2+{\displaystyle \frac{1}{3}}{\overline{\zeta }}^2$ from (1). The region into which the function f used here maps the unit disk is shown in Figure 7.

Figure 7. (a) shows the unit disk. (b) is the image of the unit disk under f.

5. Discussion

We obtained sharp coefficient bounds and growth estimates for the subclass, providing necessary and sufficient conditions for functions to be included. Through Theorem 1, we showed that the class is related to the well-established class of harmonic functions by a convolution operation, indicating structural robustness. The closure properties of the subclass under convex combinations and convolutions were established. The graphical examples provided a vivid understanding of how these functions map the unit disk, illustrating their geometric transformations. Through various examples, the graphs demonstrated the impact of different coefficients on the transformation of the unit disk, offering insights into the shape and behavior of the resulting regions. The 3D plots expanded the visual perspective, allowing a more comprehensive view of the transformations, emphasizing how harmonic functions influence the unit disk. Overall, these results contribute to the ongoing study of harmonic functions and their complex mappings. The graphical representations serve as a bridge between theory and visualization, enhancing comprehension and providing tangible insights into the behavior of harmonic functions under specific constraints. These visualizations can aid in identifying patterns and structures that may not be immediately apparent through theoretical analysis alone. The findings from this exploration open the door to further studies, particularly in the areas of geometric function theory and applied mathematics, where understanding the structure and transformation of harmonic functions is crucial.