Note on Intuitionistic Fuzzy Metric-like Spaces with Application in Image Processing

Abstract

Recently, the fixed-point theorem for fuzzy contractive mappings has been investigated within the framework of intuitionistic fuzzy metric-like spaces. This interesting topic was explored through the utilization of G-Cauchy sequences as defined by Grabiec. The aim of this study is to enhance the aforementioned results in a few aspects. Initially, the proof of the fixed-point theorem is simplified and condensed, allowing for potential generalization to papers focusing on similar fixed-point analyses. Furthermore, instead of G-Cauchy sequences, the classical Cauchy sequences proposed by George and Veeramani are examined, incorporating an additional condition on the fuzzy metric. Within this context, a solution to an old unresolved question posed by Gregory and Sapena is provided. The findings are reinforced by relevant examples. Finally, the introduced fuzzy metrics are applied to the field of image processing.

1. Introduction

Grabiec [1] adhered to the concept of fuzzy metric space introduced by Kramosil and Michalek [2] and presented a novel notion of G-Cauchy sequences, which significantly deviates from the classical definition of Cauchy sequences proposed by George and Veeramani [3]. While it is evident that G-Cauchyness is a weaker concept compared to the classical one, discussion and confusion have arisen surrounding this notion [4,5]. Additionally, it has been demonstrated (Note 3.13, [3]) that the standard fuzzy metric space $(\mathbb{R},M_d,·)$ is not G-complete, and that a compact fuzzy metric space does not necessarily guarantee G-completeness [6]. A more comprehensive study on various Cauchy and convergence types can be found in [7].

When focusing on fixed-point results related to G-Cauchyness, simpler proofs are achieved without the ease of transfer to the classical case. In this context, Gregory and Sapena [8] pose an open question regarding the fixed-point theorem in the classical case for fuzzy contractive sequences:

$${\displaystyle \frac{1}{\mathcal{M}(x_{n+1},x_{n+2},t)}}-1\le k\left({\displaystyle \frac{1}{\mathcal{M}(x_n,x_{n+1},t)}}-1\right).$$

Harandi [9] introduced a fuzzy metric-like space with a fresh perspective on the metric when $x=y$. Various authors have studied fixed-point theorems in fuzzy metric-like spaces, including Ćirić contraction [9], fuzzy contractive sequences [10], and fuzzy b-metric-like spaces [11]. Park [12] introduced intuitionistic fuzzy metric spaces inspired by the notion of intuitionistic fuzzy sets by Atanassov [13]. Further insights into intuitionistic fuzzy metric spaces, along with various fixed-point theorems and applications, can be found in [14,15,16,17].

In [18], intuitionistic fuzzy metric-like spaces are explored as a combination of concepts introduced by Harandi and Park, with direct references to fixed-point results obtained in [10]. Among numerous applications, the potential of fuzzy and probabilistic metrics and fixed-point results in image processing is highlighted [19,20,21,22]. This application is particularly realized through intuitionistic fuzzy sets [23,24,25].

The primary objectives of this paper are twofold as follows: to enhance interesting fixed-point results and examples related to intuitionistic fuzzy metric-like spaces as presented in [18], and to apply the introduced fuzzy metrics in image processing. The Introduction and Preliminaries provide essential concepts and notes on fuzzy metric-like and intuitionistic fuzzy metric spaces, with specific comments on the definition of Cauchy sequences in fuzzy metric spaces. Subsequently, the fixed-point theorem in intuitionistic fuzzy metric-like spaces is examined, incorporating the fuzzy contractive condition established by Gregory and Sapena, as well as the classical Cauchy sequences promoted by George and Veeramani. The discussion is supported by examples and appropriate fuzzy metrics utilized for image processing in the final section of the paper.

Some applications of fuzzy contractions in various fields of mathematics and engineering science through fractional differential equations are presented by Younis and Abdau in [26].

2. Preliminaries

Definition 1

([9]). Let $\Lambda \ne \varnothing .$ A mapping $\varsigma :\Lambda \times \Lambda \to \mathbb{R}$ is called metric-like on Λ if the following hold:

$(ML1)\varsigma (x,y)=0\Rightarrow x=y;$

$(ML2)\varsigma (x,y)=\varsigma (y,x);$

$(ML3)\varsigma (x,z)\le \varsigma (x,y)+\varsigma (y,z).$

The pair $(\Lambda ,\varsigma )$ is called a metric-like space (MLS) on $\Lambda .$

Clearly, $\varsigma (x,y)=max\{x,y\}$ is called metric-like on $\Lambda =[0,\infty ).$

Definition 2

([27,28]). A binary operation $★:[0,1]\times [0,1]\to [0,1]$ is a continuous t-norm if ★ satisfies the following conditions:

$(T1)★$ is commutative and associative;

$(T2)★$ is continuous;

$(T3)a★1=a,$ for all $a\in [0,1];$

$(T4)a★b\le c★d$ whenever $a\le c$ and $b\le d,$ and $a,b,c,d\in [0,1].$

Definition 3

([27,28]). A binary operation $\odot :[0,1]\times [0,1]\to [0,1]$ is a continuous t-conorm if ⊙ satisfies the following conditions:

$(C1)\odot$ is commutative and associative;

$(C2)\odot$ is continuous;

$(C3)a\odot 0=a,$ for all $a\in [0,1];$

$(C4)a\odot b\le c\odot d$ whenever $a\le c$ and $b\le d,$ and $a,b,c,d\in [0,1].$

Definition 4

([3]). The triplet $(\Lambda ,\mathcal{M},★)$ is called a fuzzy metric space (FMS), where Λ is an arbitrary set, ★ is a continuous t-norm and M is a fuzzy set on $\Lambda \times \Lambda \times (0,\infty )$ if it satisfies the following conditions, for all $x,y,z\in \Lambda$ and $t,s>0:$

$(FM1)\mathcal{M}(x,y,t)>0;$

$(FM2)\mathcal{M}(x,y,t)=1$ if and only if $x=y;$

$(FM3)\mathcal{M}(x,y,t)=\mathcal{M}(y,x,t);$

$(FM4)\mathcal{M}(x,y,t)★\mathcal{M}(y,z,s)\le \mathcal{M}(x,z,t+s);$

$(FM5)\mathcal{M}(x,y,·):(0,\infty )\to [0,1]$ is continuous.

$\mathcal{M}(x,y,·)$ is non-decreasing for all $x,y$ in $\Lambda .$

If $(\Lambda ,\mathcal{M},★)$ is an FMS, we say that $(\mathcal{M},★),$ or simply $\mathcal{M},$ is a fuzzy metric on $\Lambda .$ By

$${\mathcal{M}}_d(x,y,t)={\displaystyle \frac{t}{t+d(x,y)}},x,y\in \Lambda ,t>0,$$

is defined a standard fuzzy metric induced by metric $d.$ Every fuzzy metric $\mathcal{M}$ on $\Lambda$ generates a topology ${\tau }_{\mathcal{M}}$ on $\Lambda$, which has as a base the family of open sets of the form $\{B_{\mathcal{M}}(x,\epsilon ,t):x\in \Lambda ,0<\epsilon <1,t>0\},$ where $B_{\mathcal{M}}(x,\epsilon ,t)=\{y\in \Lambda :\mathcal{M}(x,y,t)>1-\epsilon \},$ for all $x\in \Lambda ,\epsilon \in (0,1)$ and $t>0.$

Theorem 1

([3]). A sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in a fuzzy metric space $(\Lambda ,\mathcal{M},★)$ converges to $x_0$ if, and only if, $\underset{n\to \infty }{lim}\mathcal{M}(x_0,x_n,t)=1,$ for all $t>0.$

Definition 5

([3,29]). A sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in a fuzzy metric space $(\Lambda ,\mathcal{M},★)$ is called Cauchy if for each $\epsilon \in (0,1)$ and each $t>0$ there exists $n_0\in \mathbb{N}$ such that $\mathcal{M}(x_n,x_m,t)>1-\epsilon ,$ for all $n,m\ge n_0$ or, equivalently, if $\underset{m,n\to \infty }{lim}\mathcal{M}(x_n,x_m,t)=1,$ for all $t>0.$ $(\Lambda ,\mathcal{M},★)$ is called complete if every Cauchy sequence in Λ is convergent with respect to ${\tau }_{\mathcal{M}}.$

Due to the definition of fuzzy metric spaces given by Kramosil and Michalek [2]), Grabiec established the following definition of a Cauchy sequence:

Definition 6

([1]). A sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in a fuzzy metric space $(\Lambda ,\mathcal{M},★)$ is called G-Cauchy if $\underset{n\to \infty }{lim}\mathcal{M}(x_n,x_{n+p},t)=1,$ for each $t>0$ and each $p\in \mathbb{N}.$

$(\Lambda ,\mathcal{M},★)$ is G-complete if every G-Cauchy sequence in $\Lambda$ is convergent.

Definition 7

([9]). The triplet $(\Lambda ,\mathcal{F},★)$ is a fuzzy metric-like space (FMLS), where Λ is an arbitrary set, ★ is a continuous t-norm and $\mathcal{F}$ is a fuzzy set on $\Lambda \times \Lambda \times (0,\infty )$, satisfying the following conditions, for all $x,y,z\in \Lambda$ and $t,s>0:$

$(FML1)\mathcal{F}(x,y,t)>0;$

$(FML2)$ if $\mathcal{F}(x,y,t)=1$ then $x=y;$

$(FML3)\mathcal{F}(x,y,t)=F(y,x,t);$

$(FML4)\mathcal{F}(x,y,t)★\mathcal{F}(y,z,s)\le \mathcal{F}(x,z,t+s);$

$(FML5)\mathcal{F}(x,y,·):(0,\infty )\to [0,1]$ is a continuous mapping.

Since in a fuzzy metric-like space, $\mathcal{F}(x,x,t)$ may be less than $1,$ this concept is applicable when the degree of nearness of x and y is not perfect for the case $x=y.$

Proposition 1

([10]). Let $(\Lambda ,\varsigma )$ be any metric-like space. Then, the triplet $(\Lambda ,\mathcal{F},★)$ is an FMLS, where ★ is defined by $a★b=ab,$ for all $a,b\in [0,1]$ and the fuzzy set $\mathcal{F}$ is given by

$$\mathcal{F}(x,y,t)={\displaystyle \frac{k·t^n}{k·t^n+m·\varsigma (x,y)}},$$

for all $x,y\in \Lambda ,t>0,k\in {\mathbb{R}}^{+},m>0$ and $n\ge 1.$

Proposition 1 still holds for t-norm $a★b=min\{a,b\}$ and shows that every metric-like space induces a fuzzy metric-like space. Specially, for $k=n=m=1$, we have the standard fuzzy metric-like space

$$\mathcal{F}(x,y,t)={\displaystyle \frac{t}{t+\varsigma (x,y)}},for all x,y\in \Lambda ,t>0.$$

Example 1

([10]). Let $\Lambda ={\mathbb{R}}^{+},k\in {\mathbb{R}}^{+}$ and $m>0.$ Define ★ by $a★b=ab$ and the fuzzy set $\mathcal{F}$ in $\Lambda \times \Lambda \times (0,\infty )$ by

$$\mathcal{F}(x,y,t)={\displaystyle \frac{k·t}{k·t+m·max\{x,y\}}},$$

for all $x,y\in \Lambda ,$ $t>0.$ Then, $(\Lambda ,\varsigma )$ is a MLS and $(\Lambda ,F,★)$ is an FMLS, but it is not an FMS, as $\mathcal{F}(x,x,t)={\displaystyle \frac{k·t}{k·t+m·x}}\ne 1,$ for all $x>0$ and $t>0.$

Proposition 2

([10]). Let $(\Lambda ,\varsigma )$ be any MLS. Then, the triplet $(\Lambda ,\mathcal{F},★)$ is an FMLS, where ★ is given by $a★b=ab$ or $a★b=min\{a,b\}$ for all $a,b\in [0,1]$ and the fuzzy set $\mathcal{F}$ is defined by

$$\mathcal{F}(x,y,t)=e^{{\displaystyle \frac{-\varsigma (x,y)}{t^n}}},$$

for all $x,y\in \Lambda ,$ $t>0,$ $n\ge 1.$

Example 2

([10]). Let $\Lambda ={\mathbb{R}}^{+}.$ Define ★ by $a★b=ab$ and the fuzzy set $\mathcal{F}$ in $\Lambda \times \Lambda \times (0,\infty )$ by

$$\mathcal{F}(x,y,t)=e^{-{\displaystyle \frac{max\{x,y\}}{t}}},$$

for all $x,y\in \Lambda ,$ $t>0.$ Then, $(\Lambda ,\varsigma )$ is an MLS and $(\Lambda ,\mathcal{F},★)$ is an FMLS, but it is not an FMS, as $\mathcal{F}(x,x,t)=e^{-{\displaystyle \frac{x}{t}}}\ne 1,$ for all $x>0$ and $t>0.$

Example 3

([10]). Let $\Lambda =\mathbb{N}.$ Define $a★b$ by $a★b=ab$ and the fuzzy set $\mathcal{F}$ in $\Lambda \times \Lambda \times (0,\infty )$ by:

$$\mathcal{F}(x,y,t)=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{x}{y^3}},& ifx\le y\hfill \\ \hfill {\displaystyle \frac{y}{x^3}},& ify\le x\hfill \end{array}\right.,$$

then, $(\Lambda ,\mathcal{F},★)$ is an FMLS, but it is not an FMS.

Definition 8

([12]). A 5-tuple $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is said to be an intuitionistic fuzzy metric space if Λ is an arbitrary set, ★ is a continuous t-norm, ⊙ is a continuous t-conorm and $\mathcal{F},\mathcal{G}$ are fuzzy sets on $\Lambda \times \Lambda \times (0,\infty )$, satisfying the following conditions, for all $x,y,z\in \Lambda ,s,t>0:$

$(IFM1)\mathcal{F}(x,y,t)+\mathcal{G}(x,y,t)\le 1;$

$(IFM2)\mathcal{F}(x,y,t)>0;$

$(IFM3)\mathcal{F}(x,y,t)=1$ if, and only if, $x=y;$

$(IFM4)\mathcal{F}(x,y,t)=\mathcal{F}(y,x,t);$

$(IFM5)\mathcal{F}(x,y,t)★\mathcal{F}(y,z,s)\le \mathcal{F}(x,z,t+s);$

$(IFM6)\mathcal{F}(x,y,.):(0,\infty )\to (0,1]$ is continuous;

$(IFM7)\mathcal{G}(x,y,t)<1;$

$(IFM8)\mathcal{G}(x,y,t)=0$ if, and only if, $x=y;$

$(IFM9)\mathcal{G}(x,y,t)=\mathcal{G}(y,x,t),$

$(IFM10)\mathcal{G}(x,y,t)\odot \mathcal{G}(y,z,s)\ge \mathcal{G}(x,z,t+s);$

$(IFM11)\mathcal{G}(x,y,.):(0,\infty )\to (0,1]$ is continuous.

Then, $(\mathcal{F},\mathcal{G})$ is called an intuitionistic fuzzy metric on $\Lambda .$ The functions $\mathcal{F}(x,y,t)$ and $\mathcal{G}(x,y,t)$ denote the degree of nearness and the degree of non-nearness between x and y with respect to $t,$ respectively. Also, $\mathcal{F}(x,y,·)$ is non-decreasing and $\mathcal{G}(x,y,·)$ is non-increasing for all $x,y\in \Lambda .$

Remark 1

([12,30]). Every fuzzy metric space $(\Lambda ,\mathcal{M},★)$ is an intuitionistic fuzzy metric space of the form $(\Lambda ,\mathcal{M},1-\mathcal{M},★,\odot )$ such that the t-norm ★ and t-conorm ⊙ are associated, i.e., $x\odot y=1-((1-x)★(1-y))$ for any $x,y\in \Lambda .$

Example 4

([12]). (Induced intuitionistic fuzzy metric). Let $(\Lambda ,d)$ be a metric space. Denote $a★b=ab$ and $a\odot b=min\{1,a+b\}$ for all $a,b\in [0,1]$ and let ${\mathcal{F}}_d$ and ${\mathcal{G}}_d$ be fuzzy sets on $\Lambda \times \Lambda \times (0,\infty )$ defined as follows:

$${\mathcal{F}}_d(x,y,t)={\displaystyle \frac{h·t^n}{h·t^n+m·d(x,y)}},{\mathcal{G}}_d(x,y,t)={\displaystyle \frac{d(x,y)}{k·t^n+m·d(x,y)}},$$

for all $h,k,m,n\in {\mathbb{R}}^{+}.$ Then, $(\Lambda ,{\mathcal{F}}_d,{\mathcal{G}}_d,★,\odot )$ is an intuitionistic fuzzy metric space.

The above example holds even with the t-norm $a★b=min\{a,b\}$ and the t-conorm $a\odot b=max\{a,b\}.$ If we take $h=k=m=n=1,$ we obtain the standard intuitionistic fuzzy metric:

$${\mathcal{F}}_d(x,y,t)={\displaystyle \frac{t}{t+d(x,y)}},{\mathcal{G}}_d(x,y,t)={\displaystyle \frac{d(x,y)}{t+d(x,y)}}.$$

Example 5

([12]). Let $\Lambda =\mathbb{N}.$ Define $a★b=max\{0,a+b-1\}$ and $a\odot b=a+b-ab$ for all $a,b\in [0,1]$ and let $\mathcal{F}$ and $\mathcal{G}$ be fuzzy sets on $\Lambda \times \Lambda \times (0,\infty )$ as follows:

$$\mathcal{F}(x,y,t)=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{x}{y}},& ifx\le y\hfill \\ \hfill {\displaystyle \frac{y}{x}},& ify\le x\hfill \end{array}\right.,\mathcal{G}(x,y,t)=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{y-x}{y}},& ifx\le y\hfill \\ \hfill {\displaystyle \frac{x-y}{x}},& ify\le x\hfill \end{array}\right..$$

for all $x,y\in \Lambda$ and $t>0.$ Then, $(\Lambda ,{\mathcal{F}}_d,{\mathcal{G}}_d,★,\odot )$ is an intuitionistic fuzzy metric space, where the t-norm ★ and t-conorm ⊙ are not associated. Note that the above function $(\mathcal{F},\mathcal{G})$ is not an intuitionistic fuzzy metric with the t-norm and t-conorm defined as $a★b=min\{a,b\}$ and $a\odot b=max\{a,b\}.$

Definition 9

([18]). Let Λ be an arbitrary set, ★ a continuous t-norm, and ⊙ a continuous t-conorm. Let $\mathcal{F}$ and $\mathcal{G}$ be fuzzy sets on $\Lambda \times \Lambda \times (0,\infty ).$ Then, $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is an intuitionistic fuzzy metric-like space (IFMLS) if the following conditions are satisfied, for all $x,y,z\in \Lambda$ and $t,s>0:$

$(IFML1)\mathcal{F}(x,y,t)+\mathcal{G}(x,y,t)\le 1;$

$(IFML2)\mathcal{F}(x,y,t)>0;$

$(IFML3)\mathcal{F}(x,y,t)=1\Rightarrow x=y;$

$(IFML4)\mathcal{F}(x,y,t)=\mathcal{F}(y,x,t);$

$(IFML5)\mathcal{F}(x,y,t)★\mathcal{F}(y,z,s)\le \mathcal{F}(x,z,t+s);$

$(IFML6)\mathcal{F}(x,y,.):(0,\infty )\to (0,1]$ is continuous;

$(IFML7)\mathcal{G}(x,y,t)<1;$

$(IFML8)\mathcal{G}(x,y,t)=0\Rightarrow x=y;$

$(IFML9)\mathcal{G}(x,y,t)=\mathcal{G}(y,x,t),$

$(IFML10)\mathcal{G}(x,y,t)\odot \mathcal{G}(y,z,s)\ge \mathcal{G}(x,z,t+s);$

$(IFML11)\mathcal{G}(x,y,.):(0,\infty )\to (0,1]$ is continuous.

Proposition 3

([18]). Let $(\Lambda ,\varsigma )$ be any metric-like space. Then, the 5-tuple $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is an IFMLS, where $a★b=min\{a,b\}$ and $a\odot b=max\{a,b\},$ for all $a,b\in [0,1]$ and $\mathcal{F},\mathcal{G}$ are given by

$$\mathcal{F}(x,y,t)={\displaystyle \frac{h·t^n}{h·t^n+m·\varsigma (x,y)}},\mathcal{G}(x,y,t)={\displaystyle \frac{\varsigma (x,y)}{h·t^n+m·\varsigma (x,y)}}$$

for all $x,y\in \Lambda ,t>0,h\in {\mathbb{R}}^{+},m>0,n\ge 1.$

Proposition 3 holds even with the t-norm $a★b=ab$ and $a\odot b=min\{1,a+b\}.$

Example 6

([18]). Let $\Lambda ={\mathbb{R}}^{+},h\in {\mathbb{R}}^{+}$ and $m>0.$ Let $a★b=ab$ and $a\odot b=min\{1,a+b\}$ for all $a,b\in [0,1].$ Define the fuzzy sets $\mathcal{F}$ and $\mathcal{G}$ in $\Lambda \times \Lambda \times (0,\infty )$ by

$$\mathcal{F}(x,y,t)={\displaystyle \frac{h·t}{h·t+m·max\{x,y\}}} and \mathcal{G}(x,y,t)={\displaystyle \frac{max\{x,y\}}{h·t+m·max\{x,y\}}},$$

for all $x,y\in \Lambda$ and $t>0.$ Then, $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is an IFMLS, but it is not an IFMS, as $\mathcal{F}(x,x,t)={\displaystyle \frac{h·t}{h·t+m·x}}\ne 1$ and $\mathcal{G}(x,x,t)={\displaystyle \frac{x}{h·t+m·x}}\ne 0,$ for all $x,y>0$ and $t>0.$

Note that, by (IFML1), in Proposition 3 and Example 6, parameter m must be greater than 1.

Proposition 4

([18]). Let $(\Lambda ,\varsigma )$ be any MLS. Then, the 5-tuple $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is an IFMLS, where $a★b=ab$ or $a★b=min\{a,b\}$ and $a\odot b=min\{1,a+b\}$ or $a\odot b=max\{a,b\},$ for all $a,b\in [0,1]$ and the fuzzy sets $\mathcal{F}$ and $\mathcal{G}$ are defined by

$$\mathcal{F}(x,y,t)=e^{{\displaystyle \frac{-\varsigma (x,y)}{t^n}}},\mathcal{G}(x,y,t)=1-e^{{\displaystyle \frac{-\varsigma (x,y)}{t^n}}},$$

for all $x,y\in \Lambda ,$ $t>0,n\ge 1.$

Example 7

([18]). Let $\Lambda ={\mathbb{R}}^{+},a★b=ab$ and $a\odot b=min\{1,a+b\}.$ Define the fuzzy sets $\mathcal{F}$ and G in $\Lambda \times \Lambda \times (0,\infty )$ by

$$\mathcal{F}(x,y,t)=e^{-{\displaystyle \frac{max\{x,y\}}{t}}},\mathcal{G}(x,y,t)=1-e^{-{\displaystyle \frac{max\{x,y\}}{t}}},$$

for all $x,y\in \Lambda ,$ $t>0.$ Then, $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is an IFMLS, but it is not an IFMS, as $\mathcal{F}(x,x,t)=e^{-{\displaystyle \frac{x}{t}}}\ne 1,\mathcal{G}(x,x,t)=1-e^{-{\displaystyle \frac{x}{t}}}\ne 0,$ for all $x>0$ and $t>0.$

Example 8

([18]). Let $\Lambda =\mathbb{N},a★b=ab$ and $a\odot b=min\{1,a+b\}.$ Define the fuzzy sets $\mathcal{F}$ and $\mathcal{G}$ in $\Lambda \times \Lambda \times (0,\infty )$ by:

$$\mathcal{F}(x,y,t)=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{x}{y^2}},& if x\le y\hfill \\ \hfill {\displaystyle \frac{y}{x^2}},& if y\le x\hfill \end{array}\right.,\mathcal{G}(x,y,t)=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{y^2-x}{y^2}},& if x\le y\hfill \\ \hfill {\displaystyle \frac{x^2-y}{x^2}},& if y\le x\hfill \end{array}\right.,$$

for all $x,y\in \Lambda .$ Then, $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is an IFMLS, but it is not an IFMS.

Definition 10

([9,12]). Let $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ be an IFMLS.

(a) A sequence $\left\{x_n\right\}$ in Λ is called convergent to $x\in \Lambda$ if $\underset{n\to \infty }{lim}\mathcal{F}(x_n,x,t)=\mathcal{F}(x,x,t)$ and $\underset{n\to \infty }{lim}\mathcal{G}(x_n,x,t)=\mathcal{G}(x,x,t)$ for all $t>0.$

(b) A sequence $\left\{x_n\right\}$ in Λ is called Cauchy if there are $0<A\le 1$ and $0\le B<1$, $A+B<1,$ such that,

for each $\epsilon \in (0,min\{A,1-B\})$ and each $t>0$ there exists $n_0\in \mathbb{N}$ such that

$$\mathcal{F}(x_n,x_m,t)>A-\epsilon ,and\mathcal{G}(x_n,x_m,t)<B+\epsilon ,$$

for all $n,m\ge n_0,$ or, equivalently, if

$$\underset{m,n\to \infty }{lim}\mathcal{F}(x_n,x_m,t)=A,and\underset{m,n\to \infty }{lim}\mathcal{G}(x_n,x_m,t)=B,$$

for all $t>0.$

(c) $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is called complete if every Cauchy sequence $\left\{x_n\right\}$ in Λ converges to some $x\in \Lambda$ such that

$$\underset{n,m\to \infty }{lim}\mathcal{F}(x_n,x,t)=\mathcal{F}(x,x,t)=\underset{n,m\to \infty }{lim}\mathcal{F}(x_n,x_m,t)$$

and

$$\underset{n\to \infty }{lim}\mathcal{G}(x_n,x,t)=\mathcal{G}(x,x,t)=\underset{n,m\to \infty }{lim}\mathcal{G}(x_n,x_m,t)$$

for all $t>0.$

3. Main Results

Definition 11.

Let $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ be an IFMLS. A mapping $f:\Lambda \to \Lambda$ is called an intuitionistic fuzzy contractive if there exists $\lambda \in (0,1)$ such that

$${\displaystyle \frac{1}{\mathcal{F}(f(x),f(y),t)}}-1\le \lambda \left[{\displaystyle \frac{1}{\mathcal{F}(x,y,t)}}-1\right]$$

(1)

and

$$\mathcal{G}(f(x),f(y),t)\le \lambda \mathcal{G}(x,y,t)$$

(2)

for all $x,y\in \Lambda$ and $t>0.$ Here, λ is called the intuitionistic fuzzy constant of $T.$

Remark 2.

Trivially, every intuitionistic fuzzy contractive mapping is a fuzzy contractive mapping.

Conversely, if condition (1) is satisfied, then condition (2) is not for $\mathcal{G}=1-\mathcal{F}.$

Theorem 2.

Let $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ be a complete intuitionistic fuzzy metric-like space and $f:\Lambda \to \Lambda$ an intuitionistic fuzzy contractive mapping with intuitionistic fuzzy contractive constant λ. Let

$$\underset{t\to 0^{+}}{lim}\mathcal{F}(x_n,x_{n+1},t)>0,n\in \mathbb{N},$$

(3)

and

$$\underset{t\to 0^{+}}{lim}\mathcal{G}(x_n,x_{n+1},t)<1,n\in \mathbb{N}.$$

(4)

Then, T has a unique fixed point $a\in \Lambda$ and $\mathcal{F}(a,a,t)=1,$ $\mathcal{G}(a,a,t)=0$ for all $t>0.$

Proof. 

For any arbitrary $x_0\in \Lambda ,$ a sequence $\left\{x_n\right\}\subset \Lambda$ is defined as $x_n=f(x_{n-1}),$ for all $n\in \mathbb{N}.$ If there exists an $n\in \mathbb{N}$ such that $x_n=x_{n-1},$ then $x_n$ is considered a fixed point of the function $f.$ Now, assuming that $x_n\ne x_{n-1},$ for all $n\in \mathbb{N},$ then, for $t>0$ and $n\in \mathbb{N},$ referring to the contractive condition (1), we have:

$${\displaystyle \frac{1}{\mathcal{F}(x_n,x_{n+1},t)}}-1={\displaystyle \frac{1}{\mathcal{F}(f(x_{n-1}),f(x_n),t)}}-1\le {\lambda }^n\left[{\displaystyle \frac{1}{\mathcal{F}(x_0,x_1,t)}}-1\right].$$

As we let n approach infinity, we obtain:

$$\underset{n\to \infty }{lim}\mathcal{F}(x_n,x_{n+1},t)=1,t>0.$$

(5)

It is necessary to prove that the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a Cauchy sequence. Assuming the opposite, i.e., there exist $\epsilon \in (0,A),$ $A\le 1t_0>0$ and sequences $\left\{n_k\right\}$ and $\left\{m_k\right\}$ such that $m_k>n_k>k,$ for every $k\in \mathbb{N}$ and

$$\mathcal{F}(x_{m_k},x_{n_k},t_0)\le A-\epsilon ,k\in \mathbb{N},$$

(6)

and

$$\mathcal{F}(x_{m_k-1},x_{n_k},t_0)>A-\epsilon ,k\in \mathbb{N}.$$

(7)

Clearly, from (6),

$$\underset{k\to \infty }{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)\le A-\epsilon .$$

(8)

Using (IFML5), for any $k\in \mathbb{N}$ and $p\in (0,t_0),$ it follows that

$$\mathcal{F}(x_{m_k},x_{n_k},t_0)\ge \mathcal{F}(x_{m_k},x_{m_k-1},p)★\mathcal{F}(x_{m_k-1},x_{n_k},t_0-p).$$

(9)

By letting $p\to 0^{+}$ in the inequality (9), considering the continuity of T and (3), we can deduce

$$\begin{gathered} \underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)=\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)) \\ \ge \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{m_k-1},p)★\mathcal{F}(x_{m_k-1},x_{n_k},t_0-p)) \\ =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{m_k-1},p))★\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k-1},x_{n_k},t_0-p)) \\ =1★\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k-1},x_{n_k},t_0)=\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k-1},x_{n_k},t_0)\ge A-\epsilon , \end{gathered}$$

and, together with (8), we have

$$\underset{k\to \infty }{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)=A-\epsilon .$$

To demonstrate that $\underset{k\to \infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)=A-\epsilon ,$ we utilize conditions (3) and (7) as follows:

$$\begin{gathered} \underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)) \\ \ge \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0-p)★\mathcal{F}(x_{n_k},x_{n_k+1},p)) \\ \ge \underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)★1=\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)=A-\epsilon . \end{gathered}$$

Furthermore, using conditions (3) and (7), we have:

$$\begin{gathered} A-\epsilon =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k},t_0)) \\ \ge \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0-p)★\mathcal{F}(x_{n_k+1},x_{n_k},p)) \\ \ge \underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)★1=\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0). \end{gathered}$$

Therefore, we have:

$$\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)=A-\epsilon .$$

Now,

$$\begin{gathered} \underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k+1},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k+1},x_{n_k+1},t_0)) \\ \ge \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k+1},x_{m_k},p)★\mathcal{F}(x_{m_k},x_{n_k+1},t_0-p)) \\ =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k+1},x_{m_k},p))★\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0-p)) \\ =1★\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)=A-\epsilon , \end{gathered}$$

On the other hand, we can show that

$$\begin{gathered} A-\epsilon =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{n_k+1},t_0)) \\ \ge \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{F}(x_{m_k},x_{m_k+1},t_0-p)★\mathcal{F}(x_{m_k+1},x_{n_k+1},p)) \\ \ge 1★\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k+1},x_{n_k+1},t_0),)=\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k+1},x_{n_k+1},t_0). \end{gathered}$$

So,

$$\underset{k\to +\infty }{lim}\mathcal{F}(x_{m_k+1},x_{n_k+1},t_0)=A-\epsilon .$$

Using the contractive condition for $\mathcal{F}$, we can express the relationship as follows:

$${\displaystyle \frac{1}{\mathcal{F}(x_{m_k+1},x_{n_k+1},t_0)}}-1\le \lambda \left[{\displaystyle \frac{1}{\mathcal{F}(x_{m_k},x_{n_k},t_0)}}-1\right].$$

Letting $k\to \infty$, we obtain:

$${\displaystyle \frac{1}{A}}-1\le \lambda \left[{\displaystyle \frac{1}{A}}-1\right]<{\displaystyle \frac{1}{A}}-1.$$

This leads to a clear contradiction.

By the second contractive condition (2), we have

$$\mathcal{G}(f(x_{n-1}),f{x}_n,t)=\mathcal{G}(x_n,x_{n+1},t)\le {\lambda }^n\mathcal{G}(x_0,x_1,t).$$

Therefore, we can conclude that

$$\underset{n\to \infty }{lim}\mathcal{G}(x_n,x_{n+1},t)=0,t>0.$$

(10)

To prove that sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a Cauchy sequence, we assume the contrary. That is, there exist $\epsilon \in (0,B),$ $B\le 1,t_0>0$ and sequences $\left\{n_k\right\}$ and $\left\{m_k\right\}$ such that $m_k>n_k>k,$ for every $k\in \mathbb{N}$ and the following inequalities hold:

$$\mathcal{G}(x_{m_k},x_{n_k},t_0)\ge B+\epsilon ,k\in \mathbb{N},$$

(11)

and

$$\mathcal{G}(x_{m_k-1},x_{n_k},t_0)<B+\epsilon ,k\in \mathbb{N}.$$

(12)

From (11), we have:

$$\underset{k\to \infty }{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)\ge B+\epsilon .$$

(13)

Using (IFML10), for arbitrary $k\in \mathbb{N}$ and $p\in (0,t_0),$ we obtain:

$$\mathcal{G}(x_{m_k},x_{n_k},t_0)\le \mathcal{G}(x_{m_k},x_{m_k-1},p)\odot \mathcal{G}(x_{m_k-1},x_{n_k},t_0-p).$$

(14)

If we take $p\to 0^{+}$ in the inequality (9), by continuity of ⊙ and (4), we can deduce the following:

$$\begin{gathered} \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)=\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)) \\ \le \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{m_k-1},p)\odot \mathcal{G}(x_{m_k-1},x_{n_k},t_0-p)) \\ =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{m_k-1},p))\odot \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k-1},x_{n_k},t_0-p)) \\ =0\odot \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k-1},x_{n_k},t_0)=\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k-1},x_{n_k},t_0)\le B+\epsilon , \end{gathered}$$

and in conjunction with (13), we conclude,

$$\underset{k\to \infty }{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)=B+\epsilon .$$

Let us prove that $\underset{k\to \infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)=B+\epsilon .$ By (4) and (12), we can establish that:

$$\begin{gathered} \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)) \\ \le \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0-p)\odot \mathcal{G}(x_{n_k},x_{n_k+1},p)) \\ \le \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)\odot 0=\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)=B+\epsilon . \end{gathered}$$

Additionally, based on (4) and (7),

$$\begin{gathered} B+\epsilon =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k},t_0)) \\ \le \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0-p)\odot \mathcal{G}(x_{n_k+1},x_{n_k},p)) \\ \ge \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)\odot 0=\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0). \end{gathered}$$

Therefore, we can conclude that

$$\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)=B+\epsilon .$$

Now,

$$\begin{gathered} \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k+1},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k+1},x_{n_k+1},t_0)) \\ \le \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k+1},x_{m_k},p)\odot \mathcal{G}(x_{m_k},x_{n_k+1},t_0-p)) \\ =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k+1},x_{m_k},p))\odot \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0-p)) \\ =0\odot \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)=B+\epsilon , \end{gathered}$$

Conversely, we can observe that

$$\begin{gathered} B+\epsilon =\underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{n_k+1},t_0)) \\ \le \underset{k\to +\infty }{lim}(\underset{p\to 0^{+}}{lim}\mathcal{G}(x_{m_k},x_{m_k+1},t_0-p)\odot \mathcal{G}(x_{m_k+1},x_{n_k+1},p)) \\ \le 0\odot \underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k+1},x_{n_k+1},t_0)=\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k+1},x_{n_k+1},t_0). \end{gathered}$$

So,

$$\underset{k\to +\infty }{lim}\mathcal{G}(x_{m_k+1},x_{n_k+1},t_0)=B+\epsilon .$$

In the context of a contractive condition for $\mathcal{G}$, we have

$$\mathcal{G}(x_{m_k+1},x_{n_k+1},t_0)\le \lambda \mathcal{G}(x_{m_k},x_{n_k},t_0)$$

and letting $k\to \infty$, we obtain

$$B+1\le \lambda (1+B)<1+B,$$

which is an obvious contradiction.

In both cases, the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a Cauchy sequence, implying the existence of $a\in \Lambda$ such that $\underset{n\to \infty }{lim}{x}_n=a.$ This leads to the relationships:

$$\underset{n\to \infty }{lim}\mathcal{F}(x_n,a,t)=\mathcal{F}(a,a,t)=\underset{n,m\to \infty }{lim}\mathcal{F}(x_n,x_m,t),$$

and

$$\underset{n\to \infty }{lim}\mathcal{G}(x_n,a,t)=\mathcal{G}(a,a,t)=\underset{n,m\to \infty }{lim}\mathcal{G}(x_n,x_m,t),$$

Furthermore, we have:

$${\displaystyle \frac{1}{\mathcal{F}(x_n,x_m,t)}}-1\le \lambda \left[{\displaystyle \frac{1}{\mathcal{F}(x_{n-1},x_{m-1},t)}}-1\right],$$

and as $n,m\to \infty ,$ we obtain:

$${\displaystyle \frac{1}{\mathcal{F}(a,a,t)}}-1\le \lambda \left[{\displaystyle \frac{1}{\mathcal{F}(a,a,t)}}-1\right].$$

This holds only if $\mathcal{F}(a,a,t)=1.$ Similarly from

$$\mathcal{G}(x_m,x_n,t)\le \lambda \mathcal{G}(x_{m-1},x_{n-1},t)$$

as $n,m\to \infty ,$ we arrive at:

$$\mathcal{G}(a,a,t)\le \lambda \mathcal{G}(a,a,t),$$

which is possible only if $\mathcal{G}(a,a,t)=0.$

So, we have that

$$\underset{n\to \infty }{lim}\mathcal{F}(x_n,a,t)=\mathcal{F}(a,a,t)=\underset{n,m\to \infty }{lim}\mathcal{F}(x_n,x_m,t)=1,$$

and

$$\underset{n\to \infty }{lim}\mathcal{G}(x_n,a,t)=\mathcal{G}(a,a,t)=\underset{n,m\to \infty }{lim}\mathcal{G}(x_n,x_m,t)=0.$$

The remaining part of the proof follows the same structure as discussed in [18]. □

Example 9

(Example 4 from [18]). Let $\Lambda =[0,2],a★b=ab$ and $a\odot b=max\{a,b\}$ with intuitionistic fuzzy sets defined as:

$$\mathcal{F}(x,y,t)=e^{-{\displaystyle \frac{max\{x,y\}}{t}}},\mathcal{G}(x,y,t)=1-e^{-{\displaystyle \frac{max\{x,y\}}{t}}},$$

for all $x,y\in \Lambda ,$ $t>0.$ Then, $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ forms a complete IFMLS. The mapping T, defined as

$$T(x)=\left\{\begin{array}{cc}0,& x=1\\ {\displaystyle \frac{x}{2}},& x\in [0,1)\\ {\displaystyle \frac{x}{4}},& x\in (1,2]\end{array}\right.,$$

is intuitionistic fuzzy contractive for ${\displaystyle \frac{1}{2}}\le \lambda <1.$ By Theorem 1 [18], T has a unique fixed point.

Remark 3.

The mapping T defined in Example 9 is not intuitionistic fuzzy contractive. Specifically, condition (1) is satisfied when ${\displaystyle \frac{1}{2}}\le \lambda <1.$ However, when considering condition (2), for $x,y\in [0,1),x\ge y,t>0,$ we observe that:

$$1-e^{-{\displaystyle \frac{x}{2t}}}\le \lambda (1-e^{-{\displaystyle \frac{x}{t}}})when\lambda \ge {\displaystyle \frac{e^{\frac{x}{2t}}}{1+e^{\frac{x}{2t}}}}.$$

As ${\displaystyle \frac{e^{\frac{x}{2t}}}{1+e^{\frac{x}{2t}}}\to 1}$ when $t\to 0,$ for any $x\in (0,1),$ it follows that $\lambda \ge 1.$

Remark 4.

Theorem 2 enhances the results presented in Theorem 1 [18] in several key aspects. Firstly, it is noted that the limits (5) and (10) can only be attained through the contraction conditions (1) and (2), as demonstrated in the proof of Theorem 2. Additionally, Theorem 2 highlights the presence of classical Cauchy sequences, as opposed to the G-Cauchy sequences discussed in [18]. This distinction is achieved through the introduction of supplementary conditions (3) and (4), which can be easily satisfied, as illustrated in the subsequent examples.

Furthermore, if any contractive condition leads to (5), then the sequence automatically becomes G-Cauchy, as demonstrated by the inequality:

$$\mathcal{M}(x_n,x_{n+p},t)\ge \mathcal{M}(x_n,x_{n+1},{\displaystyle \frac{t}{p}})★\mathcal{M}(x_{n+1},x_{n+2},{\displaystyle \frac{t}{p}})★\cdots ★\mathcal{M}(x_{n+p-1},x_{n+p},{\displaystyle \frac{t}{p}}),$$

which leads to the result $1★1★\cdots ★1=1,$ as $n\to \infty .$ Utilizing this, the simplification and shortening of many proofs (for example, in [10,11,18]) could be performed.

Moreover, the condition (3) along with the methodologies employed in the proof of Theorem 2 can be extended to the context of FMS. This extension provides a resolution to the open question posed by Gregory and Sapena [8] regarding the fixed-point theorem involving fuzzy contractive sequences within the classical Cauchy framework.

Example 10.

Let $\Lambda =[0,1],a★b=ab$ and $a\odot b=max\{a,b\}.$ Intuitionistic fuzzy sets are defined as:

$$\mathcal{F}(x,y,t)=e^{-{\displaystyle \frac{m·max\{x,y\}}{t+1}}},\mathcal{G}(x,y,t)=1-e^{-{\displaystyle \frac{max\{x,y\}}{t+1}}},$$

for all $x,y\in \Lambda ,$ $t>0,$ $m>1.$ Then, $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ is a complete IFMLS. Let the mapping T be defined as ${\displaystyle T(x)=\frac{x}{2},}$ where $x\in \Lambda .$ The following inequalities hold:

$$e^{{\displaystyle \frac{mx}{2t+2}}}-1\le \lambda (e^{{\displaystyle \frac{mx}{t+1}}}-1)when\lambda \ge {\displaystyle \frac{1}{e^{\frac{mx}{2t+2}}+1}},$$

and condition (1) holds for $\lambda \ge {\displaystyle \frac{1}{2}}.$ Further,

$$1-e^{-{\displaystyle \frac{x}{2t+2}}}\le \lambda (1-e^{-{\displaystyle \frac{x}{t+1}}})when\lambda \ge {\displaystyle \frac{e^{\frac{x}{2t+2}}}{1+\frac{x}{e^{\frac{x}{2t+2}}}}},$$

and condition (2) holds for $\lambda \ge {\displaystyle \frac{\sqrt{e}}{1+\sqrt{e}}}.$

Remark 5.

Example 10 essentially improves Example 4 [18] considering Remark 3. Additionally, the utilization of the parameter $m>1$ in defining the intuitionistic fuzzy sets $\mathcal{F}$ and $\mathcal{G}$ ensures that $\mathcal{F}+\mathcal{G}<1.$ This condition illustrates that an IFMLS is not directly induced by an FMLS, as outlined in Remark 1.

Example 11.

Let $\Lambda =[0,k],a★b=ab$ and $a\odot b=max\{a,b\}.$ Intuitionistic fuzzy sets are defined as:

$$\mathcal{F}(x,y,t)={\displaystyle \frac{t+1}{t+1+m·max\{x,y\}}},\mathcal{G}(x,y,t)={\displaystyle \frac{max\{x,y\}}{t+1+m·max\{x,y\}}},$$

for all $x,y\in \Lambda ,$ $t>0,$ $m>1.$ Then, the 5-tuple $(\Lambda ,\mathcal{F},\mathcal{G},★,\odot )$ forms a complete IFMLS. Let the mapping T be defined as ${\displaystyle T(x)=\frac{x}{s},s>1,x\in \Lambda .}$ It is evident that condition (1) is satisfied for $\lambda \ge {\displaystyle \frac{1}{2}}.$ Considering condition (2):

$${\displaystyle \frac{1}{st+s+mx}}\le \lambda {\displaystyle \frac{1}{t+1+mx}}$$

it holds true when ${\displaystyle \lambda \ge \frac{1+mk}{s+mk}.}$ For instance, if ${\displaystyle \Lambda =[0,1],m=2,T(x)=\frac{x}{4}}$, then ${\displaystyle \lambda \ge \frac{1}{2}.}$

Example 12.

In [24], intuitionistic fuzzy sets given by

$$A_p=\{(x,{\mathcal{F}}_A(x),{\displaystyle \frac{1-{\mathcal{F}}_A(x)}{1+p·{\mathcal{F}}_A(x)}}),x\in \Lambda \}$$

are applied in color image processing for leukocyte segmentation. From this perspective, keeping all elements from Example 11, except $\mathcal{G}$, where, for $\mathcal{F}(x,y,t)={\displaystyle \frac{t+1}{t+1+m·max\{x,y\}}}$, we have

$$\mathcal{G}(x,y,t)={\displaystyle \frac{1-\mathcal{F}(x,y,t)}{1+p·\mathcal{F}(x,y,t)}}={\displaystyle \frac{m·max\{x,y\}}{(1+p)(t+1)+m·max\{x,y\}}}.$$

Then, condition (2) holds for

$$\lambda \ge {\displaystyle \frac{1+p+mk}{s(1+p)+mk}}.$$

For example, if we take ${\displaystyle \Lambda =[0,1],m=\frac{3}{2},p=1,s=3}$, then ${\displaystyle \lambda \in [\frac{1}{2},1).}$

Remark 6.

In Example 11, more general fuzzy sets can be observed as follows:

$$\mathcal{F}(x,y,t)={\displaystyle \frac{h·t^n+1}{h·t^n+1+m·max\{x,y\}}},\mathcal{G}(x,y,t)={\displaystyle \frac{max\{x,y\}}{h·t^n+1+m·max\{x,y\}}},$$

for all $x,y\in \Lambda ,t>0$ and $m>1,h,n\in {\mathbb{R}}^{+}.$ Also, with

$$\mathcal{F}(x,y,t)={\displaystyle \frac{t+1}{t+1+m·{(\max \{x,y\})}^2}},\mathcal{G}(x,y,t)={\displaystyle \frac{{(\max \{x,y\})}^2}{t+1+m·{(\max \{x,y\})}^2}},$$

for all $x,y\in \Lambda ,t>0$ and $m>1,$ the set Λ could contain negative reals, for example, $\Lambda =[-k,k].$

4. Application

In this section, we explore the application of fuzzy metrics in filtering grayscale images. This application draws from the concept of the fuzzy filter as defined by N. M. Ralević, D. Karaklić and N. Pištinjat in [31], among other similar articles. Fuzzy metrics encompass a range of concepts that are influenced by image pixels. Each image pixel $(i,J_i)$ (“position”, “brightness level”) can be characterized by spatial coordinates of pixel $i_1,i_2$ (points $i=(i_1,i_2)\in I\times I,$ $I=\{0,1,...,n-1\}$ from the screen), and by the number $J_i$, which represents the brightness level of the pixel.

Image filtering is the process of waking up a suspect pixel replaced with the one without the sum. Typically, this is achieved by replacing the central pixel $(i,J_i)$ in the window $W=\left\{(i,J_i)\right|i\in I_1\times I_2\}$, ($i=(i_1,i_2)\in I_1\times I_2,$ (a square portion of the image of $(2n-1)\times (2n-1)$ pixels) with a pixel which represents the other pixels from V in the best possible way, that is, by the pixel that is the most similar in brightness and spatial distance to other pixels from W.

Selection bias is another potential concern because it is of enormous importance to choose a good criterion for selecting such a pixel without noise, which will replace the pixel with noise in a given window W, because the choice of pixels affects the image quality, i.e., affects the degree of the removed noise.

In the algorithm for fuzzy filtering of images, we utilize a metric $\mathit{c}:W\times W\to R$ as follows:

$$\mathit{c}((i,J_i),(j,J_j))=\mathit{\tau }(J_i,J_j)·\mathit{t}(i,j).$$

(15)

The fuzzy metric which is used in order to measure similarity in brightness level among pixels is:

$$\mathit{\tau }(J_i,J_j)={\displaystyle \frac{K+1}{K+1+m·|J_i-J_j|}}.$$

(16)

The fuzzy metric that considers the spatial distance between pixels is:

$$\mathit{t}(i,j)={\displaystyle \frac{max\left\{\right|i_1-j_1|,|i_2-j_2\left|\right\}}{t+1+m·max\left\{\right|i_1-j_1|,|i_2-j_2\left|\right\}}}.$$

(17)

In the following example, the picture Figure 1 is given in jpg format.

Figure 1. Original image kidney.jpg.

To test the quality of that image, we will use the image quality index UIQI, defined in the paper by Z. Wang and A.C. Bovik [32]. For measuring sharpness, we have used the image quality metrics introduced in the paper [33] by N.D. Narvekar and L.J. Karam.

As we can see, the filtered image given below is contaminated with $sp=5\%,10\%$ and $50\%$ salt and pepper noise. The chosen size of window is 5.

Let us present the results of the experiments we conducted and the corresponding images. We will compare the quality of the images obtained using the fuzzy filter FF and the vector median filter VMF.

Let $sp=5\%$ (Figure 2).

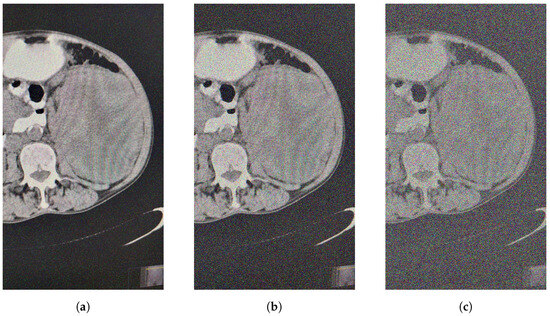
Figure 2. (a) Contaminated image $sp=5\%$. (b) Contaminated image $sp=20\%$. (c) Contaminated image $sp=50\%$.

The values of the metric of image quality UIQI for the filtered image (Figure 3a) by median filter are equal to $UIQI=0.336147196.$ The sharpness for the image filtered by VMF is 0.7578.

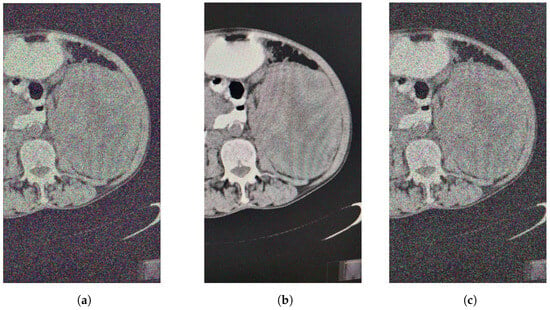
Figure 3. (a) Decontaminated image by VMF. (b) Decontaminated image by FF. (c) Decontaminated image by FF.

The tested values of the parameters appearing in those metrics ranged from 0 to 500 with a step of 100 for $K,$ while t ranged from 0 to 1.1 with a step of 0.1. The best values of the UIQI image quality metric (for each color) for the image filtered (using the method proposed in [31]) were obtained for $t=0.5$ and that is for $K=300$ (Figure 3b),

$$UIQI=0.267224408.$$

The sharpness for the image filtered by our metric is 0.9918.

The tested values of the parameters appearing in those metrics ranged from 0 to 500 with a step of 20 for $K,$ while t ranged from 0 to 500 with a step of 20. The best values of the UIQI image quality metric (for each color) for the image filtered were obtained for $t=360$ and that is for $K=420$,

$$UIQI=0.268800065.$$

The sharpness for the image filtered by our metric is 0.9915.

The tested values of the parameters appearing in those metrics ranged from 0 to 5000 with a step of 200 for $K,$ while t ranged from 0 to 1 with a step of 0.1. The best values of the UIQI image quality metric (for each color) for the images filtered were obtained for $t=0.4$ and that is for $K=400,$

$$UIQI=0.26546644.$$

The sharpness for the image filtered by our metric is 0.9901.

Let $sp=20\%$ (Figure 2b).

The values of the metric of image quality UIQI for the filtered image by median filter are equal to $UIQI=0.23954835.$ The sharpness for the image filtered by VMF is 0.6943.

The tested values of the parameters appearing in those metrics ranged from 0 to 500 with a step of 100 for $K,$ while t ranged from 0 to 500 with a step of 100. The best values of the UIQI image quality metric (for each color) for the image filtered were obtained for $t=400$ and that is for $K=500$ (Figure 3c),

$$UIQI=0.171202806.$$

The sharpness for the image filtered by our metric is 0.9967.

Let $sp=50\%$ (Figure 2c).

The values of the metric of image quality UIQI for the filtered image by median filter are equal to $UIQI=0.133346973.$ The sharpness for the image filtered by VMF is 0.8719.

The tested values of the parameters appearing in those metrics ranged from 0 to 500 with a step of 100 for $K,$ while t ranged from 0 to 500 with a step of 100. The best values of the UIQI image quality metric (for each color) for the image filtered were obtained for $t=500$ and that is for $K=500,$

$$UIQI=0.070832171.$$

The sharpness for the image filtered by our metric is 0.9985.

Our results showed that our filtered image had slightly lower values in terms of UIQI image quality but significantly higher sharpness. This emphasizes the relationship between image quality and sharpness, which is crucial when preserving important details in the image.

The previous experiments involved filtering images noised with different percentages of salt and pepper noise using the median filter (VMF) and the fuzzy filter (FF). Now, we apply other types of noise (Figure 4a–c), to the same original image Figure 1 using the appropriate functions in the MATLAB package.

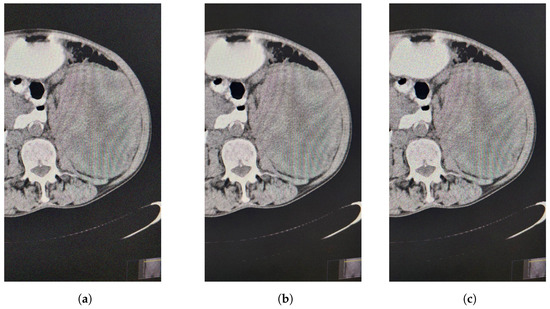
Figure 4. (a) Contaminated image by Gaussian noise. (b) Contaminated image by Poisson noise. (c) Contaminated image by speckle noise.

The programs we use are coded in the MATLAB package, and to test image quality, we use the UIQI quality index (Z. Wang and A.C. Bovik [32]). For testing the sharpness of the filtered images, we use the metrics defined in the paper by N.D. Narvekar and L.J. Karam [33]. Note that the UIQI index and sharpness values range within the interval $[0,1],$ where values closer to 1 indicate better filtering quality and image sharpness.

In the algorithm for fuzzy filtering of images, we use a metric $\mathit{c}$ defined as above in (15). The fuzzy metric used to measure similarity in brightness level among pixels is given in (16), with the parameter $m=2$. The tested values of the parameter K appearing in these metrics ranged from 0 to 5000, with a step of 500.

The fuzzy metric that considers the spatial distance between pixels is given in (17) and the tested values of the parameter t appearing in those metrics ranged from 0 to 5000 with a step of 500.

For the median filter, the obtained results are given in the Table 1:

Table 1. Values of UIQI and sharpness for VMF.

Noise	UIQI	Sharpness
$S\&P$ noise	0.119052993	0.8719
Gaussian noise	0.284389143	0.7251
Poisson noise	0.441619484	0.8024
speckle noise	0.356229611	0.7195

For the fuzzy filter, the obtained results are given in the Table 2:

Table 2. Values of UIQI and sharpness for FF.

Noise	UIQI	Sharpness
$S\&P$ noise	0.069479288	0.9980
Gaussian noise	0.251163011	0.9922
Poisson noise	0.322539216	0.9806
speckle noise	0.234211638	0.9907

When considering the fuzzy metrics with parameter $K=500$, the image filtered by FF exhibits the best UIQI index.

We note that the median filter gives a higher UIQI quality index for images obtained by removing noise from the noised original images, for all types of noise considered (Table 1 and Table 2). The sharpness of the filtered images using FF is noticeably better than that of images filtered with VMF (Table 1 and Table 2).

If we look at the fuzzy metrics parameters that occur with FF, the best UIQI index is achieved with images where $K=500.$

Research on image filtering using fuzzy metric-based filters can be found in studies such as [31,34,35].

5. Conclusions

The fixed-point theorem for fuzzy contractive mappings was explored within intuitionistic fuzzy metric-like spaces (Onbaşioğlu, Varol, Matematika, 2023, 11, 1902). As well as improvements and simplifications of the evidence, generalizations were examined for Cauchy sequences as understood by George and Veeramani.

Furthermore, we aimed to examine how intuitionistic fuzzy metric-like spaces that fulfill the conditions of the stated fixed-point theorem behave compared to other fuzzy metrics in applications. Specifically, image filtering with a fuzzy filter (FF) based on such fuzzy metrics was compared to the vector median filter (VMF). Images were subjected to different levels of pepper noise. Various parameters in the fuzzy metrics were adjusted and illustrated as part of the research. In the examples provided, the fuzzy metric proved to be more effective in enhancing the quality of the filtered image with FF compared to VMF, resulting in better image sharpness.

In future work, which will focus solely on image filtering, different classes of fuzzy metrics and their corresponding fuzzy filters will be compared, observing the quality of their filtering. Comparisons can also be made for other types of noise, such as Gaussian noise, Poisson noise, and speckle noise. Some examples of such comparisons are represented in this paper.

Distances in general, and fuzzy metrics in particular, being used in image processing can also be applied to image segmentation, as demonstrated in other works by the author (see, for example, [36,37]), and copy-move forgery detection on images [38], and others. This will demonstrate the impact of intuitionistic fuzzy metric-like segmentation on quality.