A Study of Movable Singularities in Non-Algebraic First-Order Autonomous Ordinary Differential Equations

Abstract

We studied the movable singularities of solutions of autonomous non-algebraic first-order ordinary differential equations in the form of $y^{\prime }=I\left(y\left(t\right)\right)$ and $y^{\prime }=I_1\left(y\left(t\right)\right)+I_2\left(y\left(t\right)\right)+\cdots +I_n\left(y\left(t\right)\right)$, aiming to prove that all movable singularities of all complex solutions of these equations are at most algebraic branch points. This study explores the use of the constructing triangle method to analyze complex solutions of autonomous non-algebraic first-order ordinary differential equations. For complex solutions in the form of $y=w+iv$, we treat the constructing triangle method as a way to construct a right-angled triangle in the complex plane, with the lengths of the adjacent sides being w and v. We use the definitions of the trigonometric functions sin and cos (the ratio of the adjacent side to the hypotenuse) to represent the trigonometric functions of complex solutions $y=w+iv$. Since the movable singularities of the inverse functions of trigonometric functions are easy to analyze, the properties of the movable singularities of the complex solutions are then easy to deal with.

1. Introduction

In recent years, there have been a lot of papers concerning algebraic solutions of first-order autonomous algebraic ordinary differential equations (AODEs), Grasegger [1] analyzed radical solutions of AODEs. Vo and Zhang [2] also analyzed rational solutions of AODEs. Feng and Gao [3,4] introduced an algorithm to determine the existence of non-trivial rational solutions of autonomous first-order ordinary differential equations, and Winkler [5] generalized them to systems of autonomous ordinary differential equations. Falkensteiner and Sendra [6] analyzed formal power series solutions of AODEs. They found that any formal power series solution pertaining to autonomous first-order algebraic ordinary differential equations exhibits convergence. Building upon this finding, Cano, Falkensteiner, and Sendra [7] broadened the scope to encompass fractional power series solutions and presented an algorithm capable of computing all such solutions. First-order nonlinearly coupled ordinary differential equations were studied in [8]. Singularities of singular solutions of algebraic ordinary differential equations have also been studied in recent years [9]. Saji and Takahashi studied singularities of singular solutions of first-order differential equations of the Clairaut type. In [10], Cui and Hui studied a second-order differential equation with indefinite and repulsive singularities for the first time. Nevertheless, there are merely a handful of steps involved in addressing the challenge of analyzing solutions of autonomous non-algebraic first-order ordinary differential equations. In our research, we focused on studying movable singularities of solutions of autonomous non-algebraic first-order ordinary differential equations in which we consider complex solutions only.

The distinctive features of autonomous non-algebraic first-order ODEs in comparison to other forms of ODEs are described below.

Absence of Explicit Dependence on the Independent Variable: Autonomous ODEs do not explicitly depend on the independent variable. For a first-order autonomous ODE, this means the equation can be written as $F(y,y^{\prime })=0$ or in the standard form $\frac{dy}{dx}=f\left(y\right)$, where y is the dependent variable and $y^{\prime }$ is its derivative. In contrast, non-autonomous ODEs explicitly depend on the independent variable, e.g., $F(x,y,y^{\prime })=0$.

Invariance to Time Shifts: Autonomous ODEs do not depend on the independent variable; their solutions are invariant to time shifts. This means that if $y\left(t\right)$ is a solution, then $y(t+c)$ (where c is a constant) is also a solution. This property is not shared by non-autonomous ODEs.

Simplification of the Integration Process: The absence of explicit reliance on the independent variable in autonomous ODEs leads to a streamlining of the integration process. Specifically, as these ODEs do not depend explicitly on variables like time (t), the integration is narrowed down to solely examining the dependent variable and its derivatives. This eliminates the requirement to take into account variations in the independent variable during the integration process, thereby simplifying the steps involved in solving such equations.

Absence of Algebraic Terms: As the name indicates, algebraic ODEs contain algebraic terms or expressions in addition to the derivatives. The algebraic terms can be polynomials, square roots, fractions, etc. Non-algebraic ODEs do not explicitly contain algebraic terms or expressions in their formulation.

Relationship to Dynamical Systems: Solutions of autonomous ODEs can be studied in the phase plane (the $y-y^{\prime }$ plane), where qualitative features like equilibrium points, stability, and periodic orbits can be easily visualized (see [11]). Non-autonomous ODEs depend explicitly on time or some other external parameters. This means the system’s behavior evolves not only based on its internal state but also on external influences. Due to this difference, the concept of a cocycle in dynamical systems specifically describes how trajectories of non-autonomous dynamical systems evolve under time shifts. Mathematically, consider a non-autonomous dynamical system governed by an equation of motion $x(t+1)=f\left(x\right(t),u(t),t)$, where $x\left(t\right)$ is the state at time t, $u\left(t\right)$ is an external control input, and f describes the system’s evolution. Cocycle properties describe how the system’s trajectory starting from a point $x_0$ at time $t_0$ relates to the trajectory starting from a shifted point $x_1$ at a later time $t_0$. However, since solutions of autonomous ODEs are invariant to time shifts, the concept of a cocycle does not apply to autonomous dynamical systems. For more information on this, especially the stability of non-autonomous systems, please see [12,13,14].

In this paper, we consider autonomous non-algebraic first-order ordinary differential equations of the form

$$y^{\prime }=I\left(y\left(t\right)\right)$$

(1)

and we also consider autonomous non-algebraic first-order ordinary differential equations of the form

$$y^{\prime }=I_1\left(y\left(t\right)\right)+I_2\left(y\left(t\right)\right)+\cdots +I_n\left(y\left(t\right)\right)$$

(2)

in which $I_n$ is non-algebraic in y for $t>0$.

In algebraic ordinary differential equations [15], some singularities are known as movable singularities since their locations change as we transition from one solution to another by altering the initial conditions. For example, the general solution of

$$\begin{array}{c}\hfill w^{\prime }=\frac{w}{2}(z^2{w}^2-\frac{2}{z}+\frac{1}{z^2{w}^2})\end{array}$$

(3)

is $w\left(z\right)=z^{-1}\sqrt{tan(z-c)}$, where c is an arbitrary constant. The singularity at $z=0$ is fixed, while all other singularities (which are located at $z=c+\left(\frac{n\pi }{2}\right)$, $n\in \mathbb{Z}$) are movable square-root branch points. This pertains to a specific type of algebraic singularity where, in the vicinity of such a singularity at $z=z_0$, there exists a rational number $r>0$ such that the solution can be expressed as the sum of a Laurent series in ${(z-z_0)}^r$ with a finite principal part in this region. Readers can find further details in Ince [16] or Hille [17]. This is also supported by Painlevé ’s theorem.

Theorem 1. 

(Painlevé) All movable singularities of all solutions of an equation of the form $y^{\prime }=R(z,y)$, where R is rational in y with coefficients that are analytic in z on some common open set, are either poles or algebraic branch points.

For linear equations or linear systems of algebraic ordinary differential equations, singularities are where the coefficients or inhomogeneous terms of the given differential equations or systems become singular. In the case of nonlinear equations or nonlinear systems of algebraic ordinary differential equations, singularities are those points around which the solution function could not be expressed through Taylor expansions or infinite series. For example, consider

$$\begin{array}{c}\hfill y^{″}=y^2+x.\end{array}$$

(4)

In the neighborhood of a singular point $x_0$, we can simplify to:

$$\begin{array}{c}\hfill y^{″}=y^2,\end{array}$$

(5)

and look for a power-law behavior $y\sim A{(x-x_0)}^p$. Substituting into Equation (5), we have

$$\begin{array}{c}\hfill y\sim 6{(x-x_0)}^{-2},\end{array}$$

(6)

and we can substitute $y=6{(x-x_0)}^{-2}+\delta \left(x\right)$, $z=x-x_0$ to obtain

$$\begin{array}{c}\hfill {\delta }^{″}=\frac{12}{z^2}\delta +z+x_0+{\delta }^2.\end{array}$$

(7)

Obtain the equation for $\delta$:

$$\begin{array}{ccc}\hfill \delta & =& -\frac{x_0}{10}{z}^2-\frac{z^2}{6}+C{z}^4+\frac{D}{z^3}-\frac{1}{7z^3}{\int }_0^s{s}^4{\delta }^2\left(s\right)ds+\frac{z^4}{7}{\int }_0^z{s}^{-3}{\delta }^2\left(s\right)ds\hfill \\ & =& -\frac{x_0}{10}{z}^2-\frac{z^3}{6}+C{z}^4+J\left(\delta \right),\hfill \end{array}$$

(8)

where we can see that y cannot be expressed as an infinite series around the singular point $x_0$. Also, the solution has a pole at $x_0$. For examples of solutions of algebraic ordinary differential equations that have algebraic branch points, please see [15], Theorem 2. The Painlevé theorem concerns the behavior of solutions at movable singular points and ensures that the global behavior of solutions is predictable and controllable. For equations that pass the Painlevé test but whose solutions have more complicated singularities, we can identify base points in the equivalent system of equations, as shown in [18].

Remark 1. 

All movable singularities of all solutions of an equation of the form $y^{\prime }=I(z,y)$, where I is irrational in y, are either algebraic branch points or logarithmic singularities. For example, the solutions of $y^{\prime }=\sqrt{y^2-z^2}$ are $ln(y+\sqrt{y^2-z^2})=z+C$; $y=\pm z$ are algebraic branch points. Additionally, the solutions of $y^{\prime }=\frac{1}{yln(y-z)}$ are $\int yln(y-z)dy=\int dz$; $y=z$ are logarithmic singularities. However, since equations are irrational in y, $I(z,y)$ cannot be expressed as a power series of y; intuitively, there are no poles.

If $I\left(y\right(t\left)\right)$ is algebraic in y, $y=0$ implies $y^{\prime }=0$, indicating a critical point for autonomous nonlinear equations (see more details on critical points for autonomous nonlinear equations in [19,20]). Furthermore, critical points are algebraic singularities, as shown in Section 2. However, in autonomous non-algebraic first-order ordinary differential equations, $I\left(y\right(t\left)\right)$ is non-algebraic in y; $y=0$ does not necessarily imply $y^{\prime }=0$. Readers can gain a more intuitive understanding from the examples in Section 5. Specifically, we are interested in the behaviors of the singularities in this unstudied case. We aim to prove the main theorems outlined below.

Theorem 2. 

All movable singularities of all complex solutions of an autonomous first-order ordinary differential equation of the form

$$\begin{array}{c}\hfill y^{\prime }=I\left(y\left(t\right)\right),\end{array}$$

(9)

where I is non-algebraic in y, are at most algebraic branch points.

We can extend Theorem 2 to the theorem below.

Theorem 3. 

All movable singularities of all complex solutions of an autonomous first-order ordinary differential equation of the form

$$\begin{array}{c}\hfill y^{\prime }=I_1\left(y\left(t\right)\right)+I_2\left(y\left(t\right)\right)+\cdots +I_n\left(y\left(t\right)\right),\end{array}$$

(10)

where $I_n$ is non-algebraic in y, are at most algebraic branch points.

In Section 2, we introduce categories of singularities of inverse functions. In Section 3, we present proofs of Theorems 2 and 3. In Section 5, we show some examples where all solutions of (1) and (2) have neither non-algebraic nor algebraic singularities, and other examples where all solutions of (1) and (2) exhibit algebraic singularities rather than non-algebraic ones.

The motivation for this study lies in its potential to provide a valuable tool for students and researchers to analyze more singularity problems. The motivation also lies in the potential for innovation and creativity that the constructing triangle method brings; it opens up new possibilities to transform complex solutions of autonomous non-algebraic first-order ODEs into inverse functions of certain trigonometric functions.

2. Categories of Singularities of Inverse Functions

In this section, we introduce several categories of singularities of inverse functions and some lemmas.

Consider $f:C\to G$, a non-constant holomorphic map between Riemann surfaces, where C is the complex plane. Let $z_0$ be a point in C such that $f^{\prime }\left(z_0\right)\ne 0$. Then, by Theorem 1, there exists a neighborhood V of the point $w_0=f\left(z_0\right)$ and a holomorphic map $\varphi :V\to C$ such that $f\circ \varphi =i{d}_V$. Below, we present the definitions of algebraic and non-algebraic singularities, which are referenced from Alexandre Eremeko and Walter Bergweiler [21,22].

Definition 1. 

(Algebraic Singularity of the Inverse Function) If we define a curve $\gamma :[0,1]\to G$ from $w_0$ to $w_1$, and there is an analytic continuation of ϕ along γ for $t\in [0,1)$, for the image $\Gamma \left(t\right)=\varphi \left(\gamma \right(t\left)\right)$. If $\Gamma \left(t\right)$ has a limit point at $z_1\in D$ if $t\to 1$, then by continuity $f\left(z_1\right)=w_1$, the limit set of $\Gamma \left(t\right)$ must consist of one point; otherwise, the limit set of the curve Γ would contain a continuum, while the preimage of a point under f is discrete. Therefore, Γ ends at $z_1$. If $f^{\prime }\left(z_1\right)\ne 0$, then by the inverse function theorem, an inverse function should be defined, which is differentiable through analytic continuation from ϕ to $w_1$. But in the case of $f^{\prime }\left(z_1\right)=0$, the inverse function is not defined, so ϕ has an algebraic singularity (branch point) at $w_1\in G$.

Specifically, if $f\left(z_1\right)\in C$ and $f^{\prime }\left(z_1\right)\ne 0$, or if $f\left(z_1\right)=\infty$ and $z_1$ is a simple pole of f, then $z_1$ is called an ordinary point. If $f\left(z_1\right)\in C$ and $f^{\prime }\left(z_1\right)=0$, or if $f\left(z_1\right)=\infty$ and $z_1$ is a multiple pole of f, then $z_1$ is called a critical point and a is called a critical value. Critical points are obvious algebraic singularities.

Definition 2. 

(Non-algebraic Singularity of the Inverse Function)If we define a curve $\gamma :[0,1]\to G$ from $w_0$ to $w_1$, and there is an analytic continuation of ϕ along γ for $t\in [0,1)$, for the image $\Gamma \left(t\right)=\varphi \left(\gamma \right(t\left)\right)$. Suppose $\Gamma \left(t\right)$ extends to ∞, where ∞ is the added point of the complex plane C, making C a Riemann sphere. Γ is a curve parametrized by $[0,1)$, $\Gamma \left(t\right)\to \infty$ as $t\to \infty$, and $f\left(\varphi \right(\gamma \left(t\right)\left)\right)$ has a limit point in G as $t\to 1$, so Γ is an asymptotic curve of f. The asymptotic curve of f is the  non-algebraic  singularity of the inverse function of f.

A transcendental singularity is a non-algebraic singularity. There are isolated transcendental singularities and non-isolated transcendental singularities of inverse functions. For detailed definitions, see [21]. The simplest isolated transcendental singularity of the inverse function is a logarithmic singularity, which is defined below.

Definition 3. 

(Logarithmic singularity) Given S is an isolated transcendental singularity over a point a, then there is an open disc $V=B(a,r)$ of radius r around a such that $S\left(V\right)$ is at a positive distance from other singularities. In the map $f:S\left(V\right)\setminus f^{-1}\left(a\right)\to V\setminus \left\{a\right\}$, $V\setminus \left\{a\right\}$ does not contain critical values and asymptotic values. $S\left(V\right)$ is a simply connected region bounded by a simple curve in D, and both ends of the curve tend to ∞. This type of singularity is a logarithmic singularity.

There are two kinds of branch points, logarithmic branch points and algebraic branch points, which are logarithmic singularities and algebraic singularities, respectively. A branch point is a non-isolated singularity.

Definition 4. 

(Logarithmic branch point)  A logarithmic branch point is a branch point whose neighborhood of values wraps around an infinite number of times as their complex arguments are varied.

Lemma 1. 

Let $f:z\to sin\left(z\right)$. Then $f^{-1}:sin\left(z\right)\to si{n}^{-1}\left(z\right)$ is the inverse map on the Riemann surface on which we only choose one piece of one-dimensional manifold that guarantees $sin\left(z\right)$’s invertibility. Then, $f^{-1}:sin\left(z\right)\to si{n}^{-1}\left(z\right)$ has two logarithmic branch points over ∞ and infinitely many algebraic branch points (critical points) over $-1$ and 1.

The process of expressing $arcsinz$ in the form of a logarithmic function in this proof is referenced from [23].

Proof. 

Set

$$z=sin\left(\omega \right)=\frac{e^{i\omega }-e^{-i\omega }}{2i}$$

by Euler’s formula. Let

$$v=e^{i\omega },$$

which is equivalent to analyzing the equation

$$\begin{array}{c}\hfill v-\frac{1}{v}=2iz,\end{array}$$

(11)

Multiplying by v on both sides, (11) becomes

$$v^2-1-2izv=0,$$

Using a basic method to solve quadratic equations, the solution of (11) is

$$\begin{array}{c}\hfill v=iz\pm {(1-z^2)}^{\frac{1}{2}}.\end{array}$$

(12)

Since z is a complex variable, ${(1-z^2)}^{\frac{1}{2}}$ is the complex square-root function. (12) is a multi-valued function with two possible values that differ by a sign,

$$\begin{array}{ccc}& & v=iz\pm {(1-z^2)}^{\frac{1}{2}}\hfill \\ & =& iz\pm e^{\frac{1}{2}log(1-z^2)}\hfill \\ & =& iz\pm e^{\frac{1}{2}[Log|1-z^2|+iarg(1-z^2)]}\hfill \\ & =& iz\pm {|1-z^2|}^{\frac{1}{2}}{e}^{\frac{i}{2}arg(1-z^2)},\hfill \end{array}$$

Since $v=e^{i\omega }$, it follows that

$$\omega =\frac{1}{i}logv=\frac{1}{i}log(iz\pm {|1-z^2|}^{\frac{1}{2}}{e}^{\frac{i}{2}arg(-1-z^2)}),$$

Since $\omega =arcsinz$,

$$\begin{array}{c}\hfill arcsinz=\frac{1}{i}log(iz\pm |1-z^2{|}^{\frac{1}{2}}{e}^{\frac{i}{2}arg(1-z^2)}).\end{array}$$

(13)

The principal value of the arcsine function is obtained by employing the principal value of the logarithm and the principal value of the square-root function. It is equivalent to employing the principal value of the argument. Therefore, we simplify (13) to

$$\begin{array}{c}\hfill Arcsinz=-iLog(iz\pm {(1-z^2)}^{\frac{1}{2}}).\end{array}$$

(14)

As ${(1-z^2)}^{\frac{1}{2}}$ is a square-root function, $z=\pm 1$ are branch points.

Substitute $z=\frac{1}{t}$ into (14). Then, (14) becomes

$$\begin{array}{c}\hfill Arcsinz=-iLog(\frac{i}{t}\pm \sqrt{\frac{t^2-1}{t^2}})=-iLog(\frac{i}{t}\pm \frac{\sqrt{t^2-1}}{t}),\end{array}$$

with $z\to \infty$. Thus, $t\to 0$,

$$\begin{array}{c}\hfill Arcsinz\to -iLog(\frac{i}{t}\pm \frac{\sqrt{-1}}{t}),\end{array}$$

Take

$$\begin{array}{c}\hfill \sqrt{-1}=\mp i,\end{array}$$

and then

$$\begin{array}{c}\hfill Arcsinz\to -iLog(\frac{i}{t}\pm \frac{\mp i}{t})\to -iLog\left(0\right),\end{array}$$

Since $z=0$ is a branch point of $Log\left(z\right)$, it means that $z=\infty$ is a branch point of $Arcsinz$. Therefore, $si{n}^{-1}\left(z\right)$ has a branch point at $z=\pm i$ and $z=\infty$. □

Remark 2. 

If a complex number is represented in polar form $z=r{e}^{i\theta }$, then the logarithm of z is $logz=logr+i\theta$. The logarithm has a jump discontinuity of $2\pi i$ when crossing the branch point $z=0$. The singularity of $log\left(z\right)$ at $z=0$ is a branch point, where $log\left(z\right)$ is a multi-valued function because θ can be replaced with $\theta +2\pi ni$ for any n integer. $Log\left(z\right)$ denotes the principal value of $log\left(z\right)$. Obviously, the point $z=0$ under the function $Log\left(z\right)$ is a logarithmic branch point.

3. Proof of Theorems 2 and 3

Now, we use the constructing triangle method to prove Theorems 2 and 3. The constructing triangle method utilizes the properties of triangles, such as the relationships between angles and side lengths, to construct specific triangles that are related to the solutions of autonomous first-order ODEs. For a more detailed illustration of this methodology, please see Section 4.

Proof. 

Assume $y\left(t\right)=w\left(t\right)+iv\left(t\right)$ is the solution of (9). In the following, we abbreviate it as $y=w+iv,(w,v\in \mathbb{R})$ and construct a right triangle in the complex plane, in which one of the angles is represented by $y=w+iv$, and the length of the hypotenuse is $\sqrt{v^2+w^2}$. Then, it is easy to see that

$$\begin{array}{c}\hfill siny=\frac{iv}{\sqrt{v^2+w^2}},\end{array}$$

(15)

Substitute $y=w+iv$ into $siny$,

$$\begin{array}{c}\hfill sin(w+iv)=sinwcoshv+isinhvcosw,\end{array}$$

(16)

Equating (15) and (16):

$$sinwcoshv+isinhvcosw=i\frac{v}{\sqrt{v^2+w^2}},$$

we equate the real and imaginary parts:

$$\begin{array}{c}\hfill sinwcoshv=0,\end{array}$$

(17)

$$\begin{array}{c}\hfill isinhvcosw=i\frac{v}{\sqrt{v^2+w^2}}.\end{array}$$

Therefore,

$$\begin{array}{c}\hfill sinhvcosw=\frac{v}{\sqrt{v^2+w^2}}.\end{array}$$

(18)

From (17), we have $w=0+2k\pi$ or $\pi +2k\pi$. Then, by substituting them to (18), we have

$$\begin{array}{c}\hfill sinhvcosw=1sinhv=\frac{v}{\sqrt{v^2+w^2}},\end{array}$$

$$\begin{array}{c}\hfill sinhv=\frac{e^v-e^{-v}}{2}=\frac{v}{\sqrt{v^2+w^2}}.\end{array}$$

Assume $u=e^v$. Then,

$$\begin{array}{c}\hfill u-\frac{1}{u}=\frac{2v}{\sqrt{v^2+w^2}},\end{array}$$

$$\begin{array}{c}\hfill u^2-1-\frac{2uv}{\sqrt{v^2+w^2}}=0,\end{array}$$

$$\begin{array}{c}\hfill u=\frac{v}{\sqrt{v^2+w^2}}\pm \sqrt{\frac{v^2}{v^2+w^2}+1},\end{array}$$

$$\begin{array}{c}\hfill v=log(\frac{v}{\sqrt{v^2+w^2}}\pm \sqrt{\frac{v^2}{v^2+w^2}+1}).\end{array}$$

Finally, we have the complex angle

$$\begin{array}{c}\hfill y=2k\pi +ilog(\frac{v}{\sqrt{v^2+w^2}}\pm \sqrt{\frac{v^2}{v^2+w^2}+1}),\end{array}$$

(19)

or

$$\begin{array}{c}\hfill y=\pi +2k\pi +ilog(\frac{v}{\sqrt{v^2+w^2}}\pm \sqrt{\frac{v^2}{v^2+w^2}+1}).\end{array}$$

(20)

Transform (19) and (20) into their principal value forms:

$$\begin{array}{c}\hfill y=iLog(\frac{v}{\sqrt{v^2+w^2}}\pm \sqrt{\frac{v^2}{v^2+w^2}+1}).\end{array}$$

(21)

In Section 2, two kinds of singularities were described: algebraic and non-algebraic singularities. It is obvious that (21) does not exhibit algebraic singularities for $w,v\in \mathbb{R}$.

If (21) has non-algebraic singularities, it is equivalent to

$$\begin{array}{c}\hfill \frac{v}{\sqrt{v^2+w^2}}\pm \sqrt{\frac{v^2}{v^2+w^2}+1}=0,\end{array}$$

(22)

and it is straightforward to see that there is no solution for (22).

Assume $y=w+iv$ (where $w,v\in \mathbb{C}$ are pure imaginary numbers) is the solution of (9). Construct a right triangle in the coordinate plane in which one of the angles is $y=w+iv$, and the length of the hypotenuse is $\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}$. Then, it is easy to see that

$$\begin{array}{c}\hfill cosy=\frac{iv}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}}.\end{array}$$

(23)

Substitute $y=w+iv$ into $cosy$,

$$\begin{array}{c}\hfill cos(w+iv)=coswcoshv-isinhvsinw,\end{array}$$

(24)

Equating (23) and (24):

$$\begin{array}{c}\hfill coswcoshv-isinhvsinw=i\frac{v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}},\end{array}$$

we equate the real and imaginary parts:

$$\begin{array}{c}\hfill coswcoshv=0,\end{array}$$

(25)

$$\begin{array}{c}\hfill -isinhvsinw=i\frac{v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}}.\end{array}$$

Therefore,

$$\begin{array}{c}\hfill sinhvsinw=-\frac{v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}}.\end{array}$$

(26)

From (25), we have $w=\frac{\pi }{2}+2k\pi$ or $-\frac{\pi }{2}+2k\pi$. Then, by substituting them into (26), we have

$$\begin{array}{c}\hfill sinhvsinw=1sinhv=-\frac{v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}},\end{array}$$

$$\begin{array}{c}\hfill sinhv=\frac{e^v-e^{-v}}{2}=-\frac{v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}}.\end{array}$$

Following the same process above, we have

$$\begin{array}{c}\hfill y=iLog(\frac{-v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}}\pm \sqrt{\frac{v^2}{{\left|v\right|}^2+{\left|w\right|}^2}+1}).\end{array}$$

(27)

It is obvious that (27) does not have non-algebraic singularities for $w,v\in \mathbb{R}$. If (27) has algebraic singularities, it is equivalent to

$$\begin{array}{c}\hfill \frac{-v}{\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}}=0,\end{array}$$

(28)

or

$$\begin{array}{c}\hfill \sqrt{\frac{v^2}{{\left|v\right|}^2+{\left|w\right|}^2}+1}=0.\end{array}$$

(29)

Solving (28) or (29), we have

$$\begin{array}{c}\hfill v=0,\end{array}$$

(30)

or

$$\begin{array}{c}\hfill v=-\sqrt{{\left|v\right|}^2+{\left|w\right|}^2}.\end{array}$$

(31)

If (30) holds, substitute (30) into (29). Then, we have $\sqrt{1}=0$, which is a contradiction. If (31) holds, take $w=0i$, and then (29) becomes

$$\begin{array}{c}\hfill \sqrt{\frac{v^2}{|v^2|}+1}=0,\end{array}$$

which has a solution $v=\pm i$. This proves Theorem 2.

Theorem 3 is proved in the same way as above. It is straightforward to see the general solution of (9) is $y=c_0+{\int }_0^{t}I\left(y\left(s\right)\right)ds$, and the general solution of (10) is $y=c_0+{\int }_0^t{I}_1\left(y\left(s\right)\right)ds+{\int }_0^t{I}_2\left(y\left(s\right)\right)ds+\cdots +{\int }_0^t{I}_n\left(y\left(s\right)\right)ds$, which are just linear combinations of the solutions of equations of the form (9). □

4. Methodology

In this section, we provide more detailed illustrations of how to use the constructing triangle method to solve a specific non-algebraic first-order autonomous ordinary differential equation (ODE). This section serves merely as an example of how to apply this method. For other differential equations, readers can be creative and construct other relationships based on the triangle.

Consider a differential equation,

$$\left\{\begin{array}{c}\frac{du}{dt}=cosu\left(t\right)\hfill \\ u\left(0\right)=1\hfill \end{array}\right.$$

(32)

Solve this differential equation:

$$\begin{array}{c}\hfill \int \frac{1}{cosu}du=\int secudu=ln|tanu+secu|=t+C,\end{array}$$

$$\begin{array}{c}\hfill |tanu\left(t\right)+secu\left(t\right)|=e^t{e}^C.\end{array}$$

Assume angle $u\left(t\right)$ is located in the second quadrant, as shown in the Figure 1.

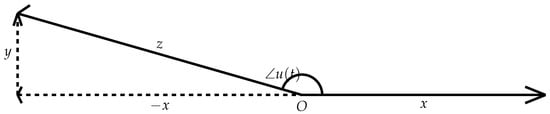
Figure 1. The angle is obtuse.

It is easy to see that

$$\begin{array}{c}\hfill tanu\left(t\right)=-\frac{y}{x},\end{array}$$

$$\begin{array}{c}\hfill secu\left(t\right)=-\frac{z}{x},\end{array}$$

where $z=\sqrt{x^2+y^2}$ is a non-negative number.

$$\begin{array}{c}\hfill |tanu\left(t\right)+secu\left(t\right)|=|-\frac{y}{x}-\frac{z}{x}|=|-\frac{(y+z)}{x}|,\end{array}$$

and square both sides,

$$\begin{array}{c}\hfill {|tanu\left(t\right)+secu\left(t\right)|}^2=|-\frac{(y+z)}{x}{|}^2=|-\frac{{(y+z)}^2}{x^2}|=|\frac{y^2+z^2+2yz}{-x^2}|.\end{array}$$

Set

$$\begin{array}{c}\hfill x^2=-2yz,\end{array}$$

and then

$$\begin{array}{c}\hfill {|tanu\left(t\right)+secu\left(t\right)|}^2=\left|\frac{y^2+z^2-x^2}{2yz}\right|.\end{array}$$

(33)

By the law of Cosines theorem,

$$\begin{array}{c}\hfill |cos(u\left(t\right)-\frac{\pi }{2})|=|\frac{y^2+z^2-x^2}{2yz}|={\left(e^t{e}^C\right)}^2=e^{2t}{e}^{2C}.\end{array}$$

Since

$$\begin{array}{c}\hfill cos(u\left(t\right)-\frac{\pi }{2})>0,\end{array}$$

$$\begin{array}{c}\hfill cos(u\left(t\right)-\frac{\pi }{2})=e^{2t}{e}^{2C}.\end{array}$$

By trigonometric relation,

$$\begin{array}{c}\hfill sin\left(u\left(t\right)\right)=cos(u\left(t\right)-\frac{\pi }{2})=e^{2t}{e}^{2C},\end{array}$$

so we have transformed $u\left(t\right)$ into an $arcsin$ function.

$$\begin{array}{c}\hfill u\left(t\right)=arcsin\left(e^{2t}{e}^{2C}\right).\end{array}$$

(34)

Now, we want to further analyze the solutions of (34), which are complex.

In the process of writing (33), we set $x^2=-2yz$, which implies $x^2<0$, $y>0$, $z>0$,

$$\begin{array}{c}\hfill x=\sqrt{-2yz}=i\sqrt{2yz}.\end{array}$$

(35)

By substituting (35) into the definition of $sin(u\left(t\right)-\frac{\pi }{2})$, we have

$$\begin{array}{c}\hfill sin(u\left(t\right)-\frac{\pi }{2})=\frac{-x}{z}=\frac{-i\sqrt{2yz}}{z}=-i\sqrt{\frac{2y}{z}}.\end{array}$$

(36)

It is apparent that $u\left(t\right)$ must be complex in order for $sin(u\left(t\right)-\frac{\pi }{2})$ to have a non-zero imaginary part. Since

$$\begin{array}{c}\hfill sin(u\left(t\right)-\frac{\pi }{2})=-i\sqrt{\frac{2y}{z}}=-{(-\frac{2y}{z})}^{\frac{1}{2}},\end{array}$$

$$\begin{array}{c}\hfill {(1-co{s}^2(u\left(t\right)-\frac{\pi }{2}))}^{\frac{1}{2}}=-{(-\frac{2y}{z})}^{\frac{1}{2}}.\end{array}$$

Squaring both sides, we have

$$\begin{array}{c}\hfill 1+\frac{2y}{z}=co{s}^2(u\left(t\right)-\frac{\pi }{2}),\end{array}$$

and then

$$\begin{array}{c}\hfill cos(u\left(t\right)-\frac{\pi }{2})=\sqrt{1+\frac{2y}{z}}.\end{array}$$

Since $u\left(t\right)$ is complex, $cos(u\left(t\right)-\frac{\pi }{2})$ must be complex, which implies $cos(u\left(t\right)-\frac{\pi }{2})=\sqrt{1+\frac{2y}{z}}>1$. This implies $\frac{2y}{z}>0$, since $y>0$.

The next steps are similar to those in Section 3. Suppose $u\left(t\right)-\frac{\pi }{2}=w+iv$. Then,

$$\begin{array}{c}\hfill sin(w+iv)=sinwcoshv+isinhvcosw,\end{array}$$

By combining it with (36), we have

$$\begin{array}{c}\hfill sinwcoshv+isinhvcosw=-i\sqrt{\frac{2y}{z}}.\end{array}$$

We equate the real and imaginary parts:

$$\begin{array}{c}\hfill sinwcoshv=0,\end{array}$$

$$\begin{array}{c}\hfill isinhvcosw=-i\sqrt{\frac{2y}{z}},\end{array}$$

$$\begin{array}{c}\hfill sinhvcosw=-\sqrt{\frac{2y}{z}}.\end{array}$$

From $sinwcoshv=0$, we have $w=0+2k\pi$ or $\pi +2k\pi$. Take $w=0+2k\pi$. Then,

$$\begin{array}{c}\hfill sinhvcosw=1sinhv=-\sqrt{\frac{2y}{z}},\end{array}$$

$$\begin{array}{c}\hfill sinhv=\frac{e^v-e^{-v}}{2}=-\sqrt{\frac{2y}{z}}.\end{array}$$

Assume $a=e^v$, and then

$$\begin{array}{c}\hfill a-\frac{1}{a}=-\sqrt{\frac{8y}{z}},\end{array}$$

$$\begin{array}{c}\hfill a^2-1+a\sqrt{\frac{8y}{z}}=0,\end{array}$$

$$\begin{array}{c}\hfill a=\frac{-\sqrt{\frac{8y}{z}}\pm \sqrt{\frac{8y}{z}+4}}{2},\end{array}$$

$$\begin{array}{c}\hfill v=ln\left(\frac{-\sqrt{\frac{8y}{z}}\pm \sqrt{\frac{8y}{z}+4}}{2}\right).\end{array}$$

Finally, we have the complex angle $u\left(t\right)$

$$\begin{array}{c}\hfill u\left(t\right)=\frac{\pi }{2}+2k\pi +iln\left(\frac{\sqrt{\frac{8y}{z}}\pm \sqrt{\frac{8y}{z}+4}}{2}\right).\end{array}$$

(37)

From (37), we can easily see that there are no singularities in the solutions of (32) based on the similar analysis in the previous sections.

Comparison with Numerical Methods

When dealing with non-algebraic first-order autonomous ODEs, we may utilize numerical methods. It is essential to check whether non-algebraic first-order autonomous ODEs in the form of (32) are convergent and stable before applying a numerical method, since if the initial value problem is not robust to small perturbations, there is no hope that any numerical method can approximate its solution.

Consider the initial value problem for a system of ODEs

$$\left\{\begin{array}{c}{y}^{\prime }=I\left(y\left(t\right)\right)\hfill \\ y\left(0\right)=c_0\hfill \end{array}\right.$$

(38)

and the perturbed problem

$$\left\{\begin{array}{c}{z}^{\prime }=I\left(z\left(t\right)\right)+\delta \left(t\right)\hfill \\ z\left(0\right)=c_0+\delta \hfill \end{array}\right.$$

(39)

where $\delta \left(t\right)$ is an integrable function and ${\delta }_0\in \mathbb{R}$.

Definition 5. 

(Stability of the Cauchy problem (see [11])). The Cauchy problem (38) is said to be stable within the time interval $[0,T]$ if for any perturbations ${\delta }_0$ and $\delta \left(t\right)$ such that

$$\begin{array}{c}\hfill \parallel {\delta }_0\parallel \le ϵ,and\parallel \delta \left(t\right)\parallel \le ϵ,\forall t\in [0,T]\end{array}$$

(40)

we have that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-y\left(t\right)\parallel \le Cϵ,\forall t\in [0,T]\end{array}$$

(41)

where C is a finite constant that does not depend on ϵ.

We also want to prove the theorem below.

Theorem 4. 

Let $D\subset R^n$ be an open set, $y_0\in D$. If $I\left(y\right(t\left)\right)$ is Lipschitz continuous in D and $\delta \left(t\right)$ is integrable, then the initial value problem (38) is stable.

Proof. 

We need to show that for any ${\delta }_0$ and $\delta \left(t\right)$, the difference between the solutions of (38) and (39) is bounded in some time interval $[0,T]$ and that the difference tends to zero as $ϵ\to 0$. First, we notice that if D is open and $ϵ$ is small enough, then the initial condition $(y_0+{\delta }_0)$ is in D. If $f\left(y\right(t\left)\right)$ is Lipschitz continuous,

$$\begin{array}{c}\hfill \parallel f\left(z\right)-f\left(y\right)\parallel \le L\parallel z-y\parallel ,\forall y,z\in D,\end{array}$$

(42)

and since $\delta \left(t\right)$ is integrable, problems (38) and (39) can be equivalently written as

$$\begin{array}{c}\hfill y\left(t\right)=y_0+{\int }_0^{t}I\left(y\left(s\right)\right)ds,\end{array}$$

(43)

$$\begin{array}{c}\hfill z\left(t\right)=y_0+{\delta }_0+{\int }_0^{t}I\left(z\left(s\right)\right)ds+{\int }_0^t\delta \left(s\right)ds,\end{array}$$

(44)

for all $t\in [0,T]$.

Subtracting (43) from (44) and taking the norm yields

$$\begin{array}{ccc}\hfill \parallel z\left(t\right)-y\left(t\right)\parallel & =& \parallel {\delta }_0+{\int }_0^t[I\left(z\left(s\right)\right)-I\left(y\left(s\right)\right)]ds+{\int }_0^t\delta \left(s\right)ds\parallel \hfill \\ & \le & \parallel {\delta }_0\parallel +{\int }_0^t\parallel I\left(z\left(s\right)\right)-I\left(y\left(s\right)\right)\parallel ds+{\int }_0^t\parallel \delta \left(s\right)\parallel ds\hfill \\ & \le & (1+t)ϵ+L{\int }_0^t\parallel z\left(s\right)-y\left(s\right)\parallel ds,\hfill \end{array}$$

(45)

and we use Grónwall’s inequality to conclude that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-y\left(t\right)\parallel \le (1+t)e^{tL}ϵ\le (1+t)e^{TL}ϵ\le Cϵ.\end{array}$$

(46)

□

This proves that if (38) is Lipschitz continuous, then it is stable. To show that (32) is stable, the remaining task is to show that (32) is Lipschitz continuous.

By the mean value theorem, there exists a $c\in (y_1,y_2)$ such that

$$\begin{array}{c}\hfill I\left(y_1\left(t\right)\right)-I\left(y_2\left(t\right)\right)=I^{\prime }\left(c\left(t\right)\right)(y_1-y_2),\end{array}$$

so that

$$\begin{array}{c}\hfill |I\left(y_1\left(t\right)\right)-I\left(y_2\left(t\right)\right)|=|I^{\prime }\left(c\left(t\right)\right)(y_1-y_2)|\le |I^{\prime }\left(c\left(t\right)\right)\left|\right|y_1-y_2|.\end{array}$$

If I is a trigonometric function in (32), it is easy to see that $|I^{\prime }\left(c\left(t\right)\right)|\le 1$. Thus, $I(t,y)$ is a Lipschitz continuous function in (32). Combined with Theorem 4, (32) is stable.

Since equations in the form of (38) are stable, a numerical scheme can be applied. Here, we use Euler’s method with $h=0.1$ to find approximate values for the solutions of the initial value problem (32) at $t\in [0,100]$. The Euler’s scheme is 0-stable and convergent, since

$$\begin{array}{c}\hfill Y_n=Y_{n-1}+h{Y}_{n-1}=(1+h)Y_{n-1}={(1+h)}^n{Y}_0,\end{array}$$

with $n\to \infty$ and $h\to 0$ in such a way that $nh=X$ a constant, then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{(1+h)}^n{Y}_0=e^X,\end{array}$$

so the method converges as $h\to 0$.

We rewrite Equation (32) as

$$\begin{array}{c}\hfill I\left(u\left(t\right)\right)=cosu\left(t\right),t_0=0and{u}_0=1.\end{array}$$

(47)

Euler’s method yields

$$\begin{array}{c}\hfill u_1=u_0+hI\left(u_0\left(t_0\right)\right)=1+0.1\left(cos\left(1\right)\right)\sim 1.0540302305868139,\end{array}$$

$$\begin{array}{ccc}\hfill u_2& =& u_1+hI\left(u_1\left(t_1\right)\right)=1.0540302305868139+0.1\left(cos\left(1.0540302305868139\right)\right),\hfill \\ & \sim & 1.1034373406650508\hfill \end{array}$$

$$\begin{array}{ccc}\hfill u_3& =& u_2+hI\left(u_2\left(t_2\right)\right)=1.1034373406650508+0.1\left(cos\left(1.1034373406650508\right)\right).\hfill \\ & \sim & 1.1484903471\hfill \end{array}$$

By repeating the above process, we eventually obtain the Figure 2 below.

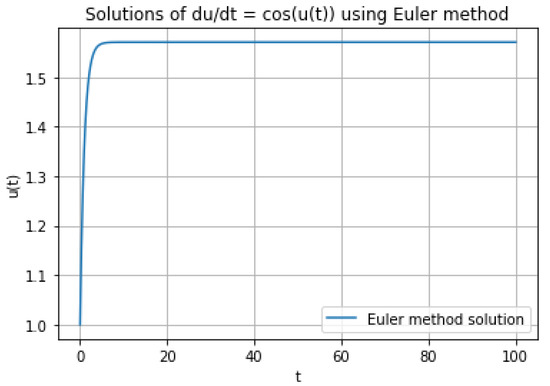
Figure 2. Graph of solutions of $\frac{du}{dt}=cos\left(u\left(t\right)\right)$.

In the graph, we can easily see that there are no singularities in the solutions of (32).

When comparing the efficiency and accuracy of numerical methods with the constructing triangle method for solving the differential equation $\frac{du}{dt}=cosu\left(t\right)$, numerical methods may not be as precise as the constructing triangle method. In practice $h\ne 0$, $Y_n$ oscillates as a trigonometric function. By using the constructing triangle method, solutions $u\left(t\right)$ have been expanded into a logarithmic equation, and the existence of singularities can be easily observed.

5. Some Examples

In Examples 1–3, we present some autonomous first-order ordinary differential equations in the form of (9) and (10), where all movable singularities of all solutions are neither non-algebraic nor algebraic singularities.

5.1. Example 1: When $I\left(y\right(t\left)\right)=cosy\left(t\right)$

Given the ordinary differential equation

$$\left\{\begin{array}{c}\frac{dy}{dt}=cosy\left(t\right),\hfill \\ y\left(0\right)=c_0.\hfill \end{array}\right.$$

(48)

$$\begin{array}{c}\hfill \frac{dy}{dt}=cosy\Rightarrow \frac{dy}{cosy}=dt\Rightarrow \int \frac{1}{cosy}dy={\int }_0^{t}dt,\end{array}$$

it is known that

$$\begin{array}{c}\hfill \frac{d}{dy}\int \frac{1}{cosy}dy=\frac{d}{dy}ln\left|tan(\frac{\pi }{4}+\frac{y}{2})\right|,\end{array}$$

$$\begin{array}{c}\hfill \int \frac{1}{cosy}dy=ln\left|tan(\frac{\pi }{4}+\frac{y}{2})\right|=t+C,\end{array}$$

(49)

$$\begin{array}{c}\hfill y\left(t\right)=2arctan\left(e^{t+C}\right)-\frac{\pi }{2},\end{array}$$

From the relation

$$\begin{array}{c}\hfill arctanx=arcsin\left(\frac{x}{\sqrt{1+x^2}}\right),\end{array}$$

we have

$$\begin{array}{c}\hfill y\left(t\right)=2arcsin\left(\frac{e^{t+C}}{\sqrt{1+e^{2(t+C)}}}\right)-\frac{\pi }{2}=arcsin(\frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1),\end{array}$$

(50)

$$\begin{array}{c}\hfill inf\frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1=\underset{t\to 0}{lim}\underset{c\to -\infty }{lim}\frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1=-1,\end{array}$$

(51)

$$\begin{array}{c}\hfill sup\frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1=\underset{t\to 0}{lim}\underset{c\to \infty }{lim}\frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1=0.\end{array}$$

(52)

From Lemma (1), $arcsin\left(z\right)$ has a logarithmic branch point at $z=\infty$. As we see in (51) and (52), $\frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1$ does not tend to ∞, which implies that the solutions of (48) do not have logarithmic singularities.

From Lemma (1), $arcsin\left(z\right)$ has an algebraic branch point at $z=\pm 1$. Solving

$$\begin{array}{c}\hfill \frac{e^{2(t+C)}}{1+e^{2(t+C)}}-1=\pm 1,\end{array}$$

there are no solutions. Therefore, the solutions of (48) do not have algebraic singularities.

5.2. Example 2: When $I_1\left(y\left(t\right)\right)=siny\left(t\right)$ and $I_2\left(y\left(t\right)\right)=cosy\left(t\right)$

Given the ordinary differential equation:

$$\left\{\begin{array}{cc}\frac{dy}{dt}=siny\left(t\right)+cosy\left(t\right)\hfill & t>0\hfill \\ y\left(0\right)=c_0\hfill \end{array}\right.$$

(53)

$$\frac{dy}{dt}=siny+cosy\Rightarrow \frac{dy}{siny+cosy}=dt\Rightarrow \int \frac{1}{siny+cosy}dy={\int }_0^{t}dt,$$

it is known that

$$\begin{array}{c}\hfill \int \frac{1}{siny+cosy}dy=\int \frac{1}{\sqrt{2}cos(y-\frac{\pi }{4})}dy.\end{array}$$

(54)

We find that (54) is in the same form as (49), so the proof process is the same as in Example 1.

5.3. Example 3: When $I\left(y\right(t\left)\right)=y\left(t\right)ln\left(y\right(t\left)\right)$

Consider the ordinary differential equation:

$$\left\{\begin{array}{cc}\frac{dy}{dt}=y\left(t\right)ln\left(y\left(t\right)\right)\hfill & t>0\hfill \\ y\left(0\right)=c_0\hfill \end{array}\right.$$

(55)

$$\begin{array}{c}\hfill \frac{dy}{dt}=y\left(t\right)ln\left(y\left(t\right)\right)\Rightarrow \frac{dy}{yln\left(y\right)}=dt\Rightarrow \int \frac{1}{yln\left(y\right)}dy={\int }_0^{t}dt.\end{array}$$

It is easy to see that

$$\begin{array}{c}\hfill y\left(t\right)=e^{e^{c_0+t}}\end{array}$$

(56)

which is an entire function that does not have singularities.

In Examples 4–6, we present some autonomous first-order ordinary differential equations in the form of (9) and (10), where all movable singularities of all solutions are non-algebraic rather than algebraic singularities.

5.4. Example 4: When $I\left(y\right(t\left)\right)=tany\left(t\right)$

Given the ordinary differential equation:

$$\left\{\begin{array}{c}\frac{dy}{dt}=tany\left(t\right),\hfill \\ y\left(0\right)=c_0.\hfill \end{array}\right.$$

(57)

$$\begin{array}{c}\hfill \frac{dy}{dt}=tany\Rightarrow \frac{dy}{tany}=dt\Rightarrow \int \frac{1}{tany}dy={\int }_0^{t}dt,\end{array}$$

it is known that

$$\begin{array}{c}\hfill \frac{d}{dy}\int \frac{1}{tany}dy=\frac{d}{dy}ln\left|sin\left(y\right)\right|,\end{array}$$

$$\begin{array}{c}\hfill \int \frac{1}{tany}dy=ln\left|sin\left(y\right)\right|=t+C,\end{array}$$

(58)

and we have

$$\begin{array}{c}\hfill y\left(t\right)=arcsin\left(e^{t+C}\right).\end{array}$$

(59)

By Lemma (1), $arcsin\left(z\right)$ has a logarithmic branch point at $z=\infty$. Let

$$\begin{array}{c}\hfill e^{t+C}\to \infty ,\end{array}$$

so then

$$\begin{array}{c}\hfill c_0=y\left(0\right)=arcsin(\infty )\end{array}$$

does not exist. Therefore, the solutions of (57) do not have non-algebraic singularities.

By Lemma (1), $arcsin\left(z\right)$ has an algebraic branch point at $z=\pm 1$. Let

$$\begin{array}{c}\hfill e^{t+C}=1,\end{array}$$

(60)

and solving (60), we have the solutions

$$\begin{array}{c}\hfill t=-C,\end{array}$$

(61)

We want time t to be a real number to guarantee that Equation (60) holds, which is equivalent to finding some initial value $c_0$ such that

$$\begin{array}{c}\hfill c_0=y\left(0\right)=arcsin\left(e^C\right),\end{array}$$

(62)

It is feasible that there exists some $C\in {\mathbb{R}}_{-}$ such that (62) holds. Therefore, the solutions of (57) have algebraic singularities.

If we set the initial value of (57) as $y\left(0\right)=1$ using the Euler method, as shown in Section 4, we obtain the Figure 3 below.

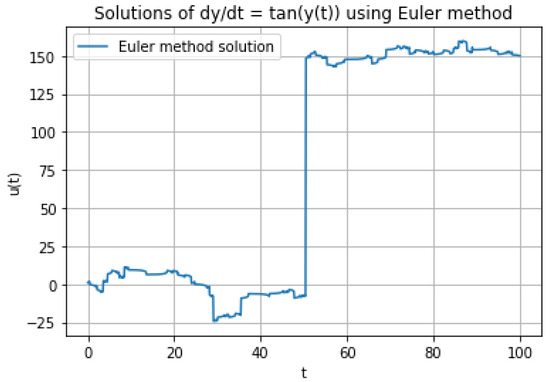
Figure 3. Graph of solutions of $\frac{dy}{dt}=tan\left(y\left(t\right)\right)$.

It is easy to observe in the graph that the singularities of the solutions of (57) exist.

5.5. Example 5: When $I\left(y\right(t\left)\right)=tany\left(t\right)$ and $I_2\left(y\left(t\right)\right)=secy\left(t\right)$

Given the ordinary differential equation:

$$\left\{\begin{array}{c}\frac{dy}{dt}=tany\left(t\right)+secy\left(t\right),\hfill \\ y\left(0\right)=c_0.\hfill \end{array}\right.$$

(63)

$$\begin{array}{c}\hfill \frac{dy}{dt}=tany+secy\Rightarrow \frac{dy}{tany+secy}=dt\Rightarrow \int \frac{1}{tany+secy}dy={\int }_0^{t}dt,\end{array}$$

it is known that

$$\begin{array}{c}\hfill \int \frac{1}{tany+secy}dy=\int \frac{cosy}{1+siny}dy=ln|1+siny|+C,\end{array}$$

$$\begin{array}{c}\hfill ln|1+siny|=t+C.\end{array}$$

(64)

We find that (64) is in the same form as (58), and the process is the same as in Example 3.

5.6. Example 6: In R-C Circuit

As shown in [24], if a circuit is described by linear differential equations, then we can simplify it by adding an imaginary part to the voltage or current:

$$\begin{array}{c}\hfill V\left(t\right)=V_{0}cos(\omega t+\varphi )+j·V_{0}sin(\omega t+\varphi )=V_0{e}^{j·(\omega +\varphi )}\end{array}$$

(65)

Consider a simple RC circuit (resistor–capacitor circuit), whose differential equation commonly describes the variation in the rate of change of the capacitor voltage with time. The magnitude of the current flowing through the capacitor is proportional to the rate of change of the voltage across the capacitor.

$$I=\frac{\partial Q}{\partial t}=C\frac{\partial V}{\partial t}.$$

where I represents the electric current, Q represents the charge on the capacitor, C represents the capacitance, and V represents the voltage across the capacitor. To relate this to the concept of singularity, we can consider a special case where the electric current I is a sinusoidal alternating current, which means that $I=\frac{\partial Q}{\partial t}=sin(\omega t+\varphi )$. Under such conditions, the differential equation becomes:

$$\begin{array}{c}\hfill I=\frac{\partial Q}{\partial t}=C\frac{\partial V}{\partial t}=sin(\omega t+\varphi ),\end{array}$$

Using basic calculation, it is easy to find that the voltage source V is a cosine function.

$$\begin{array}{c}\hfill V\sim \int sin(\omega t+\varphi )dt\sim cos(\omega t+\varphi ),\end{array}$$

The voltage across the capacitor lags behind the current by 90 degrees in sine alternating current due to the properties of $sin$ and $cos$ functions. Since the voltage V across the capacitor lags behind the current I flowing through it by a phase of $\frac{\pi }{2}$ radians, their ratio will give the reactance multiplied by an exponential with a negative phase constant. By Ohm’s law,

$$\begin{array}{c}\hfill VI=Z,\end{array}$$

where Z is the impedance of a capacitor, and we have

$$\begin{array}{c}\hfill Z=\frac{V}{I}=\frac{1}{\omega C}{e}^{-\frac{i\pi }{2}}=-\frac{i}{\omega C},\end{array}$$

where $e^{-\frac{i\pi }{2}}=cos\frac{\pi }{2}-isin\frac{\pi }{2}=-i$. $Z^{\prime }=\frac{dV}{dI}$ is the derivative of voltage V with respect to current I, which describes how the voltage changes when a small change occurs in the current. It is easy to see that $Z^{\prime }$ approximates to a secant function since V is a $cos$ function and I is a $sin$ function. Then, we can use forms of $\frac{dV}{dI}\sim tan(\Phi )\sim -i$ to analyze the singularities of the derivative of the impedance function, where $\Phi$ is some unknown function. It is easy to see that the singularities extend to $\frac{\pi }{2}+2k\pi$ throughout the entire complex plane.

In electrical or mechanical systems, much more complicated circuits, such as nonlinear circuits, can be handled by extending the mathematical techniques shown in [24]. A waveform that is not sinusoidal is called a complex wave. A complex wave can be written as a Fourier series of sines and cosines, and each term in the series can be treated using the method described here (for more information, see [25]).

6. Discussion

We firmly believe that the concepts and techniques outlined herein can be utilized to explore a wide range of singularity issues encompassing intricate ordinary differential equations. The potential avenues for future research based on this paper can be extended to a wider domain of differential equations. Solutions of partial differential equations can be constructed from solutions of ordinary differential equations. The essence of the procedure relies on identifying a suitable set of nonlinear ODEs, all of which by construction admit the solutions of non-algebraic first-order autonomous ordinary differential equations as their solutions.