Exploring Zeros of Hermite-λ Matrix Polynomials: A Numerical Approach

Abstract

This article aims to introduce a set of hybrid matrix polynomials associated with $\lambda$-polynomials and explore their properties using a symbolic approach. The main outcomes of this study include the derivation of generating functions, series definitions, and differential equations for the newly introduced two-variable Hermite $\lambda$-matrix polynomials. Furthermore, we establish the quasi-monomiality property of these polynomials, derive summation formulae and integral representations, and examine the graphical representation and symmetric structure of their approximate zeros using computer-aided programs. Finally, this article concludes by introducing the idea of 1-variable Hermite $\lambda$ matrix polynomials and their structure of zeros using a computer-aided program.

1. Introduction

The field of orthogonal matrix polynomials is rapidly advancing, yielding significant results from both theoretical and practical perspectives. The role of Orthogonal matrices is advancing due to their essence in numerical computations, geometry, signal processing, coding theory, cryptography, and quantum mechanics. Their versatility and efficiency make them indispensable across various fields, driving ongoing research and development. Special functions, as a mathematical discipline, hold paramount significance for scientists and engineers across a myriad of application areas. The theory of special functions is highly significant in the formalism of mathematical physics. Hermite and Chebyshev polynomials, fully examined in the publication by [1,2], are fundamental special functions widely recognized for their broad range of applications in physics, engineering, and mathematical physics. These applications span from theoretical number theory to solving real-world problems in the disciplines of physics and engineering. In addition, the Hermite matrix polynomials have been introduced and thoroughly researched in several articles [3,4,5,6]. Matrix polynomials in special functions have a vital role in mathematical physics, electrodynamics, and image processing.

Multi-variable special polynomials hold significant importance across various mathematical domains and applications. Defined in multiple variables, they extend the principles of classical uni-variate polynomials into higher dimensions. These polynomials find utility in algebraic geometry, mathematical physics, and computer science. The exploration of multi-variable special polynomials encompasses diverse families, each characterized by unique properties and applications, establishing them as valuable tools for scholars and practitioners alike.

Hermite polynomials stand out as highly applicable orthogonal special functions dating back to the classical period. They serve as solutions to differential equations equivalent to the Schrödinger equation for a harmonic oscillator in quantum mechanics. Furthermore, these polynomials play a crucial role in the investigation of classical boundary-value problems in parabolic regions, particularly when utilizing parabolic coordinates.

Recently, it has been shown that the symbolic method provides a powerful and efficient means to introduce, study special functions, and reform special functions [7,8]. This method is also been proven to be helpful in introducing certain extensions of several special functions. The umbral formalism can be considered as a sub-field of the symbolic methods. In umbral formalism, we obtain suitable “umbra” based on some boundary conditions of the special polynomials.

Dattoli considered the idea of umbra denoted by ${\tilde{h}}_v$, for 2VHKdFP ${\mathcal{H}}_n(u,v)$ as [9]:

$${\tilde{h}}_v^s{\widehat{\varphi }}_0=\frac{v^{\frac{s}{2}}}{\Gamma \left(\frac{s}{2}+1\right)}\left|cos\left(s\frac{\pi }{2}\right)\right|,{\widehat{\varphi }}_0\ne 0,$$

(1)

where ${\widehat{\varphi }}_0$ serve as the polynomial vacuum for 2VHKdFP ${\mathcal{H}}_n(u,v)$ thus, the action of ${\widehat{\varphi }}_0$ yields 2VHKdFP ${\mathcal{H}}_n(u,v)$.

The exponential of umbra ${\tilde{h}}_v$ is particularly important to derive the generating function for 2VHKdFP ${\mathcal{H}}_n(u,v)$. In view of Equation (1), the exponential of umbra ${\tilde{h}}_v$ is of the form [9]:

$$e^{{\tilde{h}}_{v}s}{\widehat{\varphi }}_0=e^{v{s}^2}.$$

(2)

In view of Equation (1), the umbral image of 2VHKdFP ${\mathcal{H}}_n(u,v)$ is given by

$${\mathcal{H}}_n(u,v)={(u+{\tilde{h}}_v)}^n{\widehat{\varphi }}_0.$$

(3)

Recently, Dattoli et al. discovered a link between trigonometric functions and Laguerre polynomials. They proposed a way to introduce a new family of polynomials that connects Laguerre polynomials with trigonometric functions. This family of polynomials is known as $\lambda$-polynomials [10]. They expanded on this concept by adding a parameter $\beta$ and generalizing it to associated-$\lambda$ polynomials.

The symbolic definition of associated-$\lambda$ polynomials is of the form [10]:

$${\lambda }_n^{\left(\beta \right)}(u,v)={\widehat{\ell }}^{\beta }{(v-\widehat{\ell }u)}^n{\tilde{\psi }}_0,$$

(4)

where $\widehat{\ell }$ denotes a symbolic operator given by Dattoli et al. [11], which operates on the vacuum function ${\tilde{\psi }}_z=\frac{\Gamma (z+1)}{\Gamma (2z+1)}$ as:

$${\widehat{\ell }}^w{\tilde{\psi }}_z=\frac{\Gamma (w+z+1)}{\Gamma \left(2\right(w+z)+1)},w+z\ge -1,w\in \mathbb{R}$$

(5)

and

$${\widehat{\ell }}^n{\widehat{\ell }}^m={\widehat{\ell }}^{n+m}.$$

(6)

In particular, we have

$${\widehat{\ell }}^w{\tilde{\psi }}_0:={\widehat{\ell }}^w{\tilde{\psi }}_z{|}_{z=0}=\frac{\Gamma (w+1)}{\Gamma (2w+1)},w\in \mathbb{R},w\ge -1.$$

(7)

The generating relation and explicit form of associated-$\lambda$ polynomials are [10]:

$$\sum _{n=0}^{\infty }{\lambda }_n^{\left(\beta \right)}(u,v)\frac{s^n}{n!}=e^{vs}cos(\sqrt{us};\beta )$$

(8)

and

$${\lambda }_n^{\left(\beta \right)}(u,v)=\sum _{r=0}^{\infty }\frac{{(-1)}^r\Gamma (\beta +r+1)u^r{v}^{n-r}}{r!(n-r)!\Gamma \left(2\right(\beta +r)+1)},$$

(9)

respectively.

The associated cosine function $cos(u;\beta )$ is symbolically defined as [10]:

$$cos(u;\beta ):={\widehat{\ell }}^{\beta }{e}^{-\widehat{\ell }{u}^2}{\tilde{\psi }}_0=\sum _{n=0}^{\infty }\frac{{(-1)}^n\Gamma (\beta +n+1)u^{2n}}{n!\Gamma \left(2\right(\beta +n)+1)},\beta \in \mathbb{N}.$$

(10)

Recently, Zainab and Raza [12] introduced the 1-variable $\lambda$ matrix polynomials ${\lambda }_n^{\left(P\right)}\left(u\right)$ by interchanging the role of u and v in the Equation (4) and then taking $v=1$ in the resultant expression as follows:

The symbolic image of $\lambda$ polynomials is as follows [12]:

$${\lambda }_n^{\left(P\right)}\left(u\right)={\widehat{\ell }}^P{(u-\widehat{\ell })}^n{\tilde{\psi }}_0,\forall u,v\in \mathbb{R},\forall n\in \mathbb{N},$$

(11)

where matrix exponent of symbolic operator $\widehat{\ell }$ is given by

$${\widehat{\ell }}^P{\tilde{\psi }}_0:=\Gamma (P+I){(\Gamma (2P+I))}^{-1}$$

(12)

such that

$${\widehat{\ell }}^P{\widehat{\ell }}^Q={\widehat{\ell }}^{P+Q},$$

(13)

where P and Q are positive stable matrices ${\mathbb{C}}^{m\times m}$ and $I\in {\mathbb{C}}^{m\times m}$.

The generating function and series definition of 1-variable $\lambda$ matrix polynomials ${\lambda }_n^{\left(P\right)}\left(u\right)$ is given by [12]:

$$\sum _{n=0}^{\infty }{\lambda }_n^{\left(P\right)}\left(u\right)\frac{s^n}{n!}=e^{us}cos(\sqrt{s};P)$$

(14)

and

$${\lambda }_n^{\left(P\right)}\left(u\right)=\sum _{r=0}^{\infty }\frac{{(-1)}^r\Gamma (P+(r+1)I){(\Gamma (2P+(2r+1)I))}^{-1}{u}^{n-r}}{r!(n-r)!},$$

(15)

respectively.

The associated cosine matrix function $cos(u;P)$ is defined by means of the following symbolic images [12]:

$$cos(u;P)={\widehat{\ell }}^P{e}^{-\widehat{\ell }{u}^2}{\tilde{\psi }}_0=\sum _{n=0}^{\infty }\frac{{(-1)}^n\Gamma (P+(n+1\left)I\right){(\Gamma (2P+(2n+1\left)I\right))}^{-1}{u}^{2n}}{n!}.$$

(16)

The term “quasi-monomial” figures to the polynomial sequence ${\left\{{\mathfrak{S}}_n\left(x\right)\right\}}_{n=0}^{\infty }$, having two operators, especially named as multiplicative operator ${\widehat{\Omega }}^{+}$ and derivative operator ${\widehat{\Omega }}^{-}$ satisfying the following relations [13]:

$${\widehat{\Omega }}^{+}\left\{{\mathfrak{S}}_n\left(x\right)\right\}={\mathfrak{S}}_{n+1}\left(x\right)$$

(17)

and

$${\widehat{\Omega }}^{-}\left\{{\mathfrak{S}}_n\left(x\right)\right\}=n{\mathfrak{S}}_{n-1}\left(x\right),$$

(18)

respectively.

The following commutation relation satisfy by the operators ${\widehat{\Omega }}^{+}$ and ${\widehat{\Omega }}^{-}$:

$$[{\widehat{\Omega }}^{-},{\widehat{\Omega }}^{+}]={\widehat{\Omega }}^{-}{\widehat{\Omega }}^{+}-{\widehat{\Omega }}^{+}{\widehat{\Omega }}^{-}=\tilde{1}.$$

(19)

Thus, the operators ${\widehat{\Omega }}^{+}$ and ${\widehat{\Omega }}^{-}$ satisfy a weyl group structure [13]. By making use of the operators ${\widehat{\Omega }}^{+}$ and ${\widehat{\Omega }}^{-}$, various characteristics of polynomial ${\mathfrak{S}}_n\left(x\right)$ can be obtained. If ${\widehat{\Omega }}^{+}$ and ${\widehat{\Omega }}^{-}$ have differential realizations, then the following differential equation satisfies by the polynomial ${\mathfrak{S}}_n\left(x\right)$:

$${\widehat{\Omega }}^{+}{\widehat{\Omega }}^{-}\left\{{\mathfrak{S}}_n\left(x\right)\right\}=n{\mathfrak{S}}_n\left(x\right).$$

(20)

If ${\mathfrak{D}}_0$ represents the complex plane cut along the negative real axis, and $log\left(u\right)$ denotes the principal logarithm of u, then $u^{\frac{1}{2}}$ is equivalent to $exp\left(\frac{1}{2}log\left(u\right)\right)$. For a matrix P in ${\mathbb{C}}^{\mathbb{N}\times \mathbb{N}}$, its two-norm, denoted by ${\parallel P\parallel }_2$, is defined as ${\parallel P\parallel }_2=\frac{{\parallel Pu\parallel }_2}{{\parallel u\parallel }_2}$, where ${\parallel v\parallel }_2$ for a vector $v\in {\mathbb{C}}^{\mathbb{N}}$ represents the usual Euclidean norm, given by ${\parallel v\parallel }_2={\left(v^{T}v\right)}^{\frac{1}{2}}$. The set containing all eigenvalues of P is denoted by $\sigma \left(P\right)$. If $\tilde{f}\left(u\right)$ and $\tilde{g}\left(u\right)$ are holomorphic functions of the complex variable u, defined in an open set $\Omega$ of the complex plane, and P is a matrix in ${\mathbb{C}}^{\mathbb{N}\times \mathbb{N}}$ such that $\sigma \left(P\right)\subset \Omega$, then the matrix functional calculus dictates that

$$\tilde{f}\left(P\right)\tilde{g}\left(P\right)=\tilde{g}\left(P\right)\tilde{f}\left(P\right).$$

(21)

If P is a matrix with $\sigma \left(A\right)\subset {\mathfrak{D}}_0$, then $P^{\frac{1}{2}}=\sqrt{P}=exp\left(\frac{1}{2}log\left(P\right)\right)$ denotes the image by $u^{\frac{1}{2}}=\sqrt{u}=exp\left(\frac{1}{2}log\left(u\right)\right)$ The matrix functional calculus acts on the matrix P. We say that P is a positive stable matrix [4,5,14] if

$$Re\left(u\right)>0,\mathrm{for}\mathrm{all}u\in \sigma \left(P\right).$$

(22)

In this paper, we propose a convolution between the two variables Hermite polynomials and the $\lambda$-matrix polynomials to introduce a new family of polynomials called the 2-variable Hermite $\lambda$-matrix polynomials. Section 2 delves into this newly introduced family’s generating function, series definition, differential equation, and differential recurrence relation. Also, we establish the quasi-monomiality property of these polynomials. In Section 3, we obtain some summation formulae. In Section 4, by using the computer-aided program (Wolfram Mathematica), we consider some examples of this hybrid family and give their graphical representations, mainly to observe from several angles how zeros of these polynomials are distributed and located. Section 5 concludes this paper by introducing the concept of 1-variable Hermite $\lambda$-matrix polynomials and obtaining their zeros.

2. Hermite $\mathbf{\lambda }$-Matrix Polynomials

In this section, we introduce the 2-variable Hermite $\lambda$-matrix polynomials by using a symbolic approach and obtain their generating function, series definition, multiplicative and derivative operators, differential equation, and differential recurrence relation.

Now, we recall the generating function and series definition of Classical Hermite polynomials ${\mathcal{H}}_n\left(u\right)$. The classical Hermite polynomials ${\mathcal{H}}_n\left(u\right)$ are defined by the means of the following generating function [1]:

$$exp\left(2us-s^2\right)=\sum _{n=0}^{\infty }{\mathcal{H}}_n\left(u\right)\frac{s^n}{n!}$$

(23)

and explicit representation

$${\mathcal{H}}_n\left(u\right)=n!\sum _{r=0}^{[n/2]}\frac{{(-1)}^r{\left(2u\right)}^{n-2r}}{r!(n-2r)!},$$

(24)

respectively.

2-variable Hermite Kempe de Fériet polynomials (2VHKdFP) ${\mathcal{H}}_n(u,v)$ is given by the following generating relation and series definition [15]:

$$exp\left(us+v{s}^2\right)=\sum _{n=0}^{\infty }{\mathcal{H}}_n(u,v)\frac{s^n}{n!}$$

(25)

and

$${\mathcal{H}}_n(u,v)=n!\sum _{r=0}^{[n/2]}\frac{u^{n-2r}{v}^r}{r!(n-2r)!},$$

(26)

respectively.

Now, we introduce the 2-variable Hermite $\lambda$-matrix polynomials (2vH$\lambda$MP) ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$ by replacing u in (11) with the symbolic operator of Hermite polynomial as

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)={\widehat{\ell }}^P{(u+{\widehat{h}}_v-\widehat{\ell })}^n{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(27)

We obtain the following theorem for generating function and series definition of Hermite $\lambda$-matrix polynomials ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$:

Theorem 1.

The following generating function and series definition hold true for Hermite λ-matrix polynomials ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$:

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=e^{us+v{s}^2}cos(\sqrt{s};P)$$

(28)

and

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)=\sum _{r=0}^n\left(\genfrac{}{}{0pt}{}{n}{r}\right){(-1)}^r{\mathcal{H}}_{n-r}(u,v)\Gamma (P+(r+1\left)I\right){(\Gamma (2P+(2r+1)I))}^{-1},$$

(29)

respectively.

Proof. 

From the Equation (27), we have

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }{\widehat{\ell }}^P{(u+{\widehat{h}}_v-\widehat{\ell })}^n\frac{s^n}{n!}{\widehat{\varphi }}_0{\tilde{\psi }}_0$$

(30)

or equivalently,

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }{\widehat{\ell }}^P{e}^{(u+{\widehat{h}}_v-\widehat{\ell })s}{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(31)

Since, $[(u+{\widehat{h}}_v)s,\widehat{\ell }s]=0$,

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }{\widehat{\ell }}^P{e}^{(u+{\widehat{h}}_v)s}{e}^{-\widehat{\ell }s}{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(32)

In view of Equations (2) and (16), we have assertion (28).

Again from the Equation (27), we get

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)={\widehat{\ell }}^P\sum _{r=0}^n\left(\genfrac{}{}{0pt}{}{n}{r}\right){(-1)}^r{(u+{\widehat{h}}_v)}^{n-r}{\widehat{\ell }}^r{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(33)

In view of Equation (3), we get

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)={\widehat{\ell }}^P\sum _{r=0}^n\left(\genfrac{}{}{0pt}{}{n}{r}\right){(-1)}^r{H}_{n-r}(u,v){\widehat{\ell }}^r{\tilde{\psi }}_0.$$

(34)

In view of Equation (6), we get

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)=\sum _{r=0}^n\left(\genfrac{}{}{0pt}{}{n}{r}\right){(-1)}^r{H}_{n-r}(u,v){\widehat{\ell }}^{P+rI}{\tilde{\psi }}_0.$$

(35)

Using Equation (5), we have assertion (29). □

Theorem 2.

The Hermite λ-matrix polynomials ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$ are quasi-monomial with respect to the following multiplicative and derivative operators:

$${\widehat{M}}_{{\mathcal{H}}^{\lambda }}=(u+{\widehat{h}}_v-\widehat{\ell })$$

(36)

and

$${\widehat{P}}_{{\mathcal{H}}^{\lambda }}=D_u,$$

(37)

respectively.

Proof. 

Operating $(u+{\widehat{h}}_v-\widehat{\ell })$ on both sides of Equation (27), we get

$${(u+{\widehat{h}}_v-\widehat{\ell })}_{\mathcal{H}}{\lambda }_n^{\left(P\right)}(u,v)={\widehat{\ell }}^P{(u+{\widehat{h}}_v-\widehat{\ell })}^{n+1}{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(38)

which on again using Equation (27), gives

$${(u+{\widehat{h}}_v-\widehat{\ell })}_{\mathcal{H}}{\lambda }_n^{\left(P\right)}(u,v)={}_{\mathcal{H}}{}^{ }\lambda _{n+1}^{\left(P\right)}(u,v).$$

(39)

again in view of Equations (17) and (39) we have the assertion (36).

Now, differentiating Equation (27) partially with respect to u, we find

$$D_u{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)={\widehat{\ell }}^P{(u+{\widehat{h}}_v-\widehat{\ell })}^{n-1}{\widehat{\varphi }}_0{\tilde{\psi }}_0,$$

(40)

which on again using Equation (27) gives

$$D_u{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)=n{}_{\mathcal{H}}{}^{ }\lambda _{n-1}^{\left(P\right)}(u,v).$$

(41)

In view of Equations (18) and (41) we get assertion (37). □

Theorem 3.

The differential equation satisfied by Hermite λ-matrix polynomial ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}$ is given by

$$[(u+{\widehat{h}}_v-\widehat{\ell })D_u-n]{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)=0.$$

(42)

Proof. 

In view of Equations (20), (36) and (37), we get the assertion (42). □

Theorem 4.

The Hermite λ-matrix polynomials ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$ satisfy the following differential reccurence relation:

$$\frac{\partial }{\partial u}{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)=n{}_{\mathcal{H}}{}^{ }\lambda _{n-1}^{\left(P\right)}(u,v).$$

(43)

More generally,

$$\frac{{\partial }^r}{\partial u^r}{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)=\frac{n!}{(n-r)!}{}_{\mathcal{H}}{}^{ }\lambda _{n-r}^{\left(P\right)}(u,v).$$

(44)

Proof. 

On differentiating Equation (28) with respect to u, we have

$$\frac{\partial }{\partial u}\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=s{e}^{us+v{s}^2}cos(\sqrt{s};P),$$

(45)

which in view of Equation (28), we have

$$\frac{\partial }{\partial u}\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^{n+1}}{n!}$$

(46)

or, equivalently

$$\frac{\partial }{\partial u}\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}=n\sum _{n=1}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _{n-1}^{\left(P\right)}(u,v)\frac{s^n}{n!}.$$

(47)

On comparing the equal powers of s, we get the assertion (43).

We proceed with the proof of (44) by using mathematical induction. In view of Equation (43), result (44) is true for $r=1$.

By induction, assertion (43) follows assertion (44). □

3. Summation Formulae

In this section, we obtain certain summation formulae for 2vH$\lambda$MP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$:

Theorem 5.

The following summation formula for Hermite λ- matrix polynomials ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$ holds true:

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u+w,v)=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)w^k{}_{\mathcal{H}}{}^{ }\lambda _{n-k}^{\left(P\right)}(u,v).$$

(48)

Proof. 

Replacing u by $u+w$ in the Equation (31), we have

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u+w,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }{\widehat{\ell }}^P{e}^{(u+w+{\widehat{h}}_v-\widehat{\ell })t}{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(49)

Or, equivalently

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u+w,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }{\widehat{\ell }}^P{e}^{(u+{\widehat{h}}_v-\widehat{\ell })t}{e}^{wt}{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(50)

Expanding the second exponential in the right-hand side of the above equation and using Equation (31) in the resultant equation, we have

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u+w,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)\frac{s^n}{n!}\frac{w^k{s}^n}{k!},$$

(51)

which on using the following series rearrangement

$$\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }A(n,k)=\sum _{n=0}^{\infty }\sum _{k=0}^{n}A(n-k,k),$$

(52)

in the right hand side of Equation (51), we have

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u+w,v)\frac{s^n}{n!}=\sum _{n=0}^{\infty }\left(\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)w^k{}_{\mathcal{H}}{}^{ }\lambda _{n-k}^{\left(P\right)}(u,v)\right)\frac{s^n}{n!}.$$

(53)

Comparing the equal powers of s from both sides of the above equation, we get the assertion (48). □

We obtain the following another theorem for summation formulae for Hermite $\lambda$- matrix polynomial ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$:

Theorem 6.

The following summation formula for Hermite λ- matrix polynomial ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$ holds true:

$${}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(w,v)=\sum _{n,r=0}^{k,l}\left(\genfrac{}{}{0pt}{}{k}{n}\right)\left(\genfrac{}{}{0pt}{}{l}{r}\right){(w-u)}^{n+r}{}_{\mathcal{H}}{}^{ }\lambda _{k+l-n-r}^{\left(P\right)}(u,v),$$

(54)

where ${\sum }_{n,r=0}^{k,l}:={\sum }_{n=0}^k{\sum }_{r=0}^l$.

Proof. 

Replacing s by $s+t$ in the Equation (31) and then using the formula [16]:

$$\sum _{n=0}^{\infty }f\left(n\right)\frac{{(t+s)}^n}{n!}=\sum _{n,m=0}^{\infty }f(n+m)\frac{s^n}{n!}\frac{t^m}{m!}$$

(55)

in the right-hand side of the resultant equation, we find the following generating function for Hermite $\lambda$- matrix polynomial ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$:

$${\widehat{\ell }}^P{e}^{(u+{\widehat{h}}_v-\widehat{\ell })(t+s)}=\sum _{k,l=0}^{\infty }\frac{s^n{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(u,v),$$

(56)

which can be written as

$${\widehat{\ell }}^P{e}^{({\widehat{h}}_v-\widehat{\ell })(t+s)}=e^{-u(t+s)}\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(u,v).$$

(57)

Multiplying both sides of the above equation with $e^{w(t+s)}$ and then using Equation (55) in the left-hand side of the resultant equation, we find

$$\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(w,v)=e^{(w-u)(t+s)}\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(u,v),$$

(58)

or equivalently,

$$\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(w,v)=\sum _{n=0}^{\infty }\frac{{(w-u)}^n{(t+s)}^n}{n!}\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(u,v),$$

(59)

which again, using Equation (55) in the first summation on the right-hand side gives

$$\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(w,v)=\sum _{n,r=0}^{\infty }\frac{{(w-u)}^{n+r}{s}^n{u}^r}{n!r!}\sum _{k,l=0}^{\infty }\frac{s^k{u}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(u,v),$$

(60)

Now, replacing k by $k-n$, l by $l-r$ and using Equation (52) in the right hand side of Equation (60), we find

$$\sum _{k,l=0}^{\infty }\frac{s^k{t}^l}{k!l!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l}^{\left(P\right)}(w,v)=\sum _{k,l=0}^{\infty }\sum _{n,r=0}^{k,l}\frac{{(w-u)}^{n+r}{s}^n{t}^r{s}^k{t}^l}{n!r!(k-n)!(l-r)!}{}_{\mathcal{H}}{}^{ }\lambda _{k+l-n-r}^{\left(P\right)}(u,v).$$

(61)

On comparing equal powers of t and s in the above equation, we get the assertion (54). □

4. Graphical Representation and Distribution of Zeros

In this section, we obtain certain examples and give their graphical representation and distribution of zeros of 2-variable Hermite $\lambda$-matrix polynomials.

Example 1.

For $P=\left(\begin{array}{cc}\sqrt{3}+1& \sqrt{2}\\ e& \pi -1\end{array}\right)\in {\mathbb{C}}^{2\times 2}$ and the eigenvalues of matrix P are $\{4.4196,$$0.454048\}$, so matrix P is satisfying the condition given in Equation (22) and hence, is positive stable matrix. For $n=5,$ and in view of Equation (29), 2vHλMP ${}_{\mathcal{H}}{}^{ }\lambda _5^{\left(P\right)}(u,v)$ is given by

$$\begin{array}{c}\hfill {}_{\mathcal{H}}{}^{ }\lambda _5^{\left(P\right)}(u,v):=\left(\begin{array}{ccc}-0.0072199-2.38192x^4+0.0985647x^5& & 0.00375439+1.22812x^4-0.0495848x^5\\ +x^2(-3.4672-28.583y)+(-6.9344-28.583y)y& & +x^2(1.80096+14.7374y)+y(3.60192+14.7374y)\\ +x^3(6.36242+1.97129y)& & +x^3(-3.29875-0.991696y)\\ +x(0.414261+y(38.1745+5.91388y\left)\right)& & +x(-0.215341+(-19.7925-2.97509y\left)y\right)\\ & & \\ 0.0138707+4.53732x^4-0.183192x^5& & -0.00722114-2.38938x^4+0.0997037x^5\\ +x^3(-12.1873-3.66385y)+x^2(6.6537+54.4478y)& & +x^2(-3.46914-28.6726y)+(-6.93827-28.6726y)y\\ +y(13.3074+54.4478y)& & +x^3(6.37006+1.99407y)\\ +x(-0.795583+(-73.124-10.9915y\left)y\right)& & +x(0.414383+y(38.2203+5.98222y\left)\right)\end{array}\right).\end{array}$$

Example 2.

Since in view of Equations (4) and (11), for $P=\mu \in {\mathbb{C}}^{1\times 1}$, the λ-matrix polynomials ${\lambda }_n^{\left(P\right)}(u,v)$ transform to the associated-λ polynomials ${\lambda }_n^{\left(\mu \right)}(u,v)$. Therefore, for the same choice of P, 2vHλMP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}(u,v)$ transform to 2-variable Hermite λ associated polynomials (2vHaλP) ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)$. Thus, for $P=\mu \in {\mathbb{C}}^{1\times 1}(\mu \notin {\mathbb{Z}}^{-}),$ Equations (27)–(29), (36), (37) and (42)–(44) reduce to respective symbolic definition, generating function, series definition, multiplicative operator, derivative operator, differential equation and differential recurrence relation for 2vHaλP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)$.

First, we draw the surface plots of 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)$, for $n=5,\mu =1$ and $n=6$ and same choice for $\mu$ in Figure 1 and Figure 2.

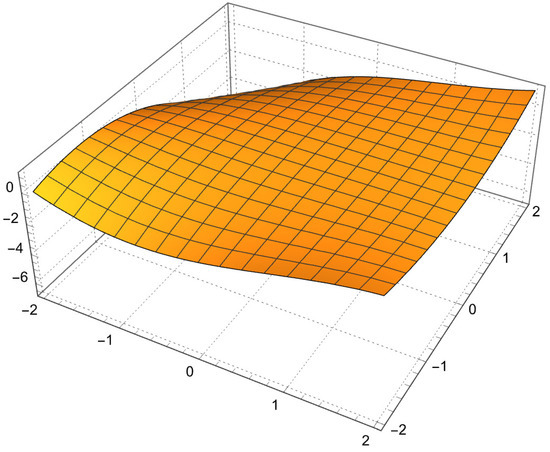
Figure 1. Surface plot of ${}_{\mathcal{H}}{}^{ }\lambda _5^{\left(1\right)}(u,v)$.

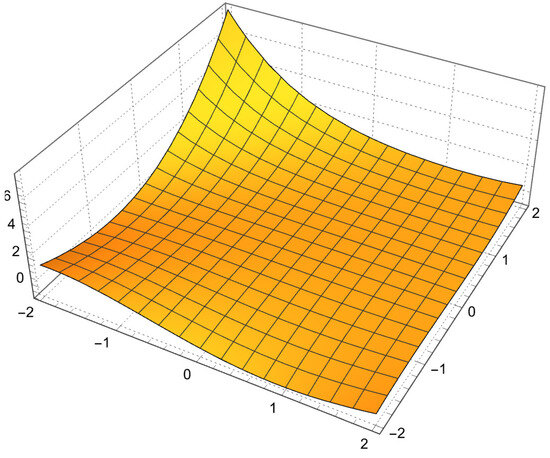
Figure 2. Surface plot of ${}_{\mathcal{H}}{}^{ }\lambda _6^{\left(1\right)}(u,v)$.

Now, we find the roots of equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)=0$ for different choices for v. Figure 3 shows the roots of the equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,1/2)=0$, Figure 4 shows the roots of the equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,2)=0$, whereas Figure 5 and Figure 6 show the roots of the equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,1/2-i)=0$ and ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,-1/3+i)=0$, respectively. Certain roots of the equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)=0$ and beautiful graphical representation are shown. We plot the zeros of the 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)$ for $n=30$ and different choices of v and $\mu$ in Figure 3, Figure 4, Figure 5 and Figure 6. Some recent developments in this field can be found in [17,18].

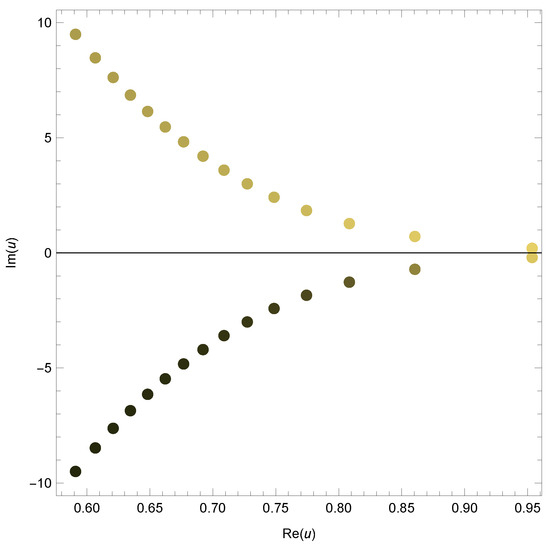
Figure 3. Zeros of 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _{30}^{\left(10\right)}(u,1/2)=0$.

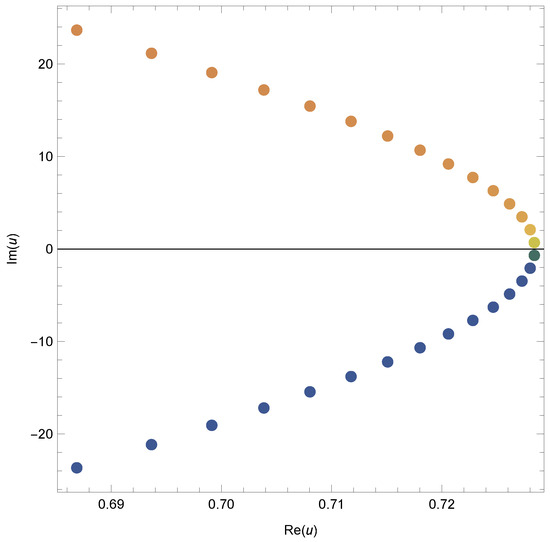
Figure 4. Zeros of 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _{30}^{\left(10\right)}(u,2)=0$.

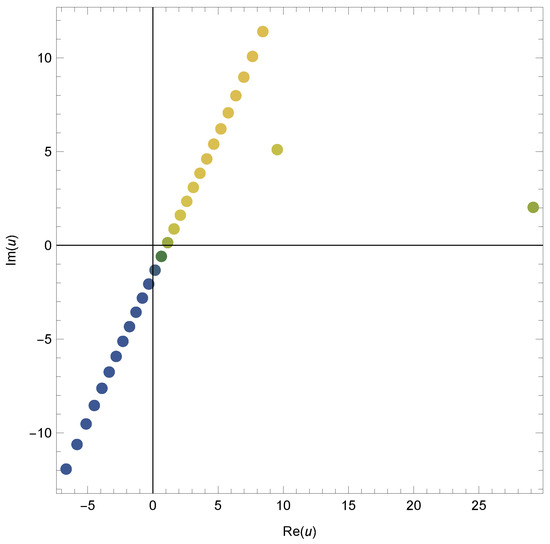
Figure 5. Zeros of 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _{30}^{\left(3\right)}(u,1/2-i)=0$.

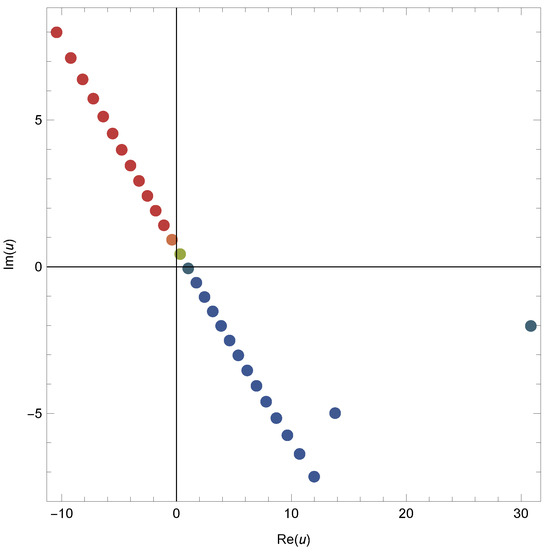
Figure 6. Zeros of 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _{30}^{\left(3\right)}(u,-1/3+i)=0$.

In Figure 3, we choose $v=1/2$ and $\mu =10$. In Figure 4, we choose $v=2$ and $\mu =10$. In Figure 5, we choose $v=1/2-i$ and $\mu =3.$ In Figure 6, we choose $v=-1/3+i$ and $\mu =3$.

Plots of real roots of the 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)$ for $1\le n\le 30$ are presented in Figure 7 and Figure 8. In Figure 7, we choose $v=-2$ and $\mu =3$. In Figure 8, we choose $v=1/2$ and $\mu =1$. It is worth noticing that for negative values of v, no of real roots are more than that of positive values of v. Stacks of roots of the 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)$ for $1\le n\le 30$, $v=\frac{1}{2}$ and $\mu =1$ from a 3D structure are presented in Figure 9.

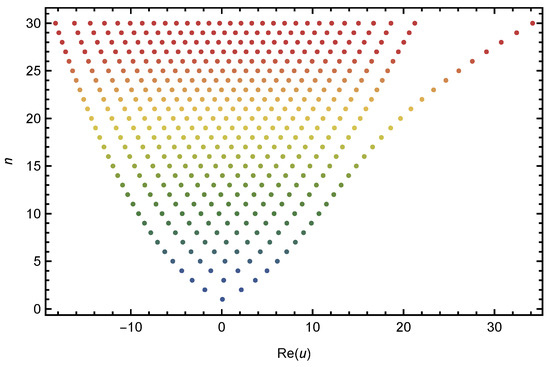
Figure 7. Real zeros of ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(3\right)}(u,-2)=0$.

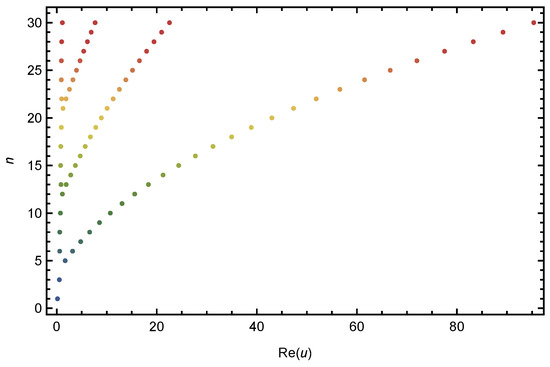
Figure 8. Real zeros of ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(1\right)}(u,1/2)=0$.

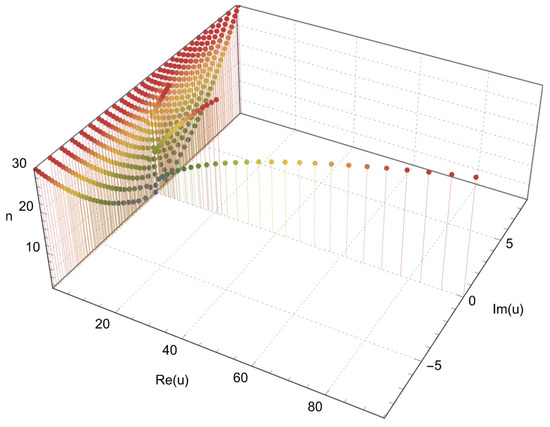
Figure 9. Stacks of zeros of ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(1\right)}(u,1/2)=0$.

Our numerical results for the solutions satisfying 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,1/2)=0$ for $n=30$ and $\mu =1$ are listed in Table 1.

Table 1. Approximate solutions of 2vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _{30}^{\left(\mu \right)}(u,1/2)=0$.

Zeros of 2vHa$\mathit{\lambda }$P ${}_{\mathcal{H}}{}^{ }\mathit{\lambda }_{30}^{\left(1\right)}(\mathit{u},1/2)=0$
$1.14237,7.67816,22.5464,95.335,1.09401-0.500339i,1.09401+0.500339i,$
$0.754911-8.94696i,0.754911+8.94696i,0.778452-7.90285i,0.778452+7.90285i,$
$0.799677-7.03036i,0.799677+7.03036i,0.82017-6.24475i,0.82017+6.24475i,$
$0.840589-5.51366i,0.840589+5.51366i,0.861359-4.82038i,0.861359+4.82038i$
$0.88286-4.15479i,0.88286+4.15479i,0.905547-3.5102i,0.905547+3.5102i,$
$0.930097-2.88186i,0.930097+2.88186i,0.957668-2.26639i,0.957668+2.26639i$
$0.990483-1.66177i,0.990483+1.66177i,1.03321-1.06879i,1.03321+1.06879i$

5. Concluding Remarks

In concluding remarks, we introduce the idea of 1-variable Hermite $\lambda$-matrix polynomials (1vH$\lambda$MP) ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)$.

From Equations (23) and (25) it is clear that the 2VHKdFP ${\mathcal{H}}_n(u,v)$ is related to the classical Hermite polynomials ${\mathcal{H}}_n\left(u\right)$ as:

$${\mathcal{H}}_n(u,v)={\mathcal{H}}_n(2u,-1).$$

(62)

In view of Equations (27) and (62), the symbolic definition of 1vH$\lambda$MP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)$ is given by

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)={\widehat{\ell }}^P{(2u+{\widehat{h}}_{-1}-\widehat{\ell })}^n{\widehat{\varphi }}_0{\tilde{\psi }}_0.$$

(63)

Similarly, taking into account Equation (63), we obtain the generating function and series definition of 1vH$\lambda$MP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)$:

$$\sum _{n=0}^{\infty }{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)\frac{s^n}{n!}=e^{2us-s^2}cos(\sqrt{s};P)$$

(64)

and

$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)=\sum _{r=0}^n\left(\genfrac{}{}{0pt}{}{n}{r}\right){(-1)}^r{\mathcal{H}}_{n-r}\left(u\right)\Gamma (P+(r+1\left)I\right){(\Gamma (2P+(2r+1)I))}^{-1},$$

(65)

respectively.

The multiplicative and derivative operators of 1vH$\lambda$MP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)$:

$${\tilde{M}}_{{\mathcal{H}}^{\lambda }}=(2u+{\widehat{h}}_{-1}-\widehat{\ell })$$

(66)

and

$${\tilde{P}}_{{\mathcal{H}}^{\lambda }}=\frac{1}{2}{D}_u,$$

(67)

respectively.

In view of Equations (20), (66) and (67), the following differential equation is satisfied by 1vH$\lambda$MP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)$:

$$\left[\frac{1}{2}(2u+{\widehat{h}}_{-1}-\widehat{\ell })D_u-n\right]{}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)=0.$$

(68)

Since in view of Equations (4) and (11), for $P=\mu \in {\mathbb{C}}^{1\times 1}(\mu \notin {\mathbb{Z}}^{-})$, the $\lambda$-matrix polynomials ${\lambda }_n^{\left(P\right)}(u,v)$ transform to the associated-$\lambda$ polynomials ${\lambda }_n^{\left(\mu \right)}(u,v)$. Therefore, for the same choice of P, 1vH$\lambda$MP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(P\right)}\left(u\right)$ transform to 1-variable Hermite associated $\lambda$ associated polynomials (1vHa$\lambda$P) ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)$. Thus, for $P=\mu \in {\mathbb{C}}^{1\times 1}(\mu \notin {\mathbb{Z}}^{-}),$ Equations (63)–(68) reduce to respective symbolic definition, generating function, series definition, multiplicative operator, derivative operator, and differential equation for 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)$.

Now, we illustrate the shape of 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)$ and examine its zeros. In Figure 10, we present the graphs of 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)$.

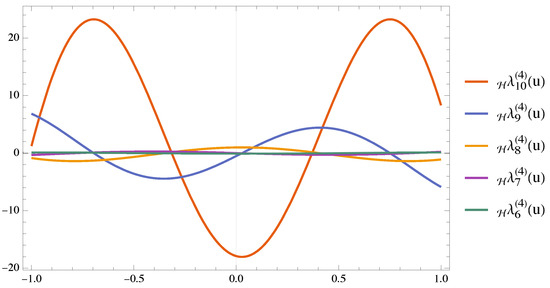
Figure 10. ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(4\right)}\left(u\right)$.

Our numerical results for the solutions satisfying 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$ for $n=40$ and $\mu =-\pi$ are listed in Table 2.

Table 2. Approximate solutions of 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _{40}^{(-\pi )}\left(u\right)=0$.

Zeros of 1vHa$\mathit{\lambda }$P ${}_{\mathcal{H}}{}^{ }\mathit{\lambda }_{40}^{(-\mathit{\pi })}\left(\mathit{u}\right)=0$
$-8.18641,-7.47314,-6.88868,-6.36866,-5.88924,-5.43833,$
$-5.00873,-4.59572,-4.19599,-3.80708,-3.42708,-3.05448,-2.68801,$
$-2.32663,-1.96941,-1.61554,-1.26429,-0.914982,-0.567005,$
$-0.219764,0.127309,0.474767,0.823165,1.17307,1.52505,1.87975,$
$2.23782,2.60003,2.96722,3.34036,3.72064,4.10948,4.50867,$
$4.92052,5.34816,5.796,6.27073,6.78346,7.3558,8.04435$

Next in Figure 11 and Figure 12, we investigate the beautiful pattern of zeros of the 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$. The plot of real zeros of the 1vHa$\lambda$P ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$ for $1\le n\le 40$ for $\mu =4$ structure are presented in Figure 11.

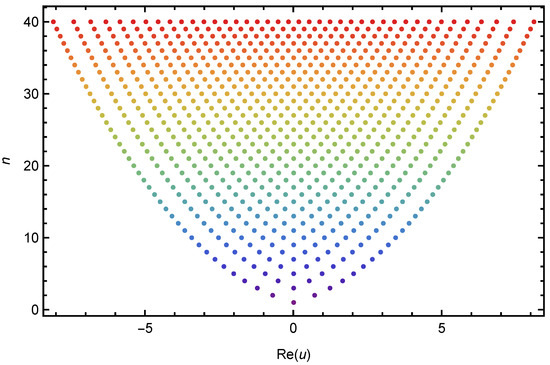
Figure 11. Real zeros of ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(4\right)}\left(u\right)$.

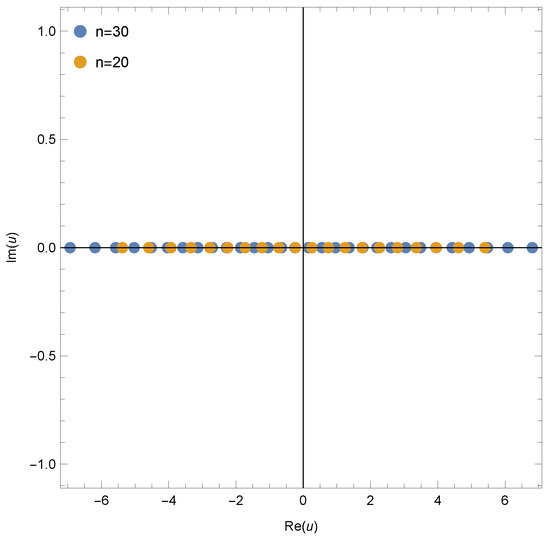
Figure 12. Zeros of ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)$.

We can discern a consistent pattern in the complex roots of the 2-variable Hermite $\lambda$ associated polynomials ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}(u,v)=0$. Consequently, the following conjectures are plausible for the equation 1vHa$\lambda \mathrm{P}$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$.

We observed that the solutions of the 1vHa$\lambda$P equations exhibit no $Im\left(u\right)=\alpha$ reflection symmetry for $\alpha \in \mathbb{R}$. It is anticipated that the solutions of the 1vHa$\lambda \mathrm{P}$${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$ equations possess $Im\left(u\right)=0$ reflection symmetry (refer to Figure 11 and Figure 12).

Conjecture 1.

Prove or disprove that 1vHaλP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$ for $u\in \mathbb{C}$ and $\mu \in \mathbb{R}$ has $Im\left(u\right)=0$ reflection symmetry analytic complex functions.

Finally, we addressed the more general problem of determining the number of zeros of the equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$. We were unable to ascertain whether this equation has n distinct solutions. Our interest lies in determining the number of complex zeros of the equation ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$.

Conjecture 2.

Prove or disprove that 1vHaλP ${}_{\mathcal{H}}{}^{ }\lambda _n^{\left(\mu \right)}\left(u\right)=0$ have n distinct roots.

As a result of investigating more n variables, it is still unknown whether the above conjectures are true or false for all variables n.

In this article, our aim is to introduce the set of hybrid matrix polynomials associated with $\lambda$-polynomials and explore their properties using a symbolic approach. The main outcomes of this study include the derivation of generating functions, series definitions, and differential equations for the newly introduced two-variable Hermite $\lambda$-matrix polynomials. Furthermore, we establish the quasi-monomiality property of these polynomials and derive summation formulae. Finally, we obtain the graphical representation and symmetric structure of their approximate zeros for different choices of $v,n$, and $\mu$ using computer-aided programs.

The results of this article have the potential to motivate researchers and readers to conduct further research on these special matrix polynomials. These results may be applied in mathematics, mathematical physics, and engineering.