New Properties of Analytic Functions

Abstract

In the present paper, we consider the class $\overline{\mathcal{A}}$ of functions $f\left(z\right)$ of the form $f\left(z\right)=z+{\sum }_{k=1}^{\infty }{a}_{1+\frac{k}{3}}{z}^{1+\frac{k}{3}}$ that are analytic in the open unit disc $\mathbb{U}.$ If $a_{1+\frac{k}{3}}=0$ for $k\ne 3n$ $(n=1,2,3,\cdots ),$ then $f\left(z\right)$ is given by $f\left(z\right)=z+{\sum }_{k=2}^{\infty }{a}_k{z}^k.$ For such functions $f\left(z\right)\in \overline{\mathcal{A}},$ some interesting properties for subordinations and strongly starlike functions are given. Also, some interesting examples for the results are shown.

1. Introduction

Let $\overline{\mathcal{A}}$ denote the class of functions $f\left(z\right)$ of the form

$$f\left(z\right)=z+\sum _{k=1}^{\infty }{a}_{1+\frac{k}{3}}{z}^{1+\frac{k}{3}},$$

(1)

which are analytic in the open unit disc $\mathbb{U}=\{z\in \mathbb{C}:|z|<1\}$ with the principal value for $\sqrt[3]{z}.$ If $a_{1+\frac{k}{3}}=0$ for $k\ne 3n$ $(n=1,2,3,\cdots ),$ then $f\left(z\right)$ can be written as

$$f\left(z\right)=z+\sum _{k=2}^{\infty }{a}_k{z}^k$$

(2)

and denoted by $f\left(z\right)\in \mathcal{A}.$

Remark 1.

A class of functions $f\left(z\right)$ given by

$$f\left(z\right)=z+\sum _{k=1}^{\infty }{a}_{1+\frac{k}{2}}{z}^{1+\frac{k}{2}}$$

(3)

which are analytic in $\mathbb{U}$ was considered by Owa [1] and Owa et al. [2].

If we consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{cc}\hfill f\left(z\right)& =\frac{z}{{\left(1-\sqrt[3]{z}\right)}^{6(1-\alpha )}}\hfill \\ \hfill & =z+\sum _{k=1}^{\infty }\frac{{\prod }_{j=1}^k(j+5-6\alpha )}{k!}{z}^{1+\frac{k}{3}}\hfill \end{array}$$

(4)

with $0\le \alpha <1,$ then $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)=Re\left(\frac{1+(1-2\alpha )\sqrt[3]{z}}{1-\sqrt[3]{z}}\right)>\alpha ,(z\in \mathbb{U}).\end{array}$$

(5)

Also, if $f\left(z\right)$ is given by

$$\begin{array}{c}\hfill f\left(z\right)=\frac{z}{1-\sqrt[3]{z}}=z+\sum _{k=1}^{\infty }{z}^{1+\frac{k}{3}},\end{array}$$

(6)

then for $z=e^{i\theta }$ $(0\le \theta <2\pi ),$ we have

$$\begin{array}{cc}\hfill Ref\left(z\right)& =Re\left(\frac{e^{i\theta }}{1-e^{i\frac{\theta }{3}}}\right)\hfill \\ \hfill & =Re\left(\frac{e^{i\left(1-\frac{1}{6}\right)\theta }}{e^{-i\frac{\theta }{6}}-e^{i\frac{\theta }{6}}}\right)\hfill \\ \hfill & =-\frac{1}{2}\left(\frac{sin\left(\frac{5}{6}\theta \right)}{sin\left(\frac{1}{6}\theta \right)}\right)\hfill \\ \hfill & =-\frac{1}{2}\left(\frac{sin\left(\frac{\theta }{6}+\frac{2}{3}\theta \right)}{sin\left(\frac{\theta }{6}\right)}\right)\hfill \\ \hfill & =-\frac{1}{2}\left\{cos\left(\frac{2}{3}\theta \right)+\frac{cos\left(\frac{\theta }{6}\right)}{sin\left(\frac{\theta }{6}\right)}\left(2sin\left(\frac{\theta }{3}\right)cos\left(\frac{\theta }{3}\right)\right)\right\}\hfill \\ \hfill & =-\frac{1}{2}\left\{2co{s}^2\left(\frac{\theta }{3}\right)-1+2\sqrt{\frac{1+cos\left(\frac{\theta }{3}\right)}{1-cos\left(\frac{\theta }{3}\right)}}sin\left(\frac{\theta }{3}\right)cos\left(\frac{\theta }{3}\right)\right\}\hfill \\ \hfill & =-\frac{1}{2}\left\{2co{s}^2\left(\frac{\theta }{3}\right)-1+2\frac{1+cos\left(\frac{\theta }{3}\right)}{sin\left(\frac{\theta }{3}\right)}sin\left(\frac{\theta }{3}\right)cos\left(\frac{\theta }{3}\right)\right\}\hfill \\ \hfill & =-\frac{1}{2}\left\{4co{s}^2\left(\frac{\theta }{3}\right)+2cos\left(\frac{\theta }{3}\right)-1\right\}\hfill \\ \hfill & \ge -\frac{5}{2}.\hfill \end{array}$$

(7)

Thus, we have

$$\begin{array}{c}\hfill Re\left(\frac{z}{1-\sqrt[3]{z}}\right)>-\frac{5}{2},(z\in \mathbb{U}).\end{array}$$

(8)

We can see this bound visualized geometrically in Figure 1.

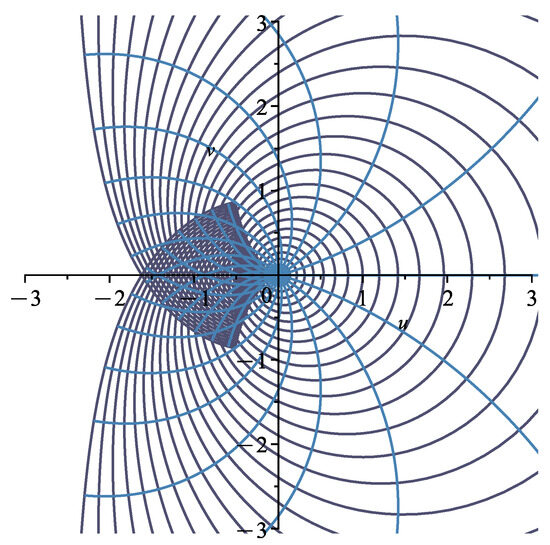
Figure 1. $Re\left(\frac{z}{1-\sqrt[3]{z}}\right)>-\frac{5}{2}$.

2. Subordination Properties

Let $f\left(z\right)$ and $g\left(z\right)$ be analytic in $\mathbb{U}.$ Then, we say that $f\left(z\right)$ is subordinate to $g\left(z\right),$ written as $f\left(z\right)\prec g\left(z\right)$ $(z\in \mathbb{U}),$ if there exists a function $w\left(z\right)$ analytic in $\mathbb{U}$ with $w\left(0\right)=0$ and $\left|w\right(z\left)\right|<1$ $(z\in \mathbb{U})$ such that $f\left(z\right)=g\left(w\right(z\left)\right).$

With the above definition, we know that if $f\left(z\right)\in \overline{\mathcal{A}}$ and

$$\begin{array}{c}\hfill g\left(z\right)=\frac{1+(1-2\alpha )\sqrt[3]{z}}{1-\sqrt[3]{z}},(z\in \mathbb{U},0\le \alpha <1)\end{array}$$

(9)

satisfy

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)\prec g\left(z\right),(z\in \mathbb{U}),\end{array}$$

(10)

then

$$\begin{array}{c}\hfill Re{f}^{\prime }\left(z\right)>\alpha ,(z\in \mathbb{U}).\end{array}$$

(11)

If $f\left(z\right)\in \overline{\mathcal{A}}$ and $g\left(z\right)$ satisfy

$$\begin{array}{c}\hfill \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec g\left(z\right),(z\in \mathbb{U}),\end{array}$$

(12)

then

$$\begin{array}{c}\hfill Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\alpha ,(z\in \mathbb{U}).\end{array}$$

(13)

Also, if $f\left(z\right)\in \overline{\mathcal{A}}$ and $g\left(z\right)$ satisfy

$$\begin{array}{c}\hfill 1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\prec g\left(z\right),(z\in \mathbb{U}),\end{array}$$

(14)

then

$$\begin{array}{c}\hfill Re\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)>\alpha ,(z\in \mathbb{U}).\end{array}$$

(15)

Remark 2.

Let us consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{cc}\hfill f\left(z\right)& =(2\alpha -1)z-6(1-\alpha )log\left(1-\sqrt[3]{z}\right)-3(1-\alpha )\sqrt[3]{z}\left(2+\sqrt[3]{z}\right)\hfill \\ \hfill & =z+6(1-\alpha )\sum _{k=1}^{\infty }\left(\frac{1}{k+3}\right)z^{1+\frac{k}{3}},\hfill \end{array}$$

(16)

and then

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)=\frac{1+(1-2\alpha )\sqrt[3]{z}}{1-\sqrt[3]{z}}.\end{array}$$

(17)

Now, we have to introduce the following lemma by Suffridge [3].

Lemma 1.

Let $p\left(z\right)$ be analytic in $\mathbb{U}$ with $p\left(0\right)=1$ and $h\left(z\right)$ be analytic and starlike in $\mathbb{U}.$ If

$$\begin{array}{c}\hfill z{p}^{\prime }\left(z\right)\prec h\left(z\right),(z\in \mathbb{U}),\end{array}$$

(18)

then

$$\begin{array}{c}\hfill p\left(z\right)\prec {\int }_0^z\frac{h\left(t\right)}{t}dt,(z\in \mathbb{U}).\end{array}$$

(19)

With the above lemma, we have the following theorem.

Theorem 1.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ and $h\left(z\right)$ be given by

$$\begin{array}{c}\hfill h\left(z\right)=\frac{z}{{\left(1-\sqrt[3]{z}\right)}^{6(1-\alpha )}},(z\in \mathbb{U})\end{array}$$

(20)

for some real α $(0\le \alpha <1).$ If $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill z{f}^{″}\left(z\right)\prec h\left(z\right)=\frac{z}{{\left(1-\sqrt[3]{z}\right)}^{6(1-\alpha )}},(z\in \mathbb{U}),\end{array}$$

(21)

then

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)\prec {\int }_0^z\frac{h\left(t\right)}{t}dt={\int }_0^z\frac{1}{{\left(1-\sqrt[3]{t}\right)}^{6(1-\alpha )}}dt,(z\in \mathbb{U}).\end{array}$$

(22)

Proof. 

Let us define a function $p\left(z\right)=f^{\prime }\left(z\right)$ for $f\left(z\right)\in \overline{\mathcal{A}}.$ Then, $p\left(z\right)$ is analytic in $\mathbb{U}$, and $p\left(0\right)=1.$ Also, $h\left(z\right)$ is analytic and starlike in $\mathbb{U}.$ Thus, using Lemma 1, we say that if

$$\begin{array}{c}\hfill z{p}^{\prime }\left(z\right)=z{f}^{″}\left(z\right)\prec h\left(z\right),(z\in \mathbb{U}),\end{array}$$

(23)

and then

$$\begin{array}{c}\hfill p\left(z\right)=f^{\prime }\left(z\right)\prec {\int }_0^z\frac{h\left(t\right)}{t}dt,(z\in \mathbb{U}).\end{array}$$

(24)

It follows that

$$\begin{array}{cc}\hfill {\int }_0^z\frac{h\left(t\right)}{t}dt& ={\int }_0^z\frac{1}{{\left(1-\sqrt[3]{t}\right)}^{6(1-\alpha )}}dt\hfill \\ \hfill & =3{\int }_{1-\sqrt[3]{z}}^1\left(u^{6\alpha -6}-2u^{6\alpha -5}+u^{6\alpha -4}\right)du\hfill \\ \hfill & =3\left\{1-{\left(1-\sqrt[3]{z}\right)}^{6\alpha -5}\left(1+(6\alpha -5)\sqrt[3]{z}\left(1+(3\alpha -2)\sqrt[3]{z}\right)\right)\right\}.\hfill \end{array}$$

(25)

□

Theorem 2.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ and $h\left(z\right)$ be given by

$$\begin{array}{c}\hfill h\left(z\right)=\frac{z}{{\left(1-\sqrt[3]{z}\right)}^{6(1-\alpha )}},(z\in \mathbb{U})\end{array}$$

(26)

for some real α $(0\le \alpha <1).$ If $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)-\frac{f\left(z\right)}{z}\prec h\left(z\right)=\frac{z}{{\left(1-\sqrt[3]{z}\right)}^{6(1-\alpha )}},(z\in \mathbb{U}),\end{array}$$

(27)

then

$$\begin{array}{cc}\hfill \frac{f\left(z\right)}{z}\prec {\int }_0^z\frac{h\left(t\right)}{t}dt& ={\int }_0^z\frac{1}{{\left(1-\sqrt[3]{t}\right)}^{6(1-\alpha )}}dt\hfill \\ \hfill & =3\left\{1-{\left(1-\sqrt[3]{z}\right)}^{6\alpha -5}\left(1+(6\alpha -5)\sqrt[3]{z}\left(1+(3\alpha -2)\sqrt[3]{z}\right)\right)\right\}.\hfill \end{array}$$

(28)

Proof. 

Letting $p\left(z\right)=\frac{f\left(z\right)}{z}$ for $f\left(z\right)\in \overline{\mathcal{A}},$ we know that

$$\begin{array}{c}\hfill z{p}^{\prime }\left(z\right)=f^{\prime }\left(z\right)-\frac{f\left(z\right)}{z}.\end{array}$$

(29)

Thus, we have the subordination (28) under the condition (27) by Lemma 1. □

Next, we introduce the lemma by Hallenbeck and Ruscheweyh [4].

Lemma 2.

Let a function $p\left(z\right)$ be analytic in $\mathbb{U}$ with $p\left(0\right)=1$, and $h\left(z\right)$ be analytic and convex in $\mathbb{U}.$ If $p\left(z\right)$ satisfies

$$\begin{array}{c}\hfill p\left(z\right)+z{p}^{\prime }\left(z\right)\prec h\left(z\right),(z\in \mathbb{U}),\end{array}$$

(30)

then

$$\begin{array}{c}\hfill p\left(z\right)\prec \frac{1}{z}{\int }_0^{z}h\left(t\right)dt,(z\in \mathbb{U}).\end{array}$$

(31)

Applying Lemma 2, we derive the following theorem.

Theorem 3.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ satisfy

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)+z{f}^{″}\left(z\right)\prec \frac{1+(1-2\alpha )\sqrt[3]{z}}{1-\sqrt[3]{z}},(z\in \mathbb{U})\end{array}$$

(32)

for some real α $(0\le \alpha <1),$ and then

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)\prec \frac{1}{z}{\int }_0^z\frac{1+(1-2\alpha )\sqrt[3]{t}}{1-\sqrt[3]{t}}dt,(z\in \mathbb{U}).\end{array}$$

(33)

Proof. 

Let us consider a function $p\left(z\right)=f^{\prime }\left(z\right)$ in Lemma 2, and let $h\left(z\right)$ be given by

$$\begin{array}{c}\hfill h\left(z\right)=\frac{1+(1-2\alpha )\sqrt[3]{z}}{1-\sqrt[3]{z}}.\end{array}$$

(34)

Then, $p\left(z\right)$ is analytic in $\mathbb{U}$ with $p\left(0\right)=1$, and $h\left(z\right)$ is analytic and convex in $\mathbb{U}.$ Thus, if $f\left(z\right)$ satisfies the subordination (32), then $f\left(z\right)$ satisfies (33). Here, we have

$$\begin{array}{cc}\hfill \frac{1}{z}{\int }_0^z\frac{1+(1-2\alpha )\sqrt[3]{t}}{1-\sqrt[3]{t}}dt& =\frac{1}{z}{\int }_0^z\left((2\alpha -1)+\frac{2(1-\alpha )}{1-\sqrt[3]{t}}\right)dt\hfill \\ \hfill & =\frac{1}{z}\left\{(2\alpha -1)z+6(1-\alpha ){\int }_{1-\sqrt[3]{z}}^1\left(\frac{1}{u}-2+u\right)du\right\}\hfill \\ \hfill & =(2\alpha -1)-6(1-\alpha )\left(\frac{1}{{\left(\sqrt[3]{z}\right)}^2}+\frac{1}{2\sqrt[3]{z}}+\frac{1}{z}log\left(1-\sqrt[3]{z}\right)\right).\hfill \end{array}$$

(35)

□

Letting $\alpha =\frac{1}{2}$ in Theorem 3, we obtain the following corollary.

Corollary 1.

If $f\left(z\right)\in \overline{\mathcal{A}}$ satisfies

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)+z{f}^{″}\left(z\right)\prec \frac{1}{1-\sqrt[3]{z}},(z\in \mathbb{U})\end{array}$$

(36)

then

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)\prec -3\left(\frac{1}{{\left(\sqrt[3]{z}\right)}^2}+\frac{1}{2\sqrt[3]{z}}+\frac{1}{z}log\left(1-\sqrt[3]{z}\right)\right).\end{array}$$

(37)

3. Applications for Strongly Starlike Functions

Let us consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{c}\hfill f\left(z\right)=-z-6\left(\sqrt[3]{z}+\frac{1}{2}{\left(\sqrt[3]{z}\right)}^2+log\left(1-\sqrt[3]{z}\right)\right),(z\in \mathbb{U}).\end{array}$$

(38)

Then, $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)=\frac{1+\sqrt[3]{z}}{1-\sqrt[3]{z}}\end{array}$$

(39)

and

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|<\frac{\pi }{2},(z\in \mathbb{U}).\end{array}$$

(40)

We say that $f\left(z\right)$ is strongly starlike in $\mathbb{U}.$ Also, if we consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{c}\hfill f\left(z\right)={\int }_0^z{\left(\frac{1+\sqrt[3]{t}}{1-\sqrt[3]{t}}\right)}^{\alpha }dt,(z\in \mathbb{U})\end{array}$$

(41)

for some real $\alpha$ $(0<\alpha \le 1),$ then $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|=\alpha \left|arg\left(\frac{1+\sqrt[3]{z}}{1-\sqrt[3]{z}}\right)\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(42)

This function $f\left(z\right)$ given by (41) is said to be a strongly starlike function of order $\alpha$ in $\mathbb{U}.$

Now, we introduce the following lemma by Fejér and Riesz [5] (also by Tsuji [6]).

Lemma 3.

Let a function $f\left(z\right)$ be analytic in $\left|z\right|\le 1.$ Then, $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill {\int }_{-1}^1{\left|f\left(z\right)\right|}^{\varrho }\left|dz\right|\le \frac{1}{2}{\int }_{\left|z\right|=1}{\left|f\left(z\right)\right|}^{\varrho }\left|dz\right|,(\varrho >0),\end{array}$$

(43)

where the above integral on the left-hand side is considered along the real axis.

Remark 3.

If we make a change of variables in Lemma 3, then the inequality (43) becomes

$$\begin{array}{c}\hfill {\int }_{-r}^r{\left|f\right(\rho e^{i\theta }\left)\right|}^{\varrho }d\rho \le \frac{r}{2}{\int }_0^{2\pi }{\left|f\left(r{e}^{i\theta }\right)\right|}^{\varrho }d\theta .\end{array}$$

(44)

Also, we need to include the lemma by Gwynme [7].

Lemma 4.

Let $f\left(z\right)$ be a complex-valued harmonic function defined on a neighborhood of a closed disk of radius 1 and center 0 in the complex plane. Then,

$$\begin{array}{c}\hfill f\left(r{e}^{i\theta }\right)=\frac{1}{2\pi }{\int }_0^{2\pi }f\left(e^{i\rho }\right)\frac{1-r^2}{1+r^2-2rcos(\theta -\rho )}d\rho \end{array}$$

(45)

and

$$\begin{array}{c}\hfill \frac{1}{2\pi }{\int }_0^{2\pi }\frac{1-r^2}{1+r^2-2rcos\rho }d\rho =1.\end{array}$$

(46)

Applying Lemma 3, we have the following theorem.

Theorem 4.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ satisfy

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|\le \frac{\alpha }{2},(z\in \mathbb{U})\end{array}$$

(47)

for some real α $(0<\alpha \le 1),$ and then

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|\le \frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(48)

Proof. 

It follows that

$$\begin{array}{c}\hfill log{f}^{\prime }\left(z\right)=log\left|f^{\prime }\left(z\right)\right|+iarg{f}^{\prime }\left(z\right)\end{array}$$

(49)

and

$$\begin{array}{c}\hfill log{f}^{\prime }\left(z\right)={\int }_0^z{\left(log{f}^{\prime }\left(t\right)\right)}^{\prime }dt={\int }_0^z\frac{f^{″}\left(t\right)}{f^{\prime }\left(t\right)}dt.\end{array}$$

(50)

This implies that

$$\begin{array}{cc}\hfill \left|arg{f}^{\prime }\left(z\right)\right|& =\left|\mathrm{Im}\left(log{f}^{\prime }\left(z\right)\right)\right|\hfill \\ \hfill & =\left|\mathrm{Im}{\int }_0^z\frac{f^{″}\left(t\right)}{f^{\prime }\left(t\right)}dt\right|\hfill \\ \hfill & =\left|\mathrm{Im}{\int }_0^r\frac{f^{″}\left(\rho e^{i\theta }\right)}{f^{\prime }\left(\rho e^{i\theta }\right)}{e}^{i\theta }d\rho \right|\hfill \\ \hfill & \le {\int }_0^r\left|\mathrm{Im}\left(\frac{e^{i\theta }{f}^{″}\left(\rho e^{i\theta }\right)}{f^{\prime }\left(\rho e^{i\theta }\right)}\right)\right|d\rho \hfill \\ \hfill & \le {\int }_{-r}^r\left|\mathrm{Im}\left(\frac{e^{i\theta }{f}^{″}\left(\rho e^{i\theta }\right)}{f^{\prime }\left(\rho e^{i\theta }\right)}\right)\right|d\rho \hfill \\ \hfill & \le {\int }_{-r}^r\left|\frac{f^{″}\left(\rho e^{i\theta }\right)}{f^{\prime }\left(\rho e^{i\theta }\right)}\right|d\rho ,\hfill \end{array}$$

(51)

where $z=r{e}^{i\theta }$ $(0\le \theta <2\pi ),$ $0\le r<1$, and $0\le \rho \le r.$ Using (44) with $\varrho =1,$ we have

$$\begin{array}{cc}\hfill \left|arg{f}^{\prime }\left(z\right)\right|& \le \frac{r}{2}{\int }_0^{2\pi }\left|\frac{f^{″}\left(r{e}^{i\theta }\right)}{f^{\prime }\left(r{e}^{i\theta }\right)}\right|d\theta \hfill \\ \hfill & =\frac{1}{2}{\int }_0^{2\pi }\left|\frac{r{e}^{i\theta }{f}^{″}\left(r{e}^{i\theta }\right)}{f^{\prime }\left(r{e}^{i\theta }\right)}\right|d\theta \hfill \\ \hfill & \le \frac{\alpha }{4}{\int }_0^{2\pi }d\theta =\frac{\pi }{2}\alpha .\hfill \end{array}$$

(52)

□

If we take $\alpha =1$ in Theorem 4, we obtain the following corollary.

Corollary 2.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ satisfy

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|\le \frac{1}{2},(z\in \mathbb{U})\end{array}$$

(53)

and then

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|<\frac{\pi }{2},(z\in \mathbb{U}).\end{array}$$

(54)

Next, we derive the following theorem.

Theorem 5.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ satisfy

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|<\frac{\alpha }{2}Re\left(\frac{1+\beta \sqrt[3]{z}}{1-\sqrt[3]{z}}\right),(z\in \mathbb{U})\end{array}$$

(55)

for some real α $(0<\alpha \le 1)$ and some real β $(\beta \ne -1),$ and then

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(56)

Proof. 

Using the method of the proof in Theorem 4, we say that

$$\begin{array}{cc}\hfill \left|arg{f}^{\prime }\left(z\right)\right|& =\frac{1}{2}{\int }_0^{2\pi }\left|\frac{r{e}^{i\theta }{f}^{″}\left(r{e}^{i\theta }\right)}{f^{\prime }\left(r{e}^{i\theta }\right)}\right|d\theta \hfill \\ \hfill & <\frac{\alpha }{4}{\int }_0^{2\pi }Re\left(\frac{1+\beta \sqrt[3]{r}{e}^{i\frac{\theta }{3}}}{1-\sqrt[3]{r}{e}^{i\frac{\theta }{3}}}\right)d\theta \hfill \\ \hfill & =\frac{\alpha }{4}{\int }_0^{2\pi }\left(\frac{1+(\beta -1)\sqrt[3]{r}cos\left(\frac{\theta }{3}\right)-\beta {\left(\sqrt[3]{r}\right)}^2}{1-2\sqrt[3]{r}cos\left(\frac{\theta }{3}\right)+{\left(\sqrt[3]{r}\right)}^2}\right)d\theta \hfill \\ \hfill & =\frac{\alpha }{4}{\int }_0^{2\pi }\left\{\frac{1-\beta }{2}+\frac{1+\beta }{2}\frac{1-{\left(\sqrt[3]{r}\right)}^2}{1+{\left(\sqrt[3]{r}\right)}^2-2\sqrt[3]{r}cos\left(\frac{\theta }{3}\right)}\right\}d\theta .\hfill \end{array}$$

(57)

Note that

$$\begin{array}{c}\hfill {\int }_0^{2\pi }\frac{1-{\left(\sqrt[3]{r}\right)}^2}{1+{\left(\sqrt[3]{r}\right)}^2-2\sqrt[3]{r}cos\left(\frac{\theta }{3}\right)}d\theta =3{\int }_0^{\frac{2\pi }{3}}\frac{1-{\left(\sqrt[3]{r}\right)}^2}{1+{\left(\sqrt[3]{r}\right)}^2-2\sqrt[3]{r}cos\rho }d\rho \le 2\pi \end{array}$$

(58)

and by Lemma 4, we obtain

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(59)

□

Example 1.

Let us consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{c}\hfill f^{\prime }\left(z\right)={\left(\frac{2}{2-\sqrt[3]{z}}\right)}^{3\alpha },(z\in \mathbb{U})\end{array}$$

(60)

with α$(0<\alpha \le 1).$ It follows from (60) that

$$\begin{array}{c}\hfill \left|arg{f}^{\prime }\left(z\right)\right|=3\alpha \left|arg\left(2-\sqrt[3]{z}\right)\right|<3\alpha \frac{\pi }{6}=\frac{\pi }{2}\alpha ,(z\in \mathbb{U})\end{array}$$

(61)

and

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|=\alpha \left|\frac{\sqrt[3]{z}}{2-\sqrt[3]{z}}\right|<\alpha ,(z\in \mathbb{U}).\end{array}$$

(62)

Therefore, if we consider some real β such that $\beta \le -3,$ then we have

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|<\alpha \le \frac{\alpha (1-\beta )}{4}<\frac{\alpha }{2}Re\left(\frac{1+\beta \sqrt[3]{z}}{1-\sqrt[3]{z}}\right),(z\in \mathbb{U}).\end{array}$$

(63)

Next, we prove the following theorem.

Theorem 6.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ satisfy

$$\begin{array}{c}\hfill \left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|<\frac{\alpha }{2}Re\left(\frac{1+\beta \sqrt[3]{z}}{1-\sqrt[3]{z}}\right),(z\in \mathbb{U})\end{array}$$

(64)

for some real α $(0<\alpha \le 1)$ and some real β $(\beta \ne -1),$ and then

$$\begin{array}{c}\hfill \left|arg\frac{f\left(z\right)}{z}\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(65)

Proof. 

It follows that

$$\begin{array}{c}\hfill log\left(\frac{f\left(z\right)}{z}\right)=log\left|\frac{f\left(z\right)}{z}\right|+iarg\left(\frac{f\left(z\right)}{z}\right)\end{array}$$

(66)

and

$$\begin{array}{cc}\hfill log\left(\frac{f\left(z\right)}{z}\right)& ={\int }_0^z{\left(log\left(\frac{f\left(t\right)}{t}\right)\right)}^{\prime }dt\hfill \\ \hfill & ={\int }_0^z\left(\frac{f^{\prime }\left(t\right)}{f\left(t\right)}-\frac{1}{t}\right)dt.\hfill \end{array}$$

(67)

Thus, we know that

$$\begin{array}{cc}\hfill \left|arg\left(\frac{f\left(z\right)}{z}\right)\right|& =\left|\mathrm{Im}\left(log\left(\frac{f\left(z\right)}{z}\right)\right)\right|\hfill \\ \hfill & =\left|\mathrm{Im}{\int }_0^z\left(\frac{f^{\prime }\left(t\right)}{f\left(t\right)}-\frac{1}{t}\right)dt\right|\hfill \\ \hfill & =\left|\mathrm{Im}{\int }_0^r\left(\frac{f^{\prime }\left(\rho e^{i\theta }\right)}{f\left(\rho e^{i\theta }\right)}-\frac{1}{\rho e^{i\theta }}\right)e^{i\theta }d\rho \right|\hfill \\ \hfill & \le {\int }_0^r\left|\mathrm{Im}\left(\frac{f^{\prime }\left(\rho e^{i\theta }\right)}{f\left(\rho e^{i\theta }\right)}-\frac{1}{\rho e^{i\theta }}\right)e^{i\theta }\right|d\rho \hfill \\ \hfill & \le {\int }_{-r}^r\left|\frac{e^{i\theta }{f}^{\prime }\left(\rho e^{i\theta }\right)}{f\left(\rho e^{i\theta }\right)}-\frac{1}{\rho }\right|d\rho \hfill \\ \hfill & \le \frac{1}{2}{\int }_0^{2\pi }\left|\frac{r{e}^{i\theta }{f}^{\prime }\left(r{e}^{i\theta }\right)}{f\left(r{e}^{i\theta }\right)}-1\right|d\theta \hfill \\ \hfill & <\frac{\alpha }{4}{\int }_0^{2\pi }Re\left(\frac{1+\beta \sqrt[3]{r}{e}^{i\frac{\theta }{3}}}{1-\sqrt[3]{r}{e}^{i\frac{\theta }{3}}}\right)d\theta \hfill \\ \hfill & \le \frac{\pi }{2}\alpha .\hfill \end{array}$$

(68)

Thus, we complete the proof of the theorem. □

Example 2.

Let us consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{c}\hfill f\left(z\right)=z{\left(\frac{2}{2-\sqrt[3]{z}}\right)}^{3\alpha },(z\in \mathbb{U})\end{array}$$

(69)

with α $(0<\alpha \le 1).$ Noting that a function $w\left(z\right)$ given by

$$\begin{array}{c}\hfill w\left(z\right)=\frac{2}{2-\sqrt[3]{z}}\end{array}$$

(70)

implies

$$\begin{array}{c}\hfill \left|w\left(z\right)-\frac{4}{3}\right|<\frac{2}{3},(z\in \mathbb{U}).\end{array}$$

(71)

This gives us

$$\begin{array}{c}\hfill \left|argw\left(z\right)\right|=\left|arg\left(\frac{2}{2-\sqrt[3]{z}}\right)\right|<\frac{\pi }{6},(z\in \mathbb{U}).\end{array}$$

(72)

Thus, we see that

$$\begin{array}{c}\hfill \left|arg\left(\frac{f\left(z\right)}{z}\right)\right|=3\alpha \left|arg\left(\frac{2}{2-\sqrt[3]{z}}\right)\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(73)

Further, $f\left(z\right)$ satisfies

$$\begin{array}{c}\hfill \left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|=\alpha \left|\frac{\sqrt[3]{z}}{2-\sqrt[3]{z}}\right|<\alpha ,(z\in \mathbb{U}).\end{array}$$

(74)

Thus, if we consider some real β such that $\beta \le -3,$ we have

$$\begin{array}{c}\hfill \left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|<\alpha \le \frac{\alpha (1-\beta )}{4}<\frac{\alpha }{2}Re\left(\frac{1+\beta \sqrt[3]{z}}{1-\sqrt[3]{z}}\right),(z\in \mathbb{U}).\end{array}$$

(75)

Using the same method, we have the following theorem.

Theorem 7.

Let $f\left(z\right)\in \overline{\mathcal{A}}$ satisfy

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}+1-\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right|<\frac{\alpha }{2}Re\left(\frac{1+\beta \sqrt[3]{z}}{1-\sqrt[3]{z}}\right),(z\in \mathbb{U})\end{array}$$

(76)

for some real α $(0<\alpha \le 1)$ and some real β $(\beta \ne -1),$ and then

$$\begin{array}{c}\hfill \left|arg\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U}).\end{array}$$

(77)

We also consider the following example for Theorem 7.

Example 3.

We consider a function $f\left(z\right)\in \overline{\mathcal{A}}$ given by

$$\begin{array}{c}\hfill \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}={\left(\frac{2}{2-\sqrt[3]{z}}\right)}^{3\alpha },(z\in \mathbb{U})\end{array}$$

(78)

with α $(0<\alpha \le 1).$ Then, we see that

$$\begin{array}{c}\hfill \left|arg\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)\right|=3\alpha \left|arg\left(\frac{2}{2-\sqrt[3]{z}}\right)\right|<\frac{\pi }{2}\alpha ,(z\in \mathbb{U})\end{array}$$

(79)

and

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}+1-\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right|<\alpha ,(z\in \mathbb{U}).\end{array}$$

(80)

Considering some real β such that $\beta \le -3,$ we have

$$\begin{array}{c}\hfill \left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}+1-\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right|<\alpha \le \frac{\alpha (1-\beta )}{4}<\frac{\alpha }{2}Re\left(\frac{1+\beta \sqrt[3]{z}}{1-\sqrt[3]{z}}\right),(z\in \mathbb{U}).\end{array}$$

(81)

4. Conclusions

In this paper, we consider functions $f\left(z\right)$ given by

$$f\left(z\right)=z+\sum _{k=1}^{\infty }{a}_{1+\frac{k}{3}}{z}^{1+\frac{k}{3}}$$

that are analytic in the open unit disc $\mathbb{U}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$ and explore new properties of $f\left(z\right)\in \overline{\mathcal{A}}.$ We present some interesting properties for subordinations and strongly starlike functions, along with some interesting examples that support our results, proven with theorems. The authors think that the results in this paper will provide new directions and contribute to the development of a new perspective on studies in Geometric Function Theory.