Fixed Point Results for Compatible Mappings in Extended Parametric S_b-Metric Spaces

Abstract

This study aims to establish common fixed point theorems for a pair of compatible self-mappings within the framework of extended parametric $S_b$-metric spaces. To support our assertions, we provide corollaries and examples accompanied with graphical representations. Moreover, we leverage our principal outcome to guarantee the existence of a common solution to a system of integral equations.

1. Introduction

Fixed point theory, a captivating area of study, is useful across many areas of research, most especially in engineering and sciences. With its wide range of applications, mathematical analysis depends heavily on this popular and very effective method for problem solving.

Maurice Fréchet [1], in his seminal work, introduced the concept of a metric space as a generalization of the traditional notion of distance. In the literature, through a variety of methodologies and alterations to the underlying axioms, the idea of metrics has been broadened and diversified. Out of the many generalizations, only a few are genuine, such as the semi-metric (proposed by Wilson [2]), quasi-metric (proposed in [3]), b-metric (proposed in [4,5]), dislocated quasi-metric (dq-metric) (proposed in [6]), S-metric (proposed by Sedghi et al. [7] through alterations to the symmetry property), parametric (proposed by Hussain et al. [8]), parametric S-metric (proposed by Taş and Özgür [9]), $S_b$-metric (proposed by Souayah and Mlaiki [10] and modified by Rohen et al. [11] in 2017), extended $S_b$-metric [12], generalized dq-metric (proposed in [13]), and parametric $S_b$-metric spaces (proposed by Taş and Özgür [14]). Recently, Mani et al. [15] introduced the notion of an extended parametric $S_b$-metric space and derived some well-known classical fixed point theorems along with its topological property. Numerous scholars have thoroughly investigated these spaces and derived several kinds of results on the existence of fixed points; a few of them are [16,17,18,19].

In 1976, Jungck [20] proved a fixed point result for a pair of maps (assuming that one of them must be continuous) by generalizing the Banach contraction principle. A considerable amount of study has been focused on the analysis of common fixed points of mappings that satisfy certain contractive conditions. Some authors have demonstrated the existence of a fixed point for a map that may exhibit a discontinuity in its domain. Nevertheless, the maps in consideration were continuous at the fixed point. Recent years have seen numerous authors using similar ideas to obtain coincidence point results for different kinds of mappings on metric spaces. We refer the reader to see [21,22,23,24].

Prior to discussing the primary findings of this research, it is necessary to provide several essential theories that include crucial definitions, illustrative instances, and supporting lemmas, all of which will significantly contribute to the proof of our main theorems.

2. Basic Principles and Relevant Literature

Definition 1

([7]). A function $S:{\mathbb{X}}^3\to [0,\infty )$ is said to be S-metric on a nonempty set X, if it satisfies the following axioms for each $\nu ,\rho ,\mu ,\tau \in \mathbb{X}$:

1.

$S(\nu ,\rho ,\mu )\ge 0$;

2.

$S(\nu ,\rho ,\mu )=0$ if and only if $\nu =\rho =\mu$;

3.

$S(\nu ,\rho ,\mu )\le S(\nu ,\nu ,\tau )+S(\rho ,\rho ,\tau )+S(\mu ,\mu ,\tau )$.

The pair $(\mathbb{X},S)$ is called an S-metric space.

Definition 2

([11]). A function $S_b:{\mathbb{X}}^3\to [0,\infty )$ is said to be $S_b$-metric on a nonempty set $\mathbb{X}$, with $b\ge 1$, if it satisfies the following axioms for each $\nu ,\rho ,\mu ,\tau \in \mathbb{X}$:

1.

$S_b(\nu ,\rho ,\mu )=0$ if and only if $\nu =\rho =\mu$;

2.

$S_b(\nu ,\rho ,\mu )\le b\left[S_b(\nu ,\nu ,\tau )+S_b(\rho ,\rho ,\tau )+S_b(\mu ,\mu ,\tau )\right].$

The pair $(\mathbb{X},S_b)$ is said to be an $S_b$-metric space.

The subsequent definition was given by Mani et al. [25].

Definition 3

([25]). A function ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ is said to be extended parametric $S_b$-metric on a nonempty set $\mathbb{X}$, where $N:{\mathbb{X}}^3\to [1,\infty )$ is a positive real-valued function, if it satisfies the following axioms for each $\nu ,\rho ,\mu ,\tau \in \mathbb{X}$:

${\mathcal{S}}_N-1$.

${\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )=0$ for all $\lambda >0$ if and only if $\nu =\rho =\mu$;

${\mathcal{S}}_N-2$.

${\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )\le N(\nu ,\rho ,\mu )[{\mathcal{S}}_N(\nu ,\nu ,\tau ,\lambda )+{\mathcal{S}}_N(\rho ,\rho ,\tau ,\lambda )+{\mathcal{S}}_N(\mu ,\mu ,\tau ,\lambda )]$.

The pair $(\mathbb{X},{\mathcal{S}}_N)$ is called an extended parametric $S_b$-metric (EPSb) space.

Example 1

([25]). Let $\mathbb{X}=\mathbb{R}.$ Define function $N:{\mathbb{X}}^3\to [1,\infty )$ by

$$N(\nu ,\rho ,\mu )=1+\mid \nu \mid +\mid \rho \mid$$

and a function ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )={\lambda }^2[\mid \nu -\rho \mid +\mid \rho -\mu \mid +\mid \nu -\mu \mid ]\end{array}$$

for each $\nu ,\rho ,\mu \in \mathbb{R}$ and for all $\lambda >0$. Then, ${\mathcal{S}}_N$ is an extended parametric $S_b$-metric space.

Example 2.

Let $\mathbb{X}=\left\{f\right|f:(0,\infty )\to \mathbb{R}\}$ and define function $N:{\mathbb{X}}^3\to [1,\infty )$ by

$$\begin{array}{c}\hfill N(\nu ,\rho ,\mu )=1+\left|\nu \right|\end{array}$$

and the function ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )={\left(\right|\nu \left(\lambda \right)-\rho \left(\lambda \right)|+|\nu \left(\lambda \right)-\mu \left(\lambda \right)|+|\rho \left(\lambda \right)-\mu \left(\lambda \right)\left|\right)}^2\end{array}$$

for each $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0.$ Then, $(\mathbb{X},{\mathcal{S}}_N)$ is an extended parametric $S_b$-metric space.

Remark 1.

It is important to mention here that a parametric S-metric space is a generalization of an S-metric space that introduces a parameter to the distance function. This parameter modifies the way distances are measured between points in the space. Some more examples of parametric S-metric and parametric $S_b$-metric spaces can be found in [8,9,14,25].

Remark 2.

It is also worth it to note that every extended parametric $S_b$-metric space, in general, is not a parametric S-metric space. Indeed, let us consider the following functions for each $\lambda \in (0,\infty )$ and $N(\nu ,\rho ,\mu )=1+\left|\nu \right|$ for all $\nu \ge 3$:

$$\nu \left(\lambda \right)=5,\rho \left(\lambda \right)=7,\mu \left(\lambda \right)=9\mathrm{and}\tau \left(\lambda \right)=6.$$

This is not a parametric S-metric space.

Definition 4

([25]). Suppose $(\mathbb{X},{\mathcal{S}}_N)$ is an extended parametric $S_b$-metric space. The pair $(\mathbb{X},{\mathcal{S}}_N)$ is said to be a symmetric extended parametric $S_b$-metric space, if for all $\nu ,\rho \in \mathbb{X},\mathrm{where}\lambda \in (0,\infty )$ is a parameter, it satisfies the following condition:

$${\mathcal{S}}_N(\nu ,\nu ,\rho ,\lambda )={\mathcal{S}}_N(\rho ,\rho ,\nu ,\lambda ).$$

Definition 5

([25]). A sequence <${\nu }_n$> in an extended parametric $S_b$-metric space $(\mathbb{X},{\mathcal{S}}_N)$ is said to be the following:

1.

Convergent if it converges to ν if and only if ${\mathcal{S}}_N({\nu }_n,{\nu }_n,\nu ,\lambda )<ϵ$ for all $n\ge n_0$ and for all $\lambda >0$.

2.

Cauchy sequence if ${lim}_{n,m\to \infty }{\mathcal{S}}_N({\nu }_n,{\nu }_n,{\nu }_m,\lambda )=0$ for all n and m, with $n>m$, and for all $\lambda >0.$

Definition 6

([25]). The space “$(\mathbb{X},{\mathcal{S}}_N)$ is called complete if every Cauchy sequence is convergent in $\mathbb{X}$”.

Definition 7.

A function $\mathcal{T}:(\mathbb{X},{\mathcal{S}}_N)\to ({\mathbb{X}}^{\prime },{\mathcal{S}}_N^{\prime })$ is said to be continuous at a point $\nu \in X$, where $(\mathbb{X},{\mathcal{S}}_N)$ and $({\mathbb{X}}^{\prime },{\mathcal{S}}_N^{\prime })$ are two extended parametric $S_b$-metric spaces, if for every sequence $\left\{{\nu }_n\right\}$ in $\mathbb{X}$ and for all $\lambda >0$,

$${\mathcal{S}}_N({\nu }_n,{\nu }_n,\nu ,\lambda )\to 0$$

implies that

$${\mathcal{S}}_N^{\prime }(\mathcal{T}\left({\nu }_n\right),\mathcal{T}\left({\nu }_n\right),\mathcal{T}\left(\nu \right),\lambda )\to 0.$$

Remark 3.

A function $\mathcal{T}$ is said to be continuous at $\mathbb{X}$ if and only if it is continuous for all $\nu \in \mathbb{X}$.

Definition 8.

Let $(\mathbb{X},{\mathcal{S}}_N)$ be an extended parametric $S_b$-metric space. A pair of self-mappings $\{\mathcal{T},\mathcal{U}\}$ is said to be compatible if and only if

$$\underset{n\to \infty }{lim}{\mathcal{S}}_N(\mathcal{T}\mathcal{U}{\nu }_n,\mathcal{T}\mathcal{U}{\nu }_n,\mathcal{U}\mathcal{T}{\nu }_n,\lambda )=0,$$

whenever $\left\{{\nu }_n\right\}$ is a sequence in $\mathbb{X}$ such that

$$\underset{n\to \infty }{lim}\mathcal{T}{\nu }_n=\underset{n\to \infty }{lim}\mathcal{U}{\nu }_n=\nu$$

for some $\nu \in \mathbb{X}$ and for all $\lambda >0$.

This study aims to establish the existence and uniqueness of a common fixed point by presenting two theorems in complete symmetric extended parametric $S_b$-metric spaces. In later sections, we provide some examples along with graphical representations, several corollaries, and an application to discuss the existence of a common solution to a system of integral equations and substantiate the main findings. The results obtained not only generalize but also expand some well-known results from the existing literature on symmetric extended parametric $S_b$-metric spaces.

3. Common Fixed Point Theorems for Pair of Self Maps

This section aims to provide a collection of significant lemmas that are valuable in the endeavor of demonstrating our fundamental theorems.

Lemma 1.

Let $(\mathbb{X},{\mathcal{S}}_N)$ be a symmetric extended parametric $S_b$-metric space. Suppose there exist two sequences $\left\{{\nu }_n\right\}$ and $\left\{{\rho }_n\right\}$ such that for all $\lambda >0$,

$$\underset{n\to \infty }{lim}{\mathcal{S}}_N({\nu }_n,{\nu }_n,{\rho }_n,\lambda )=0.$$

If the sequence $\left\{{\nu }_n\right\}\in \mathbb{X}$ exists such that ${lim}_{n\to \infty }{\nu }_n=\nu$ for some $\nu \in \mathbb{X}$, then ${lim}_{n\to \infty }{\rho }_n=\nu$.

Proof. 

Given that for any sequences $\left\{{\nu }_n\right\},\left\{{\rho }_n\right\}\in \mathbb{X}$,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\mathcal{S}}_N({\nu }_n,{\nu }_n,{\rho }_n,\lambda )=0.\end{array}$$

(1)

${lim}_{n\to \infty }{\nu }_n=\nu$ gives that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\mathcal{S}}_N({\nu }_n,{\nu }_n,\nu ,\lambda )=0.\end{array}$$

(2)

Claim: ${lim}_{n\to \infty }{\rho }_n=\nu .$

To prove this, we show that

$$\underset{n\to \infty }{lim}{\mathcal{S}}_N({\rho }_n,{\rho }_n,\nu ,\lambda )=0.$$

Suppose that on the contrary, ${lim}_{n\to \infty }{\mathcal{S}}_N({\rho }_n,{\rho }_n,\nu ,\lambda )\ne 0$.

Since $(\mathbb{X},{\mathcal{S}}_N)$ is a symmetric extended parametric $S_b$-metric space,

$$\begin{array}{cc}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,\nu ,\lambda )& \le N({\rho }_n,{\rho }_n,\nu )\{2{\mathcal{S}}_N({\rho }_n,{\rho }_n,{\nu }_n,\lambda )+{\mathcal{S}}_N(\nu ,\nu ,{\nu }_n,\lambda )\}\hfill \\ \hfill & \le N({\rho }_n,{\rho }_n,\nu )\{2{\mathcal{S}}_N({\nu }_n,{\nu }_n,{\rho }_n,\lambda )+{\mathcal{S}}_N({\nu }_n,{\nu }_n,\nu ,\lambda )\}.\hfill \end{array}$$

In taking the lim sup as $n\to \infty$ in the above inequality and making use of Equations (1) and (2), we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim\; sup}{\mathcal{S}}_N({\rho }_n,{\rho }_n,\nu ,\lambda )\le 0.\end{array}$$

Hence, ${lim}_{n\to \infty }{\rho }_n=\nu$. □

Lemma 2.

Let $(\mathbb{X},{\mathcal{S}}_N)$ be an extended parametric $S_b$-metric space and suppose that there exists a sequence $\left\{{\rho }_n\right\}\in \mathbb{X}$ such that for all $\lambda >0,$ it satisfies

$$\begin{array}{c}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n-1},\lambda )\le \theta {\mathcal{S}}_N({\rho }_{n-1},{\rho }_{n-1},{\rho }_{n-2},\lambda ).\end{array}$$

(3)

If for any ${\nu }_0\in \mathbb{X}$,

$$\begin{array}{c}\hfill \underset{n,m\to \infty }{lim}N({\nu }_n,{\nu }_n,{\nu }_m)<\frac{1}{2\theta },\end{array}$$

(4)

where $0<\theta <1,$ then $\left\{{\rho }_n\right\}$ is a Cauchy sequence in an extended parametric $S_b$-metric space.

Proof. 

Using iterations on Equation (3), we obtain

$$\begin{array}{c}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n-1},\lambda )\le {\theta }^n{\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda ).\end{array}$$

(5)

For all $m,n\in \mathbb{N}$ with $m>n$ and $\lambda >0$, in using condition ${\mathcal{S}}_N$-2 from Definition 3 and applying Equation (4), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_m,\lambda )& \le N({\rho }_n,{\rho }_n,{\rho }_m){\left(2\theta \right)}^n{\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda )\hfill \\ & +N({\rho }_n,{\rho }_n,{\rho }_m)N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m){\left(2\theta \right)}^{n+1}{\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda )\hfill \\ & ⋮\hfill \\ & +N({\rho }_n,{\rho }_n,{\rho }_m)N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m)\cdots N({\rho }_{m-1},{\rho }_{m-1},{\rho }_m)\hfill \\ & {\left(2\theta \right)}^{m-1}{\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda ).\hfill \end{array}$$

Consequently, we obtain

$$\begin{array}{cc}\hfill & {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_m,\lambda )\hfill \\ \hfill & \le {\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda )\left[\begin{array}{c}N({\rho }_1,{\rho }_1,{\rho }_m)N({\rho }_2,{\rho }_2,{\rho }_m)\cdots \hfill \\ N({\rho }_{n-1},{\rho }_{n-1},{\rho }_m)N({\rho }_n,{\rho }_n,{\rho }_m){\left(2\theta \right)}^n\hfill \\ +N({\rho }_1,{\rho }_1,{\rho }_m)N({\rho }_2,{\rho }_2,{\rho }_m)\cdots \hfill \\ N({\rho }_n,{\rho }_n,{\rho }_m)N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m){\left(2\theta \right)}^{n+1}\hfill \\ ⋮\hfill \\ +N({\rho }_1,{\rho }_1,{\rho }_m)N({\rho }_2,{\rho }_2,{\rho }_m)\cdots \hfill \\ N({\rho }_{m-2},{\rho }_{m-2},{\rho }_m)N({\rho }_{m-1},{\rho }_{m-1},{\rho }_m){\left(2\theta \right)}^{m-1}\hfill \end{array}\right]\hfill \\ \hfill & \le {\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda )\sum _{j=n}^{m-1}{\left(2\theta \right)}^j\prod _{i=1}^{j}N({\rho }_i,{\rho }_i,{\rho }_m)\hfill \end{array}$$

(6)

Suppose we have a series

$$\mathbb{B}=\sum _{n=1}^{\infty }{\left(2\theta \right)}^n\prod _{i=1}^{n}N({\rho }_i,{\rho }_i,{\rho }_m)$$

and its partial sum

$${\mathbb{B}}_n=\sum _{j=1}^n{\left(2\theta \right)}^j\prod _{i=1}^{j}N({\rho }_i,{\rho }_i,{\rho }_m).$$

In applying the ratio test and using Equation (4), the series

$$\sum _{n=1}^n{\left(2\theta \right)}^n\prod _{i=1}^{n}N({\rho }_i,{\rho }_i,{\rho }_m)$$

converges.

Hence, from Equation (6), for $m>n$, we have

$$\begin{array}{c}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_m,\lambda )\le {\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda )[{\mathbb{B}}_{m-1}-{\mathbb{B}}_n]\end{array}$$

Thus, ${\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_m,\lambda )\to 0$ as $n,m\to \infty$. In what follows, $\left\{{\rho }_n\right\}$ is a Cauchy sequence. □

Let us begin with our first result.

Theorem 1.

Suppose that $\mathcal{T},\mathcal{U},\mathcal{W}$, and $\mathcal{V}$ are self-maps defined on a complete symmetric extended parametric $S_b$-metric space $(\mathbb{X},{\mathcal{S}}_N)$, with $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right)$ and $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ such that for each $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$ with $0<k<\theta <1$, the following is satisfied:

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )\le \theta M(\nu ,\rho ,\mu ,\lambda ),\end{array}$$

(7)

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{V}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{W}\nu ,\lambda ),{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{V}\mu ,\lambda )\\ {\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ),k{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{U}\mu ,\lambda )\end{array}\right\}.\hfill \end{array}$$

Further, assume that for any ${\nu }_0\in \mathbb{X}$,

$$\begin{array}{c}\hfill \underset{n,m\to \infty }{lim}N({\nu }_n,{\nu }_n,{\nu }_m)<\frac{1}{2\theta }.\end{array}$$

(8)

Moreover, let the pairs $\{\mathcal{T},\mathcal{W}\}$ and $\{\mathcal{U},\mathcal{V}\}$ be compatible. Then, $\mathcal{T},\mathcal{U},\mathcal{W}$, and $\mathcal{V}$ have a unique common fixed point in $\mathbb{X}$ provided that $\mathcal{W}$ and $\mathcal{V}$ are continuous.

Proof. 

Let ${\nu }_0\in \mathbb{X}$. Since $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right)$, therefore, there exists ${\nu }_1\in \mathbb{X}$ such that $\mathcal{T}{\nu }_0=\mathcal{V}{\nu }_1$, and also, $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ implies that one can choose ${\nu }_2\in \mathbb{X}$ such that $\mathcal{U}{\nu }_1=\mathcal{W}{\nu }_2$. In general, we can construct sequences $\left\{{\nu }_{2n+1}\right\},\left\{{\nu }_{2n+2}\right\}\in \mathbb{X}$ such that $\mathcal{T}{\nu }_{2n}=\mathcal{V}{\nu }_{2n+1}$ and $\mathcal{U}{\nu }_{2n+1}=\mathcal{W}{\nu }_{2n+2}$.

Let us assume that ${\nu }_{2n+1}\ne {\nu }_{2n+2}$. Therefore, we can choose a sequence $\left\{{\rho }_n\right\}\in \mathbb{X}$ such that for all $n\ge 0$,

$$\begin{array}{cc}\hfill {\rho }_{2n}& =\mathcal{T}{\nu }_{2n}=\mathcal{V}{\nu }_{2n+1},\hfill \\ \hfill {\rho }_{2n+1}& =\mathcal{U}{\nu }_{2n+1}=\mathcal{W}{\nu }_{2n+2},\hfill \end{array}$$

Let us substitute $\nu ={\nu }_{2n}$, $\rho ={\nu }_{2n}$, and $\mu ={\nu }_{2n+1}$ in Equation (7). We obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )& ={\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda )\hfill \\ & \le \theta M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n+1},\lambda ),\hfill \end{array}$$

(9)

where

$$\begin{array}{cc}\hfill M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n+1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}{\nu }_{2n+1},\mathcal{U}{\nu }_{2n+1},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda )\\ k{\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{V}{\nu }_{2n},\lambda ),\end{array}\right\}\hfill \\ \hfill & =max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n+1},{\rho }_{2n+1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda ),\\ {\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda ),\\ k{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n+1},\lambda )\end{array}\right\}\hfill \\ \hfill & =max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda ),\\ kN({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n+1})\{2{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )\\ +{\mathcal{S}}_N({\rho }_{2n+1},{\rho }_{2n+1},{\rho }_{2n},\lambda )\}\end{array}\right\}\hfill \end{array}$$

$$\begin{array}{c}\hfill \le max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda ),\\ kN({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n+1})\\ max\{2{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n+1},{\rho }_{2n+1},{\rho }_{2n},\lambda )\}\end{array}\right\}\end{array}$$

In using Equation (8) and the fact that $k<\theta$, we have

$$\begin{array}{c}\hfill M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n+1},\lambda )=max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ),\\ {\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )\end{array}\right\}\end{array}$$

(10)

Here, two possibilities arise:

Choice-1

${\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )>{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )$;

Choice-2

${\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )\le {\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )$.

Suppose Choice 1 is true; then, from Equations (9) and (10), we arrive at a contradiction. Thus, Choice 2 must be true. Hence, from Equation (9), we have

$${\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )\le \theta {\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ).$$

(11)

Again, upon substituting $\nu ={\nu }_{2n}$, $\rho ={\nu }_{2n}$, and $\mu ={\nu }_{2n-1}$, in Equation (7), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )& ={\mathcal{S}}_N(y_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda )\hfill \\ & ={\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n-1},\lambda )\hfill \\ & \le \theta M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n-1},\lambda ),\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n-1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}{\nu }_{2n-1},\mathcal{U}{\nu }_{2n-1},\mathcal{V}{\nu }_{2n-1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{V}{\nu }_{2n-1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n-1},\lambda )\\ k{\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{U}{\nu }_{2n-1},\lambda ),\end{array}\right\}\hfill \\ \hfill & =max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n-2},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda ),\\ {\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n-2},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda ),\\ k{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n-1},\lambda )\end{array}\right\}\hfill \\ \hfill & =max\left\{{\mathcal{S}}_N({\rho }_{2n-2},{\rho }_{2n-2},{\rho }_{2n-1},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda )\right\}.\hfill \end{array}$$

By following an argument similar to that above, we can obtain

$${\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )\le \theta {\mathcal{S}}_N({\rho }_{2n-2},{\rho }_{2n-2},{\rho }_{2n-1},\lambda ).$$

(13)

From Equations (11) and (27), we obtain

$${\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )\le \theta {\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )\le {\theta }^2{\mathcal{S}}_N({\rho }_{2n-2},{\rho }_{2n-2},{\rho }_{2n-1},\lambda )$$

Consequently, for $n\ge 2$, it follows that

$$\begin{array}{c}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n+1},\lambda )\le \theta {\mathcal{S}}_N({\rho }_{n-1},{\rho }_{n-1},{\rho }_n,\lambda )\le {\theta }^2{\mathcal{S}}_N({\rho }_{n-2},{\rho }_{n-2},{\rho }_{n-1},\lambda )\end{array}$$

Reiterating the process n times, we obtain

$$\begin{array}{c}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n-1},\lambda )\le {\theta }^n{\mathcal{S}}_N({\rho }_1,{\rho }_1,{\rho }_0,\lambda )\end{array}$$

(14)

Lemma 2 guarantees that the sequence $\left\{{\rho }_n\right\}$ is a Cauchy sequence.

Since $\mathbb{X}$ is a complete extended parametric $S_b$-metric space, there exists some $\rho \in \mathbb{X}$ such that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\mathcal{T}{\nu }_{2n}=\underset{n\to \infty }{lim}\mathcal{V}{\nu }_{2n+1}=\underset{n\to \infty }{lim}\mathcal{U}{\nu }_{2n+1}=\underset{n\to \infty }{lim}\mathcal{W}{\nu }_{2n+2}=\rho .\end{array}$$

(15)

The continuity property of $\mathcal{W}$ provides that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\mathcal{W}}^2{\nu }_{2n+2}=\mathcal{W}\rho ,\underset{n\to \infty }{lim}\mathcal{W}\mathcal{T}{\nu }_{2n}=\mathcal{W}\rho .\end{array}$$

The compatibility property on $(\mathcal{T},\mathcal{W})$ and Lemma 1 provide that

$$\underset{n\to \infty }{lim}\mathcal{T}\mathcal{W}{\nu }_{2n}=\mathcal{W}\rho$$

(16)

Further, from Equation (7) and upon substituting $\nu =\rho =\mathcal{W}{\nu }_{2n}$ and $\mu ={\nu }_{2n+1}$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda )& \le \theta M(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},{\nu }_{2n+1},\lambda )\hfill \end{array}$$

(17)

where

$$\begin{array}{cc}\hfill M(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},{\nu }_{2n+1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}{\nu }_{2n+1},\mathcal{U}{\nu }_{2n+1},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},{\mathcal{W}}^2{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N({\mathcal{W}}^2{\nu }_{2n},{\mathcal{W}}^2{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda ),\\ k{\mathcal{S}}_N({\mathcal{W}}^2{\nu }_{2n},{\mathcal{W}}^2{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda )\end{array}\right\}\hfill \end{array}$$

(18)

Now, by taking the upper limit as $n\to \infty$ in Equations (17) and (18), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda )& =\underset{n\to \infty }{lim}{\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda )\hfill \\ & \le \theta \underset{n\to \infty }{lim}M(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},{\nu }_{2n+1},\lambda )\hfill \\ & \le \theta max\left\{\begin{array}{c}0,0,{\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda ),k{\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda )\end{array}\right\}\hfill \\ & =\theta {\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda ).\hfill \end{array}$$

Since $0<\theta <1$, it follows that $\mathcal{W}\rho =\rho$.

Also, the continuity of $\mathcal{V}$ implies that

$$\underset{n\to \infty }{lim}{\mathcal{V}}^2{\nu }_{2n+1}=\mathcal{V}\rho ,\underset{n\to \infty }{lim}\mathcal{V}\mathcal{U}{\nu }_{2n+1}=\mathcal{V}\rho .$$

Since the pair $(\mathcal{U},\mathcal{V})$ is compatible, in using Lemma (1), we obtain

$$\underset{n\to \infty }{lim}\mathcal{U}{\mathcal{V}}_{2n+1}=\mathcal{V}\rho$$

Upon substituting $\nu =\rho ={\nu }_{2n}$ and $\mu =\mathcal{V}{\nu }_{2n+1}$ in Equation (7), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\lambda )& \le \theta M({\nu }_{2n},{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda )\hfill \end{array}$$

(19)

where

$$\begin{array}{cc}\hfill M({\nu }_{2n},{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\mathcal{V}{\nu }_{2n+1},\mathcal{U}\mathcal{V}{\nu }_{2n+1},{\mathcal{V}}^2{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},{\mathcal{V}}^2{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\lambda )\\ k{\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\lambda )\end{array}\right\}\hfill \end{array}$$

(20)

By taking the upper limit as $n\to \infty$ in Equations (19) and (20), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\rho ,\rho ,\mathcal{V}\rho ,\lambda )& =\underset{n\to \infty }{lim}{\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\lambda )\hfill \\ & \le \theta \underset{n\to \infty }{lim}M({\nu }_{2n},{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda )\hfill \\ & =max\{0,0,{\mathcal{S}}_N(\rho ,\rho ,\mathcal{V}\rho ,\lambda ),{\mathcal{S}}_N(\rho ,\rho ,\mathcal{V}\rho ,\lambda ),k{\mathcal{S}}_N(\rho ,\rho ,\mathcal{V}\rho ,\lambda )\},\hfill \\ & \le {\mathcal{S}}_N(\rho ,\rho ,\mathcal{V}\rho ,\lambda ).\hfill \end{array}$$

This is possible if $\mathcal{V}\rho =\rho$.

Once again, from Equation (7),

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}{\nu }_{2n+1},\lambda )& \le \theta M(\rho ,\rho ,{\nu }_{2n+1},\lambda )\hfill \end{array}$$

(21)

where

$$\begin{array}{cc}\hfill M(\rho ,\rho ,{\nu }_{2n+1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}{\nu }_{2n+1},\mathcal{U}{\nu }_{2n+1},\mathcal{V}{\nu }_{2n+1},\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{W}\rho ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}y,\mathcal{V}{\nu }_{2n+1},\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}{\nu }_{2n+1},\lambda ),\\ k{\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\mathcal{U}{\nu }_{2n+1},\lambda )\end{array}\right\}\hfill \end{array}$$

And by taking the upper limit as $n\to \infty$ in (11) and making use of $\mathcal{W}\rho =\mathcal{V}\rho =\rho$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\rho ,\lambda )& \le \theta max\left\{\begin{array}{c}{\mathcal{S}}_N(\rho ,\rho ,\rho ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\rho ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\rho ,\lambda ),\\ k{\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\rho ,\lambda )\end{array}\right\}\hfill \\ & ={\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\rho ,\lambda ).\hfill \end{array}$$

Since $0<\theta <1$, it follows that $S(\mathcal{T}\rho ,\mathcal{T}\rho ,\rho ,\lambda )=0$ and $\mathcal{T}\rho =\rho$.

Similarly, using the same argument, from Equation (7), we can deduce that

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\rho ,\rho ,\mathcal{U}\rho ,\lambda )& ={\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\rho ,\lambda )\hfill \\ & \le \theta max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\rho ,\mathcal{U}\rho ,\mathcal{V}\rho ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{W}\rho ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\mathcal{V}\rho ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\rho ,\lambda )\\ k{\mathcal{S}}_N(\mathcal{W}\rho ,\mathcal{W}\rho ,\mathcal{U}\rho ,\lambda )\end{array}\right\}\hfill \\ & =\theta {\mathcal{S}}_N(\mathcal{U}\rho ,\mathcal{U}\rho ,\rho ,\lambda ).\hfill \end{array}$$

which implies that ${\mathcal{S}}_N(\rho ,\rho ,\mathcal{U}\rho ,\lambda )=0$ and $\mathcal{U}\rho =\rho$.

Thus, we proved that

$$\mathcal{W}\rho =\mathcal{V}\rho =\mathcal{T}\rho =\mathcal{U}\rho =\rho .$$

If there exists another common fixed point $\nu$ in $\mathbb{X}$ of all $\mathcal{T},\mathcal{U},\mathcal{W}$, and $\mathcal{V}$, then

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\nu ,\nu ,\rho ,\lambda )={\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{U}\rho ,\lambda )\le \theta M(\nu ,\nu ,\rho ,\lambda )\end{array}$$

where

$$\begin{array}{cc}\hfill M(\nu ,\nu ,\rho ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\rho ,\mathcal{U}\rho ,\mathcal{V}\rho ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\nu ,\mathcal{V}\rho ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{U}\rho ,\lambda )\\ k{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\nu ,\mathcal{U}\rho ,\lambda ).\end{array}\right\}\hfill \\ \hfill & ={\mathcal{S}}_N(\nu ,\nu ,\rho ,\lambda ).\hfill \end{array}$$

which implies that ${\mathcal{S}}_N(\nu ,\nu ,\rho ,\lambda )=0$ and $\nu =\rho$. Thus, $\rho$ is a unique common fixed point of $\mathcal{T},\mathcal{U},\mathcal{W}$, and $\mathcal{V}$. □

Remark 4.

If we eliminate the variable k from Theorem 1, then the certainty of the existence of a fixed point is doubtful.

In the following result, we used an auxiliary function $\varphi$, described below, to establish a common fixed point theorem in a symmetric complete extended parametric $S_b$-metric space.

Definition 9.

Let Φ denote the class of all functions $\varphi :[0,\infty )\to [0,\infty )$, which is increasing and continuous, such that for each fixed $t>0$, ${\sum }_{n=1}^{\infty }{\varphi }^n\left(t\right)<\infty$, ${\varphi }^n\left(t\right)\to 0$ as $n\to \infty .$

Theorem 2. 

Suppose $(\mathbb{X},{\mathcal{S}}_N)$ is an extended parametric $S_b$-metric space, which is symmetric and complete. Let $\mathcal{T},\mathcal{U},\mathcal{V},\mathcal{W}:\mathbb{X}\to \mathbb{X}$ be four self-mappings such that the following conditions are satisfied:

1.

$\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right),\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right);$

2.

$\mathcal{V}$ and $\mathcal{W}$ are continuous;

3.

The pair $(\mathcal{T},\mathcal{W})$ and $(\mathcal{U},\mathcal{V})$ are compatible;

4.

For all $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$, there exists a function $\varphi \in \Phi$ such that

$${\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )\le \varphi \left(M(\nu ,\rho ,\mu ,\lambda )\right),$$

(22)

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{V}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{V}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ).\end{array}\right\}.\hfill \end{array}$$

Further, assume that there exists $0<\theta <1$ such that for every $\nu \in \mathbb{X}$, we have

$$\underset{n\to \infty }{lim}N({\nu }_n,{\nu }_n,\nu )<\frac{1}{2\theta }.$$

Then, the maps $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$ have a unique common fixed point.

Proof. 

Let ${\nu }_0\in \mathbb{X}$ be arbitrary point in $\mathbb{X}$. We can construct a sequence $\left\{{\rho }_n\right\}$ in $\mathbb{X}$ as follows:

$${\rho }_{2n}=\mathcal{T}{\nu }_{2n}=\mathcal{V}{\nu }_{2n+1},{\rho }_{2n+1}=\mathcal{U}{\nu }_{2n+1}=\mathcal{W}{\nu }_{2n+2},n\ge 0.$$

Now, we show that $\left\{{\rho }_n\right\}$ is a Cauchy sequence.

Let $d_{n+1}={\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n+1},\lambda )$.

Then, using Equation (22), we have

$$\begin{array}{cc}\hfill d_{2n+1}={\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda )& ={\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda )\hfill \\ \hfill & \le \varphi \left(M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n+1},\lambda )\right)\hfill \end{array}$$

(23)

where

$$\begin{array}{cc}\hfill M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n+1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}{\nu }_{2n+1},\mathcal{U}{\nu }_{2n+1},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda ).\end{array}\right\}\hfill \\ \hfill & =max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}{\rho }_{2n+1},{\rho }_{2n+1},{\rho }_{2n},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n+1},\lambda ).\end{array}\right\}\hfill \\ \hfill & =max\{d_{2n},d_{2n},d_{2n+1},d_{2n+1}\}\hfill \\ \hfill & =max\{d_{2n},d_{2n+1}\}\hfill \end{array}$$

(24)

Here, two possibilities arise:

Choice-1

$d_{2n+1}>\varphi \left(d_{2n}\right)$;

Choice-2

$d_{2n+1}\le \varphi \left(d_{2n}\right)$.

Suppose Choice 1 is true; then, from Equations (23) and (24), we arrive at a contradiction. Thus, Choice 2 must be true. Hence, from Equation (23), we have

$$\begin{array}{c}\hfill d_{2n+1}\le \varphi \left(d_{2n}\right)\end{array}$$

(25)

Further,

$$\begin{array}{cc}\hfill d_{2n}=S({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n},\lambda )& ={\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda )\hfill \\ \hfill & ={\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n-1},\lambda )\hfill \\ \hfill & \le \varphi \left(M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n-1},\lambda )\right)\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill M({\nu }_{2n},{\nu }_{2n},{\nu }_{2n-1},\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{V}{\nu }_{2n-1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}{\nu }_{2n-1},\mathcal{U}{\nu }_{2n-1},\mathcal{V}{\nu }_{2n-1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}{\nu }_{2n-1},\lambda ).\end{array}\right\}\hfill \\ \hfill & =max\left\{\begin{array}{c}{\mathcal{S}}_N({\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n-2},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}{\rho }_{2n-1},{\rho }_{2n-1},{\rho }_{2n-2},\lambda ),{\mathcal{S}}_N({\rho }_{2n},{\rho }_{2n},{\rho }_{2n-1},\lambda ).\end{array}\right\}\hfill \\ \hfill & =max\{d_{2n-1},d_{2n},d_{2n-1},d_{2n}\}.\hfill \\ \hfill & =max\{d_{2n-1},d_{2n}\}.\hfill \end{array}$$

Using similar arguments as above, we have

$$\begin{array}{c}\hfill d_{2n}\le \varphi \left(d_{2n-1}\right).\end{array}$$

(26)

In combining (25) and (26), we have

$$d_{2n+1}\le \varphi \left(d_{2n}\right)\le {\varphi }^2\left(d_{2n-1}\right)$$

More precisely, for all $n\ge 2$, we have

$$\begin{array}{cc}\hfill {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n+1},\lambda )& \le \varphi \left({\mathcal{S}}_N({\rho }_{n-1},{\rho }_{n-1},{\rho }_n,\lambda )\right)\le \cdots \le {\varphi }^n\left({\mathcal{S}}_N({\rho }_0,{\rho }_0,{\rho }_1,\lambda )\right).\hfill \end{array}$$

For all $m>n$ (from Definition 3), we have

$$\begin{array}{cc}& {\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_m,\lambda )\hfill \\ & =N({\rho }_n,{\rho }_n,{\rho }_m)[2{\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n+1},\lambda )+{\mathcal{S}}_N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m,\lambda )]\hfill \\ & \le 2N({\rho }_n,{\rho }_n,{\rho }_m){\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_{n+1},\lambda )+N({\rho }_n,{\rho }_n,{\rho }_m)N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m)\hfill \\ & [2{\mathcal{S}}_N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m,\lambda )+{\mathcal{S}}_N({\rho }_{n+2},{\rho }_{n+2},{\rho }_m,\lambda )]\hfill \\ & \le 2\{\left[N({\rho }_n,{\rho }_n,{\rho }_m){\varphi }^n\left({\mathcal{S}}_N({\rho }_0,{\rho }_0,{\rho }_1,\lambda )\right)\right]\hfill \\ & +[N({\rho }_n,{\rho }_n,{\rho }_m)[N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m){\varphi }^{n+1}\left({\mathcal{S}}_N({\rho }_0,{\rho }_0,{\rho }_1,\lambda )\right)\hfill \\ & ⋮\hfill \\ & +[N({\rho }_n,{\rho }_n,{\rho }_m)N({\rho }_{n+1},{\rho }_{n+1},{\rho }_m)\cdots N({\rho }_{n-1},{\rho }_{n-1},{\rho }_m){\varphi }^{m-2}\left({\mathcal{S}}_N({\rho }_0,{\rho }_0,{\rho }_1,\lambda )\right)\}\hfill \\ & \le 2\sum _{j=n}^{m-2}{\varphi }^j\left({\mathcal{S}}_N({\rho }_0,{\rho }_0,{\rho }_1,\lambda )\right)\prod _{i=1}^{n}N({\rho }_i,{\rho }_i,{\rho }_m)\hfill \end{array}$$

Since ${\sum }_{n=1}^{\infty }{\varphi }^n\left(t\right)<\infty$ for all $t>0$, ${\mathcal{S}}_N({\rho }_n,{\rho }_n,{\rho }_m,\lambda )\to 0$ as $n\to \infty$. Hence, $\left\{{\rho }_n\right\}$ is a Cauchy sequence in $\mathbb{X}$. Since $\mathbb{X}$ is a complete extended parametric $S_b$-metric space, there exists $u\in X$ such that

$$\underset{n\to \infty }{lim}\mathcal{T}{\nu }_{2n}=\underset{n\to \infty }{lim}\mathcal{V}{\nu }_{2n+1}=\underset{n\to \infty }{lim}\mathcal{U}{\nu }_{2n+1}=\underset{n\to \infty }{lim}\mathcal{W}{\nu }_{2n+1}=u.$$

Since $\mathcal{W}$ is continuous, we have

$$\underset{n\to \infty }{lim}{\mathcal{W}}^2{\nu }_{2n+2}=\mathcal{W}u\mathrm{and}\underset{n\to \infty }{lim}\mathcal{W}\mathcal{T}{\nu }_{2n}=\mathcal{W}u.$$

Also, as $(\mathcal{T},\mathcal{W})$ is compatible, then ${lim}_{n\to \infty }{\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{W}\mathcal{T}{\nu }_{2n},\lambda )=0$. So, using Lemma 1, we have ${lim}_{n\to \infty }\mathcal{T}\mathcal{W}{\nu }_{2n}=\mathcal{W}u$.

Suppose that $\mathcal{W}u\ne u$. Then, condition (22) gives that

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{U}\mathcal{W}{\nu }_{2n+1},\lambda )\le \varphi \left(M(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n+1},\lambda )\right).\end{array}$$

(27)

where

$$\begin{array}{cc}\hfill M(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n+1},\lambda )& \le max\left\{\begin{array}{c}{\mathcal{S}}_N({\mathcal{W}}^2{\nu }_{2n},{\mathcal{W}}^2{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},{\mathcal{W}}^2{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}{\nu }_{2n+1},\mathcal{U}{\nu }_{2n+1},\mathcal{V}{\nu }_{2n+1}),\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{T}\mathcal{W}{\nu }_{2n},\mathcal{U}{\nu }_{2n+1},\lambda ).\end{array}\right\}\hfill \end{array}$$

(28)

Taking the upper limit as $n\to \infty$ in (27), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{W}u,\mathcal{W}u,u,\lambda )& \le \varphi \left({\mathcal{S}}_N(\mathcal{W}u,\mathcal{W}u,u,\lambda )\right).\hfill \end{array}$$

Using $\varphi \in \Phi$, we obtain that $\mathcal{W}u=u$, i.e., u is a fixed point of $\mathcal{W}$.

Similarly, the continuity of $\mathcal{V}$ and compatibility of the pair $(\mathcal{U},\mathcal{V})$ imply that

$$\underset{n\to \infty }{lim}{\mathcal{V}}^2{\nu }_{2n+1}=\mathcal{V}u\mathrm{and}\mathcal{V}\mathcal{U}{\nu }_{2n+1}=\mathcal{V}u.$$

$$\underset{n\to \infty }{lim}{\mathcal{S}}_N(\mathcal{U}\mathcal{V}{\nu }_{2n+1},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\mathcal{V}\mathcal{U}{\nu }_{2n+1},\lambda )=0.$$

Therefore, using Lemma (1), we have ${lim}_{n\to \infty }\mathcal{U}\mathcal{V}{\nu }_{2n+1}=\mathcal{V}u$.

Further, assume that $\mathcal{V}u\ne u$. Therefore, by condition (22), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\lambda )& \le \varphi \left(M({\nu }_{2n},{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda )\right),\hfill \end{array}$$

(29)

where

$$\begin{array}{cc}\hfill M({\nu }_{2n},{\nu }_{2n},\mathcal{V}{\nu }_{2n+1},\lambda )& \le max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}{\nu }_{2n},\mathcal{W}{\nu }_{2n},{\mathcal{V}}^2{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{W}{\nu }_{2n},\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}\mathcal{V}{\nu }_{2n+1},\mathcal{U}\mathcal{V}{\nu }_{2n+1},{\mathcal{V}}^2{\nu }_{2n+1}),\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}{\nu }_{2n},\mathcal{T}{\nu }_{2n},\mathcal{U}\mathcal{V}{\nu }_{2n+1},\lambda ).\end{array}\right\}\hfill \end{array}$$

(30)

Taking the upper limit as $n\to \infty$ in (29), we obtain

$$\begin{array}{c}\hfill {\mathcal{S}}_N(u,u,\mathcal{V}u,\lambda )\le \varphi \left({\mathcal{S}}_N(u,u,\mathcal{V}u,\lambda )\right)<{\mathcal{S}}_N(u,u,\mathcal{V}u,\lambda ).\end{array}$$

This is possible only if $\mathcal{V}u=u$. Thus, so far, we have $\mathcal{W}u=\mathcal{V}u=u$.

Again, upon considering condition (22), we have

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{U}{\nu }_{2n+1},\lambda )& \le \varphi \left(M(u,u,{\nu }_{2n+1},\lambda )\right),\hfill \end{array}$$

(31)

where

$$\begin{array}{cc}\hfill M(u,u,{\nu }_{2n+1},\lambda )& \le max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}u,\mathcal{W}u,\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{W}u,\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}{\nu }_{2n+1},\mathcal{U}{\nu }_{2n+1},\mathcal{V}{\nu }_{2n+1},\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{U}{\nu }_{2n+1},\lambda ).\end{array}\right\}\hfill \end{array}$$

(32)

Taking the upper limit as $n\to \infty$ in (31), we obtain

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,u,\lambda )& \le \varphi \left({\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,u,\lambda )\right).\hfill \end{array}$$

(33)

If $\mathcal{T}u\ne u$, then in based on the property of $\varphi$, we obtain a contradiction. This gives that $\mathcal{T}u=u$.

One more time, condition (22) gives that

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(u,u,\mathcal{U}u,\lambda )& ={\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{U}u,\lambda )\hfill \\ \hfill & \le \varphi \left(M\right(\mathcal{T}u,\mathcal{T}u,\mathcal{U}u,\lambda \left)\right),\hfill \end{array}$$

(34)

where

$$\begin{array}{cc}\hfill M(\mathcal{T}u,\mathcal{T}u,\mathcal{U}u,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}u,\mathcal{W}u,\mathcal{V}u,\lambda ),{\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{W}u,\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}u,\mathcal{U}u,\mathcal{V}u,\lambda ),{\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{U}u,\lambda ).\end{array}\right\}\hfill \\ \hfill & ={\mathcal{S}}_N(u,u,\mathcal{U}u,\lambda ).\hfill \end{array}$$

(35)

If $\mathcal{U}u\ne u$, then upon combining the above two inequalities, we have $\mathcal{U}u=u$.

Thus, we have deduced that $\mathcal{W}u=\mathcal{V}u=\mathcal{T}u=\mathcal{U}u=u$; that is, u is a common fixed point of the maps $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$.

To guarantee the uniqueness, suppose that p is another common fixed point of $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$; that is,

$$p=\mathcal{T}p=\mathcal{U}p=\mathcal{V}p=\mathcal{W}p.$$

If $u\ne p$, condition (22) implies that

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(u,u,p,\lambda )& ={\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{U}p,\lambda )\hfill \\ \hfill & \le \varphi \left(M\right(\mathcal{T}u,\mathcal{T}u,\mathcal{U}p,\lambda \left)\right)\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill M(\mathcal{T}u,\mathcal{T}u,\mathcal{U}p,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}u,\mathcal{W}u,\mathcal{V}p,\lambda ),{\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{W}u,\lambda )\\ {\mathcal{S}}_N(\mathcal{U}p,\mathcal{U}p,\mathcal{V}p,\lambda ),{\mathcal{S}}_N(\mathcal{T}u,\mathcal{T}u,\mathcal{U}p,\lambda ).\end{array}\right\}\hfill \\ \hfill & =max\left\{{\mathcal{S}}_N(u,u,p,\lambda ),{\mathcal{S}}_N(u,u,u,\lambda ),{\mathcal{S}}_N(p,p,p,\lambda ),{\mathcal{S}}_N(u,u,p,\lambda )\right\}\hfill \\ \hfill & ={\mathcal{S}}_N(u,u,p,\lambda ).\hfill \end{array}$$

Thus, we obtain that

$${\mathcal{S}}_N(u,u,p,\lambda )\le \varphi \left({\mathcal{S}}_N(u,u,p,\lambda )\right)<{\mathcal{S}}_N(u,u,p,\lambda ),$$

which is a contradiction. Hence, $u=p$. Therefore, u is the one and only fixed point of $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$. □

4. Corollaries and Numerical Illustrations

In this part, we discuss the consequential outcomes of our primary findings and provide only a few instances with graphical representations that highlight the soundness of our findings.

In letting $\mathcal{V}=\mathcal{W}$ in Theorem 1, we have the following result.

Corollary 1.

Suppose that $\mathcal{T},\mathcal{U}$, and $\mathcal{W}$ are self-maps defined on a complete symmetric extended parametric $S_b$-metric space $(\mathbb{X},{\mathcal{S}}_N)$, with $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ and $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$, such that for each $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$ with $0<k<\theta <1$, the following is satisfied:

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )\le \theta M(\nu ,\rho ,\mu ,\lambda ),\end{array}$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{W}\mu ,\lambda )\\ {\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ),k{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{U}\mu ,\lambda )\end{array}\right\}.\hfill \end{array}$$

Further, assume that for any ${\nu }_0\in \mathbb{X}$,

$$\begin{array}{c}\hfill \underset{n,m\to \infty }{lim}N({\nu }_n,{\nu }_n,{\nu }_m)<\frac{1}{2\theta },\end{array}$$

Moreover, if the pairs $\{\mathcal{T},\mathcal{W}\}$ and $\{\mathcal{U},\mathcal{W}\}$ are compatible, then the maps $\mathcal{T},\mathcal{U}$, and $\mathcal{W}$ have a unique common fixed point in $\mathbb{X}$ provided that $\mathcal{W}$ is continuous.

If we set $\mathcal{U}=\mathcal{T}$ in Corollary 1, we have the following important result as an extension and generalization of the result of Jungck [20].

Corollary 2.

Suppose that $\mathcal{T}$ and $\mathcal{W}$ are self-maps defined on a complete symmetric extended parametric $S_b$-metric space $(\mathbb{X},{\mathcal{S}}_N)$, with $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$, such that for each $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$ with $0<k<\theta <1$, the following is satisfied:

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{T}\mu ,\lambda )\le \theta M(\nu ,\rho ,\mu ,\lambda ),\end{array}$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{T}\mu ,\mathcal{T}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{W}\mu ,\lambda )\\ {\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{T}\mu ,\lambda ),k{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{T}\mu ,\lambda )\end{array}\right\}.\hfill \end{array}$$

Further, assume that for any ${\nu }_0\in \mathbb{X}$,

$$\begin{array}{c}\hfill \underset{n,m\to \infty }{lim}N({\nu }_n,{\nu }_n,{\nu }_m)<\frac{1}{2\theta },\end{array}$$

Moreover, if the pair $\{\mathcal{T},\mathcal{W}\}$ is compatible and $\mathcal{W}$ is continuous, then the maps $\mathcal{T}$ and $\mathcal{W}$ have a unique common fixed point in $\mathbb{X}$.

Corollary 3.

Suppose that $\mathcal{T},\mathcal{U}$, and $\mathcal{W}$ are self-maps defined on a complete symmetric extended parametric $S_b$-metric space $(\mathbb{X},{\mathcal{S}}_N)$, with $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ and $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right).$ For all $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$, there exists a function $\varphi \in \Phi$ such that

$${\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )\le \varphi \left(M(\nu ,\rho ,\mu ,\lambda )\right),$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ).\end{array}\right\}.\hfill \end{array}$$

Further, assume that there exists $0<\theta <1$ such that for every $\nu \in \mathbb{X}$, we have

$$\underset{n\to \infty }{lim}N({\nu }_n,{\nu }_n,\nu )<\frac{1}{2\theta }.$$

Moreover, if the pairs $\{\mathcal{T},\mathcal{W}\}$ and $\{\mathcal{U},\mathcal{W}\}$ are compatible, then the maps $\mathcal{T},\mathcal{U}$, and $\mathcal{W}$ have a unique common fixed point in $\mathbb{X}$ provided that $\mathcal{W}$ is continuous.

Proof. 

If we take $\mathcal{V}=\mathcal{W}$, then from Theorem 2, it follows that $\mathcal{T},\mathcal{U}$, and $\mathcal{W}$ have a unique common fixed point. □

Corollary 4.

Suppose that $\mathcal{T}$ and $\mathcal{W}$ are self-maps defined on a complete symmetric extended parametric $S_b$-metric space $(\mathbb{X},{\mathcal{S}}_N)$, with $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right).$ For all $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$, there exists a function $\varphi \in \Phi$ such that

$${\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{T}\mu ,\lambda )\le \varphi \left(M(\nu ,\rho ,\mu ,\lambda )\right),$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{T}\mu ,\mathcal{T}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{T}\mu ,\lambda ).\end{array}\right\}.\hfill \end{array}$$

Further, assume that there exists $0<\theta <1$ such that for every $\nu \in \mathbb{X}$, we have

$$\underset{n\to \infty }{lim}N({\nu }_n,{\nu }_n,\nu )<\frac{1}{2\theta }.$$

Moreover, if the pair $\{\mathcal{T},\mathcal{W}\}$ is compatible and $\mathcal{W}$ is continuous, then the maps $\mathcal{T}$ and $\mathcal{W}$ have a unique common fixed point in $\mathbb{X}$.

Proof. 

By letting $\mathcal{U}=\mathcal{T}$ and $\mathcal{V}=\mathcal{W}$ in Theorem 2, we obtain the result. □

Corollary 5.

Suppose $(\mathbb{X},{\mathcal{S}}_N)$ is an extended parametric $S_b$-metric space, which is symmetric and complete. Let $\mathcal{T},\mathcal{U},\mathcal{V},\mathcal{W}:\mathbb{X}\to \mathbb{X}$ be four self-mappings such that it satisfies the following conditions:

1.

$\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right),\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right);$

2.

$\mathcal{V}$ and $\mathcal{W}$ are continuous;

3.

The pair $(\mathcal{T},\mathcal{W})$ and $(\mathcal{U},\mathcal{V})$ are compatible;

4.

For all $\nu ,\rho ,\mu \in \mathbb{X}$ and for all $\lambda >0$, suppose that

$${\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )\le M(\nu ,\rho ,\mu ,\lambda ),$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{W}\nu ,\mathcal{W}\rho ,\mathcal{V}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{W}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{V}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ).\end{array}\right\}.\hfill \end{array}$$

Further, assume that there exists $0<\theta <1$ such that for every $\nu \in \mathbb{X}$, we have

$$\underset{n\to \infty }{lim}N({\nu }_n,{\nu }_n,\nu )<\frac{1}{2\theta }.$$

Then, the maps $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$ have a unique common fixed point.

Proof. 

By letting $\varphi \left(t\right)=t$ in Theorem 2, we obtain the result. □

Remark 5.

Note the following:

1.

Corollary 2 is an extension of the result of Jungck [20] in an EPS_b-metric space.

2.

Corollary 4 is an extension of the result of Saluja [26] in an EPS_b-metric space.

3.

Corollary 5 is an extension of the result of Sedghi et al. [27] in an EPS_b-metric space.

Example 3.

Let $\mathbb{X}=[0,1].$ Define function $N:{\mathbb{X}}^3\to [1,\infty )$ by

$$N(\nu ,\rho ,\mu )=max\{\nu ,\rho \}+\mu +1$$

and a function ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )=\lambda {(max\{\nu ,\rho \}-\mu )}^2\end{array}$$

where each $\lambda \in (0,\infty )$ is a parameter, and $\nu ,\rho ,\mu \in \mathbb{X}.$ Then, ${\mathcal{S}}_N$ is an EPSb space.

Define self-maps $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$ on $\mathbb{X}$ by

$$\mathcal{T}\left(\nu \right)=\frac{\nu }{32},\mathcal{U}\left(\nu \right)=\frac{\nu }{16},\mathcal{V}\left(\nu \right)=\frac{\nu }{4},\mathcal{W}\left(\nu \right)=\frac{\nu }{2}.$$

Obviously, $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ and $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right)$. Furthermore, the pairs $\{\mathcal{T},\mathcal{V}\}$ and $\{\mathcal{U},\mathcal{W}\}$ are compatible mappings.

We have

$$\begin{array}{ccc}\hfill {\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )& =& \lambda {(max\{\mathcal{T}\nu ,\mathcal{T}\rho \}-\mathcal{U}\mu )}^2\hfill \\ & =& \lambda {(max\{\frac{\nu }{32},\frac{\rho }{32}\}-\frac{\mu }{16})}^2\hfill \\ & \le & \frac{63}{64}{\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{W}\mu ,\lambda )\hfill \\ & \le & \frac{63}{64}M(\nu ,\rho ,\mu ,\lambda ),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{V}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ),\\ k{\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{U}\mu ,\lambda )\end{array}\right\}.\hfill \end{array}$$

Meanwhile, for each $\nu ,\rho ,\mu \in \mathbb{X}$, let

$${\mathcal{T}}^n=(\frac{\nu }{32}{)}^n,{\mathcal{U}}^n=(\frac{\nu }{16}{)}^n,{\mathcal{V}}^n=(\frac{\nu }{16}{{)}^n,{\mathcal{W}}^n=(\frac{\nu }{2})}^n.$$

Then,

$$\underset{n,m\to \infty }{lim}N({\mathcal{T}}^n\nu ,{\mathcal{T}}^n\rho ,{\mathcal{U}}^m\mu )=1<\frac{1}{2\theta },\forall \theta \in (0,\frac{1}{2}).$$

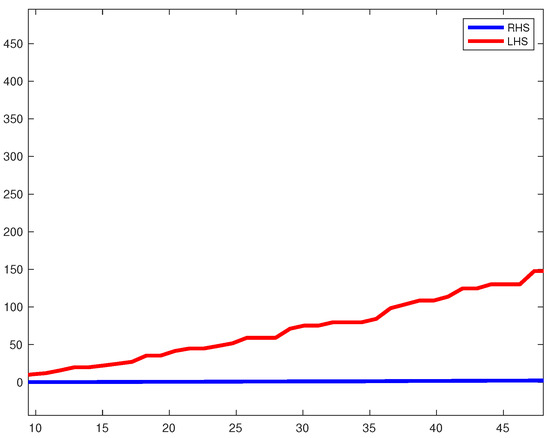
Thus, all the necessities of Theorem 1 have been accomplished. Also, the behavior of inequality (7) of Example 3 is shown graphically in Figure 1. The number 0 is the only fixed point that is common to the mappings $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$.

Figure 1. Graphical behavior of inequality (7) of Example 3.

Example 4.

Let $\mathbb{X}=[0,1).$ Define function $N:{\mathbb{X}}^3\to [1,\infty )$ by

$$N(\nu ,\rho ,\mu )=1+\mid \nu \mid +\mid \rho \mid$$

and a function ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )=\lambda [\mid \nu -\rho \mid +\mid \rho -\mu \mid +\mid \nu -\mu \mid ]\end{array}$$

where each $\lambda \in (0,\infty )$ is a parameter, and $\nu ,\rho ,\mu \in \mathbb{X}.$ Then, ${\mathcal{S}}_N$ is an EPSb space.

Define self-maps $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$ on $\mathbb{X}$ by

$$\mathcal{T}\left(\nu \right)=\frac{\nu }{16},\mathcal{U}\left(\nu \right)=\frac{\nu }{8},\mathcal{V}\left(\nu \right)=\frac{\nu }{2},\mathcal{W}\left(\nu \right)=\nu .$$

Obviously, $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ and $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right)$.

Furthermore, the pairs $\{\mathcal{T},\mathcal{V}\}$ and $\{\mathcal{U},\mathcal{W}\}$ are compatible mappings.

From inequality (7), we have

$$\begin{array}{ccc}\hfill {\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )& =& \lambda [\mid \mathcal{T}(\nu )-\mathcal{T}(\rho )\mid +\mid \mathcal{T}(\rho )-\mathcal{U}(\mu )\mid +\mid \mathcal{T}(\nu )-\mathcal{U}(\mu )\mid ]\hfill \\ & =& \lambda [\mid \frac{\nu }{16}-\frac{\rho }{16}\mid +\mid \frac{\rho }{16}-\frac{\mu }{8}\mid +\mid \frac{\nu }{16}-\frac{\mu }{8}\mid ]\hfill \\ & =& \lambda \frac{1}{8}[\mid \mathcal{V}\left(\nu \right)-\mathcal{V}\left(\rho \right)\mid +\mid \mathcal{V}\left(\rho \right)-\mathcal{W}\left(\mu \right)\mid +\mid \mathcal{V}\left(\nu \right)-\mathcal{W}\left(\mu \right)\mid ]\hfill \\ & \le & \frac{7}{8}{\mathcal{S}}_N(\mathcal{V}\left(\nu \right),\mathcal{V}\left(\rho \right),\mathcal{W}\left(\mu \right),\lambda )\hfill \\ & \le & \frac{7}{8}M(\nu ,\rho ,\mu ,\lambda );\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{V}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ),\\ k{\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{U}\mu ,\lambda )\end{array}\right\}.\hfill \end{array}$$

Also, for every $\nu ,\rho ,\mu \in \mathbb{X}$, consider

$${\mathcal{T}}^n=(\frac{\nu }{16}{)}^n,{\mathcal{U}}^n=(\frac{\nu }{8}{{)}^n,{\mathcal{V}}^n=(\frac{\nu }{2})}^n,{\mathcal{W}}^n={\left(\nu \right)}^n.$$

Then,

$$\underset{n,m\to \infty }{lim}N({\mathcal{T}}^n\nu ,{\mathcal{T}}^n\rho ,{\mathcal{U}}^m\mu )=1<\frac{1}{2\theta },\forall \theta \in (0,\frac{1}{2}).$$

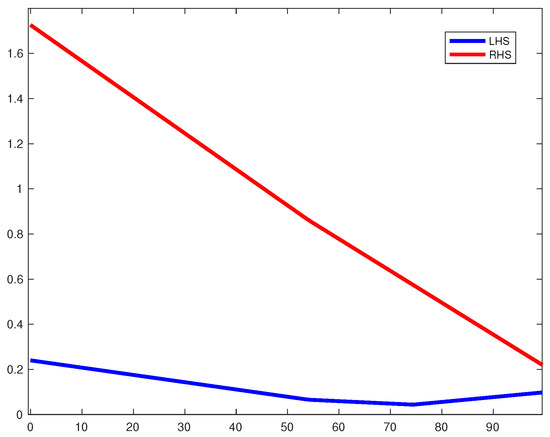
Thus, all the necessities of Theorem 1 have been accomplished. Also, the behavior of inequality (7) of Example 4 is shown graphically in Figure 2. The number 0 is the only fixed point that is common to the mappings $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$.

Figure 2. Graphical behavior of inequality (7) of Example 4.

Example 5.

Let $\mathbb{X}=[0,\frac{\pi }{2}).$ Define function $N:{\mathbb{X}}^3\to [1,\infty )$ by

$$N(\nu ,\rho ,\mu )=1+\mid \nu \mid +\mid \rho \mid$$

and a function ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ by

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\nu ,\rho ,\mu ,\lambda )=\lambda [\mid \nu -\rho \mid +\mid \rho -\mu \mid +\mid \nu -\mu \mid ]\end{array}$$

where each $\lambda \in (0,\infty )$ is a parameter, and $\nu ,\rho ,\mu \in \mathbb{X}.$ Then, ${\mathcal{S}}_N$ is an EPSb space.

Define self-maps $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$ on $\mathbb{X}$ by

$$\mathcal{T}\left(\nu \right)=\frac{sin\nu }{9},\mathcal{U}\left(\nu \right)=\frac{sin\nu }{6},\mathcal{V}\left(\nu \right)=\frac{sin\nu }{3},\mathcal{W}\left(\nu \right)=\frac{sin\nu }{2}.$$

Obviously, $\mathcal{T}\left(\mathbb{X}\right)\subseteq \mathcal{W}\left(\mathbb{X}\right)$ and $\mathcal{U}\left(\mathbb{X}\right)\subseteq \mathcal{V}\left(\mathbb{X}\right)$.

Furthermore, the pairs $\{\mathcal{T},\mathcal{V}\}$ and $\{\mathcal{U},\mathcal{W}\}$ are compatible mappings.

From inequality (7), we have

$$\begin{array}{ccc}\hfill {\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda )& =& \lambda [\mid \mathcal{T}(\nu )-\mathcal{T}(\rho )\mid +\mid \mathcal{T}(\rho )-\mathcal{U}(\mu )\mid +\mid \mathcal{T}(\nu )-\mathcal{U}(\mu )\mid ]\hfill \\ & =& \lambda [\mid \frac{sin\nu }{9}-\frac{sin\rho }{9}\mid +\mid \frac{sin\rho }{9}-\frac{sin\mu }{6}\mid +\mid \frac{sin\nu }{9}-\frac{sin\mu }{6}\mid ]\hfill \\ & =& \lambda \frac{1}{3}[\mid \mathcal{V}\left(\nu \right)-\mathcal{V}\left(\rho \right)\mid +\mid \mathcal{V}\left(\rho \right)-\mathcal{W}\left(\mu \right)\mid +\mid \mathcal{V}\left(\nu \right)-\mathcal{W}\left(\mu \right)\mid ]\hfill \\ & \le & \frac{1}{3}{\mathcal{S}}_N(\mathcal{V}\left(\nu \right),\mathcal{V}\left(\rho \right),\mathcal{W}\left(\mu \right),\lambda )\hfill \\ & \le & \varphi \left(M\right(\nu ,\rho ,\mu ,\lambda \left)\right),\hfill \end{array}$$

where $\varphi \left(t\right)=\frac{2t}{3}$, and

$$\begin{array}{cc}\hfill M(\nu ,\rho ,\mu ,\lambda )& =max\left\{\begin{array}{c}{\mathcal{S}}_N(\mathcal{U}\mu ,\mathcal{U}\mu ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\nu ,\mathcal{T}\nu ,\mathcal{V}\nu ,\lambda ),\\ {\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{W}\mu ,\lambda ),{\mathcal{S}}_N(\mathcal{T}\rho ,\mathcal{T}\rho ,\mathcal{U}\mu ,\lambda ),\\ k{\mathcal{S}}_N(\mathcal{V}\nu ,\mathcal{V}\rho ,\mathcal{U}\mu ,\lambda )\end{array}\right\}.\hfill \end{array}$$

Alternatively, for every $\nu ,\rho ,\mu \in \mathbb{X}$, let us consider

$${\mathcal{T}}^n=(\frac{sin\nu }{9}{)}^n,{\mathcal{U}}^n=(\frac{sin\nu }{6}{)}^n,{\mathcal{V}}^n=(\frac{sin\nu }{3}{{)}^n,{\mathcal{W}}^n=(\frac{sin\nu }{2})}^n.$$

Then,

$$\underset{n,m\to \infty }{lim}N({\mathcal{T}}^n\nu ,{\mathcal{T}}^n\rho ,{\mathcal{U}}^m\mu )=1<\frac{1}{2\theta },\forall \theta \in (0,\frac{1}{2}).$$

Thus, all the necessities of Theorem 2 have been accomplished. The number 0 is the only fixed point that is common to the mappings $\mathcal{T},\mathcal{U},\mathcal{V}$, and $\mathcal{W}$.

5. Common Solution of System of Integral Equations: Existence and Uniqueness

Here, we use the results obtained in Section 3 to investigate the existence of a solution for a Fredholm integral problem.

For a real number $\lambda >0$ and for all ${\varphi }_1,{\varphi }_2,{\varphi }_3\in [0,E],$ define ${\mathcal{S}}_N:{\mathbb{X}}^3\times (0,\infty )\to [0,\infty )$ by

$${\mathcal{S}}_N({\varphi }_1,{\varphi }_2,{\varphi }_3,\lambda )=\mid max\{{\varphi }_1\left(\lambda \right),{\varphi }_2\left(\lambda \right)\}-{\varphi }_3\left(\lambda \right){\mid }^2$$

and $N:{\mathbb{X}}^3\to [1,\infty )$ by

$$N({\varphi }_1,{\varphi }_2,{\varphi }_3)=max\{\mid {\varphi }_1\mid ,\mid {\varphi }_2\mid \}+{\varphi }_3+1.$$

It is evident that $(\mathbb{X},{\mathcal{S}}_N)$ is a complete extended parametric $S_b$-metric space for all $\mu ,\nu \in [0,E]$.

Theorem 3.

Let $\mathbb{X}=C[0,E]$ consists of all continuous real-valued functions defined on the closed and bounded interval $[0,E]$ in the real number system $\mathbb{R}$. Then, the system of linear integral equations

$$\begin{array}{c}\hfill {\varphi }_1\left(\mu \right)=\Xi \left(\mu \right)+{\int }_0^E{R}_1(\mu ,\nu ,{\varphi }_1\left(\nu \right))d\nu \\ \hfill {\varphi }_1\left(\mu \right)=\Xi \left(\mu \right)+{\int }_0^E{R}_2(\mu ,\nu ,{\varphi }_1\left(\nu \right))d\nu \end{array}$$

(36)

has a unique solution ${\varphi }_1\left(\mu \right)\in [0,E]$ if it satisfies the following assumptions:

(i) 

$\Xi :[0,E]\to \mathbb{R}$ is continuous;

(ii) 

$R_1,R_2:[0,E]\times [0,E]\times \mathbb{R}\to \mathbb{R}$ is continuous;

(iii) 

For every $\mu ,\nu \in [0,E],$

$$\mid R_1(\mu ,\nu ,{\varphi }_1\left(\nu \right))-R_2(\mu ,\nu ,{\varphi }_2\left(\nu \right)\mid \le \frac{1}{2}\mid {\varphi }_1\left(\nu \right)-{\varphi }_2\left(\nu \right)\mid .$$

Proof. 

Let us define $\mathcal{T},\mathcal{U}:C\left(\right[0,E\left]\right)\to C\left(\right[0,E\left]\right)$ by

$$\mathcal{T}{\varphi }_1\left(\mu \right)={\int }_0^E{R}_1(\mu ,\nu ,{\varphi }_1\left(\nu \right)d\nu +\Xi \left(\mu \right)$$

and

$$\mathcal{U}{\varphi }_1\left(\mu \right)={\int }_0^E{R}_2(\mu ,\nu ,{\varphi }_1\left(\nu \right)d\nu +\Xi \left(\mu \right),$$

where $\mu ,\nu \in [0,E]$, and ${\varphi }_1\in C\left([0,E]\right).$

Now,

$$\begin{array}{cc}\hfill \mid \mathcal{T}{\varphi }_1\left(\mu \right)-\mathcal{U}{\varphi }_2\left(\mu \right)\mid & \le {\int }_0^E\mid R_1(\mu ,\nu ,{\varphi }_1\left(\nu \right)-R_2(\mu ,\nu ,{\varphi }_2\left(\nu \right)\mid d\nu \hfill \\ \hfill & \le \frac{1}{2}{\int }_0^E\mid {\varphi }_1\left(\nu \right)-{\varphi }_2\left(\nu \right)\mid d\nu .\hfill \end{array}$$

(37)

Consider

$$\begin{array}{cc}\hfill {\mathcal{S}}_N(\mathcal{T}{\varphi }_1,\mathcal{T}{\varphi }_1,\mathcal{U}{\varphi }_2,\lambda )& =\mid max\{\mathcal{T}{\varphi }_1\left(\lambda \right),\mathcal{T}{\varphi }_1\left(\lambda \right)\}-\mathcal{U}{\varphi }_2\left(\lambda \right){\mid }^2\hfill \\ \hfill & =\mid \mathcal{T}{\varphi }_1\left(\lambda \right)-\mathcal{U}{\varphi }_2\left(\lambda \right){\mid }^2.\hfill \\ \hfill & =\frac{1}{4}{\left({\int }_0^E\mid {\varphi }_1\left(\nu \right)-{\varphi }_2\left(\nu \right)\mid d\nu \right)}^2[\mathrm{Using} \mathrm{Equation}\left(37\right)].\hfill \end{array}$$

Using the Cauchy–Schwartz inequality, we obtain

$$\begin{array}{c}\hfill {\mathcal{S}}_N(\mathcal{T}{\varphi }_1,\mathcal{T}{\varphi }_1,\mathcal{U}{\varphi }_2,\lambda )\le \frac{E^2}{4}{\mathcal{S}}_N({\varphi }_1\left(\lambda \right),{\varphi }_1\left(\lambda \right),{\varphi }_2\left(\lambda \right),\lambda ).\end{array}$$

For every $E,$$0<E<2,$$\frac{E^2}{4}<1$, and hence, all the conditions of Corollary 2 are satisfied, and therefore, there exist a ${\varphi }_1$ in $C[0,E]$ that is a common fixed point of maps $\mathcal{T}$ and $\mathcal{U}$. That is, ${\varphi }_1$ is a common solution of the integral in Equation (36). □

6. Conclusions

This study presented a more comprehensive version of the conventional fixed point problems within the context of symmetric extended parametric $S_b$-metric spaces. The discussion aimed to establish common fixed point theorems for two pairs of compatible self-maps. This paper includes two theorems and a few examples. These examples highlight the relevance and practicality of our findings. We have also shown that in the case when all functions are real-valued and continuous, specified on a closed and bounded interval $[0,E]$, with the condition $\frac{E^2}{4}<1$, the system of linear integral equations has a unique common solution.