A Deterministic Setting for the Numerical Computation of the Stabilizing Solutions to Stochastic Game-Theoretic Riccati Equations

Abstract

In this paper, we are interested in the numerical aspects of the class of generalized Riccati difference equations which are involved in linear quadratic (LQ) stochastic difference games. More specifically, we address the problem of the numerical computation of the stabilizing solutions for this class of nonlinear difference equations. We propose an iterative deterministic algorithm for the computation of such a global solution. The performances of the proposed algorithm are illustrated with some numerical examples.

1. Introduction

In this paper, we address the problem of the numerical computation of the stabilizing solutions of a class of generalized Riccati difference equations. The considered nonlinear matrix equation occurs in connection with zero-sum linear LQ stochastic difference game control problems (see [1] for more precision regarding this aspect). One of the particularities of such equations lies in the sign indefiniteness of their quadratic terms. This sign indefiniteness makes the characterization (as well as the numerical computation) of global solutions to such nonlinear matrix difference equations far more challenging when compared with the sign-definite counterpart. Even though some interesting results have already been reported in the literature (see [2,3] and the references therein), there are still substantial open problems in this field.

In [1], we addressed some theoretical aspects related to the nonlinear difference equations under consideration. The present paper can be viewed as the numerical counterpart of [1]. We propose a globally convergent iterative algorithm for the computation of the stabilizing solutions to this class of Riccati equations. To the best of the authors’ knowledge, the numerical algorithms developed in the literature for the computation of the solutions to stochastic Riccati equations are mainly based on stochastic approaches consisting of transformation of the original problem into the problem of solving a sequence of coupled stochastic Riccati equations (see [4,5] and the references therein) that rely again on some iterative procedures for their numerical resolution. One of the most remarkable features of our proposed algorithm is its deterministic nature, in the sense that one has to solve at each main iteration a system of uncoupled deterministic Riccati equations. This allows us to use direct methods (invariant or deflating subspace-based methods; see [6]) for the numerical solutions to such deterministic equations. We believe that such a fundamental difference in the construction of what we called above deterministic and stochastic algorithms will have an important impact from the computation-time point of view. This will be illustrated via numerical experiments.

We mention here that in [7], we proposed a deterministic iterative algorithm for the numerical computation of the stabilizing solutions to a class of generalized Riccati equations related to the so-called continuous-time, full-information stochastic ${\mathcal{H}}_{\infty }$ control. The discrete-time counterpart of this type of Riccati equation is a particular case of the more general class of Riccati equations considered in the present paper. We have recently shown (see [1]) that the proof of the existence and uniqueness of the stabilizing solution for this more general class of Riccati equations presents substantial differences when compared with the full-information ${\mathcal{H}}_{\infty }$-type Riccati equations, even though we followed a similar philosophy in the proof procedure. We believe that we have a similar situation from the numerical computation point of view. The results reported in the present paper are more general and contain substantial differences when compared with [7].

This paper is organized as follows. In Section 2, we describe the problem that we address. In Section 3, we introduce the main results of the paper. Some numerical experiments are included in Section 4.

Notations: $\mathfrak{N}=\{1,2,\dots ,N\}$, where $N\ge 1$ is a fixed natural number. $A^T$ stands for the transpose of the matrix A, and $Tr\left[A\right]$ denotes the trace of a matrix A. The notation $X\ge Y$ ($X>Y$), where X and Y are symmetric matrices, means that $X-Y$ is positive semi-definite (positive definite). In block matrices, ★ indicates symmetric terms, where $\left(\begin{array}{cc}A& B\\ B^T& C\end{array}\right)=\left(\begin{array}{cc}A& ★\\ B^T& C\end{array}\right)=\left(\begin{array}{cc}A& B\\ ★& C\end{array}\right)$. The expression $MN★$ is equivalent to $MN{M}^T$, while $M★$ is equivalent to $M{M}^T$. Consider the following space of matrices: ${\mathcal{M}}_{n,m}^N={\mathbb{R}}^{n\times m}\times \cdots \times {\mathbb{R}}^{n\times m}$. In the case where $n=m$, we shall write ${\mathcal{M}}_n^N$ instead of ${\mathcal{M}}_{n,n}^N$.

We introduce the following convention of notations:

• If $\mathbb{B}=\left(\begin{array}{ccc}B\left(1\right),& \cdots ,& B\left(N\right)\end{array}\right)\in {\mathcal{M}}_{n,m}^N$ and $\mathbb{D}=\left(\begin{array}{ccc}D\left(1\right),& \cdots ,& D\left(N\right)\end{array}\right)\in {\mathcal{M}}_{m,p}^N$, then $\mathbb{C}=\mathbb{B}\mathbb{D}\in {\mathcal{M}}_{n,p}^N$, where $\mathbb{C}=\left(\begin{array}{ccc}C\left(1\right),& \cdots ,& C\left(N\right)\end{array}\right)$, $C\left(i\right)=B\left(i\right)D\left(i\right)$, $1\le i\le N$.
• ${\mathbb{B}}^T=\left(\begin{array}{ccc}{B}^T\left(1\right),& \cdots ,& B^T\left(N\right)\end{array}\right)\in {\mathcal{M}}_{m,n}^N$.
• If $\mathbb{A}=\left(\begin{array}{ccc}A\left(1\right),& \cdots ,& A\left(N\right)\end{array}\right)\in {\mathcal{M}}_n^N$ with $det\left(A\right(i\left)\right)\ne 0$, $1\le i\le N$, then
  ${\mathbb{A}}^{-1}=\left(\begin{array}{ccc}{A}^{-1}\left(1\right),& \cdots ,& A^{-1}\left(N\right)\end{array}\right)$.

As usual, ${\mathcal{S}}_n\in {\mathbb{R}}^{n\times n}$ denotes the subspace of symmetric matrices of a size $n\times n$, and ${\mathcal{S}}_n^N={\mathcal{S}}_n\times \cdots \times {\mathcal{S}}_n$. ${\mathcal{S}}_n^N$ is a finite, dimensional real Hilbert space with respect to the inner product:

$$\begin{array}{c}\hfill ⟨\mathbb{X},\mathbb{Y}⟩=\sum _{i=1}^{N}Tr\left[X\left(i\right)Y\left(i\right)\right]\end{array}$$

(1)

for all $\mathbb{X}=(X\left(1\right),X\left(2\right),\dots ,X\left(N\right)),\mathbb{Y}=(Y\left(1\right),Y\left(2\right),\dots ,Y\left(N\right))\in {\mathcal{S}}_n^N$. Throughout this paper, $\mathbb{E}\left[·\right]$ stands for the mathematical expectation and $\mathbb{E}\left[·|{\theta }_t=i\right]$ denotes the conditional expectation with respect to the event $\{{\theta }_t=i\}$.

2. Problem Setting

2.1. Problem Description

Consider the following nonlinear difference equation in the space ${\mathcal{S}}_n^N$:

$$\mathbb{X}\left(t\right)={\mathsf{\Pi }}_1\left(t\right)\left[\mathbb{X}(t+1)\right]+\mathbb{M}\left(t\right)-\left[{\mathsf{\Pi }}_2\left(t\right)\left[\mathbb{X}(t+1)\right)]+\mathbb{L}\left(t\right)\right]{\left[\mathbb{R}\left(t\right)+{\mathsf{\Pi }}_3\left(t\right)\left[\mathbb{X}(t+1)\right]\right]}^{-1}★$$

(2)

where $t\in {\mathbb{Z}}_{+}=\{0,1,2,\dots \}$ with an unknown function $\mathbb{X}\left(t\right)=\left(\begin{array}{ccc}X(t,1),& \cdots ,& X(t,N)\end{array}\right)$.

Here, ${\mathsf{\Pi }}_k\left(t\right)\left[\mathbb{X}\right]=\left(\begin{array}{ccc}{\mathsf{\Pi }}_k\left(t\right)\left[\mathbb{X}\right]\left(1\right),& \cdots ,& {\mathsf{\Pi }}_k\left(t\right)\left[\mathbb{X}\right]\left(N\right)\end{array}\right)$ ($1\le k\le 3$) are defined by

$$\left\{\begin{array}{c}{\mathsf{\Pi }}_1\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=0}^r{A}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)A_j(t,i)\hfill \\ {\mathsf{\Pi }}_2\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=0}^r{A}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_j(t,i)\hfill \\ {\mathsf{\Pi }}_3\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=0}^r{B}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_j(t,i)\hfill \\ \mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)={\displaystyle \sum _{j=1}^N}{p}_t(i,j)X\left(j\right)\hfill \end{array}\right.$$

(3)

where $1\le i\le N$ for all $\mathbb{X}=\left(\begin{array}{ccc}X\left(1\right),& \cdots ,& X\left(N\right)\end{array}\right)\in {\mathcal{S}}_n^N$. In (2) $\mathbb{M}\left(t\right)=\left(M\right(t,1),\dots .,$$M(t,N))\in {\mathcal{S}}_n^N$, $\mathbb{R}\left(t\right)=(R(t,1),\dots .,R(t,N))\in {\mathcal{S}}_m^N$, and $\mathbb{L}\left(t\right)=(L(t,1),\dots ,L(t,N))\in {\mathcal{M}}_{n,m}^N$. Regarding the coefficients of Equation (2), we make the following assumption:

(H1) 

(a)

${\left\{A_j(t,i)\right\}}_{t\ge 0}\subset {\mathbb{R}}^{n\times n}$, ${\left\{B_j(t,i)\right\}}_{t\ge 0}\subset {\mathbb{R}}^{n\times m}$ ($0\le j\le r$), ${\left\{M(t,i)\right\}}_{t\ge 0}\subset {\mathcal{S}}_n$, ${\left\{L(t,i)\right\}}_{t\ge 0}\subset {\mathbb{R}}^{n\times m}$, and ${\left\{R(t,i)\right\}}_{t\ge 0}\subset {\mathcal{S}}_m$ for all $i\in \mathfrak{N}$ are periodic matrix-valued sequences of a period $\mathfrak{p}$. ${\left\{P_t\right\}}_{t\ge 0}$ with $P_t:={\left(p_t(i,j)\right)}_{(i,j)\in \mathfrak{N}\times \mathfrak{N}}$ is also assumed to be a periodic matrix-valued sequence of a period $\mathfrak{p}$.

(b)

For each $t\ge 0$, $P_t$ is a strong nondegenerate stochastic matrix (i.e., $p_t(i,j)\ge 0$,

${\sum }_{k=1}^N{p}_t(i,k)=1$, $p_t(i,i)>0$ for all $i,j\in \mathfrak{N}$).

The discrete-time backward nonlinear equation (Equation (2)) will be called a generalized discrete-time Riccati equation (GDTRE) in the rest of this paper.

We consider the following partitions of the coefficients of Equation (2):

$$\begin{array}{c}{B}_j(t,i)=\left(\begin{array}{cc}{B}_{j1}(t,i)& B_{j2}(t,i)\end{array}\right),B_{jk}(t,i)\in {\mathbb{R}}^{n\times m_k},0\le j\le r,\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}L(t,i)=\left(L_1(t,i)L_2(t,i)\right),L_k(t,i)\in {\mathbb{R}}^{n\times m_k},k=1,2\hfill \end{array}$$

(4)

and

$$R(t,i)=\left(\begin{array}{cc}{R}_{11}(t,i)& R_{12}(t,i)\\ ★& R_{22}(t,i)\end{array}\right),R_{lj}(t,i)\in {\mathbb{R}}^{m_l\times m_j},l,j=1,2.$$

(5)

Consider the following partitions corresponding to Equations (4) and (5):

$$\left\{\begin{array}{c}{\mathsf{\Pi }}_2\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\left(\begin{array}{cc}{\mathsf{\Pi }}_{21}\left(t\right)\left[\mathbb{X}\right]\left(i\right)& {\mathsf{\Pi }}_{22}\left(t\right)\left[\mathbb{X}\right]\left(i\right)\end{array}\right)\hfill \\ {\mathsf{\Pi }}_3\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\left(\begin{array}{cc}{\mathsf{\Pi }}_{311}\left(t\right)\left[\mathbb{X}\right]\left(i\right)& {\mathsf{\Pi }}_{312}\left(t\right)\left[\mathbb{X}\right]\left(i\right)\\ ★& {\mathsf{\Pi }}_{322}\left(t\right)\left[\mathbb{X}\right]\left(i\right)\end{array}\right)\hfill \end{array}\right.$$

(6)

with

$$\left\{\begin{array}{c}{\mathsf{\Pi }}_{2k}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=1}^r{A}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_{jk}(t,i)\hfill \\ {\mathsf{\Pi }}_{3lk}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=1}^r{B}_{jl}^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_{jk}(t,i)\hfill \end{array}\right.\hspace{1em};k,l=1,2.$$

The GDTRE (Equation (2)) plays a key role in the solution of a zero-sum LQ stochastic difference game control problem described by the controlled system

$$\begin{array}{c}\hfill \left\{\begin{array}{c}x(t+1)=A_0(t,{\theta }_t)x\left(t\right)+B_{01}(t,{\theta }_t)u_1\left(t\right)+B_{02}(t,{\theta }_t)u_2\left(t\right)+\sum _{k=1}^r[A_k(t,{\theta }_t)x\left(t\right)\hfill \\ +B_{k1}(t,{\theta }_t)u_1\left(t\right)+B_{k2}(t,{\theta }_t)u_2\left(t\right)]w_k\left(t\right)\hfill \\ x\left(t_0\right)=x_0\hfill \end{array}\right.\end{array}$$

(7)

and the quadratic performance criterion

$$\begin{array}{c}\hfill \mathcal{J}(x_0,u_1(·),u_2(·))=\mathbb{E}\left[\sum _{t_0}^{\infty }{\left(\begin{array}{c}{x}_u\left(t\right)\\ u_1\left(t\right)\\ u_2\left(t\right)\end{array}\right)}^T\left(\begin{array}{ccc}M(t,{\theta }_t)& L_1(t,{\theta }_t)& L_2(t,{\theta }_t)\\ ★& R_{11}(t,{\theta }_t)& R_{12}(t,{\theta }_t)\\ ★& ★& R_{22}(t,{\theta }_t)\end{array}\right)★\right]\end{array}$$

(8)

where $x_u\left(t\right)$ is the solution to the initial value problem (IVP) (Equation (7)), $t\ge t_0\ge 0$, and $u(·)={\left(\begin{array}{cc}{u}_1^T(·)& u_2^T(·)\end{array}\right)}^T$. In the first equation (Equation (7)), ${\left\{w_t\right\}}_{t\ge 0}$, $\left(w_t={\left(w_1\left(t\right),\cdots ,w_r\left(t\right)\right)}^T\right)$ is a sequence of independent random vectors, and the triple $({\left\{{\theta }_t\right\}}_{t\ge 0},{\left\{P_t\right\}}_{t\ge 0},\mathfrak{N})$ is a time non-homogeneous Markov chain defined in a given probability space $(\Omega ,\mathcal{F},\mathrm{P})$ with the finite states set $\mathfrak{N}=\{1,\cdots ,N\}$ and the sequence of transition probability matrices ${\left\{P_t\right\}}_{t\ge 0}$. Regarding processes ${\left\{{\theta }_t\right\}}_{t\ge 0}$ and ${\left\{w_t\right\}}_{t\ge 0}$, the following assumptions are made:

(H2) 

${\left\{w_t\right\}}_{t\ge 0}$ is a sequence of independent random vectors with the following properties: $\mathbb{E}\left[w\left(t\right)\right]=0$, $\mathbb{E}\left[w\left(t\right)w^T\left(t\right)\right]=I_r$, and $t\ge 0$, with $I_r$ being the identity matrix of a size r.

(H3) 

(a)

For each $t\ge 0$, the $\sigma$ algebra ${\mathcal{F}}_t$ is independent of the $\sigma$ algebra ${\mathcal{G}}_t$, where ${\mathcal{F}}_t=\sigma (w\left(s\right);0\le s\le t)$ and ${\mathcal{G}}_t=\sigma ({\theta }_s;0\le s\le t)$.

(b)

${\pi }_0\left(i\right):=\mathcal{P}\{{\theta }_0=i\}>0$ for all $i\in \mathfrak{N}$.

The following assumption regarding the weight matrices $M(t,i),R(t,i)$ and $L(t,i)$ is made:

(H4) 

For each $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$, we have

$$R_{22}(t,i)\ge {\rho }_2{I}_{m_2}$$

(9)

$$M(t,i)-L_2(t,i)R_{22}^{-1}(t,i)L_2^T(t,i)\ge 0$$

(10)

$$R_{11}(t,i)-R_{12}(t,i)R_{22}^{-1}(t,i)R_{12}^T(t,i)\le -{\rho }_1{I}_{m_1}$$

(11)

with ${\rho }_j>0$ and $j=1,2$, given constant scalars.

Let

$$\begin{array}{c}\hfill \mathcal{R}(t,\mathbb{X}(t+1),i):=R(t,i)+{\mathsf{\Pi }}_3\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right).\end{array}$$

(12)

In [1], we considered two different types of admissible strategies, namely the full-state feedback and full-information feedback strategies. We succeeded in showing that for both strategies, the solution to the LQ game relies on the unique bounded and stabilizing solution to the GDTRE (Equation (2)) satisfying a sign condition of the form

$$\begin{array}{cc}\hfill & {\mathcal{R}}_{22}^{♯}(t,\mathbb{X}(t+1),i)=R_{11}(t,i)+{\mathsf{\Pi }}_{311}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)-\left[R_{12}(t,i)+{\mathsf{\Pi }}_{312}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)\right]\hfill \\ & \times {\left[R_{22}(t,i)+{\mathsf{\Pi }}_{322}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)\right]}^{-1}★\le -{\delta }_1{I}_{m_1}\hfill \end{array}$$

(13)

$${\mathcal{R}}_{22}(t,\mathbb{X}(t+1),i)=R_{22}(t,i)+{\mathsf{\Pi }}_{322}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)\ge {\delta }_2{I}_{m_2}$$

(14)

for all $t\in \mathcal{I}$, $1\le i\le N$, ${\delta }_k>0$, and $k=1,2$ being constants.

The sign conditions in Equations (13) and (14) mean that the quadratic part of the GDTRE (Equation (2)) is of an indefinite sign. This sign indefiniteness makes the characterization and the numerical computation of the global solutions to the GDTRE (Equation (2)) much more intricate than in the sign-definite case.

Remark 1.

(i) 

The solutions ${\left\{\mathbb{X}\left(t\right)\right\}}_{t\in \mathcal{I}}$ to the GDTRE (Equation (2)) satisfying the conditions in Equations (13) and (14) will be called admissible solutions.

(ii) 

If $\mathbb{X}(·):\mathcal{I}\to {\mathcal{S}}_n^N$ is an admissible solution to the GDTRE (Equation (2)), then we have the following factorization:

$$\begin{array}{cc}\hfill R(t,i)+{\mathsf{\Pi }}_3\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)& ={\left(\begin{array}{cc}{V}_{11}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)& \mathbf{0}\\ V_{21}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)& V_{22}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)\end{array}\right)}^T\hfill \\ \hfill & \times \left(\begin{array}{cc}-I_{m_1}& \mathbf{0}\\ \mathbf{0}& I_{m_2}\end{array}\right)★\hfill \end{array}$$

(15)

where $V_{kk}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)\ge c_k{I}_{m_k}$, $k=1,2$, $i\in \mathfrak{N}$, and $t\in \mathcal{I}$.

(iii) 

For a precise definition of the stabilizing solution to the GDTRE (Equation (2)), one can refer to [1].

We derived in [1] the conditions for the existence and uniqueness of the stabilizing solution to Equation (2). In the present paper, we are interested in the numerical aspects of the GDTRE (Equation (2)). Our objective here is to propose a globally convergent algorithm for the computation of the unique stabilizing solution to Equation (2) with the sign (indefinite) conditions in Equations (13) and (14). We will propose an iterative deterministic algorithm which is based on the numerical computation of the bounded and stabilizing solutions of a sequence of Riccati difference equations arising in the deterministic framework. In order to accomplish this, we consider the following sequence of uncoupled Riccati difference equations (which are specific to the deterministic framework):

$$\begin{array}{cc}\hfill X^k(t,i)& ={\overline{A}}_0^T(t,i)X^k(t+1,i){\overline{A}}_0(t,i)+M_i^k\left(t\right)\hfill \\ \hfill & -\left({\overline{A}}_0^T(t,i)X^k(t+1,i){\overline{B}}_0(t,i)+L_i^k\left(t\right)\right){\left(R_i^k\left(t\right)+{\overline{B}}_0^T(t,i)X^k(t+1,i){\overline{B}}_0(t,i)\right)}^{-1}★\hfill \end{array}$$

(16)

where

$$\left\{\begin{array}{c}{\overline{A}}_0(t,i)=\sqrt{p_t(i,i)}{A}_0(t,i)\hfill \\ {\overline{B}}_0(t,i)=\sqrt{p_t(i,i)}{B}_0(t,i)\hfill \\ M_i^k\left(t\right)={\overline{\mathsf{\Pi }}}_1\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)+A_0^T(t,i)\overline{\mathsf{\Xi }}\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)A_0(t,i)+M(t,i)\hfill \\ {\overline{\mathsf{\Pi }}}_1\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)=\sum _{j=1}^r{A}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)A_j(t,i)\hfill \\ \overline{\mathsf{\Xi }}\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)={\displaystyle \underset{j\ne i}{{\displaystyle \sum _{j=1}^N}}}{p}_t(i,j)X^{k-1}(t+1,j)\hfill \\ L_i^k\left(t\right)={\overline{\mathsf{\Pi }}}_2\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)+A_0^T(t,i)\overline{\mathsf{\Xi }}\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)B_0(t,i)+L(t,i)\hfill \\ {\overline{\mathsf{\Pi }}}_2\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)=\sum _{j=1}^r{A}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)B_j(t,i)\hfill \\ R_i^k\left(t\right)={\overline{\mathsf{\Pi }}}_3\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)+B_0^T(t,i)\overline{\mathsf{\Xi }}\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)B_0(t,i)+R(t,i)\hfill \\ {\overline{\mathsf{\Pi }}}_3\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)=\sum _{j=1}^r{B}_j^T(t,i)\mathsf{\Xi }\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)B_j(t,i)\hfill \end{array}\right..$$

(17)

By taking $X_i^0\left(t\right)=0,1\le i\le N,t\in {\mathbb{Z}}_{+}$, we may construct the inductive sequences ${\left\{X_i^k\left(t\right)\right\}}_{k\ge 1}$, $1\le i\le N$, $X_i^k(·)$, which are the unique bounded and stabilizing solution to the Riccati difference equation (Equation (16)). The aim of this study is to provide a set of conditions which guarantee that $X_i^k(·)$ is well defined for all $k\ge 1$ and $\underset{k\to \infty }{lim}{X}_i^k\left(t\right)=X_s(t,i)$ for all $1\le i\le N$ and $t\in {\mathbb{Z}}_{+}$.

Remark 2.

Note that

$$\begin{array}{c}\hfill \widehat{\mathsf{\Pi }}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\left(\begin{array}{cc}{\mathsf{\Theta }}_1\left(t\right)\left[\mathbb{X}\right]\left(i\right)& {\mathsf{\Theta }}_2\left(t\right)\left[\mathbb{X}\right]\left(i\right)\\ ★& {\mathsf{\Theta }}_3\left(t\right)\left[\mathbb{X}\right]\left(i\right)\end{array}\right)\ge 0\end{array}$$

(18)

if $\mathbb{X}$ is such that $X\left(i\right)\ge 0$, where ${\mathsf{\Theta }}_1\left(t\right)\left[\mathbb{X}\right]\left(i\right)={\overline{\mathsf{\Pi }}}_1\left(t\right)\left[\mathbb{X}\right]\left(i\right)+A_0^T(t,i)\overline{\mathsf{\Xi }}\left(t\right)\left[\mathbb{X}\right]\left(i\right)A_0(t,i)$, ${\mathsf{\Theta }}_2\left(t\right)\left[\mathbb{X}\right]\left(i\right)={\overline{\mathsf{\Pi }}}_2\left(t\right)\left[\mathbb{X}\right]\left(i\right)+A_0^T(t,i)\overline{\mathsf{\Xi }}\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_0(t,i)$, and ${\mathsf{\Theta }}_3\left(t\right)\left[\mathbb{X}\right]\left(i\right)={\overline{\mathsf{\Pi }}}_3\left(t\right)\left[\mathbb{X}\right]\left(i\right)+B_0^T(t,i)\overline{\mathsf{\Xi }}\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_0(t,i)$, $1\le i\le N$. This follows by noticing that Equation (18) could be rewritten as

$$\widehat{\mathsf{\Pi }}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\left(\begin{array}{c}{A}_0^T(t,i)\\ B_0^T(t,i)\end{array}\right)\overline{\mathsf{\Xi }}\left(t\right)\left[\mathbb{X}\right]\left(i\right)★+\sum _{j=1}^r\left(\begin{array}{c}{A}_j^T(t,i)\\ B_j^T(t,i)\end{array}\right)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)★.$$

(19)

Remark 3.

In the Numerical Experiments section, we will clarify the deterministic nature of the proposed algorithm and highlight the contribution of such a paradigm.

2.2. Some Intermediate Results

Let us formally set $u_2\left(t\right)\equiv u_2^{\mathbb{KW}}\left(t\right)=K(t,{\theta }_t)x\left(t\right)+W(t,{\theta }_t)u_1\left(t\right)$. Hence, Equations (7) and (8) are rewritten as follows:

$$x(t+1)=A_{0\mathbb{K}}(t,{\theta }_t)x\left(t\right)+B_{0\mathbb{W}}(t,{\theta }_t)u_1\left(t\right)+\sum _{k=1}^r{w}_k\left(t\right)\left(A_{k\mathbb{K}}(t,{\theta }_t)x\left(t\right)+B_{k\mathbb{W}}(t,{\theta }_t)u_1\left(t\right)\right)$$

(20)

$${\mathcal{J}}_{\mathbb{KW}}(t_0,x_0,u_1)=\mathbb{E}\left[\sum _{t=t_0}^{\infty }{\left(\begin{array}{c}{x}_{u_1}\left(t\right)\\ u_1\left(t\right)\end{array}\right)}^T\left(\begin{array}{cc}{M}_{\mathbb{K}}(t,{\theta }_t)& L_{\mathbb{KW}}(t,{\theta }_t)\\ ★& R_{\mathbb{W}}(t,{\theta }_t)\end{array}\right)★\right]$$

(21)

where $x_{u_1}\left(t\right)$ is the solution to Equation (20) corresponding to $u_1\left(t\right)$ and

$$\left\{\begin{array}{c}{A}_{k\mathbb{K}}(t,i)=A_k(t,i)+B_{k2}(t,i)K(t,i)\hfill \\ B_{k\mathbb{W}}(t,i)=B_{k1}(t,i)+B_{k2}(t,i)W(t,i)\hfill \\ M_{\mathbb{K}}(t,i)=M(t,i)+L_2(t,i)K(t,i)+K^T(t,i)L_2^T(t,i)+K^T(t,i)R_{22}(t,i)K(t,i)\hfill \\ L_{\mathbb{KW}}(t,i)=L_1(t,i)+K^T(t,i)R_{12}^T(t,i)+\left(L_2(t,i)+K^T(t,i)R_{22}(t,i)\right)W(t,i)\hfill \\ R_{\mathbb{W}}(t,i)={\left(\begin{array}{c}{I}_{m_1}\\ W(t,i)\end{array}\right)}^{T}R(t,i)\left(\begin{array}{c}{I}_{m_1}\\ W(t,i)\end{array}\right)\hfill \end{array}\right..$$

(22)

With the above system (Equation (20)) and the corresponding quadratic functional in Equation (21), we associate the following Riccati-type difference equation of the type in Equation (2):

$$\begin{array}{cc}\hfill X(t,i)& ={\mathsf{\Pi }}_{\mathbb{K}}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)+M_{\mathbb{K}}(t,i)-\left({\mathsf{\Pi }}_{\mathbb{K}\mathbb{W}}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)+L_{\mathbb{KW}}(t,i)\right)\hfill \\ \hfill & \times {\left(R_{\mathbb{W}}(t,i)+{\mathsf{\Pi }}_{\mathbb{W}}\left(t\right)\left[\mathbb{X}(t+1)\right]\left(i\right)\right)}^{-1}★\hfill \end{array}$$

(23)

where

$$\left\{\begin{array}{c}{\mathsf{\Pi }}_{\mathbb{K}}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=0}^r{A}_{j\mathbb{K}}^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)A_{j\mathbb{K}}(t,i)\hfill \\ {\mathsf{\Pi }}_{\mathbb{K}\mathbb{W}}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=0}^r{A}_{j\mathbb{K}}^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_{j\mathbb{W}}(t,i)\hfill \\ {\mathsf{\Pi }}_{\mathbb{W}}\left(t\right)\left[\mathbb{X}\right]\left(i\right)=\sum _{j=0}^r{B}_{j\mathbb{W}}^T(t,i)\mathsf{\Xi }\left(t\right)\left[\mathbb{X}\right]\left(i\right)B_{j\mathbb{W}}(t,i)\hfill \end{array}\right.$$

(24)

for all $\mathbb{X}\in {\mathcal{S}}_n^N$.

In the following, we associate to the GDTRE (Equation (2)) the set ${\mathcal{A}}^{\mathbb{KW}}$, which consists of all pairs of feedback gains $\left(\mathbb{K}\right(·),\mathbb{W}(·\left)\right)$, where $t\to \mathbb{K}\left(t\right)=\left(\begin{array}{ccc}K(t,1),& \cdots ,& K(t,N)\end{array}\right):{\mathbb{Z}}_{+}\to {\mathcal{M}}_{m_2,n}^N$ and $t\to \mathbb{W}\left(t\right)=\left(\begin{array}{ccc}W(t,1),& \cdots ,& W(t,N)\end{array}\right):{\mathbb{Z}}_{+}\to {\mathcal{M}}_{m_2,m_1}^N$ are $\mathfrak{p}$-periodic matrix-valued sequences having the following properties:

(i)

The zero solution of the stochastic linear system

$$\begin{array}{cc}\hfill x(t+1)& =A_{0\mathbb{K}}(t,{\theta }_t)x\left(t\right)+\sum _{k=1}^r{w}_k\left(t\right)A_{k\mathbb{K}}(t,{\theta }_t)x\left(t\right)\hfill \end{array}$$

(25)

is exponentially stable in the mean square sense (ESMS) (see Definition 3.1 from [8] for details).

(ii)

The corresponding GRDE (Equation (23)) has a unique bounded and stabilizing solution ${\tilde{\mathbb{X}}}_{\mathbb{K}\mathbb{W}}(·)$ satisfying the sign condition

$$R_{\mathbb{W}}(t,i)+{\mathsf{\Pi }}_{\mathbb{W}}\left(t\right)\left[{\tilde{\mathbb{X}}}_{\mathbb{K}\mathbb{W}}(t+1)\right]\left(i\right)\le -\xi \mathbb{I}$$

(26)

for some positive scalar $\xi$ (which may depend upon $\left(\mathbb{K}(·),\mathbb{W}(·)\right)$) where $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$.

The following result gives a necessary and sufficient condition which helps us to decide if the set ${\mathcal{A}}^{\mathbb{KW}}$ is empty or not:

Proposition 1.

Under the considered assumptions, the following two assertions are equivalent:

(i) 

${\mathcal{A}}^{\mathbb{KW}}$ is not empty;

(ii) 

There exist $\mathfrak{p}$-periodic sequences $t\to \mathbb{Z}\left(t\right):{\mathbb{Z}}_{+}\to {\mathcal{S}}_n^N$, $t\to \mathbb{K}\left(t\right):{\mathbb{Z}}_{+}\to {\mathcal{M}}_{m_2,n}^N$ and $t\to \mathbb{W}\left(t\right):{\mathbb{Z}}_{+}\to {\mathcal{M}}_{m_2,m_1}^N$ solving the following matrix inequalities

$$\left(\begin{array}{cc}{\mathsf{\Pi }}_{\mathbb{K}}\left(t\right)\left[\mathbb{Z}(t+1)\right]\left(i\right)+M_{\mathbb{K}}(t,i)-Z(t,i)& {\mathsf{\Pi }}_{\mathbb{K}\mathbb{W}}\left(t\right)\left[\mathbb{Z}(t+1)\right]\left(i\right)+L_{\mathbb{KW}}(t,i)\\ ★& R_{\mathbb{W}}(t,i)+{\mathsf{\Pi }}_{\mathbb{W}}\left(t\right)\left[\mathbb{Z}(t+1)\right]\left(i\right)\end{array}\right)<0$$

(27)

Proof. 

One can apply Theorem 5.6 in [8] to the Riccati difference equation

$$\begin{array}{cc}\hfill Y(t,i)& ={\mathsf{\Pi }}_{\mathbb{K}}\left(t\right)\left[\mathbb{Y}(t+1)\right]\left(i\right)-M_{\mathbb{K}}(t,i)-\left({\mathsf{\Pi }}_{\mathbb{K}\mathbb{W}}\left(t\right)\left[\mathbb{Y}(t+1)\right]\left(i\right)-L_{\mathbb{W}}(t,i)\right)\hfill \\ \hfill & \times {\left(-R_{\mathbb{W}}(t,i)+{\mathsf{\Pi }}_{\mathbb{W}}\left(t\right)\left[\mathbb{Y}(t+1)\right]\left(i\right)\right)}^{-1}★\hfill \end{array}$$

(28)

obtained from Equation (23) by taking $Y(t,i)=-X(t,i)$, $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. □

We end this section by giving the existence conditions for the unique bounded and stabilizing solution to Equation (2). To this end, we introduce the following auxiliary system:

$$\left\{\begin{array}{c}x(t+1)={\check{A}}_0(t,{\theta }_t)x\left(t\right)+\sum _{j=1}^r{w}_j\left(t\right){\check{A}}_j(t,{\theta }_t)x\left(t\right)\hfill \\ y\left(t\right)=\check{C}(t,{\theta }_t)x\left(t\right)\hfill \end{array}\right.$$

(29)

where

$${\check{A}}_j(t,i)=A_j(t,i)-B_{j2}(t,i)R_{22}^{-1}(t,i)L_2^T(t,i),0\le j\le r$$

(30)

and $\check{C}(t,i)$ is obtained from the factorization $M(t,i)-L_2(t,i)R_{22}^{-1}(t,i)L_2^T(t,i)={\check{C}}^T(t,i)\check{C}(t,i)$ for all $i\in \mathfrak{N}$, $t\ge 0$.

Theorem 1.

Assume the following:

(a) 

Assumptions (H1–H4) are fulfilled;

(b) 

The set ${\mathcal{A}}^{\mathbb{KW}}$ is not empty;

(c) 

The auxiliary system in Equation (29) is exactly detectable at a time instant $t_0=0$;

Then, $\tilde{\mathbb{X}}(·)$, defined as $\tilde{X}(t,i)=\underset{\tau \to \infty }{lim}{X}_{\tau }(t,i)$, coincides with the unique admissible stabilizing and $\mathfrak{p}$-periodic solution ${\mathbb{X}}_s(·)$ to Equation (2), where for each $\tau >0$, ${\mathbb{X}}_{\tau }\left(t\right)=\left(\begin{array}{ccc}{X}_{\tau }(t,1),& \cdots & X_{\tau }(t,N)\end{array}\right)$ is the solution to Equation (2) satisfying the conditions $X_{\tau }(\tau +1,i)=0$ and $1\le i\le N$.

Remark 4.

For the definition of the notion of exact detectability at the time instant $t_0=0$, one can refer to [1].

Remark 5.

Note that the above theorem was proven in [1] under the assumption of stochastic detectability of the system in Equation (29) instead of exact detectability at the time instant $t_0=0$. One can show that the concept of exact detectability at the time instant $t_0=0$ is wider than the stochastic detectability one. Hence, the above result can be applied to a larger class of stochastic systems than the one reported in [1]. From the technical point of view, the improvement reported in this paper consists of the modification of Lemma 4.7 from [1], which is proven here under exact detectability at the assumption at the time instant $t_0=0$. For the reader’s convenience, we include a sketch of the proof of this Lemma in Appendix A.

3. Main Results

For each $k\ge 1$, $1\le i\le N$, the Riccati difference equation (Equation (16)) may be regarded as a special case of Equation (2). Hence, the Riccati difference equation (Equation (16)) is related to the deterministic LQ control problem described by the controlled system

$$x(t+1)={\overline{A}}_0(t,i)x\left(t\right)+{\overline{B}}_0(t,i)u\left(t\right)$$

(31)

where $t\ge 0$, $x\left(0\right)=x_0$, as well as the cost functional

$${\mathcal{J}}_i^k(x_0,u)=\sum _{t=0}^{\infty }{\left(\begin{array}{c}{x}_u\left(t\right)\\ u\left(t\right)\end{array}\right)}^T{\mathcal{M}}_i^k\left(t\right)★$$

(32)

where $x_u\left(t\right)$ is the solution to the IVP described by the controlled system in Equation (31), $t\ge 0$, $x\left(0\right)=x_0$, and

$${\mathcal{M}}_i^k\left(t\right)=\left(\begin{array}{cc}{M}_i^k\left(t\right)& L_i^k\left(t\right)\\ ★& R_i^k\left(t\right)\end{array}\right)$$

(33)

with $M_i^k\left(t\right)$, $L_i^k\left(t\right)$, and $R_i^k\left(t\right)$ being defined in Equation (17).

We formally set $u_2\left(t\right)\equiv u_{2,i}^{\mathbb{KW}}\left(t\right)=K(t,i)x\left(t\right)+W(t,i)u_1\left(t\right)$. Hence, Equations (31) and (32) are rewritten as follows:

$$x(t+1)={\overline{A}}_{0K}(t,i)x\left(t\right)+{\overline{B}}_{0W}(t,i)u_1\left(t\right)$$

(34)

$${\mathcal{J}}_{KW}^{k,i}(x_0,u_1)=\sum _{t=0}^{\infty }{\left(\begin{array}{c}{x}_{u_1}\left(t\right)\\ u_1\left(t\right)\end{array}\right)}^T\left(\begin{array}{cc}{M}_K^k(t,i)& L_{KW}^k(t,i)\\ ★& R_W^k(t,i)\end{array}\right)★$$

(35)

where $x_{u_1}\left(t\right)$ is the solution to Equation (34) corresponding to $u_1\left(t\right)$ and

$$\left\{\begin{array}{c}{\overline{A}}_{0K}(t,i)={\overline{A}}_0(t,i)+{\overline{B}}_{02}(t,i)K(t,i)\hfill \\ {\overline{B}}_{0W}(t,i)={\overline{B}}_{01}(t,i)+{\overline{B}}_{02}(t,i)W(t,i)\hfill \\ M_K^k(t,i)=M^k(t,i)+L_2^k(t,i)K(t,i)+K^T(t,i){\left(L_2^k\right)}^T(t,i)+K^T(t,i)R_{22}^k(t,i)K(t,i)\hfill \\ L_{KW}^k(t,i)=L_1^k(t,i)+K^T(t,i){R_{12}^k}^T(t,i)+\left(L_2^k(t,i)+K^T(t,i)R_{22}^k(t,i)\right)W(t,i)\hfill \\ R_W^k(t,i)={\left(\begin{array}{c}{I}_{m_1}\\ W(t,i)\end{array}\right)}^T{R}^k(t,i)★\hfill \end{array}\right.$$

(36)

With the above system (Equation (34)) and the corresponding quadratic functional in Equation (35), we associate the following Riccati difference equation:

$$\begin{array}{cc}\hfill X^k(t,i)& ={\overline{A}}_{0K}^T(t,i)X^k(t+1,i){\overline{A}}_{0K}(t,i)+M_K^k(t,i)-({\overline{A}}_{0K}^T(t,i)X^k(t+1,i){\overline{B}}_{0W}(t,i)\hfill \\ \hfill & +L_{KW}^k(t,i)){\left(R_W^k\left(t\right)+{\overline{B}}_{0W}^T(t,i)X^k(t+1,i){\overline{B}}_{0W}(t,i)\right)}^{-1}★\hfill \end{array}$$

(37)

The notion of a stabilizing solution for Equation (37) is defined in the same way as for Equation (2).

In the following, we denote with ${\mathcal{A}}_{k,i}^{\mathbb{KW}}$ the set of all pairs of feedback gains $(K_i(·),W_i(·))$, where $K_i(·):{\mathbb{Z}}_{+}\to {\mathbb{R}}^{m_2\times n}$ and $W_i\left(t\right):{\mathbb{Z}}_{+}\to {\mathbb{R}}^{m_2\times m_1}$ are $\mathfrak{p}$-periodic matrix-valued sequences having the following properties:

(i)

The zero solution of the closed-loop system

$$\begin{array}{cc}\hfill x(t+1)& ={\overline{A}}_{0K}(t,i)x\left(t\right)\hfill \end{array}$$

(38)

is exponentially stable.

(ii)

The corresponding GRDE (Equation (37)) has a unique stabilizing and $\mathfrak{p}$-periodic solution ${\tilde{\mathbb{X}}}_{\mathbb{K}\mathbb{W}}(·)$ satisfying the sign condition

$$R_W^k(t,i)+{\overline{B}}_{0W}^T(t,i)X^k(t+1,i){\overline{B}}_{0W}(t,i)\le -\xi \mathbb{I}$$

(39)

for some positive scalar $\xi$ (which may depend upon $\left(\mathbb{K}(·),\mathbb{W}(·)\right)$), and $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$.

Following similar arguments to those in the proof of Proposition 1, the following result is deduced:

Proposition 2.

Under the considered assumptions, the following two assertions are equivalent:

(i) 

${\mathcal{A}}_{k,i}^{\mathbb{KW}}$ is not empty;

(ii) 

There exist $\mathfrak{p}$-periodic sequences $t\to Z(t,i):{\mathbb{Z}}_{+}\to {\mathcal{S}}^n$, $t\to K(t,i):{\mathbb{Z}}_{+}\to {\mathbb{R}}^{m_2\times n}$, and $t\to W(t,i):{\mathbb{Z}}_{+}\to {\mathbb{R}}^{m_2\times m_1}$ solving the following matrix inequalities:

$$\left(\begin{array}{cc}{\overline{A}}_{0K}^T(t,i)Z(t+1,i)★+M_K^k(t,i)-Z(t,i)& {\overline{A}}_{0K}^T(t,i)Z(t+1,i){\overline{B}}_{0W}(t,i)+L_{KW}^k(t,i)\\ ★& R_W^k(t,i)+{\overline{B}}_{0W}^T(t,i)Z(t+1,i)★\end{array}\right)<0$$

(40)

We are now in position to prove the main result of this paper. To this end, we introduce the following auxiliary system:

$$\left\{\begin{array}{c}x(t+1)={\check{\overline{A}}}_0^k(t,i)x\left(t\right)\hfill \\ y\left(t\right)={\check{C}}^k(t,i)x\left(t\right)\hfill \end{array}\right.$$

(41)

where

$${\check{\overline{A}}}_0^k(t,i)={\overline{A}}_0(t,i)-{\overline{B}}_{02}(t,i){\left(R_{22}^k\right)}^{-1}(t,i){\left(L_2^k\right)}^T(t,i),$$

(42)

and ${\check{C}}^k(t,i)$ is obtained from the factorization

$$M^k(t,i)-L_2^k(t,i){\left(R_{22}^k\right)}^{-1}(t,i){\left(L_2^k\right)}^T(t,i)={\left({\check{C}}^k\right)}^T(t,i){\check{C}}^k(t,i)$$

for all $i\in \mathfrak{N}$, $t\ge 0$.

Theorem 2.

Assume the following:

(a) 

Assumptions (${\mathbf{H}}_{\mathbf{1}}$–${\mathbf{H}}_{\mathbf{4}})$ are fulfilled;

(b) 

The set ${\mathcal{A}}^{\mathbb{KW}}$ is not empty;

(c) 

The auxiliary system in Equation (29) is stochastically detectable.

Under these conditions, if we take $X_i^0\left(t\right)\equiv 0$, where $1\le i\le N$, then for each $k\ge 1$, $X_i^k(·)$ is well defined as the unique minimal and positive semi-definite solution to the Riccati difference equation (Equation (16)), and we have the following:

(i) 

$X_i^k(·)$ is a periodic sequence of a period $\mathfrak{p}$ and satisfies the sign conditions of the types in Equations (13) and (14);

(ii) 

$0=X_i^0\left(t\right)\le X_i^1\left(t\right)\le \cdots \le X_i^k\left(t\right)\le \cdots \le X_s(t,i)$ for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$ and ${\mathbb{X}}_s\left(t\right)=\left(\begin{array}{ccc}{X}_s(t,1),& \cdots ,& X_s(t,N)\end{array}\right)$ as the unique stabilizing and $\mathfrak{p}$-periodic solution to Equation (2);

(iii) 

If the auxiliary system in Equation (41) is detectable, then $X_i^k(·)$ is just the stabilizing solution of the Riccati difference equation (Equation (16));

(iv) 

${\displaystyle \underset{k\to \infty }{lim}}{X}_i^k\left(t\right)=X_s(t,i)$ for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$.

Proof. 

Since ${\mathcal{A}}^{\mathbb{KW}}$ is not empty, it follows from Proposition 1 that there exist $\mathfrak{p}$-periodic sequences $t\to \mathbb{Z}\left(t\right):{\mathbb{Z}}_{+}\to {\mathcal{S}}_n^N$, $t\to \mathbb{K}\left(t\right):{\mathbb{Z}}_{+}\to {\mathcal{M}}_{m_2,n}^N$, and $t\to \mathbb{W}\left(t\right):{\mathbb{Z}}_{+}\to {\mathcal{M}}_{m_2,m_1}^N$ solving the matrix inequalities in Equation(27). Note that Equation (27) could be rewritten as

$$\begin{array}{cc}\hfill & \left(\begin{array}{cc}{\overline{A}}_{0K}^T(t,i)Z(t+1,i)★+M_K^1(t,i)-Z(t,i)& {\overline{A}}_{0K}^T(t,i)Z(t+1,i){\overline{B}}_{0W}(t,i)+L_{KW}^1(t,i)\\ ★& R_W^1\left(t\right)+{\overline{B}}_{0W}^T(t,i)Z(t+1,i)★\end{array}\right)\hfill \\ \hfill & +{\widehat{\mathsf{\Pi }}}_{\mathbb{KW}}\left[\mathbb{Z}(t+1)\right]\left(i\right)<0\hfill \end{array}$$

(43)

where

$$\begin{array}{cc}\hfill {\widehat{\mathsf{\Pi }}}_{\mathbb{KW}}\left[\mathbb{Z}(t+1)\right]\left(i\right)& =\left(\begin{array}{c}{A}_{0\mathbb{K}}^T(t,i)\\ B_{0\mathbb{W}}^T(t,i)\end{array}\right)\overline{\mathsf{\Xi }}\left[\mathbb{Z}(t+1)\right]\left(i\right)★\hfill \\ \hfill & +\sum _{k=1}^r\left(\begin{array}{c}{A}_{k\mathbb{K}}^T(t,i)\\ B_{k\mathbb{W}}^T(t,i)\end{array}\right)\mathsf{\Xi }\left[\mathbb{Z}(t+1)\right]\left(i\right)★\ge 0\hfill \end{array}$$

(44)

because $Z(t,i)\ge 0$ for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. This allows us to deduce that

$$\left(\begin{array}{cc}{\overline{A}}_{0\mathbb{K}}^T(t,i)Z(t+1,i)★+M_K^1(t,i)-Z(t,i)& {\overline{A}}_{0K}^T(t,i)Z(t+1,i){\overline{B}}_{0W}(t,i)+L_{KW}^1(t,i)\\ ★& R_W^1\left(t\right)+{\overline{B}}_{0W}^T(t,i)Z(t+1,i)★\end{array}\right)<0$$

(45)

Hence, under Proposition 2, it follows that ${\mathcal{A}}_{1,i}^{\mathbb{KW}}$ is not empty. If $k=1$, then the Riccati difference equation (Equation (16)) reduces to

$$\begin{array}{cc}\hfill X(t,i)& ={\overline{A}}_0^T(t,i)X(t+1,i){\overline{A}}_0(t,i)+M(t,i)\hfill \\ \hfill & -\left({\overline{A}}_0^T(t,i)X(t+1,i){\overline{B}}_0(t,i)+L(t,i)\right){\left(R\left(t\right)+{\overline{B}}_0^T(t,i)X(t+1,i){\overline{B}}_0(t,i)\right)}^{-1}★\hfill \end{array}$$

(46)

where $1\le i\le N$. From Proposition 4.4 in [1], we deduce that if $X_{i\tau }(·)$ is the solution to Equation (46) which satisfies $X_{i\tau }\left(\tau \right)=0$, then it is well defined for all $0\le t\le \tau$ and $\tau >0$, where $1\le i\le N$, and for each $1\le i\le N$, with $X_i^1(·)$ defined by

$$X_i^1\left(t\right)=\underset{\tau \to \infty }{lim}{X}_{i\tau }\left(t\right)$$

(47)

This is the unique minimal positive semi-definite solution to Equation (46). Moreover, $t\to X_i^1\left(t\right)$ is a periodic sequence of a period $\mathfrak{p}$.

Let us notice that the Riccati difference equation (Equation (2)) satisfied by its stabilizing solution ${\mathbb{X}}_s(·)$ may be rewritten as

$$\begin{array}{cc}\hfill X_s(t,i)& ={\overline{A}}_0^T(t,i)X_s(t+1,i){\overline{A}}_0(t,i)+M_{s,i}\left(t\right)\hfill \\ \hfill & -\left({\overline{A}}_0^T(t,i)X_s(t+1,i){\overline{B}}_0(t,i)+L_{s,i}\left(t\right)\right){\left(R_{s,i}\left(t\right)+{\overline{B}}_0^T(t,i)X_s(t+1,i){\overline{B}}_0(t,i)\right)}^{-1}★\hfill \end{array}$$

(48)

where

$$\begin{array}{c}\hfill \left(\begin{array}{cc}{M}_{s,i}\left(t\right)& L_{s,i}\left(t\right)\\ ★& R_{s,i}\left(t\right)\end{array}\right)=\left(\begin{array}{cc}M(t,i)& L(t,i)\\ ★& R(t,i)\end{array}\right)+\widehat{\mathsf{\Pi }}\left(t\right)\left[{\mathbb{X}}_s\left(t\right)\right]\left(i\right).\end{array}$$

(49)

Since $X_s(t,i)\ge 0$, we deduce from Equation (18) that

$$\begin{array}{c}\hfill \left(\begin{array}{cc}{M}_{s,i}\left(t\right)& L_{s,i}\left(t\right)\\ ★& R_{s,i}\left(t\right)\end{array}\right)\ge \left(\begin{array}{cc}M(t,i)& L(t,i)\\ ★& R(t,i)\end{array}\right).\end{array}$$

Hence, by applying Theorem 4.2 in [1] in the special case of the Riccati difference equation (Equations (46) and (48)), we may infer that $X_{i\tau }\left(t\right)\le X_s(t,i)$ for all $0\le t\le \tau$, $\tau >0$, and $1\le i\le N$. By taking the limit for $\tau \to \infty$, we obtain $0\le X_i^1\left(t\right)\le X_s(t,i)$ for all $(t,i)\in {\mathbb{R}}_{+}\times \mathfrak{N}$. From the matrix inequality

$$R(t,i)+{\mathsf{\Pi }}_3\left(t\right)\left[X_i^1\left(t\right)\right]\left(i\right)\le R(t,i)+{\mathsf{\Pi }}_3\left(t\right)\left[X_s\left(t\right)\right]\left(i\right)$$

we deduce, via Lemma 4.5 in [9], that for each $1\le i\le N$, $X_i^1(·)$ satisfies the sign conditions in Equations (13) and (14). Thus, assertions (i) and (ii) from the statement are fulfilled for $k=1$.

By using the Lyapunov-type characterization of the stochastic detectability of linear stochastic systems (see, for example, Chapter 4 in [8]), one can show that the stochastic detectability of the auxiliary system (Equation (29)) implies the detectability of the deterministic system

$$\left\{\begin{array}{c}x(t+1)={\check{\overline{A}}}_0(t,i)x\left(t\right)\hfill \\ y\left(t\right)=\check{C}(t,i)x_t\hfill \end{array}\right.$$

(50)

for each $1\le i\le N$, where ${\check{\overline{A}}}_0(t,i)={\overline{A}}_0(t,i)-{\overline{B}}_{02}(t,i)R_{22}^{-1}(t,i)L_2^T(t,i)$. Therefore, under assumption (c) in the statement, it follows that $X_i^1(·)$ is just the bounded and stabilizing solution of the Riccati difference equation (Equation (16)) in the special case $k=1$, which confirms the validity of assertion (iii) from the statement for $k=1$.

Let us assume that for $k\ge 2$ and for any $1\le l\le k-1$ and $1\le i\le N$, the functions $X_i^l(·)$ are well defined as unique minimal and positive semi-definite solutions of the Riccati difference equation (Equation (16)) (written for k and replaced by l) and have properties (i–iii) from the statement. We now show that for $l=k$ and $1\le i\le N$, the Riccati difference equation (Equation (16)) has a minimal solution $X_i^k(·)$ which is positive semi-definite, and it is a $\mathfrak{p}$-periodic sequence satisfying the sign conditions in Equations (13) and (14). Moreover, we have

$$0\le X_i^1\left(t\right)\le \cdots \le X_i^l\left(t\right)\le \cdots \le X_i^{k-1}\left(t\right)\le X_i^k\left(t\right)\le \cdots \le X_s(t,i)$$

(51)

$(t,i)\in {\mathbb{R}}_{+}\times \mathfrak{N}$.

If $(\mathbb{K}(·),\mathbb{W}(·))\in {\mathcal{A}}^{\mathbb{KW}}$, then we rewrite Equation (27) in the form

$$\begin{array}{cc}\hfill & \left(\begin{array}{cc}{\overline{A}}_{0K}^T(t,i)Z(t+1,i)★+M_K^k(t,i)-Z(t,i)& {\overline{A}}_{0K}^T(t,i)Z(t+1,i){\overline{B}}_{0W}(t,i)+L_{KW}^k(t,i)\\ ★& R_W^k\left(t\right)+{\overline{B}}_{0W}^T(t,i)Z(t+1,i)★\end{array}\right)\hfill \\ \hfill & +{\widehat{\mathsf{\Pi }}}_{\mathbb{KW}}[\mathbb{Z}(t+1)-{\mathbb{X}}^{k-1}(t+1)]\left(i\right)<0\hfill \end{array}$$

(52)

in which $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$, where ${\mathbb{X}}^{k-1}\left(t\right)=\left(\begin{array}{ccc}{X}_1^{k-1}\left(t\right),& \cdots ,& X_N^{k-1}\left(t\right)\end{array}\right)$ and ${\widehat{\mathsf{\Pi }}}_{\mathbb{KW}}[\mathbb{Z}(t+1)-{\mathbb{X}}^{k-1}(t+1)]\left(i\right)$ is computed as in Equation (44) with $\mathbb{Z}(t+1)$ replaced by $\mathbb{Z}(t+1)-{\mathbb{X}}^{k-1}(t+1)$.

Recalling that stochastic detectability implies exact detectability at time instant $t_0=0$ (see Remark 5), it follows from Proposition 4.4 in [1] and Theorem 1 that $X_s(t,i)\le {\tilde{X}}_{\mathbb{KW}}(t,i)$ for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. Note also that by using similar arguments to those in Chapter 5 from [8], one can show that ${\tilde{X}}_{\mathbb{KW}}(t,i)\le Z(t,i)$ for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. Hence, we deduce that $X_i^{k-1}\le X_s(t,i)\le Z(t,i)$ for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. Thus, ${\widehat{\mathsf{\Pi }}}_{\mathbb{KW}}[\mathbb{Z}(t+1)-{\mathbb{X}}^{k-1}(t+1)]\left(i\right)\ge 0$. This allows us to conclude that the matrix-valued sequences $Z_i(·)=Z(·,i)$ satisfy

$$\left(\begin{array}{cc}{\overline{A}}_{0K}^T(t,i)Z(t+1,i)★+M_K^k(t,i)-Z(t,i)& {\overline{A}}_{0K}^T(t,i)Z(t+1,i){\overline{B}}_{0W}(t,i)+L_{KW}^k(t,i)\\ ★& R_W^k\left(t\right)+{\overline{B}}_{0W}^T(t,i)Z(t+1,i)★\end{array}\right)<0$$

(53)

Therefore, we may conclude that ${\mathcal{A}}_{k,i}^{\mathbb{KW}}$ is not empty for all $1\le i\le N$ if ${\mathcal{A}}^{\mathbb{KW}}$ is not empty. Thus, we deduce that the solutions $X_{i\tau }^k(·)$ to the difference equation (Equation (16)) which satisfy the condition $X_{i\tau }^k\left(\tau \right)=0$ are well defined for all $0\le t\le \tau$, $\forall \tau >0$, and $i\in \mathfrak{N}$. By applying Proposition 4.4 from [1] in the special case of the Riccati difference equation (Equation (16)), we infer that $X_i^k(·)$, defined by $X_i^k\left(t\right)=\underset{\tau \to \infty }{lim}{X}_{i\tau }^k\left(t\right)$, is the minimal positive semi-definite and $\mathfrak{p}$-periodic solution of the Riccati difference equation (Equation (16)).

From Equations (17) and (49), we obtain

$$\left(\begin{array}{cc}{M}_{s,i}\left(t\right)& L_{s,i}\left(t\right)\\ ★& R_{s,i}\left(t\right)\end{array}\right)-\left(\begin{array}{cc}{M}_i^k\left(t\right)& L_i^k\left(t\right)\\ ★& R_i^k\left(t\right)\end{array}\right)=\widehat{\mathsf{\Pi }}\left(t\right)\left[{\mathbb{X}}_s\left(t\right)-{\mathbb{X}}^{k-1}\left(t\right)\right]\left(i\right)$$

(54)

By again invoking the inequalities $X_i^{k-1}\left(t\right)\le X_s(t,i)$ and $\forall (t,i)\in {\mathbb{K}}_{+}\times \mathfrak{N}$, we may obtain $\widehat{\mathsf{\Pi }}\left(t\right)\left[{\mathbb{X}}_s(t+1)-{\mathbb{X}}^{k-1}(t+1)\right]\left(i\right)\ge 0$. By applying Theorem 4.2 in [1] in the special case of Equations (16) and (48), we deduce that $X_{i\tau }^k\left(t\right)\le X_s(t,i)$ for all $0\le t\le \tau$, $\tau >0$, and $1\le i\le N$. By taking the limit for $\tau \to \infty$, we deduce that

$$X_i^k\left(t\right)\le X_s(t,i)$$

(55)

for all $(t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. On the other hand, Equation (17) yields

$$\left(\begin{array}{cc}{M}_i^k\left(t\right)& L_i^k\left(t\right)\\ ★& R_i^k\left(t\right)\end{array}\right)-\left(\begin{array}{cc}{M}_i^{k-1}\left(t\right)& L_i^{k-1}\left(t\right)\\ ★& R_i^{k-1}\left(t\right)\end{array}\right)=\widehat{\mathsf{\Pi }}\left(t\right)\left[{\mathbb{X}}^{k-1}\left(t\right)-{\mathbb{X}}^{k-2}\left(t\right)\right]\left(i\right)$$

Since $X_i^{k-2}\left(t\right)\le X_i^{k-1}\left(t\right)$ and $(t,i)\in {\mathbb{K}}_{+}\times \mathfrak{N}$, one obtains $\widehat{\mathsf{\Pi }}\left(t\right)\left[{\mathbb{X}}^{k-1}(t+1)-{\mathbb{X}}^{k-2}(t+1)\right]$, where $\left(i\right)\ge 0$. This allows to us apply Theorem 4.2 from [1] in the special case of the Riccati difference equation (Equation (16)) to deduce that $X_{i\tau }^{k-1}\left(t\right)\le X_{i\tau }^k\left(t\right)$, $\forall 0\le t\le \tau$, $\tau >0$, and $1\le i\le N$. By letting $\tau \to \infty$, we obtain

$$X_i^{k-1}\left(t\right)\le X_i^k\left(t\right)$$

(56)

$\forall (t,i)\in {\mathbb{Z}}_{+}\times \mathfrak{N}$. Thus, Equations (55) and (56) confirm the validity of Equation (51).

Furthermore, Equation (55) yields

$$R(t,i)+{\mathsf{\Pi }}_3\left(t\right)\left[{\mathbb{X}}^k\left(t\right)\right]\left(i\right)\le R(t,i)+{\mathsf{\Pi }}_3\left(t\right)\left[{\mathbb{X}}_s\left(t\right)\right]\left(i\right)$$

$\forall (t,i)\in {\mathbb{Z}}_{+}\times N$. These matrix inequalities, together with Lemma 4.5 from [9], allow us to conclude that $X_i^k(·)$ satisfies the sign conditions in Equations (13) and (14).

Finally, let us remark that if the auxiliary system in Equation (41) is detectable, then the minimal solution $X_i^k(·)$ coincides with the bounded and stabilizing solution of Equation (16) for any $1\le i\le N$. Thus, we have shown inductively that $X_i^k(·)$ can be constructed for any $k\ge 1$ and $1\le i\le N$ which satisfies properties (i–iii) from the statement. Now we remark that Equation (51) allows us to conclude that the sequences ${\left\{X_i^k\left(t\right)\right\}}_{k\ge 1}$, $1\le i\le N$, and $t\ge 0$ are convergent. Let $Y(t,i)=\underset{k\to \infty }{lim}{X}_i^k\left(t\right)$, $(t,i)\in {\mathbb{R}}_{+}\times \mathfrak{N}$. By taking the limit for $k\to \infty$ in Equation (16), we obtain that ${\left\{Y\left(t\right)\right\}}_{t\in \mathbb{Z}}$ is a positive semi-definite and $\mathfrak{p}$-periodic solution of Equation (2). Based on the minimality property of the stabilizing solution of the Riccati equation (Equation (2)), we deduce that $X_s\left(t\right)\le Y\left(t\right),t\in \mathbb{Z}$, and hence

$$Y\left(t\right)=X_s\left(t\right).$$

(57)

Thus, the proof is complete. □

4. Numerical Experiments

The time-invariant case will be considered in this section. We will refer to the algorithm proposed here as Algo_Deter. In this example, and in order to evaluate the performance of Algo_Deter, we will compare it with an algorithm that belongs to the class of stochastic algorithms (see Section 1 for a description of this class of algorithms). We propose using here a stochastic algorithm that we adapted from [10] to our setting. This algorithm is referred to as Algo_Stoch. We recall here that for solving the deterministic Riccati equations appearing in Algo_Deter, one can use direct methods (invariant or deflating subspace-based methods). We refer the reader interested in direct methods to [6,11,12] and the references therein. We also recall that at each main iteration of Algo_Stoch, one has to use iterative methods. We will show, from the computation time point of view, the superiority of Algo_Deter when compared with Algo_Stoch, which is due to the direct or iterative method opposition.

We will use the following simulation protocol:

1.

Set the example numbers n_good = 0, n_Deter = 0, and n_Stoch = 0, where n_good represents the number of examples for which both Algo_Deter and Algo_Stoch converge, n_Deter is the number of examples for which Algo_Deter converges but not Algo_Stoch, and n_Stoch is the number of examples for which Algo_Stoch converges but not Algo_Deter;

2.

Choose n, $m_1$, and $m_2$ randomly and uniformly among the integers from 1 to 10 and fix $N=3$;

3.

Generate randomly the corresponding system matrices;

4.

If the assumptions in Theorem 2 are not verified, then go back to step 2;

5.

Use Algo_Deter and Algo_Stoch to solve the corresponding generalized Riccati equation. Let the stabilizing solution obtained using Algo_Deter be ${\mathbb{X}}_1$ and the solution obtained using Algo_Stoch be ${\mathbb{X}}_2$, with CPU_time_1 and CPU_time_2 being the respective CPU running times;

(a)

If neither algorithms converge, then go back to step 2;

(b)

If Algo_Deter converges but not Algo_Stoch, then set n_Deter = n_Deter + 1 and go back to step 2;

(c)

If Algo_Deter does not converge but Algo_Stoch does, then set n_Stoch = n_Stoch + 1 and go back to step 2;

(d)

If both algorithms converge, then set n_good = n_good + 1 and compute the error $R_i=\frac{1}{N}{\sum }_{j=1}^N\parallel X_1\left(j\right)-X_2\left(j\right)\parallel$ and the coefficient ${\rho }_i=\frac{\mathrm{CPU}\_\mathrm{time}\_2}{\mathrm{CPU}\_\mathrm{time}\_1}$;

6.

Repeat steps 2–6 until $\mathbf{n}\_\mathbf{good}=100$.

We generated random test samples with a specified level of accuracy $ϵ={10}^{-8}$ for both algorithms.

The obtained results are listed in Table 1 and Figure 1. In Table 1, O$\left(R_i\right)$ is the order of magnitude of $R_i$, and “Number of Examples” indicates the number of examples corresponding to the same order of magnitude of $R_i$. It follows from the obtained results that when Algo_Deter and Algo_Stoch converged, the obtained stabilizing solutions were computed with comparable accuracies.

Table 1. Accuracy comparison for 100 random examples.

O$\left({\mathit{R}}_{\mathit{i}}\right)$	Number of Examples
${10}^{-9}$	66
ine ${10}^{-10}$	34

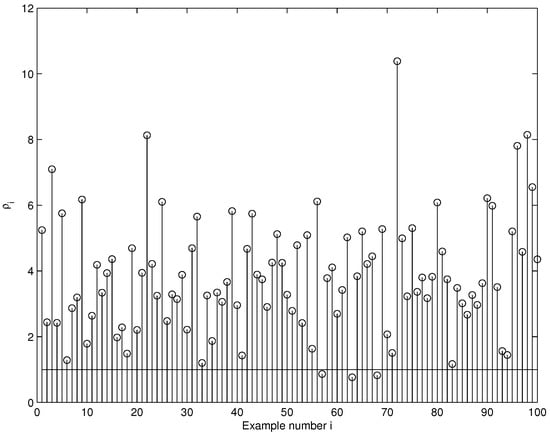
Figure 1. Plot of the quantity ${\rho }_i=\frac{\mathrm{CPU}\_\mathrm{time}\_2}{\mathrm{CPU}\_\mathrm{time}\_1}$.

As expected, and thanks to the use of direct resolution methods instead of iterative ones, one can see clearly from Figure 1 the improvement brought about by Algo_Deter from the computation time point of view.

During this experiment, we also obtained the following results: $\mathbf{n}\_\mathbf{deter}=36$ and $\mathbf{n}\_\mathbf{Stoch}=0$. This shows that Algo_Deter still worked well in cases where Algo_Stoch failed. We believe that this was due partly to the fact that in Algo_Stoch, the computation of the sequence of approximations of the stabilizing solution relies on the computation of a vanishing matrix sequence ${\left\{Z^{\left(k\right)}\left(t\right)\right\}}_{k\ge 0}$, while in Algo_Deter, one directly computes the sequence of approximations ${\left\{X^{\left(k\right)}\left(t\right)\right\}}_{k\ge 0}$. The vanishing nature of the matrix sequence ${\left\{Z^{\left(k\right)}\left(t\right)\right\}}_{k\ge 0}$ could induce ill conditioning in its computation.

5. Conclusions

In this paper, we addressed the problem of the numerical computation of the stabilizing solution for a class of generalized Riccati difference equations. We proposed an iterative deterministic algorithm for the computation of such a global solution. The performances of the proposed algorithm were illustrated via a comparison with existing algorithms in the literature. Our ongoing efforts are twofold. On one side, we are interested in the numerical computation of some global solutions to Riccati equations arising in stochastic Nash and Stackelberg games. The degree of maturity of numerical methods for such an aim is very weak when compared with its deterministic analogue. On the other side, we are also interested in generalized Riccati equations arising in mean field LQ games. Such equations present a coupling that makes this problem very challenging.