Cloud-Assisted Private Set Intersection via Multi-Key Fully Homomorphic Encryption

Abstract

With the development of cloud computing and big data, secure multi-party computation, which can collaborate with multiple parties to deal with a large number of transactions, plays an important role in protecting privacy. Private set intersection (PSI), a form of multi-party secure computation, is a formidable cryptographic technique that allows the sender and the receiver to calculate their intersection and not reveal any more information. As the data volume increases and more application scenarios emerge, PSI with multiple participants is increasingly needed. Homomorphic encryption is an encryption algorithm designed to perform a mathematical-style operation on encrypted data, where the decryption result of the operation is the same as the result calculated using unencrypted data. In this paper, we present a cloud-assisted multi-key PSI (CMPSI) system that uses fully homomorphic encryption over the torus (TFHE) encryption scheme to encrypt the data of the participants and that uses a cloud server to assist the computation. Specifically, we design some TFHE-based secure computation protocols and build a single cloud server-based private set intersection system that can support multiple users. Moreover, security analysis and performance evaluation show that our system is feasible. The scheme has a smaller communication overhead compared to existing schemes.

1. Introduction

With the rapid growth of data in the Internet era, the demand for data storage and computing capacity in various fields far exceeds the capacity of their own devices. To solve this problem, cloud computing has been proposed. Cloud computing is generally defined as an internet-based computing method. In this way, the shared software and hardware information and resources can be provided to various terminals and other devices of the computer as required. Cloud computing technology can transmit various information to the Internet and store and calculate data, and users can view the calculation results and data information. However, current security issues in the context of cloud computing are more prominent [1]. Data security issues in cloud computing mainly include storage data security, computing data security, and transmission data security. When users store data on the cloud server, the cloud server will obtain the users’ data first, but the abnormal use of malicious users can also cause a risk of data leakage. In the process of cloud server computing, the cloud server will know the calculation results and additional data. This information that should only be known by users also has a risk of leakage. In addition, data theft can easily occur during data transmission, and user data can show problems of theft and tampering [2].

Private set intersection (PSI), as an interactive encryption protocol, calculates the intersection of two data owners’ data and returns it to one of them. We generally refer to the party receiving the data as the receiver and the party receiving nothing as the sender. It is important and necessary to protect the privacy of the set in computing, especially when the information in the set is important private information such as the customer transaction information of a bank or the address book of a user. With the concerted efforts of many researchers, PSI technology has developed rapidly, and more and more efficient solutions have been proposed [3,4,5,6,7,8,9,10,11,12,13,14,15]. After several years of development, PSI technology has been applied to the fields of internet of vehicles [16], profile matching [17], and private contact search [18]. In the current situation where the data volume is large and scattered in the hands of different participants, PSI technology can well balance the relationship between privacy and information sharing. Leveraging the storage and computing power of cloud servers allows PSI protocols to compute larger datasets, but current cloud-assisted PSI schemes suffer from information leakage [19] or large communication overhead [20].

Fully homomorphic encryption (FHE) refers to the computation of data that has been homomorphically encrypted, and the computed decryption result is the same as that obtained by the same computation for unencrypted data. The concept of FHE has been proposed as early as the late 1970s, but it has only started to develop rapidly in the last two decades. The development of fully homomorphic encryption is generally divided into three stages. In 2009, the first generation of fully homomorphic encryption started to develop, and Gentry constructed the first fully homomorphic encryption scheme [21]. The scheme first constructs a somewhat homomorphic encryption (SHE) scheme that can homomorphically compute circuits of a certain depth, then compresses and decrypts the circuits and performs bootstrapping operations in an orderly manner, and finally obtains a scheme that can homomorphically compute arbitrary circuits. The second generation of fully homomorphic encryption schemes arose in 2011 when Brakerski and Vaikuntanathan implemented FHE for the first time under the LWE assumption using linearization and modulo conversion [22] and implemented FHE under the RLWE assumption [23]. These schemes do not require compression and decryption circuits, and the security and efficiency are greatly improved. In 2013, the third generation of fully homomorphic encryption schemes was born, and Gentry et al. for the first time designed a fully homomorphic encryption scheme, Gentry–Sahai–Waters (GSW), that does not require the computation of a key using the approximate eigenvector technique [24].

There are two broad categories of fully homomorphic algorithms, the BGV [25] scheme proposed by Professor Brakerski of Stanford University, Research Fellow Gentry of IBM, and Professor Vaikuntanathan of the University of Toronto, and the GSW [24] scheme proposed by Gentry of IBM, Sahai of the University of California and Waters of the University of Austin. Fully homomorphic encryption over toru (TFHE) [26] is an improvement of the GSW scheme with higher efficiency. TFHE can accomplish fast comparisons, supports arbitrary boolean circuits, and allows fast bootstrapping to reduce the noise due to ciphertext computation. In previous studies, the BGV scheme has been used to focus on the unbalanced privacy aggregation scenario [27,28,29]. Unlike previous works, this paper uses the TFHE encryption scheme for the first time to implement privacy-seeking protocol based on cloud computing. At a high level, our contributions can be summarized as follows:

• We have designed a series of security sub-protocols for the MKTFHE cryptosystem, including some basic circuit gate operations and security comparison protocols.
• We have built a cloud-assisted multi-key private set intersection (CMPSI) system based on a single cloud server. Our system can prevent collusion attacks between servers and participants.
• We strictly prove the security of the proposed CMPSI system under the semi-honest model.
• We have conducted extensive experimental evaluation on the performance of the scheme, which proves that our scheme has greatly reduced the communication cost of the participants.

The rest of the paper is organized as follows. In Section 2, we describe the related work of private set intersection. In Section 3, we provide the preliminaries. Section 4 details the system model, threat model, and design goals. Section 5 elaborates on the cryptographic protocol for the private set intersection. Section 6 analyzes the security of our proposed protocols. Section 7 conducts a series of experimental comparisons. Finally, Section 8 concludes this paper.

2. Related Work

PSI was first proposed by Freedman et al. [30], who transformed the element comparison problem into the polynomial root problem and realized PSI through multiplicative homomorphic encryption. However, when the polynomial order is large, it will lead to a costly exponential computation of the homomorphic encryption. In recent years, many researchers have intensively studied the PSI problem, and many PSI protocols with high efficiency and low communication overhead have emerged. PSI computing protocols are mainly divided into two categories according to whether there is a third party, namely, the traditional PSI computing protocol based on public key encryption, obfuscation circuit [31,32,33] and inadvertent transmission [34] technology and the cloud-assisted PSI computing protocol that uses cloud servers to complete computing.

Traditional PSI computing protocols rely on a series of basic cryptography technologies for computing. These basic cryptography technologies are mainly divided into PSI based on public key encryption mechanism, PSI based on obfuscation circuit, and PSI based on inadvertent transmission. The PSI calculation protocol proposed by Freedman et al. [34] is based on the public key encryption mechanism. This scheme represents the elements in the set as the roots of polynomials and uses polynomials to calculate the intersection. However, the cost of calculation will become large with the increase in the order of polynomials. Hazay et al. also improved the article [30] and adopted the bit commitment protocol to prevent the scenario of inconsistent input data on the server [35], so that the PSI protocol can be applied to the protocol of malicious adversaries. In 2012, Huang et al. first proposed PSI computing protocols based on obfuscated circuits [36], which are Bitwise-AND (BWA), Pairwise-Comparisons (PWC), and Sort-Compare-Suffle (SCS) protocols. In 2013, the PSI protocol proposed by Dong et al. [37] used OT technology for the first time. The author used OT technology to ensure the security of the protocol. Pinkas et al. [38] proposed a new PSI protocol based on Hash and random OT protocols and optimized the SCS protocol in [36]. The computational efficiency of the protocol was greatly improved, and the complexity of the algorithm was also reduced. Based on the article [34], Freedman et al. further optimized and improved their scheme in 2014 [39]. Specifically, the scheme uses different hash functions for the client and server when mapping the set elements. In 2018, Pinkas et al. realized PSI based on unintentional pseudorandom function [40] through the circuit. In 2020, Pinkas et al. [12] constructed a PSI protocol with malicious security based on the protocols [41] in the literature. The traditional PSI does not need the assistance of a third party, but in the application, the participants are generally resource-constrained users, who are insufficient in providing sufficient data storage and computing power.

With the development of cloud computing, the PSI protocol based on cloud servers began to develop. The cloud-assisted PSI scheme provides a new optimization method for the existing PSI scheme by the excellent storage and computing capabilities of the cloud server. The cloud-assisted PSI uses the third-party cloud computing framework to complete the calculation and uses the storage and computing resources of the cloud server to enable the protocol to calculate large-scale datasets. Kerschbaum [42] implemented the anti-collusion outsourcing PSI protocol through two single functions, but the method has the risk of brute force cracking. Then, Kerschbaum [43] proposed another kind of cloud-assisted PSI using bloom filter and homomorphic encryption. Liu et al. [19] proposed a relatively simple PSI protocol, but it can disclose the cardinality of set intersection. Abadi et al. [44] implemented the PSI protocol using homomorphic encryption and polynomial interpolation in 2015. This protocol outsources the collection of clients to a third-party server to perform infinite PSI operations. Based on this work, a verifiable cloud outsourcing PSI protocol [45] is proposed to ensure the privacy and integrity of data. Ali et al. [46] proposed an attribute-based private set intersection scheme. The cloud server can calculate the corresponding access rights of the participants. The PSI protocol based on the cloud server can use the computing and storage capabilities of the cloud server, but it has produced the privacy disclosure problem of data outsourcing, and the excessive cost of users in the operation of the protocol is another problem that needs to be solved. Table 1 shows the comparison between our scheme and the existing scheme.

Table 1. Comparison with existing schemes.

	CMPSI	[46]	[47]	[48]	[19]	[42]	[43]
The year	2023	2020	2019	2014	2014	2012	2012
Private against the CSP	52	52	52	52	56	52	52
PSI computation authorization	52	52	52	52	56	52	52
Supports multiple user queries	52	52	52	52	56	56	56
Participants can go offline after uploading data	52	52	56	56	56	56	56
CSP can collude with participants	52	56	56	56	56	56	56

3. Preliminaries

In this section, we first introduce the concept of private set intersection and have an example to better understand the concept. Then, we introduce the cryptosystem MKTFHE used in our system and present the algorithm as an example of a NAND gate. Table 2 lists some of the symbols used in this paper.

Table 2. Notation used.

Notations	Definition
$\lambda$	Security parameter
$\mathbb{Z}$	Integer set
$\mathbb{T}$	(R)LWE over the real torus
$s_i$	Private key of participant i
$({\mathbf{PK}}_i,{\mathbf{BK}}_i,{\mathbf{KS}}_i)$	Public key set of participant i
${\left[\left[x\right]\right]}_{s_i}$	Encrypted data x under $s_i$
${\mathbf{MKHE}}_{\mathbf{NAND}}$	NAND gate in multi-key TFHE
$\mathbf{CMPSI}$	Cloud-assisted multi-party private set intersection

3.1. Private Set Intersection

PSI allows two parties holding sets to compare encrypted versions of these sets to compute the intersection. Let the two parties holding the sets be sender X and receiver Y. The sender and receiver hold datasets of size $N_x$ and $N_y$ respectively, each with a number of bits $\sigma$. In a basic PSI protocol, receiver Y encrypts its own dataset and sends it to sender X. For each of Y’s data, sender X calculates the homomorphic product of the difference with all of its own terms and sends the result to receiver Y. Y decrypts the result of X’s calculation and obtains the final intersection information. The result of the calculation is sent to the receiver Y. Y decrypts the result of X’s computation and obtains the final intersection information. The basic PSI protocol is shown in Figure 1.

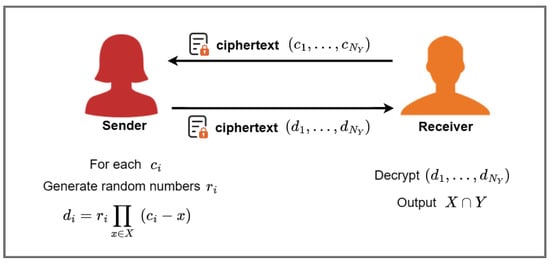
Figure 1. Basic PSI protocol.

In the scheme of this paper, the storage of data and the computation are performed on the cloud server. We construct a new PSI scheme using fully homomorphic encryption. Both the sender and the receiver encrypt the data locally and then send it to the cloud server. Suppose that the sender has encrypted data $a_1,\cdots ,a_{N_X}$ and the receiver has encrypted data $b_1,\cdots ,b_{N_Y}$. Both parties send their encrypted data to the cloud server. On the cloud server, for each data $b_i$ of the receiver, $c_i={\prod }_{0<j\le N_x}\left(b_i-a_j\right)$ is computed. $c_i$ is a Boolean value that represents whether the data $b_i$ of the receiver are in the sender X or not. Figure 2 shows the handshake model of this scheme.

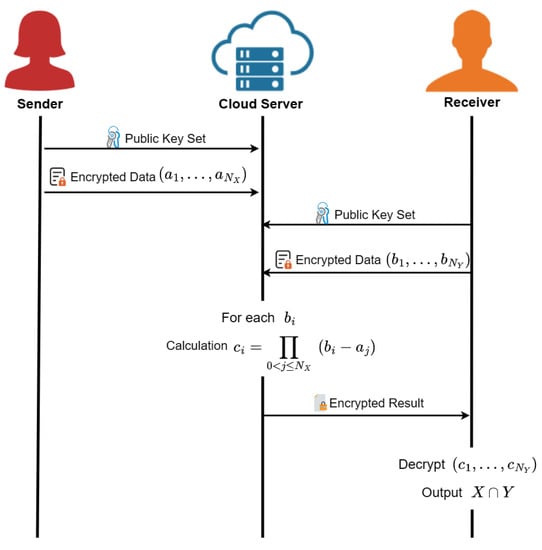
Figure 2. Handshake model.

3.2. MKTFHE Cryptosystem

Homomorphic encryption is the computation of the encrypted data to obtain the encrypted computational result, and the result of the decryption of the obtained encryption result is the same as the result obtained by performing the same operations on the unencrypted plaintext. Fully homomorphic encryption [24,25] is a homomorphic encryption that can satisfy both additive and multiplicative operations. Fully homomorphic encryption over the toru (TFHE) [26] is a type of fully homomorphic encryption that can accomplish fast comparisons and support operations on arbitrary Boolean circuits. TFHE differs from other FHE schemes in that it can be fast bootstrapping to reduce noise during ciphertext operations. In this paper, we use multi-key TFHE [49] to meet the needs of our system. MKTFHE is a multi-key version of TFHE that can compute Boolean circuits on ciphertexts encrypted under different keys, and then performs bootstrapped to refresh the noise as each binary gate is computed. However, the MKTFHE library only implements multi-key homomorphic NAND gates, which cannot meet the needs of our system. The following describes the five components of MKTFHE and gives an example of the homomorphic computation process with a multi-key homomorphic NAND gate.

1.

$\mathbf{Setup}\left(1^{\lambda }\right)$: Takes as input the security parameter $\lambda$ and returns the public parameter ${\mathbf{pp}}^{\mathbf{M}\mathbf{K}\mathbf{T}\mathbf{F}\mathbf{H}\mathbf{E}}$.

(a)

Run $\mathbf{LWE}.\mathbf{Setup}\left(1^{\lambda }\right)$ to generate the LWE parameter ${\mathbf{pp}}^{\mathbf{LWE}}=\left(n,\chi ,\alpha ,B^{\prime },d^{\prime }\right)$. In the LWE parameters, n is the dimension of the LWE secret, $\chi$ is the key distribution of the LWE secret, $\alpha$ is the error rate, $B^{\prime }$ is the decomposition basis, and $d^{\prime }$ is the dimension of the key transformation gadget vector. We use the key-switching gadget vector $g^{\prime }=\left(B^{\prime -1},\dots ,B^{\prime -d^{\prime }}\right)$.

(b)

Run $\mathbf{RLWE}.\mathbf{Setup}\left(1^{\lambda }\right)$ to generate the RLWE parameter ${\mathbf{pp}}^{\mathbf{RLWE}}=(N,\psi ,B,d,\mathbf{a})$. We define N as the dimension of RLWE secret (a power of 2), $\psi$ as the distribution of RLWE secret over R and with error rate $\alpha$, $B\ge 2$ as an integer base, decomposition dimension d, and gadget vector $g=\left(B^{-1},\dots ,B^{-d}\right)$. $\mathbf{a}$ is a uniformly distributed sample over distribution $T^d$.

(c)

Returns the generated public parameter ${\mathbf{pp}}^{\mathbf{M}\mathbf{K}\mathbf{T}\mathbf{F}\mathbf{H}\mathbf{E}}=\left(\mathbf{p}{\mathbf{p}}^{\mathbf{L}\mathbf{W}\mathbf{E}},\mathbf{p}{\mathbf{p}}^{\mathbf{R}\mathbf{L}\mathbf{W}\mathbf{E}}\right)$.

2.

$\mathbf{KeyGen}\left({\mathbf{pp}}^{\mathbf{M}\mathbf{K}\mathbf{T}\mathbf{F}\mathbf{H}\mathbf{E}}\right)$: Each participant generates its keys independently. Take the public parameter ${\mathbf{pp}}^{\mathbf{M}\mathbf{K}\mathbf{T}\mathbf{F}\mathbf{H}\mathbf{E}}$ as input and return the key ${\mathbf{s}}_i$ and the public key set $\left(\mathbf{P}{\mathbf{K}}_i,\mathbf{B}{\mathbf{K}}_i,\mathbf{K}{\mathbf{S}}_i\right)$.

(a)

Generate the LWE secret ${\mathbf{s}}_i\leftarrow \mathbf{LWE}.\mathbf{KeyGen}\left(\right)$. This step is only for sampling the key from distribution $\chi$.

(b)

Run $\left(z_i,{\mathbf{b}}_i\right)\leftarrow \mathbf{RLWE}.\mathbf{KeyGen}\left(\right)$, and set the public key to ${\mathbf{PK}}_i={\mathbf{b}}_i$. Sample z from distribution $\psi$, and then, set $\mathbf{z}=(1,z)$. Take an error vector $\mathbf{e}$ from $D_{\alpha }^d$ and calculate the public key $\mathbf{b}=-z·\mathbf{a}+\mathbf{e}(mod1)$. For $z_i=z_{1,0}+z_{i,1}X+\dots +z_{i,N-1}{X}^{N-1}$, note ${\mathbf{z}}_i^{*}=\left(z_{i,0},-z_{i,N-1},\dots ,z_{i,1}\right)\in {\mathbb{Z}}^N$.

(c)

For $j\in \left[n\right]$, generate $\left({\mathbf{d}}_{i,j},{\mathbf{F}}_{i,j}\right)\leftarrow \mathbf{RLWE}.\mathbf{UniEnc}\left(s_{i,j},z_i\right)$, this step is to encrypt the LWE secret using the RLWE secret. In addition, set the bootstrap key to ${\mathbf{BK}}_i={\left\{\left({\mathbf{d}}_{i,j},{\mathbf{F}}_{i,j}\right)\right\}}_{j\in \left[n\right]}$. Taking a random value r from $\psi$, one can think of $\mathbf{d}$ as the LWE key s under the encryption of the random value r and $\mathbf{F}$ as the random value r under the encryption of the RLWE key z.

(d)

Generate a key conversion key $\mathbf{KS}\leftarrow \mathbf{LWE}.\mathbf{KSGen}\left(z_i^{*},{\mathbf{s}}_i\right)$, capable of converting an LWE ciphertext corresponding to $\mathbf{t}\in {\mathbb{Z}}^N$ into another LWE ciphertext for the same message under $\mathbf{s}\in {\mathbb{Z}}^N$ encryption.

(e)

Returns key ${\mathbf{s}}_i$, a triple $\left(\mathbf{P}{\mathbf{K}}_i,\mathbf{B}{\mathbf{K}}_i,\mathbf{K}{\mathbf{S}}_i\right)$ of public keys, public key, bootstrap key and key transformation key, respectively.

3.

$\mathbf{Enc}\left(m\right)$: The data m to be encrypted are taken as input, and return TLWE ciphertext $\left[\left[m\right]\right]=(b,\mathbf{a})\in {\mathbb{T}}^{n+1}$ satisfies $b+⟨\mathbf{a},\mathbf{s}⟩\approx \frac{1}{4}m(mod1)$.

(a)

Using standard LWE encryption, uniformly sample from ${\mathbb{T}}^n$ to obtain $\mathbf{a}$ as the mask and sample from $D_{\alpha }$ to obtain e as the error.

(b)

Output ciphertext $\left[\left[m\right]\right]=(b,\mathbf{a})\in {\mathbb{T}}^{n+1}$, where $b+⟨\mathbf{a},\mathbf{s}⟩\approx \frac{1}{4}m(mod1)$.

4.

$\mathbf{Dec}(\left[\left[m\right]\right],{\left\{{\mathbf{s}}_i\right\}}_{i\in \left[k\right]})$: Takes as input the TLWE ciphertext $\left[\left[m\right]\right]=\left(b,{\mathbf{a}}_1,\dots ,{\mathbf{a}}_k\right)\in {\mathbb{T}}^{kn+1}$ with a set of keys $\left({\mathbf{s}}_1,\dots ,{\mathbf{s}}_k\right)$ and returns the decrypted message m which minimizes $\mid b+{\sum }_{i=1}^k⟨{\mathbf{a}}_i,{\mathbf{s}}_i⟩-\frac{1}{4}m\mid$.

(a)

Input $\left[\left[m\right]\right]=\left(b,{\mathbf{a}}_1,\dots ,{\mathbf{a}}_k\right)\in {\mathbb{T}}^{kn+1}$ with a set of keys $\left({\mathbf{s}}_1,\dots ,{\mathbf{s}}_k\right)$.

(b)

Returns the bit $m\in \{0,1\}$ that minimizes $\mid b+{\sum }_{i=1}^k⟨{\mathbf{a}}_i,{\mathbf{s}}_i⟩-\frac{1}{4}m\mid$.

5.

$\mathbf{NAND}(\left[\left[m_1\right]\right],\left[\left[m_2\right]\right],{\left\{\left(\mathbf{P}{\mathbf{K}}_i,\mathbf{B}{\mathbf{K}}_i,\mathbf{K}{\mathbf{S}}_i\right)\right\}}_{i\in \left[k\right]})$: Takes two TLWE ciphertexts and the public key as input. Expand $\left[\left[m_1\right]\right]\in {\mathbb{T}}^{k_{1}n+1}$ and $\left[\left[m_2\right]\right]\in {\mathbb{T}}^{k_{1}n+1}$ to $\left[\left[m_1^{\prime }\right]\right],\left[\left[m_2^{\prime }\right]\right]\in {\mathbb{T}}^{kn+1}$ and evaluate the gate homomorphically on encrypted bits. Then the algorithm evaluates the decryption circuit of the TLWE ciphertext and execute the multi-key switching algorithm. Finally, returning the TLWE ciphertext of the same message under joint key encryption.

(a)

Given two ciphertexts $\left[\left[m_1\right]\right]\in {\mathbb{T}}^{k_{1}n+1}$ and $\left[\left[m_2\right]\right]\in {\mathbb{T}}^{k_{1}n+1}$, let k be the number of participants, associated with either $\left[\left[m_1\right]\right]$ or $\left[\left[m_2\right]\right]$. For a public key set, ${\mathbf{PK}}_i={\mathbf{b}}_i$ represents the public key, ${\mathbf{BK}}_i={\left\{\left({\mathbf{d}}_{i,j},{\mathbf{F}}_{i,j}\right)\right\}}_{j\in \left[n\right]}$ represents the bootstrap key, and ${\mathbf{KS}}_i$ represents the key transformation key of the j-th participant. Expand ciphertext $\left[\left[m_1\right]\right]$ and $\left[\left[m_2\right]\right]$ to ${\left[\left[m_1\right]\right]}^{\prime },{\left[\left[m_2\right]\right]}^{\prime }\in {\mathbb{T}}^{kn+1}$, i.e., the same message under joint key $\overline{\mathbf{s}}=\left({\mathbf{s}}_1,\dots ,{\mathbf{s}}_k\right)\in {\mathbb{Z}}^{kn}$ encryption. The process of expansion is the process of rearrangement, and 0 is put into the empty slot. Using the expanded ciphertext to perform the calculations. Only the calculation of NAND gate is supported in the document.

(b)

Use the Mux gate to implement the main calculation, for $i\in \left[k\right]$, let ${\tilde{\mathbf{a}}}_i={\left({\tilde{a}}_{i,j}\right)}_{j\in \left[n\right]}$. For $i\in \left[k\right]$ and $j\in \left[n\right]$, recursively compute $\left[\left[\mathbf{c}\right]\right]\leftarrow \left[\left[\mathbf{c}\right]\right]+\mathbf{RLWE}.\mathbf{Prod}\left(\left[\left[\mathbf{c}\right]\right]·X^{{\tilde{a}}_{ij}}-\left[\left[\mathbf{c}\right]\right],\left({\mathbf{d}}_{i,j},{\mathbf{F}}_{i,j}\right),{\left\{{\mathbf{b}}_l\right\}}_{l\in \left[k\right]}\right)$, where $\mathbf{RLWE}.\mathbf{Prod}\left(\left[\left[\mathbf{c}\right]\right],\left({\mathbf{d}}_i,{\mathbf{F}}_i\right),{\left\{{\mathbf{b}}_j\right\}}_{j\in \left[k\right]}\right)$ is a hybrid product algorithm that multiplies a single encrypted ciphertext $({\mathbf{d}}_i,{\mathbf{F}}_i)$ by a multi-key RLWE ciphertext $\left[\right[c\left]\right]$.

(c)

For $\left[\left[\mathbf{c}\right]\right]=\left(c_0,c_1,\dots ,c_k\right)\in T^{k+1}$, let $b^{*}$ be a constant term of $c_0$ and for $i\in \left[k\right]$, let ${\mathbf{a}}_i^{*}$ be a vector of coefficients of $c_i$. Compute the LWE ciphertext ${\left[\left[m\right]\right]}^{*}=\left(b^{*},{\mathbf{a}}_1^{*},\dots ,{\mathbf{a}}_k^{*}\right)\in {\mathbb{T}}^{kn+1}$. Finally a multi-key key conversion algorithm is executed and returns the ciphertext ${\left[\left[m\right]\right]}^{″}\leftarrow \mathbf{LWE}.\mathbf{MKSwitch}\left({\left[\left[m\right]\right]}^{*},{\left\{\mathbf{K}{\mathbf{S}}_i\right\}}_{i\in \left[k\right]}\right)$, where $\mathbf{LWE}.\mathbf{MKSwitch}\left({\left[\left[m\right]\right]}^{*},{\left\{\mathbf{K}{\mathbf{S}}_i\right\}}_{i\in \left[k\right]}\right)$ inputs the expanded ciphertext and a series of key conversion keys, returning the ciphertext of the same message under joint key encryption.

4. System Model and Design Goal

4.1. Problem Formulation

Suppose the receiver Y has a dataset $T_Y$, and Y wants to know their intersection with other data owners but does not want to expose more information. The data owners encrypt their datasets separately and send them to the cloud server. The cloud server can store this encrypted information but cannot decrypt it. Data receiver Y encrypts its data and uploads it to the cloud server, which executes privacy intersection and obtains the intersection information of dataset $T_Y$ with other datasets. The cloud server computes and returns the cryptographic result to receiver Y. Y decrypts the intersection result and obtains the intersection information. Note that each data owner including the data receiver has their separate key to encrypt the data.

4.2. System Model

In Section 3.1, we mention the flow of the basic PSI protocol, in which the sender interacts directly with the receiver for information. Unlike the basic PSI protocol, our system consists of four entities, which are Parameter Generation Center (PGC), Cloud Server (CS), Data Receiver (DR), and Data Owners (DOs). DO owns its own dataset and is able to let other participants obtain information about the intersection of the dataset but does not want to expose more information. DR wants to query the intersection of its own dataset with the dataset of other participants and does not want to expose more information. Specifically, PGC is responsible for generating public parameters in the system and sending them to other entities. CS can store a large amount of data and has excellent computing resources. DR needs to query the intersection. DOs provide their encrypted data to CS. Note that in our system, the data owners can be multiple participants. The general model of our private set intersection system is shown in Figure 3.

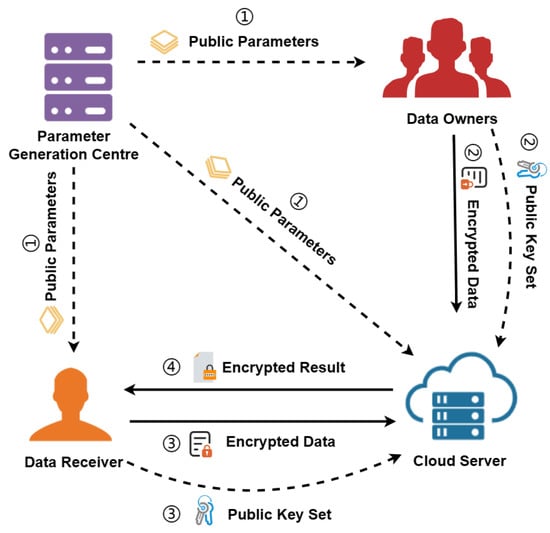
Figure 3. System model.

1.

PGC: PGC generates public parameters for our system and sends them to each entity involved in the computation (See ➀).

2.

CS: CS has huge storage resources to store the encrypted data of the participating parties. At the same time, CS has large enough computing power to satisfy the intersection of the datasets of the participating parties.

3.

DR: DR generates its own private key and public key set using public parameters, encrypts its own data using the private key and sends it to CS (See ➂), and receives the computation results sent by CS (See ➃).

4.

DOs: Each DO generates its own private key and public key set using public parameters, encrypts its own dataset using the private key, and sends it to CS (See ➁).

Please note that in our system, the participants do not need to be online all the time. Since CS can store the encrypted data, the DOs can go offline after they send their encrypted data to CS. Similarly, DR can be offline after sending data until CS returns the calculation results. In our scheme, DO can be used as DR for frequent item set queries, and the DR can query the intersection information with multiple DOs to achieve multi-user query.

4.3. Threat Model

In our system model, the participating entities are curious but honest individuals. Curious means that the server and the participants try to use existing resources and data to obtain the data of other participants and are curious about the data of other entities; honest means that the server and the participants do not falsify the experimental data and follow the developed protocols to complete the computation. $\mathcal{A}$ is the active adversary we introduce to obtain the real data from other entities. Specifically, $\mathcal{A}$ desires to obtain the real data of DOs and DR. We assume that adversary $\mathcal{A}$ has the following capabilities.

1.

$\mathcal{A}$ can obtain all the data that passes through the public channel.

2.

$\mathcal{A}$ may collude with CS. Try to obtain the original values of the encrypted data uploaded by DOs and DR.

3.

$\mathcal{A}$ may be a DR used to obtain its dataset information, the cryptographic query results returned by the CS, and the encryption and decryption capabilities of the DR.

4.

$\mathcal{A}$ may be a DO used to obtain its dataset information and encryption and decryption capabilities.

Note that in our threat model, the attacking adversary $\mathcal{A}$ can be a DR. Since the joint key of multiple participants must be used in decryption to decrypt the computed result of CS, the final decryption result is also not available when $\mathcal{A}$ has only the key of DR. Unlike existing schemes when the attacking adversary $\mathcal{A}$ is a CSP, $\mathcal{A}$ can collude with DR or DO. In our scheme, decryption requires the keys of all participants to perform; thus, CSP colluding with some DR or DO still cannot decrypt the computation results.

4.4. Design Goal

According to the system model and threat model proposed above, the design objectives of this paper are as follows.

1.

Data privacy: the original data of DR and the query intersection result as well as the original dataset of DOs cannot be revealed to adversary $\mathcal{A}$.

2.

Calculation accuracy: The accuracy of the calculation results of the system cannot be reduced compared with other methods.

3.

Low overhead: The time and upload overhead of the calculation cannot be too large compared with other methods.

4.

Offline participant: The participant should be able to go offline after encrypting the data and uploading it to ensure the scalability of the system.

5. Cloud-Assisted Multi-Party Private Set Intersection

In this section, we first introduce the initialization of the system. Then, we design the secure computing sub-protocol based on MKTFHE. Finally, we describe our private set intersection scheme.

5.1. System Initialization

Our system can satisfy the DR to query the information of its intersection with multiple participants, and we assume that there is a DR and n DOs. First, PGC generates public parameters for each participant and the cloud server and sends the public parameters to CS, DR, and n DOs. Then, each entity that receives the public parameters generates its own public key set $\left(\mathbf{P}\mathbf{K},\mathbf{B}\mathbf{K},\mathbf{K}\mathbf{S}\right)$ and private key s based on the public parameters.

5.2. Security Protocol Design

In this paper, four secure computation protocols are proposed to help complete the privacy-seeking intersection, which is a secure AND gate computation protocol (${\mathbf{SC}}_{\mathbf{AND}}$), secure OR gate computation protocol (${\mathbf{SC}}_{\mathbf{OR}}$), secure XNOR computation protocol (${\mathbf{SC}}_{\mathbf{XNOR}}$), and secure comparison protocol ($\mathbf{SCP}$).

5.2.1. Secure AND Gate Computation Protocol

We implement the AND operation between two MKLwe samples. We implement the addition between multi-key Lwe samples ($\mathbf{MKlweAddTo}$) to implement this secure computation protocol. Suppose CS has two MKLwe samples $ca$ and $cb$: initialize an intermediate sample $temp$, add $ca$ and $cb$ using $\mathbf{MKlweAddTo}$ twice, and finally return the result to $res$ (Algorithm 1).

Algorithm 1 Secure AND gate computation protocol (${\mathbf{SC}}_{\mathbf{AND}}$).

Input:  MKLwe Sample $ca$, $cb$. Output:  MKLwe Sample $res$. 1: CS initializes $temp$ using the public parameter $\mathbf{pp}$ to hold the intermediate variable LWE sample. 2: $AndConst=modSwitchToTorus32(-1,8)$ 3: $temp\leftarrow \mathbf{MKlweNoiselessTrivial}(AndConst,\mathbf{pp})$ 4: $temp\leftarrow \mathbf{MKlweAddTo}(temp+ca)$ 5: $res\leftarrow \mathbf{MKlweAddTo}(temp+cb)$

5.2.2. Secure OR Gate Computation Protocol

We implement the OR operation between two MKLwe samples. As with ${\mathbf{SC}}_{\mathbf{AND}}$ above, we use the addition $\mathbf{MKlweAddTo}$ between multi-key Lwe samples to implement this secure computation protocol. Suppose CS has two MKLwe samples $ca$ and $cb$, initialize an intermediate sample $temp$, add $ca$ and $cb$ using $\mathbf{MKlweAddTo}$ twice respectively, and finally, return the result to $res$ to obtain the result of the OR gate operation between $ca$ and $cb$ (Algorithm 2).

Algorithm 2 Secure OR gate computation protocol (${\mathbf{SC}}_{\mathbf{OR}}$).

Input:  MKLwe Sample $ca$, $cb$. Output:  MKLwe Sample $res$. 1: CS initializes $temp$ using the public parameter $\mathbf{pp}$ to hold the intermediate variable LWE sample. 2: $ORConst=modSwitchToTorus32(1,8)$ 3: $temp\leftarrow \mathbf{MKlweNoiselessTrivial}(ORConst,\mathbf{pp})$ 4: $temp\leftarrow \mathbf{MKlweAddTo}(temp+ca)$ 5: $res\leftarrow \mathbf{MKlweAddTo}(temp+cb)$

5.2.3. Secure XNOR Gate Computation Protocol

We implement the XNOR operation between two MKLwe samples. We implement this secure computation protocol using the addition and multiplication of multi-key Lwe samples $\mathbf{MKlweAddMulTo}$. Suppose CS has two MKLwe samples $ca$ and $cb$: initialize an intermediate sample $temp$, add $2\ast ca$ and $2\ast cb$ using $\mathbf{MKlweAddMulTo}$ twice, return the result to $temp$ to obtain the XOR gate operation result of $ca$ and $cb$, and use the multi-key homomorphic NOT gate ${\mathbf{SC}}_{\mathbf{NOT}}$ once to obtain the XNOR gate operation result. Note that in the cryptographic scheme we use, MKTFHE, the computation of the NOT gate does not require bootstrapping operations; thus, the computation overhead is very small (Algorithm 3).

Algorithm 3 Secure XNOR gate computation protocol (${\mathbf{SC}}_{\mathbf{XNOR}}$).

Input:  MKLwe Sample $ca$, $cb$. Output:  MKLwe Sample $res$. 1: CS initializes $temp$ using the public parameter $\mathbf{pp}$ to hold the intermediate variable LWE sample. 2: $XNORConst=modSwitchToTorus32(1,8)$ 3: $temp\leftarrow \mathbf{MKlweNoiselessTrivial}(XNORConst,\mathbf{pp})$ 4: $temp\leftarrow \mathbf{MKlweAddMulTo}(temp+2*ca)$ 5: $temp\leftarrow \mathbf{MKlweAddMulTo}(temp+2*cb)$ 6: $res\leftarrow {\mathbf{SC}}_{\mathbf{NOT}}\left(temp\right)$

5.2.4. Secure Comparison Protocol

$\mathbf{SCP}$ is important in our protocol and is used to determine whether the two input ciphertext vectors are equal or not. Suppose DR has its own encrypted data ${\left[\left[\mathbf{x}\right]\right]}_{s_{DR}}=({\left[\left[x_1\right]\right]}_{s_{DR}},\dots ,{\left[\left[x_n\right]\right]}_{s_{DR}})$ sent to CS and DO has its own encrypted data ${\left[\left[\mathbf{y}\right]\right]}_{s_{DO}}=({\left[\left[y_1\right]\right]}_{s_{DO}},\dots ,$${\left[\left[y_n\right]\right]}_{s_{DO}})$ also sent to CS, where $s_{DR}$ and $s_{DO}$ are the private keys of DR and DO, respectively. For each of ${\left[\left[\mathbf{x}\right]\right]}_{s_{DR}}=({\left[\left[x_1\right]\right]}_{s_{DR}},\dots ,{\left[\left[x_n\right]\right]}_{s_{DR}})$ and ${\left[\left[\mathbf{y}\right]\right]}_{s_{DO}}=({\left[\left[y_1\right]\right]}_{s_{DO}},\dots ,{\left[\left[y_n\right]\right]}_{s_{DO}})$, the protocol performs ${\mathbf{SC}}_{\mathbf{XNOR}}$ and ${\mathbf{SC}}_{\mathbf{AND}}$ protocols to finally obtain a ciphertext with a Boolean value (Algorithm 4).

Algorithm 4:Secure Comparison Protocol ($\mathbf{SCP}$).

Input:  Encrypted data vectors ${\left[\left[\mathbf{x}\right]\right]}_{s_{DR}}=({\left[\left[x_1\right]\right]}_{s_{DR}},\dots ,{\left[\left[x_n\right]\right]}_{s_{DR}})$,${\left[\left[\mathbf{y}\right]\right]}_{s_{DO}}=({\left[\left[y_1\right]\right]}_{s_{DO}},\dots ,{\left[\left[y_n\right]\right]}_{s_{DO}})$. Output:  Encrypted Boolean values ${\left[\left[z\right]\right]}_{s_i}$. 1: CS initializes the intermediate data vector $\left[\left[\mathbf{v}\right]\right]=(\left[\left[v_1\right]\right],\dots ,\left[\left[v_n\right]\right])$ using the public parameter $\mathbf{pp}$. 2: for $k=0$ to $n-1$ do 3:      ${\left[\left[v_k\right]\right]}_{s_i}\leftarrow {\left[\left[x_k\right]\right]}_{s_{DR}}\mathrm{XNOR}{\left[\left[y_k\right]\right]}_{s_{DO}}$ 4:      ${\left[\left[z\right]\right]}_{s_i}\leftarrow {\left[\left[v_k\right]\right]}_{s_i}\mathrm{AND}{\left[\left[z\right]\right]}_{s_i}$ 5: end for

5.3. Private Set Intersection

CMPSI is performed by CS, DR, and DOs working together. Now DR wants to obtain the intersection information of their dataset and DOs dataset. First DOs encrypt their dataset with their own private key $s_{DO}$, send the encrypted dataset $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$ with the public key set $\left(\mathbf{P}{\mathbf{K}}_{s_{DO}},\mathbf{B}{\mathbf{K}}_{s_{DO}},\mathbf{K}{\mathbf{S}}_{s_{DO}}\right)$ to CS, and then they can go offline. DR encrypts the dataset with its own private key $s_{DR}$ and then sends the encrypted dataset $B_{DR}=\left\{{\left[\left[{\mathbf{b}}_{\mathbf{1}}\right]\right]}_{s_{DR}},{\left[\left[{\mathbf{b}}_{\mathbf{2}}\right]\right]}_{s_{DR}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{n}}\right]\right]}_{s_{DR}}\right\}$ with its public key set $\left(\mathbf{P}{\mathbf{K}}_{s_{DR}},\mathbf{B}{\mathbf{K}}_{s_{DR}},\mathbf{K}{\mathbf{S}}_{s_{DR}}\right)$ to CS, and then, it can be offline until CS completes the calculation. CS receives the encrypted dataset sent by DOs and DR, saves the data, and performs the secure computation in a secure environment. Finally, DR receives the encryption result calculated by CS and decrypts it using the joint key to obtain the intersection. Let there be m items in the encrypted dataset $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$ of DOs with k Boolean values in each item, and n items in the encrypted dataset $B_{DR}=\left\{{\left[\left[{\mathbf{b}}_{\mathbf{1}}\right]\right]}_{s_{DR}},{\left[\left[{\mathbf{b}}_{\mathbf{2}}\right]\right]}_{s_{DR}},\dots ,{\left[\left[{\mathbf{b}}_{\mathbf{n}}\right]\right]}_{s_{DR}}\right\}$ of DR with k Boolean values in each item.

S1(DOs): Each DO encrypts its dataset using its own key $s_{DO}$ generated by the public parameter $\mathbf{pp}$ issued by PGC and sends it to CS. CS stores the encrypted dataset of all DOs, and for item i of dataset $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$, we have ${\left[\left[{\mathbf{a}}_{\mathbf{i}}\right]\right]}_{s_{DO}}=({\left[\left[a_1\right]\right]}_{s_{DO}},\dots ,{\left[\left[a_k\right]\right]}_{s_{DO}})$.

S2(DR): DR uses the public parameter $\mathbf{pp}$ to generate its own key $s_{DR}$ to encrypt its dataset and sends it to CS. CS uses DR’s encrypted database for secure computation and has ${\left[\left[{\mathbf{b}}_{\mathbf{j}}\right]\right]}_{s_{DR}}=({\left[\left[b_1\right]\right]}_{s_{DR}},\dots ,{\left[\left[b_k\right]\right]}_{s_{DR}})$ for item j of dataset $B_{DR}=\left\{{\left[\left[{\mathbf{b}}_{\mathbf{1}}\right]\right]}_{s_{DR}},{\left[\left[{\mathbf{b}}_{\mathbf{2}}\right]\right]}_{s_{DR}},\dots ,{\left[\left[{\mathbf{b}}_{\mathbf{n}}\right]\right]}_{s_{DR}}\right\}$.

S3(CS): CS receives the encrypted data message $B_{DR}=\left\{{\left[\left[{\mathbf{b}}_{\mathbf{1}}\right]\right]}_{s_{DR}},{\left[\left[{\mathbf{b}}_{\mathbf{2}}\right]\right]}_{s_{DR}},\dots ,{\left[\left[{\mathbf{b}}_{\mathbf{n}}\right]\right]}_{s_{DR}}\right\}$ from DR and the encrypted data message $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$ from DO. For $j\in \{1,2,\dots ,n\}$ and $i\in \{1,2,\dots ,m\}$, each item ${\left[\left[{\mathbf{b}}_{\mathbf{j}}\right]\right]}_{s_{DR}}=({\left[\left[b_1\right]\right]}_{s_{DR}},\dots ,{\left[\left[b_k\right]\right]}_{s_{DR}})$ in $B_{DR}=\left\{{\left[\left[{\mathbf{b}}_{\mathbf{1}}\right]\right]}_{s_{DR}},{\left[\left[{\mathbf{b}}_{\mathbf{2}}\right]\right]}_{s_{DR}},\dots ,{\left[\left[{\mathbf{b}}_{\mathbf{n}}\right]\right]}_{s_{DR}}\right\}$ performs $\mathbf{SCP}$ with each item ${\left[\left[{\mathbf{a}}_{\mathbf{i}}\right]\right]}_{s_{DO}}=({\left[\left[a_1\right]\right]}_{s_{DO}},\dots ,{\left[\left[a_k\right]\right]}_{s_{DO}})$ in $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$, i.e., $\mathbf{SCP}({\left[\left[{\mathbf{a}}_{\mathbf{i}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{b}}_{\mathbf{j}}\right]\right]}_{s_{DR}})$. The result ${\left[\left[{\mathbf{g}}_{\mathbf{i}}\right]\right]}_s=({\left[\left[g_1\right]\right]}_s,\dots ,{\left[\left[g_k\right]\right]}_s)$ is obtained as the result of whether the current ${\left[\left[{\mathbf{b}}_{\mathbf{j}}\right]\right]}_{s_{DR}}=({\left[\left[b_1\right]\right]}_{s_{DR}},\dots ,{\left[\left[b_k\right]\right]}_{s_{DR}})$ is the same as each item in $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$.

S4(CS): For each computed ${\left[\left[{\mathbf{g}}_{\mathbf{i}}\right]\right]}_s=({\left[\left[g_1\right]\right]}_s,\dots ,{\left[\left[g_k\right]\right]}_s)$, CS runs ${\mathbf{SC}}_{\mathbf{OR}}$ to obtain ${\left[\left[{\mathbf{c}}_{\mathbf{j}}\right]\right]}_s=({\left[\left[c_1\right]\right]}_s,\dots ,{\left[\left[c_k\right]\right]}_s)$. ${\left[\left[{\mathbf{c}}_{\mathbf{j}}\right]\right]}_s=({\left[\left[c_1\right]\right]}_s,\dots ,{\left[\left[c_k\right]\right]}_s)$ is a cryptographic Boolean value indicating whether each item in $B_{DR}=\left\{{\left[\left[{\mathbf{b}}_{\mathbf{1}}\right]\right]}_{s_{DR}},{\left[\left[{\mathbf{b}}_{\mathbf{2}}\right]\right]}_{s_{DR}},\dots ,{\left[\left[{\mathbf{b}}_{\mathbf{n}}\right]\right]}_{s_{DR}}\right\}$ exists in $A_{DO}=\left\{{\left[\left[{\mathbf{a}}_{\mathbf{1}}\right]\right]}_{s_{DO}},{\left[\left[{\mathbf{a}}_{\mathbf{2}}\right]\right]}_{s_{DO}},\dots ,{\left[\left[{\mathbf{a}}_{\mathbf{m}}\right]\right]}_{s_{DO}}\right\}$. A value of 1 means it exists and 0 means it does not.

S5 (CS): For $j\in \{1,2,\dots ,n\}$, execute S4, and send the calculated result $C=\{{\left[\left[{\mathbf{c}}_{\mathbf{1}}\right]\right]}_s$, ${\left[\left[{\mathbf{c}}_{\mathbf{2}}\right]\right]}_s,\dots ,{\left[\left[{\mathbf{c}}_{\mathbf{n}}\right]\right]}_s\}$ to DR.

S6 (DR): Receive the calculation result from $C=\left\{{\left[\left[{\mathbf{c}}_{\mathbf{1}}\right]\right]}_s,{\left[\left[{\mathbf{c}}_{\mathbf{2}}\right]\right]}_s,\dots ,{\left[\left[{\mathbf{c}}_{\mathbf{n}}\right]\right]}_s\right\}$ sent by CS and decrypt it using the joint key to obtain the result.

Please note that in our PSI scheme, the dense state computation is performed by FHE cryptography. All the calculations are performed on the cloud server, and the data on the cloud server are all cryptographic data, so that the privacy of the participants is protected. During the calculation process, the DR does not obtain any information other than its own information and the query result. The DOs do not obtain any information other than their own information and do not expose their information to other participants. The result of the CS calculation is in cryptographic form and cannot be decrypted by the participants except by the DR, which protects the privacy of the calculation result.

6. Security Analysis

In this section, we prove that our scheme is secure under a semi-honest model. We will prove the security of the MKTFHE cryptosystem, ${\mathbf{SC}}_{\mathbf{AND}}$, ${\mathbf{SC}}_{\mathbf{OR}}$, ${\mathbf{SC}}_{\mathbf{XOR}}$, $\mathbf{SCP}$ and PSI schemes separately. We first present the security of the semi-honest model below.

Definition 1 

(Security of the semi-honest model). According to protocol π, let $a_i$ be the input of participant $P_i$ and $b_i$ be the output of $P_i$. ${REAL}_i^{\Pi }\left(\pi \right)$ is the viewpoint of $P_i$ when protocol π is actually executed. ${IDEAL}_i^{\Pi }\left(\pi \right)$ is the viewpoint of $P_i$, simulated by $a_i$ and $b_i$, executed in the ideal world of protocol π. If ${REAL}_i^{\Pi }\left(\pi \right)$ is computationally indistinguishable from ${IDEAL}_i^{\Pi }\left(\pi \right)$, then protocol π is secure in the semi-fair model [50].

Note that in our protocols, the execution image usually consists of the exchanged data and the information that can be computed from these data. It follows from Definition (1) that when proving the security of these protocols, the image we simulate should be indistinguishable from the actual execution image when we compute it.

6.1. Security of MKTFHE Cryptosystem

Privacy of $\mathbf{LWE}\mathbf{Assumption}$: The j-th component ${\mathbf{K}}_j$ of a key-switching key $KS={\left\{K_j\right\}}_{j\in \left[N\right]}$ from $\mathbf{t}\in {\mathbb{Z}}^N$ to $\mathbf{s}\in {\mathbb{Z}}^N$ is generated by adding $t_j·{\mathbf{g}}^{\prime }$ to the first column of the ${\mathbb{T}}^{d^{\prime }\times (n+1)}$ matrix, the rows of which are instances of LWE under the secret $\mathbf{s}$. Therefore, $\mathrm{KS}\leftarrow \mathbf{LWE}.\mathbf{KSGen}(\mathbf{t},\mathbf{s})$ is computationally indistinguishable from a uniform distribution over ${\left({\mathbb{T}}^{d^{\prime }\times (n+1)}\right)}^N$ where LWE assumes a parameter of $(n,\chi ,\beta )$ and s is sampled according to $\chi$.

Privacy of $\mathbf{RLWE}\mathbf{Assumption}$: Under the assumption that the parameter is $(N,\psi ,\alpha )$, a uniform distribution over $T^{d\times 5}$ is computationally indistinguishable from the distribution ${\mathcal{D}}_0=\{(\mathbf{a},\mathbf{b},\mathbf{d},\mathbf{F}):{\mathbf{pp}}^{\mathbf{RLWE}}\leftarrow \mathbf{RLWE}·\mathbf{Setup}\left(1^{\lambda }\right),(z,\mathbf{b})\leftarrow \mathbf{RLWE}.\mathbf{KeyGen}\left(\right),(\mathbf{d},\mathbf{F})\leftarrow \mathbf{RLWE}·\mathbf{UniEnc}(\mu ,z)\}$ for any $\mu \in R$. We consider the following distribution: First, we transform $\mathbf{F}=\left[{\mathbf{f}}_0\mid {\mathbf{f}}_1\right]$ and $(\mathbf{b},\mathbf{a})$ into independent uniform distributions of $T^{d\times 2}$ using the RLWE assumption of a secret z. Therefore, ${\mathcal{D}}_0$ is indistinguishable from ${\mathcal{D}}_1$ in terms of calculation. ${\mathcal{D}}_1=\{(\mathbf{a},\mathbf{b},\mathbf{d},\mathbf{F}):\mathbf{a},\mathbf{b}\leftarrow U\left(T^d\right),$ $\mathbf{F}\leftarrow U\left(T^{d\times 2}\right),r\left.\leftarrow \psi ,{\mathbf{e}}_1\leftarrow D_{\alpha }^d,\mathbf{d}=r·\mathbf{a}+\mu ·\mathbf{g}+{\mathbf{e}}_1(mod1)\right\}.$ Then, $\mathbf{d}$ is made uniformly distributed using the RLWE assumption with a secret of r. Therefore, ${\mathcal{D}}_1$ is indistinguishable from the distribution ${\mathcal{D}}_2$. ${\mathcal{D}}_2=\left\{(\mathbf{a},\mathbf{b},\mathbf{d},\mathbf{F}):\mathbf{a},\mathbf{b},\mathbf{d}\leftarrow U\left(T^d\right),\mathbf{F}\leftarrow U\left(T^{d\times 2}\right)\right\}.$ Since ${\mathcal{D}}_2$ is independent from $\mu$, our RLWE scheme is semantically private.

In summary, under the (R)LWE assumption, our cryptosystem is semantically private; thus, we can appropriately choose parameters ${\mathbf{pp}}^{\mathbf{LWE}}$ and ${\mathbf{pp}}^{\mathbf{RLWE}}$ to achieve a security level of at least $\lambda$-bit.

6.2. Security of Secure Computing Protocols

In this section, we demonstrate the security of our secure computing subprotocols, including ${\mathbf{SC}}_{\mathbf{AND}}$, ${\mathbf{SC}}_{\mathbf{OR}}$, ${\mathbf{SC}}_{\mathbf{XOR}}$ and $\mathbf{SCP}$.

Theorem 1.

The ${\mathbf{SC}}_{\mathbf{AND}}$ proposed is secure under the semi-honest model.

Proof of Theorem 1.

We use ${REAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{AND}}\right)$ to denote the execution view in the real world of the of CS, where it is specified as ${REAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{AND}}\right)=$$\left\{\right[\left[ca\right]],[\left[cb\right]],[\left[AndConst\right]],[\left[temp\right]],[\left[res\right]\left]\right\}$. $\left[\right[AndConst\left]\right]$ is obtained from $\left[\right[-1\left]\right]$ and $\left[\right[8\left]\right]$ by $modSwitchToTorus32$. $\left[\right[temp\left]\right]$ is obtained from $\left[\right[AndConst\left]\right]$ and $\left[\right[ca\left]\right]$ by $\mathbf{MKlweAddTo}$ and $\mathbf{MKlweNoiselessTrival}$. We assume that ${IDEAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{AND}}\right)=$$\{\left[\left[c{a}^{\prime }\right]\right],\left[\left[c{b}^{\prime }\right]\right],\left[\left[tem{p}^{\prime }\right]\right],\left[\left[re{s}^{\prime }\right]\right],\left[\left[AndCons{t}^{\prime }\right]\right]\}$ is the execution view of the simulation in the ideal world, where $\left[\left[c{a}^{\prime }\right]\right]$, $\left[\left[c{b}^{\prime }\right]\right]$, $\left[\left[tem{p}^{\prime }\right]\right]$, $\left[\left[re{s}^{\prime }\right]\right]$ and $\left[\left[AndCons{t}^{\prime }\right]\right]$ are chosen randomly from ${\mathbb{T}}^{n+1}$. The semantic privacy of our encryption scheme makes $\left[\right[ca\left]\right]$, $\left[\right[cb\left]\right]$, $\left[\right[temp\left]\right]$ and $\left[\right[AndConst\left]\right]$ computationally indistinguishable from $\left[\left[c{a}^{\prime }\right]\right]$, $\left[\left[c{b}^{\prime }\right]\right]$, $\left[\left[tem{p}^{\prime }\right]\right]$ and $\left[\left[AndCons{t}^{\prime }\right]\right]$ respectively. In addition, $\left[\right[res\left]\right]$ is computationally indistinguishable from $\left[\left[tem{p}^{\prime }\right]\right]$ and $\left[\left[AndCons{t}^{\prime }\right]\right]$ respectively. Thus, it can be concluded that ${REAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{AND}}\right)$ and ${IDEAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{AND}}\right)$ are computationally indistinguishable. We can obtain that ${\mathbf{SC}}_{\mathbf{AND}}$ is secure under the semi-honest model. □

Theorem 2.

The ${\mathbf{SC}}_{\mathbf{OR}}$ proposed is secure under the semi-honest model.

Proof of Theorem 2.

We use ${REAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{OR}}\right)$ to denote the execution view in the real world of CS, where it is specified as ${REAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{OR}}\right)=\{\left[\left[ca\right]\right],\left[\left[cb\right]\right],\left[\left[temp\right]\right],\left[\left[ORConst\right]\right],\left[\left[res\right]\right]\}$. $\left[\right[ORConst\left]\right]$ is obtained from $\left[\right[1\left]\right]$ and $\left[\right[8\left]\right]$ by $modSwitchToTorus32$. $\left[\right[temp\left]\right]$ is obtained from $\left[\right[ca\left]\right]$ and $\left[\right[ORConst\left]\right]$ by $\mathbf{MKlweNoiselessTrivial}$ and $\mathbf{MKlweAddTo}$. $\left[\right[res\left]\right]$ is obtained from $\left[\right[temp\left]\right]$ and $\left[\right[cb\left]\right]$ by $\mathbf{MKlweAddTo}$. We assume that ${IDEAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{OR}}\right)=\{\left[\left[c{a}^{\prime }\right]\right],\left[\left[c{b}^{\prime }\right]\right],\left[\left[tem{p}^{\prime }\right]\right],\left[\left[ORCons{t}^{\prime }\right]\right],\left[\left[re{s}^{\prime }\right]\right]\}$ is the execution view of the simulation in the ideal world, where $\left[\left[c{a}^{\prime }\right]\right]$, $\left[\left[c{b}^{\prime }\right]\right]$, $\left[\left[tem{p}^{\prime }\right]\right]$, $\left[\left[ORCons{t}^{\prime }\right]\right]$ and $\left[\left[re{s}^{\prime }\right]\right]$ are chosen randomly from ${\mathbb{T}}^{n+1}$. The semantic privacy of our encryption scheme makes $\left[\right[ca\left]\right]$ and $\left[\right[cb\left]\right]$ computationally indistinguishable from $\left[\left[c{a}^{\prime }\right]\right]$, $\left[\left[c{b}^{\prime }\right]\right]$, $\left[\left[tem{p}^{\prime }\right]\right]$ and $\left[\left[ORCons{t}^{\prime }\right]\right]$, respectively. In addition, $\left[\right[res\left]\right]$ is computationally indistinguishable from $\left[\left[c{a}^{\prime }\right]\right]$, $\left[\left[c{b}^{\prime }\right]\right]$, $\left[\left[tem{p}^{\prime }\right]\right]$ and $\left[\left[ORCons{t}^{\prime }\right]\right]$ respectively. Thus, it can be concluded that ${REAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{OR}}\right)$ and ${IDEAL}_{CS}^{\Pi }\left({\mathrm{SC}}_{\mathrm{OR}}\right)$ are computationally indistinguishable. We can obtain that ${\mathbf{SC}}_{\mathbf{OR}}$ is secure under the semi-honest model. □

Theorem 3.

The ${\mathbf{SC}}_{\mathbf{XOR}}$ proposed is secure under the semi-honest model.

Proof of Theorem 3.

Since the design ideas of ${\mathbf{SC}}_{\mathbf{AND}}$ and ${\mathbf{SC}}_{\mathbf{OR}}$ are similar, we can prove the theorem based on Theorem (1). □

Theorem 4.

The $\mathbf{SCP}$ proposed is secure under the semi-honest model.

Proof of Theorem 4.

We use ${REAL}_{CS}^{\Pi }\left(\mathrm{SCP}\right)$ to denote the execution view in the real world of the CS, where it is specified as ${REAL}_{CS}^{\Pi }\left(\mathrm{SCP}\right)=\{(\left[\left[\mathbf{x}\right]\right],\left[\left[\mathbf{y}\right]\right]),\left[\left[z\right]\right]\}$. $\left[\right[\mathbf{x}\left]\right]$ and $\left[\right[\mathbf{y}\left]\right]$ are the encrypted data vectors. $\left[\right[z\left]\right]$ is the result of determining whether the encrypted data vectors $\left[\right[\mathbf{x}\left]\right]$ and $\left[\right[\mathbf{y}\left]\right]$ are equal. $\left[\right[z\left]\right]$ is a random number between 0 and 1 in the ciphertext. We assume that ${IDEAL}_{CS}^{\Pi }\left(\mathrm{SCP}\right)=\{(\left[\left[{\mathbf{x}}^{\prime }\right]\right],\left[\left[{\mathbf{y}}^{\prime }\right]\right]),\left[\left[z^{\prime }\right]\right]\}$ is the execution view of the simulation in the ideal world, where the encrypted data in both $\left[\left[{\mathbf{x}}^{\prime }\right]\right]$ and $\left[\left[{\mathbf{y}}^{\prime }\right]\right]$ are chosen randomly from ${\mathbb{T}}^{n+1}$. $\left[\left[z^{\prime }\right]\right]$ are chosen randomly from ${\mathbb{T}}^{n+1}$. The semantic privacy of our encryption scheme makes $\left[\right[\mathbf{x}\left]\right]$ and $\left[\right[\mathbf{y}\left]\right]$ computationally indistinguishable from $\left[\left[{\mathbf{x}}^{\prime }\right]\right]$ and $\left[\left[{\mathbf{y}}^{\prime }\right]\right]$, respectively. In addition, $\left[\left[z^{\prime }\right]\right]$ takes 0 or 1 with equal probability. $\left[\right[z\left]\right]$ are computationally indistinguishable from $\left[\left[z^{\prime }\right]\right]$, respectively. Thus, it can be concluded that ${REAL}_{CS}^{\Pi }\left(\mathrm{SCP}\right)$ and ${IDEAL}_{CS}^{\Pi }\left(\mathrm{SCP}\right)$ are computationally indistinguishable. We can obtain that $\mathbf{SCP}$ is secure under the semi-honest model. □

6.3. Security of CMPSI

Theorem 5.

The $\mathbf{CMPSI}$ proposed is secure under the semi-honest model, and the security of encrypted data, mining results, and query data can be guaranteed.

Proof of Theorem 5.

We can use the above method to prove that our proposed $\mathbf{CMPSI}$ is secure under the semi-honest model. In S1, CS obtains the encrypted dataset from DOs. In S2, CS obtains the encrypted dataset from DR. From Section 6.1, our cryptosystem is semantically secure, and the semi-honest CS cannot distinguish these messages from the random values of ${\mathbb{T}}^{n+1}$. In S3, $\mathbf{SCP}$ is executed to obtain the intersection information of the encryption of individual items in the dataset. Since $\mathbf{SCP}$ is secure in our system, it can be confirmed that the protocol in S3 is secure. In S4, ${\mathbf{SC}}_{\mathbf{OR}}$ is used to obtain the final encryption result. Since ${\mathbf{SC}}_{\mathbf{OR}}$ is secure in our system, the protocol in S4 is secure. In S5 and S6, the execution of S4 is repeated, the DR receives the message and decrypts it using the joint key, and the protocol is secure from the security of $\mathbf{MKTFHE}$. □

Theorem 6.

The $\mathbf{CMPSI}$ proposed is able to resist man-in-the-middle attacks.

Proof of Theorem 6.

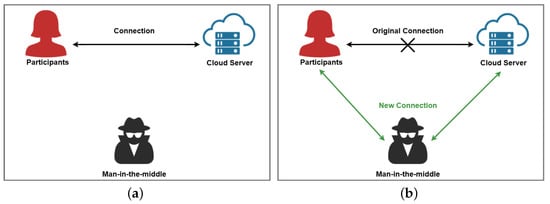
As shown in Figure 4, the participants represent the DR and DOs in our scenario. Under normal conditions, the participants can communicate with the CS, and Figure 4a shows the communication under normal conditions. The man-in-the-middle attack changes the original communication channel and can access the communication data between the participant and the cloud server, and Figure 4b shows the impact of the man-in-the-middle attack on the communication. We will prove that our model is resistant to man-in-the-middle attacks in three ways. First, DO encrypts its own dataset $T_{DO}$ into ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ using its own key $s_{DO}$ and then sends ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ to CS. Intermediary $\mathcal{A}$ obtains ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ through the new channel, but $\mathcal{A}$ does not have DO’s key, and it is known from the security of $\mathbf{MKTFHE}$ that $\mathcal{A}$ cannot decrypt ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$. Thus, our model can resist the man-in-the-middle attack during the data transmission from DO to CS. Second, DR wants to obtain the intersection information and sends the encrypted data ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ to CS. Intermediary $\mathcal{A}$ obtains ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ through the illegal channel. By the security of $\mathbf{MKTFHE}$, $\mathcal{A}$ does not have $s_{DR}$ and cannot obtain $T_{DR}$ from ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$. Thus, our model can resist the man-in-the-middle attack from DR to CS man-in-the-middle attack during the data transfer. Finally, CS needs to return the computed intersection information ${\left[\left[T_{DR\cap DO}\right]\right]}_s$ to DR. The middleman $\mathcal{A}$ obtains the information ${\left[\left[T_{DR\cap DO}\right]\right]}_s$, and it is known from the security of $\mathbf{MKTFHE}$ that $\mathcal{A}$ does not have the key to obtain $T_{DR\cap DO}$. Thus, our model can resist the man-in-the-middle attack during the data transmission from CS to DR. □

Figure 4. Man-in-the-middle attack; (a) normal communication; (b) post-attack communication.

6.4. Security Services

According to the above proof of CMPSI security, Table 3 shows the security services provided by the scheme and a demonstration from our model of how the method provides each of these functions.

Table 3. Security services provided.

Security Services	Definition	Proof
Confidentiality	Network information is not disclosed to non-authorized users, entities, or processes.	In our system, DO uses its own key $s_{DO}$ to encrypt its own dataset $T_{DO}$ into ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ and then sends ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ to CS. An unauthorized user $\mathcal{A}$ illegally obtains ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$, and according to the security of the MKTFHE cryptosystem in Section 6.1, it is known that without the key, $s_{DO}$ cannot perform decryption. Therefore, unauthorized illegal users $\mathcal{A}$ cannot obtain the information of DO’s dataset $T_{DO}$.
Integrity	Information is transmitted, exchanged, stored, and processed in such a way that it remains uncorrupted or unmodified, that it is not lost, and that it cannot be changed without authorization.	In our system, DR encrypts the dataset $T_{DR}$ as ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ using the key $s_{DR}$ and sends ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ to CS. Attacker $\mathcal{A}$ obtains the dataset ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ through the intermediate channel, and according to the definition of the semi-honest model in Section 4.3, $\mathcal{A}$ does not modify or corrupt the data, and CS can obtain the dataset ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ intact.
Availability	Assurance that information is available to authorized users, i.e., assurance that legitimate users can use the required information when needed.	In our system, DR is the legal user. When DR wants to obtain the intersection information of its dataset $T_{DR}$, DR sends ${\left[\left[T_{DR}\right]\right]}_{s_{DR}}$ to CS, and CS sends the computed intersection result ${\left[\left[T_{DR\cap DO}\right]\right]}_s$ to DR. The legitimate user DR can obtain the required data when needed, which proves the usability of our system.
Non-repudiation	The two parties of information exchange cannot deny that they send or receive information in the exchange process.	In our system, DO sends its encrypted dataset ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ to CS. According to the definition of the semi-honest model in Section 4.3, DO will not deny that the dataset ${\left[\left[T_{DO}\right]\right]}_{s_{DO}}$ is its data, proving the non-repudiation of our system.

7. Performance Analysis

In this section, we evaluate the time overhead and communication overhead of our proposed scheme. The experimental parameters we used [51] are shown in Table 4 below. According to one study [52], the parameters we use reach a privacy level of at least 110 bits, which is a common reference in this field.

Table 4. Parameter sets.

$\mathbf{LWE}\text{-}\mathbf{n}$	$\mathbf{LWE}\text{-}\mathit{\alpha }$	$\mathbf{LWE}\text{-}{\mathbf{B}}^{\prime }$	$\mathbf{LWE}\text{-}{\mathbf{d}}^{\prime }$	$\mathbf{RLWE}\text{-}\mathbf{N}$	$\mathbf{RLWE}\text{-}\mathit{\beta }$	$\mathbf{RLWE}\text{-}\mathbf{B}$	$\mathbf{RLWE}\text{-}\mathbf{d}$
560	$3.05\times {10}^{-5}$	$2^2$	8	1024	$3.72\times {10}^{-9}$	$2^9$	3

The test environment used for our experiments was as follows: a 2.30 GHz Intel (R) Core(TM) i5-8300H Dell laptop. The programming language we used was C++, and our system was based on the MKTFHE library. First, we tested the efficiency of the security subprotocols separately. Then, we tested the communication overhead of our scheme and compared it with existing schemes. Finally, we tested our scheme.

7.1. Experiments on Security Computing Protocols

Our secure subprotocol experiments were performed using the MKTFHE library (https://github.com/ilachill/MK-TFHE) (1 February 2023). MKTFHE is a proof-of-concept implementation of a multi-key version of TFHE. The code is written on top of the TFHE library (https://tfhe.github.io/tfhe/) (1 February 2023). The computation of secure NAND gates is given in the MKTFHE library. In the MKTFHE-based implementation, our goal is to implement the MKLwe sample addition and multiplication operations as a way to implement the other circuit gates needed in our scheme in addition to the NADN gate. We first performed experiments on single circuit gates, including experiments on secure AND gate computation protocol, secure OR gate computation protocol, and secure XNOR computation protocol, and the experimental results are shown in Table 5. We compared these with NAND gates and found that the efficiency of individual gate computation is close.

Table 5. Experimental results for single circuit gates.

Gate Circuit	Key Generation Time (s)	FFT Conversion Time (s)	Bootstrapping Time (s)
$AND$	1.973	0.039	0.226
$NAND$	1.982	0.038	0.227
$OR$	1.956	0.040	0.227
$XNOR$	1.975	0.039	0.220

Then, as shown in Table 6, we tested the experimental time overhead of $\mathbf{SCP}$ for k = 8, 16, and 32, where k is the bits of data. The results show that the time overhead of the $\mathbf{SCP}$ protocol is linearly related to the number of bits of input.

Table 6. Running time of $\mathbf{SCP}$.

k	8	16	32
Running time (s)	3.52	7.17	14.20

7.2. Overhead Evaluation

In our scenario, DOs and DRs are resource-constrained users; thus, it is important to have a smaller communication overhead. In our scheme, each participant uses their key to encrypt the data and uploads it to the cloud server; thus, the total communication overhead is related to the total data size. We tested the communication overhead of our scheme on datasets with aggregate sizes of $2^8$, $2^{12}$, $2^{16}$, and $2^{20}$. We compared our scheme with the scheme based on RSA [53] and the scheme based on pseudorandom permutation (PRP) [48]. As shown in Figure 5, our scheme is significantly superior to the privacy intersection scheme based on RSA. For the server-assisted scheme with limited security [48], the communication cost of our scheme is also lower. Our experimental results are the average of ten experiments.

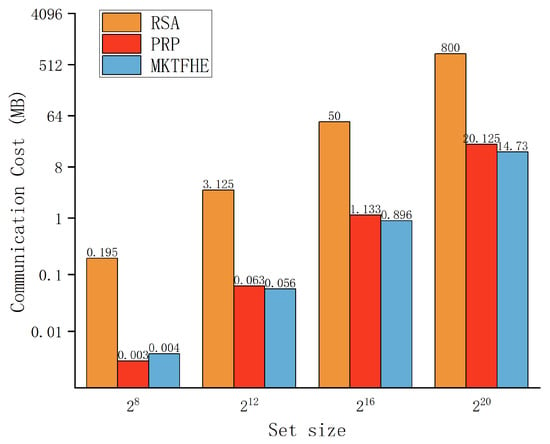
Figure 5. Communication overhead.

Our scheme is based on the underlying PSI protocol, and the computation of the ciphertext is performed directly on the cloud server. To the best of our knowledge, our proposed scheme is the first scheme that uses MKTFHE to achieve the ideal PSI, and the time overhead of the scheme is a very important metric. For users with limited resources, low overhead in the process of data encryption and decryption is necessary. We tested the time cost of using encryption and decryption and the size of ciphertext on datasets with sizes of $2^8$, $2^{12}$, $2^{16}$ and $2^{20}$. Table 7 shows that for DOs and DR with limited resources, the cost of our scheme in data encryption and decryption is very small. Finally, we tested the computing cost of the cloud server. In the experiment, we used data from 16, 32, and 64 bit systems to test the performance of our proposed scheme. Table 8 shows our experimental results. The results show that the time cost of the scheme is linearly related to the size of the dataset and the number of bits of data. Please note that the cloud has excellent computing power, so that the efficiency of the solution can be faster in actual use.

Table 7. Cost during encryption.

	$2^8$	$2^{12}$	$2^{16}$	$2^{20}$
Encryption time (ms)	13.5	208.2	3162.2	47,987.1
Cipher size (kb)	3.5	57.3	917.5	15,083.6

Table 8. Cloud computing time (min).

Data Set Size	16bit	32bit	64bit
$2^2$	0.51	0.99	1.98
$2^4$	8.47	16.02	31.70
$2^6$	137.68	273.83	547.66

8. Conclusions

In this paper, we proposed CMPSI, a cloud-assisted private set intersection via multi-key fully homomorphic encryption, which allows the participants to outsource the encrypted data to cloud servers for storage and computation. We also designed some MKTFHE-based secure computing protocols to complete the design of our system. We analytically demonstrated the security of our scheme under a semi-honest model. Through experiments, we tested the performance of our proposed scheme and proved that our scheme has less communication overhead by comparing it with existing schemes. We also proved the feasibility of the scheme.

As future research work, we plan to apply our proposed MKTFHE to a wider range of areas, such as association rule mining systems in large shopping malls. In addition, we will improve our framework to handle more complex computations and further improve the performance of our system.