Relaxation Oscillations in the Logistic Equation with Delay and Modified Nonlinearity

Abstract

We consider the dynamics of a logistic equation with delays and modified nonlinearity, the role of which is to bound the values of solutions from above. First, the local dynamics in the neighborhood of the equilibrium state are studied using standard bifurcation methods. Most of the paper is devoted to the study of nonlocal dynamics for sufficiently large values of the ‘Malthusian’ coefficient. In this case, the initial equation is singularly perturbed. The research technique is based on the selection of special sets in the phase space and further study of the asymptotics of all solutions from these sets. We demonstrate that, for sufficiently large values of the Malthusian coefficient, a ‘stepping’ of periodic solutions is observed, and their asymptotics are constructed. In the case of two delays, it is established that there is attractor in the phase space of the initial equation, whose dynamics are described by special nonlinear finite-dimensional mapping.

1. Introduction

The logistic equation with delay is the name given to the equation

$$\dot{u}=\lambda [1-u(t-T)]u.$$

(1)

Being a natural extension of the classical logistic equation, it arises in many applied problems, but most of all it is used in problems of mathematical ecology (see, for example [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]). The value u describes the dynamics of changes in the number of specimens in the population or density of an isolated biological population living in a homogeneous environment. Therefore, it makes sense to consider only non-negative solutions of Equation (1). We note that the solution of Equation (1) with a non-negative initial function $\phi \left(s\right)\in C_{[-T,0]}$ specified at some value $t_0$ (i.e., $u(t_0+s)=\phi \left(s\right)$) remains non-negative for all $t>t_0$. The coefficient $\lambda$ is called the Malthusian coefficient of linear growth and the parameter $T>0$ is called the delay time. It is associated with the age of animal units capable of procreation in the corresponding population.

The dynamic properties of the solutions of Equation (1) are well understood. Under the condition $\lambda T\le {\displaystyle \frac{\pi }{2}}$, the equilibrium state $u_0\equiv 1$ is asymptotically stable, while for $\lambda T>{\displaystyle \frac{\pi }{2}}$ it is unstable and the periodic solution $U_0(t,\lambda )$ is stable. Under the condition $0<\lambda T-{\displaystyle \frac{\pi }{2}}\ll 1$, we obtain its asymptotics on the Andronov–Hopf bifurcation theory application basis (see, for example [16,17,18]). It is shown in [7] that for sufficiently large $\lambda$ the periodic solution $U_0(t,\lambda )$ has a pronounced relaxation structure. There is a single wavelet of this function on the segment of the period $T_0\left(\lambda \right)$ length. The duration of the wavelet is close to the value of T and the period $T_0\left(\lambda \right)$ is equal to ${\left(\lambda T\right)}^{-1}exp\left(\lambda T(1+o\left(1\right))\right)$. It is important to note the asymptotic equalities.

$$\begin{array}{ccc}\hfill \underset{t}{max}{U}_0(t,\lambda )& =& exp\left(\lambda T\right(1+o\left(1\right)\left)\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \underset{t}{min}{U}_0(t,\lambda )& =& exp(-exp(\lambda T\left)\right(1+o\left(1\right)\left)\right).\hfill \end{array}$$

(3)

We also note results of [19,20], in which important results on the dynamics of logistic equations with delay and diffusion are obtained, [21], where a randomized non-autonomous logistic equation is discussed, and Ref. [22], where interesting results were obtained for an equation in which the delay itself is a function of u.

Due to the applied significance, it is of interest to study equations with various types of nonlinearity. By virtue of biological meaning, solutions must remain positive. Similar to this restriction, it is natural to require solutions to be bounded not only from below, but also from above. In addition, unlimited asymptotic growth, as in the case of Equation (1), is not always convenient, for example, for describing the dynamics of changes in the number of species.

In this paper we study the dynamics of the new model—the logistic equation with delay and modified nonlinearity

$$\dot{u}=\lambda [1-u(t-T)]u(A-u),A>1.$$

(4)

The main difference between the solutions of Equation (4) and the solutions of Equation (1) is that under the condition $0\le \phi \left(s\right)\le A$ the inequalities

$$0\le u(t,\phi )\le A$$

hold for the solution $u(t,\phi )$ of Equation (4) with the initial condition $u(t_0+s)=\phi \left(s\right)$ as $t>t_0$. Thus, the use of the factor $(A-u)$ on the right-hand side of Equation (4) leads to the restriction $u(t,\phi )\le A$ for the solutions of Equation (4). Therefore, the solutions of Equation (4) (in contrast to the solutions of Equation (1)) do not take asymptotically large values for large values of $\lambda$.

Model (4) is quite complex. At the moment, there are no analytical methods that would allow for absolutely any values of the parameters $\lambda$, T, and A to obtain results on the qualitative and quantitative behavior of all solutions of Equation (4) on the entire positive semiaxis $t\in [0,+\infty )$. In addition, numerical methods are also not very effective in the study of such models, since, firstly, it is impossible to enumerate all possible initial conditions in order to draw a qualitative conclusion about the dynamics of the model, and secondly, for some values of the model parameters, the solutions are very close will approach zero (see Section 3 and Section 4), so a relatively small error in the calculations can lead to a completely wrong result.

Therefore, in the paper, the research is carried out by analytical (asymptotic) methods. At present, the most effective among them are the methods of the theory of bifurcations in the study in the neighbourhood of the equilibrium state and the methods of a large parameter (for $\lambda \gg 1$) in the study of nonlocal processes. Large parameter methods are based on the use of singular perturbation theory, but even in cases where the $\lambda$ parameter (Malthusian coefficient in model Equation (4)) is not large enough, nevertheless, conclusions can be drawn about the trends in fluctuations with an increase in this parameter. In addition, we point out that the relaxation nature of the oscillations obtained for model Equation (4) in the case of sufficiently large values of parameter $\lambda$ corresponds to ideas about the dynamic behavior of population density dynamics in mathematical ecology [4,11].

The paper is organized as follows. In Section 2, the conditions for the parameter $\lambda$ are found using the methods of bifurcation analysis. Under them, the Andronov–Hopf bifurcation occurs in Equation (4) and a cycle arises from the equilibrium state.

The main content of Section 3 and all subsequent sections is devoted to the study of the solutions of Equation (4) on the interval $t\in [0,+\infty )$ provided that the parameter $\lambda$ is sufficiently large:

$$\lambda \gg 1.$$

(5)

In this case, the equation under consideration is singularly perturbed. After dividing by the left-hand and right-hand parts of Equation (4) by $\lambda$, we obtain an equation with a small parameter at the derivative:

$${\lambda }^{-1}\dot{u}=[1-u(t-T)]u(A-u).$$

(6)

However, the reduced equation

$$0=[1-u(t-T\left)\right]u(A-u)$$

does not describe the behavior of the Equation (6) solutions (except the simplest equilibrium states) under the condition (5).

It is important to mention that from a computational point of view, this problem is difficult, since the relaxation solution approaches A and 0 very closely, so even a small error in the calculations will take us out of the class of solutions under consideration.

Therefore, a special analytical research method was developed. First, we briefly describe it for the simplest case, for studying slowly oscillating solutions. Recall that slowly oscillating solutions are those solutions for which the time distance between adjacent roots of the equation $u\left(t\right)=1$ is greater than the delay time. Consider Equation (6). Denote by $S\subset C_{[-T,0]}$ the set of all such functions $\phi \left(s\right)\in S$$(s\in [-T,0\left]\right)$ that satisfy the conditions (see Figure 1).

$$\phi \left(0\right)=1;0\le \phi \left(s\right)\le exp\left(\frac{\lambda }{2}s\right).$$

(7)

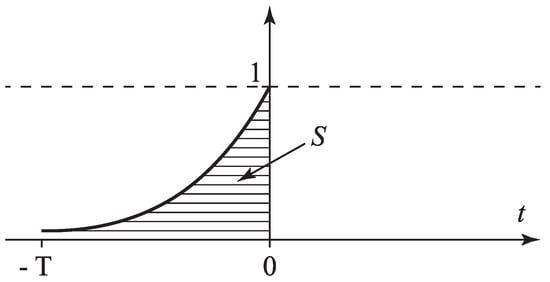
Figure 1. The set S.

Denote by $u(t,\phi )$ a solution of (6) with initial condition $\phi \left(s\right)$:$u(s,\phi )=\phi \left(s\right)$$(s\in [-T,0\left]\right)$. The method of steps will be used: for $t\in [0,T],$ taking into account the initial function $\phi \left(s\right)$, to determine $u(t,\phi )$ we obtain an ordinary differential equation of the first order. It is easy to find the asymptotics of this solution as $\lambda \to \infty$ on the indicated interval. Then we consider $u(t,\phi )$ on the interval $[T,2T],$ on which we also obtain a first-order ordinary differential equation, and find the asymptotics of the solutions. After that, we will carry out the same actions on the segment $[2T,3T]$, then on the segment $[3T,4T]$, and so on.

In Section 3.1 we study the asymptotic behavior at $\lambda \to \infty$ of all solutions $u(t,\phi )$ with initial conditions from S. In particular, the asymptotics of the first two positive roots $t_1\left(\phi \right)$ and $t_2\left(\phi \right)$ of the equation $u(t,\phi )=1$ will be found. The main conclusion is that after the time interval $t_2\left(\phi \right)$ the solution $u(t,\phi )$ will again fall on the set S:$u(s+t_2\left(\phi \right),\phi )\in S$. This gives reason to introduce the $\Pi$ operator:

$$\Pi \left(\phi \left(s\right)\right)=u(t_2\left(\phi \right)+s,\phi )$$

and justify the inclusion $\Pi S\subset S.$ From this and the well-known results of functional analysis [23], we conclude that S has a fixed point ${\phi }_0\left(s\right)$ of the operator $\Pi$: $\Pi \left({\phi }_0\left(s\right)\right)={\phi }_0\left(s\right).$ Then the function $u_0\left(t\right)=u(t,{\phi }_0)$ is periodic with period $t_2\left({\phi }_0\right)$. In Section 3.1, asymptotic formulas for $u_0\left(t\right)$ will be given.

In Section 3.2 we investigate the asymptotic behavior of rapidly oscillating solutions. As a set of initial functions, we consider the set $S({\tau }_1,{\tau }_2)$ depending on two parameters ${\tau }_1$ and ${\tau }_2$. It is shown schematically in Figure 3. In Section 3.2, a rigorous description of this set is given and the asymptotic behavior of all solutions (6) with initial conditions from $S({\tau }_1,{\tau }_2)$ is studied. Again, by $t_1\left(\phi \right)$ and $t_2\left(\phi \right)$ we denote the first and second positive roots of the equation $u(t,\phi )=1.$ We again introduce the operator $\Pi$: $\Pi \left(\phi \left(s\right)\right)=u(t_2\left(\phi \right)+s,\phi )$ and it will be shown that up to $o\left(1\right)$ the inclusion $\Pi \left(\phi \left(s\right)\right)\in S({\overline{\tau }}_1,{\overline{\tau }}_2),$ where ${\overline{\tau }}_{1,2}$ are explicitly expressed in terms of ${\tau }_{1,2}$. This gives grounds to take the function $u(s+t_2\left(\phi \right),\phi )$ as the initial one and pass to the iteration process. It is possible to find a fixed point $({\tau }_1^0,{\tau }_2^0)$ and a function ${\phi }_0\left(s\right)\in S({\tau }_1^0,{\tau }_2^0)$ such that the solution $u_0(t,{\phi }_0)$ will be periodic with period $t_2\left({\phi }_0\right)$. It is important to note that the rapidly oscillating periodic solutions found in this way are unstable.

The results of Section 4 are more interesting. We consider equations with two delays

$$\dot{u}=\lambda [1-\alpha u(t-T)-(1-\alpha )u(t-h)]u(A-u),$$

(8)

where $\alpha \in (0,1)$ and $h<T$.

It is commonly supposed that the use of two (or more) delays allows one to take into account the influence of the population age structure on the dynamics of population level changes [24,25,26,27].

One succeeded to clearly describe the nonlocal dynamic properties of Equation (8) under the condition (5). In contrast to the results of the Section 3, the relaxation step solutions for (8) can be stable.

We note that for the simpler logistic equation with two delays

$$\dot{u}=\lambda [1-\alpha u(t-T)-(1-\alpha )u(t-h)]u\left(\alpha \in (0,1),h<T\right)$$

(9)

the results were obtained in Ref. [7] as $\lambda \gg 1$. It follows from them that for sufficiently large $\lambda$ in (9) there is an orbitally stable periodic solution which is similar in appearance to the solution of Equation (1) with the same initial conditions, and the asymptotic representation (2) holds for it.

2. Andronov–Hopf Bifurcations in Equations with One Delay

We shall fix the parameters ${\lambda }_0,A_0$ and $T_0$ so that the following equality is fulfilled:

$${\lambda }_0(A_0-1)T_0=\frac{\pi }{2}.$$

(10)

Lemma 1. 

Suppose that in Equation (4)

$$\lambda (A-1)T<\frac{\pi }{2}.$$

(11)

Then the equilibrium state $u_0\equiv 1$ is asymptotically stable.

Proof. 

To prove this statement we linearize (4) on $u_0$ and consider the characteristic quasi-polynomial

$$\mu =-\lambda (A-1)exp(-\mu T).$$

(12)

Under the condition (11) all its roots have negative real parts. From this, and from known results (see Ref. [5]) on the stability in the first approximation, the proof of Lemma 1 follows. □

Next we introduce a small positive parameter $\epsilon$:

$$0<\epsilon \ll 1,$$

(13)

and assume that in Equation (4), for certain constant ${\lambda }_1,A_1$ and $T_1$, the following relations are fulfilled:

$$\lambda ={\lambda }_0+\epsilon {\lambda }_1,A=A_0+\epsilon A_1,T=T_0+\epsilon T_1.$$

(14)

We set

$$b={\left(1+\frac{{\pi }^2}{4}\right)}^{-1}\left[\left(\frac{\pi }{2}+i\right)({\lambda }_1(A_0-1)+{\lambda }_0{A}_1)+{\lambda }_0^2{(A_0-1)}^2{T}_1\left(1-i\frac{\pi }{2}\right)\right],$$

(15)

$$d=-{\lambda }_0{\left(1+\frac{{\pi }^2}{4}\right)}^{-1}\left[\frac{\pi }{2}+i+\frac{3{(A_0-2)}^2}{5(A_0-1)}\left(\frac{\pi }{2}-1+i\left(\frac{\pi }{2}+1\right)\right)\right],$$

(16)

$$\omega =\pi {\left(2T_0\right)}^{-1},$$

(17)

$$\begin{array}{cc}\hfill {\xi }_0\left(\tau \right)& ={\xi }_{0}exp\left(i\psi \tau \right),\psi =\mathrm{I}\mathrm{m} b+{\xi }_0^2\mathrm{I}\mathrm{m} d,\hfill \\ \hfill {\xi }_0& ={\left[\left(\frac{\pi }{2}({\lambda }_1(A_0-1)+{\lambda }_0{A}_1)+{\lambda }_0^2{(A_0-1)}^2{T}_1\right){\lambda }_0^{-1}{\left(\frac{\pi }{2}+\frac{3{(A_0-2)}^2}{5(A_0-1)}\left(\frac{\pi }{2}-1\right)\right)}^{-1}\right]}^{\frac{1}{2}}.\hfill \end{array}$$

(18)

Theorem 1. 

Let conditions (13)–(15), (17), and (18) hold.

1. Let $\mathrm{R}\mathrm{e} b<0$. Then all solutions of Equation (4) with initial conditions from a sufficiently small (and independent of ε) neighbourhood of the equilibrium state $u\equiv 1$ tend to 1 as $t\to \infty$.

2. Let

$$\mathrm{R}\mathrm{e} b>0.$$

(19)

Then for all sufficiently small ε Equation (4) has in the neighbourhood of the unit equilibrium state a stable periodic solution $u_0(t,\epsilon )$ for which the following asymptotic equality is fulfilled:

$$u_0(t,\epsilon )=1+{\epsilon }^{1/2}[{\xi }_0\left(\tau \right)exp\left(i\omega t\right)+{\overline{\xi }}_0\left(\tau \right)exp(-i\omega t)]+O\left(\epsilon \right),$$

where $\tau =\epsilon t$.

Proof. 

Under the condition (10) the quasi-polynomial (12) has a pair of purely imaginary roots ${\mu }_{1,2}=\pm i\omega$, where the value of $\omega$ is given in (17), and all its other roots have negative real parts. Then, under the condition (14), and for all sufficiently small $\epsilon$, Equation (4) in the neighbourhood of $u\equiv 1$ has (see Refs. [16,17,18,28]) a two-dimensional stable local invariant integral manifold, on which this equation can be written, to within higher-order terms, in the form of a complex scalar equation—a normal form:

$$\frac{d\xi }{d\tau }=B\xi \left(\tau \right)+D\xi \left(\tau \right){\left|\xi \left(\tau \right)\right|}^2,$$

(20)

where values B and D are to be determined.

In the case $\mathrm{R}\mathrm{e} B\ne 0$ and $\mathrm{R}\mathrm{e} D\ne 0$ normal form completely determines the behavior of all solutions in a neighbourhood of $u\equiv 1$ (see Refs. [16,17,18,28]). The solutions of (20) are connected with the solutions of (4) by the relation

$$\begin{array}{cc}\hfill u(t,\epsilon )=& 1+{\epsilon }^{1/2}[\xi \left(\tau \right)exp\left(i\omega t\right)+\overline{\xi }\left(\tau \right)exp(-i\omega t)]+\hfill \\ \hfill & +\epsilon u_2(t,\tau )+{\epsilon }^{3/2}{u}_3(t,\tau )+\dots \hfill \end{array}$$

(21)

Here, $\tau =\epsilon t$, the $u_j(t,\tau )$ are periodic in t with period $2\pi /\omega$. Substituting (21) into (4) and collecting coefficients of equal powers of $\epsilon$, we successively find all the elements appearing there. At ${\epsilon }^{1/2}$ we obtain true identity, and collecting coefficients of the first power of $\epsilon$ and taking into account (10), (12), and (17), we find equation for determining the function $u_2(t,\tau )$:

$$\frac{\partial u_2}{\partial t}=-{\lambda }_0(A_0-1)u_2(t-T_0,\tau )+i{\lambda }_0(A_0-2){\xi }^2\left(\tau \right)exp\left(2i\omega t\right)-i{\lambda }_0(A_0-2){\overline{\xi }}^2\left(\tau \right)exp(-2i\omega t).$$

Thus, taking into account that $u_2(t,\tau )$ is periodic in t with period $2\pi /\omega$, we find that

$$u_2(t,\tau )=\frac{(A_0-2)(2-i)}{5(A_0-1)}{\xi }^2\left(\tau \right)exp\left(2i\omega t\right)+\frac{(A_0-2)(2+i)}{5(A_0-1)}{\overline{\xi }}^2\left(\tau \right)exp(-2i\omega t).$$

Collecting coefficients of ${\epsilon }^{3/2}$ we obtain an equation for $u_3(t,\tau )$:

$$\frac{\partial u_3}{\partial t}=-{\lambda }_0(A_0-1)u_3(t-T_0,\tau )+B_{1}exp\left(i\omega t\right)+{\overline{B}}_{1}exp(-i\omega t)+B_{3}exp\left(3i\omega t\right)+{\overline{B}}_{3}exp(-3i\omega t),$$

(22)

where $B_1$ and $B_3$ are complex values.

From the condition that Equation (22) be solvable in the class of functions periodic in t with period $2\pi /\omega$ (this condition is $B_1=0$) we arrive at Equation (20) for the unknown amplitude $\xi \left(\tau \right)$, in which $B=b$ and $D=d$ (coefficient b is defined in (15) and the coefficient d is defined in (16)).

Multiplying both sides of Equation (20) by $\overline{\xi }\left(\tau \right)$ and taking into account equalities $B=b$ and $D=d$ we obtain a scalar real ordinary differential equation

$$\frac{1}{2}\dot{\rho }\left(\tau \right)=\mathrm{R}\mathrm{e} b\rho \left(\tau \right)+\mathrm{R}\mathrm{e} d{\rho }^2\left(\tau \right),$$

(23)

where $\rho \left(\tau \right)={\left|\xi \left(\tau \right)\right|}^2$.

We note that $\mathrm{R}\mathrm{e} d<0$.

That is why, if $\mathrm{R}\mathrm{e} b<0$, all solutions of (23) tend to zero as $t\to +\infty$. Thus, all solutions of (4) from the neighbourhood of $u\equiv 1$ tend to 1 as $t\to +\infty$. This completes the proof of the first part of the Theorem.

Under the condition (19) Equation (20) with $B=b$ and $D=d$ has a stable periodic solution ${\xi }_0\left(\tau \right)={\xi }_{0}exp\left(i\psi \tau \right)$, where the values ${\xi }_0$ and $\psi$ are given in (18). Taking into account here the asymptotic equality (21) we have completed the proof of the Theorem. □

It is interesting to note that the bifurcation effect considered here can be realized for fixed $\lambda ={\lambda }_0$ and $T=T_0$, i.e., for ${\lambda }_1=T_1=0$, and only upon variation of the parameter A.

3. Step-like Solutions of the Logistic Equation with Delay and with a Restriction on the Nonlinear Function

All statements below refer to the case of $\lambda \to +\infty$. For example, everywhere below $o\left(1\right)$ means that the function tends to zero as $\lambda \to +\infty$. Note that the phrase “for all sufficiently large $\lambda$” means the existence of a value ${\lambda }_0$ such that for all $\lambda >{\lambda }_0$ the corresponding assertion is true.

We separately consider questions about slowly and rapidly oscillating solutions of Equation (4).

3.1. Asymptotic Behavior of Slowly Oscillating Solutions

We shall consider the asymptotic behavior of a slowly oscillating relaxation periodic solution of Equation (4).

In (4) it is convenient to replace the time $t\to tT$ and to again denote the product $\lambda T$ by $\lambda$. Then Equation (4) takes the form

$$\dot{u}=\lambda [1-u(t-1)]u(A-u).$$

(24)

Let us introduce some notation.

By S we denote the set of all functions $\phi \left(s\right)\in C_{[-1,0]}$ that satisfy the conditions (7).

Let $u(t,\phi )$ be the solution of (24) with an initial condition $\phi \left(s\right)$ specified at $t=0$, i.e., $u(s,\phi )=\phi \left(s\right)$ for $s\in [-1,0]$. We shall construct the asymptotics for $\lambda \to \infty$ of all solutions $u(t,\phi )$ with $\phi \left(s\right)\in S$.

Theorem 2. 

For all sufficiently large λ Equation (24) has an asymptotically orbitally stable periodic (with period $T\left(\lambda \right)$) solution $u_0(t,\lambda )$, for which $u_0(0,\lambda )=u_0(t_1\left(\lambda \right),\lambda )=u_0(t_2\left(\lambda \right),\lambda )=1$, where $t_j\left(\lambda \right)$ are successive positive roots of the equation $u_0(t,\lambda )=1$, and

$$\begin{array}{cc}\hfill t_1\left(\lambda \right)& =1+{(A-1)}^{-1}+o\left(1\right),\hfill \\ \hfill T\left(\lambda \right)& =t_2\left(\lambda \right)=A+1+{(A-1)}^{-1}+o\left(1\right).\hfill \end{array}$$

For every t from the intervals $(0,t_1\left(\lambda \right))$ and $(t_1\left(\lambda \right),t_2\left(\lambda \right))$, respectively, the following equalities are fulfilled:

$$u_0(t,\lambda )=\left\{\begin{array}{cc}A+o\left(1\right),\hfill & t\in (0,t_1\left(\lambda \right)),\hfill \\ o\left(1\right),\hfill & t\in (t_1\left(\lambda \right),t_2\left(\lambda \right)).\hfill \end{array}\right.$$

Proof. 

We use the following formula for the solutions $u(t,\phi )$ of Equation (24):

$$\begin{array}{cc}\hfill u(t,\phi )=& Au(\tau ,\phi )exp\left(\lambda A{\int }_{\tau }^t\left(1-u(s-1,\phi )\right)ds\right)·\hfill \\ \hfill & {\left[A-u(\tau ,\phi )+u(\tau ,\phi )exp\left(\lambda A{\int }_{\tau }^t\left(1-u(s-1,\phi )\right)ds\right)\right]}^{-1},\hfill \end{array}$$

(25)

where t and $\tau$ are arbitrary values such that $0<\tau <t$.

We shall formulate some simple statements:

Lemma 2. 

Let $t\in (0,1]$. Then

$$u(t,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left(1+o\left(1\right)\right)t\right)\right]}^{-1}.$$

(26)

The proof of (26) follows from (25) with $\tau =0$.

Setting $\tau =1$ in (25), we immediately arrive at the following statement:

Lemma 3. 

Let $t\in (1,1+{(A-1)}^{-1}+\delta ]$, where $\delta >0$ is some small but fixed value. Then

$$u(t,\phi )=A{\left[1+(A-1)exp\left(\lambda A\left[(A-1)\left(1+o\left(1\right)\right)(t-1)-1\right]\right)\right]}^{-1}.$$

(27)

Below, we denote by $t_1\left(\phi \right)$, $t_2\left(\phi \right)$, … the first, second, … positive roots of the equation $u(t,\phi )=1$.

From (27) we arrive at the conclusion that the value $t_1\left(\phi \right)$ exists and

$$\begin{array}{cc}\hfill t_1\left(\phi \right)& =1+{(A-1)}^{-1}+o\left(1\right),\hfill \\ \hfill u(t,\phi )& =A+o\left(1\right)\mathrm{for}\mathrm{every}t\in (0,t_1\left(\phi \right)),\hfill \\ \hfill u(t,\phi )& =o\left(1\right)\mathrm{for}\mathrm{every}t\in (t_1\left(\phi \right),t_1\left(\phi \right)+1).\hfill \end{array}$$

The last equality is true, because formula (27) holds on the interval $(t_1\left(\phi \right),t_1\left(\phi \right)+1)$.

Then we construct asymptotics of solution on the interval $t>t_1\left(\phi \right)+1$. We set $\tau =t_1\left(\phi \right)$ and take into account that $u(s-1)=A+o\left(1\right)$ on the interval $s\in (t_1\left(\phi \right),$$t_1\left(\phi \right)+1)$. We use equality $u(s-1)=o\left(1\right)$ for $t_1\left(\phi \right)+1<s<t$. It follows from formula (25) that this equality holds for all $t>t_1\left(\phi \right)+1$ while

$${\int }_{t_1\left(\phi \right)}^t\left(1-u(s-1,\phi )\right)ds<0.$$

We obtain the following result:

Lemma 4. 

For $t\in [2+{(A-1)}^{-1},A+1+{(A-1)}^{-1}+\delta ]$, where $\delta >0$ is some small but fixed value

$$\begin{array}{cc}\hfill u(t,\phi )=& Aexp\left(\lambda A\left(1-A+t-\left(2+{(A-1)}^{-1}\right)+o\left(1\right)\right)\right)·\hfill \\ \hfill & {\left[A-1+exp\left(\lambda A\left(1-A+t-\left(2+{(A-1)}^{-1}+o\left(1\right)\right)\right)\right)\right]}^{-1}.\hfill \end{array}$$

(28)

From (28) the existence of $t_2\left(\phi \right)$ and the asymptotic equalities

$$t_2\left(\phi \right)=A+1+{(A-1)}^{-1}+o\left(1\right)$$

and

$$u(t,\phi )=o\left(1\right)\mathrm{for}t\in (t_1\left(\phi \right),t_2\left(\phi \right))$$

follow.

We introduce the translation along the trajectories operator $\Pi$, which links the function $u(s+t_2\left(\phi \right),\phi )$, $(s\in [-1,0\left]\right)$ to a function $\phi \left(s\right)$. From the formulas given above we arrive at the conclusion that

$$\Pi \left(\phi \left(s\right)\right)=u\left(s+t_2\left(\phi \right),\phi \right)\in S,$$

meaning that $\Pi S\subset S$.

From this and from Ref. [23] it follows that this operator has in S a fixed point ${\phi }_0\left(s\right)$, i.e.,

$$\Pi \left({\phi }_0\left(s\right)\right)={\phi }_0\left(s\right).$$

This means that the solution $u_0(t,\lambda )=u(t,{\phi }_0\left(s\right))$ is periodic, with period $T\left(\lambda \right)=t_2\left({\phi }_0\left(s\right)\right)$.

The proof of the stability of $u_0(t,\lambda )$ is rather cumbersome. In the more complicated situation discussed in Refs. [7,29] a detailed proof was given of the stability of the solution constructed there, and so we shall not give the proof here. □

It is possible to obtain the asymptotic expansion of $u_0(t,\lambda )$ to any degree of precision. Here we note only that

$$\begin{array}{cc}\hfill \underset{t}{max}{u}_0(t,\lambda )& =u_0(1,\lambda )=A[1+\left(A-1+o\left(1\right)\right)exp(-\lambda A)){]}^{-1},\hfill \\ \hfill \underset{t}{min}{u}_0(t,\lambda )& =u_0\left(t_1\left({\phi }_0\right)+1,\lambda \right)=A{(A-1)}^{-1}exp\left(\lambda A(1-A)\right)\left(1+o\left(1\right)\right).\hfill \end{array}$$

It is interesting to compare the principal characteristics of $u_0(t,\lambda )$ with the corresponding characteristics of the stable periodic solution $U_0(t,\lambda )$ of Equation (1) for $\lambda \to \infty$. To obtain formulas for ${max}_t{U}_0(t,\lambda )$ and ${min}_t{U}_0(t,\lambda )$ one should replace T by 1 in formulas (2) and (3) (see introduction of this paper and Ref. [7]). In Figure 2 we give graphs of periodic functions $u_0(t,\lambda )$ and $U_0(t,\lambda )$.

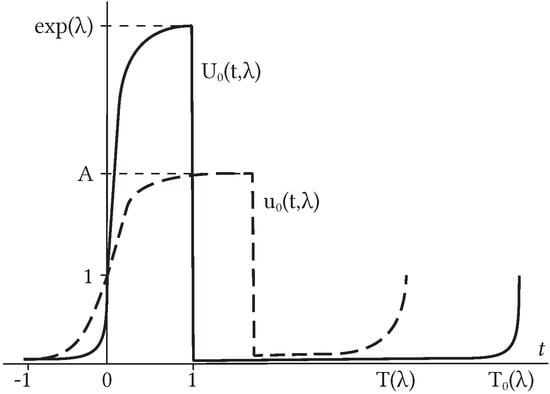
Figure 2. Form of the functions $u_0(t,\lambda )$, $U_0(t,\lambda )$.

3.2. Rapidly Oscillating Solutions of Equation (24)

We shall consider rapidly oscillating solutions of Equation (24).

These are the set of those solutions $u(t,\phi )$ that become equal to 1 at $t=0$, and have one “step” on the segment $[-1,0]$, as shown in Figure 3.

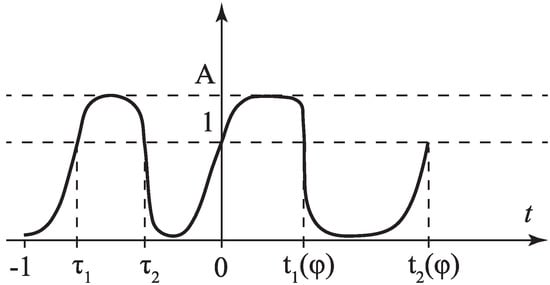
Figure 3. Graph of $\phi \left(s\right)\in S({\tau }_1,{\tau }_2)$ for $s\in [-1,0]$ and $u(t,\phi )$ for $t\ge 0$.

We shall describe the corresponding set of initial functions $\phi \left(s\right)$. We arbitrarily fix values ${\tau }_1$ and ${\tau }_2$ for which

$$-1<{\tau }_1<{\tau }_2<0.$$

Below, we shall denote by $\delta >0$ an arbitrary sufficiently small quantity that does not depend on $\lambda$ and whose precise value is unimportant. We introduce into the analysis three functions ${\kappa }_{1,2,3}(s,\lambda )$:

$$\begin{array}{cc}\hfill {\kappa }_1(s,\lambda )& =exp\left(\lambda \delta (s-{\tau }_1)\right),s\in [-1,{\tau }_1];\hfill \\ \hfill {\kappa }_2(s,\lambda )& =min{\left(A{\left[1+(A-1)exp\left(-\lambda \delta (s-{\tau }_1)\right)\right]}^{-1},A\left[1+(A-1)exp(\lambda \delta (s-{\tau }_2)\right)\right]}^{-1}),\hfill \\ \hfill & s\in ({\tau }_1,{\tau }_2);\hfill \\ \hfill {\kappa }_3(s,\lambda )& =max\left(exp\left(-\lambda \delta (s-{\tau }_2)\right),exp\left(\lambda \delta s\right)\right),s\in [{\tau }_2,0].\hfill \end{array}$$

Finally, by $S({\tau }_1,{\tau }_2)$ we denote the set of functions $\phi \left(s\right)$ from $C_{[-1,0]}$ that satisfy the conditions

$$\begin{array}{cc}\hfill \phi \left({\tau }_1\right)& =\phi \left({\tau }_2\right)=\phi \left(0\right)=1;\hfill \\ \hfill 0& \le \phi \left(s\right)\le {\kappa }_1(s,\lambda ),\mathrm{for}s\in [-1,{\tau }_1];\hfill \\ \hfill {\kappa }_2(s,\lambda )& \le \phi (s,\lambda )\le A,\mathrm{for}s\in ({\tau }_1,{\tau }_2);\hfill \\ \hfill 0& \le \phi \left(s\right)\le {\kappa }_3(s,\lambda )\mathrm{for}s\in [{\tau }_2,0].\hfill \end{array}$$

The first and the second positive roots of the equation $u(t,\phi )=1$ will be denoted by $t_1\left(\phi \right)$ and $t_2\left(\phi \right)$. We set $t_0=A{(A-1)}^{-1}({\tau }_1+1)$. Asymptotic analysis of $u(t,\phi )$ for $t\in [0,{\tau }_2+1]$ leads to the following statement:

Lemma 5. 

Suppose that the condition

$$t_0<{\tau }_2+1$$

(29)

is fulfilled. Then for $t_1\left(\phi \right)$ the following asymptotic (for $\lambda \to \infty$) equality holds:

$$t_1\left(\phi \right)=t_0+o\left(1\right).$$

Proof. 

As in Theorem 2, when constructing the asymptotics of the solution to Equation (24), we use the formula (25). It follows from (25), that on the segment $t\in [0,{\tau }_1+1]$ solution has form (26). It follows from (26), that on the interval $t\in (0,{\tau }_1+1]$ equality $u(t,\phi )=A+o\left(1\right)$ holds.

On the segment $t\in [{\tau }_1+1,{\tau }_2+1]$ the function $u(t-1,\phi )=A+o\left(1\right)$. That is why on this time segment the solution to Equation (24) satisfies the formula

$$u(t,\phi )=A{\left[1+(A-1)exp\left(\lambda A\left[-({\tau }_1+1)+(A-1)(t-({\tau }_1+1))+o\left(1\right)\right]\right)\right]}^{-1}.$$

(30)

While ${\tau }_1+1<t<t_0$, the right-hand side in formula (30) is asymptotically close to A at $\lambda \to +\infty$, and for $t>t_0$ this expression is $o\left(1\right)$ at $\lambda \to +\infty$. Therefore, if $t_0<{\tau }_2+1$, then the value $t_0$ is asymptotically close to $t_1\left(\phi \right)$ at $\lambda \to +\infty$. □

We note that for every $t\in (0,t_1\left(\phi \right))$ the relation

$$u(t,\phi )=A+o\left(1\right)$$

is fulfilled. Next, for $t\in (t_1\left(\phi \right),{\tau }_2+1)$, we have $u(t,\phi )=o\left(1\right)$, with

$$u({\tau }_2+1,\phi )=A{(A-1)}^{-1}exp(-\lambda A(A-1)({\tau }_2+1-t_0+o\left(1\right))).$$

We set $t^0=A({\tau }_2+1)+(1-A)t_0$. If

$$t^0<1,$$

(31)

then for $t\in ({\tau }_2+1,t^0+{\delta }_1)$ (where ${\delta }_1$ is some sufficiently small quantity that does not depend on $\lambda$) we find that

$$u(t,\phi )=A/\left[(A-1)exp\left(-\lambda A\left(t-A({\tau }_2+1)-(1-A)t_0+o\left(1\right)\right)\right)+1\right].$$

From this follow both the existence of $t_2\left(\phi \right)$ and the asymptotic formula $t_2\left(\phi \right)=t^0+o\left(1\right)$.

It is easy to show, that if inequality $t^0>1$ holds, then $t_2\left(\phi \right)$ exists, but $t_2\left(\phi \right)-t_1\left(\phi \right)>1$. So, in the case $t^0>1$ we return to the case of the slowly oscillating solutions.

If inequality (31) holds, then as in the preceding section, we introduce into the analysis the operator $\Pi$, using the rule $\Pi \left(\phi \left(s\right)\right)=u(s+t_2\left(\phi \right),\phi )$.

Note, that $t_2\left(\phi \right)$ corresponds to 0, $t_1\left(\phi \right)$ corresponds to ${\tau }_2$, 0 corresponds to ${\tau }_1$ (see Figure 3). That is why ${\overline{\tau }}_1=0-t^0+o\left(1\right)$ ${\overline{\tau }}_2=t_0-t^0+o\left(1\right)$.

A consequence of the formulas given here is the following statement:

Theorem 3. 

Let the conditions (29) and (31) are fulfilled. Then for all sufficiently large λ for the Equation (24) the following inclusion holds:

$$\Pi \left(\phi \left(s\right)\right)\in S({\overline{\tau }}_1+o\left(1\right),{\overline{\tau }}_2+o\left(1\right)),$$

with

$$\begin{array}{cc}\hfill {\overline{\tau }}_1& =A{\tau }_1-A{\tau }_2,\hfill \\ \hfill {\overline{\tau }}_2& =A^2{(A-1)}^{-1}{\tau }_1-A{\tau }_2+A{(A-1)}^{-1}.\hfill \end{array}$$

(32)

The system of Equation (32) is a linear inhomogeneous difference system of equations. After ${\overline{\tau }}_1$ and ${\overline{\tau }}_2$ have been determined, the situation is repeated, i.e., while for current values of ${\overline{\tau }}_1$ and ${\overline{\tau }}_2$ inequalities (29) and (31) are fulfilled, using (32) we calculate ${\stackrel{=}{\tau }}_1$ and ${\stackrel{=}{\tau }}_2$, and so on. This iteration process has a fixed point. By virtue of the fact that the determinant of the linear part in (32) is greater in modulus than 1 the iteration process is divergent, i.e., the equilibrium state in (32) is unstable.

We also remark that the number of periodic solutions of Equation (24) grows without limit as $\lambda \to \infty$. We shall show this. It was established above that for sufficiently large $\lambda$ Equation (24) has a slowly oscillating periodic solution $u_0(t,\lambda )$ with period $T\left(\lambda \right)$. This solution for each integer n satisfies the equation

$$\dot{u}=\lambda [1-u(t-1-nT\left(\lambda \right))]u(A-u).$$

(33)

In (33) we replace the time $t\to (1+nT(\lambda \left)\right)t$. We then find that the function $u_n(t,\lambda )=u_0((1+nT\left(\lambda \right))t,\lambda )$ is a solution of the equation

$$\dot{u}=\lambda (1+nT\left(\lambda \right))[1-u(t-1)]u(A-u).$$

(34)

The period of the function $u_n(t,\lambda )$ is equal to $T\left(\lambda \right){[1+nT\left(\lambda \right)]}^{-1}$. In particular, the unstable periodic solution determinable from the fixed points ${\tau }_{10}$, ${\tau }_{20}$ of the mapping (32) corresponds to the value $n=1$ in (34), i.e., to the function $u_1(t,\lambda )$.

We shall consider the more general case when on the segment $[-1,0]$ the initial functions $\phi \left(s\right)$ take the value 1 exactly $(2n+1)$ times:

$$-1<{\tau }_1<{\tau }_2<\dots <{\tau }_{2n}<0,\phi \left({\tau }_j\right)=\phi \left(0\right)=1(j=1,\dots ,2n).$$

(35)

Following the method proposed above, we arrive at the $2n$-dimensional map

$$\begin{array}{cc}\hfill {\overline{\tau }}_1={\tau }_3-t^0,& t^0=A{\tau }_2-A{\tau }_1,\hfill \\ \hfill {\overline{\tau }}_2={\tau }_4-t^0,& t_0=A{(A-1)}^{-1}({\tau }_1+1),\hfill \\ \hfill \dots & \dots \hfill \\ \hfill {\overline{\tau }}_{2n-1}=-t^0,& {\overline{\tau }}_{2n}=t_0-t^0.\hfill \end{array}$$

(36)

While we are in the class of initial conditions (conditions (35) are satisfied), we iterate this map. It can be shown that if the equilibrium state in (36) exists, then it is unstable. Since solution $u_n(t,\lambda (1+nT\left(\lambda \right)))$ corresponds to equilibrium state in map (36), then this periodic solution of (24) is unstable.

4. Step-like Solutions of the Equation with Two Delays

We normalize the time $t\to Tt$ and rename $\lambda T$ as $\lambda$ and $h{T}^{-1}$ as h$(h<1)$ again in Equation (8) with two delays. As a result, we arrive at the equation

$$\dot{u}=\lambda [1-\alpha u(t-1)-(1-\alpha )u(t-h)]u(A-u).$$

(37)

4.1. Construction of Slowly Oscillating Solutions

We shall consider the construction of slowly oscillating periodic solutions. We introduce into the analysis a set of initial conditions consisting of all those functions $\phi \left(s\right)\in C_{[-1,0]}$ for which

$$\begin{array}{cc}\hfill \phi \left(0\right)& =1,0\le \phi \left(s\right)\le 1;\hfill \\ \hfill \phi \left(s\right)& \le exp\left(\lambda \delta s\right),\hfill \end{array}$$

where $\delta >0$ is some sufficiently small but fixed value. We investigate the asymptotic form of all solutions $u(t,\phi )$ with initial conditions from S. We denote by $t_1\left(\phi \right)$ and $t_2\left(\phi \right)$ the first and second positive roots of equation $u(t,\phi )=1$. In the case when

$$t_2\left(\phi \right)-1>t_1\left(\phi \right),$$

(38)

we can determine the translation along the trajectories operator $\Pi$: $\Pi \left(\phi \left(s\right)\right)=u(s+t_2\left(\phi \right),\phi )$. From the inequality (38) we find that $\Pi \left(\phi \right(s\left)\right)\in S$. If for all $\phi \left(s\right)\in S$ we have $\Pi \left(\phi \right(s\left)\right)\in S$, i.e., $\Pi S\subset S$, we can conclude that there exists an attractor with initial conditions from S and that there exists a fixed point ${\phi }_0\left(s\right)\in S$. The solution $u_0(t,\lambda )=u(t,{\phi }_0\left(s\right))$ is thereby periodic, with period $T\left(\lambda \right)=t_2\left({\phi }_0\right)$. For the expressions $t_{1,2}\left(\phi \right)$ it is possible to obtain asymptotic formulas, and this means that we can formulate conditions on the parameters of the problem that ensure fulfilment of the inequality (38). We confine ourselves here to giving only sufficient conditions for fulfilment of this inequality.

Lemma 6. 

Let

$$1-(1-\alpha )A>0$$

(39)

and

$$1-\alpha A<0.$$

(40)

Then for all sufficiently large λ for Equation (37) we have the following inclusion:

$$\Pi S\subset S.$$

Proof. 

For each $t\in (0,h]$ the asymptotic equality

$$u(t,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left(t+o\left(1\right)\right)\right)\right]}^{-1}$$

holds. But if $t\in [h,1]$, then

$$u(t,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left((1-(1-\alpha \left)A\right)t+h(1-\alpha )A+o\left(1\right)\right)\right)\right]}^{-1}.$$

In particular,

$$u(1,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left(1-(1-\alpha )A(1-h)+o\left(1\right)\right)\right)\right]}^{-1}.$$

It follows from inequality (39) that $u(t,\phi )=A+o\left(1\right)$ on the segment $t\in [h,1+{\delta }_1]$, where ${\delta }_1$ is some positive and small (but independent on $\lambda$) constant.

Therefore, for $t>1$ while $u(t,\phi )=A+o\left(1\right)$ formula

$$u(t,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left(1-(1-\alpha )A(1-h)+(1-A)(t-1)+o\left(1\right)\right)\right)\right]}^{-1}$$

holds. From this formula we find that $t_1\left(\phi \right)$ exists and that

$$t_1\left(\phi \right)=1+\left(1-(1-\alpha )A(1-h)\right){(A-1)}^{-1}+o\left(1\right),(t_1\left(\phi \right)>1).$$

Starting from $\tau =t_1\left(\phi \right)$ we obtain that on the interval $t\in (t_1\left(\phi \right),t_1\left(\phi \right)+h]$ equality $u(t,\phi )=o\left(1\right)$ holds and that on the segment $t\in [t_1\left(\phi \right)+h,t_1\left(\phi \right)+1]$ formula

$$u(t,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left((1-A)h+(1-\alpha A)(t-h-t_1\left(\phi \right))+o\left(1\right)\right)\right)\right]}^{-1}$$

is true. It follows from (40) that $u(t,\phi )=o\left(1\right)$ on the segment $t\in [t_1\left(\phi \right)+h,t_1\left(\phi \right)+1]$. Then for $t>t_1\left(\phi \right)+1$ while $u(t,\phi )=o\left(1\right)$ we have the equality

$$u(t,\phi )=A{\left[1+(A-1)exp\left(-\lambda A\left((1-A)h+(1-\alpha A)(1-h)+(t-1-t_1\left(\phi \right))+o\left(1\right)\right)\right)\right]}^{-1}.$$

(41)

From Formula (41) we obtain both the existence of $t_2\left(\phi \right)$ and inequality $t_2\left(\phi \right)-t_1\left(\phi \right)>1$.

It follows from this that $\Pi \left(\phi \right(s\left)\right)\in S$ and $\Pi S\subset S$. The Lemma is proven. □

Theorem 4. 

Let inequalities (39) and (40) hold. Then for all sufficiently large λ Equation (37) has an asymptotically orbitally stable slowly oscillating periodic (with period $T\left(\lambda \right)$) solution $u_0(t,\lambda )$, for which $u_0(0,\lambda )=u_0(t_1\left(\lambda \right),\lambda )=u_0(t_2\left(\lambda \right),\lambda )=1$, where $t_j\left(\lambda \right)$ are successive positive roots of the equation $u_0(t,\lambda )=1$, and

$$\begin{array}{cc}\hfill t_1\left(\lambda \right)& =1+\left(1-(1-\alpha )A(1-h)\right){(A-1)}^{-1}+o\left(1\right),\hfill \\ \hfill T\left(\lambda \right)& =t_2\left(\lambda \right)=2+\left(1-(1-\alpha )A(1-h)\right){(A-1)}^{-1}+(A-1)h-(1-\alpha A)(1-h)+o\left(1\right).\hfill \end{array}$$

For every t from the intervals $(0,t_1\left(\lambda \right))$ and $(t_1\left(\lambda \right),t_2\left(\lambda \right))$, respectively, the following equalities are fulfilled:

$$u_0(t,\lambda )=\left\{\begin{array}{cc}A+o\left(1\right),\hfill & t\in (0,t_1\left(\lambda \right)),\hfill \\ o\left(1\right),\hfill & t\in (t_1\left(\lambda \right),t_2\left(\lambda \right)).\hfill \end{array}\right.$$

The proof of existence of the periodic solution in Theorem 4 follows from the proof of the Lemma 6, and proof of stability of this solution is rather cumbersome. In the more complicated situation discussed in Refs. [7,29] a detailed proof was given of the stability of the solution constructed there, and so we shall not give the proof here.

4.2. Construction of More Complicated Solutions

We shall consider the construction of rapidly oscillating periodic solutions. We arbitrarily fix $\tau$, satisfying condition

$$\tau \in \left(max\left(h,1-h-h(1-\alpha A){(A-1)}^{-1}\right),1\right)$$

(42)

and consider the set

$$\begin{array}{cc}\hfill S\left(\tau \right)& =\{\phi \left(s\right)\in C_{[-1,0]}:0\le \phi \left(s\right)\le A;\hfill \\ \hfill \phi (-\tau )& =\phi \left(0\right)=1,\hfill \\ \hfill \phi \left(s\right)& \le max\left(exp\left(-\lambda \delta (s+\tau )\right),exp\left(\lambda \delta s\right)\right),s\in [-\tau ,0];\hfill \\ \hfill \phi \left(s\right)& \ge min{\left(A{\left[1+(A-1)exp\left(-\lambda \delta (s+1)\right)\right]}^{-1},A\left[1+(A-1)exp\left(\lambda \delta \right(s+\tau )\right)\right]}^{-1}),\hfill \\ \hfill & s\in [-1,-\tau ]\}.\hfill \end{array}$$

We shall give the final asymptotic formulas for $u(t,\phi )$$(\phi \in S(\tau \left)\right)$. In them we denote by $g\left(x\right)$ the function

$$g\left(x\right)=\left\{\begin{array}{cc}x,\hfill & \mathrm{if}x>0;\hfill \\ 0,\hfill & \mathrm{if}x\le 0.\hfill \end{array}\right.$$

We shall assume that the inequalities

$$1-\alpha A>0,1-(1-\alpha )A<0,$$

(43)

and

$$h<1-h$$

(44)

are fulfilled. Let $t\in (0,h]$. Then $u(t,\phi )=A+o\left(1\right)$, and

$$\begin{array}{cc}\hfill u(h,\phi )=& A{\left[1+(A-1)exp\left(-\lambda A\left[h-\alpha Amin(h,1-\tau )+o\left(1\right)\right]\right)\right]}^{-1}.\hfill \end{array}$$

It follows from condition (42), that for $t\in [h,max(h,1-\tau \left)\right]$ we also have $u(t,\phi )=A+o\left(1\right)$, and

$$\begin{array}{c}\hfill u(max(h,1-\tau ),\phi )=A[1+(A-1)exp(-\lambda A[max(h,1-\tau )-\alpha Amin(h,1-\tau )\\ \hfill -Ag(1-\tau -h)+o\left(1\right)\left]\right){]}^{-1}.\end{array}$$

We set

$$\begin{array}{cc}\hfill t_1^0=& \frac{\alpha A(1-\tau +h)-Ah}{1-(1-\alpha )A}.\hfill \end{array}$$

From (42) and (43) we get that $t_1^0>max(h,1-\tau )$. Then $t_1\left(\phi \right)=t_1^0+o\left(1\right)$, and for every $t\in (0,t_1\left(\phi \right))$ we have the relation $u(t,\phi )=A+o\left(1\right)$.

Suppose that the following inequality is fulfilled:

$$t_1^0<1-h.$$

(45)

Then on the interval $(t_1\left(\phi \right),t_1\left(\phi \right)+h]$ we have the equality $u(t,\phi )=o\left(1\right)$, and

$$\begin{array}{cc}\hfill u\left(t_1\left(\phi \right)+h,\phi \right)& =A{\left[1+(A-1)exp\left(-\lambda A\left[(1-(1-\alpha \left)A\right)h+o\left(1\right)\right]\right)\right]}^{-1}.\hfill \end{array}$$

If condition

$$(1-(1-\alpha )A)h+1-t_1^0-h<0$$

(46)

is true, then on the interval $(t_1\left(\phi \right)+h,1]$ equality $u(t,\phi )=o\left(1\right)$ holds, and

$$u\left(1,\phi \right)=A{\left[1+(A-1)exp\left(-\lambda A\left[(1-(1-\alpha )A)h+(1-t_1^0-h)+o\left(1\right)\right]\right)\right]}^{-1}.$$

We set

$$t_2^0=1+\left((1-\alpha )Ah+t_1^0-1\right){[1-\alpha A]}^{-1}.$$

Suppose

$$t_2^0<t_1^0+1,$$

(47)

then $t_2\left(\phi \right)=t_2^0+o\left(1\right)$, and for every $t\in [1,t_2\left(\phi \right))$ the equality $u(t,\phi )=o\left(1\right)$ is fulfilled. Finally, we introduce the quantity $\overline{\tau }=t_2\left(\phi \right)-t_1\left(\phi \right)$. Then, to order $o\left(1\right)$ (for $\lambda \to \infty$), we obtain the equality

$$\overline{\tau }=f\left(\tau \right),$$

(48)

where $f\left(\tau \right)=t_2^0-t_1^0$.

After $\overline{\tau }$ has been determined, the situation is repeated, i.e., while for current value of $\overline{\tau }$ inequalities (42), (45)–(47) are fulfilled, using (48) we calculate $\stackrel{=}{\tau }$ and so on.

The one-dimensional mapping (48) plays a central role in the study of the solutions from $S\left(\tau \right)$. When the conditions (42)–(47) are fulfilled its attractors determine the structure of the periodic solutions from $S\left(\tau \right)$. For example, to the equilibrium state ${\tau }_0$:

$${\tau }_0=f\left({\tau }_0\right)$$

(49)

there corresponds, under the condition $|f^{\prime }\left({\tau }_0\right)|<1$, a stable one-step periodic solution $u_0(t,\lambda )$ with the initial conditions in $S\left({\tau }_0\right)$.

Lemma 7. 

Let the inequality

$$1-A+A^2\alpha <0$$

(50)

hold. Then there exist values of h such that the map (48) has a stable fixed point $\tau ={\tau }_{*}$, where

$${\tau }_{*}=\frac{A(A-1)(\alpha +(\alpha -1\left)h\right)}{1-A+A^2\alpha },$$

(51)

such that inequalities (42)–(47) are fulfilled.

Proof. 

First, let us show, that if inequality (50) holds, then inequalities (43) are true.

It is easy to see, that inequalities (43) are equivalent to inequality $\alpha <min(1/A,1-1/A)$. Inequality (50) is equivalent to $\alpha <1/A-1/A^2$. This value is less than $min(1/A,1-1/A)$ (parameter $A>1$), therefore, if (50) is true, then conditions (43) hold.

Second, let us substitute the values of $t_1^0$ and $t_2^0$ into the map (48):

$$\overline{\tau }=\frac{A^2{\alpha }^2}{(-1+\alpha A)(1-(1-\alpha \left)A\right)}\tau +\frac{A(A-1)\left(h\right(1-\alpha )-\alpha )}{(-1+\alpha A)(1-(1-\alpha \left)A\right)}.$$

(52)

This map has a fixed point ${\tau }_{*}$ satisfying formula (51). We should check whether this value ${\tau }_{*}$ satisfies conditions (42), (45)–(47), because map (52) corresponds to the initial equation only when all these inequalities hold, and we should study stability of the fixed point (51).

Let us begin with the study of stability. The fixed point ${\tau }_{*}$ is stable if and only if

$$-1<\frac{A^2{\alpha }^2}{(-1+\alpha A)(1-(1-\alpha \left)A\right)}<1.$$

From the condition (43) we get that this value is greater than zero, and this value is less than 1 if and only if inequality (50) holds. Therefore, this fixed point is stable.

Now let us prove that if $\tau ={\tau }_{*}$ satisfies (51), then conditions (42), (45)–(47) hold.

Below, we always assume that inequalities (43) and (50) hold.

Substituting ${\tau }_{*}$ in inequality $\tau <1$ from (42) we obtain, that this condition is equivalent to

$$h<\frac{(1-\alpha )A-1}{A(A-1)(1-\alpha )}=:{\gamma }_1,$$

(53)

inequality $h<\tau$ from (42) is equivalent to

$$h>\frac{\alpha A(A-1)}{{(A-1)}^2+\alpha A}=:{\beta }_1,$$

and condition $\tau >1-h-h(1-\alpha A){(A-1)}^{-1}$ from (42) is equivalent to

$$h>\frac{A-1}{A^2(1-\alpha )}=:{\beta }_2.$$

(54)

Condition (45) at $\tau ={\tau }_{*}$ can be rewritten in the form

$$h<\frac{(A-1)(1-\alpha A)}{\left(A\right(1-\alpha A)-(1-(1-\alpha )A\left)\right)}=:{\gamma }_2.$$

Condition (46) holds, if $\tau ={\tau }_{*}$ and (54) is true, and inequality (47) holds, if $\overline{\tau }={\tau }_{*}<1$ (the last inequality is equivalent to (53)).

Thus, at $\tau ={\tau }_{*}$ and under condition (50) the system of inequalities (42), (43), (45)–(47) is equivalent to

$$max({\beta }_1,{\beta }_2)<h<min({\gamma }_1,{\gamma }_2).$$

Parameter h must satisfy condition $h<1/2$ (we obtain this inequality from condition (44)).

Let us prove that under condition (50) interval $(max({\beta }_1,{\beta }_2),min(1/2,{\gamma }_1,{\gamma }_2))$ is not empty.

$$\begin{array}{cc}\hfill {\beta }_1-{\beta }_2& =\frac{(A-1)(1-(1-\alpha )A)(1-A+A^2\alpha )}{A^2(-1+\alpha )({(A-1)}^2+\alpha A)}<0,\hfill \end{array}$$

therefore $max({\beta }_1,{\beta }_2)={\beta }_2$. Let us estimate the values of ${\gamma }_1-{\beta }_2$, ${\gamma }_2-{\beta }_2$, $1/2-{\beta }_2$.

$$\begin{array}{cc}\hfill {\gamma }_1-{\beta }_2& =\frac{1-A+A^2\alpha }{(A-1)A^2(-1+\alpha )}>0,\hfill \\ \hfill {\gamma }_2-{\beta }_2& =\frac{(A-1)(1-A+A\alpha )(1-A+A^2\alpha )}{A^2(1-\alpha )\left(A(1-\alpha A)-(1-(1-\alpha \left)A\right)\right)}>0.\hfill \end{array}$$

Inequality

$$\begin{array}{cc}\hfill 1/2-{\beta }_2& =\frac{2-2A+A^2-A^2\alpha }{2A^2(1-\alpha )}>0\hfill \end{array}$$

is equivalent to inequality $2-2A+A^2-A^2\alpha >0$. Function $q\left(\alpha \right)=2-2A+A^2-A^2\alpha$ is decreasing on the interval $\alpha \in (0,1/A-1/A^2)$. Therefore, $q(1/A-1/A^2)\le q\left(\alpha \right)$ for all $\alpha \in (0,1/A-1/A^2)$.

$$q(1/A-1/A^2)=2-2A+A^2-A^2(1/A-1/A^2)=A^2-3A+3>0,$$

thus inequality $1/2-{\beta }_2>0$ holds for all $\alpha \in (0,1/A-1/A^2)$. The Lemma is proven. □

From the constructions and the reasoning given above we obtain the following statement.

Theorem 5. 

Let the inequality (50) hold. Then for all sufficiently large λ there exist h and $\tau ={\tau }_{*}$, satisfying (51), such that equation (37) has an asymptotically orbitally stable rapidly oscillating periodic (with period $T\left(\lambda \right)$) solution $u_{*}(t,\lambda )$, for which $u_{*}(0,\lambda )=u_{*}(t_1\left(\lambda \right),\lambda )=u_{*}(t_2\left(\lambda \right),\lambda )=1$, where $t_j$ are successive positive roots of the equation $u_{*}(t,\lambda )=1$, and

$$\begin{array}{cc}\hfill t_1\left(\lambda \right)=& \frac{A(\alpha +(\alpha -1\left)h\right)}{1-A+A^2\alpha }+o\left(1\right),\hfill \\ \hfill T\left(\lambda \right)=& t_2\left(\lambda \right)=\frac{A^2(\alpha +(\alpha -1)h)}{1-A+A^2\alpha }+o\left(1\right),\hfill \\ \hfill t_2\left(\lambda \right)-t_1\left(\lambda \right)=& {\tau }_{*}+o\left(1\right)<1.\hfill \end{array}$$

For every t from intervals $(0,t_1\left(\lambda \right))$ and $(t_1\left(\lambda \right),t_2\left(\lambda \right))$, respectively, the following equalities are fulfilled:

$$u_{*}(t,\lambda )=\left\{\begin{array}{cc}A+o\left(1\right),\hfill & t\in (0,t_1\left(\lambda \right)),\hfill \\ o\left(1\right),\hfill & t\in (t_1\left(\lambda \right),t_2\left(\lambda \right)).\hfill \end{array}\right.$$

In a similar way, one can determine the existence conditions and find the asymptotics of multi-step periodic solutions on the segment $[-1,0]$ and obtain an n-dimensional (in terms of the number of steps on the segment $[-1,0]$) mapping for their description.

5. Conclusions

The dynamics of the logistic equation with delays and with bounding modified nonlinearity are studied.

First, oscillations close to harmonic are studied. Using the methods of bifurcation analysis, we singled out the critical case in the problem of stability of stationary state and constructed the normal form. Its nonlocal dynamics determine the local behavior of the initial equation solutions in the neighborhood of the equilibrium state.

The solutions of the relaxation (step-like) type are studied for sufficiently large values of the parameter $\lambda$. We stress that, from a computational point of view, Equations (4) and (8) are difficult, since the relaxation solution approaches A and 0 very closely, so even a small error in the calculations will take us out of the class of solutions under consideration. Therefore, asymptotic methods play a special role. They not only allow one to find an approximation of the solution, but also reduce the problem of the dynamics of the original infinite-dimensional problem to the problem of the dynamics of the constructed finite-dimensional mapping (this object is much more simpler than the initial equation). Asymptotic formulas that couple the solutions of (4) and (8) with such mappings trajectories are obtained. The resulting formulas are suitable for engineering calculations. It is important to note that this method is applicable to equations with different types of nonlinearities [30,31] and to systems of two, three, and more singular perturbed equations with delay [30,32,33].

The use of the modified nonlinearity leads to the fact that the oscillations turn out to be ‘safer’ in comparison with Equation (1): their largest value A is significantly less than the value of $exp\left(\lambda T\right)$ for Equation (1), and the smallest value of $exp(-\lambda const)$ is significantly greater than the value of $exp(-exp\lambda T)$.

As a generalization of the obtained results, we note that they do not change if the function $(A-u)$ in (8) is replaced by a more general function $F_0\left(u\right)$ for which the conditions $F_0\left(u\right)>0$ as $0<u<A$, $F_0\left(0\right)=F_0\left(A\right)=0$ and $F_0^{\prime }\left(0\right)\ne 0$, $F_0^{\prime }\left(A\right)\ne 0$ are satisfied. We also note that the proposed method allows extension to the case of more than two delays in Equation (8).